Момент инерции | это… Что такое Момент инерции?

У этого термина существуют и другие значения, см. Момент.

Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения СИ: кг·м².

Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.

Содержание 1 Осевой момент инерции 1.1 Теорема Гюйгенса-Штейнера 1.2 Осевые моменты инерции некоторых тел 1.3 Вывод формул 1.4 Безразмерные моменты инерции планет и их спутников 2 Центробежный момент инерции 3 Геометрический момент инерции 4 Центральный момент инерции 5 Тензор инерции и эллипсоид инерции 6 См. также 7 Примечания 8 Литература 9 Ссылки

Осевой момент инерции

Осевые моменты инерции некоторых тел.

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

где:

• m_i — масса i-й точки,
• r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела

J_a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

,

где:

•  — масса малого элемента объёма тела ,
•  — плотность,
•  — расстояние от элемента до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то

Теорема Гюйгенса-Штейнера

Основная статья: Теорема Штейнера

Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси.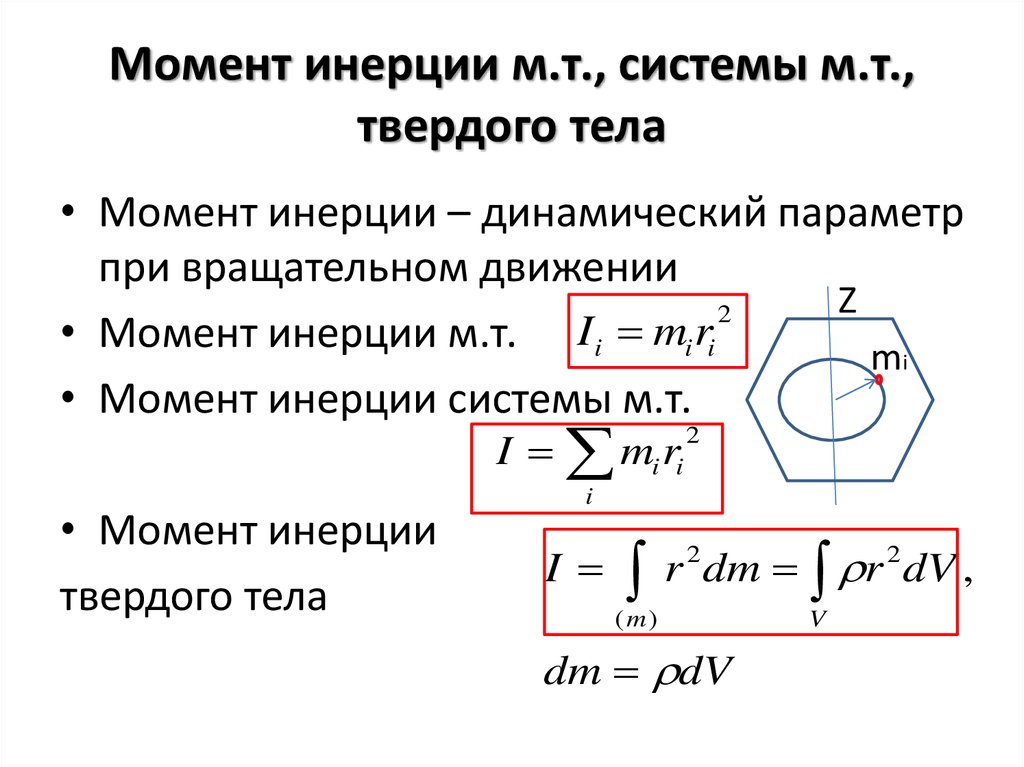 Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

,

где  — полная масса тела.

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

Осевые моменты инерции некоторых тел

Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения

Тело	Описание	Положение оси a	Момент инерции Ja
	Материальная точка массы m	На расстоянии r от точки, неподвижная
	Полый тонкостенный цилиндр или кольцо радиуса r и массы m	Ось цилиндра
	Сплошной цилиндр или диск радиуса r и массы m	Ось цилиндра
	Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1	Ось цилиндра
	Сплошной цилиндр длины l, радиуса r и массы m	Ось перпендикулярна к цилиндру и проходит через его центр масс
	Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m	Ось перпендикулярна к цилиндру и проходит через его центр масс
	Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его центр масс
	Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его конец
	Тонкостенная сфера радиуса r и массы m	Ось проходит через центр сферы
	Шар радиуса r и массы m	Ось проходит через центр шара
	Конус радиуса r и массы m	Ось конуса
	Равнобедренный треугольник с высотой h, основанием a и массой m	Ось перпендикулярна плоскости треугольника и проходит через вершину
	Правильный треугольник со стороной a и массой m	Ось перпендикулярна плоскости треугольника и проходит через центр масс
	Квадрат со стороной a и массой m	Ось перпендикулярна плоскости квадрата и проходит через центр масс

Вывод формул

Тонкостенный цилиндр (кольцо, обруч)

Вывод формулы  

Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJ_i. Тогда

Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду

Толстостенный цилиндр (кольцо, обруч)

Вывод формулы  

Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R₁, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит

Момент инерции толстого кольца найдём как интеграл

Поскольку объём и масса кольца равны

получаем окончательную формулу для момента инерции кольца

Однородный диск (сплошной цилиндр)

Вывод формулы  

Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R₁ = 0), получим формулу для момента инерции цилиндра (диска):

Сплошной конус

Вывод формулы  

Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен

где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят

Интегрируя, получим

Сплошной однородный шар

Вывод формулы  

Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле

Масса и момент инерции такого диска составят

Момент инерции сферы найдём интегрированием:

Тонкостенная сфера

Вывод формулы  

Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:

Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину

dR.

Тонкий стержень (ось проходит через центр)

Вывод формулы  

Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна

Интегрируя, получим

Тонкий стержень (ось проходит через конец)

Вывод формулы  

При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен

Безразмерные моменты инерции планет и их спутников^[1][2]

Безразмерные моменты инерции планет и их спутников

Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr²). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение допплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра. ^[3][4]

Центробежный момент инерции

Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:

где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.

Ось OX называется главной осью инерции тела, если центробежные моменты инерции J_xy и J_xz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела.

Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции.

Геометрический момент инерции

Геометрический момент инерции — геометрическая характеристика сечения вида

где  — расстояние от центральной оси до любой элементарной площадки относительно нейтральной оси.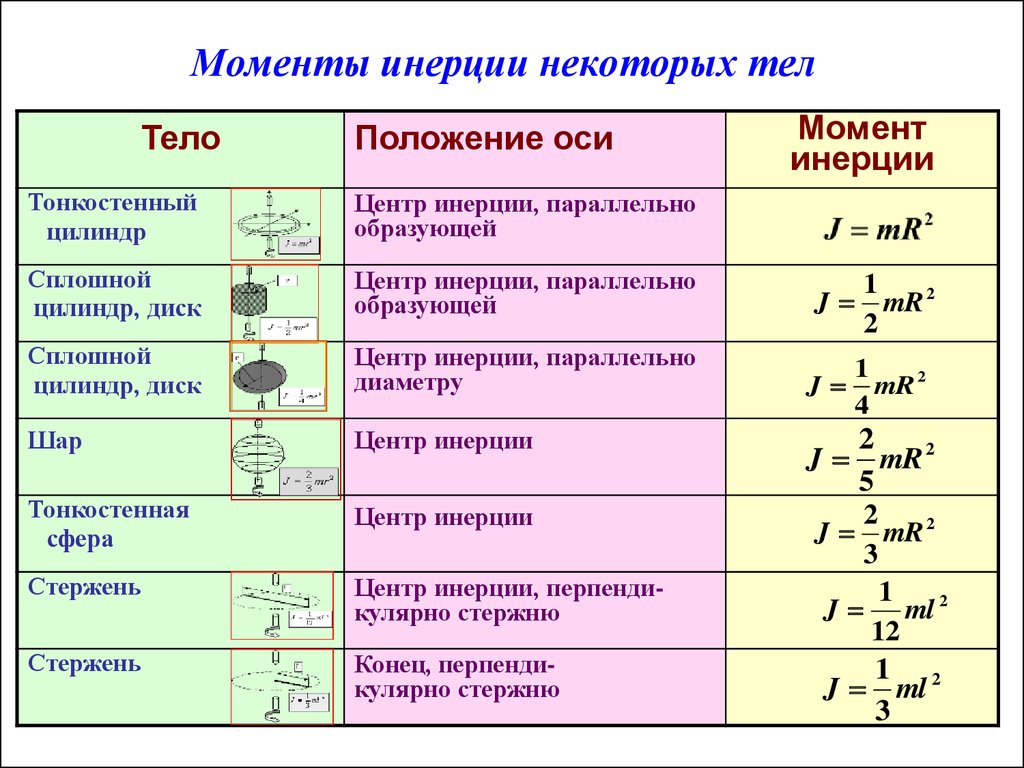

Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости сечения. Используется для вычисления радиуса инерции, прогиба балки, подбора сечения балок, колонн и др.

Единица измерения СИ — м⁴

. В строительных расчетах, литературе и сортаментах металлопроката в частности указывается в см⁴.

Из него выражается момент сопротивления сечения:

.

Геометрические моменты инерции некоторых фигур
Прямоугольника высотой и шириной :
Прямоугольного коробчатого сечения высотой и шириной по внешним контурам и , а по внутренним и соответственно
Круга диаметром

Центральный момент инерции

Центральный момент инерции (или момент инерции относительно точки O) — это величина

,

где:

•  — масса малого элемента объёма тела ,
•  — плотность,
•  — расстояние от элемента до точки O.

Центральный момент инерции можно выразить через главные осевые или центробежные моменты инерции: .

Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором , можно представить в виде квадратичной (билинейной) формы:

(1),

где  — тензор инерции. Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:

,
.

Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :
,
где  — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины  — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:

,

откуда получается уравнение эллипсоида в собственных координатах.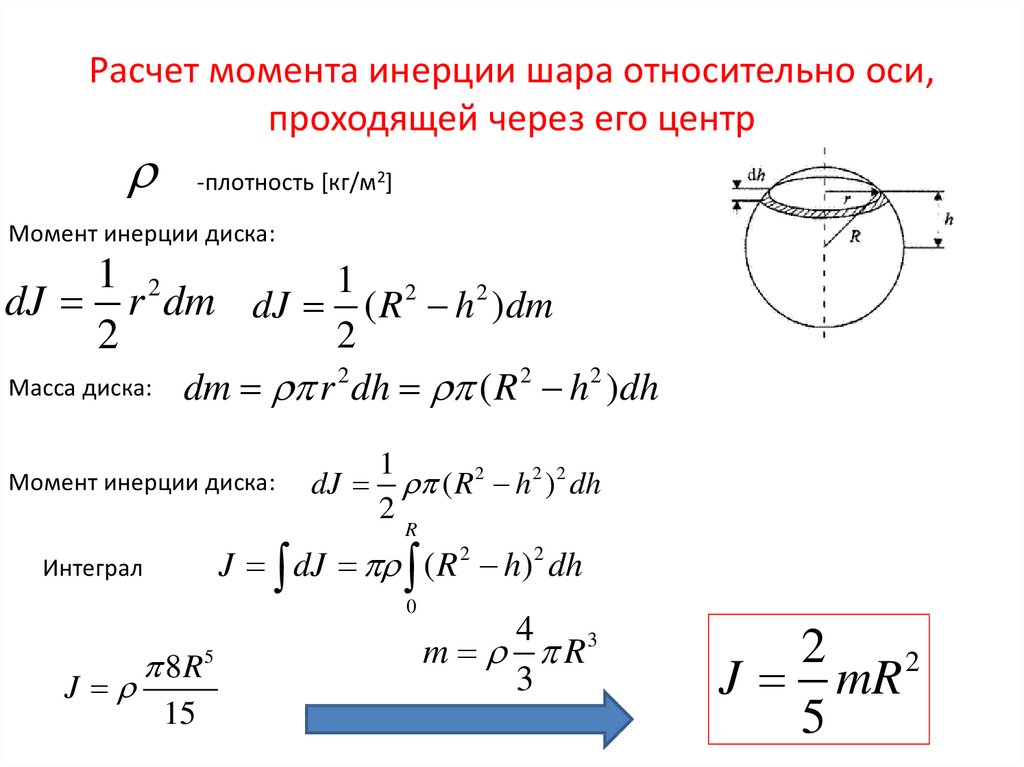 Разделив обе части уравнения на

и произведя замены:

,

получаем канонический вид уравнения эллипсоида в координатах :

Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:

См. также

• Движение твёрдого тела
• Метод главных компонент
• Сопротивление материалов
• Теорема Штейнера
• Механические приложения тройного интеграла
• Механические приложения двойного интеграла
• Полярный момент инерции
• Список моментов инерции

Примечания

1. ↑ Planetary Fact Sheet
2. ↑ Showman, Adam P.; Malhotra, Renu (1999). «The Galilean Satellites» (PDF). Science 286 (5437): 77–84. DOI:10.1126/science.286.5437.77. PMID 10506564.
3. ↑ Галкин И.Н. Внеземная сейсмология.  — М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X
4. ↑ Пантелеев В. Л. Физика Земли и планет. Гл. 3.4 — Гравитационное поле планеты

Литература

• Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.) http://www.alleng.ru/d/phys/phys108.htm
• Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
• Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997. http://nature.web.ru/db/msg.html?mid=1186208&s=120000000
• Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с. http://www.alleng.ru/d/phys/phys99.htm
• Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
• Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm
• Беляев Н. М., Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.

Ссылки

• Определение момента инерции тел простой формы
• Осевые моменты инерции, моменты сопротивления и радиусы инерции плоских фигур
• Online Калькулятор осевых моментов инерции, моментов сопротивления и радиусов инерции плоских фигур

Вращение твердого тела

Для кинематического описания вращения твердого тела удобно использовать угловые величины: угловое перемещение Δφ, угловую скорость ω

и угловое ускорение ε

В этих формулах углы выражаются в радианах. При вращении твердого тела относительно неподвижной оси все его точки движутся с одинаковыми угловыми скоростями и одинаковыми угловыми ускорениями. За положительное направление вращения обычно принимают направление против часовой стрелки.

Рисунок 1.23.1. Вращение диска относительно оси, проходящей через его центр O

При малых угловых перемещениях Δφ модуль вектора линейного перемещения некоторого элемента массы Δm вращающегося твердого тела выражается соотношением:

Δs = rΔφ,

где r – модуль радиус-вектора (рис. 1.23.1). Отсюда следует связь между модулями линейной и угловой скоростей:

υ = rω,

и между модулями линейного и углового ускорения:

a = aτ = rε.

Векторы и направлены по касательной к окружности радиуса r. Следует вспомнить, что при движении тела по окружности возникает также нормальное или центростремительное ускорение, модуль которого есть

Разобьем вращающееся тело на малые элементы Δmi. Расстояния до оси вращения обозначим через ri, модули линейных скоростей – через υi. Тогда кинетическую энергию вращающегося тела можно записать в виде:

Физическая величина зависит от распределения масс вращающегося тела относительно оси вращения. Она называется моментом инерции I тела относительно данной оси:

В пределе при Δm → 0 эта сумма переходит в интеграл. Единица измерения момента инерции в СИ – килограмм-метр в квадрате (кг∙м2). Таким образом, кинетическую энергию твердого тела, вращающегося относительно неподвижной оси, можно представить в виде

Эта формула очень похожа на выражение для кинетической энергии поступательно движущегося тела только теперь вместо массы m в формулу входит момент инерции I, а вместо линейной скорости υ – угловая скорость ω.

Момент инерции в динамике вращательного движения играет ту же роль, что и масса тела в динамике поступательного движения. Но есть и принципиальная разница. Если масса – внутреннее свойство данного тела, не зависящее от его движения, то момент инерции тела зависит от того, вокруг какой оси оно вращается. Для разных осей вращения моменты инерции одного и того же тела различны.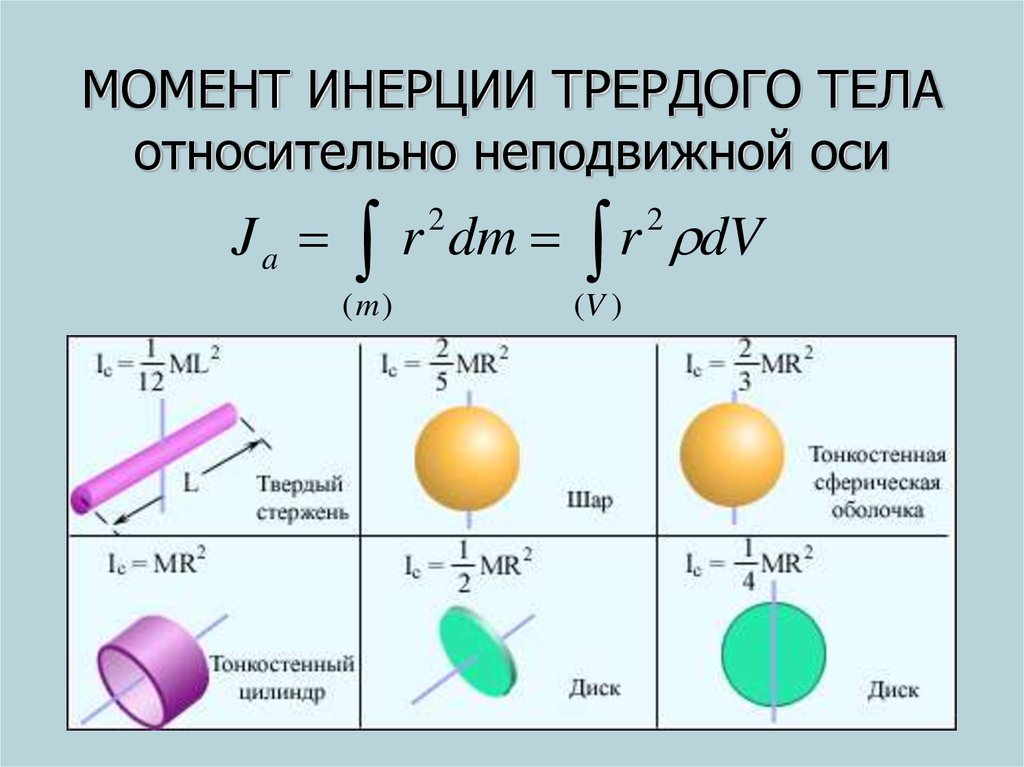

Во многих задачах рассматривается случай, когда ось вращения твердого тела проходит через его центр массы. Положение xC, yC центра масс для простого случая системы из двух частиц с массами m1 и m2, расположенными в плоскости XY в точках с координатами x1, y1 и x2, y2 (рис. 1.23.2), определяется выражениями:

Рисунок 1.23.2. Центр масс C системы из двух частиц

В векторной форме это соотношение принимает вид:

Аналогично, для системы из многих частиц радиус-вектор центра масс определяется выражением

Для сплошного тела суммы в выражении для заменяются интегралами. Легко видеть, что в однородном поле тяготения центр масс совпадает с центром тяжести. Если в однородном поле тяготения твердое тело сложной формы подвесить за центр масс, то оно будет находиться в безразличном состоянии равновесия. Поэтому положение центра масс тела сложной формы можно практически определить путем последовательного подвешивания его за несколько точек и отмечая по отвесу вертикальные линии (рис. 1.23.3).

Рисунок 1.23.3. Определение положения центра масс C тела сложной формы. A1, A2, A3 точки подвеса

Равнодействующая сил тяжести в однородном поле тяготения приложена к центру масс тела. Если тело подвешено за центр масс, то оно находится в состоянии безразличного равновесия (см. §1.14).

Любое движение твердого тела можно представить как сумму двух движений: поступательного движения со скоростью центра масс тела и вращения относительно оси, проходящей через центр масс. Примером может служить колесо, которое катится без проскальзывания по горизонтальной поверхности (рис. 1.23.4). При качении колеса все его точки движутся в плоскостях, параллельных плоскости рисунка. Такое движение называется плоским.

При плоском движении кинетическая энергия движущегося твердого тела равна сумме кинетической энергии поступательного движения и кинетической энергии вращения относительно оси, проходящей через центр масс тела и перпендикулярной плоскостям, в которых движутся все точки тела:

где m – полная масса тела, IC – момент инерции тела относительно оси, проходящей через центр масс.

Рисунок 1.23.4. Качение колеса как сумма поступательного движения со скоростью и вращения с угловой скоростью относительно оси O, проходящей через центр масс

В механике доказывается теорема о движении центра масс: под действием внешних сил центр масс любого тела или системы взаимодействующих тел движется как материальная точка, в которой сосредоточена вся масса системы.

Иллюстрацией этого утверждения может служить рис. 1.23.5, на котором изображено движение тела под действием силы тяжести. Центр масс тела движется по параболической траектории как материальная точка, в то время как все другие точки движутся по более сложным траекториям.

Рисунок 1.23.5. Движение твердого тела под действием силы тяжести

Если твердое тело вращается относительно некоторой неподвижной оси, то его момент инерции I можно выразить через момент инерции IC этого тела относительно оси, проходящей через центр масс тела и параллельной первой.

Рисунок 1.23.6. К доказательству теоремы о параллельном переносе оси вращения

Рассмотрим сечение твердого тела произвольной формы, изображенное на рис. 1.23.6. Выберем координатную систему XY с началом координат O в центре масс C тела. Пусть одна из осей вращения проходит через центр масс C, а другая через произвольную точку P, расположенную на расстоянии d от начала координат. Обе оси перпендикулярны плоскости чертежа. Пусть Δmi – некоторый малый элемент массы твердого тела. По определению момента инерции:

 

Выражение для IP можно переписать в виде:

Поскольку начало координат совпадает с центром масс C, последние два члена обращаются в нуль. Это следует из определения центра масс. Следовательно,

IP = IC + md2,

где m – полная масса тела. Этот результат называют теоремой Штейнера (теоремой о параллельном переносе оси вращения).

 

Модель. Момент инерции

На рис. 1.23.7 изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.

Рисунок 1.23.7. Моменты инерции IC некоторых однородных твердых тел

Второй закон Ньютона может быть обобщен на случай вращения твердого тела относительно неподвижной оси. На рис. 1.23.8 изображено некоторое твердое тело, вращающееся относительно оси, перпендикулярной плоскости рисунка и проходящей через точку O. Выделим произвольный малый элемент массы Δmi. На него действуют внешние и внутренние силы. Равнодействующая всех сил есть Ее можно разложить на две составляющие: касательную составляющую и радиальную Радиальная составляющая создает центростремительное ускорение an.

Рисунок 1.23.8. Касательная и радиальная составляющие силы действующей на элемент Δmi твердого тела

Касательная составляющая вызывает тангенциальное ускорение массы Δmi. Второй закон Ньютона, записанный в скалярной форме, дает

Δmiaiτ = Fiτ = Fi sin θ или Δmiriε = Fi sin θ,

где – угловое ускорение всех точек твердого тела.
Если обе части написанного выше уравнения умножить на ri, то мы получим:

Здесь – плечо силы – момент силы.

Теперь нужно аналогичные соотношения записать для всех элементов массы Δmi вращающегося твердого тела, а затем просуммировать левые и правые части. Это дает:

Стоящая в правой части сумма моментов сил, действующих на различные точки твердого тела, состоит из суммы моментов всех внешних сил и суммы моментов всех внутренних сил.

Но сумма моментов всех внутренних сил согласно третьему закону Ньютона равна нулю, поэтому в правой части остается только сумма моментов всех внешних сил, которые мы будем обозначать через M. В итоге:

Iε = M.

Это и есть основное уравнение динамики вращательного движения твердого тела. Угловое ускорение ε и момент сил M в этом уравнении являются величинами алгебраическими. Обычно за положительное направление вращения принимают направление против часовой стрелки.

Возможна и векторная форма записи основного уравнения динамики вращательного движения, при которой величины , , определяются как векторы, направленные по оси вращения.

При изучении поступательного движения тел вводится понятие импульса тела (см. §1.16). Аналогично, при изучении вращательного движения вводится понятие момента импульса.

Моментом импульса вращающегося тела называют физическую величину, равную произведению момента инерции тела I на угловую скорость ω его вращения. Момент импульса обозначается буквой L:

L = Iω.

Поскольку уравнение вращательного движения можно представить в виде:

Окончательно будем иметь:

Это уравнение, полученное здесь для случая, когда I = const, справедливо и в общем случае, когда момент инерции тела изменяется в процессе движения.

Если суммарный момент M внешних сил, действующих на тело, равен нулю, то момент импульса L = Iω относительно данной оси сохраняется:

ΔL = 0, если M = 0.

Следовательно,

L = Iω = const.

Это и есть закон сохранения момента импульса. Иллюстрацией этого закона может служить неупругое вращательное столкновение двух дисков, насажанных на общую ось (рис. 1.23.9).

Рисунок 1.23.9. Неупругое вращательное столкновение двух дисков. Закон сохранения момента импульса: I1ω1 = (I1 + I2)ω

Закон сохранения момента импульса справедлив для любой замкнутой системы тел. Он выполняется, например, при движении планет по эллиптическим орбитам вокруг Солнца (второй закон Кеплера).

Уравнение вращательного движения тела можно записывать не только относительно неподвижной или равномерно движущейся оси, но и относительно оси, движущейся с ускорением.

Основное уравнение динамики вращательного движения не изменяет своего вида и в случае ускоренно движущихся осей при условии, что ось вращения проходит через центр массы тела и что ее направление в пространстве остается неизменным. Примером может служить качение тела (обруч, цилиндр, шар) по наклонной плоскости с трением (рис. 1.23.10).

Рисунок 1.23.10. Качение симметричного тела по наклонной плоскости

Ось вращения O проходит через центр масс тела. Моменты силы тяжести и силы реакции относительно оси O равны нулю. Момент M создает только сила трения: M = FтрR.

Уравнение вращательного движения:

где ε – угловое ускорение катящегося тела, a – линейное ускорение его центра масс, IC – момент инерции относительно оси O, проходящей через центр масс.
Второй закон Ньютона для поступательного движения центра масс записывается в виде:

ma = mg sin α – Fтр.

Исключая из этих уравнений Fтр, получим окончательно:

Из этого выражения видно, что быстрее будет скатываться с наклонной плоскости тело, обладающее меньшим моментом инерции. Например, у шара а у сплошного однородного цилиндра Следовательно, шар будет скатываться быстрее цилиндра.

[Решено] От какого из следующих свойств зависит момент инерции тела

От какого из следующих свойств зависит момент инерции тела?

1. Угловая скорость

2. Положение оси вращения

3. Распределение массы

1. 1 и 2
2. 1 и 3
3. 2 и 3
4. 1, 2 и 3

Вариант 3 и 3

1, 2 и 3

Вариант 3 и 3 : 2 и 3

Бесплатно

Электрические заряды и закон Кулона (основной)

78 тыс. пользователей

10 вопросов

10 баллов

10 минут

ПОНЯТИЕ :

• Момент инерции: Величина, выражающая тенденцию тела сопротивляться угловому ускорению, называется моментом инерции.
• Для точечной массы. Момент инерции – это просто произведение массы на квадрат перпендикулярного расстояния до оси вращения.

I = m × r​2 

где I – момент инерции, m – масса точки, r – расстояние по перпендикуляру от оси вращения. 9{2}\)

где I — момент инерции, m — масса точки, r — расстояние по перпендикуляру от оси вращения.

ОБЪЯСНЕНИЕ :

• Если масса расположена близко к оси, то момент инерции будет мал, потому что расстояние частиц массы от оси вращения будет мало.
• Если масса расположена на большом расстоянии от оси, момент инерции будет большим, потому что расстояние частиц массы от оси вращения будет большим.
• Итак, момент Инерции зависит от положения оси вращения, а также от распределения масс.
• Момент инерции — это физическое свойство распределения массы конфигурации и оси вращения.
• Но угловая скорость не играет роли для нахождения момента инерции. (см. также формулу)
• Итак, зависит от 2. Положения оси вращения 3. Распределения массы, но не зависит от 1. Угловой скорости .
• Следовательно, правильный ответ – вариант 3 (т.е. 2 и 3)

Скачать решение PDF

Поделиться в WhatsApp

Последние обновления Airforce Group X

Последнее обновление: 11 ноября 2022 г.

Предварительный список IAF Group X, опубликованный для приема на 01/2022. Индийские ВВС (IAF) также опубликовали официальное уведомление для IAF Group X (01/2023) 7 ноября 2022 года.  Отбор кандидатов будет зависеть от трех этапов: этапа 1 (письменный онлайн-тест), этапа 2. (DV, тест физической подготовки, тест на адаптацию I и II) и Фаза 3 (медицинское обследование). Экзамен запланирован с 18 по 24 января 2023 года. Кандидаты, прошедшие все этапы процесса отбора, будут отобраны на должности группы X ВВС и получат зарплату в размере рупий. 30 000. Это одна из самых востребованных вакансий. Кандидаты могут проверить соответствие требованиям Airforce Group X здесь. 92 + …$ . Затем используйте уравнения, чтобы уточнить, как момент инерции зависит от массы и расстояния от оси вращения.

Полный пошаговый ответ:
Момент инерции — Его также называют массовым моментом инерции или вращательной инерцией тела. Момент инерции представляет собой сумму произведений массы каждой частицы на квадрат расстояния каждой частицы от оси вращения. Момент инерции основан на понятии центра масс. Центр масс — это воображаемая точка тела, в которой можно считать, что вся масса тела собрана. 92 + …$
Из приведенного выше уравнения мы узнаем некоторые важные моменты. Проще говоря, момент инерции тела зависит от распределения массы тела и расстояния от оси вращения.
Момент инерции тела прямо пропорционален его массе и расстоянию частиц тела от оси вращения.
Следовательно, момент инерции зависит от массы и расстояния от оси вращения, а сила и плотность не влияют на момент инерции тела.
Следовательно, варианты A и C являются правильными вариантами.

Примечание: Понятие центра масс очень важно для расчета момента инерции. Понятие центра масс очень интересно. Мы знаем, что для расчета электростатической и гравитационной сил, действующих на тело, мы также рассматриваем их как точечный заряд и точечную массу соответственно. По существу, мы считаем, что все заряды и масса сосредоточены в центре. Помните, что этот заряд или масса всегда считается находящейся внутри тела, но в случае с центром масс он также может быть расположен вне тела, например – Центр масс Банана.

Недавно обновленные страницы

Большинство эубактериальных антибиотиков получены из биологии ризобия класса 12 NEET_UG

Биоинсектициды саламина были извлечены из биологии класса 12 NEET_UG

Какое из следующих утверждений, касающихся Baculovirusses, Neet_ug

.