Момент силы | Virtual Laboratory Wiki
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Файл:Fysik vridmoment.pngОтношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы $ \tau $ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние, до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
$ \boldsymbol{\tau} = \mathbf{r} \times \mathbf{F}, $
где $ \mathbf{F} $ — сила, действующая на частицу, а $ ~\mathbf{r} $ — радиус-вектор частицы.
Предыстория
Файл:Moment Sili2.JPGСтрого говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы $ \vec F $ на рычаг $ \vec r $, совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок $ ~dl $, которому соответствует бесконечно малый угол $ d\varphi $. Обозначим через $ \vec dl $ вектор, который направлен вдоль бесконечно малого отрезка $ ~dl $ и равен ему по модулю. Угол между вектором силы $ \vec F $ и вектором $ \vec dl $ равен $ ~\beta $, а угол $ ~\alpha $ $ \vec r $ и вектором силы $ \vec F $.
Следовательно, бесконечно малая работа $ ~dA $, совершаемая силой $ \vec F $ на бесконечно малом участке $ ~dl $ равна скалярному произведению вектора $ \vec dl $ и вектора силы, то есть $ dA = \vec F \cdot \vec dl $.
Теперь попытаемся выразить модуль вектора $ \vec dl $ через радиус вектор $ \vec r $, а проекцию вектора силы $ \vec F $ на вектор $ \vec dl $, через угол $ ~\alpha $.
В первом случае, используя теорему Пифагора, можно записать следующее равенство $ \sin \frac {d\varphi}{2} = \frac {~dl}{2} $, где в случае малого угла справедливо $ \frac {d\varphi}{2} = \frac {~dl}{2} $ и следовательно $ \left| \vec{dl} \right| = \left| \vec{r} \right| d\varphi $
Теперь запишем бесконечно малую работу через новые равенства $ dA=\left| \vec{r} \right| d\varphi \left| \vec{F} \right| \sin{\alpha} $ или $ dA=\left| \vec{r} \right| \left| \vec{F} \right| \sin{\left (\alpha \right )} d\varphi $.
Теперь видно, что произведение $ \left| \vec{r} \right| \left| \vec{F} \right| \sin{\left (\alpha \right )} $ есть ни что иное как модуль векторного произведения векторов $ \vec F $ и $ \vec r $, то есть $ \left| \vec F \times \vec r \right| $, которое и было принято обозначить за момент силы $ ~M $ или модуля вектора момента силы $ \left|\vec M\right| $.
И теперь полная работа записывается очень просто $ A = \int\limits_ 0^ \varphi \left| \vec F \times \vec r \right| d\varphi $ или $ A = \int\limits_ 0^ \varphi\left| \vec M \right| d\varphi $.
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- $ E= \tau \theta\ $ ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Файл:Moment arm.pngОчень интересен особый случай, представляемый как определение момента силы в поле:
- $ {\tau} $ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- $ \boldsymbol{T} $ = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- $ \boldsymbol{\tau} ={d\mathbf{L} \over dt} \,\! $ ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- $ \mathbf{L}=I\,\boldsymbol{\omega} \,\! $ ,
То есть если I постоянная, то
- $ \boldsymbol{\tau}=I{d\boldsymbol{\omega} \over dt}=I\boldsymbol{\alpha} \,\! $ ,
где α — угловое ускорение измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- $ \boldsymbol{P} $ = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность $ \boldsymbol{P} $ измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Превращение в другие единицы
Если угловая скорость измеряется в оборотах вместо радиан, то приходится домножать на коэффициент 2*π.
- $ \boldsymbol{P} $ = МОМЕНТ СИЛЫ * 2π * УГЛОВАЯ СКОРОСТЬ,
Где угловая скорость измеряется в оборотах в секунду. Некоторые люди используют лошадиные силы для измерения мощности, футофунты для измерения момента силы и обороты в минуты для угловой скорости. Общая формула тогда:
- $ \boldsymbol{P} $(л.с.)= (МОМЕНТ СИЛЫ(lbf*ft) * УГЛОВАЯ СКОРОСТЬ(rpm))/5252
Отношение между моментом силы и работой
- $ \boldsymbol{E} $ = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа $ \boldsymbol{E} $ измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость $ \boldsymbol{w} $ в радианах в секунду и время действия МОМЕНТА $ \boldsymbol{t} $.
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- $ \boldsymbol{E} $ = МОМЕНТ СИЛЫ * $ \boldsymbol{w} $ * $ \boldsymbol{t} $
Момент силы относительно точки
Если имеется материальная точка $ O_F\,\! $, к которой приложена сила $ \vec F $, то момент силы относительно точки $ O\,\! $ равен векторному произведению радиус-вектора $ \vec r $, соединяющий точки $ O $ и $ O_F $, на вектор силы $ \vec F $:
$ \vec M_O = \left[ \vec r \times \vec F \right] $.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Момент силы. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .
Момент силы — Википедия (с комментариями)
Материал из Википедии — свободной энциклопедии
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора, проведённого от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
Общие сведения
В физике момент силы можно понимать как «вращающая сила». В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метра от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров от оси вращения. Более точно момент силы частицы определяется как векторное произведение:
- <math>\vec M = \left[\vec r\times\vec F\right]</math>,
где <math>\vec F</math> — сила, действующая на частицу, а <math>\vec r</math> — радиус-вектор частицы.
Предыстория
Для того чтобы понять, откуда появилось обозначение момента сил и как к нему пришли, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси. Работа, совершаемая при действии силы <math>\vec F</math> на рычаг <math>\vec r</math>, совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок <math>dl</math>, которому соответствует бесконечно малый угол <math>d\varphi</math>. Обозначим через <math>\vec dl</math> вектор, который направлен вдоль бесконечно малого отрезка <math>dl</math> и равен ему по модулю. Угол между вектором силы <math>\vec F</math> и вектором <math>\vec dl</math> равен <math>\beta</math>, а угол между векторами <math>\vec r</math> и <math>\vec F</math> — <math>\alpha</math>.
Следовательно, бесконечно малая работа <math>dA</math>, совершаемая силой <math>\vec F</math> на бесконечно малом участке <math>dl</math>, равна скалярному произведению вектора <math>\vec dl</math> и вектора силы, то есть <math>dA = \vec F \cdot \vec dl</math>.
Теперь попытаемся выразить модуль вектора <math>\vec dl</math> через радиус-вектор <math>\vec r</math>, а проекцию вектора силы <math>\vec F</math> на вектор <math>\vec dl</math> — через угол <math>\alpha </math>.
Так как для бесконечно малого перемещения рычага <math>dl</math> можно считать, что траектория перемещения перпендикулярна рычагу <math>\vec r</math>, используя соотношения для прямоугольного треугольника, можно записать следующее равенство: <math>dl = r \mathrm{tg}\,d\varphi</math>, где в случае малого угла справедливо <math>\mathrm{tg}\,d\varphi = d\varphi</math> и, следовательно, <math>\left|\vec{dl}\right| = \left|\vec r\right| d\varphi</math>.
Для проекции вектора силы <math>\vec F</math> на вектор <math>\vec dl</math> видно, что угол <math>\beta = \alpha — \frac{\pi}{2}</math>, а так как <math>\cos{\left(\alpha — \frac{\pi}{2}\right)} = \sin\alpha</math>, получаем, что <math>\left|\vec F\right|\cos\beta = \left|\vec F\right|\sin\alpha</math>.
Теперь запишем бесконечно малую работу через новые равенства: <math>dA = \left|\vec r\right|d\varphi\left|\vec F\right|\sin\alpha</math>, или <math>dA = \left|\vec r\right|\left|\vec F\right|\sin(\alpha) d\varphi</math>.
Теперь видно, что произведение <math>\left|\vec r\right|\left|\vec F\right|\sin\alpha</math> есть не что иное, как модуль векторного произведения векторов <math>\vec r</math> и <math>\vec F</math>, то есть <math>\left|\vec r\times\vec F\right|</math>, которое и было принято обозначить за момент силы <math>M</math>, или модуль вектора момента силы <math>\left|\vec M\right|</math>.
Теперь полная работа записывается просто: <math>A = \int\limits_0^\varphi \left|\vec r\times\vec F\right| d\varphi</math>, или <math>A = \int\limits_0^\varphi \left|\vec M\right| d\varphi</math>.
Единицы
Момент силы имеет размерность «сила на расстояние» и единицу измерения ньютон-метр в системе СИ. Энергия и механическая работа также имеют размерность «сила на расстояние» и измеряются в системе СИ в джоулях. Следует заметить, что энергия — это скалярная величина, тогда как момент силы — величина (псевдо) векторная. Совпадение размерностей этих величин не случайность: момент силы 1 Н·м, приложенный через целый оборот, совершает механическую работу и сообщает энергию <math>2\pi</math> джоулей. Математически:
- <math>E = M\theta</math>,
где Е — энергия, M — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- <math>\left|\vec M\right| = \left|\vec{M}_1\right| \left|\vec F\right|</math>, где: <math>\left|\vec{M}_1\right|</math> — момент рычага, <math>\left|\vec F\right|</math> — величина действующей силы.
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину. Если сила перпендикулярна вектору <math>\vec r</math>, момент рычага будет равен расстоянию до центра и момент силы будет максимален:
- <math>\left|\vec{T}\right| = \left|\vec r\right| \left|\vec F\right| </math>
Сила под углом
Если сила <math>\vec F</math> направлена под углом <math>\theta</math> к рычагу r, то <math>M = r F \sin\theta</math>.
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для двумерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении ΣM=0.
Момент силы как функция от времени
Момент силы — производная по времени от момента импульса,
- <math>\vec M = \frac{d\vec L}{dt}</math>,
где <math>\vec L</math> — момент импульса.
Возьмём твердое тело. Движение твёрдого тела можно представить как движение конкретной точки и вращения вокруг неё.
Момент импульса относительно точки O твёрдого тела может быть описан через произведение момента инерции и угловой скорости относительно центра масс и линейного движения центра масс.
- <math>\vec{L_o} = I_c\,\vec\omega + [M(\vec{r_o} — \vec{r_c}), \vec{v_c}]</math>
Будем рассматривать вращающиеся движения в системе координат Кёнига, так как описывать движение твёрдого тела в мировой системе координат гораздо сложнее.
Продифференцируем это выражение по времени. И если <math>I</math> — постоянная величина во времени, то
- <math>\vec M = I\frac{d\vec\omega}{dt} = I\vec\alpha</math>,
где <math>\vec\alpha</math> — угловое ускорение, измеряемое в радианах в секунду за секунду (рад/с2). Пример: вращается однородный диск.
Если тензор инерции меняется со временем, то движение относительно центра масс описывается с помощью динамического уравнения Эйлера:
<math>\vec{M_c} = I_c\frac{d\vec\omega}{dt} + [\vec w, I_c\vec w]</math>.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Так же и момент силы, если совершает действие через угловое расстояние, он совершает работу.
- <math>P = \vec M \cdot \vec\omega</math>
В системе СИ мощность <math>P</math> измеряется в Ваттах, момент силы — в ньютон-метрах, а угловая скорость — в радианах в секунду.
Отношение между моментом силы и работой
- <math>A = \int_{\theta_1}^{\theta_2} \left|\vec M\right| \mathrm{d}\theta</math>
В случае постоянного момента получаем:
- <math>A = \left|\vec M\right|\theta</math>
В системе СИ работа <math>A</math> измеряется в джоулях, момент силы — в ньютон·метр, а угол — в радианах.
Обычно известна угловая скорость <math>\omega</math> в радианах в секунду и время действия момента <math>t</math>.
Тогда совершённая моментом силы работа рассчитывается как:
- <math>A = \left|\vec M\right|\omega t </math>
Момент силы относительно точки
Если имеется материальная точка <math>O_F</math>, к которой приложена сила <math>\vec F</math>, то момент силы относительно точки <math>O</math> равен векторному произведению радиус-вектора <math>\vec r</math>, соединяющего точки <math>O</math> и <math>O_F</math>, на вектор силы <math>\vec F</math>:
<math>\vec{M_O} = \left[\vec r \times \vec F\right]</math>.
Момент силы относительно оси
Момент силы относительно оси равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную этой оси относительно точки пересечения оси с плоскостью, то есть <math>M_z(F) = M_o(F’) = F’h'</math>.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н·м — это момент, который производит сила 1 Н на рычаг длиной 1 м, приложенная к концу рычага и направленная перпендикулярно ему.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки.
См. также
К:Википедия:Статьи без источников (тип: не указан)Напишите отзыв о статье «Момент силы»
Отрывок, характеризующий Момент силы
Но хотя уже к концу сражения люди чувствовали весь ужас своего поступка, хотя они и рады бы были перестать, какая то непонятная, таинственная сила еще продолжала руководить ими, и, запотелые, в порохе и крови, оставшиеся по одному на три, артиллеристы, хотя и спотыкаясь и задыхаясь от усталости, приносили заряды, заряжали, наводили, прикладывали фитили; и ядра так же быстро и жестоко перелетали с обеих сторон и расплюскивали человеческое тело, и продолжало совершаться то страшное дело, которое совершается не по воле людей, а по воле того, кто руководит людьми и мирами.Тот, кто посмотрел бы на расстроенные зады русской армии, сказал бы, что французам стоит сделать еще одно маленькое усилие, и русская армия исчезнет; и тот, кто посмотрел бы на зады французов, сказал бы, что русским стоит сделать еще одно маленькое усилие, и французы погибнут. Но ни французы, ни русские не делали этого усилия, и пламя сражения медленно догорало.
Русские не делали этого усилия, потому что не они атаковали французов. В начале сражения они только стояли по дороге в Москву, загораживая ее, и точно так же они продолжали стоять при конце сражения, как они стояли при начале его. Но ежели бы даже цель русских состояла бы в том, чтобы сбить французов, они не могли сделать это последнее усилие, потому что все войска русских были разбиты, не было ни одной части войск, не пострадавшей в сражении, и русские, оставаясь на своих местах, потеряли половину своего войска.
Французам, с воспоминанием всех прежних пятнадцатилетних побед, с уверенностью в непобедимости Наполеона, с сознанием того, что они завладели частью поля сраженья, что они потеряли только одну четверть людей и что у них еще есть двадцатитысячная нетронутая гвардия, легко было сделать это усилие. Французам, атаковавшим русскую армию с целью сбить ее с позиции, должно было сделать это усилие, потому что до тех пор, пока русские, точно так же как и до сражения, загораживали дорогу в Москву, цель французов не была достигнута и все их усилия и потери пропали даром. Но французы не сделали этого усилия. Некоторые историки говорят, что Наполеону стоило дать свою нетронутую старую гвардию для того, чтобы сражение было выиграно. Говорить о том, что бы было, если бы Наполеон дал свою гвардию, все равно что говорить о том, что бы было, если б осенью сделалась весна. Этого не могло быть. Не Наполеон не дал своей гвардии, потому что он не захотел этого, но этого нельзя было сделать. Все генералы, офицеры, солдаты французской армии знали, что этого нельзя было сделать, потому что упадший дух войска не позволял этого.
Не один Наполеон испытывал то похожее на сновиденье чувство, что страшный размах руки падает бессильно, но все генералы, все участвовавшие и не участвовавшие солдаты французской армии, после всех опытов прежних сражений (где после вдесятеро меньших усилий неприятель бежал), испытывали одинаковое чувство ужаса перед тем врагом, который, потеряв половину войска, стоял так же грозно в конце, как и в начале сражения. Нравственная сила французской, атакующей армии была истощена. Не та победа, которая определяется подхваченными кусками материи на палках, называемых знаменами, и тем пространством, на котором стояли и стоят войска, – а победа нравственная, та, которая убеждает противника в нравственном превосходстве своего врага и в своем бессилии, была одержана русскими под Бородиным. Французское нашествие, как разъяренный зверь, получивший в своем разбеге смертельную рану, чувствовало свою погибель; но оно не могло остановиться, так же как и не могло не отклониться вдвое слабейшее русское войско. После данного толчка французское войско еще могло докатиться до Москвы; но там, без новых усилий со стороны русского войска, оно должно было погибнуть, истекая кровью от смертельной, нанесенной при Бородине, раны. Прямым следствием Бородинского сражения было беспричинное бегство Наполеона из Москвы, возвращение по старой Смоленской дороге, погибель пятисоттысячного нашествия и погибель наполеоновской Франции, на которую в первый раз под Бородиным была наложена рука сильнейшего духом противника.
Для человеческого ума непонятна абсолютная непрерывность движения. Человеку становятся понятны законы какого бы то ни было движения только тогда, когда он рассматривает произвольно взятые единицы этого движения. Но вместе с тем из этого то произвольного деления непрерывного движения на прерывные единицы проистекает большая часть человеческих заблуждений.
Известен так называемый софизм древних, состоящий в том, что Ахиллес никогда не догонит впереди идущую черепаху, несмотря на то, что Ахиллес идет в десять раз скорее черепахи: как только Ахиллес пройдет пространство, отделяющее его от черепахи, черепаха пройдет впереди его одну десятую этого пространства; Ахиллес пройдет эту десятую, черепаха пройдет одну сотую и т. д. до бесконечности. Задача эта представлялась древним неразрешимою. Бессмысленность решения (что Ахиллес никогда не догонит черепаху) вытекала из того только, что произвольно были допущены прерывные единицы движения, тогда как движение и Ахиллеса и черепахи совершалось непрерывно.
Принимая все более и более мелкие единицы движения, мы только приближаемся к решению вопроса, но никогда не достигаем его. Только допустив бесконечно малую величину и восходящую от нее прогрессию до одной десятой и взяв сумму этой геометрической прогрессии, мы достигаем решения вопроса. Новая отрасль математики, достигнув искусства обращаться с бесконечно малыми величинами, и в других более сложных вопросах движения дает теперь ответы на вопросы, казавшиеся неразрешимыми.
Эта новая, неизвестная древним, отрасль математики, при рассмотрении вопросов движения, допуская бесконечно малые величины, то есть такие, при которых восстановляется главное условие движения (абсолютная непрерывность), тем самым исправляет ту неизбежную ошибку, которую ум человеческий не может не делать, рассматривая вместо непрерывного движения отдельные единицы движения.
В отыскании законов исторического движения происходит совершенно то же.
Движение человечества, вытекая из бесчисленного количества людских произволов, совершается непрерывно.
Постижение законов этого движения есть цель истории. Но для того, чтобы постигнуть законы непрерывного движения суммы всех произволов людей, ум человеческий допускает произвольные, прерывные единицы. Первый прием истории состоит в том, чтобы, взяв произвольный ряд непрерывных событий, рассматривать его отдельно от других, тогда как нет и не может быть начала никакого события, а всегда одно событие непрерывно вытекает из другого. Второй прием состоит в том, чтобы рассматривать действие одного человека, царя, полководца, как сумму произволов людей, тогда как сумма произволов людских никогда не выражается в деятельности одного исторического лица.
Историческая наука в движении своем постоянно принимает все меньшие и меньшие единицы для рассмотрения и этим путем стремится приблизиться к истине. Но как ни мелки единицы, которые принимает история, мы чувствуем, что допущение единицы, отделенной от другой, допущение начала какого нибудь явления и допущение того, что произволы всех людей выражаются в действиях одного исторического лица, ложны сами в себе.
Всякий вывод истории, без малейшего усилия со стороны критики, распадается, как прах, ничего не оставляя за собой, только вследствие того, что критика избирает за предмет наблюдения большую или меньшую прерывную единицу; на что она всегда имеет право, так как взятая историческая единица всегда произвольна.
Только допустив бесконечно малую единицу для наблюдения – дифференциал истории, то есть однородные влечения людей, и достигнув искусства интегрировать (брать суммы этих бесконечно малых), мы можем надеяться на постигновение законов истории.
Первые пятнадцать лет XIX столетия в Европе представляют необыкновенное движение миллионов людей. Люди оставляют свои обычные занятия, стремятся с одной стороны Европы в другую, грабят, убивают один другого, торжествуют и отчаиваются, и весь ход жизни на несколько лет изменяется и представляет усиленное движение, которое сначала идет возрастая, потом ослабевая. Какая причина этого движения или по каким законам происходило оно? – спрашивает ум человеческий.
Историки, отвечая на этот вопрос, излагают нам деяния и речи нескольких десятков людей в одном из зданий города Парижа, называя эти деяния и речи словом революция; потом дают подробную биографию Наполеона и некоторых сочувственных и враждебных ему лиц, рассказывают о влиянии одних из этих лиц на другие и говорят: вот отчего произошло это движение, и вот законы его.
Но ум человеческий не только отказывается верить в это объяснение, но прямо говорит, что прием объяснения не верен, потому что при этом объяснении слабейшее явление принимается за причину сильнейшего. Сумма людских произволов сделала и революцию и Наполеона, и только сумма этих произволов терпела их и уничтожила.
момент силы — с русского на английский
Момент силы — Размерность L2MT−2 Единицы измерения СИ Ньютон метр … Википедия
МОМЕНТ СИЛЫ — величина, характеризующая вращат. эффект силы при действии её на тв. тело; одно из осн. понятий механики. Различают М. с. относительно центра (точки) и относительно оси. М. с. относительно центра О величина векторная. Его модуль MO=Fh, где F… … Физическая энциклопедия
Момент (силы) — – в статике сооружений произведение величины силы на кратчайшее расстояние от линии действия силы до точки, относительно которой определяется момент. [Полякова, Т.Ю. Автодорожные мосты: учебный англо русский и русско английский… … Энциклопедия терминов, определений и пояснений строительных материалов
МОМЕНТ СИЛЫ — относительно точки (Moment of a force) произведение величин силы на длину перпендикуляра, опущенного из точки на направление силы. М. С. относительно оси произведение проекции силы на плоскость, перпендикулярную оси, на расстояние между осью и… … Морской словарь
момент силы — произведение силы на плечо. вращающий момент. плечо. кручение. см. равновесие … Идеографический словарь русского языка
МОМЕНТ СИЛЫ — МОМЕНТ СИЛЫ, см. ВРАЩАЮЩИЙ МОМЕНТ … Научно-технический энциклопедический словарь
момент силы — величина, характеризующая вращательный эффект силы при действии её на твёрдое тело. Различают моменты силы относительно центра (точки) и относительно оси. Момент силы относительно центра O (рис. а) векторная величина, численно равная… … Энциклопедический словарь
Момент силы — величина, характеризующая вращательный эффект силы при действии её на твёрдое тело; является одним из основных понятий механики. Различают М. с. относительно центра (точки) и относительно оси. М. с. относительно центра О величина … Большая советская энциклопедия
момент силы — [moment of force] величина, характеризизующая вращательный эффект силы при действии ее на твердое тело. Момент силы, Н • м, рассчитывается относительно центра (точки) вращения. Смотри также: Момент момент сопротивления сечения момент прокатки … Энциклопедический словарь по металлургии
МОМЕНТ СИЛЫ — механич. величина, характеризующая внеш. воздействие на тело (или систему тел) и определяющая изменение вращат. движения тела. М. с. относительно полюса (точки) О (см. рис.) наз. вектор М, равный векторному произведению радиус вектора r,… … Большой энциклопедический политехнический словарь
МОМЕНТ СИЛЫ — величина, характеризующая вращат. эффект силы при действии её на тв. тело. Различают М. с. относительно центра (точки) и относительно осн. М. с. относительно центра О (рис. а) векторная величина, численно равная произведению модуля силы F на… … Естествознание. Энциклопедический словарь
МОМЕНТ СИЛ — с русского на все языки
Момент сил — Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) физическая величина, характеризующая вращательное действие силы на твёрдое тело. Момент силы приложенный к гаечному ключу Отношение между векторами силы, момента силы … Википедия
МОМЕНТ СИЛ — В технике: показание действия сил. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. МОМЕНТ СИЛ Произведение сил на их расстояние от точки опоры до точки приложения. Объяснение 25000 иностранных слов, вошедших в… … Словарь иностранных слов русского языка
приведенный момент сил — Момент приведенной пары сил. [Сборник рекомендуемых терминов. Выпуск 99. Теория механизмов и машин. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики теория механизмов и машин Обобщающие термины динамический анализ… … Справочник технического переводчика
входной вращающий момент сил — input torque Вращающий момент сил, приложенный к входному звену механизма. Шифр IFToMM: 3.2.42 Раздел: ДИНАМИКА МЕХАНИЗМОВ … Теория механизмов и машин
входной момент сил — input torque Момент сил, приложенных к входному звену механизма. Шифр IFToMM: 3.2.42 Раздел: ДИНАМИКА МЕХАНИЗМОВ … Теория механизмов и машин
выходной вращающий момент сил — output torque Вращающий момент сил, обеспечиваемый выходным звеном механизма. Шифр IFToMM: 3.2.43 Раздел: ДИНАМИКА МЕХАНИЗМОВ … Теория механизмов и машин
выходной момент сил — output torque Момент сил, приложенных к выходному звену механизма. Шифр IFToMM: 3.2.43 Раздел: ДИНАМИКА МЕХАНИЗМОВ … Теория механизмов и машин
приведённый момент сил — Момент приведенной пары сил … Политехнический терминологический толковый словарь
Момент силы — Размерность L2MT−2 Единицы измерения СИ Ньютон метр … Википедия
момент вращения — момент сил скручивающее усилие В океанах сила, обусловленная полем напряжений поверхностных ветров. Ответственна за крупномасштабное движение, подъем и опускание поверхностных вод. Сила, вызывающая завихренность.… … Справочник технического переводчика
Момент ядровый — – момент сил, заменяющий действие отброшенной части стержня на оставшуюся, при плоском внецентренном сжатии, взятый относительно оси, проходящей через точку пересечения контура ядра сечения с главной осью сечения, лежащей в плоскости… … Энциклопедия терминов, определений и пояснений строительных материалов
Момент силы — Вики
Момент силы, приложенный к гаечному ключу. Направлен от зрителя
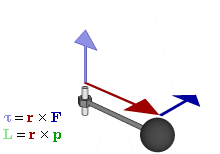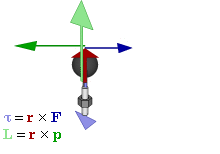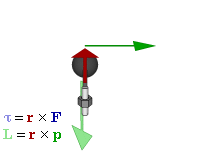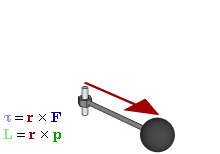
Моме́нт си́лы (синонимы: кру́тящий момент, враща́тельный момент, вертя́щий момент, враща́ющий момент) — векторная физическая величина, равная векторному произведению радиус-вектора, проведённого от оси вращения к точке приложения силы и вектора этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
Общие сведения
В физике момент силы можно понимать как «вращающая сила». В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр (Н·м). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метра от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров от оси вращения. Более точно момент силы частицы определяется как векторное произведение:
- M→=[r→×F→],{\displaystyle {\vec {M}}=\left[{\vec {r}}\times {\vec {F}}\right],}

