4. Векторное произведение и его свойства.
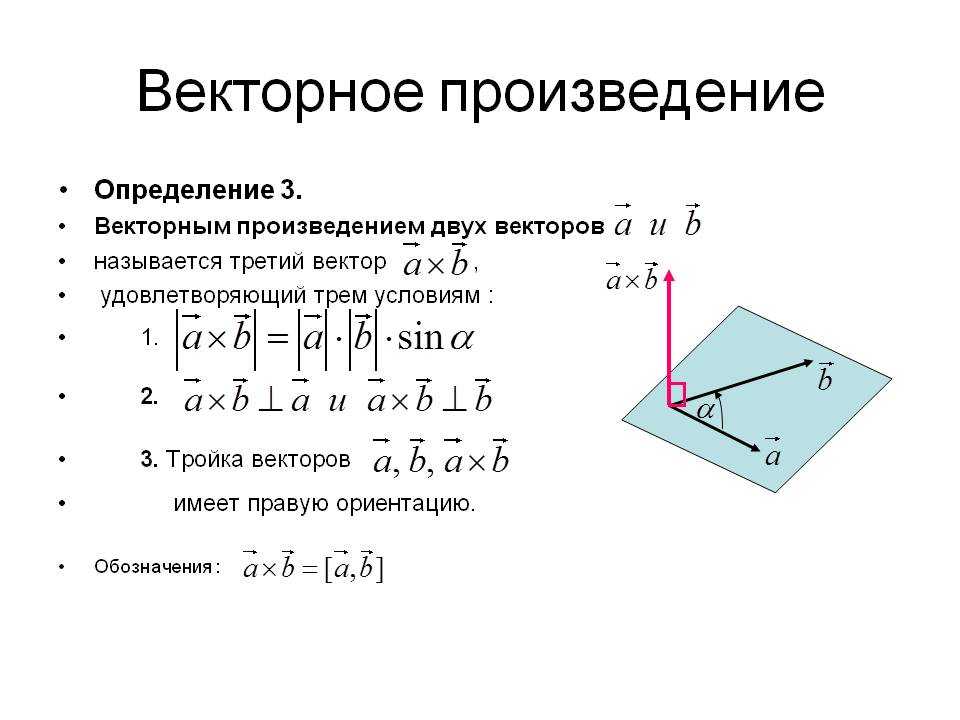
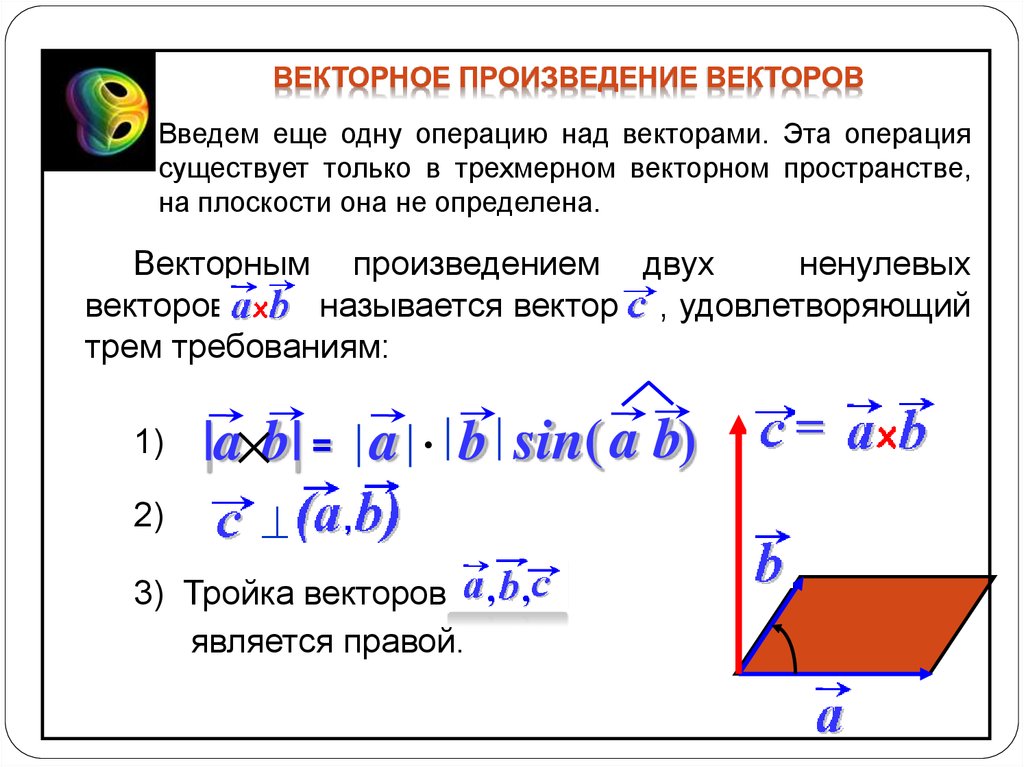
Определение. Векторным произведением двух векторов и называется новый вектор , модуль которого равен площади параллелограмма, построенного на векторах и , приведенных к общему началу, и который перпендикулярен к перемножаемым векторам (иначе говоря, перпендикулярен к плоскости построенного на них параллелограмма) и направлен в такую строну, чтобы кратчайший поворот от к вокруг полученного вектора представлялся происходящим против часовой стрелки, если смотреть из конца вектора (см .рис.).
Если векторы и коллинеарны, то их векторное произведение считается равным нулевому вектору.
Из этого определения следует, что ,
где – угол между векторами и ().
Векторное произведение векторов и обозначается символом
или или
.
Выясним физический смысл векторного произведения. Если вектор изображает приложенную в некоторой точке M силу, а вектор идет из некоторой точки O в точку M, то вектор представляет собой момент силы относительно точки O.
Свойства векторного произведения:
При перестановке сомножителей векторное произведение меняет знак, т.е.
.
Это свойство следует из определения векторного произведения.
Таким образом, векторное произведение не обладает переместительным свойством.
,
Свойство 2 непосредственно вытекает из смысла произведения вектора на скаляр и определения векторного произведения.
Векторное произведение подчиняется распределительному закону, т.е.
.
Если векторное произведение двух векторов равно нулевому вектору, то либо равен нулевому вектору хотя бы один из перемножаемых векторов (тривиальный случай), либо равен нулю синус угла между ними, т.е. векторы коллинеарны.
Обратно, если два ненулевых вектора коллинеарны, то их векторное произведение равно нулевому вектору. Таким образом,
Пусть даны три
вектора
, и
.
Представим себе, что вектор умножается векторно на и полученный вектор умножается скалярно на вектор
,
тем самым определяется число
.
Оно называется векторно-скалярным или смешанным произведением трех
, и
.
Для краткости смешанное произведение будем обозначать или ().
Выясним геометрический смысл смешанного произведения . Пусть рассматриваемые векторы , и некомпланарны. Построим параллелепипед на векторах , и как на ребрах. Векторное произведение есть вектор , численно равный площади параллелограмма OADB (основание построенного параллелепипеда), построенного на векторах и , и направленный перпендикулярно к плоскости параллелограмма (см. рис.).
E
C1
C
O B
A D
Скалярное произведение есть произведение модуля вектора и проекции вектора на .
Высота построенного параллелепипеда есть абсолютная величина этой проекции.
Следовательно,
произведение по абсолютной величине равно произведению
площади основания параллелепипеда на
его высоту, т. е. объему параллелепипеда,
построенного на векторах
, и
.
е. объему параллелепипеда,
построенного на векторах
, и
.
При этом важно отметить, что скалярное произведение дает объем параллелепипеда иногда с положительным, а иногда с отрицательным знаком. Положительный знак получается, если угол между векторами и острый; отрицательный – если тупой.
Таким образом, смешанное произведение есть число, абсолютная величина которого выражает объем параллелепипеда, построенного на векторах , , как на ребрах
Знак произведения положителен, если векторы , , образуют систему, одноименную с основной, и отрицателен в противном случае.
Абсолютная величина
смешанного произведения остается той
же, в каком бы порядке мы ни брали
сомножители. Что касается знака, то он
будет в одних случаях положительным, в
других – отрицательным; это зависит от
того, образуют ли наши три вектора,
взятые в определенном порядке, систему
одноименную с основной, или нет.
Смешанное произведение не меняется при круговой (циклической) перестановке его сомножителей. Перестановка двух соседних сомножителей меняет знак произведения:
.
Наконец, из геометрического смысла смешанного произведения непосредственно следует следующее утверждение.
Необходимым и достаточным условием компланарности векторов , , является равенство нулю их смешанного произведения:
.
Как найти векторное произведение векторов? Ответ на webmath.ru
Содержание:
- Формула
- Примеры вычисления векторного произведения векторов
Формула
Для того чтобы найти векторное произведение $[\bar{a}, \bar{b}]$ двух векторов, заданных своими координатами $\bar{a}=\left(a_{x} ; a_{y} ; a_{z}\right)$ и $\bar{b}=\left(b_{x} ; b_{y} ; b_{z}\right)$ соответственно, необходимо вычислить следующий определитель
$$[\bar{a}, \bar{b}]=\left|\begin{array}{ccc}\bar{i} & \bar{j} & \bar{k} \\ a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z}\end{array}\right|$$
Обычно такой определитель вычисляют разложением по первой строке. Отметим также, что результатом векторного произведения является вектор.
Отметим также, что результатом векторного произведения является вектор.
Примеры вычисления векторного произведения векторов
Пример
Решение. Для вычисления векторного произведения заданных векторов воспользуемся формулой
$$[\bar{a}, \bar{b}]=\left|\begin{array}{ccc}\bar{i} & \bar{j} & \bar{k} \\ a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z}\end{array}\right|$$
Подставляя координаты заданных векторов, получим:
$$[\bar{a}, \bar{b}]=\left|\begin{array}{lll}\bar{i} & \bar{j} & \bar{k} \\ 1 & 0 & 0 \\ 0 & 1 & 0\end{array}\right|$$
Раскладываем определитель по первой строке:
Первые два определителя равны нулю, так как они содержат нулевой столбец, а третий определитель вычисляем
как определитель второго порядка: от произведения элементов главной диагонали отнимаем произведение элементов побочной.
Итак, координаты искомого вектора равны коэффициентам при ортах, то есть
$$[\bar{a}, \bar{b}]=(0 ; 0 ; 1)$$
Ответ. $[\bar{a}, \bar{b}]=(0 ; 0 ; 1)$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Даны векторы $\bar{a}=(5 ; 3 ;-4)$ и $\bar{b}=(6 ; 7 ;-8)$ . Найти координаты векторного произведения $[\bar{a}, \bar{b}]$
Решение. Координаты векторного произведения $[\bar{a}, \bar{b}]$ вычисляются по формуле
$$[\bar{a}, \bar{b}]=\left|\begin{array}{ccc}\bar{i} & \bar{j} & \bar{k} \\ a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z}\end{array}\right|$$
Подставляя координаты заданных векторов, получим:
$$[\bar{a}, \bar{b}]=\left|\begin{array}{ccc}\bar{i} & \bar{j} & \bar{k} \\ 5 & 3 & -4 \\ 6 & 7 & -8\end{array}\right|$$
Раскладываем полученный определитель по первой строке:
$$=\bar{i} \cdot\left|\begin{array}{cc}3 & -4 \\ 7 & -8\end{array}\right|-\bar{j} \cdot\left|\begin{array}{cc}5 & -4 \\ 6 & -8\end{array}\right|+\bar{k} \cdot\left|\begin{array}{cc}5 & 3 \\ 6 & 7\end{array}\right|=$$ $$=[3 \cdot(-8)-7 \cdot(-4)] \cdot \bar{i}-[5 \cdot(-8)-6 \cdot(-4)] \cdot \bar{j}+$$ $$+[5 \cdot 7-6 \cdot 3] \cdot \bar{k}=(-24+28) \bar{i}-(-40+24) \bar{j}+(35-18) \bar{k}=$$ $$=4 \cdot \bar{i}+16 \cdot \bar{j}+17 \cdot \bar{k}$$
Тогда
$$[\bar{a}, \bar{b}]=(4 ; 16 ; 17)$$
Ответ. $[\bar{a}, \bar{b}]=(4 ; 16 ; 17)$
$[\bar{a}, \bar{b}]=(4 ; 16 ; 17)$
Читать дальше: как найти смешанное произведение векторов.
Перекрестное произведение двух векторов
Просмотр обсуждения
Улучшить статью
Сохранить статью
- Последнее обновление: 15 фев, 2022
Посмотреть обсуждение
Улучшить статью
Сохранить статью
Вектор — это двумерный объект, имеющий как величину, так и направление. Вектор можно рассматривать геометрически как направленный отрезок линии со стрелкой, обозначающей направление, и длиной, равной величине вектора. Направление вектора от хвоста к голове. Если два вектора имеют одинаковую величину и направление, они одинаковы. Это указывает на то, что если мы возьмем вектор и перенесем его в новую точку (не поворачивая его), то вектор, который мы получим в конце, будет таким же, как и тот, с которого мы начали.
Перекрестное произведение двух векторов В трехмерном пространстве перекрестное произведение представляет собой бинарную операцию над двумя векторами. Он генерирует перпендикулярный вектор к обоим заданным векторам. a × b представляет векторное произведение двух векторов, a и b. Он создает вектор, который перпендикулярен как a, так и b. Взаимные товары — это другое название векторных продуктов. Результатом перекрестного произведения двух векторов является вектор, который можно определить с помощью правила правой руки.
Он генерирует перпендикулярный вектор к обоим заданным векторам. a × b представляет векторное произведение двух векторов, a и b. Он создает вектор, который перпендикулярен как a, так и b. Взаимные товары — это другое название векторных продуктов. Результатом перекрестного произведения двух векторов является вектор, который можно определить с помощью правила правой руки.
a × b = |a||b|sinθ
Матрица перекрестного произведения
Мы также можем вывести формулу векторного произведения двух векторов, используя определитель матрицы, как указано ниже.
A = ai + bj + ck
B = xi + yj + zk
Примеры задачA × B =
=
= (bz – cy)i + (cx – az)j + (ay – bx) k
Вопрос 1. Найдите векторное произведение векторов: и
Решение:
Дано:
Вопрос 2. Найдите перекрестный продукт векторов:
Найдите перекрестный продукт векторов:
. Решение: 9 9003
9003 8.Вопрос 3. Найдите векторное произведение векторов: и .
Решение:
Дано: и .
Вопрос 4. Найдите векторное произведение векторов: и .
Решение:
Дано: .
Вопрос 5. Найдите векторное произведение векторов: и .

Решение:
Дано: и
Вопрос 5. Найдите векторное произведение векторов: и .
Решение:
Дано: и .
Вопрос 6. Найдите векторное произведение векторов: и .
Решение:
Дано: и .
Вопрос 7. Найдите векторное произведение векторов: и .
Решение:
Дано: и .
Руководство по перекрестным продуктам
- Дом
- О
- Страницы математики и статистики
- R Программирование
- Предметы Python
Этот пост будет о перекрестном произведении.
Эту тему можно найти в курсе исчисления и векторов средней школы (который я знаю в Онтарио, Канада) или во вводном курсе линейной алгебры.
Здесь мы будем иметь дело с векторами в трехмерном пространстве. Кроме того, легче вычислять произведения, если знать, как вычислять (2 на 2) определители. При этом я предполагаю, что читатель знаком с детерминантами.
Содержание
- Перекрестное произведение
- Вспомогательные средства памяти
- Свойства перекрестных произведений
- Примеры
- Практические задачи
- Решения
- Ссылки
Перекрестное произведение
Предположим, у нас есть два вектора \(\mathbf{u} = (u_1, u_2, u_{3})\) и \(\mathbf{v} = (v_1, v_2, v_{3})\) в трех измерениях. Перекрестное произведение $ ( ) $ двух векторов представляет собой (другой) вектор, перпендикулярный двум векторам.
Источник: https://upload.
wikimedia.org/wikipedia/commons/thumb/b/b0/Cross_product_vector.svg/220px-Cross_product_vector.svg.png
Существует два способа вычисления перекрестных произведений. Первая формула не предполагает, что читатель знает определители. Эта формула задается следующим образом:
\[ \mathbf{u} \times \mathbf{v} = (u_{2}v_{3} — u_{3}v_{2}, u_{3}v_{ 1} — u_{1}v_{3}, u_{1}v_{2} — u_{2}v_{1} )\]
Вторая формула фактически аналогична приведенной выше, но в детерминантной записи . Эта формула:
Источник: http://quicklatex.com/cache3/c4/ql_926219b87045b16e28f37e299ca0d7c4_l3.png
Напомним, что определитель 2 на 2 равен \(ad — bc\).
Вспомогательные средства для запоминания
Посмотрев на эти две формулы, вы, возможно, задаетесь вопросом, как мне все это запомнить!? При внимательном наблюдении вы можете обнаружить несколько закономерностей и придумать некоторые вспомогательные средства для запоминания.
В первой формуле все члены имеют формат \(uv\). Если вы внимательно посмотрите на пронумерованные нижние индексы, то увидите, что числа зеркальны. В первой части имеем \(u_{2}v_{3} — u_{3}v_{2}\). Первый нижний индекс — это 2, который идет с u, а второй нижний индекс — это 3 с v. После знака минус индексы зеркально отражены в порядке 3 и 2. Вторая часть имеет индексы 3,1,1, 3, а последняя часть имеет 1,2,2,1.
Для первой формулы одним из возможных вспомогательных средств памяти будут 2332, 3113 и 1221. Альтернативой могут быть 23, 31 и 12, поскольку у нас есть \(u_{2}v_{3}\), представляющий 23, и \(- u_ {3}v_{2}\), 31 для \(u_{3}v_{1} — u_{1}v_{3}\) и 12 для \(u_{1}v_{2} — u_{2 }v_{1}\).
Вторая формула предполагает, что читатель знаком с концепцией детерминантов в линейной алгебре. Обратите внимание, что верхняя строка в каждом определителе соответствует вектору \(\textbf{u}\), а нижняя строка — вектору \(\textbf{v}\). Одним из возможных вспомогательных средств для запоминания могут быть 23, -13 и 12, поскольку числа с индексами используются при переходе от крайнего левого столбца к крайнему правому столбцу.
Отрицательное значение для -13 представляет собой отрицательный определитель.
Другой способ получить вторую формулу — использовать этот метод, состоящий из нескольких частей.
Сформируйте матрицу 2 на 3 в формате
Первую составляющую перекрестного произведения можно вычислить, удалив первый столбец приведенной выше матрицы и взяв полученный определитель 2 на 2.
Второй компонент состоит из удаления второго столбца матрицы 2 на 3 и взятия определителя
Последним и третьим компонентом перекрестного произведения \(\textbf{u} \times \textbf{v}\) будет удаление последнего столбца матрицы и вычисление определителя
Результатом будет вторая формула, преобразованная в первую формулу.
Свойства перекрестных произведений
Как и с любой новой математической операцией, такой как перекрестное произведение, с ними связаны правила. В начальной школе были правила сложения, вычитания, умножения и деления.
Вот свойства перекрестного произведения для векторов \(\textbf{u}\), \(\textbf{v}\) и \(\textbf{w}\) в трехмерном пространстве с \(k \) как числовой скаляр. (\(\textbf{0}\) здесь нулевой вектор в трехмерном пространстве)
\[ \textbf{u} \times \textbf{v} = — (\textbf{v} \times \textbf{u})\]
\[ \textbf{u} \times (\textbf{v} + \textbf{w}) = (\textbf{u} \times \textbf{v}) + (\textbf{u} \times \textbf {w}) \text{ (Умножение слева) }\]
\[(\textbf{u} + \textbf{v}) \times \textbf{w} = (\textbf{u} \times \textbf{w}) + (\textbf{v} \times \textbf {w}) \text{ (Умножение справа) }\]
\[k(\textbf{u} \times \textbf{v}) = (k \textbf{u}) \times \textbf{v} = \textbf{u} \times (k \textbf{v} ) \]
\[\textbf{u} \times \textbf{0} = \textbf{0} \times \textbf{u} \]
- Пример 1 -2, 1)\), Найдите \(\textbf{u} \times \textbf{v}\) и \(\textbf{v} \times \textbf{u}.
\[\textbf{u} \times \textbf{u} = \textbf{0} \]
\)
Мы можем использовать формулу \[\textbf{u} \times \textbf{v} = (u_{2}v_{3} — u_{3}v_{2}, u_{3}v_{1} — u_{1}v_{3 }, u_{1}v_{2} — u_{2}v_{1} )\] или обозначение определителя формулы. Здесь будет использоваться детерминантная запись формулы.
Мы также вычисляем \(\textbf{v} \times \textbf{u}\).
Вы также можете проверить свойство \(\textbf{u} \times \textbf{v} = — (\textbf{v} \times \textbf{u})\). В этом случае \(\textbf{u} \times \textbf{v} = (1, 10, 15 ) = — (-1, -10, -15) = — (\textbf{v} \times \textbf{ у})\). Пример 2 , -1)\). Найдите вектор, который перпендикулярен/ортогонален обоим векторам \(\textbf{u}\) и \(\textbf{v}\).
Векторное перекрестное произведение двух векторов представляет собой (третий) вектор, который перпендикулярен обоим двум векторам.
Найдем перекрестное произведение \(\textbf{u} \times \textbf{v}\) следующим образом:
Вектор, перпендикулярный векторам \(\textbf{u}\) и \(\textbf{ v}\) равно \(\textbf{u} \times \textbf{v} = (1, -3, 2)\).


 Эту тему можно найти в курсе исчисления и векторов средней школы (который я знаю в Онтарио, Канада) или во вводном курсе линейной алгебры.
Эту тему можно найти в курсе исчисления и векторов средней школы (который я знаю в Онтарио, Канада) или во вводном курсе линейной алгебры.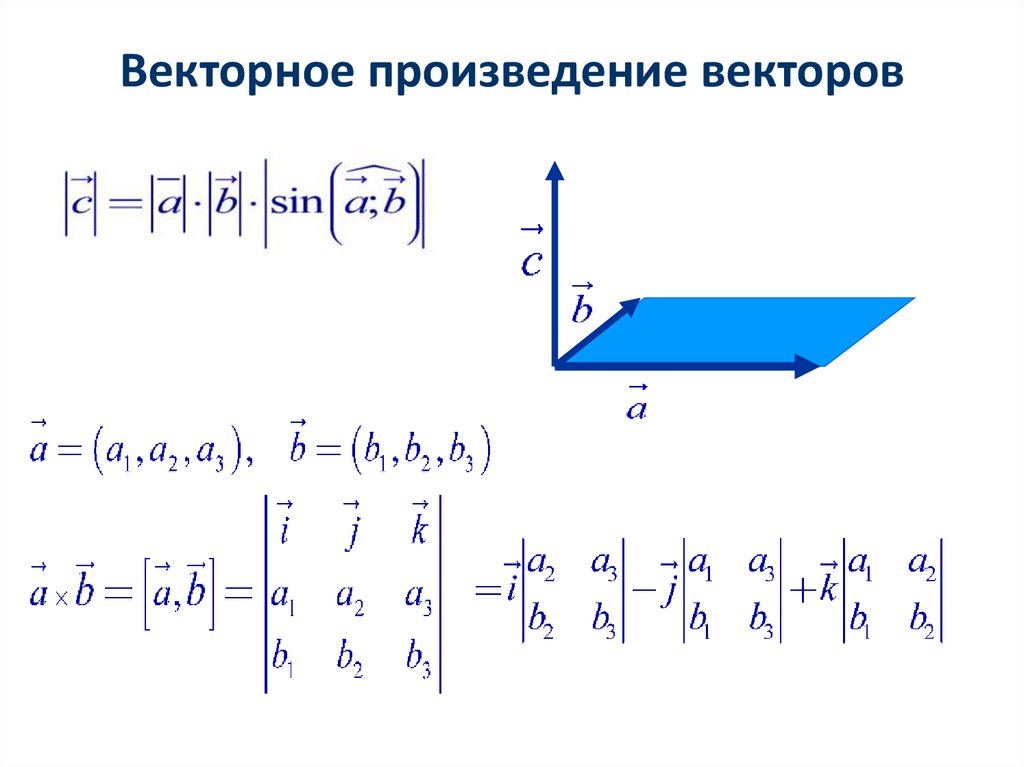 wikimedia.org/wikipedia/commons/thumb/b/b0/Cross_product_vector.svg/220px-Cross_product_vector.svg.png
wikimedia.org/wikipedia/commons/thumb/b/b0/Cross_product_vector.svg/220px-Cross_product_vector.svg.png
 Отрицательное значение для -13 представляет собой отрицательный определитель.
Отрицательное значение для -13 представляет собой отрицательный определитель.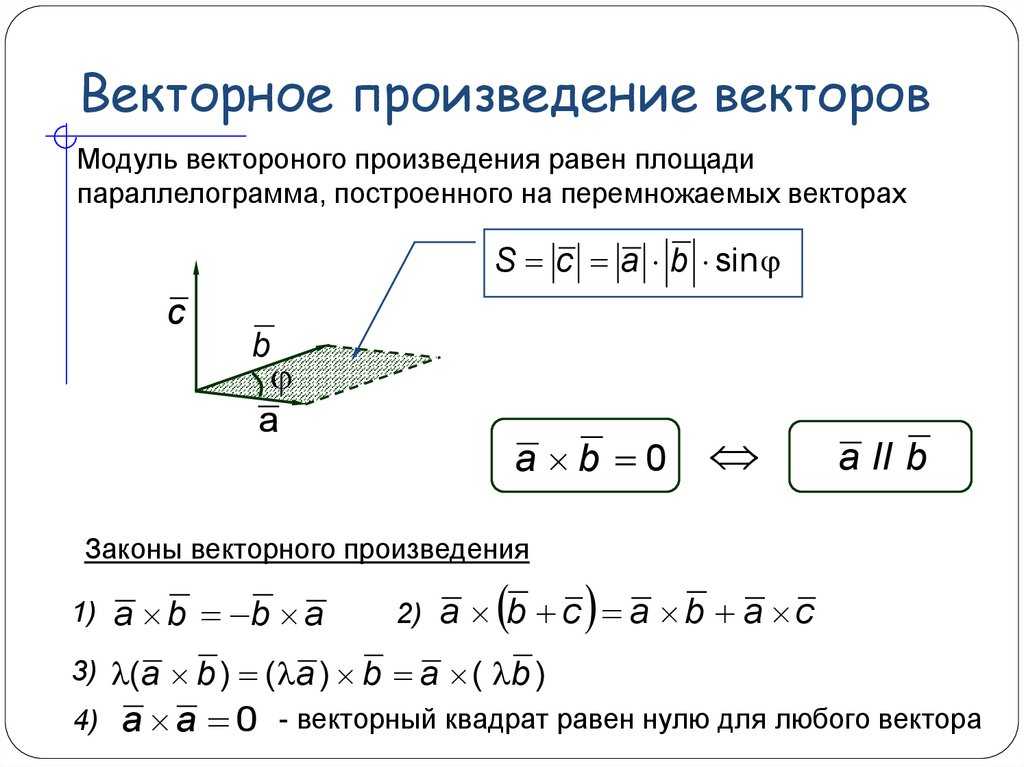
 \)
\)