3. Электрическое поле постоянного тока

К частным случаям электромагнитного поля относятся электрическое и магнитное поля постоянного тока. Эти поля являются стационарными, т.е. не зависящими от времени.

Так как магнитное поле постоянного тока не зависит от времени, явление электромагнитное индукции отсутствует, следовательно, стационарное магнитное поле не оказывает влияния на электрическое поле постоянного тока, и эти поля можно рассматривать отдельно.

3.1. Электрическое поле в диэлектрике, окружающем проводники с постоянными токами

При отсутствии токов в диэлектрике rotE = 0, т.е. E = – grad; D = E; divD = 0.

В случае однородной среды, когда  = const, эти уравнения дают divE = 0 или div grad  = 0, т.е. потенциал удовлетворяет уравнению Лапласа.

Таким образом, в самом диэлектрике такое поле ничем не отличается от электростатического. Однако граничные условия на поверхности проводников уже не соответствуют тем, которые имеют место в электростатике. В случае электростатической задачи поверхность каждого проводника является поверхностью равного потенциала. При прохождении по проводнику электрического тока в проводнике возникает падение потенциала, и, следовательно, поверхность проводника уже не будет равнопотенциальной. Линии напряженности электрического поля в диэлектрике подходят к поверхности проводника не под прямым углом, так как на поверхности проводника появляется касательная составляющая напряженности поля в направлении линии тока. На рис. 3.1 показан характер линий напряженности электрического поля около проводов линии передачи. С принципиальной точки зрения, указанное обстоятельство существенно осложняет расчет поля, однако практически во многих случаях его можно не учитывать, так как обычно падение напряжения вдоль проводников на длине, сравнимой с расстоянием между проводниками, ничтожно мало по сравнению с разностью потенциалов проводников. Поэтому при рассмотрении электрического поля в диэлектрике, окружающем проводники с постоянными токами, можно использовать решения, полученные при рассмотрении соответствующих электростатических задач.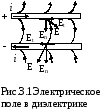

3.2.Электрическое поле постоянного тока в проводящей среде

Рассмотрим электрическое поле постоянного тока в неподвижных проводящих средах, или проводниках.

3.2.1. Уравнения и основные соотношения электрического поля постоянного тока

Рассмотрим электрическое поле постоянного тока в неподвижных проводящих средах, или проводниках.

Из полной системы уравнений Максвелла выберем только те уравнения, которые описывают электрическое поле постоянного тока в проводящей среде:

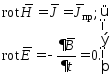(1)

Применим к обеим частям первого уравнения системы (1) операцию дивергенции, с учетом получим

.

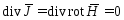Тогда уравнения Максвелла для электрического поля постоянного тока примут вид

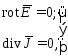(2)

где согласно (3.6)

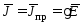. (3)

Одно из основных отличий электрического поля постоянного тока от электростатического обусловлено наличием внешних источников энергии неэлектростатического происхождения, без которых невозможно возникновение тока. В области действия этих источников, характеризуемых напряженностью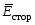

, (3) примет вид

. (4)

Выражение (3) представляет собой закон Ома в дифференциальной форме. Соотношение (4) является обобщенным законом Ома, или вторым законом Кирхгофа, в дифференциальной форме. Второе уравнение системы (2) называют первым законом Кирхгофа в дифференциальной форме.

Условие rotE = 0 свидетельствует, что вне источника ЭДС электрическое поле постоянных токов является так же, как и электростатическое поле, безвихревым. Такое поле является потенциальным, т.е. для характеристики может быть введена потенциальная функция φ, причем E = – grad .

Из второго уравнения системы (2) следует, что линии вектора плотности тока непрерывны и замкнуты.

Два уравнения (2) можно объединить в одно, подобное уравнениям Пуассона-Лапласа.

Область, во всех точках которой .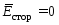

Для однородной проводящей среды (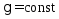) из второго уравнения (2) с учетом (3) получим:

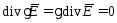. (5)

Подставляя в (5) выражение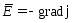

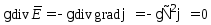,имеем:

,

т.е.

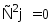. (6)

Таким образом, электрическое поле в однородной проводящей среде в области вне источников энергии описывается уравнением Лапласа (6), как и электростатическое поле в однородной среде, где нет свободных зарядов.

ЭЛЕКТРИЧЕСКОЕ ПОЛЕ — это… Что такое ЭЛЕКТРИЧЕСКОЕ ПОЛЕ?



ЭЛЕКТРИЧЕСКОЕ ПОЛЕ

ЭЛЕКТРИЧЕСКОЕ ПОЛЕ (электростатическое поле), область вокруг электрического заряда, в которой на каждую заряженную частицу действует некоторая сила. Объект с противоположным зарядом испытывает силу притяжения. Объект, имеющий такой же заряд, как и окружающее его поле, испытывает отталкивающее воздействие. Сила поля относительно единичного заряда на расстоянии r от заряда Q равна: Q/4pr²e, где e — диэлектрическая проницаемость среды, окружающей заряд. Переменное магнитное поле также может создать электрическое поле. см. также ЭЛЕКТРОМАГНЕТИЗМ.

Научно-технический энциклопедический словарь.

• ЭЛЕКТРИЧЕСКИЙ ТОК
• ЭЛЕКТРИЧЕСТВО

Смотреть что такое «ЭЛЕКТРИЧЕСКОЕ ПОЛЕ» в других словарях:

• ЭЛЕКТРИЧЕСКОЕ ПОЛЕ — частная форма проявления (наряду с магн. полем) электромагнитного поля, определяющая действие на электрич. заряд (со стороны поля) силы, не зависящей от скорости движения заряда. Представление об Э. п. было введено М. Фарадеем в 30 х гг. 19 в.… …   Физическая энциклопедия

• ЭЛЕКТРИЧЕСКОЕ ПОЛЕ — ЭЛЕКТРИЧЕСКОЕ ПОЛЕ, одна из форм электромагнитного поля. Создается электрическими зарядами или переменным магнитным полем. Характеризуется напряженностью электрического поля (или электрической индукцией). Напряженность электрического поля у… …   Современная энциклопедия

• ЭЛЕКТРИЧЕСКОЕ ПОЛЕ — (14, а) …   Большая политехническая энциклопедия

• ЭЛЕКТРИЧЕСКОЕ ПОЛЕ — частная форма проявления электромагнитного поля; создается электрическими зарядами или переменным магнитным полем и характеризуется напряженностью электрического поля …   Большой Энциклопедический словарь

• Электрическое поле — одна из двух сторон электромагнитного поля, характеризующаяся воздействием на электрически заряженную частицу с силой, пропорциональной заряду этой частицы и не зависящей от ее скорости… Источник: ЭЛЕКТРОТЕХНИКА . ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ ОСНОВНЫХ …   Официальная терминология

• электрическое поле — Одна из двух сторон электромагнитного поля, характеризующаяся воздействием на электрически заряженную частицу с силой, пропорциональной заряду этой частицы и не зависящей от ее скорости. [ГОСТ Р 52002 2003] EN electric field constituent of an… …   Справочник технического переводчика

• Электрическое поле —     Классическая электродинамика …   Википедия

• электрическое поле — 06.01.07 электрическое поле [ electric field]: Составляющая электромагнитного поля, которая характеризуется векторами напряженности электрического поля Е и электрической индукции D. Примечание Во французском языке термин «champ electrique»… …   Словарь-справочник терминов нормативно-технической документации

• Электрическое поле — Демонстрация поля электростатического заряда. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ, одна из форм электромагнитного поля. Создается электрическими зарядами или переменным магнитным полем. Характеризуется напряженностью электрического поля (или электрической… …   Иллюстрированный энциклопедический словарь

• электрическое поле — частная форма проявления электромагнитного поля; создаётся электрическими зарядами или переменным магнитным полем и характеризуется напряжённостью электрического поля. * * * ЭЛЕКТРИЧЕСКОЕ ПОЛЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ, частная форма проявления… …   Энциклопедический словарь

Книги

• Почему у свитых проводников с током отсутствует электромагнитное поле? Электромагнитное поле, магнитное поле, электрическое поле проводника с током. Импульсное поле витка с током и катушки (теория аб, Гуревич Гарольд Станиславович, Каневский Самуил Наумович. В книге доказано, что электромагнитное поле проводника с током образовано электронами. Электромагнитное поле — есть пространство, заполненное направленно движущимися по винтовым траекториям… Подробнее  Купить за 916 грн (только Украина)
• Теоретические основы электротехники. Электромагнитное поле, Л. А. Бессонов. Рассмотрены традиционные и появившиеся за последние годы новые вопросы теории и методы расчета физических процессов в электрических, магнитных и электромагнитных полях, предусмотренные… Подробнее  Купить за 750 руб
• Почему у свитых проводников с током отсутствует электромагнитное поле? Теория абсолютности, Гуревич Гарольд Станиславович, Каневский Самуил Наумович. Почему у свитых проводников с током отсутствует электромагнитное поле? Электромагнитное поле, магнитное поле, электрическое поле проводника с током. Импульсивноеполе витка с током и катушки… Подробнее  Купить за 715 руб

Другие книги по запросу «ЭЛЕКТРИЧЕСКОЕ ПОЛЕ» >>

Электрическое поле — это… Что такое Электрическое поле?

Электрическое поле — одна из составляющих электромагнитного поля; особый вид материи, существующий вокруг тел или частиц, обладающих электрическим зарядом, а также при изменении магнитного поля (например, в электромагнитных волнах). Электрическое поле непосредственно невидимо, но может быть обнаружено благодаря его силовому воздействию на заряженные тела.

Для количественного определения электрического поля вводится силовая характеристика — напряжённость электрического поля — векторная физическая величина, равная отношению силы, с которой поле действует на положительный пробный заряд, помещённый в данную точку пространства, к величине этого заряда. Направление вектора напряженности совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд.

В классической физике, применимой при рассмотрении крупномасштабных (больше размера атома) взаимодействий, электрическое поле рассматривается как одна из составляющих единого электромагнитного поля и проявление электромагнитного взаимодействия. В квантовой электродинамике — это компонент электрослабого взаимодействия.

В классической физике система уравнений Максвелла описывает взаимодействие электрического поля, магнитного поля и воздействие зарядов на эту систему полей.

Сила Лоренца описывает воздействие электромагнитного поля на частицу.

Эффект поля заключается в том, что при воздействии электрического поля на поверхность электропроводящей среды в её приповерхностном слое изменяется концентрация свободных носителей заряда. Этот эффект лежит в основе работы полевых транзисторов.

Основным действием электрического поля является силовое воздействие на неподвижные (относительно наблюдателя) электрически заряженные тела или частицы. Если заряженное тело фиксировано в пространстве, то оно под действием силы не ускоряется. На движущиеся заряды силовое воздействие оказывает и магнитное поле (вторая составляющая силы Лоренца).

Энергия электрического поля

Электрическое поле обладает энергией. Плотность этой энергии определяется величиной поля и может быть найдена по формуле

где E — напряжённость электрического поля, D — индукция электрического поля.

Классификация

Однородное поле

Направление линий напряжённости между двумя разнозаряженными пластинами

Однородное поле — это электрическое поле, в котором напряжённость одинакова по модулю и направлению во всех точках пространства. Приблизительно однородным является поле между двумя разноимённо заряженными плоскими металлическими пластинами. В однородном электрическом поле линии напряжённости направлены параллельно друг другу.

Наблюдение электрического поля в быту

Для того, чтобы создать электрическое поле, необходимо создать электрический заряд. Натрите какой-нибудь диэлектрик о шерсть или что-нибудь подобное, например, пластиковую ручку о собственные чистые волосы. На ручке создастся заряд, а вокруг — электрическое поле. Заряженная ручка будет притягивать к себе мелкие обрывки бумаги. Если натирать о шерсть предмет большей ширины, например, резиновую ленту, то в темноте можно будет видеть мелкие искры, возникающие вследствие электрических разрядов.

Электрическое поле часто возникает возле телевизионного экрана (относится к телевизорам с ЭЛТ) при включении или выключении телеприёмника. Это поле можно почувствовать по его действию на волоски на руках или лице.

Электрическое поле внутри проводников с избыточными зарядами

Из опытов, приводимых в электростатике, известно, что избыточные заряды привнесённые в проводник извне, перемещаются к поверхности проводника и остаются у поверхности проводника. Само перемещение избыточных зарядов к поверхности проводника свидетельствует о наличии электрического поля внутри проводника в период перемещения к поверхности проводника.

Электрическое поле внутри проводников с недостатком собственных электронов

При недостатке собственных электронов тело получает положительный заряд «дырочной» природы. Дырки при этом ведут себя подобно электронам и также распределяются по поверхности тела.

См. также

Литература

• Орир, Джей — Популярная физика: [пер. с англ.].: Мир, 1966. — 446 с.
• Учебник «Элементарный учебник физики» под ред. Ландсберга Г. С., Часть 2 (Электричество и магнетизм.)
• Трофимова Т. И. Курс физики: Учеб. пособие для вузов.—2-е изд., перераб. и доп.— М.: Высш. шк., 1990.—478 с.: ил. ISBN 5-06-001540-8

В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 15 мая 2011.

08 Электрическое поле постоянных токов

Лекция № 8

Электрическое поле постоянных токов

1. Уравнения электромагнитного поля постоянных токов

Рассмотрим поле постоянных токов в неподвижных проводниках и проводящих средах. Постоянный ток может протекать только в замкнутой проводящей цепи. Уравнения электромагнитного поля для случая постоянных токов в неподвижной проводящей среде вне источников э.д.с. имеют вид

rotH = j, rotE= 0, divD = divB = 0.
j = E,	B = H,	D= E.	(1)

Условие rotE = 0 свидетельствует, что вне источника э.д.с. электрическое поле постоянных токов является так же, как и электростатическое поле, безвихревым и потенциальным.

Уравнение непрерывности в случае постоянных токов сводится к уравнению divj =0,

которое выражает то, что линии вектора плотности тока в этом случае не имеют ни начала, ни конца. Соотношение (2) называют также первым законом Кирхгофа в дифференциальной форме.

Вычислим интеграл jdl , взятый вдоль некоторого замкнутого контура L,

L

совпадающего с замкнутой силовой линией. Если имеется только электростатическое поле E кулоновского происхождения, то плотность тока связана с напряженностью уравнением j = = E, где E=-grad . Тогда

jdl	= Edl grad dl — d 0.			(3)
L	L	L	L

Так как интегрирование в интеграле jdl ведется вдоль линии плотности тока, то элемент

L

пути интегрирования dl в каждой точке параллелен вектору плотности тока. Следовательно, jdl= jdl. C учетом сказанного равенство (3) приобретает вид

jdl = jdl 0.

L L

Подынтегральное выражение на всем пути интегрирования не меняет знака. При таком условии из равенства нулю интеграла следует равенство нулю подынтегрального выражения: j=0. Тем самым доказано, что существование постоянного тока при наличии только кулоновских сил электростатического поля невозможно.

Постоянные токи могут существовать только при наличии полей неэлектростатического происхождения. Такие поля существуют в источниках тока — гальванических элементах, аккумуляторах, генераторах. Эти поля, называются сторонними, связанные с этими полями силы, обеспечивающие движение зарядов и возникновение тока, называются сторонними электродвижущими силами (сторонними э.д.с.).

Обобщение закона Ома. Плотность тока обусловливается не только электростатическим полем, но и полем сторонних сил. Поле сторонних сил характеризуется вектором Естор, который определяется как напряженность электрического поля, порождающего такую же плотность электрического поля, какая порождается сторонними силами неэлектростатического происхождения. В связи с этим закон Ома должен быть написан в виде

Уравнение (4) называют обобщенным законом Ома в дифференциальной форме. Если от обеих частей уравнения (4) взять интеграл по замкнутому контуру, включающему в себя

Электрическое поле постоянных токов

2

________________________________________________________________________________

источник э.д.с., то будет получен второй закон Кирхгофа, поэтому уравнение (4) называют также вторым законом Кирхгофа в дифференциальной форме.

Закон Джоуля-Ленца в дифференциальной форме. Мощность тепловых потерь в проводнике равна произведению тока и напряжения P=IU. Если рассмотреть в проводящей среде элемент объема dV, то мощность, которая тратится в этом объеме на тепловые потери, будет равна:

dP=dIdU=jdSEdl=jEdV,

откуда

dP jE E2 j2 / . dV

Это и есть дифференциальная форма закона Джоуля-Ленца.

Мощность тепловых потерь в объеме V можно выразить следующим образом: P E2dV

V

2. Электрическое поле в диэлектрике, окружающем проводники с постоянными токами

Так как токи в диэлектрике отсутствуют, то следует положить в нем поэтому поле в диэлектрике характеризуется уравнениями:

rotE = 0, divD = 0 D= E.

В случае однородной среды, когда const, эти уравнения дают divE = 0 или =0, т.е. потенциал удовлетворяет уравнению Лапласа.

Таким образом, в самом диэлектрике такое поле ничем не отличается от электростатического. Однако граничные условия на поверхности проводников уже не соответствуют тем, которые имели место в электростатике. В случае электростатической задачи поверхность каждого проводника является поверхностью равного потенциала. Это следует из закона j = E. Математически проводники характеризуются тем, что их проводимость 0, поэтому, если j = 0, то при электростатическом равновесии E=0, т.е. поле в проводнике равно нулю только тогда, когда в нем отсутствуют токи, а заряды находятся в равновесии.

При прохождении по проводнику электрического тока в проводнике возникает падение потенциала, и, следовательно, поверхность проводника уже не будет эквипотенциальной. Линии напряженности электрического поля в диэлектрике подходят к поверхности проводника не под прямым углом, так как на поверхности проводника появляется касательная составляющая напряженности поля в направлении линий тока.

С принципиальной точки зрения, указанное обстоятельство существенно осложняет расчет поля, однако практически во многих случаях его можно не учитывать, так как обычно касательная составляющая напряженности поля много меньше нормальной составляющей. Касательная составляющая может быть определена из выражения Et = j/ . Если принять для медных проводов См/м и j = 5 А/м2, то получим для Et = 0,086 В/м. В случае проводов линии низкого напряжения величина Еn имеет величину порядка 1000 В/м, тогда En/Et > 104. Для линий высокого напряжения эта величина достигает 107.

Полученные цифры показывают, что составляющая Et ничтожно мала по сравнению с En – (Et En), и при рассмотрении поля около проводов ею можно пренебречь без опасения внести этим заметную ошибку. В таком случае граничные условия на поверхности проводников оказываются тождественными условиям в электростатике.

Электрическое поле постоянных токов

3

________________________________________________________________________________

3. Электрическое поле и поле вектора плотности тока в проводящей среде

Внутри проводников, по которым проходит ток, также существует электрическое поле. Внутри проводящей среды вне источников э.д.с. всюду соблюдается условие Edl=0

L

или rotE = 0, что выражает также второй закон Кирхгофа соответственно в интегральной и дифференциальной формах в области, где нет источников э.д.с.

Электрическое поле и поле вектора плотности тока в проводящей среде вне

источников э.д.с. определяются системой уравнений:
rotE = 0, divj =0,	j = E.	(5)

Эти уравнения вытекают из приведенной в начале лекции системы уравнений (1), причем уравнение divj =0, как уже отмечалось, является следствием уравнения rotH = j, так как divrotH = 0.

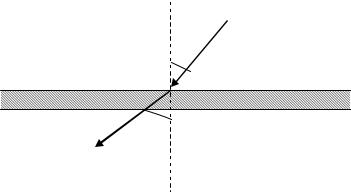
При переходе тока через поверхность раздела сред с различными удельными проводимостями направление тока изменяется, если только линии тока не направлены нормально к поверхности раздела. Установим соотношение между углом падения 1и углом преломления 2.

j1

1

j2

2

Из уравнений (5) следуют два граничных условия для касательной составляющей вектора E и нормальной составляющей вектора j:

				E1t=E2t
				j1n=j2n					(6)
Записав эти граничные условия с помощью тригонометрических функций, и приняв
во внимание E j, получим:				E1sin 1= E2sin 2
			1E1cos 1= 2E2cos 2.
Разделив первую строчку на вторую, найдем
	tg 1		tg 2	или	tg 1		1	.	(7)
	1		2		tg 2
							2

Закон преломления линий тока по форме аналогичен закону преломления линий электрического смещения на границе двух диэлектриков и закону преломления линий магнитной индукции на границе двух магнетиков.

Во многих практических случаях мы встречаемся с переходом тока из металлических тел в окружающую среду, удельная проводимость которой во много раз меньше удельной проводимости металла. Такие условия имеют место, например, в случае токов утечки через изоляцию между проводами, находящимися под разными потенциалами. В этом случае отношение удельной проводимости меди к удельной проводимости изоляции имеет порядок 1020. В качестве другого примера можно указать на случай перехода тока в землю через

Электрическое поле постоянных токов

4

________________________________________________________________________________

зарытые в землю металлические электроды. В этом случае отношение удельной проводимости материала заземлителя к удельной проводимости почвы имеет порядок 108.

Во всех этих случаях при рассмотрении поля в среде с малой проводимостью можно пренебречь падением напряжения внутри металлических тел и считать поверхности металлических тел поверхностями равного потенциала.

4. Аналогия электрического поля в проводящей среде с электростатическим полем

Между соотношениями, характеризующими стационарное электрическое поле в проводящей среде, и соотношениями, характеризующими электростатическое поле в диэлектрике, можно провести формальную аналогию.

Электрическое поле	Электростатическое
в проводящей среде	поле
rotE = 0	rotE = 0
B	B
Edl UA UB	Edl UA UB
A	A
j = E	D = 0E
divj = 0	divD = 0
jdS i	DdS q
S	S

Если заменить вектор электрического смещения D вектором плотности тока j, электрический заряд q током i и абсолютную диэлектрическую проницаемость удельной проводимостью , то выражения в левой и правой колонках полностью совпадут

Если условия для вектора j на границе данной проводящей среды с удельной проводимостью совпадают с условиями для вектора D на такой же формы границе диэлектрика с абсолютной диэлектрической проницаемостью , то электрические поля в проводящей среде и в диэлектрике должны быть аналогичны друг другу.

На этом основан так называемый метод электростатической аналогии, позволяющий при расчете токов в проводящей среде воспользоваться готовыми решениями соответствующих задач электростатики. Метод электростатической аналогии дает также возможность заменить исследование электростатического поля экспериментальным исследованием поля тока в проводящей среде.

Проще всего удается экспериментально исследовать электрическое поле в проводящей среде. Важно при этом, чтобы при моделировании было соблюдено геометрическое подобие областей, в которых существует поле, а также соблюдены требуемые граничные условия.

Для исследования плоскопараллельных полей используют металлические листы или листы из проводящей бумаги, можно применять также ванну со слабо проводящей жидкостью, в которую погружены электроды.

Формулы для электрической проводимости среды G =i/U, в которой протекает ток, могут быть получены из соответствующих формул для емкости C = q/U тел, так как в аналогичных задачах ток i заменяется зарядом q.

Электрическое поле постоянных токов

5

________________________________________________________________________________

q

DdS 0

EdS

i

jdS

EdS

C

,

G

,

S

S

S

S

UAB

B

B

UAB

B

B

Edl

Edl

Edl

Edl

A

A

A

A

G

.

C 0

Сопротивление заземления. Для осуществления соединения какой-либо точки электрической цепи с землей зарывают в землю металлические проводники, к которым и присоединяют соответствующую точку цепи. При повреждении изоляции одного из фазных проводов возникает ток короткого замыкания, проходящий от мест повреждения через землю и заземлитель к нейтральной точке трансформатора. Электрический ток, проходя через землю, встречает некоторое сопротивление, называемое сопротивлением заземления. По существу это — сопротивление земли, которое встречает ток при растекании от заземлителя. Вдоль поверхности земли создается падение напряжения, которое вблизи от места заземления может достигать опасных для жизни человека значений уже на длине шага человека. Поэтому необходимо уметь вычислить сопротивление растеканию тока в земле при различных конструкциях заземлителей. Формулы для проводимости заземления могут быть написаны на основании метода электростатической аналогии по имеющимся формулам для расчета емкости соответственно расположенных тел.

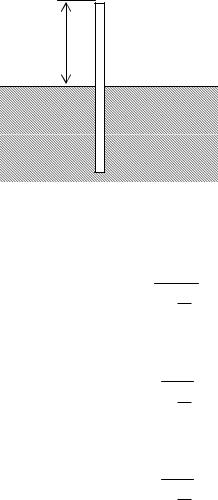
Часто применяют заземлители в виде труб, забитых вертикально в землю.

l

Пусть l — длина трубы и r — ее радиус. Предположим, что один конец трубы находится у самой поверхности земли. Длина трубы вместе с ее зеркальным отражением равна 2l. Емкость цилиндра, имеющего длину 2l и радиус r при 2l>>r, приближенно равна

C 4 0l . ln 2l

r

Следовательно, проводимость для системы из электрода и его зеркального изображения равна

G 4 l . ln 2l

r

Таким образом, проводимость заземления для электрода в форме вертикальной трубы выражается формулой

G 2 l . ln 2l

r

Электрическое поле постоянных токов

6

________________________________________________________________________________

5. Понятие идеального проводника и идеального изолятора

Уравнение непрерывности divj+ =0 преобразуем следующим образом. Значение

t

объемной плотности возьмем из уравнения Максвелла divD, а плотность тока — из закона Ома j = E. Тогда получаем

div( E	divD	) div( E				E	) 0.	(8)
	t				0 t
Для того чтобы равенство (8) выполнялось, достаточно предположить, что
E E0 exp(				t).
			0

Из уравнения divD видно, что аналогично будет зависеть от времени и плотность заряда

0 exp(		t) 0 exp(	t	).
	0
			M

Величина 0 играет роль характерного для данной среды времени релаксации M (максвелловское время релаксации). Оно равно времени, в течение которого объемный заряд уменьшается в е = 2,71 раза. Значение M изменяется в очень широких пределах. В плохо проводящих веществах (изоляторах) оно может измеряться многими минутами. В металлах вследствие их большой проводимости M равно по порядку величины 10-17 с.

У идеального диэлектрика M = , у идеального проводника M = 0.

Время релаксации Максвелла определяет порядок величины времени, в течение которого восстанавливается стационарность электрических процессов. Чтобы токи можно было считать квазистационарными, характерное время рассматриваемого процесса Т должно быть много больше времени релаксации M

Т >> M.

Если токи изменяются периодически, то под Т следует понимать период колебаний Т = 2 / , где — круговая частота колебаний. Тогда сформулированное выше условие квазистационарности примет вид

M << 1.

Диэлектрик может сохранять заряд достаточно долго, в проводнике же заряды, внесенные внутрь среды, быстро исчезают (релаксируют). Из закона сохранения заряда видно, что если проводник занимает все пространство, то заряды уходят на бесконечность, если же он ограничен диэлектрической средой, то заряды могут задержаться на граничной поверхности между проводником и диэлектриком.

6. Поток энергии в случае провода с постоянным током

Будем рассматривать проводник с током I как уединенный проводящий цилиндр. Воспользуемся законом Ома j= E и найдем напряженность электрического поля на

поверхности проводника (r=a) — E Izo a2 . Из закона полного тока найдем напряженность магнитного поля H Ir 2 a. Вектора напряженности электрического и

магнитного полей взаимно перпендикулярны. Вектор Пойнтинга в произвольной точке на поверхности проводника равен

I2

S E H -ro 2 2a3 .

Электрическое поле постоянных токов

7

________________________________________________________________________________

z0

r r0

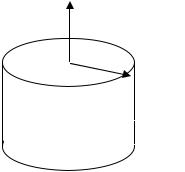
Вектор Пойнтинга направлен радиально внутрь проводника, таким образом, энергия внешнего поля «втекает» в проводник. Поток энергии на участке длиной L имеет следующее значение

	2					L
SdΣ	I				2 aL I2			I2R ,
	2	a	3			2
	2					a

где R — сопротивление участка проводника. Это есть мощность тепловых потерь. На основании баланса энергии можно утверждать, что энергия внешнего поля проникает в проводник именно постольку, поскольку она им поглощается. При переходе к идеальному сверхпроводнику ( ) исчезает поглощение, а вместе с ним, как это видно из полученного результата, и поток энергии в проводник.

Рассмотрим постоянный ток, сосредоточенный в ограниченной области пространства. Выбрав какую-либо поверхность , отделяющую область V, вне которой нет тока, из теоремы Пойнтинга получим (изменение энергии электромагнитного поля равно нулю)

V

Будем неограниченно увеличивать объем V, относя поверхность в бесконечность. На достаточно больших расстояниях электрическое поле подобно полю точечного заряда, а магнитное – полю магнитного диполя. Таким образом, поверхностный интеграл в пределе равен нулю и мы получаем

Величина интеграла в последнем равенстве не может зависеть от V, если только внутри локализован не весь ток (а именно это мы и предположили вначале). Поэтому в правой части (9) всегда нуль, а отсюда

при условии, что поверхность охватывает весь ток. Полученное равенство выражает важное свойство стационарных полей: поток энергии через поверхность, содержащую внутри себя весь ток, обязательно равен нулю. Можно сказать, что постоянный ток не излучает энергию.

В электростатическом поле также нет движения энергии, так как Н=0 и вектор Пойнтинга в каждой точке пространства равен нулю. Нет потока энергии и в магнитостатическом поле, где Е=0.

Заменим в равенстве (10) плотность тока через напряженность электрического поля

	по закону Ома. При этом получится	j2	dV 0. Отсюда следует, j = 0. Но при отсутствии
	V

тока нет и стационарного электромагнитного поля. Если использовать обобщенный закон

Электрическое поле постоянных токов

8

________________________________________________________________________________

	Ома j = E+Eстор), то получится равенство		j2	dV jEсторdV, показывающее, что
		V		V

постоянный ток (вместе со своим полем) существует лишь при наличии сторонних сил, т.е. источника энергии неэлектромагнитного происхождения.

Электрическое поле — Википедия

Материал из Википедии — свободной энциклопедии

Электрическое поле — одна из двух компонент электромагнитного поля, представляющая собой векторное поле^[1], существующее вокруг тел или частиц, обладающих электрическим зарядом, а также возникающее при изменении магнитного поля (например, в электромагнитных волнах). Электрическое поле непосредственно невидимо, но может быть обнаружено благодаря его силовому воздействию на заряженные тела^[2].

Для количественного определения электрического поля вводится силовая характеристика — напряжённость электрического поля — векторная физическая величина, равная отношению силы, с которой поле действует на положительный пробный заряд, помещённый в данную точку пространства, к величине этого заряда. Направление вектора напряженности совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд.

В классической физике, применимой при рассмотрении крупномасштабных (больше размера атома) взаимодействий, электрическое поле рассматривается как одна из составляющих единого электромагнитного поля и проявление электромагнитного взаимодействия. В квантовой электродинамике — это компонент электрослабого взаимодействия.

В классической физике система уравнений Максвелла описывает взаимодействие электрического поля, магнитного поля и воздействие зарядов на эту систему полей.

Основным действием электрического поля является силовое воздействие на неподвижные относительно наблюдателя электрически заряженные тела или частицы. На движущиеся заряды силовое воздействие оказывает и магнитное поле (вторая составляющая силы Лоренца).

Энергия электрического поля

Электрическое поле обладает энергией. Плотность этой энергии определяется величиной поля и может быть найдена по формуле

u=12(E→D→),{\displaystyle u={\frac {1}{2}}\left({\vec {E}}{\vec {D}}\right),}

где E — напряжённость электрического поля, D — индукция электрического поля.

Классификация

Однородное поле

Направление линий напряжённости между двумя разнозаряженными пластинами

Однородное поле — это электрическое поле, в котором напряжённость одинакова по модулю и направлению во всех точках пространства. Приблизительно однородным является поле между двумя разноимённо заряженными плоскими металлическими пластинами. В однородном электрическом поле линии напряжённости направлены параллельно друг другу.

Наблюдение электрического поля в быту

Для того, чтобы создать электрическое поле, необходимо создать электрический заряд. Натрите какой-нибудь диэлектрик о шерсть или что-нибудь подобное, например, пластиковую ручку о собственные чистые волосы. На ручке создастся заряд, а вокруг — электрическое поле. Заряженная ручка будет притягивать к себе мелкие обрывки бумаги. Если натирать о шерсть предмет большей ширины, например, резиновую ленту, то в темноте можно будет видеть мелкие искры, возникающие вследствие электрических разрядов.

Электрическое поле часто возникает возле телевизионного экрана (относится к телевизорам с ЭЛТ) при включении или выключении телеприёмника. Это поле можно почувствовать по его действию на волоски на руках или лице.

Электрическое поле внутри проводников с избыточными зарядами

Из опытов, приводимых в электростатике, известно, что избыточные заряды привнесённые в проводник извне, перемещаются к поверхности проводника и остаются у поверхности проводника. Само перемещение избыточных зарядов к поверхности проводника свидетельствует о наличии электрического поля внутри проводника в период перемещения к поверхности проводника.

Электрическое поле внутри проводников с недостатком собственных электронов

При недостатке собственных электронов тело получает положительный заряд «дырочной» природы. Дырки при этом ведут себя подобно электронам и также распределяются по поверхности тела.

Методы расчета электрического поля

Расчёты электрического поля можно проводить аналитическими^[3][4][5] или численными методами^[6]. Аналитические методы удается применить лишь в простейших случаях, на практике в основном используются численные методы. Численные методы включают в себя: метод сеток или метод конечных разностей; вариационные методы; метод конечных элементов; метод интегральных уравнений; метод эквивалентных зарядов^[6].

См. также

Примечания

Литература

• Орир, Джей — Популярная физика: [пер. с англ.].: Мир, 1966. — 446 с.
• Учебник «Элементарный учебник физики» под ред. Ландсберга Г. С., Часть 2 (Электричество и магнетизм.)
• Трофимова Т. И. Курс физики: Учеб. пособие для вузов.—2-е изд., перераб. и доп.— М.: Высш. шк., 1990.—478 с.: ил. ISBN 5-06-001540-8

Постоянное электрическое поле (электростатическое поле) | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Постоянное (не изменяющееся во времени) электриче­ское поле создается распределением неподвижных заря­дов. Силовые линии начинаются на положительных и окан­чиваются на отрицательных зарядах.

Существование поля проявляется в том, что на заряженные частицы действует сила, которая может быть измерена. Ра­бота, совершаемая этой силой при перемещении заряда из одной точки пространства в другую, зависит только от рас­положения этих точек и не зависит от пути перемещения.

Если распределение зарядов и тока не меняется во времени, то создаваемое им электромагнитное поле также не будет меняться. Электрическое поле полностью описывается двумя первыми уравнениями Максвелла, ко­торые приобретают вид:

1) ∮_SE̅ × n̅ • dS = (1 / ε₀) • Σ_iq_i,

2) ∮_SE̅ × dl̅ = 0.

Силовые линии поля позволяют судить не только о на­правлении вектора напряженности в каждой точке про­странства, но и о величине напряженности.  

Трубка, образованная силовыми линиями поля

Рассмотрим тонкую трубку в пустоте, боковая поверхность которой образована силовыми линиями. Два сечения этой трубки и поверхность трубки между ними образуют замк­нутую поверхность, к которой применимо первое уравне­ние. При условии, что внутри поверхности нет зарядов, по­лучим из первого уравнения Максвелла:

∮_SE̅ × n̅ • dS = E̅₁ × n̅₁S₁ + E̅₂ × n̅₂S₂ = E₂S₂ –E₁S₁ = 0.

Произведение модуля напряженности поля в некоторой точке внутри трубки, образованной силовыми линиями в пустоте, на площадь сечения трубки в этой точке не меня­ется вдоль трубки.

Если трубка расширяется, величина напряженности поля падает, и наоборот. Материал с сайта http://worldofschool.ru

Если в некоторой ограни­ченной области простран­ства заключен поло­жительный заряд, то силовые линии поля вы­ходят из этой области и, если никаких других за­рядов больше нет, уходят на бесконечность. При­чем на достаточно боль­шом расстоянии от заря­да силовые линии будут ортогональны сферичес­ким поверхностям, в цен­тре которых находится заряд. Если в другой об­ласти присутствует отри­цательный заряд такой же величины, то все ли­нии, вышедшие из первой области, войдут в замкну­тую поверхность, внутри которой находится отри­цательный заряд. Если знаки зарядов поменять, картина силовых линий останется прежней, но их направление изме­нится.

20 Лекция 20. Электрическое поле постоянного тока

Цель лекции: изучить основные физические величины, характеризующие электрическое поле и связь между ними.

20.1 Ток и плотность тока

Если в проводнике существует электрическое поле, оно вызывает упорядоченное движение зарядов, представляю­щее собой ток проводимости. В металлических проводни­ках ток проводимости определяется движением электронов. Мерой тока служит предел отношения заряда q, про­ходящего сквозь заданную поверхность в течение некото­рого времени t, к t, когда t стремится к нулю как к пределу .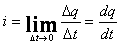

Ток — величина скалярная. Если значе­ние тока не зависит от времени, ток называется постоянным. Ток измеряется в амперах (А). Плотностью тока называют векторную величину 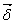, числен­ное значение которой равно пределу отношения тока, про­текающего через некоторую площадку, расположенную нормально к направлению движения зарядов, к площади этой площадки, когда она стремится к нулю как к пре­делу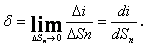

Направление вектора 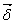выбирается таким образом, чтобы оно совпадало с направлением движения положительных зарядов (или было противоположно направлению движе­ния oтрицательных зарядов).

Ток и плотность тока связаны соотношением

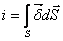. (20.1)

Ток сквозь поверхность S равен потоку вектора плот­ности тока сквозь ту же поверхность. Плотность тока измеряется в амперах, деленных на квадратные метры (А/м²).

20.2 Закон Ома в дифференциальной форме

В изотропном проводнике плотность тока проводимо­сти 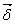пропорциональна напряженности электрического поля Е

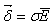. (20.2)

Эта формула представляет собой закон Ома в диффе­ренциальной форме. Коэффициент  называется удельной прово­димостью и измеряется в См/м.

Для того, чтобы в проводнике длительно протекал ток, необходимо наличие электрического поля, силы которого будут перемещать заряды. Такое поле может быть создано и будет поддерживаться процессами не электростатического происхождения (химическими, термоэлектрическими) и носит название стороннего электрического поля. Напряженность стороннего электрического поля обо­значаем Е_стор. Если в проводнике одновременно действуют и электро­статические и сторонние силы, напряженность результи­рующего поля будет равна .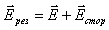

Рассмотрим проводящий контур а— 1 — b— 2 — а (рисунок 20.1).

На уча­стке b — 2 — а действуют сторонние си­лы и на этом участке

.

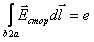На участке a — 1 — b сторонних сил нет, поэтому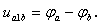

В замкнутой цепи сумма падений напряжения равна э. д. с.

или.

Разность потенциалов между двумя точками рассматри­ваемого контура меньше э. д. с., действующей в этом кон­туре. Ток на участке a — 1 — b идет от точки а (точки высшего потенциала) к точке b (точке низшего потенциала).

Если бы в цепи не было сторонних сил, то потенциалы точек а и b выровнялись бы и ток прекратился. Наличие сторонних сил заставляет заряды перемещаться от точки b к точке а по пути b — 2 — а и поддерживает потенциалы точек а и b постоянными. Энергия стороннего поля расхо­дуется на тепловые потери как на участке а — 1 — b, так и на участке b — 2 — а. В тех областях проводника, в ко­торых имеются сторонние силы, закон Ома записывается следующим образом

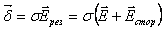. (20.3)

Закон Ома в дифференциальной форме справедлив как для постоянных, так и для переменных электрических по­лей.

20.3 Закон Джоуля- Ленца в дифференциальной форме

Мощность тепловых потерь в проводнике равна произве­дению тока и напряжения .

Если рассмотреть в проводящей среде элемент объема dV, то мощность, которая тратится в этом объеме на тепловые потери, будет равна

,

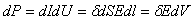откуда 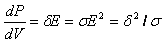. (20.4)

Мощность тепловых потерь в объеме V можно выразить следующим образом 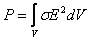. (20.5)

Формула (20.4) является дифференциальной формой за­кона Джоуля—Ленца.

20.4 Первый закон Кирхгофа в дифференциальной форме

Замкнутая поверхность S охватывает узел цепи, к кото­рому подтекают токи I₁ и I₂ и из которого вытекают токи I₃ и I₄ (рисунок 20.2).

Согласно первому закону Кирхгофа I₁ +I₂ =I₃+I_4.

Выразим токи через плотность тока, тогда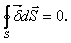

Поток вектора плотности тока проводимости сквозь зам­кнутую поверхность равен нулю. Это значит, что заряд, входящий в любой объем, равен заряду, выходящему из него за тот же промежуток времени. Постоянный ток непрерывен. Линии вектора плотности тока 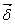замкнуты.

По теореме Остроградского

.

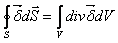Так как поверхность S, а следовательно, и объем V выбраны произвольно, то можно считать, что

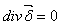. (20.6)

Плотность тока проводимости не имеет источников. При постоянном токе заряд в любом объеме проводника остается неизменным.

Так как дивергенция плотности тока проводимости равна нулю, то линии вектора 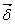замкнуты, поэтому формулу (20.6) называют уравнением непрерывности для постоянного тока.

20.5 Граничные условия

Рассмотрим границу двух проводящих сред, удельные проводимости которых равны σ₁ и σ₂. Граничные условия:

а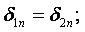) нормальная составляющая вектора плотности тока на границе двух проводящих сред непрерывна

в) если на границе этих сред нет сторонних сил, то танген­циальные составляющие вектора напряженности электриче­ского поля также должны быть непрерывны у границы

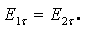
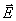Если векторы и образуют с нормалью к границе угол 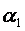в первой среде и угол 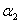—во второй (рисунок 20.3), то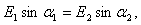

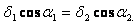
Так как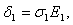

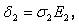
то

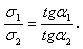
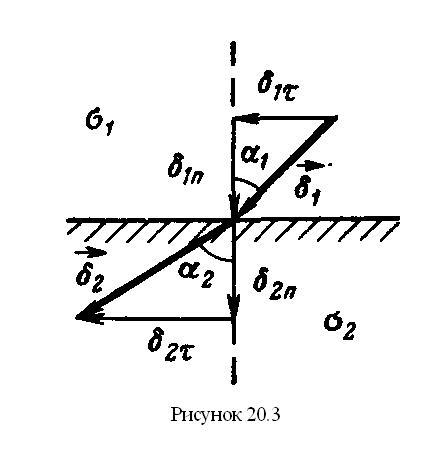
20.6 Аналогия между электрическим и электростатическим полями

В области, в которой нет сторонних э. д. с., поле посто­янного тока потенциальное. Потенциал и напряженность поля в такой области связаны соотношением

Так как постоянный ток непрерывен, поле такого тока не имеет источников

.

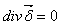По закону Ома в дифференциальной форме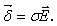

В среде с постоянной проводимостью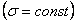

.

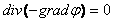Следовательно

Для определения потенциала поля в рассматриваемой области необходимо решить уравнение Лапласа и учесть гра­ничные условия.

Электростатическое поле в диэлектрике при отсутствии свободных объемных зарядов также описывается уравне­нием Лапласа. Поэтому, если две одинаково ограниченные области: проводящая (без сторонних э. д. с.) и диэлектри­ческая (без свободных объемных зарядов) имеют на гранич­ной поверхности одинаковое распределение потенциала, то внутри каждой из этих областей распределение потенциала будет также одинаковым. Это обстоятельство позволяет пользоваться формулами, полученными при расчете электро­статических полей, в случае поля постоянного тока. При этом емкость необходимо заменить проводимостью, абсолютную диэлектрическую проницаемость — удельной проводимостью.

Например, чтобы определить проводимость изоляции коаксиального кабеля, можно воспользоваться формулой емкости кабеля 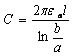. Произведя замену, получим 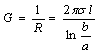.