Как определить направление силы лоренца. Сила Лоренца и правило левой руки. Движение заряженных частиц в магнитном поле
Содержание
- 1 Немного истории
- 2 Определение и формула
- 2.1 В чём измеряется?
- 2.2 Когда возникает?
- 3 Формула силы Лоренца при наличии магнитного и электрического полей
- 3.1 Направление силы Лоренца
- 4 Следствия свойств силы Лоренца
- 4.1 Формула силы Лоренца при наличии магнитного и электрического полей
- 4.2 Единицы измерения силы Лоренца
- 5 Понятие напряженности электрического поля
- 5.1 Напряженность электрического поля
- 6 Примеры задачи
- 6.1 Задача 1
- 6.2 Задача 2
- 6.3 Задача 3
- 7 Что такое сила Лоренца — определение, когда возникает, получение формулы
- 7.1 Определение направления силы Лоренца с помощью правила левой руки
- 7.2 Движение заряженной частицы в магнитном поле
- 8 Применение силы Лоренца в технике
- 8.
 1 Кинескоп
1 Кинескоп - 8.2 Масс-спектрограф
- 8.
- 9 Циклотрон
- 9.1 Магнетрон
- 9.2 Магнитное поле Земли
- 10 Траектории частиц под действием силы Лоренца
- 10.1 Значение силы Лоренца
- 10.2 ЭДС
- 11 Единицы измерения силы Лоренца
- 11.1 Понятие напряженности электрического поля
- 11.2 Напряженность электрического поля
Немного истории
Первые попытки описать электромагнитную силу были сделаны еще в XVIII веке. Ученые Генри Кавендиш и Тобиас Майер высказали предположение, что сила на магнитных полюсах и электрически заряженных объектах подчиняется закону обратных квадратов. Однако экспериментальное доказательство этого факта не было полным и убедительным. Только в 1784 году Шарль Августин де Кулон при помощи своего торсионного баланса смог окончательно доказать это предположение.
В 1820 году физиком Эрстедом был открыт факт, что на магнитную стрелку компаса действует ток вольта, а Андре-Мари Ампер в этом же году смог разработать формулу угловой зависимости между двумя токовыми элементами. По сути, эти открытия стали фундаментом современной концепции электрических и магнитных полей. Сама же концепция получила свое дальнейшее развитие в теориях Майкла Фарадея, особенно в его представлении о силовых линиях. Лорд Кельвин и Джеймс Максвелл дополнили теории Фарадея подробным математическим описанием. В частности Максвеллом было создано так званное, «уравнение поля Максвелла» – представляющее собой систему дифференциальных и интегральных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах.
По сути, эти открытия стали фундаментом современной концепции электрических и магнитных полей. Сама же концепция получила свое дальнейшее развитие в теориях Майкла Фарадея, особенно в его представлении о силовых линиях. Лорд Кельвин и Джеймс Максвелл дополнили теории Фарадея подробным математическим описанием. В частности Максвеллом было создано так званное, «уравнение поля Максвелла» – представляющее собой систему дифференциальных и интегральных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах.
Джей Джей Томпсон был первым физиком, кто попытался вывести из уравнения поля Максвелла электромагнитную силу, которые действует на движущийся заряженный объект. В 1881 году он опубликовал свою формулу F = q/2 v x B. Но из-за некоторых просчетов и неполного описания тока смещения она оказалась не совсем правильной.
И вот, наконец, в 1895 году голландский ученый Хендрик Лоренц вывел правильную формулу, которая используется и поныне, а также носит его имя, как и та сила, что действует на летящую частицу в магнитном поле, отныне называется «силой Лоренца».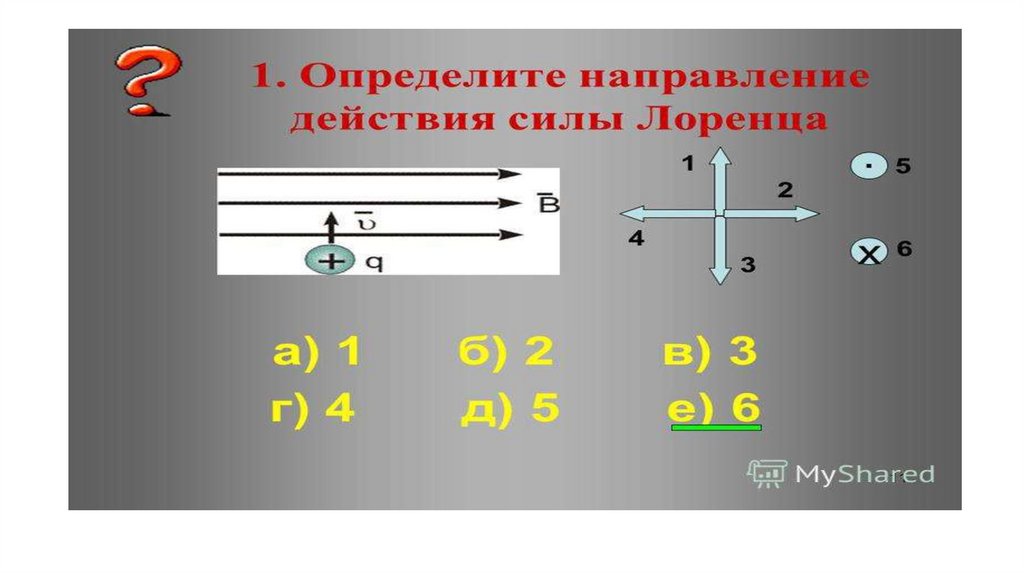
Определение и формула
Хендрик Лоренц доказал, что электромагнитная индукция взаимодействует с заряженными частицами. Эти взаимодействия приводят к возникновению силы Лоренца. Рассматриваемая сила возникает под действием магнитной индукции. Она перпендикулярна вектору скорости движущейся частицы (см. рис. 1). Необходимым условием возникновения этой силы является движение электрического заряда.
Рис. 1. Выводы Лоренца
Обратите внимание на расположение векторов (рисунок слева, вверху). Векторы, указывающие направления скорости и силы Лоренца, лежат в одной плоскости XOY, причём они расположены под углом 90º. Вектор магнитной индукции сориентирован вдоль оси Z, перпендикулярной плоскости XOY, а значит, в выбранной системе координат он перпендикулярен к векторам силы и скорости.
По закону Ампера:
Учитывая, что
(здесь j – плотность тока, q – единичный заряд, n – количество зарядов на бесконечно малую единицу длины проводника, S – сечение проводника, символом v обозначен модуль скорости движущейся частицы), запишем формулу Ампера в виде:
Так, как nSdl – общее число зарядов в объёме проводника, то для нахождения силы, действующей на точечный заряд, разделим выражение на количество частиц:
Модуль F вычисляется по формуле:
Из формулы следует:
- Сила Лоренца приобретает максимальное значение, если угол α прямой.

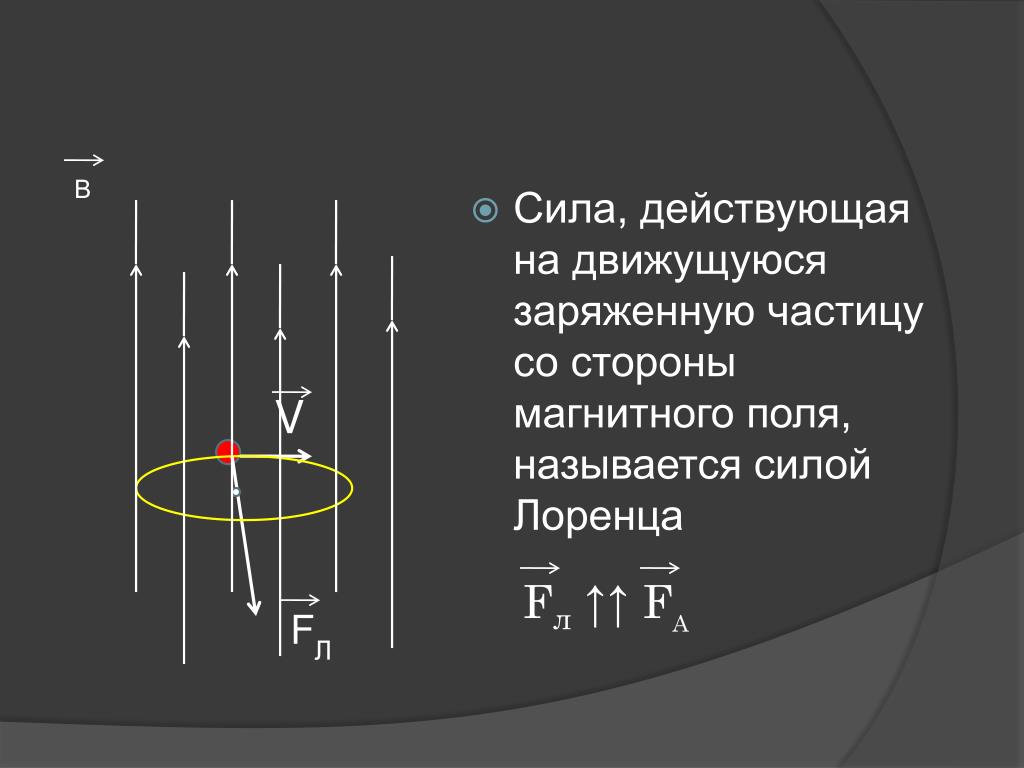
- Если точечный заряд, например, электрон, попадает в среду однородного магнитного поля, обладая некой начальной скоростью, перпендикулярной к линиям электромагнитной индукции, тогда вектор F будет перпендикулярен к вектору скорости. На точечный заряд будет действовать центробежная сила, которая заставит его вращаться по кругу. При этом работа равняется нулю (см. рис.2).
- Если угол между вектором индукции и скоростью частицы не равняется 90º, тогда заряд будет двигаться по спирали. Направление вращения зависит от полярности заряда (рис. 3).
Рис. 2. Заряженная частица между полюсами магнитов
Рис. 3. Ориентация вектора в зависимости от полярности заряда
Из рисунка 3 видно, что вектор F направлен в противоположную сторону, если знак заряда меняется на противоположный (при условии, что направления остальных векторов остаются неизменными).
Траекторию движения частицы правильно называть винтовой линией. Радиус этой винтовой линии (циклотронный радиус) определяется перпендикулярной к полю составной начальной скорости частицы.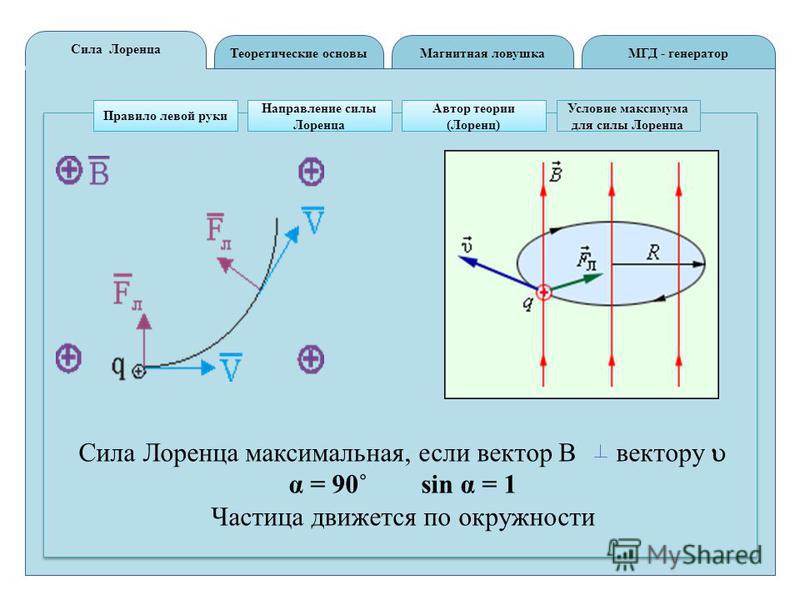 Шаг винтовой линии, вдоль которой перемещается частица, определяется составной начальной скорости заряда, вошедшего в однородное магнитное поле. Эта составная направлена параллельно к электромагнитным линиям.
Шаг винтовой линии, вдоль которой перемещается частица, определяется составной начальной скорости заряда, вошедшего в однородное магнитное поле. Эта составная направлена параллельно к электромагнитным линиям.
В чём измеряется?
Размерность силы Лоренца в международной системе СИ – ньютон (Н). Разумеется, модуль силы Лоренца настолько крохотная величина, по сравнению с ньютоном, что её записывают в виде К×10-n Н, где 0к
Когда возникает?
Магнитные поля не реагируют на неподвижный электрический заряд, так же как не действует сила Ампера на обесточенный проводник.
Для возникновения силы Лоренца необходимо выполнить три условия:
- У частицы должен быть отрицательный или положительный заряд.
- Заряженная частица должна находиться в магнитном поле.
- Частица должна быть в движении, то есть вектор v ≠ 0.
Если хотя бы одно из условий не выполняется, сила Лоренца не возникает.
Формула силы Лоренца при наличии магнитного и электрического полей
Рассмотрим случай, когда заряженная частица находится в движении в двух полях одновременно (в электрическом и магнитном), тогда на заряд подействуют две составляющие:
Тогда:
Поскольку эту формулу вывел Лоренц, то её также называют именем учёного-физика.
Направление силы Лоренца
Мы уже упоминали, что направление возникшей силы Лоренца, кроме магнитных параметров, определяется (в том числе) полярностью заряда. Если бы мы имели возможность наблюдать заряженную элементарную частицу, пребывающую в магнитном поле, то по вектору её перемещения можно было бы определить направление вектора силы F.
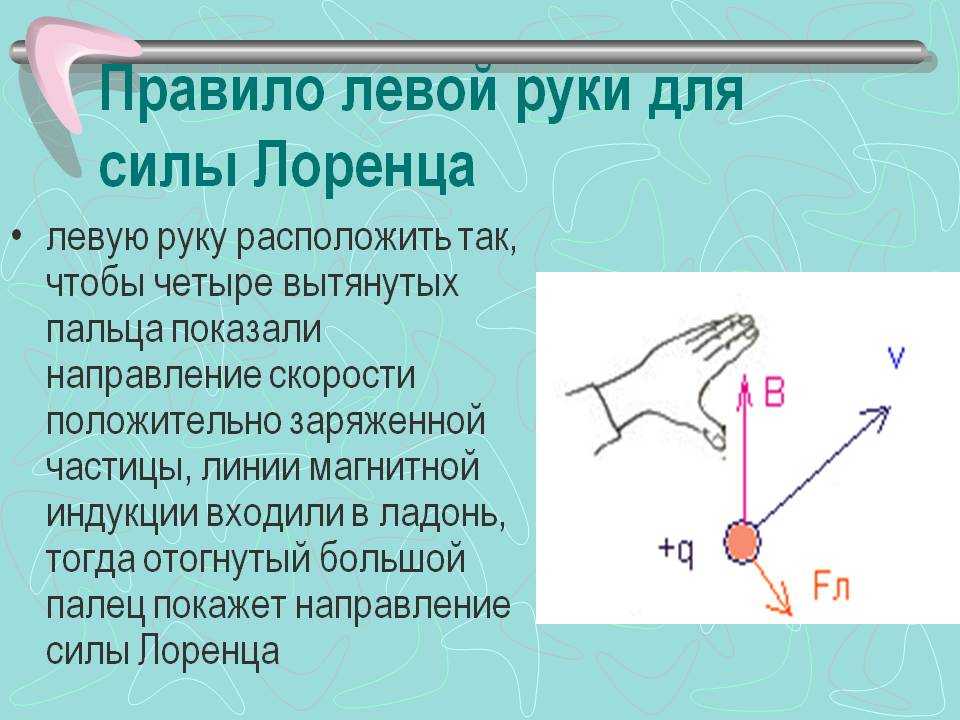
Но на практике наблюдать элементарные заряды очень сложно из-за крохотных размеров. Поэтому для определения этого направления применяют способ, известен, как правило левой руки (рис. 4).
Рис. 4. Нахождение вектора силы Лоренца
Ладонь необходимо развернуть так, чтобы вектор индукции входил в неё. В случае с положительным зарядом, вытянутые пальцы располагают по движению частицы. (для отрицательного заряда пальцы направляют в противоположную сторону). Большой палец под прямым углом указывает искомое направление.
Если известна ориентация вектора скорости частицы, то определить направления остальных векторов можно, применяя правило правой руки, которое понятно из рисунка 5.
Рис. 5. Пример применения правила правой руки
Ученые заметили, что есть определенная закономерность между тем, как частица влетает в магнитное поле и тем, куда оно ее отклоняет. Чтобы ее было легче запомнить, они разработали специальное мнемоническое правило. Для его запоминания нужно совсем немного усилий, ведь в нем используется то, что всегда под рукой – рука. Точнее, левая ладонь, в честь чего оно носит название правила левой руки.
Итак, ладонь должна быть раскрыта, четыре пальца смотрят вперед, большой палец оттопырен в сторону. Угол между ними составляет 900. Теперь необходимо представить, что магнитный поток представляет собой стрелу, которая впивается в ладонь с внутренней стороны и выходит с тыльной. Пальцы при этом смотрят туда же, куда летит воображаемая частица. В таком случае большой палец покажет, куда она отклонится.
Интересно!
Важно отметить, что правило левой руки действует только для частиц со знаком «плюс». Чтобы узнать, куда отклонится отрицательный заряд, нужно четыре пальца направить в сторону, откуда летит частица.
Все остальные манипуляции остаются прежними.
Следствия свойств силы Лоренца
Тело влетает в магнитном поле под каким-то определённым углом. Интуитивно понятно, что его величина имеет какое-то значение на характер воздействия на него поля, здесь нужно математическое выражение, чтобы стало понятнее. Следует знать, что как сила, так и скорость являются векторными величинами, то есть имеют направление. То же самое относится и к линиям магнитной напряженности. Тогда формулу можно записать следующим образом:
FЛ=qvBsinα,
sin α здесь – это угол между двумя векторными величинами: скоростью и потоком магнитного поля.
Как известно, синус нулевого угла также равен нулю. Получается, что если траектория движения частицы проходит вдоль силовых линий магнитного поля, то она никуда не отклоняется.
В однородном магнитном поле силовые линии имеют одинаковое и постоянное расстояние друг от друга. Теперь представим, что в таком поле перпендикулярно этим линиям движется частица. В этом случае сила Лоуренса заставит двигаться ее по окружности в плоскости, перпендикулярной силовым линиям. Чтобы найти радиус этой окружности, нужно знать массу частицы:
В этом случае сила Лоуренса заставит двигаться ее по окружности в плоскости, перпендикулярной силовым линиям. Чтобы найти радиус этой окружности, нужно знать массу частицы:
R=mvqB
Значение заряда не случайно взято как модуль. Это означает, что неважно, отрицательная или положительная частица входит в магнитное поле: радиус кривизны будет одинаков. Изменится только направление, в котором она полетит.
Во всех остальных случаях, когда заряд имеет определенный угол α с магнитным полем, он будет двигаться по траектории, напоминающей спираль с постоянным радиусом R и шагом h. Его можно найти по формуле:
R=mvsinαqB
h=2mvcosαqB
Еще одним следствием свойств этого явления является тот факт, что она не совершает никакой работы. То есть она не отдает и не забирает энергию у частицы, а лишь меняет направление ее движения.
Самая яркая иллюстрация этого эффекта взаимодействия магнитного поля и заряженных частиц – это северное сияние. Магнитное поле, окружающее нашу планету, отклоняет заряженные частицы, прилетающие от Солнца.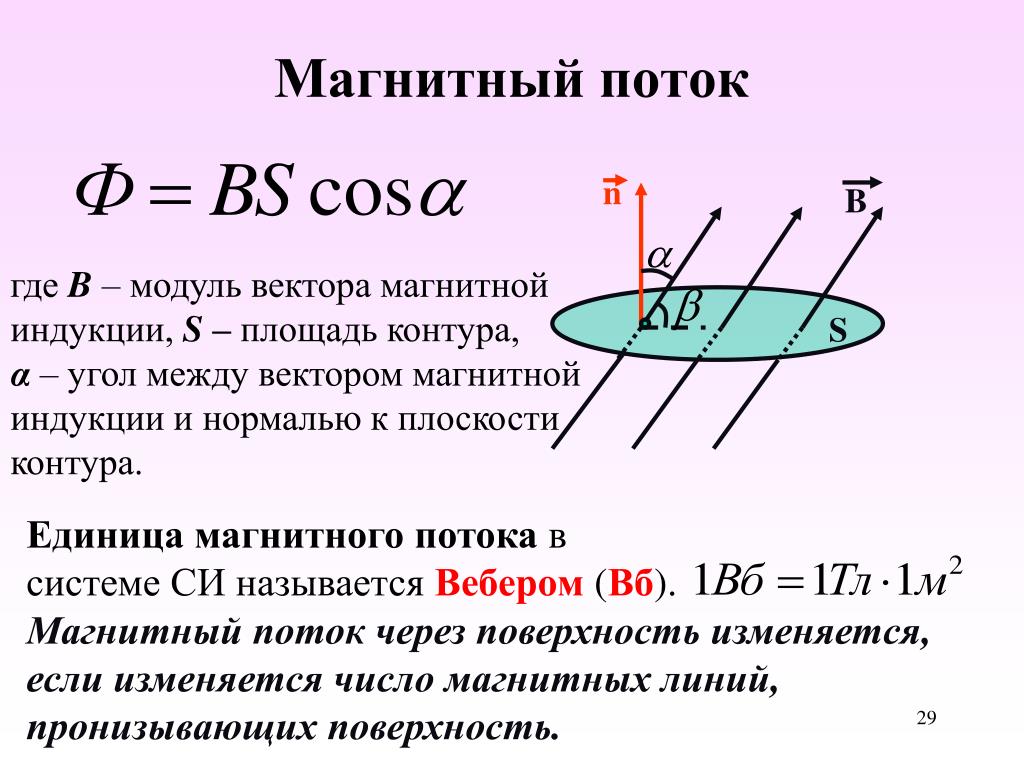 Но так как оно слабее всего на магнитных полюсах Земли, то туда проникают электрически заряженные частицы, вызывая свечение атмосферы.
Но так как оно слабее всего на магнитных полюсах Земли, то туда проникают электрически заряженные частицы, вызывая свечение атмосферы.
Центростремительное ускорение, которое придается частицам, используется в электрических машинах – электродвигателях. Хотя уместнее здесь говорить о силе Ампера – частном проявлении силы Лоуренса, которая воздействует на проводник.
Принцип действия ускорителей элементарных частиц также основан на этом свойстве электромагнитного поля. Сверхпроводящие электромагниты отклоняют частицы от прямолинейного движения, заставляя их двигаться по кругу.
Самое любопытное заключается в том, что сила Лоренца не подчиняется третьему закону Ньютона, который гласит, что всякому действию есть свое противодействие. Связано это с тем, что Исаак Ньютон верил, что всякое взаимодействие на любом расстоянии происходит мгновенно, однако это не так. На самом деле оно происходит с помощью полей. К счастью, конфуза удалось избежать, так как физикам удалось переработать третий закон в закон сохранения импульса, который выполняется в том числе и для эффекта Лоуренса.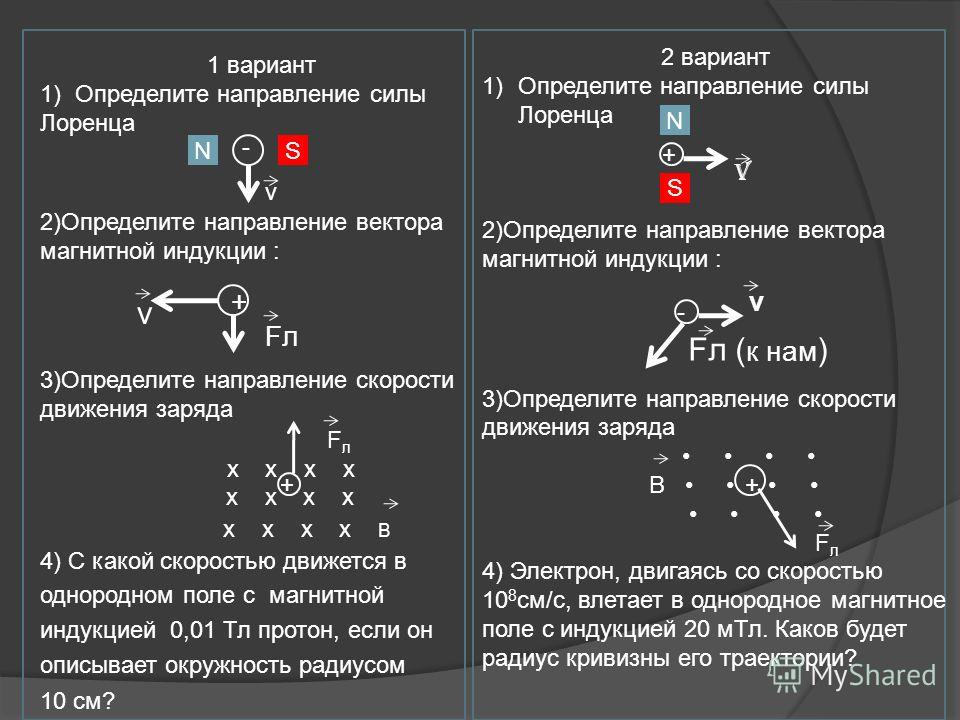
Формула силы Лоренца при наличии магнитного и электрического полей
Магнитное поле имеется не только у постоянных магнитов, но и у любого проводника электричества. Только в данном случае помимо магнитной составляющей, в ней присутствует еще и электрическая. Однако даже в этом электромагнитном поле эффект Лоуренса продолжает свое воздействие и определяется по формуле:
FЛ=qE+vB
где v – скорость электрически заряженной частицы, q – ее заряд, B и E – напряженности магнитного и электрических полей поля.
Единицы измерения силы Лоренца
Как и большинство других физических величин, которые действуют на тело и изменяют его состояние, она измеряется в ньютонах и обозначается буквой Н.
Понятие напряженности электрического поля
Электромагнитное поле на самом деле состоит из двух половин – электрической и магнитной. Они точно близнецы, у которых все одинаково, но вот характер разный. А если приглядеться, то во внешности можно заметить небольшие различия.
То же самое касается и силовых полей. Электрическое поле тоже обладает напряженностью – векторной величиной, которая является силовой характеристикой. Она воздействует на частицы, которые в неподвижности находятся в нем. Само по себе оно не является силой Лоренца, ее просто нужно принимать во внимание, когда вычисляется воздействие на частицу в условиях наличия электрического и магнитного полей.
Напряженность электрического поля
Напряженность электрического поля воздействует только на неподвижный заряд и определяется по формуле:
E=Fq
Единицей измерения является Н/Кл или В/м.
Примеры задачи
Задача 1
На заряд в 0,005 Кл, который движется в магнитном поле с индукцией 0,3 Тл, действует сила Лоренца. Вычислить ее, если скорость заряда 200 м/с, а движется он под углом 450 к линиям магнитной индукции.
| Дано: q = 0,005 Кл B = 0,3 Тл v = 200 м/с α = 450 | Решение: В условиях задачи нет упоминания электрического поля, поэтому силу Лоренца можно найти по следующей формуле: FЛ=qvBsinα=0,005×200×0,3×sin 450 =0,3×22=0,21 Н |
Задача 2
Определить скорость тела, имеющего заряд и которое движется в магнитном поле с индукцией 2 Тл под углом 900. Величина, с которой поле воздействует на тело, равна 32 Н, заряд тела – 5 × 10-3 Кл.
Величина, с которой поле воздействует на тело, равна 32 Н, заряд тела – 5 × 10-3 Кл.
| Дано: q = 0,005 Кл B = 2 Тл FЛ = 32 Н α = 900 | Решение: Чтобы найти скорость заряда, необходимо несколько видоизменить формулу для нахождения силы Лоренца:
FЛ=qvBsinαv=FЛqBsinα v=320,005×2×sin900=320,01×1=32000мс=32 км/с |
Задача 3
Электрон движется в однородном магнитном поле под углом 900 ее силовым линиям. Величина, с которой поле воздействует на электрон, равна 5 × 10-13 Н. Величина магнитной индукции равна 0,05 Тл. Определить ускорение электрона.
| Дано: q = -1,6 × 10-19 Кл B = 0,05 Тл FЛ = 5 × 10-13 Н α = 900 | Решение: В этой задаче сила Лоренца ко всему прочему еще и заставляет двигаться электрон по окружности. Поэтому здесь под ускорением следует понимать центростремительное ускорение: aц=v2R На данный момент неизвестны ни скорость электрона, ни радиус окружности, по которой он движется.
v=FЛqBsinα=5×10-13-1,6×10-19×0,05∙sin900=6×107мс R=mvqB=9×10-31×6×107-1,6×10-19×0,05=6,8×10-3мс
|
aц=v2R=6×10726,8×10-3=5×1017мс2
Электродинамика оперирует такими понятиями, которым трудно подобрать аналогию в обычном мире. Но это совсем не значит, что их невозможно постичь. С помощью различных наглядных экспериментов и природных явлений процесс познания мира электричества может стать по настоящему захватывающим.
Что такое сила Лоренца — определение, когда возникает, получение формулы
Известно, что электрический ток – это упорядоченное перемещение заряженных частиц. Установлено также, что во время движения в магнитном поле каждая из этих частиц подвергается действию силы.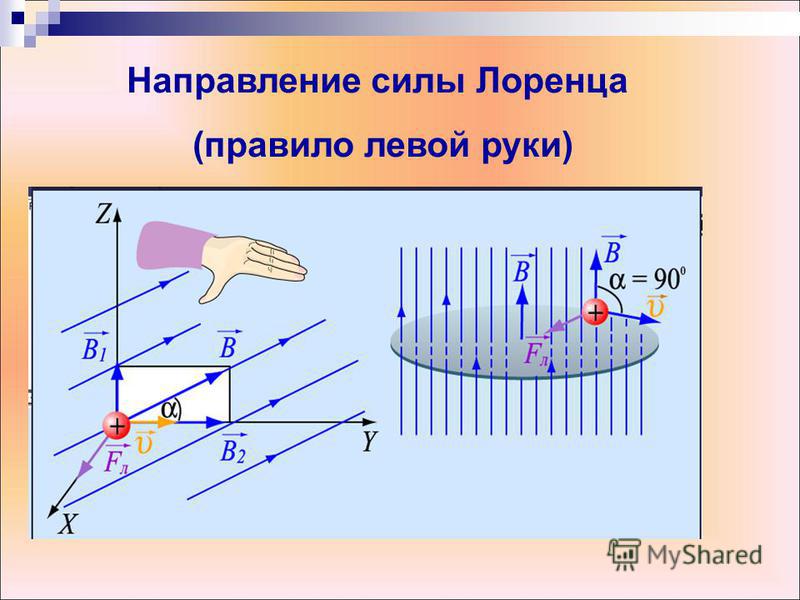 Для возникновении силы требуется, чтобы частица находилась в движении.
Для возникновении силы требуется, чтобы частица находилась в движении.
Сила Лоренца – это сила, которая действует на электрически заряженную частицу при её движении в магнитном поле. Её направление ортогонально плоскости, в которой лежат векторы скорости частицы и напряженности магнитного поля. Равнодействующая сил Лоренца и есть сила Ампера. Зная ее, можно вывести формулу для силы Лоренца.
Время, требуемое для прохождения частицей отрезка проводника,
, где
– длина отрезка,
– скорость частицы. Суммарный заряд, перенесенный за это время через поперечное сечение проводника,
. Подставив сюда значение времени из предыдущего равенства, имеем
(2)
В то же время
, где
– количество частиц, находящееся в рассматриваемом проводнике. При этом
, где
– заряд одной частицы. Подставив в формулу значение
из (2), можно получить:
Таким образом,
Используя (1), предыдущее выражение можно записать как
После сокращений и переносов появляется формула для вычисления силы Лоренца
С учетом того, что формула записана для модуля силы, ее необходимо записать так:
(3)
Поскольку
, то для вычисления модуля силы Лоренца неважно, куда направлена скорость, – по направлению силы тока или против, – и можно сказать, что
– это угол, образуемый векторами скорости частицы и магнитной индукции.
Запись формулы в векторном виде будет выглядеть следующим образом:
– это векторное произведение, результатом которого является вектор с модулем, равным
.
Исходя из формулы (3), можно сделать вывод о том, что сила Лоренца является максимальной в случае перпендикулярности направлений электрического тока и магнитного поля, то есть при
, и исчезать при их параллельности (
).
Необходимо помнить, что для получения правильного количественного ответа – например, при решении задач, – следует пользоваться единицами системы СИ, в которой магнитная индукция измеряется в теслах (1 Тл = 1 кг·с−2·А−1), сила – в ньютонах (1 Н = 1 кг·м/с2), сила тока – в амперах, заряд в кулонах (1 Кл = 1 А·с), длина – в метрах, скорость – в м/с.
Определение направления силы Лоренца с помощью правила левой руки
Поскольку в мире макрообъектов сила Лоренца проявляется как сила Ампера, для определения ее направления можно пользоваться правилом левой руки.
Нужно поставить левую руку так, чтобы раскрытая ладонь находилась перпендикулярно и навстречу линиям магнитного поля, четыре пальца следует вытянуть в направлении силы тока, тогда сила Лоренца будет направлена туда, куда указывает большой палец, который должен быть отогнут.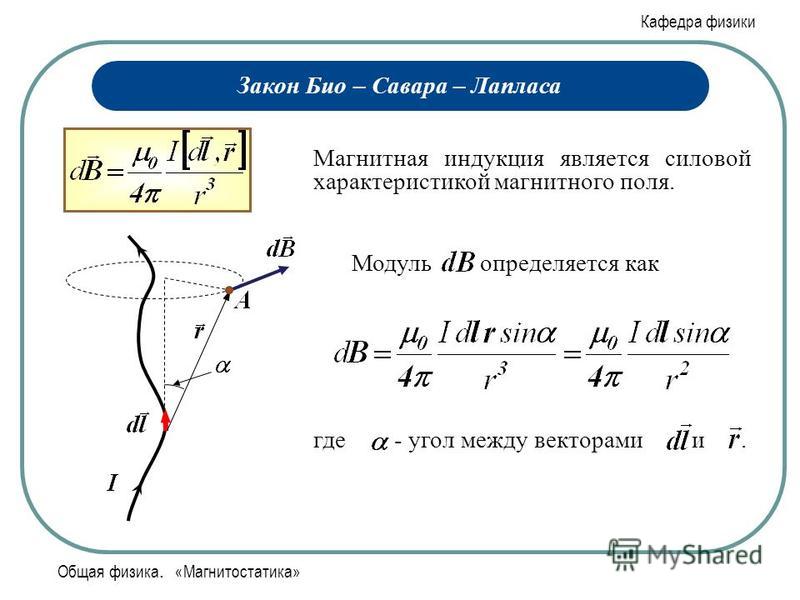
Движение заряженной частицы в магнитном поле
В простейшем случае, то есть при ортогональности векторов магнитной индукции и скорости частицы сила Лоренца, будучи перпендикулярной к вектору скорости, может менять только её направление. Величина скорости, следовательно, и энергия будут оставаться неизменными. Значит, сила Лоренца действует по аналогии с центростремительной силой в механике, и частица перемещается по окружности.
В соответствии со II законом Ньютона (
) можно определить радиус вращения частицы:
.
Необходимо обратить внимание, что с изменением удельного заряда частицы (
) меняется и радиус.
При этом период вращения T =
=
. Он не зависит от скорости, значит, взаимное положение частиц с различными скоростями будет неизменным.
В более сложном случае, когда угол между скоростью частицы и напряженностью магнитного поля является произвольным, она будет перемещаться по винтовой траектории – поступательно за счет составляющей скорости, направленной параллельно полю, и по окружности под влиянием ее перпендикулярной составляющей.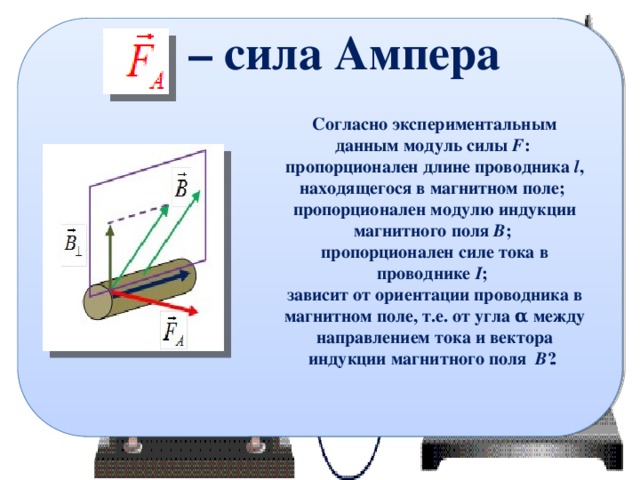
Применение силы Лоренца в технике
Кинескоп
Кинескоп, стоявший до недавнего времени, когда на смену ему пришел LCD-экран (плоский), в каждом телевизоре, не смог бы работать, не будь силы Лоренца. Для формирования на экране телевизионного растра из узкого потока электронов служат отклоняющие катушки, в которых создается линейно изменяющееся магнитное поле. Строчные катушки перемещают электронный луч слева направо и возвращают обратно, кадровые отвечают за вертикальное перемещение, двигая бегающий по горизонтали луч сверху вниз. Такой же принцип используется в осциллографах – приборах, служащих для изучения переменного электрического напряжения.
Масс-спектрограф
Масс-спектрограф – прибор, использующий зависимость радиуса вращения заряженной частицы от ее удельного заряда. Принцип его работы следующий:
Источник заряженных частиц, которые набирают скорость с помощью созданного искусственно электрического поля, с целью исключения влияния молекул воздуха помещается в вакуумную камеру. Частицы вылетают из источника и, пройдя по дуге окружности, ударяются в фотопластинку, оставляя на ней следы. В зависимости от удельного заряда меняется радиус траектории и, значит, точка удара. Этот радиус легко измерить, а зная его, можно вычислить массу частицы. С помощью масс-спектрографа, например, изучался состав лунного грунта.
Частицы вылетают из источника и, пройдя по дуге окружности, ударяются в фотопластинку, оставляя на ней следы. В зависимости от удельного заряда меняется радиус траектории и, значит, точка удара. Этот радиус легко измерить, а зная его, можно вычислить массу частицы. С помощью масс-спектрографа, например, изучался состав лунного грунта.
Циклотрон
Независимость периода, а значит, и частоты вращения заряженной частицы от её скорости в присутствии магнитного поля используется в приборе, называемом циклотроном и предназначенном для разгона частиц до высоких скоростей. Циклотрон – это два полых металлических полуцилиндров – дуанта (по форме каждый из них напоминает латинскую букву D), помещенных прямыми сторонами навстречу друг другу на небольшом расстоянии.
Дуанты помещаются в постоянное однородное магнитное поле, а между ними создается переменное электрическое поле, частота которого равна частоте вращения частицы, определяемой напряженностью магнитного поля и удельным зарядом. Попадая дважды за период вращения (при переходе из одного дуанта в другой) под воздействие электрического поля, частица каждый раз ускоряется, увеличивая при этом радиус траектории, и в определенный момент, набрав нужную скорость, вылетает из прибора через отверстие. Таким способом можно разогнать протон до энергии в 20 МэВ (мегаэлектронвольт).
Попадая дважды за период вращения (при переходе из одного дуанта в другой) под воздействие электрического поля, частица каждый раз ускоряется, увеличивая при этом радиус траектории, и в определенный момент, набрав нужную скорость, вылетает из прибора через отверстие. Таким способом можно разогнать протон до энергии в 20 МэВ (мегаэлектронвольт).
Магнетрон
Устройство, называемое магнетроном, который установлен в каждой микроволновой печи, – еще один представитель приборов, использующих силу Лоренца. Магнетрон служит для создания мощного СВЧ-поля, которое разогревает внутренний объем печи, куда помещается пища. Магниты, входящие в его состав, корректируют траекторию движения электронов внутри прибора.
Магнитное поле Земли
А в природе сила Лоренца играет крайне важную для человечества роль. Её наличие позволяет магнитному полю Земли защитить людей от смертоносного ионизирующего излучения космоса. Поле не дает возможности заряженным частицам бомбардировать поверхность планеты, заставляя их менять направление движения.
Траектории частиц под действием силы Лоренца
Заряженная частица дрейфует в однородном магнитном поле. (A) Нет возмущающей силы (B) В электрическом поле, E (C) С независимой силой, F (например, гравитация) (D) В неоднородном магнитном поле, grad H
Во многих случаях, представляющих практический интерес, движение в магнитном поле электрически заряженной частицы (например, электрона или иона в плазме) можно рассматривать как суперпозицию относительно быстрого кругового движения вокруг точки, которая дрейфует в направлении перпендикулярном электрическому и магнитным полям. Скорости дрейфа могут различаться в зависимости от их зарядового состояния, массы или температуры, что может привести к электрическим токам или химическому разделению.
Значение силы Лоренца
В то время как современные уравнения Максвелла описывают то, как электрически заряженные частицы и токи или движущиеся заряженные частицы вызывают электрические и магнитные поля, сила Лоренца дополняет эту картину, описывая силу, действующую на движущийся точечный заряд q в присутствии электромагнитных полей.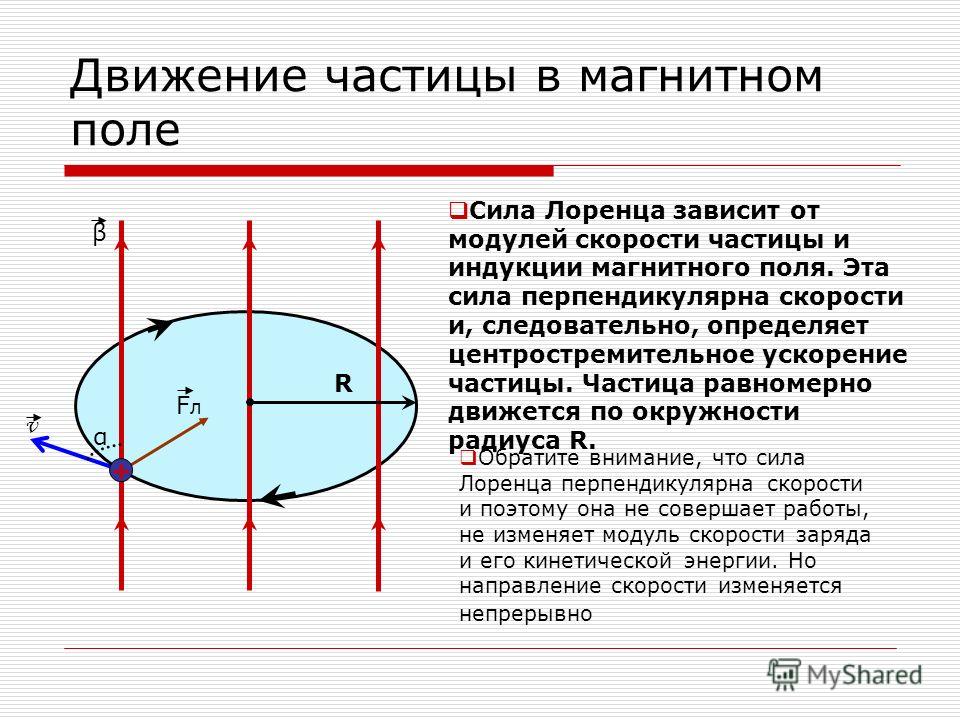 Хотя сила Лоренца описывает действие E и B на точечный заряд, но такие электромагнитные силы не являются всей картиной. Заряженные частицы, возможно, связаны с другими силами, особенно с гравитацией и ядерными силами. Таким образом, уравнения Максвелла не отделены от других физических законов, а связаны с ними через плотности заряда и тока. Реакция точечного заряда на закон Лоренца — это один из аспектов; генерация E и B токами и зарядами — другое.
Хотя сила Лоренца описывает действие E и B на точечный заряд, но такие электромагнитные силы не являются всей картиной. Заряженные частицы, возможно, связаны с другими силами, особенно с гравитацией и ядерными силами. Таким образом, уравнения Максвелла не отделены от других физических законов, а связаны с ними через плотности заряда и тока. Реакция точечного заряда на закон Лоренца — это один из аспектов; генерация E и B токами и зарядами — другое.
В реальных материалах сила Лоренца неадекватно описывает коллективное поведение заряженных частиц как в принципе, так и с точки зрения вычислений. Заряженные частицы в материальной среде не только реагируют на поля E и B, но и создают эти поля сами. Для определения временной и пространственной реакции зарядов необходимо решать сложные уравнения переноса, например, уравнение Больцмана, уравнение Фоккера — Планка или уравнения Навье — Стокса . Например, см. Магнитогидродинамику, гидродинамику, электрогидродинамику, сверхпроводимость, звездную эволюцию .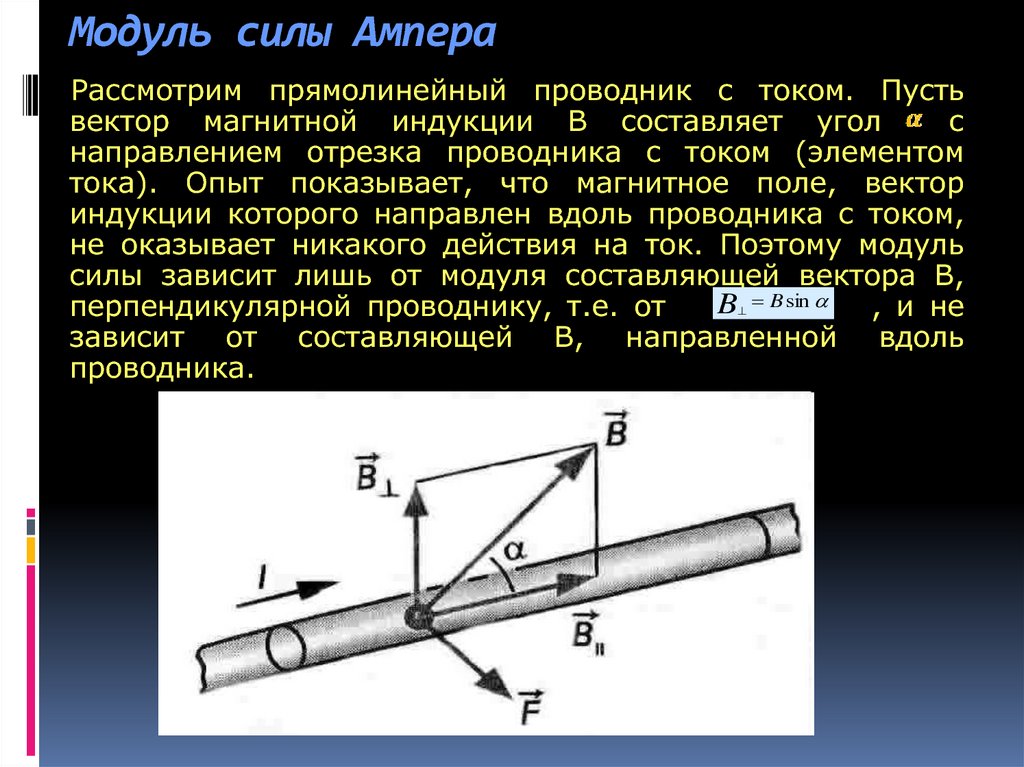 Разработан целый физический аппарат для решения этих вопросов. См., Например, формулы Грина — Кубо и функцию Грина (теория многих тел) .
Разработан целый физический аппарат для решения этих вопросов. См., Например, формулы Грина — Кубо и функцию Грина (теория многих тел) .
ЭДС
Магнитная сила (qv × B) в выражении силы Лоренца отвечает за двигательную электродвижущую силу (или двигательную ЭДС), явление, лежащее в основе действия многих электрических генераторов. Когда проводник перемещается через область магнитного поля, магнитное поле оказывает противоположно направленные силы на электроны и ядра в проводе, и это создает ЭДС. Термин «двигательная ЭДС» применяется к этому явлению, поскольку ЭДС возникает из-за движения провода.
В других электрических генераторах магниты движутся, а проводники — нет. В этом случае ЭДС возникает из-за электрической силы (qE) в уравнении для силы Лоренца. Рассматриваемое электрическое поле создается изменяющимся магнитным полем, приводящим к возникновению индуцированной ЭДС, как описано уравнением Максвелла — Фарадея.
Обе эти ЭДС, несмотря на их явно различное происхождение, описываются одним и тем же уравнением, а именно ЭДС — это скорость изменения магнитного потока через провод.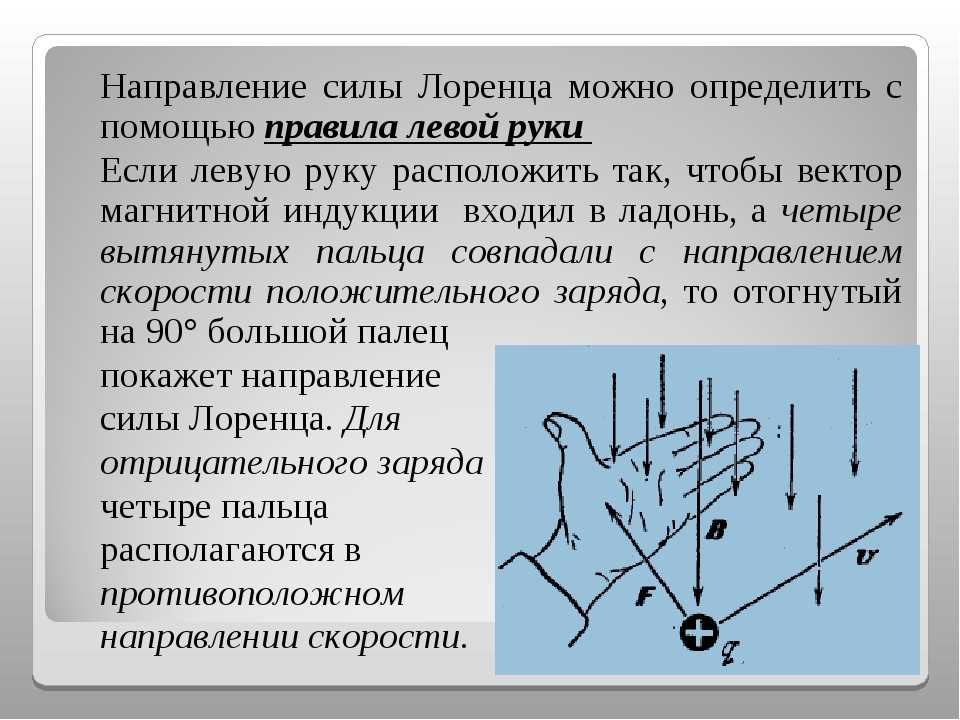 Это закон электромагнитной индукции Фарадея, см. Ниже . Специальная теория относительности Эйнштейна была частично мотивирована желанием лучше понять эту связь между двумя эффектами. Фактически, электрическое и магнитное поля представляют собой разные грани единого электромагнитного поля, и при переходе от одной инерциальной системы отсчета к другой часть электромагнитного векторного поля E можно полностью или частично заменить на B или наоборот.
Это закон электромагнитной индукции Фарадея, см. Ниже . Специальная теория относительности Эйнштейна была частично мотивирована желанием лучше понять эту связь между двумя эффектами. Фактически, электрическое и магнитное поля представляют собой разные грани единого электромагнитного поля, и при переходе от одной инерциальной системы отсчета к другой часть электромагнитного векторного поля E можно полностью или частично заменить на B или наоборот.
Единицы измерения силы Лоренца
Как и большинство других физических величин, которые действуют на тело и изменяют его состояние, она измеряется в ньютонах и обозначается буквой Н.
Понятие напряженности электрического поля
Электромагнитное поле на самом деле состоит из двух половин – электрической и магнитной. Они точно близнецы, у которых все одинаково, но вот характер разный. А если приглядеться, то во внешности можно заметить небольшие различия.
То же самое касается и силовых полей. Электрическое поле тоже обладает напряженностью – векторной величиной, которая является силовой характеристикой. Она воздействует на частицы, которые в неподвижности находятся в нем. Само по себе оно не является силой Лоренца, ее просто нужно принимать во внимание, когда вычисляется воздействие на частицу в условиях наличия электрического и магнитного полей.
Она воздействует на частицы, которые в неподвижности находятся в нем. Само по себе оно не является силой Лоренца, ее просто нужно принимать во внимание, когда вычисляется воздействие на частицу в условиях наличия электрического и магнитного полей.
Напряженность электрического поля
Напряженность электрического поля воздействует только на неподвижный заряд и определяется по формуле:
Единицей измерения является Н/Кл или В/м.
Модуль силы Ампера вычисляется по формуле
где α – угол между векторами и .
Два параллельных тока одинакового направления притягиваются друг к другу с силой
(2.10)
На рисунке 2.15 приведен пример взаимодействия параллельных токов одинакового направления.
Рис. 2.15
Если
токи имеют противоположные направления,
то, используя правило левой руки, можно
показать, что между ними действует сила
отталкивания, определяемая формулой
(2. 10).
10).
II. 12. Каково действие магнитного поля (силы Лоренца) и электромагнитного с магнитным на движущийся заряд?
Сила, действующая со стороны магнитного поля на электрический заряд Q, движущийся в этом поле со скоростью , называется силой Лоренца и выражается формулой
(2.11)
где – индукция магнитного поля, в котором заряд движется.
Направление
силы Лоренца определяется с помощью
правила левой руки: если ладонь левой
руки расположить так, чтобы в нее входил
вектор
,
а четыре вытянутых пальца направить
вдоль вектора скорости положительного
заряда, то отогнутый под углом 900 большой палец покажет направление силы,
действующей на положительный заряд. На
рис. 2.16 показана взаимная ориентация
векторов
,
и
для положительного заряда. На отрицательный
заряд сила действует в противоположном
направлении. Модуль силы Лоренца равен
Модуль силы Лоренца равен
где α – угол между и .
Рис. 2.16
Магнитное поле не действует на покоящийся электрический заряд. В этом существенное отличие магнитного поля от электрического. Магнитное поле действует только на движущиеся в нем заряды.
Если на движущийся электрический заряд помимо магнитного поля с индукцией действует и электрическое поле с напряженностью , то результирующая сила , приложенная к заряду, равна векторной сумме сил – силы, действующей со стороны электрического поля, и силы Лоренца:
(2.12)
Это выражение называется формулой Лоренца. Скорость в этой формуле есть скорость заряда относительно магнитного поля.
II. 13. Каково движение заряженных частиц в магнитном поле под действием силы Лоренца?
а)
Если заряженная частица массой m
влетает параллельно силовым линиям,
то на нее магнитное поле не действует,
сила Лоренца Fл=0. Траектория ее движения есть прямая
линия (рис. 2.17).
Траектория ее движения есть прямая
линия (рис. 2.17).
Рис. 2.17
б) Если заряженная частица движется в магнитном поле со скоростью , перпендикулярной вектору , то сила Лоренца (рис. 2.18) постоянна по модулю и нормальна к траектории частицы. Согласно 2-му закону Ньютона, эта сила создает центростремительное ускорение. Отсюда следует, что частица будет двигаться по окружности, радиус r которой определяется из условия qVB = mV2/r, откуда
Рис. 2.18
Период вращения частицы, т. е. время Т, за которое она совершит один полный оборот,
Или с учетом r
в)
Если скорость
заряженной частицы направлена под углом
α к вектору
(рис. 2.19), то ее движение можно представить
в виде суперпозиции:
2.19), то ее движение можно представить
в виде суперпозиции:
1) равномерного прямолинейного движения вдоль поля со скоростью
= соs α;
2) равномерного движения со скоростью = sin α по окружности в плоскости, перпендикулярной полю. Радиус окружности определяется формулой
В результате сложения обоих движений возникает движение по спирали, ось которого параллельна магнитному полю.
Рис. 2.19
Шаг винтовой линии
Подставив сюда Т, получим выражение,
Направление, в котором закручивается спираль, зависит от знака заряда частицы.
Если
скорость
заряженной частицы составляет угол α
с направлением вектора неоднородного
магнитного поля, индукция которого
возрастает в направлении движения
частицы, то r
и h
уменьшаются с ростом
. На этом основана фокусировка заряженных
частиц в магнитном поле.
На этом основана фокусировка заряженных
частиц в магнитном поле.
Формула силы лоренца центростремительного ускорения. Сила лоренца. Определение силы Лоренца
«Физика — 11 класс»
Магнитное поле действует с силой на движущиеся заряженные частицы, в то числе и на проводники с током.
Какова же сила, действующая на одну частицу?
1.
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца в честь великого голландского физика X. Лоренца, создавшего электронную теорию строения вещества.
Силу Лоренца можно найти с помощью закона Ампера.
Модуль силы Лоренца равен отношению модуля силы F, действующей на участок проводника длиной Δl, к числу N заряженных частиц, упорядоченно движущихся в этом участке проводника:
Так как сила (сила Ампера), действующая на участок проводника со стороны магнитного поля
равна F = | I | BΔl sin α ,
а сила тока в проводнике равна I = qnvS
где
q — заряд частиц
n — концентрация частиц (т. е. число зарядов в единице объема)
е. число зарядов в единице объема)
v — скорость движения частиц
S — поперечное сечение проводника.
Тогда получаем:
На каждый движущийся заряд со стороны магнитного поля действует сила Лоренца , равная:
где α — угол между вектором скорости и вектором магнитной индукции.
Сила Лоренца перпендикулярна векторам и .
2.
Направление силы Лоренца
Направление силы Лоренца определяется с помощью того же правила левой руки , что и направление силы Ампера:
Если левую руку расположить так, чтобы составляющая магнитной индукции, перпендикулярная скорости заряда, входила в ладонь, а четыре вытянутых пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90° большой палец укажет направление действующей на заряд силы Лоренца F л
3.
Если в пространстве, где движется заряженная частица, существует одновременно и электрическое поле, и магнитное поле, то суммарная сила, действующая на заряд, равна:
= эл + л
где сила, с которой электрическое поле действует на заряд q, равна F эл = q.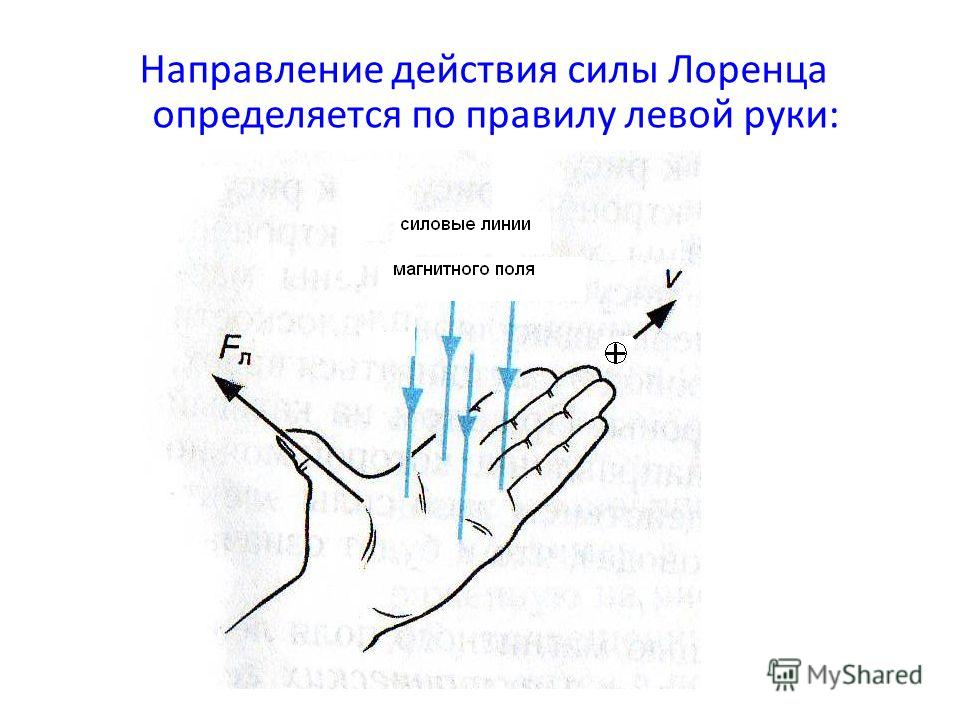
4.
Cила Лоренца не совершает работы , т.к. она перпендикулярна вектору скорости частицы.
Значит сила Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль ее скорости.
Под действием силы Лоренца меняется лишь направление скорости частицы.
5.
Движение заряженной частицы в однородном магнитном поле
Есть однородное магнитное поле , направленное перпендикулярно к начальной скорости частицы .
Сила Лоренца зависит от модулей векторов скорости частицы и индукции магнитного поля.
Магнитное поле не меняет модуль скорости движущейся частицы, значит остается неизменным и модуль силы Лоренца.
Сила Лоренца перпендикулярна скорости и, следовательно, определяет центростремительное ускорение частицы.
Неизменность по модулю центростремительного ускорения частицы, движущейся с постоянной по модулю скоростью, означает, что
В однородном магнитном поле заряженная частица равномерно движется по окружности радиусом r .
Согласно второму закону Ньютона
Тогда радиус окружности по которой движется частица, равен:
Время, за которое частица делает полный оборот (период обращения), равно:
6.
Использование действия магнитного поля на движущийся заряд.
Действие магнитного поля на движущийся заряд используют в телевизионных трубках-кинескопах, в которых летящие к экрану электроны отклоняются с помощью магнитного поля, создаваемого особыми катушками.
Сила Лоренца используется в циклотроне — ускорителе заряженных частиц для получения частиц с большими энергиями.
На действии магнитного поля основано также и устройство масс-спектрографов, позволяющих точно определять массы частиц..
Нигде еще школьный курс физики так сильно не перекликается с большой наукой, как в электродинамике. В частности, ее краеугольный камень – воздействие на заряженные частицы со стороны электромагнитного поля, нашло широкое применение в электротехнике.
Формула силы Лоренца
Формула описывает взаимосвязь магнитного поля и основных характеристик движущегося заряда.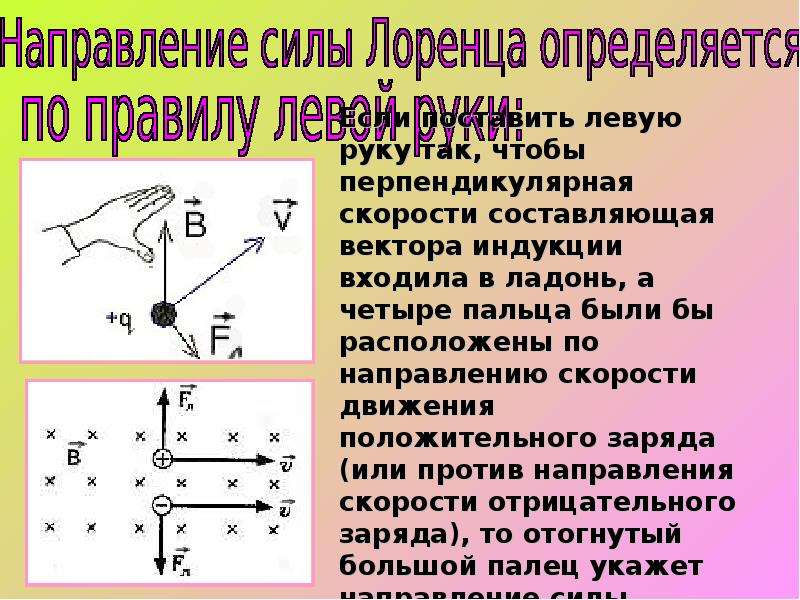 Но сперва нужно разобраться, что же оно собой представляет.
Но сперва нужно разобраться, что же оно собой представляет.
Определение и формула силы Лоренца
В школе очень часто показывают опыт с магнитом и железными опилками на бумажном листе. Если расположить его под бумагой и слегка потрясти, то опилки выстроятся по линиям, которые принято называть линиями магнитной напряженности. Говоря простыми словами, это силовое поле магнита, которое окружает его подобно кокону. Оно замкнуто само на себя, то есть не имеет ни начала, ни конца. Это векторная величина, которая направлена от южного полюса магнита к северному.
Если бы в него влетела заряженная частица, то поле воздействовало бы на него очень любопытным образом. Она бы не затормозилась и не ускорилась, а всего лишь отклонилась в сторону. Чем она быстрее и чем сильнее поле, тем больше на нее действует эта сила. Ее назвали силой Лоренца в честь ученого-физика, впервые открывшего это свойство магнитного поля.
Вычисляют ее по специальной формуле:
здесь q – величина заряда в Кулонах, v – скорость, с которой движется заряд, в м/с, а B – индукция магнитного поля в единице измерения Тл (Тесла).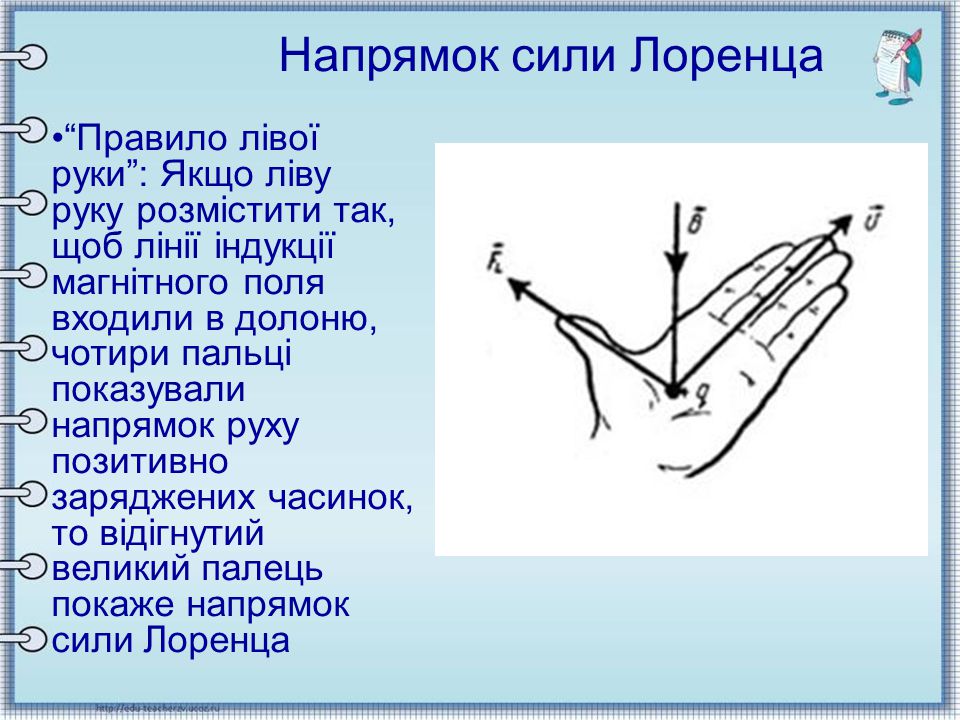
Направление силы Лоренца
Ученые заметили, что есть определенная закономерность между тем, как частица влетает в магнитное поле и тем, куда оно ее отклоняет. Чтобы ее было легче запомнить, они разработали специальное мнемоническое правило. Для его запоминания нужно совсем немного усилий, ведь в нем используется то, что всегда под рукой – рука. Точнее, левая ладонь, в честь чего оно носит название правила левой руки.
Итак, ладонь должна быть раскрыта, четыре пальца смотрят вперед, большой палец оттопырен в сторону. Угол между ними составляет 900. Теперь необходимо представить, что магнитный поток представляет собой стрелу, которая впивается в ладонь с внутренней стороны и выходит с тыльной. Пальцы при этом смотрят туда же, куда летит воображаемая частица. В таком случае большой палец покажет, куда она отклонится.
Интересно!
Важно отметить, что правило левой руки действует только для частиц со знаком «плюс». Чтобы узнать, куда отклонится отрицательный заряд, нужно четыре пальца направить в сторону, откуда летит частица.
Все остальные манипуляции остаются прежними.
Следствия свойств силы Лоренца
Тело влетает в магнитном поле под каким-то определённым углом. Интуитивно понятно, что его величина имеет какое-то значение на характер воздействия на него поля, здесь нужно математическое выражение, чтобы стало понятнее. Следует знать, что как сила, так и скорость являются векторными величинами, то есть имеют направление. То же самое относится и к линиям магнитной напряженности. Тогда формулу можно записать следующим образом:
sin α здесь – это угол между двумя векторными величинами: скоростью и потоком магнитного поля.
Как известно, синус нулевого угла также равен нулю. Получается, что если траектория движения частицы проходит вдоль силовых линий магнитного поля, то она никуда не отклоняется.
В однородном магнитном поле силовые линии имеют одинаковое и постоянное расстояние друг от друга. Теперь представим, что в таком поле перпендикулярно этим линиям движется частица. В этом случае сила Лоуренса заставит двигаться ее по окружности в плоскости, перпендикулярной силовым линиям. Чтобы найти радиус этой окружности, нужно знать массу частицы:
В этом случае сила Лоуренса заставит двигаться ее по окружности в плоскости, перпендикулярной силовым линиям. Чтобы найти радиус этой окружности, нужно знать массу частицы:
Значение заряда не случайно взято как модуль. Это означает, что неважно, отрицательная или положительная частица входит в магнитное поле: радиус кривизны будет одинаков. Изменится только направление, в котором она полетит.
Во всех остальных случаях, когда заряд имеет определенный угол α с магнитным полем, он будет двигаться по траектории, напоминающей спираль с постоянным радиусом R и шагом h. Его можно найти по формуле:
Еще одним следствием свойств этого явления является тот факт, что она не совершает никакой работы. То есть она не отдает и не забирает энергию у частицы, а лишь меняет направление ее движения.
Самая яркая иллюстрация этого эффекта взаимодействия магнитного поля и заряженных частиц – это северное сияние. Магнитное поле, окружающее нашу планету, отклоняет заряженные частицы, прилетающие от Солнца. Но так как оно слабее всего на магнитных полюсах Земли, то туда проникают электрически заряженные частицы, вызывая свечение атмосферы.
Но так как оно слабее всего на магнитных полюсах Земли, то туда проникают электрически заряженные частицы, вызывая свечение атмосферы.
Центростремительное ускорение, которое придается частицам, используется в электрических машинах – электродвигателях. Хотя уместнее здесь говорить о силе Ампера – частном проявлении силы Лоуренса, которая воздействует на проводник.
Принцип действия ускорителей элементарных частиц также основан на этом свойстве электромагнитного поля. Сверхпроводящие электромагниты отклоняют частицы от прямолинейного движения, заставляя их двигаться по кругу.
Самое любопытное заключается в том, что сила Лоренца не подчиняется третьему закону Ньютона, который гласит, что всякому действию есть свое противодействие. Связано это с тем, что Исаак Ньютон верил, что всякое взаимодействие на любом расстоянии происходит мгновенно, однако это не так. На самом деле оно происходит с помощью полей. К счастью, конфуза удалось избежать, так как физикам удалось переработать третий закон в закон сохранения импульса, который выполняется в том числе и для эффекта Лоуренса.
Формула силы Лоренца при наличии магнитного и электрического полей
Магнитное поле имеется не только у постоянных магнитов, но и у любого проводника электричества. Только в данном случае помимо магнитной составляющей, в ней присутствует еще и электрическая. Однако даже в этом электромагнитном поле эффект Лоуренса продолжает свое воздействие и определяется по формуле:
где v – скорость электрически заряженной частицы, q – ее заряд, B и E – напряженности магнитного и электрических полей поля.
Единицы измерения силы Лоренца
Как и большинство других физических величин, которые действуют на тело и изменяют его состояние, она измеряется в ньютонах и обозначается буквой Н.
Понятие напряженности электрического поля
Электромагнитное поле на самом деле состоит из двух половин – электрической и магнитной. Они точно близнецы, у которых все одинаково, но вот характер разный. А если приглядеться, то во внешности можно заметить небольшие различия.
То же самое касается и силовых полей. Электрическое поле тоже обладает напряженностью – векторной величиной, которая является силовой характеристикой. Она воздействует на частицы, которые в неподвижности находятся в нем. Само по себе оно не является силой Лоренца, ее просто нужно принимать во внимание, когда вычисляется воздействие на частицу в условиях наличия электрического и магнитного полей.
Электрическое поле тоже обладает напряженностью – векторной величиной, которая является силовой характеристикой. Она воздействует на частицы, которые в неподвижности находятся в нем. Само по себе оно не является силой Лоренца, ее просто нужно принимать во внимание, когда вычисляется воздействие на частицу в условиях наличия электрического и магнитного полей.
Напряженность электрического поля
Напряженность электрического поля воздействует только на неподвижный заряд и определяется по формуле:
Единицей измерения является Н/Кл или В/м.
Примеры задачи
Задача 1
На заряд в 0,005 Кл, который движется в магнитном поле с индукцией 0,3 Тл, действует сила Лоренца. Вычислить ее, если скорость заряда 200 м/с, а движется он под углом 450 к линиям магнитной индукции.
Задача 2
Определить скорость тела, имеющего заряд и которое движется в магнитном поле с индукцией 2 Тл под углом 900. Величина, с которой поле воздействует на тело, равна 32 Н, заряд тела – 5 × 10-3 Кл.
Задача 3
Электрон движется в однородном магнитном поле под углом 900 ее силовым линиям. Величина, с которой поле воздействует на электрон, равна 5 × 10-13 Н. Величина магнитной индукции равна 0,05 Тл. Определить ускорение электрона.
aц=v2R=6×10726,8×10-3=5×1017мс2
Электродинамика оперирует такими понятиями, которым трудно подобрать аналогию в обычном мире. Но это совсем не значит, что их невозможно постичь. С помощью различных наглядных экспериментов и природных явлений процесс познания мира электричества может стать по настоящему захватывающим.
Определение силы Лоренца
Сила Лоренца представляет собой комбинацию магнитной и электрической силы на точечном заряде, который вызван электромагнитными полями. Или другими словами, сила Лоренца – это сила, действующая на всякую заряженную частицу, которая падает в магнитном поле с определенной скоростью. Ее величина зависит от величины магнитной индукции В , электрического заряда частицы q и скорости, с которой частица падает в поле – V . О том какая формула расчета силы Лоренца, а также ее практическое значение в физике читайте далее.
О том какая формула расчета силы Лоренца, а также ее практическое значение в физике читайте далее.
Немного истории
Первые попытки описать электромагнитную силу были сделаны еще в XVIII веке. Ученые Генри Кавендиш и Тобиас Майер высказали предположение, что сила на магнитных полюсах и электрически заряженных объектах подчиняется закону обратных квадратов. Однако экспериментальное доказательство этого факта не было полным и убедительным. Только в 1784 году Шарль Августин де Кулон при помощи своего торсионного баланса смог окончательно доказать это предположение.
В 1820 году физиком Эрстедом был открыт факт, что на магнитную стрелку компаса действует ток вольта, а Андре-Мари Ампер в этом же году смог разработать формулу угловой зависимости между двумя токовыми элементами. По сути, эти открытия стали фундаментом современной концепции электрических и магнитных полей. Сама же концепция получила свое дальнейшее развитие в теориях Майкла Фарадея, особенно в его представлении о силовых линиях.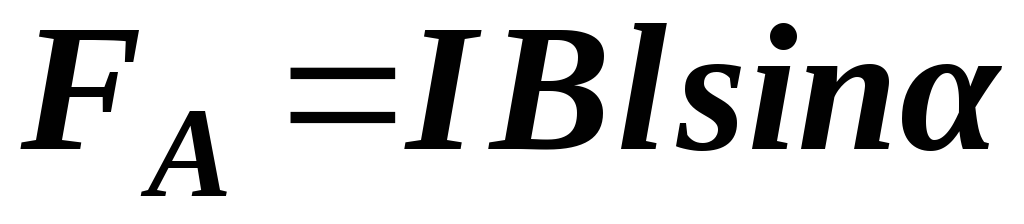 Лорд Кельвин и Джеймс Максвелл дополнили теории Фарадея подробным математическим описанием. В частности Максвеллом было создано так званное, «уравнение поля Максвелла» – представляющее собой систему дифференциальных и интегральных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах.
Лорд Кельвин и Джеймс Максвелл дополнили теории Фарадея подробным математическим описанием. В частности Максвеллом было создано так званное, «уравнение поля Максвелла» – представляющее собой систему дифференциальных и интегральных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах.
Джей Джей Томпсон был первым физиком, кто попытался вывести из уравнения поля Максвелла электромагнитную силу, которые действует на движущийся заряженный объект. В 1881 году он опубликовал свою формулу F = q/2 v x B. Но из-за некоторых просчетов и неполного описания тока смещения она оказалась не совсем правильной.
И вот, наконец, в 1895 году голландский ученый Хендрик Лоренц вывел правильную формулу, которая используется и поныне, а также носит его имя, как и та сила, что действует на летящую частицу в магнитном поле, отныне называется «силой Лоренца».
Формула силы Лоренца
Формула для расчета силы Лоренца выглядит следующим образом:
Где q – электрический заряд частицы, V – ее скорость, а B – величина магнитной индукции магнитного поля.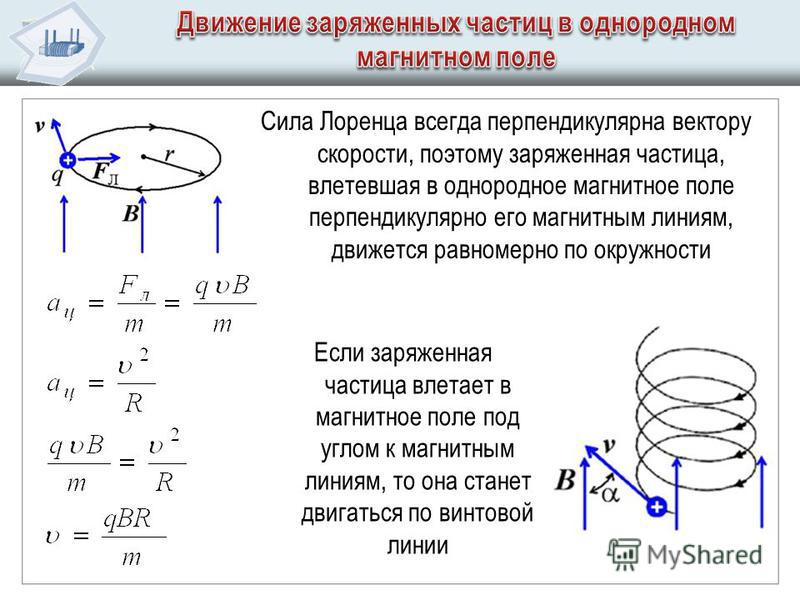
При этом поле B выступает в качестве силы, перпендикулярной к направлению вектора скорости V нагрузок и направлению вектора B. Это можно проиллюстрировать на диаграмме:
Правило левой руки позволяет физикам определять направление и возврат вектора магнитной (электродинамической) энергии. Представьте себе, что наша левая рука расположена таким образом, что линии магнитного поля направлены перпендикулярно внутренней поверхности руки (так, что они проникают внутрь руки), а все пальцы за исключением большого указывают на направление протекания положительного тока, отклоненный большой палец указывает на направление электродинамической силы, действующий на положительный заряд, помещенный в это поле.
Вот так это будет выглядеть схематически.
Есть также и второй способ определения направления электромагнитной силы. Он заключается в расположении большого, указательного и среднего пальцев под прямым углом. В этом случае указательный палец будет показывать направление линий магнитного поля, средний – направление движение тока и большой – направление электродинамической силы.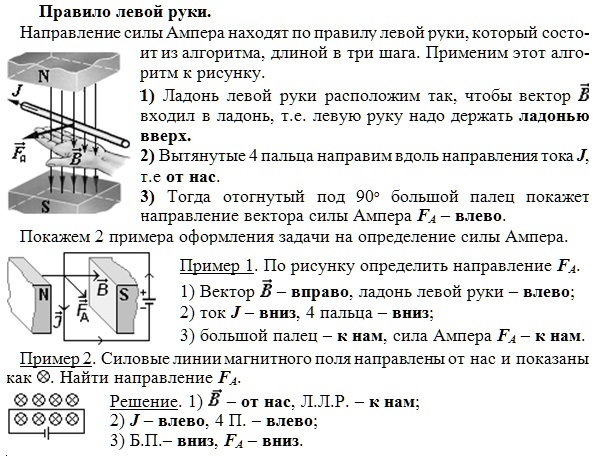
Применение силы Лоренца
Сила Лоренца и ее расчеты имеет свое практическое применение при создании как специальных научных приборов – масс-спектрометров, служащих для идентификации атомов и молекул, так и создании многих других устройств самого разнообразного применения. Среди устройств есть и электродвигатели, и громкоговорители, и рельсовые пистолеты.
 Гидравлический пресс. Золотое правило механики
Гидравлический пресс. Золотое правило механики Свойства идеального газа. Основное уравнение МКТ. Температура. Уравнение состояния идеального газа. Уравнение Менделеева-Клайперона. Газовые законы — изотерма, изобара, изохора
Свойства идеального газа. Основное уравнение МКТ. Температура. Уравнение состояния идеального газа. Уравнение Менделеева-Клайперона. Газовые законы — изотерма, изобара, изохора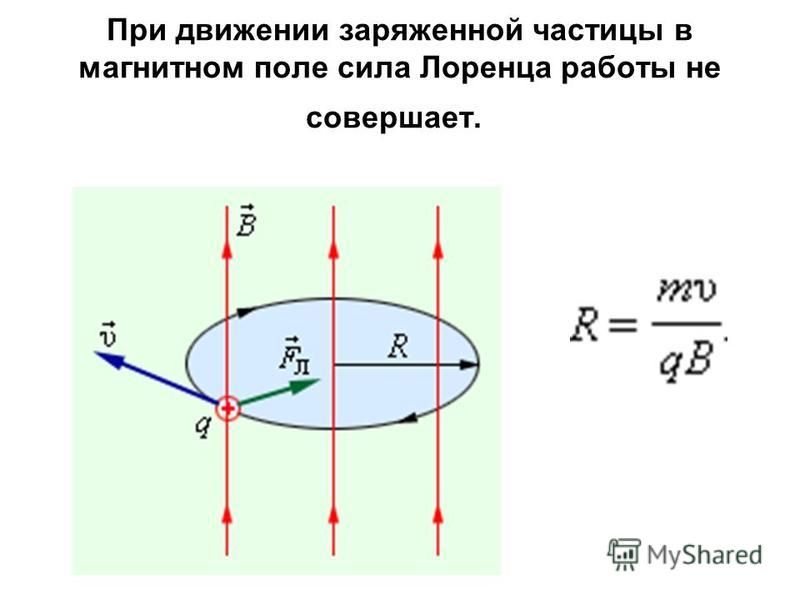 Электрические цепи — последовательное и параллельное соединение. Правила Кирхгофа.
Электрические цепи — последовательное и параллельное соединение. Правила Кирхгофа. Зависимость массы от скорости. Основной закон релятивистский динамики…
Зависимость массы от скорости. Основной закон релятивистский динамики…Силой Лоренца называют силу, которая действует со стороны электромагнитного поля на движущийся электрический заряд. Весьма нередко силой Лоренца называют лишь магнитную составляющую этого поля. Формула для определения:
F = q(E+vB),
где q — заряд частицы; Е — напряжённость электрического поля; B — магнитная индукция поля; v — скорость частицы.
Сила Лоренца очень похожа по своему принципу на , разница заключается в том, что последняя действует на весь проводник, который в целом электрически нейтральный, а сила Лоренца описывает влияние электромагнитного поля лишь на единичный движущийся заряд.
Она характеризуется тем, что не изменяет скорость перемещения зарядов, а лишь воздействует на вектор скорости, то есть способна изменять направление движения заряженных частиц.
В природе сила Лоренца позволяет защищать Землю от воздействия космической радиации. Под её воздействием падающие на планету заряженные частицы отклоняются от прямой траектории благодаря присутствию магнитного поля Земли, вызывая полярные сияния.
В технике сила Лоренца используется очень часто: во всех двигателях и генераторах именно она приводит во вращение ротор под действием электромагнитного поля статора.
Таким образом, в любых электромоторах и электроприводах основным видом силы является Лоренцева. Кроме того, она применяется в ускорителях заряженных частиц, а также в электронных пушках, которые раньше устанавливались в ламповых телевизорах. В кинескопе испускаемые пушкой электроны отклоняются под влиянием электромагнитного поля, что происходит при участии Лоренцевой силы.
Кроме того, эта сила используется в масс-спектрометрии и масс-электрографии для приборов, способных сортировать заряженные частицы в зависимости от их удельного заряда (отношение заряда к массе частицы). Это позволяет с высокой точностью определять массу частиц. Также находит применение в других КИП, например, в бесконтактном способе измерения расхода электропроводящих жидких сред (расходомеры). Это очень актуально, если жидкая среда обладает очень высокой температурой (расплав металлов, стекла и др.).
Контрольная в устной форме по физике для 8, 9, 11 классов
Пробники ОГЭ ↓
Математика, Физика, Информатика, Химия, Русский, Обществознание, Литература, История, Иностранные языки, География, Биология
21 августа 2020
В закладки
Обсудить
Жалоба
Пробные работы ОГЭ по физике
Pеклaмa Бесплатные уроки для подготовки к ОГЭ каждый день от MAXIMUM Education →
Готовим к ЕГЭ бесплатно и проводим более 300 уроков в месяц по всем предметам. Начни учиться прямо сейчас!
Начни учиться прямо сейчас!
Перечень контрольных вопросов для промежуточной аттестации в устной форме по физике.
kr-ust-fiz.docx
8 класс
1. Какие существуют виды энергии?
2. От чего зависит температура тела?
3. Какие явления называют тепловыми?
4. Что называют тепловым движением?
5. Формула кинетической энергии
6. Формула потенциальной энергии
7. Что есть внутренняя энергия тела?
8. От чего зависит внутренняя энергия тела?
9. От чего не зависит внутренняя энергия?
10. Какие есть способы изменения внутренней энергии?
11. Что такое теплопередача?
12. Что такое теплопроводность?
13. Привести примеры большей / меньшей теплопроводности
14. Что такое конвекция?
15. Какова особенность излучения?
16. Что такое количество теплоты и в чём оно измеряется?
17. Что такое удельная теплоёмкость? Какая уд. теплоёмкость у воды, эфира, стали?
18. Назвать формулу количества теплоты нагревания/охлаждения
19. Формула уд. теплоты сгорания топлива? Какова УТС топлива если взято 15 кг антрацита
Формула уд. теплоты сгорания топлива? Какова УТС топлива если взято 15 кг антрацита
20. Закон сохранения и превращения энергии
21. Что такое плавление, кристаллизация вещества?
22. Формула удельной теплоты плавления. Выразить из неё массу и УТ плавления
23. УТ плавления льда / ртути / спирта
24. Что такое парообразование и испарение / конденсация?
25. Что такое кипение и как называется температура, при которой жидкость кипит?
26. Температура кипения воды, железа, водорода, эфира, ртути
27. Что такое влажность воздуха и по какой формуле она вычисляется?
28. Что такое точка росы?
29. Какими приборами измеряется относительная влажность воздуха?
30. Что показывает УТ парообразования и конденсации? По какой формуле она рассчитывается?
31. Что такое тепловой двигатель?
32. По какой формуле вычисляется КПД теплового двигателя?
33. Из скольких тактов состоит цикл двигателя? Как они называются?
9 класс
1. Что такое материальная точка?
2. Что такое поступательное движение?
Что такое поступательное движение?
3. Что образует систему отсчёта?
4. Что такое перемещение тела?
5. Что такое скорость равномерного прямолинейного движения?
6. Назовите формулу по вопросу №5
7. Что такое ускорение тела и по какой формуле оно измеряется?
8. Что такое мгновенная скорость?
9. Формула для расчёта проекции вектора перемещения при равноускоренном движении
10. В чём проявляется относительность движения?
11. Какие системы мира были открыты и кем?
12. Назовите первый закон Ньютона
13. Что называется инерциальными / неинерциальными системами отсчёта?
14. Словесная формулировка второго закона Ньютона
15. Математическая запись второго закона Ньютона
16. Словесная и математическая формулировки третьего закона Ньютона
17. Что называется свободным падением тел?
18. Что такое ускорение свободного падения?
19. Закон всемирного тяготения. Чему равна гравитационная постоянная?
20. Что такое центростремительное ускорение?
21. Формула центростремительного ускорения
Формула центростремительного ускорения
22. Модуль вектора силы, под действием которой тело движется по окружности с постоянной скоростью по модулю
23. Формула для расчёта первой круговой скорости
24. Что такое импульс тела?
25. По какой формуле рассчитывается импульс тела?
26. Закон сохранения импульса
27. Привести примеры реактивного движения
28. Закон сохранения механической энергии
29. Что такое механические колебания?
30. Какие колебания называются свободными?
31. Что такое колебательные системы
32. Что называют маятником?
33. Какие величины характеризуют колебательное движение?
34. Что есть частота / период колебаний?
11 класс
1. В каком пространстве возникает магнитное поле?
2. Перечислите основные свойства МП, установленные экспериментально?
3. Что принимается за направление вектора магнитной индукции?
4. Куда направлена положительная нормаль вектора магнитной индукции?
5. Назовите правило буравчика
6. Что называют линиями магнитной индукции?
Что называют линиями магнитной индукции?
7. Кем был установлен закон, определяющий силу, действующую на отдельный небольшой участок проводника?
8. Сформулируйте закон Ампера
9. В чем измеряется модуль вектора магнитной индукции?
10. Что называют силой Лоренца?
11. Формула силы Лоренца
12. Магнитные свойства вещества
13. Что такое магнитный поток и в чём он измеряется. Назовите формулу
14. Правило Ленца
15. Закон ЭМИ
16. Что такое самоиндукция?
17. Что такое индуктивность?
18. Что такое колебания?
19. Что называют периодическими / свободными / вынужденными колебаниями?
20. Что есть математический маятник?
21. При каких условиях математический маятник будет свободно кол:)ся?
22. Что называется гармоническими колебаниями?
23. Что называют фазой колебаний?
24. Что такое резонанс?
25. Назовите формулу Томсона
26. Что такое ёмкостное сопротивление?
27. Что такое индуктивное сопротивление?
28. Строение трансформатора
29. Коэффициент трансформации – это …
Коэффициент трансформации – это …
30. Что такое волна? Виды волн
31. Что такое длина волны?
32. Назовите уравнение гармонической бегущей волны
33. Что такое плоская / линейная / сферическая волна?
34. Что такое акустика и акустические колебания?
35. Скорость звука равна …
Новости вузов | Вчера, 23:45
Минобрнауки России установило единые сроки приёма в вузы для поступающих на очное и заочное отделения, пишет ТАСС со ссылкой на пресс-службу министерства.
Пробные работы ЕГЭ по русскому языку | Вчера, 17:57
Практика.
Русский | Вчера, 14:29
По предмету «Русский язык».
По какой формуле определяют силу лоренца. Сила лоренца и ее воздействие на электрический заряд
Почему одних ученых история вносит на свои страницы золотыми буквами, а некоторых стирает бесследно? Каждый пришедший в науку обязан оставить в ней свой след. Именно по величине и глубине этого следа судит история.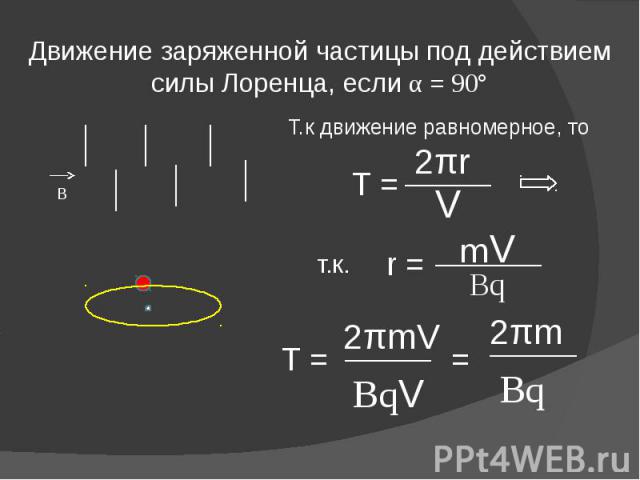 Так, Ампер и Лоренц внесли неоценимый вклад в развитие физики, что дало возможность не только развивать научные теории, но получило весомую практическую ценность. Как появился телеграф? Что такое электромагниты? На все эти вопросы даст ответ сегодняшний урок.
Так, Ампер и Лоренц внесли неоценимый вклад в развитие физики, что дало возможность не только развивать научные теории, но получило весомую практическую ценность. Как появился телеграф? Что такое электромагниты? На все эти вопросы даст ответ сегодняшний урок.
Для науки представляют огромную ценность полученные знания, которые впоследствии могут найти свое практическое применение. Новые открытия не только расширяют исследовательские горизонты, но и ставят новые вопросы, проблемы.
Выделим основные открытия Ампера в области электромагнетизма.
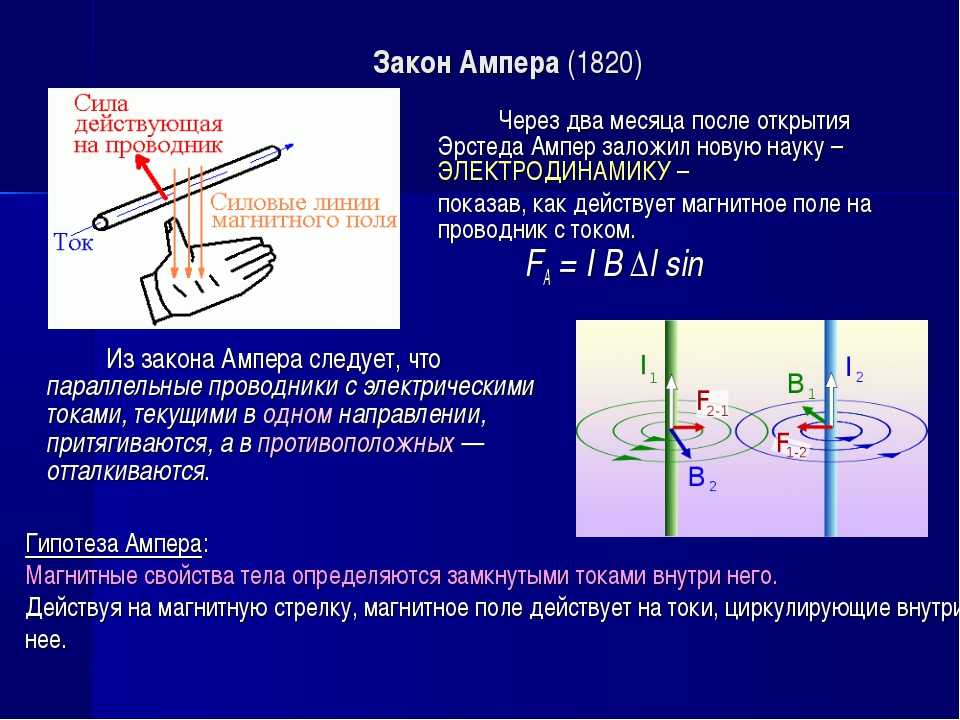
Во-первых, это взаимодействия проводников с током. Два параллельных проводника с токами притягиваются друг к другу, если токи в них сонаправлены, и отталкиваются, если токи в них противонаправлены (рис. 1).
Рис. 1. Проводники с током
Закон Ампера гласит:
Сила взаимодействия двух параллельных проводников пропорциональна произведению величин токов в проводниках, пропорциональна длине этих проводников и обратно пропорциональна расстоянию между ними.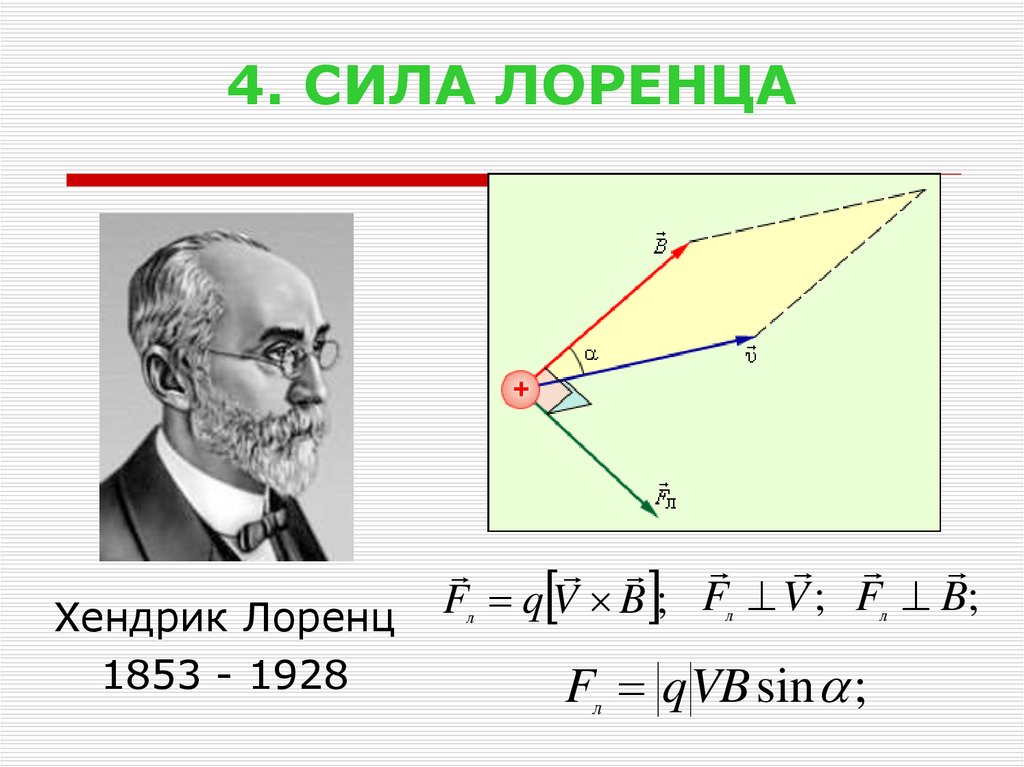
Сила взаимодействия двух параллельных проводников,
Величины токов в проводниках,
− длина проводников,
Расстояние между проводниками,
Магнитная постоянная.
Открытие этого закона позволило ввести в единицы измерения величину силы тока, которой до того времени не существовало. Так, если исходить из определения силы тока как отношения количества заряда перенесенного через поперечное сечение проводника в единицу времени, то мы получим принципиально не измеряемую величину, а именно количество заряда, переносимое через поперечное сечение проводника. На основании этого определения мы не сможем ввести единицу измерения силы тока. Закон Ампера позволяет установить связь между величинами сил тока в проводниках и величинами, которые можно измерить опытным путем: механической силой и расстоянием. Таким образом, получена возможность ввести в рассмотрение единицу силы тока — 1 А (1 ампер).
Ток в один ампер — это такой ток, при котором два однородных параллельных проводника, расположенных в вакууме на расстоянии один метрот друга взаимодействуют с силой Ньютона.
Закон взаимодействия токов — два находящихся в вакууме параллельных проводника, диаметры которых много меньше расстояний между ними, взаимодействуют с силой, прямо пропорциональной произведению токов в этих проводниках и обратно пропорциональной расстоянию между ними.
Еще одно открытие Ампера – это закон действия магнитного поля на проводник с током. Он выражается прежде всего в действии магнитного поля на виток или рамку с током. Так, на виток с током в магнитном поле действует момент силы, которая стремится развернуть этот виток таким образом, чтобы его плоскость стала перпендикулярна линиям магнитного поля. Угол поворота витка прямо пропорционален величине тока в витке. Если внешнее магнитное поле в витке постоянно, то значение модуля магнитной индукции также величина постоянная. Площадь витка при не очень больших токах также можно считать постоянной, следовательно, справедливо то, что сила тока равна произведению момента сил, разворачивающих виток с током, на некоторую постоянную при неизменных условиях величину.
– сила тока,
– момент сил, разворачивающих виток с током.
Следовательно, появляется возможность измерять силу тока по величине угла поворота рамки, которая реализована в измерительном приборе – амперметре (рис. 2).
Рис. 2. Амперметр
После открытия действия магнитного поля на проводник с током Ампер понял, что это открытие можно использовать для того, чтобы заставить проводник двигаться в магнитном поле. Так, магнетизм можно превратить в механическое движение – создать двигатель. Одним из первых, работающих на постоянном токе, был электродвигатель (рис. 3), созданный в 1834 г. русским электротехником Б.С. Якоби.
Рис. 3. Двигатель
Рассмотрим упрощенную модель двигателя, которая состоит из неподвижной части с закрепленными на ней магнитами – статора. Внутри статора может свободно вращаться рамка из проводящего материала, которая называется ротором. Для того чтобы по рамке мог протекать электрический ток, она соединена с клеммами при помощи скользящих контактов (рис.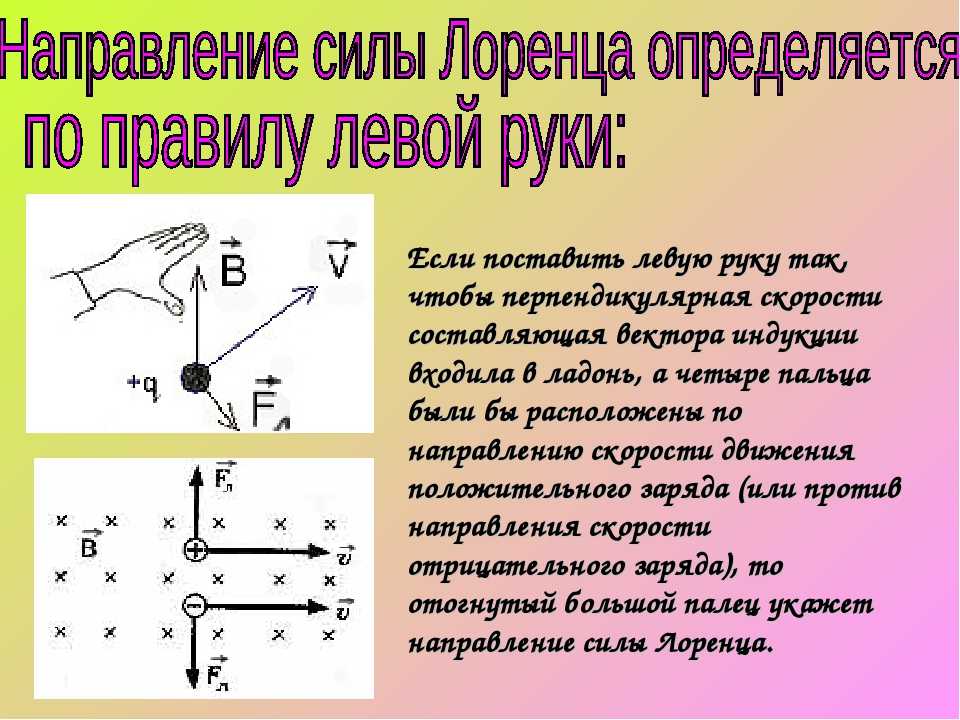 4). Если подключить двигатель к источнику постоянного тока в цепь с вольтметром, то при замыкании цепи рамка с током начнет вращение.
4). Если подключить двигатель к источнику постоянного тока в цепь с вольтметром, то при замыкании цепи рамка с током начнет вращение.
Рис. 4. Принцип работы электродвигателя
В 1269 г. французский естествоиспытатель Пьер де Марикур написал труд под названием «Письмо о магните». Основной целью Пьера де Марикура было создание вечного двигателя, в котором он собирался использовать удивительные свойства магнитов. Насколько успешными были его попытки, неизвестно, но достоверно то, что Якоби использовал свой электродвигатель для того, чтобы привести в движение лодку, при этом ему удалось ее разогнать до скорости 4,5 км/ч.
Необходимо упомянуть еще об одном устройстве, работающем на основе законов Ампера. Ампер показал, что катушка с током ведет себя подобно постоянному магниту. Это значит, что можно сконструировать электромагнит – устройство, мощность которого можно регулировать (рис. 5).
Рис. 5. Электромагнит
Именно Амперу пришла идея о том, что, скомбинировав проводники и магнитные стрелки, можно создать устройство, которое предает информацию на расстояние.
Рис. 6. Электрический телеграф
Идея телеграфа (рис. 6) возникла в первые же месяцы после открытия электромагнетизма.
Однако широкое распространение электромагнитный телеграф приобрел после того, как Самюэль Морзе создал более удобный аппарат и, главное, разработал двоичную азбуку, состоящую из точек и тире, которая так и называется: азбука Морзе.
С передающего телеграфного аппарата с помощью «ключа Морзе», который замыкает электрическую цепь, в линии связи формируются короткие или длинные электрические сигналы, соответствующие точкам или тире азбуки Морзе. На приемном телеграфном аппарате (пишущий прибор) на время прохождения сигнала (электрического тока) электромагнит притягивает якорь, с которым жестко связано пишущее металлическое колесико или писец, которые оставляют чернильный след на бумажной ленте (рис. 7).
Рис. 7. Схема работы телеграфа
Математик Гаусс, когда познакомился с исследованиями Ампера, предложил создать оригинальную пушку (рис. 8), работающую на принципе действия магнитного поля на железный шарик – снаряд.
8), работающую на принципе действия магнитного поля на железный шарик – снаряд.
Рис. 8. Пушка Гаусса
Необходимо обратить внимание на то, в какую историческую эпоху были сделаны эти открытия. В первой половине XIX века Европа семимильными шагами шла по пути промышленной революции – это было благодатное время для научно-исследовательских открытий и быстрого внедрения их в практику. Ампер, несомненно, внес весомый вклад в этот процесс, дав цивилизации электромагниты, электродвигатели и телеграф, которые до сих пор находят широкое применение.
Выделим основные открытия Лоренца.
Лоренц установил, что магнитное поле действует на движущуюся в нем частицу, заставляя ее двигаться по дуге окружности:
Cила Лоренца — центростремительная сила, перпендикулярная направлению скорости. Прежде всего, открытый Лоренцем закон, позволяет определять такую важнейшую характеристику, как отношение заряда к массе — удельный заряд .
Значение удельного заряда — величина уникальная для каждой заряженной частицы, что позволяет их идентифицировать, будь то электрон, протон или любая другая частица. Таким образом, ученые получили мощный инструмент для исследования. Например, Резерфорд сумел провести анализ радиоактивного излучения и выявил его компоненты, среди которых присутствуют альфа-частицы — ядра атома гелия — и бета-частицы — электроны.
Таким образом, ученые получили мощный инструмент для исследования. Например, Резерфорд сумел провести анализ радиоактивного излучения и выявил его компоненты, среди которых присутствуют альфа-частицы — ядра атома гелия — и бета-частицы — электроны.
В ХХ веке появились ускорители, работа которых основана на том, что заряженные частицы ускоряются в магнитном поле. Магнитное поле искривляет траектории частиц (рис. 9). Направление изгиба следа позволяет судить о знаке заряда частицы; измерив радиус траектории, можно определить скорость частицы, если известны ее масса и заряд.
Рис. 9. Искривление траектории частиц в магнитном поле
На этом принципе разработан Большой адронный коллайдер (рис. 10). Благодаря открытиям Лоренца наука получила принципиально новый инструмент для физических исследований, открывая дорогу в мир элементарных частиц.
Рис. 10. Большой адронный коллайдер
Для того чтобы охарактеризовать влияние ученого на технический прогресс, вспомним о том, что из выражения для силы Лоренца вытекает возможность рассчитать радиус кривизны траектории частицы, которая движется в постоянном магнитном поле.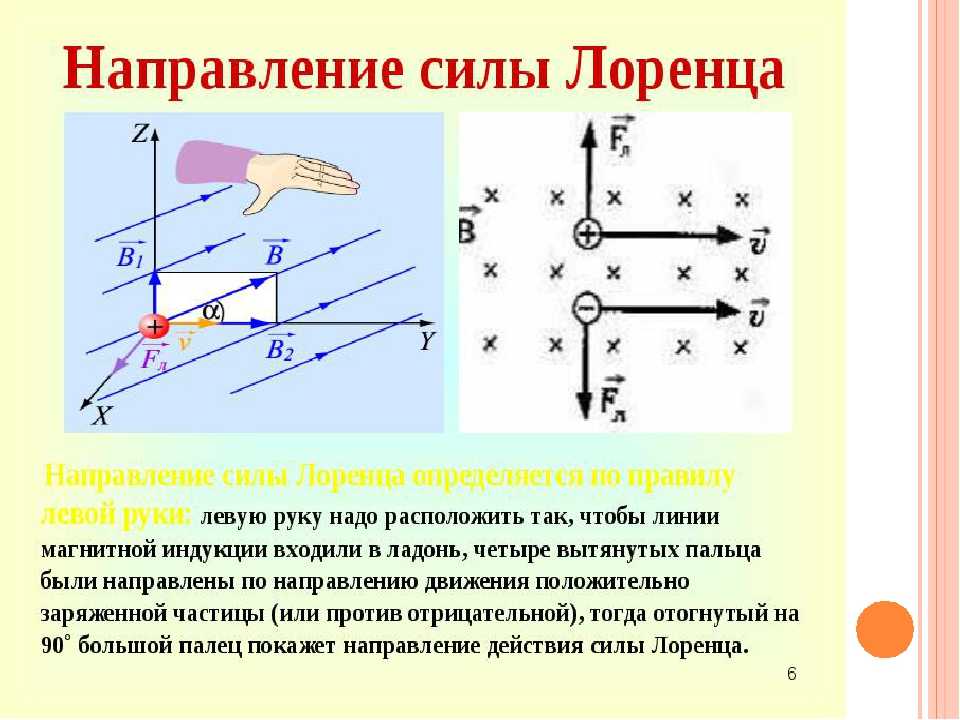 При неизменных внешних условиях этот радиус зависит от массы частицы, ее скорости и заряда. Таким образом, получаем возможность классифицировать заряженные частицы по этим параметрам и, следовательно, можем проводить анализ какой-либо смеси. Если смесь веществ в газообразном состоянии ионизировать, разогнать и направить в магнитное поле, то частицы начнут двигаться по дугам окружностей с различными радиусами — частицы будут покидать поле в разных точках, и остается только зафиксировать эти точки вылета, что реализуется при помощи экрана, покрытого люминофором, который светится при попадании на него заряженных частиц. Именно по такой схеме работает масс-анализатор (рис. 11). Масс-анализаторы широко применяют в физике и химии для анализа состава смесей.
При неизменных внешних условиях этот радиус зависит от массы частицы, ее скорости и заряда. Таким образом, получаем возможность классифицировать заряженные частицы по этим параметрам и, следовательно, можем проводить анализ какой-либо смеси. Если смесь веществ в газообразном состоянии ионизировать, разогнать и направить в магнитное поле, то частицы начнут двигаться по дугам окружностей с различными радиусами — частицы будут покидать поле в разных точках, и остается только зафиксировать эти точки вылета, что реализуется при помощи экрана, покрытого люминофором, который светится при попадании на него заряженных частиц. Именно по такой схеме работает масс-анализатор (рис. 11). Масс-анализаторы широко применяют в физике и химии для анализа состава смесей.
Рис. 11. Масс-анализатор
Это еще не все технические устройства, которые работают на основе разработок и открытий Ампера и Лоренца, ведь научное знание рано или поздно перестает быть исключительной собственностью ученых и становится достоянием цивилизации, при этом оно воплощается в различных технических устройствах, которые делают нашу жизнь более комфортной.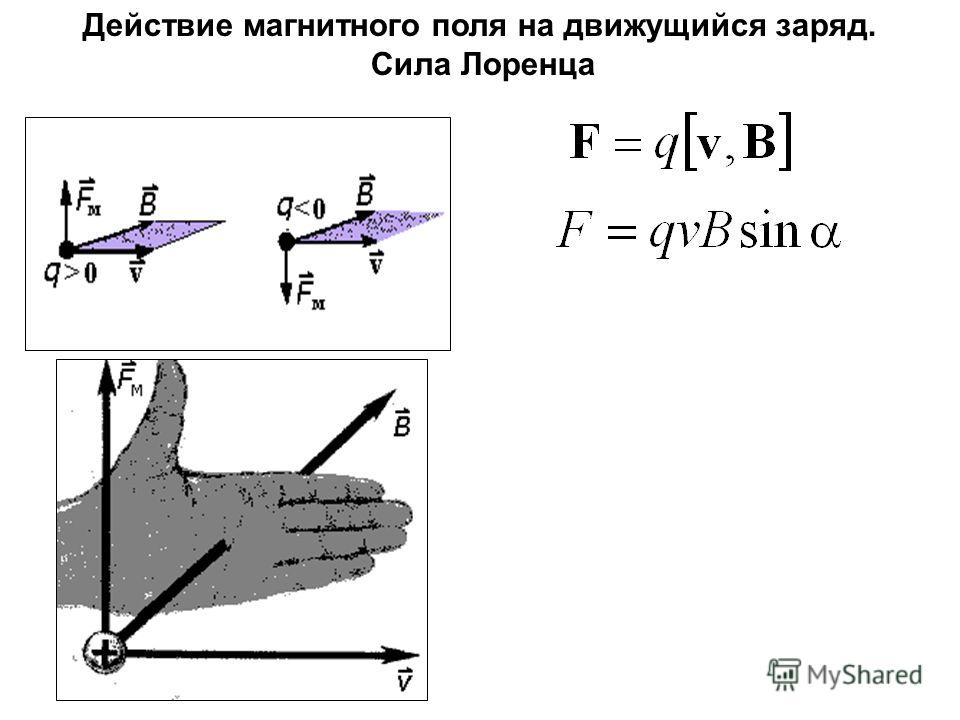
Список литературы
- Касьянов В.А., Физика 11 кл.: Учебн. для общеобразоват. учреждений. — 4-е изд., стереотип. — М.: Дрофа, 2004. — 416с.: ил., 8 л. цв. вкл.
- Генденштейн Л.Э., Дик Ю.И., Физика 11. — М.: Мнемозина.
- Тихомирова С.А., Яворский Б.М., Физика 11. — М.: Мнемозина.
- Интернет-портал «Чип и Дип» ().
- Интернет-портал «Киевская городская библиотека» ().
- Интернет-портал «Институт дистанционного образования» ().
Домашнее задание
1. Касьянов В.А., Физика 11 кл.: Учебн. для общеобразоват. учреждений. — 4-е изд., стереотип. — М.: Дрофа, 2004. — 416с.: ил., 8 л. цв. вкл., ст. 88, в. 1-5.
2. В камере Вильсона, которая размещена в однородном магнитном поле с индукцией 1,5 Тл, альфа-частица, влетая перпендикулярно к линиям индукции, оставляет след в виде дуги окружности радиусом 2,7 см. Определите импульс и кинетическую энергию частицы. Масса альфа-частицы 6,7∙10 -27 кг, а заряд 3,2∙10 -19 Кл.
3. Масс-спектрограф. Пучок ионов, разогнанных разницей потенциалов 4 кВ, влетает в однородное магнитное поле с магнитной индукцией 80 мТл перпендикулярно линиям магнитной индукции. Пучок состоит из ионов двух типов с молекулярными массами 0,02 кг/моль и 0,022 кг/моль. Все ионы обладают зарядом 1,6 ∙ 10 -19 Кл. Ионы вылетают из поля двумя пучками (рис. 5). Найти расстояние между пучками ионов, которые вылетают.
4. * С помощью электродвигателя постоянного тока поднимают груз на тросе. Если отключить электродвигатель от источника напряжения и замкнуть ротор накоротко, груз будет опускаться с постоянной скоростью. Объясните это явление. В какую форму переходит потенциальная энергия груза?
Электрические заряды, движущиеся в определенном направлении, создают вокруг себя магнитное поле, скорость распространения которого в вакууме равно скорости света, а в других средах чуть меньше. Если движение заряда происходит во внешнем магнитном поле, то между внешним магнитным полем и магнитным полем заряда возникает взаимодействие.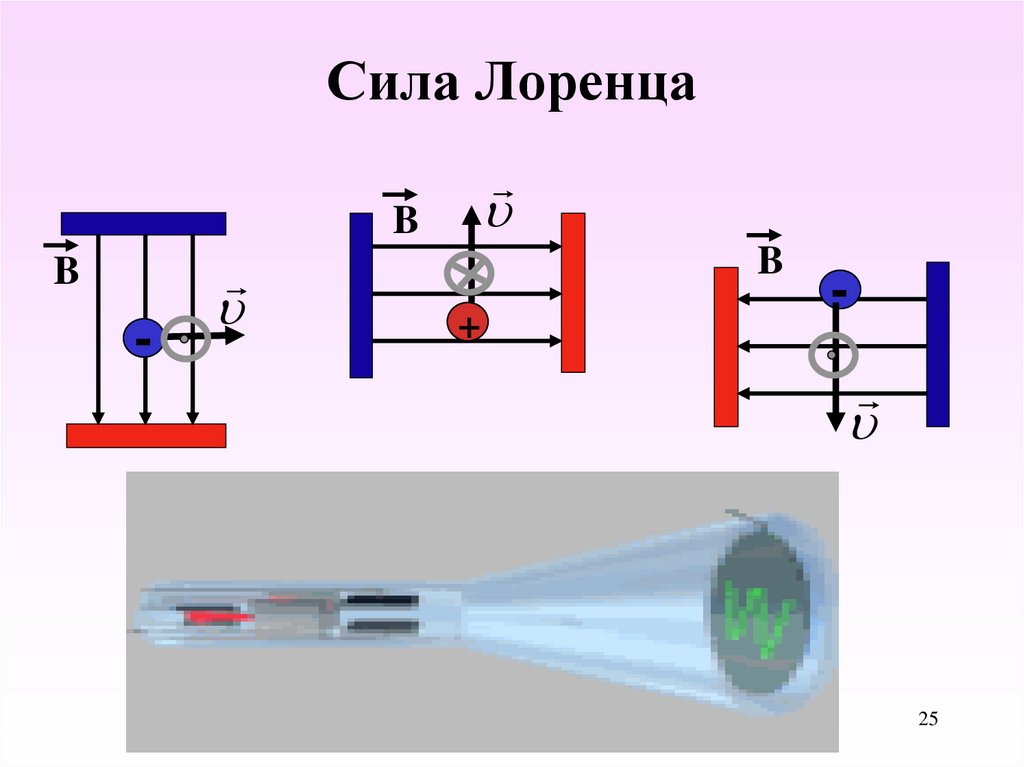 Так как электрический ток – это направленное движение заряженных частиц, то сила, которая будет действовать в магнитном поле на проводник с током, будет являться результатом отдельных (элементарных) сил, каждая из которых прикладывается к элементарному носителю заряда.
Так как электрический ток – это направленное движение заряженных частиц, то сила, которая будет действовать в магнитном поле на проводник с током, будет являться результатом отдельных (элементарных) сил, каждая из которых прикладывается к элементарному носителю заряда.
Процессы взаимодействия внешнего магнитного поля и движущихся зарядов исследовались Г. Лоренцом, который в результате многих своих опытов вывел формулу для расчета силы, действующей на движущуюся заряженную частицу со стороны магнитного поля. Именно поэтому силу, которая действует на движущийся в магнитном поле заряд, называют силой Лоренца.
Сила, действующая на проводник стоком (из закона Ампера), будет равна:
По определению сила тока равна I = qn (q – заряд, n – количество зарядов, проходящее через поперечное сечение проводника за 1 с). Отсюда следует:
Где: n 0 – содержащееся в единице объема количество зарядов, V – их скорость движения, S – площадь поперечного сечения проводника. Тогда:
Подставив данное выражение в формулу Ампера, мы получим:
Данная сила будет действовать на все заряды, находящиеся в объеме проводника: V = Sl. Количество зарядов, присутствующих в данном объеме будет равно:
Количество зарядов, присутствующих в данном объеме будет равно:
Тогда выражение для силы Лоренца будет иметь вид:
Отсюда можно сделать вывод, что сила Лоренца, действующая на заряд q, который двигается в магнитном поле, пропорциональна заряду, магнитной индукции внешнего поля, скорости его движения и синусу угла между V и В, то есть:
За направление движения заряженных частиц принимают направление движения положительных зарядов. Поэтому направление данной силы может быть определено с помощью правила левой руки.
Сила, действующая на отрицательные заряды, будет направлена в противоположную сторону.
Сила Лоренца всегда направлена перпендикулярно скорости V движения заряда и поэтому работу она не совершает. Она изменяет только направление V, а кинетическая энергия и величина скорости заряда при его движении в магнитном поле остаются неизменными.
Когда заряженная частица движется одновременно в магнитном и электрическом полях, на него будет действовать сила:
Где Е – напряженность электрического поля.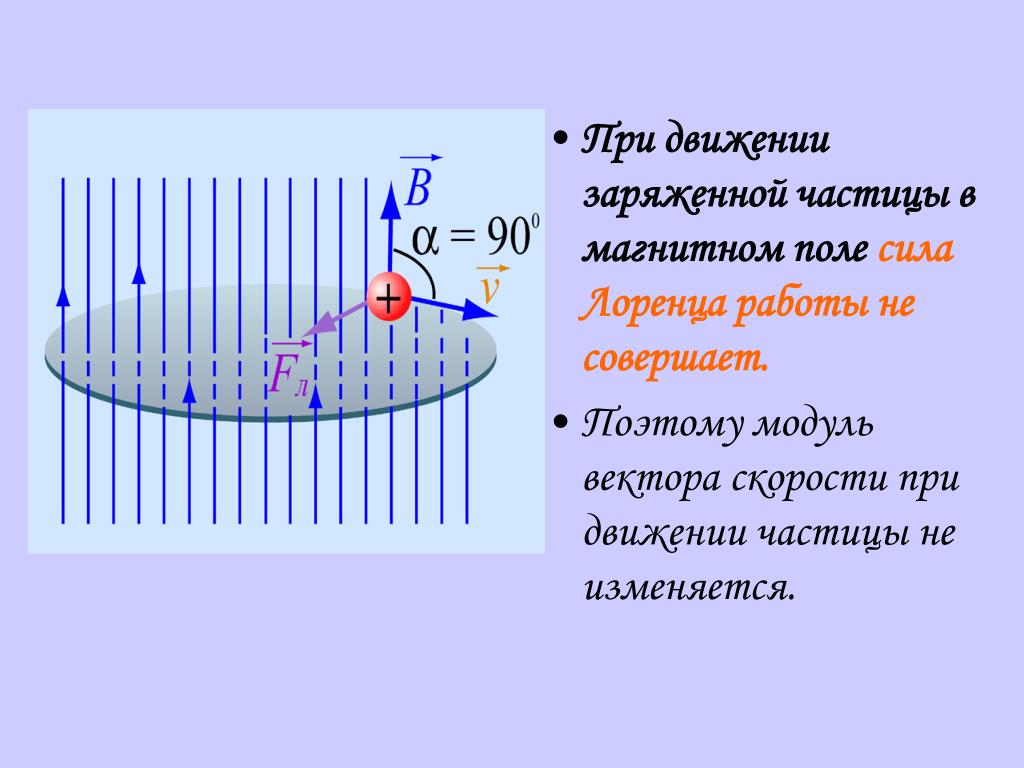
Рассмотрим небольшой пример:
Электрон, прошедший ускоряющую разность потенциалов 3,52∙10 3 В, попадает в однородное магнитное поле перпендикулярно линиям индукции. Радиус траектории r = 2 см, индукция поля 0,01 Т. Определить удельный заряд электрона.
Удельный заряд – это величина, равная отношению заряда к массе, то есть e/m.
В магнитном поле с индукцией В на заряд, движущийся со скоростью V перпендикулярно линиям индукции, действует сила Лоренца F Л = BeV. Под ее действием заряженная частица будет перемещаться по дуге окружности. Так как при этом сила Лоренца вызовет центростремительное ускорение, то согласно 2-му закону Ньютона можно записать:
Кинетическую энергию, которая будет равна mV 2 /2, электрон приобретает за счет работы А сил электрического поля (А = eU), подставив в уравнение получим.
Определение силы магнитной силы
Определение
Если заряд движется в магнитном поле, то на него действует сила ($\overrightarrow{F}$), которая зависит от величины заряда (q), скорости движения частицы ($\overrightarrow{v}$) относительно магнитного поля, и индукции магнитного поля ($\overrightarrow{B}$).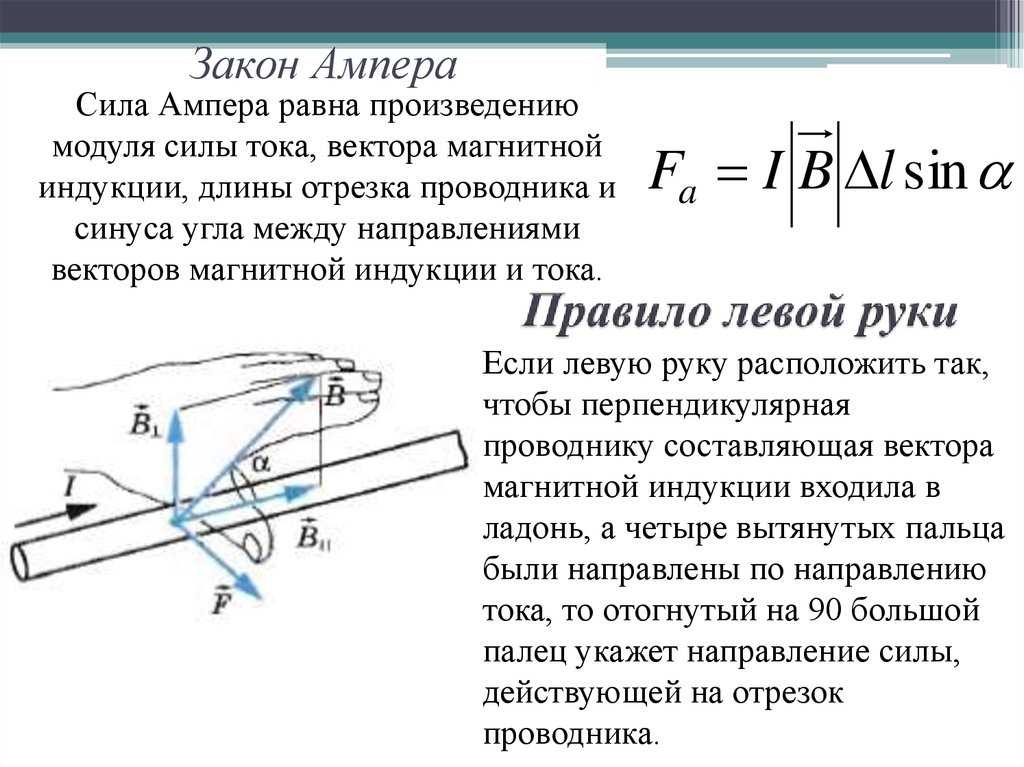 Эта сила была установлена экспериментально, называется она магнитной силой.
Эта сила была установлена экспериментально, называется она магнитной силой.
И имеет в системе СИ вид:
\[\overrightarrow{F}=q\left[\overrightarrow{v}\overrightarrow{B}\right]\ \left(1\right).\]
Модуль силы в соответствии с (1) равен:
где $\alpha $ — угол между векторами $\overrightarrow{v\ }и\ \overrightarrow{B}$. Из уравнения (2) следует, что если заряженная частица движется вдоль линии магнитного поля, то не испытывает действия магнитной силы.
Направление магнитной силы
Магнитная сила, исходя из (1) направлена перпендикулярно плоскости, в которой лежат векторы $\overrightarrow{v\ }и\ \overrightarrow{B}$. Ее направление совпадает с направлением векторного произведения $\overrightarrow{v\ }и\ \overrightarrow{B}$ в том случае, если величина движущегося заряда больше нуля, и направлена в противоположную сторону, если $q
Свойства силы магнитной силы
Магнитная сила работы над частицей не свершает, так как всегда направлена перпендикулярно скорости ее движения. Из этого утверждения следует, что с помощью воздействия на заряженную частицу с помощью постоянного магнитного поля ее энергию изменить нельзя.
Из этого утверждения следует, что с помощью воздействия на заряженную частицу с помощью постоянного магнитного поля ее энергию изменить нельзя.
Если на частицу, обладающую зарядом, действуют одновременно электрическое и магнитное поля, то равнодействующая сила может быть записана как:
\[\overrightarrow{F}=q\overrightarrow{E}+q\left[\overrightarrow{v}\overrightarrow{B}\right]\ \left(3\right).\]
Сила, указанная в выражении (3) называется силой Лоренца. Часть $q\overrightarrow{E}$ является силой, действующей со стороны электрического поля на заряд, $q\left[\overrightarrow{v}\overrightarrow{B}\right]$ характеризует силу действия магнитного поля на заряд. Сила Лоренца проявляется при движении электронов и ионов в магнитных полях.
Пример 1
Задание: Протон ($p$) и электрон ($e$), ускоренный одинаковой разностью потенциалов влетают в однородное магнитное поле. Во сколько раз радиус кривизны траектории движения протона $R_p$отличается от радиуса кривизны траектории электрона $R_e$. {-31}}}\approx 42.\]
{-31}}}\approx 42.\]
Ответ: Радиус кривизны протона в 42 раза больше, чем радиус кривизны электрона.
Пример 2
Задание: Найдите напряженность электрического поля (E), если протон в скрещенном магнитном и электрическом полях движется прямолинейно. В эти поля он влетел, пройдя ускоряющую разность потенциалов равную U. Поля скрещены под прямым углом. Индукция магнитного поля равна B.
На частицу, по условиям задачи действует сила Лоренца, имеющая две составные части: магнитную и электрическую. Первая составляющая магнитная она равна:
\[\overrightarrow{F_m}=q\left[\overrightarrow{v}\overrightarrow{B}\right]\ \left(2.1\right).\]
$\overrightarrow{F_m}$ — направлена перпендикулярно $\overrightarrow{v\ }и\ \overrightarrow{B}$. Электрическая составляющая силы Лоренца равна:
\[\overrightarrow{F_q}=q\overrightarrow{E}\left(2.2\right).\]
Сила $\overrightarrow{F_q}$- направлена по напряженности $\overrightarrow{E}$. Мы помним, что протон имеет положительный заряд. 2}{2}=qU\to v=\sqrt{\frac{2qU}{m}}\left(2.5\right).\]
2}{2}=qU\to v=\sqrt{\frac{2qU}{m}}\left(2.5\right).\]
Подставим (2.5) в (2.4), получим:
Ответ: $E=B\sqrt{\frac{2qU}{m}}.$
Нигде еще школьный курс физики так сильно не перекликается с большой наукой, как в электродинамике. В частности, ее краеугольный камень – воздействие на заряженные частицы со стороны электромагнитного поля, нашло широкое применение в электротехнике.
Формула силы Лоренца
Формула описывает взаимосвязь магнитного поля и основных характеристик движущегося заряда. Но сперва нужно разобраться, что же оно собой представляет.
Определение и формула силы Лоренца
В школе очень часто показывают опыт с магнитом и железными опилками на бумажном листе. Если расположить его под бумагой и слегка потрясти, то опилки выстроятся по линиям, которые принято называть линиями магнитной напряженности. Говоря простыми словами, это силовое поле магнита, которое окружает его подобно кокону. Оно замкнуто само на себя, то есть не имеет ни начала, ни конца. Это векторная величина, которая направлена от южного полюса магнита к северному.
Это векторная величина, которая направлена от южного полюса магнита к северному.
Если бы в него влетела заряженная частица, то поле воздействовало бы на него очень любопытным образом. Она бы не затормозилась и не ускорилась, а всего лишь отклонилась в сторону. Чем она быстрее и чем сильнее поле, тем больше на нее действует эта сила. Ее назвали силой Лоренца в честь ученого-физика, впервые открывшего это свойство магнитного поля.
Вычисляют ее по специальной формуле:
здесь q – величина заряда в Кулонах, v – скорость, с которой движется заряд, в м/с, а B – индукция магнитного поля в единице измерения Тл (Тесла).
Направление силы Лоренца
Ученые заметили, что есть определенная закономерность между тем, как частица влетает в магнитное поле и тем, куда оно ее отклоняет. Чтобы ее было легче запомнить, они разработали специальное мнемоническое правило. Для его запоминания нужно совсем немного усилий, ведь в нем используется то, что всегда под рукой – рука. Точнее, левая ладонь, в честь чего оно носит название правила левой руки.
Итак, ладонь должна быть раскрыта, четыре пальца смотрят вперед, большой палец оттопырен в сторону. Угол между ними составляет 900. Теперь необходимо представить, что магнитный поток представляет собой стрелу, которая впивается в ладонь с внутренней стороны и выходит с тыльной. Пальцы при этом смотрят туда же, куда летит воображаемая частица. В таком случае большой палец покажет, куда она отклонится.
Интересно!
Важно отметить, что правило левой руки действует только для частиц со знаком «плюс». Чтобы узнать, куда отклонится отрицательный заряд, нужно четыре пальца направить в сторону, откуда летит частица. Все остальные манипуляции остаются прежними.
Следствия свойств силы Лоренца
Тело влетает в магнитном поле под каким-то определённым углом. Интуитивно понятно, что его величина имеет какое-то значение на характер воздействия на него поля, здесь нужно математическое выражение, чтобы стало понятнее. Следует знать, что как сила, так и скорость являются векторными величинами, то есть имеют направление.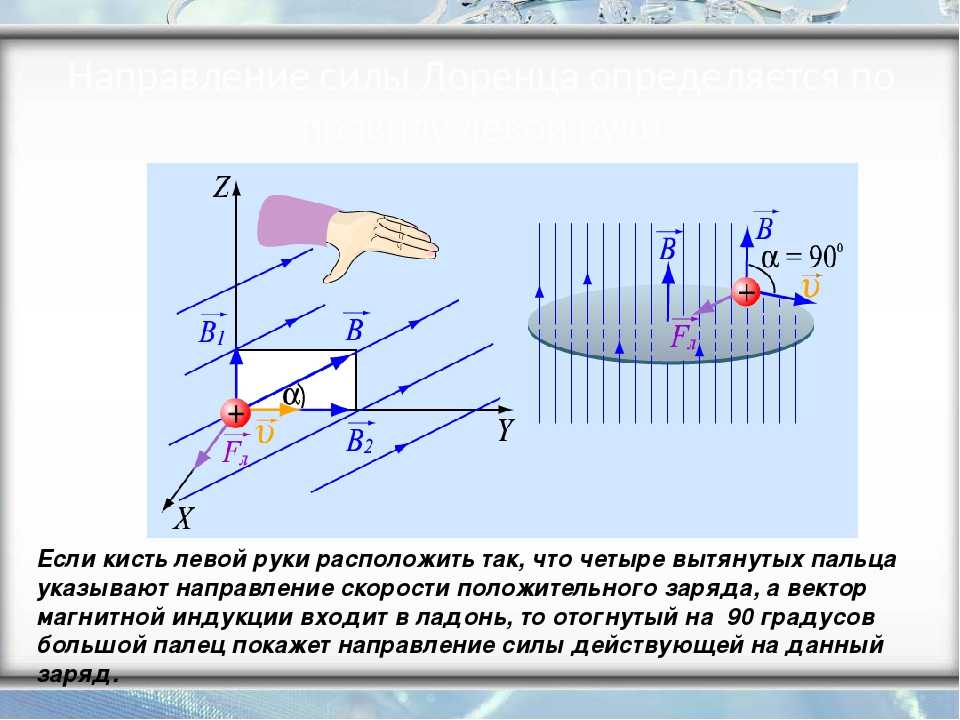 То же самое относится и к линиям магнитной напряженности. Тогда формулу можно записать следующим образом:
То же самое относится и к линиям магнитной напряженности. Тогда формулу можно записать следующим образом:
sin α здесь – это угол между двумя векторными величинами: скоростью и потоком магнитного поля.
Как известно, синус нулевого угла также равен нулю. Получается, что если траектория движения частицы проходит вдоль силовых линий магнитного поля, то она никуда не отклоняется.
В однородном магнитном поле силовые линии имеют одинаковое и постоянное расстояние друг от друга. Теперь представим, что в таком поле перпендикулярно этим линиям движется частица. В этом случае сила Лоуренса заставит двигаться ее по окружности в плоскости, перпендикулярной силовым линиям. Чтобы найти радиус этой окружности, нужно знать массу частицы:
Значение заряда не случайно взято как модуль. Это означает, что неважно, отрицательная или положительная частица входит в магнитное поле: радиус кривизны будет одинаков. Изменится только направление, в котором она полетит.
Во всех остальных случаях, когда заряд имеет определенный угол α с магнитным полем, он будет двигаться по траектории, напоминающей спираль с постоянным радиусом R и шагом h. Его можно найти по формуле:
Его можно найти по формуле:
Еще одним следствием свойств этого явления является тот факт, что она не совершает никакой работы. То есть она не отдает и не забирает энергию у частицы, а лишь меняет направление ее движения.
Самая яркая иллюстрация этого эффекта взаимодействия магнитного поля и заряженных частиц – это северное сияние. Магнитное поле, окружающее нашу планету, отклоняет заряженные частицы, прилетающие от Солнца. Но так как оно слабее всего на магнитных полюсах Земли, то туда проникают электрически заряженные частицы, вызывая свечение атмосферы.
Центростремительное ускорение, которое придается частицам, используется в электрических машинах – электродвигателях. Хотя уместнее здесь говорить о силе Ампера – частном проявлении силы Лоуренса, которая воздействует на проводник.
Принцип действия ускорителей элементарных частиц также основан на этом свойстве электромагнитного поля. Сверхпроводящие электромагниты отклоняют частицы от прямолинейного движения, заставляя их двигаться по кругу.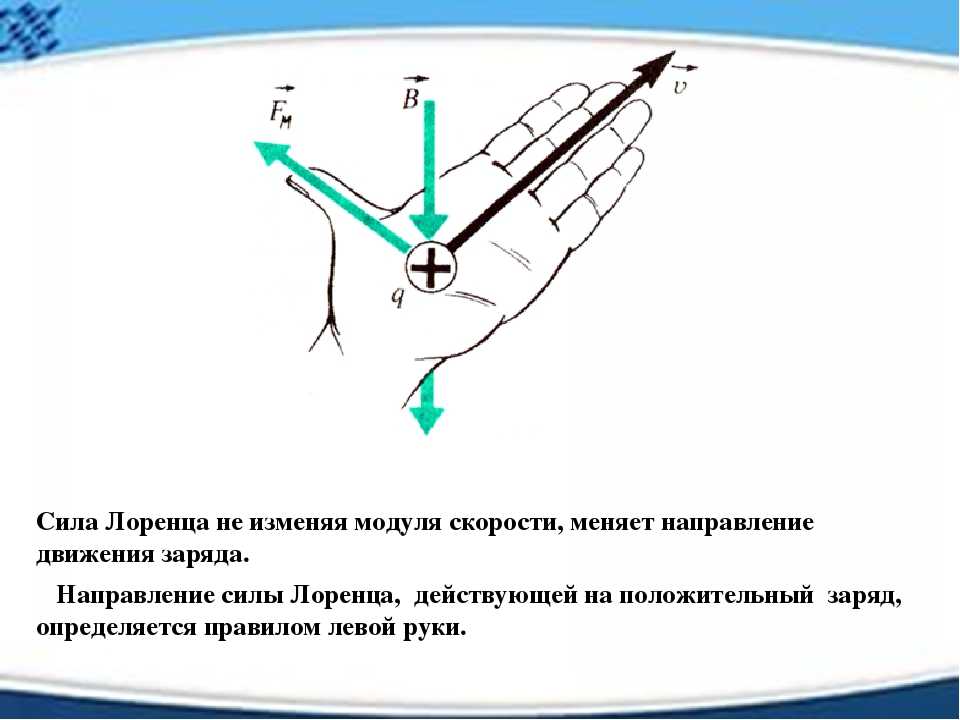
Самое любопытное заключается в том, что сила Лоренца не подчиняется третьему закону Ньютона, который гласит, что всякому действию есть свое противодействие. Связано это с тем, что Исаак Ньютон верил, что всякое взаимодействие на любом расстоянии происходит мгновенно, однако это не так. На самом деле оно происходит с помощью полей. К счастью, конфуза удалось избежать, так как физикам удалось переработать третий закон в закон сохранения импульса, который выполняется в том числе и для эффекта Лоуренса.
Формула силы Лоренца при наличии магнитного и электрического полей
Магнитное поле имеется не только у постоянных магнитов, но и у любого проводника электричества. Только в данном случае помимо магнитной составляющей, в ней присутствует еще и электрическая. Однако даже в этом электромагнитном поле эффект Лоуренса продолжает свое воздействие и определяется по формуле:
где v – скорость электрически заряженной частицы, q – ее заряд, B и E – напряженности магнитного и электрических полей поля.
Единицы измерения силы Лоренца
Как и большинство других физических величин, которые действуют на тело и изменяют его состояние, она измеряется в ньютонах и обозначается буквой Н.
Понятие напряженности электрического поля
Электромагнитное поле на самом деле состоит из двух половин – электрической и магнитной. Они точно близнецы, у которых все одинаково, но вот характер разный. А если приглядеться, то во внешности можно заметить небольшие различия.
То же самое касается и силовых полей. Электрическое поле тоже обладает напряженностью – векторной величиной, которая является силовой характеристикой. Она воздействует на частицы, которые в неподвижности находятся в нем. Само по себе оно не является силой Лоренца, ее просто нужно принимать во внимание, когда вычисляется воздействие на частицу в условиях наличия электрического и магнитного полей.
Напряженность электрического поля
Напряженность электрического поля воздействует только на неподвижный заряд и определяется по формуле:
Единицей измерения является Н/Кл или В/м.
Примеры задачи
Задача 1
На заряд в 0,005 Кл, который движется в магнитном поле с индукцией 0,3 Тл, действует сила Лоренца. Вычислить ее, если скорость заряда 200 м/с, а движется он под углом 450 к линиям магнитной индукции.
Задача 2
Определить скорость тела, имеющего заряд и которое движется в магнитном поле с индукцией 2 Тл под углом 900. Величина, с которой поле воздействует на тело, равна 32 Н, заряд тела – 5 × 10-3 Кл.
Задача 3
Электрон движется в однородном магнитном поле под углом 900 ее силовым линиям. Величина, с которой поле воздействует на электрон, равна 5 × 10-13 Н. Величина магнитной индукции равна 0,05 Тл. Определить ускорение электрона.
aц=v2R=6×10726,8×10-3=5×1017мс2
Электродинамика оперирует такими понятиями, которым трудно подобрать аналогию в обычном мире. Но это совсем не значит, что их невозможно постичь. С помощью различных наглядных экспериментов и природных явлений процесс познания мира электричества может стать по настоящему захватывающим.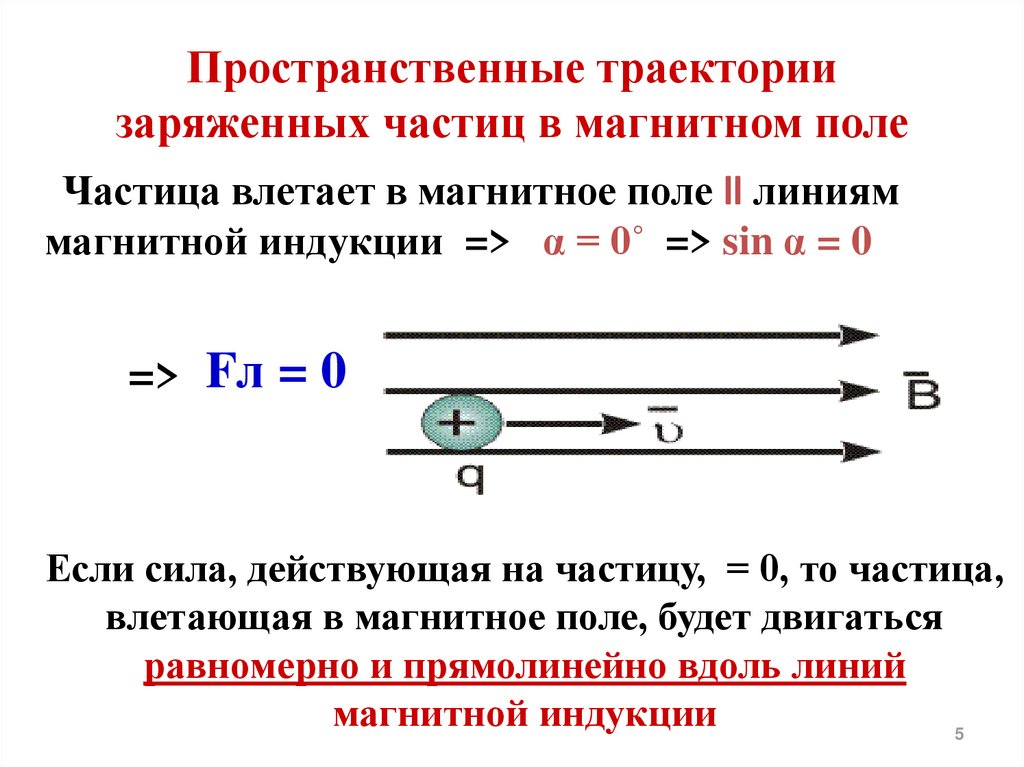
 Связь линейной и угловой скорости
Связь линейной и угловой скорости Поляризация света
Поляризация света Понятие электромагнитной волны. Свойства электромагнитных волн. Волновые явления
Понятие электромагнитной волны. Свойства электромагнитных волн. Волновые явленияФизика всем! — Магнетизм
Сила Ампера
Заряженные тела способны создавать кроме электрического еще один вид поля.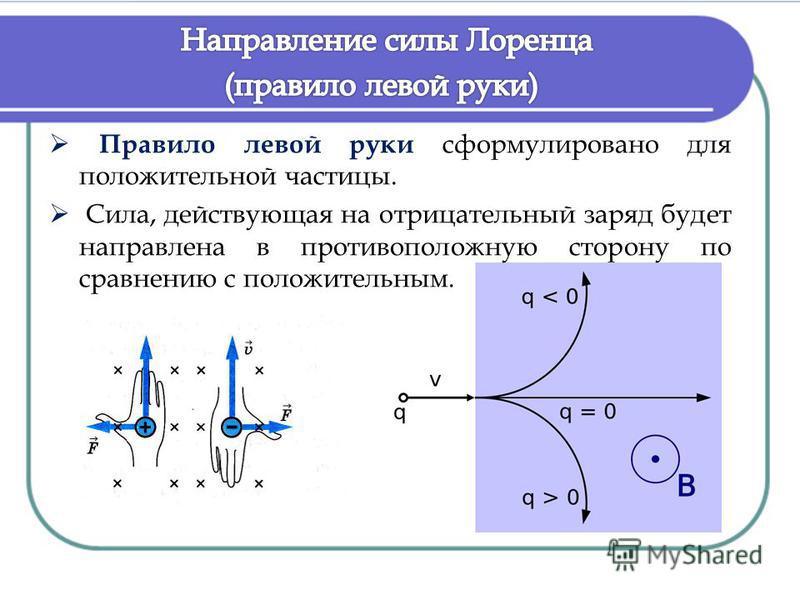 Если заряды движутся, то в пространстве вокруг них создается особый вид материи, называемый магнитным полем.
Если заряды движутся, то в пространстве вокруг них создается особый вид материи, называемый магнитным полем.
Сила Лоренца направлена перпендикулярно векторам скорости и индукции магнитного поля. При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется. Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору индукции магнитного поля, то частица будет двигаться по окружности, радиус которой можно вычислить по следующей формуле:
Сила Лоренца в этом случае играет роль центростремительной силы. Период обращения частицы в однородном магнитном поле равен:
Последнее выражение показывает, что для заряженных частиц заданной массы m период обращения (а значит и частота, и угловая скорость) не зависит от скорости (следовательно, и от кинетической энергии) и радиуса траектории R.
Теория о магнитном поле
Магнитное взаимодействие токов
Если по двум параллельным проводам идёт ток в одном направлении, то они притягиваются; если в противоположных направлениях, то отталкиваются. Закономерности этого явления были экспериментально установлены Ампером. Взаимодействие токов вызывается их магнитными полями: магнитное поле одного тока действует силой Ампера на другой ток и наоборот. Опыты показали, что модуль силы, действующей на отрезок длиной Δl каждого из проводников, прямо пропорционален силам тока I1 и I2 в проводниках, длине отрезка Δl и обратно пропорционален расстоянию R между ними:
где: μ0 – постоянная величина, которую называют магнитной постоянной. Введение магнитной постоянной в СИ упрощает запись ряда формул. Ее численное значение равно:
μ0 = 4π·10–7 H/A2 ≈ 1,26·10–6 H/A2.
Сравнивая приведенное только что выражение для силы взаимодействия двух проводников с током и выражение для силы Ампера нетрудно получить выражение для индукции магнитного поля создаваемого каждым из прямолинейных проводников с током на расстоянии R от него:
где: μ – магнитная проницаемость вещества (об этом чуть ниже). Если ток протекает по круговому витку, то в центре витка индукция магнитного поля определяется по формуле:
Если ток протекает по круговому витку, то в центре витка индукция магнитного поля определяется по формуле:
Силовыми линиями магнитного поля называют линии, по касательным к которым располагаются магнитные стрелки. Магнитной стрелкой называют длинный и тонкий магнит, его полюса точечны. Подвешенная на нити магнитная стрелка всегда поворачивается в одну сторону. При этом один её конец направлен в сторону севера, второй — на юг. Отсюда название полюсов: северный (N) и южный (S). Магниты всегда имеют два полюса: северный (обозначается синим цветом или буквой N) и южный (красным цветом или буквой S). Магниты взаимодействуют так же, как и заряды: одноименные полюса отталкиваются, а разноименные – притягиваются. Невозможно получить магнит с одним полюсом. Даже если магнит разломать, то у каждой части будет по два разных полюса.
Вектор магнитной индукции
Вектор магнитной индукции — векторная физическая величина, являющаяся характеристикой магнитного поля, численно равная силе, действующей на элемент тока в 1 А и длиной 1 м, если направление силовой линии перпендикулярно проводнику.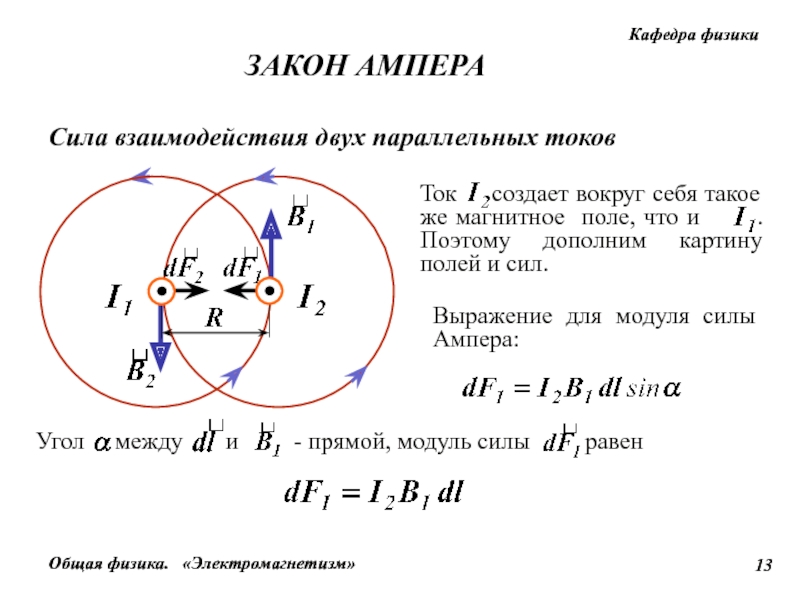 Обозначается В, единица измерения — 1 Тесла. 1 Тл — очень большая величина, поэтому в реальных магнитных полях магнитную индукцию измеряют в мТл.
Обозначается В, единица измерения — 1 Тесла. 1 Тл — очень большая величина, поэтому в реальных магнитных полях магнитную индукцию измеряют в мТл.
Вектор магнитной индукции направлен по касательной к силовым линиям, т.е. совпадает с направлением северного полюса магнитной стрелки, помещённой в данное магнитное поле. Направление вектора магнитной индукции не совпадает с направлением силы, действующей на проводник, поэтому силовые линии магнитного поля, строго говоря, силовыми не являются.
Силовая линия магнитного поля постоянных магнитов направлена по отношению к самим магнитам так, как показано на рисунке:
В случае магнитного поля электрического тока для определения направления силовых линий используют правило «Правой руки»: если взять проводник в правую руку так, чтобы большой палец был направлен по току, то четыре пальца, обхватывающие проводник, показывают направление силовых линий вокруг проводника:
В случае прямого тока линии магнитной индукции — окружности, плоскости которых перпендикулярны току. Вектора магнитной индукции направлены по касательной к окружности.
Вектора магнитной индукции направлены по касательной к окружности.
Соленоид — намотанный на цилиндрическую поверхность проводник, по которому течёт электрический ток I. Магнитное поле соленоида подобно полю прямого постоянного магнита. Внутри соленоида длиной l и количеством витков N создается однородное магнитное поле с индукцией (его направление также определяется правилом правой руки):
Линии магнитного поля имеют вид замкнутых линий — это общее свойство всех магнитных линий. Такое поле называют вихревым. В случае постоянных магнитов линии не оканчиваются на поверхности, а проникают внутрь магнита и замыкаются внутри. Это различие электрического и магнитного полей объясняется тем, что, в отличие от электрических, магнитных зарядов не существует.
Магнитные свойства вещества
Все вещества обладают магнитными свойствами. Магнитные свойства вещества характеризуются относительной магнитной проницаемостью μ, для которой верно следующее:
Данная формула выражает соответствие вектора магнитной индукции поля в вакууме и в данной среде. В отличие от электрического, при магнитном взаимодействии в среде можно наблюдать и усиление, и ослабление взаимодействия по сравнению с вакуумом, у которого магнитная проницаемость μ = 1. У диамагнетиков магнитная проницаемость μ немного меньше единицы. Примеры: вода, азот, серебро, медь, золото. Эти вещества несколько ослабляют магнитное поле. Парамагнетики — кислород, платина, магний — несколько усиливают поле, имея μ немного больше единицы. У ферромагнетиков — железо, никель, кобальт — μ >> 1. Например, у железа μ ≈ 25000.
В отличие от электрического, при магнитном взаимодействии в среде можно наблюдать и усиление, и ослабление взаимодействия по сравнению с вакуумом, у которого магнитная проницаемость μ = 1. У диамагнетиков магнитная проницаемость μ немного меньше единицы. Примеры: вода, азот, серебро, медь, золото. Эти вещества несколько ослабляют магнитное поле. Парамагнетики — кислород, платина, магний — несколько усиливают поле, имея μ немного больше единицы. У ферромагнетиков — железо, никель, кобальт — μ >> 1. Например, у железа μ ≈ 25000.
Магнитный поток. Электромагнитная индукция
ОПРЕДЕЛЕНИЕ
Явление электромагнитной индукции было открыто выдающимся английским физиком М.Фарадеем в 1831 году. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур. Магнитным потоком Φ через площадь S контура называют величину:
где: B – модуль вектора магнитной индукции, α – угол между вектором магнитной индукции B и нормалью (перпендикуляром) к плоскости контура, S – площадь контура, N – количество витком в контуре. Единица магнитного потока в системе СИ называется Вебером (Вб).
Единица магнитного потока в системе СИ называется Вебером (Вб).
Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции εинд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум возможным причинам.
- Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
- Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре.
При решении задач важно сразу определить за счет чего меняется магнитный поток. Возможно три варианта:
Возможно три варианта:
- Меняется магнитное поле.
- Меняется площадь контура.
- Меняется ориентация рамки относительно поля.
При этом при решении задач обычно считают ЭДС по модулю. Обратим внимание также внимание на один частный случай, в котором происходит явление электромагнитной индукции. Итак, максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S, вращающемся с угловой скоростью ω в магнитном поле с индукцией В:
Движение проводника в магнитном поле
При движении проводника длиной l в магнитном поле B со скоростью v на его концах возникает разность потенциалов, вызванная действием силы Лоренца на свободные электроны в проводнике. Эту разность потенциалов (строго говоря, ЭДС) находят по формуле:
где: α — угол, который измеряется между направлением скорости и вектора магнитной индукции. В неподвижных частях контура ЭДС не возникает.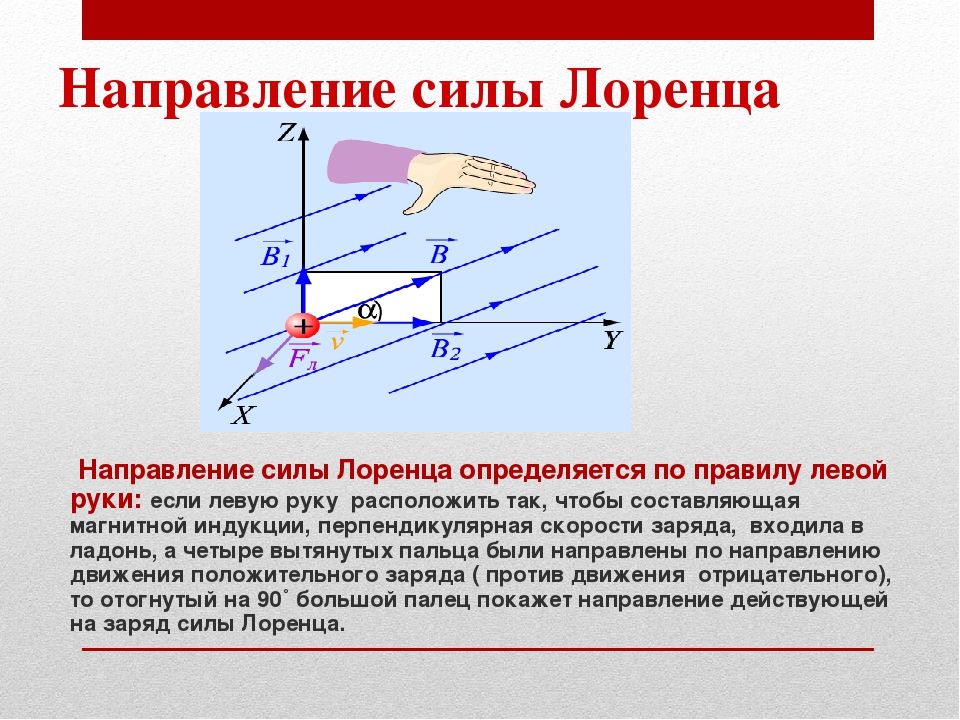
Если стержень длиной L вращается в магнитном поле В вокруг одного из своих концов с угловой скоростью ω, то на его концах возникнет разность потенциалов (ЭДС), которую можно рассчитать по формуле:
Индуктивность. Самоиндукция. Энергия магнитного поля
ОПРЕДЕЛЕНИЕ
Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре. Собственный магнитный поток Φ, пронизывающий контур или катушку с током, пропорционален силе тока I:
Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции или индуктивностью катушки.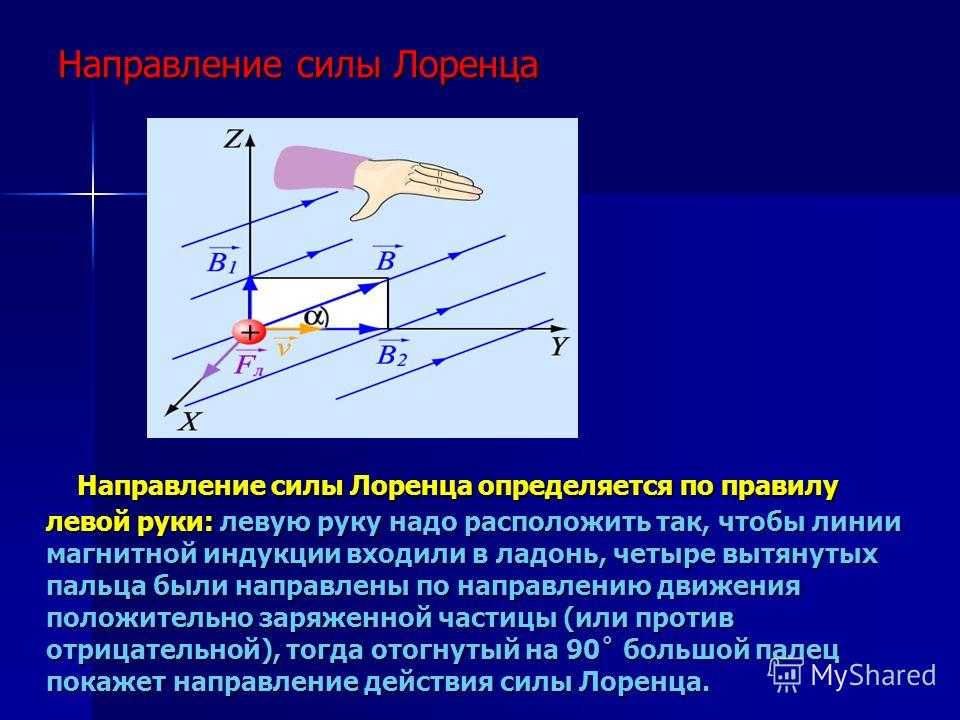 Единица индуктивности в СИ называется Генри (Гн).
Единица индуктивности в СИ называется Генри (Гн).
Запомните: индуктивность контура не зависит ни от магнитного потока, ни от силы тока в нем, а определяется только формой и размерами контура, а также свойствами окружающей среды. Поэтому при изменении силы тока в контуре индуктивность остается неизменной. Индуктивность катушки можно рассчитать по формуле:
где: n — концентрация витков на единицу длины катушки:
ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно формуле Фарадея равна:
Итак ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.
Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I, может быть рассчитана по одной из формул (они следуют друг из друга с учётом формулы Φ = LI):
Соотнеся формулу для энергии магнитного поля катушки с её геометрическими размерами можно получить формулу для объемной плотности энергии магнитного поля (или энергии единицы объёма):
Правило Ленца
Инерция – явление, происходящее и в механике (при разгоне автомобиля мы отклоняемся назад, противодействуя увеличению скорости, а при торможении отклоняемся вперёд, противодействуя уменьшению скорости), и в молекулярной физике (при нагревании жидкости увеличивается скорость испарения, самые быстрые молекулы покидают жидкость, уменьшая скорость нагревания) и так далее. В электромагнетизме инерция проявляется в противодействии изменению магнитного потока, пронизывающего контур. Если магнитный поток нарастает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать нарастанию магнитного потока, а если магнитный поток убывает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать убыванию магнитного потока.
В электромагнетизме инерция проявляется в противодействии изменению магнитного потока, пронизывающего контур. Если магнитный поток нарастает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать нарастанию магнитного потока, а если магнитный поток убывает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать убыванию магнитного потока.
Правило Ленца для определения направления индукционного тока: возникающий в контуре индукционный ток имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, которое вызывало этот ток.
Пройдите тест по теме магнетизм
Что такое сила Лоренца. Что такое сила Лоренца, каковы величина и направление этой силы. Эту зависимость можно выразить формулой
Раскройте ладонь левой руки и выпрямите все пальцы. Согните большой палец под углом 90 градусов по отношению ко всем остальным пальцам, в одной плоскости с ладонью.
Представьте, что четыре пальца ладони, которые вы держите вместе, указывают направление скорости заряда, если он положительный, или противоположное направление скорости, если заряд отрицательный.
Таким образом, на ладонь войдет вектор магнитной индукции, который всегда направлен перпендикулярно скорости. Теперь посмотрите, куда указывает большой палец — это направление силы Лоренца.
Сила Лоренца может быть равна нулю и не иметь векторной составляющей. Это происходит, когда траектория заряженной частицы параллельна силовым линиям магнитного поля. В этом случае частица имеет прямолинейную траекторию движения и постоянную скорость. Сила Лоренца никак не влияет на движение частицы, потому что в данном случае она вообще отсутствует.
В простейшем случае заряженная частица имеет траекторию движения, перпендикулярную силовым линиям магнитного поля. Тогда сила Лоренца создает центростремительное ускорение, заставляющее заряженную частицу двигаться по окружности.
note
Сила Лоренца была открыта в 1892 году голландским физиком Хендриком Лоренцем. Сегодня он довольно часто используется в различных электроприборах, действие которых зависит от траектории движения электронов. Например, это электронно-лучевые трубки в телевизорах и мониторах. Всевозможные ускорители, разгоняющие заряженные частицы до огромных скоростей, с помощью силы Лоренца задают орбиты их движения.
Полезный совет
Частным случаем силы Лоренца является сила Ампера. Его направление рассчитывается по правилу левой руки.
Источники:
- Сила Лоренца
- Сила Лоренца Правило левой руки
Действие магнитного поля на проводник с током означает, что магнитное поле воздействует на движущиеся электрические заряды. Сила, действующая на движущуюся заряженную частицу со стороны магнитного поля, называется силой Лоренца в честь голландского физика Г. Лоренца
Инструкция
Прочность — так можно определить ее числовое значение (модуль) и направление (вектор).
Модуль силы Лоренца (Fl) равен отношению модуля силы F, действующей на отрезок проводника с током длиной ∆l, к числу N заряженных частиц, упорядоченно движущихся по этому сечение проводника: Fl = F/N (1). В силу простых физических преобразований силу F можно представить в виде: F = q*n*v*S*l*B*sina (формула 2), где q — заряд движущегося , n — на участке проводника, v — скорость частицы, S — площадь поперечного сечения сечения проводника, l — длина сечения проводника, B — магнитная индукция, sina — синус угла между векторами скорости и индукции . А количество движущихся частиц преобразуется к виду: N=n*S*l (формула 3). Подставляем формулы 2 и 3 в формулу 1, уменьшаем значения n, S, l, получается для силы Лоренца: Fl = q * v * B * sin a. Итак, для решения простых задач нахождения силы Лоренца определим в условии задания следующие физические величины: заряд движущейся частицы, ее скорость, индукция магнитного поля, в котором движется частица, и угол между скоростью и индукция.
Перед решением задачи убедитесь, что все величины измерены в единицах, соответствующих друг другу или международной системе. Чтобы в ответе получить ньютоны (Н — единица силы), заряд надо измерять в кулонах (К), скорость — в метрах в секунду (м/с), индукцию — в теслах (Тл), синус альфа — нет измеримое число.
Чтобы в ответе получить ньютоны (Н — единица силы), заряд надо измерять в кулонах (К), скорость — в метрах в секунду (м/с), индукцию — в теслах (Тл), синус альфа — нет измеримое число.
Пример 1. В магнитном поле с индукцией 49 мТл заряженная частица массой 1 нКл движется со скоростью 1 м/с. Векторы скорости и магнитной индукции взаимно перпендикулярны. 9(12).
Направление силы Лоренца определяется по правилу левой руки. Чтобы применить его, представьте себе следующее расположение трех векторов перпендикулярно друг другу. Левую руку расположить так, чтобы вектор магнитной индукции входил в ладонь, четыре пальца направлены в сторону движения положительной (против движения отрицательной) частицы, тогда большой палец, согнутый на 90 градусов, укажет направление лоренцевской усилие, см. рисунок).
Сила Лоренца применяется в телевизионных трубках мониторов, телевизоров.
Источники:
- Мякишев Г.Я., Буховцев Б.Б. Учебник физики. 11 класс. Москва. «Образование».
 2003
2003 - решение задач на силу Лоренца
Истинное направление тока — то, в котором движутся заряженные частицы. Он, в свою очередь, зависит от знака их заряда. Кроме того, техники используют условное направление движения заряда, не зависящее от свойств проводника.
Инструкция
Чтобы определить истинное направление движения заряженных частиц, следуйте следующему правилу. Внутри источника они вылетают из электрода, заряжающегося от этого с обратным знаком, и движутся к электроду, который по этой причине приобретает заряд, близкий по знаку к частицам. Во внешней же цепи они вырываются электрическим полем из электрода, заряд которого совпадает с зарядом частиц, и притягиваются к противоположно заряженному электроду.
В металле носителями тока являются свободные электроны, перемещающиеся между узлами кристалла. Так как эти частицы заряжены отрицательно, внутри источника считайте их движущимися от положительного электрода к отрицательному, а во внешней цепи — от отрицательного к положительному.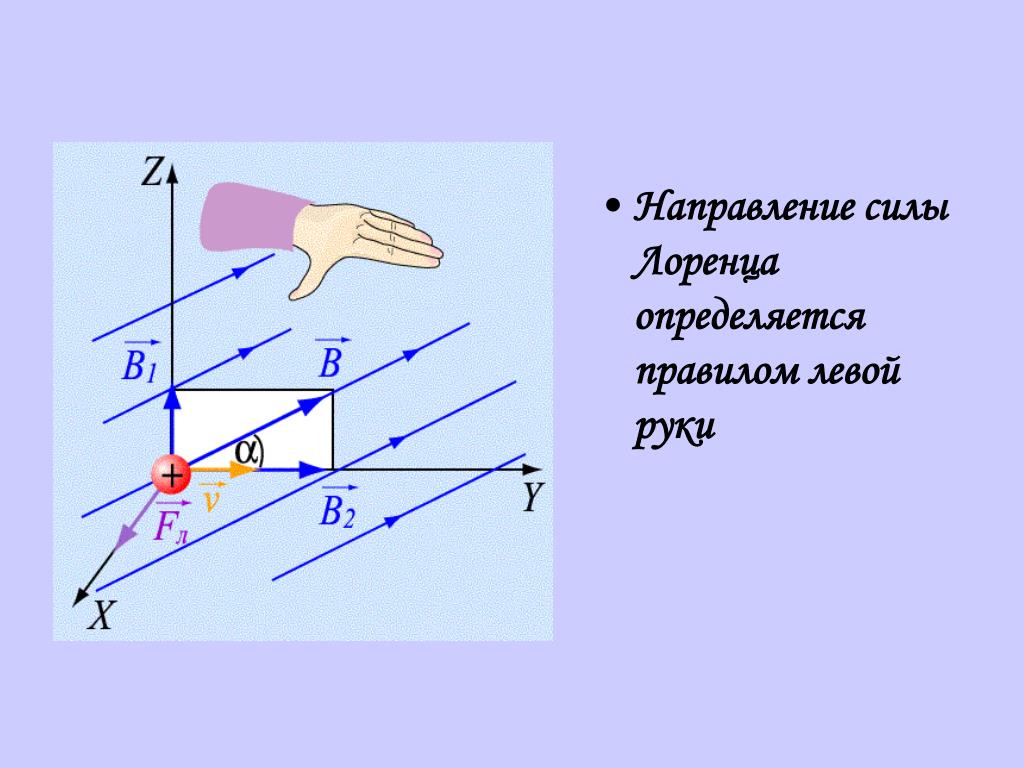
В неметаллических проводниках электроны тоже несут заряд, но механизм их движения иной. Электрон, покидая атом и тем самым превращая его в положительный ион, заставляет его захватить электрон от предыдущего атома. Тот же самый электрон, который покинул атом, отрицательно ионизирует следующий. Процесс повторяется непрерывно, пока в цепи есть ток. При этом считать направление движения заряженных частиц таким же, как и в предыдущем случае.
Полупроводники двух типов: с электронной и дырочной проводимостью. В первом случае переносчиками являются электроны, и поэтому направление движения частиц в них можно считать таким же, как в металлах и неметаллических проводниках. Во втором заряд несут виртуальные частицы — дырки. Упрощенно можно сказать, что это какие-то пустые места, в которых нет электронов. Из-за попеременного смещения электронов дырки движутся в противоположном направлении. Если соединить два полупроводника, один из которых имеет электронную, а другой дырочную проводимость, то такой прибор, называемый диодом, будет обладать выпрямляющими свойствами.
В вакууме заряд переносится электронами, движущимися от нагретого электрода (катода) к холодному (аноду). Обратите внимание, что при выпрямлении диода катод отрицателен по отношению к аноду, а вот по отношению к общему проводу, к которому подключен вторичный вывод трансформатора напротив анода, катод заряжается положительно. Противоречия здесь нет, учитывая наличие падения напряжения на любом диоде (как вакуумном, так и полупроводниковом).
В газах положительные ионы несут заряд. Направление движения зарядов в них считают обратным направлению их движения в металлах, неметаллических твердых проводниках, вакууме, а также полупроводниках с электронной проводимостью и аналогичным направлению их движения в полупроводниках с дырочной проводимостью. Ионы намного тяжелее электронов, поэтому газоразрядные устройства имеют большую инерцию. Ионные приборы с симметричными электродами не имеют односторонней проводимости, а с несимметричными имеют ее в определенном диапазоне разности потенциалов.
В жидкостях заряд всегда переносится тяжелыми ионами. В зависимости от состава электролита они могут быть как отрицательными, так и положительными. В первом случае считайте, что они ведут себя как электроны, а во втором — как положительные ионы в газах или дырки в полупроводниках.
При указании направления тока в электрической цепи, независимо от того, куда фактически движутся заряженные частицы, считайте их движением в источнике от отрицательного к положительному, а во внешней цепи от положительного к отрицательному. Указанное направление считается условным, и оно было принято до открытия строения атома.
Источники:
- текущее направление
В статье поговорим о магнитной силе Лоренца, как она действует на проводник, рассмотрим правило левой руки для силы Лоренца и момент силы, действующей на цепь с током.
Сила Лоренца — это сила, действующая на заряженную частицу, падающую с определенной скоростью в магнитное поле. Величина этой силы зависит от величины магнитной индукции магнитного поля B , электрический заряд частицы q и скорость v , с которой частица попадает в поле.
То, как магнитное поле B ведет себя по отношению к нагрузке, совершенно отличается от того, как оно наблюдается для электрического поля E . Во-первых, поле B не реагирует на загрузку. Однако при перемещении груза в поле B появляется сила, которая выражается формулой, которую можно рассматривать как определение поля B :
Таким образом, видно, что поле B действует как сила, перпендикулярная направлению вектора скорости V нагрузки и направлению вектора B . Это можно проиллюстрировать на диаграмме:
На q-диаграмме есть положительный заряд!
Единицы поля B можно получить из уравнения Лоренца. Таким образом, в системе СИ единица В равна 1 тесла (1Тл). В системе СГС полевой единицей является Гаусс (1G). 1Т=104Г
Для сравнения показана анимация движения как положительных, так и отрицательных зарядов.
Когда поле B охватывает большую площадь, заряд q, движущийся перпендикулярно направлению вектора b, , стабилизирует свое движение по круговой траектории. Однако, когда вектор v имеет составляющую, параллельную вектору b, , тогда путь заряда будет спиральным, как показано на анимации
Однако, когда вектор v имеет составляющую, параллельную вектору b, , тогда путь заряда будет спиральным, как показано на анимации
Сила Лоренца, действующая на проводник с током
Сила, действующая на проводник с током, является результатом действия силы Лоренца на движущиеся носители заряда, электроны или ионы. Если на участке длины направляющей l, как на чертеже
, движется полный заряд Q, то сила F, действующая на этот отрезок, равна
. протекающий ток I и, следовательно, сила, действующая на участок с током, выражается формулой
Для учета зависимости силы F от угла между вектором B и осью отрезка, длина отрезка l составила задается характеристикой вектора.
В металле под действием разности потенциалов движутся только электроны; ионы металлов остаются неподвижными в кристаллической решетке. В растворах электролитов подвижны анионы и катионы.
Правило левой руки Сила Лоренца – определяющее направление и возврат вектора магнитной (электродинамической) энергии.
Если левая рука расположена так, что силовые линии магнитного поля направлены перпендикулярно внутренней поверхности руки (так, что они проникают внутрь руки), а все пальцы, кроме большого, указывают направление потока положительного тока (движущейся молекулы) отведенный большой палец указывает направление электродинамической силы, действующей на положительный электрический заряд, помещенный в это поле (для отрицательного заряда сила будет противоположной).
Второй способ определить направление электромагнитной силы — расположить большой, указательный и средний пальцы под прямым углом. При таком расположении указательный палец показывает направление линий магнитного поля, направление среднего пальца — направление тока, а направление большого пальца — направление силы.
Момент силы, действующей на цепь с током в магнитном поле
Определяется также момент силы, действующей на цепь с током в магнитном поле (например, на проволочную катушку в обмотке двигателя) силой Лоренца.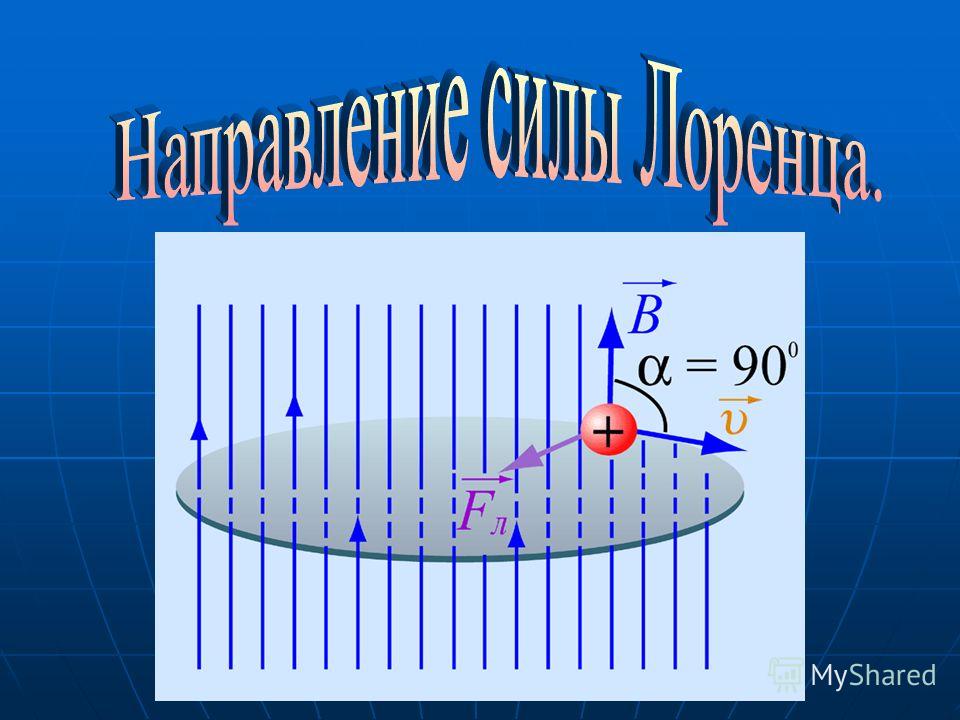 Если петля (отмеченная красным на схеме) может вращаться вокруг оси, перпендикулярной к полю В, и проводит ток I, то появляются две неуравновешенные силы F, действующие от рамы параллельно оси вращения.
Если петля (отмеченная красным на схеме) может вращаться вокруг оси, перпендикулярной к полю В, и проводит ток I, то появляются две неуравновешенные силы F, действующие от рамы параллельно оси вращения.
Сила Ампера , действующая на отрезок проводника длиной Δ l с током I находящимся в магнитном поле B ,
Выражение для силы Ампера можно записать в виде:
Это сила называется сила Лоренца . Угол α в этом выражении равен углу между скоростью и вектором магнитной индукции . Направление силы Лоренца, действующей на положительно заряженную частицу, как и направление силы Ампера, можно найти из правило левой руки или правило буравчика . Взаимное расположение векторов и для положительно заряженной частицы показано на рис. 1.18.1.
Рисунок 1.18.1. Взаимное расположение векторов , а модуль силы Лоренца численно равен площади параллелограмма, построенной на векторах и умноженной на заряд q |
Сила Лоренца направлена перпендикулярно векторам и
Когда заряженная частица движется в магнитном поле, сила Лоренца не действует. Следовательно, модуль вектора скорости не меняется при движении частицы.
Следовательно, модуль вектора скорости не меняется при движении частицы.
Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору, то частица будет двигаться по окружности радиусом
Период обращения частица в однородном магнитном поле равна
вызываемый циклотронная частота . Циклотронная частота не зависит от скорости (а значит, и от кинетической энергии) частицы. Этот факт используется в циклотронах – ускорители тяжелых частиц (протонов, ионов). Принципиальная схема циклотрона представлена на рис. 1.18.3.
Между полюсами сильного электромагнита помещают вакуумную камеру, в которой находятся два электрода в виде полых металлических полуцилиндров ( де ). На дуанты подается переменное электрическое напряжение, частота которого равна циклотронной частоте . Заряженные частицы инжектируются в центр вакуумной камеры.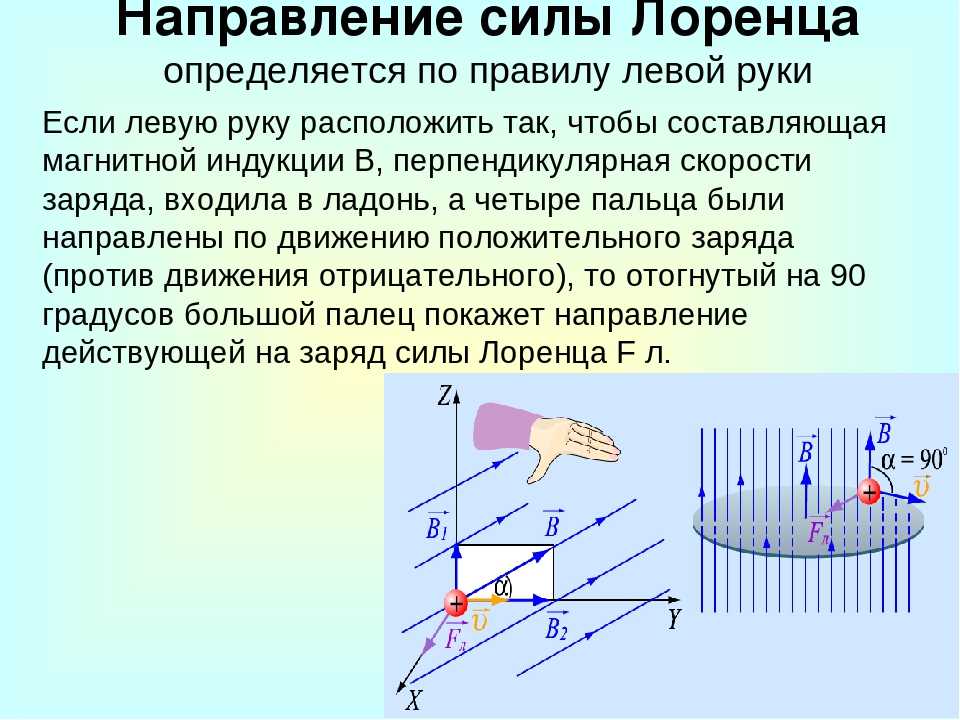 Частицы ускоряются электрическим полем в зазоре между дуантами. Внутри дуа частицы движутся под действием силы Лоренца по полуокружностям, радиус которых увеличивается по мере увеличения энергии частиц. Каждый раз, когда частица проходит через зазор между дуантами, она ускоряется электрическим полем. Таким образом, в циклотроне, как и во всех других ускорителях, заряженная частица ускоряется электрическим полем, а удерживается на траектории магнитным полем. Циклотроны позволяют ускорять протоны до энергии порядка 20 МэВ.
Частицы ускоряются электрическим полем в зазоре между дуантами. Внутри дуа частицы движутся под действием силы Лоренца по полуокружностям, радиус которых увеличивается по мере увеличения энергии частиц. Каждый раз, когда частица проходит через зазор между дуантами, она ускоряется электрическим полем. Таким образом, в циклотроне, как и во всех других ускорителях, заряженная частица ускоряется электрическим полем, а удерживается на траектории магнитным полем. Циклотроны позволяют ускорять протоны до энергии порядка 20 МэВ.
Однородные магнитные поля используются во многих приборах и, в частности, в масс-спектрометрах — приборы, с помощью которых можно измерять массы заряженных частиц — ионов или ядер различных атомов. Масс-спектрометры используются для разделения изотопов , то есть ядер атомов с одинаковым зарядом, но разными массами (например, 20 Ne и 22 Ne). Простейший масс-спектрометр показан на рис. 1.18.4. Ионы, испускаемые источником S , проходят через несколько небольших отверстий, образующих узкий пучок. Затем они попадают в Переключатель скоростей , в котором частицы движутся в скрещенных однородных электрическом и магнитном полях . Между пластинами плоского конденсатора создается электрическое поле, в зазоре между полюсами электромагнита создается магнитное поле. Начальная скорость заряженных частиц направлена перпендикулярно векторам и
Затем они попадают в Переключатель скоростей , в котором частицы движутся в скрещенных однородных электрическом и магнитном полях . Между пластинами плоского конденсатора создается электрическое поле, в зазоре между полюсами электромагнита создается магнитное поле. Начальная скорость заряженных частиц направлена перпендикулярно векторам и
На частицу, движущуюся в скрещенных электрическом и магнитном полях, действует электрическая сила и магнитная сила Лоренца . При условии E = υ B эти силы точно уравновешивают друг друга. При выполнении этого условия частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. Для заданных значений электрического и магнитного полей селектор выберет частицы, движущиеся со скоростью υ = E / B .
Далее частицы с той же скоростью попадают в камеру масс-спектрометра, в которой создается однородное магнитное поле. Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусом R = м υ / qB» . Путем измерения радиусов траекторий при известных значениях υ и B» можно определить отношение q / м . В случае изотопов ( q 1 = q 2) масс-спектрометр позволяет разделить частицы с разными массами.
Траектории частиц представляют собой окружности радиусом R = м υ / qB» . Путем измерения радиусов траекторий при известных значениях υ и B» можно определить отношение q / м . В случае изотопов ( q 1 = q 2) масс-спектрометр позволяет разделить частицы с разными массами.
Современные масс-спектрометры позволяют измерять массы заряженных частиц с точностью лучше 10–4.
Если скорость частицы имеет составляющую вдоль направления магнитного поля, то такая частица будет двигаться в однородном магнитном поле по спирали. При этом радиус спирали R зависит от модуля составляющей υ Á вектора, перпендикулярного магнитному полю и шагу спирали p – от модуля продольной составляющей υ || (рис. 1.18.5).
Таким образом, траектория заряженной частицы как бы наматывается вокруг линий магнитной индукции. Это явление используется в технологии магнитной теплоизоляции высокотемпературной плазмы , то есть полностью ионизированного газа при температуре около 10 6 К. Вещество в таком состоянии получают в установках типа «Токамак» при изучении контролируемых термоядерные реакции. Плазма не должна соприкасаться со стенками камеры. Теплоизоляция достигается созданием магнитного поля особой конфигурации. В качестве примера на рис. 1.18.6 показана траектория заряженной частицы в магнитная бутылка (или ловушка ).
Вещество в таком состоянии получают в установках типа «Токамак» при изучении контролируемых термоядерные реакции. Плазма не должна соприкасаться со стенками камеры. Теплоизоляция достигается созданием магнитного поля особой конфигурации. В качестве примера на рис. 1.18.6 показана траектория заряженной частицы в магнитная бутылка (или ловушка ).
Аналогичное явление происходит и в магнитном поле Земли, являющемся защитой всего живого от потоков заряженных частиц из космоса. Быстрые заряженные частицы из космоса (в основном от Солнца) «захватываются» магнитным полем Земли и образуют так называемые радиационные пояса (рис. 1.18.7), в котором частицы, как и в магнитных ловушках, перемещаются вперед и назад по спиральным траекториям между северным и южным магнитными полюсами за времена порядка долей секунды. Только в полярных регионах некоторые частицы проникают в верхние слои атмосферы, вызывая полярные сияния. Радиационные пояса Земли простираются от расстояний порядка 500 км до десятков радиусов Земли.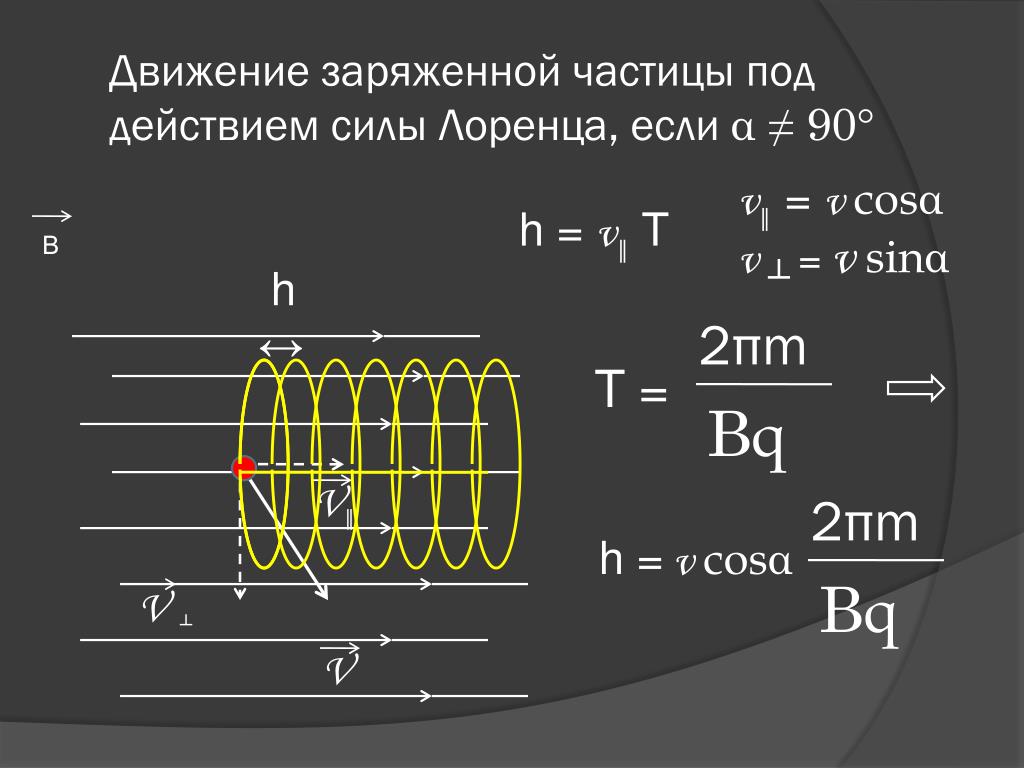 Следует помнить, что южный магнитный полюс Земли находится недалеко от северного географического полюса (на северо-западе Гренландии). Природа земного магнетизма еще не изучена.
Следует помнить, что южный магнитный полюс Земли находится недалеко от северного географического полюса (на северо-западе Гренландии). Природа земного магнетизма еще не изучена.
контрольные вопросы
1. Опишите опыты Эрстеда и Ампера.
2. Что является источником магнитного поля?
3. В чем заключается гипотеза Ампера, объясняющая существование магнитного поля постоянного магнита?
4. В чем принципиальное отличие магнитного поля от электрического?
5. Сформулировать определение вектора магнитной индукции.
6. Почему магнитное поле называют вихревым?
7. Сформулировать законы:
А) Ампер;
Б) Био-Савар-Лаплас.
8. Чему равно абсолютное значение вектора магнитной индукции поля постоянного тока?
9. Сформулировать определение единицы силы тока (ампер) в Международной системе единиц.
10. Запишите формулы, выражающие величину:
А) модуль вектора магнитной индукции;
Б) силы Ампера;
Б) силы Лоренца;
Г) период обращения частицы в однородном магнитном поле;
Е) радиус кривизны окружности при движении заряженной частицы в магнитном поле;
Тест на самообладание
Что наблюдалось в опыте Эрстеда?
1) Взаимодействие двух параллельных проводников с током.
2) Взаимодействие двух магнитных стрелок
3) Вращение магнитной стрелки вблизи проводника при пропускании через него тока.
4) Возникновение электрического тока в катушке при вталкивании в нее магнита.
Как взаимодействуют два параллельных проводника, если по ним проходят токи в одном направлении?
Привлечены;
отталкивать;
Сила и момент сил равны нулю.
Сила равна нулю, но крутящий момент не равен нулю.
Какая формула определяет выражение для модуля силы Ампера?
Какая формула определяет выражение для модуля силы Лоренца?
Б)
В)
Ж)
0,6 Н; 2) 1 Н; 3) 1,4 Н; 4) 2,4 Н.
1) 0,5 т; 2) 1 т; 3) 2 т; 4) 0,8 Т .
Электрон со скоростью V влетает в магнитное поле с модулем индукции B перпендикулярно магнитным линиям. Какое выражение соответствует радиусу орбиты электрона?
Какое выражение соответствует радиусу орбиты электрона?
Ответ: 1)
2)
4)
8. Как изменится период обращения заряженной частицы в циклотроне при увеличении ее скорости в 2 раза? (V
1) увеличится в 2 раза; 2) Увеличится в 2 раза;
3) Увеличение в 16 раз; 4) Не изменится.
9. Какая формула определяет модуль индукции магнитного поля, создаваемого в центре кругового тока с радиусом окружности R?
1)
2)
3)
4)
10. Ток в катушке I . Какая из формул определяет модуль индукции магнитного поля в середине витка длиной л с числом витков N ?
1)
2)
3)
4)
№ лаб.
Определение горизонтальной составляющей индукции магнитного поля Земли.
Краткая теория для лабораторной работы.
Магнитное поле – это материальная среда, передающая так называемые магнитные взаимодействия.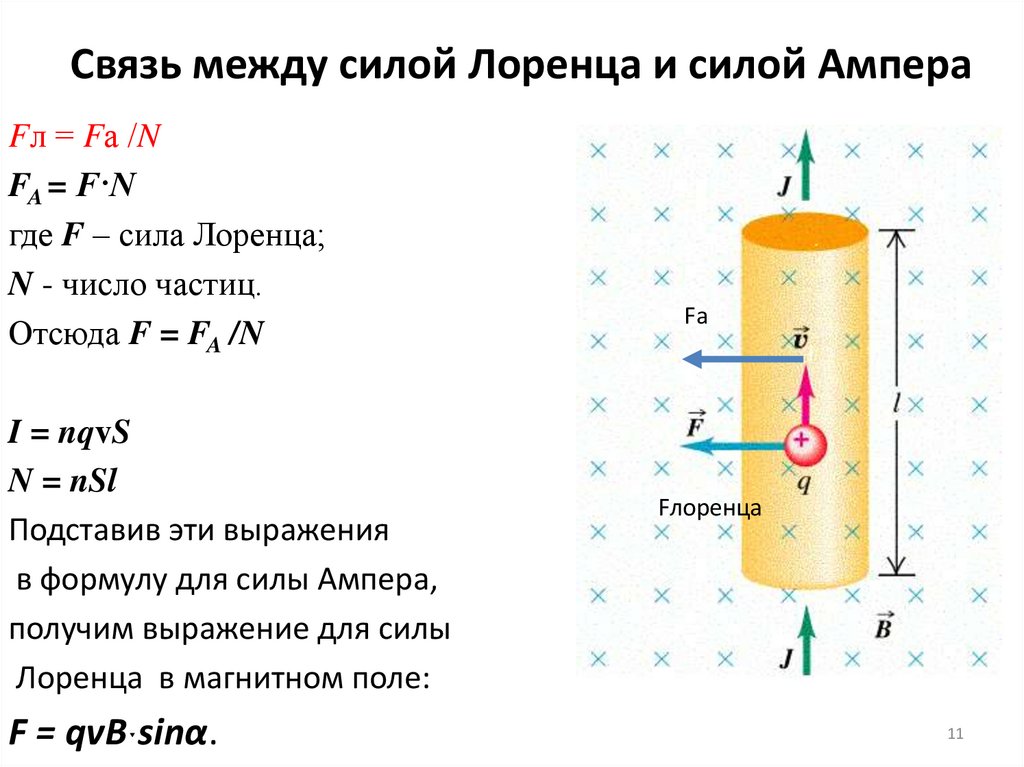 Магнитное поле является одним из проявлений электромагнитного поля.
Магнитное поле является одним из проявлений электромагнитного поля.
Источниками магнитных полей являются движущиеся электрические заряды, проводники с током и переменные электрические поля. Создаваемое движущимися зарядами (токами) магнитное поле, в свою очередь, действует только на движущиеся заряды (токи), а на неподвижные заряды не действует.
Основной характеристикой магнитного поля является вектор магнитной индукции:
Модуль вектора магнитной индукции численно равен максимальной силе, действующей со стороны магнитного поля на проводник единичной длины, по которому протекает ток единичной силы. Вектор образует правильную тройку с вектором силы и направлением тока. Таким образом, магнитная индукция – это силовая характеристика магнитного поля.
Единицей магнитной индукции в системе СИ является Тесла (Тл).
Силовыми линиями магнитного поля называются воображаемые линии, в каждой точке которых касательные совпадают с направлением вектора магнитной индукции.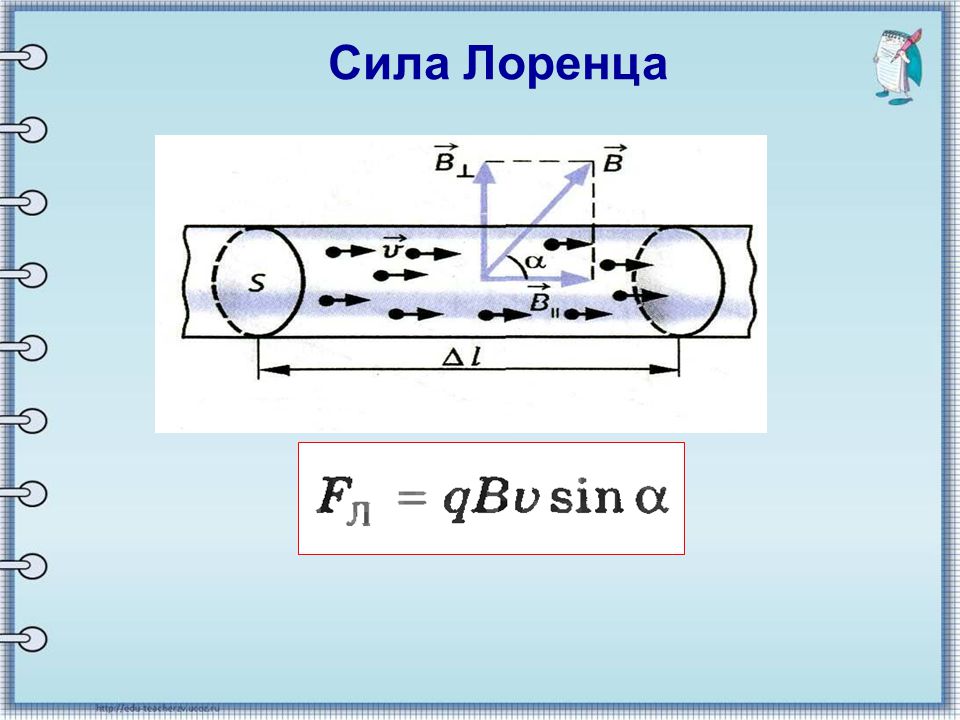 Силовые линии магнитного поля всегда замкнуты, никогда не пересекаются.
Силовые линии магнитного поля всегда замкнуты, никогда не пересекаются.
Закон Ампера определяет силовое воздействие магнитного поля на проводник с током.
Если в магнитном поле с индукцией помещается токоведущая жила, затем на каждый токонаправленный элемент проводник, действует сила Ампера, определяемая соотношением
. |
Направление силы Ампера совпадает с направлением векторного произведения
, т.е. перпендикулярно плоскости, в которой лежат векторы и (рис. 1).
Рис. 1. Определить направление силы Ампера
Если перпендикулярно, то направление силы Ампера можно определить по правилу левой руки: четыре вытянутых пальца направить вдоль тока, ладонь расположить перпендикулярно силовым линиям, тогда большой палец покажет направление силы Ампера. В основу определения магнитной индукции положен закон Ампера, т. е. соотношение (1) следует из формулы (2), записанной в скалярной форме.
е. соотношение (1) следует из формулы (2), записанной в скалярной форме.
Сила Лоренца — это сила, с которой электромагнитное поле действует на заряженную частицу, движущуюся в этом поле. Формула силы Лоренца была впервые получена Г. Лоренцем в результате обобщения опыта и имеет вид:
. |
где
— сила, действующая на заряженную частицу в электрическом поле напряженностью ;
– сила, действующая на заряженную частицу в магнитном поле.
Формулу для магнитной составляющей силы Лоренца можно получить из закона Ампера, учитывая, что ток представляет собой упорядоченное движение электрических зарядов. Если бы магнитное поле не действовало на движущиеся заряды, оно не действовало бы и на проводник с током. Магнитная составляющая силы Лоренца определяется как:
. |
Эта сила направлена перпендикулярно плоскости, в которой лежат векторы скорости и индукция магнитного поля; его направление совпадает с направлением векторного произведения
для q > 0 и с направлением
для q >0 (рис. 2).
Рис. 2. Определить направление магнитной составляющей силы Лоренца
Если вектор перпендикулярно вектору , то направление магнитной составляющей силы Лоренца для положительно заряженных частиц можно найти по правилу левой руки, а для отрицательно заряженных частиц по правилу правой руки. Так как магнитная составляющая силы Лоренца всегда направлена перпендикулярно скорости , то работы по перемещению частицы она не совершает. Он может только изменить направление скорости, искривляют траекторию частицы, т.е. действуют как центростремительная сила.
Закон Био-Савара-Лапласа используется для расчета магнитных полей (определения), создаваемых проводниками с током.
Согласно закону Био-Савара-Лапласа каждый элемент проводника с током направлен создает в точке на расстоянии от этого элемента, магнитное поле, индукция которого определяется соотношением:
. |
где
Гн/м — магнитная постоянная; мк — магнитная проницаемость среды.
Рис. 3. К закону Био-Савара-Лапласа
Направление
совпадает с направлением векторного произведения
, т.е.
перпендикулярно плоскости, в которой лежат векторы и . Одновременно
— касательная к силовой линии, направление которой можно определить по правилу буравчика: если поступательное движение острия буравчика направлено по течению, то направление вращения рукоятки будет определять направление линия магнитного поля (рис. 3).
Чтобы найти магнитное поле, создаваемое всем проводником, нужно применить принцип суперпозиции полей:
. |
Например, рассчитаем магнитную индукцию в центре кругового тока (рис. 4).
Рис. 4. К расчету поля в центре кругового тока
Для кругового тока
и
, поэтому соотношение (5) в скалярной форме имеет вид:
Закон полного тока (теорема циркуляции магнитной индукции) — еще один закон расчета магнитных полей.
Закон полного тока для магнитного поля в вакууме имеет вид:
. |
где В л – выступ на токопроводящем элементе направленного тока.
Циркуляция вектора магнитной индукции по любой замкнутой цепи равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этой цепью.
Теорема Остроградского-Гаусса для магнитного поля выглядит следующим образом:
. |
где В п – векторная проекция в нормальный на сайт dS .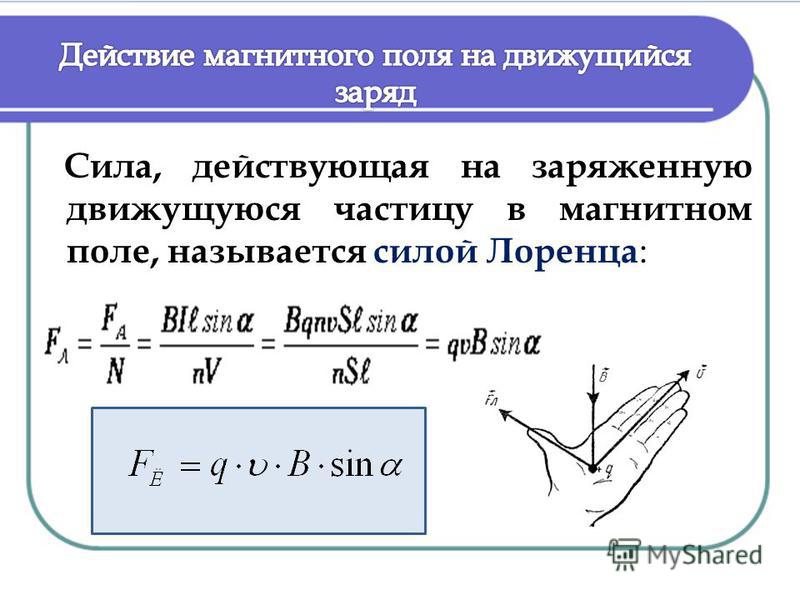
Поток вектора магнитной индукции через произвольную замкнутую поверхность равен нулю.
Характер магнитного поля следует из формул (9), (10).
Условием потенциальности электрического поля является равенство нулю циркуляции вектора напряженности
.
Потенциальное электрическое поле создается неподвижными электрическими зарядами; силовые линии не замкнуты, они начинаются на положительных зарядах и заканчиваются на отрицательных.
Из формулы (9) видно, что в магнитном поле циркуляция вектора магнитной индукции отлична от нуля, следовательно, магнитное поле не является потенциальным.
Из соотношения (10) следует, что не существует магнитных зарядов, способных создавать потенциальные магнитные поля. (В электростатике тлеет аналогичная теорема вида
.
Магнитные силовые линии замыкаются сами на себя. Такое поле называется вихревым полем. Таким образом, магнитное поле является вихревым полем. Направление силовых линий определяется по правилу буравчика В прямолинейном бесконечно длинном проводнике с током силовые линии имеют вид концентрических окружностей, охватывающих проводник (рис. 3).
3).
Наряду с силой Ампера, кулоновским взаимодействием, электромагнитными полями в физике часто встречается понятие силы Лоренца. Это явление является одним из основных в электротехнике и электронике, наряду с , и др. Он действует на заряды, движущиеся в магнитном поле. В этой статье мы кратко и наглядно рассмотрим, что такое сила Лоренца и где она применяется.
Определение
Когда электроны движутся через проводник, вокруг него возникает магнитное поле. В то же время, если поместить проводник в поперечное магнитное поле и переместить его, возникнет ЭДС электромагнитной индукции. Если по проводнику, находящемуся в магнитном поле, течет ток, на него действует сила Ампера.
Его значение зависит от протекающего тока, длины проводника, величины вектора магнитной индукции и синуса угла между силовыми линиями магнитного поля и проводником. Она рассчитывается по формуле:
Рассматриваемая сила чем-то похожа на рассмотренную выше, но действует не на проводник, а на движущуюся заряженную частицу в магнитном поле. Формула выглядит так:
Формула выглядит так:
Важно! Сила Лоренца (Fl) действует на электрон, движущийся в магнитном поле, а сила Ампера действует на проводник.
Из двух формул видно, что как в первом, так и во втором случае, чем ближе синус угла альфа к 90 градусам, тем большее влияние оказывает Fa или Fl на проводник или заряд соответственно.
Итак, сила Лоренца характеризует не изменение величины скорости, а то, какое воздействие происходит со стороны магнитного поля на заряженный электрон или положительный ион. При воздействии на них Фл не работает. Соответственно, меняется направление скорости заряженной частицы, а не ее величина.
Что касается единицы измерения силы Лоренца, то, как и в случае с другими силами в физике используется такая величина как Ньютон. Его компоненты:
Как направлена сила Лоренца?
Для определения направления силы Лоренца, как и для силы Ампера, работает правило левой руки. Значит, чтобы понять, куда направлена величина Fl, нужно раскрыть ладонь левой руки так, чтобы линии магнитной индукции вошли в руку, а вытянутые четыре пальца указывали направление вектора скорости. Затем большой палец, согнутый под прямым углом к ладони, указывает направление силы Лоренца. На картинке ниже вы видите, как определить направление.
Затем большой палец, согнутый под прямым углом к ладони, указывает направление силы Лоренца. На картинке ниже вы видите, как определить направление.
Внимание! Направление лоренцевского действия перпендикулярно движению частицы и линиям магнитной индукции.
В то же время, если быть точнее, для положительно и отрицательно заряженных частиц имеет значение направление четырех вытянутых пальцев. Описанное выше правило левой руки сформулировано для положительной частицы. Если он заряжен отрицательно, то линии магнитной индукции должны быть направлены не на раскрытую ладонь, а на ее тыльную сторону, и направление вектора Fl будет противоположным.
Теперь расскажем простыми словами, что дает нам это явление и какое реальное влияние оно оказывает на заряды. Предположим, что электрон движется в плоскости, перпендикулярной направлению линий магнитной индукции. Мы уже упоминали, что Fl не влияет на скорость, а только меняет направление движения частицы. Тогда сила Лоренца будет иметь центростремительное действие. Это отражено на рисунке ниже.
Тогда сила Лоренца будет иметь центростремительное действие. Это отражено на рисунке ниже.
Применение
Из всех областей, где используется сила Лоренца, одной из крупнейших является движение частиц в магнитном поле Земли. Если рассматривать нашу планету как большой магнит, то частицы, находящиеся вблизи северных магнитных полюсов, совершают ускоренное движение по спирали. В результате этого они сталкиваются с атомами из верхних слоев атмосферы, и мы видим северное сияние.
Однако есть и другие случаи, когда это явление применимо. Например:
- электронно-лучевые трубки. В их электромагнитных отклоняющих системах. ЭЛТ уже более 50 лет используются в самых разных устройствах, начиная от простейшего осциллографа и заканчивая телевизорами различных форм и размеров. Любопытно, что в вопросах цветопередачи и работы с графикой некоторые до сих пор используют ЭЛТ-мониторы.
- Электрические машины — генераторы и двигатели. Хотя здесь скорее действует сила Ампера.
 Но эти величины можно считать смежными. Однако это сложные устройства, при работе которых наблюдается влияние многих физических явлений.
Но эти величины можно считать смежными. Однако это сложные устройства, при работе которых наблюдается влияние многих физических явлений. - В ускорителях заряженных частиц для задания их орбит и направлений.
Заключение
Подытожим и кратко изложим четыре основных тезиса этой статьи:
- Сила Лоренца действует на заряженные частицы, движущиеся в магнитном поле. Это следует из основной формулы.
- Прямо пропорциональна скорости заряженной частицы и магнитной индукции.
- Не влияет на скорость частиц.
- Влияет на направление частицы.
Его роль довольно велика в «электрических» областях. Специалист не должен упускать из виду основные теоретические сведения об основных физических законах. Эти знания будут полезны, а также тем, кто занимается научной работой, дизайном и просто для общего развития.
Теперь вы знаете, что такое сила Лоренца, чему она равна и как действует на заряженные частицы. Если у вас остались вопросы, задавайте их в комментариях под статьей!
материалы
Сила, действующая на электрический заряд Q , движущаяся в магнитном поле со скоростью v , называется силой Лоренца и выражается формулой
(114.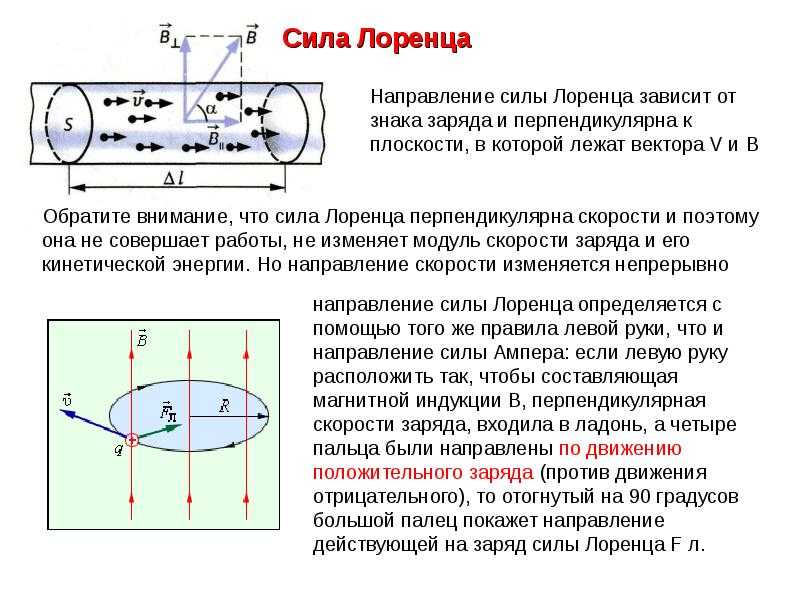 1)
1)
где B — индукция магнитного поля, в котором движется заряд.
Направление силы Лоренца определяется по правилу левой руки: если ладонь левой руки расположить так, что она включает в себя вектор В, а четыре вытянутых пальца направлены вдоль вектора v ( для Q > 0 направления I и v матч, на В — напротив), то согнутый большой палец покажет направление силы, действующей на положительный заряд. На рис. 169 показана взаимная ориентация векторов v , B (поле направлено к нам, показано точками на рисунке) и F для положительного заряда. На отрицательный заряд сила действует в противоположном направлении. Модуль силы Лоренца (см. (114.1)) равен
где — угол между v и V.
Выражение для силы Лоренца (114.1) позволяет найти ряд закономерностей движения заряженных частиц в магнитном поле.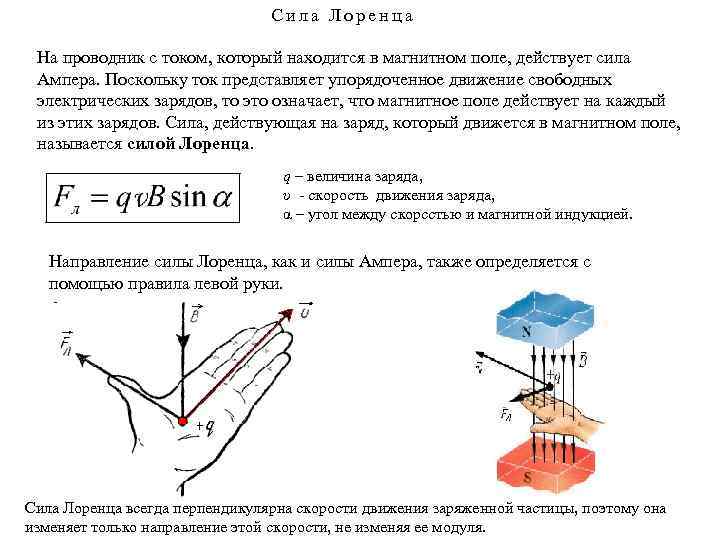 Направление силы Лоренца и направление вызванного ею отклонения заряженной частицы в магнитном поле зависят от знака заряда Q частиц. На этом основано определение знака заряда частиц, движущихся в магнитных полях.
Направление силы Лоренца и направление вызванного ею отклонения заряженной частицы в магнитном поле зависят от знака заряда Q частиц. На этом основано определение знака заряда частиц, движущихся в магнитных полях.
Если заряженная частица движется в магнитном поле со скоростью v , перпендикулярно вектору B, то сила Лоренца F знак равно В [ vB ] постоянна по модулю и нормальна к траектории частицы. Согласно второму закону Ньютона эта сила создает центростремительное ускорение. Отсюда следует, что частица будет двигаться по окружности радиусом r который определяется из условия QvB знак равно мв 2 / р , где
(115.1)
Период вращения частицы, т.е. время Т , , за которое он делает один полный оборот,
Подставляя сюда выражение (115. 1), получаем
1), получаем
(115,2)
т. е. период вращения частицы в однородном магнитном поле определяется только обратной величиной удельного заряда ( Q / m ) частиц и магнитной индукции поля, но не зависит от его скорости (при v ≪ с ). Это основа работы циклических ускорителей заряженных частиц (см. § 116).
Если скорость v заряженная частица направлена под углом к вектору В (рис. 170), то его движение можно представить в виде суперпозиции: 1) равномерное прямолинейное движение по полю со скоростью v 1 знак равно Vcos ; 2) равномерное движение со скоростью v = всин по кругу в плоскости, перпендикулярной полю. Радиус окружности определяется по формуле (115.1) (в этом случае необходимо заменить в на v = всин ).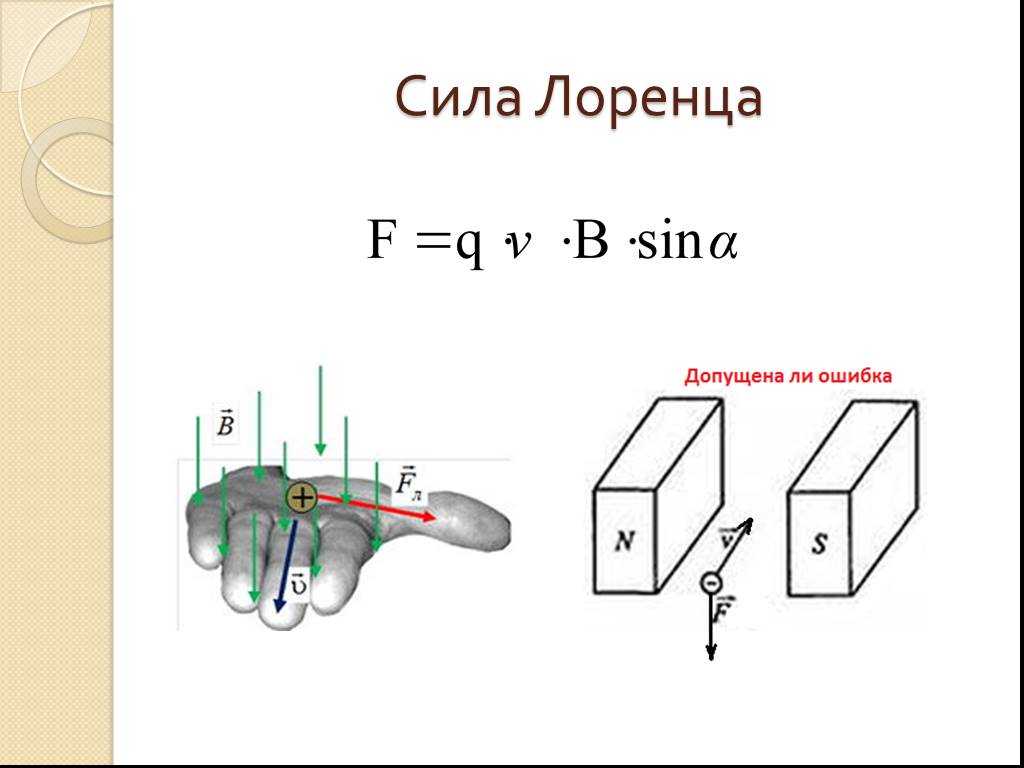 В результате сложения обоих движений возникает спиральное движение, ось которого параллельна магнитному полю (рис. 170).
В результате сложения обоих движений возникает спиральное движение, ось которого параллельна магнитному полю (рис. 170).
Рис. 170
Шаг спирали
Подставляя в последнее выражение (115.2), получаем
Направление закручивания спирали зависит от знака заряда частицы.
Если скорость m заряженной частицы составляет угол a с направлением вектора B неоднородная магнитного поля, индукция которого возрастает в направлении движения частицы, то r и A уменьшаются с увеличением B . Это основа для фокусировки заряженных частиц в магнитном поле.
Сила, действующая на движущийся заряд в магнитном поле – Колледж физики
Глава 22 Магнетизм
Резюме
- Опишите влияние магнитных полей на движущиеся заряды.
- Используйте правило правой руки 1, чтобы определить скорость заряда, направление магнитного поля и направление магнитной силы, действующей на движущийся заряд.

- Рассчитайте магнитную силу, действующую на движущийся заряд.
Каков механизм, посредством которого один магнит воздействует на другой? Ответ связан с тем фактом, что весь магнетизм вызван током, потоком заряда. Магнитные поля воздействуют на движущиеся заряды , и поэтому они воздействуют на другие магниты, все из которых имеют движущиеся заряды.
Магнитная сила, действующая на движущийся заряд, является одной из самых фундаментальных известных. Магнитная сила так же важна, как электростатическая или кулоновская сила. И все же магнитная сила более сложна как по количеству воздействующих на нее факторов, так и по своему направлению, чем относительно простая кулоновская сила. Величина магнитной силы [латекс]{F}[/латекс] на заряд [латекс]{q}[/латекс], движущийся со скоростью [латекс]{v}[/латекс] в магнитном поле прочность [латекс]{B}[/латекс] равна
[латекс] {F = qvB \;\text{sin} \theta},[/latex]
, где [latex]{\theta}[/latex] — угол между направлениями [latex]\textbf{v}[/latex] и [latex]\textbf{B}[/latex]. Эту силу часто называют силой Лоренца . Фактически именно так мы определяем напряженность магнитного поля [латекс]{В}[/латекс] — через силу, действующую на заряженную частицу, движущуюся в магнитном поле. Единица СИ для напряженности магнитного поля [латекс]{B}[/латекс] называется тесла (Тл) в честь эксцентричного, но блестящего изобретателя Николы Теслы (1856–1819 гг.).43). Чтобы определить, как тесла соотносится с другими единицами СИ, мы решаем [латекс]{F = qvB \;\text{sin} \theta}[/latex] для [латекс]{B}[/латекс].
Эту силу часто называют силой Лоренца . Фактически именно так мы определяем напряженность магнитного поля [латекс]{В}[/латекс] — через силу, действующую на заряженную частицу, движущуюся в магнитном поле. Единица СИ для напряженности магнитного поля [латекс]{B}[/латекс] называется тесла (Тл) в честь эксцентричного, но блестящего изобретателя Николы Теслы (1856–1819 гг.).43). Чтобы определить, как тесла соотносится с другими единицами СИ, мы решаем [латекс]{F = qvB \;\text{sin} \theta}[/latex] для [латекс]{B}[/латекс].
[латекс] {B =} [/ латекс] [латекс] {\ гидроразрыва {F} {qv \; \ текст {грех} \; \ тета}} [/ латекс]
Поскольку [латекс]{\текст{грех} \;\тета}[/латекс] не имеет единиц измерения, тесла равен
. [латекс] {1 \;\textbf{T} =}[/латекс] [латекс]{\frac{1 \;\textbf{N}}{\text{C} \cdot \;\text{m/ s}}}[/латекс] [латекс]{=}[/латекс] [латекс]{\ гидроразрыва {1 \;\textbf{N}}{\textbf{A} \cdot \;\text{m}} }[/латекс] 9{-5} \;\textbf{T}}[/latex], или 0,5 г.
Направление магнитной силы [латекс]\textbf{F}[/латекс] перпендикулярно плоскости, образованной [латекс]\текстбф{в}[/латекс] и [латекс]\текстбф{В}[ /латекс], как определено правилом правой руки 1 (или RHR-1), которое показано на рисунке 1. RHR-1 утверждает, что для определения направления магнитной силы на положительно движущемся заряде вы большой палец правой руки в направлении [латекс]\textbf{v}[/латекс], пальцы в направлении [латекс]\текстбф{В}[/латекс], а перпендикуляр к ладони указывает на направление [латекс]\textbf{F}[/латекс]. Один из способов запомнить это состоит в том, что существует одна скорость, и поэтому ее представляет большой палец. Есть много линий поля, поэтому пальцы представляют их. Сила направлена в том направлении, куда вы бы толкнули ладонью. Сила, действующая на отрицательный заряд, направлена прямо противоположно силе на положительном заряде.
Рис. 1. Магнитные поля воздействуют на движущиеся заряды. Эта сила является одной из самых основных известных. Направление магнитной силы на движущийся заряд перпендикулярно плоскости, образованной v и B , и следует правилу правой руки-1 (RHR-1), как показано. Величина силы пропорциональна q , v , B и синусу угла между v и B .
Эта сила является одной из самых основных известных. Направление магнитной силы на движущийся заряд перпендикулярно плоскости, образованной v и B , и следует правилу правой руки-1 (RHR-1), как показано. Величина силы пропорциональна q , v , B и синусу угла между v и B .Выполнение соединений: заряды и магниты
На статические заряды не действует магнитная сила. Однако на движущиеся заряды действует магнитная сила. Когда заряды неподвижны, их электрические поля не действуют на магниты. Но когда заряды движутся, они создают магнитные поля, которые воздействуют на другие магниты. При относительном движении возникает связь между электрическим и магнитным полями — одно влияет на другое.
Пример 1. Расчет магнитной силы: магнитное поле Земли на заряженном стеклянном стержне
За исключением компаса, вы редко видите или лично испытываете на себе силы, обусловленные слабым магнитным полем Земли. Чтобы проиллюстрировать это, предположим, что в физической лаборатории вы натираете стеклянную палочку шелком, помещая на нее положительный заряд в 20 нКл. Вычислите силу, действующую на стержень со стороны магнитного поля Земли, если бросить его с горизонтальной скоростью 10 м/с строго на запад в месте, где поле Земли направлено строго на север параллельно земле. (Направление силы определяется правилом правой руки 1, как показано на рисунке 2.)
Чтобы проиллюстрировать это, предположим, что в физической лаборатории вы натираете стеклянную палочку шелком, помещая на нее положительный заряд в 20 нКл. Вычислите силу, действующую на стержень со стороны магнитного поля Земли, если бросить его с горизонтальной скоростью 10 м/с строго на запад в месте, где поле Земли направлено строго на север параллельно земле. (Направление силы определяется правилом правой руки 1, как показано на рисунке 2.)
Стратегия
Нам известны заряд, его скорость, напряженность и направление магнитного поля. Таким образом, мы можем использовать уравнение [латекс]{F = qvB \;\text{sin} \;\theta}[/latex], чтобы найти силу.
Решение 9{-11} \;\textbf{N}} \end{array}.[/latex]
Обсуждение
Этой силой можно пренебречь на любом макроскопическом объекте, что согласуется с опытом. (Оно вычисляется только с точностью до одной цифры, поскольку поле Земли меняется в зависимости от местоположения и выражается только одной цифрой.) Однако магнитное поле Земли оказывает очень важное воздействие, особенно на субмикроскопические частицы. Некоторые из них рассматриваются в главе 22.5 «Сила движущегося заряда в магнитном поле: примеры и приложения».
- Магнитные поля воздействуют на движущийся заряд силой q , величина которой равна
[латекс] {F = qvB \;\text{sin} \;\theta},[/latex]
, где [latex]{\theta}[/latex] — угол между направлениями [latex]\textbf{v}[/latex] и [latex]\textbf{B}[/latex].
- Единицей СИ для напряженности магнитного поля [латекс]\textbf{B}[/латекс] является тесла (Тл), которая связана с другими единицами соотношения
[латекс] {1 \;\textbf{T} =}[/латекс] [латекс]{\frac{1 \;\textbf{N}}{\text{C} \cdot \;\text{m/ s}}}[/латекс] [латекс]{=}[/латекс] [латекс]{\ гидроразрыва {1 \;\textbf{N}}{\textbf{A} \cdot \;\text{m}} }[/латекс]
- Направление силы на движущийся заряд задается правилом правой руки 1 (RHR-1): Направьте большой палец правой руки в направлении [латекс]{v}[/латекс], пальцы в направление [латекс]{B}[/латекс], а перпендикуляр к ладони указывает в направлении [латекс]{F}[/латекс].

- Сила перпендикулярна плоскости, образованной [латексом]\textbf{v}[/латексом] и [латексом]\текстбф{В}[/латексом]. Поскольку сила равна нулю, если [латекс]\textbf{v}[/латекс] параллелен [латексу]\текстбф{В}[/латексу], заряженные частицы часто следуют за силовыми линиями магнитного поля, а не пересекают их.
- Правило правой руки 1 (RHR-1)
- правило для определения направления магнитной силы на положительно движущийся заряд: когда большой палец правой руки указывает в направлении скорости заряда [latex]\textbf{v}[/latex], а остальные пальцы указывают в направление магнитного поля [латекс]\textbf{B}[/латекс], тогда сила на заряд перпендикулярна и направлена от ладони; сила на отрицательный заряд перпендикулярна и направлена на ладонь
- сила Лоренца
- сила, действующая на заряд, движущийся в магнитном поле
- тесла
- Тл — единица напряженности магнитного поля в системе СИ; [латекс]{1 \;\textbf{T} = \frac{1 \;\textbf{N}}{\textbf{A} \cdot \;\text{m}}}[/latex]
- магнитная сила
- сила, действующая на заряд при его движении через магнитное поле; сила Лоренца
- Гаусс
- Гс — единица напряженности магнитного поля; [латекс]{1 \;\textbf{G} = 10^{-4} \;\textbf{T}}[/латекс]
Как определить правило левой руки силы Лоренца.
 сила Лоренца. Единицы силы Лоренца
сила Лоренца. Единицы силы Лоренца« Физика – 11 класс
Магнитное поле действует с силой на движущиеся заряженные частицы, в том числе на проводники с током.
Какая сила действует на одну частицу?
1.
Сила, действующая на движущаяся заряженная частица со стороны магнитного поля называется силой Лоренца в честь великого голландского физика Г. Лоренца, создавшего электронную теорию строения вещества.
Силу Лоренца можно найти с помощью закона Ампера.
Модуль силы Лоренца равен отношению модуля силы F, действующей на отрезок проводника длиной Δl, к числу N заряженных частиц, упорядоченно движущихся в этом сечении проводника:
Так как сила (сила Ампера), действующая на сечение проводника со стороны магнитного поля
, равна F = | я | BΔl sin α ,
и сила тока в проводнике равна I = qnvS
где
q — заряд частицы
n — концентрация частицы (т.е. количество зарядов в единице объема)
v — скорость частицы
S — сечение проводника.
Тогда получим:
На каждый движущийся заряд со стороны магнитного поля действует сила Лоренца равная:
где α угол между вектором скорости и вектором магнитной индукции.
Сила Лоренца перпендикулярна векторам и.
2.
Направление силы Лоренца
Направление силы Лоренца определяется с помощью тех же правил левой руки , что и направление силы Ампера:
Если левая рука расположена так, что составляющая магнитная индукция, перпендикулярная скорости заряда, поступает на ладонь, а четыре вытянутых пальца направлены по ходу движения положительного заряда (против движения отрицательного), затем большой палец отгибается 90° укажет направление силы Лоренца, действующей на заряд F л
3.
Если в пространстве, где движется заряженная частица, имеется и электрическое поле, и магнитное поле, то полная сила, действующая на заряд равно: = el + l где сила, с которой электрическое поле действует на заряд q, равна F el = q . ..
..
4.
Сила Лоренца не совершает работу , так как она перпендикулярна частице вектор скорости.
Это означает, что сила Лоренца не изменяет кинетическую энергию частицы и, следовательно, модуль ее скорости.
Под действием силы Лоренца изменяется только направление скорости частицы.
5.
Движение заряженной частицы в однородном магнитном поле
Существует однородное магнитное поле, направленное перпендикулярно начальной скорости частицы.
Сила Лоренца зависит от модулей векторов скорости частиц и индукции магнитного поля.
Магнитное поле не изменяет модуль скорости движущейся частицы, а значит, модуль силы Лоренца остается неизменным.
Сила Лоренца перпендикулярна скорости и, следовательно, определяет центростремительное ускорение частицы.
Неизменность по модулю центростремительного ускорения частицы, движущейся с постоянной по модулю скоростью, означает, что
В однородном магнитном поле заряженная частица движется равномерно по окружности радиусом r .
По второму закону Ньютона
Тогда радиус окружности, по которой движется частица, равен:
Время, за которое частица совершает полный оборот (орбитальный период), равно:
6.
С помощью действия магнитного поля на движущийся заряд.
Действие магнитного поля на движущийся заряд используется в телевизионных кинескопах, в которых летящие к экрану электроны отклоняются магнитным полем, создаваемым специальными катушками.
Сила Лоренца используется в циклотроне, ускорителе заряженных частиц, для получения частиц высокой энергии.
Устройство масс-спектрографов также основано на действии магнитного поля, что позволяет точно определять массы частиц.
Голландский физик Х. А. Лоренц в конце XIX века. установил, что сила, действующая со стороны магнитного поля на движущуюся заряженную частицу, всегда перпендикулярна направлению движения частицы и силовым линиям магнитного поля, в котором движется эта частица. Направление силы Лоренца можно определить по правилу левой руки. Если расположить ладонь левой руки так, чтобы четыре вытянутых пальца указывали направление движения заряда, а вектор магнитной индукции поля входил в отведенный большой палец, то он укажет направление силы Лоренца, действующей на положительный заряд.
Если расположить ладонь левой руки так, чтобы четыре вытянутых пальца указывали направление движения заряда, а вектор магнитной индукции поля входил в отведенный большой палец, то он укажет направление силы Лоренца, действующей на положительный заряд.
Если заряд частицы отрицательный, то сила Лоренца будет направлена в противоположную сторону.
Модуль силы Лоренца легко определяется из закона Ампера и равен:
F = | q | vB грех? ,
где q — заряд частицы, v — скорость ее движения, ? — угол между векторами скорости и индукции магнитного поля.
Если кроме магнитного поля существует еще и электрическое поле, действующее на заряд с силой , то общая сила, действующая на заряд, равна:
.
Часто именно эту силу называют силой Лоренца, а силу выражают формулой ( F = | q | vB грех? ) называются магнитной частью силы Лоренца .
Так как сила Лоренца перпендикулярна направлению движения частицы, то она не может изменить свою скорость (не совершает работу), а может только изменить направление своего движения, то есть искривить траекторию.
Такое искривление траектории электронов в телевизионном кинескопе легко наблюдать, если поднести к его экрану постоянный магнит — изображение исказится.
Движение заряженной частицы в однородном магнитном поле. Пусть заряженная частица влетает со скоростью v в однородное магнитное поле перпендикулярно линиям напряженности.
Сила, действующая на частицу со стороны магнитного поля, заставит ее равномерно вращаться по окружности радиусом r , которое легко найти, используя второй закон Ньютона, выражение целенаправленного ускорения и формулу ( F = | q | vB грех? ):
.
Отсюда получаем
.
, где m — масса частицы.
Применение силы Лоренца.

Действие магнитного поля на движущиеся заряды используется, например, в масс-спектрографах , которые позволяют разделять заряженные частицы по их удельным зарядам, т. е. отношению заряда частицы к ее массе, и по полученным результатам точно определять массы частиц.
Вакуумная камера прибора помещена в поле (вектор индукции перпендикулярен рисунку). Заряженные частицы (электроны или ионы), ускоренные электрическим полем, описывая дугу, падают на фотопластинку, где оставляют след, что позволяет с большой точностью измерить радиус траектории r … Этот радиус используется для определения удельного заряда иона. Зная заряд иона, можно легко вычислить его массу.
Электрические заряды, движущиеся в определенном направлении, создают вокруг себя магнитное поле, скорость распространения которого в вакууме равна скорости света, а в других средах немного меньше. Если движение заряда происходит во внешнем магнитном поле, то происходит взаимодействие между внешним магнитным полем и магнитным полем заряда.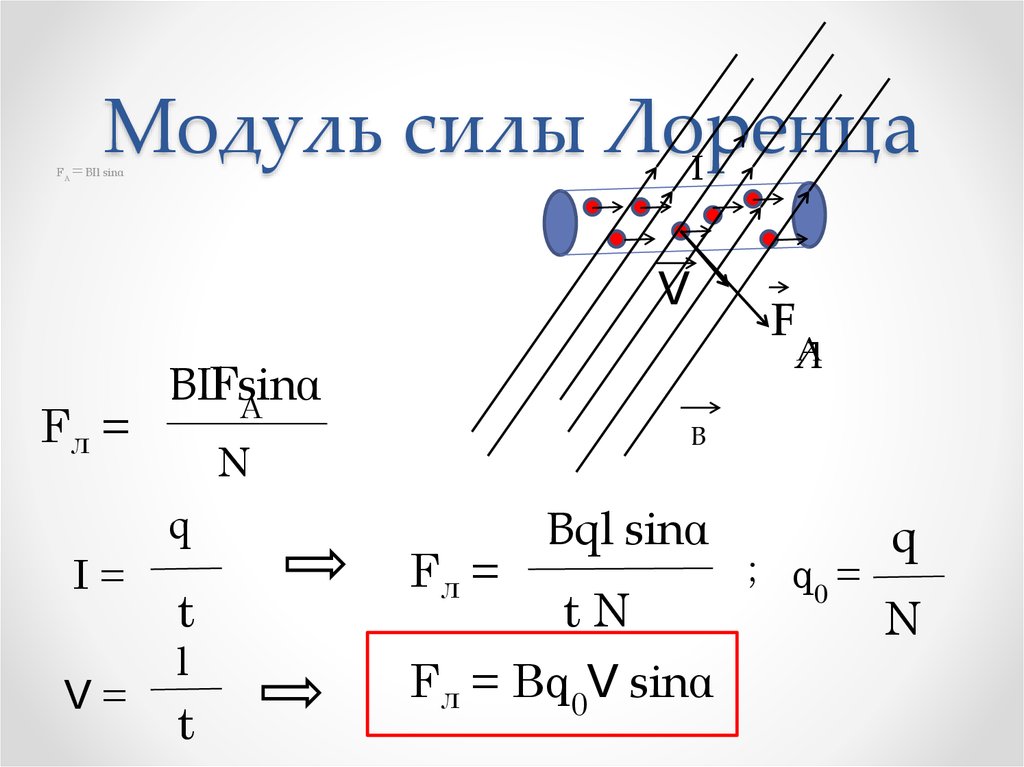 Поскольку электрический ток представляет собой направленное движение заряженных частиц, то сила, которая будет действовать в магнитном поле на проводник с током, будет результатом действия отдельных (элементарных) сил, каждая из которых приложена к элементарному носителю заряда.
Поскольку электрический ток представляет собой направленное движение заряженных частиц, то сила, которая будет действовать в магнитном поле на проводник с током, будет результатом действия отдельных (элементарных) сил, каждая из которых приложена к элементарному носителю заряда.
Процессы взаимодействия внешнего магнитного поля и движущихся зарядов исследовал Г. Лоренц, который в результате многих своих опытов вывел формулу для расчета силы, действующей на движущуюся заряженную частицу со стороны магнитное поле. Вот почему сила, действующая на заряд, движущийся в магнитном поле, называется силой Лоренца.
Сила, действующая на проводник со стороны стока (из закона Ампера), будет равна:
По определению сила тока равна I = qn (q — заряд, n — число зарядов, прошедших через сечение проводника за 1 с). Отсюда следует:
Где: n 0 — количество зарядов, содержащихся в единице объема, V — скорость их движения, S — площадь поперечного сечения проводника. Тогда:
Подставив это выражение в формулу Ампера, получим:
Эта сила будет действовать на все заряды в объеме проводника: V = Sl. Число зарядов, находящихся в данном объеме, будет равно:
Число зарядов, находящихся в данном объеме, будет равно:
Тогда выражение для силы Лоренца будет:
Отсюда можно заключить, что сила Лоренца, действующая на заряд q, движущийся в магнитном поле поля, пропорциональна заряду, магнитной индукции внешнего поля, скорости его движения и синусу угла между V и B, то есть:
Направление движения заряженных частиц принимается за направление движения положительных зарядов. Следовательно, направление данной силы можно определить с помощью правила левой руки.
Сила, действующая на отрицательные заряды, будет направлена в противоположную сторону.
Сила Лоренца всегда направлена перпендикулярно скорости V движения заряда и поэтому не совершает работы. Меняется только направление V, а кинетическая энергия и величина скорости заряда при его движении в магнитном поле остаются неизменными.
Когда заряженная частица движется одновременно в магнитном и электрическом полях, на нее будет действовать сила:
Где Е — напряженность электрического поля.
Рассмотрим небольшой пример:
Электрон, прошедший ускоряющую разность потенциалов 3,52∙10 3 В, попадает в однородное магнитное поле, перпендикулярное линиям индукции. Радиус траектории r = 2 см, индукция поля 0,01 Тл. Определить удельный заряд электрона.
Удельный заряд — величина, равная отношению заряда к массе, то есть е/м.
В магнитном поле с индукцией B сила Лоренца F L = BeV действует на заряд, движущийся со скоростью V перпендикулярно линиям индукции. Под его действием заряженная частица будет двигаться по дуге окружности. Так как в этом случае сила Лоренца вызовет центростремительное ускорение, то согласно второму закону Ньютона можно записать:
Кинетическая энергия, которая будет равна мВ 2/2, электрон приобретает за счет работы А силы электрического поля (A = eU), подставив его в уравнение, получим.
Сила, действующая со стороны магнитного поля на движущуюся электрически заряженную частицу.
где q — заряд частицы;
В – скорость заряда;
а — угол между вектором скорости заряда и вектором магнитной индукции.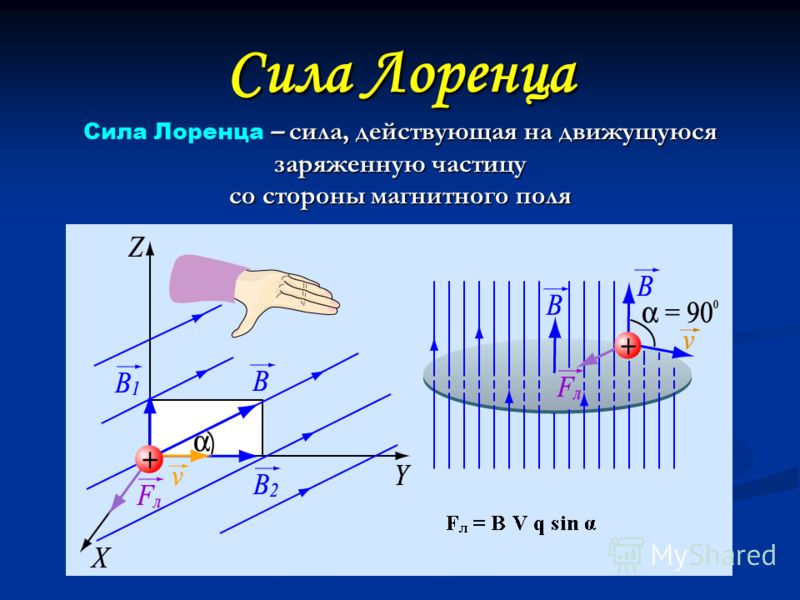
Направление силы Лоренца определяется по правилу левой руки:
Если положить левую руку так, чтобы составляющая вектора индукции, перпендикулярная скорости, попадала на ладонь, а четыре пальца располагались в направление скорости движения положительного заряда (или против направления скорости отрицательного заряда), то согнутый большой палец укажет направление силы Лоренца:
Поскольку сила Лоренца всегда перпендикулярна скорости заряда, она не совершает работы (т. е. не меняет величину скорости заряда и его кинетической энергии).
Если заряженная частица движется параллельно силовым линиям магнитного поля, то Fl = 0, и заряд в магнитном поле движется равномерно и прямолинейно.
Если заряженная частица движется перпендикулярно силовым линиям магнитного поля, то сила Лоренца центростремительна:
и создает центростремительное ускорение, равное:
В этом случае частица движется по окружности.
Согласно второму закону Ньютона: сила Лоренца равна произведению массы частицы на центростремительное ускорение:
тогда радиус окружности равен:
и период обращения заряда в магнитном поле:
Так как электрический ток есть упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды. Если ввести проводник с током в магнитное поле (рис. 96, а), то мы увидим, что в результате сложения магнитных полей магнита и проводника результирующее магнитное поле увеличится с одной стороны проводника (на рисунке выше) и ослабит магнитное поле с другой стороны проводника (на рисунке ниже). В результате действия двух магнитных полей произойдет искривление магнитных линий и они, стремясь сжаться, будут толкать проводник вниз (рис. 96, б).
Если ввести проводник с током в магнитное поле (рис. 96, а), то мы увидим, что в результате сложения магнитных полей магнита и проводника результирующее магнитное поле увеличится с одной стороны проводника (на рисунке выше) и ослабит магнитное поле с другой стороны проводника (на рисунке ниже). В результате действия двух магнитных полей произойдет искривление магнитных линий и они, стремясь сжаться, будут толкать проводник вниз (рис. 96, б).
Направление силы, действующей на проводник с током в магнитном поле, можно определить по «правилу левой руки». Если левую руку поместить в магнитное поле так, что магнитные линии, выходящие из Северного полюса, как бы входят в ладонь, а четыре вытянутых пальца совпадают с направлением тока в проводнике, то согнутый большой палец руки будет показать направление силы. Сила Ампера, действующая на элемент длины проводника, зависит от: величины магнитной индукции В, величины тока в проводнике I, от элемента длины проводника и от синуса угла а между направлением элемента длины проводника и направлением магнитного поля.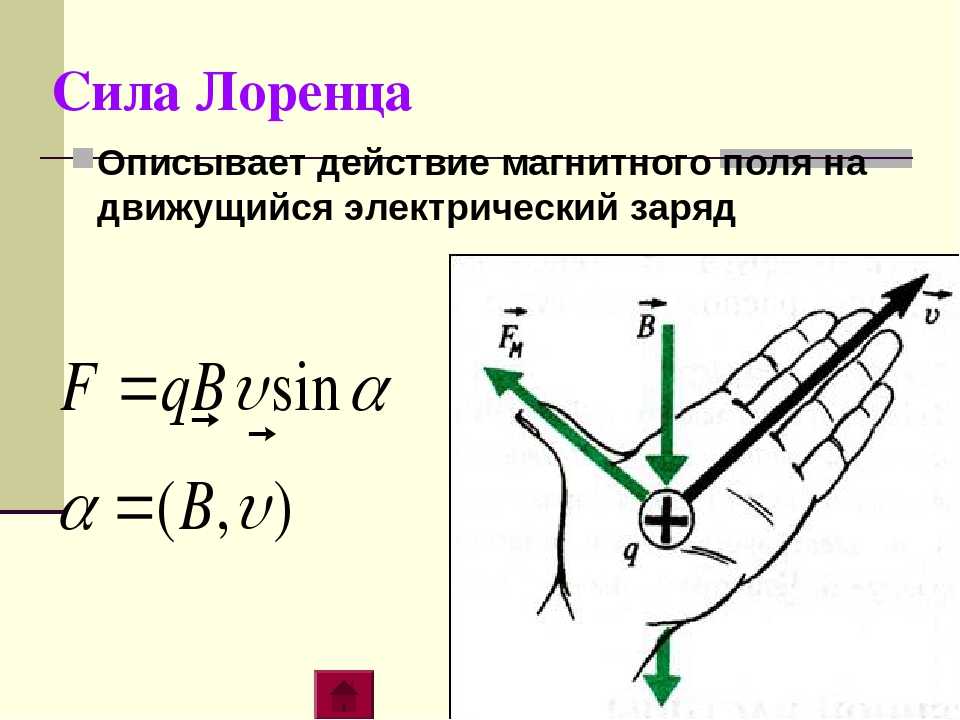
Эту зависимость можно выразить формулой:
Для прямого проводника конечной длины, расположенного перпендикулярно направлению однородного магнитного поля, сила, действующая на проводник, будет:
Из последней формулы, определяем размерность магнитной индукции.
Так как размерность силы:
то есть размерность индукции такая же, как была получена нами из закона Био и Савара.
Тесла (единица магнитной индукции)
Тесла, единица магнитной индукции Международная система единиц, равна магнитной индукции, при которой магнитный поток проходит через поперечное сечение площадью 1 м 2 равно 1 Вебера. Назван в честь Н. Теслы. Условные обозначения: русский tl, международный т. 1 tl = 104 rs ( gauss ) .
Магнитный момент , магнитный дипольный момент — основная величина, характеризующая магнитные свойства вещества. Магнитный момент измеряется в А⋅м 2 или Дж/Тл (СИ), или эрг/Гс (СГС), 1 эрг/Г = 10 -3 Дж/Тл. Специфической единицей элементарного магнитного момента является магнетон Бора. В случае плоской цепи с электрическим током магнитный момент рассчитывается как
Магнитный момент измеряется в А⋅м 2 или Дж/Тл (СИ), или эрг/Гс (СГС), 1 эрг/Г = 10 -3 Дж/Тл. Специфической единицей элементарного магнитного момента является магнетон Бора. В случае плоской цепи с электрическим током магнитный момент рассчитывается как
где — сила тока в контуре, — площадь контура, — единичный вектор нормали к плоскости контура. Направление магнитного момента обычно находят по правилу буравчика: если вращать ручку карданного подвеса в направлении тока, то направление магнитного момента совпадет с направлением поступательного движения карданного подвеса.
Для произвольного замкнутого контура магнитный момент находится из:
где радиус-вектор, проведенный от начала координат к элементу длины контура
В общем случае произвольного распределения токов в среде:
где — плотность тока в элементе объема.
Итак, на цепь с током в магнитном поле действует крутящий момент. Контур ориентирован в данной точке поля только одним способом. Примем положительное направление нормали за направление магнитного поля в данной точке. Крутящий момент прямо пропорционален величине тока I , площадь контура S и синус угла между направлением магнитного поля и нормалью.
Примем положительное направление нормали за направление магнитного поля в данной точке. Крутящий момент прямо пропорционален величине тока I , площадь контура S и синус угла между направлением магнитного поля и нормалью.
здесь M — крутящий момент или момент силы , — магнитный момент Схема (аналогично — электрический момент диполя).
В неоднородном поле () формула справедлива, если размер контура достаточно мал (тогда поле можно считать примерно однородным в пределах контура). Следовательно, цепь с током все же стремится повернуться так, чтобы ее магнитный момент был направлен по линиям вектора.
Но, кроме того, на контур действует результирующая сила (в случае однородного поля и. Эта сила действует на контур с током или на постоянный магнит с моментом и втягивает их в область более сильного магнитном поле
Работа по перемещению контура с током в магнитном поле
Нетрудно доказать, что работа по перемещению контура с током в магнитном поле равна, где и — магнитные потоки через площадь контура в конечном и начальном положениях. Эта формула справедлива, если ток контура постоянен , т.е. при перемещении контура не учитывается явление электромагнитной индукции.
Эта формула справедлива, если ток контура постоянен , т.е. при перемещении контура не учитывается явление электромагнитной индукции.
Формула справедлива и для больших контуров в сильно неоднородном магнитном поле (при условии I = const).
Наконец, если цепь с током не сместить, а изменить магнитное поле, т.е. изменить магнитный поток через поверхность, охваченную контуром, от значения до, то для этого нужно проделать ту же работу. Эта работа называется работой по изменению магнитного потока, связанного с цепью. Поток вектора магнитной индукции (магнитный поток) через площадь dS называется скалярной физической величиной, которая равна
где B n = Вcosα — проекция вектора V на направление нормали к участку dS (α — угол между векторами n и V ), d S = dS n — вектор, модуль которого равен dS, а его направление совпадает с направлением нормали n на сайт. Векторный поток V может быть как положительным, так и отрицательным, в зависимости от знака cosα (задается выбором положительного направления нормали n ). Вектор потока V обычно связан с цепью, по которой протекает ток. В данном случае мы указали положительное направление нормали к контуру: оно связано с током по правилу правого винта. Это означает, что магнитный поток, создаваемый контуром через ограниченную им самим поверхность, всегда положителен.
Вектор потока V обычно связан с цепью, по которой протекает ток. В данном случае мы указали положительное направление нормали к контуру: оно связано с током по правилу правого винта. Это означает, что магнитный поток, создаваемый контуром через ограниченную им самим поверхность, всегда положителен.
Поток вектора магнитной индукции Ф B через произвольную заданную поверхность S равен
Для однородного поля и плоской поверхности, перпендикулярной вектору В , B n = B = const и
От В этой формуле за единицу магнитного потока устанавливается вебер (Вб): 1 Вб — магнитный поток, проходящий через плоскую поверхность площадью 1 м 2 , которая расположена перпендикулярно однородному магнитному полю и индукция которого составляет 1 Тл (1 Втб = 1 Тл м2).
Теорема Гаусса для поля B : поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:
Эта теорема является отражением того факта, что отсутствуют магнитные заряды , в результате чего линии магнитной индукции не имеют ни начала, ни конца и замкнуты.
Поэтому для потоков векторов V и E через замкнутую поверхность в вихревых и потенциальных полях получаются разные формулы.
В качестве примера найдем поток вектора V через соленоид. Магнитная индукция однородного поля внутри соленоида с сердечником с магнитной проницаемостью μ равна
. Магнитный поток через один виток соленоида площадью S равен
, а полный магнитный поток, связанный с все витки соленоида и называется потокосцепление ,
ОПРЕДЕЛЕНИЕ
сила Лоренца — сила, действующая на точечную заряженную частицу, движущуюся в магнитном поле.
Равен произведению заряда, модуля скорости частицы, модуля вектора индукции магнитного поля и синуса угла между вектором магнитного поля и скоростью частицы.
Здесь – сила Лоренца, – заряд частицы, – модуль вектора индукции магнитного поля, – скорость частицы, – угол между вектором индукции магнитного поля и направлением движения.
Единица силы — Н (ньютон) .
Сила Лоренца является векторной величиной. Сила Лоренца принимает наибольшее значение, когда векторы индукции и направления скорости частицы перпендикулярны ().
Направление силы Лоренца определяется по правилу левой руки:
Если вектор магнитной индукции входит в ладонь левой руки и четыре пальца вытянуты в направлении направления вектора движения тока, то большой палец, отогнутый в сторону, показывает направление силы Лоренца.
В однородном магнитном поле частица будет двигаться по окружности, при этом сила Лоренца будет центростремительной. Работа не будет сделана.
Примеры решения задач по теме «Сила Лоренца»
ПРИМЕР 1
ПРИМЕР 2
| Упражнение | Под действием силы Лоренца частица массы m с зарядом q движется по окружности. Магнитное поле однородное, его напряженность равна В. Найти центростремительное ускорение частицы. |
| Раствор | Вспомним формулу силы Лоренца: Кроме того, по 2-му закону Ньютона: В этом случае сила Лоренца направлена к центру окружности и туда же направлено создаваемое ею ускорение, то есть это и есть центростремительное ускорение. |
По какой формуле можно рассчитать силу Лоренца. Сила Лоренца в магнитном поле. направление силы Лоренца
Электрические заряды, движущиеся в определенном направлении, создают вокруг себя магнитное поле, скорость распространения которого в вакууме равна скорости света, а в других средах немного меньше. Если движение заряда происходит во внешнем магнитном поле, то происходит взаимодействие между внешним магнитным полем и магнитным полем заряда. Поскольку электрический ток представляет собой направленное движение заряженных частиц, то сила, которая будет действовать в магнитном поле на проводник с током, будет результатом действия отдельных (элементарных) сил, каждая из которых приложена к элементарному носителю заряда.
Процессы взаимодействия внешнего магнитного поля и движущихся зарядов исследовал Г. Лоренц, который в результате многих своих опытов вывел формулу для расчета силы, действующей на движущуюся заряженную частицу со стороны магнитное поле. Вот почему сила, действующая на заряд, движущийся в магнитном поле, называется силой Лоренца.
Вот почему сила, действующая на заряд, движущийся в магнитном поле, называется силой Лоренца.
Сила, действующая на проводник со стороны стока (из закона Ампера), будет равна:
По определению сила тока равна I = qn (q — заряд, n — число зарядов, прошедших через сечение проводника за 1 с). Отсюда следует:
Где: n 0 — количество зарядов, содержащихся в единице объема, V — скорость их движения, S — площадь поперечного сечения проводника. Тогда:
Подставив это выражение в формулу Ампера, получим:
Эта сила будет действовать на все заряды в объеме проводника: V = Sl. Число зарядов, находящихся в данном объеме, будет равно:
Тогда выражение для силы Лоренца будет:
Отсюда можно заключить, что сила Лоренца, действующая на заряд q, движущийся в магнитном поле поля, пропорциональна заряду, магнитной индукции внешнего поля, скорости его движения и синусу угла между V и B, то есть:
Направление движения заряженных частиц принимается за направление движения положительных зарядов.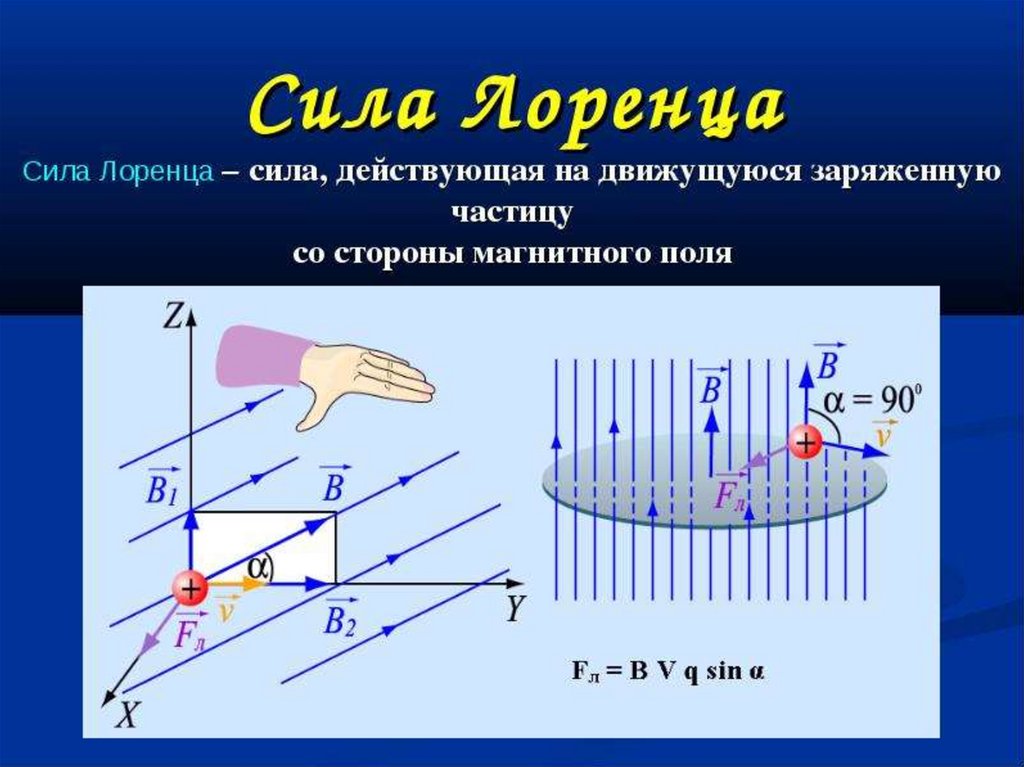 Следовательно, направление данной силы можно определить с помощью правила левой руки.
Следовательно, направление данной силы можно определить с помощью правила левой руки.
Сила, действующая на отрицательные заряды, будет направлена в противоположную сторону.
Сила Лоренца всегда направлена перпендикулярно скорости V движения заряда и поэтому не совершает работы. Меняется только направление V, а кинетическая энергия и величина скорости заряда при его движении в магнитном поле остаются неизменными.
Когда заряженная частица движется одновременно в магнитном и электрическом полях, на нее будет действовать сила:
Где Е — напряженность электрического поля.
Рассмотрим небольшой пример:
Электрон, прошедший ускоряющую разность потенциалов 3,52∙10 3 В, попадает в однородное магнитное поле, перпендикулярное линиям индукции. Радиус траектории r = 2 см, индукция поля 0,01 Тл. Определить удельный заряд электрона.
Удельный заряд — величина, равная отношению заряда к массе, то есть е/м.
В магнитном поле с индукцией B сила Лоренца F L = BeV действует на заряд, движущийся со скоростью V перпендикулярно линиям индукции.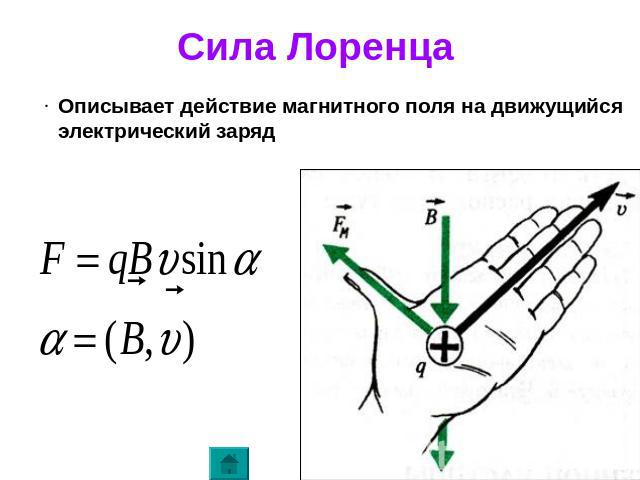 Под его действием заряженная частица будет двигаться по дуге окружности. Так как в этом случае сила Лоренца вызовет центростремительное ускорение, то по второму закону Ньютона можно написать:
Под его действием заряженная частица будет двигаться по дуге окружности. Так как в этом случае сила Лоренца вызовет центростремительное ускорение, то по второму закону Ньютона можно написать:
Электрон приобретает кинетическую энергию, которая будет равна мВ 2/2, за счет работы А электрического поля сил (A = eU), подставив его в уравнение, получим.
Определение силы магнитной силы
Определение
Если заряд движется в магнитном поле, то на него действует сила ($\overrightarrow(F)$), которая зависит от величины заряда (q ), скорость частицы ($\overrightarrow(v)$) относительно магнитного поля и поля магнитной индукции ($\overrightarrow(B)$). Эта сила установлена экспериментально, она называется магнитной силой.
И имеет вид в системе СИ:
\ [\ стрелка вверх (F) = q \ влево [\ стрелка вверх (v) \ стрелка вправо (B) \ вправо] \ \ влево (1 \ вправо). \]
Модуль силы в соответствии с (1) равен:
где $\alpha$ — угол между векторами $\overrightarrow(v\) и \\overrightarrow(B)$. Из уравнения (2) следует, что если заряженная частица движется вдоль линии магнитного поля, то на нее не действует магнитная сила.
Из уравнения (2) следует, что если заряженная частица движется вдоль линии магнитного поля, то на нее не действует магнитная сила.
Направление магнитной силы
Исходя из (1), магнитная сила направлена перпендикулярно плоскости, в которой лежат векторы $\overrightarrow(v\) и \\overrightarrow(B)$. Его направление совпадает с направлением векторного произведения $\overrightarrow(v\) и \\overrightarrow(B)$, если значение движущегося заряда больше нуля, и направлено в противоположную сторону, если $q
Сила свойства магнитной силы
Магнитная сила не действует на частицу, так как она всегда направлена перпендикулярно скорости ее движения. Из этого утверждения следует, что воздействуя на заряженную частицу с помощью постоянного магнитного поля, нельзя изменить ее энергию.
Если на частицу с зарядом действует одновременно электрическое и магнитное поля, то результирующая сила может быть записана как:
\ [\ overrightarrow (F) = q \ overrightarrow (E) + q \ left [\верхняя стрелка(v)\верхняя стрелка(B)\правая]\\левая(3\правая). \]
\]
Сила, указанная в выражении (3), называется силой Лоренца. Часть $q\overrightarrow(E)$ есть сила, действующая на заряд со стороны электрического поля, $q\left[\overrightarrow(v)\overrightarrow(B)\right]$ характеризует силу магнитного поля на заряд обвинение. Сила Лоренца проявляется при движении электронов и ионов в магнитных полях. 92) (2) = qU \ влево (1,3 \ вправо). \]
Из формулы (1.3) выразим скорость частицы:
Подставив (1.2), (1.4) в (1.1), выразим радиус кривизны траектории:
Подставив данные для разных частиц , находим отношение $\frac(R_p)(R_e)$:
\[\frac(R_p)(R_e)=\frac(\sqrt(2Um_p))(B\sqrt(q_p)sin\alpha)\ cdot\frac(B\sqrt(q_e)sin\alpha)(\sqrt(2Um_e)) = \frac(\sqrt(m_p))(\sqrt(m_e)). \] 9(- 31))) \ ок 42 . \]
Ответ: Радиус кривизны протона в 42 раза больше радиуса кривизны электрона.
Пример 2
Задача: Найти напряженность электрического поля (Е), если протон движется прямолинейно в скрещенных магнитном и электрическом полях. Он влетел в эти поля, пройдя ускоряющую разность потенциалов, равную U. Поля пересекаются под прямым углом. Магнитная индукция равна В.
Он влетел в эти поля, пройдя ускоряющую разность потенциалов, равную U. Поля пересекаются под прямым углом. Магнитная индукция равна В.
По условиям задачи на частицу действует сила Лоренца, имеющая две составляющие: магнитную и электрическую. Первая составляющая магнитная, она равна:
\[\вправо (F_m) = q\влево [\вверхвправо(v) \вверхвправо(В)\вправо] \\влево (2.1\вправо). \]
$\overrightarrow(F_m)$ — направлены перпендикулярно к $\overrightarrow(v\) и \\overrightarrow(B)$. Электрическая составляющая силы Лоренца равна:
\[\overrightarrow (F_q) = q \ overrightarrow (E) \ left (2,2 \ right). \]
Сила $\overrightarrow(F_q)$ — направлена по напряжению $\overrightarrow(E)$. Мы помним, что протон имеет положительный заряд. Для того чтобы протон двигался прямолинейно, необходимо, чтобы магнитная и электрическая составляющие силы Лоренца уравновешивали друг друга, то есть их геометрическая сумма была равна нулю. Изобразим силы, поля и скорость протона, выполняющие условия их ориентации на рис. 2. 92) (2) = qU \ to v = \ sqrt (\ frac (2qU) (m)) \ влево (2,5 \ вправо). \]
2. 92) (2) = qU \ to v = \ sqrt (\ frac (2qU) (m)) \ влево (2,5 \ вправо). \]
Подставляя (2.5) в (2.4), получаем:
Ответ: $E = B\ sqrt(\frac(2qU)(m)). $
Определение силы Лоренца
Сила Лоренца представляет собой комбинацию магнитной и электрической сил на точечный заряд, вызванную электромагнитными полями. Или другими словами, сила Лоренца — это сила, действующая на любую заряженную частицу, падающую в магнитном поле с определенной скоростью. Его значение зависит от величины магнитной индукции В , электрический заряд частицы q и скорость, с которой частица попадает в поле — В … О том, что такое формула для расчета силы Лоренца, а также ее практическое значение в физике , читать дальше.
Немного истории
Первые попытки описания электромагнитной силы были предприняты в 18 веке. Ученые Генри Кавендиш и Тобиас Мейер предположили, что сила на магнитных полюсах и электрически заряженных объектах подчиняется закону обратных квадратов. Однако экспериментальное подтверждение этого факта не было полным и убедительным. Только в 1784 году Шарль Августин де Кулон с помощью своих крутильных весов смог окончательно доказать это предположение.
Однако экспериментальное подтверждение этого факта не было полным и убедительным. Только в 1784 году Шарль Августин де Кулон с помощью своих крутильных весов смог окончательно доказать это предположение.
В 1820 году физик Эрстед открыл факт действия вольтового тока на магнитную стрелку компаса, а Андре-Мари Ампер в том же году смог вывести формулу угловой зависимости между двумя элементами тока. Фактически эти открытия стали основой современной концепции электрических и магнитных полей. Само понятие получило дальнейшее развитие в теориях Майкла Фарадея, особенно в его концепции силовых линий. Лорд Кельвин и Джеймс Максвелл дополнили теории Фарадея подробными математическими описаниями. В частности, Максвелл создал так называемое «уравнение поля Максвелла» — систему дифференциальных и интегральных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах.
Дж. Дж. Томпсон был первым физиком, который попытался вывести из уравнения поля Максвелла электромагнитную силу, действующую на движущийся заряженный объект. В 1881 году он опубликовал свою формулу F = q/2 v x B. Но из-за некоторых просчетов и неполного описания тока смещения она оказалась не совсем правильной.
В 1881 году он опубликовал свою формулу F = q/2 v x B. Но из-за некоторых просчетов и неполного описания тока смещения она оказалась не совсем правильной.
И, наконец, в 1895 году голландский ученый Хендрик Лоренц вывел правильную формулу, которая используется до сих пор, а также носит его имя, как и сила, действующая на летящую частицу в магнитном поле, теперь называется «Сила Лоренца».
Формула силы Лоренца
Формула для расчета силы Лоренца выглядит следующим образом:
Где q — электрический заряд частицы, V — ее скорость, а B — величина магнитной индукции частицы. магнитное поле.
В этом случае поле B действует как сила, перпендикулярная направлению вектора скорости V нагрузок и направлению вектора B. Это можно проиллюстрировать на схеме:
Правило левой руки позволяет физикам определять направление и возврат вектора магнитной (электродинамической) энергии. Представим, что наша левая рука расположена таким образом, что линии магнитного поля направлены перпендикулярно внутренней поверхности руки (так, что они проникают внутрь руки), а все пальцы, кроме большого, указывают направление положительного тока потока, отклоненный большой палец указывает направление электродинамической силы, действующей на положительный заряд, помещенный в это поле.
Вот так это будет выглядеть схематически.
Существует также второй способ определения направления электромагнитной силы. Он заключается в расположении большого, указательного и среднего пальцев под прямым углом. При этом указательный палец покажет направление силовых линий магнитного поля, средний — направление движения тока, а большой — направление электродинамической силы.
Приложение силы Лоренца
Сила Лоренца и ее расчеты имеют свое практическое применение при создании как специальных научных приборов — масс-спектрометров, служащих для идентификации атомов и молекул, так и при создании многих других приборов самого широкого применения. Устройства включают электродвигатели, громкоговорители и рельсовые пистолеты.
Определение
Сила, действующая на движущуюся заряженную частицу в магнитном поле, равна:
называется Сила Лоренца (магнитная сила) .
Исходя из определения (1), модуль рассматриваемой силы:
где – вектор скорости частицы, q – заряд частицы, – вектор магнитной индукции поля в точке нахождения заряда, – угол между векторами и . Из выражения (2) следует, что если заряд движется параллельно силовым линиям магнитного поля, то сила Лоренца равна нулю. Иногда, пытаясь выделить силу Лоренца, обозначают с помощью индекса:
Из выражения (2) следует, что если заряд движется параллельно силовым линиям магнитного поля, то сила Лоренца равна нулю. Иногда, пытаясь выделить силу Лоренца, обозначают с помощью индекса:
Направление силы Лоренца
Сила Лоренца (как и любая другая сила) представляет собой вектор. Его направление перпендикулярно вектору скорости и вектору (то есть перпендикулярно плоскости, в которой расположены векторы скорости и магнитной индукции) и определяется правилом правого большого пальца (правого винта) рис. 1 (а) . Если мы имеем дело с отрицательным зарядом, то направление силы Лоренца противоположно результату векторного произведения (рис. 1 (б)).
вектор направлен перпендикулярно плоскости рисунков на нас.
Последствия свойств силы Лоренца
Поскольку сила Лоренца всегда направлена перпендикулярно направлению скорости заряда, ее работа над частицей равна нулю. Оказывается, воздействуя на заряженную частицу постоянным магнитным полем, нельзя изменить ее энергию.
Если магнитное поле однородно и направлено перпендикулярно скорости движения заряженной частицы, то заряд под действием силы Лоренца будет двигаться по окружности радиусом R = const в плоскости, которая перпендикулярна вектору магнитной индукции. В этом случае радиус окружности равен:
где m — масса частицы, | д | – модуль заряда частицы, – релятивистский фактор Лоренца, c – скорость света в вакууме.
Сила Лоренца является центростремительной силой. По направлению отклонения элементарной заряженной частицы в магнитном поле делается вывод о его знаке (рис. 2).
Формула силы Лоренца при наличии магнитного и электрического полей
Если заряженная частица движется в пространстве, в котором одновременно присутствуют два поля (магнитное и электрическое), то действующая на нее сила равна:
где – вектор напряженности электрического поля в точке нахождения заряда. Выражение (4) было получено Лоренцем опытным путем. Сила, входящая в формулу (4), также называется силой Лоренца (силой Лоренца). Разделение силы Лоренца на составляющие: электрическую и магнитную относительно, так как оно связано с выбором инерциальной системы отсчета. Так, если система отсчета движется с той же скоростью, что и заряд, то в такой системе сила Лоренца, действующая на частицу, будет равна нулю.
Разделение силы Лоренца на составляющие: электрическую и магнитную относительно, так как оно связано с выбором инерциальной системы отсчета. Так, если система отсчета движется с той же скоростью, что и заряд, то в такой системе сила Лоренца, действующая на частицу, будет равна нулю.
Единицы силы Лоренца
Основная единица измерения силы Лоренца (как и любой другой силы) в системе СИ: [F] = H
В SGS: [F] = ding
Примеры решения задач
Пример
Упражнение. Какова угловая скорость электрона, движущегося по окружности в магнитном поле с индукцией B?
Раствор. Так как электрон (частица с зарядом) движется в магнитном поле, то на него действует сила Лоренца вида:
где q = q e — заряд электрона. Поскольку условие говорит о том, что электрон движется по окружности, это означает, что, следовательно, выражение для модуля силы Лоренца будет иметь вид:
Сила Лоренца является центростремительной и, кроме того, согласно второму закону Ньютона закону, в нашем случае она будет равна:
Приравнивая правые части выражений (1. 2) и (1.3), имеем:
2) и (1.3), имеем:
Из выражения (1.3) получаем скорость:
Период обращения электрона по окружности можно найти как:
Зная период, можно найти угловую скорость как:
Ответ.
Пример
Упражнение. Заряженная частица (заряд q, масса m) со скоростью v влетает в область, где есть электрическое поле напряженностью E и магнитное поле с индукцией B. Вектора и совпадают по направлению. Чему равно ускорение частицы в момент начала движения в полях, если?
Наряду с силой Ампера, кулоновским взаимодействием, электромагнитными полями в физике часто встречается понятие силы Лоренца. Это явление является одним из основных в электротехнике и электронике, наряду с , и др. Он действует на заряды, движущиеся в магнитном поле. В этой статье мы кратко и наглядно рассмотрим, что такое сила Лоренца и где она применяется.
Определение
Когда электроны движутся вдоль проводника, вокруг него возникает магнитное поле. В то же время, если поместить проводник в поперечное магнитное поле и переместить его, возникнет ЭДС электромагнитной индукции. Если по проводнику, находящемуся в магнитном поле, течет ток, на него действует сила Ампера.
В то же время, если поместить проводник в поперечное магнитное поле и переместить его, возникнет ЭДС электромагнитной индукции. Если по проводнику, находящемуся в магнитном поле, течет ток, на него действует сила Ампера.
Его значение зависит от протекающего тока, длины проводника, величины вектора магнитной индукции и синуса угла между линиями магнитного поля и проводником. Они рассчитываются по формуле:
Рассматриваемая сила отчасти аналогична рассмотренной выше, но действует не на проводник, а на движущуюся заряженную частицу в магнитном поле. Формула:
Важно! На электрон, движущийся в магнитном поле, действует сила Лоренца (Fl), а на проводник — Ампер.
Из двух формул видно, что и в первом, и во втором случае чем ближе синус угла альфа к 90 градусам, тем больше влияние на проводник или заряд Fа или Fl соответственно.
Итак, сила Лоренца характеризует не изменение величины скорости, а действие магнитного поля на заряженный электрон или положительный ион. При воздействии на них Фл не совершает работы. Соответственно, меняется направление скорости движения заряженной частицы, а не ее величина.
При воздействии на них Фл не совершает работы. Соответственно, меняется направление скорости движения заряженной частицы, а не ее величина.
Что касается единицы измерения силы Лоренца, то, как и в случае с другими силами в физике используется такая величина как Ньютон. Его компоненты:
Как направлена сила Лоренца
Для определения направления силы Лоренца, как и в случае с силой Ампера, работает правило левой руки. Значит, чтобы понять, куда направлена величина Fl, нужно раскрыть ладонь левой руки так, чтобы в руку вошли линии магнитной индукции, а вытянутые четыре пальца указали направление вектора скорости. Затем большой палец, согнутый под прямым углом к ладони, указывает направление силы Лоренца. На картинке ниже вы можете увидеть, как определить направление.
Внимание! Направление действия Лоренца перпендикулярно движению частицы и линиям магнитной индукции.
В данном случае, если быть точнее, для положительно и отрицательно заряженных частиц имеет значение направление четырех вытянутых пальцев. Приведенное выше правило левой руки сформулировано для положительной частицы. Если он заряжен отрицательно, то линии магнитной индукции должны быть направлены не в сторону раскрытой ладони, а в сторону ее тыльной стороны, а направление вектора Fl будет противоположным.
Приведенное выше правило левой руки сформулировано для положительной частицы. Если он заряжен отрицательно, то линии магнитной индукции должны быть направлены не в сторону раскрытой ладони, а в сторону ее тыльной стороны, а направление вектора Fl будет противоположным.
Теперь расскажем простыми словами, что дает нам это явление и какое реальное влияние оно оказывает на заряды. Предположим, что электрон движется в плоскости, перпендикулярной направлению линий магнитной индукции. Мы уже упоминали, что Fl не влияет на скорость, а только меняет направление движения частиц. Тогда сила Лоренца будет иметь центростремительное действие. Это отражено на рисунке ниже.
Приложение
Из всех сфер, где используется сила Лоренца, одной из крупнейших является движение частиц в магнитном поле Земли. Если рассматривать нашу планету как большой магнит, то частицы, находящиеся вблизи северных магнитных полюсов, совершают ускоренное спиральное движение. В результате они сталкиваются с атомами из верхних слоев атмосферы, и мы видим северное сияние.
Однако есть и другие случаи, когда это явление применимо. Например:
- Электронно-лучевые трубки. В их электромагнитных системах отклонения. ЭЛТ используются более 50 лет подряд в устройствах, начиная от простейшего осциллографа и заканчивая телевизорами различных форм и размеров. Любопытно, что в вопросах цветопередачи и работы с графикой некоторые до сих пор используют ЭЛТ-мониторы.
- Электрические машины — генераторы и двигатели. Хотя тут скорее действует сила Ампера. Но эти величины можно рассматривать как смежные. Однако это сложные устройства, при работе которых наблюдается влияние многих физических явлений.
- В ускорителях заряженных частиц, чтобы задать их орбиты и направления.
Заключение
Резюмируем и обрисовываем четыре основных тезиса этой статьи простыми словами:
- Сила Лоренца действует на заряженные частицы, движущиеся в магнитном поле. Это следует из основной формулы.
- Прямо пропорциональна скорости заряженной частицы и магнитной индукции.

- Не влияет на скорость частиц.
- Влияет на направление частицы.
Его роль достаточно велика в «электрических» областях. Специалист не должен упускать из виду основные теоретические сведения об основных законах физики. Эти знания будут полезны, а также тем, кто занимается научной работой, дизайном и просто для общего развития.
Теперь вы знаете, что такое сила Лоренца, чему она равна и как действует на заряженные частицы. Если у вас остались вопросы, задавайте их в комментариях под статьей!
Материалы (редактировать)
Формула силы Лоренца. сила Лоренца
- движение заряженной частицы в однородном магнитном поле;
- приложение силы Лоренца.
В зависимости от планирования материала для изучения данной темы можно взять от 1 до 3 уроков, включая уроки по решению задач.
Цели занятия
Изучить движение заряженной частицы в однородном магнитном поле, отработать решение задач по теме «Действие магнитного поля на движущийся заряд. сила Лоренца.
сила Лоренца.
Новый материал на этом уроке изучается при одновременной работе учащихся с компьютерной моделью. Студенты должны получить ответы на вопросы рабочего листа, используя возможности этой модели.
| № п/п | Этапы урока | Время, мин | Методы и методы |
| 1 | Организационное время | 2 | |
| 2 | Повторение изученного материала по теме «Сила Лоренца» | 10 | Фронтальный разговор |
| 3 | Исследование нового материала с использованием компьютерной модели «Движение заряженной частицы в однородном магнитном поле» | 30 | Работа с рабочим листом и моделью |
| 4 | Объяснение домашнего задания | 3 | |
Домашнее задание: § 6, № 849 (Сборник заданий.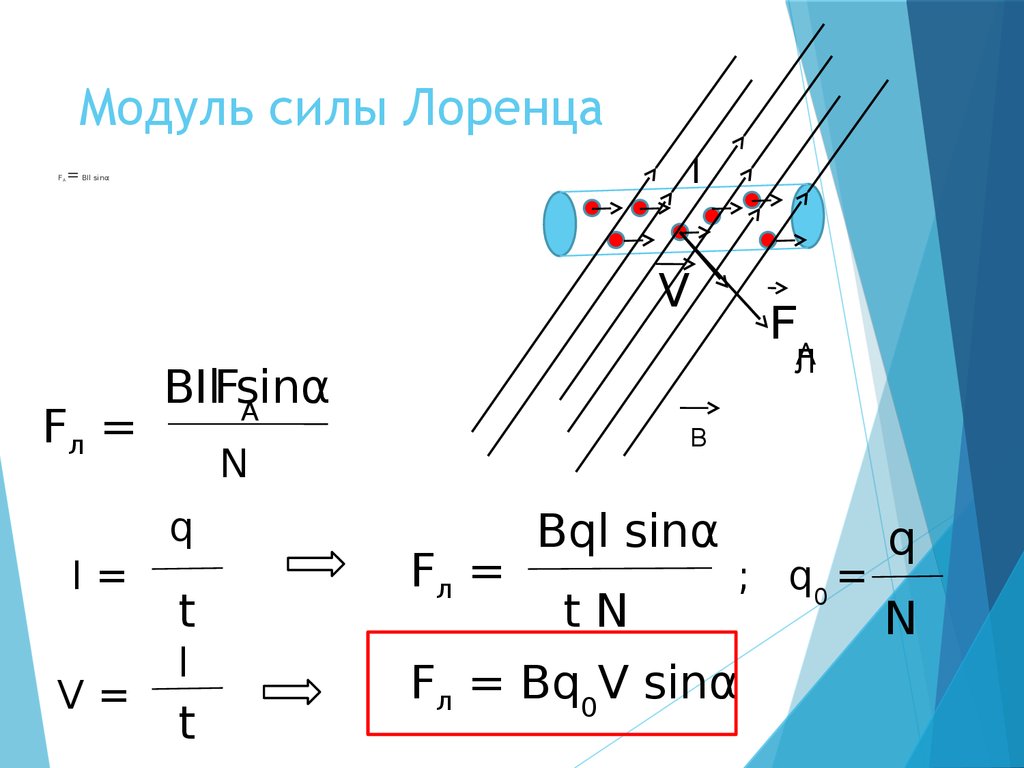 10–11 классы Рымкевич А.П. — Дрофа московская, 2001).
10–11 классы Рымкевич А.П. — Дрофа московская, 2001).
Рабочий лист к занятию
Примеры ответов
Модель «Движение заряда в магнитном поле»
Ф.И.О., класс _______________________________________________________
| 1. | При каких условиях частица движется по окружности? Ответ: частица движется по окружности, если вектор скорости перпендикулярен вектору индукции магнитного поля. |
| 2. | Предполагая, что частица движется по окружности, установите максимальные значения скорости частицы и величины индукции магнитного поля. Каков радиус окружности, по которой движется частица? Ответ: R = 22,76 см. |
| 3. | Уменьшить скорость частицы в 2 раза. Не изменяйте магнитное поле. Каков радиус окружности, по которой движется частица? Ответ: R = 11,38 см. |
| 4. | Снова уменьшить скорость частицы в 2 раза. Не изменяйте магнитное поле. Каков радиус окружности, по которой движется частица? Ответ: R = 5,69 см. |
| 5. | Как зависит радиус окружности, по которой движется частица, от величины вектора скорости частицы? Ответ: радиус окружности, по которой движется частица, прямо пропорционален модулю вектора скорости частицы. |
| 6. | Переустановить максимальные значения скорости и величины магнитной индукции поля (частица движется по кругу). |
| 7. | Уменьшить значение магнитной индукции в 2 раза. Не меняйте скорость частицы. Каков радиус окружности, по которой движется частица? Ответ: R = 45,51 см. |
8.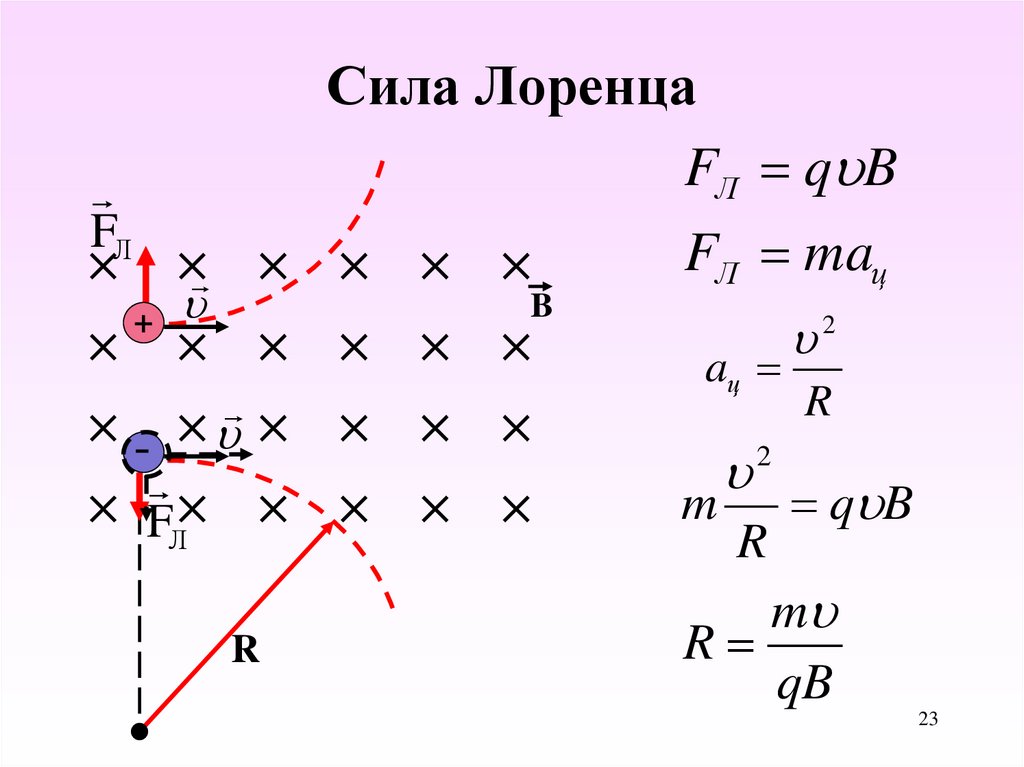 | Уменьшить значение магнитной индукции еще раз в 2 раза. Не меняйте скорость частицы. Каков радиус окружности, по которой движется частица? Ответ: R = 91,03 см. |
| 9. | Как зависит радиус окружности, по которой движется частица, от величины индукции магнитного поля? Ответ: радиус окружности, по которой движется частица, обратно пропорционален величине индукции магнитного поля. |
| 10. | Используя формулу радиуса окружности, по которой движется заряженная частица в магнитном поле (формула 1.6 в учебнике), вычислить удельный заряд частицы (отношение заряда частицы к ее массе). |
Сравните удельный заряд частицы с удельным зарядом электрона. Сделайте вывод.
Ответ: полученный результат соответствует табличному значению удельного заряда электрона.
Используя правило левой руки, определите знак заряда частицы в компьютерном эксперименте. Сделайте вывод.
Ответ: Анализ траектории частицы по правилу левой руки позволяет сказать, что это отрицательно заряженная частица. Принимая во внимание ранее полученный результат о равенстве удельных зарядов исследуемой частицы и электрона, можно сделать вывод, что частица, представленная в модели, является электроном.
Рассчитайте силу Лоренца, действующую на заряд.

Рассчитайте ускорение, сообщаемое этому заряду этой силой (согласно второму закону Ньютона).
|
Рассчитайте радиус окружности, по которой движется частица, используя формулу центростремительного ускорения.
|
Похожие вопросы
- Для младших школьников дали всего 200 билетов: 74 билета в Театр Лялькового. большая часть решти — в цирке. и все инши — в кино. Скилки пришли в кино,
- Напишите текст и продолжите его двумя-тремя предложениями. Жаркий летний день. В знойном воздухе разлита духота. Безоблачное голубое небо окутано легкой дымкой.
- 1. Мяч упал с высоты 3 м, отскочил от пола и был пойман на высоте 1 м. Найдите путь и переместите мяч. 2. Скорость движения шагающего экскаватора при работе 0,18 км/ч. Какое расстояние проедет экскаватор за 5 минут? 3. Расстояние между городами А и Б составляет 250 км. При этом из обоих городов навстречу друг другу выезжают две машины, одна со скоростью 60 км/ч, другая со скоростью 40 км/ч. Как скоро они встретятся? 4. Движение материальной точки описывается уравнением x=-25+5t. Найти начальную координату точки, модуль и направление скорости, координату точки через 5 с.
 Нарисуйте график зависимости координат от времени. 5. Какое из тел не двигалось? Какое тело движется с наименьшей скоростью? Тела движутся в одном направлении?
Нарисуйте график зависимости координат от времени. 5. Какое из тел не двигалось? Какое тело движется с наименьшей скоростью? Тела движутся в одном направлении? - «Основные причины формирования климата» Составьте схему.
- Вместо многоточия необходимо вставить слово: 1) Предком домашней собаки считается волк (1)… очень умное животное. Волки путешествуют стаями, и их территория может быть где угодно (2)… от 40 до 400 квадратных миль. Помимо обозначения границ своей территории запахом, они (3)… другие волки узнают, что они рядом, по лаю и вою. 2) В стае может быть (4)… до 30 волков, хотя там, где (5)… запасы пищи ограничены, в стае может быть только шесть или семь животных. Во время охоты они работают вместе, чтобы преследовать животное, блокировать (6) … убежать и, наконец, поймать его. В (7) … способе они (8) … ловят крупных животных, таких как олени или лоси. 3) Если имеются сельскохозяйственные животные, они (9) … волки с легким источником пищи. Это, конечно, приводит затем (10) .
 .. к контакту с людьми. Отравления и отстрелы способствовали (11)… сокращению популяции волков по всему миру. Красный волк в настоящее время почти вымер (12) … дикий, в то время как серый волк (13) … его ареал сократился до нескольких районов в Европе, Северной Америке и Азии. (14) … много других крупных млекопитающих, волк все чаще (15) … угроза от деятельности человека.
.. к контакту с людьми. Отравления и отстрелы способствовали (11)… сокращению популяции волков по всему миру. Красный волк в настоящее время почти вымер (12) … дикий, в то время как серый волк (13) … его ареал сократился до нескольких районов в Европе, Северной Америке и Азии. (14) … много других крупных млекопитающих, волк все чаще (15) … угроза от деятельности человека.
1. Рассчитайте силу Лоренца, действующую на протон, движущийся со скоростью 106 м/с в однородном магнитном поле с индукцией 0,3 Тл перпендикулярно линиям индукции.
2. В однородном магнитном поле с индукцией 0,8 Тл на проводник с током 30 А, длина активной части которого 10 см, действует сила 1,5 Н. Под каким углом к вектор магнитной индукции расположен в проводнике?
3. Какие из частиц электронного пучка
отклоняются на больший угол в одном и том же магнитном поле — быстрые или медленные? (почему?)
4. Протон, ускоренный в электрическом поле разностью потенциалов 1,5·105 В, влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции и движется равномерно по окружности радиусом 0,6 м. Определить скорость протона, величину вектора магнитной индукции и силу, с которой магнитное поле действует на протон.
Определить скорость протона, величину вектора магнитной индукции и силу, с которой магнитное поле действует на протон.
Литература: —
Интернет-ресурсы.
—
Тема № 10 Электромагнитные колебания.
Решение задач и упражнений по образцу.
Прочтите теоретический материал, выбрав один из источников, перечисленных в библиографии.
Найдите формулы для решения задач.
Напишите «Дано» в условии задачи.
Задача 1. В колебательном контуре индуктивность катушки 0,2 Гн. Амплитуда силы тока 40 мА. Найти энергию магнитного поля катушки и энергию электрического поля конденсатора в момент, когда мгновенное значение тока в 2 раза меньше амплитуды. Не обращайте внимания на сопротивление контура.
Задача 2. Рамка площадью 400 см 2 имеет 100 витков. Он вращается в однородном магнитном поле с индукцией 0,01 Тл, а период вращения рамки равен 0,1 с. Напишите зависимость ЭДС от времени, возникающую в системе отсчета, если ось вращения перпендикулярна линиям магнитной индукции.
Задача 3. На первичную обмотку трансформатора подается напряжение 220В. Какое напряжение можно снять со вторичной обмотки этого трансформатора, если коэффициент трансформации равен 10? Будет ли он потреблять энергию из сети, если его вторичная обмотка разомкнута?
Литература: — Г.Я. Мякишев Б.Б. Буховцев Физика. Учебник для 11 кл. — М., 2014.
Интернет-ресурсы.
— Ландсберг Г.С. Начальный учебник физики — М. Высшая школа 1975.
Яворский Б.М. Селезнев Ю.А. Справочник по физике — М.Наука, 1984.
Решение задач на расчет параметров колебательного контура.
Прочтите теоретический материал, выбрав один из источников, перечисленных в библиографии.
Найдите формулы для решения задач.
Напишите «Дано» в условии задачи.
1. Какую емкость надо взять в колебательном контуре, чтобы при индуктивности 250 мГн его можно было настроить на звуковую частоту 500 Гц .
2. Найти индуктивность катушки, если амплитуда напряжения 160 В, амплитуда тока 10 А, частота 50 Гц .
3. Конденсатор включается в цепь переменного тока стандартной частоты напряжением 220В. Какова емкость конденсатора, если сила тока в цепи 2,5 А .
4. В одном ящике резистор, в другом конденсатор, в третьем индуктор. Провода подключаются к внешним клеммам. Как, не открывая коробок, узнать, что в каждой из них? (Даны источники постоянного и переменного напряжения одинаковой величины и лампочка накаливания.)
Литература: — Г.Я. Мякишев Б.Б. Буховцев Физика. Учебник для 11 кл. — М., 2014.
Интернет-ресурсы.
— Ландсберг Г.С. Начальный учебник физики — М. Высшая школа 1975.
Яворский Б.М. Селезнев Ю.А. Справочник по физике — М.Наука, 1984.
ОПРЕДЕЛЕНИЕ
Сила Лоренца — сила, действующая на точечную заряженную частицу, движущуюся в магнитном поле.
Равен произведению заряда, модуля скорости частицы, модуля вектора индукции магнитного поля и синуса угла между вектором магнитного поля и скоростью частицы.
Здесь – сила Лоренца, – заряд частицы, – модуль вектора индукции магнитного поля, – скорость частицы, – угол между вектором индукции магнитного поля и направлением движения.
Единица измерения силы — Н (ньютон) .
Сила Лоренца является векторной величиной. Сила Лоренца принимает наибольшее значение, когда векторы индукции и направления скорости частиц перпендикулярны ().
Направление силы Лоренца определяется по правилу левой руки:
Если вектор магнитной индукции входит в ладонь левой руки и четыре пальца вытянуты в сторону направления текущего вектора движения, то большой палец согнут в сторону показывает направление силы Лоренца.
В однородном магнитном поле частица будет двигаться по окружности, при этом сила Лоренца будет центростремительной силой. Работа не будет сделана.
Примеры решения задач по теме «Сила Лоренца»
ПРИМЕР 1
ПРИМЕР 2
| Упражнение | Под действием силы Лоренца частица массы m с зарядом q движется по окружности. Магнитное поле однородное, его напряженность равна В. Найти центростремительное ускорение частицы. Магнитное поле однородное, его напряженность равна В. Найти центростремительное ускорение частицы. |
| Раствор | Вспомним формулу силы Лоренца: Также по 2-му закону Ньютона: В этом случае сила Лоренца направлена к центру окружности и туда же направлено создаваемое ею ускорение, то есть это и есть центростремительное ускорение. Значит: |
Голландский физик X. А. Лоренц в конце XIX века. установил, что сила, действующая со стороны магнитного поля на движущуюся заряженную частицу, всегда перпендикулярна направлению движения частицы и силовым линиям магнитного поля, в котором движется эта частица. Направление силы Лоренца можно определить по правилу левой руки. Если расположить ладонь левой руки так, чтобы четыре вытянутых пальца указывали направление движения заряда, а вектор магнитной индукции поля входил в отведенный большой палец, то он укажет направление силы Лоренца, действующей на заряд. положительный заряд.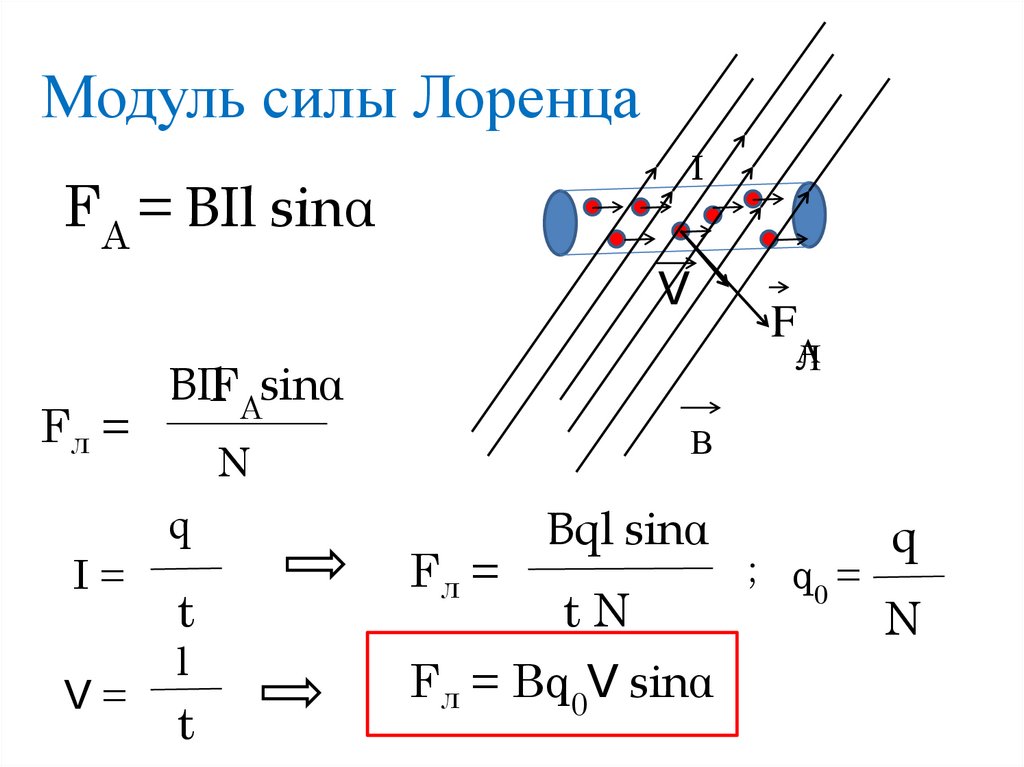
Если заряд частицы отрицательный, то сила Лоренца будет направлена в противоположную сторону.
Модуль силы Лоренца легко определяется из закона Ампера и равен:
F = | q | vB грех? ,
где q — заряд частицы, v — скорость ее движения, ? — угол между векторами скорости и индукции магнитного поля.
Если, кроме магнитного поля, есть еще электрическое поле, действующее на заряд с силой , то общая сила, действующая на заряд, равна:
.
Часто эту силу называют силой Лоренца, а силу выражают формулой ( F = | q | vB грех? ) называются магнитной частью силы Лоренца .
Так как сила Лоренца перпендикулярна направлению движения частицы, то она не может изменить свою скорость (не совершает работу), а может только изменить направление своего движения, т. е. искривить траекторию.
Такое искривление траектории электрона в телевизионном кинескопе легко наблюдать, если поднести к его экрану постоянный магнит — изображение исказится.
Движение заряженной частицы в однородном магнитном поле. Пусть заряженная частица влетает со скоростью v в однородное магнитное поле перпендикулярно линиям напряженности.
Сила, действующая на частицу со стороны магнитного поля, заставит ее равномерно вращаться по окружности радиусом r , которое легко найти, используя второй закон Ньютона, выражение целенаправленного ускорения и формулу ( F = | q | vB грех? ):
.
Отсюда получаем
.
, где m — масса частицы.
Применение силы Лоренца.
Действие магнитного поля на движущиеся заряды используется, например, в масс-спектрографах , которые позволяют разделять заряженные частицы по их удельным зарядам, т. е. по отношению заряда частицы к ее массе, и на основании полученных результатов точно определять массы частиц.
Вакуумная камера прибора помещена в поле (вектор индукции перпендикулярен рисунку).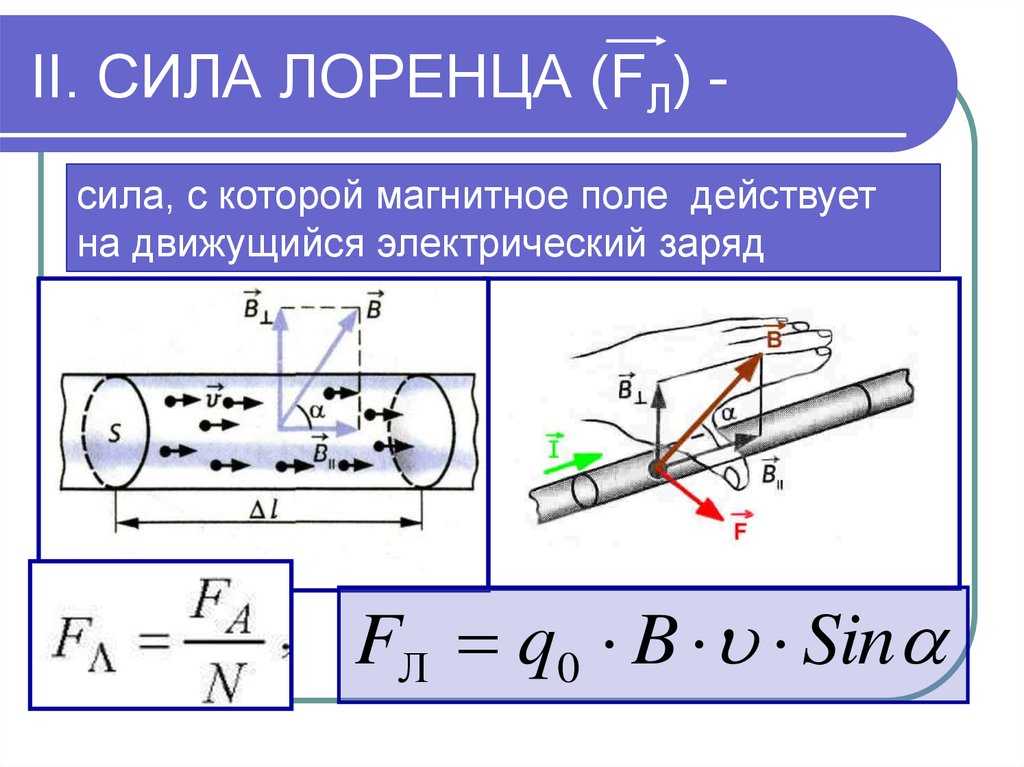 Заряженные частицы (электроны или ионы), ускоренные электрическим полем, описав дугу, падают на фотопластинку, где оставляют след, что позволяет с большой точностью измерить радиус траектории р . По этому радиусу определяется удельный заряд иона. Зная заряд иона, можно легко вычислить его массу.
Заряженные частицы (электроны или ионы), ускоренные электрическим полем, описав дугу, падают на фотопластинку, где оставляют след, что позволяет с большой точностью измерить радиус траектории р . По этому радиусу определяется удельный заряд иона. Зная заряд иона, можно легко вычислить его массу.
Напряжение и деформация – главы физики колледжа 1–17
5 Дополнительные применения законов Ньютона: трение, сопротивление и упругость
Резюме
- Закон штата Гука.
- Объясните закон Гука, используя графическое изображение между деформацией и приложенной силой.
- Обсудите три типа деформации, такие как изменение длины, боковой сдвиг и изменение объема.
- Опишите на примерах модуль Юнга, модуль сдвига и объемный модуль.
- Определить изменение длины по массе, длине и радиусу.
Теперь мы переходим от рассмотрения сил, влияющих на движение объекта (таких как трение и сопротивление), к тем, которые влияют на форму объекта. Если бульдозер втолкнет машину в стену, то машина не сдвинется с места, но заметно изменит форму. Изменение формы из-за приложения силы представляет собой деформацию . Известно, что даже очень малые силы вызывают некоторую деформацию. При малых деформациях наблюдаются две важные характеристики. Во-первых, объект возвращается к своей первоначальной форме при снятии силы, то есть деформация является упругой при малых деформациях. Во-вторых, величина деформации пропорциональна силе, то есть при малых деформациях выполняется закон Гука . В форме уравнения закон Гука имеет вид
Если бульдозер втолкнет машину в стену, то машина не сдвинется с места, но заметно изменит форму. Изменение формы из-за приложения силы представляет собой деформацию . Известно, что даже очень малые силы вызывают некоторую деформацию. При малых деформациях наблюдаются две важные характеристики. Во-первых, объект возвращается к своей первоначальной форме при снятии силы, то есть деформация является упругой при малых деформациях. Во-вторых, величина деформации пропорциональна силе, то есть при малых деформациях выполняется закон Гука . В форме уравнения закон Гука имеет вид
[латекс]\boldsymbol{F=k\Delta{L},}[/латекс]
, где[латекс]\boldsymbol{\Delta{L}}[/латекс]является величиной деформации (например, изменение длины), вызванной силой[латекс]\жирныйсимвол{F},[/латекс]и [латекс]\boldsymbol{k}[/латекс]является константой пропорциональности, которая зависит от формы и состава объекта и направления силы. Обратите внимание, что эта сила является функцией деформации [латекс] \boldsymbol{\Delta{L}}[/латекс] — она не постоянна, как кинетическая сила трения.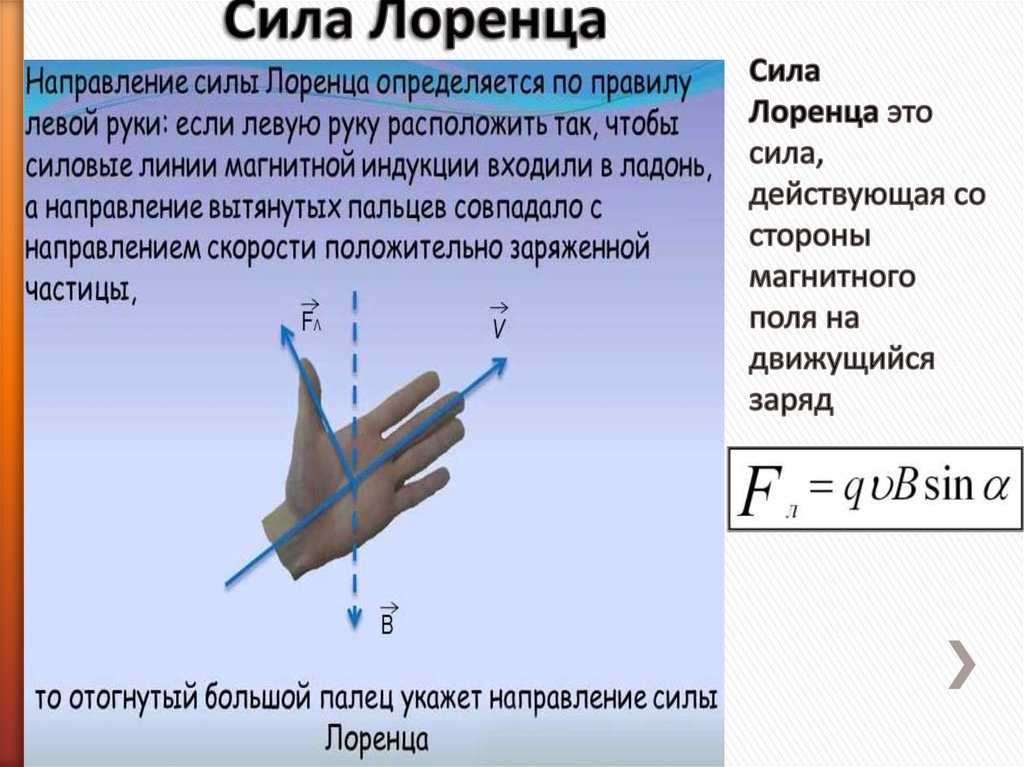 Переставить это на
Переставить это на
[латекс]\boldsymbol{\Delta{L}\:=}[/латекс][латекс]\boldsymbol{\frac{F}{k}}[/латекс]
дает понять, что деформация пропорциональна приложенной силе. На рис. 1 показана зависимость по закону Гука между растяжением [латекс]\жирныйсимвол{\Delta{L}}[/латекс]пружины или человеческой кости. Для металлов или пружин прямолинейная область, к которой относится закон Гука, намного больше. Кости хрупкие, эластичная область мала, а перелом внезапный. В конце концов, достаточно большое напряжение на материале приведет к его разрыву или разрушению. Прочность на растяжение — это разрушающее напряжение, вызывающее необратимую деформацию или разрушение материала.
ЗАКОН ГУКА
[латекс]\boldsymbol{F=k\Delta{L},}[/latex]
где [латекс]\boldsymbol{\Delta{L}}[/latex]является величиной деформации ( например, изменение длины), производимое силой[латекс]\boldsymbol{F},[/латекс]и[латекс]\жирныйсимвол{к}[/латекс]является константой пропорциональности, которая зависит от формы и состава объект и направление силы.
[латекс]\boldsymbol{\Delta{L}\:=}[/латекс][латекс]\boldsymbol{\frac{F}{k}}[/латекс]
Рисунок 1. График деформации Δ L в зависимости от приложенной силы F . Прямой отрезок — это линейный участок, на котором соблюдается закон Гука. Наклон прямой области равен 1 / k . Для больших сил график искривлен, но деформация остается упругой — Δ L вернется к нулю, если усилие будет устранено. Еще большие силы постоянно деформируют объект, пока он окончательно не сломается. Форма кривой вблизи разрушения зависит от нескольких факторов, в том числе от того, как сила F . Обратите внимание, что на этом графике наклон увеличивается непосредственно перед переломом, указывая на то, что небольшое увеличение F приводит к большому увеличению L вблизи перелома.
Константа пропорциональности[латекс]\boldsymbol{k}[/латекс]зависит от ряда факторов, влияющих на материал.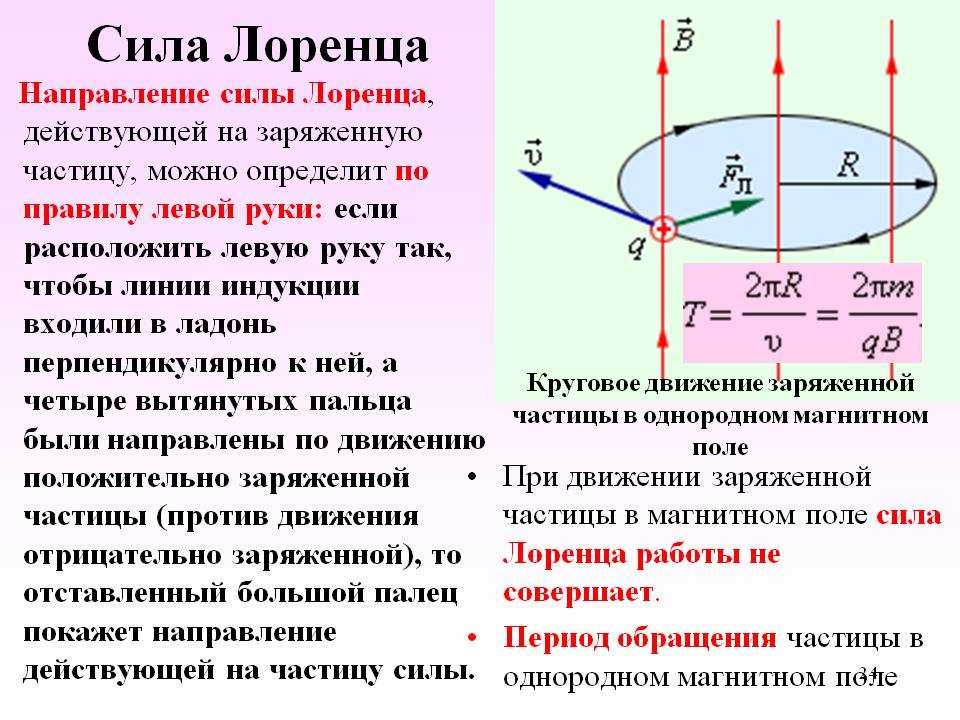 3}.[/латекс]
3}.[/латекс]
НЕМНОГО ПОТЯНИТЕСЬ
Как бы вы измерили константу пропорциональности[латекс]\жирныйсимвол{к}[/латекс]резиновой ленты? Если резиновая лента растянулась на 3 см, когда к ней прикреплен груз массой 100 г, то насколько сильно она растянется, если две одинаковые резиновые ленты будут прикреплены к одной и той же массе, даже если их сложить параллельно или, наоборот, связать вместе последовательно?
Теперь рассмотрим три конкретных типа деформации: изменение длины (растяжение и сжатие), боковой сдвиг (напряжение) и изменение объема. Все деформации предполагаются малыми, если не указано иное.
Изменение длины[латекс]\boldsymbol{\Delta{L}}[/latex] происходит, когда к проволоке или стержню прикладывается сила, параллельная его длине[латекс]\boldsymbol{L_0},[/latex] либо растягивая его (напряжение), либо сжимая его. (См. рис. 3.)
(См. рис. 3.)
Эксперименты показали, что изменение длины ([латекс]\boldsymbol{\Delta{L}}[/латекс]) зависит лишь от нескольких переменных. Как уже отмечалось, [латекс]\boldsymbol{\Delta{L}}[/латекс] пропорционален силе[латекс]\жирный символ{F}[/латекс] и зависит от вещества, из которого сделан объект. Кроме того, изменение длины пропорционально исходной длине[латекс]\boldsymbol{L_0}[/латекс]и обратно пропорционально площади поперечного сечения проволоки или стержня. Например, длинная гитарная струна растянется больше, чем короткая, а толстая струна растянется меньше, чем тонкая.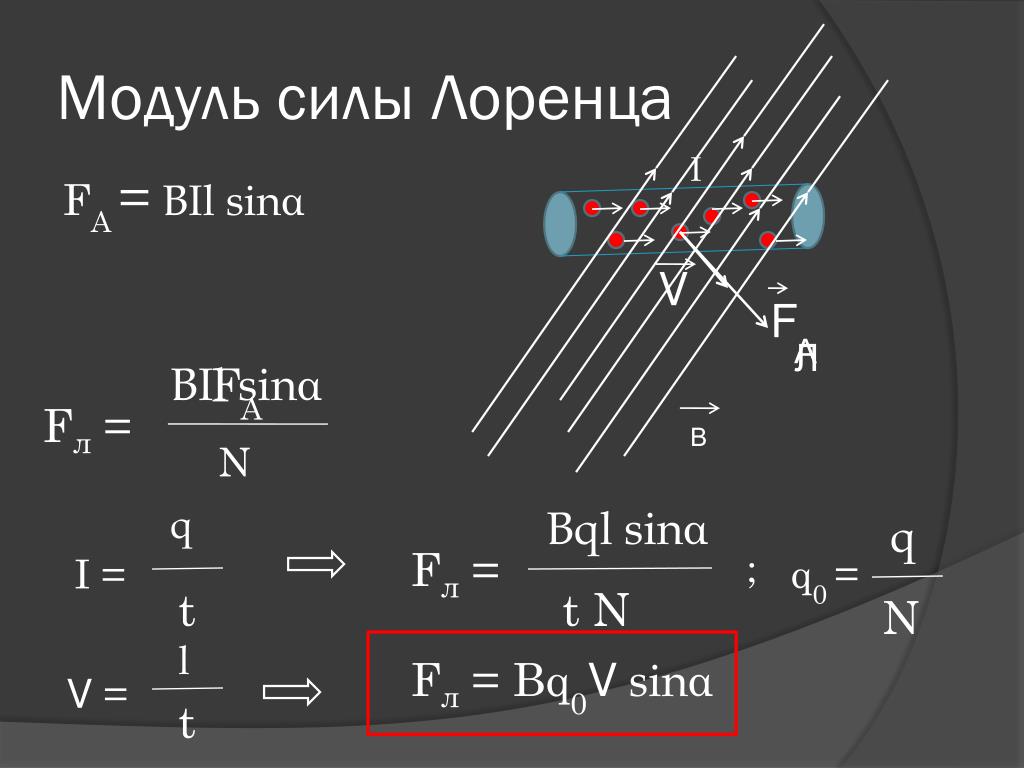 Мы можем объединить все эти факторы в одно уравнение для[латекс]\жирныйсимвол{\Delta{L}}:[/латекс]
Мы можем объединить все эти факторы в одно уравнение для[латекс]\жирныйсимвол{\Delta{L}}:[/латекс]
[латекс]\boldsymbol{\Delta{L}\:=}[/латекс][латекс]\boldsymbol{\frac{1}{Y}\frac{F}{A}}[/latex][латекс] \boldsymbol{L_0},[/латекс]
где[латекс]\boldsymbol{\Delta{L}}[/латекс]изменение длины,[латекс]\жирныйсимвол{F}[/латекс]приложенная сила,[латекс]\жирныйсимвол{Y}[/ латекс] — это коэффициент, называемый модулем упругости или модулем Юнга, который зависит от вещества, [латекс]\boldsymbol{A}[/latex]— площадь поперечного сечения и[латекс]\boldsymbol{L_0}[/ латекс] — исходная длина. В таблице 3 приведены значения[латекс]\жирныйсимвол{Y}[/латекс]для нескольких материалов. Говорят, что материалы с большим[латекс]\жирнымсимволом{Y}[/латекс] имеют большую жесткость при растяжении, потому что они меньше деформируются при заданное напряжение или сжатие. 92)}[/латекс]
 Модули упругости 1 .
Модули упругости 1 .Модули Юнга для жидкостей и газов не указаны в таблице 3, поскольку они не могут растягиваться или сжиматься только в одном направлении. Обратите внимание, что предполагается, что объект не ускоряется, так что на самом деле есть две приложенные силы величины [латекс]\boldsymbol{F}[/латекс], действующие в противоположных направлениях. Например, струны на рис. 3 тянутся силой величины[latex]\boldsymbol{w}[/latex] и удерживаются потолком, который также оказывает силу величины[latex]\boldsymbol{w }.[/латекс] 92})(3020\textbf{ m})}[/latex]
[latex]\boldsymbol{=18\textbf{ m}}.[/latex]
Обсуждение
Это довольно натянуто, но только около 0,6% длины без поддержки. Влияние температуры на длину может быть важным в этих условиях.
Кости в целом не ломаются при растяжении или сжатии. Скорее, они обычно ломаются из-за бокового удара или изгиба, что приводит к сдвигу или хрусту кости. Поведение костей при растяжении и сжатии важно, поскольку оно определяет нагрузку, которую кости могут нести. Кости классифицируются как несущие конструкции, такие как колонны в зданиях и деревьях. Несущие конструкции имеют особенности; колонны в здании имеют стальные арматурные стержни, а деревья и кости — волокнистые. Кости в разных частях тела выполняют разные структурные функции и подвержены разным нагрузкам. Таким образом, кость в верхней части бедренной кости располагается тонкими пластинками, разделенными костным мозгом, тогда как в других местах кости могут быть цилиндрическими и наполненными костным мозгом или просто сплошными. Люди с избыточным весом склонны к повреждению костей из-за постоянного сжатия в суставах и сухожилиях.
Поведение костей при растяжении и сжатии важно, поскольку оно определяет нагрузку, которую кости могут нести. Кости классифицируются как несущие конструкции, такие как колонны в зданиях и деревьях. Несущие конструкции имеют особенности; колонны в здании имеют стальные арматурные стержни, а деревья и кости — волокнистые. Кости в разных частях тела выполняют разные структурные функции и подвержены разным нагрузкам. Таким образом, кость в верхней части бедренной кости располагается тонкими пластинками, разделенными костным мозгом, тогда как в других местах кости могут быть цилиндрическими и наполненными костным мозгом или просто сплошными. Люди с избыточным весом склонны к повреждению костей из-за постоянного сжатия в суставах и сухожилиях.
Другой биологический пример закона Гука происходит в сухожилиях. Функционально сухожилие (ткань, соединяющая мышцу с костью) должно сначала легко растягиваться при приложении силы, но обеспечивать гораздо большую восстанавливающую силу при большем напряжении.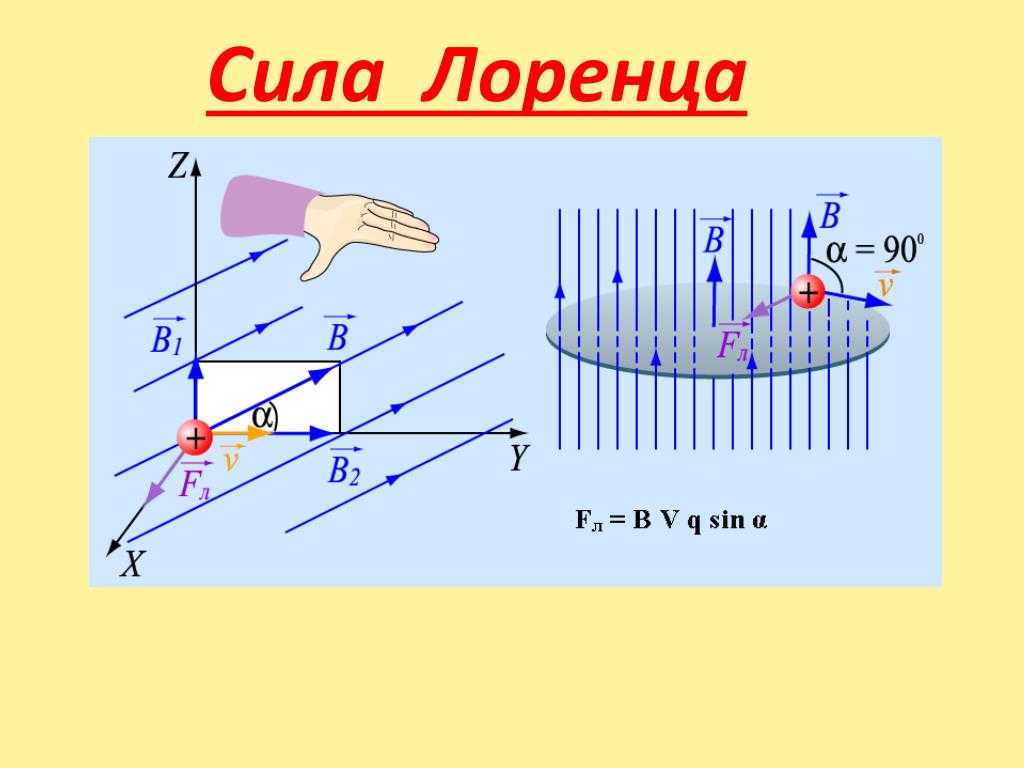 На рис. 5 показана зависимость между напряжением и деформацией сухожилия человека. Некоторые сухожилия имеют высокое содержание коллагена, поэтому напряжение или изменение длины относительно невелики; другие, такие как опорные сухожилия (как в ноге), могут изменять длину до 10%. Обратите внимание, что эта кривая напряжения-деформации нелинейна, поскольку наклон линии изменяется в разных областях. В первой части растяжения, называемой областью пальцев, волокна сухожилия начинают выстраиваться в направлении напряжения — это называется 9.1128 разжимной . В линейной области фибриллы будут растягиваться, а в области разрушения отдельные волокна начинают рваться. Простую модель этой взаимосвязи можно проиллюстрировать параллельными пружинами: разные пружины активируются при разной длине растяжения. Примеры этого приведены в задачах в конце этой главы. Связки (ткань, соединяющая кость с костью) ведут себя аналогичным образом.
На рис. 5 показана зависимость между напряжением и деформацией сухожилия человека. Некоторые сухожилия имеют высокое содержание коллагена, поэтому напряжение или изменение длины относительно невелики; другие, такие как опорные сухожилия (как в ноге), могут изменять длину до 10%. Обратите внимание, что эта кривая напряжения-деформации нелинейна, поскольку наклон линии изменяется в разных областях. В первой части растяжения, называемой областью пальцев, волокна сухожилия начинают выстраиваться в направлении напряжения — это называется 9.1128 разжимной . В линейной области фибриллы будут растягиваться, а в области разрушения отдельные волокна начинают рваться. Простую модель этой взаимосвязи можно проиллюстрировать параллельными пружинами: разные пружины активируются при разной длине растяжения. Примеры этого приведены в задачах в конце этой главы. Связки (ткань, соединяющая кость с костью) ведут себя аналогичным образом.
 Показаны три области: (1) область носка (2) линейная область и (3) область разрушения.
Показаны три области: (1) область носка (2) линейная область и (3) область разрушения. В отличие от костей и сухожилий, которые должны быть прочными и эластичными, артерии и легкие должны быть очень растяжимыми. Эластические свойства артерий необходимы для кровотока. Давление в артериях увеличивается, и стенки артерий растягиваются, когда кровь выталкивается из сердца. Когда аортальный клапан закрывается, давление в артериях падает, и стенки артерий расслабляются, чтобы поддерживать кровоток. Когда вы чувствуете свой пульс, вы чувствуете именно это — эластичное поведение артерий по мере того, как кровь течет через них при каждом толчке сердца. Если бы артерии были жесткими, вы бы не почувствовали пульс. Сердце также является органом с особыми эластическими свойствами. Легкие расширяются за счет мышечного усилия, когда мы вдыхаем, но свободно и эластично расслабляются, когда мы выдыхаем. Наша кожа особенно эластична, особенно у молодых. Молодой человек может похудеть со 100 кг до 60 кг без видимых провисаний кожи. 2)= 607.6\textbf{N}},[/латекс] 9{-5}\textbf{ м}}.[/latex]
2)= 607.6\textbf{N}},[/латекс] 9{-5}\textbf{ м}}.[/latex]
Обсуждение
Это небольшое изменение длины кажется разумным, согласующимся с нашим опытом, что кости жесткие. На самом деле, даже довольно большие силы, возникающие при напряженной физической работе, не сильно сжимают или сгибают кости. Хотя кости более жесткие по сравнению с жиром или мышцами, некоторые из веществ, перечисленных в таблице 3, имеют более высокие значения модуля Юнга[латекс]\жирныйсимвол{Y}.[/латекс]Другими словами, они более жесткие. 92}[/latex]), а отношение изменения длины к длине,[latex]\boldsymbol{\frac{\Delta{L}}{L_0}},[/latex]определяется как штамм ( безразмерная величина). Другими словами,
[латекс]\boldsymbol{\textbf{стресс}=Y\times\textbf{штамм}}.[/латекс]
В этой форме уравнение аналогично закону Гука, где напряжение аналогично силе, а деформация аналогична деформации. Если мы снова перепишем это уравнение к виду
[латекс]\boldsymbol{F=YA}[/латекс][латекс]\boldsymbol{\frac{\Delta{L}}{L_0}},[/latex]
видим, что это то же самое, что и закон Гука с константой пропорциональности
[латекс]\boldsymbol{k\:=}[/латекс][латекс]\boldsymbol{\frac{YA}{L_0}}. [/latex]
[/latex]
Эта общая идея о том, что сила и вызываемая ею деформация пропорциональны малым деформациям, применима к изменениям длины, боковому изгибу и изменениям объема.
НАПРЯЖЕНИЕ
Отношение силы к площади [латекс]\boldsymbol{\frac{F}{A}},[/латекс] определяется как напряжение, измеренное в Н/м 2 .
НАПРЯЖЕНИЕ
Отношение изменения длины к длине,[латекс]\жирныйсимвол{\frac{\Delta{L}}{L_0}},[/латекс] определяется как напряжение (безразмерная величина). Другими словами,
[латекс]\boldsymbol{\textbf{напряжение}=Y\times\textbf{напряжение}}.[/latex]
На рис. 6 показано, что подразумевается под боковым напряжением или силой сдвига . Здесь деформация называется [латекс]\boldsymbol{\Delta{x}}[/latex], и она перпендикулярна [латексу]\boldsymbol{L_0},[/latex], а не параллельна, как при растяжении и сжатии. Деформация сдвига ведет себя аналогично растяжению и сжатию и может быть описана аналогичными уравнениями. Выражение для деформации сдвига равно
Выражение для деформации сдвига равно
[латекс]\boldsymbol{\Delta{x}\:=}[/latex][латекс]\boldsymbol{\frac{1}{S}\frac{F}{A}}[/latex][латекс] \boldsymbol{L_0},[/латекс]
, где[латекс]\boldsymbol{S}[/латекс]– модуль сдвига (см. Таблицу 3), а[латекс]\boldsymbol{F}[/латекс]– сила, приложенная перпендикулярно [латексу]\boldsymbol{L_0} [/latex]и параллельно площади поперечного сечения[latex]\boldsymbol{A}.[/latex]Опять же, чтобы объект не ускорялся, на самом деле существуют две равные и противоположные силы[latex]\boldsymbol{F} [/latex]применяется к противоположным граням, как показано на рисунке 6. Уравнение логично — например, легче согнуть длинный тонкий карандаш (small[latex]\boldsymbol{A}[/latex]), чем короткий толстый, и оба легче сгибаются, чем аналогичные стальные стержни (большой[латекс]\boldsymbol{S}[/латекс]).
ДЕФОРМАЦИЯ СДВИГА
[латекс]\boldsymbol{\Delta{x}\:=}[/latex][латекс]\boldsymbol{\frac{1}{S}\frac{F}{A}}[/latex ][latex]\boldsymbol{L_0},[/latex]
, где[latex]\boldsymbol{S}[/latex]– модуль сдвига, а[latex]\boldsymbol{F}[/latex]– приложенная сила перпендикулярно[латекс]\boldsymbol{L_0}[/латекс]и параллельно площади поперечного сечения[латекс]\жирныйсимвол{А}. [/латекс]
[/латекс]
Рис. 6. Силы сдвига приложены перпендикулярно длине L 0 и параллельно площади A , вызывая деформацию Δx . Вертикальные силы не показаны, но следует иметь в виду, что в дополнение к двум силам сдвига, F , должны существовать поддерживающие силы, удерживающие объект от вращения. При таком подходе искажающие эффекты этих поддерживающих сил игнорируются. Вес объекта также не показан, так как он обычно ничтожен по сравнению с силами, достаточно большими, чтобы вызвать значительные деформации.
Изучение модулей сдвига в Таблице 3 показывает некоторые закономерности. Например, для большинства материалов модули сдвига меньше модулей Юнга. Кость — замечательное исключение. Его модуль сдвига не только больше модуля Юнга, но и такой же большой, как у стали. Вот почему кости такие жесткие.
Позвоночный столб (состоящий из 26 позвоночных сегментов, разделенных дисками) обеспечивает основную опору для головы и верхней части тела. Позвоночник имеет нормальную кривизну для стабильности, но эта кривизна может быть увеличена, что приводит к увеличению сдвигающих усилий на нижние позвонки. Диски лучше противостоят силам сжатия, чем силам сдвига. Поскольку позвоночник не является вертикальным, вес верхней части тела оказывает и то, и другое. Беременные женщины и люди с избыточным весом (с большим животом) должны отводить плечи назад, чтобы сохранить равновесие, тем самым увеличивая искривление позвоночника и, таким образом, увеличивая сдвигающий компонент нагрузки. Увеличенный угол из-за большей кривизны увеличивает силы сдвига вдоль плоскости. Эти более высокие силы сдвига увеличивают риск травм спины из-за разрывов дисков. Пояснично-крестцовый диск (клиновидный диск под последним позвонком) особенно подвержен риску из-за своего расположения.
Позвоночник имеет нормальную кривизну для стабильности, но эта кривизна может быть увеличена, что приводит к увеличению сдвигающих усилий на нижние позвонки. Диски лучше противостоят силам сжатия, чем силам сдвига. Поскольку позвоночник не является вертикальным, вес верхней части тела оказывает и то, и другое. Беременные женщины и люди с избыточным весом (с большим животом) должны отводить плечи назад, чтобы сохранить равновесие, тем самым увеличивая искривление позвоночника и, таким образом, увеличивая сдвигающий компонент нагрузки. Увеличенный угол из-за большей кривизны увеличивает силы сдвига вдоль плоскости. Эти более высокие силы сдвига увеличивают риск травм спины из-за разрывов дисков. Пояснично-крестцовый диск (клиновидный диск под последним позвонком) особенно подвержен риску из-за своего расположения.
Модули сдвига для бетона и кирпича очень малы; они слишком сильно различаются, чтобы их можно было перечислить. Бетон, используемый в зданиях, может выдерживать сжатие, например, в колоннах и арках, но очень плохо сопротивляется сдвигу, который может возникнуть в сильно нагруженных полах или во время землетрясений. Современные конструкции стали возможными благодаря использованию стали и сталежелезобетона. Почти по определению, жидкости и газы имеют модули сдвига, близкие к нулю, потому что они текут под действием сил сдвига.
Современные конструкции стали возможными благодаря использованию стали и сталежелезобетона. Почти по определению, жидкости и газы имеют модули сдвига, близкие к нулю, потому что они текут под действием сил сдвига.
Пример 3. Расчет силы, необходимой для деформации: гвоздь не сильно прогибается под нагрузкой 1.80\:\mu\textbf{m}}.[/latex](Предположим, что модуль сдвига известен до двух значащих цифр.)
Рис. 7. Вид сбоку на гвоздь с подвешенным к нему изображением. Гвоздь очень слабо изгибается (показан намного больше, чем на самом деле) из-за эффекта сдвига поддерживаемого веса. Также показано восходящее усилие стены на гвозде, иллюстрирующее, что есть равные и противоположные силы, приложенные к противоположным поперечным сечениям гвоздя. См. пример 3 для расчета массы картины.Стратегия
Сила[латекс]\жирныйсимвол{F}[/латекс]на гвозде (без учета собственного веса гвоздя) равна весу изображения[латекс]\жирныйсимвол{w}.[/латекс]Если мы можем найти[латекс]\boldsymbol{w},[/latex],тогда масса изображения равна просто[латекс]\boldsymbol{wg}. [/latex]Уравнение[латекс]\boldsymbol{\Delta{x} =\frac{1}{S}\frac{F}{A}L_0}[/latex]можно решить для[latex]\boldsymbol{F}.[/latex]
[/latex]Уравнение[латекс]\boldsymbol{\Delta{x} =\frac{1}{S}\frac{F}{A}L_0}[/latex]можно решить для[latex]\boldsymbol{F}.[/latex]
Решение
Решение уравнения [латекс]\boldsymbol{\Delta{x}=\frac{1}{S}\frac{F}{A}L_0}[/latex]для[латекс]\boldsymbol{F},[/latex]мы видим что все остальные величины могут быть найдены: 9{-6}\textbf{ m})}[/latex][latex]\boldsymbol{=\:51\textbf{ N}}.[/latex]
Эта сила в 51 Н является весом[latex]\boldsymbol {w}[/latex]картинки, поэтому масса картинки равна
[латекс]\boldsymbol{m\:=}[/latex][латекс]\boldsymbol{\frac{w}{g}}[/ латекс][латекс]\boldsymbol{=}[/латекс][латекс]\boldsymbol{\frac{F}{g}}[/latex][латекс]\boldsymbol{=\:5.2\textbf{кг}}. [/latex]
Обсуждение
Это довольно массивная картинка, и впечатляет то, что гвоздь сгибается только[latex]\boldsymbol{1.80 \:\mu\textbf{m}}[/latex]— количество, неразличимое невооруженным глазом.
Объект будет сжиматься во всех направлениях, если внутренние силы приложены равномерно ко всем его поверхностям, как показано на рис. 8. Газы сжимать относительно легко, а жидкости и твердые тела сжимать чрезвычайно трудно. Например, воздух в винной бутылке сжимается, когда ее закупоривают. Но если вы попытаетесь закупорить полную до краев бутылку, вы не сможете сжать вино — часть вина придется вынуть, если нужно вставить пробку. Причина такой разной сжимаемости заключается в том, что атомы и молекулы разделены большими пустыми пространствами в газах, но плотно упакованы в жидкостях и твердых телах. Чтобы сжать газ, вы должны сблизить его атомы и молекулы. Чтобы сжать жидкости и твердые тела, нужно фактически сжать их атомы и молекулы, и очень сильные электромагнитные силы в них противодействуют этому сжатию .
8. Газы сжимать относительно легко, а жидкости и твердые тела сжимать чрезвычайно трудно. Например, воздух в винной бутылке сжимается, когда ее закупоривают. Но если вы попытаетесь закупорить полную до краев бутылку, вы не сможете сжать вино — часть вина придется вынуть, если нужно вставить пробку. Причина такой разной сжимаемости заключается в том, что атомы и молекулы разделены большими пустыми пространствами в газах, но плотно упакованы в жидкостях и твердых телах. Чтобы сжать газ, вы должны сблизить его атомы и молекулы. Чтобы сжать жидкости и твердые тела, нужно фактически сжать их атомы и молекулы, и очень сильные электромагнитные силы в них противодействуют этому сжатию .
Мы можем описать сжатие или объемную деформацию объекта с помощью уравнения. Во-первых, отметим, что сила, «приложенная равномерно», определяется как имеющая одинаковое напряжение или отношение силы к площади [латекс] \ жирный символ {\ гидроразрыва {F} {A}} [/латекс] на всех поверхностях. Произведенная деформация представляет собой изменение объема[латекс]\жирныйсимвол{\Delta{V}},[/латекс], которое, как установлено, ведет себя очень похоже на сдвиг, растяжение и сжатие, обсуждавшиеся ранее. (Это неудивительно, поскольку сжатие всего объекта эквивалентно сжатию каждого из его трех измерений.) Связь изменения объема с другими физическими величинами определяется выражением
Во-первых, отметим, что сила, «приложенная равномерно», определяется как имеющая одинаковое напряжение или отношение силы к площади [латекс] \ жирный символ {\ гидроразрыва {F} {A}} [/латекс] на всех поверхностях. Произведенная деформация представляет собой изменение объема[латекс]\жирныйсимвол{\Delta{V}},[/латекс], которое, как установлено, ведет себя очень похоже на сдвиг, растяжение и сжатие, обсуждавшиеся ранее. (Это неудивительно, поскольку сжатие всего объекта эквивалентно сжатию каждого из его трех измерений.) Связь изменения объема с другими физическими величинами определяется выражением
[латекс]\boldsymbol{\Delta{V}\:=}[/латекс][латекс]\boldsymbol{\frac{1}{B}\frac{F}{A}}[/latex][латекс] \boldsymbol{V_0},[/латекс]
, где[latex]\boldsymbol{B}[/latex] — объемный модуль (см. Таблицу 3), [latex]\boldsymbol{V_0}[/latex] — первоначальный объем, а [latex]\boldsymbol{\frac {F}{A}}[/latex] — сила на единицу площади, равномерно приложенная внутрь ко всем поверхностям. Обратите внимание, что объемные модули для газов не приводятся.
Каковы некоторые примеры объемного сжатия твердых тел и жидкостей? Одним из практических примеров является производство алмазов промышленного качества путем сжатия углерода с чрезвычайно большой силой на единицу площади. Атомы углерода перестраивают свою кристаллическую структуру в более плотно упакованную структуру алмазов. В природе аналогичный процесс происходит глубоко под землей, где чрезвычайно большие силы возникают из-за веса вышележащего материала. Еще одним естественным источником больших сжимающих сил является давление, создаваемое весом воды, особенно в глубоких частях океанов. Вода оказывает внутреннюю силу на все поверхности подводного объекта и даже на саму воду. На больших глубинах вода заметно сжимается, как показывает следующий пример. 92}.[/latex]
Стратегия
Уравнение[latex]\boldsymbol{\Delta{V}=\frac{1}{B}\frac{F}{A}V_0}[/latex]is правильные физические отношения. Все величины в уравнении, кроме [latex]\boldsymbol{\frac{\Delta{V}}{V_0}}[/latex], известны.
Решение
Нахождение неизвестного }}{V_0}}[/latex][latex]\boldsymbol{=}[/latex][latex]\boldsymbol{\frac{1}{B}\frac{F}{A}}.[/latex] 92}}[/latex]
[latex]\boldsymbol{=0.023=2.3\%}.[/latex]
Обсуждение
единица площади составляет около 500 атмосфер (1 миллион фунтов на квадратный фут). Жидкости и твердые тела чрезвычайно трудно сжимать.
И наоборот, очень большие силы создаются жидкостями и твердыми телами, когда они пытаются расшириться, но не могут этого сделать, что эквивалентно их сжатию до меньшего, чем их нормальный объем. Это часто происходит, когда содержащийся в нем материал нагревается, поскольку большинство материалов расширяются при повышении их температуры. Если материалы плотно сжаты, они деформируют или ломают свой контейнер. Другой очень распространенный пример возникает, когда вода замерзает. Вода, в отличие от большинства материалов, расширяется при замерзании и может легко разбить валун, биологическую клетку или блок двигателя, который встанет у нее на пути.
Другие виды деформации, такие как кручение или скручивание, ведут себя аналогично рассматриваемым здесь деформациям растяжения, сдвига и объемной деформации.
- Закон Гука определяется выражением
[латекс]\boldsymbol{F=k\Delta{L}},[/латекс]
, где [латекс]\boldsymbol{\Delta{L}}[/латекс] — степень деформации (изменение длины), [латекс]\жирный символ {F}[/латекс] — приложенная сила, а [латекс ]\boldsymbol{k}[/latex]является константой пропорциональности, которая зависит от формы и состава объекта и направления силы. Связь между деформацией и приложенной силой также можно записать как
[латекс]\boldsymbol{\Delta{L}\:=}[/латекс][латекс]\boldsymbol{\frac{1}{Y}\frac{F}{A}}[/latex][латекс] \boldsymbol{L_0},[/латекс]
где[латекс]\boldsymbol{Y}[/латекс]является модулем Юнга , который зависит от вещества,[латекс]\жирныйсимвол{А}[/латекс]является площадью поперечного сечения, а[латекс]\ жирный символ{L_0}[/latex] — исходная длина.
- Отношение силы к площади, [латекс]\boldsymbol{\frac{F}{A}},[/латекс] определяется как напряжение , измеренное в Н/м 2 .

- Отношение изменения длины к длине,[латекс]\жирныйсимвол{\frac{\Delta{L}}{L_0}},[/латекс]определяется как штамм (безразмерная величина). Другими словами,
[латекс]\boldsymbol{\textbf{стресс}=Y\times\textbf{штамм}}.[/латекс]
- Выражение для деформации сдвига:
[латекс]\boldsymbol{\Delta{x}\:=}[/latex][латекс]\boldsymbol{\frac{1}{S}\frac{F}{A}}[/latex][латекс] \boldsymbol{L_0},[/латекс]
, где[латекс]\boldsymbol{S}[/латекс]– модуль сдвига, а[латекс]\boldsymbol{F}[/латекс]– сила, приложенная перпендикулярно [латексу]\boldsymbol{L_0}[/латекс]и параллельно площади поперечного сечения[латекс]\boldsymbol{A}.[/латекс]
- Связь изменения объема с другими физическими величинами определяется выражением
[латекс]\boldsymbol{\Delta{V}\:=}[/латекс][латекс]\boldsymbol{\frac{1}{B}\frac{F}{A}}[/latex][латекс] \boldsymbol{V_0},[/латекс]
, где [латекс]\boldsymbol{B}[/latex]– объемный модуль, [латекс]\boldsymbol{V_0}[/latex]– первоначальный объем, а [латекс]\boldsymbol{\frac{F}{A }}[/latex] — сила на единицу площади, приложенная равномерно внутрь ко всем поверхностям.

Задачи и упражнения
1: Во время циркового номера один артист качается вверх ногами, свисая с трапеции, держа за ноги другого, также перевернутого артиста. Если восходящая сила, действующая на нижнюю часть тела, в три раза превышает ее вес, насколько растянутся кости (бедренные кости) ее верхней части ног? Вы можете предположить, что каждый из них эквивалентен однородному стержню длиной 35,0 см и радиусом 1,80 см. Ее масса 60,0 кг.
2: Во время борцовского поединка борец весом 150 кг ненадолго стоит на одной руке во время маневра, призванного сбить с толку своего уже умирающего противника. На сколько укорачивается плечевая кость? Кость может быть представлена однородным стержнем длиной 38,0 см и радиусом 2,10 см. 92}.[/latex]Рассчитайте изменение длины грифеля автоматического карандаша, если вы постучите им прямо по карандашу с силой 4,0 Н. Диаметр грифеля 0,50 мм, а длина 60 мм. б) разумен ли ответ? То есть согласуется ли это с тем, что вы наблюдали при использовании карандашей?
б) разумен ли ответ? То есть согласуется ли это с тем, что вы наблюдали при использовании карандашей?
4: Телевизионные антенны — самые высокие искусственные сооружения на Земле. В 1987 году физик весом 72,0 кг разместил себя и 400 кг оборудования на вершине одной антенны высотой 610 м для проведения гравитационных экспериментов. На сколько была сжата антенна, если считать ее эквивалентом стального цилиндра радиусом 0,150 м?
5: (a) Насколько альпинистка весом 65,0 кг растянет нейлоновую веревку диаметром 0,800 см, когда она свисает на 35,0 м ниже выступа скалы? (b) Соответствует ли ответ тому, что вы наблюдали для нейлоновых веревок? Был бы смысл, если бы веревка была на самом деле эластичным шнуром?
6: Полый алюминиевый флагшток высотой 20,0 м эквивалентен по жесткости сплошному цилиндру диаметром 4,00 см. Сильный ветер изгибает шест так сильно, как горизонтальная сила 900 Н приложено наверху. Насколько далеко в сторону изгибается верхняя часть шеста?
7: При бурении нефтяной скважины каждая новая секция бурильной трубы несет собственный вес, а также вес трубы и бурового долота под ней.


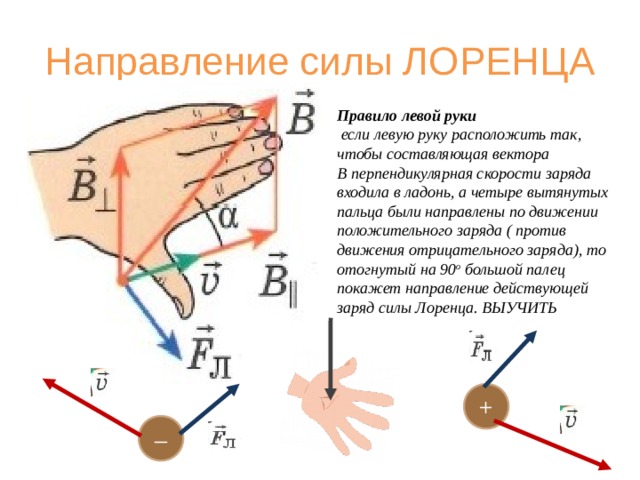
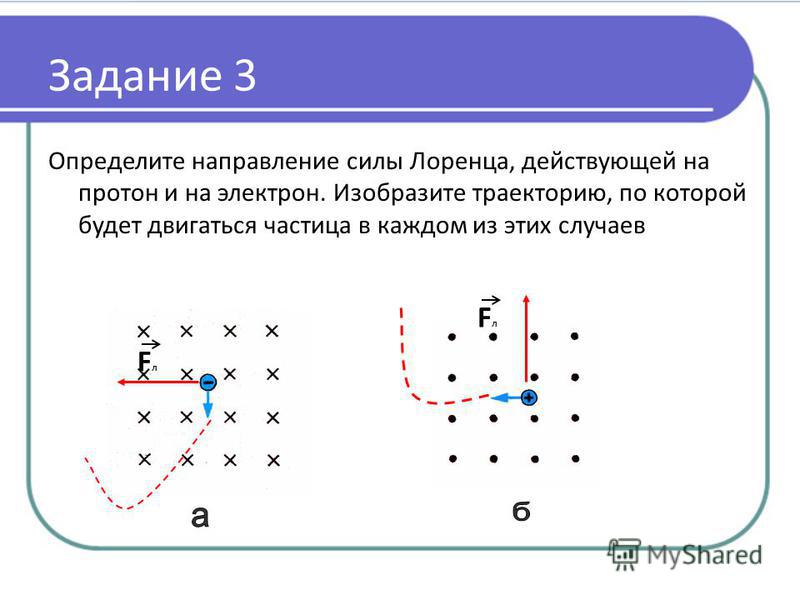 Все остальные манипуляции остаются прежними.
Все остальные манипуляции остаются прежними.
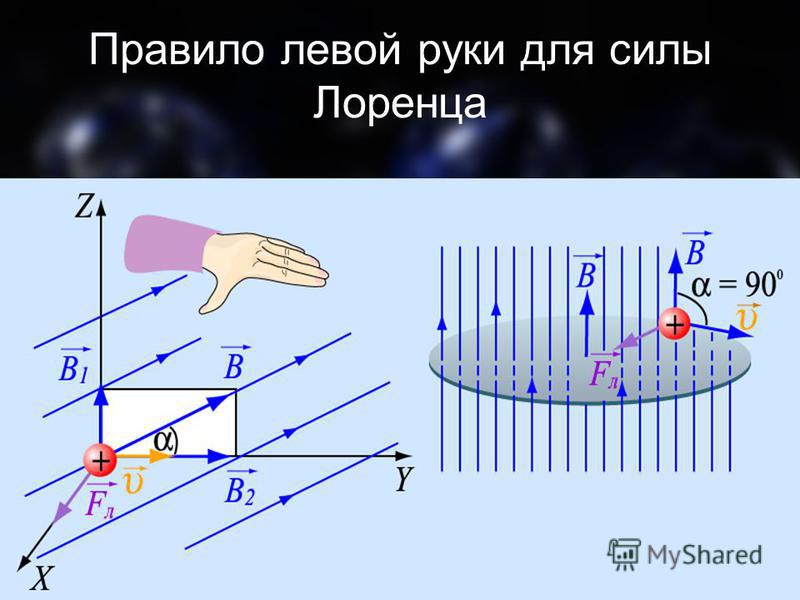 Все остальные манипуляции остаются прежними.
Все остальные манипуляции остаются прежними.
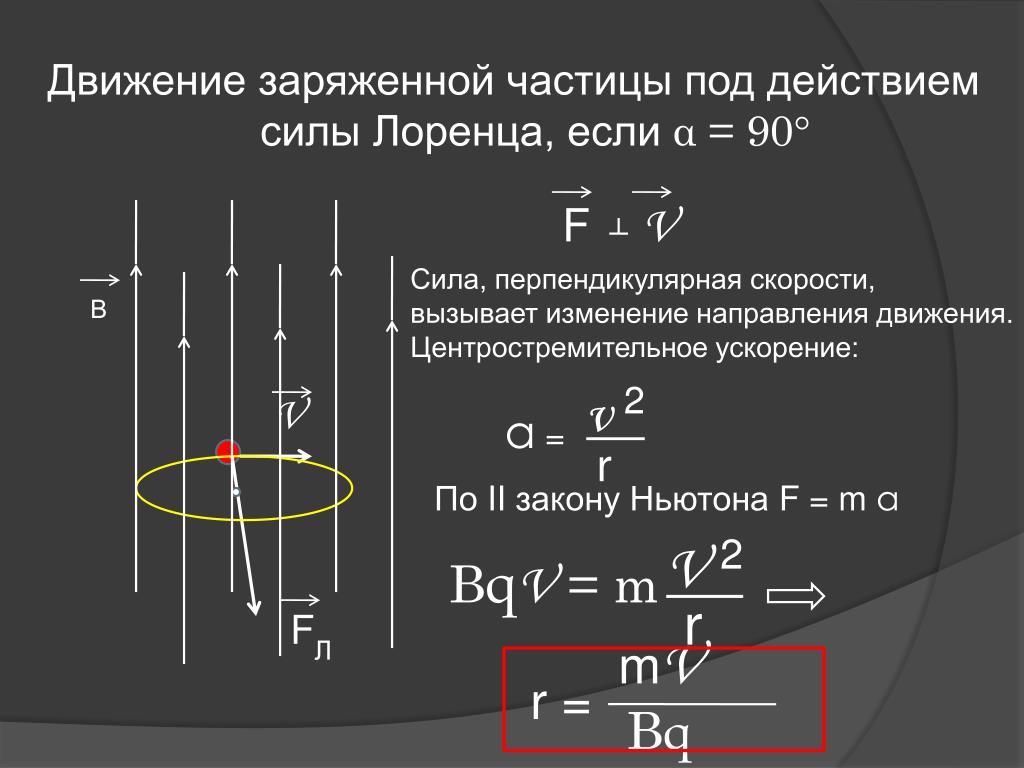 2003
2003
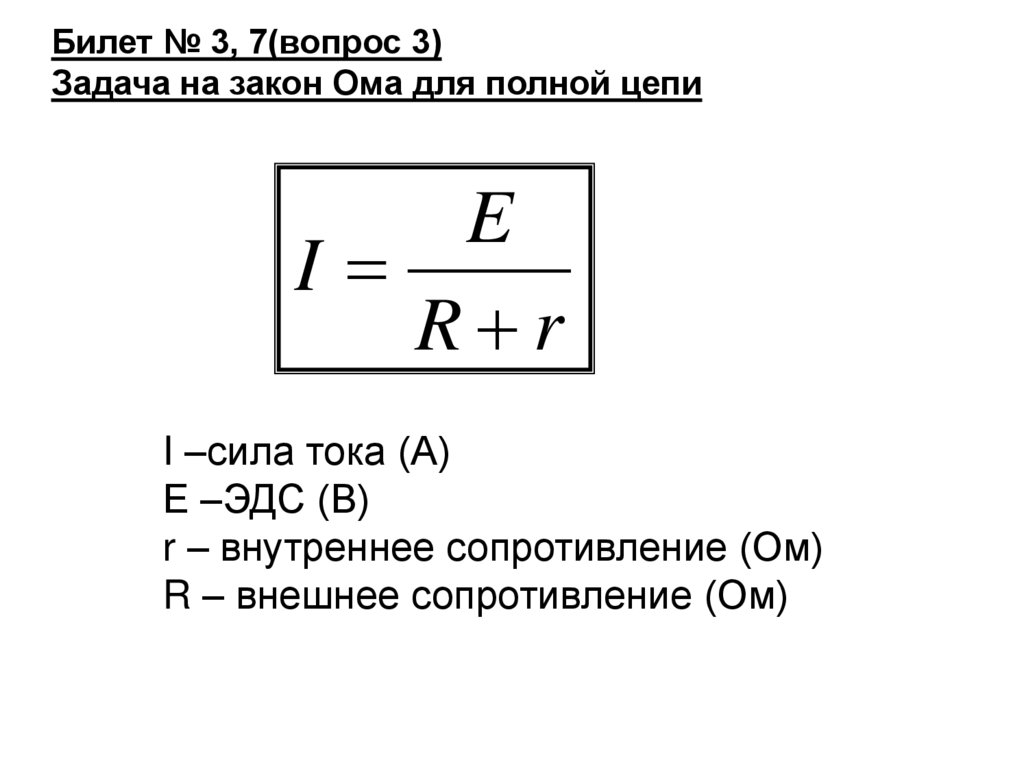
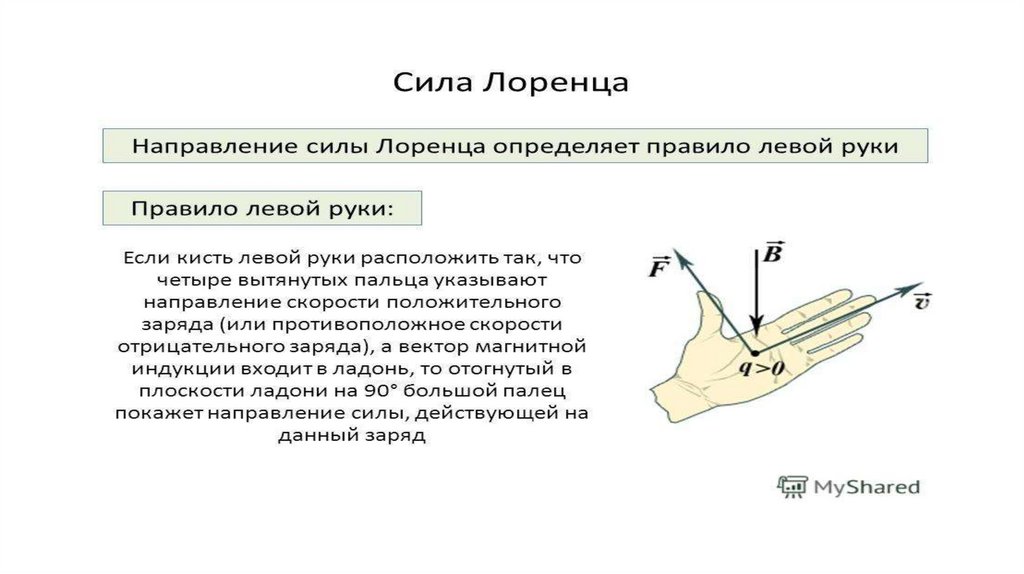 Но эти величины можно считать смежными. Однако это сложные устройства, при работе которых наблюдается влияние многих физических явлений.
Но эти величины можно считать смежными. Однако это сложные устройства, при работе которых наблюдается влияние многих физических явлений.

 Средства:
Средства:


 Нарисуйте график зависимости координат от времени. 5. Какое из тел не двигалось? Какое тело движется с наименьшей скоростью? Тела движутся в одном направлении?
Нарисуйте график зависимости координат от времени. 5. Какое из тел не двигалось? Какое тело движется с наименьшей скоростью? Тела движутся в одном направлении? .. к контакту с людьми. Отравления и отстрелы способствовали (11)… сокращению популяции волков по всему миру. Красный волк в настоящее время почти вымер (12) … дикий, в то время как серый волк (13) … его ареал сократился до нескольких районов в Европе, Северной Америке и Азии. (14) … много других крупных млекопитающих, волк все чаще (15) … угроза от деятельности человека.
.. к контакту с людьми. Отравления и отстрелы способствовали (11)… сокращению популяции волков по всему миру. Красный волк в настоящее время почти вымер (12) … дикий, в то время как серый волк (13) … его ареал сократился до нескольких районов в Европе, Северной Америке и Азии. (14) … много других крупных млекопитающих, волк все чаще (15) … угроза от деятельности человека.