Мощность переменного тока. Мощность тока через катушку, резистор, конденсатор
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.
Переменный ток несёт энергию. Поэтому крайне важным является вопрос о мощности в цепи переменного тока.
Пусть и — мгновенные значение напряжения и силы тока на данном участке цепи. Возьмём малый интервал времени — настолько малый, что напряжение и ток не успеют за это время сколько-нибудь измениться; иными словами, величины и можно считать постоянными в течение интервала .
Пусть за время через наш участок прошёл заряд (в соответствии с правилом выбора знака для силы тока заряд считается положительным, если он переносится в положительном направлении, и отрицательным в противном случае). Электрическое поле движущихся зарядов совершило при этом работу
Мощность тока — это отношение работы электрического поля ко времени, за которое эта работа совершена:
(1)
Точно такую же формулу мы получили в своё время для постоянного тока. Но в данном случае мощность зависит от времени, совершая колебания вместе током и напряжением; поэтому величина (1) называется ещё мгновенной мощностью.
Из-за наличия сдвига фаз сила тока и напряжение на участке не обязаны совпадать по знаку (например, может случиться так, что напряжение положительно, а сила тока отрицательна, или наоборот). Соответственно, мощность может быть как положительной, так и отрицательной. Рассмотрим чуть подробнее оба этих случая.
1. Мощность положительна: . Напряжение и сила тока имеют одинаковые знаки. Это означает, что направление тока совпадает с направлением электрического поля зарядов, образующих ток. В таком случае
2. Мощность отрицательна: . Напряжение и сила тока имеют разные знаки. Стало быть, ток течёт против поля движущихся зарядов, образующих этот самый ток.
Как такое может случиться? Очень просто: электрическое поле, возникающее на участке, как бы «перевешивает» поле движущихся зарядов и «продавливает» ток против этого поля. В таком случае энергия участка убывает: участок отдаёт энергию во внешнюю цепь (например, конденсатор разряжается).
Если вы не вполне поняли, о чём только что шла речь, не переживайте — дальше будут конкретные примеры, на которых вы всё и увидите.
Мощность тока через резистор
Пусть переменный ток протекает через резистор сопротивлением . Напряжение на резисторе, как нам известно, колеблется в фазе с током:
Поэтому для мгновенной мощности получаем:
(2)
График зависимости мощности (2) от времени представлен на рис. 1. Мы видим, что мощность всё время неотрицательна — резистор забирает энергию из цепи, но не возвращает её обратно в цепь.

Рис. 1. Мощность переменного тока через резистор
Максимальное значение нашей мощности связано с амплитудами тока и напряжения привычными формулами:
На практике, однако, интерес представляет не максимальная, а средняя мощность тока. Это и понятно. Возьмите, например, обычную лампочку, которая горит у вас дома. По ней течёт ток частотой Гц, т. е. за секунду совершается колебаний силы тока и напряжения. Ясно, что за достаточно продолжительное время на лампочке выделяется некоторая средняя мощность, значение которой находится где-то между и . Где же именно?
Посмотрите ещё раз внимательно на рис. 1. Не возникает ли у вас интуитивное ощущение, что средняя мощность соответствует «середине» нашей синусоиды и принимает поэтому значение ?
Это ощущение совершенно верное! Так оно и есть. Разумеется, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу догадку прямым вычислением, но нам это не нужно. Достаточно интуитивного понимания простого и важного факта:
среднее значение квадрата синуса (или косинуса) за период равно .
Этот факт иллюстрируется рисунком 2.

Рис. 2. Среднее значение квадрата синуса равно
Итак, для среднего значения мощности тока на резисторе имеем:
(3)
В связи с этими формулами вводятся так называемые действующие (или эффективные) значения напряжения и силы тока (на самом деле это есть не что иное, как средние квадратические значения напряжения и тока. Такое у нас уже встречалось: средняя квадратическая скорость молекул идеального газа (листок «Уравнение состояния идеального газа»):
(4)
Формулы (3), записанные через действующие значения, полностью аналогичны соответствующим формулам для постоянного тока:
Поэтому если вы возьмёте лампочку, подключите её сначала к источнику постоянного напряжения , а затем к источнику переменного напряжения с таким же действующим значением , то в обоих случаях лампочка будет гореть одинаково ярко.
Действующие значения (4) чрезвычайно важны для практики. Оказывается, вольтметры и амперметры переменного тока показывают именно действующие значения (так уж они устроены). Знайте также, что пресловутые вольт из розетки — это действующее значение напряжения бытовой электросети.
Мощность тока через конденсатор
Пусть на конденсатор подано переменное напряжение . Как мы знаем, ток через конденсатор опережает по фазе напряжение на :
Для мгновенной мощности получаем:
График зависимости мгновенной мощности от времени представлен на рис. 3.

Рис. 3. Мощность переменного тока через конденсатор
Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в данном случае равно нулю! Мы видим это сейчас как математический факт. Но интересно было бы с физической точки зрения понять, почему мощность тока через конденсатор оказывается нулевой.
Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе на протяжении одного периода колебаний (рис. 4).

Рис. 4. Напряжение на конденсаторе и сила тока через него
Рассмотрим последовательно все четыре четверти периода.
1. Первая четверть, . Напряжение положительно и возрастает. Ток положителен (течёт в положительном направлении), конденсатор заряжается. По мере увеличения заряда на конденсаторе сила тока убывает.
Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счёт работы внешнего электрического поля, продвигающего заряды на конденсатор.
2. Вторая четверть, . Напряжение продолжает оставаться положительным, но идёт на убыль. Ток меняет направление и становится отрицательным: конденсатор разряжается против направления внешнего электрического поля.В конце второй четверти конденсатор полностью разряжен.
Мгновенная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать).
3. Третья четверть, . Внешнее электрическое поле меняет направление: напряжение отрицательно и возрастает по модулю. Сила тока отрицательна: идёт зарядка конденсатора в отрицательном направлении.
Ситуация полностью аналогична первой четверти, только знаки напряжения и тока — противоположные. Мощность положительна: конденсатор вновь накапливает энергию.
4. Четвёртая четверть, . Напряжение отрицательно и убывает по модулю. Конденсатор разряжается против внешнего поля: сила тока положительна.
Мощность отрицательна: конденсатор возвращает энергию в цепь. Ситуация аналогична второй четверти — опять-таки с заменой заменой знаков тока и напряжения на противоположные.
Мы видим, что энергия, забранная конденсатором из внешней цепи в ходе первой четверти периода колебаний, полностью возвращается в цепь в ходе второй четверти. Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.
Мощность тока через катушку
Пусть на катушку подано переменное напряжение . Ток через катушку отстаёт по фазе от напряжения на :
Для мгновенной мощности получаем:
Снова средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики напряжения и силы тока через катушку за период (рис. 5).

Рис. 5. Напряжение на катушке и сила тока через неё
Мы видим, что в течение второй и четвёртой четвертей периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по модулю; для создания тока внешнее электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на увеличение энергии магнитного поля катушки.
В первой и третьей четвертях периода напряжение и сила тока имеют разные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против внешнего электрического поля и совершает тем самым положительную работу. А за счёт чего совершается эта работа? За счёт энергии, накопленной ранее в катушке.
Таким образом, энергия, запасаемая в катушке за одну четверть периода, полностью возвращается в цепь в ходе следующей четверти. Поэтому средняя мощность, потребляемая катушкой, оказывается равной нулю.
Мощность тока на произвольном участке
Теперь рассмотрим самый общий случай. Пусть имеется произвольный участок цепи — он может содержать резисторы, конденсаторы, катушки…На этот участок подано переменное напряжение .
Как мы знаем из предыдущего листка «Переменный ток. 2», между напряжением и силой тока на данном участке имеется некоторый сдвиг фаз . Мы записывали это так:
Тогда для мгновенной мощности имеем:
(5)
Теперь нам хотелось бы определить, чему равна средняя мощность. Для этого мы преобразуем выражение (5), используя формулу:
В результате получим:
(6)
Но среднее значение величины равно нулю! Поэтому средняя мощность оказывается равной:
(7)
Данную формулу можно записать с помощью действующих значений (4) напряжения и силы тока:
Формула (7) охватывает все три рассмотренные выше ситуации. В случае резистора имеем , и мы приходим к формуле (3). Для конденсатора и катушки , и средняя мощность равна нулю.
Кроме того, формула (7) даёт представление о весьма общей проблеме, связанной с передачей электроэнергии. Чрезвычайно важно, чтобы у потребителя был как можно ближе к единице. Иначе потребитель начнёт возвращать значительную часть энергии назад в сеть (что ему совсем невыгодно), и к тому же возвращаемая энергия будет безвозвратно расходоваться на нагревание проводов и других элементов цепи.
С этой проблемой приходится сталкиваться разработчикам электрических схем, содержащих электродвигатели. Обмотки электродвигателей обладают большими индуктивностями, и возникает ситуация, близкая к «чистой» катушке. Чтобы избежать бесполезного циркулирования энергии по сети, в цепь включают дополнительные элементы, сдвигающие фазу — например, так называемые компенсирующие конденсаторы.
Мгновенная мощность
В отличие от цепей постоянного тока, где мощность в течение определенного промежутка времени остается неизменной, в цепях переменного тока дело обстоит иначе. Так как ток и напряжение постоянно меняют своё значение, то и мощность соответственно будет меняться в каждый момент времени. Такая мощность называется мгновенной.
Мгновенной мощностью p(t) называют произведение приложенного к цепи мгновенного напряжения u(t) на мгновенное значение тока i(t) в этой цепи.

График мгновенной мощности представлен на рисунке ниже

Мощность обозначена заштрихованной областью. Знак мощности зависит от сдвига фаз между током и напряжением. В данном случае в цепи присутствуют только активные сопротивления, которые не создают сдвига фаз, поэтому мощность имеет только положительные значения.
Рассмотрим другой график

На данном графике имеются области отрицательных значений мгновенной мощности. Такой график может соответствовать цепи, в которой присутствуют конденсатор или катушка, причем положительные участки — это мощность, которая пошла в цепь и рассеялась на сопротивлении, либо запаслась в качестве энергии полей конденсаторов или катушек, а отрицательные участки это мощность, которая была возвращена обратно источнику.
Активная мощность
Чтобы понять какое количество энергии потребляет источник, целесообразнее взять среднюю мощность за период. Для этого вернемся к первому графику.
На графике мгновенной мощности выделяют прямоугольник со сторонами

В нашем случае сдвиг фаз равен нулю, поэтому коэффициент мощности равен единице, но в случаях с реактивными элементами нужно этот момент учитывать.

Активная мощность измеряется в ваттах – Вт.
cosφ – коэффициент мощности, который показывает отношение активной мощности к полной мощности.

Реактивная мощность
Реактивная мощность – это энергия, которая периодически циркулирует между источником и приемником. Реактивная мощность возникает потому, что конденсатор и катушка способны накапливать энергию, а затем снова отдавать её в сеть. На практике от реактивной мощности зачастую стараются избавиться.

Реактивная мощность измеряется в вольт амперах реактивных – ВАр.
Полная мощность
Полная мощность — это максимальное значение активной мощности.

Для наглядного представления существует треугольник мощностей, в котором гипотенузой является полная мощность, а катетами – активная и реактивная составляющие.

Читайте также — Последовательная RL-цепь
Энергетический процесс в цепи с резистором
Мгновенная мощность в цепи с резистором равна произведению мгновенного значения напряжения на мгновенное значение тока.
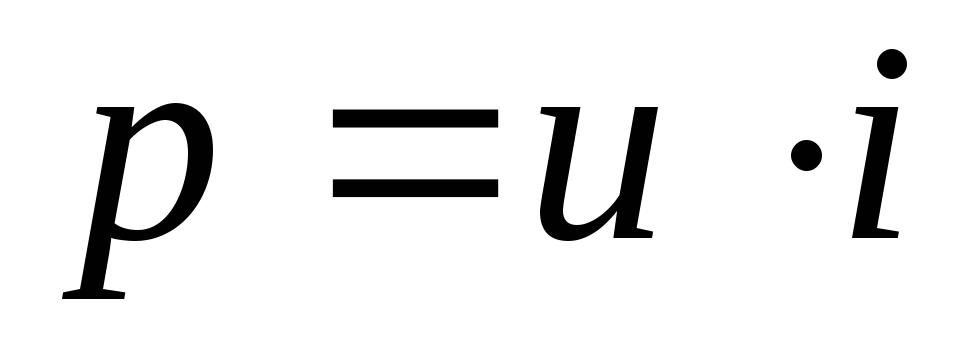
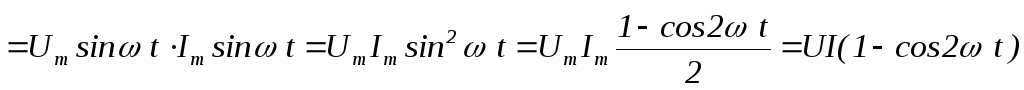
Перемножим напряжение и ток графически.
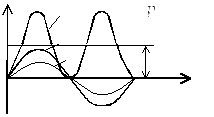
Вывод: в цепи с резистором мгновенная мощность всегда положительна. Это значит, что в любой момент времени происходит необратимый процесс преобразования электрической энергии в тепловую. Средняя скорость этого преобразования называется активная мощность (
 )
и разделить на время равное периоду.
)
и разделить на время равное периоду. 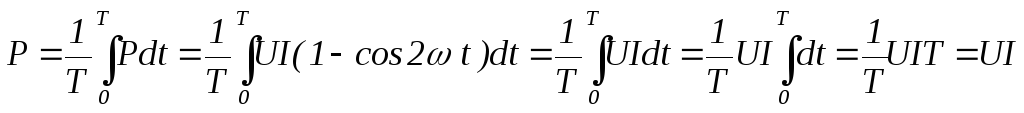
Получаем разность
интервалов, где интеграл за период от 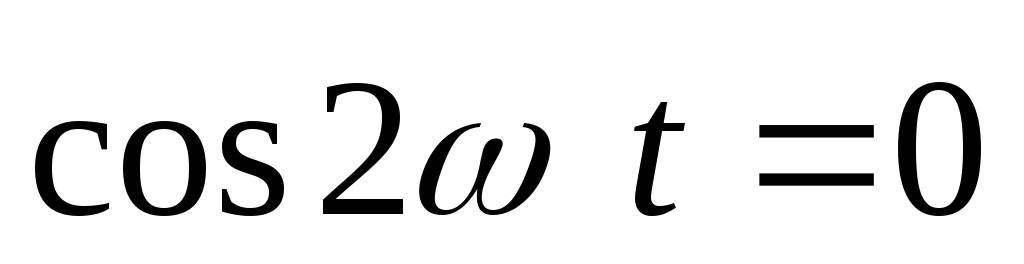
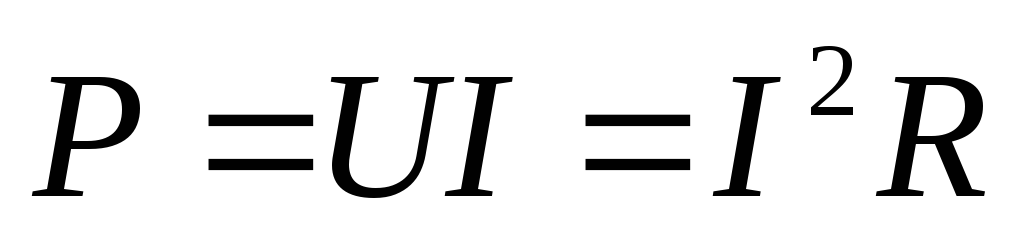 ,
где
,
где 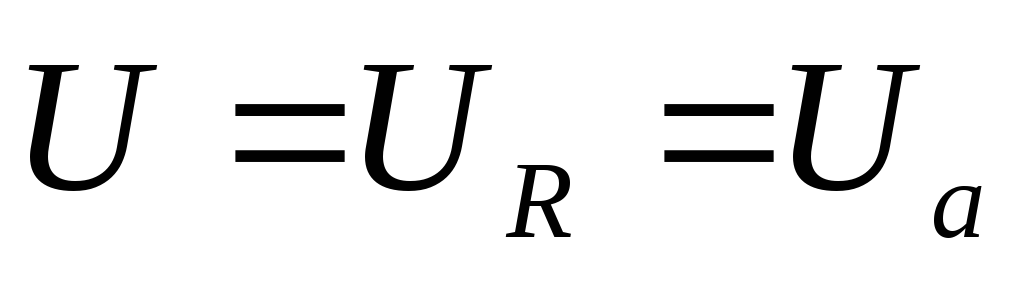
Измеряется активная мощность в ваттах (Вт).
Пример решения задачи.
1) Дано: 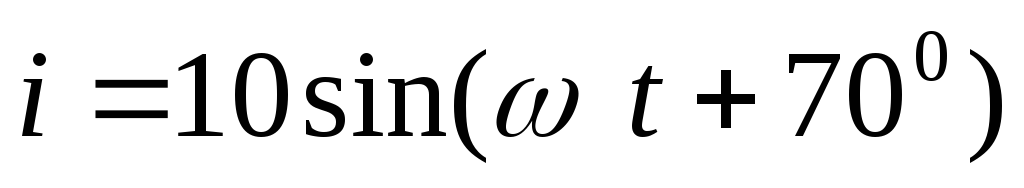
R=50 Ом
Определить:  .
Построить векторную
диаграмму тока и напряжения.
.
Построить векторную
диаграмму тока и напряжения.
Um=Im·R=10·50=500 В
I=
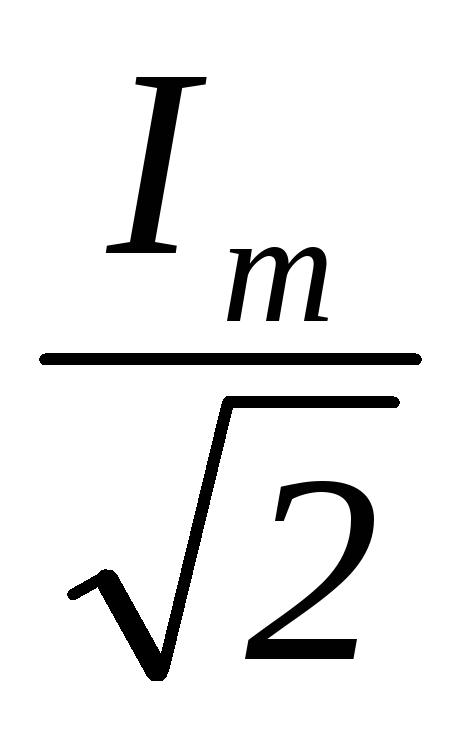 =7,14
А
=7,14
А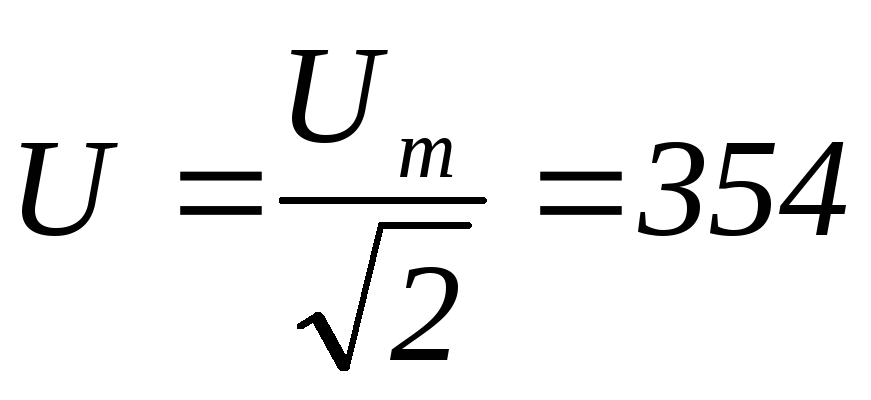 В
В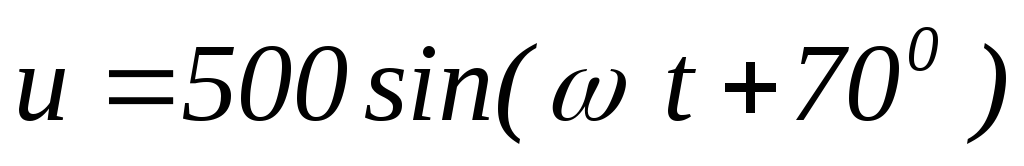
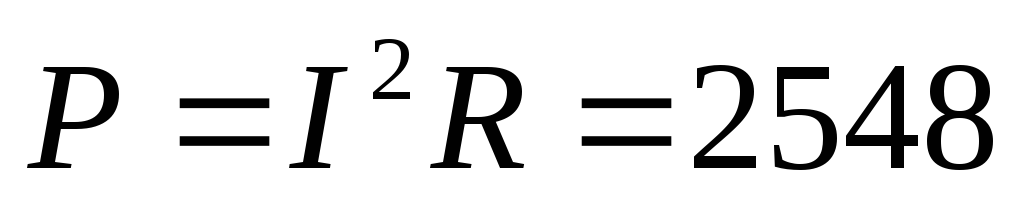 Вт
Вт 
Тестовые задания:
Задание | |
1.Верно ли, что в цепи с R напряжения и совпадают по фазе? | Да; Нет. |
2.Какая единица измерения активной мощности? | а) Вт; б) вар; в) B·A. |
Цепь с идеальной катушкой индуктивности при гармоническом воздействии
Пусть по цепи
течет ток 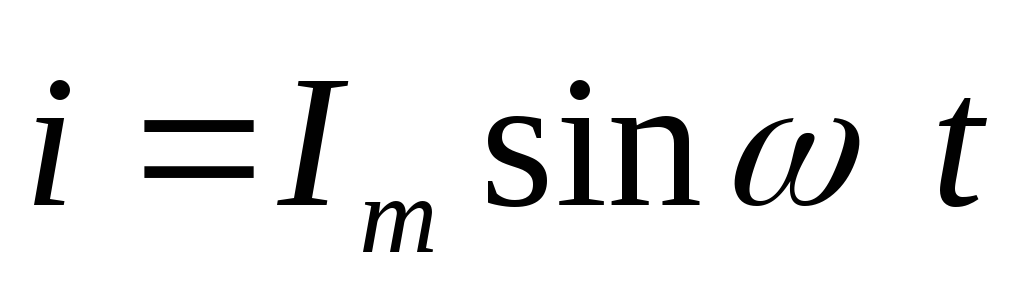
При прохождении тока в катушке возникает ЭДС самоиндукции
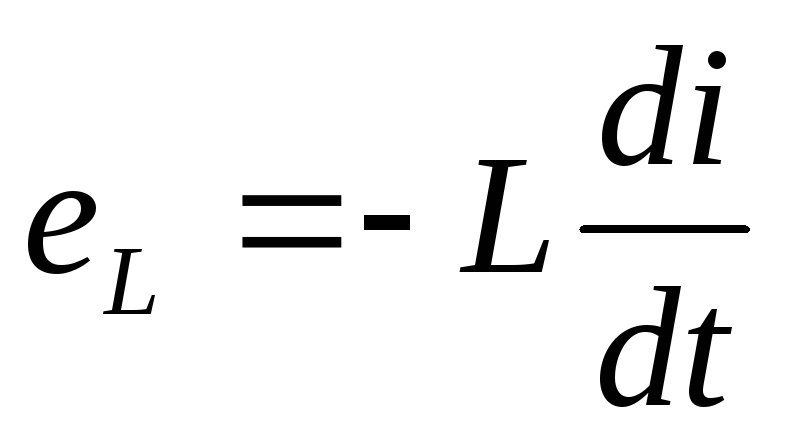
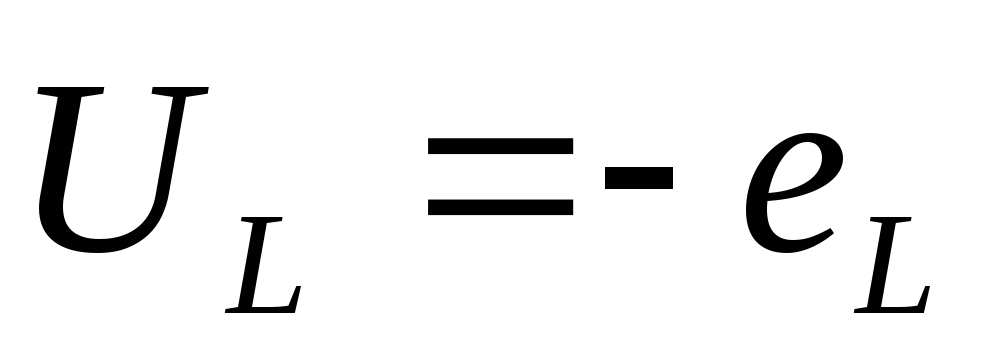 -напряжение
на входе уравновешивает эту ЭДС.
Подставим в эту формулу значение тока
-напряжение
на входе уравновешивает эту ЭДС.
Подставим в эту формулу значение тока 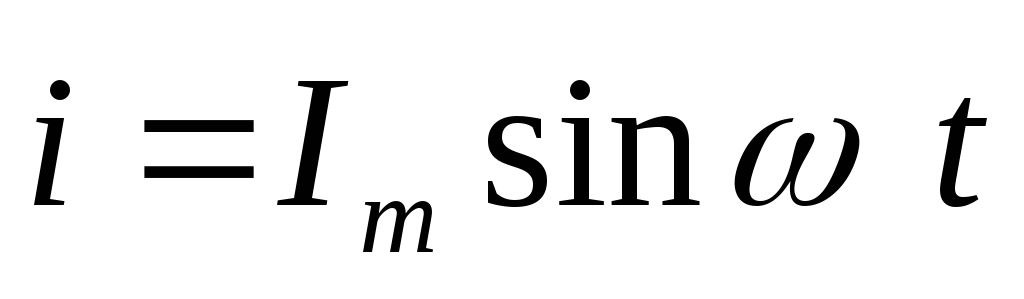 и продифференцируем
и продифференцируем
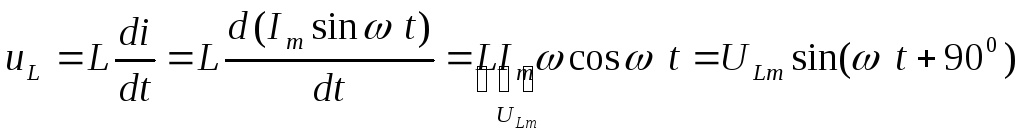
Угол сдвига фаз 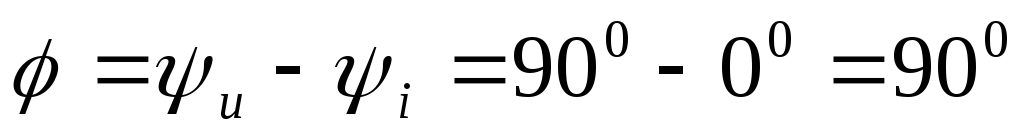
Вывод: в цепи с идеальной катушкой напряжение опережает ток на угол 900
ЭДС самоиндукции уравновешивает напряжение, значить ЭДС будет отставать от тока на угол равный 900.
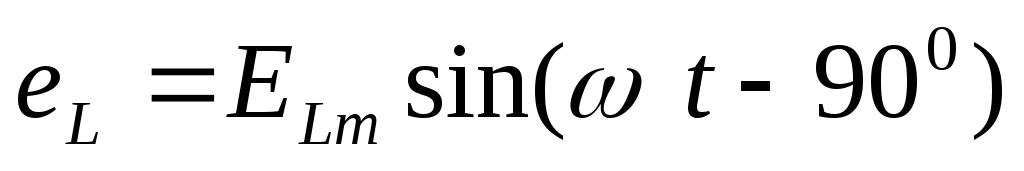
 —
потокосцепление катушки.
—
потокосцепление катушки. 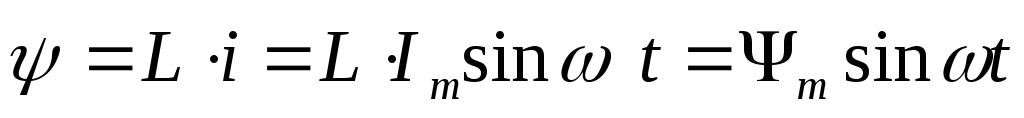
Вывод: в цепи с идеальной катушкой ток, потокосцепление и магнитный поток совпадает по фазе.
Построим временную и векторную диаграммы
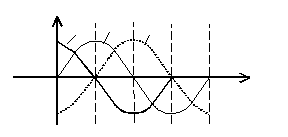
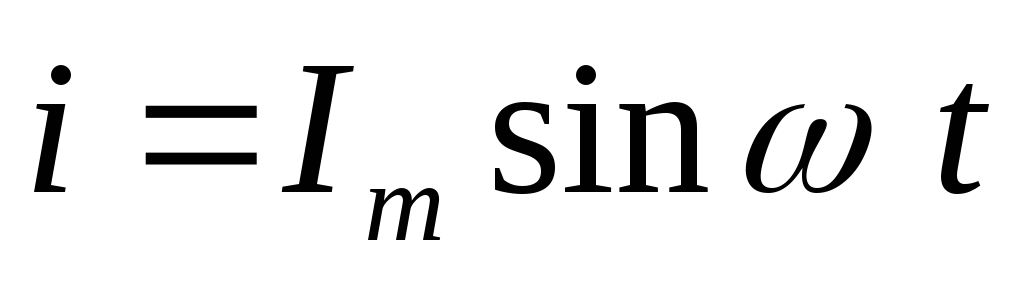
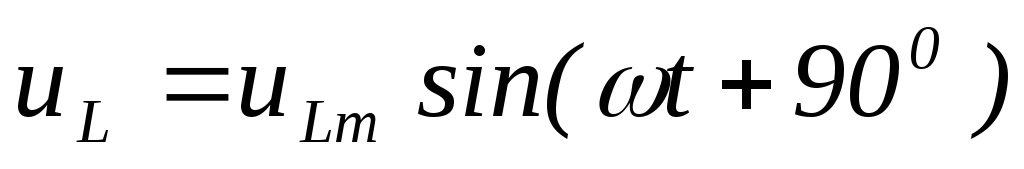
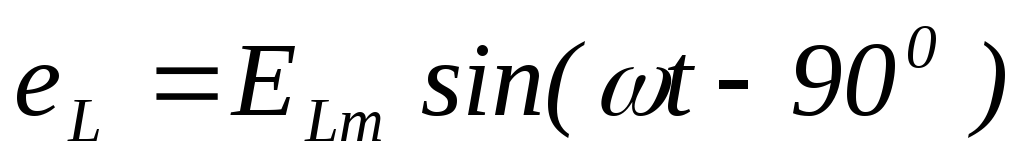
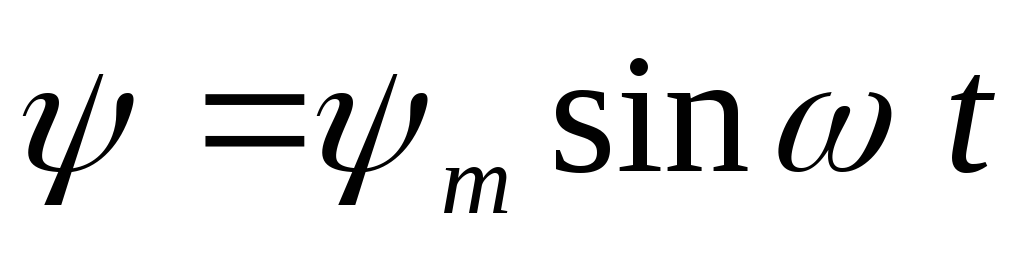
Закон Ома для цепи с идеальной катушкой. Индуктивное сопротивление
Запишем отдельно
выражение 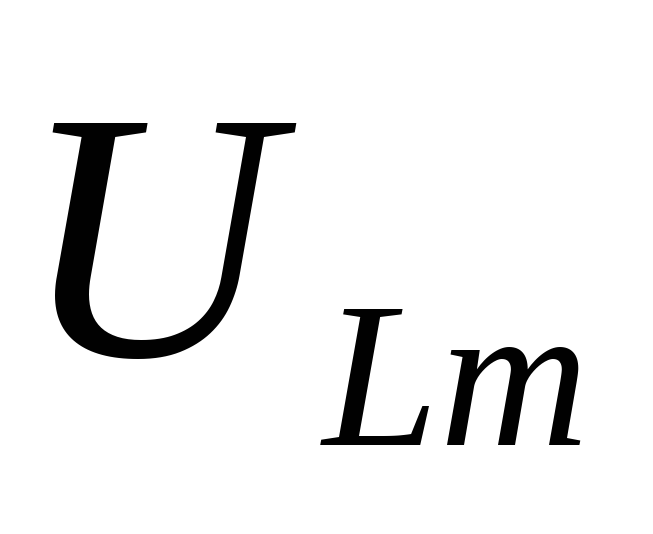
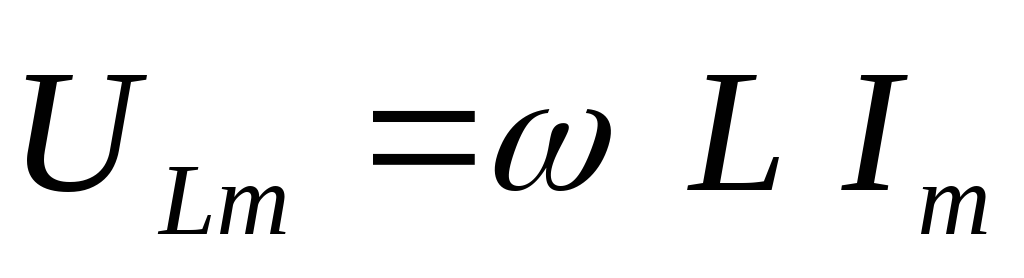 ,
отсюда
,
отсюда 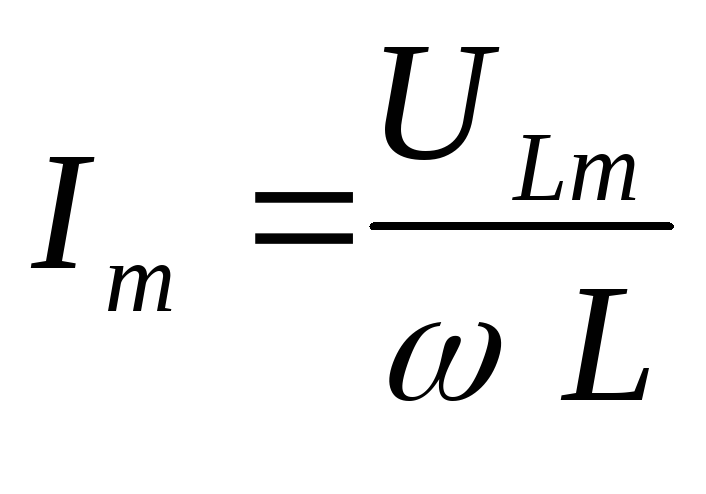 ,
где обозначаем
,
где обозначаем 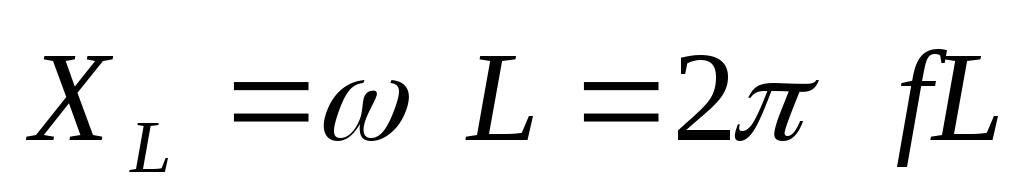 — индуктивное сопротивление
— индуктивное сопротивление
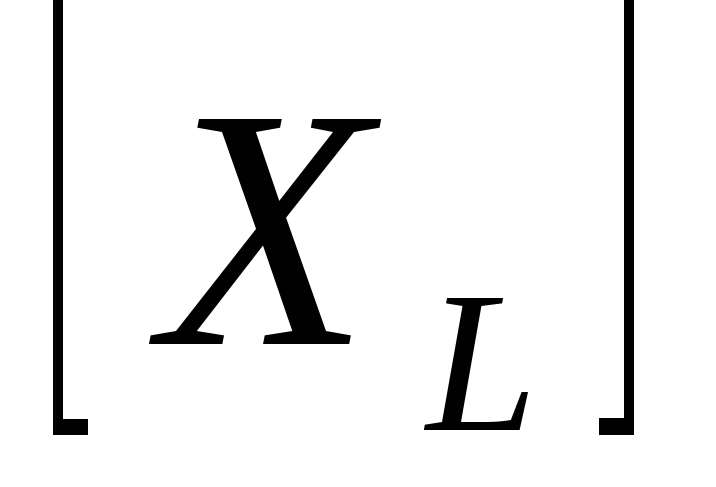 =Ом
=Ом
Получаем закон Ома для максимальных и действующих значений в цепи с идеальной катушкой
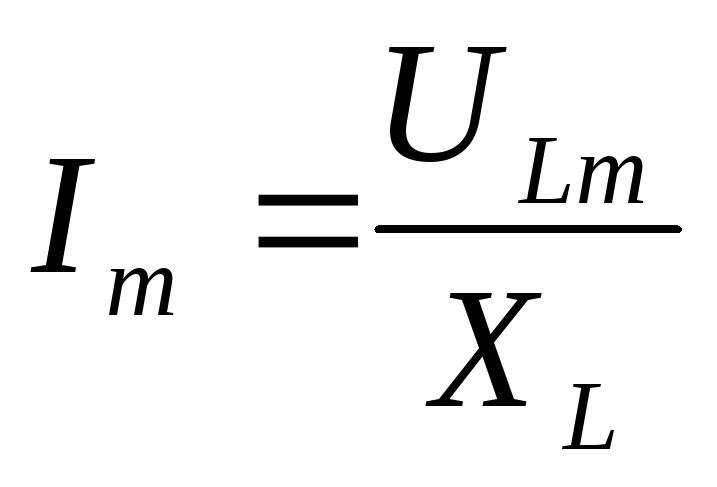
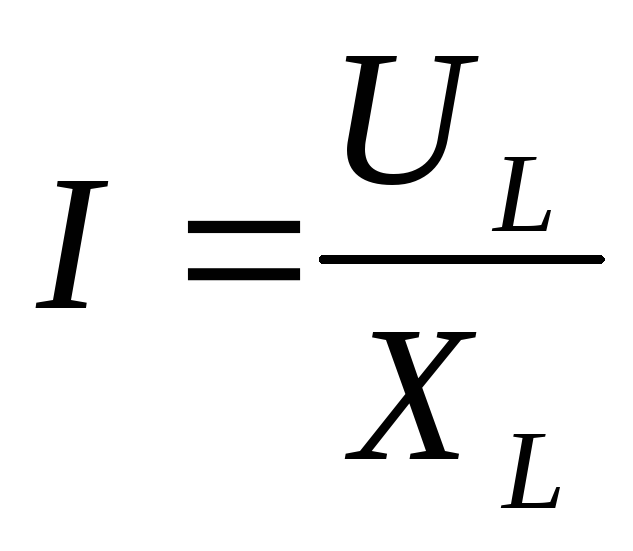
Вывод: в цепи с
идеальной катушкой закон Ома справедлив
для максимальных и действующих значений,
но не справедлив для мгновенных (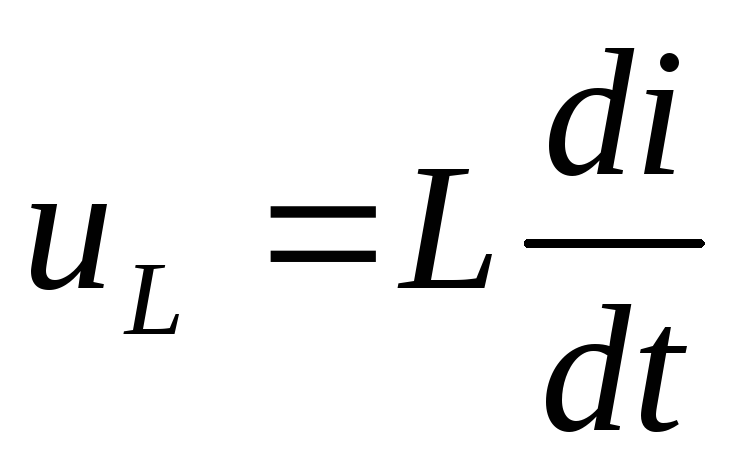 ).
).
Построим зависимость
,
где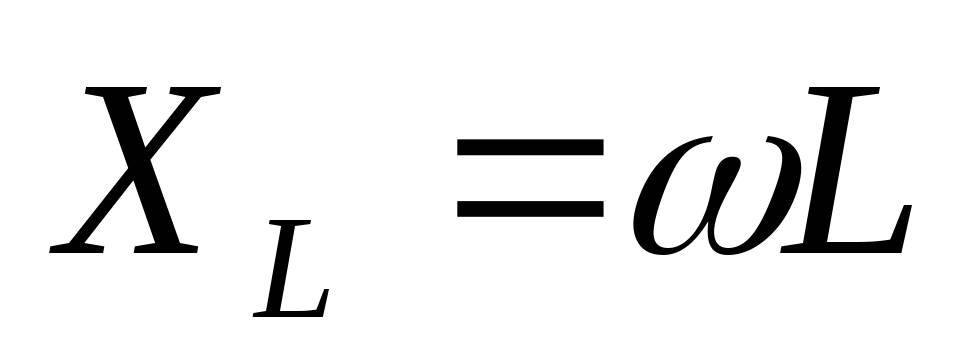
Вывод: с ростом частоты индуктивное сопротивление растет, значит, катушка хорошо пропускает токи нижних и плохо токи верхних частот. Катушка-фильтр нижних частот.
На постоянном
токе 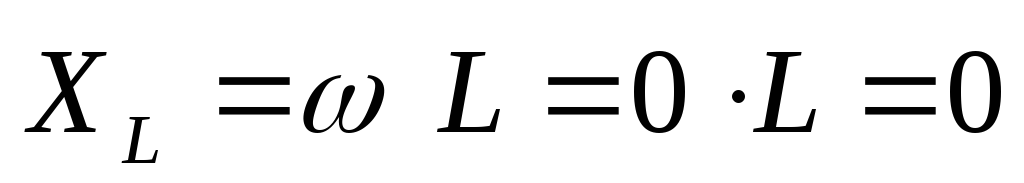
Индуктивное сопротивление равно 0, значит, на постоянном токе вместо идеальной катушки стоит провод.
Энергетический процесс в цепи с идеальной катушкой.
Мгновенная мощность равна произведению мгновенного значения напряжения на мгновенное значение тока.
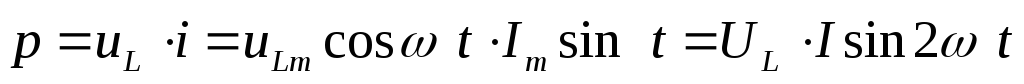
Перемножим напряжение и ток графически.
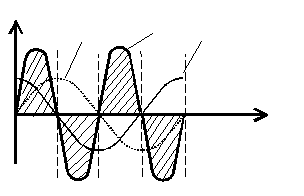
Вывод: первую и третью четверти периода напряжение и ток имеют одинаковые знаки, следовательно, источник работает в режиме генератора и отдает свою энергию в магнитное поле катушки, мгновенная мощность положительна. Ворую и четвертую четверти напряжение и ток имеют разные знаки, следовательно, источник работает в режиме потребителя, энергия возвращается обратно к источнику, мгновенная мощность отрицательна.
Вывод: в цепи с
идеальной катушкой источник и катушка
обмениваются энергией и мерой этого
обмена, является реактивная мощность,
которая обозначается 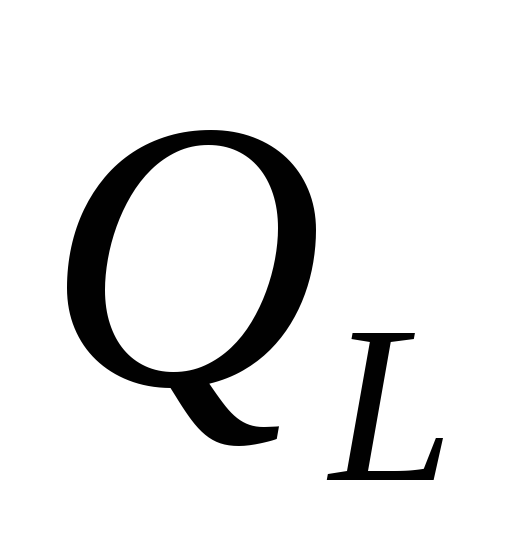 .
.
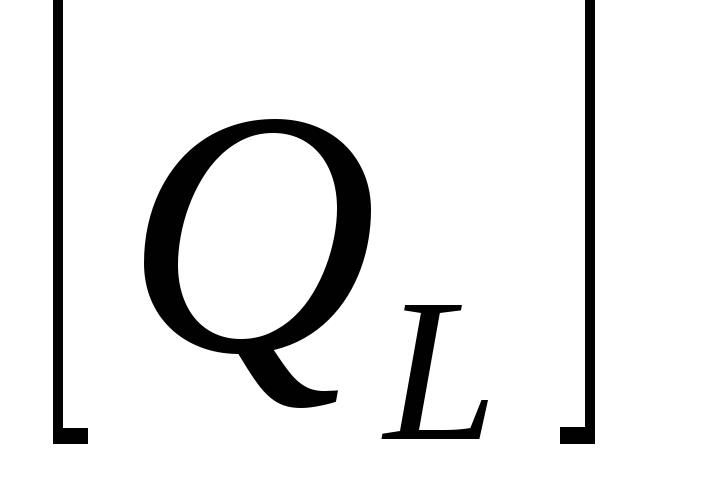 =
вар
=
вар
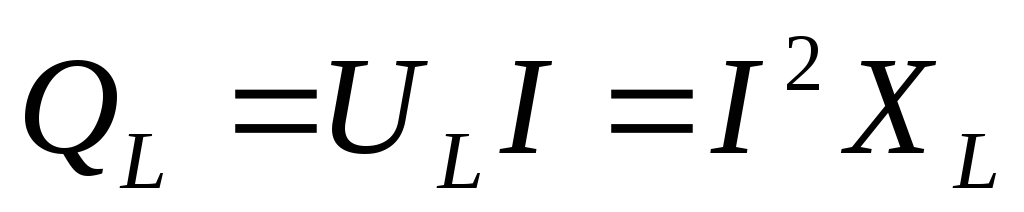
Пример решения задачи
Дано:
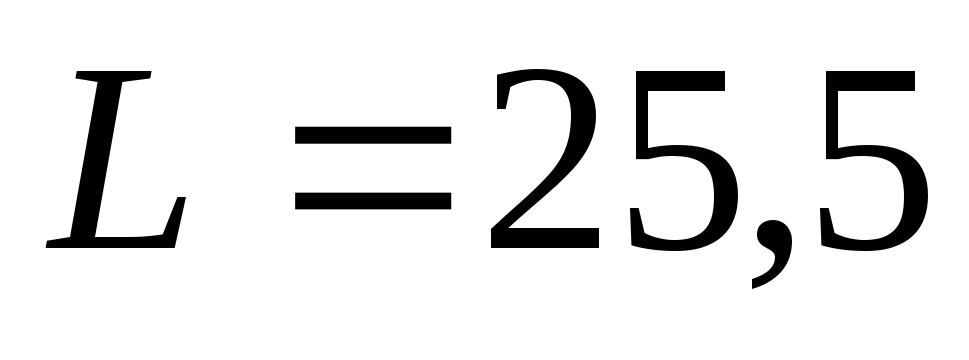 мГн
мГн
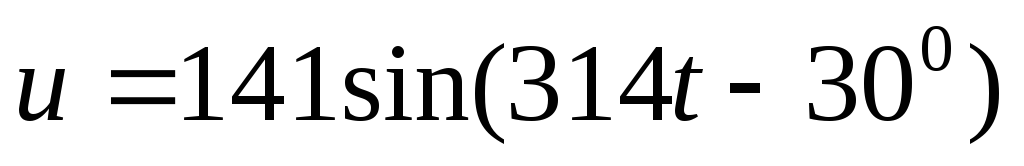
Найти:
 ,
построить векторные диаграммы напряжения
и тока
,
построить векторные диаграммы напряжения
и тока
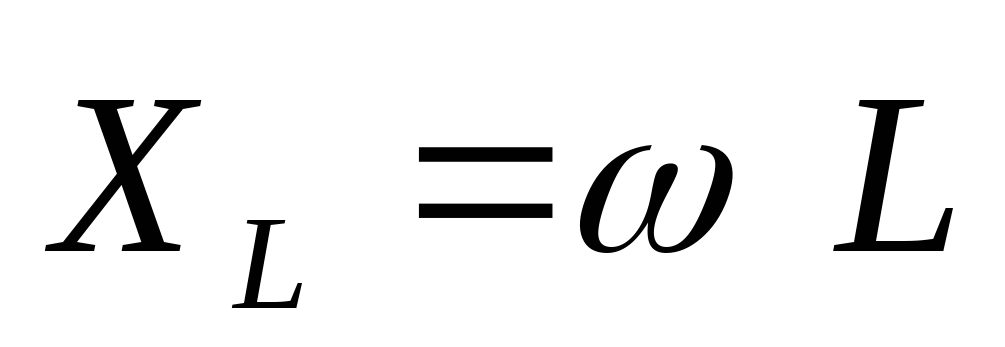
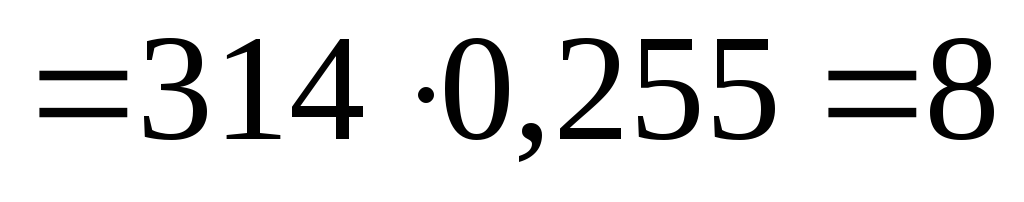 Ом
Ом
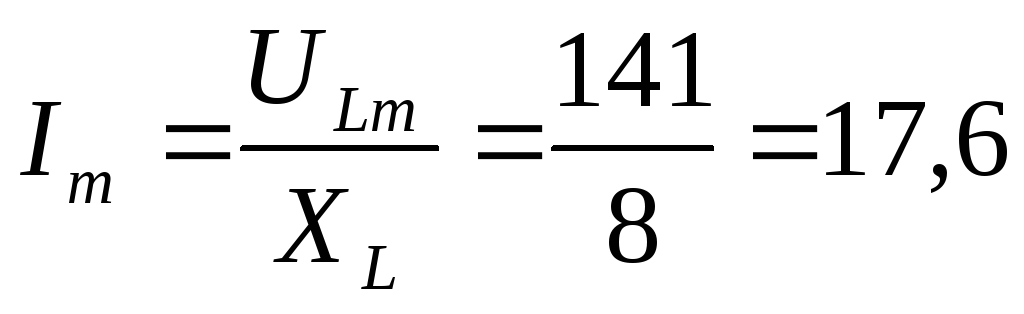 А
А
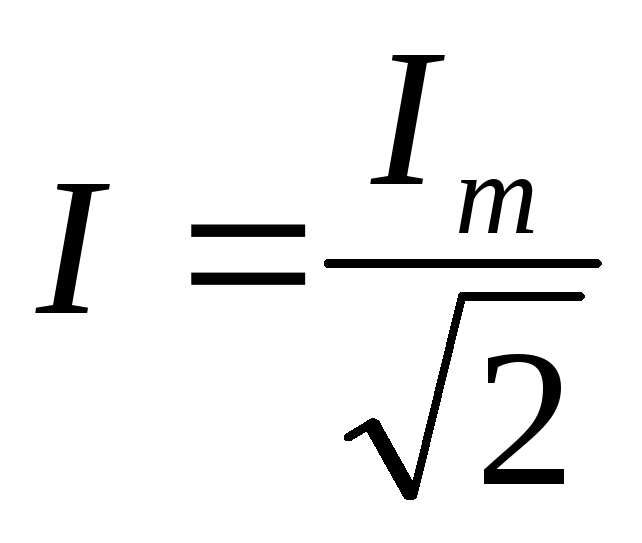
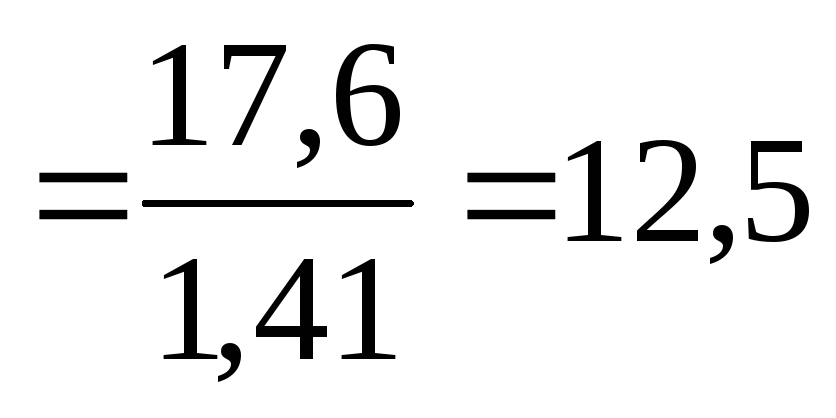 А
А
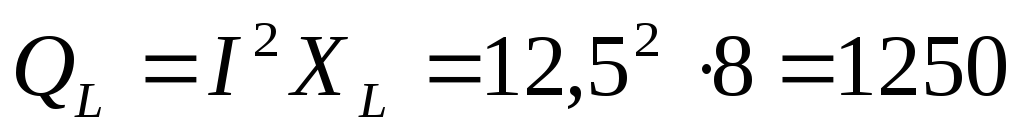 вар
вар
расскажите про мощность переменного тока (очень надо)
Мощность равна произведению напряжения на зажимах цепи на ток, протекающий в этой цепи: р — и г. Поскольку напряжение и ток изменяются, то по отношению к переменному току можно говорить о мощности D данный момент, т. е. о мгновенной мощности. Мгновенная мощность равна нулю в те моменты, когда равны нулю и или i. Мгновенная мощность положительна, когда направление напряжения и тока на нагрузке одинаковы, и отрицательна, когда и и i разных анаков. Измерить мгновенную мощность относительно сложно. Поэтому для оценки энергетических соотношений в цепи переменного тока возьмем среднее значение мгновенной мощности за период. Среднее значение мощности за период называют активной мощностью. Рассмотрим энергетические процессы в цепях переменного тока. В цепи переменного тока только с активным сопротивлением ток и напряжение совпадают по фазе, следовательно, I = IM sinwt, и = UM sinwt. Мгновенная мощность будет равна: р = и г = UMIM sin2wt Средняя мощность в цепи переменного тока, содержащей только активное сопротивление, будет равна: Р = U I. На рис. 5 приведены кривые напряжения, тока и мощности для этой цепи. Из графика видно, что мгноиенная мощность всегда положительна. Это значит, что независимо от направления тока в цепи энергия пере¬дается всегда в одном направлении от источника к приемнику. В приемнике электрическая энергия преобразуется в другие формы энергии (тепло, механическую работу) . Пока ток возрастает, мгновенная мощность положительна, т. е. энергия передается от источника к индуктивности. В это время происходит накапливание энергии в магнитном поле индуктивности. К концу первой четверти периода эта энергия достигает своего максимума. Во второй четверти периода, когда ток убывает, мгновенная мощность отрицательна, т. е. вся энергия, запасенная магнитным полем индуктивности, возвращается назад к источнику. Среднее значение мощности за период будет равно нулю. Следовательно, и активная мощность в такой цепи равна нулю. Ток в цепи не совершает работы, а обуславливается лишь колебаниями энергии между источником и магнитным полем индуктивности. Этот ток называется реактивным. Он бесполезно загружает источники энергии и провода линий передач. В цепи с емкостью, так же как и в цепи с индуктивностью, мгновенная мощность изменяется с двойной частотой по отношению к току. В этой цепи мощность положительна, т. е. энергия передается от источника к емкости, пока возрастает напряжение. В это время происходит накапливание энергии D электрическом поле между обкладками конденсатора. Во второй четверти периода, когда напряжение понижается, мощность отрицательна, так как емкость разряжается на источник электроэнергии. За это время вся энергии, напасенная в электрическом поле между обкладками конденсатора, возвращается источнику. Среднее значение мощности за период равно нулю. В цепи будет протекать реактивный емкостный ток, обусловленный колебаниями энергии между источником и емкостью. Большинство промышленных электрических цепей содержит активное сопротивление и индуктивность. В этом случае ток отстает от напряжения на некоторый угол ф. Величина этого угла зависит от соотношения активного и реактивного (индуктивного) сопротивлений цепи. Чем больше индуктивность цепи при одном и том же активном сопротивлении, тем на больший угол ток отстает от напряжения. Среднее значение за период составляющей U I cos(2wt + ср) равно нулю. Поэтому средняя (активная) мощность цепи будет равна: Р = U I coscp. Последнее выражение для активной мощности является общим, и оно справедливо при наличии сдвига фаз между током и напряжением, вызванного любой причиной. Электрические машины и аппараты конструируют для работы при определенных значениях тока и напряжения. Поэтому некоторые из них характеризуют не активной мощностью, зависящей от сдвига фаз ср между напряжением и током, а полной мощностью (S = U I), представляющей собой произведение действующих значений напряжения и тока. Очевидно, что полная мощность равна
<a rel=»nofollow» href=»http://ru.wikipedia.org/wiki/Электрическая_мощность» target=»_blank»>http://ru.wikipedia.org/wiki/Электрическая_мощность</a>
Мгновенная мощность и энергия
Если из одной точки в другую, имеющие разность потенциалов u, перемещать бесконечно малый заряд dq, то затрачивается работа, равная энергии:
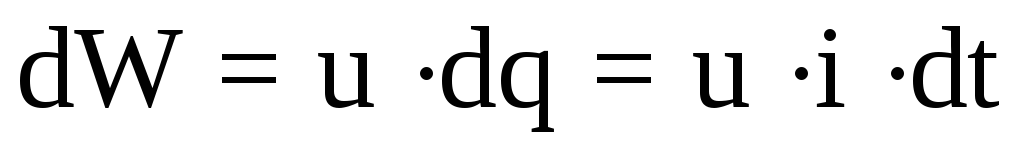 .
.
Производная энергии по времени является мгновенной мощностью:
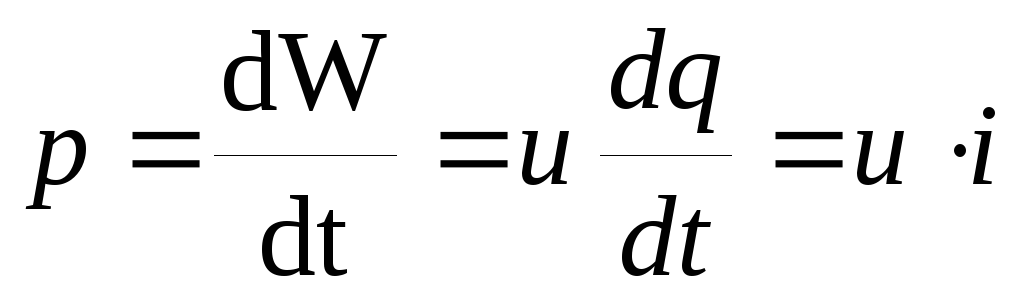
Следовательно, мгновенная мощность, поступающая в приемник, равна произведению мгновенных значений тока и напряжения. Она положительна при одинаковых знаках u и i и отрицательна при разных. Положительное значение мощности означает, что мощность поступает в приемник, отрицательное – возвращается в источник питания.
Энергию, потребляемую приемником за промежуток времени от t1 до t2, можно определить как
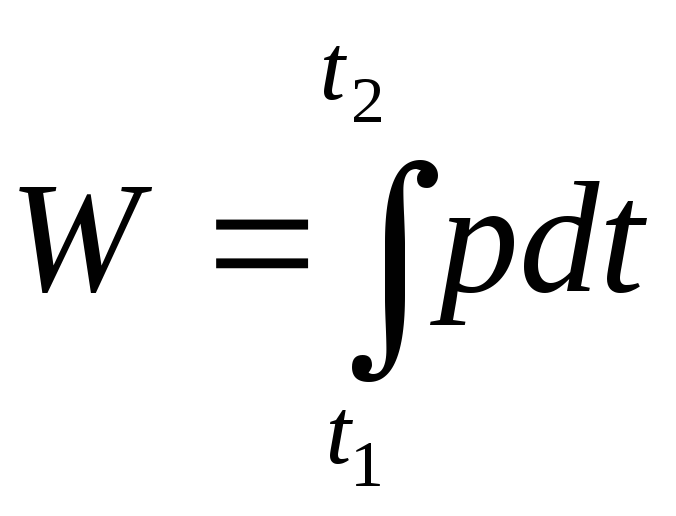 .
.
Измеряется мощность
в ваттах (Вт), [Вт]=[В А],
энергия – в джоулях (Дж), [Дж]=[В
А],
энергия – в джоулях (Дж), [Дж]=[В А
А с].
с].
Пассивные элементы электрической цепи Сопротивление
Сопротивлением называется идеализированный элемент цепи в котором происходит необратимый процесс преобразования электрической энергии в тепловую. Обозначение резистора приведено на рис. 1.1, буквенное обозначение – R или r.
Между напряжением на элементе, током и сопротивлением элемента существует соотношение:
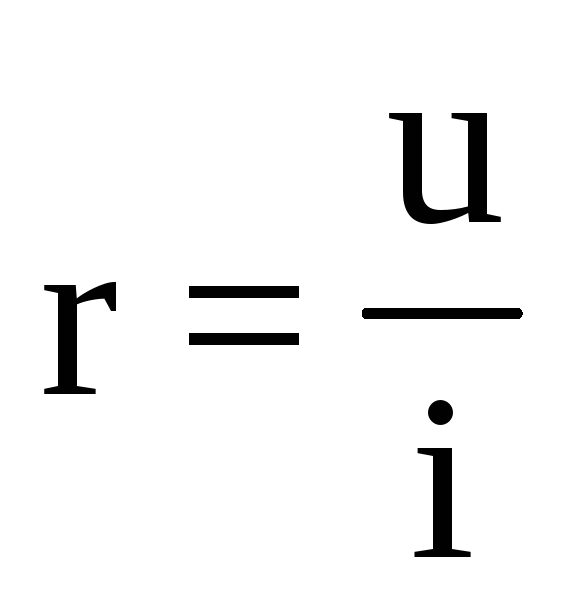 , (1.2)
, (1.2)
известное как закон Ома, экспериментально установленный немецким ученым Омом в 1826 г. Величина сопротивления измеряется в омах (Ом). [Ом] = [В/А].
Сопротивление всегда положительное, т.е., направления тока через сопротивление и напряжения на нем совпадают.
Величина, обратная сопротивлению
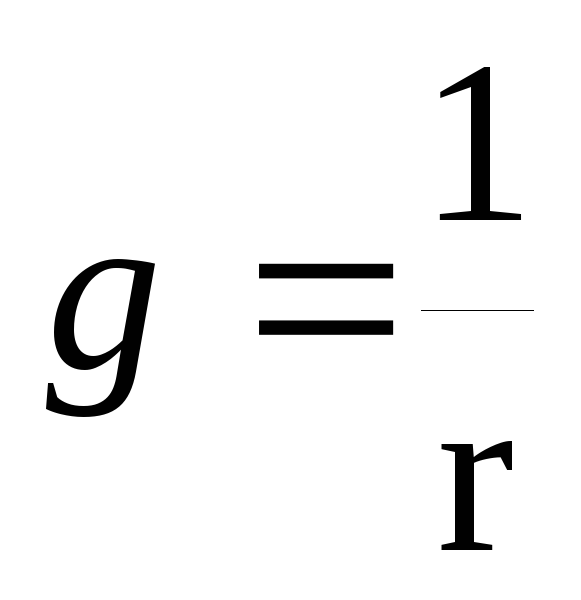 ,
,
называется проводимостью. Измеряется проводимость в сименсах (См). [См] = [А/В].
Мгновенная мощность, выделяемая на сопротивлении, равна произведению мгновенных значений тока и напряжения:
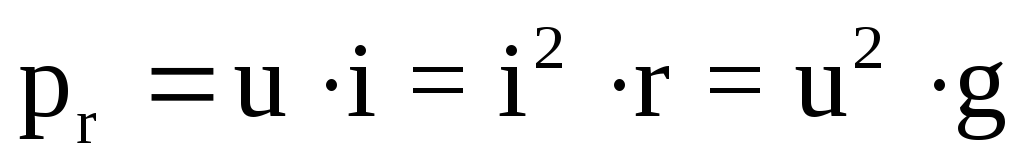 ,
,
т.е.,
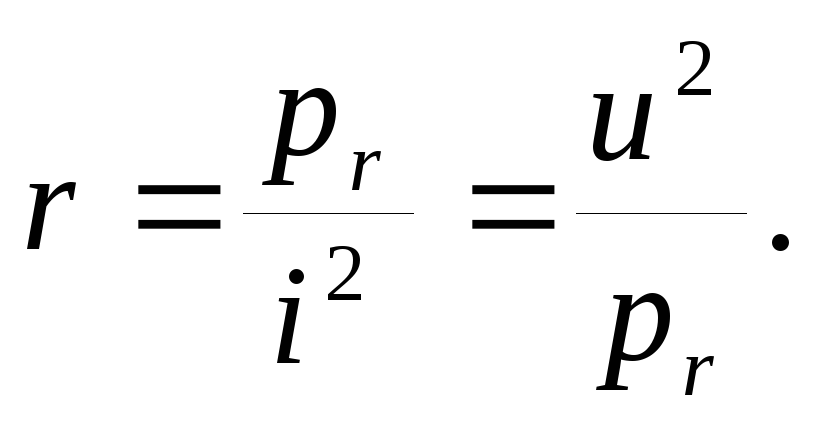
Электрическая энергия, поглощаемая сопротивлением, равна:
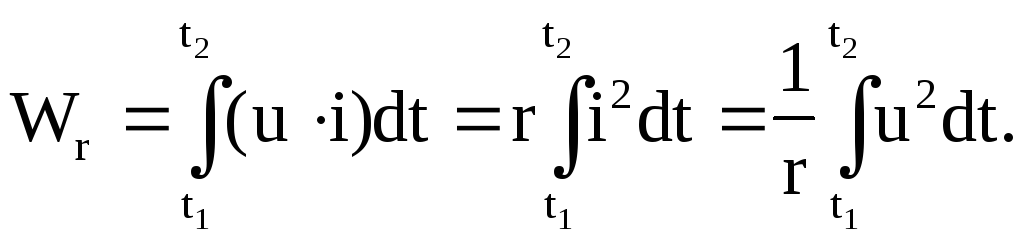
Если ток постоянный (i = I = const), то
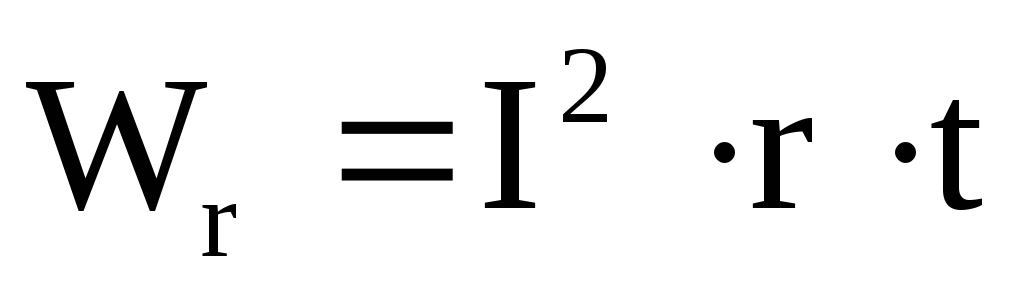 .
.
1.4.2. Емкость
Емкостью называется идеализированный элемент электрической цепи, приближенно заменяющий конденсатор, в котором накапливается энергия электрического поля. Буквенное обозначение емкости – С.
Величина емкости определяет, какой заряд q можно получить при заданном напряжении u:
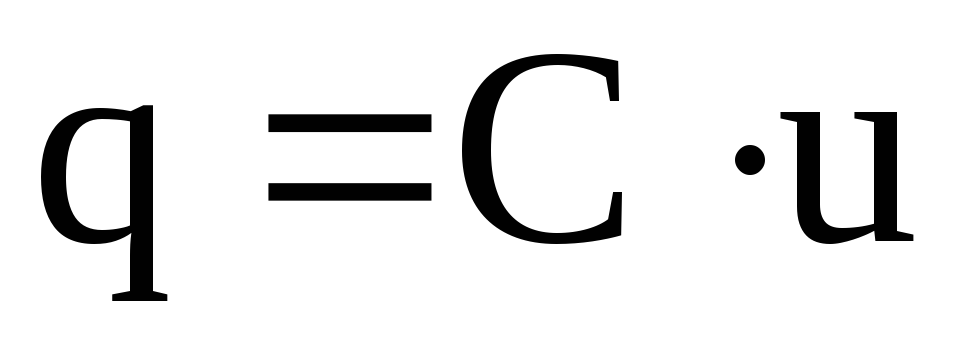 (1.3)
(1.3)
или
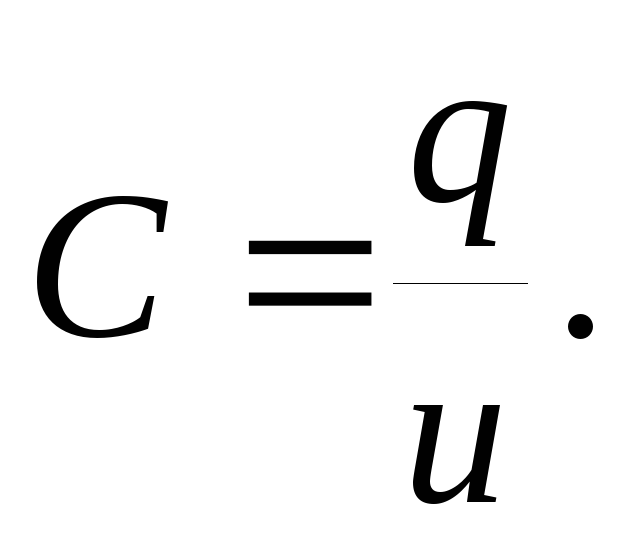
Величина емкости измеряется в фарадах (Ф):
 .
.
Заряд и напряжение всегда имеют одинаковый знак, так как емкость С>0 .
При изменении напряжения, приложенного к емкости, изменится в соответствии с (1.3) и электрический заряд. Подставив (1.3) в (1.1), получаем:
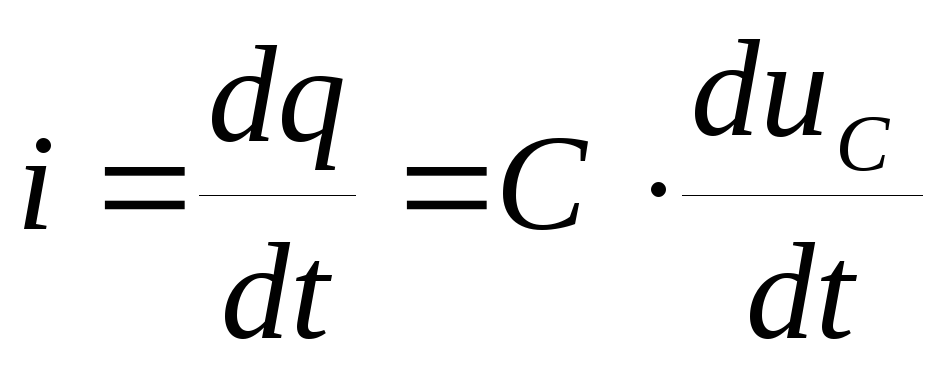 (1.
4.)
(1.
4.)
Не рассматривая процессы с позиций теории электромагнитного поля, отметим только, что в проводниках, соединенных с емкостью, будет протекать ток, величина которого определяется в соответствии с (1.4).
На основании
выражения (1.4) напряжение на емкости 
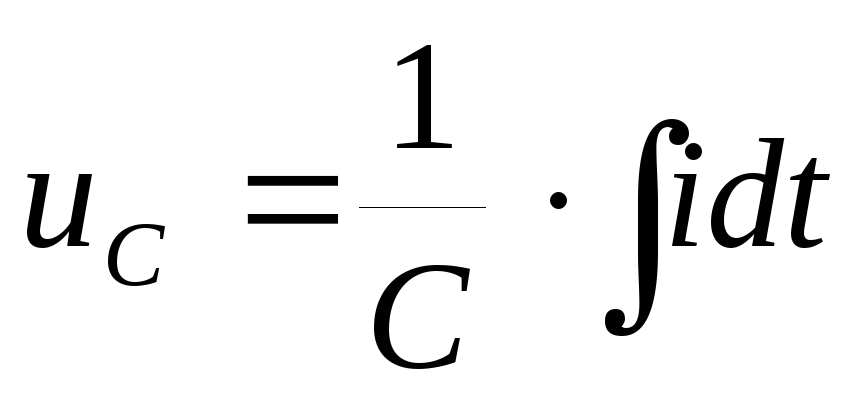
или
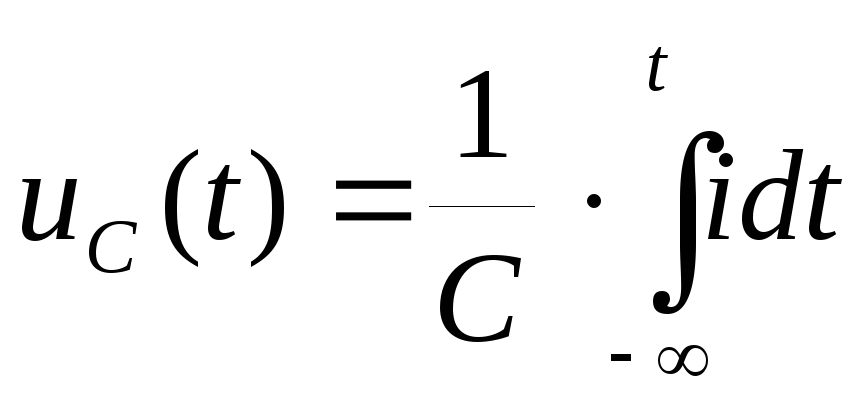 ,
,
где предполагается,
что до момента времени t процесс мог
длиться сколь угодно долго, поэтому
нижний предел интеграла принят равным
(– ).
При t = 0 напряжение на емкости равно:
).
При t = 0 напряжение на емкости равно:
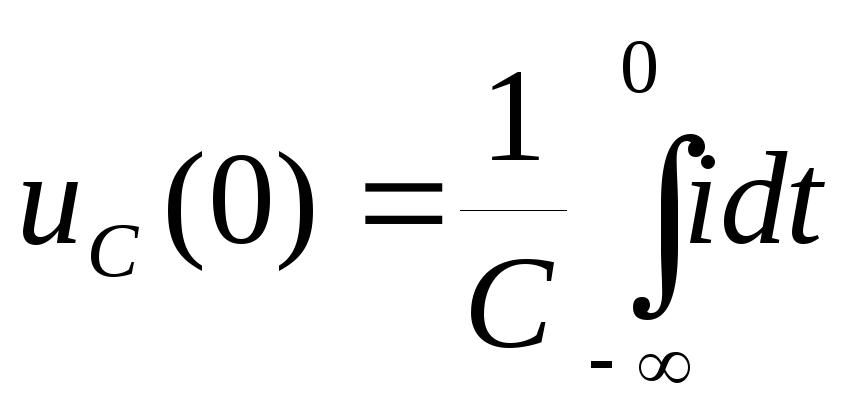 ,
,
или
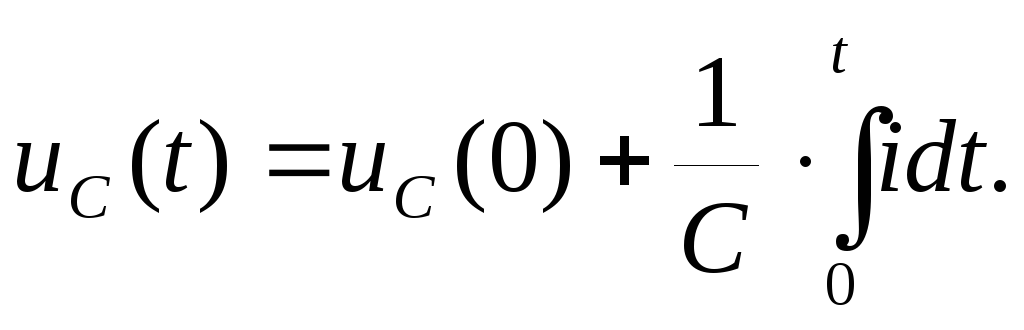 (1.5)
(1.5)
Условное графическое обозначение емкости с положительными направлениями токов и напряжений приведено на рис. 1.5.
 Мгновенная
мощность, поступающая в емкость, равна:
Мгновенная
мощность, поступающая в емкость, равна:
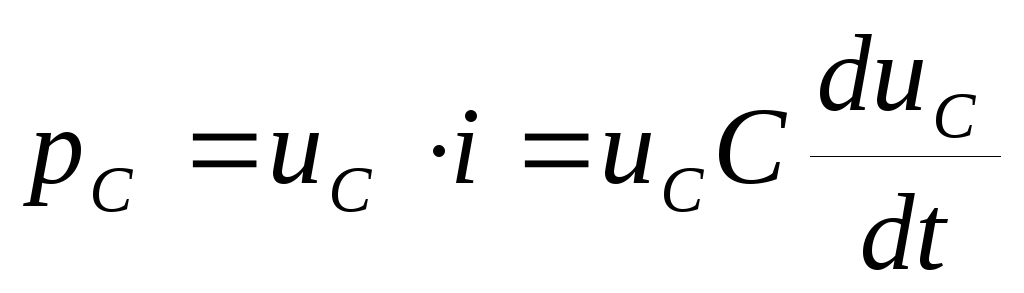 ,
,
откуда видно, что
если 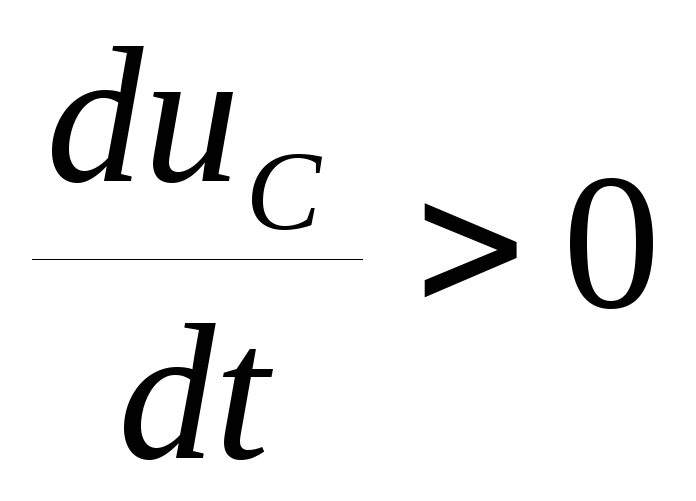 ,
мгновенная мощность pc>0,
т.е., емкость накапливает энергию
(происходит заряд емкости), иначе
происходит возврат энергии источнику
питания (разряд емкости).
,
мгновенная мощность pc>0,
т.е., емкость накапливает энергию
(происходит заряд емкости), иначе
происходит возврат энергии источнику
питания (разряд емкости).
Энергия электрического
поля в произвольный момент времени t
определится по формуле:
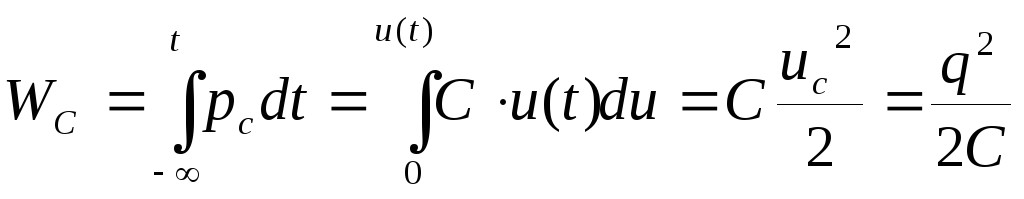 .
(1.6)
.
(1.6)
В выражении (1.6) предполагается, что при
t = (– )
напряжение на емкости С: Uc(
)
напряжение на емкости С: Uc(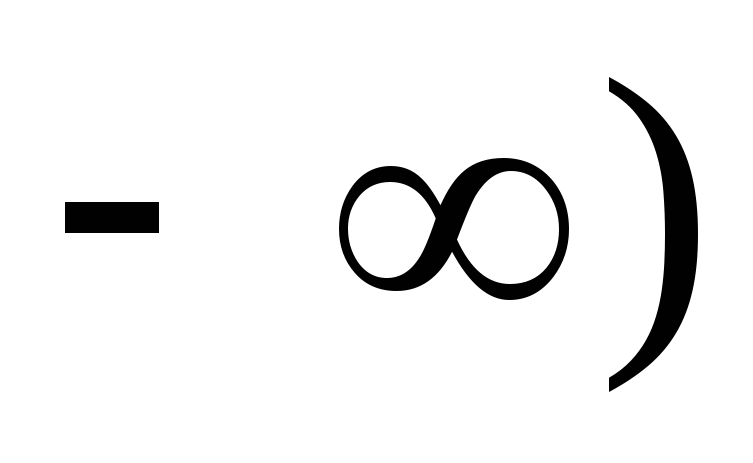 =
0.
=
0.
Мощность на резисторе в цепи переменного тока
По закону Джоуля-Ленца, мгновенное значение тепловой мощности на участке цепи определяется как произведение силы тока на напряжение:
P = UI =U0cos ω t* I0cos ω t = I0U0cos 2ωt
Эта величина непрерывно изменяется. В промышленной сети частота изменения равна 50 Гц, то есть 50 раз в секунду изменяется значение тепловой мощности. Поэтому практического значения знание мгновенной мощности не имеет.
Вычислим среднее значение мощности за период колебаний:
<P> = <I0U0cos 2 ω t> = I0U0<cos 2 ω t>
<cos2ωt> = ½
<P> = 1/2I0U0
Введем определение:
Действующим значением силы тока (или напряжения) называется сила такого постоянного тока (или напряжения), который, протекая по данной цепи, выделяет в ней мощность, равную средней мощности в цепи переменного тока за период
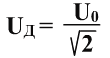
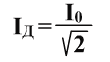
<P> = IДUД
Средняя мощность, выделяющаяся на резисторе в цепи переменного тока за период, равна произведению действующего значения силы тока на действующее значение напряжения.
Домашнее задание Повторить: конденсатор, емкость конденсатора, единицы измерения электроемкости, энергия заряженного конденсатора, последовательное и параллельное соединение конденсаторов, энергия электрического поля заряженного конденсатора, закон Ома для участка цепи.
Лекция 6 Конденсатор в цепи переменного тока
Включим конденсатор в цепь постоянного тока. Некоторый заряд перетечет от источника тока на обкладки конденсатора. В цепи возникает кратковременный импульс зарядного тока. Конденсатор заряжается до напряжения источника, после чего ток прекращается. Через конденсатор постоянный ток течь не может!
Р ассмотрим
процессы, происходящие при включении
конденсатора в цепь переменного тока
ассмотрим
процессы, происходящие при включении
конденсатора в цепь переменного тока
зарядный ток
.
Через диэлектрик, разделяющий обкладки конденсатора, электрический ток протекать, как и прежде, не может. Но в результате периодически повторяющихся процессов зарядки и разрядки конденсатора в цепи появится переменный ток.
Если напряжение в цепи изменяется по гармоническому закону,
U = U0cos ωt
т о
заряд на обкладках конденсатора
изменяется
о
заряд на обкладках конденсатора
изменяется
также по гармоническому закону
q=Cu = CU0cos ωt
и силу тока в цепи можно найти как производную заряда
i = q/
i= -CU0 ω sin ωt = CU0ω cos(ωt+π/2),
i= I0ω cos(ωt+π/2)
Амплитуда силы тока I0 = CU0ω
Из полученной формулы видно, что в любой момент времени
фаза тока больше фазы напряжения на π/2.
В цепи переменного напряжение на конденсаторе тока отстает по фазе от тока на π/2, или на четверть периода.
Емкостное сопротивление
Величину 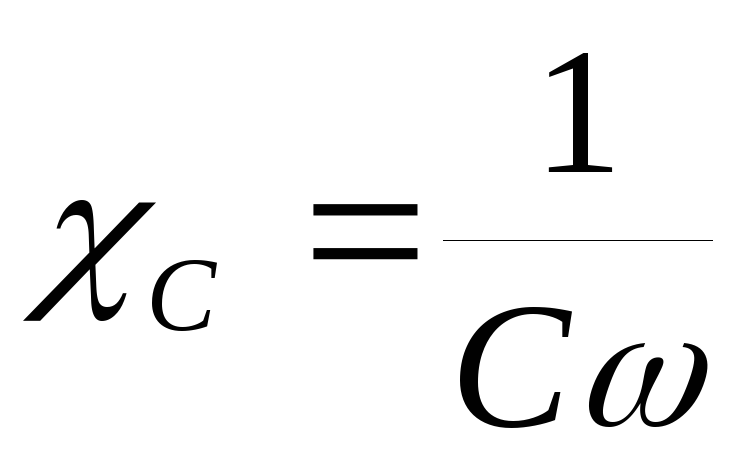
называют емкостным сопротивлением.
Связь между амплитудными значениями силы тока и напряжения формально совпадает с законом Ома для участка цепи
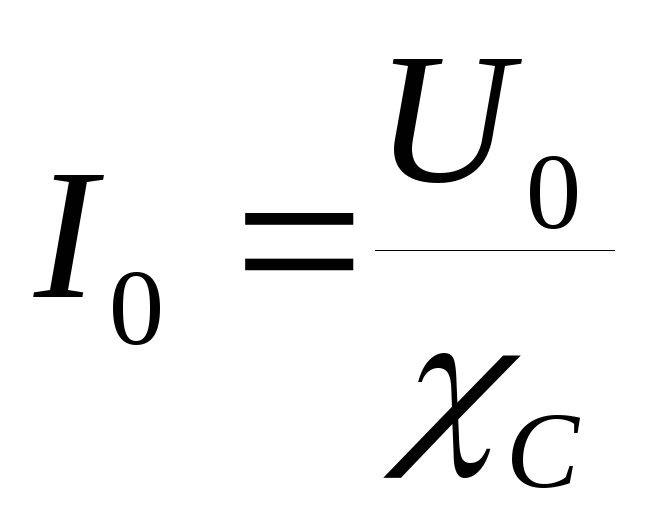
Такое же соотношение выполняется для действующих значений силы тока и напряжения.
Емкостное сопротивление конденсатора зависит от частоты переменного напряжения. С увеличением частоты колебаний напряжения емкостное сопротивление уменьшается, поэтому амплитуда силы тока увеличивается прямо пропорционально частоте I0 = CU0ω.
При уменьшении частоты амплитуда силы тока уменьшается и при ω=0 обращается в 0. Отметим, что нулевая частота колебаний означает, что в цепи протекает постоянный ток.
Задача 8: максимальная мощность на реостате
 | Резистор, сопротивление которого постоянно, и реостат подсоединены к источнику постоянного напряжения, как показано на рисунке. При силе тока в цепи I1 = 2 A на реостате выделяется мощность P1 = 48 Вт, а при силе тока I2 = 5 A на нем выделяется мощность P2 = 30 Вт.
|
Решение
1. Пусть в первом случае сопротивление реостата равно R1, во втором — равно R2. По закону Ома имеем систему:| I2(r + R2) = U, (1) |
| U = | P1I22 − P2I12 | = 36 B, |
| I1I2(I2 − I1) |
| r = | P1I2 − P2I1 | = 6 Ом. |
| I1I2(I2 − I1) |
 3. В общем случае мощность, которая выделяется на переменном напряжении R, можно представить в виде:
3. В общем случае мощность, которая выделяется на переменном напряжении R, можно представить в виде:
| Pmax = | U2 | = | U2Rм | => Rм = r. |
| 4r | (Rм + r)2 |
Далее: максимальная сила тока в предохранителе [тема: задачи на минимум и максимум]

