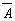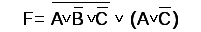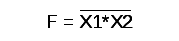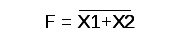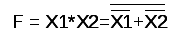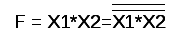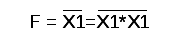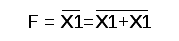Логические схемы. Решение задач.

Просмотр содержимого документа
«Логические схемы. Решение задач.»

Решение задач

Пример

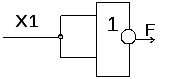
Составить логическую схему для следующего логического выражения найдите ответ:

F = X V Y & X

( пусть Х – истина, Y – ложь)

Строим схему:

Ответ: 1 V 0 & 1 =

&

V

Пример

Постройте логическую схему, соответствующую логическому выражению F = X & Y V ¬(Y V X) . Вычислить значения выражения для X=1 , Y=0 .

Постройте логическую схему по логическому выражению и найдите значение логического выражения

F = A V B& ¬ C , если А=1, В=1, С=1

F = ¬ ( A V B&C ), если А=0, В=1, С=1

F = ¬ A V B&C , если А=1, В=0, С=1

F = ( A V B ) & (

C V B ), если А=0, В=1, С= 0

Постройте логическую схему по логическому выражению и найдите значение логического выражения

F = ¬ ( A&B&C ) V (B&C V ¬A ) , если

А= 1 , В=1, С= 0

F = ¬ ( A&B&C ), если А=0, В= 0 , С=1

F = B& ¬ A V ¬B &A , если А=0, В= 0

Постройте логическое выражение по логической схеме

&

V

Ответ : F = A & (B V C)

Постройте логическое выражение по логической схеме

V

&

¬

&

¬

Ответ : F = (A V( ¬A & B)) & ¬B

Постройте логическое выражение по логической схеме

&

&

V

¬

V

¬

Ответ : F = A&B&( ¬ B V ¬ C) V D

Постройте логическое выражение по логической схеме

&

¬

V

&

V

¬

&

Ответ : F = (¬A& C ) V ¬ (A&BVB&C)

Домашнее задание

Составьте логические схемы к логическим выражениям:

F = BV(C& ¬A)V(A&B)

F = ¬(A&B)VC&D

ПРИМЕР 2

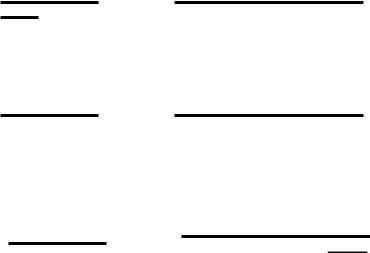
Упростить логические выражения:

A C A (B C)

A B (B A C)

A C (B A C )

Пример 3

Составить таблицу истинности для выражения

Перемен-				Промежуточные формулы						ИТОГ
	ные
x		y
0		0	1	0	0	1			1	1
0		1	1	1	1	0			1	1
1		0	0	0	1	0			0	1
1		1	0	0	1	0			0	1

Пример 4

Какому логическому выражению соответствует таблица истинности

A	B	C	A B	?
0	0	0	0	0
0	0	1	0	0
0	1	0	1	0
0	1	1	1	1
1	0	0	1	0
1	0	1	1	1
1	1	0	1	0
1	1	1	1	1

1.(A B) & C

2.(A B) & (C C)

3.(A B) C

4.A B

ПРИМЕР 5

При каких значениях переменных А и В логическая

функция

F A B (A B)

принимает значение ложь?

1.Построить таблицу истинности исходной логической функции

2.Упростить выражение и построить таблицу истинности преобразованной логической функции

Лаб_6_Построение логических схем

Лабораторная работа №4.

Схемотехническая реализация логических элементов. Построение логических схем.

Теоретическая часть.

В основе обработки компьютером информации лежит алгебра логики, разработанная Дж. Булем. Было доказано, что все электронные схемы ЭВМ могут быть реализованы с помощью логических элементов И, ИЛИ, НЕ.

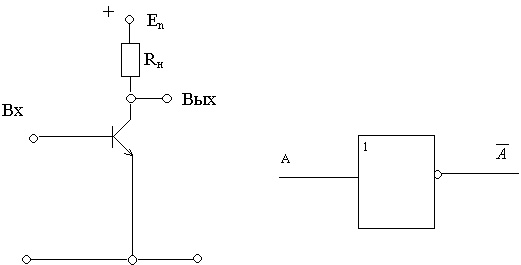
Элемент НЕ

A
0	1
1	0

При подаче на вход схемы сигнала низкого уровня (0) транзистор будет заперт, т.е. ток через него проходить не будет, и на выходе будет сигнал высокого уровня (1). Если же на вход схемы подать сигнал высокого уровня (1), то транзистор “откроется”, начнет пропускать электрический ток. На выходе за счет падения напряжения установится напряжение низкого уровня. Таким образом, схема преобразует сигналы одного уровня в другой, выполняя логическую функцию.

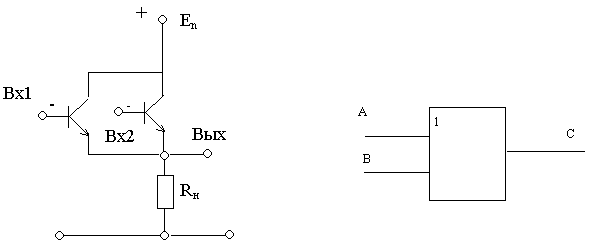
Элемент ИЛИ

А	В	С
0	0	0
0	1	1
1	0	1
1	1	1

Функция “ИЛИ” — логическое сложение (дизъюнкция), ее результат равен 1, если хотя бы 1 из аргументов равен 1. Здесь транзисторы включены параллельно друг другу. Если оба закрыты, то их общее сопротивление велико и на выходе будет сигнал низкого уровня (логический “0”). Достаточно подать сигнал высокого уровня (“1”) на один из транзисторов, как схема начнет пропускать ток, и на сопротивлении нагрузки установится также сигнал высокого уровня (логическая “1”).

Элемент И

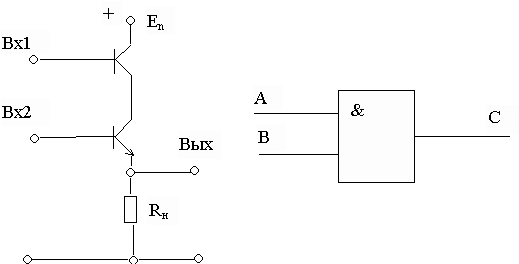
A	B	C
0	0	0
0	1	0
1	0	0
1	1	1

Если на входы Вх1 и Вх2 поданы сигналы низкого уровня (логические “0”), то оба транзистора закрыты, ток через них не проходит, выходное напряжение на R_н близко к нулю. Пусть на один из входов подано высокое напряжение (“1”). Тогда соответствующий транзистор откроется, однако другой останется закрытым, и ток через транзисторы и сопротивление проходить не будет. Следовательно, при подаче напряжения высокого уровня лишь на один из транзисторов, схема не переключается и на выходе остается напряжение низкого уровня. И лишь при одновременной подаче на входы сигналов высокого уровня (“1”) на выходе мы также получим сигнал высокого уровня.

Таким образом, каждой базовой логической функции – «И», «ИЛИ», «НЕ» — соответствует особым образом сконструированная схема, называемая логическим элементом. Комбинируя сигналы, обозначающие логические переменные, и выходы, соответствующие логическим функциям, с помощью логических элементов, пользуясь таблицей истинности или представлением логической функции в виде КНФ и ДНФ, можно составить структурную или функциональную схему (см. примеры ниже), являющуюся основой для аппаратной реализации схемы.

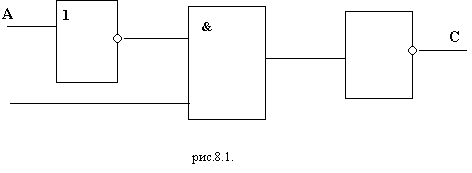
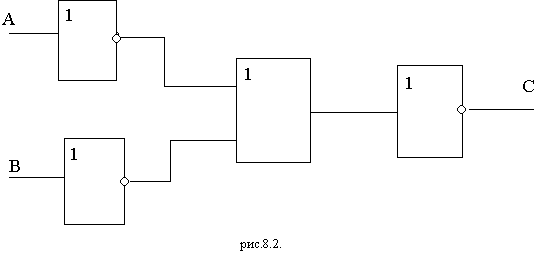
Анализируя функциональную схему, можно понять, как работает логическое устройство, т.е. дать ответ на вопрос: какую функцию она выполняет. Не менее важной формой описания логических устройств является структурная формула. Покажем на примере как выписывают формулу по заданной функциональной схеме (1 схема). Ясно, что элемент “И” осуществляет логическое умножение значений 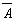и В. Над результатом в элементе “НЕ” осуществляется операция отрицания, т.е. вычисляется значение выражения: Формула и есть структурная формула логического устройства.

Итак, основные логические функции обозначаются

Инверсия
Конъюнкция
Дизъюнкция

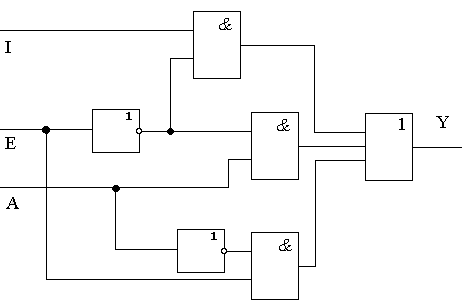
Пример: дана логическая схема:

A E I Y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 0 1 1 1 0

Она построена на основании булева выражения — Y = Ē /\ I \/ Ē /\ A \/ Ā /\ E

Практическая часть.

Задание 1. Для каждой из функциональных схем выписать соответствующую структурную формулу.

 

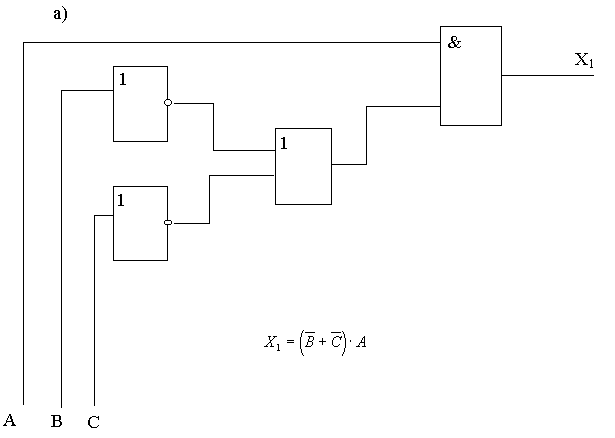
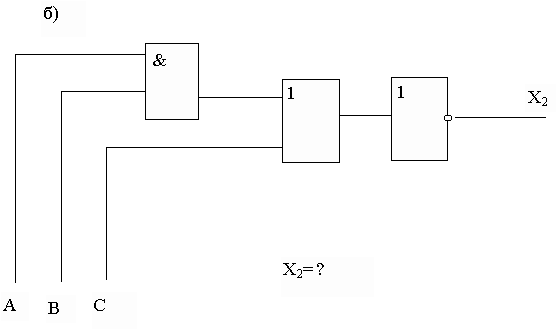
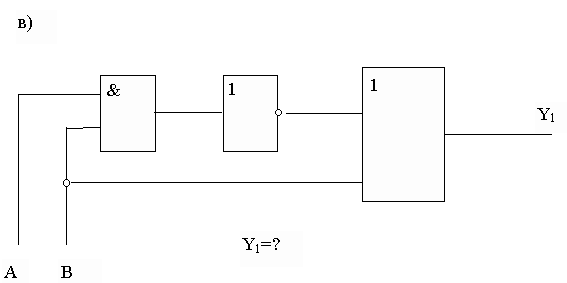
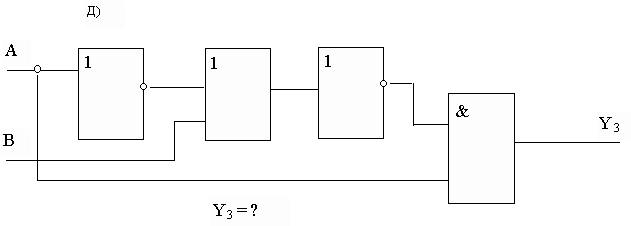
2) Для КНФ и ДНФ из лабораторной работы 5 построить функциональные схемы.

34. Логический базис и-не. Синтез логических схем по логическому выражению в базисе и-не.

Булевый базис не является единственной функционально полной системой логических функций. Среди других наибольшее распространение получили базис И–НЕ и базис ИЛИ–НЕ.

Чтобы доказать логическую полноту любого базиса, достаточно показать, что в этом базисе можно реализовать базовые функции И, ИЛИ, НЕ.

Для базиса И-НЕ в качестве базового элемента используется элемент приведенный на рисунке рис. 2.5,а.

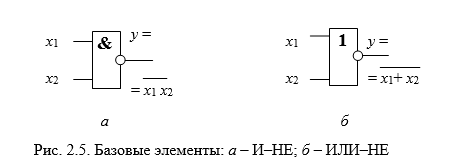
Реализация с помощью функции И-НЕ базовых функций алгебры Буля осуществляется следующим образом.

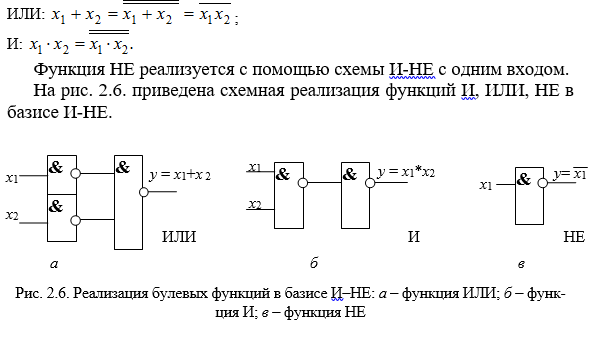
Реализация с помощью логической функции ИЛИ-НЕ базовых функций алгебры Буля осуществляется следующим образом.

При синтезе логических схем в заданном базисе логических элементов (например, в базисах И–НЕ, или ИЛИ–НЕ) целесообразно предварительно исходное выражение привести к форме, в которой в выражении будут использованы только логические операции, соответствующие используемым логическим элементам в заданном базисе.

Вопрос 35.Логический базис или-не.Синтез логических схем по логическому выражению в базисе или-не.

Реализация с помощью логической функции ИЛИ-НЕ базовых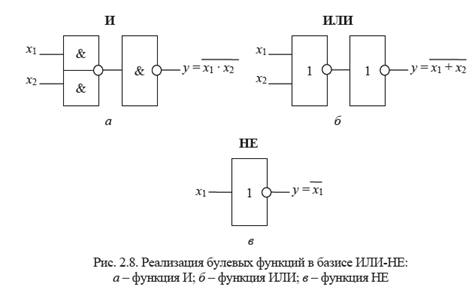

функций алгебры Буля осуществляется следующим образом.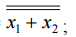

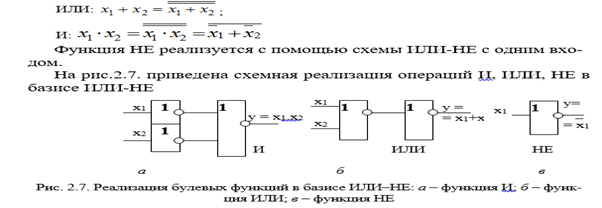
ИЛИ: x1 + x2 =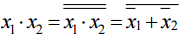

И:

Функция НЕ реализуется с помощью схемы ИЛИ-НЕ с одним

входом.

На рис. 2.8. приведена схемная реализация операций И, ИЛИ, НЕ

в базисе ИЛИ-НЕ

При синтезе логических схем в заданном базисе логических элементов (например, в базисах И–НЕ, или ИЛИ–НЕ) целесообразно предварительно исходное выражение привести к форме, в которой в выражении будут использованы только логические операции, соответствующие используемым логическим элементам в заданном базисе.

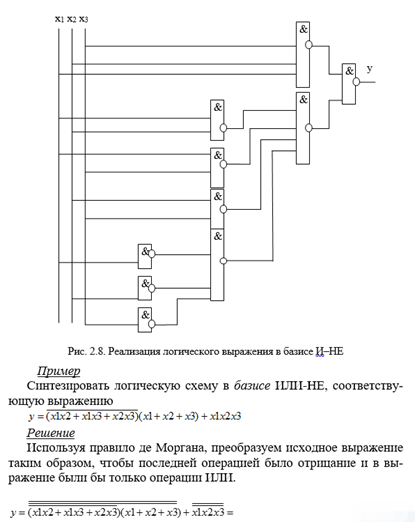
Пример:

Синтезировать логическую схему в базисе ИЛИ-НЕ, соответствующую выражению:

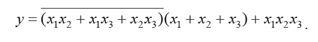
Решение

Используя правило де Моргана, преобразуем исходное выражение таким образом, чтобы последней операцией было отрицание и в выражение были бы только операции ИЛИ.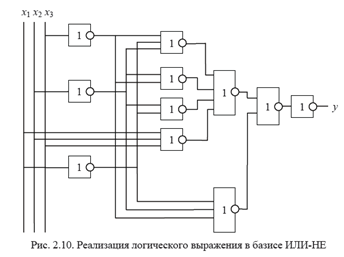

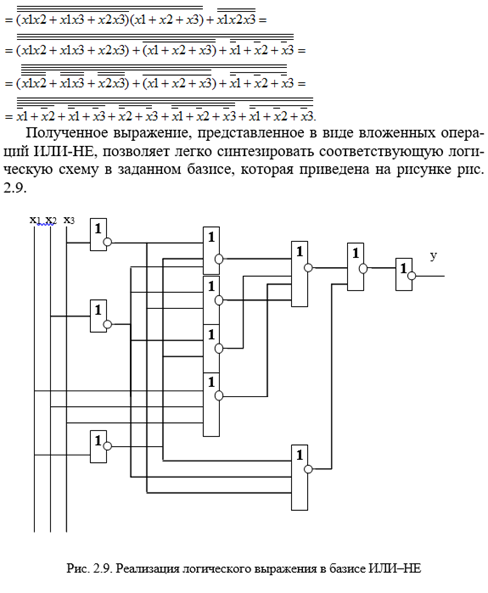
Полученное выражение, представленное в виде вложенных операций ИЛИ-НЕ, позволяет легко синтезировать соответствующую логическую схему в заданном базисе, которая приведена на рисунке рис. 2.10.

36.Логические элементы. Реализация простейших логических элементов с помощью резистивно-диодной логики. Большинство современных цвм состоят из двух и более архитектурных уровней (до шести).

Элементы ЭВМ, являющиеся представителями низшего иерархического уровня архитектуры компьютера – цифрового логического уровня (схемотехнического), реализованные на радиотехнических деталях, представляют собой мельчайшие компоненты, на основе которых строятся более крупные составляющие вычислительной машины.

— Можно выделить три основные разновидности элементов – логические элементы, запоминающие, специальные.

Логические элементы, так же как и элементы алгебры логики, реализуют логические функции, но эти функции, оставаясь сравнительно простыми, все же сложней, чем базовые функции в алгебре логики. В одном логическом элементе может быть реализовано несколько простых функций. Кроме того, логические элементы характеризуются дополнительными параметрами, такими, как количество входов, нагрузочная способность (количество входов других элементов, к которым можно подключать выход данного элемента).

На рис. 1.1. приведены примеры некоторых логических элементов.

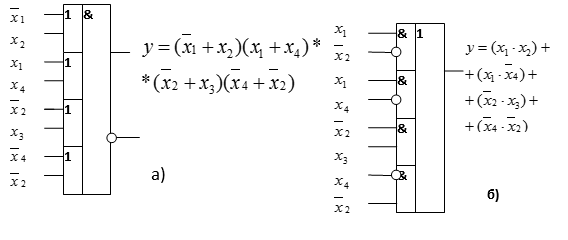
Рис. 1.1. Примеры логических элементов:

а – ИЛИ-И-НЕ; б – И-ИЛИ-НЕ

На выходах элементов указаны логические выражения для выходных сигналов в соответствии с приведенными входными сигналами. На рис. 1, б приведен логический элемент с инверсными входами (в логическом выражении сигнал по такому входу используется в обратном значении).

Примеры реализации простейших логических элементов с помощью диодно—резисторной схемы приведены на рис. 1.2.

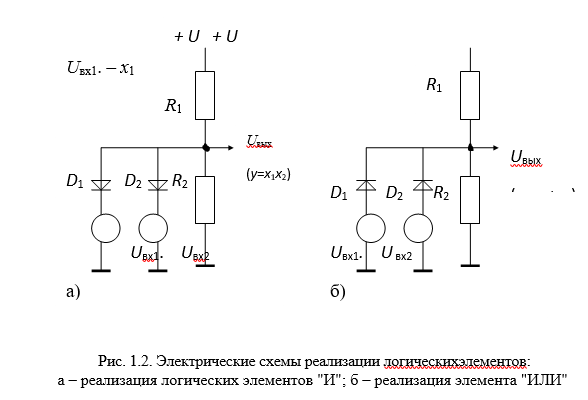
На рис.1.2,а приведена реализация логических элементов И. Реализация элемента ИЛИ приведена на рис.1.2,б. Схемы логических элементов построены с условием, что логическая «1» соответствует высокому уровню («+»), а логический ноль – низкому уровню напряжения, близкому «земле». Это соответствие используется и в других реализациях. На рис. 1.2,а соотношение сопротивления резисторов R1 и R2 при заданном напряжении «+U» выбирается таким образом, что без учета шунтирующего действия диодных цепочек напряжение на выходе имеет значение высокого уровня (уровня, соответствующего логической «1»). Источники входных сигналов Uвх1 и Uвх2 имеют малое внутреннее сопротивления. Поэтому, если один или оба источника подают низкий уровень (логический «0»), то из-за шунтирующего воздействия диодных цепочек на резистора R2 на выходе будет иметь место низкий уровень напряжения, соответствующий логическому нулю. Высокий уровень на выходе (логическая «1») будет иметь место только тогда, когда на оба входа подаются единицы, так как соответствующие им высокие уровни напряжения закрывают оба диода. Таким образом, единица на выходе будет иметь место только тогда, когда и x1, и x2 имеют единичные значения. Это означает, что рассматриваемая схема реализует логику И.

Для схемы на рис. 1.2,б соотношение сопротивления резисторов R1 и R2 при заданном напряжении «+U» выбирается таким образом, что без учета воздействия диодных цепочек напряжение на выходе имеет значение низкого уровня (уровня, соответствующего логическому «0»). Если хотя бы один или оба источника входных сигналов подают высокий уровень (логическая «1»), то этот высокий уровень проходит через открытый диод и появляется на выходе. Низкий уровень, т.е. логический «0», будет иметь место только тогда, когда оба входных сигнала имеют низкий уровень. Это означает, что рассматриваемая схема реализует логику ИЛИ.

На рис.1.3 приведены примеры реализации логических функций НЕ (рис. 1.3,а) и ИЛИ-НЕ (рис. 1.3,b) на транзисторах. Транзисторы обозначены символом «Т».

На рис. 1.3,а транзистор открыт, следовательно, на его коллекторе напряжение, близкое к нулевому уровню, тогда, когда на его базе высокий уровень логической единицы, и, наоборот, транзистор закрыт, а следовательно на его коллекторе высокий уровень тогда, когда входной сигнал соответствует низкому уровню нуля. Выходом схемы является коллектор транзистора, поэтому выходной сигнал реализует функцию НЕ.

На рис. 1.3,б на выходе схемы «y» будет низкий уровень (логический нуль) тогда, когда открыт хотя бы один транзистор T1 , T2 , T3 , т.е. тогда, когда хотя бы одна из входных переменныхx1,x2,x3, имеет значение логической единицы. Это означает, что выходной сигнал «y» зависит от входных сигналов по логике ИЛИ- НЕ.

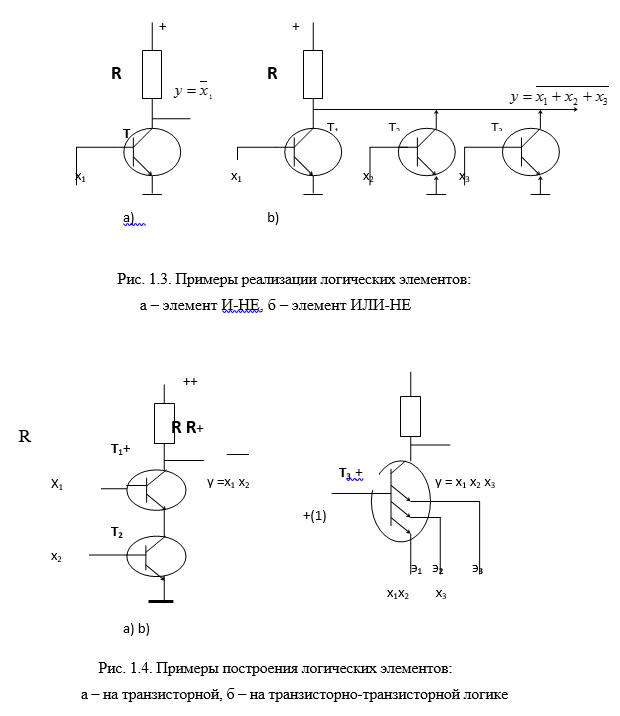
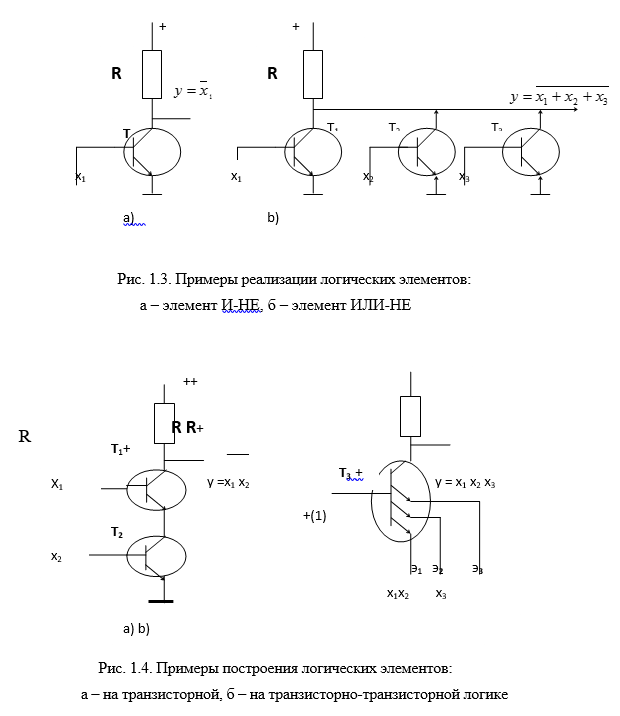
На рис. 1.4 приведены примеры реализации логических функции И-НЕ и функции И на транзисторах.

На рис. 1.4,а на выходе схемы «y» будет низкий уровень (логический нуль) только тогда, когда открыты оба транзистора T1 , T2 , т.е. тогда, когда обе входные переменныеx1,x2 имеют значение логической единицы. Это означает, что выходной сигнал «y» зависит от входных сигналов по логике И-НЕ.

На рис.1.4,б приведена схема, использующая многоэмиттерный транзистор T3 .Транзистор такого типа пропускает ток только тогда, когда имеет место высокий уровень на его базе и низкий уровень хотя бы на одном из его эмиттеров. В приведенной схеме на базу T3 подается постоянный высокий уровень (логическая константа, равная «1»). В этом случае на выходе схемы «y» будет низкий уровень (логический нуль) тогда, когда есть условия протекания тока хотя бы по одному из его эмиттеров, т.е. хотя бы одна из входных переменных x1, x2 , x3 имеет значение логического нуля. Если на все эмиттеры подается логическая единица, то T3 закрыт, а на выходе схеме имеет место высокий уровень, т.е. логическая единица.Это означает, что выходной сигнал «y» зависит от входных сигналов по логике И.

Практическая работа №5,6 по Информатике и ИКТ

Практическая работа №5,6

Тема: Логические величины, операции, выражения. Построение логических схем.

Цель работы: научиться составлять аналитические выражения по  табличному значению функции, строить схемы из элементарных логических  элементов по заданному аналитическому выражению функции.

Студент должен

знать:

    основной базис логики;

    особенности применения логических элементов;

уметь:

    производить синтез и анализ аналитических выражений логических функций

    строить схемы из элементарных логических  элементов по заданному аналитическому выражению функции.

 

Теоретическое обоснование.

1. Логические элементы

Функция отрицание НЕ или инверсия

Таблица истинности функции отрицания имеет вид:

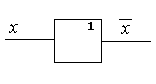
Логический элемент НЕ обозначается на схемах следующим образом:
(пишется X c чертой сверху)

Логическое ИЛИ (логическое сложение, дизъюнкция): Y= X1 + X2 = X1VX2

Таблица истинности логического ИЛИ имеет вид:

Логический элемент ИЛИ обозначается на схемах следующим образом:

 

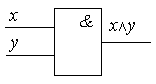
Логическое И (логическое умножение, конъюнкция): Y = X1X2 = X1&X2

Таблица истинности логического И имеет вид:

Логический элемент И обозначается на схемах следующим образом:

Функция ИЛИ-НЕ: Y = (X1+X2)

Таблица истинности функции ИЛИ-НЕ имеет вид:

Логический элемент ИЛИ-НЕ обозначается на схемах следующим образом:

Функция И-НЕ: Y =  (X1^X2)

Таблица истинности функции И-НЕ имеет вид:

Логический элемент И-НЕ обозначается на схемах следующим образом:

 

2. Алгоритм построение логических схем.

1.                Определить число логических переменных.

2.                Определить количество базовых логических операций и их порядок.

3.                Изобразить для каждой логической операции соответствующий ей вентиль.

4.                Соединить вентили в порядке выполнения логических операций.

Пример 1.
Составить логическую схему для логического выражения: F=A v B & A.
Две переменные – А и В.
Две логические операции: 1-&, 2-v.
Строим схему:

Пример 2.
Постройте логическую схему, соответствующую логическому выражению F=А&Вv (ВvА). Вычислить значения выражения для А=1,В=0.
Переменных две: А и В;
Логических операций три: & и две v; А&Вv (Вv А).
Схему строим слева направо в соответствии с порядком логических операций:

3.  Составление аналитического выражения функции  и построение логической схемы по табличному заданию функции.

Синтез комбинационных устройств может быть произведен по табличному заданию функции по «0» и «1». Рассмотрим для примера синтез по «1». Для всех значений аргументов х1, х2, х3, где функция задана как «1» берется их конъюнкция, если аргумент равен «1», если же 0 – конъюнкция их инверсий. От полученных конъюнкций берется дизъюнкция.

Например,  функция от трех аргументов задана следующей таблицей:

 

 

х1

х2

Х3

у

1

0

0

0

0

2

0

0

1

1

3

0

1

0

0

4

0

1

1

0

5

1

0

0

0

6

1

0

1

0

7

1

1

0

0

8

1

1

1

1

               

Это значит, что при любых наборах аргументов ч кроме второго и последнего, аргумент у будет равен 0. Составляем для второго набора выражение: .

 Для последнего набора:  х1 х2 х3

Составим аналитическое выражение функции:

 

Схема должна содержать инверсию сигналов х1, х2, две схемы «И» и одну двухвходовую схему «ИЛИ»

 

 

 

 

 

 

 

 

 

 

Ход работы:

1.     Изучить теоретическое обоснование;

2.     Выполнить практическое задание по вариантам;

3.     Оформить отчет.

4.     Ответить на контрольные вопросы по указанию преподавателя.

 

Практические задания:

Задание 1
Записать логическую функцию, описывающую состояние логической схемы. Составить таблицу истинности.

Вариант 1

а)

б)

 

Вариант 2

Вариант 3

а)

б)

 

 

Вариант 4

а)

&

 

б)

Задание 2

Построить логические схемы по формулам и составить таблицу истинности

Вариант 1

а) F= (AvB)&(Cv`B)

б) F= (A&B&C)

Вариант 2

а) F=(X&`Y)vZ.

б) F=X&Yv`Z.

В ариант 3

   

 

 

а)F= (XvY) & (Yv`X).

   

 

 

б)F= ((XvY) & (`ZvX)) & (ZvY).

Вариант 4

а) F= A&B&C&`D.

б) F= (AvB) &(`AvB).

 

Задание 3

По табличному заданию функции найти аналитическое выражение функции и построить логическую схему в соответствии со своим вариантом.

 

 

 

 

Вариант 1

Вариант 2

Вариант 3

Вариант 4

 

х1

х2

Х3

у1

у2

у3

У4

у5

у6

у7

у8

1

0

0

0

1

0

0

0

1

1

0

0

2

0

0

1

0

1

0

0

0

1

0

0

3

0

1

0

1

0

1

0

0

1

0

1

4

0

1.2. Синтез схемы по заданному логическому выражению

На практике часто требуется синтезировать схему по заданному логическому выражению.

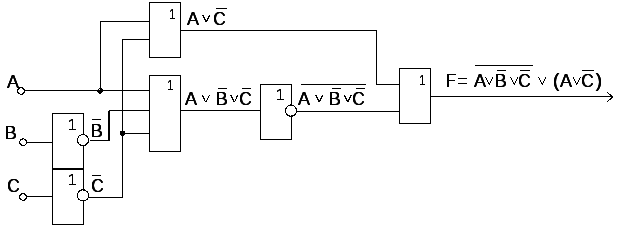
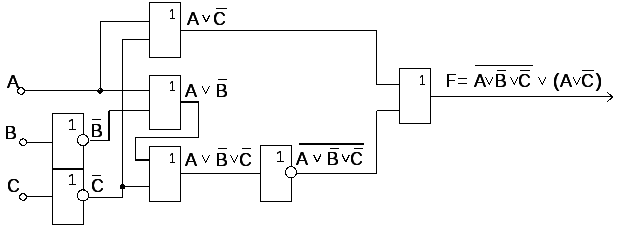
В качестве примера синтезируем цифровую схему, работа которой описывается логическим выражением

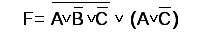
Определим количество входных сигналов. Из логического выражения видно, что входными сигналами являются сигналы А, В и С, т.е. схема будет иметь три входа.

Реализовать логическое выражение схемотехнически возможно только пошагово:

1 шаг – получение инверсии входных сигналов В и С;

2 шаг – получение логических сумм сигналов 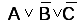и;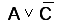

3 шаг – получение инверсии логической суммы сигнала ;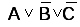

4 шаг – получение логической суммы сигналов 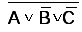и.

Для получения 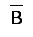и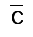необходимы два элемента НЕ.

Выражение 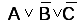получают при помощи элемента ИЛИ с тремя входами.

К этому элементу последовательно подключается ЛЭ НЕ, обеспечивающий получение сигнала .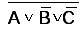

Выражение 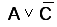получают при помощи элемента ИЛИ с двумя входами.

Выходы с сигналам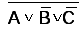и и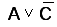поступают на вход элемента ИЛИ.

Таким образом, для схемотехнической реализации заданного логического выражения необходимы 3 ЛЭ НЕ, 2 ЛЭ ИЛИ с двумя входами, 1 ЛЭ ИЛИ с тремя входами. Цифровая схема, реализующая заданное логическое выражение, представлена на рисунке 1.2.

Рис. 1.2 – Цифровая схема, работа которой описывается логическим выражением

Для схемотехнической реализации логической суммы сигналов 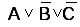можно использовать два ЛЭ ИЛИ с двумя входами, что более экономично, т.к. используется полностью корпус ИС с двухвходовыми ЛЭ ИЛИ и не требуется корпус ИС с ЛЭ на три входа.

Цифровая схема, реализующая такое схемотехническое решение, представлена на рисунке 1.3.

Рис. 1.3 – Цифровая схема, не содержащая ЛЭ 3ИЛИ

1.3. Реализация цифровых схем на базовых лэ

В цифровой электронике имеется набор ЛЭ, реализующих функции, с помощью которых могут быть получены все остальные функции булевой алгебры (конъюнкция, дизъюнкция, инверсия). К таким элементам относятся элементы И-НЕ и ИЛИ-НЕ.

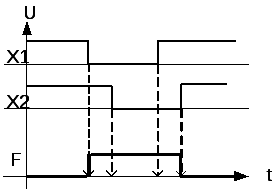
Логический элемент И-НЕ является комбинацией логических схем И и НЕ. На выходе логического элемента И-НЕ сигнал уровня 0 будет только в том случае, когда на обоих его входах присутствует сигнал уровня 1. УГО, таблица истинности и диаграмма работы ЛЭ И-НЕ представлены в таблице 1.2.

Логический элемент ИЛИ-НЕ является комбинацией логических схем ИЛИ и НЕ. На выходе логического элемента ИЛИ-НЕ сигнал уровня 1 будет только в том случае, когда на обоих его входах присутствует сигнал уровня 0. УГО, таблица истинности и диаграмма работы ЛЭ ИЛИ-НЕ представлены в таблице 1.2.

Таблица 1.2 – УГО, таблицы истинности и диаграммы работы базовых ЛЭ

Наименование. Логическое выражение	Условное обозначение	Таблица истинности	Диаграмма работы
Элемент И-НЕ		Х1 Х2 F 0 0 1 0 1 1 1 0 1 1 1 0
Элемент ИЛИ-НЕ		Х1 Х2 F 0 0 1 0 1 0 1 0 0 1 1 0

Схемотехнически любая цифровая схема может быть выполнена или на ЛЭ И-НЕ, или на ЛЭ ИЛИ-НЕ.

Преобразования выполняются с помощью теоремы Де-Моргана, правила двойного отрицания и правила повторения.

Первая теорема Де-Моргана: .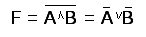

Вторая теорема Де-Моргана: .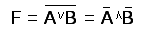

Правило двойного отрицания: .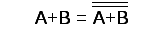

Правило повторения: 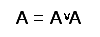или.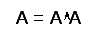

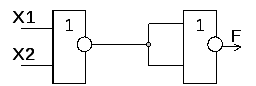
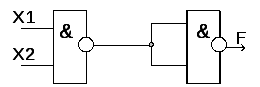
Преобразование функции ИЛИ (дизъюнкция) к базовому элементу И-НЕ осуществляется с помощью теоремы Де-Моргана, рисунок 1.4.а.

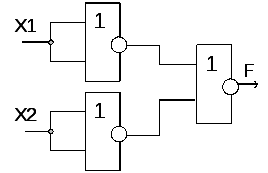
Преобразование функции ИЛИ к базовому элементу ИЛИ-НЕ осуществляется согласно правилу двойного отрицания, рисунок 1.4.б.

а)	б)
Рис. 1.4 – Реализация функции ИЛИ с помощью базового элемента И-НЕ (а) и базового элемента ИЛИ-НЕ (б)

Преобразование функции И (конъюнкция) к базовым элементам ИЛИ-НЕ и И-НЕ представлено на рисунке 1.5.

а)	б)
Рис. 1.5 – Реализация функции И с помощью базового элемента ИЛИ-НЕ (а) и базового элемента И-НЕ (б)

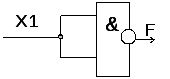
Преобразование функции НЕ (инверсия) к базовым элементам И-НЕ и ИЛИ-НЕ представлено на рисунке 1.6.

Функция НЕ реализуется элементами И-НЕ или ИЛИ-НЕ при объединении их входов. Используется правило повторения.

а)	б)
Рис. 1.6 – Реализация функции НЕ с помощью базового элемента И-НЕ (а) и базового элемента ИЛИ-НЕ (б)

Логические схемы. Переход от логического выражения к логической схеме и наоборот

Цели:

1. Образовательные

• Основные логические операции.
• Построение таблиц истинности сложных высказываний.
• Логические схемы и логические выражения.

2. Развивающие

• Развитие исследовательской и познавательной деятельности.
• Лаконично, полно и содержательно отвечать и делать обобщающие выводы.

3. Воспитательные

• Формирование аккуратности при работе с компьютером.
• Понимание связей между другими учащимися, культурой поведения.

Тип урока: комбинированный

Методы организации учебной деятельности:

• фронтальная
• индивидуальная
• ученик-компьютер

Программно-дидактическое обеспечение: ПК, презентация, задание для практической работы, раздаточный материал, Electronics Workbench (EWB512), PowerPoint.

ХОД УРОКА

I. Организационный момент.

II. Актуализация ранее изученного материала и проверка домашнего задания.

Задания для выполнения в тетради и у доски.

№1. Составьте таблицы истинности для следующих логических выражений:

№3. Нарисовать на доске логические элементы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ.

III. Новый материал.

Над возможностями применения логики в технике ученые и инженеры задумывались уже давно. Например, голландский физик Пауль Эренфест (1880 - 1933), еще в 1910 году писал: «…Пусть имеется проект схемы проводов автоматической телефонной станции. Надо определить:

1) будет ли она правильно функционировать при любой комбинации, могущей встретиться в ходе деятельности станции;
2) не содержит ли она излишних усложнений.

Каждая такая комбинация является посылкой, каждый маленький коммутатор есть логическое «или-или», воплощенное в эбоните и латуни; все вместе — система чисто качественных… «посылок», ничего не оставляющая желать в отношении сложности и запутанности… правда ли, что, несмотря на существование алгебры логики, своего рода «алгебра распределительных схем» должна считаться утопией?».

Созданная позднее М.А. Гавриловым (1903 — 1979) теория релейно-контактных схем показала, что это вовсе не утопия.

Посмотрим на микросхему. На первый взгляд ничего того, что нас бы удивило, мы не видим!
Но если рассматривать ее при сильном увеличении, она поразит нас своей стройной архитектурой. Чтобы понять, как она работает, вспомним, что компьютер работает на электричестве, то есть любая информация представлена в компьютере в виде электрических импульсов.

Почему необходимо уметь строить логические схемы?

Дело в том, что из вентилей составляют более сложные схемы, которые позволяют выполнять арифметические операции и хранить информацию. Причем схему, выполняющую определенные функции, можно построить из различных по сочетанию и количеству вентилей. Поэтому значение формального представления логической схемы чрезвычайно велико. Оно необходимо для того, чтобы разработчик имел возможность выбрать наиболее подходящий ему вариант построения схемы из вентилей. Процесс разработки общей логической схемы устройства (в том числе и компьютера в целом), становится иерархическим, причем на каждом следующем уровне в качестве «кирпичиков» используются логические схемы, созданные на предыдущем этапе.
Алгебра логики дала в руки конструкторам мощное средство разработки, анализа и совершенствования логических схем. В самом деле, гораздо проще, быстрее и дешевле изучать свойства и доказывать правильность работы схемы с помощью выражающей ее формулы, чем создавать реальное техническое устройство. Именно в этом состоит смысл любого математического моделирования.

Логические схемы необходимо строить из минимально возможного количества элементов, что в свою очередь, обеспечивает большую скорость работы и увеличивает надежность устройства.

Правило построения логических схем:

1) Определить число логических переменных.
2) Определить количество базовых логических операций и их порядок.
3) Изобразить для каждой логической операции соответствующий ей вентиль и соединить вентили в порядке выполнения логических операций.

Рассмотрение двух примеров перехода от выражения к схеме. (Презентация)

Рассмотрение двух примеров перехода от схемы к выражению. (Презентация)

Чаще в жизни возникает ситуация, когда известен результат и для его реализации необходимо построить устройство.

Рассмотрим следующую задачу: (Презентация)

Задача 1. В двухэтажном доме лестница освещается одной лампой Х. На первом этаже установлен один выключатель А, на втором этаже - выключатель В. Если включают А, то лампа загорается. При поднятии на второй этаж и включении В лампа гаснет. Если кто-то выходит и нажмет В, то лампа включается, при спуске на первый этаж и нажатии А лампа должна погаснуть.

Алгоритм решения:

• Составить таблицу истинности.
• Определить логическую функцию.
• Построить логическую схему.

 

A	B	X
0	0	0
1	0	1
1	1	0
0	1	1
0	0	0

Чтобы создать логическую функцию по таблице истинности, надо записывать значения выходной переменной.

Между строками таблицы будет стоять знак логического сложения, а между столбцами — знак логического умножения .

Задача 2. (Презентация)

IV. Закрепление изученного материала.

Работа у доски и в тетради по карточкам.

№1. По логическому выражению построить логическую схему:

№2. По логической схеме составьте логическое выражение:

V. Компьютерный практикум.

Практическая работа с использованием электронной лаборатории Electronics Workbench (EWB512).

Вариант 1

1. Упростите логическое выражение

2. Проверьте свою работу, используя программу Electronics Workbench:

— Запишите исходное выражение в Logic Converter;
— Составьте таблицу истинности
— Упростите выражение используя
— Постройте упрощенную логическую схему .

3. Проверьте правильность выполненных упрощений.

VI. Домашнее задание:

а) упростите логическое выражение, постройте логическую схему и таблицу истинности
б) по таблице истинности (00001011) составьте выражение, упростите его, нарисуйте схему.