16. Момент инерции. Вычисление моментов инерции ноторых тел относительно оси симметрии (тонкий стержень, обруч, диск). Теорема Штейнера.

Момент инерции — скалярная физическая величина, характеризующая распределение масс в теле, равная сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения СИ: кг·м².

Обозначение: I или J.

Для расчета моментов инерции тонкого диска массы m и радиуса R выберем систему координат так, чтобы ее оси совпадали с главными центральными осями (рис.32). Определим момент инерции тонкого однородного диска относительно оси z , перпендикулярной к плоскости диска. Рассмотрим бесконечно тонкое кольцо с внутренним

радиусом r и наружным r+dr. Площадь такого кольца ds=2r $\pi$ dr, а его масса , гдеS= $\pi$ R² — площадь всего диска. Момент инерции тонкого кольца найдется по формуле dJ=dmr². Момент инерции всего диска определяется интегралом

Вычисление момента инерции тонкого стержня:

Пусть тонкий стержень имеет длину l и массу m. Разделим его на малые элементы длины dx (рис.27), масса которых . Если выбранный элемент находится на расстоянии x от оси, то его момент инерции, т.е.     Интегрируя последнее соотношение в пределах от 0 до l/2 и удваивая полученное выражение (для учета левой половины стержня), получим

Момент инеpции обручаотносительно оси, пpоходящей чеpез центp кольца пеpпендикуляpно к его плоскости. В этом случае все элементаpные массы обруча удалены от оси на одинаковое pасстояние, поэтому в сумме (3.18) r2 можно вынести за знак суммы, т. е.    

Теорема Штейнера:

В общем случае вращения тела произвольной формы вокруг произвольной оси, вычисление момента инерции может быть произведено с помощью теоремы Штейнера: момент инерции относительно произвольной оси равен сумме момента инерции J0 относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния между осями: J=J0+ma^2.

Например, момент инерции диска относительно оси О’ в соответствии с теоремой Штейнера:

Линия — ось вращения.

— масса на квадрат радиуса окружности, по которой движется материальная точка.

Все тело мысленно разбиваем на маленькие объемы. Масса этого кусочка .

Твердое тело представляется как совокупность системы точечных масс.

— расстояние, на котором находится точка от оси вращения.

— общий алгоритм определения собственного момента инерции твердого тела, относительно оси проходящей через центр инерции данного тела.

Момент инерции шара.

     Сплошной шар массы m и радиуса R можно рассматривать как совокупность бесконечно тонких сферических слоев с массами dm , радиусом r, толщиной dr (рис.35).

     Рассмотрим малый элемент сферического слоя $\delta$ m с координатами x, y, z. Его моменты инерции относительно осей проходящих через центр слоя — $\delta$ J_x, $\delta$ J_y, $\delta$ J_z, равны Т. е. можно записать     (п.26)

     Так как для элементов сферического слоя x²+y²+z²=r² то      После интегрирования по всему объему слоя получим     (п.27)

     Так как, в силу симметрии для сферического слоя dJ_x=dJ_y=dJ_z=dJ , а , тоИнтегрируя по всему объему шара, получаем      Окончательно (после интегрирования) получим, что момент инерции шара относительно оси, проходящей через его центр равен

Разобьём КОНУС на цилиндрические слои   ось толщиной dr. Масса такого слоя   dm = r²dr,

где ρ – плотность материала, из которого изготовлен конус. Момент инерции этого слоя dI = dm^.r².

Момент инерции всего конуса   складывается из моментов инерции всех слоёв: 

 I = = ρπ r ⁴dr = ρR⁵.

Остаётся выразить его через массу всего цилиндра: m = == R³,

отсюда    ρ = , I =  = mR².

Определение момента инерции тел методом трифилярного подвеса — Студопедия

Поделись  

ЦЕЛЬ РАБОТЫ

Экспериментальное определение с помощью трифилярного подвеса момента инерции тел простой формы (диска, полого цилиндра, прямоугольного бруска).

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ

Трифилярный подвес.

Секундомер.

Рулетка или линейка.

Штангенциркуль.

Весы.

Набор тел (диск, полый цилиндр, прямоугольный брусок).

ОПИСАНИЕ УСТАНОВКИ.

ВЫВОД РАСЧЕТНОЙ ФОРМУЛЫ

Трифилярный подвес (рис.1) состоит из двух цилиндрических дисков разного диаметра, соединенных упругими нитями длиной ℓ.

Точки крепления нитей на дисках расположены симметрично по вершинам равностороннего треугольника.

Верхний диск Q жестко закреплен. Нижний диск P имеет возможность совершать крутильные колебания относительно оси ОО’. Для этого нижний диск необходимо повернуть вокруг вертикальной оси на некоторый угол φ₀ и отпустить. Период колебания диска зависит от его момента инерции и упругих свойств нити. Если на диск Р помещать разные тела, то период колебаний будет меняться. Это обстоятельство используется для экспериментального определения момента инерции тел.

Выведем расчетную формулу для определения момента инерции твердых тел.

При закручи-вании диска Р на угол φ₀ его центр масс поднимается на высоту (рис. 2). В этом положении диск, имею-щий массу m, обладает максимальной потенциаль-ной энергией .

В отсутствии трения в системе механи-ческая энергия сохраняет-ся

Через промежуток времени, равный четверти периода колебаний , диск Р проходит положе-ние равновесия. Потенци-альная энергия переходит в кинетическую энергию

,

где – момент инерции диска относительно вертикальной оси ОО’, – угловая скорость диска при прохождении положения равновесия.

Из закона сохранения механической энергии следует, что кинетическая энергия диска в положении равновесия равна максимальному значению его потенциальной энергии. Следовательно, момент инерции диска

. (1)

Для вычисления момента инерции диска необходимо определить и .

Для свободных гармонических крутильных колебаний диска угол поворота относительно оси вращения с течением времени t изменяется по закону

,

где – амплитуда угла поворота, Т – период колебаний.

Найдем угловую скорость вращения диска

В момент времени от начала движения диска, соответствующий прохождению диском положения равновесия, абсолютное значение угловой скорости

(2)

Определим высоту в формуле (1). При закручивании диска Р на угол (рис.2) точка крепления одной из нитей переходит из положения А в положение А₁. Центр масс диска поднимается на высоту . Из прямоугольных треугольников ABC и A

1BC₁ находим

, (3)

,

где х=А₁С₁, ℓ=АВ=А₁В, H=ВС.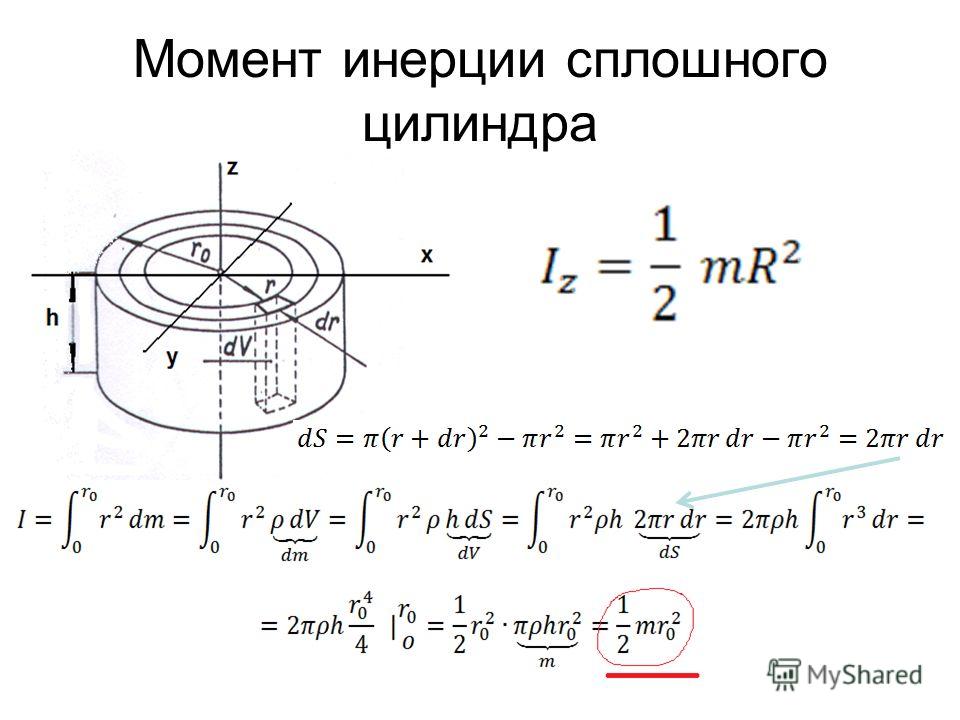

По теореме косинусов длину отрезка х найдем из треугольника О₁С₁А₁.

, (4)

где r=О₁С₁, R=О₁А₁.

Решая совместно уравнения (3) и (4) получим

(5)

При выводе выражения (5) принимаем , а – малая величина, которой можно пренебречь. Для малых углов закручивания . В результате выражение для принимает вид

(6)

Подставляя в уравнение (1) значения (2) и (6), получим выражение для момента инерции

. (7)

Величины в правой части формулы (7) могут быть непосредственно измерены в опыте.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Определение момента инерции диска.

1. Измерьте несколько раз диаметры дисков Р и Q с помощью штангенциркуля, вычислите среднее значение величин и найдите радиусы дисков R и r.

2. Измерьте длину нити ℓ с помощью линейки или рулетки.

3. Убедитесь, что колебания трифилярного подвеса являются гармоническими колебаниями.

Для этого поверните нижний диск Р вокруг вертикальной оси на угол φ

0≤30º и отпустите. Определите число колебаний N, за которое их амплитуда уменьшается в 2–3 раза. Если N≥10, то затухание маятника мало и можно считать колебания гармоническими.

Измерьте с помощью секундомера время t для 15–20 полных колебаний. Определите период колебаний диска Р по формуле , N – число полных колебаний. Измерения повторите 5 раз и вычислите среднее значение периода колебаний.

4. По средним значениям измеренных величин вычислите момент инерции диска I_д по формуле (7).

Определение момента инерции полого цилиндра.

1. На диск Р поместите полый цилиндр и так же, как в предыдущем опыте

, определите период колебаний системы диска с полым цилиндром.

2. По формуле (7) вычислите момент инерции системы I_с. Масса системы равна сумме масс диска и цилиндра.

3. Величину момента инерции полого цилиндра вычислите, как разность момента инерции системы и момента инерции диска по формуле I_ц=I_c–I_д.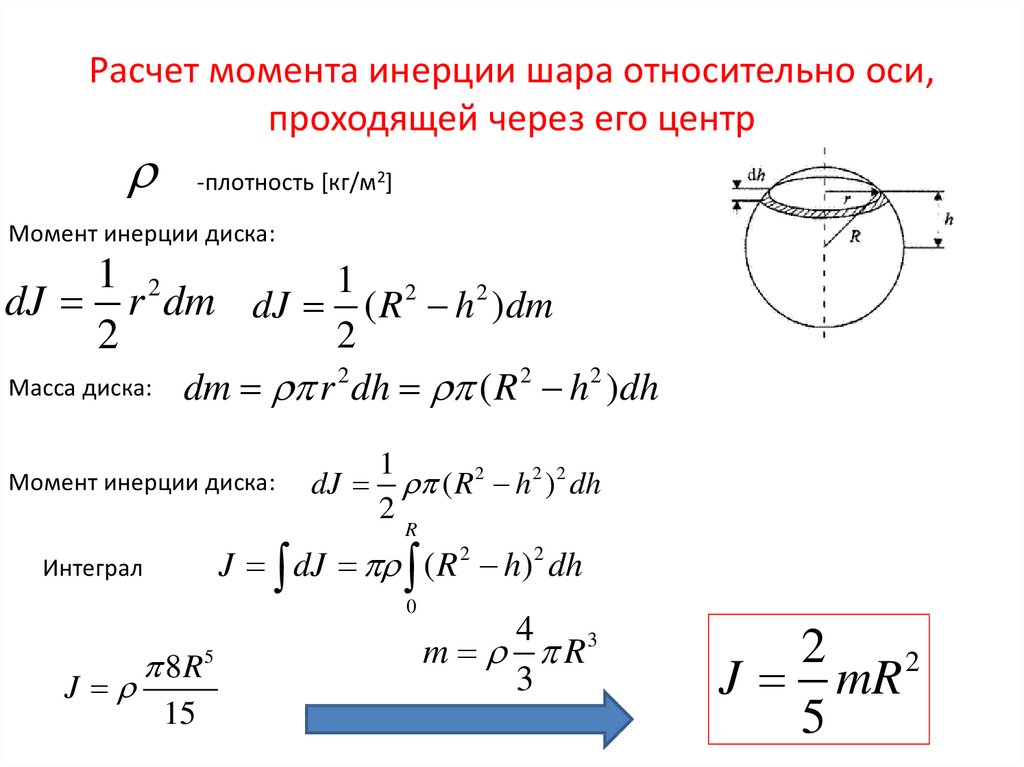

Определение момента инерции прямоугольного бруска.

1–3. Поместите на диск Р прямоугольный брусок и так же, как в предыдущем опыте определяли момент инерции полого цилиндра, найдите момент инерции бруска I_Б

.

Результаты измерений и вычислений моментов инерции тел занести в таблицу (см. образец, табл.1). Массы диска m_Д, полого цилиндра m_Ц и прямоугольного бруска m_Б указаны на телах. При необходимости можно произвести взвешивание тел на технических весах.

Таблица 1

Опыт	m,кг	Т,с	R,м	r,м	ℓ,м	Ic, кг·м2	Iт, кг·м2
Диск
Диск и цилиндр
Диск и брусок

Сравнение экспериментальных и теоретических значений моментов инерции тел. Оценка погрешности

1. Измерьте с помощью штангенциркуля внутренний R₁ и внешний R₂ радиусы полого цилиндра (рис. 3), длину ℓ и ширину d бруска (рис. 4). Измерения проведите несколько раз и определите среднее значение указанных величин.

2. Вычислите теоретические значения моментов инерции тел.

Момент инерции диска относительно оси, проходящей через его середину перпендикулярно плоскости диска

, (8)

момент инерции полого цилиндра относительно оси, проходящей через его ось симметрии

(9)

момент инерции прямоугольного бруска относительно оси, проходящей через его центр масс перпендикулярно плоскости бруска

. (10)

3. Вычислите относительные погрешности , и – экспериментальное и теоретическое значения моментов инерции исследуемых тел. Результаты вычислений и моментов инерции занесите в таблицу (см. образец, табл.2).

Таблица 2

	Диск (8)	Полый цилиндр (9)	Брусок (10)
Эксперимент Момент инерции , кг·м2
Теория Момент инерции , кг·м2
, %

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Сформулируйте основную идею эксперимента. Какие физические законы применяются для решения задач эксперимента?

2. Выведите рабочую формулу для вычисления момента инерции с помощью трифилярного подвеса.

3. Что такое период колебаний? Каковы единицы его измерения?

4. Опишите экспериментальную установку. Из каких основных частей она состоит?

5. Какие колебания называются гармоническими?

6. При каких условиях крутильные колебания будут гармоническими?

7. Сохраняется ли механическая энергия при гармонических колебаниях? Запишите закон сохранения механической энергии для данного опыта.

8. Как рассчитывается момент инерции материальной точки?

9. Как определяется момент инерции твердого тела относительно оси? Каков физический смысл момента инерции?

10. Что является мерой инертности в поступательном движении? В колебательном? Во вращательном?

11. Как момент инерции зависит от массы тела?

12. Как распределение массы тела вдоль радиуса вращения влияет на момент инерции?

13. Сколько моментов инерции у стержня? у обруча? у цилиндра?

14. Выведите формулу для момента инерции полого цилиндра относительно оси, проходящей через центр инерции.

15. Выведите формулу для момента инерции прямоугольного бруска относительно оси, проходящей через центр инерции.

16. Выведите формулу для кинетической энергии тела твердого тела, вращающегося вокруг закрепленной оси.

17. Запишите выражение для работы момента силы относительно оси.

18. От чего и как зависит кинетическая энергия вращающегося тела?

БИБЛИОГРАФИЧЕСКИЙ СПИСОК ЛИТЕРАТУРЫ

1. Савельев, И. В. Курс физики. В 3-х т. Т. 1. Механика. Молекулярная физика./ И. В. Савельев.- М.: Наука, 1989.- 352 с.

2. Иродов, И. Е. Механика. Основные законы./ И. Е. Иродов.- М.: Лаборатория Базовых Знаний, 2001.- 256 с.

3. Волков, В. Н. Физика. В 3-х т. Т. 1. Механика. Молекулярная физика./ В. Н. Волков, Г. И. Рыбакова, М. Н. Шипко; Иван. гос. энерг. ун-т.- Иваново, 1993. -230 с.



Расчет момента инерции диска

Расчет момента инерции диска

19/11/2015 by RhEvans

В физике вращательный эквивалент массы называется моментом инерции . Определение момента инерции элемента объема, имеющего массу, дается формулой

, где — расстояние по перпендикуляру от оси вращения до элемента объема. Чтобы найти общий момент инерции объекта, нужно просуммировать моменты инерции всех элементов объема объекта по всем значениям расстояния от оси вращения. Обычно мы рассматриваем момент инерции относительно вертикали (оси z) и обычно обозначаем его . Мы можем написать

Момент инерции относительно двух других основных осей обозначается и , но мы можем рассматривать момент инерции относительно любой удобной оси.

Вывод момента инерции диска

В этом блоге я выведу момент инерции диска. В следующих блогах я выведу другие моменты инерции, например. для кольца, твердой сферы, сферической оболочки и полой сферы с очень тонкой оболочкой.

Для наших целей диск представляет собой сплошной круг с небольшая толщина (маленькая по сравнению с радиусом диска). Если он имеет толщину, сравнимую с его радиусом, он становится цилиндром, о чем мы поговорим в следующем блоге. Итак, наш диск выглядит примерно так.

Диск малой толщины, радиусом

Для расчета момента инерции этого диска относительно оси z суммируем момент инерции элемента объема от центра (где ) до внешнего радиуса .

Элемент массы связан с элементом объема уравнением
(где плотность элемента объема). Будем считать в этом примере, что плотность диска однородна; но в принципе, если бы мы знали его зависимость от , это не было бы проблемой.

Элемент объема можно рассчитать, рассматривая кольцо на радиусе с шириной и толщиной.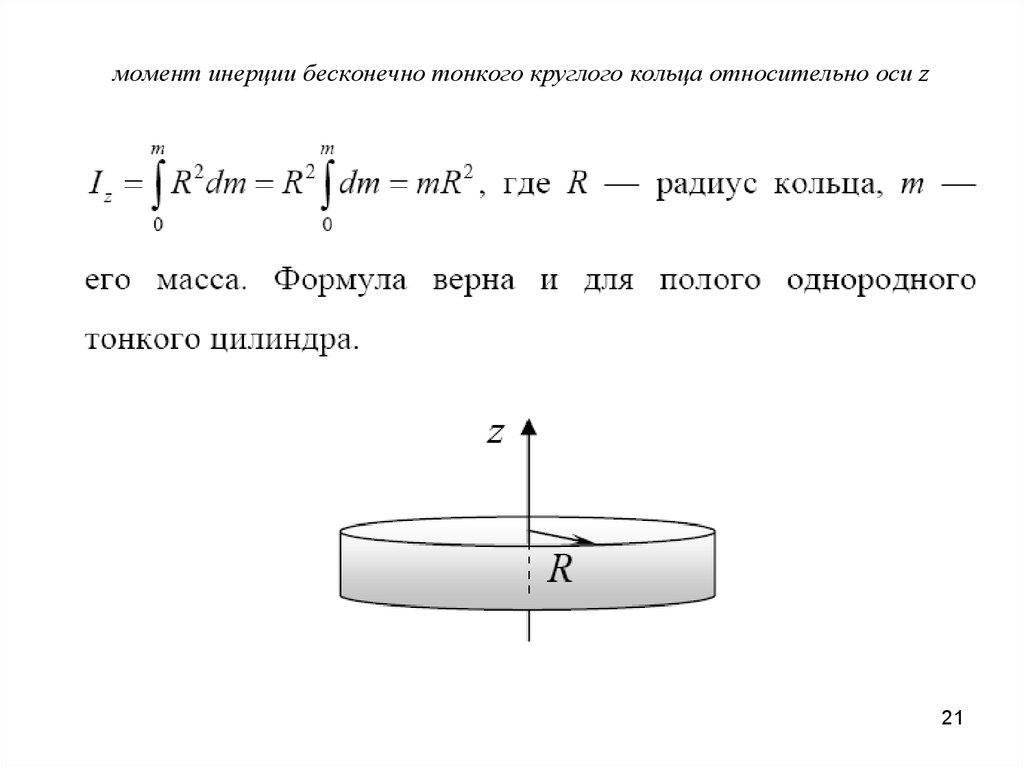 Объем этого кольца равен произведению окружности этого кольца на его ширину, умноженной на его толщину.

, поэтому мы можем записать

и, следовательно, мы можем записать уравнение (1) как

Интегрируя между радиусом и , мы получаем

Если мы теперь определим полную массу диска как , где

и общий объем диска. Общий объем диска — это просто его площадь, умноженная на его толщину,

, поэтому общая масса равна

. Используя это, мы можем переписать уравнение (2) как

. Каковы моменты инерции относительно x и оси Y?

Чтобы найти момент инерции относительно оси x или оси y, мы используем Теорема перпендикулярной оси . Это утверждает, что для объектов, которые лежат внутри плоскости, момент инерции относительно оси, параллельной этой плоскости, определяется выражением

, где и — два момента инерции в плоскости и перпендикулярно друг другу.

Из симметрии диска видно, что момент инерции относительно осей x и y будет одинаковым, поэтому . Поэтому мы можем написать

Маховики

Маховики используются для накопления энергии вращения. Это полезно, когда источник энергии не является непрерывным, поскольку они могут помочь обеспечить непрерывный источник энергии. Они используются во многих типах двигателей, включая современные автомобили.

Именно из-за момента инерции диска он может хранить энергию вращения таким образом. Как и в случае с массой в линейном случае, для изменения скорости вращения (угловой скорости) объекта требуется сила. Чем больше момент инерции, тем большая сила требуется для изменения его угловой скорости. Как мы видим выше из уравнения для момента инерции диска, для двух маховиков одинаковой массы более тонкий больший будет запасать больше энергии, чем более толстый меньший, потому что его момент инерции увеличивается пропорционально квадрату радиуса диск.

Иногда масса является критическим фактором, и в следующий раз я рассмотрю случай кольца, в котором удалена внутренняя часть диска.