крутящий момент силы — английский перевод

Крутящий момент.	You know, torque.
Реальный крутящий момент ( крутящего момента макс. крутящий момент 100)	Actual torque ( per cent torque x max. torque 100)
крутящий момент 100)	torque 100)
Реальный крутящий момент	The OBD system shall also perform rationality monitoring on the information coming from or provided to components that do not belong to the engine system when this information compromises the emission control system and or the engine system for proper performance.
Максимальный крутящий момент	Maximum torque speed
Крутящий момент двигателя	Engine torque
8. 1.7.1 крутящий момент	8.1.7.1 torque
Крутящий момент процент	Torque per cent
Крутящий момент, корректирующий направление	E ECE TRANS 505
Крутящий момент, корректирующий направление	Regulation No. 83
1.9 Максимальный крутящий момент	Maximum torque speed
Крутящий момент, корректирующий направление	Rev.1 Add.82 Rev.2
2.2 Реальный крутящий момент	Actual torque
приведенный крутящий момент 82	As an example, the following test point shall be unnormalized
приведенный крутящий момент 82	In order for engines with a unit cylinder displacement of  0. 75 dm³ to be considered to belong to the same engine family, the spread of their individual cylinder displacements shall not exceed 30 per cent of the largest individual cylinder displacement within the family.
Максимальный крутящий момент (Н.м)	Fuel delivery per stroke (mg)
2.2 Фактический крутящий момент	2.2. Actual torque
3.3.1.8 Максимальный крутящий момент . . . . . . . .	Maximum net power output kW at min 1 3.3.1.8.
1.9 Максимальный крутящий момент	.. Maximum torque speed
приведенный крутящий момент 82	per cent torque 82 per cent
Фактический крутящий момент (5)	Actual torque (5)
Измеренный крутящий момент, Н м	Measured torque, Nm
Полезный крутящий момент, Н м	Net torque, Nm
3. 3.1.8 Максимальный крутящий момент . . . . . . . .	Net maximum torque . . . . . . . . . . . . .
мощность и крутящий момент	power and torque
приведенный крутящий момент 82 .	per cent torque 82 per cent
L крутящий момент в .	L per cent torque
Максимальный полезный крутящий момент .	Maximum net torque .
Максимальный крутящий момент (Н.м)	Maximum torque (Nm)
2.2 Реальный крутящий момент	2.2. Actual torque
приведенный крутящий момент 82	per cent speed per cent torque
Максимальный крутящий момент (Нм)	Max. torque (Nm)
2.2 Фактический крутящий момент	Actual torque
5.2.1.2.4 Крутящий момент Ct1 представляет собой средний крутящий момент, полученный по следующей формуле	The torque Ct1 is the average torque derived from the following formula
5.2.1.2.4 Крутящий момент Ct1 представляет собой средний крутящий момент, полученный по следующей формуле	5.2.1.2.4. The torque Ct1 is the average torque derived from the following formula
пороговый входной крутящий момент (минимальный крутящий момент, необходимый для создания измеримого тормозного момента)	Threshold input torque (minimum torque necessary to produce a measurable brake torque)
реальный крутящий момент 574 Нм	actual torque 574 Nm
11. 1.2 Максимальный полезный крутящий момент . . .	Maximum net torque . . . . . . . . .
12.1.2 Максимальный полезный крутящий момент . . .	Maximum net torque . . . . . . . . .
1.12 Максимальный полезный крутящий момент .	1.12. Maximum net torque .Nm at min 1 1.13.
1.12 Максимальный полезный крутящий момент .	1.12. Maximum net torque .Nm at .min 1 1.13.
1.12 Максимальный полезный крутящий момент .	Combustion system compression ignition positive ignition (2)
MT испытательный крутящий момент Н м	MT test torque Nm
Исходный максимальный крутящий момент двигателя	Reference engine maximum torque
реальный крутящий момент 574 Нм	actual torque pic 574 Nm

Крутящий момент, что это и зачем он нужен? Примеры момента силы

Каждый двигатель внутреннего сгорания рассчитан на определенную максимальную мощность, которую он может выдавать при наборе определенного количества оборотов коленчатого вала. Однако помимо максимальной мощности существует еще и такая величина в характеристике двигателя, как максимальный крутящий момент, достигаемый на оборотах отличных от оборотов максимальной мощности.

Что же означает понятие крутящий момент?

Говоря научным языком, крутящий момент равен произведению силы на плечо ее применения и измеряется в ньютон — метрах. Значит если к гаечному ключу длиной 1 метр (плечо), приложить силу в 1 Ньютон (перпендикулярно на конце ключа), то мы получим крутящий момент равный 1 Нм.

Для наглядности. Если гайка затянута с усилием 3 кгс, то для ее откручивания придется к ключу с длиной плеча в 1 метр приложить усилие 3 кг. Однако, если на ключ длиной 1 метр надеть дополнительно 2-х метровый отрезок трубы, увеличив тем самым рычаг до 3 метров, то тогда для отворачивания этой гайки потребуется лишь усилие в 1 кг. Так поступают многие автолюбители при откручивании колесных болтов: либо добавляют отрезок трубы, а за неимением такового просто надавливают на ключ ногой, увеличив тем самым силу приложения к баллонному ключу.

Так же если на рычаг метровой длины повесить груз равный 10 кг, то появится крутящий момент равный 10 кгм. В системе СИ это значение (перемножается на ускорение свободного падения — 9,81 м/см2) будет соответствовать 98,1 Нм.

Результат всегда един — крутящий момент, это произведение силы на длину рычага, стало быть, нужен либо длиннее рычаг, либо большее количество прикладываемой силы.

Все это хорошо, но для чего нужен крутящий момент в автомобиле и как его величина влияет на его поведение на дороге?

Мощность двигателя лишь косвенно отражает тяговые возможности мотора, и ее максимальное значение проявляется, как правило, на максимальных оборотах двигателя. В реальной жизни в таких режимах практически никто не ездит, а вот ускорение двигателю требуется всегда и желательно с момента нажатия на педаль газа. На практике одни автомобили уже с низких оборотов (с низов) ведут себя достаточно резво, другие напротив предпочитают лишь высокие обороты, а на низах показывают вялую динамику.

Так у многих возникает масса вопросов, когда они с авто с бензиновым мотором мощностью 105-120 л.с. пересаживаются на 70-80 – сильный дизель, то последний с легкостью обходит машину с бензиновым мотором. Как такое может быть?

Связано это с величиной тяги на ведущих колесах, которая различна для этих двух автомобилей. Величина тяги напрямую зависит от произведения таких показателей как, величины крутящего момента, передаточного числа трансмиссии, ее КПД и радиуса качения колеса.

Как создается крутящий момент в двигателе

В двигателе нет метровых рычагов и грузов, и их заменяет кривошипно-шатунный механизм с поршнями. Крутящий момент в двигателе образуется за счет сгорания топливо — воздушной смеси, которая расширяясь в объеме с усилием толкает поршень вниз. Поршень в свою очередь через шатун передает давление на шейку коленчатого вала. В характеристике двигателя нет значения плеча, но есть величина хода поршня (двойное значение радиуса кривошипа коленвала).

Для любого мотора крутящий момент рассчитывается следующим образом. Когда поршень с усилием 200 кг двигает шатун на плечо 5 см, появляется крутящий момент 10 кГс или 98,1Нм. В данном случает для увеличения крутящего момента нужно либо увеличить радиус кривошипа, или же увеличить давление расширяющихся газов на поршень.

До определенной величины можно увеличить радиус кривошипа, но будут расти и размеры блока цилиндров как в ширину, так и в высоту и увеличивать радиус до бесконечности невозможно. Да и конструкцию двигателя придется значительно упрочнять, так как будут нарастать силы инерции и другие отрицательные факторы. Следовательно, у разработчиков моторов остался второй вариант – нарастить силу, с которой поршень передает усилие для прокручивания коленвала. Для этих целей в камере сгорания нужно сжечь больше горючей смеси и к тому же более качественно. Для этого меняют величину и конфигурацию камеры сгорания, делают «вытеснители» на головках поршней и повышают степень сжатия.

Однако максимальный момент доступен не на всех оборотах мотора и у различных двигателей пик момента достигается на различных режимах. Одни моторы выдают его в диапазоне 1800- 3000 об/мин, другие на 3000-4500 об/мин. Это зависит от конструкции впускного коллектора и фаз газораспределения, когда эффективное наполнение цилиндров рабочей смесью происходит при определенных оборотах.

Наиболее простое решение для увеличения крутящего момента, а следовательно и тяги, это применение или механического наддува, либо применение их в комплексе. Тогда крутящий момент можно уже использовать с 800-1000 об/мин, т.е. практически сразу при нажатие на педаль акселератора. К тому же это закрывает такую проблему, как провалы при наборе скорости, так как величина КМ становится практически одинакова во всем диапазоне оборотов двигателя. Достигается это различными путями: увеличивают количество клапанов на цилиндр, делают управляемыми фазы газораспределения для оптимизации сгорания топлива, повышают степень сжатия, применяют выпускной коллектор по формуле 1-4 -2-3, в турбинах применяют крыльчатки с изменяемым и регулируемым углом атаки лопаток и т.

д.

Всем привет! Сегодня рассмотрим недорогую ноунейм аккумуляторную трещотку. Наверняка кто-то заметил, что есть сходство с M12 IR-201B. Да что там сходство — это практически полная желтая копия милуоки с мелкими изменениями. Нам обещают 35 Нм крутящего момента — представьте, что на гайку накинут ключ с рукоятью 1 метр, на конце которой груз 3.5 кг. Да, не очень много, но нужно понимать, что трещотками не откручивают колеса, на это так же намекает не самый крупный 3/8 квадрат. Под катом подробные характеристики, демонстрация возможностей и «расчлененка».

Сразу же напишу насчет цены чтобы информация не потерялась. Необходимо применить купон

Elec

Доставка заняла около двух недель

Характеристики

Торцевой гайковерт (так их называют в оффлайн магазинах)
Модель: 963126
Цвет: Желтый
Материал: металл + пластик(и немного резины)
Размер: 28 см x 4.5 см
Емкость аккумулятора: 1. 5 Ач
Напряжение аккумулятора: 12 Вольт
Крутящий момент: 35 Нм
Максимальная скорость: 280 об/мин
Размер квадрата: 3/8″ дюйма

Время зарядки: 90 минут
Время работы: около 3 часов

Упаковка и внешний вид

Серый пакет

Пупырчатая пленка

В комплект закинули переходник для ЗУ, принт коробки минималистичный

Внутри трещотка с аккумулятором, головка на 15, инструкция и зарядное устройство.

Языки только английский и китайский, есть перечисление комплектующих

Во время зарядки индикатор блока горит красным

Постепенно перетекая в зеленый

Аккумулятор не умеет отображать уровень заряда, но есть трехуровневый индикатор в основном корпусе.

Так же имеется механический предохранитель для защиты от случайных нажатий

Функционал
Принцип работы немного отличается от механических собратьев, в которых обычно используют парочку подпружиненных фиксаторов. Но оно и понятно, т.к. в данном случае происходят колебания, а не вращение. Подробнее покажу после разборки.
Кнопка включения с регулятором оборотов — чем сильнее утапливаем, тем больше оборотов и крутящий момент.

Реверс включается поворотом «язычка» с тыльной стороны.

Вообще 3/8 не самый распространенный размер квадрата, поэтому я купил парочку переходников

После этого можно смело пользоваться всеми удлинителями и головками до 17, что лежат в данном чемоданчике. Так то можно и на 24 нацепить, но обычно откручивание болтов таких размеров требует немалых усилий, чего трещотки не очень любят.

Вот так выглядит с переходником, вполне нормально.

Сама себя трещотка не сломает за счет не очень большого крутящего момента, но механизм имеет фиксацию, а это значит, что можно помочь руками в разумных пределах. В нашем случае рукоять толстая, не впивается в руку, а еще гайка точно вот-вот начнет крутиться, надо только упереться во что-то ногой и потянуть сильнее. В таких случаях лучше спросить себя — «а выкручивал бы я эту гайку средней механической трещоткой или взял ключ и трубу?»

Нужно было заменить масло в машине и открутить 6 болтов на 17 для снятия защиты двигателя. Часть срывались вручную, но усилие было не очень большим

В основном выкручивались самостоятельно

С гайками и болтами ниже 17 проблем никаких не было. Единственный минус — нет ограничителя момента и можно запросто раздавить пластиковые элементы во время монтажа. Приходится снижать обороты, ориентируясь на остаток хода или ослаблять хват.

Бампер затянули до упора, ключом докручивать уже было некуда.

Гайки багажника ваз 2110, правда не ржавые, но окрашены

Нашел переходник под биту, решил сравнить сабж с шуруповертом.

Трещоткой пользоваться не так удобно — сложно обеспечить перпендикулярный нажим

Шуруповерт на первой скорости справился аналогично, но удобнее, хотя трещотка за счет бОльшего рычага меньше выворачивает кисть во время затяжки.

Чуть позже масло с фильтром поменяли, закрепили на место поддон, в итоге как было 3 индикатора, так и осталось.

Еще через некоторое время меняли колодки — суппорты поддались без проблем, при чем верхний болт крайне неудобно располагался — между стойкой и тормозным механизмом, так что инструмент был очень кстати. После этого зеленая лампочка индикатора заряда стала заметно тускнее. Процесс не снимал, т.к. руки стали грязные моментально.
Еще сабж использовался для сборки дивана с нуля.

Думаю найдутся люди, которым интересно какие звуки издает инструмент во время работы. Для примера вставлю кусок видео, где в дерево вкручивается здоровый шуруп. Вероятно у него есть какое-то название, но для меня он шуруп. Немного не по назначению, но зато есть плавное нарастание нагрузки вплоть до остановки, так что должно быть довольно показательно.

Расчлененка

10 винтов и один фиксатор рычага спустя, корпус разбирается на 2 части

Двигатель без опознавательных знаков, в верхней части закреплен кусок редуктора

Кнопка поближе, мосфет с запасом, 60 Вольт, 60 Ампер

Остальная часть редуктора. Смазки как-то пожалели

Весь механизм редуктора

Маятник совершает колебательные движения за счет шарнира

Так выглядит механизм храповика. Внутренняя часть имеет две многозубые фиксирующие «собачки».

При прокручивании «язычка» подпружиненные рычажки меняют угол

И при совершении колебательных движений корпуса, внутренняя часть практически не встречает сопротивления в одну сторону, проскальзывая с характерными щелчками, но фиксируется при обратном движении на внешней шестерне и двигается вместе с ней.

Вот и вся магия. Редуктор смазал и собрал всё на место. На самом деле смазки не очень много, ракурс такой.

Аккумулятор так же разбирается, состоит из трех элементов 18650 емкостью 1500 мАч. Есть термистор.

Дополнительные провода свидетельствуют о наличии балансировки

и

Итоги

Да, это специализированный элемент и не каждому может понадобиться. Я знаю людей, у которых вообще ни одного ключа в машине нет — благо сервисных центров куча. Но если заниматься ремонтом самостоятельно, можно сэкономить прилично времени и сил. Все ведь понимают преимущества механической трещотки перед ключами. Я сейчас не представляю себе ремонт без неё. Не, конечно при желании можно где-то подлезть рожковым или накидным, где-то вороток использовать, но процесс будет идти гораздо медленнее.
Аккумуляторная же версия позволяет подлезть даже в узкие места без необходимости освобождать место, снимая патрубки, выхлопную или еще чего, что мешается и заставляет набивать чечетку по кузову. Главное втиснуть корпус, надеть головку на болт/гайку, нажать на кнопку а дальше оно само.
Благодаря редуктору имеется неплохой крутящий момент, плюс можно срывать вручную не очень податливые соединения, главное меру знать. С другой стороны, размер ручки не такой большой чтобы можно было легко слизать шестерню механизма, учитывая особенности строения. Даже колеса снимал/надевал, предварительно сорвав гайки ключом с трубой — всё быстрее, чем руками.
Ну и напоследок по цене — насколько могу судить, она вполне гуманна. Та же милуоки с аналогичными характеристиками официально стоит около 250 долларов, онлайн можно найти от 80+$ без аккумулятора.

Не уверен, что все примененные мною термины правильные, т.к. что-то слышал от мастеров, что-то видел в форумах, так что поправляйте в комментариях — я исправлю текст. Всем добра =)

Товар предоставлен для написания обзора магазином. Обзор опубликован в соответствии с п.18 Правил сайта.

Планирую купить +11 Добавить в избранное Обзор понравился +45 +64

Конвертер длины и расстояния Конвертер массы Конвертер мер объема сыпучих продуктов и продуктов питания Конвертер площади Конвертер объема и единиц измерения в кулинарных рецептах Конвертер температуры Конвертер давления, механического напряжения, модуля Юнга Конвертер энергии и работы Конвертер мощности Конвертер силы Конвертер времени Конвертер линейной скорости Плоский угол Конвертер тепловой эффективности и топливной экономичности Конвертер чисел в различных системах счисления Конвертер единиц измерения количества информации Курсы валют Размеры женской одежды и обуви Размеры мужской одежды и обуви Конвертер угловой скорости и частоты вращения Конвертер ускорения Конвертер углового ускорения Конвертер плотности Конвертер удельного объема Конвертер момента инерции Конвертер момента силы Конвертер вращающего момента Конвертер удельной теплоты сгорания (по массе) Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему) Конвертер разности температур Конвертер коэффициента теплового расширения Конвертер термического сопротивления Конвертер удельной теплопроводности Конвертер удельной теплоёмкости Конвертер энергетической экспозиции и мощности теплового излучения Конвертер плотности теплового потока Конвертер коэффициента теплоотдачи Конвертер объёмного расхода Конвертер массового расхода Конвертер молярного расхода Конвертер плотности потока массы Конвертер молярной концентрации Конвертер массовой концентрации в растворе Конвертер динамической (абсолютной) вязкости Конвертер кинематической вязкости Конвертер поверхностного натяжения Конвертер паропроницаемости Конвертер плотности потока водяного пара Конвертер уровня звука Конвертер чувствительности микрофонов Конвертер уровня звукового давления (SPL) Конвертер уровня звукового давления с возможностью выбора опорного давления Конвертер яркости Конвертер силы света Конвертер освещённости Конвертер разрешения в компьютерной графике Конвертер частоты и длины волны Оптическая сила в диоптриях и фокусное расстояние Оптическая сила в диоптриях и увеличение линзы (×) Конвертер электрического заряда Конвертер линейной плотности заряда Конвертер поверхностной плотности заряда Конвертер объемной плотности заряда Конвертер электрического тока Конвертер линейной плотности тока Конвертер поверхностной плотности тока Конвертер напряжённости электрического поля Конвертер электростатического потенциала и напряжения Конвертер электрического сопротивления Конвертер удельного электрического сопротивления Конвертер электрической проводимости Конвертер удельной электрической проводимости Электрическая емкость Конвертер индуктивности Конвертер Американского калибра проводов Уровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др.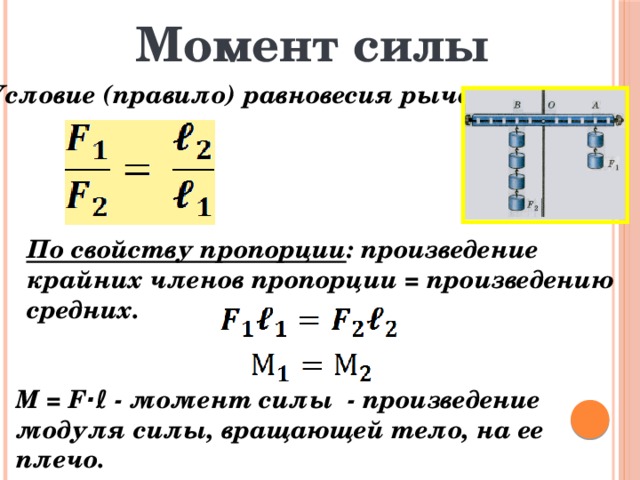 единицах Конвертер магнитодвижущей силы Конвертер напряженности магнитного поля Конвертер магнитного потока Конвертер магнитной индукции Радиация. Конвертер мощности поглощенной дозы ионизирующего излучения Радиоактивность. Конвертер радиоактивного распада Радиация. Конвертер экспозиционной дозы Радиация. Конвертер поглощённой дозы Конвертер десятичных приставок Передача данных Конвертер единиц типографики и обработки изображений Конвертер единиц измерения объема лесоматериалов Вычисление молярной массы Периодическая система химических элементов Д. И. Менделеева

1 ньютон-метр [Н·м] = 0,1019716212978 килограмм-сила-метр [кгс·м]

Исходная величина

Преобразованная величина

ньютон-метр килоньютон-метр миллиньютон-метр микроньютон-метр тонна-сила (короткая)-метр тонна-сила (длинная)-метр тонна-сила (метрическая)-метр килограмм-сила-метр грамм-сила-сантиметр фунт-сила-фут паундаль-фут паундаль-дюйм

Общие сведения

Момент силы — это физическая величина, характеризующая насколько сила, приложенная к телу, вызывает вращение тела вокруг оси. В английском и некоторых других языках это явление называют разными словами, в зависимости от контекста. Поскольку эта статья написана для сайта переводчиков, мы немного поговорим о терминологии в других языках. Величина момента силы равна векторному произведению силы, приложенной к телу на вычисленное по перпендикуляру расстояние между осью вращения и точкой приложения силы, которая вызывает вращение. В английском языке для момента силы используют два термина, момент силы (moment of force ) и отдельный термин, torque . Английский термин torque используют для обозначения физической величины, которую измеряют так же, как и момент силы (в английском), но только в контексте, в котором сила, ответственная за это свойство, обязательно вызывает вращение тела. Эту величину также измеряют, умножив силу на расстояние между осью вращения и точкой приложения силы. В русском языке термину «torque» соответствуют термины «вращающий момент» и «вращательный момент», которые являются синонимами. Русский термин «крутящий момент» относится к внутренним усилиям, возникающим в объектах под действием приложенных к ним нагрузок. Этому термину соответствуют английские термины «torsional movement», «torque effect», «torsional shear» и некоторые другие.

Как уже упоминалось выше, в этой статье мы уделяем много внимания контексту, в котором используется тот или иной английский термин. Наша задача — объяснить разницу, чтобы помочь читателю, если он в будущем столкнется с этими терминами в английском тексте. Самое главное, что следует помнить — оба термина, момент силы и torque, используют для одной и той же физической величины, но в разных контекстах. Во многих языках, как и в русском, используют только один термин. Ниже рассмотрим в каком же контексте используют каждый из этих терминов.

Терминология в английском языке

Как мы уже упоминали выше, английские термины «момент силы» и «torque» используют для одного и того же понятия, но в разных контекстах. В этом разделе обсудим, когда в английском наиболее часто используют термин «момент силы» и почти не используют «torque». Часто о понятии «torque» говорят в контексте, когда сила, действующая на тело вызывает изменение углового ускорения тела. С другой стороны, когда в английском языке говорят о моменте силы, то сила, действующая на тело не обязательно вызывает такое ускорение. То есть, «torque» — это частный пример момента силы, но не наоборот. Можно также сказать, что «torque» — это момент силы, но момент силы — не «torque».

Ниже рассмотрим несколько примеров. Стоит еще раз напомнить, что разница в использовании этих двух терминов зависит от контекста, но используют их для одного и того же физического явления. Нередко оба эти термина используют попеременно.

Чтобы понять, что такое момент силы, рассмотрим вначале, что такое момент в общем. Момент — это интенсивность, с которой сила действует на тело на определенном расстоянии относительно тела. Величина момента силы зависит от величины силы, которая действует на тело, и от расстояния от точки приложения силы до точки на теле. Как мы увидели из определения выше, эта точка часто находится на оси вращения.

Момент силы пропорционален силе и радиусу. Это значит, что если сила приложена к телу на определенном расстоянии от оси вращения, то вращательное действие этой силы умножается на радиус, то есть чем дальше от оси вращения приложена сила, тем более вращающее действие она оказывает на тело. Это принцип используется в системах рычагов, шестерней и блоков, чтобы получить выигрыш в силе. В этом контексте чаще всего говорят о моменте силы и о его использовании в различных системах, например в системах рычагов. Примеры работы рычагов показаны в . Стоит заметить, что в этой статье мы в основном обсуждаем вращающий момент, что соответствует английскому термину «torque».

Иногда понятия момент силы и вращающий момент различают с помощью понятия «пары сил». Пара сил — это две силы одинаковой величины, действующие в противоположном направлении. Эти силы вызывают вращение тела, и их векторная сумма равна нулю. То есть, термин «момент силы» используют в более общем контексте, чем вращающий момент.

В некоторых случаях термин «вращающий момент» используют, когда тело вращается, в то время как термин «момент силы» используют, когда тело не вращается, например, если речь идет об опорных балках и других конструктивных элементах зданий в строительстве. В таких системах концы балки либо жестко закреплены (жесткая заделка), либо крепление позволяет балке вращаться. Во втором случае говорят, что эта балка закреплена на шарнирной опоре. Если на эту балку действует сила, например, перпендикулярно ее поверхности, то в результате образуется момент силы. Если балка не фиксирована, а прикреплена на шарнирной опоре, то она свободно движется в ответ на действующие на нее силы. Если же балка фиксирована, то в противодействие моменту силы образуется другой момент, известный как изгибающий момент . Как видно из этого примера, термины момент силы и вращающий момент различаются тем, что момент силы не обязательно изменяет угловое ускорение. В этом примере угловое ускорение не изменяется потому, что силам извне, действующим на балку, противодействуют внутренние силы.

Примеры момента силы

Хороший пример момента силы в быту — это действие на тело одновременно момента силы и изгибающего момента, о котором мы говорили выше. Момент силы часто используют в строительстве и в проектировании строительных конструкций, так как, зная момент силы, можно определить нагрузку, которую должна выдержать эта конструкция. Нагрузка включает нагрузку от собственного веса, нагрузку, вызванную внешними воздействиями (ветром, снегом, дождем, и так далее), нагрузку от мебели и нагрузку, вызванную посетителями и обитателями здания (их вес). Нагрузка, вызванная людьми и интерьером, называется в строительстве полезной нагрузкой , а нагрузка, вызванная весом самого здания и окружающей средой называется статической или постоянной нагрузкой .

При постройке в 1900 году моста Александры через реку Оттава использовано много двутавровых балок

Если на балку или другой конструктивный элемент действует сила, то в ответ на эту силу возникает изгибающий момент, под действием которого некоторые части этой балки сжимаются, в то время как другие, наоборот, растягиваются. Представим, к примеру, балку, на которую действует сила, направленная вниз и приложенная по центру. Под воздействием этой силы балка принимает вогнутую форму. Верхняя часть балки, на которую действует сила, сжимается под воздействием этой силы, в то время как нижняя, наоборот, растягивается. Если нагрузка больше, чем этот материал может выдержать, то балка разрушается.

Наибольшая нагрузка — на самый верхний и самый нижний слои балки, поэтому в строительстве и при проектировании сооружений эти слои часто укрепляют. Хороший пример — использование двутавровых конструкций . Двутавр — конструктивный элемент с поперечным сечением в форме буквы Н или латинской буквы “I ” с верхней и нижней засечками (поэтому английском языке используют термин I -beam, Такая форма очень экономична, так как она позволяет упрочнить самые слабые части балки, используя при этом наименьшее количество материала. Чаще всего двутавровые балки сделаны из стали, но для прочной балки двутавровой конструкции вполне можно использовать и другие материалы.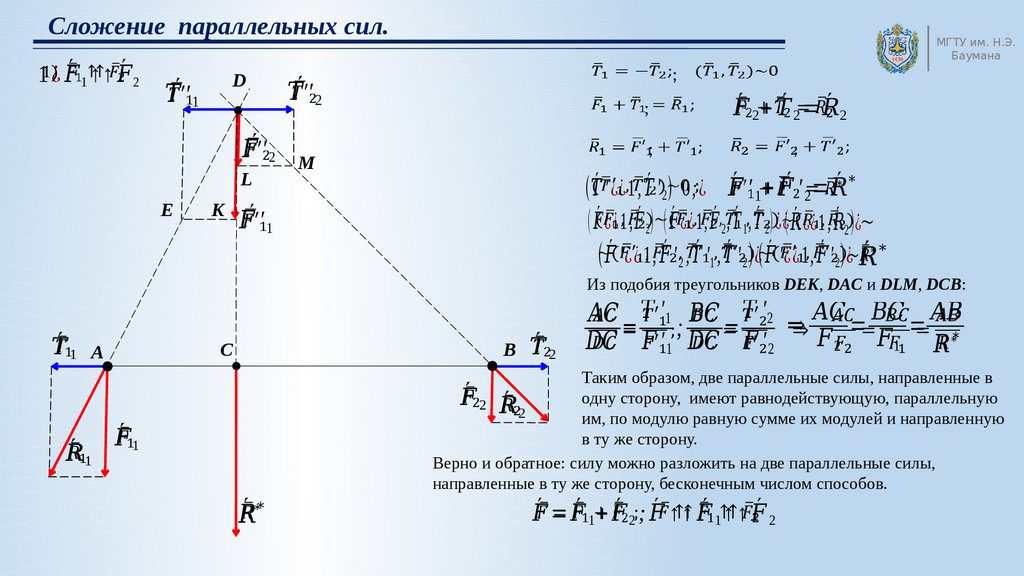 На YouTube можно найти видеосюжеты испытания двутавровых балок, сделанных из материалов, менее прочных, чем сталь, например из пенопласта и фанеры (нужно искать plywood beam test). Двутавровые балки из фанеры и древесностружечных плит появились на российском рынке стройматериалов относительно недавно, хотя они давно и очень широко применяются при строительстве каркасных домов в Северной Америке.

Если на конструкцию действует изгибающий момент, то двутавровые балки — решение проблем, связанных с прочностью. Двутавровые балки также используют в конструкциях, которые подвергаются напряжению сдвига . Края двутавровой балки противодействуют изгибающему моменту, в то время как центральная опора противостоит напряжению сдвига. Несмотря на ее достоинства, двутавровая балка не может противостоять . Чтобы уменьшить эту нагрузку на поверхность конструкции, ее делают круглой и полируют поверхность, чтобы предотвратить скопление нагрузки в точках с неровной поверхностью. Увеличение диаметра и изготовление такой конструкции полой внутри может помочь уменьшить ее вес.

Заключение

В это статье мы рассмотрели, чем отличаются термины «момент силы» и «вращающий момент», а также английские термины «moment of force» и «torque», и увидели несколько примеров момента силы. В основном мы говорили о случаях, когда момент силы создает проблемы в строительстве, но часто бывает наоборот и момент силы приносит пользу. Примеры использования момента силы на практике — в . Стоит также упомянуть, что разница в терминологии в английском языке чаще всего значительна в американском и британском машиностроении и строительстве, в то время как в физике эти термины часто взаимозаменяемы.

Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.

что это, на что влияет, почему он важнее мощности :: Autonews

Многие уверены, что главной характеристикой двигателя автомобиля является мощность, которая обычно измеряется в лошадиных силах (на самом деле — в ваттах, но применительно к машинам часто используют «лошадей»). Но ведь есть еще такая характеристика как крутящий момент.

• Что это такое
• На что влияет
• Что важнее — момент или мощность
• Дизель и бензин

www.adv.rbc.ru

Что такое крутящий момент?

Крутящий момент – это векторная величина, определяемая как произведение радиус-вектора точки приложения силы и вектора силы. В простейшем случае – это произведение прикладываемой силы на плечо рычага, к которому она прикладывается. Единица измерения у крутящего момента – соответствующая: ньютоны на метры (Н∙м).

Звучит сложно, но попытаемся объяснить на простом примере. Представьте себе механическую мясорубку, которую нужно крутить за ручку. Так вот, в ней прикладываемая сила – это та сила, с которой вы крутите ручку. А плечо – это сама ручка. И чем она длиннее, тем выше крутящий момент при тех же ваших усилиях.

Как это всё относится к двигателю автомобиля? Очень просто. В моторе сила давления сгорающей смеси бензина и воздуха передаётся через поршень на кривошипно-шатунный механизм. Сила «берётся» из сгорания топлива, а в качестве рычага выступают детали механизма.

На что влияет крутящий момент

Крутящий момент характеризует «итоговую» тягу двигателя. Он говорит «насколько двигатель сильный», какую силу тяги может создавать. При этом надо понимать, что на колёса крутящий момент доходит уже изменённым, ведь шины связаны с мотором не напрямую, а через трансмиссию, в которой момент изменяется в зависимости от передаточного соотношения.

Крутящий момент — величина не постоянная. Момент изменяется вместе с количеством поступающей в цилиндр смеси и оборотами двигателями. Поэтому для оценки возможностей двигателя обычно используют график крутящего момента, который иллюстрирует его зависимость от оборотов.

Особенность двигателей внутреннего сгорания в том, что с ростом оборотов крутящий момент рано или поздно начинает снижаться (Фото: Shutterstock)

Чем большее усилие развивает двигатель — тем лучше автомобиль разгоняется. Поэтому максимальное ускорение получается на тех оборотах, при которых момент достигает пиковых значений.

Но особенность двигателей внутреннего сгорания в том, что с ростом оборотов крутящий момент рано или поздно начинает снижаться. Решить эту проблему помогает коробка передач: при разгоне мы включаем нужную передачу, поддерживая обороты на оптимальном уровне. И поэтому так важно, чтобы двигатель на как можно большем промежутке оборотов выдавал максимальную тягу.

Крутящий момент и мощность: что важнее

Но что важнее? Крутящий момент или мощность двигателя? Чтобы ответить на этот вопрос, сначала нужно понять, что такое вообще мощность.

С точки зрения физики мощность получается путём деления совершенной работы на время, за которое работа совершилась. То есть, эта характеристика показывает не «что было сделано», а «что было сделано за определённое время». Например, перенести из пункта А в пункт Б десять ящиков можно за пять минут, а можно за сорок. Выполненная работа будет одинакова.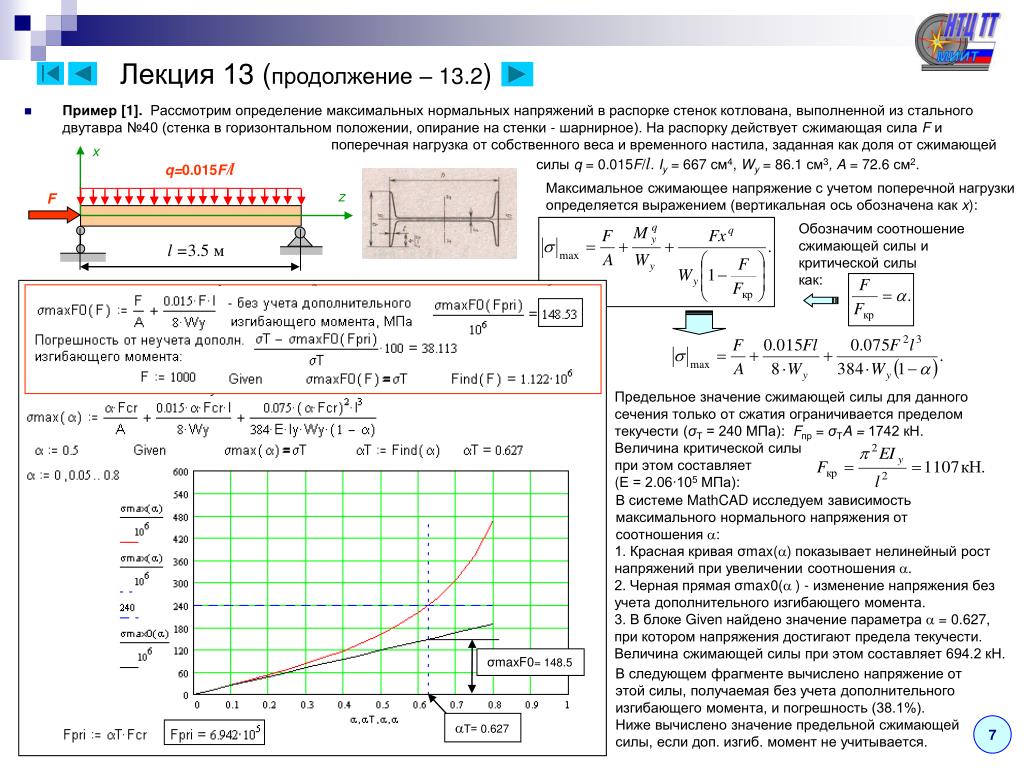 А вот мощность — нет.

Применительно к автомобильному двигателю мощность тоже является такой же «оценочной» характеристикой. При этом, можно сказать, что работой двигателя, по сути, является… крутящий момент. Ведь работа мотора — это крутить коленвал. Следовательно, крутящий момент и мощность — величины взаимосвязанные.

Вернемся к воображаемой мясорубке. Длинная ручка обеспечивает высокий крутящий момент, то есть вы можете прокручивать, например, не обычное мясо, а замороженное. Допустим, за один оборот сквозь мясорубку проходит 10 граммов такого мяса, а если у вас получится делать 100 оборотов в минуту — на выходе получится килограмм фарша. Это и есть ваша мощность.

В автомобилях мощность мотора равняется его крутящему моменту на данных оборотах в минуту, умноженному на число этих оборотов и разделённому на определённый коэффициент. Она показывает «суммарное количество» крутящего момента, то есть, работы, совершённой двигателем за определённое время. Чем больше момент, «сила кручения» — тем больше мощность.

Часто на графике отображаются сразу две линии: одна обозначает момент, а другая — мощность. (Фото: drive2.ru)

Отметим, что как для крутящего момента, так и для мощности существуют графики, демонстрирующие зависимость от числа оборотов. Более того, часто на графике отображаются сразу две линии: одна обозначает момент, а другая — мощность.

Вот и получается, что вопрос о том, что из этих показателей важнее — не совсем корректен. Во-первых, они взаимосвязаны. А, во-вторых, значение имеют не только сами эти показатели, но и обороты.

Крутящий момент в дизельных и бензиновых двигателях

Какой двигатель обладает большим крутящим моментом — бензиновый или дизельный? Как правило, у дизеля крутящий момент заметно выше, чем у аналогичного бензинового мотора. Причём на низких оборотах эта разница наиболее значительна. Дизель развивает хорошую тягу «сразу», чуть ли не с холостых оборотов. А бензиновый должен сперва раскрутиться.

Максимальное ускорение получается на тех оборотах, при которых момент достигает пиковых значений (Фото: Shutterstock)

С другой стороны, у дизельных двигателей в силу особенности конструкции меньше рабочий диапазон оборотов: когда при разгоне бензиновый двигатель продолжает раскручиваться, дизельный уже требует перехода на высшую передачу.

Значит ли это, что дизель со своим большим крутящим моментом подходит только ля грузовиков и внедорожников? Когда-то многие были в этом уверены. Однако современные дизельные двигатели отлично ведут себя на быстрых спортивных автомобилях.

• Топ-5 автоподстав. Видеопримеры и разбор от экспертов
• Антидождь для автомобиля — что это за средство и как оно работает
• Автомагистраль: что это и чем она отличается от других дорог
   

Объяснение урока: Момент силы относительно точки в 2D: скаляр

В этом объяснении мы узнаем, как найти сумму моментов группы сил, действующих на тело относительно точки в 2D.

Ненулевая результирующая сила, действующая на твердое тело, создает линейное ускорение тела в направлении, в котором действует результирующая сила, что приводит к смещению центра масс тела в этом направлении.

Сила, действующая на тело, может также приводить к угловому ускорению тела относительно точки, вызывая вращение тела. Величина углового ускорения тела от действия силы пропорциональна моменту силы относительно точки.

На следующем рисунке показан тонкий стержень, подвешенный вертикально в точке 𝑃. На стержень горизонтально действует сила ⃑𝐹. Момент силы действует так, что стержень поворачивается на 𝑃.

На следующем рисунке показано, что стержень вращается по часовой стрелке из-за момента ⃑𝐹 относительно 𝑃.

Предположим, что линия действия ⃑𝐹 меняется так, что линия проходит через 𝑃, как показано на следующем рисунке.

Стержень не вращается вокруг 𝑃 из-за момента ⃑𝐹. Чтобы ⃑𝐹 имел ненулевой момент относительно 𝑃, должно быть ненулевое расстояние между 𝑃 и линией действия ⃑𝐹.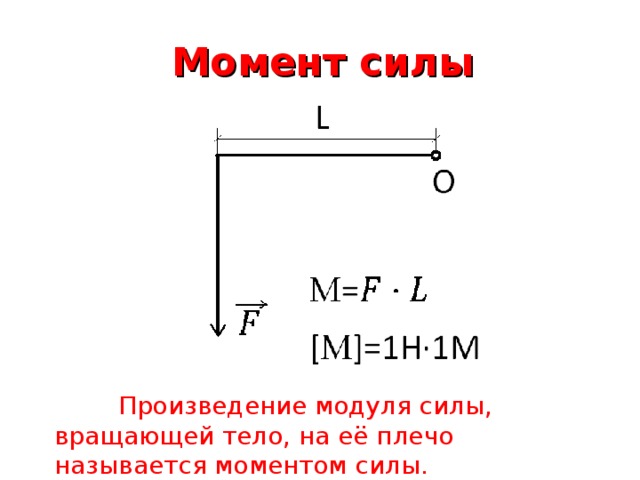

Когда линия, соединяющая точку 𝑃 и точку, в которой действует сила ⃑𝐹, и линия действия силы ⃑𝐹 перпендикулярны, модуль момента силы относительно точки 𝑃 является произведением модуля ⃑𝐹 и расстояние 𝑑 между точкой и линией действия силы. Это можно выразить как 𝑀=𝐹𝑑.

Используя ньютоны в качестве единицы силы и метры в качестве единицы расстояния, единицей момента силы является ньютон-метр (Н⋅м).

Единица ньютон-метр кажется той же единицей, что и работа, совершаемая силой, но расстояние в метрах имеет совсем другое значение для момента силы, чем для работы, совершаемой силой . Для работы, совершаемой силой, 𝑑 — это расстояние, на которое тело перемещается вдоль линии действия силы, действующей на тело для его перемещения. Для момента силы 𝑑 — это расстояние между линией действия силы и точкой, относительно которой создается момент.

Теперь рассмотрим пример расчета момента относительно точки.

Пример 1: Определение модуля момента силы относительно точки

Если сила величиной 498 Н находится на расстоянии 8 см от точки 𝐴, найдите норму момента силы относительно точки 𝐴, ответив в ньютон-метры.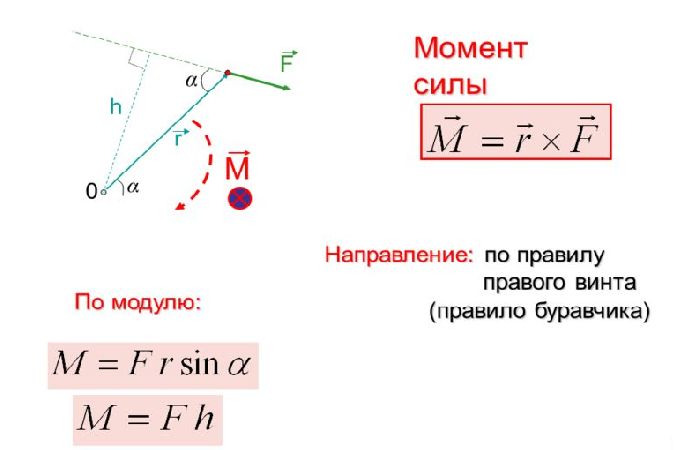

Ответ

Вопрос говорит нам, что существует сила величины 498 Н, действующая в точке на расстоянии 8 см от точки 𝐴. В вопросе не уточняется, что расстояние 8 см и линия действия силы перпендикулярны, но это можно предположить, если ничто не указывает на обратное. Вопрос задает норму силы, то есть ее величину.

Момент можно рассчитать по формуле 𝑀=𝐹𝑑.

Ответ должен быть дан в ньютон-метрах. Величина силы равна 498 Н.

Значение 𝑑 не равно 8, так как расстояние не 8 м, а 8 см. 8 см необходимо преобразовать в значение в метрах, поэтому 𝑑=0,08 м.

Значения силы теперь используются в формуле для решения: 𝑀=498×0,08=39,84⋅.Нм

Момент силы может вызвать вращение тела по часовой стрелке или против часовой стрелки, как показано на следующем рисунке.

Сила ⃑𝐹 создает момент по часовой стрелке 𝑀 относительно 𝑃, а сила ⃑𝐹 создает момент против часовой стрелки 𝑀 относительно 𝑃. Сумма 𝑀 и 𝑀 равна 𝑀net, где 𝑀=𝑀−𝑀,net, поскольку моменты против часовой стрелки считаются положительными.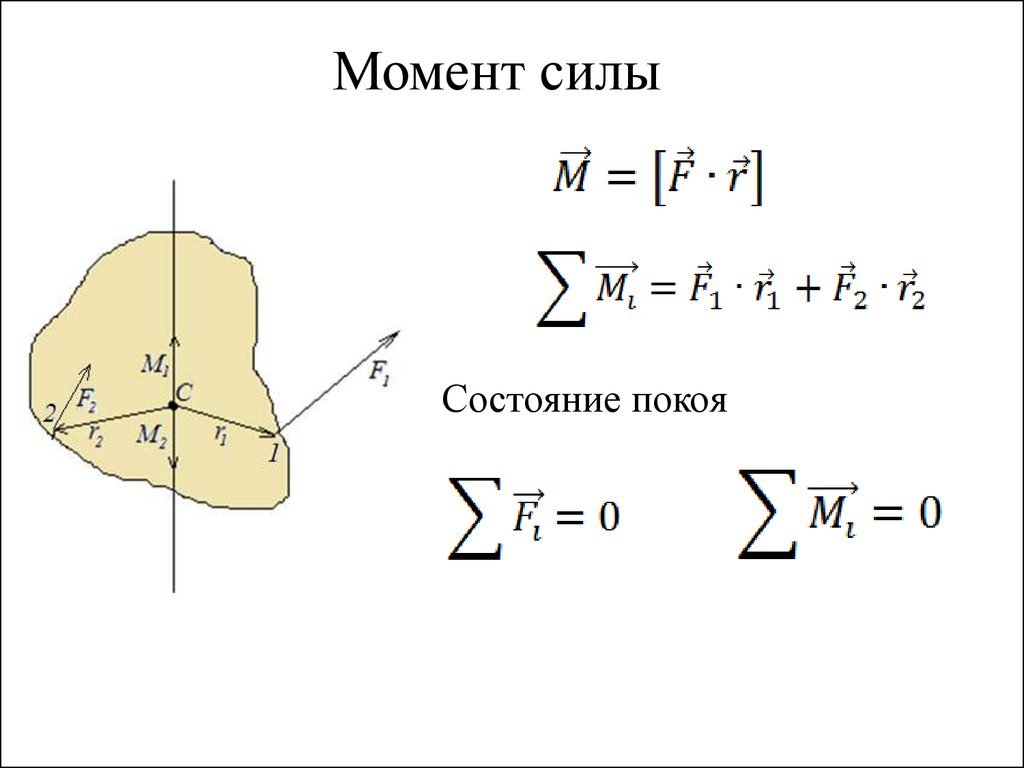

Теперь рассмотрим пример расчета момента относительно точки, в которой учитывается направление вращения, обусловленное моментом, и расстояние от точки, в которой момент приближается, до точки, на которую действует сила, равно прямо не дано.

Пример 2: Момент силы относительно точки в двух измерениях

Определите момент силы величины 11 Н относительно точки 𝑂, дав ответ в Н⋅м.

Ответ

Чтобы ответить на этот вопрос, мы должны предположить, что сила 11 Н является единственной силой, действующей на объект. Поскольку никакие другие значения не приводятся, это разумное предположение.

Вопрос кажется довольно сложным, поэтому полезно помнить, что для определения момента силы относительно 𝑂 требуются только два значения. Одним из требуемых значений является величина силы, которая составляет 11 Н. Другое требуемое значение — это расстояние от 𝑂 до линии действия силы. Это расстояние показано на следующем рисунке как 𝑑.

Момент, создаваемый силой, действующей на тело, эквивалентен силе, действующей в точке на расстоянии 𝑑 по горизонтали и на нулевом расстоянии по вертикали от 𝑂.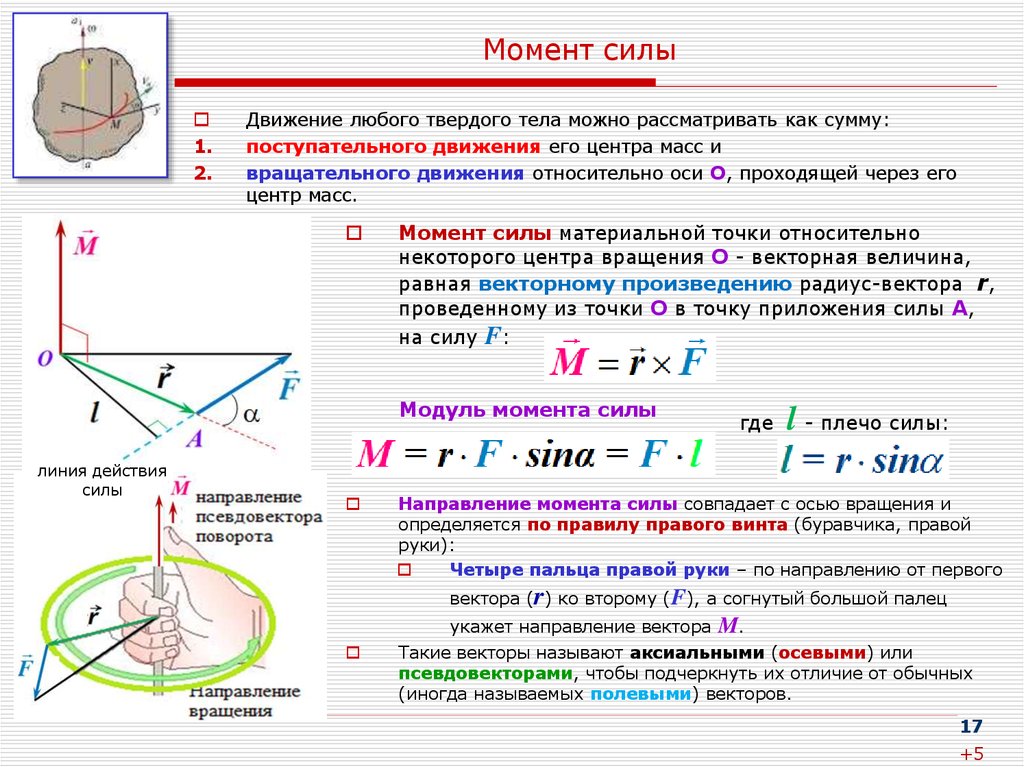 Сила может действовать на тело в любой точке тела вдоль линии действия силы, создавая такой же момент.

Можно определить 𝑑, построив прямоугольный треугольник с вертикальной стороной, соединяющей точку на теле, отстоящую на 36 см по горизонтали от 𝑂, с точкой, расположенной ниже по вертикали, которая пересекает прямую, перпендикулярную линии действия силы, проходит через точку, в которой действует сила, как показано на следующем рисунке.

Сторона треугольника, образованного противоположным углу 𝜃, равна 𝐷, и определение 𝐷 позволяет определить 𝑑 с помощью уравнения 𝑑=0,36−(0,26−𝐷).

Обратите внимание, что расстояния 36 см и 26 см были преобразованы в 0,36 м и 0,26 м соответственно, так что ответ можно дать в ньютон-метрах.

Значение 𝐷 можно найти, если известен угол 𝜃, так как 𝜃 — это угол прямоугольного треугольника напротив 𝐷, где гипотенуза 𝐷 имеет длину 29 см. 29 см также преобразуются в 0,29.м, чтобы ответ можно было дать в ньютон-метрах.

Для определения 𝐷 используется следующее уравнение: sin𝜃=𝐷0,29.

Поскольку угол 60∘, показанный на рисунке, является частью прямого угла, состоящего из угла 60∘ и угла 𝜃, отсюда следует, что 𝜃=(90−60)=30,∘∘∘

As sin(30 )=12∘, 12=𝐷0,29.

Создание 𝐷 субъектом дает 𝐷=0,292=0,145.

Ранее было установлено, что 𝑑=0,36−0,26+𝐷, поэтому 𝑑 находится из 𝑑=0,36−0,26+0,145=0,245 м

Поскольку 𝑀=𝐹𝑑,𝑀=11×0,245=2,695⋅.Нм

Однако это не полное решение, поскольку вращение из-за 𝑀 происходит либо по часовой стрелке, либо против часовой стрелки. На следующем рисунке показано, что сила должна перемещать объект вниз, что приводит к вращению тела по часовой стрелке.

Поскольку моменты по часовой стрелке считаются отрицательными, момент определяется выражением 𝑀=−2,695⋅.Нм

Теперь рассмотрим пример, в котором определяется чистый момент от действия нескольких сил.

Пример 3. Нахождение суммы моментов сил, действующих на стержень

𝐴𝐵 представляет собой стержень длиной 114 см и незначительным весом. На стержень действуют силы величиной 83 Н, 225 Н, 163 Н и 136 Н, как показано на следующем рисунке. 𝐶 и 𝐷 — точки трисекции 𝐴𝐵, а точка 𝑂 — середина стержня. Найдите алгебраическую сумму моментов этих сил относительно точки 𝑂.

Ответ

Длина стержня 114 см, а длины 𝐵𝐷, 𝐷𝐶 и 𝐶𝐴 равны 𝑑=1143=38 см

Длина 𝐵𝑂 определяется как 𝐵𝑂 см, что равно длине 𝐴𝑂.

Длина 𝐷𝑂 определяется как 𝐷𝑂=3812=19 см, что равно длине 𝐶𝑂.

Силы, действующие в точках 𝐴 и 𝐷, создают моменты против часовой стрелки относительно 𝑂, а силы, действующие в точках 𝐵 и 𝐶, создают моменты по часовой стрелке около 𝑂. Таким образом, чистый момент относительно 𝑂 определяется выражением 𝑀=(83×57)+(163×19)−(136×57)−(225×19)=−4199⋅.netNcm

Чтобы сила создавала момент, сила должна иметь ненулевую составляющую, действующую перпендикулярно к линии, соединяющей точку, вокруг которой создается момент, и точку, на которую действует сила. Рассмотрим следующий рисунок.

Если 𝜃 равно нулю, то силовая линия ⃑𝐹 должна проходить через 𝑃 и, таким образом, это даст нулевой момент относительно 𝑃. Если 𝜃=90∘, тогда ⃑𝐹 производит свой максимальный момент около 𝑃. Следовательно, расчет момента силы должен включать угол, под которым действует сила.

Определение

Момент силы относительно точки 𝑃 представляет собой расстояние 𝑑 от 𝑃 до точки, где действует сила, умноженное на составляющую силы, перпендикулярную направлению линии, пересекающей 𝑃, и точке, где действует сила действует. Это можно записать как 𝑀=𝐹𝑑𝜃,sin, где 𝐹 — величина силы, а 𝜃 — угол между направлением силы и направлением линии, пересекающей 𝑃, и точкой, в которой действует сила.

Теперь давайте теперь рассмотрим пример, где необходимо учитывать углы, под которыми действуют силы.

Пример 4. Нахождение величины суммы моментов трех сил, действующих вдоль равностороннего треугольника

Три силы, измеряемые в ньютонах, действуют вдоль сторон равностороннего треугольника 𝐴𝐵𝐶 как показано на рисунке. Учитывая, что длина стороны треугольника равна 7 см, определите алгебраическую сумму моментов сил относительно середины треугольника 𝐴𝐵, округленную до двух знаков после запятой.

Ответ

Вопрос касается моментов относительно середины 𝐴𝐵, которая показана как точка 𝑃 на следующем рисунке. Длина 𝐴𝐵 7 см. Поскольку 𝑃 находится в середине 𝐴𝐵, длинадлинасм𝐴𝑃=𝐵𝑃=3,5.

Линия действия силы 300 Н проходит вдоль 𝐴𝐵, поэтому она проходит через 𝑃, создавая нулевой момент относительно 𝑃, и ею можно пренебречь.

Поскольку треугольник 𝐴𝐵𝐶 равносторонний, все его внутренние углы равны 60∘. На следующем рисунке показаны ненулевые моменты относительно 𝑃.

Треугольник 𝑃𝐵𝐶 — прямоугольный треугольник с углом 60∘, для которых длина стороны, прилегающей к углу, равна 3,5 см и длина стороны, противоположной углу, равна 𝑃𝐶. У нас есть, следовательно, tan(60)=𝑃𝐶3,5; ∘ следовательно, 𝑃𝐶=3,5√3.cm

На следующем рисунке показаны величины действующих сил, углы, под которыми они действуют, и их расстояния от 𝑃.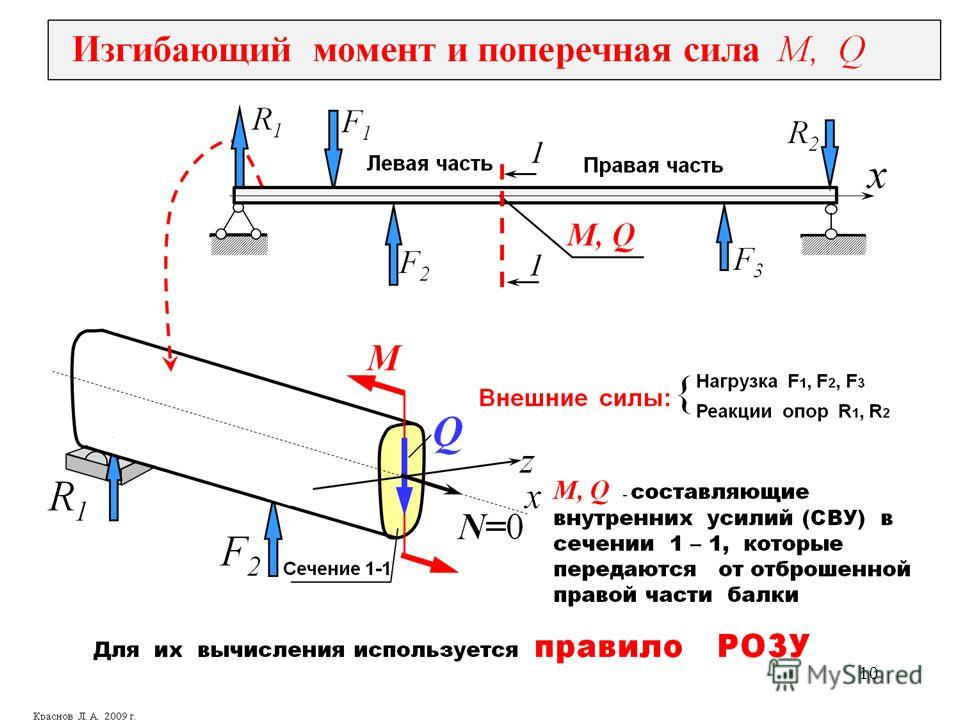

Сила 150 Н и сила 100 Н действуют по часовой стрелке, поэтому обе отрицательны.

Используя формулу 𝑀=𝐹𝑑𝜃, грех в момент около 𝑃 из-за Сила 150 Н определяется выражением 𝑀=−150×3.5√3(30)⋅𝑀=−525√32⋅.∘sinNcmNcm

Момент около 𝑃 из-за силы 100 Н определяется выражением 𝑀=−100×3.5(60)⋅,𝑀=−175√3⋅.∘sinNcmNcm

Сумма моментов относительно 𝑃 равна 𝑀net, которая является суммой 𝑀 и 𝑀. Вопрос запрашивает это значение до двух знаков после запятой: 𝑀=−525√32+175√3=−875√32=−757,77⋅.netNcm

Давайте теперь рассмотрим другой такой пример.

Пример 5. Нахождение точки на прямоугольнике по сумме моментов сил, действующих вокруг нее действующие вдоль 𝐵𝐴, 𝐵𝐶, 𝐶𝐷 и 𝐶𝐴 соответственно. Если точка 𝐸∈𝐵𝐶, где сумма моментов сил относительно 𝐸 равна 53 Н⋅см в направлении 𝐴𝐵𝐶𝐷, определить длину 𝐵𝐸.

Ответ

Силы, действующие на прямоугольник, и точки, в которых они действуют, показаны на следующем рисунке.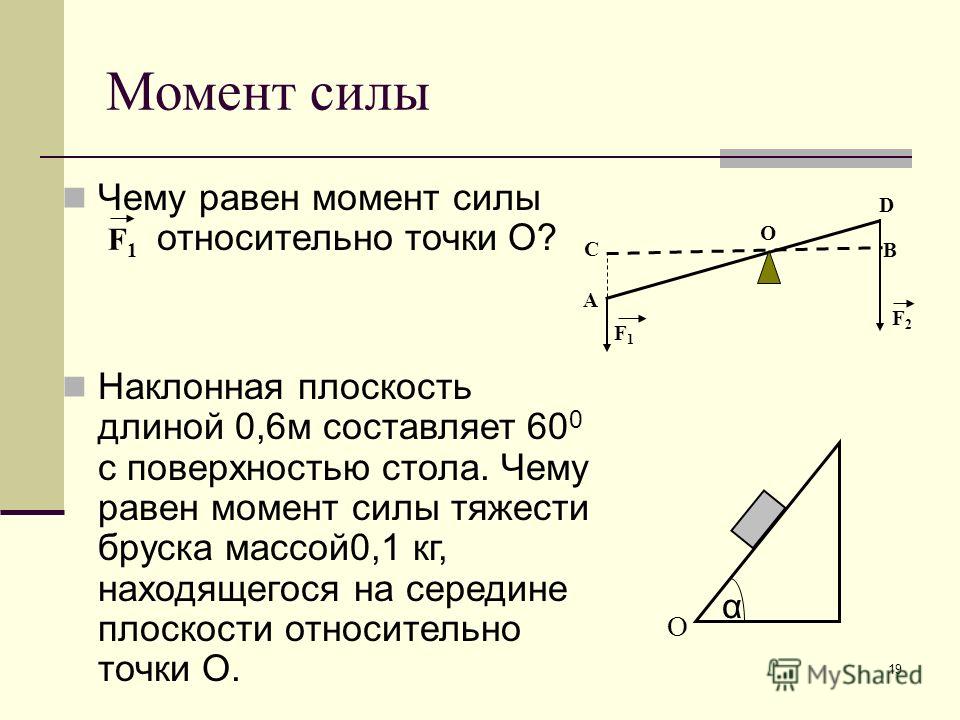

Силу в точке 𝐴, действующую вдоль 𝐶𝐴, можно разложить на перпендикулярные составляющие. Для решения этой силы необходимо знать угол от 𝐴𝐵 к линии действия силы, который показан как 𝜃 на следующем рисунке и равен углу, образуемому линией действия силы с 𝐶𝐷.

𝐴𝐷𝐶 — прямоугольный треугольник. Длина 𝐴𝐶 определяется как 𝐴𝐶=√8+6=√100=10.см

Таким образом, мы имеем, что sincos𝜃=810=45,𝜃=610=35.

Составляющая силы в 30 ньютонов вдоль 𝐷𝐴 равна 𝐹=3045=24,Н, а составляющая силы в 30 ньютонов вдоль 𝐵𝐴 равна 𝐹=3035=18.N

𝐹 и сила в 24 ньютона, действующая в 𝐴, действуют вдоль одной и той же линии, поэтому результирующая сила, действующая в 𝐴, равна 𝐹=24+18=42.N

На следующем рисунке показаны компоненты сил действующая перпендикулярно и параллельно 𝐵𝐶, которая пересекает точку 𝐸, о которой известен суммарный момент.

Момент около 𝐸, обусловленный каждым компонентом, представляет собой расстояние от линии действия компонента до 𝐸, перпендикулярное направлению компонента.

На следующем рисунке показаны величины и направления моментов относительно 𝐸 от каждой силы, а также суммарный момент относительно 𝐸.

Чистый момент относительно 𝐸 можно приравнять к сумме моментов относительно 𝐸 за счет компонентов: 144+64−8𝑦−42𝑦=53.

Мы можем изменить это выражение, чтобы сделать 𝑦 подлежащим следующим образом: −50𝑦=53−64−144=−155𝑦=−155−50=3,1 см

Подведем итог тому, что мы узнали из этих примеров.

Ключевые точки

• Момент силы ⃑𝐹 относительно точки 𝑃 представляет собой расстояние 𝑑 от 𝑃 до точки, где действует сила, умноженное на составляющую силы, перпендикулярную направлению линии, пересекающей 𝑃 и точку где действует сила. Это можно записать как 𝑀=𝐹𝑑𝜃,sin, где 𝐹 — величина силы, а 𝜃 — угол между направлением силы и направлением линии, пересекающей 𝑃, и точкой, в которой действует сила.
• Чистый момент, обусловленный набором моментов относительно точки, представляет собой сумму моментов относительно точки по часовой стрелке и против часовой стрелки, где моменты против часовой стрелки положительны.

Консольные балки — моменты и отклонения

Консольный луча — одиночная нагрузка на конце

Максимальная сила реакции

на фиксированном конце может быть выражена как:

R _A = F (1a)

R _A = F (1a)

0186

where

R _A = reaction force in A (N, lb)

F = single acting force in B (N, lb)

Maximum Moment

at the fixed Конец может быть выражен как

M _MAX = M _A

= — F L (1B)

, где

M

444443. фунт дюймов)

L = длина балки (м, мм, дюйм)

Максимальный прогиб

на конце консольной балки можно выразить как

δ _B = F L ^{3 (1C)}

, где

Δ _B = максимальный отклонение в B (M, MM, In)

E = Modulus (N/M ² (PA), N Modulus (N/M ^{2 9024 (PA), N Modulus (N/M 2 9024 (PA), N Modulus (N/M 2 9018 /мм 2 , фунт/дюйм 2 (psi))}

I = момент инерции (м ⁴ , мм ⁴ , дюйм ⁴ )

b = длина между B и

Стресс

Стресс в изгибающем луче может быть выражена как

σ = y m / i (1d)

, где

σ = стресс (N / M ²

σ = стресс (N / M ²

σ = стресс (N / M ²

) , Н/мм ² , psi)

y = расстояние до точки от нейтральной оси (м, мм, дюйм)

M = изгибающий момент (Нм, фунт·дюйм)

I = момент инерции (м ⁴ , мм 4 , in ⁴ )

Максимальный момент в консольной балке находится в фиксированной точке, и максимальное напряжение можно рассчитать путем объединения 1b и 1d по

σ 8 max 1 _max F L / I                (1e)

Пример — консольная балка с одинарной нагрузкой на конце, метрические единицы

Максимальный момент на закрепленном конце консольной балки UB 305 x 127 x 42 со стальными полками 5000 мм длинная, с моментом инерции 8196 см ⁴ (8196000000 мм ⁴ ) , Модуль эластичности 200 ГПа (200000 н/мм ² ).

M _MAX = (3000 N) (5000 мм)

= 1,5 10 ⁷ NMM

= 1,5 10 ⁴ NM

.

δ _B = (3000 N) (5000 mm) ³ / (3 (2 10 ⁵ N/mm ² ) (8.196 10 ⁷ mm ⁴ )) 

    = 7,6 мм

Высота балки 300 мм и расстояние от крайней точки до нейтральной оси 150 мм . Максимальное напряжение в луче может быть рассчитано как

σ _MAX = (150 мм) (3000 N) (5000 мм) / ( 8.196 10 ⁷ мм ⁴ )

⁴ )

9000 29103 29241. 40242 )

9000 29103 241.^{. =} )

⁴ )

40242 ). (N/mm ² )

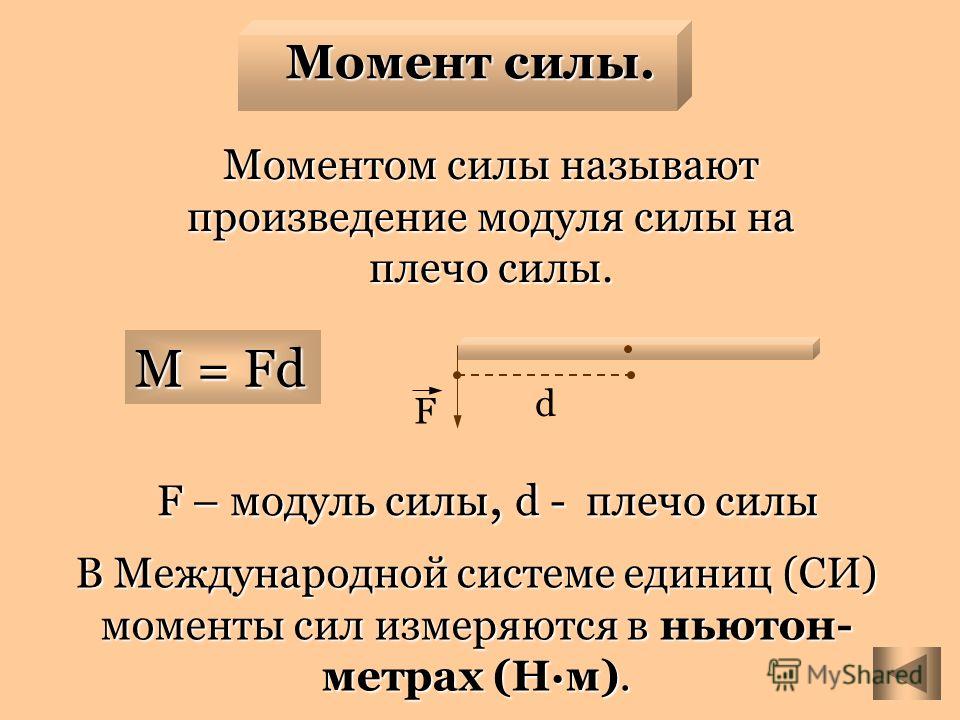
    = 27.4 10 ⁶ (N/m ² , Pa)

    = 27. 4 MPa

Максимальное напряжение намного ниже предела прочности при растяжении для большинства сталей.

Cantilever Beam — Single Load

Maximum Reaction Force

at the fixed end can be expressed as:

R _A = F                              (2a)

where

R _A = сила реакции в A (Н, фунт)

F = сила одностороннего действия в B (Н, фунт)

Максимальный момент

на фиксированной конце может быть выражена как

M _MAX = M _A

= — F A (2B)

, где

, где

, где

. A (Н·м, Н·мм, фунт·дюйм)

a = длина между A и B (м, мм, дюйм)

Максимальный прогиб

на конце консольной балки можно выразить как

дельта _C = (F A ³ / (3 E I)) (1 + 3 B / 2 A) (2C)

, где

Δ _C = максимальная отклонение в C (M, MM MM _C = максимальное отклонение в C (M, M, M, MM MM MM. , дюйм)

E = модуль упругости (Н/м ² (Па), Н/мм ² , фунт/дюйм ² (psi))

I = момент инерции ( м ⁴ , мм ⁴ , дюйм ⁴ )

b = длина между B и C (м, мм, дюйм)

Maximum Deflection

at the action of the single force can be expressed as

δ _B = F a ³ / (3 E I)                              (2d)

where

δ _B = максимальный прогиб в B (м, мм, дюйм)

Максимальное напряжение

Максимальное напряжение можно рассчитать, объединив 1d и 2b в

σ _max = y _max F a / I               (2e)   

Консольная балка — калькулятор одинарной нагрузки

Общий калькулятор — будьте последовательны и используйте метрические значения, основанные на м или миллиметрах, или британские значения, основанные на дюймах. Типичные значения по умолчанию указаны в метрических миллиметрах.

F — нагрузка (Н, фунты)

a — длина балки между A и B (м, мм, дюйм)

b — длина балки между B и C (м, мм, в)

I — Момент инерции (м ⁴ , mm ⁴ , in ⁴ )

E — Modulus of Elasticity (N/m ² , N/mm ² , psi)

y — Distance from neutral axis (m, mm, in)

Cantilever Beam — Uniform Distributed Load

Maximum Reaction

at the fixed end can be expressed as:

R _A = q L                                (3a)

где

R _A = сила реакции в А (Н, фунт)

q = равномерная распределенная нагрузка (Н/м, Н/мм, фунт/дюйм) Консольный луч (M, MM, In)

Максимальный момент

на фиксированном конце может быть выражен как

M _A = — Q L ² /2 (3B)

41 2

/2 (3b)

817881788178817881788178817881788178817881788.

в конце можно выразить как

Δ _B = Q L ⁴ / (8 E I) (3C)

, где

Δ _B = максимум дефекция в B (MM, MM, MM, в MM, in) _B = Maximum Defluction In B (MM, MM, MM, в MM, в MM, в) _B = Maximum Defluction In B (MM, MM, MM, в MM, в MM, в MM, в) _B = MAXILILE в B (MM, MM, MM, MM, в MM, в MM, в MM, в) _B = Maximum Defluction. Балка — Калькулятор равномерной нагрузки

Универсальный калькулятор — используйте метрические значения, основанные на м или миллиметрах, или британские значения, основанные на дюймах. Типичные значения по умолчанию указаны в метрических миллиметрах.

q — Равномерная нагрузка (Н/м, Н/мм, фунт/дюйм)

L — Длина балки (м, мм, дюйм)

I — Момент инерции (м ⁴ , мм ⁴ , дюйм ⁴ )

3 9 Модуль упругости 30

9 Па, Н/мм ² , psi)

y — Расстояние от нейтральной оси (м, мм, дюйм)

Более чем одноточечная нагрузка и/или равномерная нагрузка, действующая на консольную балку

Если на консольную балку действует более одной точечной нагрузки и/или равномерной нагрузки — результирующий максимальный момент на закрепленном конце А и результирующий максимальный прогиб на конце В можно рассчитать путем суммирования максимального момента в А и максимального прогиба в В для каждую точку и/или равномерную нагрузку.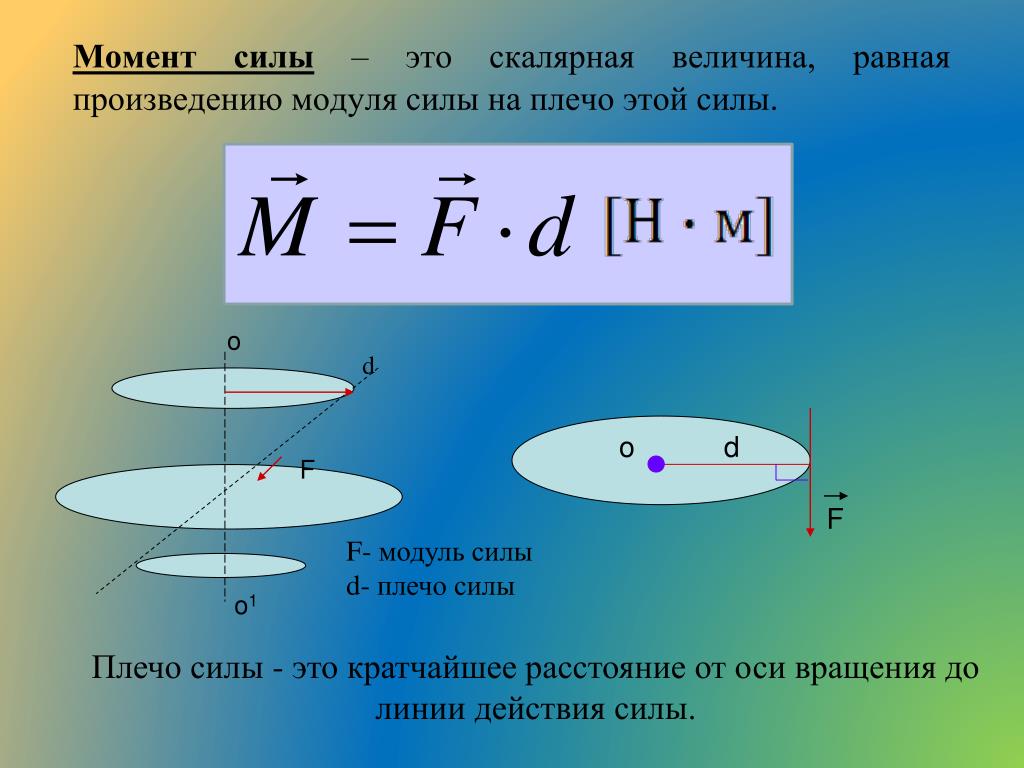

Cantilever Beam — Declining Distributed Load

Maximum Reaction Force

at the fixed end can be expressed as:

R _A = q L / 2                              (4a)

where

R _A = сила реакции в A (Н, фунт)

q = падающая распределенная нагрузка — максимальное значение в A — ноль в B (Н/м, фунт/фут)

Максимальный момент

в фиксированный конец может быть выражен как

M _MAX = M _A

= — Q L ² /6 (4B)

, где

, где

.

L = длина балки (м, мм, дюйм)

Максимальный прогиб

на конце консольной балки можно выразить как

δ _B = L ⁴ / (30 E I)                                    (4c)

где

δ _B = максимальный прогиб в B (м, мм, дюйм)

E = модуль упругости (Н/м ^{2 Па), 2 Н/мм 9 (Па)} , фунт/дюйм ² (psi))

I = момент инерции (м ⁴ , мм ⁴ , дюйм ⁴ )

90 Расширение Sketchup

Сила 120 Н приложена, как показано, к одному концу класса 11 физики CBSE

Подсказка: Используйте уравнение для момента силы в терминах силы и перпендикулярного расстояния между точкой действия силы и точкой, относительно которой должен быть определен момент силы. Используйте горизонтальную и вертикальную составляющие силы для расчета конечного момента силы. Воспользуйтесь условием максимального момента силы и снова определите требуемый угол и момент силы.

Используемая формула:
Момент силы равен 9{ — 1}}\left( {\dfrac{{{\tau _y}}}{{{\tau _x}}}} \right)\] …… (2)
Здесь, \[{\tau _x} \] и \[{\tau _y}\] — горизонтальная и вертикальная составляющие момента силы.

Полный пошаговый ответ:
Приведенная диаграмма в терминах составляющих силы выглядит следующим образом:

В задаче дано, что сила \[F = 120\,{\text{N} }\] действует на один конец ключа. Мы видим, что на рисунке сила имеет две составляющие \[F\sin \alpha \] и \[F\cos \alpha \] в горизонтальном и вертикальном направлениях соответственно. Вычислим перпендикулярное расстояние \[{r_h}\] между горизонтальной силой \[F\sin \alpha \] и точкой O.
\[{r_h} = \left( {25\,{\text{мм}}} \right) + \left( {70\,{\text{мм}}} \right) + \left( {70 \,{\text{мм}}} \right) + \left( {25\,{\text{мм}}} \right)\]
\[ \Rightarrow {r_h} = 190\,{\text{ мм}}\]
Расстояние по перпендикуляру между горизонтальной силой \[F\sin \alpha \] и точкой O равно \[190\,{\text{мм}}\].