5.1. Когда была изобретена позиционная система счисления?. Великая смута. Конец Империи
5.1. Когда была изобретена позиционная система счисления?
Сегодня считается, что позиционная система записи чисел была изобретена в Индии «очень давно» [821], с. 88. И затем заимствована арабами, которые наконец-то и принесли ее в средневековую Европу. Именно в Европе «арабские цифры» послужили толчком к быстрому развитию математики и вычислений во второй половине XVI — начале XVII века. В 1585 году были уже изобретены десятичные дроби [821], с. 119. Историк математики Д.Л. Стройк пишет: «Это было одним из больших усовершенствований, которые стали возможными благодаря всеобщему принятию индийско-арабской системы счисления. Другим большим усовершенствованием вычислительной техники было изобретение логарифмов» [821], с. 120. Напомним, что логарифмы были изобретены в первой половине XVII века [821], с. 120–121.
Подчеркнем, что как десятичные дроби, так и логарифмы могли появиться лишь ПОСЛЕ ВВЕДЕНИЯ ПОЗИЦИОННОЙ ДЕСЯТИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ.

Чуть более сложным, но тоже не представляющим из себя принципиальных затруднений является изобретение ДЕСЯТИЧНЫХ ЛОГАРИФМОВ — опять-таки на основе десятичной позиционной системы счисления. Дело в том, что целая часть десятичного логарифма это ДЛИНА ЗАПИСИ ЧИСЛА в позиционной десятичной системе, уменьшенная на единицу. Не трудно заметить — и это, скорее всего, было достаточно быстро сделано, — что при умножении двух натуральных чисел длины их записей, в общем-то, складываются (с точностью до единицы, которую иногда приходится вычитать). Последнее связано с тем, что при умножении чисел их логарифмы складываются, следовательно, целые части логарифмов тоже складываются с точностью до единицы. Лишняя единица возникает тогда, когда сумма дробных частей складываемых логарифмов больше или равна единице. Естественная задача для средневекового математика — уточнить характеристику, задаваемую длиной числа, таким образом, чтобы при перемножении чисел эти характеристики В ТОЧНОСТИ СКЛАДЫВАЛИСЬ.
Следовательно, от появления идеи позиционного десятичного счисления до создания десятичных дробей и логарифмов не могло пройти очень много времени. А поскольку логарифмы были созданы лишь в начале XVII века, то можно уверенно предположить, что распространение позиционной десятичной системы счисления началось НЕ РАНЕЕ СЕРЕДИНЫ XVI ВЕКА Н. Э. Причем на первых порах — среди математиков и вычислителей, то есть представителей сравнительно узкого круга ученых. И лишь затем эта идея проникла в общество, и ею стали пользоваться издатели, художники, школьные учителя и т. п.
И лишь затем эта идея проникла в общество, и ею стали пользоваться издатели, художники, школьные учителя и т. п.
Но сегодня нас хотят убедить, что в западноевропейском обществе такие далекие от математики люди, как, например, художники, свободно пользовались позиционной десятичной системой счисления уже в XV веке и даже в более ранние эпохи. Не говоря уж об индусах, которые якобы пользовались этой системой аж в 500 году до н. э. (!) [755], с. 20. Правда, как потом рассказывает нам та же скалигеровская история науки, «древние» индусы почему-то «забыли» об этих своих выдающихся математических открытиях. Но, по счастью, успели рассказать о них арабам. Которые и донесли этот светоч «древнейших знаний» до необразованной Европы. Произошло это в Средние века. Индия в это время (как, впрочем, и Европа) была погружена в мрачную эпоху средневекового невежества. По крайней мере, математического. Во всяком случае, как нам говорят сегодня, «относительно математики в Китае и в Индии мы располагаем очень ограниченным запасом сведений.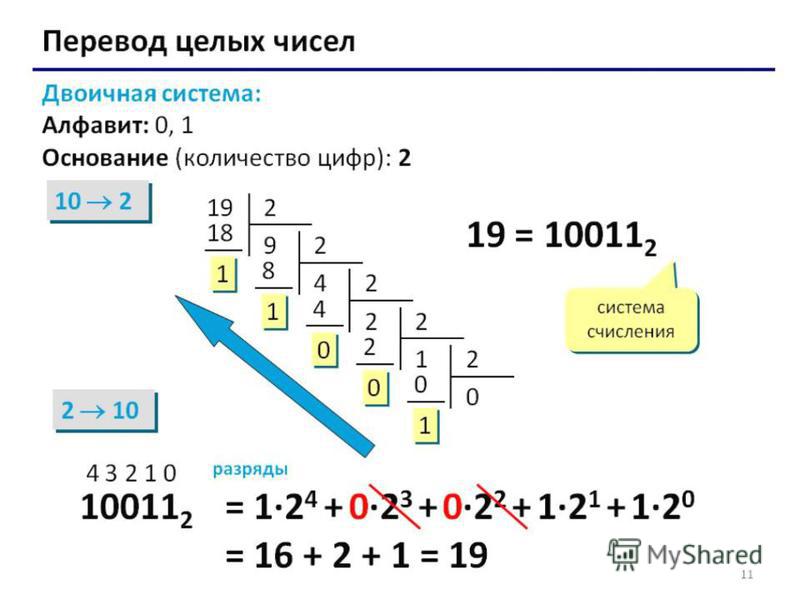
По нашему мнению, нарисованная историками картина неестественна и даже нелепа. Определить примерную дату изобретения позиционной десятичной системы счисления можно по бурному развитию и внедрению этой идеи, которое началось лишь в конце XVI века [821]. Следовательно, сама идея возникла где-то в середине XVI века, а не в глубокой древности. Нельзя отделять идею от ее прямых и ОЧЕВИДНЫХ следствий СОТНЯМИ и даже ТЫСЯЧАМИ лет. Поэтому все те «древне»-вавилонские, «древне»-индийские, «древне»-арабские и вообще «очень-очень древние» тексты, в которых использована идея позиционного десятичного счисления, не могли появиться ранее XVI века.
Это в полной мере относится и к якобы «древнейшей» КЛИНОПИСИ Двуречья. Сегодня нам говорят, будто «древние шумеры» еще в ТРЕТЬЕМ ТЫСЯЧЕЛЕТИИ ДО Н. Э. широко пользовались позиционной системой [821], с. 40. А якобы за ДВЕ ТЫСЯЧИ ЛЕТ ДО Н. Э. они уже свободно решают линейные и квадратные уравнения с двумя неизвестными. Д.Л. Стройк сообщает: «Вавилоняне времен Хаммурапи ПОЛНОСТЬЮ владели техникой решения квадратных уравнений. Они решали линейные и квадратные уравнения с двумя неизвестными, решали даже задачи, сводящиеся к кубическим и биквадратным уравнениям» [821], с. 42. А В ПЕРВОМ ТЫСЯЧЕЛЕТИИ ДО Н. Э. «древние шумеры» производят вычисления «которые доведены до СЕМНАДЦАТОГО шестидесятичного знака. СТОЛЬ СЛОЖНЫЕ ВЫЧИСЛИТЕЛЬНЫЕ работ уже нельзя связывать с вычислением налогов или измерением, — стимулом для них были астрономические задачи» [821], с. 44.
Д.Л. Стройк сообщает: «Вавилоняне времен Хаммурапи ПОЛНОСТЬЮ владели техникой решения квадратных уравнений. Они решали линейные и квадратные уравнения с двумя неизвестными, решали даже задачи, сводящиеся к кубическим и биквадратным уравнениям» [821], с. 42. А В ПЕРВОМ ТЫСЯЧЕЛЕТИИ ДО Н. Э. «древние шумеры» производят вычисления «которые доведены до СЕМНАДЦАТОГО шестидесятичного знака. СТОЛЬ СЛОЖНЫЕ ВЫЧИСЛИТЕЛЬНЫЕ работ уже нельзя связывать с вычислением налогов или измерением, — стимулом для них были астрономические задачи» [821], с. 44.
По нашему мнению, все эти «древне»-шумерские математические высоты были достигнуты лишь в XVI–XVII или даже в ВОСЕМНАДЦАТОМ веках НАШЕЙ ЭРЫ. А отнюдь не до нашей эры, как полагают историки, основываясь на ошибочной хронологии Скалигера. Недаром даже Джон Непер, изобретатель логарифмов, «избегал операций с дробями» [755], с. 130. Хотя историки математики считают, что он производил действия с дробями «легко», тем не менее, сам факт избегания дробей весьма красноречив.
Данный текст является ознакомительным фрагментом.
ГЛАВА 10 КОГДА БЫЛА СОЗДАНА АНТИГИТЛЕРОВСКАЯ КОАЛИЦИЯ?
 И.Сталин. Сочинения. Т. 7. С. 287.
1Я знаю ваше возражение. Что там Британия, скажете, главная поддержка вовсе
И.Сталин. Сочинения. Т. 7. С. 287.
1Я знаю ваше возражение. Что там Британия, скажете, главная поддержка вовсе11.14. Когда и как была создана китайская история
11.14. Когда и как была создана китайская история Как, кем и когда была написана «древняя китайская история»? Оказывается, что в XVII–XVIII веках, при манжурах, в Китае происходила какая-то исключительно бурная деятельность ПО НАПИСАНИЮ КИТАЙСКОЙ ИСТОРИИ [151]. Она сопровождалась
5.1. Когда изобрели позиционную систему счисления
5.1. Когда изобрели позиционную систему счисления Сегодня считается, что позиционная система записи чисел изобретена в Индии «очень давно» [821], с. 88. И затем была заимствована арабами, которые, наконец-то, и принесли ее в средневековую Европу. Именно в Европе «арабские
Когда была катастрофа?
Когда была катастрофа?
Воспоминания об отдаленном потопе и о сопровождавших его гибельных землетрясениях поддерживались последующими катастрофами местного порядка. Так, около 1450 года до н. э. произошел прорыв вод Атлантического океана в Средиземное море, уровень
Так, около 1450 года до н. э. произошел прорыв вод Атлантического океана в Средиземное море, уровень
Когда была установлена Пасхалия
Когда была установлена Пасхалия Приведем резюме исследования Г.В. Носовского [6 тЗ], гл. 2. Речь идет о двух важнейших вехах исторической хронологии – датировках Рождества Христова и Первого Вселенского собора в Никее, часто называемого Никейским собором. На этих датах в
XXIV. День, когда была уничтожена империя
XXIV. День, когда была уничтожена империя Атауальпе, тринадцатому Инке, правителю десятимиллионной империи, под началом которого находится четвертьмиллионная армия, противостоят 177 авантюристов, прибывших из Европы. В ходе предыдущих экспедиций эти люди пытались найти
Когда Албания была Кавказской
Когда Албания была Кавказской Порой мне кажется, из недосказанности соткан мир… Прочитав иные монографии, видишь, будто он такой же, как платье голого короля, что нахваливали в сказке Андерсена прожженные мошенники… Почему нет? Иные исторические события абсолютно
Когда книга была уже написана… (Необходимое послесловие)
Когда книга была уже написана…
(Необходимое послесловие)
Действительно, жарким летом 2007 года, когда работа над данным текстом была, в целом, завершена, к автору пришла еще одна, только что опубликованная книга, вплотную примыкающая к рассматривавшимся выше проблемам. Как
Как
• 2. Медный век – время, когда Империя была еще в Египте
• 2. Медный век – время, когда Империя была еще в Египте Историки не могут прийти к однозначному мнению, где и когда человек впервые открыл медь. «Где произошло впервые применение меди для изготовления из нее орудий и других изделий, а равно изобретение бронзы – трудно
• 4. Когда была изобретена бронза?
• 4. Когда была изобретена бронза? Сегодня считается, что бронза (сплав меди с оловом) была известна с древнейших времен. А медный век историки часто называют «бронзовым веком». Если верить скалигеровским датировкам, то в «античности» якобы было изготовлено огромное
Когда Албания была кавказской
Когда Албания была кавказской Порой мне кажется, из недосказанности соткан мир… Прочитав иные монографии, видишь, будто он такой же, как платье голого короля, что нахваливали в сказке Андерсена прожженные мошенники… Почему нет? Иные исторические события абсолютно
5.
 1. Когда изобрели позиционную систему счисления
1. Когда изобрели позиционную систему счисления5.1. Когда изобрели позиционную систему счисления
Сегодня считается, что позиционная система записи чисел изобретена в Индии «очень давно» [821], с. 88. И затем была заимствована арабами, которые, наконец-то, и принесли ее в средневековую Европу. Именно в Европе «арабские цифры» послужили толчком к быстрому развитию математики и вычислений во второй половине XVI — начале XVII века. В частности, в 1585 году изобрели десятичные дроби [821], с. 119. Историк математики Д.Я. Стройк пишет: «Это было одним из больших усовершенствований, которые стали возможными благодаря всеобщему принятию индийско-арабской системы счисления. Другим большим усовершенствованием вычислительной техники было изобретение логарифмов» [821], с. 120. Логарифмы были изобретены в первой половине XVII века [821], с. 120–121.
Подчеркнем, что как десятичные дроби, так и логарифмы, могли появиться лишь ПОСЛЕ ВВЕДЕНИЯ ПОЗИЦИОННОЙ ДЕСЯТИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ. Причем, после появления этой системы, изобретение дробей и логарифмов не заключало в себе принципиальной сложности. В самом деле, рассмотрим вопрос о возникновении десятичных дробей. Если мы имеем позиционную систему счисления, то перемещение какой-то цифры на разряд вверх, «повышает ее вес», — то есть вклад этой цифры в значение результирующего числа, — в десять раз. В области целых чисел самым младшим разрядом является разряд единиц. Естественная мысль состоит в том, чтобы продолжить разряды «вниз», то есть «под разряд единиц». По тому же правилу: перемещение цифры на разряд вниз уменьшает «ее вес», то есть вклад в результирующее число, в десять раз. Чтобы это сделать, нужно только придумать разделитель целых и дробных разрядов. То есть десятичную запятую. Например, в записи числа 16,234 запятая отделяет два целых разряда от трех дробных. Вряд ли для такого изобретения потребовались СОТНИ лет, как на том настаивает скалигеровская история науки. Скорее всего, это сделали довольно быстро, всего лишь через десятки лет, сразу после изобретения нуля и позиционной системы счисления.
Причем, после появления этой системы, изобретение дробей и логарифмов не заключало в себе принципиальной сложности. В самом деле, рассмотрим вопрос о возникновении десятичных дробей. Если мы имеем позиционную систему счисления, то перемещение какой-то цифры на разряд вверх, «повышает ее вес», — то есть вклад этой цифры в значение результирующего числа, — в десять раз. В области целых чисел самым младшим разрядом является разряд единиц. Естественная мысль состоит в том, чтобы продолжить разряды «вниз», то есть «под разряд единиц». По тому же правилу: перемещение цифры на разряд вниз уменьшает «ее вес», то есть вклад в результирующее число, в десять раз. Чтобы это сделать, нужно только придумать разделитель целых и дробных разрядов. То есть десятичную запятую. Например, в записи числа 16,234 запятая отделяет два целых разряда от трех дробных. Вряд ли для такого изобретения потребовались СОТНИ лет, как на том настаивает скалигеровская история науки. Скорее всего, это сделали довольно быстро, всего лишь через десятки лет, сразу после изобретения нуля и позиционной системы счисления.
Чуть более сложным, но тоже не представляющим из себя принципиальных затруднений, является изобретение ДЕСЯТИЧНЫХ ЛОГАРИФМОВ на основе десятичной позиционной системы счисления. Дело в том, что целая часть десятичного логарифма — это, попросту, ДЛИНА ЗАПИСИ ЧИСЛА в позиционной десятичной системе, уменьшенная на единицу. Нетрудно заметить, — что, скорее всего, и было быстро сделано, — следующее простое обстоятельство. При умножении двух чисел длины их записи, в общем-то, складываются. Иногда приходится вычитать единицу. Это связано с тем, что при умножении двух чисел их логарифмы складываются. Следовательно, целые части логарифмов тоже складываются. Но иногда возникает лишняя единица, в том случае, когда сумма дробных частей логарифмов перемножаемых чисел больше или равна единице. Естественная задача для средневекового математика — уточнить характеристику, задаваемую длиной числа, таким образом, чтобы при перемножении чисел эти характеристики СКЛАДЫВАЛИСЬ. Правильное понимание идеи мгновенно приводит к понятию логарифма. Именно эту задачу и пытался решить Джон Непер при создании логарифмов в начале XVII века. Известно, что именно он придумал логарифмы. Сначала в несколько неуклюжей форме, но затем идея была мгновенно доведена до ее практически современного состояния [821], с. 121. Д.Я. Стройк сообщает, что полная таблица десятичных логарифмов целых чисел от единицы до ста тысяч была опубликована в 1627 году [821], с. 121. То есть всего лишь через 13 лет после первой работы Джона Непера на эту тему [821], с. 120–121.
Именно эту задачу и пытался решить Джон Непер при создании логарифмов в начале XVII века. Известно, что именно он придумал логарифмы. Сначала в несколько неуклюжей форме, но затем идея была мгновенно доведена до ее практически современного состояния [821], с. 121. Д.Я. Стройк сообщает, что полная таблица десятичных логарифмов целых чисел от единицы до ста тысяч была опубликована в 1627 году [821], с. 121. То есть всего лишь через 13 лет после первой работы Джона Непера на эту тему [821], с. 120–121.
Следовательно, от появления идеи позиционного десятичного счисления до создания десятичных дробей и логарифмов не могло пройти очень много времени. А поскольку логарифмы созданы лишь в начале XVII века, то можно уверенно предположить, что распространение позиционной десятичной системы счисления началось НЕ РАНЕЕ СЕРЕДИНЫ XVI ВЕКА. Причем на первых порах среди математиков и вычислителей, то есть представителей сравнительно узких специальностей. И лишь затем эта идея проникла в общество, и ею стали пользоваться издатели, художники, преподаватели в школах и т. д.
д.
Нас же сегодня хотят убедить, что в западно-европейском обществе неспециалисты, например художники, свободно пользовались позиционной десятичной системой счисления в XV веке и даже в более ранние эпохи. Не говоря уж об индусах, которые якобы пользовались этой системой аж в 500 году до н. э. [755], с. 20. Правда, как потом рассказывает нам та же скалигеровская история науки, «древние» индусы почему-то «забыли» об этих своих выдающихся математических открытиях. Нам говорят, что они, правда, успели рассказать о них арабам. Которые и донесли этот светоч «древнейших знаний» до необразованной Европы где-то в средние века. Индия же в это время, как, впрочем, и вся Европа, погрузилась в мрачную эпоху средневекового невежества. По крайней мере, математического. Во всяком случае, как нам говорят сегодня, «относительно математики в Китае и в Индии мы располагаем очень ограниченным запасом сведений. Либо исчезли, либо еще не найдены многие материальные свидетельства» [755], с. 45.
По нашему мнению, рисуемая нам картина совершенно неестественна и неверна. Мы легко можем увидеть примерную дату изобретения позиционной десятичной системы счисления по бурному развитию и внедрению этой идеи, которое началось лишь в конце XVI века [821]. Следовательно, сама идея возникла где-то в середине XVI века. Не ранее. НЕЛЬЗЯ ОТДЕЛЯТЬ ИДЕЮ И ЕЕ ПРЯМЫЕ ОЧЕВИДНЫЕ СЛЕДСТВИЯ СОТНЯМИ И ДАЖЕ ТЫСЯЧАМИ ЛЕТ, как это делает скалигеровская история. Поэтому все те «древне»-вавилонские, «древне»-индийские, «древне»-арабские и вообще все «очень-очень древние» тексты, использующие идею позиционного десятичного счисления, не могли появиться ранее XVI века. Это замечание в полной мере относится и к знаменитой «древнейшей» клинописи Двуречья. Сегодня нас уверяют, будто «древние шумеры» еще в ТРЕТЬЕМ ТЫСЯЧЕЛЕТИИ ДО Н.Э. широко использовались позиционной системой [821], с. 40. А якобы за ДВЕ ТЫСЯЧИ ЛЕТ ДО Н.Э. они уже свободно решали линейные и квадратные уравнения с двумя неизвестными. Д.Я. Стройк сообщает: «Вавилоняне времен Хаммурапи ПОЛНОСТЬЮ владели техникой решения квадратных уравнений.
Мы легко можем увидеть примерную дату изобретения позиционной десятичной системы счисления по бурному развитию и внедрению этой идеи, которое началось лишь в конце XVI века [821]. Следовательно, сама идея возникла где-то в середине XVI века. Не ранее. НЕЛЬЗЯ ОТДЕЛЯТЬ ИДЕЮ И ЕЕ ПРЯМЫЕ ОЧЕВИДНЫЕ СЛЕДСТВИЯ СОТНЯМИ И ДАЖЕ ТЫСЯЧАМИ ЛЕТ, как это делает скалигеровская история. Поэтому все те «древне»-вавилонские, «древне»-индийские, «древне»-арабские и вообще все «очень-очень древние» тексты, использующие идею позиционного десятичного счисления, не могли появиться ранее XVI века. Это замечание в полной мере относится и к знаменитой «древнейшей» клинописи Двуречья. Сегодня нас уверяют, будто «древние шумеры» еще в ТРЕТЬЕМ ТЫСЯЧЕЛЕТИИ ДО Н.Э. широко использовались позиционной системой [821], с. 40. А якобы за ДВЕ ТЫСЯЧИ ЛЕТ ДО Н.Э. они уже свободно решали линейные и квадратные уравнения с двумя неизвестными. Д.Я. Стройк сообщает: «Вавилоняне времен Хаммурапи ПОЛНОСТЬЮ владели техникой решения квадратных уравнений. Они решали линейные и квадратные уравнения с двумя неизвестными, решали даже задачи, сводящиеся к кубическим и биквадратным уравнениям» [821], с. 42. А В ПЕРВОМ ТЫСЯЧЕЛЕТИИ ДО Н.Э. «древние шумеры» производят вычисления, «которые доведены до СЕМНАДЦАТОГО шестидесятичного знака. СТОЛЬ СЛОЖНЫЕ ВЫЧИСЛИТЕЛЬНЫЕ работы уже нельзя связывать с вычислением налогов или измерением, — стимулом для них были астрономические задачи» [821], с. 44.
Они решали линейные и квадратные уравнения с двумя неизвестными, решали даже задачи, сводящиеся к кубическим и биквадратным уравнениям» [821], с. 42. А В ПЕРВОМ ТЫСЯЧЕЛЕТИИ ДО Н.Э. «древние шумеры» производят вычисления, «которые доведены до СЕМНАДЦАТОГО шестидесятичного знака. СТОЛЬ СЛОЖНЫЕ ВЫЧИСЛИТЕЛЬНЫЕ работы уже нельзя связывать с вычислением налогов или измерением, — стимулом для них были астрономические задачи» [821], с. 44.
По нашему мнению, все эти «древне»-шумерские математические высоты достигнуты лишь в XVI–XVII или даже в XVIII веках нашей эры. А отнюдь не до нашей эры. Недаром даже Джон Непер, изобретатель логарифмов, «избегал операций с дробями» [755], с. 130. Хотя историки математики добавляют, что он это делал «легко», тем не менее, сам факт избегания дробей весьма красноречив. И неудивителен. Поскольку, как мы видели, десятичные дроби изобретены лишь в 1585 году, когда Джону Неперу (1550–1617) было уже 35 лет [821], с. 121. А до этого, операции с дробями (не десятичными) были громоздки и неудобны. Математики, бухгалтеры, счетоводы, астрономы XVI–XVIII веков нашей эры, жившие на территории Междуречья, по-видимому, еще не имели в достаточном количестве бумаги. Поэтому были вынуждены записывать свои вычисления на неудобных глиняных табличках. Которые быстро вышли из употребления в XVIII–XIX веках, когда здесь, наконец-то, появилась бумага в достаточном количестве. Затем, лет через сто, эти таблички обнаружили западно-европейские археологи и тут же с восторгом объявили «древнейшим свидетельством могущества шумерской науки». Расцветшей якобы в III тысячелетии до н. э. Местные жители не возражали. Приятно оказаться потомками «невероятно древней» цивилизации.
Математики, бухгалтеры, счетоводы, астрономы XVI–XVIII веков нашей эры, жившие на территории Междуречья, по-видимому, еще не имели в достаточном количестве бумаги. Поэтому были вынуждены записывать свои вычисления на неудобных глиняных табличках. Которые быстро вышли из употребления в XVIII–XIX веках, когда здесь, наконец-то, появилась бумага в достаточном количестве. Затем, лет через сто, эти таблички обнаружили западно-европейские археологи и тут же с восторгом объявили «древнейшим свидетельством могущества шумерской науки». Расцветшей якобы в III тысячелетии до н. э. Местные жители не возражали. Приятно оказаться потомками «невероятно древней» цивилизации.
Данный текст является ознакомительным фрагментом.
5. Когда китайцы изобрели подзорную трубу
5. Когда китайцы изобрели подзорную трубу
Все мы думаем, что подзорная труба была изобретена Галилеем, или его непосредственными предшественниками, в XVII веке. Он додумался до революционной идеи – использовать оптические линзы для разглядывания удаленных объектов, в том
Он додумался до революционной идеи – использовать оптические линзы для разглядывания удаленных объектов, в том
5.1. Когда была изобретена позиционная система счисления?
5.1. Когда была изобретена позиционная система счисления? Сегодня считается, что позиционная система записи чисел была изобретена в Индии «очень давно» [821], с. 88. И затем заимствована арабами, которые наконец-то и принесли ее в средневековую Европу. Именно в Европе
КАКУЮ СИСТЕМУ ХОТЕЛ СОЗДАТЬ КАНО ДЗИГАРО?
КАКУЮ СИСТЕМУ ХОТЕЛ СОЗДАТЬ КАНО ДЗИГАРО? По сути Кано стремился создать целую этическую систему «обновленного самурая», выдержанную в классическом духе традиционной Японии. Говоря о достижении «максимума эффективности в использовании тела и духа», Кано
а) Воздействие на социальную систему
а) Воздействие на социальную систему Мы уже замечали ранее в данном «Исследовании», что в столкновениях между современниками, в которых воздействие нападающей стороны заканчивается успешным проникновением в систему подвергшейся нападению стороны культурного
2.
 Когда китайцы изобрели подзорную трубу
Когда китайцы изобрели подзорную трубу2. Когда китайцы изобрели подзорную трубу Все мы думаем, что подзорная труба изобретена Галилеем, или его непосредственными предшественниками, в XVII веке. Он додумался до революционной идеи — использовать оптические линзы для разглядывания удаленных объектов, в том
Глава II. МОЖНО ЛИ БЫЛО РЕФОРМИРОВАТЬ СОВЕТСКУЮ СИСТЕМУ?
Глава II. МОЖНО ЛИ БЫЛО РЕФОРМИРОВАТЬ СОВЕТСКУЮ СИСТЕМУ? Теперь, имея чёткие и непредвзятые представления о сути вопроса, мы можем спросить себя, какие из главных компонентов старой советской системы были реально реформированы при Горбачёве? Что касается официальной
Под систему подкапываются!
Под систему подкапываются!
Именно так охарактеризовал свои впечатления от «закрытого доклада» Хрущева на XX съезде КПСС один старый большевик. Реакция советской и мировой общественности, которой основное содержание доклада вскоре стало известно, была крайне
Реакция советской и мировой общественности, которой основное содержание доклада вскоре стало известно, была крайне
ГЛАВА 1 М. Горбачев: последняя попытка спасти советскую систему
ГЛАВА 1 М. Горбачев: последняя попытка спасти советскую систему Реформы в России начались не с Ельцина и далеко не в 1991 году. Реальные перемены в стране начались еще в 1985 году с избранием Михаила Горбачева на пост Генерального секретаря коммунистической партии. Однако и
Инфраструктурная катастрофа Пора не латать, а всю систему менять
Инфраструктурная катастрофа Пора не латать, а всю систему менять В воскресенье в Брянске мама с ребёнком провалилась в промоину.8-го января 26-летняя Татьяна Диденко с полуторагодовалым сыном Кириллом провалилась в неожиданную промоину под тротуарной плиткой сквера
Про системы счисления / Хабр
Что же это, чёрт возьми, такое, как работают нули-единицы, и кто и зачем это вообще придумал.
Начинаю серию статей с простым объяснением всяких фундаментальных вещей с иллюстрациями. Школьнику, которого учитель информатики заставляет переводить числа туда-сюда, а он вообще не врубается, что происходит. Дизайнеру, который не знает, что значит цвет #FFDD00. Тем, кто всё знает, но не против ещё раз укрепить модель.
В статье всё замаскировано под исторические события. Это фикция, я не знаю историю, поэтому придумал свою, чтобы было проще рассказывать.
Жил-был древний человек.
И были у него овцы.
И решил он однажды посчитать, сколько у него овец. Но считать ещё не умел.
Древний человек придумал оставлять засечки на камне. Одна засечка — одна овца. Когда рождается овца, человек рисовал засечку, когда умирала — стирал.
И жил так прекрасно древний человек, пока не поумнел и не решил узнать что-нибудь об окружающем его мире. И захотел он посчитать количество звёзд на небе — тем же способом.
И умер.
Это, конечно, такой естественный отбор был. Человек должен с копьём на кабана охотиться, а не звёзды считать.
Человек должен с копьём на кабана охотиться, а не звёзды считать.
Потом были древние римляне. Их было много, поэтому, очевидно, были те, кто поумнее, и все остальные. Последние охотились на кабана с копьём, а умные считали добычу и столкнулись с той же проблемой, что и древний человек.
И они подумали: «а давайте нарисуем ещё больше разных закорючек, и они будут кратко обозначать большие числа».
И придумали, что эти закорючки будут такими:
V = IIIII,
X = VV,
L = XXXXX,
C = LL,
D = CCCCC,
M = DD.
Ещё они придумали хитрые правила, чтобы, например, вместо VIIII писать IX, но для простоты повествования мы про эти правила забудем.
И смогли римляне посчитать, что средняя продолжительность жизни — лет L, а звёзд на небе видно примерно MMD. Им этого хватало.
Но время шло, и человечеству понадобилось записывать всё большие числа. Латинского алфавита, чтобы придумать ещё больше обозначений, не хватило бы, да и не очень это было удобно.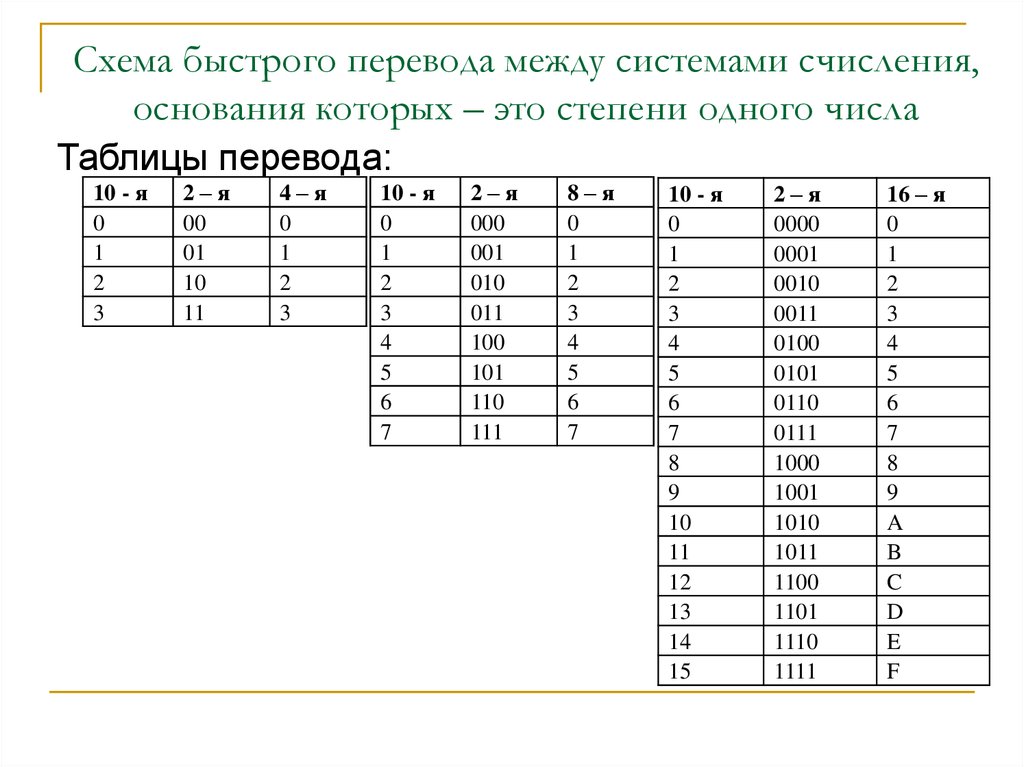
И нашёлся один умный человек, который придумал такую сложную и непонятную систему, что я не удивлюсь, если его за это потом сожгли.
Заметьте, что во всех предыдущих способах записи закорючки (цифры), стоящие рядом, просто складываются. Если древний человек написал II, это значит «I засечка и ещё I засечка». Если римлянин написал VII, это значит буквально IIIII + I + I, то есть IIIIIII.
Умный человек (горе ему) придумал вот что:
Пусть у нас будет сколько-то закорючек, например, X (здесь и дальше X — римская цифра, а не «неизвестное»). Позвал знакомого араба, сказал ему: «придумай мне X закорючек». Араб почесал репу и нарисовал: 0123456789.
Пусть 0 означает «ничего», а каждая следующая цифра сама по себе означает число, больше предыдущего на 1.
А дальше вообще отвал башки.
Пусть чем раньше в числе стоит цифра, тем большую «значимость» она имеет. Если цифра стоит в конце, она значит ровно столько, сколько написано.
 3 и так далее.
3 и так далее.Немного терминологии, чтобы привязать знания к реальности.
Система счисления — это способ записывать количество какими-то чёрточками. Способ подсчёта овец древним человеком — система счисления. Запись чисел с помощью V, X и M римлянами — система счисления. Новый и прогрессивный способ, придуманный умным человеком, — тоже.
Непозиционная система счисления — та, где от положения цифры её значение не меняется. Древний человек придумал именно такую систему — I всегда значит I.
Позиционная система счисления — та, где, наоборот, положение цифры влияет на её значение. Такую систему изобрёл умный человек. Например, в числе 456 цифра 4 означает 400, а в числе 546 — всего 40.
Основание системы счисления — общее количество закорючек (цифр) в ней. Умный человек придумал систему счисления с основанием X (в этой системе, в свою очередь, X записывается как 10).
Разряд — положение цифры в числе.
Что будет, если изменить основание системы счисления, например, на 2?
В целом, то же самое, только: — цифры остались всего две — можем придумать любые, но для удобства обычно берут символы из нашей системы счисления.
 3 = 0 + 2 + 0 + 8 = 10.
3 = 0 + 2 + 0 + 8 = 10.Выходит, 1010 в двоичной системе счисления обозначает такое же количество, какое 10 — в нашей, десятичной.
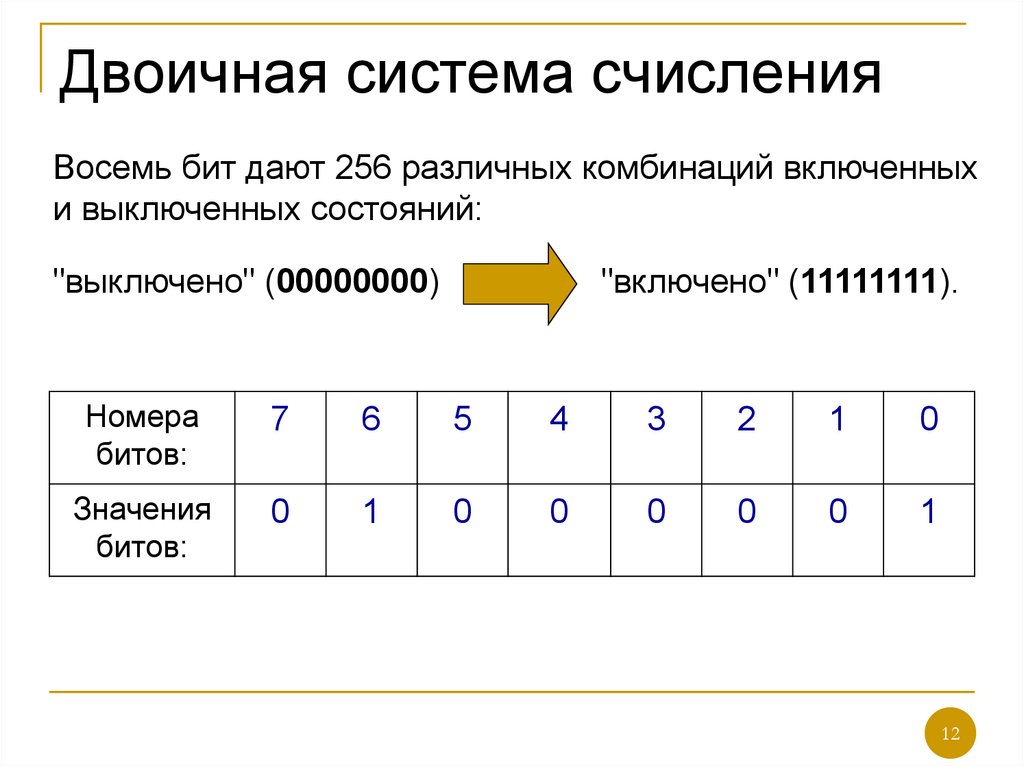
Двоичная система удобна, потому что в ней достаточно иметь всего две возможные позиции в каждом из разрядов — «ток течёт» или «ток не течёт», «палец загнут» или «палец выпрямлен».
Например, загибая пальцы рук, можно посчитать от 00000 00000 до 11111 11111, если принять левый мизинец за старший разряд, а правый мизинец — за младший, нулевой. Получается, в переводе на десятичную систему счисления на пальцах можно посчитать от нуля до 1023.
Первое, на что я хочу обратить внимание, — основание системы счисления в этой же системе всегда записывается как «10». В двоичной системе счисления число 2 записывается как «10», потому что 1 * 2 + 0 = 2. В шестнадцатеричной системе счисления число 16 записывается как «10», потому что 1 * 16 + 0 = 16. Ну вы поняли.
В связи с этим есть мем:
Инопланетянин говорит, что камней «10», потому что использует систему счисления с основанием 4 по-нашему.
 В его системе счисления наше «4» записывается как раз как «10». А что такое «4», инопланетянин вообще не знает, потому что у него цифры 0, 1, 2 и 3.
В его системе счисления наше «4» записывается как раз как «10». А что такое «4», инопланетянин вообще не знает, потому что у него цифры 0, 1, 2 и 3.Кстати, про шестнадцатеричную систему счисления. Десять привычных нам цифр уже есть, а где ещё шесть взять? Да давайте просто возьмём ещё шесть букв. После 9 идёт A, потом B, потом C, D, E, F, и только потом — 10. Получается, что последние цифробуквы шестнадцатеричной системы счисления переводятся в десятичную так:
A = 10,
B = 11,
C = 12,
D = 13,
E = 14,
F = 15.И последнее на сегодня — для дизайнеров. Что означает запись #FFDD00 для цвета? Наверняка вы знаете, что каждый пиксель на экране состоит из трёх лампочек — красного, зелёного и синего цвета, а все остальные цвета получаются смешиванием этих трёх в разной пропорции.
Каждая из лампочек может светить с условной яркостью от 0 до 255. #FFDD00 — это три числа: FF, DD и 00, где каждое число обозначает яркость каждой лампочки.
FF = 15 * 16 + 15 = 255.

DD = 13 * 16 + 13 = 221.
00 = 0.Получается, красная лампочка включена на все 255, зелёная на 221, а синяя полностью выключена.
#FFFFFF — все лампочки горят на максимум и дают белый цвет. #000000 — все выключены, чёрный цвет.
Вот так, короче.
Следующая статья будет (наверное) про то, что такое, чёрт возьми, электричество, сила тока, чем она отличается от напряжения, что такое заряд, сопротивление и потенциал.
Подписывайтесь на меня в Твиттере: https://twitter.com/adam_arutyunov
А ещё есть канал — «Адам Арутюнов поднимается до мидла». В нём — вы не поверите. t.me/cdarr
Кто изобрел ноль? | Живая наука
Живая наука поддерживается своей аудиторией. Когда вы покупаете по ссылкам на нашем сайте, мы можем получать партнерскую комиссию. Вот почему вы можете доверять нам.
Понятие нуля как заполнителя и символа «ничего» появилось сравнительно недавно. (Изображение предоставлено: html»>Ираидка | Shutterstock )Хотя люди всегда понимали концепцию ничего или неимения ничего, концепция нуля относительно нова; он полностью развился в Индии примерно в пятом веке нашей эры, возможно, на пару столетий раньше. До этого математики изо всех сил пытались выполнить простейшие арифметические вычисления. Сегодня ноль — и как символ (или число), и как понятие, означающее отсутствие какой-либо величины, — позволяет нам выполнять вычисления, составлять сложные уравнения и изобретать компьютеры.
«Индийский [или числовой] ноль, который многие считают одним из величайших нововведений в истории человечества, является краеугольным камнем современной математики и физики, а также побочной технологии», — сказал Питер Гобетс, секретарь фонда ZerOrigIndia, или нулевой проект. Фонд, базирующийся в Нидерландах, исследует происхождение нулевой цифры.
Ранняя история: Угловые клинья
Ноль в качестве заполнителя был независимо изобретен цивилизациями по всему миру, говорит д-р Аннет ван дер Хук, индиолог и координатор исследований Zero Project.
 Вавилоняне получили свою систему счисления от шумеров, первых людей в мире, разработавших систему счета. Разработанная 4000–5000 лет назад шумерская система была позиционной — значение символа зависело от его положения относительно других символов.
Вавилоняне получили свою систему счисления от шумеров, первых людей в мире, разработавших систему счета. Разработанная 4000–5000 лет назад шумерская система была позиционной — значение символа зависело от его положения относительно других символов.Роберт Каплан, автор книги «Ничто, что есть: естественная история нуля», предполагает, что предком нулевого заполнителя могла быть пара угловых клиньев, используемых для представления пустого числового столбца. Однако Чарльз Сейф, автор книги «Ноль: биография опасной идеи», не согласен с тем, что клинья представляли собой заполнитель.
Шумерская система перешла через Аккадскую империю к вавилонянам около 300 г. до н.э. Там, соглашается Каплан, появился символ, который явно был заполнителем — способом отличить 10 от 100 или обозначить, что в числе 2025 нет числа в столбце сотен. Первоначально вавилоняне оставили пустое место в своей клинописной системе счисления, но когда это стало запутанно, они добавили символ — клинья с двойным углом — для обозначения пустого столбца.
 Однако они никогда не развивали идею нуля как числа.
Однако они никогда не развивали идею нуля как числа.Ноль в Америке
Шестьсот лет спустя и в 12 000 милях от Вавилона майя разработали ноль в качестве заполнителя около 350 г. н.э. и использовали его для обозначения заполнителя в своих сложных календарных системах. Однако, несмотря на то, что они были высококвалифицированными математиками, майя никогда не использовали ноль в уравнениях. Каплан описывает изобретение нуля майя как «наиболее яркий пример того, как ноль был изобретен полностью с нуля».
Индия: где ноль стал цифрой
Некоторые ученые утверждают, что вавилонская концепция проникла в Индию, но другие, в том числе участники проекта «Ноль», отдают должное индийцам за то, что они самостоятельно разработали числовой ноль. «Мы придерживаемся мнения, что в древней Индии были найдены многочисленные так называемые «культурные предшественники», которые делают вероятным, что математический нуль был изобретен там», — сказал Гобетс, чья организация состоит из ученых и аспирантов, посвятивших себя изучению развития нуля в Индии.
 «Нулевой проект предполагает, что математический ноль («шунья» на санскрите) мог возникнуть из современной философии пустоты или шуньяты», — сказал Гобец. Если бы философские и культурные факторы, обнаруженные в Индии, были важны для развития нуля как математической концепции, это объяснило бы, почему другие цивилизации не разработали ноль как математическую концепцию, сказал ван дер Хук.
«Нулевой проект предполагает, что математический ноль («шунья» на санскрите) мог возникнуть из современной философии пустоты или шуньяты», — сказал Гобец. Если бы философские и культурные факторы, обнаруженные в Индии, были важны для развития нуля как математической концепции, это объяснило бы, почему другие цивилизации не разработали ноль как математическую концепцию, сказал ван дер Хук.Согласно книге доктора Джорджа Гевергезе Джозефа «Гребень павлина: неевропейские корни математики», концепция нуля впервые появилась в Индии примерно в 458 году нашей эры. , что означало «пустой» или «пустой» и произошло от слова «рост» в сочетании с ранним определением, найденным в Ригведе, «недостаток» или «недостаток». Производным от двух определений является Śūnyata, буддийское учение о «пустоте», или освобождении ума от впечатлений и мыслей.
«Из этой философии мы думаем, что появилось число для использования в математических уравнениях», — сказал ван дер Хук. «Мы ищем мост между индийской философией и математикой».

«Ноль и его действие впервые были определены [индуистским астрономом и математиком] Брахмагуптой в 628 году», — сказал Гобетс. Он разработал символ нуля: точку под цифрами. «Но он тоже не претендует на то, что изобрел ноль, который, по-видимому, должен был существовать уже какое-то время», — добавил Гобец.
Надпись на стене храма в Гвалиоре, Индия, датируется девятым веком и считается старейшим зарегистрированным примером нуля, по данным Оксфордского университета. Другим примером является древний индийский свиток, называемый рукописью Бхакшали. Обнаруженный в поле в 1881 году, исследователи думали, что он также возник в девятом веке. Однако недавнее углеродное датирование показало, что оно, вероятно, было написано в третьем или четвертом веке, что отодвигает самое раннее зарегистрированное использование нуля на 500 лет назад.
Маркус дю Сотуа, профессор математики Оксфордского университета, сказал: «Сегодня мы считаем само собой разумеющимся, что концепция нуля используется во всем мире и является ключевым строительным блоком цифрового мира.
 ноль как самостоятельный номер, который произошел от символа-заполнителя, найденного в рукописи Бахшали, был одним из величайших прорывов в истории математики.
ноль как самостоятельный номер, который произошел от символа-заполнителя, найденного в рукописи Бахшали, был одним из величайших прорывов в истории математики.«Теперь мы знаем, что еще в математики в Индии посеяли семена идеи, которая впоследствии стала фундаментальной для современного мира. Полученные данные показывают, насколько яркой была математика на Индийском субконтиненте на протяжении столетий».0003
От Ближнего Востока до Уолл-Стрит
В течение следующих нескольких столетий концепция нуля прижилась в Китае и на Ближнем Востоке. По словам Нильса-Бертила Валлина из YaleGlobal, к 773 году ноль достиг Багдада, где стал частью арабской системы счисления, основанной на индийской системе.
Персидский математик Мохаммед ибн-Муса аль-Хорезми предложил использовать в вычислениях маленький кружок, если в разряде десятков не появляется число. Арабы называли этот круг «сифр», или «пустой». Ноль имел решающее значение для аль-Ховаризми, который использовал его для изобретения алгебры в девятом веке.
 Аль-Ховаризми также разработал быстрые методы умножения и деления чисел, которые известны как алгоритмы — искажение его имени.
Аль-Ховаризми также разработал быстрые методы умножения и деления чисел, которые известны как алгоритмы — искажение его имени.Ноль попал в Европу благодаря мавританскому завоеванию Испании и был развит итальянским математиком Фибоначчи, который использовал его для решения уравнений без счетов, тогда наиболее распространенного инструмента для выполнения арифметических операций. Эта разработка была очень популярна среди торговцев, которые использовали уравнения Фибоначчи с нулем, чтобы сбалансировать свои бухгалтерские книги.
Средневековые религиозные лидеры в Европе не поддерживали использование нуля, сказал ван дер Хук. Они считали это сатанинским. «Бог был во всем, что было. Все, чего не было, было от дьявола», — сказала она.
Валлин отмечает, что итальянское правительство с подозрением относилось к арабским числам и запретило использование нуля. Торговцы продолжали использовать его нелегально и тайно, а арабское слово «сифр», обозначающее ноль, породило слово «шифр», которое означает не только числовой символ, но и «код».

К 1600-м годам нуль довольно широко использовался по всей Европе. Это было основополагающим в декартовой системе координат Рене Декарта и в исчислении, разработанном независимо сэром Исааком Ньютоном и Готфридом Вильгельмом Либницем. Исчисление проложило путь физике, технике, компьютерам и большей части финансовой и экономической теории.
«Концепция пустоты сейчас занимает центральное место в современной физике: вся известная вселенная рассматривается как «игра с нулевой суммой» среди прочих, таких как Стивен Хокинг», — сказал Гобетс.
Цифра и понятие ноль, привезенные из Индии, проявлялись по-разному. «Ноль стал настолько обыденным, что лишь немногие осознают его поразительную роль в жизни каждого человека в мире», — сказал Гобетс.
Дополнительные ресурсы
- Scientific American: The Origin of Zero
- Йельский университет: история нуля
- Американское математическое общество: все напрасно
Кто изобрел числа? | Вандополис
МАТЕМАТИКА — Числа
Задумывались ли вы когда-нибудь.
 ..
..- Кто изобрел числа?
- Кто из известных математиков помог разработать числа?
- Какое влияние числа оказали на развивающиеся общества?
Теги:
Просмотреть все теги
- История,
- Математика,
- Один,
- Номер,
- Подсчет,
- Математика,
- Доисторический,
- Резьба,
- Кость,
- Кость Ишанго,
- Африка,
- Малоберцовая кость,
- Бабуин,
- Счетная метка,
- Общество,
- Торговля,
- Город,
- Шумер,
- Месопотамия,
- Ирак,
- Письмо,
- Дополнение,
- Вычитание,
- арабский,
- Число, Система
- ,
- Индия,
- Математик,
- Брахмагупта,
- Арьябхат,
- Египетский,
- Измерение,
- Пирамида,
- Геометрия,
- История,
- Математика,
- Один,
- Номер,
- Подсчет,
- Математика,
- Доисторический,
- Резьба,
- Кость,
- Кость Ишанго,
- Африка,
- Малоберцовая кость,
- Бабуин,
- Счетная отметка,
- Общество,
- Торговля,
- Город,
- Шумер,
- Месопотамия,
- Ирак,
- Письмо,
- Дополнение,
- Вычитание,
- арабский,
- Число, Система
- ,
- Индия,
- Математик,
- Брахмагупта,
- Арьябхат,
- Египетский,
- Измерение,
- Пирамида,
- Геометрия
Сегодняшнее чудо дня было вдохновлено Сарой из Леандера, штат Техас.
 Сара Уондерс , » Откуда наши номера 1-9родом из? «Спасибо, что ДУМАЕТЕ вместе с нами, Сара!
Сара Уондерс , » Откуда наши номера 1-9родом из? «Спасибо, что ДУМАЕТЕ вместе с нами, Сара!Один плюс один равно двум. В одной минуте 60 секунд. Шестьдесят минут равны одному часу. В одних сутках 24 часа. Один год состоит из 365 дней. Все это основные факты, которые мы знаем наизусть, но они подчеркивают важность одной вещи: цифр.
Можете ли вы представить мир без чисел? Можно с уверенностью сказать, что общество, каким мы его знаем сегодня, никогда бы не развилось без чисел. Научные и технические достижения, на которых построено общество, зависят от математики, которая, в свою очередь, зависит от чисел.
Несмотря на их важность, развитие чисел остается в основном загадкой. Это потому, что первые древние доисторические люди, которые, вероятно, разработали простые методы счета, не оставили никаких записей, чтобы объяснить себя.
Здравый смысл и древние свидетельства указывают на то, что числа и счет начались с единицы.
 Хотя они, вероятно, не называли это «единицей», доисторические люди, вероятно, считали единицами и отслеживали, вырезая линии на кости.
Хотя они, вероятно, не называли это «единицей», доисторические люди, вероятно, считали единицами и отслеживали, вырезая линии на кости.Доказательства того, что это произошло 20 000 лет назад, можно найти на древнем артефакте, известном как кость Ишанго. Найденная в Африке в 1960 году кость Ишанго (малоберцовая кость бабуина) имеет серию линий, которые выглядят как то, что мы сегодня назвали бы «счетными метками».
Отслеживание небольшого количества предметов с подсчетными метками было достаточно для отдельных лиц и небольших групп. Однако по мере того, как общества начали формироваться и расти, торговля стала более сложной, требуя развития чисел для выполнения простых математических расчетов.
Историки считают, что числа и счет расширились за пределы единицы около 4000 г. до н.э. в Шумере, который располагался в южной Месопотамии на территории нынешнего южного Ирака. Шумеру, одной из первых цивилизаций, в которой появились города, которые были центрами торговли, понадобились новые методы подсчета и ведения записей.

Пока в Шумере разрабатывались новые системы счисления и счета, также разрабатывались основы арифметики и письма. Отслеживание продаваемых товаров требовало письма и базовых операций сложения и вычитания в дополнение к расширенной системе счисления и счета.
Все эти основополагающие идеи развивались одновременно с ростом городов и расцветом торговли. Некоторые историки считают, что некоторые из этих идей независимо развивались и в других регионах мира.
Например, арабская система счисления, с которой мы все сегодня знакомы, обычно приписывается двум математикам из древней Индии: Брахмагупте из 6 — века до н.э. и Арьябхат с 5 по век до н.э.
В конце концов, числа стали необходимы не только для подсчета вещей. Мы можем поблагодарить древних египтян за то, что они совершили скачок от использования чисел для счета к использованию их для измерения вещей. Историки считают, что их использование чисел для измерения позволило древним египтянам построить пирамиды и заложить основу для передовых математических концепций, таких как геометрия.

Common Core, Научные стандарты следующего поколения и Национальный совет по социальным исследованиям.»> Стандарты: CCRA.L.3, CCRA.L.6, CCRA.R.1, CCRA.R.2, CCRA.R.4, CCRA.R.10, CCRA.SL.1, CCRA.W.2, CCRA .W.4, CCRA.W.9, CCRA.L.1, CCRA.L.2
Интересно, что дальше?
Завтрашнее чудо дня имеет катастрофический конец!
Попробуйте
Вы готовы считать? Не забудьте проверить следующие действия с другом или членом семьи:
- Можете ли вы поверить, что некоторые из самых старых свидетельств чисел были найдены на кости? Зайдите в Интернет, чтобы проверить страницу «Математическое сокровище: кость Ишанго», чтобы узнать больше об этом интересном артефакте. Если бы вы нашли эту кость, поняли бы вы, что на ней изображено и насколько она важна?
- Вы ежедневно сильно полагаетесь на цифры? Вы можете быть удивлены! Попробуйте идти так долго, как только сможете, не используя никаких чисел.
 Это означает отсутствие телевидения, так как вам нужны цифры, чтобы выбрать правильный канал. Вы также не можете бросить закуску в микроволновую печь, так как вам понадобятся числа, чтобы запрограммировать ее на приготовление в течение определенного времени. Как еще появляются числа? Как только вы начнете думать об этом, вы будете поражены тем, как переплетены числа в вашей повседневной жизни!
Это означает отсутствие телевидения, так как вам нужны цифры, чтобы выбрать правильный канал. Вы также не можете бросить закуску в микроволновую печь, так как вам понадобятся числа, чтобы запрограммировать ее на приготовление в течение определенного времени. Как еще появляются числа? Как только вы начнете думать об этом, вы будете поражены тем, как переплетены числа в вашей повседневной жизни! - Вы знакомы с обычной системой счисления с основанием 10, в которой используются числа от 0 до 9., но знаете ли вы, что существует множество других систем счисления, таких как основание 8, основание 2 и даже основание 16? Ознакомьтесь с онлайн-системами счисления, чтобы узнать, как работают эти другие интересные системы счисления!
Wonder Sources
- https://www.deseretnews.com/article/865560110/A-brief-history-of-numbers-and-counting-Part-1-Mathematics-advanced-with-civilization.html
- http://www.smithsonianmag.com/innovation/how-humans-invented-numbersand-how-numbers-resized-our-world-180962485/
- http://www.
 whoinvented.org/who-invented-numbers/
whoinvented.org/who-invented-numbers/
Получили?
Проверьте свои знанияWonder Contributors
Благодарим:
Алексис из Кентукки, Тревор и Сара
за ответы на вопросы по сегодняшней теме Wonder!Удивляйтесь вместе с нами!
Что вас интересует?
Wonder Words
- идея
- сейф
- простой
- общество
- объяснить
- бабуин
- тайна
- представить
- выделить
- произошло
- доказательство
- авансы
- цивилизаций
- важность
- расчеты
- математика
- разработка
- технологический
Примите участие в конкурсе Wonder Word
Оцените это чудо
Поделись этим чудом
×ПОЛУЧАЙТЕ СВОЕ ЧУДО ЕЖЕДНЕВНО
Подпишитесь на Wonderopolis и получайте Wonder of the Day® по электронной почте или SMS
Присоединяйтесь к Buzz
Не пропустите наши специальные предложения, подарки и рекламные акции.
 Узнай первым!
Узнай первым!Поделитесь со всем миром
Расскажите всем о Вандополисе и его чудесах.
Поделиться Wonderopolis
Wonderopolis Widget
Хотите делиться информацией о Wonderopolis® каждый день? Хотите добавить немного чуда на свой сайт? Помогите распространить чудо семейного обучения вместе.
Добавить виджет
Ты понял!
Продолжить
Не совсем!
Попробуйте еще раз
Как люди изобрели числа и как числа изменили наш мир | Инновация
«Числа — это человеческое изобретение, а не то, что мы автоматически получаем от природы», — говорит Калеб Эверетт. Квангмузаа/iStockКак только вы выучите цифры, вам будет трудно освободиться от их объятий. Они кажутся естественными, врожденными, чем-то, с чем рождаются все люди.
 Но когда адъюнкт-профессор Университета Майами Калеб Эверетт и другие антропологи работали с коренными жителями Амазонки, известными как пираха, они поняли, что у членов этого племени нет слова, которое последовательно использовалось для идентификации любое количество , даже не одно.
Но когда адъюнкт-профессор Университета Майами Калеб Эверетт и другие антропологи работали с коренными жителями Амазонки, известными как пираха, они поняли, что у членов этого племени нет слова, которое последовательно использовалось для идентификации любое количество , даже не одно.Заинтригованные исследователи разработали дополнительные тесты для взрослых пираха, которые были психически и биологически здоровы. Антропологи выстроили ряд батареек на столе и попросили участников пираха разместить такое же число в параллельном ряду с другой стороны. При подаче одной, двух или трех батарей задача решалась без труда. Но как только первоначальная линия включала в себя четыре и более батарей, пираха начинали ошибаться. По мере увеличения количества батарей в линии росли и их ошибки.
Исследователи обнаружили нечто экстраординарное: отсутствие чисел у пираха означало, что они не могли точно различить количество больше трех. Как пишет Эверетт в своей новой книге «Числа и создание нас »: «Математические понятия не связаны с человеческими условиями.
 Они усваиваются, приобретаются посредством культурной и языковой передачи. И если они усваиваются, а не унаследованы генетически, то из этого следует, что они не являются компонентом человеческого ментального оборудования, а в значительной степени являются частью нашего ментального программного обеспечения — функцией приложения, которое мы сами разработали».
Они усваиваются, приобретаются посредством культурной и языковой передачи. И если они усваиваются, а не унаследованы генетически, то из этого следует, что они не являются компонентом человеческого ментального оборудования, а в значительной степени являются частью нашего ментального программного обеспечения — функцией приложения, которое мы сами разработали».Чтобы узнать больше об изобретении чисел и огромной роли, которую они сыграли в человеческом обществе, Smithsonian.com поговорил с Эвереттом о его книге.
Как вы заинтересовались изобретением чисел?
Это косвенно связано с моей работой над языками в Амазонии. Столкновение с языками, в которых нет чисел или много чисел, неизбежно приводит вас к вопросу о том, каким был бы ваш мир без чисел, и к пониманию того, что числа — это человеческое изобретение, а не то, что мы получаем автоматически от природы.
В книге вы подробно рассказываете о том, как наше увлечение нашими руками — и пятью пальцами на каждой — вероятно, помогло нам изобретать числа, и оттуда мы могли использовать числа, чтобы делать другие открытия.
 Так что же появилось раньше — числа или математика?
Так что же появилось раньше — числа или математика? Я думаю, это может вызвать некоторую путаницу, когда я говорю об изобретении чисел. Очевидно, что в природе существуют закономерности. Как только мы изобретаем числа, они открывают нам доступ к этим закономерностям в природе, которых иначе у нас не было бы. Мы можем видеть, что длина окружности и диаметр круга имеют постоянное соотношение между кругами, но практически невозможно понять это без чисел. В природе существует множество закономерностей, таких как число Пи, которые на самом деле существуют. Эти вещи существуют вне зависимости от того, можем ли мы последовательно различать их. Когда у нас есть числа, мы можем последовательно различать их, и это позволяет нам находить интересные и полезные закономерности природы, которые мы никогда не смогли бы уловить без точности.
Числа — это очень простое изобретение. Эти слова, овеществляющие понятия, являются инструментом познания. Но так удивительно думать о том, что они делают как вид.
 Без них мы, кажется, изо всех сил пытаемся последовательно отличить семь от восьми; с ними мы можем отправить кого-нибудь на Луну. Все это можно проследить до того, как кто-то где-то сказал: «Эй, у меня тут кое-что есть». Без этого первого шага или без подобных первых шагов, сделанных для изобретения чисел, вы не доберетесь до этих других шагов. Многие люди думают, что из-за того, что математика настолько сложна, и существуют числа, они думают, что это то, что вы начинаете узнавать. Меня не волнует, насколько вы умны, если у вас нет цифр, вы не добьетесь этого. В большинстве случаев изобретение, вероятно, началось с этого эфемерного осознания [что у вас пять пальцев на одной руке], но если они не приписывают этому ни слова, то это осознание очень быстро проходит и умирает вместе с ними. Это не передается следующему поколению.
Без них мы, кажется, изо всех сил пытаемся последовательно отличить семь от восьми; с ними мы можем отправить кого-нибудь на Луну. Все это можно проследить до того, как кто-то где-то сказал: «Эй, у меня тут кое-что есть». Без этого первого шага или без подобных первых шагов, сделанных для изобретения чисел, вы не доберетесь до этих других шагов. Многие люди думают, что из-за того, что математика настолько сложна, и существуют числа, они думают, что это то, что вы начинаете узнавать. Меня не волнует, насколько вы умны, если у вас нет цифр, вы не добьетесь этого. В большинстве случаев изобретение, вероятно, началось с этого эфемерного осознания [что у вас пять пальцев на одной руке], но если они не приписывают этому ни слова, то это осознание очень быстро проходит и умирает вместе с ними. Это не передается следующему поколению.Числа и создание нас: счет и курс человеческих культур
Еще одна интересная параллель — связь между числами, сельским хозяйством и торговлей.
 Что там было первым?
Что там было первым? Я думаю, что наиболее вероятным сценарием является совместная эволюция. Вы разрабатываете числа, которые позволяют вам торговать более точными способами. Поскольку это облегчает такие вещи, как торговля и сельское хозяйство, это заставляет изобретать больше чисел. В свою очередь, эти усовершенствованные системы счисления сделают возможными новые виды торговли и более точные карты, так что все они связаны друг с другом. Это похоже на ситуацию с курицей и яйцом, может быть, цифры были первыми, но они не должны были быть там в очень надежной форме, чтобы обеспечить определенные виды поведения. Кажется, что во многих культурах, когда люди получают цифру пять, она их запускает. Как только они поймут, что могут опираться на такие вещи, как пять, они смогут со временем усилить свое числовое знание. Это ключевое осознание того, что «рука — это пять вещей», во многих культурах является когнитивным ускорителем.
Насколько большую роль сыграли числа в развитии нашей культуры и общества?
Мы знаем, что они должны играть огромную роль.
 Они позволяют использовать все виды материальных технологий. Помимо того, что они помогают нам думать о количествах и изменять нашу ментальную жизнь, они позволяют нам делать что-то для создания сельского хозяйства. У пираха есть подсечно-огневая техника, но если вы собираетесь заниматься систематическим сельским хозяйством, им нужно больше. Если вы посмотрите на майя и инков, они явно очень полагались на числа и математику. Числа кажутся воротами, которые имеют решающее значение и необходимы для других видов образа жизни и материальных культур, которые мы все разделяем сейчас, но которых в какой-то момент у людей не было. В какой-то момент более 10 000 лет назад все люди жили относительно небольшими группами, прежде чем мы начали формировать вождества. Вождества происходят прямо или косвенно от сельского хозяйства. Числа имеют решающее значение для всего, что вы видите вокруг себя из-за всех технологий и медицины. Все это происходит от поведения, которое прямо или косвенно связано с числами, включая системы письма.
Они позволяют использовать все виды материальных технологий. Помимо того, что они помогают нам думать о количествах и изменять нашу ментальную жизнь, они позволяют нам делать что-то для создания сельского хозяйства. У пираха есть подсечно-огневая техника, но если вы собираетесь заниматься систематическим сельским хозяйством, им нужно больше. Если вы посмотрите на майя и инков, они явно очень полагались на числа и математику. Числа кажутся воротами, которые имеют решающее значение и необходимы для других видов образа жизни и материальных культур, которые мы все разделяем сейчас, но которых в какой-то момент у людей не было. В какой-то момент более 10 000 лет назад все люди жили относительно небольшими группами, прежде чем мы начали формировать вождества. Вождества происходят прямо или косвенно от сельского хозяйства. Числа имеют решающее значение для всего, что вы видите вокруг себя из-за всех технологий и медицины. Все это происходит от поведения, которое прямо или косвенно связано с числами, включая системы письма. Мы не развиваем письмо без предварительного развития чисел.
Мы не развиваем письмо без предварительного развития чисел.Как цифры привели к написанию?
Письменность была изобретена лишь в нескольких случаях. Центральная Америка, Месопотамия, Китай, затем из этих систем развилось множество систем письма. Мне кажется интересным, что числа были своего рода первыми символами. Эти записи сильно ориентированы на числовые значения. У нас есть письменные знаки возрастом 5000 лет из Месопотамии, и они сосредоточены на количестве. Я должен быть честным, потому что письменность была изобретена только в нескольких случаях, [ссылка на числа] могла быть случайной. Это более спорный случай. Я думаю, что есть веские причины полагать, что числа привели к написанию, но я подозреваю, что некоторые ученые сказали бы, что это возможно, но мы не знаем этого наверняка.
Вы еще коснетесь того, являются ли числа врожденными человеческими или другие животные могут обладать этой способностью. Могут ли птицы или приматы создавать числа?
Не похоже, чтобы они сами по себе справились.
 Мы не знаем наверняка, но у нас нет конкретных доказательств того, что они могут сделать это самостоятельно. Если вы посмотрите на Алекса, африканского серого попугая [и предмет 30-летнего исследования психолога животных Ирэн Пепперберг), то, что он был способен делать, было довольно замечательно, последовательно считать и складывать, но он развил эту способность только тогда, когда ее научили. снова и снова, эти числовые слова. В некотором роде это можно передать и другим видам — некоторые шимпанзе, кажется, способны выучить некоторые основные числа и основы арифметики, но они не делают этого самостоятельно. Они похожи на нас в том, что, кажется, способны на это, если им дать количество слов. Это открытый вопрос, насколько это легко. Нам это кажется легким, потому что у нас это было с самого раннего возраста, но если вы посмотрите на детей, это не происходит естественным образом.
Мы не знаем наверняка, но у нас нет конкретных доказательств того, что они могут сделать это самостоятельно. Если вы посмотрите на Алекса, африканского серого попугая [и предмет 30-летнего исследования психолога животных Ирэн Пепперберг), то, что он был способен делать, было довольно замечательно, последовательно считать и складывать, но он развил эту способность только тогда, когда ее научили. снова и снова, эти числовые слова. В некотором роде это можно передать и другим видам — некоторые шимпанзе, кажется, способны выучить некоторые основные числа и основы арифметики, но они не делают этого самостоятельно. Они похожи на нас в том, что, кажется, способны на это, если им дать количество слов. Это открытый вопрос, насколько это легко. Нам это кажется легким, потому что у нас это было с самого раннего возраста, но если вы посмотрите на детей, это не происходит естественным образом.Какие дальнейшие исследования по этому вопросу вы хотели бы увидеть?
Когда вы смотрите на население, которое является основой того, что мы знаем о мозге, это узкий диапазон человеческих культур: много американских старшекурсников, европейских старшекурсников, немного японцев.
 Хорошо представлены люди из определенного общества и культуры. Было бы неплохо, если бы жители Амазонки и коренные народы подверглись исследованиям фМРТ, чтобы получить представление о том, насколько это различается в разных культурах. Учитывая пластичность коры, культура играет роль в развитии мозга.
Хорошо представлены люди из определенного общества и культуры. Было бы неплохо, если бы жители Амазонки и коренные народы подверглись исследованиям фМРТ, чтобы получить представление о том, насколько это различается в разных культурах. Учитывая пластичность коры, культура играет роль в развитии мозга.Как вы надеетесь, что люди вынесут из этой книги?
Я надеюсь, что люди получат от этого увлекательное чтение, и я надеюсь, что они в большей степени осознают, что большая часть их жизни, которую они считают основной, на самом деле является результатом определенных культурных линий. Мы унаследовали на протяжении тысячелетий вещи от определенных культур: индоевропейцев, чья система счисления у нас все еще есть, основание десять. Я надеюсь, что люди увидят это и поймут, что это происходит не просто так. Людям на протяжении тысячелетий приходилось дорабатывать и развивать систему. Мы благотворители этого.
Я думаю, одна из основных вещей в книге заключается в том, что мы склонны думать о себе как об особом виде, и мы таковыми и являемся, но мы думаем, что у нас действительно большой мозг.



 3 и так далее.
3 и так далее. 3 = 0 + 2 + 0 + 8 = 10.
3 = 0 + 2 + 0 + 8 = 10. В его системе счисления наше «4» записывается как раз как «10». А что такое «4», инопланетянин вообще не знает, потому что у него цифры 0, 1, 2 и 3.
В его системе счисления наше «4» записывается как раз как «10». А что такое «4», инопланетянин вообще не знает, потому что у него цифры 0, 1, 2 и 3.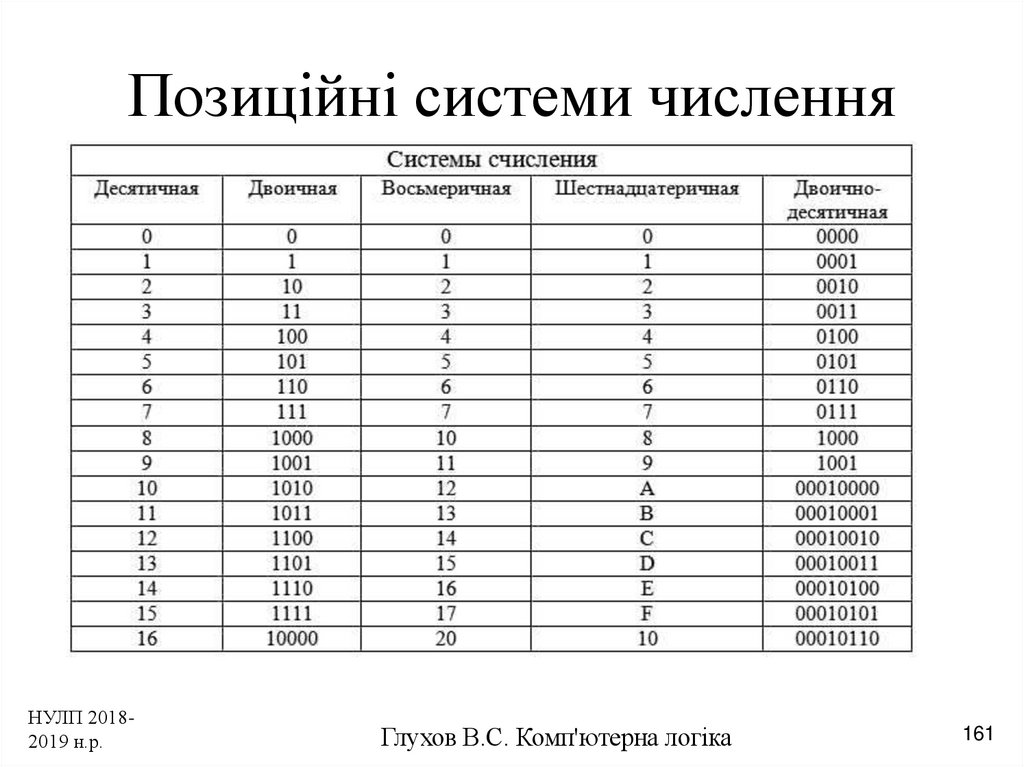
 Вавилоняне получили свою систему счисления от шумеров, первых людей в мире, разработавших систему счета. Разработанная 4000–5000 лет назад шумерская система была позиционной — значение символа зависело от его положения относительно других символов.
Вавилоняне получили свою систему счисления от шумеров, первых людей в мире, разработавших систему счета. Разработанная 4000–5000 лет назад шумерская система была позиционной — значение символа зависело от его положения относительно других символов. Однако они никогда не развивали идею нуля как числа.
Однако они никогда не развивали идею нуля как числа. «Нулевой проект предполагает, что математический ноль («шунья» на санскрите) мог возникнуть из современной философии пустоты или шуньяты», — сказал Гобец. Если бы философские и культурные факторы, обнаруженные в Индии, были важны для развития нуля как математической концепции, это объяснило бы, почему другие цивилизации не разработали ноль как математическую концепцию, сказал ван дер Хук.
«Нулевой проект предполагает, что математический ноль («шунья» на санскрите) мог возникнуть из современной философии пустоты или шуньяты», — сказал Гобец. Если бы философские и культурные факторы, обнаруженные в Индии, были важны для развития нуля как математической концепции, это объяснило бы, почему другие цивилизации не разработали ноль как математическую концепцию, сказал ван дер Хук.
 ноль как самостоятельный номер, который произошел от символа-заполнителя, найденного в рукописи Бахшали, был одним из величайших прорывов в истории математики.
ноль как самостоятельный номер, который произошел от символа-заполнителя, найденного в рукописи Бахшали, был одним из величайших прорывов в истории математики. Аль-Ховаризми также разработал быстрые методы умножения и деления чисел, которые известны как алгоритмы — искажение его имени.
Аль-Ховаризми также разработал быстрые методы умножения и деления чисел, которые известны как алгоритмы — искажение его имени.
 ..
.. Сара Уондерс , » Откуда наши номера 1-9родом из? «Спасибо, что ДУМАЕТЕ вместе с нами, Сара!
Сара Уондерс , » Откуда наши номера 1-9родом из? «Спасибо, что ДУМАЕТЕ вместе с нами, Сара! Хотя они, вероятно, не называли это «единицей», доисторические люди, вероятно, считали единицами и отслеживали, вырезая линии на кости.
Хотя они, вероятно, не называли это «единицей», доисторические люди, вероятно, считали единицами и отслеживали, вырезая линии на кости.
 Это означает отсутствие телевидения, так как вам нужны цифры, чтобы выбрать правильный канал. Вы также не можете бросить закуску в микроволновую печь, так как вам понадобятся числа, чтобы запрограммировать ее на приготовление в течение определенного времени. Как еще появляются числа? Как только вы начнете думать об этом, вы будете поражены тем, как переплетены числа в вашей повседневной жизни!
Это означает отсутствие телевидения, так как вам нужны цифры, чтобы выбрать правильный канал. Вы также не можете бросить закуску в микроволновую печь, так как вам понадобятся числа, чтобы запрограммировать ее на приготовление в течение определенного времени. Как еще появляются числа? Как только вы начнете думать об этом, вы будете поражены тем, как переплетены числа в вашей повседневной жизни!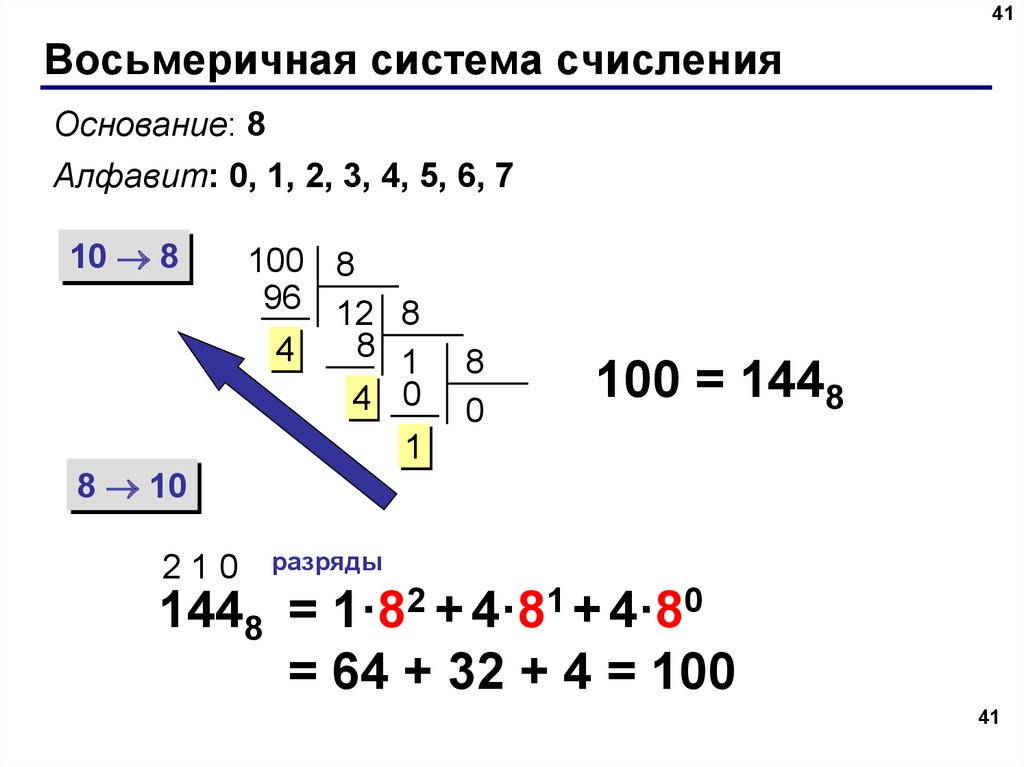 whoinvented.org/who-invented-numbers/
whoinvented.org/who-invented-numbers/ Узнай первым!
Узнай первым! Но когда адъюнкт-профессор Университета Майами Калеб Эверетт и другие антропологи работали с коренными жителями Амазонки, известными как пираха, они поняли, что у членов этого племени нет слова, которое последовательно использовалось для идентификации любое количество , даже не одно.
Но когда адъюнкт-профессор Университета Майами Калеб Эверетт и другие антропологи работали с коренными жителями Амазонки, известными как пираха, они поняли, что у членов этого племени нет слова, которое последовательно использовалось для идентификации любое количество , даже не одно. Они усваиваются, приобретаются посредством культурной и языковой передачи. И если они усваиваются, а не унаследованы генетически, то из этого следует, что они не являются компонентом человеческого ментального оборудования, а в значительной степени являются частью нашего ментального программного обеспечения — функцией приложения, которое мы сами разработали».
Они усваиваются, приобретаются посредством культурной и языковой передачи. И если они усваиваются, а не унаследованы генетически, то из этого следует, что они не являются компонентом человеческого ментального оборудования, а в значительной степени являются частью нашего ментального программного обеспечения — функцией приложения, которое мы сами разработали».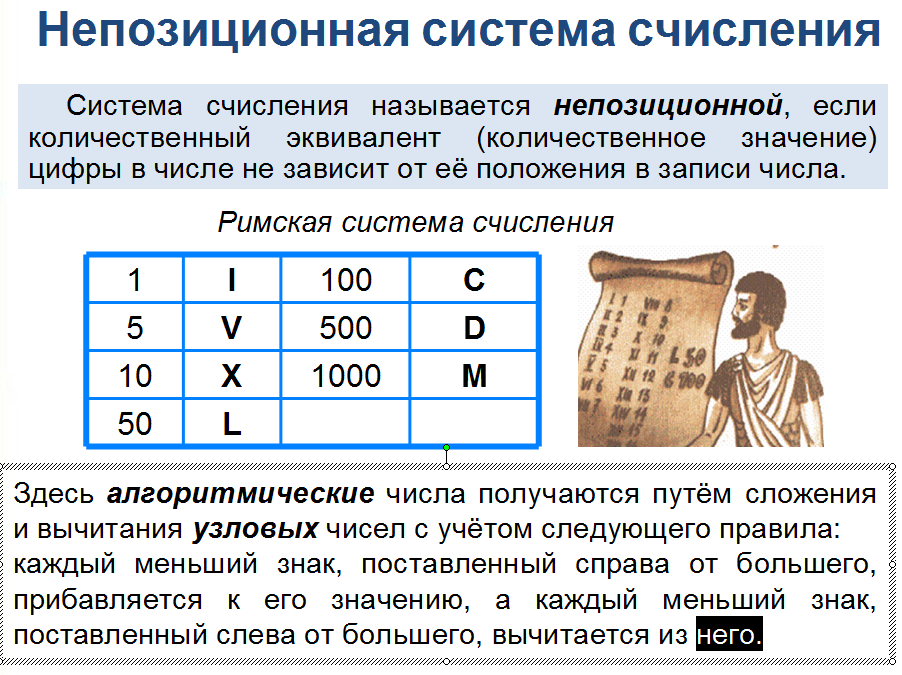 Так что же появилось раньше — числа или математика?
Так что же появилось раньше — числа или математика?  Без них мы, кажется, изо всех сил пытаемся последовательно отличить семь от восьми; с ними мы можем отправить кого-нибудь на Луну. Все это можно проследить до того, как кто-то где-то сказал: «Эй, у меня тут кое-что есть». Без этого первого шага или без подобных первых шагов, сделанных для изобретения чисел, вы не доберетесь до этих других шагов. Многие люди думают, что из-за того, что математика настолько сложна, и существуют числа, они думают, что это то, что вы начинаете узнавать. Меня не волнует, насколько вы умны, если у вас нет цифр, вы не добьетесь этого. В большинстве случаев изобретение, вероятно, началось с этого эфемерного осознания [что у вас пять пальцев на одной руке], но если они не приписывают этому ни слова, то это осознание очень быстро проходит и умирает вместе с ними. Это не передается следующему поколению.
Без них мы, кажется, изо всех сил пытаемся последовательно отличить семь от восьми; с ними мы можем отправить кого-нибудь на Луну. Все это можно проследить до того, как кто-то где-то сказал: «Эй, у меня тут кое-что есть». Без этого первого шага или без подобных первых шагов, сделанных для изобретения чисел, вы не доберетесь до этих других шагов. Многие люди думают, что из-за того, что математика настолько сложна, и существуют числа, они думают, что это то, что вы начинаете узнавать. Меня не волнует, насколько вы умны, если у вас нет цифр, вы не добьетесь этого. В большинстве случаев изобретение, вероятно, началось с этого эфемерного осознания [что у вас пять пальцев на одной руке], но если они не приписывают этому ни слова, то это осознание очень быстро проходит и умирает вместе с ними. Это не передается следующему поколению. Что там было первым?
Что там было первым?  Они позволяют использовать все виды материальных технологий. Помимо того, что они помогают нам думать о количествах и изменять нашу ментальную жизнь, они позволяют нам делать что-то для создания сельского хозяйства. У пираха есть подсечно-огневая техника, но если вы собираетесь заниматься систематическим сельским хозяйством, им нужно больше. Если вы посмотрите на майя и инков, они явно очень полагались на числа и математику. Числа кажутся воротами, которые имеют решающее значение и необходимы для других видов образа жизни и материальных культур, которые мы все разделяем сейчас, но которых в какой-то момент у людей не было. В какой-то момент более 10 000 лет назад все люди жили относительно небольшими группами, прежде чем мы начали формировать вождества. Вождества происходят прямо или косвенно от сельского хозяйства. Числа имеют решающее значение для всего, что вы видите вокруг себя из-за всех технологий и медицины. Все это происходит от поведения, которое прямо или косвенно связано с числами, включая системы письма.
Они позволяют использовать все виды материальных технологий. Помимо того, что они помогают нам думать о количествах и изменять нашу ментальную жизнь, они позволяют нам делать что-то для создания сельского хозяйства. У пираха есть подсечно-огневая техника, но если вы собираетесь заниматься систематическим сельским хозяйством, им нужно больше. Если вы посмотрите на майя и инков, они явно очень полагались на числа и математику. Числа кажутся воротами, которые имеют решающее значение и необходимы для других видов образа жизни и материальных культур, которые мы все разделяем сейчас, но которых в какой-то момент у людей не было. В какой-то момент более 10 000 лет назад все люди жили относительно небольшими группами, прежде чем мы начали формировать вождества. Вождества происходят прямо или косвенно от сельского хозяйства. Числа имеют решающее значение для всего, что вы видите вокруг себя из-за всех технологий и медицины. Все это происходит от поведения, которое прямо или косвенно связано с числами, включая системы письма. Мы не развиваем письмо без предварительного развития чисел.
Мы не развиваем письмо без предварительного развития чисел. Мы не знаем наверняка, но у нас нет конкретных доказательств того, что они могут сделать это самостоятельно. Если вы посмотрите на Алекса, африканского серого попугая [и предмет 30-летнего исследования психолога животных Ирэн Пепперберг), то, что он был способен делать, было довольно замечательно, последовательно считать и складывать, но он развил эту способность только тогда, когда ее научили. снова и снова, эти числовые слова. В некотором роде это можно передать и другим видам — некоторые шимпанзе, кажется, способны выучить некоторые основные числа и основы арифметики, но они не делают этого самостоятельно. Они похожи на нас в том, что, кажется, способны на это, если им дать количество слов. Это открытый вопрос, насколько это легко. Нам это кажется легким, потому что у нас это было с самого раннего возраста, но если вы посмотрите на детей, это не происходит естественным образом.
Мы не знаем наверняка, но у нас нет конкретных доказательств того, что они могут сделать это самостоятельно. Если вы посмотрите на Алекса, африканского серого попугая [и предмет 30-летнего исследования психолога животных Ирэн Пепперберг), то, что он был способен делать, было довольно замечательно, последовательно считать и складывать, но он развил эту способность только тогда, когда ее научили. снова и снова, эти числовые слова. В некотором роде это можно передать и другим видам — некоторые шимпанзе, кажется, способны выучить некоторые основные числа и основы арифметики, но они не делают этого самостоятельно. Они похожи на нас в том, что, кажется, способны на это, если им дать количество слов. Это открытый вопрос, насколько это легко. Нам это кажется легким, потому что у нас это было с самого раннего возраста, но если вы посмотрите на детей, это не происходит естественным образом. Хорошо представлены люди из определенного общества и культуры. Было бы неплохо, если бы жители Амазонки и коренные народы подверглись исследованиям фМРТ, чтобы получить представление о том, насколько это различается в разных культурах. Учитывая пластичность коры, культура играет роль в развитии мозга.
Хорошо представлены люди из определенного общества и культуры. Было бы неплохо, если бы жители Амазонки и коренные народы подверглись исследованиям фМРТ, чтобы получить представление о том, насколько это различается в разных культурах. Учитывая пластичность коры, культура играет роль в развитии мозга.