Крутящий момент | это… Что такое Крутящий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Содержание
|
Момент силы
В физике момент силы можно понимать как «вращающая сила».
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.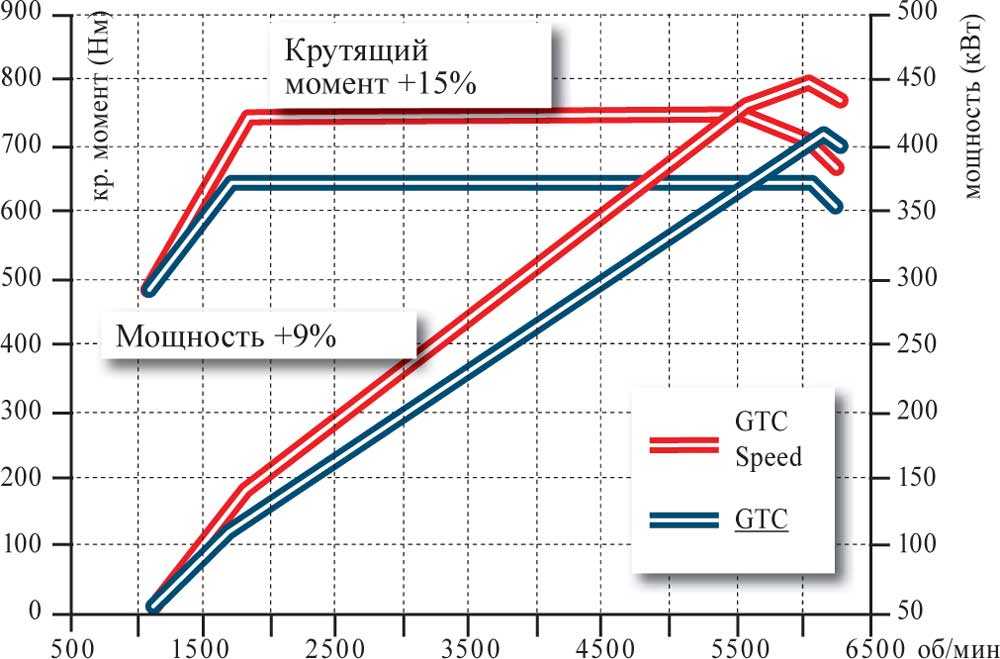
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
- Момент инерции
- Момент импульса
- Теорема Вариньона
Крутящий момент | это… Что такое Крутящий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Содержание
|
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.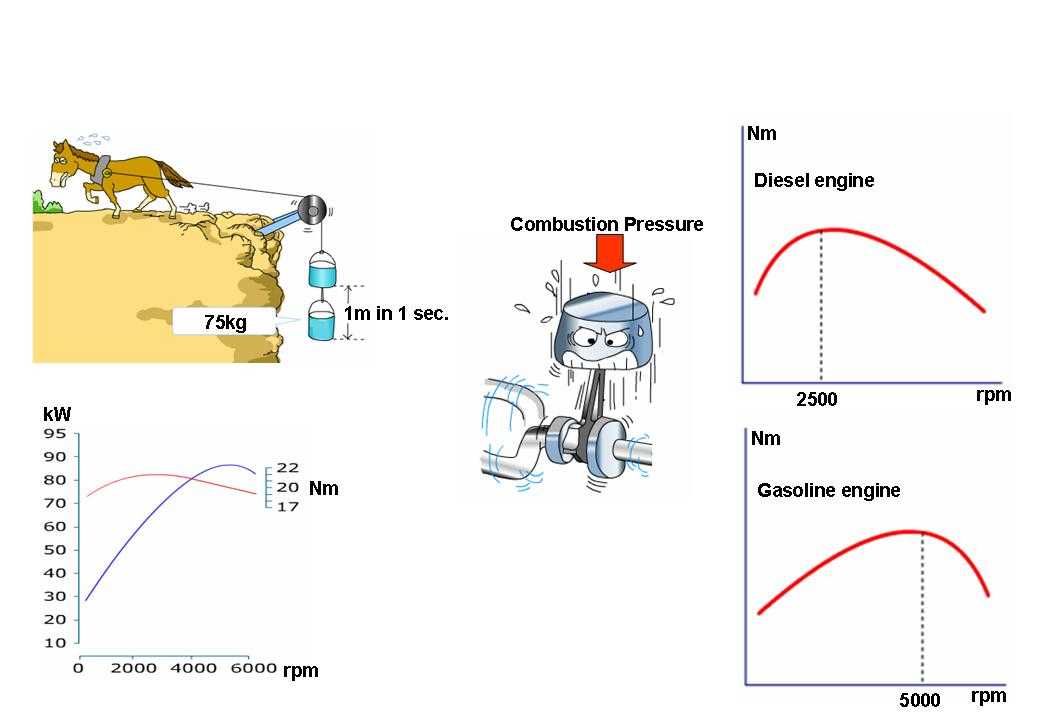
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
- Момент инерции
- Момент импульса
- Теорема Вариньона
Преобразование единиц измерения крутящего момента
Преобразование значений крутящего момента и единиц измерения в соответствии с вашими потребностями!
«Сколько Нм составляют 12,7 фут-фунта?»
Страница преобразования крутящего момента немедленно выполняет для вас
преобразований! Значения во всех общепринятых единицах измерения крутящего момента могут быть немедленно преобразованы в другие распространенные единицы измерения крутящего момента.
Найдите исходную единицу измерения и введите исходное значение, чтобы преобразовать значения крутящего момента в другие единицы измерения.
дюймовых граммов
| Блок | Значение |
|---|---|
| Дюйм-грамм | |
| Дюймы Фунты | |
| Миллиньютон-метры | |
| Сенти Ньютон Метры | |
| Деци Ньютон Метры | |
| Ньютон-метры | |
| Килограмм Сантиметры |
дюймовых унций
| Блок | Значение |
|---|---|
| Дюймовые унции | |
| Дюйм-грамм | |
| Дюймы Фунты | |
| Фунты Фунты | |
| Миллиньютон-метры | |
| Сенти Ньютон Метры | |
| Деци Ньютон Метры | |
| Ньютон-метры | |
| Грамм Сантиметры | |
| Килограмм Сантиметры | |
| Килограммы |
дюйма фунта
| Блок | Значение |
|---|---|
| Дюймы Фунты | |
| Дюйм-грамм | |
| Дюймовые унции | |
| Фунты Фунты | |
| Миллиньютон-метры | |
| Сенти Ньютон Метры | |
| Деци Ньютон Метры | |
| Ньютон-метры | |
| Килограмм Сантиметры | |
| Килограммы |
футо-фунта
| Блок | Значение |
|---|---|
| Фунт-фунт | |
| Дюйм-грамм | |
| Дюймовые унции | |
| Дюймы Фунты | |
| Миллиньютон-метры | |
| Сенти Ньютон Метры | |
| Деци Ньютон Метры | |
| Ньютон-метры | |
| Килограмм Сантиметры | |
| Килограммы |
миллиньютон-метра
| Блок | Значение |
|---|---|
| Миллиньютон-метры | |
| Дюйм-грамм | |
| Дюймовые унции | |
| Дюймы Фунты | |
| Фунты Фунты | |
| Сенти Ньютон Метры | |
| Деци Ньютон Метры | |
| Ньютон-метры | |
| Килограмм Сантиметры | |
| Килограммы | |
| Грамметры |
санти ньютон метры
| Блок | Значение |
|---|---|
| Санти Ньютон Метры | |
| Дюйм-грамм | |
| Унции в дюймах | |
| Дюймы Фунты | |
| Фунты Фунты | |
| Миллиньютон-метры | |
| Деци Ньютон Метры | |
| Ньютон-метры | |
| Килограмм Сантиметры | |
| Килограммы | |
| Грамм Сантиметр |
Деци Ньютон Метров
| Блок | Значение |
|---|---|
| Деци Ньютон Метры | |
| Дюйм-грамм | |
| Дюймовые унции | |
| Дюймы Фунты | |
| Фунты Фунты | |
| Миллиньютон-метры | |
| Сенти Ньютон Метры | |
| Ньютон-метры | |
| Килограмм Сантиметры | |
| Килограммы |
ньютон-метра
| Блок | Значение |
|---|---|
| Ньютон-метры | |
| Дюйм-грамм | |
| Дюймовые унции | |
| Дюймы Фунты | |
| Фунты Фунты | |
| Миллиньютон-метры | |
| Сенти Ньютон Метры | |
| Деци Ньютон Метры | |
| Килограмм Сантиметров | |
| Килограммы |
Килограмм Сантиметров
| Блок | Значение |
|---|---|
| Килограмм Сантиметры | |
| Дюйм-грамм | |
| Дюймовые унции | |
| Дюймы Фунты | |
| Фут Фунт | |
| Миллиньютон-метры | |
| Сенти Ньютон Метры | |
| Деци Ньютон Метры | |
| Ньютон Сантиметры |
килограмма метров
| Блок | Значение |
|---|---|
| Килограммы | |
| Унции в дюймах | |
| Дюймы Фунты | |
| Фунты Фунты | |
| Миллиньютон-метры | |
| Сенти Ньютон Метры | |
| Деци Ньютон Метры | |
| Ньютон-метры | |
| Килограмм Сантиметры |
NEMA Конструкция электрического двигателя A, B, C и D
NEMA установила четыре различных конструкции A, B, C и D для электрических асинхронных двигателей.

Рекламные ссылки
Различные двигатели с одинаковой номинальной мощностью могут иметь разные пусковой ток, кривые крутящего момента, скорости и другие параметры. При выборе конкретного двигателя для поставленной задачи необходимо учитывать все технические параметры.
Четыре конструкции NEMA (Национальной ассоциации производителей электрооборудования) имеют уникальное соотношение скорости, крутящего момента и скольжения, что делает их подходящими для различных типов приложений.
Конструкция NEMA A
- максимальное скольжение 5 %
- пусковой ток от высокого до среднего
- нормальный крутящий момент заторможенного ротора
- нормальный крутящий момент
- подходит для широкого спектра применений, например, вентиляторы и насосы 6 NEMA исполнение B
- максимальное проскальзывание 5 %
- низкий пусковой ток
- высокий крутящий момент при заторможенном роторе
- нормальный пробивной крутящий момент
- подходит для широкого спектра применений с нормальным пусковым крутящим моментом — общее в Системы HVAC с вентиляторами, воздуходувками и насосами
- максимальное проскальзывание 5 %
- низкий пусковой ток
- высокий крутящий момент при блокировке ротора
- нормальный разрывной крутящий момент
- подходит для оборудования с высокой инерцией и пуском крутящий момент при запуске — как у объемных насосов, конвейеров
- максимальное скольжение 5-13%
- низкий пусковой ток
- очень высокий крутящий момент заблокированного ротора
- подходит для оборудования с очень высокой инерцией пуска, такого как краны, подъемники и т.
 д.
д.
NEMA исполнение C
NEMA исполнение D
Рекламные ссылки
Связанные темы !
Добавляйте стандартные и настраиваемые параметрические компоненты, такие как балки с полками, пиломатериалы, трубопроводы, лестницы и т. д., в свою модель Sketchup с помощью Engineering ToolBox — расширения SketchUp, которое можно использовать с потрясающими, интересными и бесплатными приложениями SketchUp Make и SketchUp Pro. .Добавьте расширение Engineering ToolBox в свой SketchUp из хранилища расширений SketchUp Pro Sketchup!
Перевести
О Engineering ToolBox!
Мы не собираем информацию от наших пользователей. В нашем архиве сохраняются только электронные письма и ответы. Файлы cookie используются только в браузере для улучшения взаимодействия с пользователем.
Некоторые из наших калькуляторов и приложений позволяют сохранять данные приложения на локальном компьютере. Эти приложения будут — из-за ограничений браузера — отправлять данные между вашим браузером и нашим сервером.


 также
также д.
д.