Сила трения скольжения – формула, от чего зависит
4.4
Средняя оценка: 4.4
Всего получено оценок: 72.
4.4
Средняя оценка: 4.4
Всего получено оценок: 72.
Большое количество задач классической механики требуют учета силы трения скольжения, ее учитывают и при проектировании различных механизмов, чтобы подобрать смазочные материалы или сделать конструкцию, при которой трение минимизируется. Поэтому необходимо понимать ее причины и уметь рассчитывать.
Природа силы трения скольжения
Простейший опыт, который позволяет обнаружить трение, ставится в бытовых условиях. Для это необходимо привязать к грузу веревку и потянуть его. Тянущую силу можно измерить с помощью динамометра или ручных весов с крючком.
Рис. 1. Иллюстрация опыта.Пока сила меньше предельного значения, груз остается на месте, и причина этого – трение покоя. По модулю его сила равна внешней силе и направлена в противоположную сторону.
Трение обусловлено тем, что на микроуровне всякая поверхность шероховата.
Если внешняя сила достигает предельного значения, равного наибольшей силе трения покоя, груз начинает двигаться. Тогда возникает трение скольжения. Существует набор законов, названных в честь Кулона, открывшего их, которые описывают это явление.
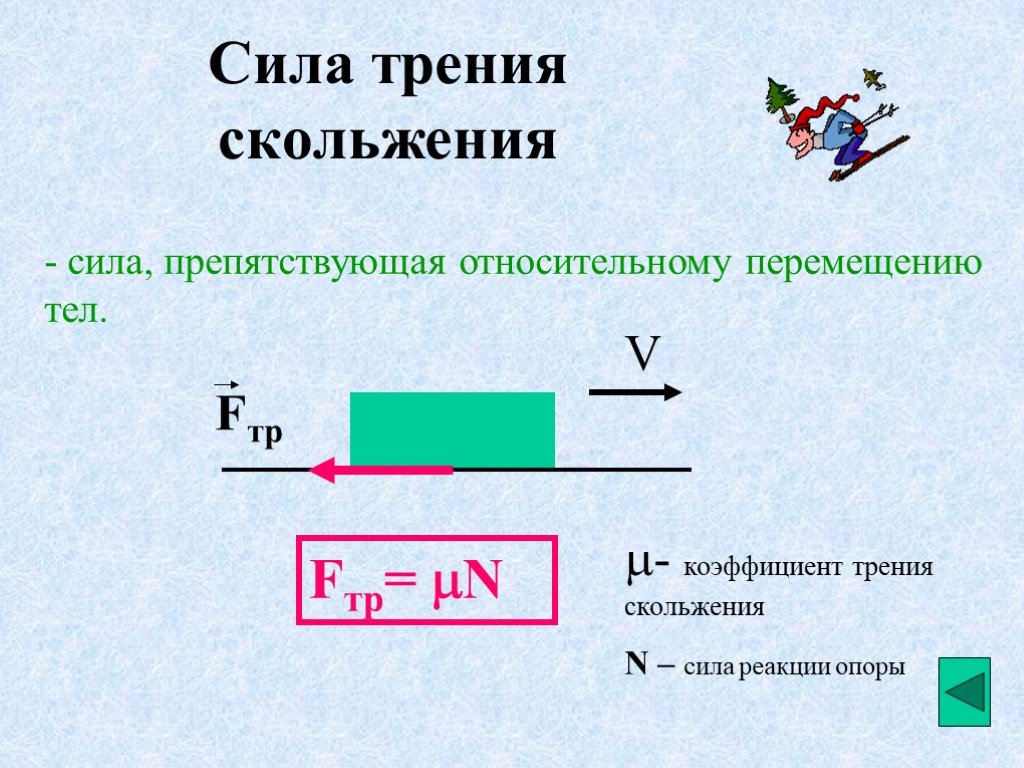
Сила трения скольжения:
- Направлена вдоль поверхности соприкосновения и препятствует причинам движения.
- Не зависит от площади соприкосновения.
- Пропорциональна нормальной реакции опоры.
- Пропорциональна безразмерному коэффициенту трения.
Расчет силы трения скольжения
Для расчета силы трения скольжения допускают, что она не зависит от скорости и приблизительно равна наибольшему значению трения покоя. При невысоких скоростях такое приближение позволяет производить расчеты с достаточной точностью. Тогда формула силы трения скольжения запишется так:
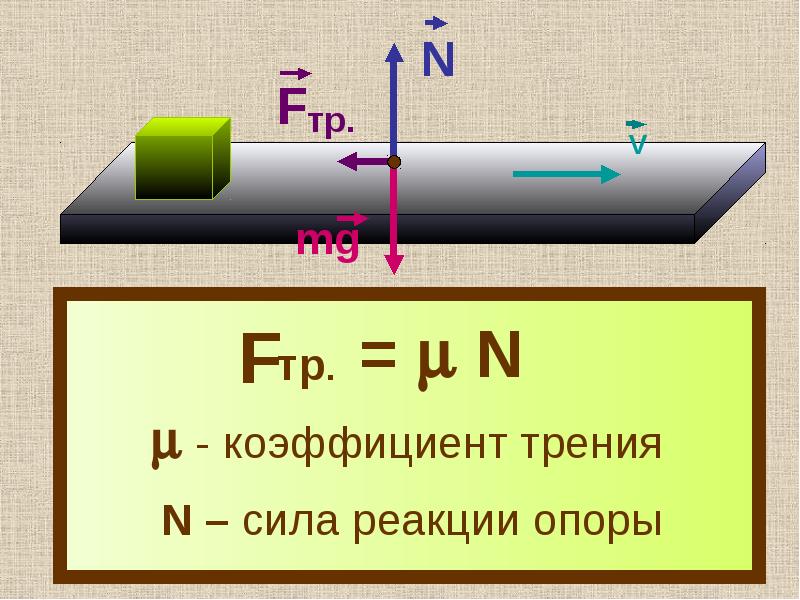
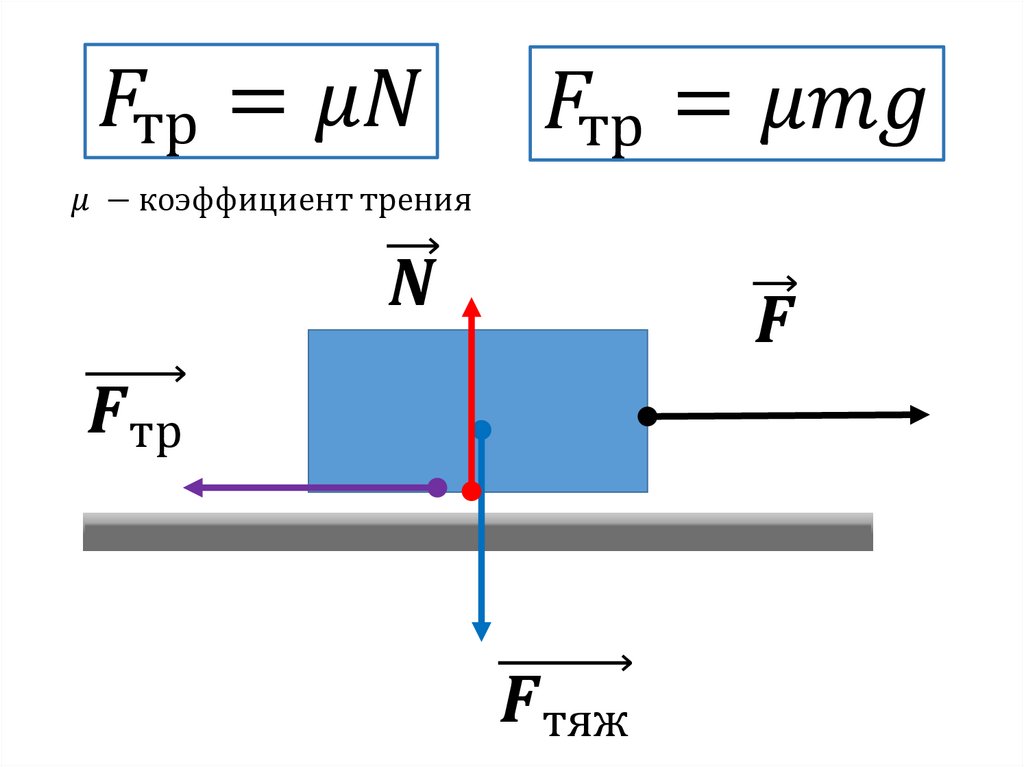
$F_{тр} = \mu N$, которая называется формулой Кулона-Амонтона и является математическим выражением третьего закона Кулона.
При движении по горизонтальной поверхности $N = mg$
$\mu$ – коэффициент трения скольжения, значение которого примерно равно коэффициенту трения покоя.
В том случае, если тело движется по наклонной поверхности, $F_{тр} = \mu mgsin \varphi$, где $\varphi$ – угол наклона поверхности.
Когда поверхности сухие, трение называют сухим. Выделяют и другие виды: с сухой смазкой, жидкостное (влажная смазка), смешанное, когда чередуются влажные и сухие участки поверхностей.
Задачи
- Тело тянут на вершину горы с силой, равной 28 Н. Масса тела – 2 кг, угол наклона горы – 30˚, ускорение – 1 м/c2. Найти коэффициент трения скольжения.
Решение первой задачи
Запишем второй закон Ньютона в векторной форме:
$$m \vec a = \vec F_{тр} + m \vec g + \vec N + \vec F$$
И в проекциях на оси:
Ох: $ma =F – F_{тр} – mgcos \varphi$ – (1)
Оу: $N=mgsin \varphi$ – (2)
Подставляя (2) в (1), получим:
$ma =F – \mu mgsin \varphi – mgcos \varphi$, тогда коэффициент трения скольжения будет равен:
$$\mu ={F \over mgsin \varphi} – {a \over gsin \varphi} – ctg \varphi = 0,87$$.
2 \over Rg} = {100 \over 10g} = 1$. Отсюда следует, что предельный угол равен 45˚.
Что мы узнали?
В ходе урока было установлено, от чего зависит сила трения скольжения и какова ее природы, были рассмотрены законы, характеризующие ее, и расчетные формулы, введены понятие коэффициента трения скольжения и виды трения скольжения. В завершении урока решены несколько задач.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Роман Гаврилов
10/10
Оценка доклада
4.4
Средняя оценка: 4.4
Всего получено оценок: 72.
А какая ваша оценка?
исчерпывающие подходы и факты —
Как найти ускорение с помощью коэффициента трения — еще одна важная и общепринятая тема, которую необходимо решить. Это фактор, который определенным образом увеличивает ускорение.
Когда тело находится в движении, оно будет продолжать движение до тех пор, пока на него не подействует сила, изменяющая размеры объекта.
Таким образом, этот процесс будет продолжаться до тех пор, пока скорость не будет увеличена или уменьшена.
Как только объект изменяет скорость, он либо ускоряется (положительно), либо замедляется (отрицательно), обычно в направлении, противоположном движению. Изменение скорости также известно как скорость с точки зрения физики.
Изменение скорости происходит в другое время, и, следовательно, это будет влиять на ускорение движущегося тела либо положительно, либо отрицательно. Внезапный рывок в системе также влияет на ускорение.
Когда тело находится в движении, на него влияет несколько факторов, и одним из них является ускорение, на которое будет влиять термин, называемый трением. Постепенно мы будем иметь дело с нахождением ускорения с помощью коэффициент трения.
Мы можем продолжать говорить об ускорении по-разному, но когда на ускорение влияет другой фактор, нам нужно сосредоточиться на этом. Трение — это, по сути, фактор, присутствующий между телом и активной поверхностью.
Прежде чем мы углубимся в это подробно, необходимы первые знания о трении и коэффициенте трения. Трение по сути, это сила, которая сопротивляется движению при ходьбе, беге и т. д.
Между объектом и поверхностью присутствует небольшой фактор, который называется трением. Эта конкретная сила называется силой трения. Эта сила помогает любому случайному телу в действии двигаться.
Когда поверхность шероховатая, трение больше, а когда поверхность гладкая, трение меньше. Таким образом, когда трение увеличивается, ускорение уменьшается, а когда трение уменьшается, ускорение уменьшается. Это также базовое понимание в знакомых терминах.
Теперь давайте посмотрим, что именно означает коэффициент трения. Этот коэффициент трения представляет собой безразмерный коэффициент, представляющий собой соотношение между нормальной силой и силой трения движущегося тела.
Итак, все мы знаем, что движению тела способствуют несколько различных аспектов.
Так или иначе, он будет ускоряться. Во-первых, это изменение скорости, называемое скоростью, которое помогает в подвижности тела.
В некоторых случаях это тоже кажется существенным. Это будет внешняя сила или любая другая сила и чистая сила в целом. Фактор, называемый трением, вносит большой вклад в движение любого объекта или тела. Коэффициент трения будет определять, сколько силы потребуется для такого движения тела.
Поскольку это мера отношения, она будет иметь нулевые размеры, а значение будет варьироваться от минимального 0 до максимального значения 0.5. Также может быть коэффициент трения, который может быть больше единицы.
Как найти ускорение по коэффициенту тренияТребуется знание формулы для определения ускорения. Согласно второму закону Ньютона, ускорение пропорционально силе и косвенно пропорционально массе объекта.
Следовательно, мы получаем его как а = Ф / м. это формула базового ускорения без каких-либо атрибутов.
Когда трение действует на тело и его движение, не менее важен тип поверхности.
Таким образом, формула изменяется в соответствии с коэффициентом трения, a = (fn-μ) / m. μ известен как коэффициент трения, и он указывает количество силы, необходимой для дальнейшего движения тела.
Давайте посмотрим, как это сделать, на лучшем примере. Трение весом 10 кг прикладывается к правому трению 7 Н. Допускается ускорение на неровной поверхности. Сила трения имеет значение 0.3 Н. Теперь вычислите ускорение объекта.
а = (20 — 0.3) / 7
а = 19.7 / 7
a = 2.81 мс-2
Вот как найти ускорение с коэффициентом трения. Но где использовать коэффициент трения — это вопрос. Мы тоже с этим разберемся. В вопросе прямо дана постоянная силы трения.
Сила трения и сила нормали не будут указаны явно, но значения могут быть нарисованы с использованием коэффициента трения. По приведенным данным мы должны рассчитать коэффициент трения, чтобы применить его к формуле и найти ускорение.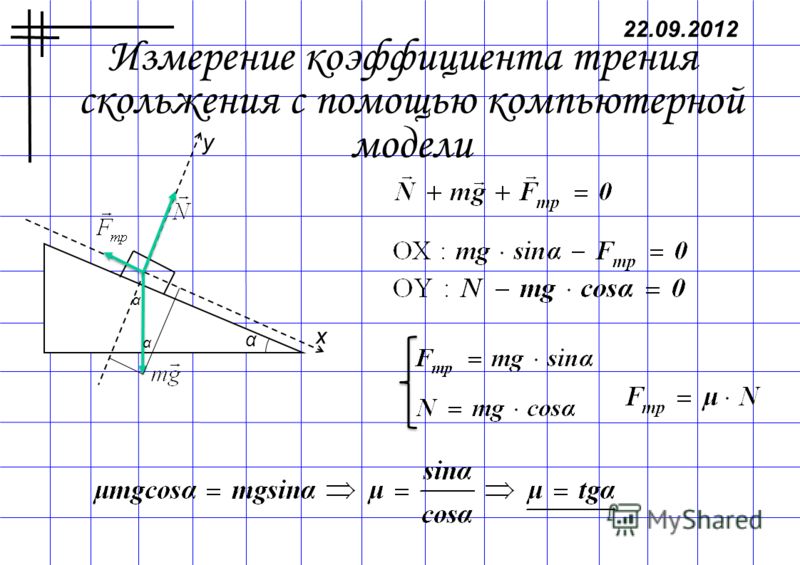
Проблема:
Автомобиль весом 1100 кг с коэффициентом трения μ = 0.95 относительно шин. Теперь определим ускорение. Он движется с силой 880 Н.
Решение:
Нам нужно понять эту проблему, используя диаграмму свободного тела. Теперь давайте погрузимся в движение автомобиля и силы, действующие на него. Поскольку автомобиль находится в движении, на него будет воздействовать как можно больше сил.
Мы знаем, что по умолчанию на тело действует нормальная сила; теперь, когда он находится в движении, действует также сила трения.
Значение, данное для коэффициента трения: μ = 0.95. Здесь нам нужно найти фрикционную и нормальные силы, так как коэффициент значение трения уже задано.
Отметим, что нормальная сила равна силе гравитации. Известно, что сила тяжести составляет 9.8 мс-1. А теперь это значение, умноженное на массу, дает нормальную силу.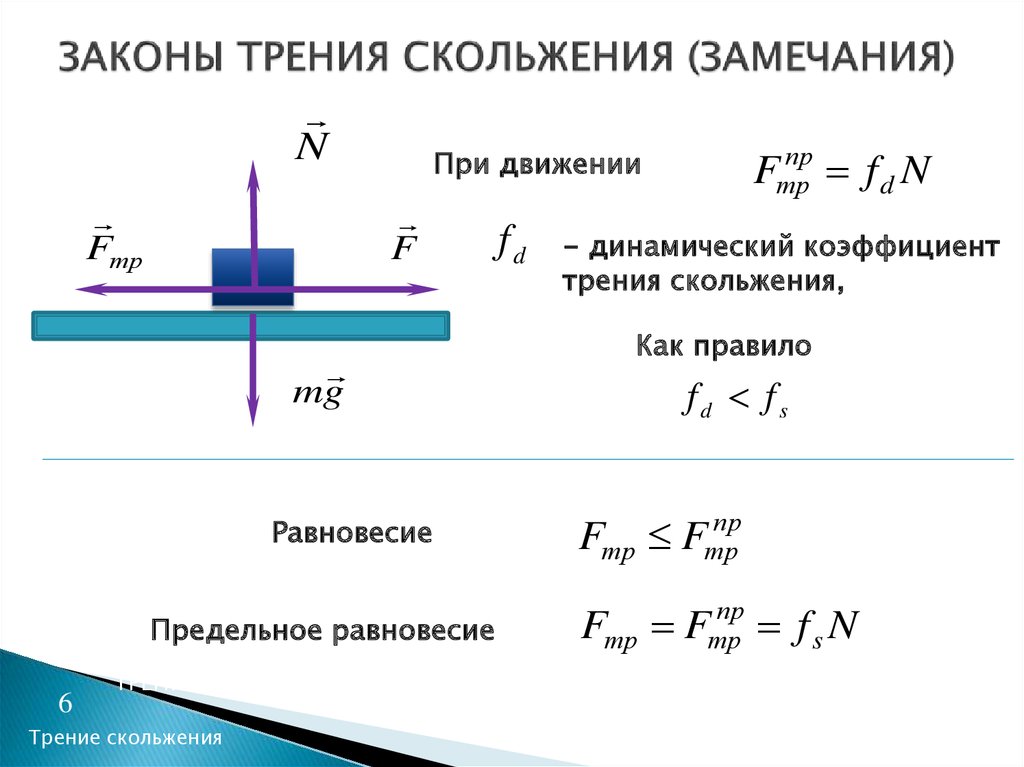
Fn = 1100 × 9.8 = 10780.
Сила трения — это коэффициент трения, умноженный на нормальную силу. Следовательно ff = 10241. Теперь, когда сила трения найдена, следующим шагом будет определение ускорения. Сила трения также считается чистой силой.
а = ф / м
а = 10241/1100
а = 9.31 мс-2
Часто задаваемые вопросыКак найти скорость с трением?Поскольку ускорение можно найти с помощью трения, можно найти и скорость, поскольку это не что иное, как изменение скорости.
Во-первых, нам нужно известна начальная скорость и сила тяжести. Таким образом, скорость с учетом трения находится по формуле: начальная скорость минус коэффициент трения, умноженный на силу тяжести и заданное время. v(t) = v0 – µ g t.
Как найти коэффициент трения?Коэффициент трения — это фактор, который присутствует между движущимся телом и поверхностью, с которой оно движется.
Формула для коэффициента трения: μ = (сила трения) / (сила в норме). Еще один момент, который следует отметить, заключается в том, что сила трения иногда равна чистой силе, действующей на тело, что упрощает вычисление ускорения. Нормальная сила рассчитывается путем умножения силы тяжести и массу тела.
Какие бывают типы трения?Статическое и кинетическое трение — это два разных типа, которые подпадают под одну тему трения.
Статическое трение называется трением, когда тело не движется. Из самого слова «статика» очевидно, что ничего не движется. В таких случаях найденное трение называется трением покоя. Когда тело выходит из равновесия, это также происходит из-за трения, которое называется кинетическим трением. Статическое и кинетическое трение различается в зависимости от случая и условий.
Почему статическое трение называется так?Статическое трение называется так, потому что это сила, противодействующая неподвижному телу.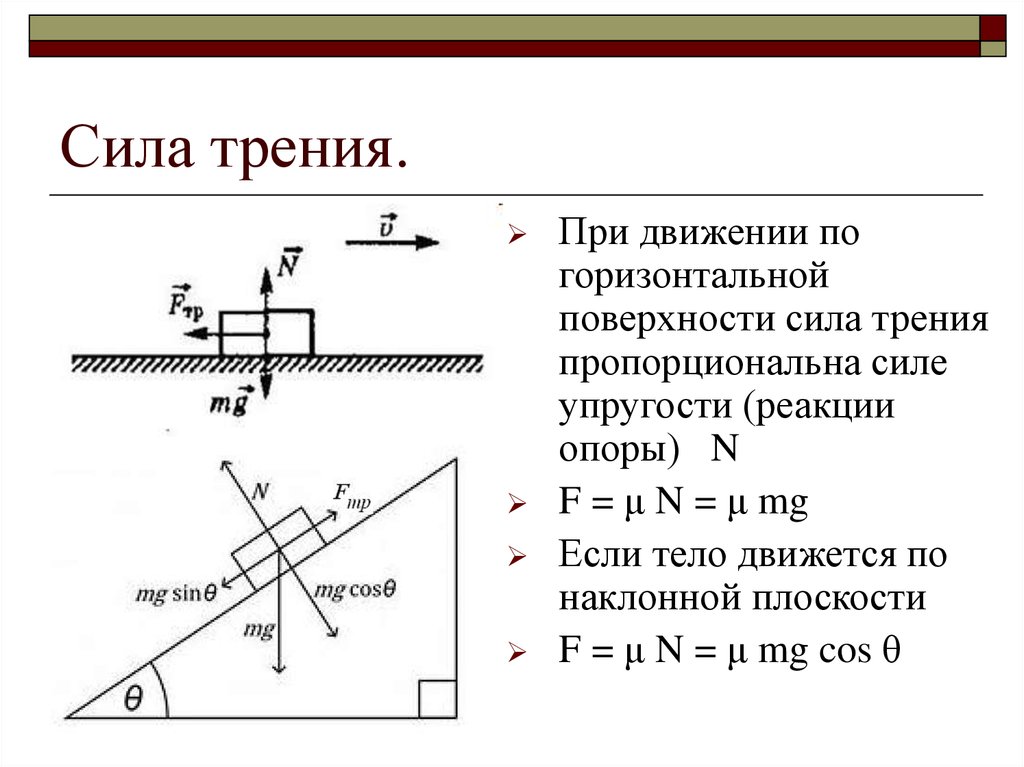
Когда тело не движется и остается в положении равновесия, трение, действующее на тело, называется трением покоя. Это трение всегда действует в направлении, противоположном силе, действующей вместе с движением тела, даже когда оно не действует.
ньютоновская механика — Как я могу рассчитать замедление из-за трения?
спросил
Изменено 2 года, 6 месяцев назад
Просмотрено 10 тысяч раз
$\begingroup$
Мне было интересно, как я могу рассчитать замедление объекта из-за трения и, следовательно, найти максимальное расстояние, которое он может преодолеть?
Например, если автомобиль внезапно затормозит посреди дороги, как я могу узнать, сколько времени потребуется ему для полной остановки, его замедление, расстояние, которое он преодолеет до остановки?
Или, если кто-то катается на лыжах и достигает подножия горы, где земля становится плоской, как я могу узнать, сколько времени потребуется лыжнику, чтобы полностью остановиться?
Раньше я использовал формулу (в которой я не слишком уверен): $deceleration = -g \times \mu_{static}$.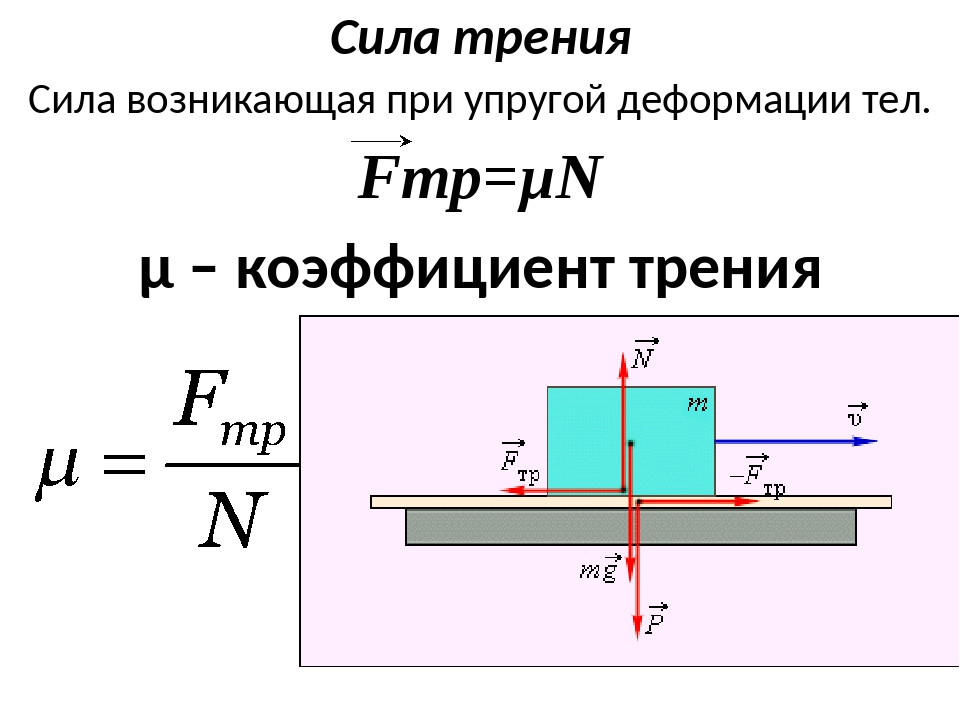
- ньютоновская механика
- ускорение
- трение
- скорость
- расстояние
$\endgroup$
1
$\begingroup$
Мне было интересно, как я могу рассчитать замедление объекта из-за трения — и, следовательно, найти максимальное расстояние, которое он может достигать?
Если вы знаете скорость объекта до того, как трение начнет его останавливать, вы можете рассчитать тормозной путь, используя теорему о работе-энергии, которая утверждает, что чистая работа, выполненная над объектом, равна изменению его кинетической энергии. Если единственной силой, действующей на объект и останавливающей его, является сила трения, то 92}{2μg}$$
Где $d$ = тормозной путь, $v$ = скорость объекта до столкновения с трением, $µ$ = коэффициент трения и $g$= ускорение под действием силы тяжести.
В случае тормозного пути транспортного средства, если автомобиль скользит, вы используете коэффициент кинетического трения между шинами и дорогой. Если колеса продолжают катиться, вы используете коэффициент статического трения. Обычно сопротивлением качению можно пренебречь.
Вы можете рассчитать величину замедления по второму закону Ньютона 92}{2}$$
$$t=\sqrt \frac{2d}{a}$$
Надеюсь, это поможет.
$\endgroup$
$\begingroup$
Ну g×коэффициент трения покоя – неправильный способ определения замедления из-за трения.
Первая очевидная причина заключается в том, что если объект движется, то в игру вступает кинетическое трение, или же в реальных условиях качения играет роль трение качения.
Только в совершенно идеальном сценарии чистого качения мы можем учитывать статическое трение в наших расчетах.
Однако большинство вопросов касаются идеальных случаев, поэтому эта часть в основном верна.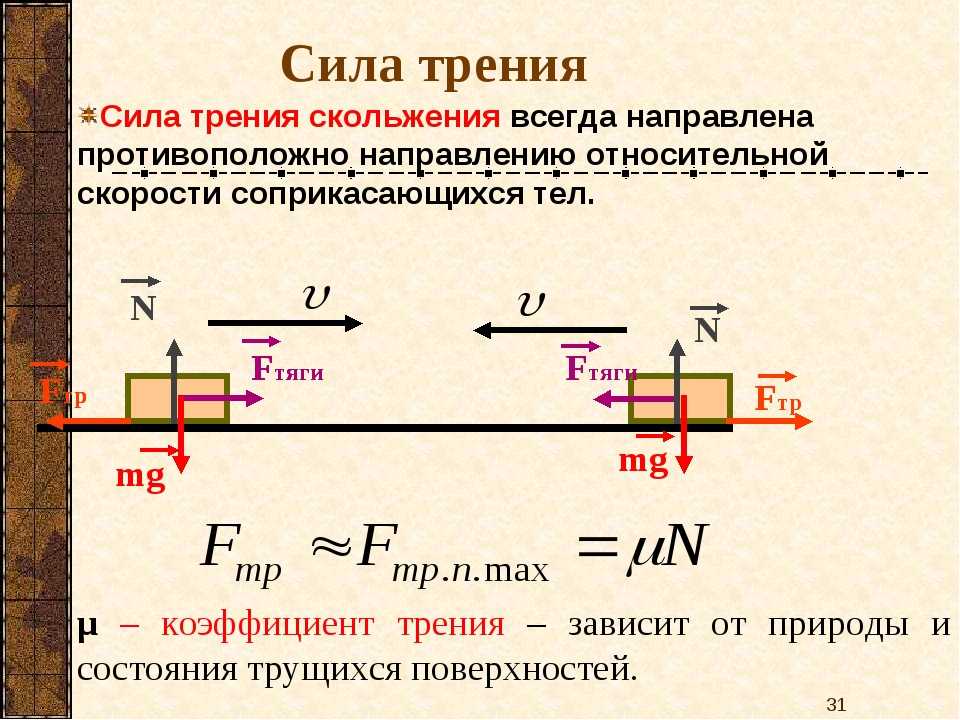
Также другой термин «g» будет правильным только в таких случаях, как автомобиль, движущийся по прямой дороге и т. д.
Если объект двигался по наклонной, ваша формула даст вам неправильное значение.
Это связано с тем, как определяется трение.
Когда объект движется. Трение = Коэффициент кинетического трения × Нормальная сила
Только на плоской поверхности нормальная сила будет равна мг.
На плоскости, наклоненной под углом $\theta $ к земле, это будет $mg \cos\theta $
Таким образом, замедление здесь будет иметь член gcos $\theta $ вместо члена g в вашей формуле.
Надеюсь помог!
$\endgroup$
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
В «эксперименте с трением» вы собрали данные о расстояниях и времени для задействованных масс. Эти данные позволяют производить расчеты энергий, участвующих в движениях. Одной из фундаментальных симметрий природы является сохранение энергии: «Энергия не создается и не уничтожается». Это означает, что для любого физического эксперимента вы должны иметь возможность «балансировать энергетическую чековую книжку» и учитывать энергии, задействованные в различных частях эксперимента. Эксперимент начинается с энергетического баланса в виде гравитационной потенциальной энергии массы, висящей на струне. Когда масса падает на пол, вы забираете весь этот баланс, выплачивая его в виде кинетической энергии падающей массы и движущегося блока на столе выше. Веревка, прикрепленная к бруску на деревянной дорожке, совершает над ним работу, которая равна силе, умноженной на расстояние. Ниже приведен пример анализа данных, полученных в лаборатории. Детальный анализ имеет параллельные поля ввода, в которые вы можете ввести свои данные для сравнения и определить коэффициент трения на основе ваших собственных данных. В полях данных по умолчанию будут значения для примеров, поэтому вам нужно будет убедиться, что ваши значения для измерений введены. Первым шагом в анализе является определение вашего начального энергетического баланса, потенциальной энергии висящей массы. Потенциальная энергия = мгч = (0,1502 кг)(9,8 м/с 2 )(0,3 м) = 0,44 джоуля. Потенциальная энергия = мгч = ( кг)(9,8 м/с 2 )( м) = джоули. Рассматриваемый нами «энергетический счет» состоит только из висящей массы и блока, к которому она прикреплена на веревке. Мы пренебрегаем струной из-за ее крошечной массы, поэтому наш счет состоит из энергии этих двух объектов. Любая энергия, передаваемая земле (стол, пол, деревянная дорожка, по которой она скользит и т. д.), рассматривается как отвод энергии из нашей системы. Эта энергия, конечно, не теряется, поскольку в конечном счете энергия никогда не теряется, а просто переносится из нашего счета энергии для эксперимента. Первый отвод происходит, когда висящая масса врезается в пол: до столкновения у нее была кинетическая энергия, а после столкновения ее нет. Так как кинетическая энергия = (1/2)mv 2 , нам нужна скорость удара о пол. Мы можем рассчитать среднюю скорость по расстоянию, деленному на время, но скорость удара вдвое больше средней. Этот этап энергетической оценки выглядит следующим образом: v среднее = h/t = 0,30 м/0,6 с = 0,5 м/с v среднее = ч/т = м/с = м/с v удар = 2v среднее = 1 м/с v удар = 2v среднее = м/с Кинетическая энергия = (1/2)мв 2 = (1/2)(0,1502 кг)(1 м/с) 2 = 0,075 Дж Кинетическая энергия = (1/2)мв 2 = (1/2)(кг)(м/с) 2 = Дж Это количество энергии теперь снимается со счета, и это завершает анализ энергии для висящей массы. Он сидит на полу, и у него не осталось ни потенциальной, ни кинетической энергии. Оставшаяся часть энергии должна была быть использована для выполнения работы над деревянным бруском, другой частью нашей системы.  |
Эта работа перемещает блок против сопротивления трения mmg, где вес равен W=mg. Это также придает ему кинетическую энергию, так что он все еще движется некоторое время после того, как висящая масса упадет на пол. В конечном счете, трение побеждает и останавливает скользящий блок, и в этот момент вы можете сказать, что вся работа, проделанная над блоком, была «снята» с вашего счета энергии, поскольку она рассеивается на сопротивление трению. Балансируя энергетическую чековую книжку, мы можем подразумевать работу, совершаемую против трения, и определить значение коэффициента трения, действовавшего между бруском и деревянной дорожкой, по которой он скользит.
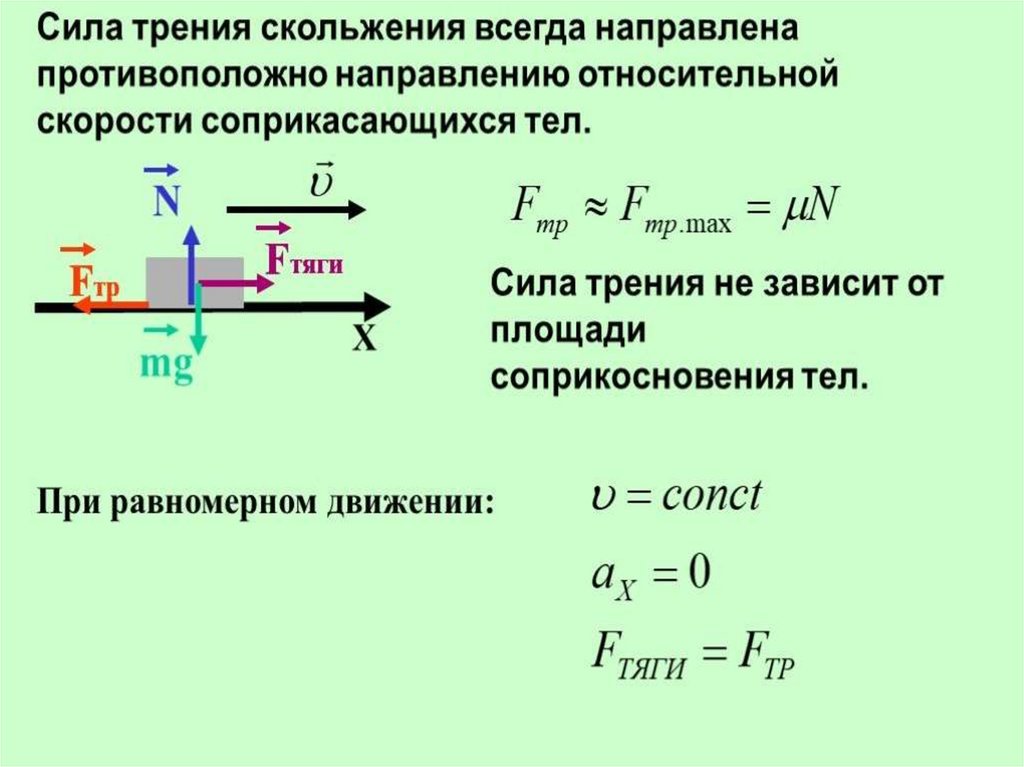
Следующим шагом является расчет этого вывода.