формула определения значения, обозначение в физике, измерительные действия
Физика
12.11.21
15 мин.
Процесс взаимодействия тел при их относительном движении можно отобразить с помощью формулы трения скольжения. Коэффициент определяется только путём проведённых исследований. Изучением процессов трения занимается раздел физики, который называется трибологией (механикой фрикционного взаимодействия). Определяемый коэффициент является совокупной характеристикой пары материалов, которые не зависят от площади соприкосновения тел.
Оглавление:
- Краткое описание
- Сила трения скольжения
- Правила расчёта
- Измерительные манипуляции
- Основные характеристики
- Практическое значение
- Ключевые нюансы
Процесс взаимодействия тел при их относительном движении можно отобразить с помощью формулы трения скольжения.
Коэффициент определяется только путём проведённых исследований. Изучением процессов трения занимается раздел физики, который называется трибологией (механикой фрикционного взаимодействия). Определяемый коэффициент является совокупной характеристикой пары материалов, которые не зависят от площади соприкосновения тел.
Краткое описание
Трение можно рассматривать как способ взаимодействия двух объектов. Но у этого процесса есть свои нюансы. Между двумя объектами трение возникает только в результате их соприкосновения с определённой площадью поверхности. Этот процесс попадает под действие третьего закона Ньютона.
Например, если взять 2 небольших бруска из дерева и просто их передвигать, то в итоге можно наблюдать соприкосновение по площадям. Во время эксперимента можно заметить, что двигать предметами относительно друг друга гораздо сложнее, нежели совершать с ними какие-либо манипуляции в воздухе. Именно в этом случае в действие вступает закон трения.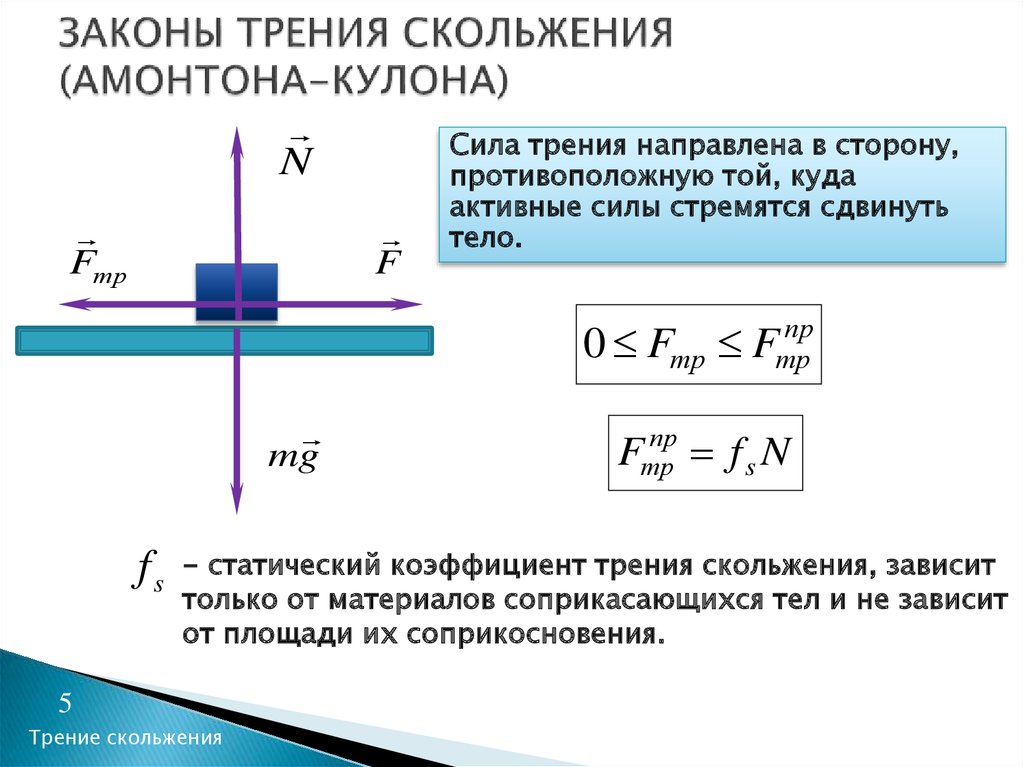
В третьем законе Ньютона описано правило, которое касается того, что по модулю силы равны, но направлены совершенно в разные стороны. Получается, что сила μ является векторной величиной. Этот процесс имеет электромагнитную природу. Трение возникает в результате того, что молекулы и атомы тел, участвующих в соприкосновении, начинают взаимодействовать друг с другом. На этом правиле основано много задач по физике. Латинской буквой k или греческой μ обозначается коэффициент трения.
Сила трения скольжения
Коэффициент трения скольжения показывает отношение μ к силе давления на поверхность. Это правило изучают на уроках физики в 10 классе. Силы трения всегда воздействуют на объекты. Они возникают в результате соприкосновения твёрдых тел, газов и жидкостей, подчиняются закону Ньютона.
Для решения сложных задач нужно понимать, что направление силы трения противоположно движению объекта и факторам, которые стремятся изменить его положение. Исключений не предусмотрено.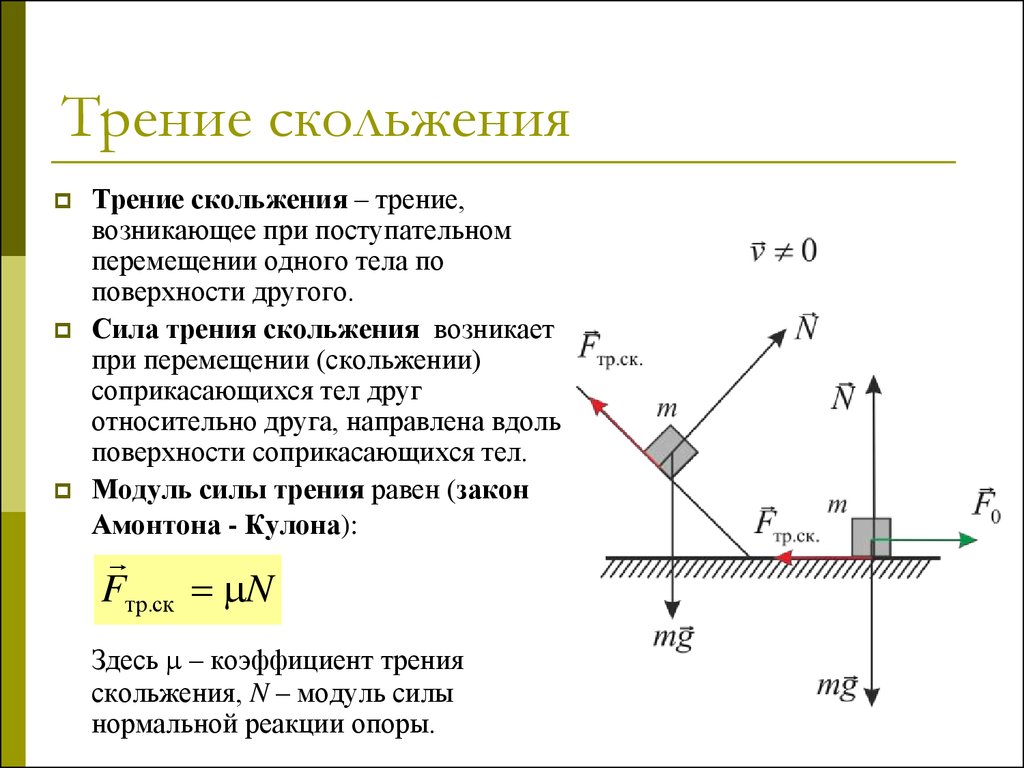
- скорости движения;
- коэффициента трения скольжения (µ), от которого напрямую зависят свойства, а также состояние поверхностей соприкосновения;
- силы нормальной реакции опоры (N→).
Итоговый коэффициент во многом зависит от свойств задействованного материала.
Например, чем шероховатее будет поверхность, тем больше станет значение μ. У скользких оснований коэффициент окажется минимальным. Трение во многом зависит от скорости, но этим значением часто пренебрегают, если речь не идет о точных измерениях. По этой причине показатель μ является постоянным.
Правила расчёта
С максимальной точностью силу трения скольжения можно определить с помощью формулы F = µ* N. Значение N рассчитывается как производное массы тела на ускорение свободного падения.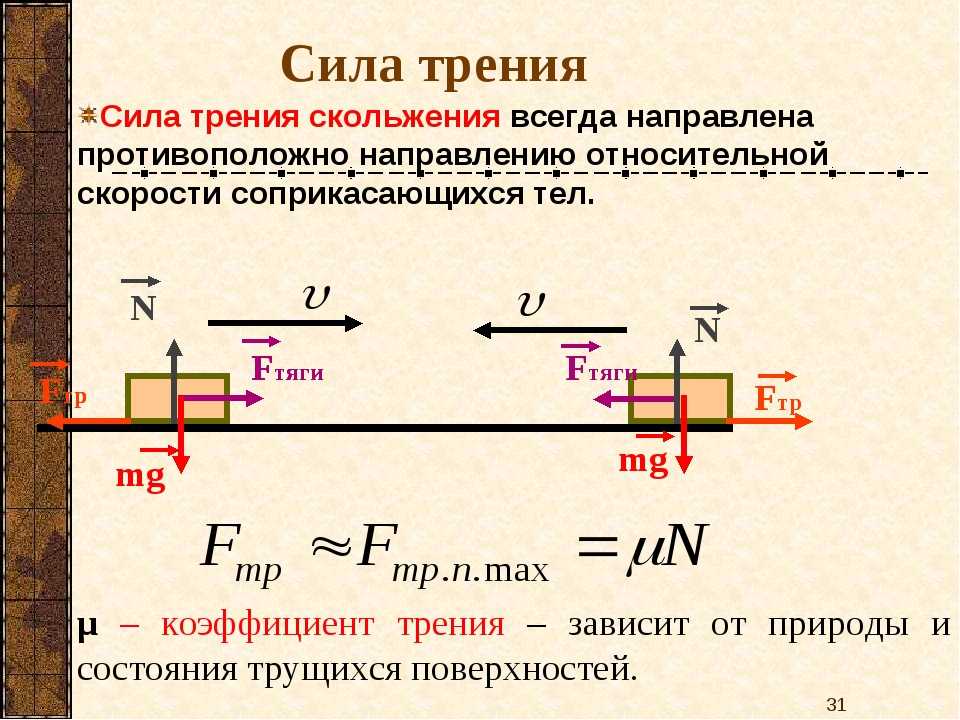
Учитывается также косинус угла к поверхности: N = m * g * cosa. Формула коэффициента трения скольжения выглядит следующим образом: µ = F/N.
На уроках физики можно узнать, что для основного количества всех пар материалов коэффициент рассчитывается во время опытов. Значение находится в пределах от 0,1 до 0,5. В такой ситуации μ будет являться переменной величиной.
В физике используются специальные таблицы, в которых указаны переменные величины для каждого из материалов. Но эти данные являются актуальными только при соблюдении определённых условий. Если нужно получить максимально точный результат, тогда следует самостоятельно выполнить расчёты для конкретной ситуации.
Измерительные манипуляции
Динамометр используется для измерения реальных показателей механической силы. Этот прибор включает в себя силовой элемент (пружину) и отчётное звено (линейку). Принцип использования стандартного пружинного динамометра прост.
Чтобы правильно найти величину μ, которая передаётся на брусок в процессе его движения по конкретной поверхности, нужно постараться прикрепить к объекту динамометр. Необходимо потянуть устройство за пружину в горизонтальной плоскости.
Чтобы полученный результат не имел погрешностей, нужно следить за тем, чтобы прибор перемещался максимально равномерно и с постоянной скоростью.
На анализируемую величину будут действовать сразу 2 силы, одна из которых препятствует движению бруска, а вторая старается снизить вероятность деформации пружины. Так как движение динамометра равномерное, силы имеют одинаковое значение и уравновешивают друг друга. На измерительной шкале регистрируется показатель упругости пружины, из-за чего полученная величина и будет искомой цифрой.
Проведённый опыт может доказать, что итоговое значение μ во многом зависит от веса задействованного объекта.
Если применить дополнительный груз и повторить исследование, тогда можно заметить, что значение на линейке увеличится.
Основные характеристики
Сила трения может рассматриваться как процесс, который возникает в результате соприкосновения двух объектов и препятствует их относительному движению. Основными причинами трения являются специфическая шероховатость трущихся поверхностей и взаимодействие имеющихся молекул. Существует определённый характер фрикционного взаимодействия, который принято делить на несколько категорий:
- Граничное. В области контакта содержатся участки и слои разной природы (например, жидкость, оксидные плёнки). Это самый распространённый случай, когда дело касается скольжения.
- Сухое. Взаимодействующие твёрдые тела не разделены между собой дополнительными слоями. На практике крайне редко фиксируются ситуации, которые свойственны сухому трению.
Для этого случая характерно наличие большого значения μ в состоянии покоя. - Жидкостное. Задействованные тела разделены слоем твёрдого тела (например, порошок графита), газом либо жидкостью. Эта ситуация чаще всего фиксируется при трении качения. Твёрдые тела погружены в жидкость, а величина μ отличается вязкой средой.
- Смешанное. Зона контакта содержит участки жидкостного и сухого трения.
- Вязкоупругое. Решающую роль играет внутреннее трение в смазывающем материале. Это фрикционное взаимодействие возникает при увеличении относительных скоростей перемещения.
Для этого случая характерно наличие большого значения μ в состоянии покоя.Многочисленные исследования показали, что для многих пар материалов итоговое значение µ не превышает 1. В противном случае можно говорить, что между контактирующими телами присутствует сила адгезии.
Для решения элементарных задач используется следующая формула: µ = (F + F adhesion)/ N. Значение μ измеряется стандартным образом, никакие дополнительные буквы для обозначения полученного результата не используются (указываются только цифры).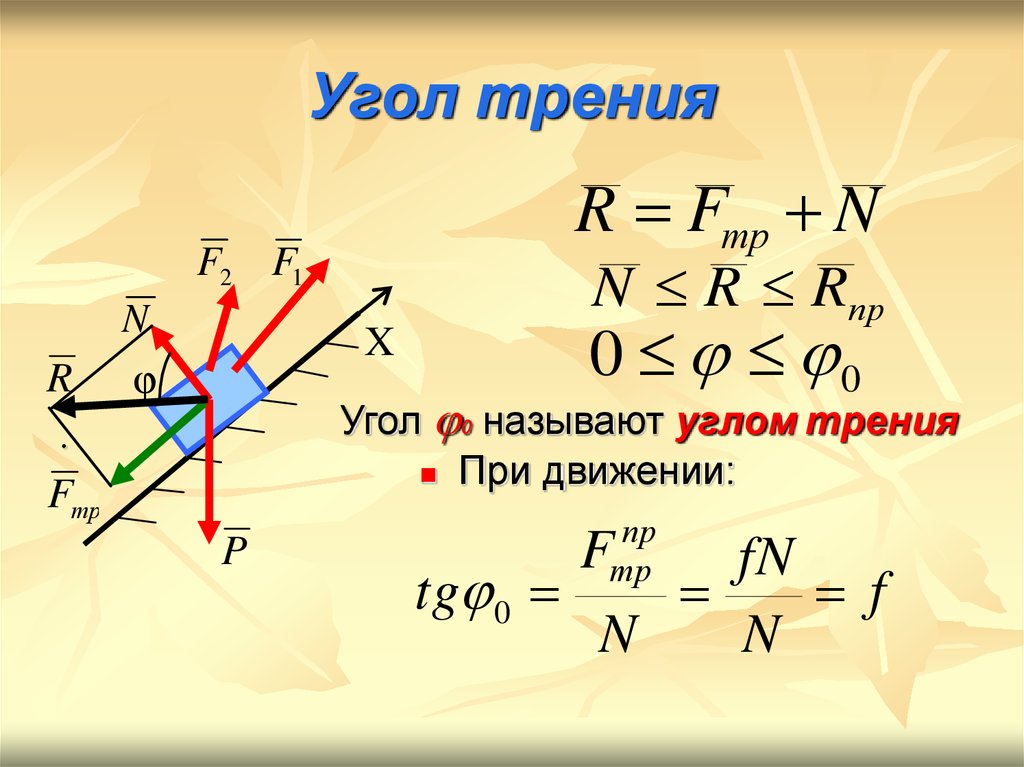
Практическое значение
Трение играет отрицательную роль во многих механизмах, например, в транспортных средствах, двигателях внутреннего сгорания, зубчатых шестеренках. Негативное значение сказывается на снижении коэффициента полезного действия механизма. Смазки, масла на синтетической и натуральной основе позволяют существенно уменьшить силу трения. На многих широко распространённых деталях присутствует защитное напыление.
Если речь идет о миниатюризации МЭМС (микроэлектромеханических систем) и НЭМС (наноэлектромеханических систем), тогда показатель μ будет существенно увеличиваться. Для решения этих проблем используется усовершенствованный подход в рамках трибологии.
Благодаря трению объекты могут перемещаться. Например, при ходьбе неизбежным является сцепление стопы с полом, из-за чего человек отталкивается от поверхности и движется дальше. Аналогичным образом происходит сцепление колёс транспортного средства с дорогой. Для повышения эксплуатационных характеристик автомобилей выпускаются инновационные формы и специальные разновидности резины для колёс.
На спортивные машины устанавливают универсальные антикрылья, которые прижимают транспортное средство к трассе.
Ключевые нюансы
Сила трения имеет место и при качении какого-либо тела. Но этим параметром часто пренебрегают, так как итоговые показатели недостаточно велики, чтобы брать их в расчёт. Такой подход позволяет упростить процесс решения различных задач. Но даже в этом случае можно сохранить высокую степень точности итогового результата.
Для закрепления полученных знаний можно изучить пример решения задачи по физике. На пол поставили ящик весом 7 кг. Между этим объектом и напольным покрытием значение μ составляет 0,3. К ящику прикладывают силу, которая соответствует 14 Н. Нужно совершить необходимые расчёты, чтобы понять, можно ли сдвинуть объект с места. Для определения силы реакции необходимо массу ящика умножить на ускорение:
- N = m * g.
- N = 10 кг * 9,8 м/с² = 98 кг * м/с² = 98 Н.
- F = k * N.
- F = 0,3 * 98 Н = 29,4 Н.
Полученный результат позволяет сделать вывод, что ящик останется на прежнем месте. Это связано с тем, что итоговое значение превышает усилия, приложенные к объекту: 29,4 Н > 14 Н.
Силы трения имеют большое значение в жизни людей и животных.
Благодаря этому явлению человек может ходить и держать в руках различные предметы. За счёт действия закона сцепления на скалах удерживаются огромные валуны и не падают в пропасть, а плетущиеся растения тянутся к солнечному свету и скрепляются с ближайшей опорой.
Люди и животные от природы умеют избавляться от негативного воздействия торможения. К примеру, всё тело рыбы покрыто специальной слизью, что позволяет существенно уменьшить трение о воду. Человек при работе с техникой научился использовать различные смазывающие материалы, благодаря чему увеличивается срок эксплуатации, а также качество работы устройства.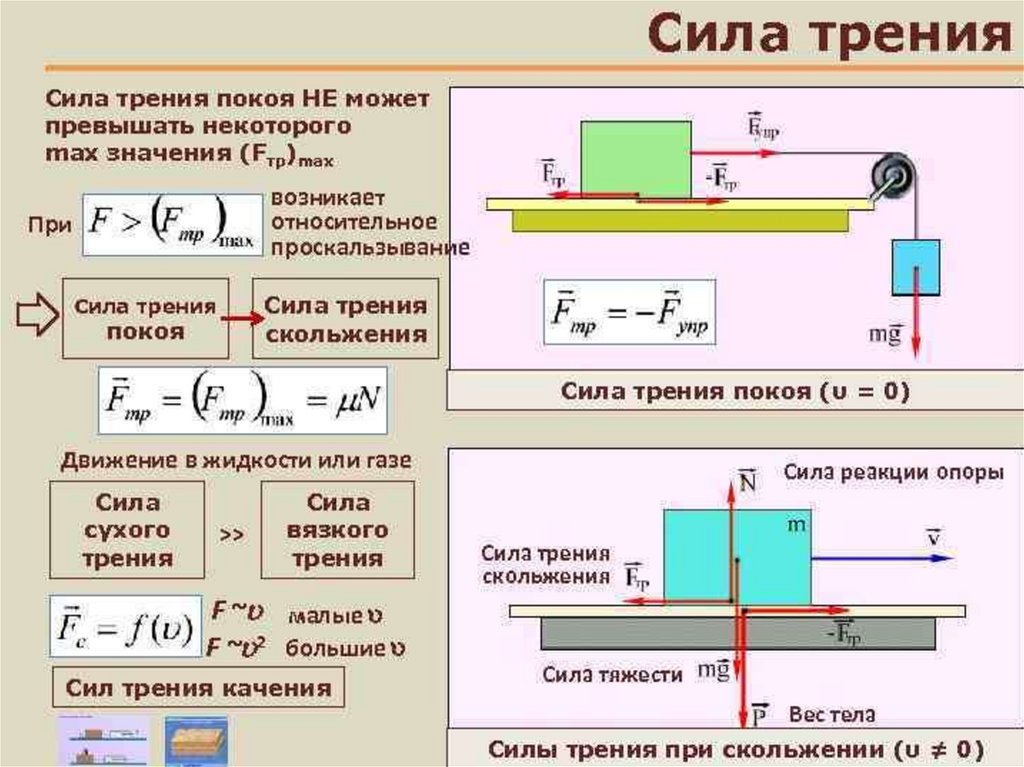
Сила трения. Коэффициент трения скольжения реферат по физике | Сочинения Физика
Скачай Сила трения. Коэффициент трения скольжения реферат по физике и еще Сочинения в формате PDF Физика только на Docsity! Сила трения. Коэффициент трения скольжения Трением называется взаимодействие между различными соприкасающимися поверхностями, препятствующее их относительному перемещению. Сила трения направлена вдоль поверхностей соприкасающихся тел противоположно скорости их относительного перемещения. Различают: трение покоя – при отсутствии относительного перемещения соприкасающихся тел и трение скольжения – при их движении. Если к телу находящемуся в соприкосновении с другим телом приложить вдоль линии соприкосновения постепенно увеличивающуюся от нуля силу, то движения не возникает, до того момента пока действующая сила не достигнет определённого значения. Пока не началось движение, сила трения покоя равна действующей на тело силе, то есть является переменной величиной от нуля до некоторой максимальной силы трения покоя.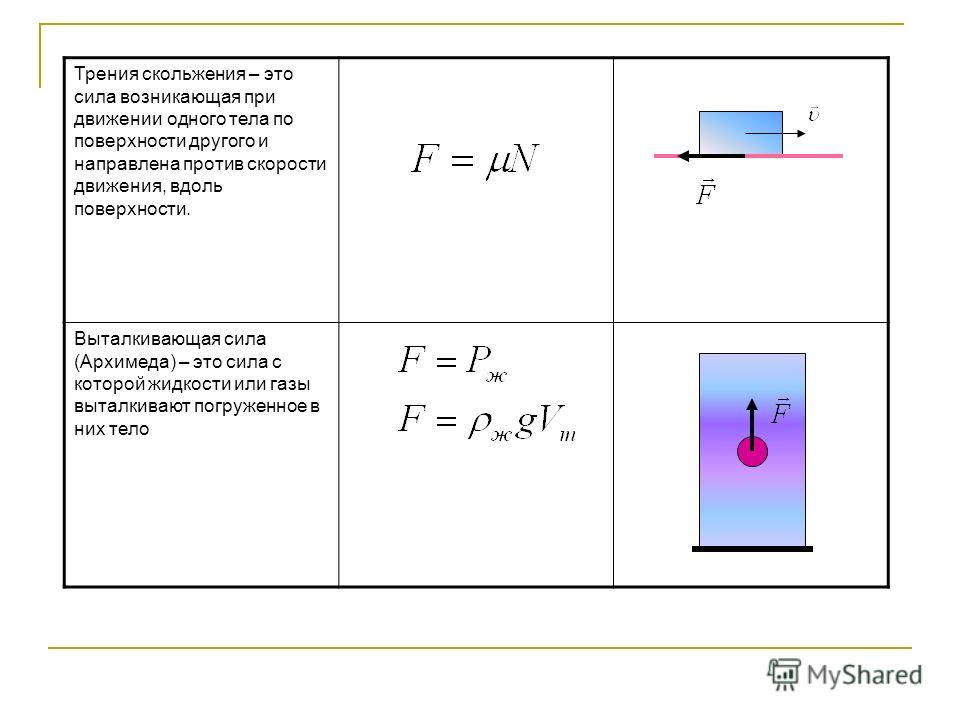
При скольжении тел друг по другу сила трения скольжения пропорциональна силе прижимающей эти тела по нормали к поверхности соприкосновения (перпендикулярно поверхности соприкосновения). Эта прижимающая сила называется силой нормального давления и она по третьему закону Ньютона равна силе нормальной реакции . Величина силы трения скольжения вычисляется по формуле , где µ — коэффициент трения скольжения (во многих случаях вместо µ используют k). При движении по горизонтальной поверхности сила нормального давления, как правило, равна весу тела и может совпадать с силой тяжести. При движении по наклонной плоскости необходимо раскладывать силу тяжести на составляющие параллельную наклонной плоскости и перпендикулярную ей. Перпендикулярная составляющая силы тяжести обеспечивает силу нормального давления, а, следовательно, и силу трения скольжения . Первый закон Ньютона. Существуют такие системы отсчёта, относительно которых поступательно движущиеся тела сохраняют свою скорость постоянной, если на них не действуют другие тела или действие других тел компенсируется.
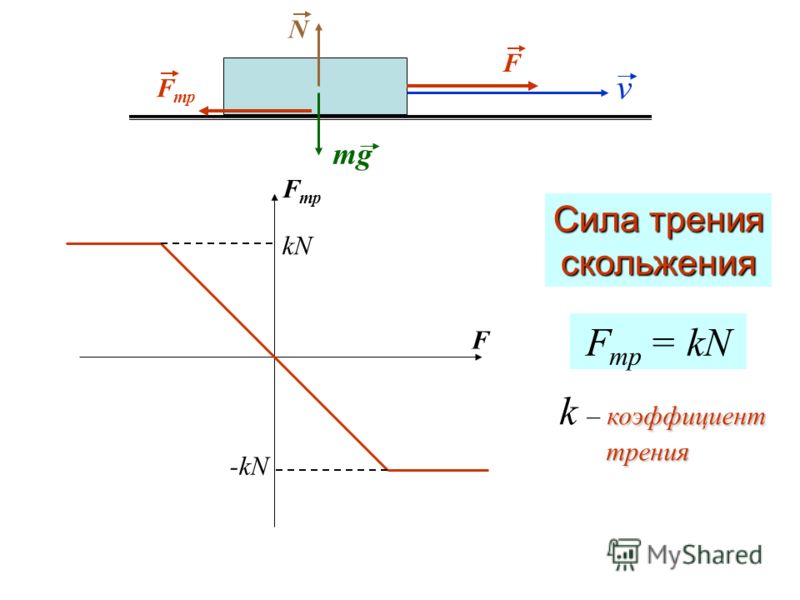Инерциальная система отсчёта. Это система отсчёта, относительно которой свободная материальная точка, не подверженная действию других тел, движется равномерно и прямолинейно. Принцип относительности Галилея. Все механические явления в различных инерциальных системах отсчёта протекают одинаково. Это означает, что никакими механическими опытами проводимыми в данной инерциальной системе отсчёта невозможно установить покоится она или движется равномерно прямолинейно. Принцип Галилея справедлив при движении систем отсчёта со скоростью малой по сравнению со скоростью света. Масса. Физическая величина, являющаяся мерой инерционных свойств тела называется инертной массой этого тела. В этом смысле масса выступает как свойство тел не поддаваться изменению скорости как по величине, так и по направлению. Сила. Векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры (деформируется).
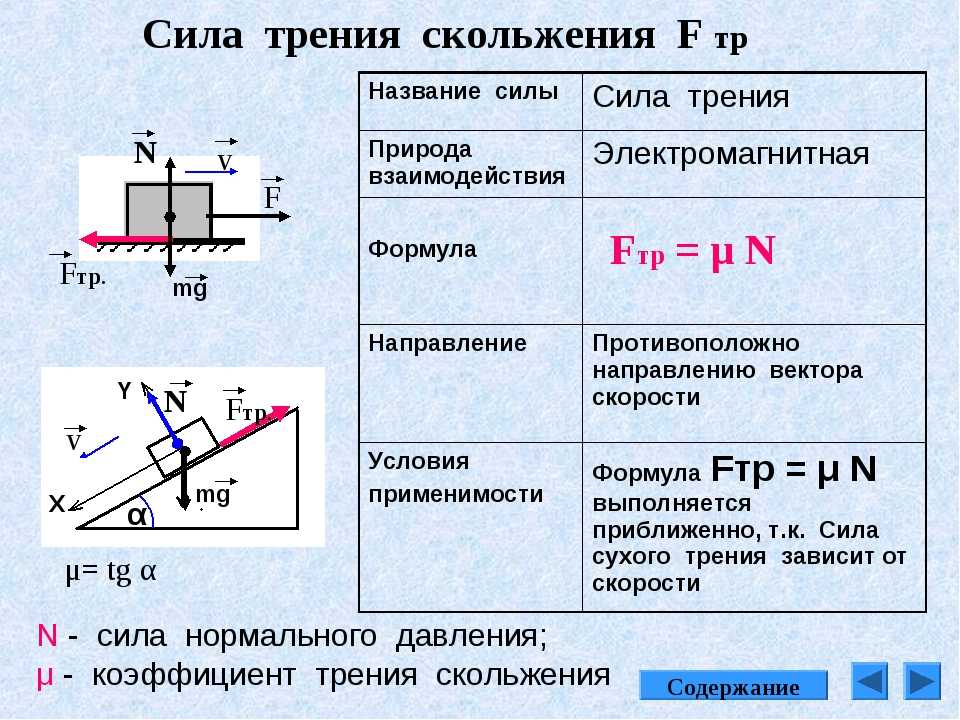В каждый момент времени сила характеризуется величиной, направлением в пространстве и точкой приложения. Второй закон Ньютона. Второй закон Ньютона составляет основу не только классической механики, но и всей классической физики. Несмотря на простоту его математической формулировки при объяснении его «физического смысла» возникают вполне определенные методические трудности. До сих пор в различные учебных курсах используются различные подходы к «физической» формулировке этого важнейшего закона, причем каждый из них обладает как определенными преимуществами, так и недостатками. В нашем случае реализован подход, основанный на использовании независимого определении силы при помощи описания процедуры ее измерения. В его рамках две входящие в уравнение (1) векторные величины оказываются определенными еще до формулировки второго закона, что позволяет придать ей весьма простой и элегантный вид: Опыт показывает, что ускорение, приобретаемое телом, движущимся под действием сил, пропорционально равнодействующей этих сил: .
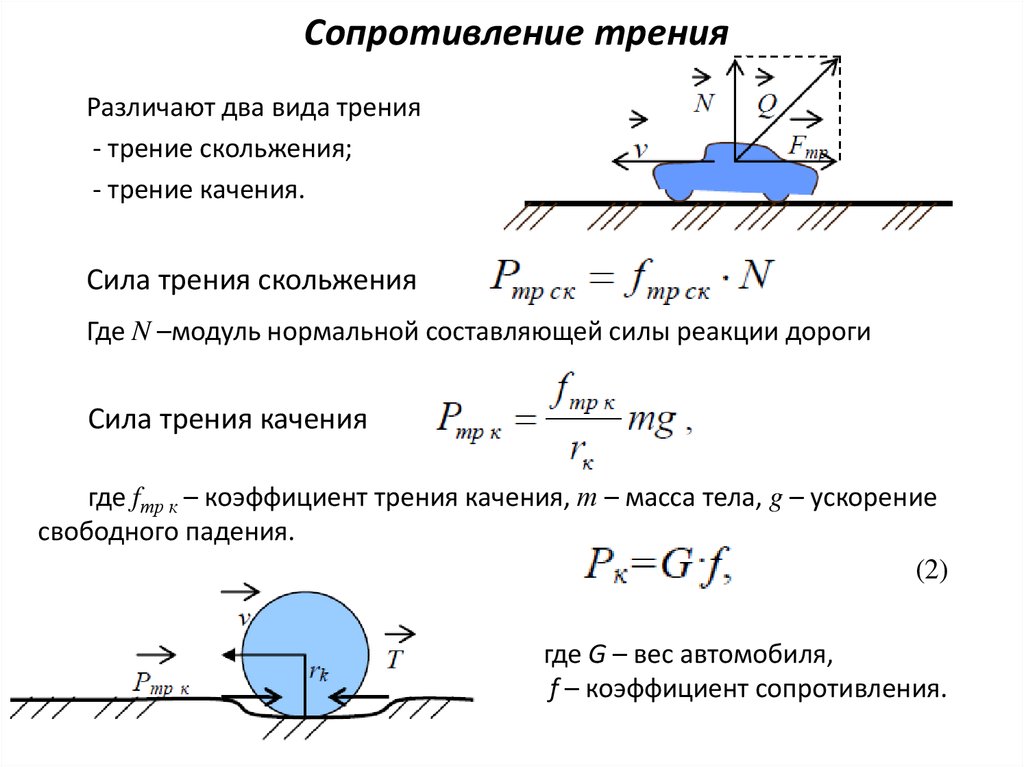В рамках такого подхода инертная масса тела может быть определена Попытайтесь приписать такое значение инертной массе тела Strange, чтобы оно вело себя подобно телу с бесконечно большой эффективной массой. Математические свойства инертной массы: скалярный характер Мыслима ситуация, при которой воздействие на тело одинаковых сил, приложенных в различных направлениях, вызывает различные ускорения. Если бы такая ситуация действительно реализовывалась в природе, инертную массу такого тела следовало бы считать тензорной величиной. В данной демонстрации моделируется движение двух тел: «обычной гири» (Normal) и тела с тензорной массой (Strange). Ускорение гири позволяет судить о действующей внешней силе. Ускорение объекта Strange вообще не совпадает с направлением ускорения обычного тела! Как и в предыдущем случае кажущееся необычным поведение тела объясняется не свойствами его инертной массы, а его участием в дополнительных взаимодействиях. В данной ситуации помимо основной силы Force тело Strange испытывает воздействие сил сухого трения, величина которых различна при движении вдоль различных направлений.
Подобная ситуация может реализовываться в природе, например, при движении электронов в кристалле с некубической решеткой. При этом часто оказывается удобным исключить из рассмотрения взаимодействия с кристаллической решеткой, «расплатившись» за это введением тензорной массы, т.е. заменой реальной частицы на квазичастицу. Изменяя направление внешней силы Force, убедитесь, что в случае ее действия вдоль ребер кристаллической решетки ускорения частицы и квазичастицы совпадают по направлению. Аддитивность массы Масса тела обладает свойством аддитивности, т.е. равна сумме масс частей, составляющих это тело. В качестве примера моделируется ускоренное движение автопоездов, головные автомобили у которых обеспечивают одинаковые силы тяги. Массы всех автомобилей равны. Всилу аддитивности массы автопоездов относятся как 1:2:3, в чем несложно убедиться, сравнивая из ускорения, которые относятся как 3:2:1. Из-за того, что автомобили связаны между собой упругой сцепкой, на равноускоренное движение автопоездов накладываются небольшие колебания, которые можно уменьшить, увеличив жесткость пружин.
Отцепляя вагоны от автопоездов, убедитесь в том, что сила тяги головных автомобилей всех трех составов действительно одинакова. (Для того, чтобы расцепить составы автопоездов, достаточно «отключить» взаимодействия медлу телами). Релятивистская масса При движении заряженной частицы (электрона) в однородном электрическом поле, соласно классической динамике, его скорость должна неограниченно возрастать во времени по линейному закону. В реальности она стремится к предельному значению с=137. Этот эффект может быть отнесен за счет возрастания массы частицы при приближении ее скорости к скорости света. Убедитесь, что в данном случае импульсная формулировка второго закона Ньютона остается более удобной: релятивистской импульс частицы возрастает во времени по линейному закону (p=Ft). Обратите внимание на то, что в пределе малых скоростей релятивистский и классический законы движения приводят к одному и тому же результату. Третий закон Ньютона. Согласно третьему закону Ньютона при взаимодействии тел возникают силы, приложенные к каждому из партнеров.
При этом силы всегда оказываются равными друг другу по величине и противоположно направленными. Из законов Ньютона следует, что в случае взаимодействия двух тел, не взаимодействующих с другими, каждое из них должно двигаться с ускорением. Если масса одного из взаимодйствующих тел существенно превосходит массу другого, то его ускорение оказывается малым. Силы, возникающие при взаимодействиях тел При взаимодействии двух тел, согласно третьему закону, между ними возникают равные и противоположно — направленные силы. Для изменения величины гравитационного взаимодействия поменяйте массу любого из взаимодействующих тел. Убедитесь при этом, что обе силы изменят свою величину, но по-прежнему остануться равными друг другу по модулю. Ускорения взаимодействующих тел В данной демонстрации масса планеты существенно превосходит массу яблока. В результате яблоко ускоренно падает на пактически неподвижную планету. На самом деле планета так же испытывает ускорние, но его величина меньше ускорения яблока в число, равное отношению массы яблока к массе планеты.
Увеличте массу яблока в 10, 100 и т.д. раз и убедитесь, что в этом случае планета начнет «заметно падать» на яюлоко. Центральные силы и третий закон Ньютона Многие почему-то считают, что третий заколн Ньютона подраземевает ориентацию сил вдоль прямой, соединяющкей взаимодействующие тела. На самом деле подобное утверждение не имеет непосредственого отношения к третьему закону. В данной демонстрации моделируется движение тел, взаимодействиющих друг с другом нецентральными силами. Приведенный в данной демонстрации пример не является «физически реальным» и не может быть реализован непосредственным определением взаимодействий в программе физического конструктора (автором программы просто не была предусмотрена возможность создания столь «нефизических» ситуаций). Для реализации данной демонстрации в систему пришлось ввести дополнительное силовое поле Unreal, обладающее весьма специфическими свойствами. Проанализируйте параметры данной физической модели и убедитесь, что созданная на компьютере ситуация действительно отвечает нецентральному взаимодействию и не противоречит системе законов Ньютона.
Попытайтесь самостоятельно придумать другие примеры аналогичных «странных» систем. Гравитационные силы. Взаимное притяжение всех без исключения материальных тел наблюдаемое в любой среде, называют гравитационным взаимодействием, а соответствующие силы притяжения между притягивающимися телами называются гравитационными силами.. Закон всемирного тяготения Две материальные точки массами m1 и m2 притягиваются друг к другу с силой F прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния r между ними: . Коэффициент пропорциональности G называется гравитационной постоянной и показывает с какой силой притягиваются две материальные точки с массами по 1 кг находящиеся на расстоянии 1 м друг от друга (G=6,67? 10-11 Н? м2/кг2). Сила тяжести. Вес тела.
H i g h коэффициент трения скольжения , e ve n во влажном состоянии. | e l eva do Coeficiente D E Atrito D E DESL IZAM EN TO MESMO EM BONDIE например ura» на […] «muito segura» torrotimber.net torrotimber.net | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Высокая коррозионная стойкость ta n t Слайд U N IT с чрезвычайным S MA L L Коэффициент трения . thk.com thk.com | Uma un id ade deslizante alt am ente resistente corroso co m umba ix ssi thk.com thk.com Угол наклона, обычно равный или около 10 градусов, [. плюс воздух низкого давления, действующий как […]
Смазка, уменьшает T H E Коэффициент из Струйный трению A N D Conveys FINE […] FINE […] FINE …] FINE […] FINE …] FINE …] FINE […] FINAL […] FINAL […] N D A N D . с легкостью сушат сыпучие материалы вниз по склону, как воду. dynamicair.com dynamicair.com Онгуло де инклинао, нормальный ао […] redor de 10 graus, somado ao ar de baixa pr esso que atua como um […]
смазка и te, redu z o coeficiente d e frico e tr anspo rt a o материал [. com facilidade, quase como gua. dynamicair.com dynamicair.com OPT IM U M Коэффициент из . oks-germany.com oks-germany.com Coeficiente D E FRICO I DEA L PAR A F или AS E TENSO E LEVAD AS . oks-germany.com oks-germany.com Фрикционная найтовка заключается в натяжении найтов для увеличения […] сила предварительного натяжения и […]
consequently t h e friction coefficient b e tw een the load and the supporting surface to prevent the load fr o m раздвижной . uirr.com uirr.com A marrao por atrito состоят без напряжения das amarraes […] пункт […]
Aumentar A FORA DE PR-TENSO E, следующий за EN TEMEN TE, O COEFECIENTE DE Atrito ENT RE A C ARGA E Superfc DE APO DE APO DE APO DE APO DE DE APO DE AT A ATA SAUPER пункт […] impedir o deslizamento da carga. uirr.com uirr.com Т H E Коэффициент скольжения из Фрик B E TW EEN ATENT […] и его ответный кулачок был примерно 0,40, что приводило к сильному абразивному износу. whitfordww.com whitfordww.com O coeficiente corredio de frico en tr e a ling e ta e seu [. пришел около эры приблизительно 0,40, что в результате em uso abrasivo severo. whitfordww.com.br whitfordww.com.br WI TH A Коэффициент из Фрикция 0 . 02 -0,25, подшипники GGB DU обеспечивают превосходство le n t friction p e rf ormance in rotat in g , sliding a n d колебательные движения. cn.ggbearings.com cn.ggbearings.com C om um coeficiente de atrito de 0,02 — 0,25 , os m ancais DU da GGB apresentam um excelente desempenho de deslizamento em aplicaes com movimento s rotat ivo s, линейный e osc ilat ri os. ggbearings.com.br ggbearings.com.br Для обеспечения безопасности не все wi n g sliding o f t he cargo the st at i c coefficient of трение i s u sed еще динамическое трение. uirr.com uirr.com Р ар a equipamentos d e fixao que no permitem o deslizamento d a car ga, o coeficiente de atrito est t ico utilizado em conjunto co m o atrito din m ico. uirr.com uirr.com Могут использоваться как для пациентов со средней0025 [. веса и бариатрических пациентов и изготовлены […]
В высококачественном, L O W — Фрикция F A BR IC, который сохраняет свои GO O D O D O D c a pa способности даже после […] длительный срок использования. лико.се лико.се Podem ser usados para pacientes com […] нормальный или баритрикос, фабрикад os num te cido de alta […]
Qualid AD E CO M UM A FRICO B AIXA , QU E MANTM A BOA CAPA CI DADE DE CI DADE DE CI DADE DE CI DADE DE CI DADE DE CI DADE DE CI DADE DE CI . можно продлить использование. лико.се лико.се Изучение […]
износ и T H E Фрик O F A Металлическая пара под смазочной в E D .0008 скользящий . портал conhecimento.br портал conhecimento.br Estudo D O DES GAS TE E Atrito D E U M P AR ME T LICO SO B DESLIZATION L LICO TO B Deslizamento L LICO. портал conhecimento.br портал conhecimento.br Осталось взять […] t h e коэффициент трения o f t он копыт. europarl.europa.eu europarl.europa.eu Tudo o que […]
falta ter e m co nta o coeficiente d e frico do s cas co s на рампе. europarl.europa.eu europarl.europa.eu Например, […]
снижение на 20 % в t h e коэффициент трения i n коробка передач […] может снизить потери энергии на процент […] варьируется от 0,64 % до 0,80 %, обеспечивая экономию в размере 26 миллиардов евро в год только в транспортном секторе. eur-lex.europa.eu eur-lex.europa.eu Например, […]
DIMINUI O DE 20 % DO Coeficiente DE Atrito NA CA IXA D E Velocidades [. de um automvel capaz de reduzir […] Пердас де Энергия Нума Процентная разница между 0,64 % и 0,80 %, o Que Equivale a uma Economia de 26 mil milhes de euro ao ano no no сектору dos transports. eur-lex.europa.eu eur-lex.europa.eu Для предотвращения проскальзывания основной ролик имеет накатку или […]
окрашен hi г ч коэффициент трения k e nt аний плазменный спрей. shwallong.co.uk shwallong.co.uk Para previnir derrapagens, o rolo main serrilhado ou pintados […]
ком спрей плазмы де Кен та ниум де альт и фрико . shwallong.com.pt shwallong.com.pt износостойкость и [. amorim.pt amorim.pt Сопротивление ао десгасте — […]
резист n cia a o atrito e o seu ele va do coeficiente de f rico amorim.pt amorim.pt The chain slides with li tt l e friction a n d wear over a pla st i c sliding л а уе р. schaeffler-aftermarket.com.mx schaeffler-aftermarket.com.mx Corprent E Desliza C OM POU COATRITO E DES GAS TE PO R UMA CAMAD A PLST ICA . schaeffler-aftermarket.com.br schaeffler-aftermarket.com.br Уменьшение диапазона допусков внутреннего диаметра до верхней половины диапазона допусков класса N, что […] обеспечивает надлежащий допуск для регулировки скольжения на внутреннем […]
Кольца и, в то же время, уменьшает сокращение SI V E Сдвиг A N D Frction . nsk.com.br nsk.com.br Reduo na faixa de tolerncia do dimetro interno para a metade Superior da faixa de tolerncia da classe N, o que garante […] tolerncia adequada para o ajuste deslizante nos anis […]
internos e, ao mesmo tempo, reduz o ex ce ssiv o deslizament o e atrito . nsk.com.br nsk.com.br Может использоваться как для нормального, так и для очень тяжелого веса […] пациентов и состоит из […]
качественный, l o w — friction f a br ic which has a very go o d sliding c a pa город даже […] после длительного использования. лико.се лико.се Pode ser usado para pacientes de peso normal ou muito pesados, sendo feito de […] um tecido de alta […]
Qualidade M AS DE B AIX A FRICO, COM UMA BOA C APACID AD E DE DESLIZE MESM O DESLIZIZE MESM O DESLIZIZE MESM O MESM O MESM O MESM a ] срок использования. лико.се лико.се Его новая формула и спец. CI A L Фрикция P R OP . т он отличается […] . cepsa.com cepsa.com A sua nova frmula e as suas […]
свойства особенно EC IAIS DE FRICO на MITE M U M DESLIZAR C на TROL AD O DOS D IF [… … … …] O DOS D IF [… … … … …] O DOS D IF [… … …] O DOS D IF [… … … …] O DOS DS IF . элементы передачи. cepsa.com cepsa.com Трение скольжения i s l за счет трения покоя. uirr.com uirr.com O atrito di nmi co in ferio rao atrito est ti co. uirr.com uirr.com Пластмассовый наполнитель дозировка 1-5%, основа на пленке краски […] применение спрос, во время продукции […]
низкого производства ту r e коэффициент трения , o r более тонкая пленка, […] может увеличить дозировку добавки. tianyichemical.com tianyichemical.com Agente deslizante de дозировка enchimento de plstico de 1-5%, базовый sobre a requirea de aplicao de pintura do […] пленка, срок изготовления и изготовления [. fina, que pode aumentar дозировка aditivos. tianyichemical.com.pt tianyichemical.com.pt Во-первых, эффективное привет г ч — коэффициент трения r o ad поверхность может уменьшить […] тормозной путь транспортного средства на целых 50%. europarl.europa.eu europarl.europa.eu Примьер-лугар, гм […]
тротуар o com elev ad o coeficiente d e atrito po de reduz ir em 50% […] distncia de paragem de um veculo. europarl.europa.eu europarl. 5 0 Коэффициент трения F (D RY) GGBearings.com GGBearings.com 5 0 Coeficiente de atrito f 9 Ролик основной с накаткой или […]
с покрытием hi g h коэффициент трения k e nt аниум плазменный спрей. shwallong.co.uk shwallong.co.uk O rolo main serrilhado ou revestidos com spray de […]
плазма ke ntan ium coeficiente alt a frico . shwallong.com.pt shwallong.com.pt Подшипник с перекрестными роликами с сепаратором или изолятором [. скорость использования и полный ролик […]
Подшипник типа подходит для низких скоростей вращения и больших нагрузок. sbibearings.com sbibearings.com O rolamento de rolos cruzados vindo com uma […] gaiola ou um isolador apropriada […]
пункт ты SO S DE BAI XA FRICO E Coeficiente D E AL TA V EL Ocidade […] де ротао, э ос роламентос де […] rolos типо интеграл aplicvel для baixa velocidade де ротао и usa carga pesada. sbibearings.com.pt sbibearings.com.pt Используется для увеличения [. используется в производстве […] демаркационной краски, краски для пола на спортивных площадках и для текстуры. ourobranco.com.br ourobranco.com.br Тема заключительной проверки […]
reestncia Abra SO, O Coeficiente DE Atrito E DAR TEX TU RA, Utilizado […] на завод по производству красок […] de demarcao, de piso de quadras esportivas e textura. ourobranco.com.br ourobranco.com.br Одна рама неподвижная, а другая подвижная, они собираются на [. 4 опоры с резьбой в […]
ковкий чугун с l o w коэффициент трения . T he y облегчают обращение […] и обеспечивают длительный срок службы […] винты, регулирующие открытие. legnotre.com legnotre.com Um bastidor fixo e o outro mvel e so montados sobre 4 […] опоры roscados em ferro fundido […]
ESFEROI DA L CO M BA IX O Coeficiente D E Atrito, Q E P ERMIT EM UMA FCIL […] manobra e longa durao dos […] grandes parafusos que regulam a abertura. legnotre.com legnotre.com Example measurement unit: static and kin et i c coefficients of friction ( C oF ) calculated wh e № раздвижная f i лм при x см/мин. b-i-b.com b-i-b.com Пример […]
unida de de m edi o : coeficientes e st tic os e cin tico s de frico calc ula dos ao deslizar o f ilm e a x c м/мин. b-i-b.com b-i-b.com Так было с самого начала […] сухих смазочных материалов, когда древняя механика использовала графит, тальк, слюду и др. […]
«гладкие» порошки по re du c e трение скольжения . whitfordww.com whitfordww.com Isto foi uma verdade desde o incio dos […] Secos lubrificantes, quando antigamente, mecnicos usavam графит, тальк, слюда и внешние части ps [. whitfordww.com.br whitfordww.com.br Покрытие из ксилана герметизирует прорези лопастей в […]
the rotor and red uc e d friction o n t h e sliding v a ne с. whitfordww.com whitfordww.com Uma camada de Xylan vedou as aberturas das palhetas […]
do roto r e re duzi u a frico n as palheta s whitfordww.com.br whitfordww.com.br Фрикция R E SU LTS из двух серфингов AC E S SPITION0007 a c ro сс друг друга и [. измеряется числом, которое описывает сопротивление (силу) между скользящими частями. whitfordww.com whitfordww.com FRICO O AT O DE DU AS SUPERFC IE S QUE DESLIZAM UMA N A OUTRA […] e esto medidos por um nmero que descreve o arraste (fora) entre partes corredias. whitfordww.com.br whitfordww.com.br Деван Мухаммад Нуруззаман , Мохаммад Асадуззаман Чоудхури Факультет машиностроения, Даккский инженерно-технологический университет, Газипур-1700, Бангладеш Адрес для переписки: Деван Мухаммад Нуруззаман, факультет машиностроения, Даккский инженерно-технологический университет, Газипур-1700, Бангладеш. Copyright © 2012 Научное и академическое издательство. Все права защищены. Аннотация В настоящем исследовании исследуются и сравниваются коэффициенты трения при скольжении алюминия по различным материалам штифтов. Для этого разработан и изготовлен штифт на дисковом аппарате. Проводятся эксперименты, когда различные типы штифтов, такие как алюминий, медь и латунь, скользят по алюминиевому диску. Опыты проводят при нормальной нагрузке 5, 7,5 и 10 Н, скорости скольжения 0,5, 0,75 и 1 м/с и относительной влажности 70%. Исследованы изменения коэффициента трения в зависимости от продолжительности трения при различных нормальных нагрузках и скоростях скольжения. Результаты показывают, что коэффициент трения зависит от продолжительности трения, нормальной нагрузки и скорости скольжения. В целом коэффициент трения увеличивается в течение определенного времени трения и после этого остается постоянным в течение всего остального времени эксперимента. Ключевые слова: коэффициент трения, нормальная нагрузка, скорость скольжения, продолжительность трения, алюминий, медь, латунь Ссылайтесь на эту статью: Деван Мухаммад Нуруззаман, Мохаммад Асадуззаман Чоудхури, «Влияние нагрузки и скорости скольжения на коэффициент трения алюминия, скольжения по различным материалам штифтов», Американский журнал материаловедения , Vol. 2 № 1, 2012. С. 26-31. doi: 10.5923/j.materials.20120201.05. |
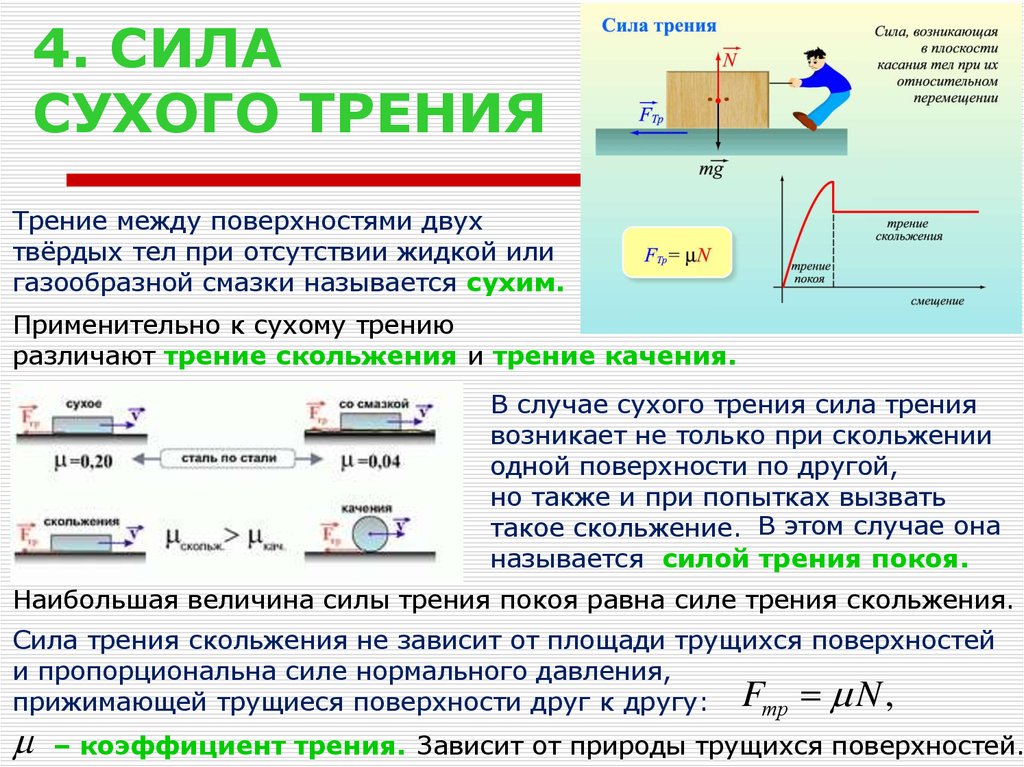
Это означает, что сопротивление скольжению находится в диапазоне от «безопасного» до «чрезвычайно безопасного».
..]
..]
..]