|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства… Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует… Интересное: Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным… Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 15 из 40Следующая ⇒ Режим работы электрической цепи, при котором ток и напряжение на входе цепи совпадают по фазе, называют резонансом.
Резонанс напряжений Резонанс напряжений может иметь место в цепи с последовательно соединенными индуктивным и емкостным элементами. Рассмотрим схему последовательного соединения резистора, индуктивности и емкости (рис. 6.1). Второй закон Кирхгофа для данной цепи можно записать: .
Отсюда комплексное сопротивление цепи . (6.1) Построим векторную диаграмму. При этом могут иметь место три случая. 1. Пусть индуктивное сопротивление больше емкостного XL> XC , тогда и индуктивное напряжение будет больше емкостного UL> UC. Векторная диаграмма будет иметь вид (рис. Реактивная составляющая напряжения UХ = UL – UC – положительна, и угол сдвига фаз между током и напряжением φ> 0. Такой характер цепи является активно-индуктивным. 2. Пусть индуктивное сопротивление меньше емкостного XL < XC . Тогда и индуктивное напряжение станет меньше емкостного UL< UC, так как ток через элементы протекает один и тот же, а напряжение пропорционально току и сопротивлению. Векторная диаграмма будет иметь вид (рис. 6.3). Реактивная составляющая напряжения UХ = UL – U 3. Пусть XL = XC, в этом случае индуктивное и емкостное напряжения равны по величине UL= UC. Так как они всегда противоположны по фазе, то они полностью компенсируют друг друга, следовательно, реактивная составляющая UХ = UL – UC = 0. Общее напряжение будет активным и совпадет по фазе с током φ = 0, следовательно, в цепи имеет место резонанс напряжений. Векторная диаграмма для данного случая показана на рис. 6.4. Из вышесказанного следует, что условием, при котором наступит резонанс напряжений, является равенство индуктивного и емкостного сопротивлений. , или . Из выражения (6.1) следует, что при резонансе полное сопротивление цепи имеет активный характер. Резонанс напряжений можно достигнуть подбором трех параметров: 1) изменением частоты колебательного контура , L, C = const; 2) изменением индуктивности контура , , С = const; 3) изменением емкости колебательного контура , , L = const . При этом все три параметра связаны между собой. Из условия получаем: , отсюда: , , . Частоту ω0, определяемую из такого условия, называют резонансной. Если напряжение на зажимах цепи и активное сопротивление цепи R не изменяются, то ток при резонансе имеет максимальное значение , так как . Если реактивные сопротивления превосходят при резонансе активное сопротивление: , , то напряжения на зажимах катушки и конденсатора могут существенно превышать напряжение на входе цепи. Превышение напряжения на реактивных элементах над напряжением на входе принято характеризовать величиной , называемой волновым или характеристическим сопротивлением цепи. Волновое сопротивление численно равно индуктивному или емкостному сопротивлению на резонансной частоте. Кратность превышения напряжения на зажимах индуктивного и емкостного сопротивлений над входным определяют отношением напряжения на реактивном элементе к напряжению на входе цепи на резонансной частоте: . Эта величина называется добротностью контура. Величина, обратная добротности , называется затуханием контура. Избирательные свойства колебательного контура определяются его добротностью. Чем больше добротность контура, тем более узкой будет резонансная кривая (рис. 6.5). Избирательность контура характеризуется полосой пропускания. Полоса пропускания – это диапазон частот, для которых ток ослабляется не более чем в раз по отношению к максимальному значению . Ширину полосы пропускания можно определить по формуле . Рассмотрим резонансные кривые тока и напряжений (рис. 6.6). При неизменных параметрах цепи и неизменном входном напряжении ток определится выражением . Рассмотрим это выражение в реперных точках: ; . Напряжение на индуктивности пропорционально частоте, следовательно, при нулевой частоте напряжение на индуктивности . При все напряжение, подаваемое от источника, приложено к индуктивности, и . Напряжение на емкости обратно пропорционально частоте, следовательно, при все напряжение приложено к емкости . При , так как равно нулю емкостное сопротивление. При резонансной частоте индуктивное и емкостное напряжения равны . Напряжение на резистивном элементе пропорционально току и, следовательно, повторяет форму кривой тока при и , при . Рассмотрим энергетические соотношения при резонансе. Мгновенные значения мощности на зажимах катушки и конденсатора определяются выражениями: ; . Так как при резонансе , эти мощности в любой момент времени равны и противоположны по знаку. Это значит, что происходит обмен энергией между магнитным полем катушки и электрическим полем конденсатора, но не происходит обмена между источником и реактивными элементами, так как и , то есть суммарная энергия электрического и магнитного полей остается постоянной. Энергия переходит из конденсатора в катушку в течение четверти периода, когда напряжение на конденсаторе убывает, а ток растет. В течение следующей четверти периода энергия переходит из катушки в конденсатор. Источник энергии питает только активное сопротивление.
Резонанс токов Резонанс в идеальной цепи Резонанс токов наступает при параллельном соединении индуктивности и емкости. Для обобщения анализов включим в цепь параллельно индуктивности и емкости активное сопротивление (рис. 6.7). По первому закону Кирхгофа можно записать: . Запишем это выражение в комплексной форме: , где , , . Вынесем напряжение за скобку, получим . Условием резонанса токов является равенство индуктивной и емкостной проводимостей: . Векторная диаграмма для режима резонанса представлена на рис. 6.8. При равенстве индуктивной и емкостной проводимостей будут равны и токи . Направленные в противофазе, эти токи компенсируют друг друга, в цепи остается только активная составляющая тока, и общий ток будет совпадать по фазе с напряжением . Поэтому резонанс называют резонансом токов. Общий ток в цепи можно представить как , где – полная комплексная проводимость, модуль которой равен . С учетом условия резонанса, получим, что , то есть проводимость цепи минимальна, следовательно, и ток будет минимальным – это признак резонанса токов. Из условия резонанса получим выражение для резонансной частоты . То есть, как и при резонансе напряжений, добиться резонанса токов можно, изменяя один из трех параметров ω, L, C.
Резонанс в реальной цепи Реальная катушка и реальный конденсатор обладают не только реактивным, но и активным сопротивлением. Катушка – сопротивлением обмотки, конденсатор – сопротивлением токам утечки. В этом случае при большой добротности катушки или конденсатора активное сопротивление может оказаться функцией частоты. Под добротностью катушки будем понимать отношение её индуктивного сопротивления к активному. . Под добротностью конденсатора – отношение его емкостного сопротивления к активному . Рассмотрим цепь, содержащую реальные катушку и конденсатор, представленную на рис. 6.9. Условием резонанса токов в такой цепи является равенство нулю реактивной проводимости . Комплексную проводимость цепи можно выразить через комплексные сопротивления ветвей: . При резонансе b=0, то есть . Из полученного выражения видно, что в отличие от идеальной цепи резонанс можно получить, регулируя не три параметра, а пять: . Решая уравнение (6.1) относительно частоты, получим выражение для резонансной частоты , Рассмотрим частные случаи: 1. , тогда резонансная частота будет равна , как и в случае идеальной цепи. 2. , тогда при любом значении частоты реактивная проводимость равна нулю, то есть резонанс имеет место при любой частоте. 3. , – добротность невелика, тогда выражение под корнем отрицательно. Резонансная частота мнимая, резонанс невозможен. При резонансе в реальной цепи, так же, как и в идеальной, ток минимален и имеет чисто активный характер. Векторная диаграмма для режима резонанса представлена на рис. 6.10. Из диаграммы видно, что токи в ветвях, содержащих катушку и конденсатор, различны, но равны их реактивные составляющие.
Контрольные вопросы и задания 1. Какой режим работы электрической цепи называют резонансом? 2. В каких цепях возможен резонанс напряжений? 3. Что является условием и признаком резонанса напряжений? 4. Поясните, какова природа резонанса напряжений. 5. Какой характер электрической цепи называют активно-индуктивным, активно-емкостным? 6. Как по векторной диаграмме определить характер электрической цепи? 7. Что называют волновым сопротивлением контура? 8. Что называют добротностью контура? 9. На какие свойства контура влияет добротность? 10. Что называется полосой пропускания? 11. В каких цепях возможен резонанс токов? 12. Что является условием и признаком резонанса токов? 13. Поясните природу резонанса токов. 14. Чем отличается резонанс токов в идеальной и реальной цепях? 15. Что называется добротностью катушки, конденсатора? 16. Какие частные случаи могут иметь место при резонансе в реальной электрической цепи? 17.
⇐ Предыдущая10111213141516171819Следующая ⇒ Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… |
Магнитотеллурический метод в геофизике. (Лекция 7.6) презентация, доклад
7.6 Магнитотеллурический метод
Напоминание о вариациях магнитного поля Земли: поле – переменно!
Закон электромагнитной индукции Фарадея: ε=-dФ/dt, следовательно, переменное магнитное поле создаст переменное электрическое поле!
Высокочастотные (1-2000 Гц) вариации магнитного поля, созданные грозами на экваторе
20-80 км
ρ=1013Ом. м
м
ρ=105Ом.м
ионосфера
100 В/м
15 kA
10-250 мкс
>1000 км
Параметры магнитотеллурического поля
Длина волны
Глубина проникновения поля
Волновое сопротивление среды – импеданс
Кажущееся сопротивление
Как и в случае метода сопротивления, кажущееся сопротивление, вычисленное по формуле Тихонова-Каньяра, есть эффективное удельное сопротивление Земли, вычисленное в предположении о её однородности.
Магнитотеллурическое зондирование
Длина волны электромагнитного поля зависит от периода поля и удельного сопротивления среды. Изменяя период поля ”регулируют” глубину исследования.
7.7 Индукционные методы с активными источниками
Принцип индуктивного возбуждения электромагнитного поля.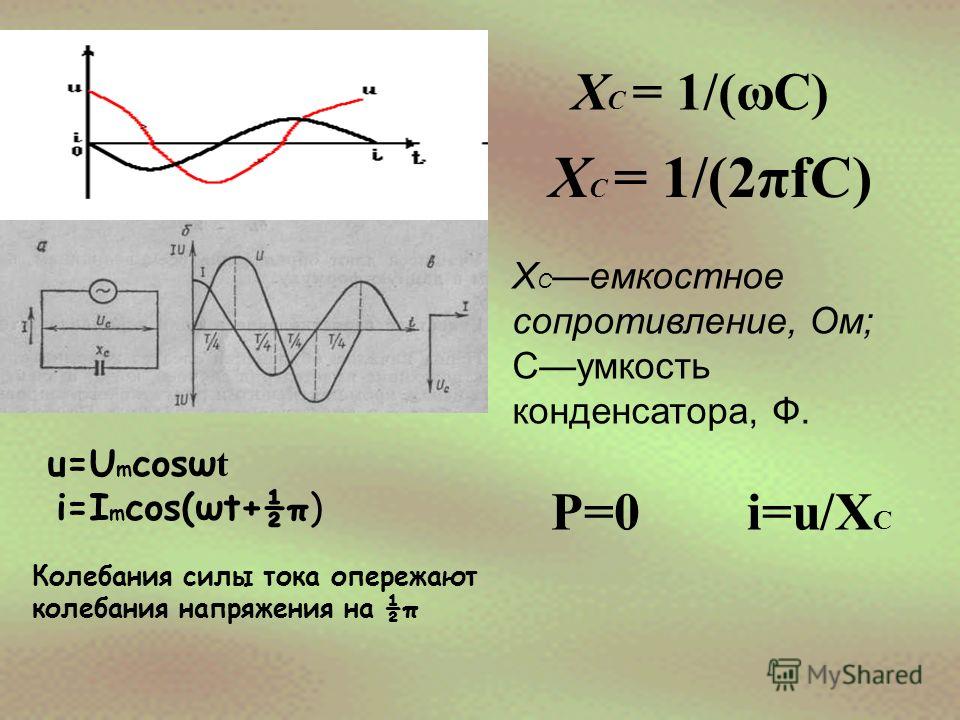
На поверхности земли расположена петля с током (черный овал), силовые линии магнитного поля показаны синим цветом, а вторичные вихревые токи – красным.
Идея индукционного измерения поля
Виды источников и приемников поля
Длинный кабель
Горизонтальный
электрический диполь
=
Магнитный диполь
Вертикальный
электрический
диполь
Петля
Горизонтальный
электрический диполь
Магнитный диполь
M
N
M
N
Переменные поля: частотная и временная области (аналогия с ВП)
Частотная область: вещественная и мнимая компоненты магнитного поля
Временная область: зависимость поля от времени – “становление” поля
Профилирование: одна частота
Зондирование много частот или зависимость поля от времени
Архангельская область: трубка Пионерская: зондирование становлением поля (ЗСБ)
Песчаники
и известняки
С
Песчаники
D3
Трубка
“Пионерская”
D3-C1
Архангельская область: трубка Пионерская: зондирование становлением поля (ЗСБ)
7. 8 Георадиолокация
8 Георадиолокация
Скорость волны:
. Пример радарограммы, с отражающей границей, образованной коренными породами, перекрытыми слоем супеси
Георадиолокация: профилирование
Георадиолокация: томография
Распределение скорости электромагнитной волны в железнодорожной насыпи по результатам георадиолокационного просвечивания (ООО ”Технотерра”, Санкт-Петербург)
Резюме – геоэлектрика:
От каких факторов зависит электропроводность пород?
Какие руды являются проводниками и полупроводниками?
В каких экспериментах проявляется вызванная поляризация?
Какие явления приводят к спонтанной поляризации?
В чем суть электрической индукции, электромагнитной индукции?
Дайте определение кажущегося удельного электрического сопротивления.
В чем суть электропрофилирования, электрозондирования, электротомографии?
Какие геологические объекты исследуют методом заряда?
Назовите параметры, которые измеряют методом ВП
Резюме – геоэлектрика:
Какие объекты исследуют методом ЕП?
Какова природа электромагнитного поля, используемого в магнитотеллурическом методе?
Как в магнитотеллурическом методе достигается эффект зондирования?
В чем суть индукционных методов?
Сравните теорию сейсморазведки и георадиолокации. В чем сходства и различия?
Какие геологические результаты можно получить методом георадиолокации?
Скачать презентацию
23.11 Реактивное, индуктивное и емкостное сопротивление – Физика колледжа 2e
Цели обучения
К концу этого раздела вы сможете:
- Схема зависимости напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.

- Расчет индуктивных и емкостных реактивных сопротивлений.
- Расчет тока и/или напряжения в простых индуктивных, емкостных и резистивных цепях.
Многие схемы также содержат конденсаторы и катушки индуктивности в дополнение к резисторам и источнику переменного напряжения. Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы рассмотрим, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.
Катушки индуктивности и индуктивное сопротивление
Предположим, что катушка индуктивности подключена непосредственно к источнику переменного напряжения, как показано на рис. 23.43. Разумно предположить пренебрежимо малое сопротивление, так как на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что оно окажет незначительное влияние на цепь. Также показан график зависимости напряжения и тока от времени.
Рисунок 23.43 (a) Источник переменного напряжения последовательно с катушкой индуктивности, имеющей пренебрежимо малое сопротивление. (б) График тока и напряжения на катушке индуктивности в зависимости от времени.
График на рис. 23.43(b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и достигает своего пика после управляющего им напряжения, как это было в случае, когда в предыдущем разделе было включено постоянное напряжение. Когда напряжение в точке а становится отрицательным, ток начинает уменьшаться; он становится равным нулю в точке b, где напряжение является самым отрицательным. Затем ток становится отрицательным, снова следуя за напряжением. Напряжение становится положительным в точке с и начинает делать ток менее отрицательным. В точке d ток проходит через нуль как раз в тот момент, когда напряжение достигает своего положительного пика, чтобы начать новый цикл. Это поведение резюмируется следующим образом:
Напряжение переменного тока в индукторе
Когда на катушку индуктивности подается синусоидальное напряжение, напряжение опережает ток на одну четвертую периода или на
90º90º фазовый угол.
Ток отстает от напряжения, так как катушки индуктивности препятствуют изменению тока. Изменение тока индуцирует противоЭДС V=-L(ΔI/Δt)V=-L(ΔI/Δt). Это считается эффективным сопротивлением катушки индуктивности переменному току. Действующее значение тока II через катушку индуктивности LL определяется вариантом закона Ома:
·I=VXL,I=VXL,
23,51
где VV — среднеквадратичное напряжение на катушке индуктивности, а XLXL определяется как
XL=2πfL, XL=2πfL,
23,52
с ff частотой источника переменного напряжения в герцах (анализ цепи с использованием правила контура Кирхгофа и исчисления фактически дает это выражение). XLXL называется индуктивным реактивным сопротивлением, потому что индуктор препятствует протеканию тока. XLXL имеет единицы измерения в омах (1 Гн=1 Ом⋅с1 Г=1 Ом⋅с, так что частота, умноженная на индуктивность, имеет единицы (циклы/с)(Ом⋅с)=Ω(циклы/с)(Ом⋅с) = Ω), в соответствии с его ролью эффективного сопротивления. Имеет смысл, что XLXL пропорциональна LL, поскольку чем больше индукция, тем больше ее сопротивление изменению. Также разумно, что XLXL пропорционально частоте ff, так как большая частота означает большее изменение тока. То есть ΔI/ΔtΔI/Δt велико для больших частот (большие ff , малое ΔtΔt). Чем больше изменение, тем больше сопротивление индуктора.
Имеет смысл, что XLXL пропорциональна LL, поскольку чем больше индукция, тем больше ее сопротивление изменению. Также разумно, что XLXL пропорционально частоте ff, так как большая частота означает большее изменение тока. То есть ΔI/ΔtΔI/Δt велико для больших частот (большие ff , малое ΔtΔt). Чем больше изменение, тем больше сопротивление индуктора.
Пример 23.10
Расчет индуктивного сопротивления, а затем тока
(a) Рассчитайте индуктивное сопротивление катушки индуктивности 3,00 мГн при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока на каждой частоте, если приложенное среднеквадратичное напряжение равно 120 В?
Стратегия
Индуктивное сопротивление находится непосредственно из выражения XL=2πfLXL=2πfL. Как только XLXL найден на каждой частоте, можно использовать закон Ома, сформулированный в уравнении I=V/XLI=V/XL, для определения тока на каждой частоте.
Решение для (a)
Ввод частоты и индуктивности в уравнение XL=2πfLXL=2πfL дает
XL=2πfL=6,28(60,0/с)(3,00 мГн)=1,13 Ом при 60 Гц.XL=2πfL=6,28 (60,0/с)(3,00 мГн)=1,13 Ом при 60 Гц.
23,53
Аналогично, на 10 кГц
XL=2πfL=6,28(1,00×104/с)(3,00 мГн)=188 Ом на 10 кГц.XL=2πfL=6,28(1,00×104/с)(3,00 мГн)=188 Ом при 10 кГц.
23,54
Решение для (b)
Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в уравнении I=V/XLI=V/XL, при условии, что приложенное среднеквадратичное напряжение равно 120 В. Для первой частоты это дает
I=VXL=120 В1.13 Ом=106 А при 60 Гц. I=VXL=120 В1.13 Ом=106 А при 60 Гц.
23,55
Аналогично, при 10 кГц
I=VXL=120 В188 Ом=0,637 А при 10 кГц. I=VXL=120 В188 Ом=0,637 А при 10 кГц.
23,56
Обсуждение
Катушка индуктивности очень по-разному реагирует на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток мал, что соответствует тому, как индуктор препятствует быстрому изменению. Таким образом, высокие частоты препятствуют больше всего. Индукторы можно использовать для фильтрации высоких частот; например, большой индуктор можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выходящий из ваших динамиков, или высокочастотные скачки мощности в вашем компьютере.
Обратите внимание, что хотя сопротивление в рассматриваемой цепи незначительно, переменный ток не очень велик, поскольку индуктивное сопротивление препятствует его протеканию. При переменном токе нет времени для того, чтобы ток стал чрезвычайно большим.
Конденсаторы и емкостные реактивные сопротивления
Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рис. 23.44. Сопротивление такой цепи можно сделать настолько малым, что оно оказывает незначительное влияние по сравнению с конденсатором, и поэтому мы можем предположить пренебрежимо малое сопротивление. Напряжение на конденсаторе и ток представлены на рисунке как функции времени.
23.44. Сопротивление такой цепи можно сделать настолько малым, что оно оказывает незначительное влияние по сравнению с конденсатором, и поэтому мы можем предположить пренебрежимо малое сопротивление. Напряжение на конденсаторе и ток представлены на рисунке как функции времени.
Рисунок 23.44 (a) Источник переменного напряжения последовательно с конденсатором C , имеющим пренебрежимо малое сопротивление. (б) График тока и напряжения на конденсаторе в зависимости от времени.
График на рис. 23.44 начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, а ток становится отрицательным по мере разряда конденсатора. В точке а конденсатор полностью разряжен ( Q=0Q=0 ) и напряжение на нем равно нулю. Ток между точками a и b остается отрицательным, что приводит к изменению напряжения на конденсаторе. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и сводя напряжение к нулю в точке c, что позволяет току достигать своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла:
Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и сводя напряжение к нулю в точке c, что позволяет току достигать своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла:
Напряжение переменного тока в конденсаторе
Когда на конденсатор подается синусоидальное напряжение, напряжение следует за током на одну четвертую периода или на 90º90º угол фазы.
Конденсатор влияет на ток, имея возможность полностью остановить его при полной зарядке. Поскольку применяется переменное напряжение, существует среднеквадратичное значение тока, но оно ограничено конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока II в цепи, содержащей только конденсатор CC, по другой версии закона Ома составляет
I=VXC,I=VXC,
23,57
, где VV — среднеквадратичное напряжение, а XCXC определяется (как и в случае XLXL, это выражение для XCXC получается в результате анализа цепи с использованием правил Кирхгофа и расчета) равно
XC=12πfC,XC=12πfC,
23,58
, где XCXC называется емкостным реактивным сопротивлением, потому что конденсатор реагирует на сопротивление току. XCXC имеет единицы измерения в омах (проверка оставлена читателю в качестве упражнения). XCXC обратно пропорциональна емкости CC; чем больше конденсатор, тем больший заряд он может хранить и тем больший ток может протекать. Он также обратно пропорционален частоте ff; чем больше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.
XCXC имеет единицы измерения в омах (проверка оставлена читателю в качестве упражнения). XCXC обратно пропорциональна емкости CC; чем больше конденсатор, тем больший заряд он может хранить и тем больший ток может протекать. Он также обратно пропорционален частоте ff; чем больше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.
Пример 23.11
Расчет емкостного реактивного сопротивления, а затем тока
(a) Рассчитайте емкостное реактивное сопротивление конденсатора емкостью 5,00 мкФ при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока, если приложенное среднеквадратичное напряжение равно 120 В?
Стратегия
Емкостное реактивное сопротивление находится непосредственно из выражения XC=12πfCXC=12πfC. Один раз
XCXC
была найдена на каждой частоте, закон Ома, сформулированный как I=V/XCI=V/XC, можно использовать для нахождения тока на каждой частоте.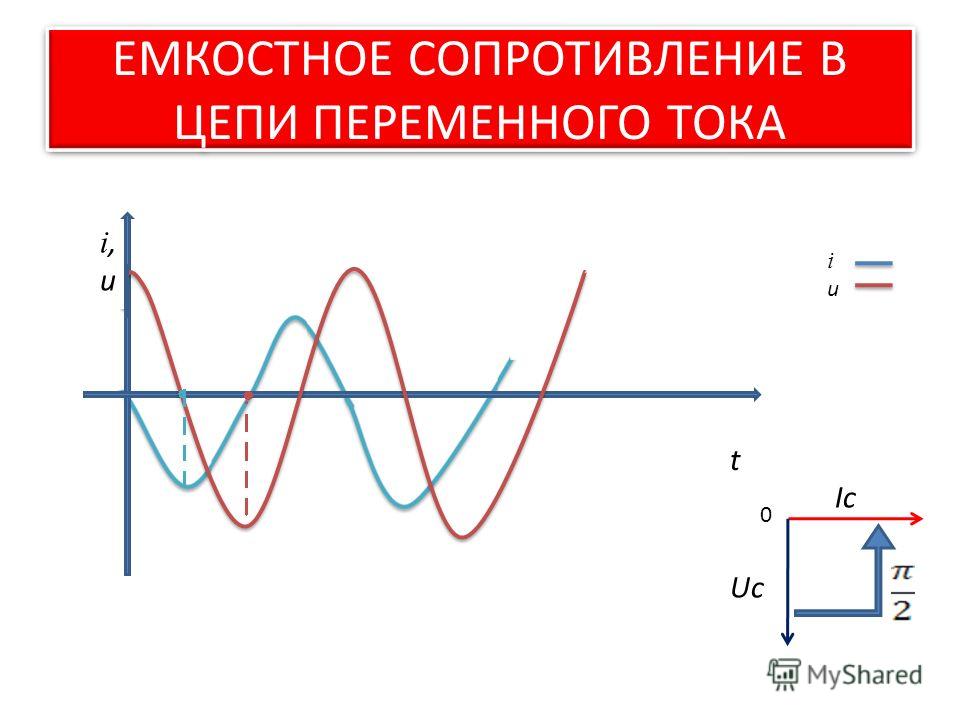
Решение для (a)
Ввод частоты и емкости в XC=12πfCXC=12πfC дает
XC=12πfC=16,28(60,0/с)(5,00 мкФ)=531 Ом при 60 Гц.XC=12πfC=16,28( 60,0/с) (5,00 мкФ) = 531 Ом при 60 Гц.
23,59
Аналогично, на частоте 10 кГц
XC=12πfC=16,28(1,00×104/с)(5,00 мкФ)=3,18 Ом на 10 кГц.XC=12πfC=16,28(1,00×104/с) мкФ) = 3,18 Ом при 10 кГц.
23,60
Решение для (b)
Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в I=V/XCI=V/XC, при условии, что приложенное среднеквадратичное напряжение равно 120 В. Для первой частоты это дает
I=VXC=120 В531 Ом=0,226 А при 60 Гц. I=VXC=120 В531 Ом=0,226 А при 60 Гц.
23,61
Аналогично, при 10 кГц,
I=VXC=120 В3,18 Ом=37,7 А при 10 кГц. I=VXC=120 В3,18 Ом=37,7 А при 10 кГц.
23,62
Обсуждение
Конденсатор очень по-разному реагирует на двух разных частотах, и совершенно противоположным образом реагирует индуктор. На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы способствуют изменениям, тогда как индукторы сопротивляются изменениям. Конденсаторы больше всего препятствуют низким частотам, поскольку низкая частота дает им время зарядиться и остановить ток. Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно со звуковоспроизводящей системой, избавляет ее от гула частотой 60 Гц.
На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы способствуют изменениям, тогда как индукторы сопротивляются изменениям. Конденсаторы больше всего препятствуют низким частотам, поскольку низкая частота дает им время зарядиться и остановить ток. Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно со звуковоспроизводящей системой, избавляет ее от гула частотой 60 Гц.
Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с переменным напряжением, приложенным к конденсатору, существует среднеквадратичное значение тока. Это связано с тем, что напряжение постоянно меняется, заряжая и разряжая конденсатор. Если частота стремится к нулю (постоянный ток), XCXC стремится к бесконечности, а ток равен нулю, как только конденсатор заряжен. На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет пренебрежимо малое реактивное сопротивление и не препятствует протеканию тока (он действует как простой провод). Конденсаторы оказывают противоположное влияние на цепи переменного тока по сравнению с катушками индуктивности .
Конденсаторы оказывают противоположное влияние на цепи переменного тока по сравнению с катушками индуктивности .
Резисторы в цепи переменного тока
В качестве напоминания рассмотрим рис. 23.45, на котором показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени. Напряжение и ток равны в фазе в резисторе. Поведение простого сопротивления в цепи не зависит от частоты:
Рисунок 23.45 (a) Источник переменного напряжения последовательно с резистором. (b) График зависимости тока и напряжения на резисторе от времени, показывающий, что они точно совпадают по фазе.
Напряжение переменного тока в резисторе
Когда на резистор подается синусоидальное напряжение, напряжение точно совпадает по фазе с током — они имеют фазовый угол 0º0º.
Индуктивное реактивное сопротивление
Электрика переменного тока. Введение в переменный ток
Противодействие протеканию тока в этой цепи называется индуктивным реактивным сопротивлением.
Это называется реактивным сопротивлением, а не сопротивлением, потому что влияние индуктивности зависит от частоты питания, а также от значения индуктивности.
Индуктивное реактивное сопротивление измеряется в омах и обозначается символом XL.
Для определения индуктивного сопротивления можно использовать следующую формулу.
XL = 2 π f L
где π — постоянная, f — частота, L — индуктивность снижаться. И наоборот, что более важно, по мере уменьшения частоты цепи индуктивное сопротивление уменьшается, а ток цепи увеличивается.
Емкость в цепях переменного тока
Емкость — это способность цепи накапливать электрический заряд. Устройство, используемое для введения емкости в цепь, известно как конденсатор. Конденсатор состоит из двух пластин, разделенных диэлектриком, см. рис. 11.10. Диэлектриками могут быть, среди прочего, воздух, слюда или вощеная бумага.
рис. 11.10. Диэлектриками могут быть, среди прочего, воздух, слюда или вощеная бумага.
На количество заряда, которое может удерживать конденсатор, влияют три фактора.
Это:
• Площадь тарелок.
•Расстояние между пластинами.
•Материал, используемый для разделения пластин, диэлектрик.
Конденсатор накапливает электрический заряд подобно тому, как гидроаккумулятор хранит жидкость под давлением, но сначала его необходимо зарядить.
При подключении к батарее, как показано на рис. 11.10, электроны будут удаляться с пластины, подключенной к положительной клемме батареи, и добавляться к пластине, подключенной к отрицательной клемме, обычный ток будет течь от положительного к отрицательному. Этот процесс будет продолжаться до тех пор, пока пластины не насытятся и ток не прекратится.
11
Электрика переменного тока — Введение в переменный ток 11
169
11 Электрика переменного тока — Введение в переменный ток
Электрика переменного тока в Введение — Электрика переменного тока 11
пластин достигает своего максимума, и теперь конденсатор полностью заряжен, его напряжение равно напряжению батареи.
Если теперь перевести переключатель в среднее положение, цепь зарядки отключится, и конденсатор будет сохранять свой заряд неопределенное время, подобно аккумулятору. (На практике будет некоторая утечка, которая позволяет конденсатору разряжаться в течение определенного периода времени).
Использование переключателя для подключения конденсатора к внешней цепи позволит конденсатору разрядиться, и ток будет течь по цепи в противоположном направлении, пока разность потенциалов на пластинах не станет равной. Обратите внимание, что конденсатор разряжается в направлении, противоположном тому, в котором он был заряжен. Отметим также, что электроны не проходят между пластинами через диэлектрик
Рис. 11.11 Конденсатор в цепи переменного тока.
170
Электрика переменного тока – Введение в AC 11
При установке в цепь переменного тока, как показано на рис. 11.11, конденсатор будет постоянно заряжаться и разряжаться, так как приложенное напряжение и ток постоянно меняют полярность и направление. Когда приложенное напряжение падает, конденсатор разряжает ток обратно в цепь в противоположном направлении, и его напряжение падает.
Когда приложенное напряжение падает, конденсатор разряжает ток обратно в цепь в противоположном направлении, и его напряжение падает.
Это приводит к сдвигу напряжения в противофазе с током, и в чисто емкостной цепи ток опережает напряжение на 90°. См. рисунок 11.12.
Единицей измерения емкости является фарад, а конденсатору дается символ C. Если ток в 1 ампер, протекающий в течение 1 секунды, создает разность потенциалов в 1 вольт между пластинами конденсатора, то это конденсатор емкостью 1 фарад. Из-за задействованных значений конденсатор емкостью 1 фарад не является практичным размером, и более распространенной единицей измерения является микрофарад или пикофарад.
Рисунок 11.12 Соотношение фаз в чисто емкостной цепи
Емкостное реактивное сопротивление
Противодействие протеканию тока в этой цепи называется емкостным реактивным сопротивлением. Как и в индуктивной цепи, величина реактивного сопротивления зависит от частоты и емкости конденсатора в фарадах. Емкостное реактивное сопротивление измеряется в омах и обозначается символом XC. Его можно рассчитать по следующей формуле:
Емкостное реактивное сопротивление измеряется в омах и обозначается символом XC. Его можно рассчитать по следующей формуле:
ХС | = |
| 1 | |
2 | π f C | |||
|
|
Из этой формулы видно, что с увеличением частоты значение емкостного сопротивления уменьшается, поэтому ток в цепи будет увеличиваться. И наоборот, если частота уменьшается, емкостное сопротивление увеличивается, а ток цепи уменьшается.
Электрика переменного тока — введение в переменный ток 11
171
11 Электрика переменного тока — Введение в переменный ток
Полное сопротивление
Переменный ток в Введение — Электрика переменного тока 11
Полное противодействие току в цепи переменного тока представляет собой комбинацию сопротивления, индуктивного сопротивления и емкостного сопротивления. Но поскольку в каждой цепи соотношение фаз между напряжением и током разное, их нельзя просто сложить.
Но поскольку в каждой цепи соотношение фаз между напряжением и током разное, их нельзя просто сложить.
Индуктивное реактивное сопротивление можно рассматривать как эффект, противоположный емкостному реактивному сопротивлению, поскольку в одной цепи ток отстает от напряжения на 90°, а в другом ток опережает напряжение на 90°, поэтому они разнесены на 180°, и полное реактивное сопротивление можно найти, вычитая одно из другого. Полное сопротивление представляет собой векторную сумму сопротивления и полного реактивного сопротивления и представляет собой полное сопротивление протекающему току, измеренное в омах и обозначенное символом Z.
Рис. видно, что сопротивление не совпадает по фазе с реактивным сопротивлением на 90°:
Математически сумма векторов двух может быть выражена с помощью теоремы Пифагора.
Резонансные цепи
Изменения частоты питания в цепи будут иметь противоположное влияние на емкость и индуктивность. Увеличение частоты питания увеличивает индуктивное сопротивление (XL) и уменьшает емкостное сопротивление (XC).




 6.2).
6.2).


 При нулевой частоте ток в цепи будет постоянным, величина тока , так как конденсатор не пропускает постоянный ток, при резонансной частоте ток максимален – это признак резонанса напряжений . На высоких частотах ток , так как сопротивление катушки становится равным .
При нулевой частоте ток в цепи будет постоянным, величина тока , так как конденсатор не пропускает постоянный ток, при резонансной частоте ток максимален – это признак резонанса напряжений . На высоких частотах ток , так как сопротивление катушки становится равным .


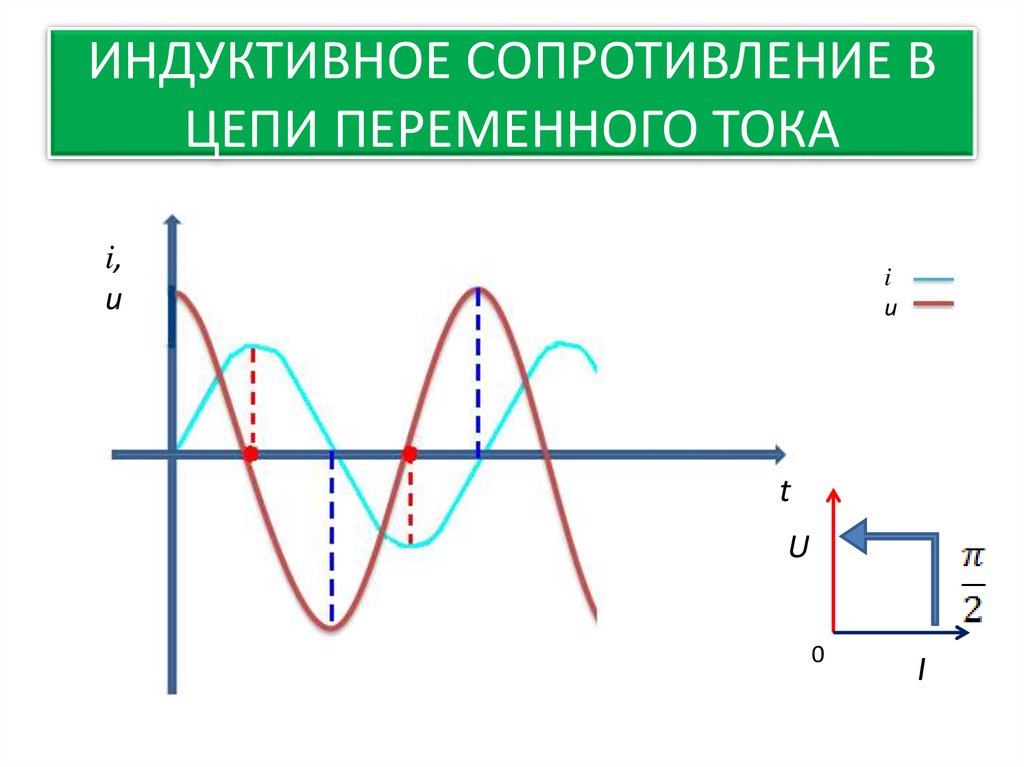
 (6.1)
(6.1)
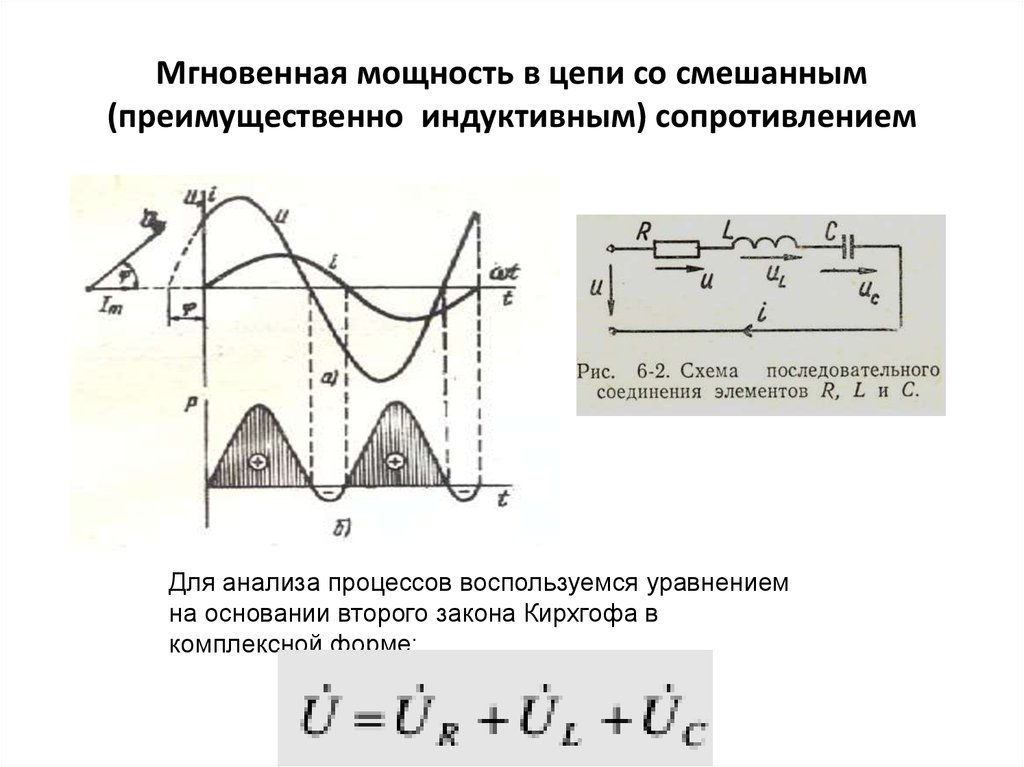 Какие энергетические соотношения справедливы при резонансе?
Какие энергетические соотношения справедливы при резонансе?