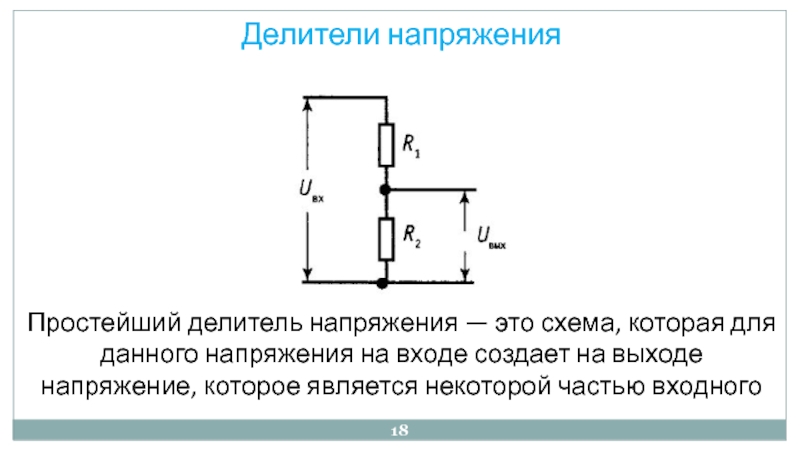
Схемы делителей напряжения
Добавлено 13 января 2021 в 05:06
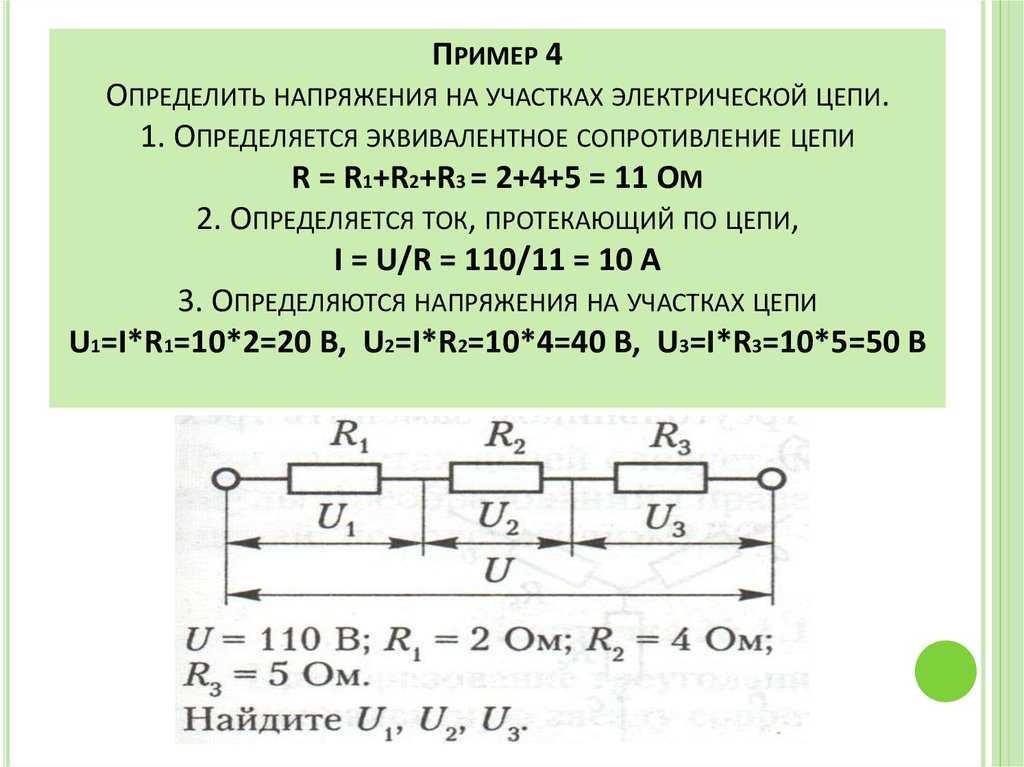
Давайте проанализируем простую последовательную схему и определим падение напряжения на отдельных резисторах:
Рисунок 1 – Схема последовательной цепиРисунок 2 – Табличный метод. Шаг 1По заданным значениям отдельных сопротивлений мы можем определить общее сопротивление цепи, зная, что последовательные сопротивления суммируются.
Рисунок 3 – Табличный метод. Шаг 2Теперь мы можем использовать закон Ома (I = E/R) для определения общего тока, который, как мы знаем, будет таким же, как ток каждого резистора, поскольку токи во всех частях последовательной цепи одинаковы.
Рисунок 4 – Табличный метод. Шаг 3Теперь, зная, что ток в цепи равен 2 мА, мы можем использовать закон Ома (E = IR) для расчета напряжения на каждом резисторе:
Рисунок 5 – Табличный метод. Шаг 4Должно быть очевидно, что падение напряжения на каждом резисторе пропорционально его сопротивлению, учитывая, что ток одинаков на всех резисторах.
Обратите внимание, что напряжение на R2 вдвое больше, чем на R1, так же как сопротивление R2 в два раза больше, чем у R1.
Если бы мы изменили общее напряжение, то обнаружили бы, что эта пропорциональность падений напряжения остается постоянной.
Рисунок 6 – Пропорциональность падений напряжения остается постояннойНесмотря на то, что напряжение источника изменилось, напряжение на R2 по-прежнему ровно вдвое больше, чем на R1. Пропорциональность падений напряжения (соотношение между ними) строго зависит от значений сопротивлений.
При более внимательном наблюдении становится очевидным, что падение напряжения на каждом резисторе также является фиксированной долей напряжения питания. Например, напряжение на R1 составляло 10 вольт при питании от батареи 45 вольт. Когда напряжение аккумулятора было увеличено до 180 вольт (в 4 раза больше), падение напряжения на R1 также увеличилось в 4 раза (с 10 до 40 вольт).
Однако соотношение между падением напряжения R1 и общим напряжением не изменилось:
\[\frac{E_{R1}}{E_{общ}} = \frac{10 \ В}{45 \ В} = \frac{40 \ В}{180 \ В} = 0,22222\]
Точно так же ни один из других коэффициентов падения напряжения не изменился с увеличением напряжения питания:
\[\frac{E_{R2}}{E_{общ}} = \frac{20 \ В}{45 \ В} = \frac{80 \ В}{180 \ В} = 0,44444\]
\[\frac{E_{R3}}{E_{общ}} = \frac{15 \ В}{45 \ В} = \frac{60 \ В}{180 \ В} = 0,33333\]
Формула делителя напряжения
По этой причине последовательную цепь часто называют делителем напряжения из-за ее способности пропорционально делить общее напряжение на дробные части с постоянными коэффициентами. Применив немного алгебры, мы можем вывести формулу для определения падения напряжения на последовательном резисторе, не учитывая ничего, кроме общего напряжения, сопротивления отдельного резистора и общего сопротивления.
Падение напряжения на любом резисторе:
\[E_n = I_n R_n\]
Сила тока в последовательной цепи:
\[I_{общ} = \frac{E_{общ}}{R_{общ}}\]
Подставляем Eобщ/Rобщ вместо In в первую формулу.
..
Падение напряжения на любом резисторе в последовательнй цепи:
\[E_n = \frac{E_{общ}}{R_{общ}} R_n\]
или
\[\large E_n = \frac{R_n}{R_{общ}} E_{общ}\]
В схеме делителя напряжения отношение отдельного сопротивления к общему сопротивлению равно отношению отдельного падения напряжения к общему напряжению питания. Эта формула известна как формула делителя напряжения, и это сокращенный метод определения падения напряжения в последовательной цепи без проведения расчетов тока по закону Ома.
Пример использования формулы делителя напряжения
Используя эту формулу, мы можем повторно проанализировать падение напряжения в примере схемы за меньшее количество шагов:
Рисунок 7 – Схема последовательной цепи\[E_{R1} = 45 \ В \ \frac{5 \ кОм}{22,5 \ кОм} = 10 В\]
\[E_{R2} = 45 \ В \ \frac{10 \ кОм}{22,5 \ кОм} = 20 В\]
\[E_{R3} = 45 \ В \ \frac{7,5 \ кОм}{22,5 \ кОм} = 15 В\]
Компоненты, делящие напряжение
Делители напряжения находят широкое применение в измерительных схемах, где как часть схемы измерения напряжения для «деления» напряжения на точные пропорции используются определенные комбинации последовательных резисторов.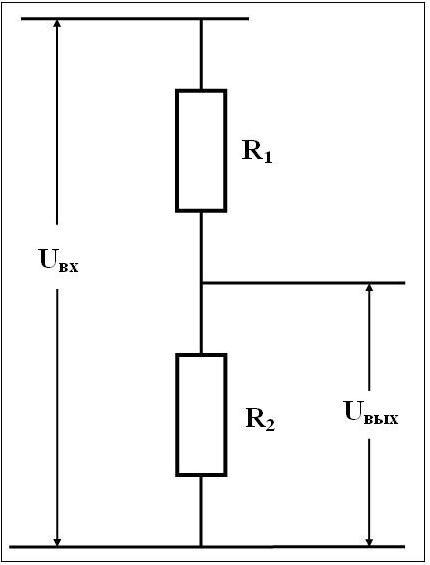
Потенциометры как компоненты, делящие напряжение
Одним из устройств, часто используемых в качестве элемента деления напряжения, является потенциометр, который представляет собой резистор с подвижным элементом, перемещаемым ручкой или рычагом. Подвижный элемент, обычно называемый ползунком, вступает в контакт с резистивной полосой материала в любой, выбранной вручную точке:
Рисунок 9 – ПотенциометрКонтакт ползунка – это обращенная влево стрелка, нарисованная в середине вертикального обозначения резистора. При перемещении вверх он контактирует с резистивной полосой ближе к клемме 1 и дальше от клеммы 2, уменьшая сопротивление от него до клеммы 1 и повышая сопротивление от него до клеммы 2. При перемещении вниз происходит противоположный эффект. Сопротивление, измеренное между клеммами 1 и 2, постоянно для любого положения ползунка.
Рисунок 10 – Принцип действия потенциометраПоворотные и линейные потенциометры
Ниже показано внутреннее устройство двух типов потенциометров: поворотного и линейного.
Линейные потенциометры
Рисунок 11 – Конструкция линейного потенциометраНекоторые линейные потенциометры приводятся в действие прямолинейным движением рычага или ползунковой кнопки. Другие, подобные изображенному на рисунке выше, приводятся в действие поворотным винтом для точной регулировки. Потенциометры последнего типа иногда называют «подстроечниками» потому, что они хорошо работают в приложениях, требующих «подстройки» переменного сопротивления до некоторого точного значения.
Следует отметить, что не все линейные потенциометры имеют такое же назначение выводов, как показано на этом рисунке. У некоторых вывод ползунка находится посередине между двумя крайними выводами.
Поворотный потенциометр
На изображении ниже показана конструкция поворотного потенциометра.
Рисунок 12 – Поворотный потенциометрНа фотографии ниже показан реальный поворотный потенциометр с открытыми для удобства просмотра ползунком и резистивным элементом. Вал, который перемещает ползунок, повернут почти до конца по часовой стрелке, поэтому ползунок почти касается левого конечного вывода резистивного элемента:
Рисунок 13 – Поворотный потенциометр с открытыми ползунком и резистивным элементомВот тот же потенциометр с валом ползунка, перемещенным почти до упора против часовой стрелки, поэтому ползунок теперь находится рядом с другим крайним концом хода:
Рисунок 14 – Потенциометр с валом ползунка, повернутым до упора против часовой стрелкиВлияние регулировки потенциометра на схему
Если между внешними выводами (по всей длине резистивного элемента) приложено постоянное напряжение, положение ползунка будет отводить часть приложенного напряжения, измеряемого между контактом ползунка и любым из двух других выводов.
Значение коэффициента деления полностью зависит от физического положения ползунка:
Важность потенциометров
Как и в случае с фиксированным делителем напряжения, коэффициент деления напряжения потенциометра строго зависит от сопротивления, а не от величины приложенного напряжения. Другими словами, если ручка потенциометра или рычаг перемещается в положение 50 процентов (точное центральное положение), падение напряжения между ползунком и любым крайним выводом будет составлять ровно 1/2 от приложенного напряжения, независимо от того, что с этим напряжением происходит, или каково полное сопротивление потенциометра. Другими словами, потенциометр работает как регулируемый делитель напряжения, где коэффициент деления напряжения устанавливается положением ползунка.
Это применение потенциометра является очень полезным средством получения изменяемого напряжения от источника фиксированного напряжения, такого как аккумулятор.
Если для схемы, которую вы собираете, требуется определенная величина напряжения, которая меньше, чем значение напряжения доступной батареи, вы можете подключить внешние выводы потенциометра к этой батарее и «выбрать» для использования в вашей цепи любое необходимое напряжение между ползунком и одним из внешних выводов потенциометра:
При таком использовании название «потенциометр» имеет смысл: он «измеряет» (контролирует) приложенный к нему потенциал (напряжение), создавая изменяемый коэффициент деления напряжения. Такое использование трехполюсного потенциометра в качестве переменного делителя напряжения очень популярно в схемотехнике.
Примеры небольших потенциометров
Ниже показано несколько небольших потенциометров, которые обычно используются в бытовом электронном оборудовании, а также любителями и студентами при построении схем:
Рисунок 17 – Примеры небольших потенциометровМеньшие устройства слева и справа предназначены для подключения к беспаечной макетной плате или для пайки в печатную плату.
Устройства посередине предназначены для установки на плоской панели с проводами, припаянными к каждому из трех выводов.
Ниже показано еще три потенциометра, более специализированных, чем только что показанный набор:
Рисунок 18 – Примеры потенциометров размером побольшеБольшое устройство «Helipot» – это лабораторный потенциометр, предназначенный для быстрого и легкого подключения к цепи. Устройство в нижнем левом углу фотографии представляет собой потенциометр того же типа, только без корпуса и поворотного счетного диска. Оба этих потенциометра представляют собой прецизионные устройства, в которых используются многооборотные спиралевидные резистивные ленты и ползунковые механизмы для точной регулировки. Устройство в правом нижнем углу представляет собой потенциометр для монтажа на панели, предназначенный для работы в тяжелых промышленных условиях.
Резюме
- Последовательные цепи делят общее напряжение питания на отдельные падения напряжения, коэффициенты деления строго зависят от сопротивлений: ERn = Eобщ(Rn/Rобщ)
- Потенциометр – это элемент переменного сопротивления с тремя точками подключения, часто используемый в качестве регулируемого делителя напряжения.
Оригинал статьи:
- Voltage Divider Circuits
Теги
Делитель напряженияДля начинающихЗакон ОмаОбучениеПоследовательная цепьПотенциометрСхемотехникаОглавление
Вперед
Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | |||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva. Поделиться:
| ||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления.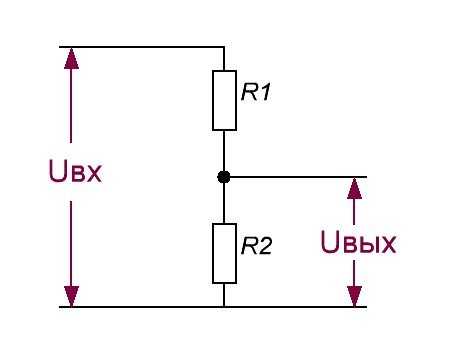 Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.
Free xml sitemap generator | ||||||
engineeringtoolbox.com (классный сайт)Потенциометр как делитель напряжения
Скорость потока электронов через проводник называется электрическим током. Его можно просто определить как количество заряда, прошедшего через проводник за определенный период времени. Таким образом, мы можем генерировать формулы для электрического тока из вышеуказанного определения как
I = Q/T
Где,
Q = Заряд
T = время
SI единицы электрический ток Ампер(А).
1 Ампер определяется как 1 кулон заряда, проходящего через проводник за 1 секунду.
Направление потока электрического тока противоположно направлению потока электронов.
Виды электрического тока
Электрический ток может быть двух видов в зависимости от его величины и направления.
Постоянный ток
Тип тока, величина и направление которого остаются неизменными во времени, называется постоянным током. В постоянном токе постоянный ток протекает через проводник, и нет колебаний величины тока, т.е. величина постоянна, а не переменна.
Например. Ячейка, батарея и т. д.
Переменный ток
Ток, амплитуда которого изменяется, а направление меняется периодически, называется переменным током. В переменном токе величина сначала постепенно увеличивается от 0 до максимума, а затем снова уменьшается до 0. Затем снова увеличивается до максимума, но в отрицательном направлении, а затем снова достигает нуля. Это завершает один цикл переменного тока.
Описанный выше процесс настолько быстр, что за одну секунду может выполняться любое количество циклов.
Количество циклов в секунду измеряется в герцах (Гц). Например, электроснабжение в Индии происходит на частоте 50 Гц. Это означает, что за одну секунду совершается 50 циклов.
Например. AC Dynamo, Поставка в наши дома через электростанцию.
Электрическое сопротивление
Противодействие протеканию электрического тока по проводнику известно как электрическое сопротивление. Закон Ома гласит, что разность потенциалов на проводнике прямо пропорциональна току, протекающему по проводнику.
В ∝ I
В = IR
, где R — константа пропорциональности, которая представляет собой сопротивление.
Формулы для электрического сопротивления можно вывести из закона Ома следующим образом: R = V/I
где V = разность потенциалов
I = электрический ток
Единицей сопротивления в системе СИ является Ом.
1 Ом определяется как сопротивление, создаваемое проводником, когда к проводнику приложена разность потенциалов в 1 вольт, а ток, протекающий через проводник, составляет 1 ампер.
Сопротивление может быть представлено в виде зигзага на цепи.
Разность потенциалов
Разность потенциалов между двумя точками представляет собой меру энергии, вовлеченной или высвобождаемой при переносе носителей заряда из одной точки в другую. Он определяется как произведение сопротивления провода на ток, протекающий по проводу. Из приведенного выше определения можно вывести следующие формулы: V = IR
Единицей разности потенциалов в системе СИ является вольт (В).
Потенциометр
Потенциометр представляет собой резистор с тремя выводами, два из которых являются фиксированными, а один — переменным или подвижным. если разбить слово «потенциометр», то получится два слова «потенциал» и «метр». Итак, становится совершенно ясно, что потенциометр — это устройство, которое используется для измерения разности потенциалов между проводниками.
Принцип Принцип работы потенциометра заключается в том, что он находит значение неизвестного напряжения путем сравнения его с известным напряжением.
Вольтметр и потенциометр
Не следует часто путать вольтметр и потенциометр. Это разные вещи. Вольтметр используется для определения напряжения на клеммах цепи, тогда как потенциометр используется для определения ЭДС цепи.
Применение
- Потенциометр используется для определения неизвестного напряжения путем сравнения его с известным напряжением.
- Используется для определения значения ЭДС и внутреннего сопротивления данной ячейки.
- Может также использоваться как делитель напряжения.
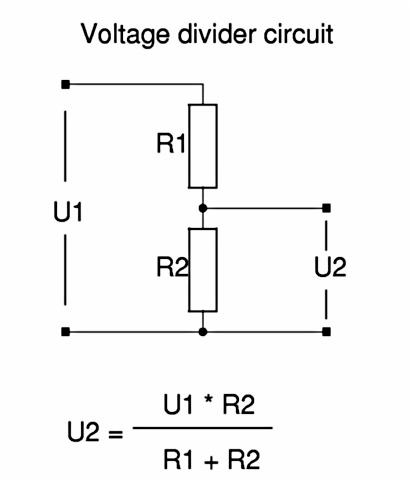
Потенциометр в качестве делителя напряжения
Чтобы сделать делитель напряжения, входное напряжение источника подключается к сопротивлению через цепь. Два конца сопротивления закреплены, а между сопротивлениями находится ползунок, который делит данное сопротивление на две части R 1 и R 2 . Требуемое напряжение V out достигается на R 2 .
Приведенная ниже диаграмма более ясно пояснит ситуацию.
Пусть V R1 и V R2 — падение напряжения на резисторах R1 и R2 соответственно. Применяя Закон о напряжении Кирхгофа,
V в = V R1 + V R2
С V R1 = I X R1 и V R2 = I X R2
3 3 3 3 3 3 3 3 3 9000 3 3 3 3 3 3 9000 3 9000 3 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 . = I x R1 + I x R2В в = I x ( R1 + R2)
I = V в / (R1 + R2)
Следовательно,
В R1 = (V в / (R1 + R2)) x R1
V R1 = V в x (R1 / (R1 + R2))
и
V R2 = 2 (R1 / (R1 + R2)) in / (R1 + R2)) x R2
В R2 = V in x ( R2 / (R1 + R2))
Заданное входное напряжение (V в ) может быть изменено на требуемое выходное напряжение (V из ) путем перемещения клеммы переменной по сопротивлению.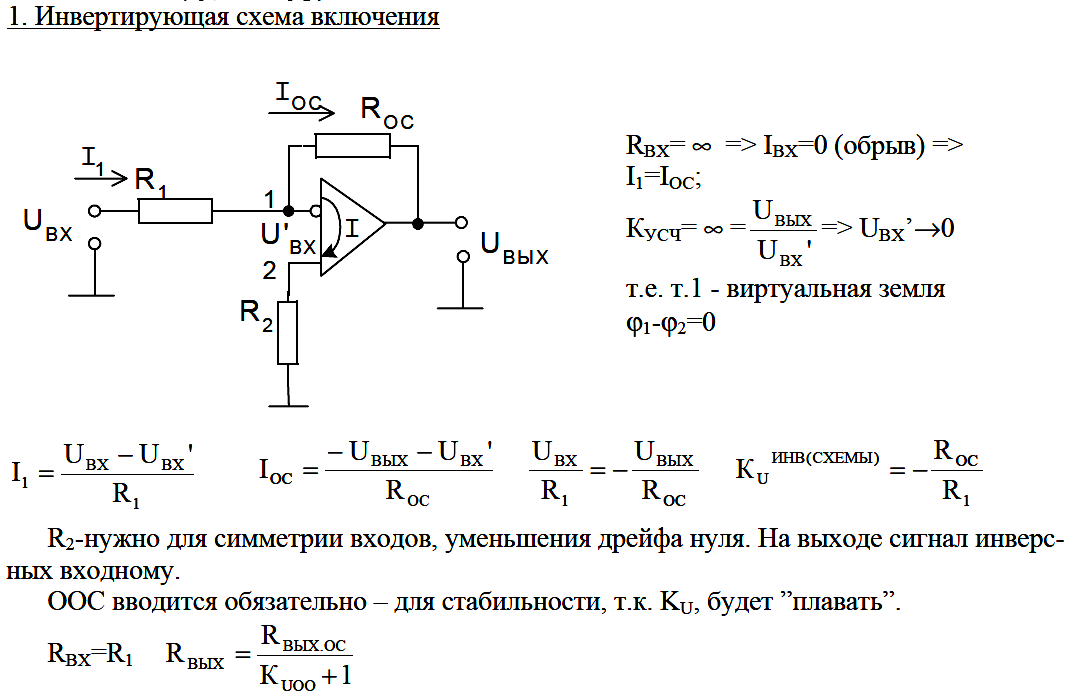
Перемещая движок, мы можем изменить значение R1 и R2, и, следовательно, падение напряжения на R2 также изменится.
Так как величина напряжения и сопротивления зависят друг от друга. Мы знаем, что отношение напряжений равно отношению сопротивлений.
V в / V OUT = (R 1 + R 2 / R 2 )
SO, V OUT = V в 222222221 (V OUT = V ). 1 + R 2 )
Обобщения:
Случай 1: Если R 1 = R 2 = R,
V out = V in × (R / 2R)
V out = V in / 2
Case 2: If R 1 << R 2
V out ≈ V in (R 2 /R 2 )
V out = V in
Case 3: If R 2 << R 1
В вых ≈ В вх (0/R 1 )
В вых = 0
Примеры задач
Задача 1: Если ток 5А протекает по проводу за 2 сек.
Найдите заряд провода в кулонах.
Решение:
q = I x t
q = 5 x 2
= 10 кулонов
Итак, заряд в проводе равен 10 кулонам.
Задача 2: Найдите сопротивление проводника, если течет ток 2А, а разность потенциалов 5В.
Решение:
R=V/I
= 5/2
= 2,5 Ом
Итак, сопротивление поперек проводника равно 2,5 Ом.
Задача 3: Найдите напряжение на сопротивлении 3 кОм. Если ток протекает через сопротивление 2 A.
Решение:
V = IR
= 2 x 3 x 10 3
= 6 К. .
Задача 4: Найдите деленное напряжение потенциометра, если сопротивление R1 равно 2 Ом, сопротивление R2 равно 4 Ом, а входное напряжение равно 3 В.
Решение:
Выходное напряжение = 3 x (4/2+4)
= 3 x (2/3)
= 2 В
Таким образом, выходное напряжение потенциометра составляет 2 В.
Задача 5: Найти входное напряжение потенциометра, если сопротивление разделено поровну, а выходное напряжение равно 6 В
Решение:
Входное напряжение = 2 x 6
= 12 В
Итак, входное напряжение потенциометра равно 12 В.
Задача 6: Найдите напряжение на резисторе R1. Если напряжение источника 5 В, R1 = 3 Ом и R2 = 6 Ом.
Решение:
Напряжение на R1 = 5 x (3/3 + 6)
= 5 x (3/9)
= 5 x (1/3)
= 1,67 В
Итак, падение напряжения на резисторе R1 составляет 1,67 В.
Задача 7: Найдите выходное напряжение, если R1 = 30 мкОм и R2 = 2 кОм. Напряжение источника 50В.
Решение:
Поскольку R2>>R1,
Итак, V из почти равно V из .
В вых = В вх
В вых = 50 В
Итак, выходное напряжение 50 В.
Разделение напряжения и простые RC-фильтры
| Выходное напряжение всегда меньше, чем V входное. В идеальной схеме соотношение между входом и выходом совершенно линейно. Затухание пропорционально отношению R Потенциометр представляет собой реализацию простой схемы делителя напряжения в виде простого механического устройства, позволяющего плавно регулировать соотношение R1 и R2. Название «потенциометр» происходит от термина «потенциальная электродвижущая сила», который является синонимом напряжения. Возможно, это было выбрано потому, что «вольтметр» уже использовался в качестве устройства для измерения напряжения. Важные конструктивные особенности: R 1 добавляет последовательное сопротивление к V в , повышая импеданс источника. R 2 загрузки V в . Если общая сумма R 1 + R 2 меньше, чем ≈10-кратное сопротивление источника V в , тогда вы должны добавить полное сопротивление источника к R 1 , чтобы формулы были точными. Аналогичным образом, «нагрузка», подключенная к клемме V out , должна иметь входное сопротивление ≈10x R 1 + R 2 . Как правило, лучше всего поддерживать R 1 +R 2 настолько низким, насколько это позволяет импеданс источника, чтобы результирующий выходной импеданс делителя был лишь небольшим увеличением импеданса по сравнению с источником. Управление входом делителя напряжения с источником напряжения с очень низким импедансом (например, выход операционного усилителя) позволяет использовать конструкцию с минимальным импедансом (см. Douglas Self Полезные формулы: V out = V in * ( R 2 / (R 1 + R 2 ) ) R 1 = R 2 (V in — V OUT ) / V OUT R 2 = (-V OUT ) (R 1) / (V OUT -V в ) 1212121. 12121 2 -v в ) IF -V . 2 , затем V out = V in / 2 Википедия: Делитель напряжения Если требуется симметричный аттенюатор, я рекомендую конфигурацию «U» и размещение его рядом с симметричным входом. Проектирование начинается с расчета минимального входного импеданса, допустимого для импеданса источника. Это можно найти, проверив лист данных производителя, руководство пользователя, схему, открыв устройство и нарисовав схему, или проверив. Для профессионального аудиоустройства общего назначения (источник неизвестен) примите минимальное входное сопротивление 10 кОм. Затем выберите желаемые потери, например -6 дБ, -20 дБ, -40 дБ и т. д. В потерях напряжения они соответствуют делениям 1/2, 1/10 и 1/100 соответственно. Используйте несимметричную схему с 2 резисторами и формулы, чтобы найти значения резисторов для желаемого деления напряжения. Следуя практике проектирования с низким импедансом, оставьте R 2 настолько низким, насколько позволяет минимальный импеданс. Чтобы преобразовать несбалансированную схему в симметричную U-образную схему, просто разделите несимметричную R Расчеты могут привести к нестандартным значениям резисторов. Я выберу R 2 в качестве стандартного значения, затем рассчитайте R 1 . Необходимо рассчитать допуски как для входного импеданса, так и для фактических потерь напряжения. После того, как допуски установлены, попробуйте округлить рассчитанное значение R 1 в большую или меньшую сторону до ближайших значений стандартных резисторов и проверьте, соответствует ли окончательный проект заданным допускам. Распространенной альтернативой конфигурации «U» является конфигурация «H». Буква «H» является реверсивной и «согласованной», т. е. подходит для передачи максимальной мощности. При передаче напряжения в виде сигнала с незначительным потреблением тока мы не пытаемся передать мощность. По сравнению с простыми цепями RC-фильтра: Замена верхнего резистора конденсатором создает фильтр верхних частот. Основная идея такая же, как у делителя постоянного напряжения, за исключением того, что конденсатор можно рассматривать как «резистор, зависящий от частоты». Когда частота переменного напряжения снижается, «сопротивление» C увеличивается. При постоянном токе (частота = 0 или очень близка к 0) конденсатор полностью блокирует напряжение, аналогично эффекту увеличения R1 в первой схеме делителя напряжения. На высоких частотах «сопротивление» C очень мало, и выход очень близок к входу. Мы называем это «зависимым от частоты сопротивлением» специальным термином: реактивное сопротивление. Конденсаторы имеют емкостное сопротивление, а катушки индуктивности — индуктивное сопротивление. Символы реактивного сопротивления: X 9(-1/x) показывает логарифмическую кривую зарядки крышки, где e — число Эйлера, y — заряд на крышке, x — емкость, а сопротивление и время в секундах равны 1 (и имеют уже исключены из данного уравнения). Использование простых RC-фильтров в качестве «делителей напряжения переменного тока» становится проблематичным, когда мы хотим выбрать произвольное деление или затухание для данного входа. С двумя резисторами очень легко выбрать любое произвольное деление, которое вам нравится. После введения конденсатора с его извилистыми скоростями заряда и разряда решение для конкретных величин затухания вдоль кривой возможно, но гораздо сложнее. Вместо того, чтобы пытаться разобраться со сложностью всей кривой, принято просто фокусироваться на точке, где R = C. Если мы сосредоточимся на этой точке, то сможем вернуться к нашему относительно простому Vout = Vin (R2/ R1+R2), обновите ее для использования с конденсаторами, и мы найдем полезное «эмпирическое правило», которое можно применить для быстрых расчетов фильтра. Когда мы установим R = C, будет определенная частота, которая будет ослаблена на -3 дБ при прохождении через фильтр. Почему -3 дБ? Эта точка аналогична равным резисторам в чисто резистивном делителе напряжения, и поэтому ее относительно легко вычислить, если вы понимаете формулы. Чтобы рассмотреть другие варианты, вы можете вернуться к извилистым функциям, производимым зарядкой и разрядкой конденсатора. Можно рассчитать точку -1 дБ, точку -2 дБ и т. д., но, поскольку все эти точки лежат на кривой линии, решение для этих других точек, возможно, сложнее. Точка -3 дБ, возможно, является самой простой точкой для расчета, и она полезна в реальных приложениях. -3дБ примерно соответствует уменьшению на 30%. В следующем разделе показано, как рассчитывается это число. Деление напряжения с импедансом При объединении реактивного сопротивления и сопротивления получается импеданс. Наша формула делителя напряжения с использованием конденсаторов имеет ту же структуру, что и делитель только с резисторами, но она должна быть выражена через импеданс. Z означает импеданс. Z total означает комбинацию реактивного сопротивления C1 и сопротивления R1 (аналогично выражению R 1 + R 2 мы использовали ранее). Z Всего = Z 1 +Z 2 Z 1 = x C Z 2 = R 1 2 Z 2 = R 1 2 1 2 . всего ). Чтобы найти импеданс любого компонента, мы должны добавить сопротивление компонента к реактивному сопротивлению компонента. Это рассчитывается с использованием декартовой плоскости (также известной как график «xy»), где сопротивление отложено по горизонтальной оси или оси «x», а реактивное сопротивление нанесено по вертикальной оси или оси «y». Мы не можем суммировать их напрямую (x+y), но мы можем суммировать их как вектор, что означает, что мы будем измерять длину отрезка прямой от начала координат (0,0) до нашей точки (x,y). Наш отрезок образует гипотенузу треугольника с длиной x и высотой y. Теорема Пифагора говорит, что длина гипотенузы будет равна квадратному корню из суммы x 2 + y 2 : Z всего = √(R 1 2 + X 2 ), где X C — емкостное реактивное сопротивление C 1 . Чтобы показать аналогию с чисто резистивным делителем, мы решим Ztotal для случая, когда R1 = 1 и XC = 1, z Всего = √ (1 2 + 1 2 ) Z Итого = √ (1 + 1) Z Итого = √2 Z 2 2, = √2 Z 2 2, = √2 Z 2 2 , с момента IT = √2 Z . резистор, будет = √(1 2 + 0 2 ), = 1. . Vout = Vin (1 / √2) Если мы оценим √2 равным 1,414, то уравнение может стать следующим: Vout = Vin * 0,707, что можно интерпретировать как «выходное напряжение будет составлять около 70% входного напряжения». Как выражение в децибелах, умножение на 1/√2 выражается как -3 дБ. Гораздо более аккуратное и легкое для восприятия выражение. Как вычислить частоту -3 дБ Вы можете найти «частоту среза -3 дБ», сокращенную до f -3 дБ , используя следующую формулу: f -3 дБ = 1 / ( 2πRC) Эта формула получена из того, где реактивное сопротивление C = сопротивление R на желаемой частоте (надеюсь, теперь мы понимаем, почему это имеет смысл). Если частота известна, и вам просто нужно найти R или C, их удобно просто поменять местами после переключения вещей с помощью алгебры: R = 1 / (2πCf -3dB ) C = 1 / (2πRf -3dB ) Как только вы определили точку -3dB, затухание уменьшается по мере увеличения входной частоты и увеличивается по мере ее снижения. Если вы не понимаете, почему константа «2π» выскочила в уравнении, она выражает 360° сигнала переменного тока в радианах. Замена нижнего резистора делителя напряжения конденсатором создает фильтр нижних частот. Конденсатор по-прежнему имеет низкое реактивное сопротивление на высоких частотах и высокое реактивное сопротивление на высоких частотах, но теперь его роль в делителе напряжения изменилась. Теперь низкие частоты, вплоть до постоянного тока, проходят нормально, поскольку C «выглядит» как большой резистор, тогда как высокие частоты «видят» C как очень маленький резистор и соответственно ослабляются. Применимы все приведенные выше формулы, но теперь затухание уменьшается при снижении входной частоты и увеличивается при повышении входной частоты. Эксперимент/Лаборатория Необходимые предметы: 9 В батарея Клипы аллигатора ДВА 1K 1/4 Вт (или любые два резистора того же значения, больше 1K) VOLTMETER 2 .OLTAGE). – очень важное понятие. Если вы можете понять деление напряжения, вы можете понять базовые усилители, а базовые усилители являются сердцем большинства аудиосхем. До сих пор ожидается, что вы понимаете, что такое блок питания /источник напряжения , по крайней мере, на самом базовом уровне. Для целей нашего первого деления напряжения нам просто нужно что-то вроде 9-вольтовой батареи. Он может подавать 9 В на нагрузку 2 кОм без чрезмерной «нагрузки» (см. страницу «Батареи и резисторы»). Аккумулятор 9 В обеспечивает около 9 В… может быть, немного больше, и все меньше и меньше по мере разрядки… но что, если нам нужно другое напряжение? Для выше , нам либо нужно выбрать другую батарею (например, батарею на 12 В), использовать специальную схему (немного продвинутую для нас на данный момент!), либо поместить 2 9 В в серии , чтобы получить 18 В. Хм. Как сделать с меньшим напряжением ? (Простой) ответ: деление напряжения . Вот эксперимент: Соедините два резистора вместе последовательно . Возьмите один из двух резисторов одинакового номинала (1 кОм или выше) и обмотайте один провод вокруг одного вывода другого резистора. Если это резисторы номиналом 1 кОм, это эквивалентно одному резистору на 2 кОм, за исключением того, что у нас есть место, где мы можем измерить напряжение в середине нашего нового резистора «2 кОм». Соедините с помощью зажимов типа «крокодил» клемму «+» 9-вольтовой батареи с одним из неподсоединенных выводов резистора, а клемму «–» батареи с другим неподсоединенным выводом резистора. Цепь должна идти от клеммы 9В + к резистору 1к, к другому резистору 1к, к клемме 9В -. Измерить напряжение на аккумуляторе. Красный щуп к клемме +, черный щуп к клемме -. Это должно показывать 9В или больше. Держите черный щуп на клемме -, а красный щуп поднесите к соединению двух резисторов. Обратите внимание на это показание напряжения. Что ты получил? Было ли оно около 4,5 В или 1/2 от показаний на аккумуляторе + клемма? Поздравляем, вы «создали» точку 4,5 В, которую можно использовать во многих схемах. Это мощный навык, позволяющий «создавать» новые напряжения из фиксированного напряжения. Теперь, когда вы это сделали, возникает следующий вопрос: почему это сработало? Давайте подумаем об этом с помощью закона Ома. Что касается резистора «2k», мы знаем, что на одной стороне резистора есть +9 В, а на другой — 0 В. Закон Ома говорит, что будет протекать ток в следующей величине: Ток = Напряжение / Сопротивление Ток = 9 В / 2000 Ом Ток = 0,0045 А Ток одинаков для всех наших последовательно соединенных элементов . Снова используя закон Ома, мы определяем напряжение на каждом резисторе 1 кОм, используя 0,0045 А в качестве тока. Напряжение = ток x сопротивление Напряжение = 0,0045 А x 1000 Ом Напряжение = 4,5 В Это означает, что от клеммы +9 аккумулятора до места соединения двух резисторов падает 4,5 В. «Глядя» с другой стороны, есть падение 4,5 В от клеммы 0 В или — до соединения двух резисторов. В любом случае у нас есть 9В-4,5В = 4,5В на стыке двух резисторов. Эти простые расчеты очень сложны, но они помогут вам понять более сложные расчеты. В эксперименте «Батарея и резистор как источник и нагрузка» мы наблюдали эффект «нагрузки», который резистор 1k может иметь на 9батарея В. Без нагрузки 9 В может иметь 9,5 В или около того, а нагрузка 1 кОм или около того вызовет небольшое падение напряжения на клеммах аккумулятора. Для батарей 9 В я использую 3 Ом в качестве внутреннего импеданса батареи. Допустим, ненагруженные 9В на нашем вольтметре измеряли 9,5В. Мы подключаем 3 Ом + 1000 Ом через клеммы. Посмотрим, каким будет ток: Ток = (9 В) / (1003 Ом) = 0,00897 А Посмотрим падение напряжения на резисторе 3 Ом. Для моего свежего источника 9 В с импедансом источника 3 Ом я испытываю только 0,0269V Падение напряжения питания при подключении нагрузки 1к. Мы бы прочитали около 9,47 В на вольтметре. Подключим более тяжелую нагрузку. Ток = 9 В / 503 Ом = 0,01789 А А теперь вычисляем падение на 3 Ом: Напряжение = 0,01789 x 3 Ом = 0,0537 В Все еще в порядке. Вольтметр показывает около 9,44 В. Еще более тяжелый груз. Теперь 50 Ом. Снова ток: 9 В / 53 Ом = 0,17 А Падение напряжения: 0,17 А x 3 Ом = 0,5 В. Сейчас «загрузка» значительна. Наша незаряженная батарея на 9,5 В теперь едва соответствует названию «9 В». Еще тяжелее . Переходим к 10 Ом. 9 В / 13 Ом = 0,7 А 0,7 А x 3 Ом = 2,1 В Теперь наша разряженная батарея на 9,5 В поддается большой нагрузке и становится батареей на 6,9 В. 9 В — плохой источник напряжения для такого низкого импеданса нагрузки. Нам понадобится источник с сопротивлением намного меньше 3 Ом для управления нагрузкой 10 Ом. Это приводит к практическому правилу при «управлении» нагрузками от источников напряжения. Эмпирическое правило: импеданс источника должен быть примерно в десять раз меньше импеданса нагрузки .  |
Частоту -3 дБ часто называют «частотой среза». «Частота среза» не всегда означает точку -3 дБ, но в большинстве случаев вы можете сделать предположение, если не указано что-то еще, например -1 дБ.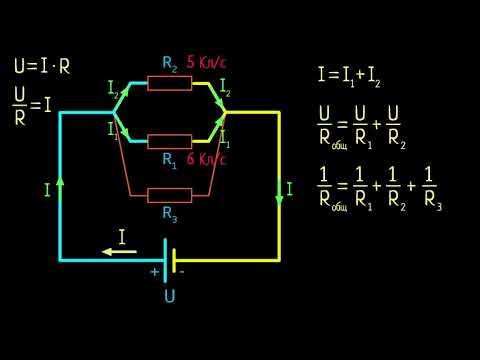
(Консультируйтесь с учебником физики для более глубокого объяснения.)
Значение «C» имеет неотъемлемую связь с частотой, которая выражается в формуле емкостного реактивного сопротивления, которая отличается от приведенной выше формулы «R = …» только добавлением X 92 + 1)), домен x равен 0-1, это показывает, что произойдет, если вы замените R1 линейным потенциометром. Объясняет ограничения и проблемы простых регулируемых RC-фильтров.]
.. в данном случае это батарея и 2 резистора.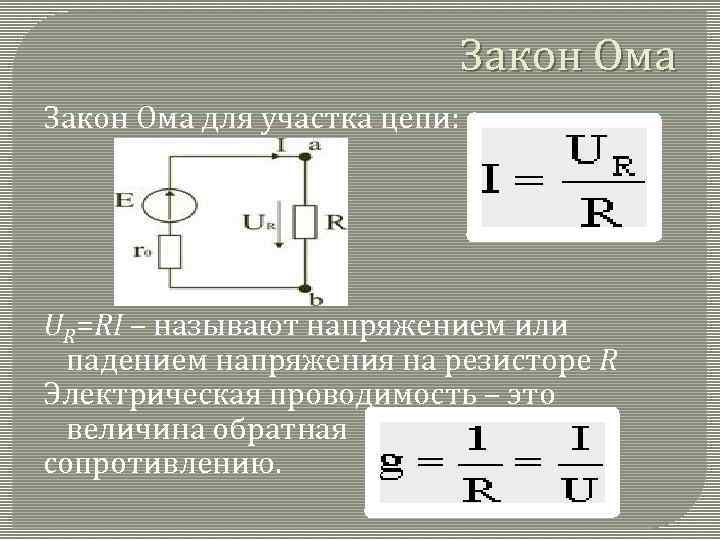
Это похоже на постоянный резистор 3 Ом, постоянно подключенный к плюсовой клемме аккумулятора. Это может быть либо терминал, либо воображаемый «между» терминалами. Дело в том, что это в серии с нагрузкой, и, таким образом, снова с нашим 1k примером, нам нужно рассчитать наше «выходное напряжение» по отношению к деление напряжения , которое будет происходить между нашим сопротивлением источника 3 Ом и сопротивлением нагрузки 1000 Ом .
Попробуем 500 Ом. Снова вычисляем ток: