Параллельное соединение резисторов | Электротехника
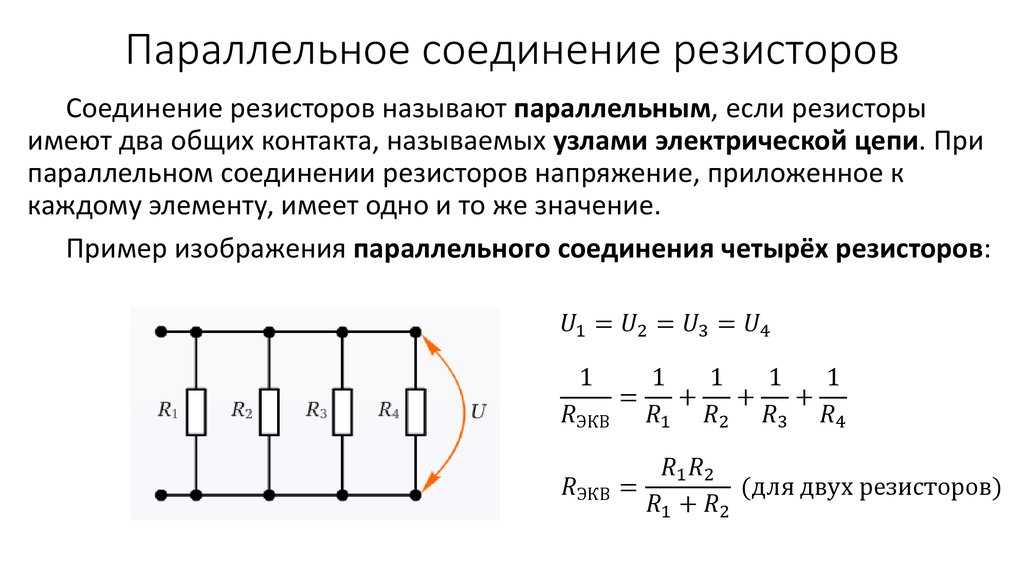
Параллельное соединение резисторов. При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
Рис. 26. Схемы параллельного соединения приемников
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I1=U/R1; I2=U/R2; I3=U/R3.
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I1+I2+I3, или
I = U / R1 + U / R2 + U / R3 = U (1/R1 + 1/R2 + 1/R3) = U / Rэк (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/Rэк = 1/R1 + 1/R2 + 1/R3 (24)
Вводя в формулу (24) вместо значений 1/Rэк, 1/R1, 1/R2 и 1/R3 соответствующие проводимости Gэк, G1, G2 и G3, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:
Gэк = G1+ G2 +G3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I1 : I2 : I3 = 1/R1 : 1/R2 : 1/R3 = G1 + G2 + G3 (26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
Rэк=R1R2/(R1+R2)
при трех параллельно включенных резисторах
Rэк=R1R2R3/(R1R2+R2R3+R1R3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.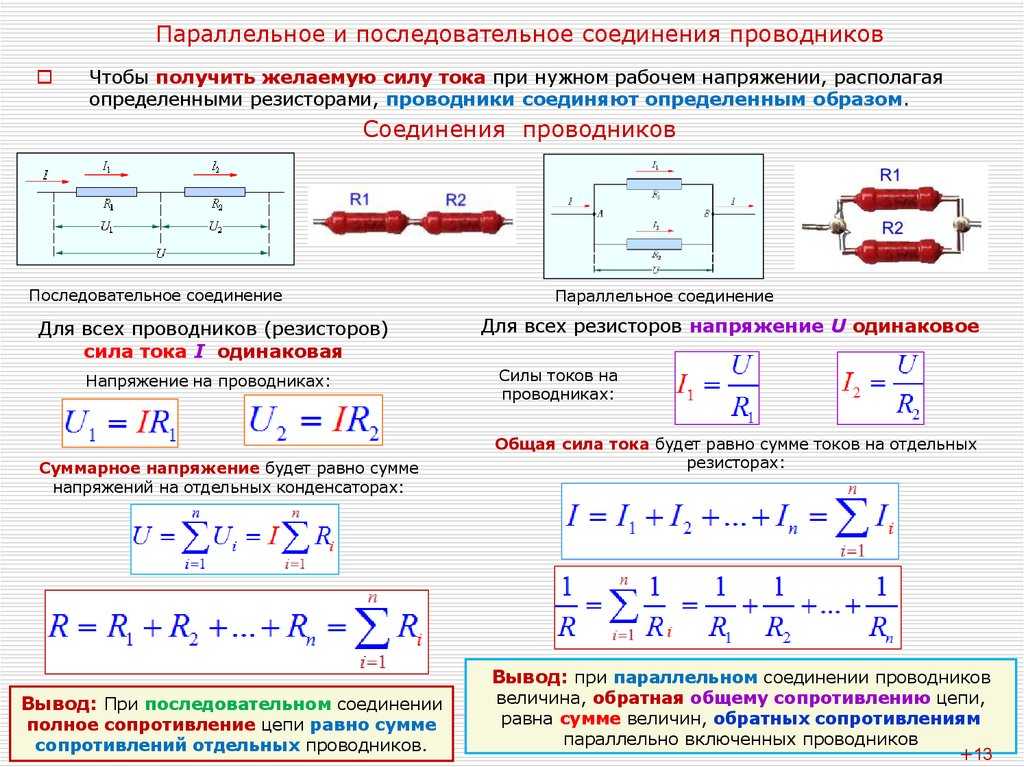
Rэк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
Параллельное включение резисторов. Как рассчитать сложные схемы соединения резисторов. Способы соединения проводников
Определение параллельного соединения
Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) — это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.
Резисторы представляют собой пассивные электронные компоненты, основным параметром которых является сопротивление, также называемое электрическим сопротивлением, отсюда и другой называемый резистор. Сопротивление — это параметр, полностью не зависящий от напряжения.
Согласно «старой школе» резисторы были отмечены «сломанной» ветвью схемы, символизирующей избыток на проводнике. В настоящее время представление идеальных резисторов в схемах замещения использует тот же символ, что и в случае идеального однооборотного элемента, описываемого импедансом. Это связано с тем, что резистор является самым элементарным электронным компонентом, а определение импеданса идеального резистора на основе резистора сводится к определению сопротивления резистора, которое рассматривается в конце раздела под названием «Импеданс».
Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.
Графическое обозначение схемы параллельного соеднинения
На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).
Согласно обобщенному закону Ома, сопротивление определяется. Если вы измеряете напряжение и ток, протекающие в резистивный контур, черный ящик, тогда закон Ома может быть заменен одним резистором. Внутренняя структура такого черного ящика не должна играть абсолютно никакой роли, он может содержать любое количество резисторов, свободно взаимосвязанных — замена их одним резистором всегда возможна.
Резисторы-резисторы, соединенные последовательно в данной ветви цепи, равны сумме их сопротивлений. При последовательном подключении резисторов через ветвь, согласно первому закону Кирхгофа, течет ток, т.е. каждый из параллельных подключенных резисторов будет равномерно течь для каждого тока.
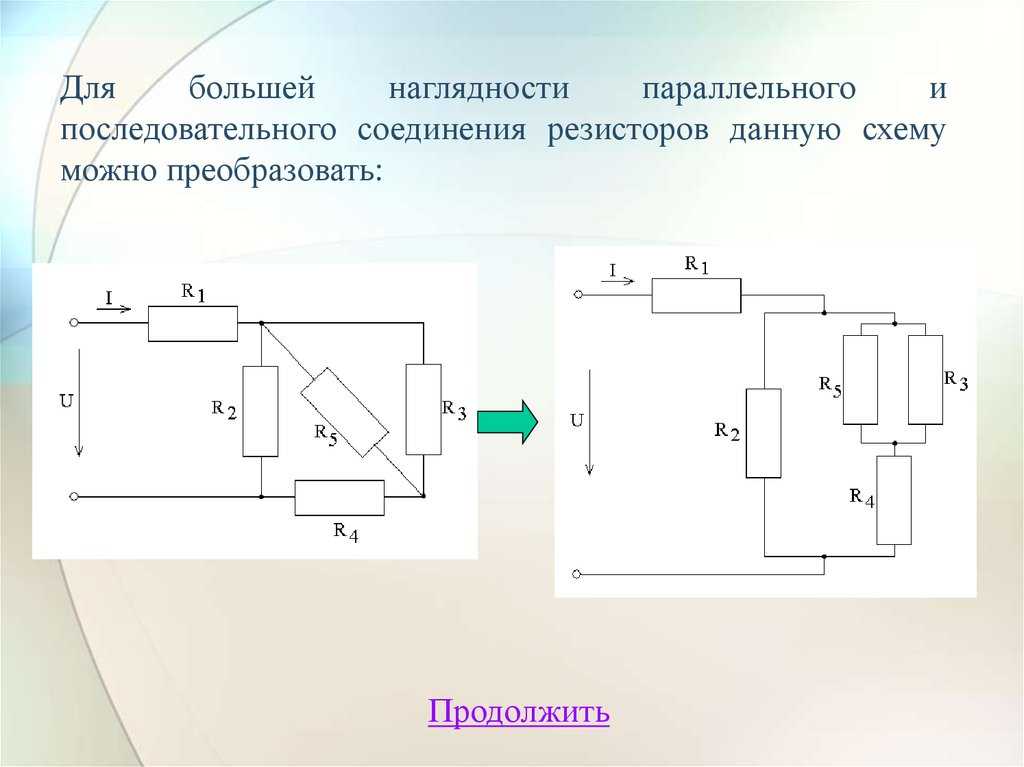
В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.
Формула для расчета параллельного соединения сопротивлений
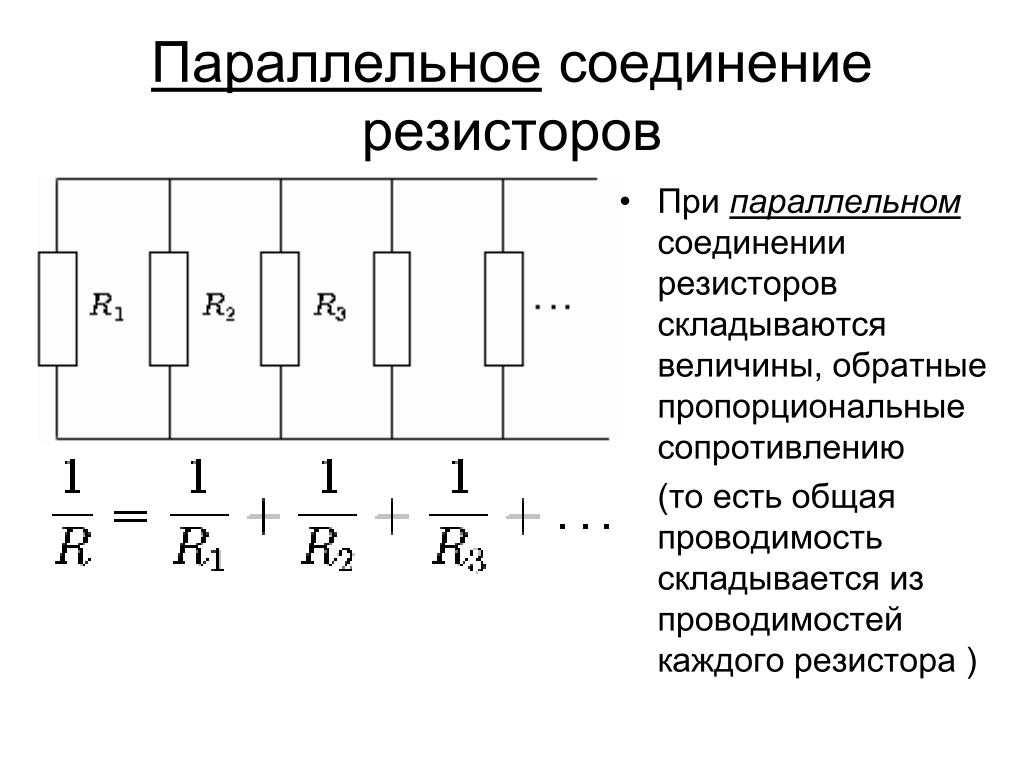
При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.
После преобразования мы получаем. Разделите две стороны током, который мы получаем. Для двух резисторов этот шаблон имеет вид. При параллельном соединении резисторов напряжение на них равно, равно. Согласно закону Кирхгофа сумма течений, протекающих из «верхнего» узла, равна влиянию, которое выражает зависимость. Разделите с обеих сторон напряжение.
Резисторы, отмеченные цветовым кодом. Резисторы чаще всего встречаются в виде дискретных элементов, продаваемых отдельно или в «ленте» с бумажной связью. Резисторы имеют форму небольшого корпуса, напоминающего поперечное сечение принципиальной схемы замены, из которой выводятся два провода, чтобы они могли быть включены в схему.
Резисторы имеют форму небольшого корпуса, напоминающего поперечное сечение принципиальной схемы замены, из которой выводятся два провода, чтобы они могли быть включены в схему.
Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:
В частном случае при подключении параллельно двух сопротивлений:
Резисторы с различными сопротивлениями доступны. Из-за их часто небольших размеров и цилиндрических характеристик, препятствующих описательному процессу, был принят общий стандарт для описания резисторов, чтобы избежать ошибок внедрения. Маркировка выполняется с помощью системы цветового кодирования, показанной в таблице ниже. Коды обычно считываются с самых экстремальных полос — чаще всего первые две полосы определяют сопротивление, третий множитель и следующий допуск, а иногда и температурный коэффициент сопротивления.
Дополнительная информация приведена ниже таблицы. Полосы обычно три, четыре или шесть, если есть 3 полосы — тогда все три являются сопротивлением, а допуск равен ± 20%, если есть 4 полосы — тогда первые три означают сопротивление, а четвертый — толерантность, если их шесть, значит, мы имеем работа с прецизионным резистором, а первые три обозначают номера сопротивлений, четвертый — множитель, пятый — допуск, шестой — коэффициент сопротивления температуры. Публикуется для обеспечения согласованности материала и самого быстрого доступа.
Публикуется для обеспечения согласованности материала и самого быстрого доступа.
Эквивалентное сопротивление цепи определяется по формуле:
В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:
Информация о сопротивлении резистора кодируется в цвете. В Интернете вы можете найти несколько калькуляторов, которые позволяют конвертировать из слайдов в сленг и наоборот. Ниже графика показаны 4 наиболее популярных значения сопротивления: 100 Ом, 220 Ом, 4, 7 кОм, 10 кОм. Золотая полоса справа указывает на сопротивление резистора ± 5%.
Другие любители — 10% серебра и 2% красные. Цветовые коды наиболее часто используемых значений резисторов. Обратите внимание, что, комбинируя резисторы, мы можем получить другие отсутствующие значения. Резистивное сопротивление резисторов, соединенных параллельно, равно инверсии обратной суммы единичных сопротивлений. Диоды не должны соединяться параллельно друг с другом — в этом случае каждый должен иметь свой собственный резистор. Диоды можно подключать последовательно и параллельно-параллельно, но вам нужно выбрать правильные резисторы.
Диоды можно подключать последовательно и параллельно-параллельно, но вам нужно выбрать правильные резисторы.
Формулы для частного рассчета вытекают из основной формулы.
Формула для расчета параллельного соединения емкостей (конденсаторов)
При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:
Формула для расчета параллельного соединения индуктивностей
При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении:
Стол со стандартными значениями должен быть достаточным. Таблица: Значения резисторов для отдельных светодиодов. Ток, протекающий через диод: 20 мА. Подробные способы расчета и объединения можно найти в Интернете. Хотя энергосберегающие технологии в электронике становятся все более популярными, маловероятно, что механические охлаждающие устройства когда-либо будут полностью оставлены. В настоящее время, помимо жидкостных систем охлаждения, вентиляторы чаще всего используются в корпусах. В статье представлены основные способы их классификации, оценки производительности в отношении требований конкретного приложения и элементов дизайна, на которые вы должны обратить внимание.
В настоящее время, помимо жидкостных систем охлаждения, вентиляторы чаще всего используются в корпусах. В статье представлены основные способы их классификации, оценки производительности в отношении требований конкретного приложения и элементов дизайна, на которые вы должны обратить внимание.
Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.
Пример свертывания параллельного сопротивления
Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.
Центробежные вентиляторы разделены на величину угла выхода лопастей для вентиляторов с изогнутыми передними и задними лезвиями. Вентиляторы в основном разделены в зависимости от направления потока воздушного потока относительно оси вентилятора, выделяя в этом отношении три группы: осевые, радиальные и диагональные. При охлаждении электронных устройств используются вентиляторы первого типа, в которых поток воздуха протекает в осевом направлении.
В применениях этого типа вентилятор, характерная особенность которого представляет собой лопасти ротора в виде пропеллера, чаще всего размещается в корпусе вместе с электродвигателем, встроенным в ступицу ротора. Такая компактная конструкция с монтажными отверстиями на фланце вентилятора позволяет устанавливать даже в ограниченных пространственных условиях. Однако проблема с компактным дизайном — это распорки, соединяющие корпус двигателя с фланцем.
Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к E1. R1 — одним концом подключено к R5, а не к узлу. R5 — одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.
Они обеспечивают стабильность, но в то же время препятствуют потоку воздуха. Во время работы лопасти ротора подметают стойки, вызывая скачки давления в их окрестностях. Это один из основных источников шума, создаваемых осевыми вентиляторами.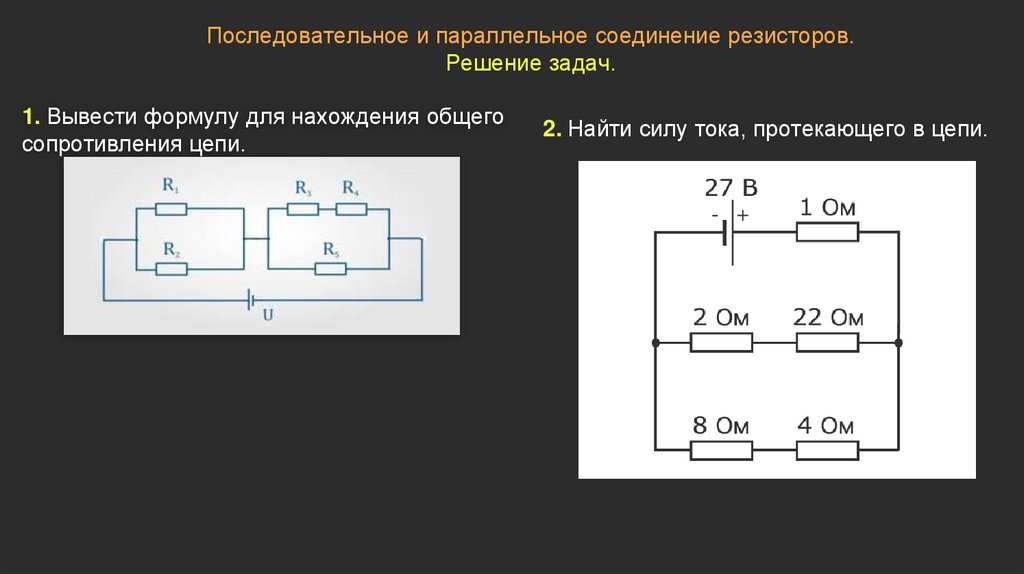 Поэтому на этапе проектирования этого устройства форму и количество распорок тщательно анализируют на предмет их влияния на поток воздуха через вентилятор.
Поэтому на этапе проектирования этого устройства форму и количество распорок тщательно анализируют на предмет их влияния на поток воздуха через вентилятор.
Устройство в одном корпусе вентилятора. Наиболее распространенными являются осевые вентиляторы со спирально изогнутыми распорками. На практике соблюдаются некоторые основные правила относительно их установки. Один из них касается разрыва между лезвиями и стойками — чем они крупнее, тем меньше шума. Значительно большое количество лезвий и прокладок. Чем меньше стойки, тем меньше шума, особенно при высоких скоростях вращения ротора.
Ток при параллельном соединении
При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.
Напряжение при параллельном соединении
При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.
В свою очередь, чем больше лезвий, тем больше поток воздуха, но в то же время лезвия чаще сметают стойки, что создает больше шума.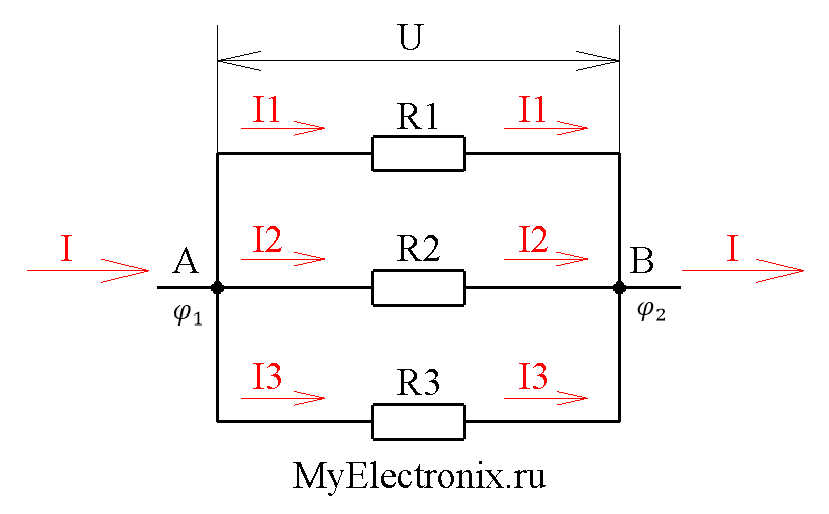 Также важно, чтобы стойки располагались на выходной стороне воздуха от вентилятора, что оправдано характеристиками потока. Воздушный поток у входа вентилятора является ламинарным потоком, а на выходе вентилятора поток изменяет свой характер на турбулентный.
Также важно, чтобы стойки располагались на выходной стороне воздуха от вентилятора, что оправдано характеристиками потока. Воздушный поток у входа вентилятора является ламинарным потоком, а на выходе вентилятора поток изменяет свой характер на турбулентный.
Когда на пути ламинарного потока возникает препятствие, слышится определенная частота, слышится как свисток. С другой стороны, когда турбулентный поток сталкивается с препятствием, появляются звуки разных частот, что делает шум менее раздражающим для людей.
Применение параллельного соединения
1. В промышленности изготавливаются сопротивления определенных величин. Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.
Центробежные и диагональные вентиляторы
В дополнение к осевым вентиляторам при охлаждении электронных компонентов используются, хотя и реже, радиальные вентиляторы.
2. Делитель токов.
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую или параллельно для того, чтобы создать более сложные электронные схемы.
Третий тип — вентиляторы с смешанным потоком. диагональ, которая, хотя с точки зрения внешнего вида, более похожа на осевые вентиляторы, благодаря принципу работы представляет собой промежуточную конструкцию между осевыми и радиальными вентиляторами: входное отверстие для воздуха находится в осевом направлении на выходе, но выход по диагонали.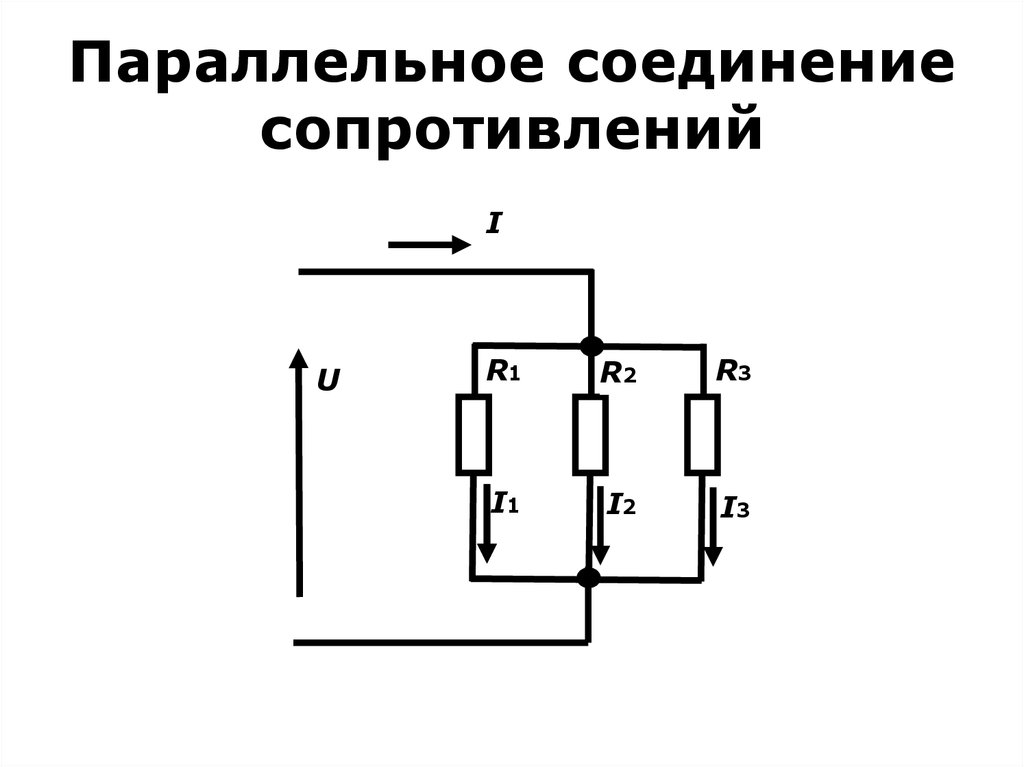 В результате вентиляторы смешанного потока создают более высокое давление при тех же размерах и рабочих скоростях, что и осевые вентиляторы, а под этим углом образуются радиальные вентиляторы.
В результате вентиляторы смешанного потока создают более высокое давление при тех же размерах и рабочих скоростях, что и осевые вентиляторы, а под этим углом образуются радиальные вентиляторы.
Схема замены устройства на рис. Резисторы соответствуют сопротивлению потока отдельных компонентов устройства. Производительность вентилятора описывает его характеристическую кривую, которая представляет объемный расход перекачиваемого газа, в зависимости от увеличения давления, создаваемого вентилятором. Основываясь на этой характеристике, можно сравнивать разные типы вентиляторов, но на практике ее чаще всего используют для оценки производительности вентилятора в соответствии с требованиями конкретного приложения.
Схема параллельного соединения показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
В этом случае характеристики вентилятора анализируются вместе с кривой, которая показывает падение давления в охлаждаемом устройстве в зависимости от количества проходящего через него воздуха.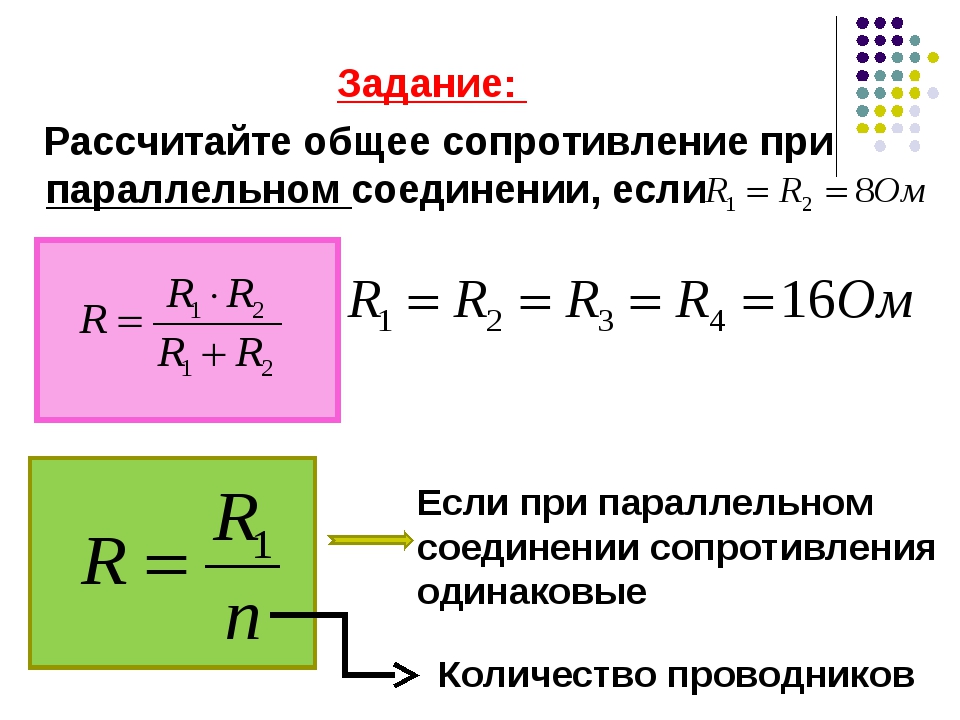 Чтобы определить характеристики устройства, сначала определите текущее сопротивление потока. Точные расчеты сопротивления потоку обычно используют специализированное программное обеспечение, которое использует сложные модели и численные методы.
Чтобы определить характеристики устройства, сначала определите текущее сопротивление потока. Точные расчеты сопротивления потоку обычно используют специализированное программное обеспечение, которое использует сложные модели и численные методы.
Однако на практике также используются упрощенные методы. Один из них будет рассмотрен на примере устройства, в котором монтируется один вентилятор и вентиляционная решетка. Он состоит из пяти параллельных монтажных плат с компонентами и блоком питания, заключенных в отдельный корпус с отверстиями на передней и задней панелях. На рисунке 3 показана схема замены рассматриваемого устройства. Отдельные компоненты и компоненты корпуса показаны на нем в виде резисторов с определенным сопротивлением потоку.
Ток, протекающий через отдельно взятый резистор, согласно , можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Определение характеристик устройства
Характеристики системы вентиляции: охлажденное устройство — вентилятор. Соответствующие формулы используются для определения значений сопротивлений, в которых предполагается, что сопротивление зависит от площади поперечного сечения препятствия, а в случае вентиляционной решетки — от площади поверхности, через которую протекает поток воздуха. Следующий шаг — рассчитать общее сопротивление всей системы.
Для этой цели используются аналоги, применяемые при замене последовательного сопротивления и параллельных электрических сопротивлений. Затем эту характеристику следует разместить на общем графике с характеристиками вентилятора. Тогда в точке пересечения двух кривых определяется точка действия вентилятора. В нем описывается фактическая производительность конкретного вентилятора в этой установке, то есть количество воздуха, которое вентилятор может охлаждать при охлаждении устройства.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
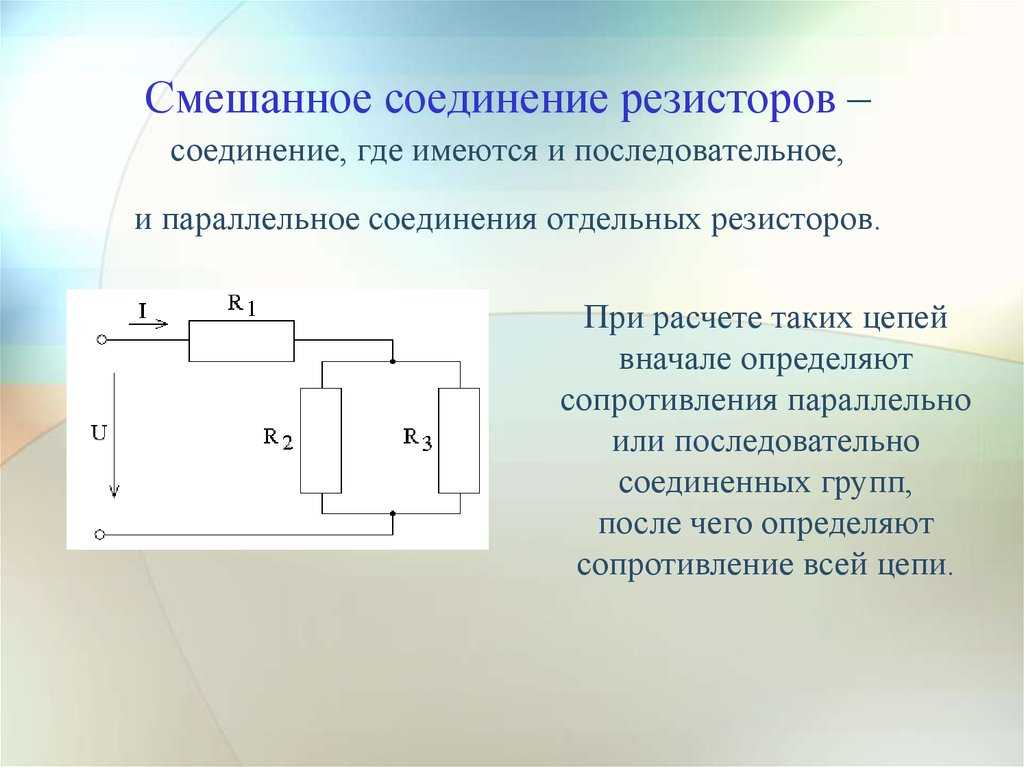
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов (I1 и I2) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать .
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
Резисторы параллельно | Вращающиеся числа
Компоненты находятся в параллельном , если они имеют два узла, например,
Мы раскрываем свойства параллельного соединения, рассматривая схемы резисторов. Разобраться с параллельными резисторами немного сложнее, чем с последовательными резисторами.
Разобраться с параллельными резисторами немного сложнее, чем с последовательными резисторами.
Автор Вилли Макаллистер.
Содержимое
- Параллельное соединение
- Резисторы параллельно
- Эквивалентный параллельный резистор
- $\text N$ резисторов параллельно
- Ток распределяется между резисторами параллельно
- Проверка концепции
- Особый случай — параллельное подключение резисторов $2$
- Особый случай — параллельные резисторы $2$
Параллельное соединение
Компоненты параллельны, когда их два терминала соединяются с одними и теми же узлами.
На следующем изображении $\text R1$, $\text R2$ и $\text R3$ параллельны. Две горизонтальные линии представляют два узла, общие для всех трех резисторов.
Просмотр определения узла Ознакомьтесь с определениями узла и распределенного узла в этой статье, посвященной терминологии цепей.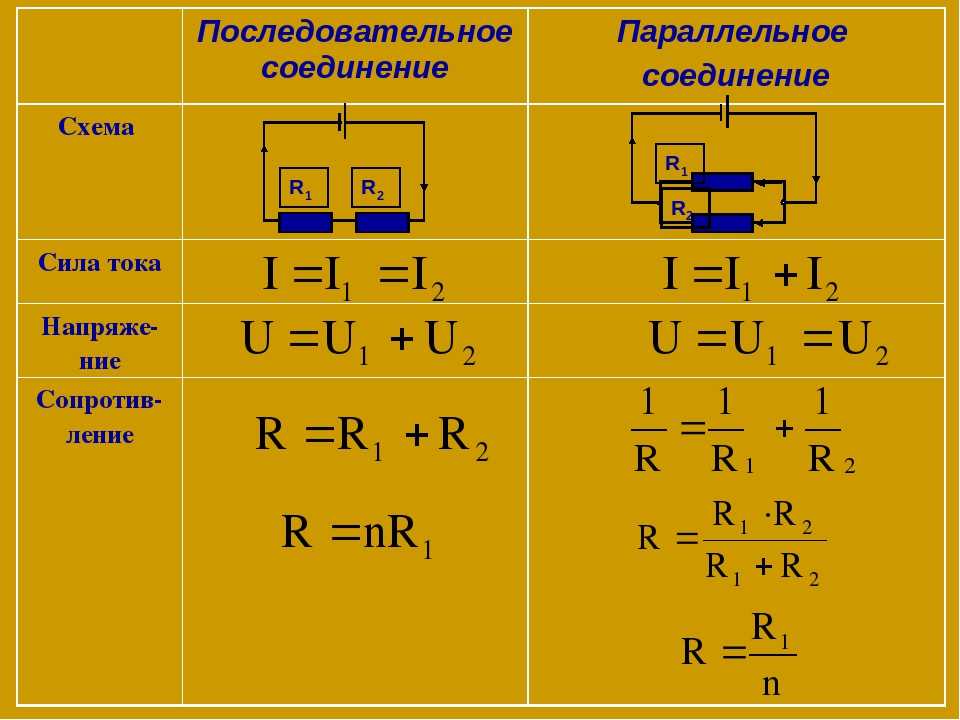 Еще один хороший ресурс, который поможет вам понять параллельные схемы, — это статья об эквивалентности схем.
Еще один хороший ресурс, который поможет вам понять параллельные схемы, — это статья об эквивалентности схем.
Поскольку резисторы подключены к одним и тем же узлам, на каждом параллельном резисторе появляется одинаковое напряжение.
На следующем изображении резисторы , а не , соединены параллельно. Есть дополнительные компоненты (оранжевые прямоугольники), разбивающие общие узлы между резисторами. Эта схема имеет четыре отдельных узла, поэтому $\text R1$, $\text R2$ и $\text R3$ не имеют одинаковое напряжение.
Параллельные резисторы
Вот схема с параллельными резисторами. Эта цепь имеет источник тока. Мы не можем использовать их очень часто, так что это должно быть весело.
Источник тока $\text I_\text s$ направляет ток $i$ в направлении $\text R1$, $\text R2$ и $\text R3$. Текущий $i$ возвращается к нижнему терминалу текущего источника. но мы еще не знаем ни напряжения $v$, ни того, как $i$ разделяется на три тока резистора.
То, что мы знаем, это,
- Текущий $i$ — это некоторая заданная постоянная величина.
- Сумма токов трех резисторов должна составлять $i$.
- Напряжение $v$ появляется на всех трех резисторах.
Обладая этими небольшими знаниями и законом Ома, мы можем найти то, чего не знаем.
- Мы еще не знаем напряжения $v$, возникающего на резисторах и источнике тока.
- Мы не знаем, как $i$ делится на три тока резистора.
Используя то, что мы знаем, мы можем записать следующие выражения:
$i = i_{\text R1} + i_{\text R2} + i_{\text R3} $
$v = i_{\text R1} \, \text R1 \qquad v = i_{\text R2} \, \text R2 \qquad v = i_{\text R3} \, \text R3$
Переставьте три выражения закона Ома, чтобы найти ток,
$i_{\text R1} = \dfrac{v}{\text R1} \qquad i_{\text R2} = \dfrac{v}{\text R2} \qquad i_{\text R3} = \dfrac{ v}{\text R3}$
Подставим эти выражения в сумму токов,
$i = \dfrac{v}{\text R1} +\dfrac{v}{\text R2} + \dfrac{v}{\text R3}$
Вынести общий член $v$,
$i = v \left (\dfrac{1}{\text R1} +\dfrac{1}{\text R2} + \dfrac{1}{\text R3} \right )$
Помните, что мы уже знаем $i$ (задается текущим источником), поэтому мы можем найти $v$,
$v = i \,\dfrac{1}{\left (\dfrac{1}{\text R1} +\ dfrac{1}{\text R2} + \dfrac{1}{\text R3} \right )}$
Взгляните на это уравнение.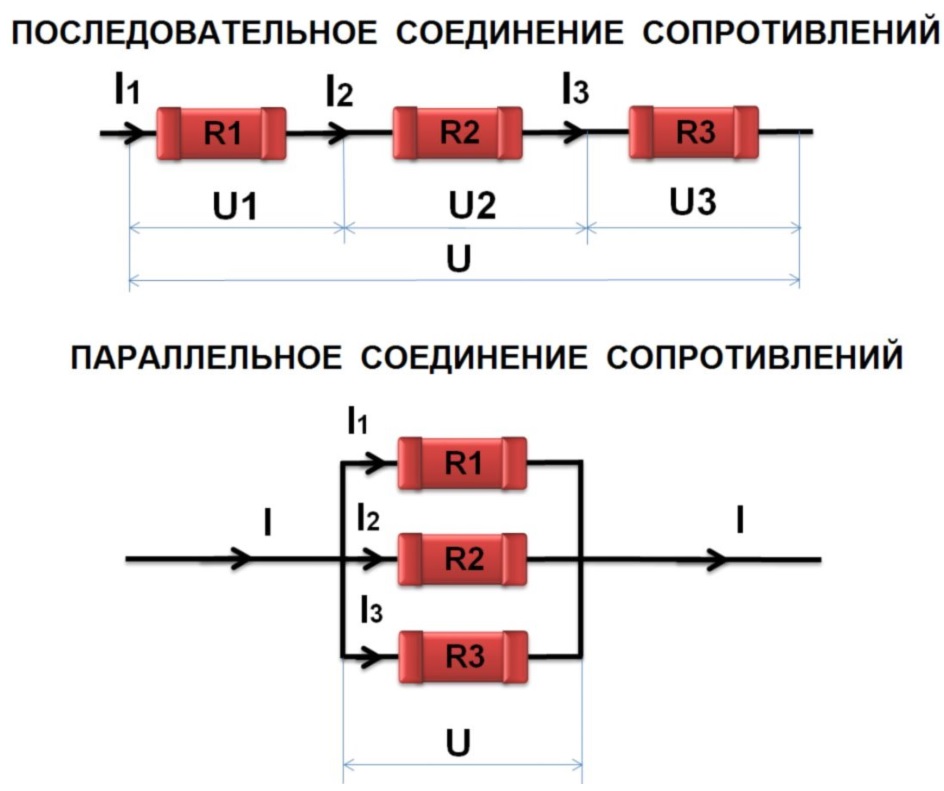 Это похоже на закон Ома, $v = i\,\text R$, но с резисторами, представленными в виде большого двойного обратного выражения, где обычно появляется $\text R$.
Это похоже на закон Ома, $v = i\,\text R$, но с резисторами, представленными в виде большого двойного обратного выражения, где обычно появляется $\text R$.
Мы заключаем,
Для резисторов, включенных параллельно, общее сопротивление является обратной величиной суммы обратных величин отдельных резисторов.
(Это полный рот. Легче понять уравнение, чем произнести его вслух.)
Эквивалент параллельного резистора
Предыдущее уравнение предлагает способ определить новый резистор , эквивалентный , для трех параллельных резисторов.
$\text R_{\text{параллельно}} = \dfrac{1}{\left (\dfrac{1}{\text R1} +\dfrac{1}{\text R2} + \dfrac{1} {\текст R3} \справа )}$
Новый резистор является обратной величиной суммы обратных величин. Оно эквивалентно в том смысле, что при данном $i$, вытекающем из источника тока, возникает одно и то же напряжение $v$.
Мы можем записать это немного меньше, перевернув гигантское обратное число,
$\dfrac{1}{\text R _{\text{parallel}}} = \dfrac{1}{\text R1} +\dfrac{ 1}{\text R2} + \dfrac{1}{\text R3}$
Вы можете заменить три параллельных резистора одним эквивалентным резистором, и $i$ и $v$ останутся точно такими же.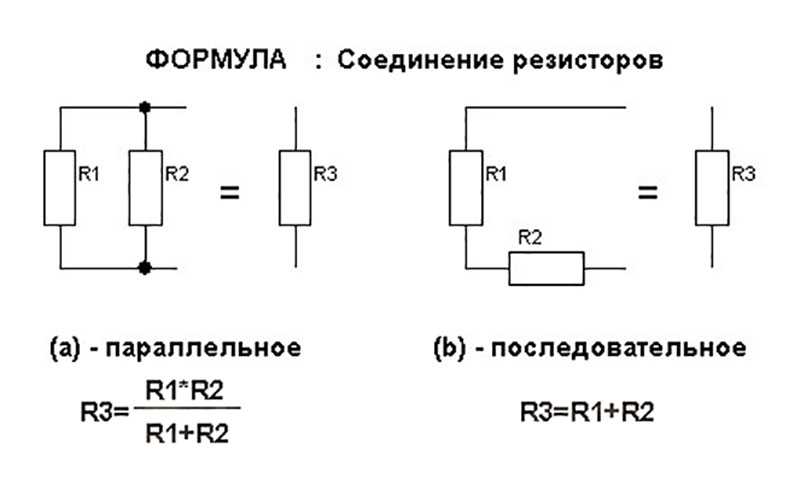
С «точки зрения» источника тока вы не можете отличить эквивалентный резистор от трех параллельных резисторов.
$\text N$ резисторов, соединенных параллельно
Мы можем обобщить уравнение параллельного резистора для любого количества параллельно соединенных резисторов. Вывод этой формулы для $\text N$ резисторов, соединенных параллельно, выполняется точно так же, как мы делали выше для трех параллельных резисторов.
$\dfrac{1}{\text R_{\text{parallel}}} = \dfrac{1}{\text R1} +\dfrac{1}{\text R2} + \ldots + \dfrac{1 }{\text{R}_\text N}$
$\qquad\quad$
Ток распределяется между параллельными резисторами
Выясним, как распределяется основной ток $i$ и протекает через каждый резистор. Мы ищем $i_{\text R1}$, $i_{\text R2}$ и $i_{\text R3}$.
Примените закон Ома к отдельным резисторам. $v$ одно и то же в каждом уравнении,
$i_{\text R1} = v/\text R_1 \qquad i_{\text R2} = v/\text R_2 \qquad i_{\text R3} = v/ \text R_3$
Основной ток $i$ распадается на три отдельных потока.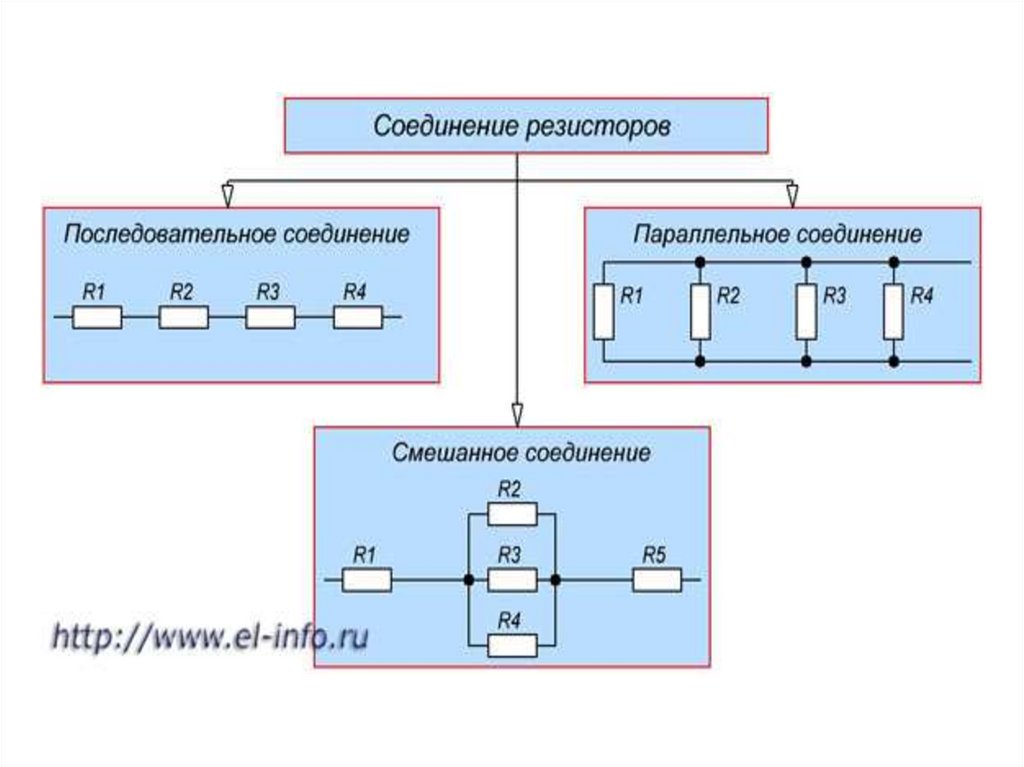 Эти токи воссоединяются и текут обратно к текущему источнику. Это означает, что токи отдельных резисторов должны суммироваться с основным током.
Эти токи воссоединяются и текут обратно к текущему источнику. Это означает, что токи отдельных резисторов должны суммироваться с основным током.
Величина тока в каждом резисторе обратно пропорциональна номиналу резистора.
Это лучше усвоится, если мы сделаем пример с действительными числами.
Проверка концепции
ПРОБЛЕМА 1
а. Найдите напряжение $v$.
б. Найдите токи в трех резисторах.
в. Покажите, как сумма токов отдельных резисторов составляет $i$.
Шаги к решению:
- Найдите эквивалентное параллельное сопротивление $\text R_{\text{parallel}}$.
- Найдите напряжение $v$ по закону Ома.
- Найдите отдельные токи, снова используя закон Ома.
- Убедитесь, что сумма токов резисторов соответствует ожидаемой.
Часть а. Эквивалент $\text R_{\text{параллельный}}$ равен обратной величине обратной суммы трех резисторов.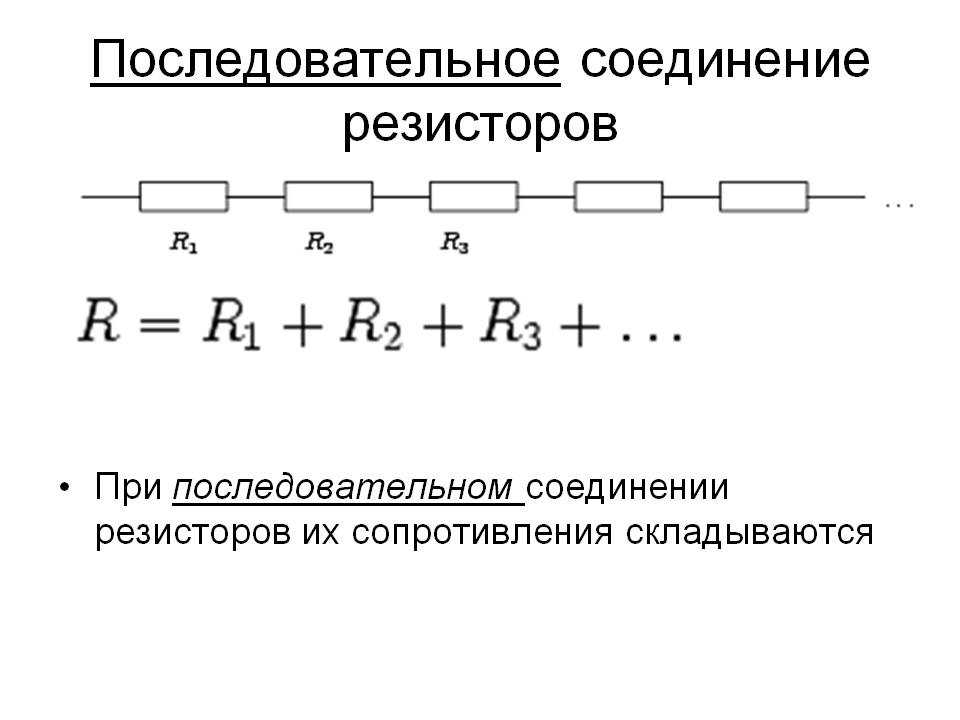
$\text R_{\text{параллельно}} = \dfrac{1}{\left (\dfrac{1}{50\,\Omega} + \dfrac{1}{100\,\Omega} + \dfrac {1}{500\,\Omega} \right )}$
$\text R_{\text{параллельно}} = \dfrac{1}{(0,02 + 0,01 + 0,002)} = \dfrac{1}{0,032} = 31,25\,\Omega$
Теперь мы знаем ток и эквивалентное сопротивление. Мы можем найти напряжение $v$ на всех резисторах, используя закон Ома,
.$v = i\,\text R_{\text{параллельно}}$
$v = 100\,\text{мА} \cdot 31,25\,\Omega = 3,125\,\text V$
Часть б. Зная $v$, мы можем вернуться назад и вычислить токи отдельных резисторов,
$i_{\text R1} = \dfrac{v}{\text R1} = \dfrac{3,125\,\text V}{\text{50}} = 62,5\,\text{мА}$
$i_{\text R2} = \dfrac{v}{\text R2} = \dfrac{3,125\,\text V}{\text{100}} = 31,25\,\text{мА}$
$i_{\text R3} = \dfrac{v}{\text R3} = \dfrac{3,125\,\text V}{\text{500}} = \phantom{0}6,25\,\text{мА }$
Вот как выглядит решение,
Часть в.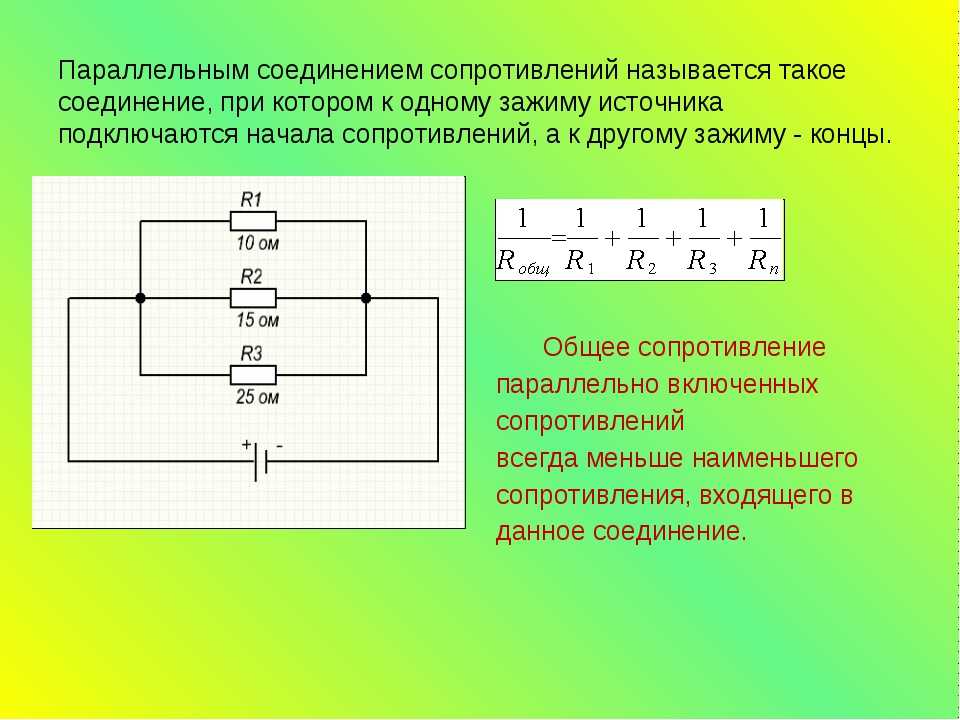 Проверить: сумма токов резисторов равна току источника?
Проверить: сумма токов резисторов равна току источника?
$62,5\,\text{мА} + 31,25\,\text{мА} + 6,25\,\text{мА} = 100\,\text{мА}\qquad \checkmark$ Да!
Откуда электроны «знают», через какой резистор им протечь?Обычный вопрос о параллельных цепях: «Когда ток достигает первого резистора, как электроны «выбирают» или «знают», через какой резистор течь?» или «Как электроны «решают», куда течь? ”
Как известно, электроны — не люди, у них нет маленьких электронных мозгов (насколько нам известно). Здесь нет выбора или решения. Они не выбирают и не решают, через какое сопротивление течь, точно так же, как молекула воды не «решает» или не «выбирает», с какой стороны скалы она потечет в потоке. В любой цепи, в том числе и в параллельных, каждый электрон реагирует только на электрические силы от напряжения и от отталкивающего роя окружающих электронов.
Исходя из токов резисторов, которые вы только что нашли,
ПРОБЛЕМА 2
Через какой резистор проходит наибольшая доля тока?
Выберите один: $\quad$ самый маленький $\quad$ средний $\quad$ самый большой
показать ответ Самый маленький резистор несет наибольшую долю тока.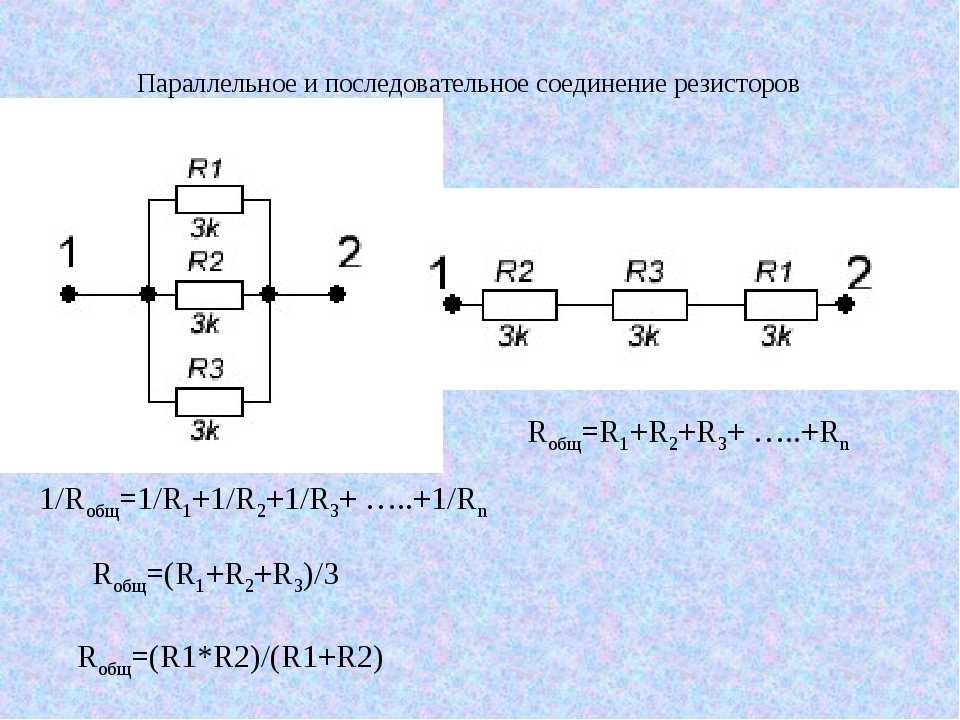
ЗАДАЧА 3
Через какой резистор проходит наименьшая доля тока?
Выберите один: $\quad$ наименьший $\quad$ средний $\quad$ наибольший
показать ответСамый большой резистор несет наименьшую долю тока.
ЗАДАЧА 4
Каков относительный размер эквивалентного резистора по сравнению с параллельными резисторами?
- $\text{R}_\text{parallel}$ больше, чем самый большой резистор.
- $\text{R}_\text{parallel}$ находится между наибольшим и наименьшим резистором.
- $\text{R}_\text{parallel}$ меньше самого маленького резистора.
Эквивалентный параллельный резистор меньше наименьшего параллельного резистора. Всегда.
Проблема 5
Какой резистор имеет самое высокое напряжение?
Выберите один: $\quad$ самый маленький $\quad$ средний $\quad$ самый большой
показать ответ Вопрос с подвохом.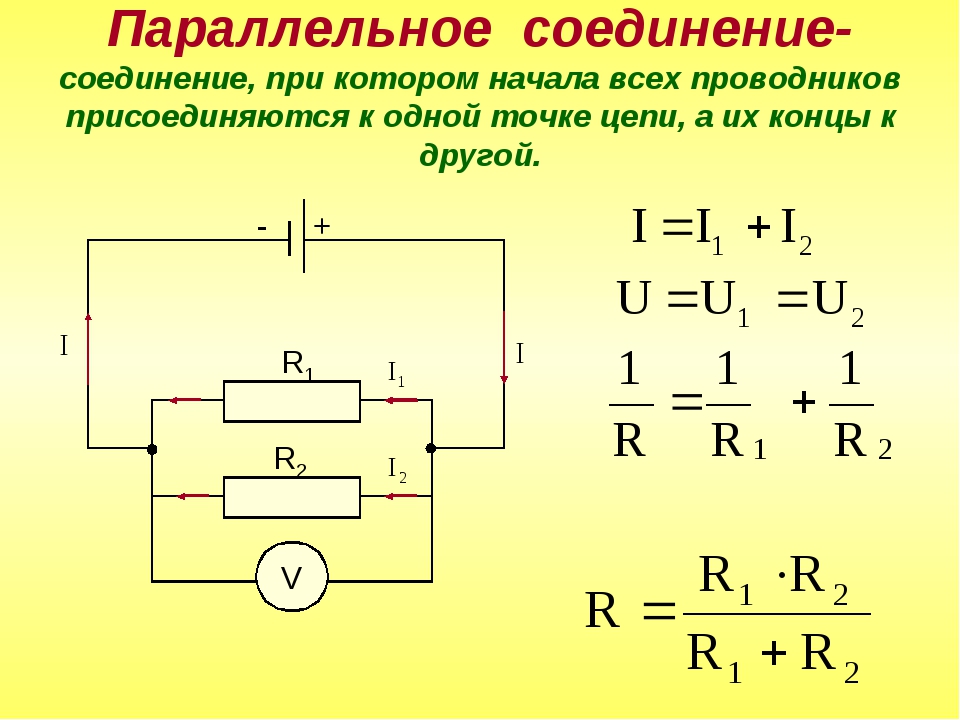 Все три резистора имеют одинаковое напряжение. Вот что значит быть параллельно. Все они имеют одинаковое напряжение.
Все три резистора имеют одинаковое напряжение. Вот что значит быть параллельно. Все они имеют одинаковое напряжение.
Особый случай — параллельное подключение резисторов $2$
Согласно общему уравнению два параллельно соединенных резистора имеют эквивалентное сопротивление,
$\text R _{\text{параллель}} = \dfrac{1} {\left (\dfrac{1}{\text R1} +\dfrac{1}{\text R2} \right )}$
Мы можем сделать немного алгебры, чтобы найти альтернативное выражение всего с одной дробью. Вместо того, чтобы просто дать вам ответ, это обряд посвящения, когда вы сами решаете алгебру в первый раз. Ответ спрятан, так что вы можете попробовать это самостоятельно, прежде чем заглянуть. Посмотрите, сможете ли вы вывести выражение для $\text R_{\text{parallel}}$ в виде одной дроби.
Два резистора параллельно$\text R _{\text{параллельно}} = \dfrac{1} {\left (\dfrac{1}{\text R1} +\dfrac{1}{\text R2} \right)}$
Поработайте со знаменателем, чтобы очистить дроби.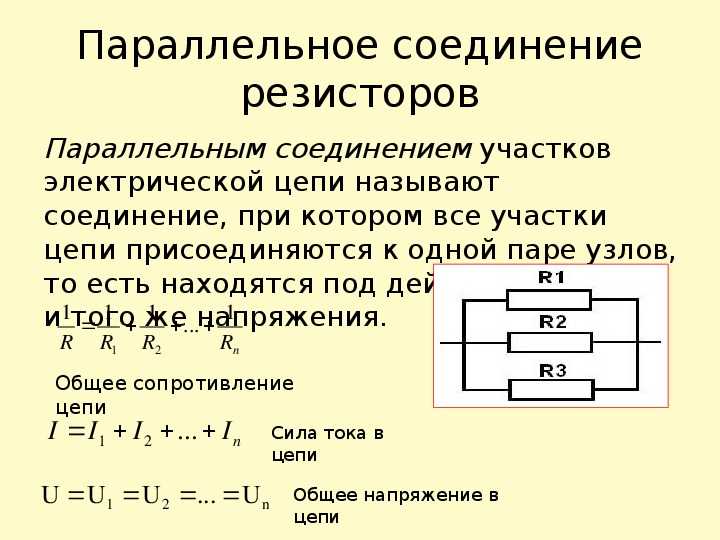 Общий знаменатель $\text R1 \, \text R2$.
Общий знаменатель $\text R1 \, \text R2$.
$\text R_{\text{параллельно}} = \dfrac{1}{\left (\dfrac{1}{\text R1}\,\dfrac{\text R2}{\text R2}\right ) + \left (\dfrac{1}{\text R2}\,\dfrac{\text R1}{\text R1} \right )}$
$\text R _{\text{параллельно}} = \dfrac{1} {\left ( \dfrac{\text R2}{\text R1\,\text R2} \right ) + \left (\dfrac{\ text R1}{\text R1\,\text R2} \right )}$
$\text R _{\text{параллельно}} = \dfrac{1} {\left (\dfrac{\text R1 + \text R2}{\text R1\,\text R2} \right )}$
Переверните большую дробь, чтобы получить уравнение для двух параллельных резисторов,
$\text R_{\text{параллельно}} = {\dfrac{\text R1\,\text R2} {\text R1 + \text R2}}$
Произведение сверх суммы. Это стоит запомнить.
Особый случай — $2$ равных резистора, соединенных параллельно
Что делать, если два параллельных резистора имеют одинаковое значение. Что эквивалентно $\text R_{\text{parallel}}$?
Пусть $\text R1 = \text R2$. Мы будем называть его просто $\text R$.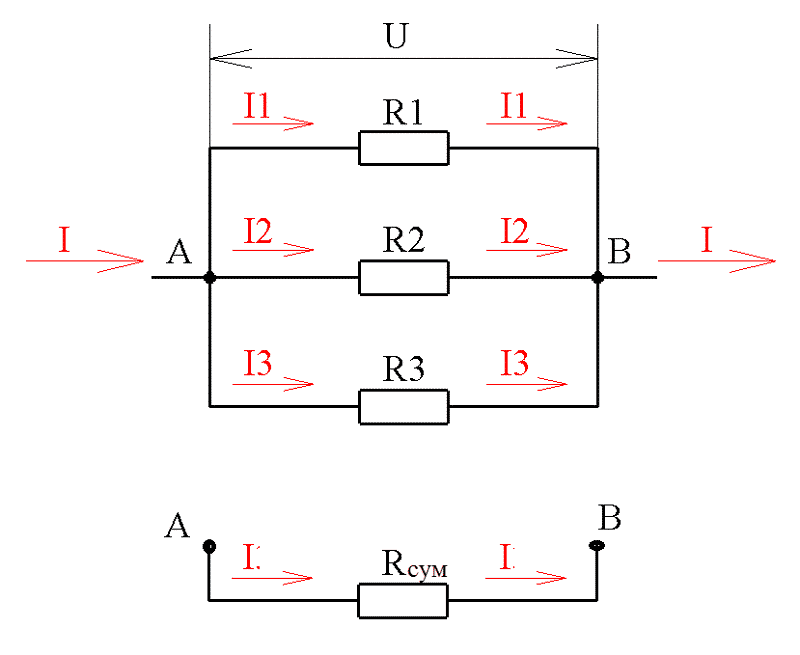
$\text R_{\text{параллельно}} = \dfrac{\text R \, \text R}{\text R + \text R} = \dfrac{\text R \, \text R}{2 \,\text R}$
$\text R_{\text{parallel}} = \dfrac{1}{2} \,\text R$
Два одинаковых резистора, включенных параллельно, имеют эквивалентное сопротивление, равное половине значения любого резистора. Ток делится поровну между ними.
Резюме
Параллельно подключенные компоненты имеют одинаковое напряжение.
Общая форма для параллельных резисторов:
$\dfrac{1}{\text R_{\text{parallel}}} = \dfrac{1}{\text R1} +\dfrac{1}{\ text R2} + \ldots + \dfrac{1}{\text{R}_\text N} $
Используйте это уравнение, если у вас есть три или более резисторов, соединенных параллельно.
Если у вас есть два параллельных резистора, вы можете использовать общую форму или объединить их как произведение на сумму,
$\text R _{\text{параллель}} = \dfrac{\text R1\,\text R2}{\text R1+\text R2}$
Эквивалентный резистор $\text R_{\text{параллельный}}$ всегда меньше наименьшего параллельного резистора.
Наибольший ток протекает через наименьший резистор.
Комбинация резисторов — GeeksforGeeks
Поток заряженных частиц обозначается как электрический ток . В текущем электричестве поток заряда будет непрерывным. Электрический ток движется от более высокого электрического потенциала к более низкому.
Для протекания тока требуется цепь, состоящая из замкнутого контура из проводящего материала. Цепь состоит из проводов, которые соединены друг с другом и движутся в одном направлении.
Когда поток электронов движется по проводнику, он представляет собой электрический ток. Условно утверждается, что направление тока (I) всегда принимается противоположным направлению потока электронов или заряда.
Сопротивление
Физик Георг Симон Ом установил зависимость между протекающим током I, протекающим по металлическому проводу, имеющему разность потенциалов на его выводах (концах). Он заявил, что: Разность потенциалов в вольтах V на клеммах данного металлического провода в электрической цепи прямо пропорциональна току I, протекающему через него, при условии, что его температура остается неизменной.
Это известно как закон Ома . Другими словами, это можно записать как: Разность потенциалов на концах ∝ Ток
или
В ∝ I
В = I R, где R — константа пропорциональности, называемая Сопротивление .
Сопротивление – это свойство, которое противодействует (сопротивляется) потоку тока, или, можно сказать, потоку электронов в проводнике. Он контролирует величину (величину) тока, протекающего по цепи.
Единица сопротивления в СИ измеряется в омах, что обозначается цифрой Ом .
Математически сопротивление можно определить как:
R = V / I
Здесь I — ток, а V — разность потенциалов.
- Ток обратно пропорционален сопротивлению. Следовательно, чем больше ток, тем меньше сопротивление и наоборот.
- Устройства сопротивления, такие как реостат или переменный резистор, позволяют изменять сопротивление в цепи, сохраняя разность потенциалов одинаковой на концах.

- В проводнике электроны притягиваются атомами проводника. Существует сила сопротивления, которая ниже для хорошего проводника (металлы, такие как железо, медь), но очень высока для изолятора (дерево, одежда, тапочки). Проводник, имеющий некоторое сопротивление, известен как Резистор .
Эксперимент по закону Ома
Согласно закону Ома: Разность потенциалов на концах резистора прямо пропорциональна протекающему через него току при условии, что его температура остается неизменной.
При одном и том же сопротивлении R, когда берутся три разных источника напряжения, результирующая разность потенциалов всегда будет пропорциональна току, протекающему по цепи. Это подразумевает, что:
V 1 ∝ I 1 ,
V 2 ∝ I 2 и
V 3 ∝ I 3
6:.
6.1661616.161616:, , , , , : 3
. Я график для нихромовой проволоки.
Я график для нихромовой проволоки.Факторы, от которых зависит сопротивление
Сопротивление проводника зависит от:
- его длины (l),
- площади поперечного сечения (A) и
- природы его материала.
Сопротивление равномерно распределенного металлического проводника прямо пропорционально его длине и обратно пропорционально площади его поперечного сечения.
Следовательно, R ∝ l и R ∝ 1/A.
⇒ R ∝ l / A
или
⇒ R = ρl / A
, где ρ — константа пропорциональности, известная как удельное электрическое сопротивление материала проводника.
- Единицей СИ является Ом·м.
- Удельное сопротивление зависит от температуры (T).
- Удельное сопротивление проводников очень низкое, тогда как у изоляторов очень высокое удельное сопротивление.
- Сплавы с более высоким удельным сопротивлением, чем у металлов, используются в электронагревательных устройствах, таких как железо и тостеры, медь и алюминий используются для линий электропередач, а вольфрам используется в нити накала электрических ламп.

- Следовательно, удельное сопротивление изоляторов > удельное сопротивление сплавов > удельное сопротивление проводников.
Комбинация резисторов
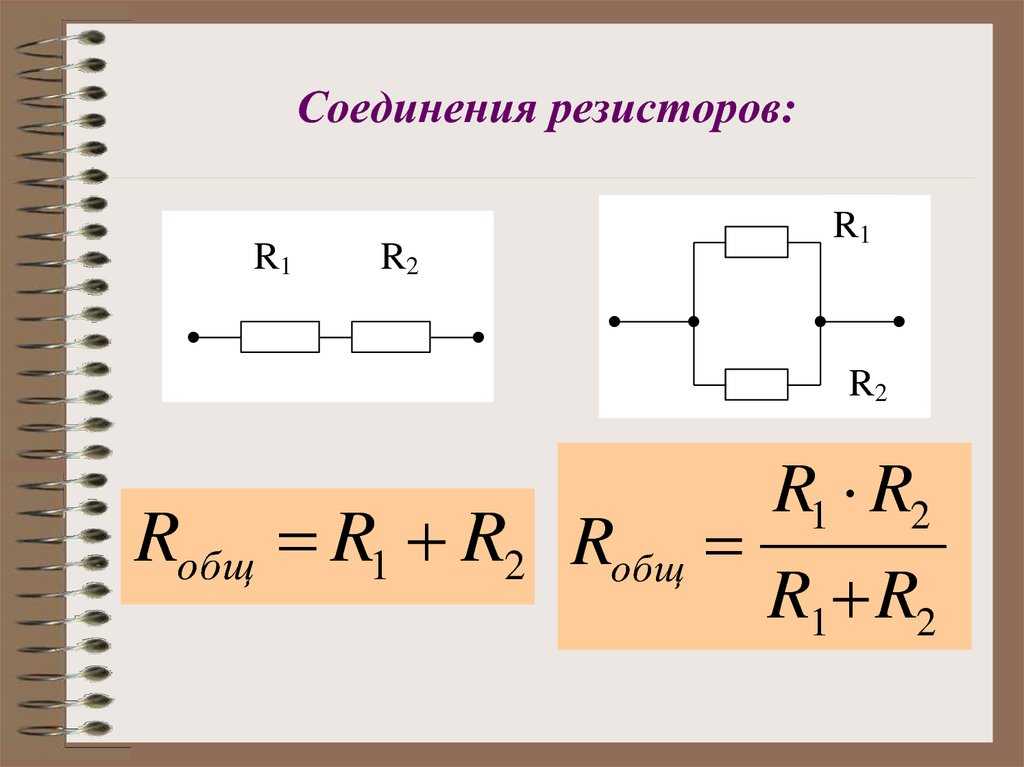
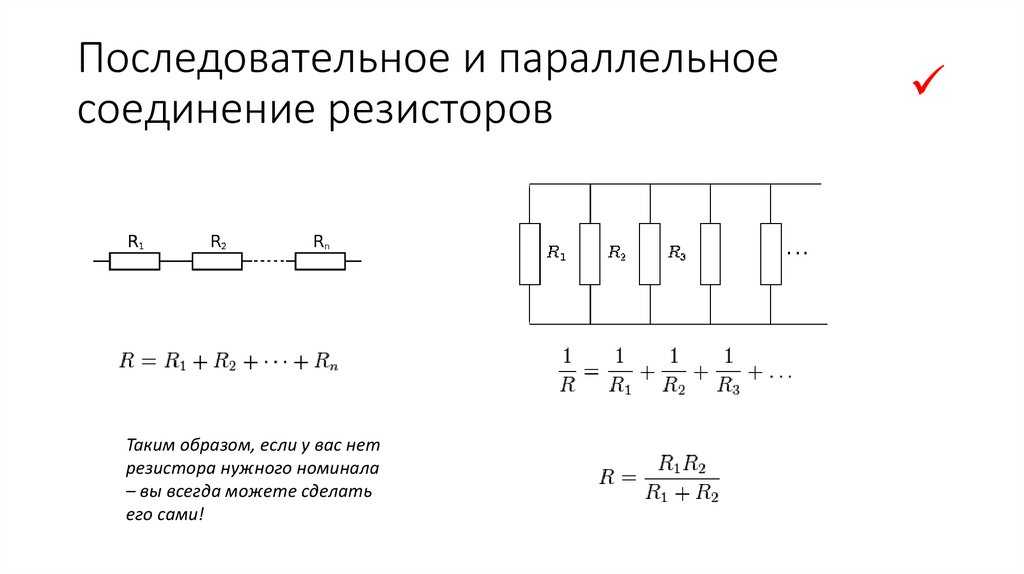
Резисторы используются в различных комбинациях. Существует два метода расположения резисторов в различных комбинациях:
(i) Резисторы последовательно
(ii) Резисторы параллельно
последовательно равны сумме их индивидуальных сопротивлений в цепи.
Последовательное соединение резисторов:
Говорят, что два или более резистора соединены последовательно, если они соединены встык и через каждый из них по очереди протекает один и тот же ток. В этом случае эквивалентное или общее сопротивление равно сумме количества отдельных сопротивлений, присутствующих в последовательной комбинации.
Математически эквивалентное сопротивление любого количества сопротивлений (R 1 , R 2 , R 3 , R 4 , R 5 , ……. .), соединенных последовательно, определяется как:
.), соединенных последовательно, определяется как:
R eq = R 1 + R 2 + R 2 4 3 9044 + R 5 + ……..
Рассмотрим случай трех сопротивлений (R 1 , R 2 и R 3 ), соединенных последовательно друг с другом с соответствующим источником напряжения (V 1 , V 2 и V 3 ) в цепи, показанной ниже:
Резисторы серии
Эквивалентный ток, протекающий через него, равен I, определяемый амперметром A и ключом K.
Эквивалентная разность потенциалов равна сумме индивидуальных разностей потенциалов на каждом резисторе, т. е.
В eq = В 1 + V 2 + V 3
Ток I через каждый резистор одинаков, т. е. I = I 1 = I 2 = I 3
эквивалентный одиночный резистор сопротивлением R eq , так что разность потенциалов V eq на его выводах и ток I в цепи остаются неизменными.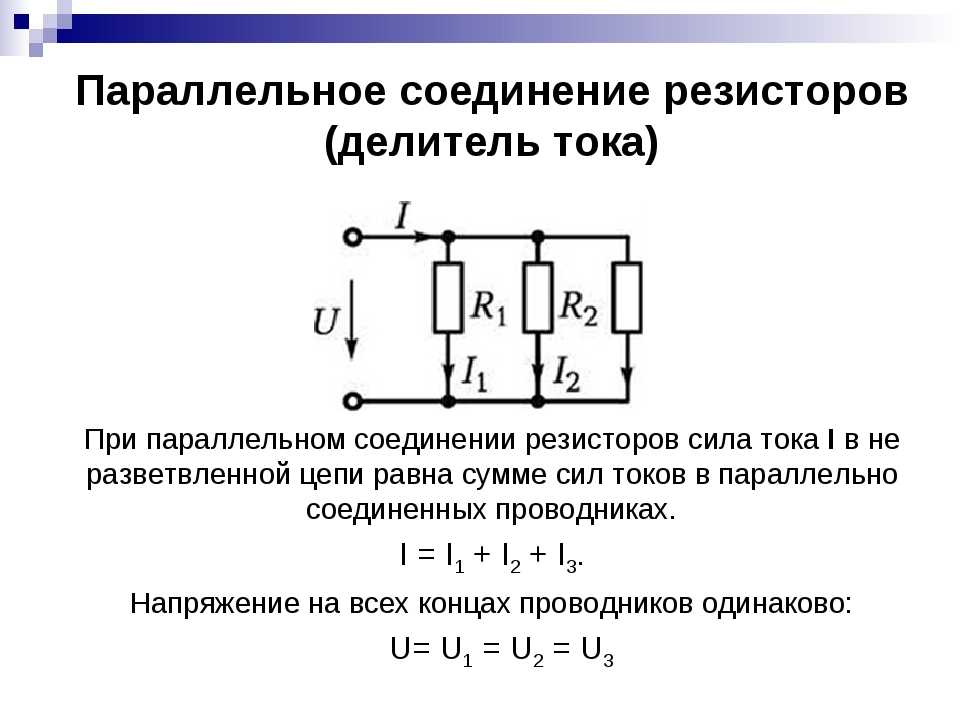
Applying Ohm’s law to the circuit:
V eq = IR eq
By applying Ohm’s law to all resistors individually as:
V 1 = IR 1
V 2 = IR 2
V 3 = IR 3
Следовательно, IR= IR 1 + IR 2 + IR 3
или
R Уравнение = R 1 + R 2 + R 3
- . ОБЩАЯ СРЕДНА. СРЕДИ .
- Эквивалентная разность потенциалов представляет собой сумму индивидуальных разностей потенциалов на каждом резисторе.
- В результате эквивалентное сопротивление становится суммой индивидуальных сопротивлений.
- Единственным недостатком последовательного соединения является то, что при выходе из строя любого резистора в последовательном соединении или отказе вся цепь отключается.
- Последовательная комбинация необходима для увеличения сопротивления и разделения больших разностей потенциалов на множество сопротивлений.

- Такая комбинация используется в коробках сопротивлений, декоративных светильниках и т. д. разное направление тока. В таких цепях ток разветвляется и рекомбинируется по мере пересечения ветвей в общей точке.
Математически эквивалентное сопротивление любого количества сопротивлений (R 1 , R 2 , R 3 , R 4 , R 5 , ……..), соединенных параллельно, определяется как:
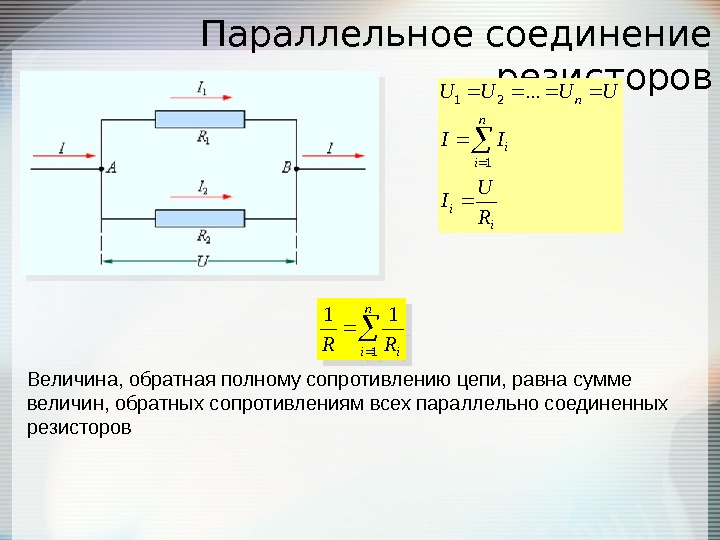
1/R eq = 1/R 1 + 1/R 2 + 1/R 3 + 1/R 4 + 1/R 5 90,5190 + … 90,5120 Рассмотрим случай трех сопротивлений (R 1 , R 2 и R 3 ), соединенных параллельно друг другу с соответствующим источником напряжения (V 1 , V 2 и V 3 ) в цепи, показанной ниже:
Параллельное соединение резисторов
Здесь ток, протекающий через каждый резистор, различен, поэтому эквивалентный ток, протекающий через цепь, равен:
I eq = I 1 + I 2 + I 3
Замените три резистора, соединенных параллельно, эквивалентным одиночным резистором из параллельной комбинации резисторов R eq .

Теперь, применяя закон Ома к параллельной комбинации резисторов как:
I eq = V / R eq
Применяя закон Ома к отдельным резисторам как:
I 2 904 1
I 2 = V / R 2
I 3 = V / R 3
Отсюда, V / R EQ = V / R 12+ V / R EQ = V / R 2+ V / R . 2 + В/Р 3
или
1 / R eq = 1 / R 1 + 1 / R 2 + 1 / R 3
В заключение можно сказать, что эквивалентное сопротивление обратной группы Сопротивления, соединенные параллельно, равно сумме обратных величин сопротивлений отдельных элементов.
- Эквивалентный ток в цепи представляет собой сумму отдельных токов в каждой ветви цепи.
- Разность потенциалов на двух конечных точках цепи остается неизменной.
- В результате обратная величина эквивалентного сопротивления цепи представляет собой сумму обратных величин отдельных сопротивлений.

- В параллельной цепи резистор или какой-либо другой компонент можно легко подключить или отключить, не мешая другим компонентам.
- При параллельном соединении ток, протекающий по цепи, разделяется на разные ветви, и, следовательно, каждый компонент получает необходимое количество тока.
- Здесь эквивалентное сопротивление всегда меньше, чем все сопротивления по отдельности.
- При выходе из строя или коротком замыкании одного из компонентов остальные компоненты цепи работают нормально.
Примеры задач
Задача 1. Какой ток потребляет электрическая лампа от источника 220 В, если сопротивление лампы равно 1000 Ом?
Решение:
Учитывая, что
Напряжение источника V равно 220 В.
Сопротивление лампы R равно 1000 Ом.
Формула для расчета потребляемого тока:
I = V / R
Подставьте указанные значения в приведенное выше выражение следующим образом:
I = 220 В / 1000 Ом
= 0,22 A
Следовательно, ток, проходящий через электрическую лампу, равен 0,22 A .

Задача 2. Если сопротивление нити накала лампы 200 Ом, какой ток потребляет электрическая лампочка от источника 220 В?
Решение:
Учитывая, что
Напряжение источника V равно 220 В.
Сопротивление лампы R составляет 200 Ом.
Формула для расчета потребляемого тока:
I = V / R
Подставьте указанные значения в приведенное выше выражение следующим образом:
I = 220 В / 200 Ом ток через электрическую лампочку равен 1,1 А .
Задача 3: Разность потенциалов между контактами электрической лампочки составляет 30 В, когда она потребляет от источника ток силой 6 А. Какой ток будет потреблять лампочка, если разность потенциалов увеличить до 120 В?
Учитывая, что
Разность потенциалов на электрической лампочке, В, составляет 30 В.
Потребляемый ток, I, составляет 6 А. Закон Ома, формула для расчета сопротивления:
R = V / I
= 30 В / 6 A
= 5 Ω
Когда разность потенциалов увеличивается до 120 В, потребляемый ток равен:
I ‘ = V / R’
Замените данные значения в приведенном выше выражении следующим образом:
I’ = 120 В / 5 Ом
= 24 А
Следовательно, ток, проходящий через электрическую лампочку, равен 24 А .

Задача 4: Провод имеет сопротивление 4 Ом из некоторого данного материала длиной l и площадью поперечного сечения A. Сколько будет сопротивление другого провода из того же материала, имеющего длину l/2 и поперечное сечение -площадь сечения 2А?
Решение:
Рассмотрим сопротивление первого провода как:
R 1 = ρl / A
, где ρ — удельное сопротивление, l — длина, а A — площадь поперечного сечения первого провода.
Но известно, что сопротивление R 1 равно 4 Ом.
Следовательно,
4 ω = ρl / a …… (1)
Теперь, в случае второго провода:
Длина провода, L 2 IS L / 2 и
площадь, А 2 – это 2А.
Следовательно, сопротивление для второго провода становится:
R 2 = ρl 2 / A 2
= ρ (L / 2) / (2A)
= ρl / 4A
. Ω для ρl/A, из уравнения (1) в приведенном выше выражении.

R 2 = 4 Ом / 4
= 1 Ом
Следовательно, сопротивление второго провода равно 1 Ом.
Задача 5: Электроприбор, подключенный к батарее сопротивлением 40 Ом и провод сопротивлением 12 Ом последовательно к батарее 8 В. Рассчитать :
(a) Общее сопротивление цепи,
(b) Ток в цепи, и
(c) Разность потенциалов на каждом сопротивлении.
Solution:
The given problem can be represented diagrammatically as:
(a) Given that,
The resistance of electric lamp, R 1 = 40 Ω,
The сопротивление проводника, соединенного последовательно, R 2 = 12 Ом.
Следовательно, общее сопротивление цепи равно:
R = R 1 + R 2
Подставьте указанные значения в приведенное выше выражение.

R eq = 40 Ом + 12 Ом
= 52 Ом
Следовательно, общее сопротивление в цепи равно 52 Ом.
(b) Опять же, в задаче указано, что
Суммарная разность потенциалов на двух выводах батареи, В, равна 8 В.
По закону Ома ток в цепи равен:
I = V / R eq
I = 8 В / 52 Ом
= 0,15 А
Следовательно, ток в цепи равен 0,15 А.
(c) Опять же, применим закон Ома отдельно к электрической лампе и проводнику, разность потенциалов на электрической лампе равна:
= 6 В
, а разность потенциалов на проводниках —
V 2 = I × R 2
= 12 ω × 0,15 A
= 1,8 В
Проблема 6: Рассмотри. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние.
 Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. три резистора: R 1 = 6 Ом, R 2 = 18 Ом и R 3 = 36 Ом, соединенные параллельно, через источник питания 12 В. Рассчитать:
Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. три резистора: R 1 = 6 Ом, R 2 = 18 Ом и R 3 = 36 Ом, соединенные параллельно, через источник питания 12 В. Рассчитать: (a) Ток через каждый резистор,
(b) Общий ток в цепи и
(c) Общее сопротивление цепи.
Решение:
Данную задачу можно представить схематически как:
Параллельно соединенные сопротивления: 3
Разность потенциалов на аккумуляторе, В, составляет 12 В.
Поскольку в цепи параллельно соединены резисторы, то разность потенциалов на клеммах отдельного резистора будет одинаковой.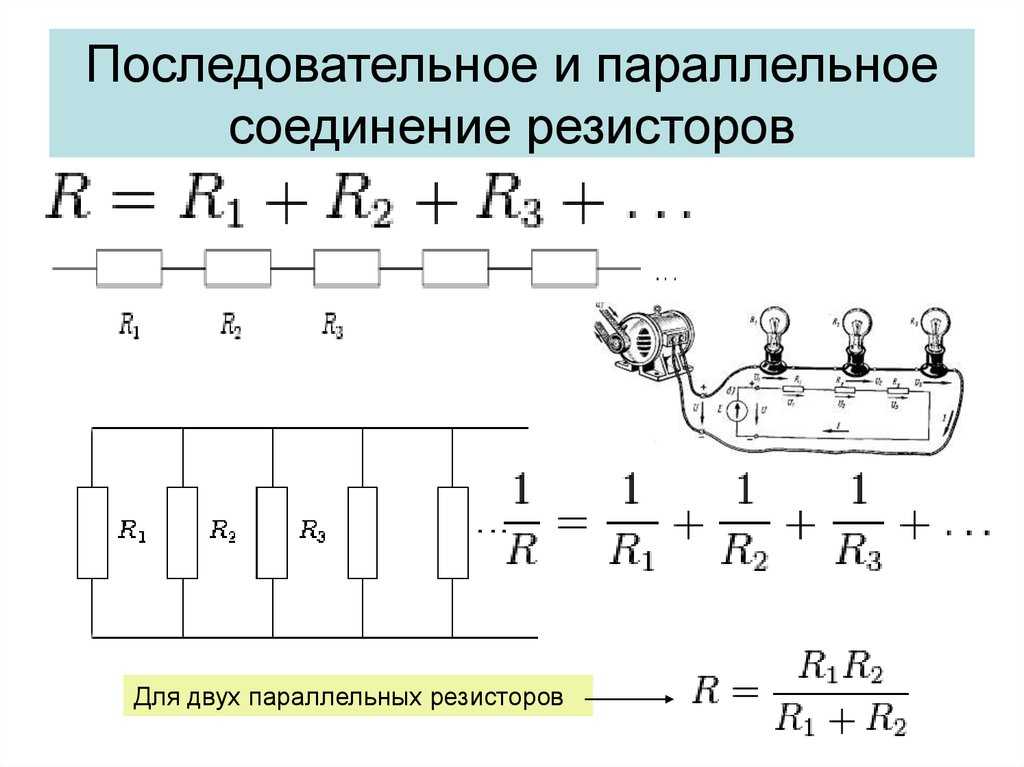





 Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. три резистора: R 1 = 6 Ом, R 2 = 18 Ом и R 3 = 36 Ом, соединенные параллельно, через источник питания 12 В. Рассчитать:
Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. Состояние. три резистора: R 1 = 6 Ом, R 2 = 18 Ом и R 3 = 36 Ом, соединенные параллельно, через источник питания 12 В. Рассчитать: