Увеличиваются ли молекулы при нагревании? / Хабр

Все мы знаем, что если надуть пластиковую бутылку горячим воздухом, крепко-накрепко закрыть крышкой, а потом охладить, то бутылка сожмётся. Причина этого лежит в физике 8-го класса, или, если точнее, в законе Гей-Люссака, утверждающем, что отношение объёмов при разных температурах равно отношению абсолютных температур. То есть ещё со школьных времён (а может и раньше) нам всем известно, что при нагревании некоторого количества газа его объём увеличивается, а при охлаждении — уменьшается.

А что насчёт того, из чего этот газ состоит? Увеличивается ли объём самих частичек газа, то есть размер атомов и молекул? Банальный ответ на этот банальный вопрос под катом.

Ха-ха, попались!

Ответ на этот вопрос весьма прост: как мы определим

объём

размер частиц (что такое размер атома/молекулы в зависимости от температуры), такой ответ мы и получим. Поскольку атомы по-своей сути — это одноатомные молекулы, то дальше мы будем называть все эти частицы единым термином «молекула«.

Если взять бутылку с газом, и из этой бутылки взять одну единственную молекулу, то окажется, что для неё не возможно (по-честному) даже принципиально измерить температуру. Частица находится в каком-то конкретном (квантовом) состоянии, которое мы можем определить и измерить, но при этом мы не сможем засунуть ей в в неё термометр и узнать сколько там у неё градусов. Связанно это с тем, что «температура» — это свойство макроскопических (т.е. больших) систем, состоящих из большого числа частиц. А значит если молекул в системе мало, то и измерять у этой системы нечего. «Большое число частиц», конечно, это плавающее понятие, но обычно оно измеряется в молях, или в числах Авогадро (), поэтому очевидно, что одна молекула горааааздо меньше этого порядка величин, а значит само понятие температуры не применимо к одной, двум, да даже десяти молекулам.

Что такое температура?

Но что вообще такое температура? Ещё со школы мы знаем, что есть т.н. абсолютная температура T, измеряемая в градусах Кельвина. Именно она стоит во всех газовых законах, в частности в уравнении Менделеева-Клайперона.

Для забывших, как выглядит уравнение Менделеева-Клайперона

Это уравнение имеет вид , где P — давление, V — объём, n — количество вещества (в молях), R = 8.314 Дж/(моль · К) — универсальная газовая постоянная, а T — абсолютная температура в Кельвинах (К).

Абсолютная температура связанна с относительной температурой t, измеряемой в градусах Цельсия, как , и абсолютный ноль (T=0, или же ) — это недостижимая величина. Ещё всем в голову вбивают мантру:

абсолютная температура является мерой средней кинетической энергии молекул.

Но эта мантра не объясняет, что же именно из себя представляет температура.

Попробуем разобраться. Начнём с простого примера. Закроем глаза и представим себе Африку: жаркую, солнечную, заполненную равнинными саваннами, и с горой Килиманджаро торчащей посередине. А ещё там есть слоны.

Каждый слон имеет определённую (большую) массу, и поэтому любое поднятие своей туши из равнинной местности в горную — это большая затрата энергии.

Представим, что слоны голодные, поэтому энергии у них мало. Будучи слоном, я бы в таком состоянии не попёрся бы в гору, а тусовался бы в саванне. В горы бы я ходил только по очень-очень большой нужде. В результате, если бы мы сняли фотографию Африки со спутника, она бы выглядела примерно так, как показано на картинке ниже: много-много слонов на равнине, и очень мало смелых и отчаянных в горах, причём, чем выше — меньше вероятность найти слона.

А теперь представим, что слоны хорошенько поели, да ещё какой-нибудь [Роскомнадзор] ещё для скорости им в еду подсыпали, так что энергии у слонов много. В этом случае, что равнина, что гора, слоны будут туда переться без особой устали, поэтому теперь вероятность отыскать слона на равнине и в горах будет отличаться уже меньше, чем в предыдущем примере (см. картинку ниже), хотя всё ещё будет сохраняться правило: чем выше на гору — тем меньше слонов.

Эти два примера весьма точно иллюстрируют случаи газа с низкой (первый) и высокой (второй) температурой. У каждой молекулы (слона) есть какая-то своя энергия, в нашем примере — это гравитационная энергия , где m — масса, g = 9.8 м/c² — ускорение свободного падения, а h — высота над равниной. Из энергии каждой конкретной частицы (места, где нашли слона) мы не можем ничего сказать о том, как всех слонов покормили в целом, но именно то, сколько на всех выделили еды, или другими словами, сколько энергии вкачали в среднем во всю систему, даст нам распределение слонов по ландшафту Африки. Собственно, температура в наших примерах — это общая величина накормленности всех слонов во всей Африке.

Именно поэтому мантра из школьного курса физики и оказывается верна — температура — это то, сколько в среднем энергии (причем, как кинетической, так и потенциальной) имеет каждая молекула, или, что в данном случае эквивалентно, какова вероятность найти частицу с очень большой энергией. Но более точно, температура — это параметр распределения Больцмана (или Гиббса) — распределения частиц по состояниям с различной энергией. Это распределение говорит нам, что чем выше температура, тем больше высокоэнергетических молекул относительно числа низкоэнергетических мы имеем.

Распределение Больцмана

Собственно, распределение Больцмана имеет вид:

где n(E) — это число частиц с энергией E, R — универсальная газовая постоянная (см. предыдущий спойлер), а T, само собой, температура.

В примере же со слонами мы иллюстрировали т.н. барометрическую формулу: частный случай распределения Больцмана, показывающий как меняется давление газа с увеличением высоты:

где P(h) — это давление на высоте

h, , а M — это молярная масса газа.

Растут ли атомы от температуры?

Теперь, собственно, можно перейти к вопросу: а растут ли, например, атомы при росте температуры. Само собой, каждый конкретный атом находится в каком-то квантовом состоянии, поэтому от температуры его размер не зависит, но вот средний размер всех атомов в сосуде с газом от той самой температуры зависеть уже будет.

Представим себе, например, атом водорода: тяжёлый протон, а вокруг него летает электрон. Поскольку протон положительный, а электрон отрицательный, то один притягивает другой по закону Кулона, который выглядит точно так же как ньютоновская гравитация, поэтому в этом смысле атом вполне себе напоминает, например, Солнце и Землю, летающую вокруг него. Только, как говорит нам (далеко не полностью удачная, см. например, тут) атомная модель Бора, в отличие от системы «звезда + планета», электрон летает вокруг ядра только по орбитам определённого радиуса.

Так или иначе, чем больше энергии мы закачиваем в атом водорода, тем более широкая орбита будет доступна электрону для полёта вокруг ядра. Естественно, если мы возьмём один конкретный атом, мы можем узнать его орбиту, и она ничего нам о температуре всех атомов не скажет. Но вот если мы измерим радиусы у множества атомов, а потом усредним полученные величины, то у нас действительно возникнет зависимость от температуры для этого среднего числа. В результате получится что-то типа такой картинки:

Из неё видно, что чтобы начать замечать хоть какие-то изменения в размере электронной оболочки, нужно ооочень сильно нагреть атом (в данном случае до более 10000 градусов). Это в целом общий тренд.

Как была посчитана эта зависимость

Подробнее о формулах можно узнать в этом посте.

Если кратко, то радиус орбиты (R) в зависимости от главного квантового числа

n=1,2,3… — это

где R₀=5.3×10⁻¹¹ метра − это боровский радиус. Энергия (E) же орбиты имеет вид

где E_h= 4.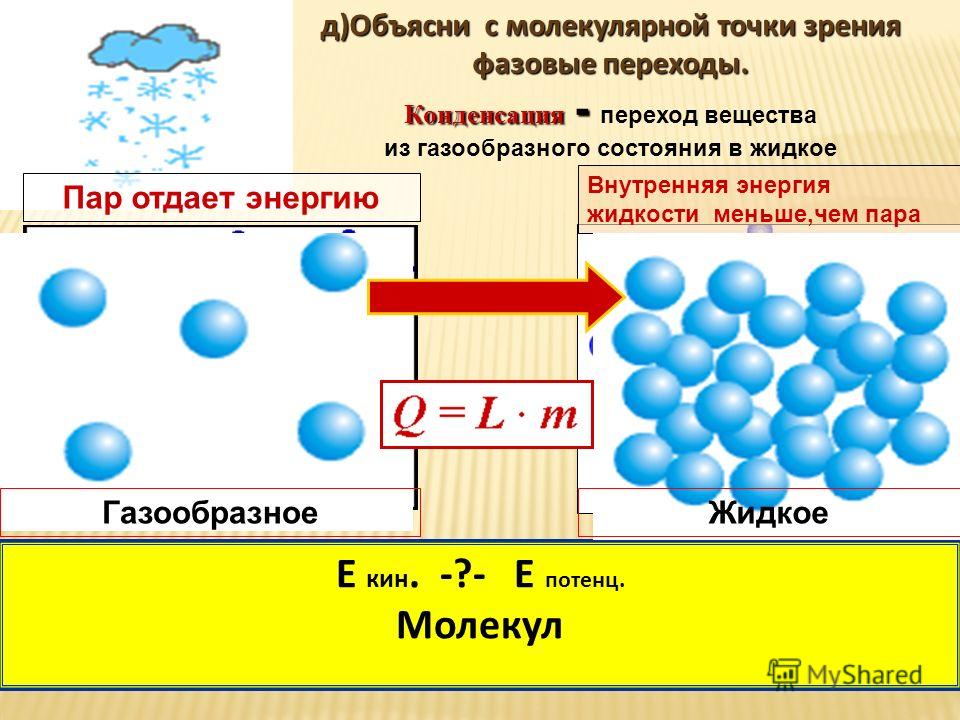 3597447222071(85)×10⁻¹⁸ Джоулей − это энергия Хартри.
Далее используя распределение Больцмана для одной частицы, мы можем посчитать среднее значение радиуса от температуры как

Знаменатель у нас появляется из-за того, что полная вероятность всех исходов измерений должна быть равна единице.

Иными словами,

ответ на вопрос поста: да, при нагревании электронные оболочки атомов (и молекул) в среднем расширяются

. Но, это увеличение очень маленькое, и требует нагрева до очень высоких температур, к которым мы в обыденной жизни не привыкли.

Растут ли молекулы от температуры?

Теперь зададимся вопросом: а что если наша молекула составлена не из одного, а из двух, трёх или более атомов? Можем ли мы что-то сказать о межатомных расстояниях в ней, как ведут они себя при повышении температуры? Для простоты, естественно, ограничимся двухатомными молекулами, кои, в частности, составляют как минимум 98.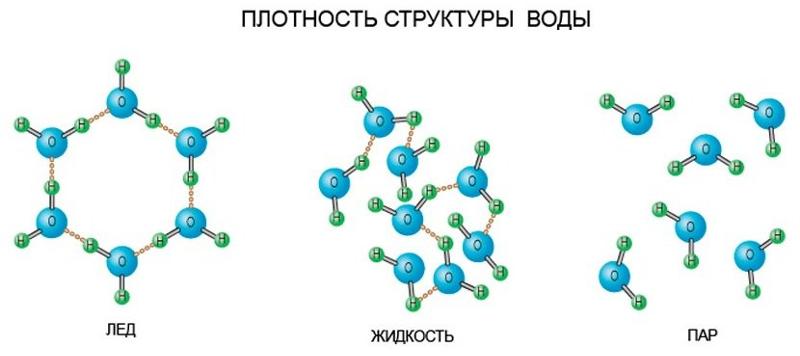

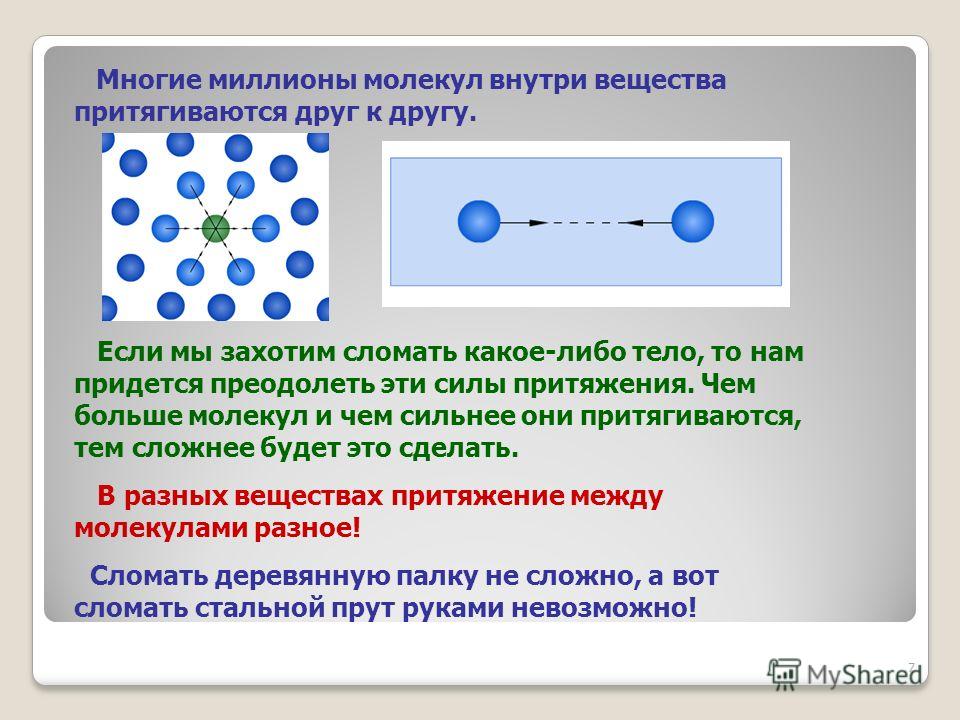
7 % нашей атмосферы (азот и кислород).

У нас есть один атом, у нас есть второй атом: ммммм, и расстояние между ними, обозначим его как R. Как ведёт себя потенциальная энергия взаимодействия этих атомов в зависимости от R?

• Если мы разведём атомы оооочень далеко друг от друга, то химическая связь между ними давно будет разорвана. Поэтому особой разницы от того, что расстояние мы увеличим от «очень много» до «очень много и ещё чуть-чуть», мы не заметим. Иными словами при R → ∞ у нас должна быть горизонтальная асимптота.
• Если же, наоборот, мы будем пытаться впихнуть один атом в другой (R → 0), то в какой-то момент мы выгоним из пространства между этими атомами все электроны, ибо те не идиоты, чтобы тусоваться в токсичной высокоэнергетической атмосфере, и у нас останутся два голых положительно заряженных ядра, отталкивающиеся друг от друга через Кулоновскую силу. Т.е. при R → 0 у нас будет вертикальная асимптота, стремящая потенциальную энергию взаимодействия атомов в высокоэнергетическую бесконечность.
  
• Ну и, логично, что не будь какого-то минимума на этой потенциальной кривой между R=0 и R → ∞, то самих молекул о которых мы говорим, не существовало бы.
  

В итоге мы понимаем, что кривая потенциальной энергии взаимодействия имеет следующий вид:

Атомы в молекуле всегда колеблются, даже при абсолютном нуле, когда никакой лишней энергии не осталось. Из-за принципа неопределённости они не могут просто скатиться в минимальную по энергии точку на потенциале и сдохнуть лежать, свернувшись калачиком: им приходится совершать т.н. нулевые колебания. Если же энергия у них выше, то и колеблются они с большей амплитудой. Поэтому возникает вопрос: а как конкретно колеблются атомы?

Если бы слева и справа от точки минимума потенциал был одинаков, как, например, в случае закона Гука, то атомы во время колебаний отклонялись бы в область малых значений межатомных расстояний ровно то же количество времени, сколько и в область больших значений. В этом случае бы среднее значение межатомного расстояния при любой температуре было бы равно значению расстояния в точке минимума. Иными словами, если бы мы взяли газ, и в любой момент времени сфоткали все молекулы, а потом посчитали бы среднее значение для всех расстояний между атомами, то в итоге получили бы расстояние в точке минимума.

Но реальность у нас другая: слева от точки минимума (при R → 0) у молекулы стоит жёсткая стенка, а справа (при R → ∞) — мягкий диван. Вопрос: где будет больше времени проводить молекула: долбиться о стенку, или валяться на диване? Правильно: конечно на диване. Иными словами, распределение расстояний в молекуле, что при абсолютном нуле, что при какой-то температуре, будет несимметричным, поэтому среднее значение расстояний будет сдвинуто в сторону больших расстояний относительно минимального. Мало того, при повышении температуры, т.е. когда мы будем закачивать больше кинетической энергии в систему, увеличивая амплитуду колебаний, молекула будет видеть гораздо более жёсткую стенку, и гораздо более мягкий диван.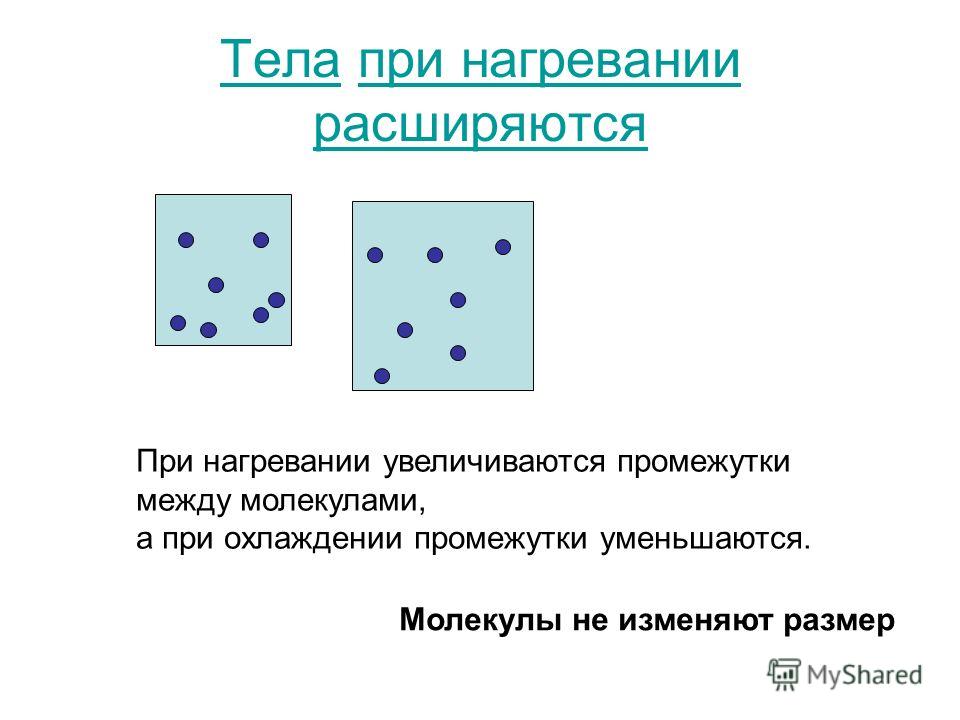 Поэтому среднее значение межатомных расстояний будет расти с ростом температуры, а значит и средний размер молекул, причём всех, не только двухатомных, будет увеличиваться.

К сожалению, чтобы посчитать этот рост среднего расстояния, потребуется много больше усилий, чем в случае атома водорода. Но можно пойти другим путём, и поискать, а не исследовался ли этот вопрос в экспериментах?

И порывшись на просторах этих наших Интернетов, можно набрести на следующую работу: J. Chem. Phys. 79, 170 (1983). В ней делали эксперимент буквально описанный выше:

• брали кучу молекул углекислого газа (CO₂) и нагревали их до разных температур, в диапазоне температур от комнатной (300 K ≈ 25^oC) до «ай как горячо» (1000 К ≈ 730^oC ),
• при каждой выбранной температуре делали «фотку» всех молекул при помощи электронов (этот метод зовётся газовой электронографией, о нём можно немного почитать здесь),
• ну а дальше буквально измеряли средние значения для межатомных расстояний на каждой фотке.

В результате они, в частности, получили следующую зависимость средней длины двойной связи C=O в молекуле углекислого газа (O=C=O):

Из графика видно, что при нагреве от комнатной температуры до 1000 градусов К это среднее значение выросло почти на 0.004 Å (1 ангстрем, Å, = 10^—10 метров). Конечно, в наших привычных величинах это очень мало, но сама длина связи C=O в этой молекуле составляет 1.2 Å, так что это рост на почти 0.3 %! Вполне себе заметная величина при нагреве, достижимом привычными средствами (например, газовой плитой).

Зачем это вообще знать?

Да хотя бы просто ради любопытства. Разве не прикольно поспорить с коллегой на чашку кофе, что при нагреве контейнера с едой в микроволновке помимо объёма газа увеличится и размер частиц газа? Ну и в практическом смысле это тоже важно. Все эти температурные расширения/уменьшения всяких макроскопических объектов, таких как рельсы, провода линий электропередач, да даже крышки банки под горячей водой, работают ровно по тому же механизму, что и для молекул газа: средние межатомные расстояния увеличиваются, т. к. в систему при увеличении температуры закачивается больше энергии движения частиц. И по-моему, осознание того, что за такими обыденными явлениями стоят такие нетривиальные процессы, вдохновляет на новые подвиги и свершения.

Всех благ, и да пребудет с Вами межатомная сила.

Три смерти и обожённое лицо за одну ночь. Почему газ вышел из-под контроля? — Новости Магнитогорска

Прошлые выходные омрачились трагедией. В челябинской многоэтажке от отравления бытовым газом погибли 17-летний подросток, двухгодовалый ребёнок и 79-летняя старушка — их соседка сверху. В это же время в Магнитогорске духовой шкаф полил пенсионерку огнём. Она отделалась лёгкими ожогами.

Встретилась с огненной стеной

Шестидесятиоднолетняя Ольга Ивановна выносит из комнаты электрическую плитку на две конфорки. Новую. Говорит, купила в супермаркете неподалёку, по скидке. И тут же жалуется на пенсию: получает восемь тысяч.

В её квартире газа нет. Перекрыли после воскресной аварии. Тогда, вечером, она выходила из ванны. Собиралась включить духовку, чтобы нагреть воду для стирки второй партии вещей. Из духового шкафа на неё обрушился столб пламени.

— Я духовку открываю, спичку зажигаю, подношу. А пламя оттуда как поднялось! И мне по лицу. Ладно подруга моя была рядом, быстро перекрыла газ. И волосы мокрые были. А то лысая бы осталась, — рассказывает Ольга Горбуль.

Ольга Ивановна «отделалась» лёгкими ожогами лица, губ, выпавшими зубами и опалёнными бровями. Вещи на кухне не пострадали. Лишь духовка закоптилась.

Виноваты соседи?

Пенсионерка рассказывает: в квартиру не единожды наведывались газовщики. Проверяли печку, говорили: с ней всё хорошо, но тяги в вентиляции нет. Так и в этот раз «отдушина» оказалась забита. Газ сконцентрировался на кухне. И вспыхнул.

— Я пошла в ЖЭУ с этим актом. А они мне говорят: в четверг придёте. А что мне до четверга делать? — волнуется Ольга Ивановна.

В том, что вентиляция не тянет, пенсионерка обвиняет соседей сверху. Дескать они затеяли ремонт. И забили трубу строительным мусором. По её словам, из-за них обрушился потолок в комнате у соседа.

Обрушившийся потолок мы видели. А его «разрушителей» дома не застали. Открыла несовершеннолетняя девушка. Сказала, что взрослых в доме нет.

— Я с ними уже говорила как-то. Встретила, когда приносила кота с улицы. Говорю: «всё рушится, совесть хоть имейте». А они отвечают: «А что вы хотели? Дом старый», — негодует Ольга Горбуль.

Людьми из квартиры выше недовольна не только Ольга Ивановна, но и домуправление. От комментариев там отказались, сказали: все заняты. По телефону пояснили: те жильцы самовольно устроили перепланировку и забили вентиляцию.

Выемки вентиляции важнее, чем вы думаете

Окончательное ли это решение — неизвестно. Разбираться, кто виноват, всё-равно придётся управляющей компании. Им же придётся восстанавливать вытяжку. Трубы вентиляции — их зона ответственности. Так объяснили в службе газа.

— Газовая служба проверяет только наличие тяги. А за исправность, надлежащее содержание, своевременную очистку, ремонт дымоходов и дымканалов несёт ответственность управляющая компания, — рассказала Елена Короткова, ведущий инженер промбезопасности филиала АО «Газпром газораспределение Челябинск» в г. Магнитогорске.

По нормам, «газовщики» не могут «принять» к работе газовую плиту, если в вентиляции нет тяги. Потому и заглушили газ Ольге Ивановне.

Чтобы не случилось беды, горожанам советуют самим проверять тягу. Нужно поднести листочек к вентиляции. Если он всасывается, значит плиту использовать можно.

Иначе может произойти небольшой взрыв, как случилось с Ольгой Ивановной. А ещё газ может копиться, концентрироваться — и привести к гибели. Как в Челябинске.

Челябинская трагедия

В то же воскресенье от отравления угарным газом умерли подросток, двухлетний малыш и пенсионерка, жившая на этаж выше. В квартире у первых сломалась «водогрейка». Газ утекал в помещение. Выйти ему было некуда — вытяжки заклеили.

В управляющей компании Челябинска отказались общаться с журналистами. Разговаривать с ними будут следователи и прокуратура. Возбуждено дело о халатности, идёт разбирательство.

Таких квартир, с газовыми водонагревателями, 2 544. Авария может произойти в каждой. Ещё больше водогреек в своих домах. А газовые плиты стоят почти на каждой кухне.

Газ, огонь — это опасно для человека. Есть техника безопасности. Но кто её соблюдает, прежде чем зажечь конфорку?

— Нужно периодически проверять наличие тяги. Ни в коем случае не заклеивать вентиляционные отверстия, не вставлять патрубки вытяжных устройств в вентиляционные каналы. Обязательно открывать форточки. Потому что на одну молекулу газа приходится две молекулы кислорода, — советует горожанам Елена Короткова.

термодинамика — Может ли отдельная молекула иметь температуру?

Полное раскрытие, этот ответ основан на статье, которую я недавно опубликовал по этой теме. Название статьи «Определение температуры изолированной молекулы» говорит о том, что мой ответ — да, мы можем определить такую ​​температуру.

Действительно, концепция температуры изолированной молекулы в вакууме не нова. Он использовался в течение десятилетий в таких областях, как астрофизика и столкновения молекулярных пучков (я даю много ссылок в статье).

Например, ПАУ (полициклические ароматические углеводороды) были открыты в межзвездных средах в 1984 г., когда К. Селлгрен отнес некоторые особенности в ближнем ИК-диапазоне, появляющиеся в спектрах некоторых туманностей, к тепловому излучению очень мелких зерен (радиус 10 Å). которые кратковременно нагреваются до ~1000 К за счет поглощения отдельных ультрафиолетовых фотонов 90 008 ». Такие зерна оказались крупными молекулами ПАУ.

Для определения температуры необходимо учитывать, что изолированная молекула представляет собой микроканоническую систему, сохраняющую полную энергию. (По крайней мере, в краткосрочной перспективе, поскольку оно медленно излучает избыток энергии как черное тело. ) Поэтому мы работаем с микроканоническими температурами, а не с обычными каноническими температурами. Основное отличие состоит в том, что микроканоническая температура является функцией $T\left(E\right)$ от полной энергии $E$, а каноническая температура противоположна; энергия $E\left(T\right)$ является функцией температуры. 9{-1}} $$ для конечной системы с несколькими степенями свободы. В этом уравнении $S$ — энтропия, которая, по Больцману, равна $$ {{S}_{B}}\left( E \right)={{k}_{B}}\ln \left[ \varepsilon \,\omega \left( E \right) \right],$$ где $\omega\left( E \right)$ — плотность микросостояний с энергией $E$.

В принципе, дискретный характер $E$ для небольшой конечной квантовой системы может создавать значительные трудности при вычислении производной, определяющей температуру. Однако численные тесты показывают, что пока избыток энергии не слишком мал (около нулевого уровня), $ \omega\left( E \right) $ хорошо дифференцируема.

Тогда мы можем продолжить. Мы можем вычислить $ \omega\left( E \right) $ для изолированной молекулы численно, получить производную и получить ее микроканоническую температуру. Если нас устраивает гармоническое приближение для нормальных колебательных мод, мы можем даже получить $\omega\left(E\right)$ аналитически и написать красивое замкнутое выражение для $T\left(E\right)$.

Перед этим мы должны рассмотреть еще одну проблему: определение энтропии неоднозначно. По Гиббсу, например, энтропия должна учитывать все микросостояния с энергией, малой или равной $E$, т. е. $$ {{S}_{G}}\left( E \right)={{k}_{B}}\ln \left[ \Omega \left( E \right) \right], $$ где $\Omega \left( E \right)$ — интегральное число состояний.

Оба функционала энтропии в термодинамическом пределе дают одинаковые результаты для больших систем. Однако для небольшой конечной системы, такой как изолированная молекула, предсказания обоих подходов могут не совпадать. Действительно, это имеет место для молекул примерно до десяти атомов.

Во всяком случае, для большой молекулы объемные микроканонические температуры Больцмана и Гиббса хорошо согласуются. Вы можете оценить их с помощью этого простого уравнения $$ T\left(E\right)={{\left[\ln \left(\frac{E+{{E}_{ZP}}}{E-{{E}_{ZP}}} \right) \ справа]}^{-1}}\frac{2{{E}_{ZP}}}{N{{k}_{B}}}, $$ где $E_{ZP}$ — гармоническая нулевая энергия, а $N$ — число колебательных степеней свободы $\left(N = 3N_{атомов}-6\right)$.

На рисунке ниже показано несколько примеров микроканонической температуры изолированных молекул в гармоническом приближении.

Какую работу может выполнить одна молекула?

Существует множество неправильных представлений о том, как работают атмосферные процессы, и одна из них, которая часто кажется мысленным барьером, — это идея . Какую работу может выполнить одна молекула?

Эта идея, представленная разными способами, регулярно появлялась здесь в комментариях, а также появляется во многих блогах с красноречивыми эссе о «реальной роли» CO2 в атмосфере, обычно не обремененными какими-либо фактическими знаниями о научных исследованиях. дисциплина, известная как физика.

Нам всем нужны мысленные образы того, как на самом деле работают невидимые или микроскопические вещества.

Когда мы рассматриваем CO2 (или любой другой газ), поглощающий длинноволновое излучение, мысленная картина сначала представляет собой попытку найти иголку в стоге сена.

А во-вторых, мы его нашли, но он такой крошечный и незначительный, что не может сам выполнять всю эту работу ?

Сколько на самом деле может сделать один мужчина или женщина?

Эта статья на самом деле о втором ментальном образе, но краткое описание первого мысленного образа для новых читателей этого блога..

Иголка в стоге сена

Представьте себе луч энергии около 15,5 мкм. Вот график поглощения CO2 вокруг этой длины волны. Это линейный график, чтобы не путать людей, менее знакомых с логарифмическими графиками. Водяной пар также нанесен на этот график, но вы его не видите, потому что поглощающая способность водяного пара в этой полосе намного ниже, чем у CO2.

Поглощение СО2, 15,4-15,6 мкм, линейное, взято со Spectrecalc.com

Вертикальная ось сбоку имеет какое-то значение, но пока просто думайте об этом как об относительной мере того, насколько эффективен СО2 на каждой конкретной длине волны.

Вот логарифмический график водяного пара и CO2. Ниже на графике вы можете увидеть несколько черных вертикальных линий — водяной пар. Помните, что по мере того, как вы перемещаетесь вниз по каждой черной горизонтальной линии сетки на графике, способность поглощения падает в 100 раз. Если двигаться вниз по двум черным линиям сетки, способность поглощения снижается в 10 000 раз.

Поглощение CO2 — логарифмический график — 15,4–15,6 мкм, взято с сайта speckalc.com

Теперь я добавлю поглощающую способность O2 и N2 — газов, составляющих большую часть атмосферы — проверьте разницу:

O2 и N2 добавлены..

Spectralcalc ничего не выдаст — ничего в базе данных.

Фотоны размером 15,5 мкм проходят сквозь O2 и N2, как будто их не существует. Они прозрачны на этой длине волны.

Итак, на нашей иголке в стоге сена идея , представьте себе поле – очень-очень длинное поле. Стога сена идут один за другим на мили.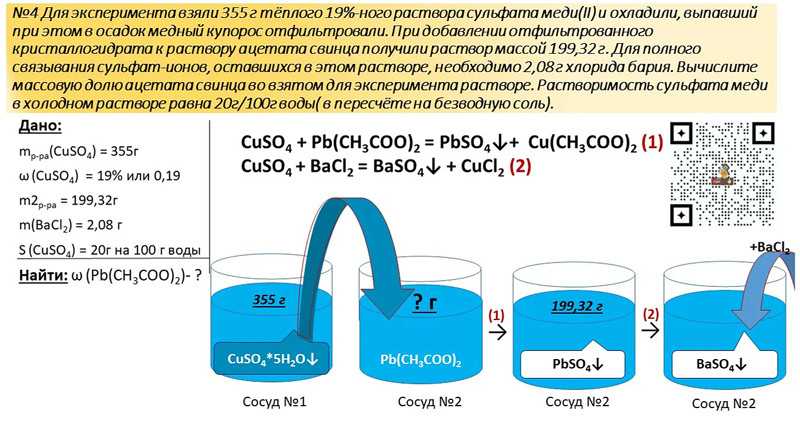 В каждом стоге сена по одной иголке. Вы приседаете и смотрите вдоль линии обзора всех этих стогов — конечно, вы можете видеть только сено прямо перед собой в первом.

Происходит какое-то волшебство, и внезапно вы можете видеть сквозь сено.

Представь.. Хэй теперь невидим.

Сможете ли вы увидеть иголки?

Это мир фотона размером 15,5 мкм, путешествующего через атмосферу. Несмотря на то, что CO2 составляет всего 380 частей на миллион, или около 0,04% атмосферы, CO2 — это все, что существует для этого фотона, и вероятность того, что этот 15,5-микронный фотон будет поглощен молекулой CO2, прежде чем покинуть этот мир и отправиться в лучшее место , очень мала. довольно высоко.

На самом деле существует математическое уравнение, которое точно определяет долю поглощаемого излучения любой длины волны, но в этом посте мы будем держаться подальше от математики. Вы можете увидеть уравнение в CO2 — незначительный следовый газ? Часть третья. И если вы увидите какой-либо «анализ» эффективности CO2 или любого следового газа, в котором делается вывод о его незначительности, но не упоминает это уравнение, вы поймете, что это скорее поэма, чем наука. Нет ничего плохого в том, чтобы немного стихов, если они хорошо написаны..

В любом случае, это всего лишь мысленная картина, которую я хотел создать. Это не идеальная мысленная картина, это просто аналогия — стихотворение, если хотите. Если вам нужна настоящая наука, ознакомьтесь с серией CO2 — незначительные следовые количества газа.

СО2 – Стахановец атмосферного мира?

Еще в лихие дни сталинской России была создана мифологическая фигура (как и большинство мифов, вероятно, из доли правды), когда Алексей Стаханов якобы добыл за одну смену в 14 раз больше нормы угля. И поэтому остальная часть рабочей силы была призвана внести свой реальный вклад в движение. Стахановцами стать.

Похоже, это изображение атмосферных газов.

Большинство молекул просто слоняются без дела, возможно, как работа на _____ (мысленно вставьте название наименее любимой и самой ленивой организации, но не делитесь – мы стараемся не обижать людей здесь, за исключением плохой науки)

Итак, вот большая организация, мало что делается, а теперь вводим стахановцев — этих поборников трудовой этики. Ну, даже если они делают в 14 или 100 раз больше работы, чем их коллеги, какая разница?

В конце концов, они составляют всего 0,04% рабочей силы.

Но настоящая атмосфера не такая..

Попробуем объяснить, как на самом деле работает атмосфера, и помочь этому процессу..

Мысленный эксперимент

молекула может», рассмотрим небольшой «участок» атмосферы при 0°С.

Просвечиваем этот участок атмосферы излучением 15,5 мкм и постепенно накручиваем интенсивность. Поскольку это мысленный эксперимент, все задействованные молекулы просто остаются и не уплывают по ветру.

Молекулы CO2 поглощают энергию – все больше и больше. Молекулы O2 и N2 просто игнорируют это, они не знают, почему молекулы CO2 так возбуждаются.

Какова ваша ментальная картина? Что происходит с этими молекулами CO2?

а) они становятся все горячее и горячее? Итак, молекулы O2 и N2 все еще находятся при 0°C, а CO2 сначала имеет температуру 10°C, затем 100°C, затем 1000°C?

б) они достигают определенной температуры и просто подают сигнал «тайм-аут», чтобы фотоны «отступили»?

c) другие предложения?

Реальная атмосфера – от каждого по способностям, каждому по потребностям

Какова повседневная жизнь молекулы?

Очень сильно зависит от температуры. Абсолютная температура молекулы (в К) пропорциональна кинетической энергии молекулы. Кинетическая энергия зависит от скорости и массы. Молекулы вращаются очень быстро, если они находятся при любой типичной атмосферной температуре.

Вот хорошая иллюстрация этой идеи (с http://www.chem.ufl.edu/~itl/2045/lectures/lec_d.html).

На уровне моря типичная молекула испытывает около 10 ¹⁰ (10 миллиардов) столкновений с другими молекулами каждую секунду. Цифры меняются в зависимости от температуры и молекулы.

Подумайте иначе – на уровне моря 8×10 ²³ молекул ударяются о каждый ² см поверхности в секунду.

Каждый раз, когда молекулы сталкиваются, они эффективно «делятся» энергией.

Следовательно, если молекула СО2 начнет получать огромное количество энергии от фотонов, которые «попадают в точку» (имеют правильную длину волны), то она нагревается, движется еще быстрее, и не успеет сказать «¤» она столкнется с другими молекулами и поделится своей энергией.