Как составить таблицу истинности? — Студопедия
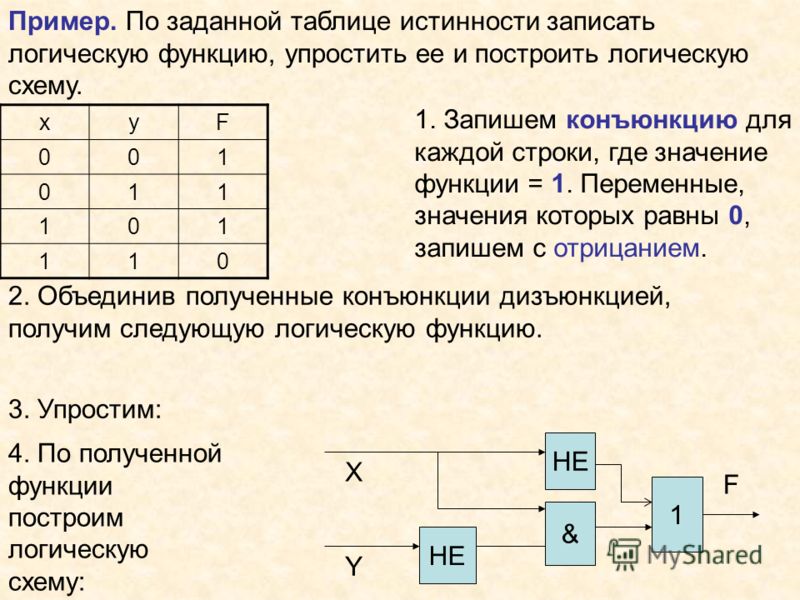
Пример 1. Установить истинность высказывания · С
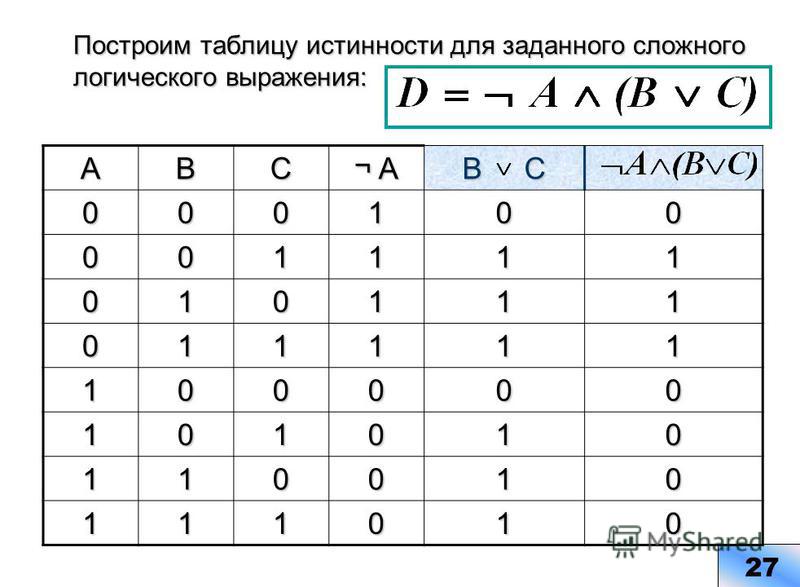
Решение. В состав сложного высказывания входят 3 простых высказывания: А, В, С. В таблице заполняются колонки значениями (0, 1). Указываются все возможные ситуации. Простые высказывания от сложных отделяются двойной вертикальной чертой.
При составлении таблицы надо следить за тем, чтобы не перепутать порядок действий; заполняя столбцы, следует двигаться “изнутри наружу”, т.е. от элементарных формул к более и более сложным; столбец, заполняемый последним, содержит значения исходной формулы.
| А | В | С | А+ | · С | ||
| 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 |
Из таблицы видно, что данное высказывание истинно только в случае, когда А=0, В=1, С=1. Во всех остальных случаях оно ложно.
Во всех остальных случаях оно ложно.
1. Составим таблицу истинности для формулы , которая содержит две переменные x и y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу:
Переменные | Промежуточные логические формулы | Формула | |||||
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 1, то есть является тождественно истинной.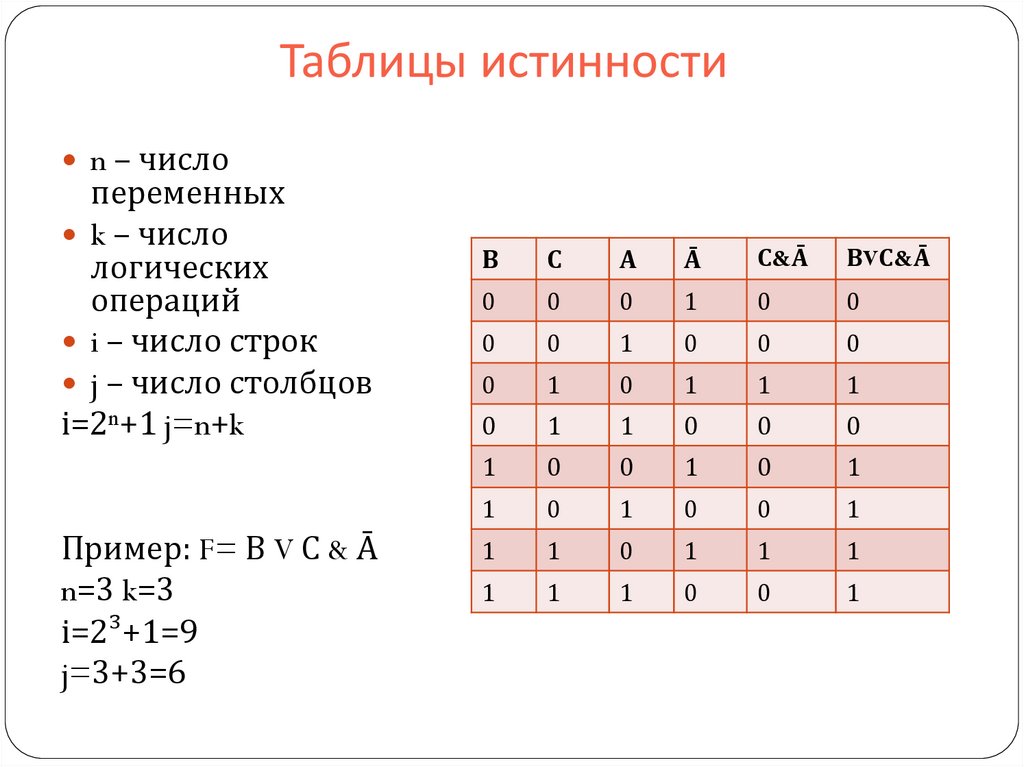
2. Таблица истинности для формулы :
Переменные | Промежуточные логические формулы | |||||
| 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Из таблицы видно, что при всех наборах значений переменных x и y формула
3. Таблица истинности для формулы :
Переменные | Промежуточные логические формулы | Формула | ||||||
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
Из таблицы видно, что формула в некоторых случаях принимает значение 1, а в некоторых — 0, то есть является 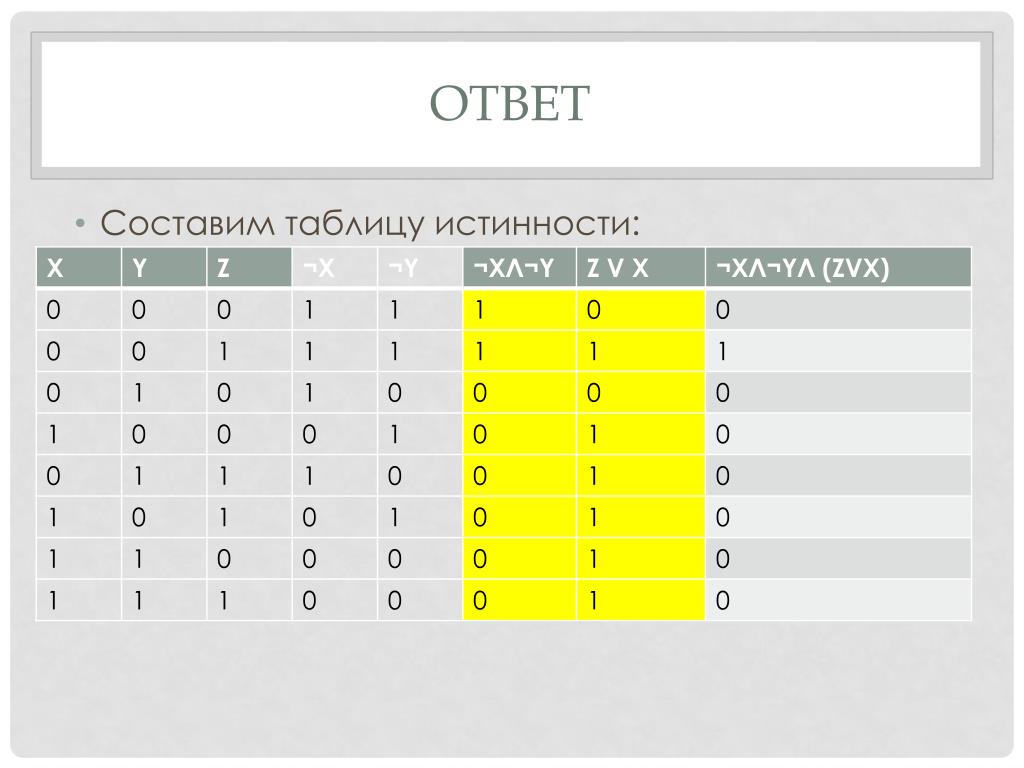
Равносильности формул логики высказываний часто называют законами логики.
Знание законов логики позволяет проверять правильность рассуждений и доказательств.
Нарушения этих законов приводят к логическим ошибкам и вытекающим из них противоречиям.
Перечислим наиболее важные из них:
| Закон | Для ИЛИ | Для И |
| Переместительный | ||
| Сочетательный | ||
| Распределительный | ||
| Правила де Моргана | ||
| Идемпотенции | ||
| Поглощения | ||
| Склеивания | ||
| Операция переменной с ее инверсией | ||
| Операция с константами | ||
| Двойного отрицания | ||
Алгоритмы и способы их описания.
Алгоритмомназывается точное и понятное предписание исполнителю совершить последовательность действий, направленных на решение поставленной задачи. Слово «алгоритм» происходит от имени математика Аль Хорезми, который сформулировал правила выполнения арифметических действий. Первоначально под алгоритмом понимали только правила выполнения четырех арифметических действий над числами. В дальнейшем это понятие стали использовать вообще для обозначения последовательности действий, приводящих к решению любой поставленной задачи. Говоря об алгоритме вычислительного процесса, необходимо понимать, что объектами, к которым применялся алгоритм, являются данные. Алгоритм решения вычислительной задачи представляет собой совокупность правил преобразования исходных данных в результатные.
Детерминированность (определенность). Предполагает получение однозначного результата вычислительного процесса при заданных исходных данных. Благодаря этому свойству процесс выполнения алгоритма носит механический характер;
Благодаря этому свойству процесс выполнения алгоритма носит механический характер;
Результативность. Указывает на наличие таких исходных данных, для которых реализуемый по заданному алгоритму вычислительный процесс должен через конечное число шагов остановиться и выдать искомый результат;
Массовость.
Дискретность. Означает расчлененность определяемого алгоритмом вычислительного процесса на отдельные этапы, возможность выполнения которых исполнителем (компьютером) не вызывает сомнений.
Алгоритм должен быть формализован по некоторым правилам посредством конкретных изобразительных средств. К ним относятся следующие способы записи алгоритмов:
· словесный,
· формульно-словесный,
· графический,
· язык операторных схем,
· алгоритмический язык.
Наибольшее распространение благодаря своей наглядности получил графический (блок-схемный) способ записи алгоритмов.
Блок-схемой называется графическое изображение логической структуры алгоритма, в котором каждый этап процесса обработки информации представляется в виде геометрических символов (блоков), имеющих определенную конфигурацию в зависимости от характера выполняемых операций.
При всем многообразии алгоритмов решения задач в них можно выделить три основных вида вычислительных процессов:
· линейный;
· ветвящийся;
· циклический.
Линейнымназывается такой вычислительный процесс, при котором все этапы решения задачи выполняются в естественном порядке следования записи этих этапов.
Ветвящимся называется такой вычислительный процесс, в котором выбор направления обработки информации зависит от исходных или промежуточных данных (от результатов проверки выполнения какого-либо логического условия).
Циклом называется многократно повторяемый участок вычислений. Вычислительный процесс, содержащий один или несколько циклов, называется циклическим. По количеству выполнения циклы делятся на циклы с определенным (заранее заданным) числом повторений и циклы с неопределенным числом повторений. Количество повторений последних зависит от соблюдения некоторого условия, задающего необходимость выполнения цикла. При этом условие может проверяться в начале цикла — тогда речь идет о цикле с предусловием, или в конце — тогда это цикл с постусловием.
| Обозначение | Описание |
| Терминатор начала и конца работы функции | Терминатором начинается и заканчивается любая функция. Тип возвращаемого значения и аргументов функции обычно указывается в комментариях к блоку терминатора. |
| Операции ввода и вывода данных | В ГОСТ определено множество символов ввода/вывода, например вывод на магнитные ленты, дисплеи и т. п. Если источник данных не принципиален, обычно используется символ параллелограмма. Подробности ввода/вывода могут быть указаны в комментариях. п. Если источник данных не принципиален, обычно используется символ параллелограмма. Подробности ввода/вывода могут быть указаны в комментариях.
|
| Выполнение операций над данными | В блоке операций обычно размещают одно или несколько (ГОСТ не запрещает) операций присваивания, не требующих вызова внешних функций. |
| Блок, иллюстрирующий ветвление алгоритма | Блок в виде ромба имеет один вход и несколько подписанных выходов. В случае, если блок имеет 2 выхода (соответствует оператору ветвления), на них подписывается результат сравнения — «да/нет». Если из блока выходит большее число линий (оператор выбора), внутри него записывается имя переменной, а на выходящих дугах — значения этой переменной. |
| Вызов внешней процедуры | Вызов внешних процедур и функций помещается в прямоугольник с дополнительными вертикальными линиями. |
| Начало и конец цикла | Символы начала и конца цикла содержат имя и условие. Условие может отсутствовать в одном из символов пары. Расположение условия, определяет тип оператора, соответствующего символам на языке высокого уровня — оператор с предусловием (while) или постусловием (do … while). Условие может отсутствовать в одном из символов пары. Расположение условия, определяет тип оператора, соответствующего символам на языке высокого уровня — оператор с предусловием (while) или постусловием (do … while).
|
| Подготовка данных | Символ «подготовка данных» в произвольной форме (в ГОСТ нет ни пояснений, ни примеров), задает входные значения. Используется обычно для задания циклов со счетчиком. |
| Соединитель | В случае, если блок-схема не умещается на лист, используется символ соединителя, отражающий переход потока управления между листами. Символ может использоваться и на одном листе, если по каким-либо причинам тянуть линию не удобно. |
| Комментарий | Комментарий может быть соединен как с одним блоком, так и группой. Группа блоков выделяется на схеме пунктирной линией. |
Логический преобразователь
Логический преобразователь
Логический преобразователь — мощное устройство,
производящее некоторые преобразования
представления схем. Он используется для
преобразования:
Он используется для
преобразования:
— схемы в таблицу истинности
— таблицы истинности в логическое выражение
— таблицы истинности в упрощенное логическое выражение
— логического выражения в таблицу истинности
— логического выражения в схему
— логического выражения в схему на базе элементов И-НЕ
Клавиши преобразования находятся на правой стороне панели логического преобразователя.
Ввод таблицы истинности
Для этого
отметьте с помощью мыши входы таблицы
истинности, необходимые для ее составления
(подведите указатель мыши к необходимому входу и
нажмите левую кнопку мыши). При этом значения
возможных состояний на входах схемы будут
заполнены автоматически. Затем поместите
указатель мыши в столбец “out” для заполнения
выходных значений схемы и нажмите левую кнопку
мыши. Введите значения выходных сигналов схемы,
соответствующих входным по таблице, причем если
таблица истинности содержит неопределенности,
то необходимо поставить символ “?”.
Введите значения выходных сигналов схемы,
соответствующих входным по таблице, причем если
таблица истинности содержит неопределенности,
то необходимо поставить символ “?”.
Преобразование схемы в таблицу истинности
Логический преобразователь может создавать таблицу истинности для схем с максимальным числом входов равным 8 и всего с одним выходом.
Присоедините входы схемы к выводам “
A”… “H” логического преобразователя. Затем присоедините выход схемы в выводу “OUT”.Далее осуществите преобразование нажатием кнопки на панели логического преобразователя.
Также вы можете редактировать или преобразовывать таблицу истинности к другим видам, используя кнопки логического преобразователя.
Преобразование таблицы истинности в логическое выражение
Для
получения логического выражения из таблицы
истинности необходимо воспользоваться этим
типом преобразования.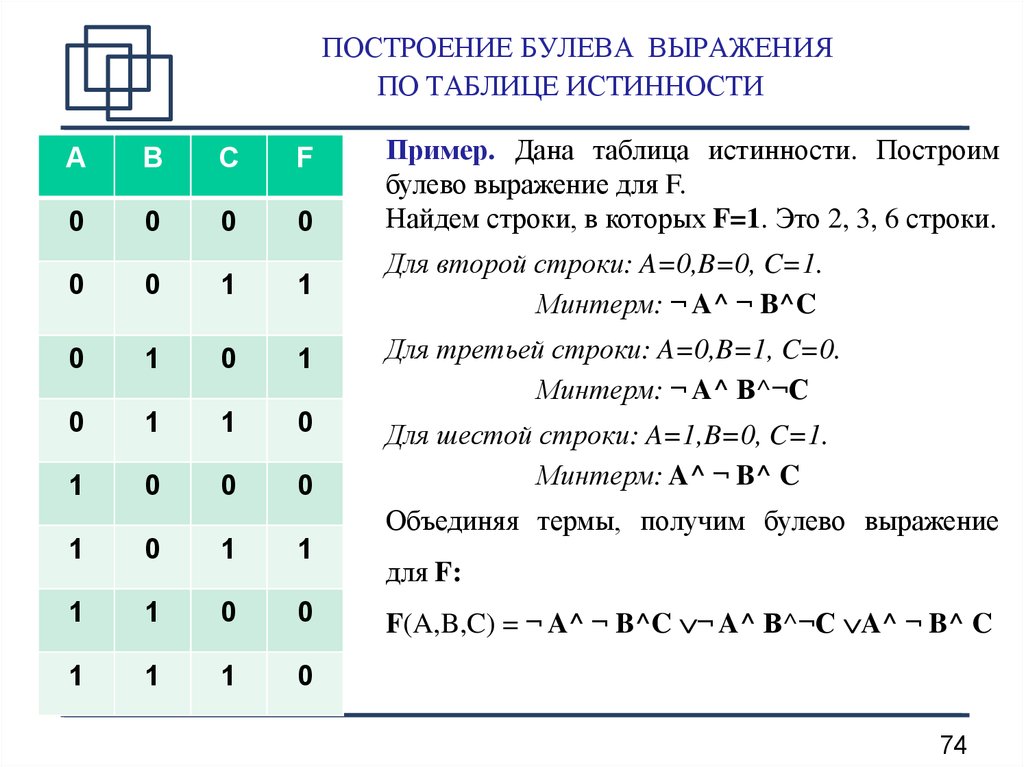 Сначала введите таблицу
истинности в рабочую область прибора. Далее
нажмите с помощью мыши кнопку на панели таблицы истинности,
соответствующую преобразованию таблицы
истинности в логическое выражение. В нижней
строке панели логического преобразователя будет
показана полученное выражение. Если выражение не
помещается полностью в отведенном для нее окне,
то просмотреть остальную ее часть можно
передвинув область просмотра выражения с
помощью указателя в правом нижнем углу панели
логического преобразователя.
Сначала введите таблицу
истинности в рабочую область прибора. Далее
нажмите с помощью мыши кнопку на панели таблицы истинности,
соответствующую преобразованию таблицы
истинности в логическое выражение. В нижней
строке панели логического преобразователя будет
показана полученное выражение. Если выражение не
помещается полностью в отведенном для нее окне,
то просмотреть остальную ее часть можно
передвинув область просмотра выражения с
помощью указателя в правом нижнем углу панели
логического преобразователя.
Далее вы можете упростить полученное логическое выражение или преобразовать его в схему.
Упрощение логического выражения
Для получения упрощенной формы записи логического выражения нажмите мышью кнопку на панели логического преобразователя.
EWB
использует метод Куайна-МакКласки (Quine-McCluskey) для упрощения логического выражения. Этот метод гарантирует
упрощение систем, имеющих большее число входов,
чем может быть просчитано вручную при помощи
карт Карно.
Этот метод гарантирует
упрощение систем, имеющих большее число входов,
чем может быть просчитано вручную при помощи
карт Карно.
Подсказка:
Логическое упрощение требует много памяти. Если ваш компьютер не имеет достаточного количества памяти, он не сможет завершить эту операцию.Преобразование логического выражения в таблицу истинности
Если
известна логическое выражение, описывающее
требуемый цифровой автомат, то получить таблицу
истинности по этому выражению можно с помощью
этой опции на панели управления прибора. Для
этого преобразования установите курсор с
помощью мыши в строку логического выражения,
нажмите левую клавишу мыши и наберите имеющееся
выражение. Входные значения обозначаются
буквами от “a” до “h” (по названиям входов
логического преобразователя). Для обозначения
инверсии сигнала используется символ “’”
после соответствующего входа.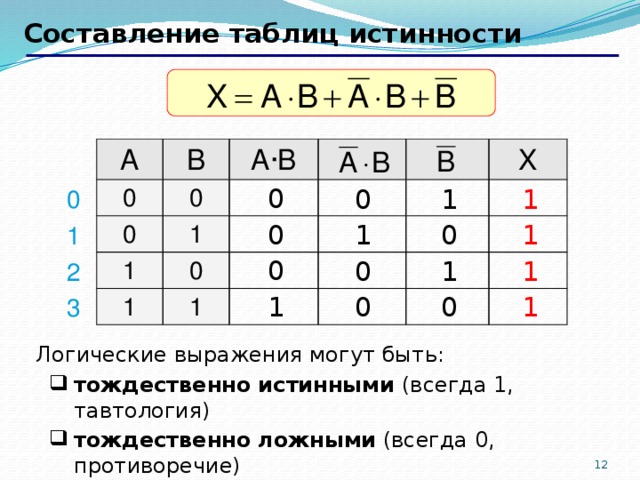 Для обозначения
инверсии группы входов эта группа записывается в
скобках и после закрывающей скобки ставится
символ “’”. Логическая операция
“&” обозначается последовательной записью
входных значений (например, “a & h” запишется как ah).
Логическая операция “E ” обозначается
символом “+”. После того как вы набрали функцию,
нажмите с помощью мыши кнопку преобразования .
Для обозначения
инверсии группы входов эта группа записывается в
скобках и после закрывающей скобки ставится
символ “’”. Логическая операция
“&” обозначается последовательной записью
входных значений (например, “a & h” запишется как ah).
Логическая операция “E ” обозначается
символом “+”. После того как вы набрали функцию,
нажмите с помощью мыши кнопку преобразования .
В поле таблицы истинности появится таблица истинности, построенная по набранному вами логическому выражению.
Для упрощения логического выражения сначала преобразуйте его в таблицу истинности, а затем упростите
Преобразование логического уравнения в схему
Данное преобразование используется для получения схемы по имеющемуся логическому выражению. Введите логическое выражение и нажмите мышью клавишу преобразования:
Логические элементы, которые составляют
введенное логическое выражение будут помещены в
рабочее пространство.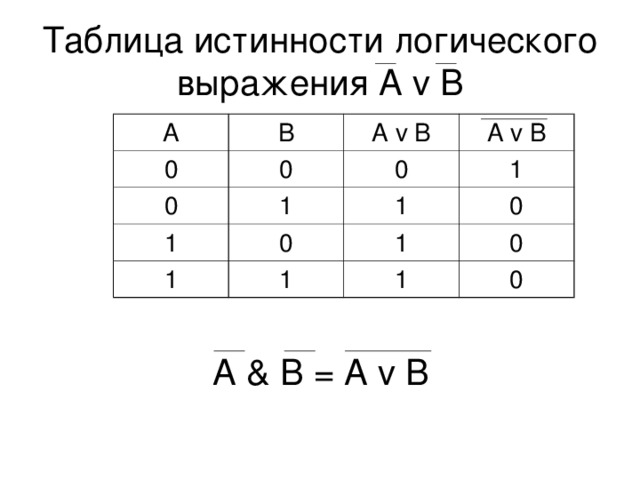 Все эти элементы будут
выделены, таким образом вы сможете перемещать их
по рабочему пространству в любое место или
скопировать и поместить их в подсхему.
Все эти элементы будут
выделены, таким образом вы сможете перемещать их
по рабочему пространству в любое место или
скопировать и поместить их в подсхему.
Подсказка:
Таким образом вы можете разрабатывать сложные схемы, например, декодеры. Создание схемы из элементов И-НЕ (NAND)Этот тип преобразования используется при необходимости получения схемы, состоящей только из логических элементов И-НЕ. Введите логическое выражение и нажмите клавишу преобразования:
Сайт создан в системе uCoz
логика — Где математики научились составлять таблицы истинности?
@ Дуг Спунвуд: Я не могу точно датировать первое использование таблиц истинности среди (профессиональных) математиков, хотя Чарльз С. Пирс и Готтлоб Фреге могли сделать хорошие приближения (неявные ссылки на известную статью, опубликованную Пирсом в 1885 г. и к «Begriffsschrift» Фреге 1879 г.). В частности, Пирс знал [около 1900-1902] о истинностно-функциональном поведении ВСЕХ [двузначных] пропозициональных связок (включая НЕ-И и НЕ-ИЛИ, обычно приписываемых Генри М. Шефферу 19).13), хотя подробностей он не публиковал при жизни: его находки остались в рукописях. В этом отношении приведенная ранее ссылка на SEP вводит в заблуждение: Людвиг Витгенштейн появляется позже (где-то в начале двадцатых годов или чуть раньше).
Пирс и Готтлоб Фреге могли сделать хорошие приближения (неявные ссылки на известную статью, опубликованную Пирсом в 1885 г. и к «Begriffsschrift» Фреге 1879 г.). В частности, Пирс знал [около 1900-1902] о истинностно-функциональном поведении ВСЕХ [двузначных] пропозициональных связок (включая НЕ-И и НЕ-ИЛИ, обычно приписываемых Генри М. Шефферу 19).13), хотя подробностей он не публиковал при жизни: его находки остались в рукописях. В этом отношении приведенная ранее ссылка на SEP вводит в заблуждение: Людвиг Витгенштейн появляется позже (где-то в начале двадцатых годов или чуть раньше).
Мы знаем, однако, достоверно, что таблицы истинности были популярны уже примерно за 21 век до Фреге и Пирса, среди философов, точнее их нашел Хрисипп Сол[о]и, около 279-206 до н.э., основатель Стоическая логика. Даже Хрисипп был основан на предыдущих открытиях философа V века до нашей эры Евклида Мегарского, бывшего ученика Сократа и основателя мегарской школы (или, что более вероятно, одного из его «мегарских» последователей).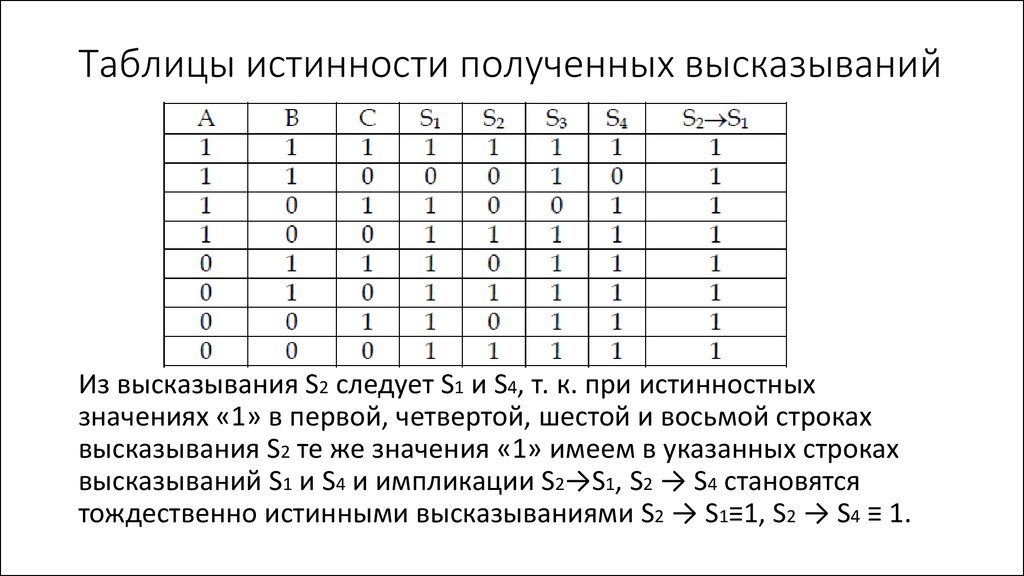 Подробнее см., например. SEP-запись о «Диалектической школе», принадлежащая Сюзанне Бобзиен, ее SEP-запись по «Древней логике» и, возможно, статьи в Википедии о мегарской школе и тому подобное.
Подробнее см., например. SEP-запись о «Диалектической школе», принадлежащая Сюзанне Бобзиен, ее SEP-запись по «Древней логике» и, возможно, статьи в Википедии о мегарской школе и тому подобное.
Между прочим, следует отметить, что, в отличие от Аристотеля и других членов платоновской Академии, Хрисипп и его последователи не особенно любили математику (в смысле того времени).
Я надеюсь опубликовать на днях длинную заметку о (наиболее правдоподобном) «математическом» методе построения так называемой «стоической логики» («логики Хрисиппа»), включая таблицу истинности вещи (как они могли понять это 22 века назад) [следите за academia.edu для потенциальных препринтов].
@ Митч, на сегодняшний день 20150323 [ответ слишком длинный, чтобы поместиться в поле для комментариев]:
> [Митч:] Вы говорите, что существуют доказательства того, что некоторые греческие философы имели концепцию функций истинности (функций, чьи входы и выходы чем-то вроде истинности и ложности) и графического представления таблиц истинности (табличного представления)? Я не сомневаюсь в первом, но я верю во второе.
Кроме того, у меня есть вопрос об интеллектуальном происхождении отображения таблицы истинности в современной математике, а не о многочисленных, возможно, не влияющих переизобретениях по всему миру. <
На первую половину вашего вопроса можно ответить утвердительно: Хрисипп и некоторые более поздние стоики «имели понятие о функциях истины», так сказать, для всех практических целей. В его/их терминах, конечно: они знали, как манипулировать функциями истинности, чтобы объяснять «семантически» сложные предложения (стоические аксиомы) в терминах простых, то есть атомарных предложений. (Вы не ожидаете, что философ второго века до нашей эры будет знаком с нашей современной — теоретико-множественной — концепцией, даже со «старомодным» доканторианским способом мышления функций в традиционной математике — скажем, функций как правил. Кроме того, как я уже говорил, стоики меньше интересовались математикой своего времени.) Так что в отношении «интеллектуального происхождения» (понятия) честь, без сомнения, принадлежит Хрисиппу.
Однако на вторую половину вопроса (о фактическом представлении истинностных назначений) нельзя ответить должным образом, главным образом потому, что у нас недостаточно (текстовых или иных исторических) свидетельств, чтобы сказать что-то определенное о. Даже молодой Рассел значительно позже, на рубеже XIX века, немного запутался в понятии «пропозициональная функция», да и Витгенштейн был не намного блестяще в этом вопросе…
Говоря современным языком, стоики, вероятно, использовали что-то эквивалентное нашим таблицам истинности (в конце концов, конкретное представление ad hoc) только для того, чтобы, так сказать, семантически оправдать свои теоретико-доказательные размышления. Хотя играть с ними приятно — в конце концов, это часть детской математики, — функционально-истинное объяснение логических связок не было центральным в их логических доктринах: стоики привыкли думать о бинарных связках (connector = syndesmos по-гречески) в термины «полярные оппозиции» (или конфликт = «маше», по-гречески; более или менее: противоречия).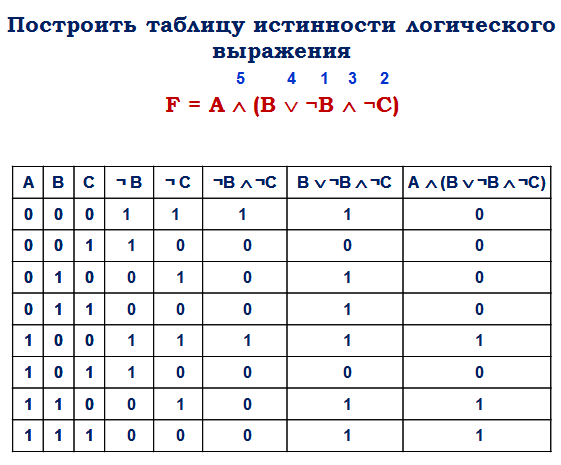
Примеры: пара сложных предложений, читающихся (А И Б, А НА И Б) на нашем жаргоне — оба засвидетельствованные, кстати, в оставшихся стоических фрагментах — составляют «полярную пару» (противоположностей), и аналогично для «полярные пары», включая IF (материальное условное выражение) и обратное ему, читая приблизительно С. На самом деле полярные противоположности IF [IF A THEN B] и SINCE [A SINCE B], соответственно, также засвидетельствованы в сохранившихся стоических фрагментах: первое читается как «A mallon he B» [«A больше, чем B»], в Греческий язык Хрисиппа — семантически = А И (НЕ В) —, в то время как полярная противоположность ТАК КАК [А ПОСКОЛЬКУ В = ЕСЛИ В, ТО А] будет читаться как «A etton he B» [«А меньше, чем В»], семантически = ( НЕ А) И Б. (Истинностно-функциональная интерпретация «маллон…» / «эттон…» была также недавно подтверждена профессором Бобзиеном, крупным специалистом по доктринам стоиков, между прочим.) Наконец, полярная пара ( A NOR B, A OR B) также исторически засвидетельствованы в позднестоических текстах. Итак, мы имеем фактически «экспрессивную полноту» (двуусловное IFF и исключающая дизъюнкция, XOR, могут быть объяснены в терминах вышеизложенного. Это также можно найти в стоических текстах!) Откуда мы знаем, что такое *(C ) — полярная противоположность С — для любого С. При этом «двойное отрицание» допускается для каждой формы (комплексного) С.
Итак, мы имеем фактически «экспрессивную полноту» (двуусловное IFF и исключающая дизъюнкция, XOR, могут быть объяснены в терминах вышеизложенного. Это также можно найти в стоических текстах!) Откуда мы знаем, что такое *(C ) — полярная противоположность С — для любого С. При этом «двойное отрицание» допускается для каждой формы (комплексного) С.
Чтобы предвосхитить более длинное (техническое) примечание, обещанное ранее: Когда полярный трюк хорошо понят, становится относительно ясно, как строить противоречивые последовательности предложений (elenchoi, или опровержения по-гречески) формы A_1, …, A_n || — Falsum, в духе стоиков, такой, что действительное следствие (силлогизмы), A_1, …, A_n ||- C, может быть объяснено в терминах … ||- Falsum by:
A_1, …, A_n ||- C тогда и только тогда, когда A_1, …, A_n, *(C) ||- Falsum,
, где Falsum — произвольное ложное суждение, а *(C) — полная противоположность C.
По этому плану — учитывая тот факт, что мы можем систематически анализировать сложные *(C) на их «полярные» компоненты — относительно легко получить что-то очень похожее на систему «естественной дедукции» Генцена, соотв. резолюция/таблоподобная система (а-ля Хинтикка, Бет, Смаллиан и т. д.) для классической (то есть хрисипповской) логики!
резолюция/таблоподобная система (а-ля Хинтикка, Бет, Смаллиан и т. д.) для классической (то есть хрисипповской) логики!
Ну, я не буду заходить так далеко, чтобы утверждать, что Хрисипп доказал полноту своей логики (= классической логики) по отношению к предполагаемому описанию классических связок в терминах таблиц истинности 22 века назад, но во всяком случае, он был довольно близок к этому!
Таблицы истинности для последовательностей
Таблицы истинности для последовательностейМы также можем построить таблицу истинности для всей секвенции. Процедура точно такая же мы только что сделали, за исключением того, что мы начинаем с нескольких столбцов справа: по одному для каждой предпосылки и один для заключения. Вот простой пример:
Последовательность:(P v Q) → R, ~R |- ~Q
Начать с колонн под помещения и вывод:
| (P v Q) → R | ~R | |- ~Q |
|---|---|---|
Разложить wffs:
| Q | (P v Q) → R | ~ R | |- Q |
|---|---|---|---|
| Q | R | (P v Q) → R | ~R | |- ~Q |
|---|---|---|---|---|
| Вопрос | R | (P v Q) | (P v Q) → R | ~R | |- ~Q |
|---|---|---|---|---|---|
| P | Q | R | (P v Q) | (P v Q) → R | ~R | |- ~Q |
|---|---|---|---|---|---|---|
Разбери комбинации (букв в предложении три, поэтому нам понадобится 2 × 2 × 2 = 8 рядов)
| P | Q | R | (P v Q) | (P v Q) → R | ~R | |- ~Q |
|---|---|---|---|---|---|---|
| T | T | T | ||||
| T | T | F | ||||
| T | F | T | ||||
| T | F | F | ||||
| F | T | T | ||||
| F9 | ||||||
| F9 | ||||||
| F | ||||||
| F | ||||||
| F | ||||||
| 0194 T | F | |||||
| F | F | T | ||||
| F | F | F |
Вычислить:
| Р | Q | R | (P v Q) | (P v Q) → R | ~R | |- ~Q |
|---|---|---|---|---|---|---|
| T | T | T | T | T | F | F |
| T | T | F | T | F | T | F |
| T | F | T | T | T | F | T |
| T | F | F | T | F | T | T |
| F | T | T | T | T | F | F |
| F | T | F | T | F | T | F |
| F | F | T | F | T | F | T |
| F | F | F | F | T | T | T |
Теперь изучите значения истинности для двух предпосылок и заключения в каждой из них.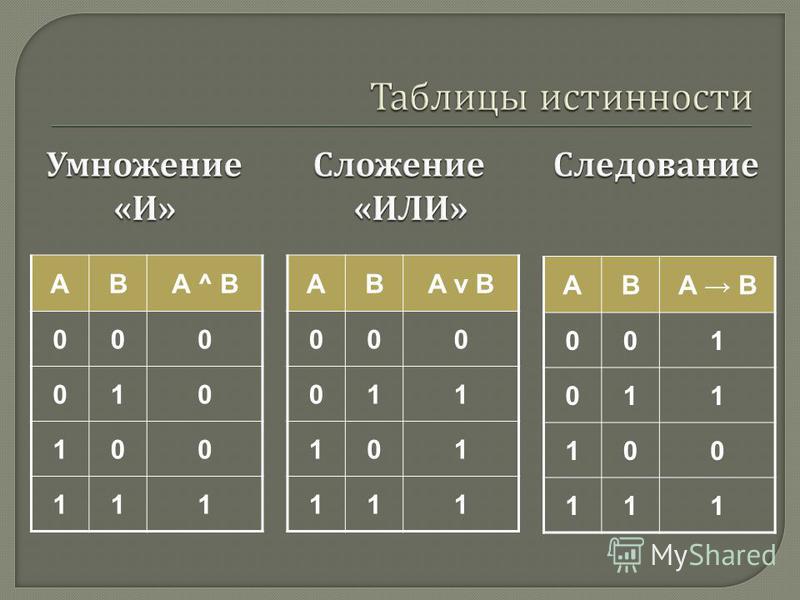 ряд. Есть ли ряд, в котором заключение ложно, а посылки верны?
ряд. Есть ли ряд, в котором заключение ложно, а посылки верны?
| Premise 1 | Premise 2 | Conclusion | ||||
|---|---|---|---|---|---|---|
| P | Q | R | (P v Q) | (P v Q) → R | ~R | | — ~Q |
| T | T | T | T | T | F | F |
| T | T | F | T | F | T | F |
| T | F | T | T | T | F | T |
| T | F | F | T | F | T | T |
| F | T | T | T | T | F | F |
| F | T | F | T | F | T | F |
| F | F | T | F | T | F | T |
| F | F | F | F | T | T | T |
In fact, there isn’t.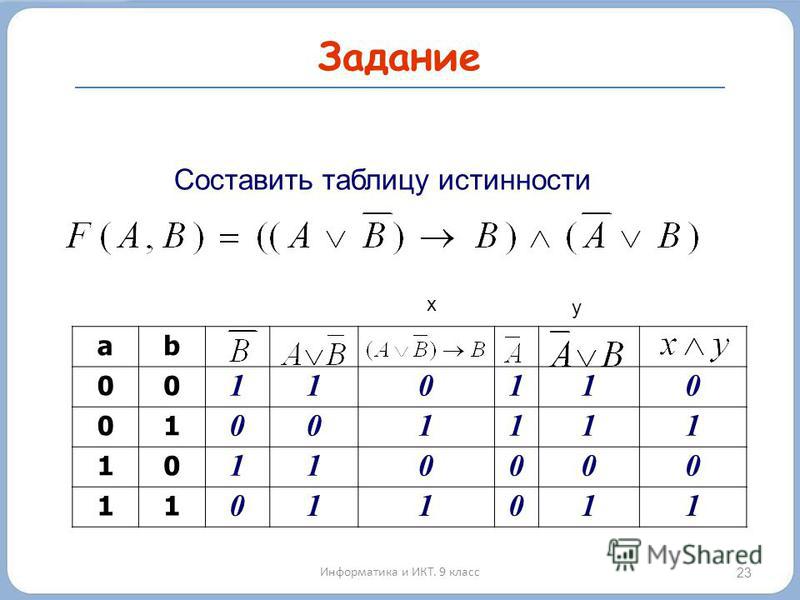 Есть четыре строки, в которых заключение
ложно (отмечено красным), но в каждом случае хотя бы одна посылка также ложна.
Есть один случай, когда обе посылки верны (отмечены желтым), но
в этом случае вывод также верен. Итак, можно сказать, что в этом
аргумент, посылки не могут быть истинными, а вывод
одновременно и ложно. Следовательно, этот аргумент действителен.
Есть четыре строки, в которых заключение
ложно (отмечено красным), но в каждом случае хотя бы одна посылка также ложна.
Есть один случай, когда обе посылки верны (отмечены желтым), но
в этом случае вывод также верен. Итак, можно сказать, что в этом
аргумент, посылки не могут быть истинными, а вывод
одновременно и ложно. Следовательно, этот аргумент действителен.
Теперь рассмотрим недопустимый аргумент:
P v Q, Q → S, T |- S и T
| P | Q | S | T | P v Q | Q → S | T | |- S & T | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T | T | T | T | T | Т | Т | Т | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Т | Т | Т | F | T | T | F | F | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| T | T | F | T | T | F | T | F | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| T | T | F | F | T | F | F | F | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| T | F | T | T | T | T | T | T | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| T | F | T | F | T | T | F | F | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| T | F | F | T | T | T | T | F | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| T | F | F | F | T | T | F | F | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| F | T | T | T | T | T | T | T | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| F | T | T | F | T | T | F | F | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| F | T | F | T | T | F | T | F | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| F | T | F | F | T | F | F | F | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| F | F | T | T | F | T | T | T | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| F | F | T | F | F | T | F | F | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| F | F | F | T | F | T | T | F | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| F | F | F | F | F | T | F | 9.
| P | Q | S | T | P v Q | Q → S | T | |- S & T | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T | T | T | T | T | T | T | T | ||||||
| T | T | T | F | T | T | F | F | ||||||
| T | T | F | T | Т | F | T | F | ||||||
| T | T | F | F | T | F | F | F | ||||||
| T | F | T | T | T | T | T | T | ||||||
| T | F | T | F | T | T | F | F | ||||||
| T | F | F | T | T | T | T | F | ||||||
| T | F | F | F | ||||||||||
| F | T | T | T | . | F | T | |||||||
| F | T | F | F | ||||||||||
| F | F | T | T | ||||||||||
| F | F | T | F | ||||||||||
| F | F | F | T | ||||||||||
| F | F | F | F |
We can use это для разработки сокращенного теста таблицы истинности с помощью
пытаясь работать в обратном направлении от предположения, что аргумент
недействителен. Возьмем тот же пример, предположим, что он действительно имел
посылки и ложный вывод. Мы можем представить это, начав
из «таблицы истинности» с справа сбоку сначала заполняется:
Возьмем тот же пример, предположим, что он действительно имел
посылки и ложный вывод. Мы можем представить это, начав
из «таблицы истинности» с справа сбоку сначала заполняется:
| P | Q | S | T | P v Q | Q → S | T | |- S & T |
|---|---|---|---|---|---|---|---|
| T | T | T | T | F |
Что мы можем добавить к этому? Во-первых, если S & T ложно, а T истинно, тогда S должно быть ложным:
| П | В | S | T | P v Q | Q → S | T | |- S & T |
|---|---|---|---|---|---|---|---|
| F | T | T | T | T | F |
Далее, если Q → S истинно, а S ложно, то Q должно быть ложным:
| P | Q | S | T | P v Q | Q → S | T | |- S & T | 89F | F | T | T | T | T | F |
|---|
| P | Q | S | T | P V Q | Q → S | T | |- S & T |
|---|---|---|---|---|---|---|---|
| 8 | |- S & T | ||||||
| | | Т | Т | Ж |
В данном случае мы выяснили единственно возможную комбинацию правды
значения для букв предложения в этих wffs, которые делают вывод
ложь и посылки истинны: P = T , Q = F , S = F , и
Т = Т .
Что произойдет, если мы попробуем этот метод с допустимым аргументом? Первый, давайте обратим внимание на разницу между тем, что нужно, чтобы показать, что аргумент действителен и что нужно, чтобы показать, что он недействителен:
Чтобы показать, что аргумент недействителен, нам нужно только найти одну строку его таблицы истинности, в которой посылки истинны, а вывод ложный.
Чтобы показать, что аргумент действителен, нам нужно показать, что нет строки его таблицы истинности, в которой посылки верны и вывод неверный.
Важным отличием является то, что как только мы нашли одну строку с истинными посылками и ложным заключением мы можем остановиться (поскольку мы знаем что аргумент недействителен), но для того, чтобы доказать, что он действителен нам придется проверить каждую строку .
В качестве примечания: вы можете подумать, что причина, подтверждающая аргумент, действительна.


 Кроме того, у меня есть вопрос об интеллектуальном происхождении отображения таблицы истинности в современной математике, а не о многочисленных, возможно, не влияющих переизобретениях по всему миру. <
Кроме того, у меня есть вопрос об интеллектуальном происхождении отображения таблицы истинности в современной математике, а не о многочисленных, возможно, не влияющих переизобретениях по всему миру. < 9 29 29 29 29 2. заключение
ЛОЖЬ. Следовательно, этот аргумент недействителен. Неважно, сколько
такие строки есть до тех пор, пока есть хотя бы одна: если есть в
хотя бы одна строка, в которой посылки верны, а заключение ложно ,
тогда аргумент недействителен.
9 29 29 29 29 2. заключение
ЛОЖЬ. Следовательно, этот аргумент недействителен. Неважно, сколько
такие строки есть до тех пор, пока есть хотя бы одна: если есть в
хотя бы одна строка, в которой посылки верны, а заключение ложно ,
тогда аргумент недействителен.
 0389 T
0389 T