5.11. Вывод закона Ома

16

Постоянный ток Н. Ф. Шемяков

___________________________________________________________________________________________________________________

Лекция 8

5.10. Классическая теория электропроводности металлов

На основании ряда экспериментальных данных, полученных учеными Рикке, Мандельштамом и Папалекси, Толменом и Стюартом в начале XX в. было установлено, что носителями тока в металлах являются электроны.

Некоторые свойства электрона были описаны Томсоном в 1895-97 гг.

Большая концентрация электронов в металлах (n_o  10²⁸ — 10²⁹ м^3) обуславливает в них высокую тепло- и электопроводимость. Позднее была создана классическая теория электропроводности металлов

Друде—Лоренца.

В основу теории были положены выводы классической молекулярно-кинетической теории, в которой электроны проводимости рассматриваются как электронный газ и его свойства подобны свойствам одноатомного, идеального газа. Число свободных электронов равно примерно числу атомов.

Согласно классической электронной теории проводимости металлов в отсутствии электрического поля в них электроны проводимости (электронный газ) находятся в состоянии теплового хаотического движения в кристаллической решетке, образованной положительно заряженными ионами.

Ионы совершают тепловые колебания около положений равновесия — узлов кристаллической решетки. При своем движении электроны испытывают столкновения с ионами. Длина свободного пробега электронов , т. е. по порядку равна периоду кристаллической решетки. В соответствии с выводами молекулярно-кинетической теории средняя кинетическая энергия теплового движения электронов ,

где m — масса электрона; v_кв — средняя квадратичная скорость теплового движения. Например, при температуре Т = 273 К, v_кв  10⁵ м/c.

При создании электрического поля в металлических проводниках возникает электрический ток, плотность которого

, (5.38)

где n₀ — концентрация электронов; q_e — заряд электрона; v — средняя скорость упорядоченного движения. Электроны имеют скорость v = <u> + v.

Следовательно, под действием напряженности электрического поля электроны в проводнике приходят в упорядоченное движение в направлении противоположном вектору напряженности электрического поля.

При максимально допустимой плотности тока в металлах cредняя скорость упорядоченного движения v  10

³ м/c, т. е. v  u, что объясняется малым значением средней длины свободного пробега электрона между двумя последовательными столкновениями его с ионами.

По классической теории проводимости металлов при соударении электрона с ионом он полностью теряет свою скорость.

Уравнение движения электрона в электрическом поле в процессе свободного пробега является равноускоренным.

Поэтому на основании второго закона Ньютона

F = ma = m,

где F = q_eE; Е — напряженность электрического поля.

Средняя скорость упорядоченного движения

v =.

Если средняя продолжительность времени свободного пробега t, то после интегрирования

F = ma = m

получим, что v_мах =

или

v =. (5.39)

Если u всех электронов одинаковы, но v  u, найдем среднее время пробега электрона

.

С учетом этого формулу (5.39) перепишем в виде:

. (5.40)

Следовательно, плотность тока

, (5.41)

где (5.42)

— удельная электропроводимость проводника.

Таким образом, на основании классической теории проводимости металлов был теоретически получен закон Ома в дифференциальной форме

j =  E.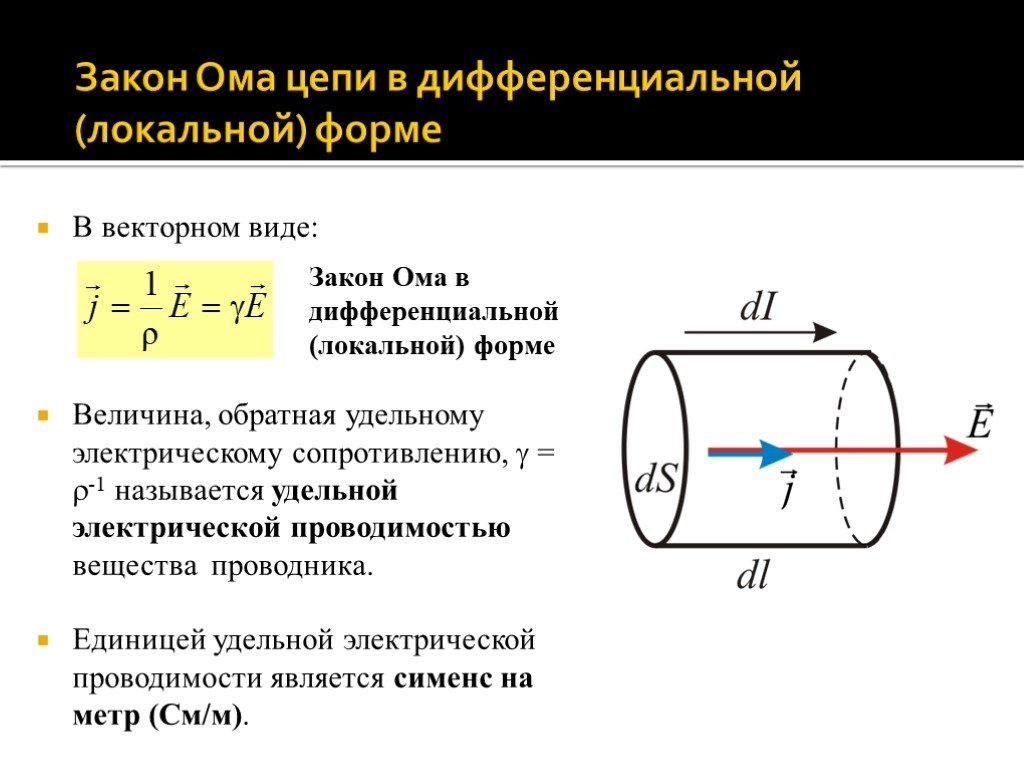

После соударения электрона с ионами кристаллической решетки его энергия упорядоченного движения переходит во внутреннюю энергию, что приводит к нагреванию проводника.

Под действием электрического поля за время свободного пробега электрон увеличивает свою кинетическую энергию на величину

. (5.43)

Из-за теплового хаотического движения электронов, их средняя кинетическая энергия

. (5.44)

В единице объема проводника содержится n₀ электронов, причем ежесекундно каждый из них испытывает в среднем число столкновений с ионами

. (5.45)

Энергия электрического тока, которая преобразуется во внутреннюю энергию за 1 с в единице объема, называется объемной плотностью тепловой мощности

, (5.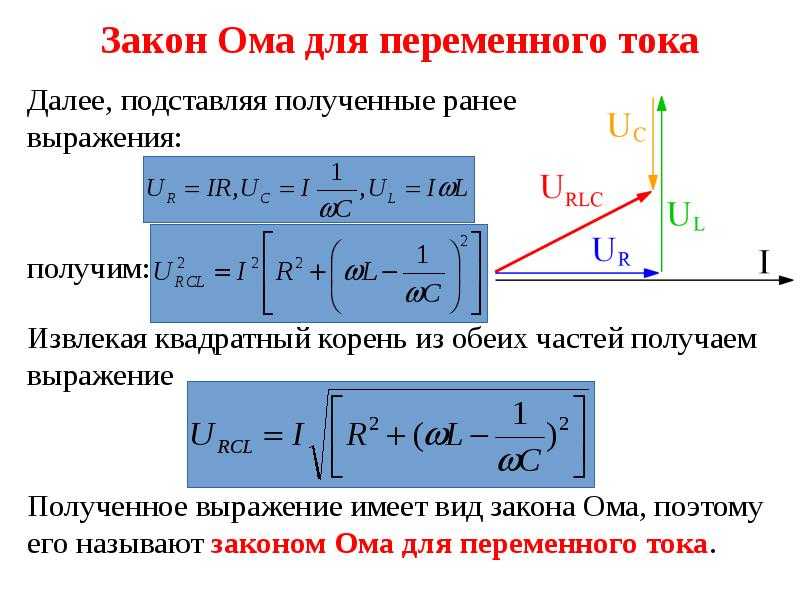 46)

где

v_мах = 2v.

Используя формулу (5.39) и

окончательно получим

(5.47)

или

w = E².

Последняя формула выражает закон Джоуля-Ленца в дифференциальной форме, т. е.

. (5.48)

Вывод законов Ома и Джоуля—Ленца в классической электронной теории — Студопедия

Поделись  

Важнейшей задачей классической электронной теории проводимости металлов является теоретический вывод основных законов электрического тока — законов Ома и Джоуля-Ленца, установленных опытным путем. Рассмотрим вывод этих законов.

1. Предположим, что при соударениях с узлами кристаллической решетки электроны полностью теряют скорость упорядоченного движения, которую они приобретают под действием внешнего электрического поля за время t свободного пробега. В процессе свободного пробега электроны движутся равноускоренно. Поэтому средняя скорость упорядоченного движения электронов равна:

где _макс—среднее значение максимальной скорости, приобретаемой электроном под действием электрического поля за время свободного пробега.

Пусть т—масса электрона, е—его заряд и Е—напряженность стационарного электрического поля в проводнике. Тогда уравнение движения электрона имеет следующий вид

Интегрируя это уравнение по v от 0 до v

макс и по t от 0 до t(t — средняя продолжительность свободного пробега электрона), получаем:

(20.24)

и

. (20.25)

Среднее время свободного пробега электронов можно выразить через среднюю длину свободного пробега и среднюю скорость движения электронов относительно кристаллической решетки проводника. Эта скорость равна сумме средней скорости их теплового движения и средней скорости и упорядоченного движения. Поэтому

Выше было показано, что . Поэтому в предыдущей формуле величиной по сравнению с можно пренебречь

Подставим значение в формулу (20.25):

(20.25`)

Заменив в (20.24) его выражением из(20.25`), получим:

. (20.26)

Величина

называетсяудельной электропроводностью, а обратная ей величина — удельным сопротивлением проводника.

Следовательно,

(20.27)

Формула (20.27) совпадает с (20.12) и выражаетзакон Ома в дифференциальной форме для плотности тока:

плотность тока в проводнике равна произведению удельной проводимости проводника на напряженность электрического поля.

Векторы Е и j имеют одинаковое направление. Поэтому закон Ома можно записать также в векторной форме (20.12).

2. Рассмотрим превращение энергии, происходящее при соударениях электронов проводимости с узлами кристаллической решетки. В конце свободного пробега каждый электрон теряет скорость упорядоченного движения. Средняя энергия, передаваемая при этом электроном тому иону, с которым он столкнулся, равна . За единицу времени электрон в среднем претерпевает столкновений с узлами решетки, причем

(20.28)

Все п_о электронов проводимости, находящихся в единице объема проводника, испытывают столкновений в единицу времени и передают узлам решетки металла энергию, которая идет на увеличение теплового движения ионов металла, т. е. на нагревание проводника

(20.29)

Подставив в (20.29) выражения для из (20.28) и из (20.24), получим величину энергии, которая передается ионам решетки в единице объема проводника за единицу времени:

(20.30)

Эта величина по своему физическому смыслу являетсяплотностью тепловой мощности тока,рассмотренная нами в уравнении (20.17).

Коэффициент есть не что иное, как удельная электропроводность

металла, поэтому (20.30) можно записать в следующем виде:

. (20.31)

Формула (20.31) представляет математическое выражениезакона Джоуля—Ленца для плотности тепловой мощности тока:

плотность тепловой мощности тока в проводнике равна произведению его удельной электропроводности на квадрат напряженности электрического поля,

и совпадает с ранее полученным выражением (20.19) дифференциальной формы закона.

В приведенных выше выводах законов Ома и Джоуля—Ленца мы предполагали, что при соударениях электронов с узлами кристаллической решетки электроны полностью теряют скорость упорядоченного движения. Г. Лоренц показал, что это предположение несущественно. К тем же результатам можно прийти, считая, что соударения электронов с узлами решетки являются абсолютно упругими.



электромагнетизм — Вывод закона Ома

спросил 10 лет, 2 месяца назад

Изменено 2 года, 8 месяцев назад

Просмотрено 7к раз

$\begingroup$

Можно ли вывести закон Ома (возможно, в каком-то соответствующем пределе) из уравнений Максвелла?

• электромагнетизм
• электрические цепи
• физика твердого тела
• электрический ток
• электрическое сопротивление

$\endgroup$

1

$\begingroup$

Закон Ома $\vec\jmath=\sigma\vec{E}$ может быть строго выведен в пределе малых электрических полей с использованием теории линейного отклика. Это приводит к формуле Кубо для электропроводности, которая связывает $\sigma$ с пределом нулевой частоты корреляционной функции запаздывающий ток-ток. 9\beta(-\omega,-q)]\rangle \right\} $$

(Конечно, этот вывод включает в себя больше, чем просто уравнение Максвелла. Оно правильно выводится в контексте неравновесной теории поля.) Модель Друде представляет собой модель спектральной функции корреляционной функции ток-ток. с точки зрения одного «времени столкновения». Эта модель может быть получена в рамках кинетической теории, которая применима, когда взаимодействия слабые, а корреляционная функция может быть вычислена в терминах квазичастиц.

$\endgroup$

3

$\begingroup$

Нет, не так, как вы, вероятно, думаете. Вы можете многое сделать с уравнениями Максвелла, но вам придется выйти за их пределы, чтобы вывести закон Ома. Существует тривиальное отношение, идущее от точек к макроскопическим объектам (например, умножение на длины и площади поперечного сечения), но это просто дает разные формы того, что до сих пор называют законом Ома.

Как я указал в комментарии к принятому в настоящее время ответу Томаса, я думаю, что решение Кубо неявно предполагает (, т.е. , не выводится с нуля) линейную зависимость между током и полем. Это уже выходит за рамки законов Максвелла.

Полный ответ требует большего. См. , например , Riess (2004). Вот почему я говорю, что нет — правильный ответ на ваш фактический вопрос.

Важно отметить, что я не думаю, что оригинальная статья Кубо по этому вопросу пытается вычислить какие-либо фактические значения $\sigma.$ Таким образом, Кубо не вывел ни один из аспектов закона Ома. Скорее, формализм Кубо позволяет вычислять $\sigma$, предполагая существование линейной зависимости.

По этим причинам я бы возражал против использования Томасом фразы «выведено строго» при описании вклада Кубо в том виде, как он описан. Это также частично, почему я думаю, что мой собственный ответ стоит представить. (Меня несколько беспокоит использование этой фразы в этом контексте, особенно если я также говорю, что проблемная модель Друде также дает это, как будто это тривиальное уравнение для вывода или что-то в этом роде.)

$\endgroup$

$\begingroup$

Нет, это приближение, а не выведенное из первых принципов. Он основан на эмпирических наблюдениях.

$\endgroup$

2

$\begingroup$

Я добавил этот ответ, потому что в некоторых комментариях к этому и другим подобным вопросам (помеченным как повторяющиеся) запрашивались дополнительные подробности квантово-механического вывода закона Ома.

Приведенный здесь вывод подходит для квантовой механики одиночных частиц и пытается вывести закон Ома в форме: $$ j_i = \sigma_{ij}E_j\;, $$ где $j_i$ — i-я компонента тока (плотность), E_j — j-я компонента электрического поля, а $\sigma_{ij}$ — проводимость (тензор). {-iH_0t}\;. $$ 9I_j(t’),p_i]|0\rangle\;. $$

Эта специфическая связь между j и E также основана на предположении об отсутствии тока в невозмущенном основном состоянии $|0\rangle$.

$\endgroup$

$\begingroup$

Сначала имеем следующее уравнение, полученное из определяющих соотношений:

$$\vec{J}=\sigma(\vec{r},t)*\vec{E}$$

что сигма постоянна во всей среде и не является временно дисперсионной. Поэтому оператор свертки эквивалентен умножению. 92_{1}\vec{E}\cdot\vec{dl} ==> V=E \cdot l$$

Предыдущее соотношение ( $V=E \cdot l$ ) справедливо, только если электрическое поле константа вдоль кривой l . Поэтому мы будем применять то приближение, которое выполняется в материалах с малыми потерями, т. е. диэлектрическую проницаемость $\epsilon$ не является временно дисперсионным и постоянным во всей среде $\epsilon(\vec{r},t)\cong\epsilon$.

Наконец, мы можем вывести закон Ома как:

$$\int\vec{J}\cdot\vec{dS} = \int\sigma\cdot\vec{E}\cdot\vec{dS} == > I = \int\sigma\cdot\frac{V}{l}\cdot dS = \sigma \cdot \frac{V}{l}\cdot S$$

$$V=I\cdot R$$ $$R= \frac{1}{\sigma} \cdot \frac{l}{S}$$ $$Resistivity=\rho= \frac{1}{\sigma}$$

Напоминание: Диэлектрическая проницаемость среды $\epsilon$ должна быть постоянной и временно не рассеивается. Это условие выполняется в подавляющем большинстве материалов проводников.

$\endgroup$

3

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

(1) Закон Ома и его выводы(2) Дрейфовая скорость свободных электронов и ее связь с током $I = neA{v_d}$

Ответ

Проверено

229.2k+ просмотров

Подсказка Закон Ома объясняет связь между разностью потенциалов и током. Нам нужно вывести выражение для этого отношения. Свободные электроны имеют дрейфовую скорость, и мы также должны вывести связь между дрейфовой скоростью электронов и током.

Полный пошаговый ответ:
Джордж Саймон Ом установил связь между разностью потенциалов на проводнике и током, протекающим по проводнику. Этот закон называется законом Ома.
Согласно закону Ома, при постоянной температуре ток, протекающий по проводнику, будет прямо пропорционален разности потенциалов между концами проводника.
Примем разность потенциалов равной $V$
Пусть ток через проводник равен $I$
По закону Ома $V$ и $I$ прямо пропорциональны
Т. е.
$V \propto I$
Мы можем изменить знак пропорциональности на знак равенства, умножив на константу пропорциональности.
Следовательно, мы можем написать,
$V = IR$
Где константа пропорциональности $R$ известна как сопротивление проводника. Единицей сопротивления является Ом $\left( \Omega \right)$
Дрейфовая скорость электронов.
Средняя скорость, с которой дрейфуют свободные электроны под действием электрического поля, называется скоростью дрейфа.
Скорость дрейфа можно обозначить как ${v_d}$.
Связь между течением и скоростью дрейфа может быть получена следующим образом:
Рассмотрим проводник длиной $l$ и площадью поперечного сечения $A$. Пусть число свободных электронов в единице объема равно $n$. ${v_d}$ — скорость дрейфа.
Ток, протекающий через проводник за секунду, можно записать в виде:
$I = \dfrac{q}{t}$
Пусть $N$ — общее число электронов, а $e$ — заряд электрона. .
Тогда мы можем записать полный заряд $q$ в виде $q = Ne$
Тогда $I = \dfrac{{Ne}}{t}$
Объем проводника можно записать в виде
$V = Al $
Где $A$ — площадь проводника, а $l$ — длина проводника.
Количество электронов в единице объема будет
$n = \dfrac{N}{{Al}}$
Отсюда можно написать:
$N = nAl$
Подставив это значение в уравнение тока, получим
$I = \dfrac{{nAle}}{t}$
Пусть число зарядов, пересекающих любой крест -сечением в одну секунду будут электроны, содержащиеся на длине, равной дрейфовой скорости проводника.
т.е.
$l = {v_d}t$
Подставив это значение в приведенное выше уравнение для тока, получим
$I = \dfrac{{nA{v_d}te}}{t} = nAe{v_d}$

Примечание
Закон Ома действует только тогда, когда по проводнику течет постоянный ток. По закону Ома график, соединяющий напряжение и ток, будет представлять собой прямую линию. Подвижность можно определить как скорость дрейфа на единицу электрического поля. Это положительная величина.

Недавно обновленные страницы

Большинство эубактериальных антибиотиков получены из биологии ризобия класса 12 NEET_UG

Биоинсектициды саламин были извлечены из класса 12 Biology NEET_UG

Какое из следующих утверждений, касающихся Baculovirus, NEET_UG

.