массивы — Как сложить два разных, по размеру, вектора в R

Вопрос задан 2 года 4 месяца назад

Изменён 2 года 4 месяца назад

Просмотрен 486 раз

Допустим есть вектора:

a <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
b <- c(1, 2, 3, 4)

Как сложить все элементы из a с элементами b циклично, чтобы на выходе был вот такой результат:

2, 4, 6, 8, 6, 8, 10, 12, 10, 12

Если можно срезами, то было бы замечательно

• массивы
• r
• вектор

для сложения двух векторов (любой длины) служит оператор +:

> rep(1, 8) + 1:4
[1] 2 3 4 5 2 3 4 5

в случае, когда длина большего вектора не кратна длине меньшего, вдобавок к результату получаем предупреждение:

> rep(1, 10) + 1:4
 [1] 2 3 4 5 2 3 4 5 2 3
Warning message:
In rep(1, 10) + 1:4 :
  longer object length is not a multiple of shorter object length

при желании вывод предупреждения можно подавить, например, с помощью функции suppressWarnings():

> suppressWarnings(rep(1, 10) + 1:4)
 [1] 2 3 4 5 2 3 4 5 2 3

я бы делал так:

a <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
b <- c(1, 2, 3, 4)
a+rep(b, ceiling(length(a)/length(b)))[1:length(a)]
 [1]  2  4  6  8  6  8 10 12 10 12

1

чтобы сложить надо использовать плюс a+b

https://ideone. com/rVcBu9

a <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
b <- c(1, 2, 3, 4)
print(a+b)

2

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

в чем оно состоит, примеры решения задач

Основные понятия

Определение 1

Направленный вектор — это отрезок, для которого указано, какая из его граничных точек является началом, а какая концом.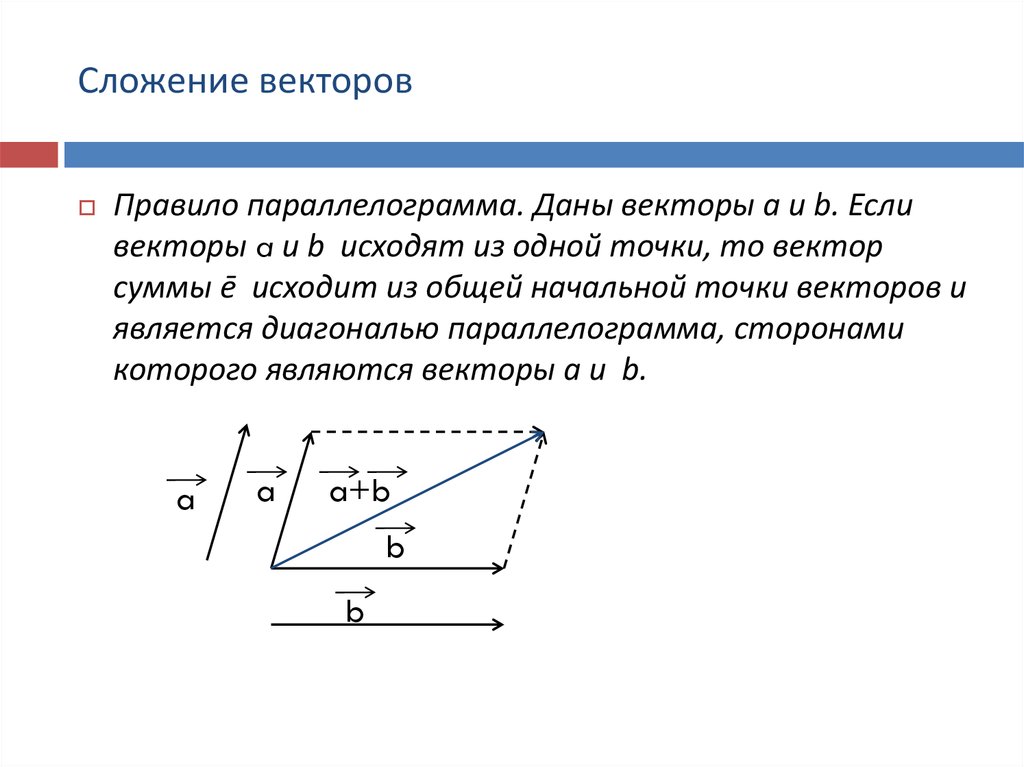

Обозначается следующим образом:

 

Коллинеарность векторов означает: ненулевые векторы, которые лежат на одной прямой или на параллельных прямых. Нулевой вектор (вектор нулевой длины) является коллинеарным любому вектору.

Определение 2

Сонаправленные векторы — векторы, направленные в одну сторону.

Определение 3

Противонаправленные векторы — векторы, направленные в разные стороны.

 

Определение 4

Равные векторы — векторы, которые коллинеарны, сонаправлены и имеют одинаковую длину.

Формулировка компланарности векторов: векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.

Три вектора, среди которых имеются два коллинеарных, также компланарны.

Некомпланарный вектор не имеет равный ему вектор, лежащий в одной плоскости.

Складывать векторы можно несколькими способами. Мы рассмотрим сложение векторов методом параллелограмма.

Сложение векторов по правилу параллелограмма

Чтобы получить сумму двух векторов, нужно из произвольной точки отложить эти векторы и построить на них параллелограмм.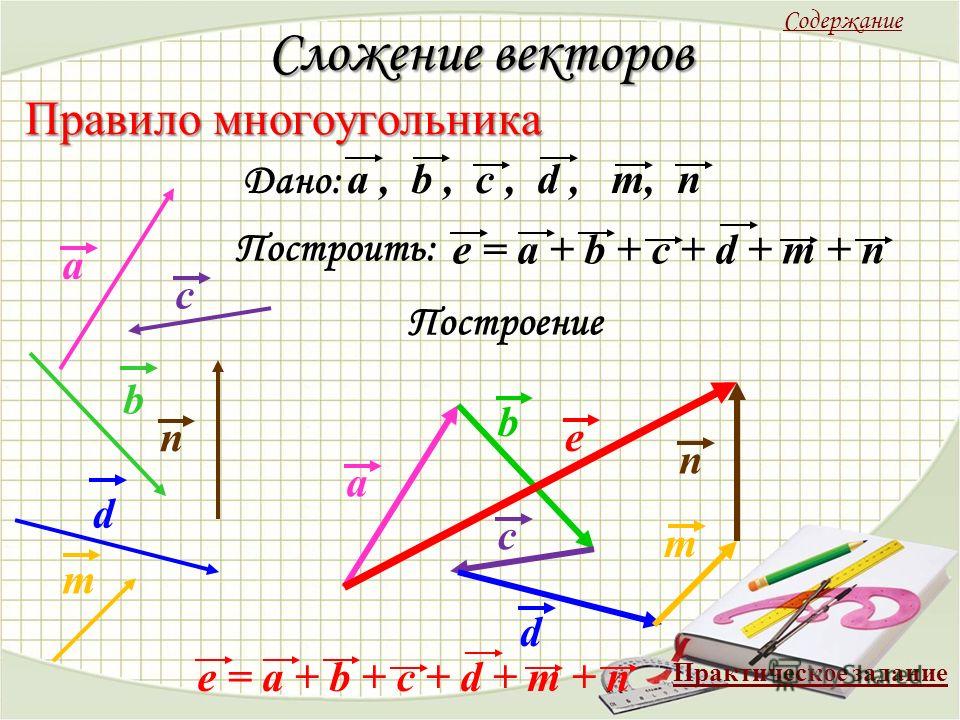 Диагональ параллелограмма, исходящая из этой точки, и будет суммой векторов.

На рисунке все наглядно проиллюстрировано.

сочетательный закон:

 

Из произвольной точки А отложим вектор , прибавим к нему вектор , получим их сумму . К этой сумме прибавим вектор , получим результат:

 

В правой части выражения мы сначала получили сумму векторов , после прибавили ее к вектору  и получили результат: 

Таким образом, мы провели доказательство сочетательного закона сложения векторов.

Когда векторы расположены в пространстве и они не компланарны, для их сложения применяется правило параллелепипеда.

Для начала проводят построение:

1. Векторы приводят к общему началу А.

    2. На этих трех ребрах строиться параллелепипед.

    3. Диагональ параллелепипеда, которая выходит из этой же точки, изображает суммы векторов АВ, AD, AA1.

Примеры решения задач

Пример 1

Определить вид четырехугольника ABCD, если:

 

 

Решение:

Данный четырехугольник — ромб.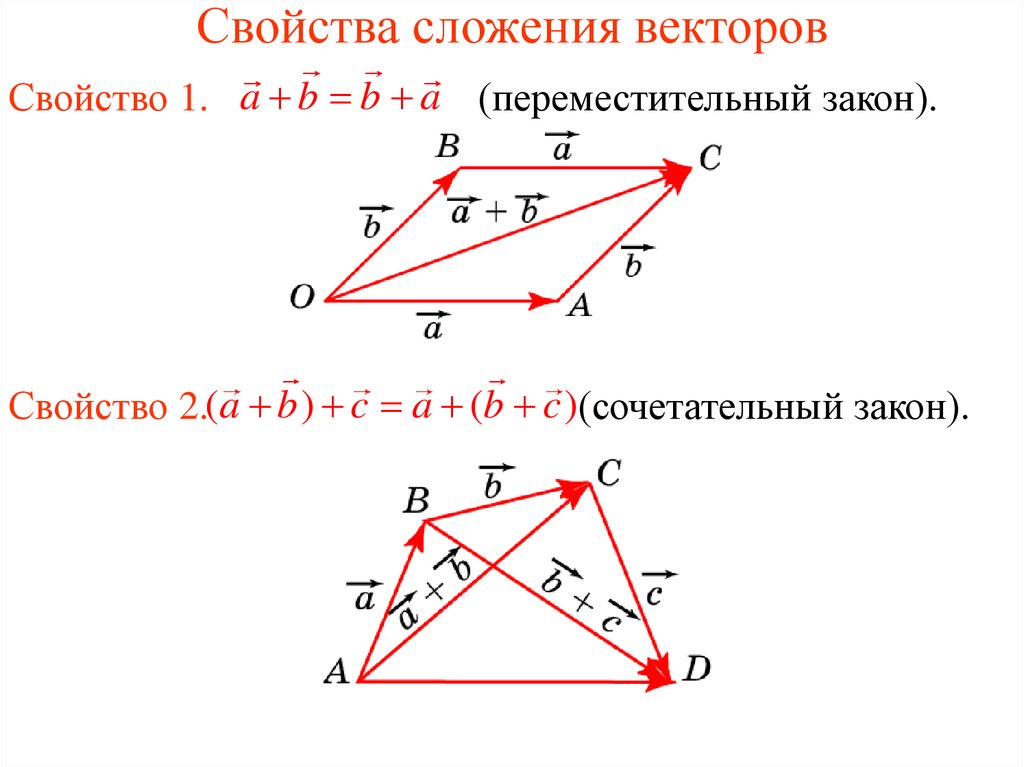 Обоснуем это.

Мы знаем, что векторы  и  равны, отсюда следует, что равны их модули — то есть длины отрезков.

Векторы по условию сонаправлены и коллинеарны, то есть принадлежат параллельным прямым. Таким образом, заданный четырехугольник — параллелограмм.

Данный факт обоснован признаком параллелограмма: если две стороны четырехугольника принадлежат параллельным прямым и длины их равны, то данный четырехугольник — параллелограмм.

Согласно второму условию: , соседние стороны параллелограмма равны друг другу, а такой параллелограмм является ромбом.

Пример 2

Дан параллелепипед ABCDА1B1С1D1. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов: AB+AD+AА1.

Решение:

AB+AD=AC, AC+AA1=AC1

Ответ: AC1.

Задания для самостоятельной работы

Задание 1

Дан параллелограмм ABCD. Найдите сумму векторов CD+DB+BA.

Задание 2

Дан параллелепипед ABCDА1B1С1D1. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов: DA+DC+DD1.

Видео с вопросами: Графическое сложение трех векторов

Стенограмма видео

Какой из векторов 𝐏, 𝐐, 𝐑, 𝐒 и 𝐓, показанных на диаграмме, равен 𝐀 плюс 𝐁 плюс 𝐂?

Когда мы представляем вектор стрелкой, мы называем его острый конец головой, а другой конец хвостом. Чтобы добавить второй вектор к этому первому вектору, мы начинаем с рисования второго вектора с хвостом в начале первого вектора. Если теперь мы нарисуем третий вектор с хвостом в конце первого вектора и головой в начале второго вектора, этот третий вектор будет в точности суммой двух векторов, которые мы изначально нарисовали.

Все это хорошо, но задача состоит в том, чтобы найти сумму трех векторов, а не двух. Однако сложение векторов является ассоциативным. Таким образом, сложение трех векторов вместе — это то же самое, что сложение двух векторов, а затем добавление третьего вектора к этой сумме. Таким образом, чтобы добавить третий вектор к 𝐔 и 𝐕, мы просто рисуем этот третий вектор с хвостом в начале 𝐔 плюс 𝐕.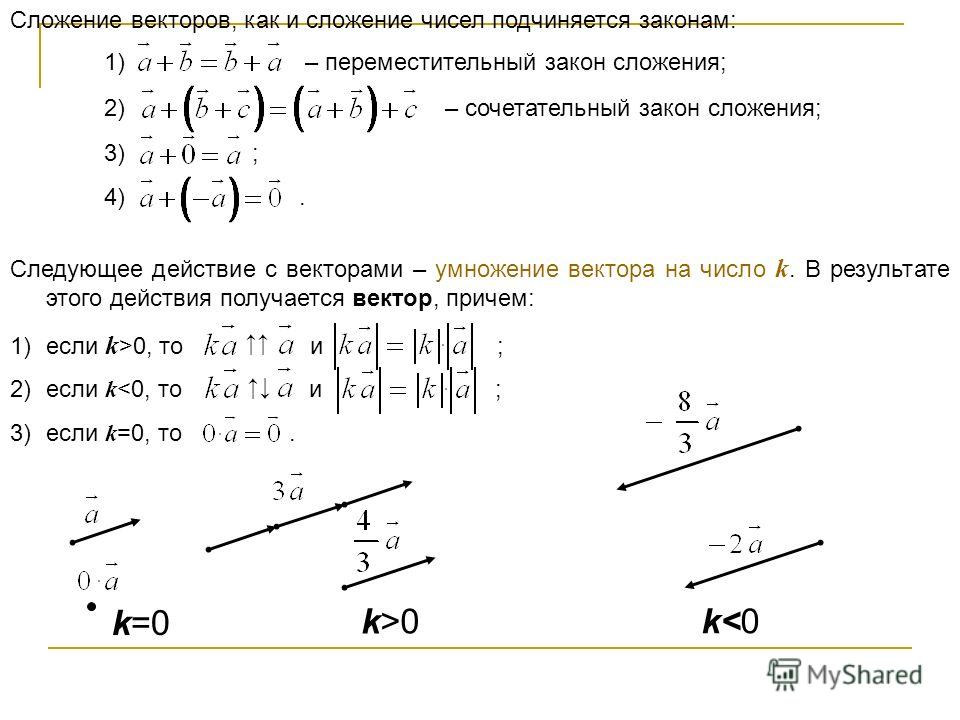 А затем мы соединим хвост 𝐔 плюс 𝐕 с головой этого третьего вектора. Мы нарисовали наш третий вектор 𝐖. И теперь мы рисуем наш окончательный вектор, представляющий общую сумму, с хвостом в хвосте 𝐔 плюс 𝐕 и головой в голове 𝐖.

Теперь, когда у нас есть окончательная сумма, когда мы стираем промежуточный вектор 𝐔 плюс 𝐕, мы видим, что, соединив три вектора от хвоста к голове, четвертый вектор с хвостом на оставшемся хвосте и головой на оставшейся голове точно равен сумме этих трех векторов. На самом деле, это работает для любого количества векторов. И для любого конкретного набора векторов не имеет значения, в каком порядке мы их рисуем. Мы всегда будем получать один и тот же ответ, потому что сложение векторов является одновременно коммутативным и ассоциативным.

Возвращаясь к диаграмме, мы видим, что для ответа на этот вопрос нам нужно соединить 𝐀, 𝐁 и 𝐂 от хвоста к голове, а затем найти, какой из остальных векторов соединяет оставшийся хвост с оставшейся головой. Поскольку порядок не имеет значения, мы можем также соединить хвост 𝐁 с головой 𝐀, а затем хвост 𝐂 с головой 𝐁. 𝐁 расширяет на одну единицу влево и на пять единиц вверх. Итак, начиная с головы 𝐀, мы рисуем стрелку, которая простирается на одну единицу влево и на пять единиц вверх.

Теперь нам нужно включить 𝐂. 𝐂 расширяет четыре единицы влево и четыре единицы вниз. Когда мы соединим эту стрелку с уже нарисованными нами стрелками, мы увидим, что острие совпадает с острием вектора 𝐓. Теперь эта голова, наконечник стрелки, которую мы пометили 𝐂, является нашей оставшейся головой. А наш оставшийся хвост — это хвост вектора 𝐀, находящийся в начале координат. И, как мы видим, вектор 𝐓 имеет хвост в начале координат и голову в оставшейся голове. Таким образом, 𝐓 должно быть суммой 𝐀, 𝐁 и 𝐂.

Если бы мы сложили векторы в другом порядке, возможно, 𝐂, затем 𝐀, а затем 𝐁, как показано, мы бы обнаружили, что оставшаяся голова по-прежнему совпадает с головой 𝐓, а оставшийся хвост по-прежнему совпадает с хвостом 𝐓, что подтверждает, что наш ответ — 𝐓, а также наглядно показывает, как сложение векторов является коммутативным.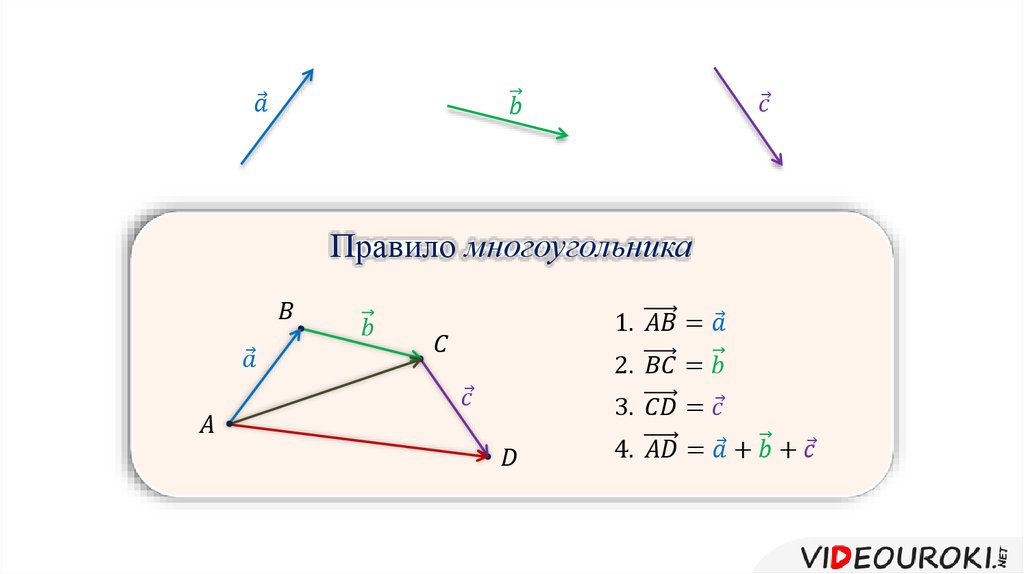

Сложение трех векторов Важные концепции и советы для JEE

Что такое сложение векторов?

Дата последнего обновления: 26 марта 2023 г.

•

Всего просмотров: 76,5 тыс.

•

Просмотров сегодня: 0,53 тыс.

Как мы знаем, вектор определяется как физическая величина, которая имеет как направление, так и величину. Любой вектор можно представить в плоскости XYZ, используя его компоненты. Если два вектора определены путем задания их компонентов направления на плоскости XYZ и если они добавляются, мы можем просто добавить компоненты X, компоненты Y и компоненты Z двух векторов соответственно. Когда векторы определяются их величиной, у нас есть два разных закона сложения векторов, посредством которых можно складывать векторы.

Это аналитические методы, используемые для сложения векторов, а именно закон треугольника и закон параллелограмма сложения векторов. Давайте рассмотрим, как закон треугольника и закон параллелограмма выполняются при сложении векторов.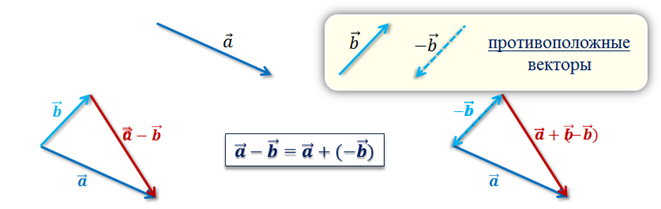

Законы сложения векторов

Закон треугольника

Закон треугольника сложения векторов гласит, что если два вектора провести как две смежные стороны треугольника как по величине, так и по направлению, то третья сторона треугольника является эти два вектора после сложения как по величине, так и по направлению. Давайте возьмем два вектора, а именно C и D, и нарисуем их как две упорядоченные стороны треугольника, как показано на рисунке ниже. 9{2}+2 c d \cos \theta}$

Здесь c и d — величины двух векторов C и D соответственно. θ — это угол между двумя векторами C и D. Давайте посмотрим на закон сложения векторов в виде параллелограмма, а также на некоторые примеры сложения векторов.

 

Закон параллелограмма 

Закон сложения векторов параллелограмма гласит, что если два вектора, как по величине, так и по направлению, представлены как две смежные стороны параллелограмма, то диагональ, проходящая через эти два вектора, покоится в точке результат векторов после сложения. Давайте продемонстрируем закон параллелограмма с помощью диаграммы. 9{2}+2 c d \cos \theta}$

Если мы хотим узнать угол между результирующим вектором  и вектором D, отношение между $\phi$ и $\theta$ определяется выражением 

$\ tan \phi=\dfrac{c \sin \theta}{d+c \cos \theta}$

Это формулы сложения векторов, используемые с законом сложения векторов.

Сложение трех векторов

Предположим, что есть три вектора C, D и E, которые нужно сложить по закону формул сложения векторов. Для сложения трех векторов мы можем выполнить сложение векторов для первых двух векторов C и D, где мы получим результирующую R. Затем добавьте этот результат к третьему вектору, E, чтобы получить конечную результирующую сложения трех векторов, т. е. R’.

Сложение трех векторов

Вот как три вектора складываются с использованием законов сложения векторов, и этот процесс также аналогичен для вычитания векторов.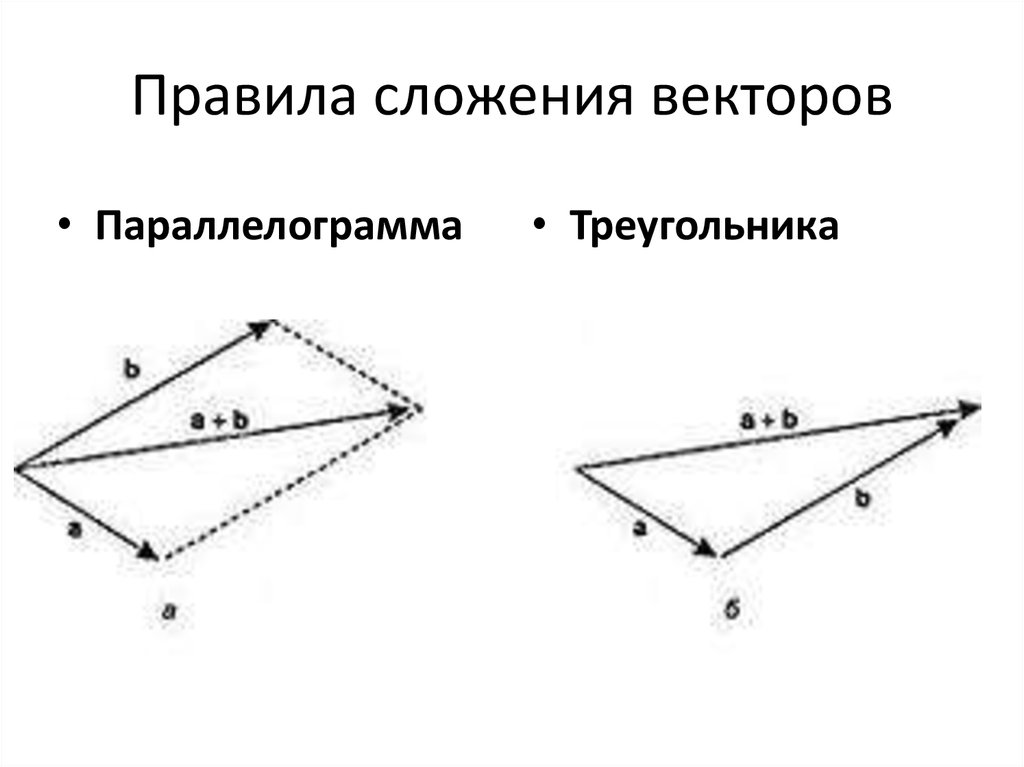 Ниже приведены примеры задач, чтобы понять, как складываются три вектора.

Примеры сложения векторов 

Пример 1. Учитывая, что величина векторов |C| = 4единицы, |D| = 5 единиц и |E| = 7 единиц соответственно. Найдите модуль результирующего вектора после сложения трех векторов, если угол между C и D равен 9.{2}+2(7) \sqrt{41} \cos 60} \\ &=\sqrt{41+49+7 \sqrt{41}} \\ &=11,611 \text {единицы} \end{align} $

Это требуемое значение результирующего вектора после сложения трех векторов, C, D и E. 

Пример 2. Три вектора задаются их компонентами X, Y и Z следующим образом.

C = 2i + 4j + 7k

D = i + 3j + 8k

E = -4i + 2j — 5k

Найдите модуль результирующего вектора после сложения этих трех векторов.

Решение: 9{2}}=\sqrt{182}=13,49 \text { единиц }$ 

Требуемое значение модуля равнодействующей трех векторов равно 13,49 единиц.