Момент силы. Движение. Теплота

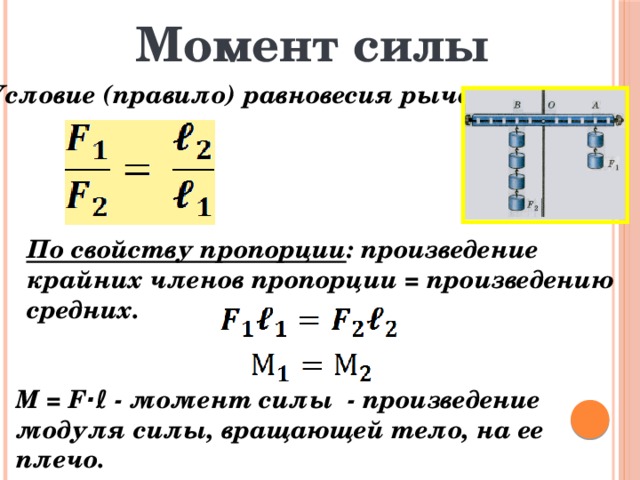
Момент силы

Попробуйте рукой привести во вращение тяжелое маховое колесо. Тяните за спицу. Вам будет тяжело, если вы ухватитесь рукой слишком близко к оси. Переместите руку к ободу, и дело пойдет легче.

Что же изменилось? Ведь сила в обоих случаях одна и та же. Изменилась точка приложения силы.

Во всем предыдущем изложении вопрос о месте приложения силы не возникал, так как в рассмотренных задачах форма и размер тела роли не играли. По сути дела мы мысленно заменяли тело точкой.

Пример с вращением колеса показывает, что вопрос о точке приложения силы далеко не праздный, когда речь идет о вращении или повороте тела.

Для того чтобы понять роль точки приложения силы, вычислим работу, которую надо проделать, чтобы повернуть тело на некоторый угол. При этом расчете, конечно, предполагается, что все частички твердого тела жестко сцеплены между собой (мы оставляем пока без внимания способность тела гнуться, сжиматься – вообще менять свою форму).

Поэтому сила, приложенная к одной точке тела, сообщает кинетическую энергию всем его частям.

При вычислении этой работы роль точки приложения сил отчетливо видна.

На рис. 49 показано закрепленное на оси тело. При повороте тела на маленький угол ? точка приложения силы переместилась по дуге – прошла путь s.

Проектируя силу на направление движения, т.е. на касательную к окружности, по которой движется точка приложения, напишем знакомое выражение работы A:

A = F_прод·s

Но дуга s может быть представлена как

s = r?,

где r – расстояние от оси вращения до точки приложения силы. Итак,

A = F_прод·r?.

Поворачивая тело на один и тот же угол разными способами, мы можем затратить различную работу в зависимости от того, где приложена сила.

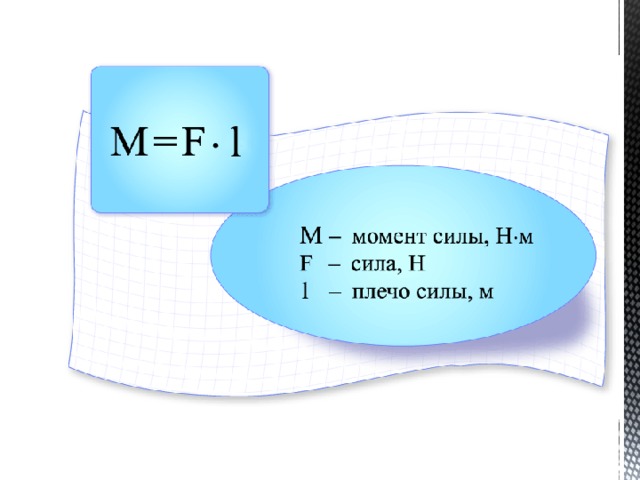
Если угол задан, то работа определяется произведением F_прод·r.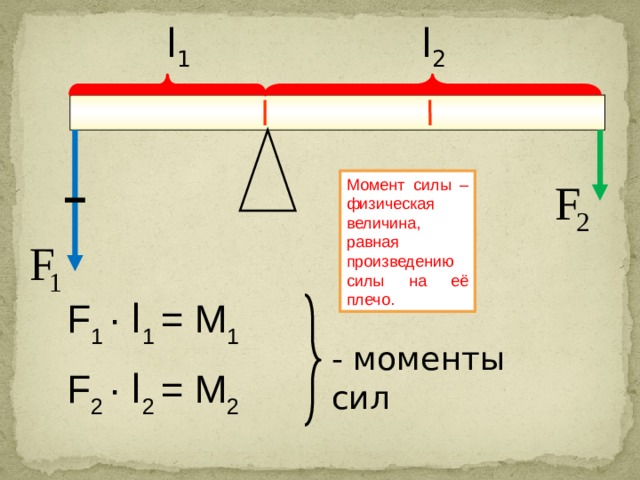 Такое произведение называют моментом силы:

M = F_прод·r

Формуле момента силы можно придать другой вид. Пусть O – ось вращения и B – точка приложения силы (рис. 50). Буквой d обозначена длина перпендикуляра, опущенного из

O на направление силы. Два треугольника, построенные на рисунке, подобны. Поэтому

Величина d называется плечом силы. Новая формула M = Fd читается так: момент силы равен произведению силы на ее плечо.

Если точку приложения силы перемещать вдоль направления силы, то плечо d, а вместе с ним и момент силы не будут меняться. Значит, безразлично, где именно на линии силы лежит точка приложения.

При помощи нового понятия формула для работы запишется короче:

A = M?,

т.е. работа равняется произведению момента силы на угол поворота.

Пусть на тело действуют две силы с моментами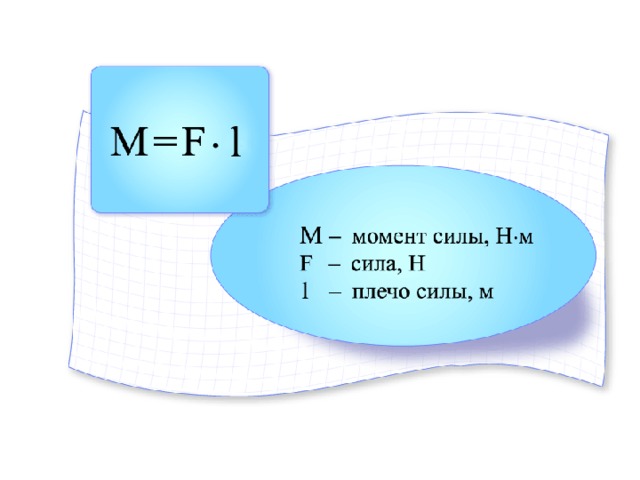

M₁ и M₂. При повороте тела на угол ? будет совершена работа M₁? + M₂? = (M₁ + M₂)?. Эта краткая запись показывает, что две силы с моментами M₁ и M₂ вращают тело так, как это делала бы одна сила с моментом M, равным сумме M₁ + M₂. Моменты сил могут как помогать, так и мешать друг другу. Если моменты M₁ и M₂ стремятся повернуть тело в одну и ту же сторону, то мы должны считать их величинами, имеющими одинаковый алгебраический знак. Напротив, моменты сил, поворачивающие тело в разные стороны, имеют разные знаки.

Как мы знаем, работа всех сил, действующих на тело, идет на изменение кинетической энергии.

Вращение тела замедлилось или ускорилось – значит, изменилась его кинетическая энергия. Это может произойти лишь в том случае, если суммарный момент сил не равен нулю.

А если суммарный момент равен нулю? Ответ ясен – кинетическая энергия не изменяется, следовательно, тело или вращается равномерно по инерции, или покоится.

Итак, равновесие способного вращаться тела требует уравновешивания действующих на него моментов сил. Если действуют две силы, равновесие требует равенства

M₁ + M₂ = 0.

Пока нас интересовали такие задачи, в которых тело можно было рассматривать как точку, условия равновесия были проще: чтобы тело покоилось или двигалось равномерно, говорил закон Ньютона для таких задач, надо, чтобы результирующая сила равнялась нулю; силы, действующие вверх, должны уравновеситься силами, направленными вниз; сила вправо должна компенсироваться силой влево.

Этот закон действителен и для нашего случая. Если маховое колесо находится в покое, то действующие на него силы уравновешиваются реакцией оси, на которую насажено колесо.

Но этих необходимых условий становится недостаточно. Кроме уравновешивания сил требуется еще уравновешивание моментов сил. Уравновешивание моментов является вторым необходимым условием покоя или равномерного вращения твердого тела.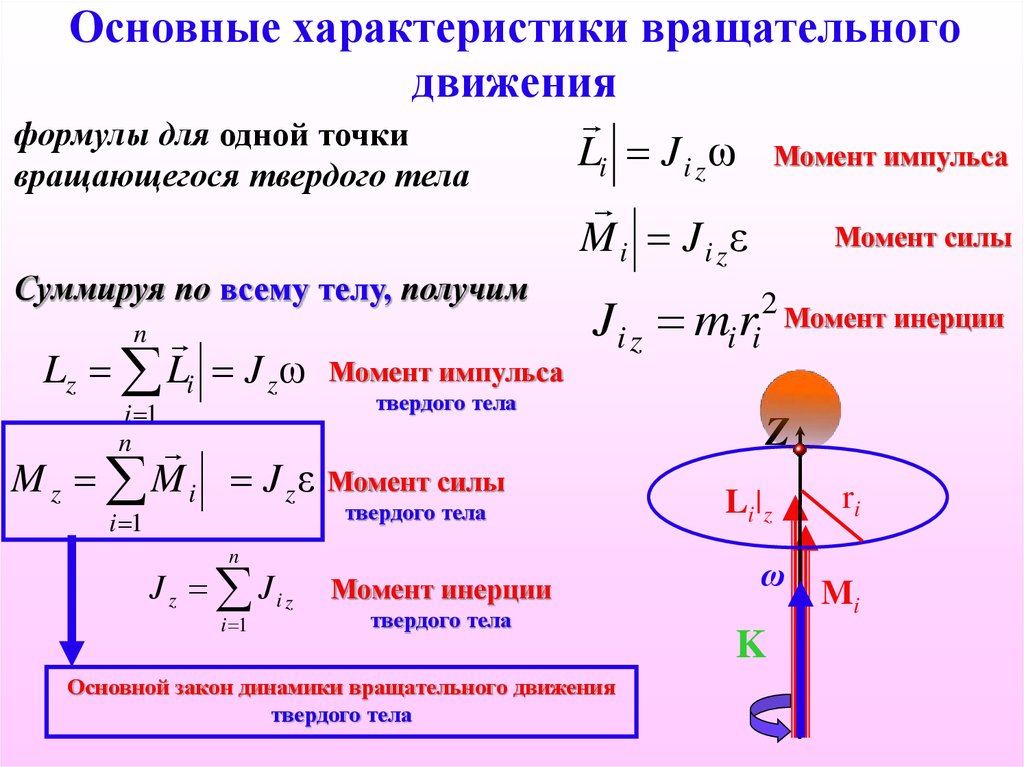

Моменты сил, если их много, без труда разбиваются на две группы: одни стремятся вращать тело вправо, другие – влево. Эти-то моменты и должны компенсироваться.

НА НАС ВЛИЯЮТ ПРИРОДНЫЕ СИЛЫ

НА НАС ВЛИЯЮТ ПРИРОДНЫЕ СИЛЫ Приняв, что все это истинно, мы приходим к рассмотрению некоторых сил и влияний, которые воздействуют на этот чудесный сложный автоматический механизм с органами невообразимо чувствительными и изящными, когда его несет вращающийся

IV Можно ли укрыться от силы тяжести?

IV Можно ли укрыться от силы тяжести? Мы слишком привыкли к тому, что все вещи, все физические тела прикованы своим весом к земле; нам трудно поэтому даже мысленно отрешиться от силы тяжести и представить себе картину того, что было бы, если бы мы обладали способностью

Заслон от силы тяжести

Заслон от силы тяжести Остроумный английский писатель Герберт Уэльс подробно развил эту мысль в научно-фантастическом романе „Первые люди на Луне»[4]. Ученый герой романа, изобретатель Кевор, открыл способ изготовления именно такого вещества, непроницаемого для

К главе II 1. Силы тяготения

К главе II 1. Силы тяготения Приведенные в начале главы II примеры действия силы тяготения могут быть проверены несложными расчетами, основанными, на законе Ньютона и элементах механики. Напомним сначала, что в механике за единицу измерения силы принята сила, которая,

IV. Откуда же берутся эти силы?

IV. Откуда же берутся эти силы? Наш разговор мы начали с того, что фундаментальные силы похожи на игры, однако в нашей игре не хватает одного компонента, без которого ничего не получится: это мяч. Задумайтесь об этом. Без мяча теннис — не более чем конвульсивное размахивание

16. Без юридической силы

16.  Без юридической силы Хотя меня в некоторой степени утешала новообретенная независимость духа, семейный катаклизм на самом деле сломил меня. Во тьме поражения я чувствовала, что опозорена и что от меня все отреклись, что я неуклюже пытаюсь вновь найти свою личность, как

Четыре силы

Четыре силы Словно мало было хлопот с новыми частицами, в те же 1930 — е годы были открыты еще и новые поля. К уже известному тяготению и электромагнетизму добавились силы ядерного взаимодействия, удерживающие протоны и нейтроны в ядре, и силы слабого взаимодействия,

83 Еще раз про силы сцепления

83 Еще раз про силы сцепления Для опыта нам потребуются: два кусочка стекла или два маленьких зеркальца. Мы помним, как иголка плавала на воде в одном из наших опытов. Помогали ей плавать силы поверхностного натяжения. Но вот вопрос: можно ли почувствовать силу

Движение под действием силы тяжести

Движение под действием силы тяжести Будем скатывать небольшую тележку с двух очень гладких наклонных плоскостей.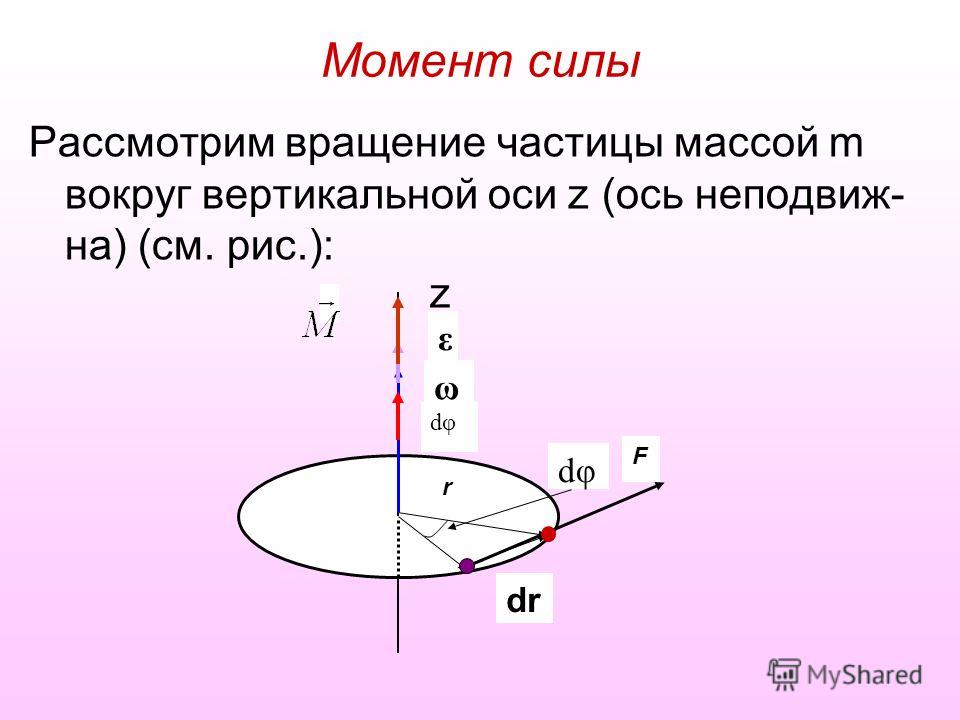 Одну доску возьмем значительно короче другой и положим их на одну и ту же опору. Тогда одна наклонная плоскость будет крутой, а другая – пологой. Верхушки

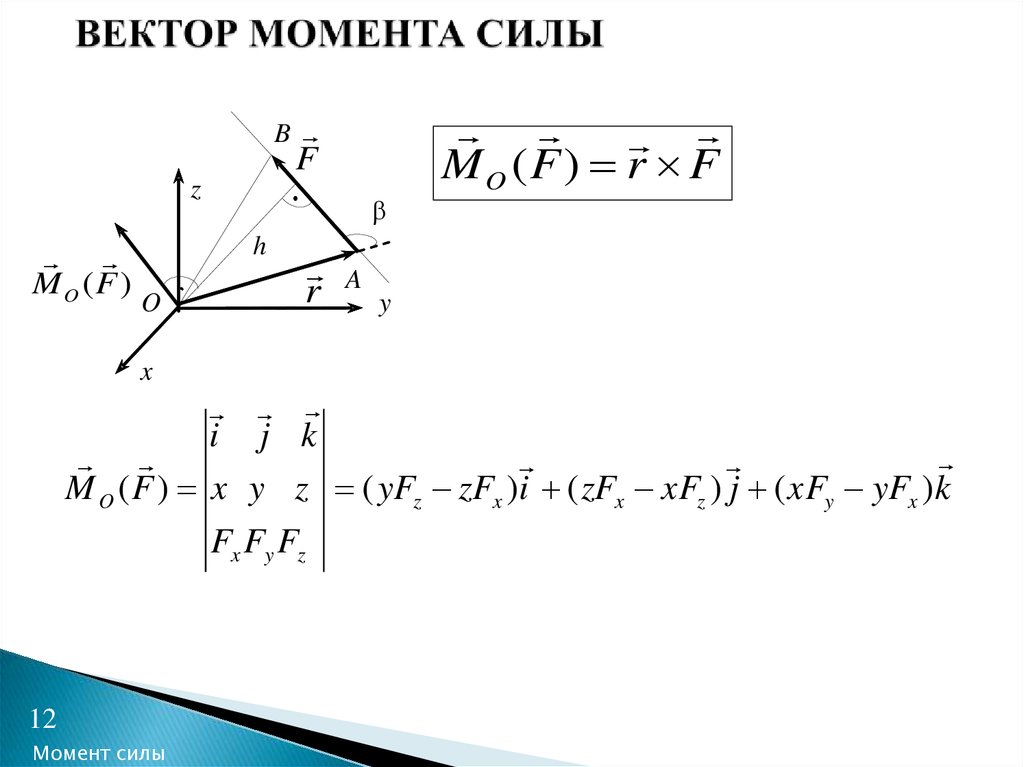
Вращательный момент

Вращательный момент Сейчас мы познакомимся еще с одним механическим понятием, которое позволяет сформулировать новый для нас важный закон движения.Это понятие называется вращательным моментом, или моментом импульса, или моментом количества движения. Уже названия

Вращательный момент как вектор

Вращательный момент как вектор До сих пор речь шла о величине вращательного момента. Но вращательный момент обладает свойствами векторной величины.Рассмотрим вращение точки по отношению к какому-либо «центру». На рис. 62 изображены два близких положения точки.

Поверхностные силы

Поверхностные силы Можно ли выйти сухим из воды? Конечно, для этого нужно смазаться несмачивающимся водой веществом. Натрите палец парафином и опустите в воду. Когда вы его вынете, окажется, что воды на пальце нет, если не считать двух-трех капелек. Небольшое движение – и

Силы трения

Силы трения Мы не в первый раз говорим о трении. И правда, как можно было, рассказывая о движении, обойтись без упоминания о трении? Почти любое движение окружающих нас тел сопровождается трением. Останавливается автомобиль, у которого водитель выключил мотор,

Силы сопротивления при больших скоростях

Силы сопротивления при больших скоростях Но вернемся к законам «мокрого» трения. Как мы выяснили, при малых скоростях сопротивление зависит от вязкости жидкости, скорости движения и линейных размеров тела. Рассмотрим теперь законы трения при больших скоростях. Но

IV. Откуда же берутся эти силы?

IV.  Откуда же берутся эти силы? Наш разговор мы начали с того, что фундаментальные силы похожи на игры, однако в нашей игре не хватает одного компонента, без которого ничего не получится: это мяч. Задумайтесь об этом. Без мяча теннис – не более чем конвульсивное размахивание

Момент силы Калькулятор | Вычислить Момент силы

✖Сила — это любое взаимодействие, которое, если ему не противодействовать, изменит движение объекта. Другими словами, сила может заставить объект с массой изменить свою скорость.ⓘ Сила [F]		Атомная единица силыАттоньютонСантиньютонДеканьютонДециньютондинаэксаньютонFemtonewtonГиганьютонГрамм-силаГраве-силагектоньютонДжоуль / СантиметрДжоуль на метрКилограмм-силаКилоньютонКилопруд Килофунт-силаКип-силаМеганьютонМикроньютонMilligrave — силаМиллиньютонНаноньютонНьютонУнция-силаPetanewtonPiconewtonпрудФунт-фут в квадратную секундуПаундалФунт-силастенТераньютонТон-сила (Long)Тон-сила (метрическая система)Тон-сила (короткий)Йоттаньютон	+10% -10%
✖Перпендикулярное расстояние между силой и точкой является важным фактором при расчете момента силы. ⓘ Перпендикулярное расстояние между силой и точкой [rFP]		створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр	+10% -10%

✖Момент силы – это произведение силы на расстояние, перпендикулярное линии действия силы. ⓘ Момент силы [M]

дина метрдина ммГрамм-сила-сантиметрграмм-сила-метрграмм-сила ммКилограмм-метрКилограмм-сила-сантиметрКилограмм-сила-метркгс ммКилоньютон-метрНьютон-сантиметрНьютон-метрНьютон Миллиметрунция силы-футУнция-сила-дюймфунт-сила футафунт силы дюйм

⎘ копия

👎

Формула

сбросить

👍

Момент силы Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Сила: 2.5 Ньютон —> 2.5 Ньютон Конверсия не требуется
Перпендикулярное расстояние между силой и точкой: 4 метр —> 4 метр Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

10 Ньютон-метр —> Конверсия не требуется

< 11 Статика частиц Калькуляторы

Наклон равнодействующей двух сил, действующих на частицу

Идти Наклон равнодействующих сил = atan((Вторая сила*sin(Угол))/(Первая сила+Вторая сила*cos(Угол)))

Результат двух сил, действующих на частицу под углом

Идти Равнодействующая сила = sqrt(Первая сила^2+(2*Первая сила*Вторая сила*cos(Угол))+Вторая сила^2)

Разрешение силы с углом по горизонтали

Идти Горизонтальная составляющая силы = Сила под углом тета*cos(Угол)

Разрешение силы с углом по вертикали

Идти Вертикальная составляющая силы = Сила под углом тета*sin(Угол)

Результат двух сил, действующих на частицу под углом 90 градусов

Идти Равнодействующая сила = sqrt(Первая сила^2+Вторая сила^2)

Момент силы

Идти Момент силы = Сила*Перпендикулярное расстояние между силой и точкой

момент пары

Идти Момент силы = Сила*Перпендикулярное расстояние между двумя силами

Результат двух разнородных параллельных сил, не равных по величине

Идти Равнодействующая сила = Первая сила-Вторая сила

Результат двух сил, действующих на частицу под углом 180 градусов

Идти Равнодействующая сила = Первая сила-Вторая сила

Результат двух сил, действующих на частицу под углом 0 градусов

Идти Равнодействующая сила = Первая сила+Вторая сила

Результат двух одинаковых параллельных сил

Идти Равнодействующая сила = Первая сила+Вторая сила

Момент силы формула

Момент силы = Сила*Перпендикулярное расстояние между силой и точкой
M = F*r_FP

Что такое момент силы?

Момент силы — это мера ее тенденции заставить тело вращаться вокруг определенной точки или оси. Чтобы на мгновение развиться, сила должна воздействовать на тело таким образом, чтобы оно начало скручиваться.

Share

Copied!

Расчет моментов и сил. SINADRIVES Direct Drive Experts

Перейти к содержимому

Предыдущий Следующий

Расчет моментов и сил

Привет, мехатронисты,

Добро пожаловать в последний пост в блоге Sinadrives.

Сентябрь 2022

В сегодняшней статье мы обсудим, как рассчитать статические и динамические моменты силы. Эти простые расчеты позволяют нам определить, являются ли модули с выбранными линейными двигателями наиболее подходящими для разрабатываемого нами приложения.

Расчет статической силы

Начнем с физической части расчета, где мы будем использовать формулу 1:

F = m x g

Где:
F – сила в Н
м – масса в кг
г – ускорение свободного падения м/с2

Пример:
Если мы поместим на поверхность груз массой 10 кг, статическая сила, которую он оказывает, составит 98 Н (10 х 9,8 = 98 Н).

Расчет динамической силы

Для расчета динамической силы мы заменяем g (ускорение свободного падения) на A (ускорение). Важно знать, что это ускорение должно действовать в том же направлении, что и масса.

F = m x A

Где:
F – сила в Н
m – масса в кг
A – ускорение в м/с2

Пример:
и ускорить его в вертикальном направлении (A = 5 м/с2), динамическая сила, которую он оказывает, составляет 50 Н (10 х 5 = 50 Н).

Совместный расчет статических и динамических сил

Предположим, нам нужно рассчитать силу, с которой лифт действует на конструкцию здания при вертикальном движении.

Данные:

Масса лифта: 1000 кг
Ускорение: 4,5 м/S2

F = M x A + M x g = 1000 x 4,5 + 1000 x 9,8 = 4500 + 9800 = 14300n

Расчет STATIC

. Для расчета статического момента воспользуемся приведенной ниже формулой:

M = m x g x X

Где:
M – крутящий момент в Нм
X – расстояние между центром масс и зажимом в м
м – масса в кг
г – ускорение свободного падения м/с2

Пример:
Если мы поместим груз массой 10 кг на поверхность на расстоянии 300 мм, статический момент будет равен 29,4 Нм (10 х 9,8 х 0,3 = 29,4 Нм).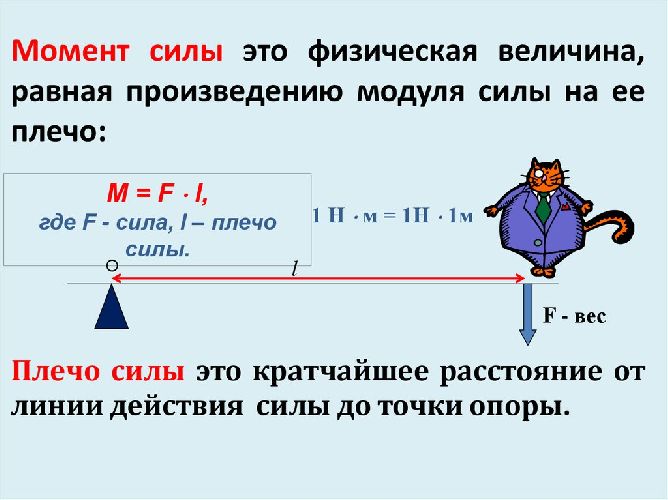 Изображение 1 является примером приложения.

Расчет динамического момента

Для расчета динамического момента воспользуемся приведенной ниже формулой.

M = m x A x X

Где:
M – крутящий момент в Нм
X – расстояние между центром масс и зажимом в м
m – масса в кг
A – ускорение в м/с2

Пример:
Если мы поместим массу 10 кг на подвижную тележку на расстоянии 300 мм и также переместим эту тележку с ускорением 15 м /с2 динамический момент составит 45 Нм (10 х 15 х 0,3 = 45 Нм).

На рис. 2 показан пример приложения.

Совместный расчет статических и динамических сил и моментов

Рассмотрим пример. Мы собираемся рассчитать статические и динамические силы и моменты. Мы будем использовать данные из двух приведенных выше примеров и применим порядок, как показано на рисунке 3.

В этом случае у нас есть:

Статические силы и моменты :
FZ = 98N
MX = 29,4 нм

Динамические силы и моменты :
MZ = 45 нм

Коэффициент максимальной.

выбрали линейный модуль MLE30420 для нашего приложения, и мы должны проверить моменты силы. На изображении ниже показаны значения по каталогу для модуля с линейным двигателем MLE30420HS:

. Если использовать формулу, приведенную в каталоге, получим:

Fy/Fycat + Fz/Fzcat + Mx/Mxcat + My/Mycat + Mz/Mzcat ≤ 1

Значения, рассчитанные в главах 1, 4 и 5, помещаем в верхнюю строку, а каталожные — в нижнюю. , что дает нам следующие результаты:

98/1500 + 29,4/180 + 45/320 = 0,07 + 0,16 + 0,14 = 0,23

Мы видим, что результат ≤ 1, что означает наличие хорошего запаса прочности. По каталогу результат меньше 1 гарантирует срок службы более 30 000 км.

Некоторые соображения

Отдельно рассчитанные значения никогда не могут превышать максимальное каталожное значение. Чем ниже это значение, тем дольше будет срок службы. Если скорость и ускорение превышают значения 3 м/с и 30 м/с2, соответственно, общая сумма не должна превышать 0,7, если не считается приемлемым более короткий срок службы.

Если у вас есть приложение, в котором вы хотите улучшить производительность своей машины, будь то скорость, динамика, точность или просто сокращение потребностей в обслуживании, свяжитесь с нами.

Наши специалисты по технологиям прямого привода и линейным модулям с технологией линейных двигателей будут рады бесплатно проконсультировать вас.

Делайте выводы сами. Решите, какие инновации вы хотите внедрить в свою машину, чтобы быть конкурентоспособными. Мы можем помочь тебе.

Ваша команда SINADRIVES.

Подпишитесь на наш блог

Область ползунка переключения

Поиск

Поиск:

Общение

Ссылка для загрузки страницы

Перейти к началу

Сила, энергия и моменты: определение, формула, примеры

Проще говоря, сила — это не что иное, как толчок или притяжение. С научной точки зрения, сила — это движение, производимое объектом в результате его взаимодействия с другим объектом или полем, таким как электрическое или гравитационное поле.

Рис. 1. Сила может быть толчком или притяжением объекта

Конечно, сила используется не только для того, чтобы толкать или тянуть объекты. Фактически мы можем выполнять три типа функций с помощью силы.

• Изменение формы объекта: если, например, вы сгибаете, растягиваете или сжимаете объект, вы изменяете его форму.
• Изменение скорости объекта: если во время езды на велосипеде вы увеличиваете педаль или кто-то толкает вас сзади, скорость велосипеда увеличивается. Таким образом, приложение большей силы заставляет велосипед ускоряться.
• Изменение направления движения объекта: в крикетном матче, когда игрок с битой ударяет по мячу, сила, прилагаемая битой, вызывает изменение направления мяча. Здесь сила используется для изменения направления уже движущегося объекта.

Что такое энергия?

Энергия — это способность совершать работу, а работа равна силе, приложенной для перемещения объекта на определенное расстояние в направлении, определяемом этой силой. Таким образом, энергия — это то, сколько работы совершается этой силой над объектом. Уникальность энергии в том, что ее можно трансформировать.

Сохранение энергии

Сохранение энергии утверждает, что энергия передается только из одного состояния в другое, так что полная энергия замкнутой системы сохраняется.

Например, когда объект падает, его потенциальная энергия преобразуется в кинетическую энергию, но общая сумма обеих энергий (механическая энергия системы) одинакова в каждый момент падения.

Рис. 2 – Преобразование кинетической энергии в потенциальную в случае американских горок

Что такое момент?

Эффект поворота или сила, создаваемая вокруг оси, называется моментом силы или крутящим моментом. Примерами шарниров являются петли открывающейся двери или гайка, поворачиваемая гаечным ключом. Ослабление затянутой гайки и открывание двери на неподвижной петле требуют некоторого момента.

Рис. 3. Сила на расстоянии от неподвижной оси создает момент

Хотя это вращательное движение вокруг неподвижной оси, существуют и другие типы эффектов поворота.

Какие бывают виды моментов силы?

Помимо аспекта вращения, нам также необходимо отметить направление, в котором движется объект. Например, в случае аналоговых часов все их стрелки вращаются в одном направлении вокруг неподвижной оси, расположенной в их центре. Направление, в данном случае, по часовой стрелке.

Момент по часовой стрелке

Когда момент или эффект вращения силы вокруг точки вызывает движение по часовой стрелке, этот момент направлен по часовой стрелке. В расчетах мы принимаем момент по часовой стрелке как отрицательный.

Момент против часовой стрелки

Точно так же, когда момент или вращательное действие силы вокруг точки вызывает движение против часовой стрелки, этот момент является вращением против часовой стрелки. В расчетах мы принимаем момент против часовой стрелки как положительный.

Рис. 4 — По часовой и против часовой стрелки

Как рассчитать момент силы?

Вращающее действие силы, также известное как крутящий момент, можно рассчитать по формуле:

\[T = r \cdot F \sin(\theta)\]

1. T = крутящий момент.
2. r = расстояние от приложенной силы.
3. F = приложенная сила.
4. 𝜭 = Угол между F и плечом рычага.

Рис. 5 – Моменты, приложенные к перпендикулярному уровню (F1) и моменту, действующему под углом (F2)

На этой диаграмме действуют две силы: F ₁ и F ₂ . Если мы хотим найти момент силы F ₁ вокруг точки вращения 2 (где сила F ₂ актов), это можно рассчитать, умножив F ₁ на расстояние от точки 1 до точки 2:

\[\text{Момент силы} = F_1 \cdot D\]

Однако для расчета момент силы F ₂ вокруг точки вращения 1 (где действует сила F ₁ ) приходится немного импровизировать. Взгляните на рисунок 6 ниже.

Рис. 6 – Разрешение вектора F2 для расчета момента силы F2

F ₂ не перпендикулярно стержню. Поэтому нам нужно найти составляющую силы F ₂ , который перпендикулярен линии действия этой силы.

В этом случае формула принимает вид F ₂ sin𝜭 (где 𝜭 — угол между F ₂ и горизонталью). Итак, формула для расчета крутящего момента вокруг силы F ₂ :

\[\text{Момент силы} = F_2 \cdot \sin(\theta) \cdot D\]

Принцип момента

Принцип момента гласит, что когда тело балансирует вокруг точки вращения, сумма момента по часовой стрелке равна сумме момента против часовой стрелки. Мы говорим, что объект находится в равновесии и не будет двигаться, пока не изменится одна из сил или не изменится расстояние от центра вращения любой из сил. См. иллюстрацию ниже:

Рис. 7 – Примеры равновесия

Рассчитайте расстояние от точки опоры силы 250 Н, которое необходимо приложить, чтобы качели уравновесились, если сила на другом конце качелей составляет 750 Н при расстоянии 2,4. м от стержня.

Сумма моментов по часовой стрелке = сумма моментов против часовой стрелки.

\[F_1 \cdot d_1 = F_2 \cdot d_2\]

\[750 \cdot d_1 = 250 \cdot 2. 4\]

\[d_1 = 7.2 \space m\]

Следовательно, расстояние сила 250 Н должна находиться на расстоянии 7,2 м от оси, чтобы качели были сбалансированы.

Что такое пара?

В физике момент пары – это две равные параллельные силы, находящиеся в противоположных направлениях друг от друга и на одинаковом расстоянии от точки вращения, действующие на объект и производящие эффект вращения. Примером может быть водитель, поворачивающий руль своей машины обеими руками.

Отличительной чертой пары является то, что, несмотря на эффект вращения, результирующая сила в сумме равна нулю. Следовательно, нет поступательного, а есть только вращательное движение.

Рис. 8. Пара образуется, если две равные силы действуют в противоположных направлениях на одинаковом расстоянии от точки вращения

Чтобы вычислить момент пары, нам нужно умножить любую из сил на расстояние между ними. В случае нашего примера выше, вычисление:

\[\text{Момент пары} = F \cdot S\]

Какова единица момента силы?

Поскольку единицей силы является ньютон, а единицей расстояния — метр, единицей момента становится ньютон на метр (Нм). Таким образом, крутящий момент является векторной величиной, поскольку он имеет величину и направление.

Момент силы 10 Н относительно точки равен 3 Нм. Вычислите расстояние между точками опоры и линией действия силы.

\[\text{Момент силы} = \text{Сила} \cdot \text{Расстояние}\]

\(3 \space Nm = 10 \cdot r\)

\(r = 0.3 \space м\)

Сила Энергия — Ключевые выводы

• Сила – это толчок или притяжение объекта.
• Сила может изменить форму объекта вместе с его скоростью и направлением, в котором он движется.
• Сохранение энергии означает, что энергия передается только из одного состояния в другое, так что сохраняется полная энергия замкнутой системы.
• Эффект поворота или сила, создаваемая вокруг оси вращения, представляет собой момент силы или крутящего момента.
• Момент может быть направлен по часовой стрелке или против часовой стрелки.
• Принцип момента гласит, что когда тело балансирует вокруг точки вращения, сумма моментов по часовой стрелке равна сумме моментов против часовой стрелки.