Сложение ⭐ двух сил, направленных по одной прямой в физике: правило и способы сложения
Как понять какие силы действуют на тело
Источник: otvet.imgsmail.ru
На любое тело, находящееся в природных условиях, как правило, действует несколько сил. Их векторы могут совпадать, а могут быть разнонаправленными. Чтобы определить, каким образом проявится одновременное воздействие всех сил на тело, необходимо понимать, какие они бывают и каковы правила их сложения.
В физике понятие «сила» обозначается буквой F со стрелкой сверху. Это обозначает, что величина является векторной и имеет направленное воздействие на тело в момент приложения силы. Величина воздействия (силы) выражается в Ньютонах.
Перед тем, как сформулировать, какое суммарное воздействие будет на тело, если оно испытывает одновременное воздействие нескольких сил, необходимо охарактеризовать некоторые их них.
Сила тяжести
В основе лежат процессы гравитации.
Определение 1Сила, с которой тело притягивается к земле, называется силой тяжести. Ее вектор направлен вертикально вниз, в каком бы положении тело ни находилось.
Ее вектор направлен вертикально вниз, в каком бы положении тело ни находилось.
Источник: fizmat.by
Сила трения
Когда тело движется по какой-либо поверхности, его движению всегда противодействует сила трения. Ее возникновение связано с особенностями структуры этой поверхности, дефекты которой при отсутствии силы, компенсирующей это воздействие, способны замедлить движение или даже свести его к нулю. В задачах на тему силы трения используется следующая формула:
Источник: fizmat.by
Векторная составляющая силы трения направлена по прямой — в сторону, противоположную движению.
Сила реакции опоры
В ситуации, когда тело лежит на опоре, на него действует не только силы тяжести. Поверхность остается ровной по причине наличия ее сопротивления. Можно сказать, что стол «реагирует» на оказываемое давление силой, направленной противоположно силе тяжести. Третий закон Ньютона говорит, что наравне с противоположной направленностью, по величине сила опоры равняется силе тяжести.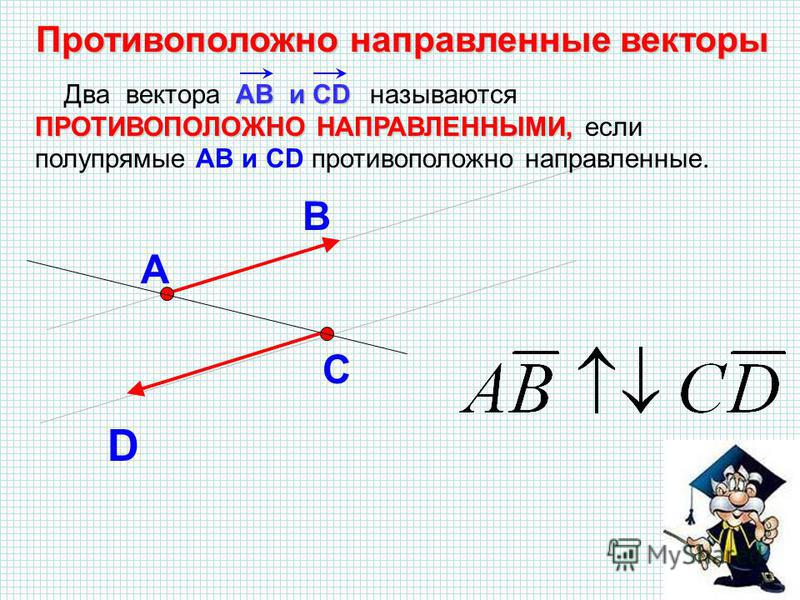
Характеристика силы опоры связана с особенностями структуры материала, из которого изготовлена опора. На уроке физики объясняется, что специальной формулы для качественной оценки силы опоры не существует, поскольку это — разновидность силы упругости, которая обозначается буквой N со стрелкой сверху (демонстрация направленности величины). Закономерно, что направлена сила опоры перпендикулярно поверхности этой опоры.
Сила упругости
В природе силы действуют не только в результате движения тела либо его лежания на ровной поверхности. На предметы, подвешенные на пружине, действует сила упругости, величина которой определяется свойствами материала.
Источник: fizmat.by
Подобно тому, как сила трения поверхности направлена противоположно движению, сила упругости направлена противоположно деформации.
Равнодействующая
Определение 1Равнодействующей нескольких сил называется сила, при воздействии которой на тело оказывается воздействие, аналогичное нескольким одновременно действующим силам.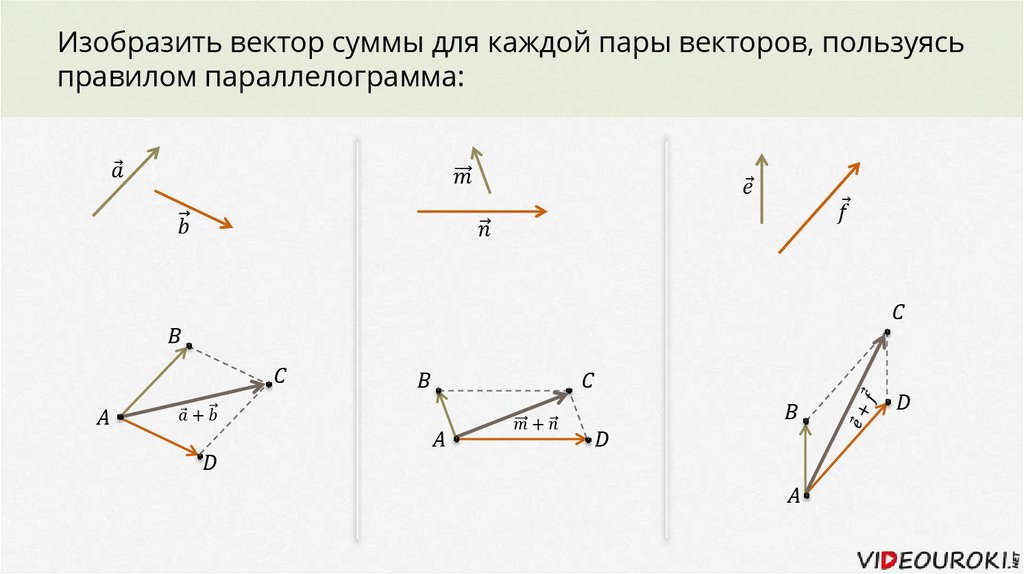
В большинстве случаев прибегают к описанию именно этой силы, а не к характеристике каждой, приложенной к телу в конкретный момент времени. Для того, чтобы правильно ее определить, необходимо четко представлять себе, как сложить две (или больше) сил. Ведь они могут быть не только различными по величине, но и иметь разную направленность.
Правило сложения двух сил, направленных по одной прямой
Когда на одно тело воздействует две силы, вектора которых лежат на одной прямой, действуют следующие правила их сложения.
Пояснения на примерах
Пример 1На тело действуют две силы, направления которых совпадают.
Источник: class-fizika.ru
Обозначим равнодействующую этих двух сил буквой R, сами силы — F1, F2.
Тогда будет справедливым утверждение, что
R=F1+F2
Однако необходимо помнить, что сила — векторная величина. Поэтому при сложении происходит не только суммирование значений, но и определение вектора этой равнодействующей.
Исходя из рассматриваемого рисунка, при одинаково направленных F1+F2 равнодействующая направлена в ту же сторону, а ее значение по модулю равно сумме модулей действующих сил.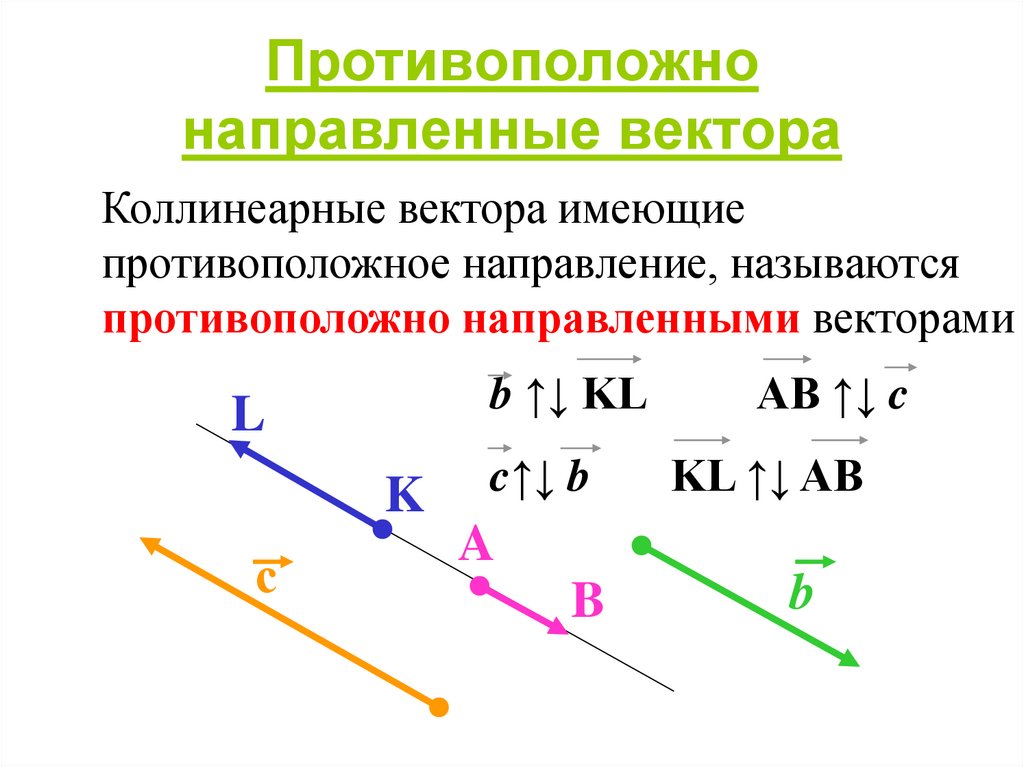
Рассмотрим пример. Отец посадил к себе на шею ребенка. Вес отца 80 кг, сына — 20 кг. Чтобы найти, с какой силой мужчина будет давить на землю, необходимо их общий вес (80+20) умножить на постоянную g (коэффициент свободного падения).
Пример 2На тело действуют две силы, направления которых не совпадают, а являются противоположными.
Источник: class-fizika.ru
Исходя из рассматриваемого рисунка, при противоположно направленных F1 и F2 равнодействующая направлена в сторону той силы, которая больше. Ее значение при этом по модулю равно разности модулей действующих сил.
R=F1-F2
Пример. Два человека перетягивают канат: один с силой 20 Н, другой — 15 Н. Необходимо определить, в какую сторону будет перетянут канат и чему будет равна равнодействующая двух сил.
Понятно, что направления прикладываемых к канату сил противоположны. Применяя приведенную выше формулу и учитывая, что равнодействующая будет направлена в сторону большей силы, а ее значение равно разности их модулей, получаем решение: канат будет двигаться в сторону человека, прикладывающего силу 20Н.
R=20-15=5 Н
Два описанных случая содержат указания на действие сил, направленных по одной прямой в одну или разные стороны. Результат их действия оценивается через сложение модулей (либо вычитание).
Пример 3Определенный интерес представляет тот случай, когда действующие силы имеют одинаковое значение (равны по модулю), но противоположное направление. Ситуация отображена на следующем рисунке:
Источник: class-fizika.ru
Для такой ситуации характерен признак: равнодействующая двух сил (слагаемых в приведенной формуле), направленных в противоположные стороны и имеющих одинаковое значение по модулю, равна нулю. Другими словами, тело не будет двигаться (его скорость станет равной нулю) либо его движение будет равномерным и прямолинейным.
Примером аналогичных случаев является движение парашютиста в воздухе. Его перемещение вниз будет равномерным с постоянной скоростью в тот период времени, когда его сила тяжести сравняется с силой сопротивления атмосферы.
Тело, подвешенное на пружине, уравновесится и будет в покое в тот момент, когда произойдет уравновешивание его силы тяжести и силы упругости пружины.
В обоих случаях силы будут иметь противоположное направление, но равны по модулю.
Приведенные закономерности действуют, если силы воздействуют на предмет по одной прямой. Если же одну из них направить под углом к вектору другой, характеристики движения будут иными.
3 Пример 4
ПримечаниеНа практике бывает, что на тело действует не две, а несколько сил, векторы которых лежат в одной плоскости.
Например, в перетягивании каната с каждой стороны участвуют по 2 человека.
Схематически этот процесс можно представить так:
Источник: obrazavr.ru
Как видно из рисунка, с каждой стороны на тело действует сумма двух сил, пара из которых имеет одно направление, а вторая пара — противоположное. Для таких случаев формула равнодействующей будет такова:
R=(F1+F2)-(F3+F4)
Вторым способом является решение по этапам:
R=R1-R2
R1=F1+F2
R2=F3+F4
Направление равнодействующей четырех сил будет таким, куда будет направлена большая сумма.
Векторы в пространстве
Векторы
В ектором в пространстве называется направленный отрезок, т.е. отрезок, в котором указаны его начало и конец.
Вектор с началом в точке А и концом в точке В обозначается и изображается стрелкой с началом в точке А и концом в точке В .
Длиной , или модулем , вектора называется длина соответствующего отрезка. Длина векторо в , обозначается соответственно , .
Два вектора называются равными , если они имеют одинаковую длину и направление.
В режиме слайдов ответы появляются после кликанья мышкой
Рассматривают также нулевые векторы, у которых начало совпадает с концом. Все нулевые векторы считаются равными между собой. Они обозначаются , и их длина считается равной нулю.
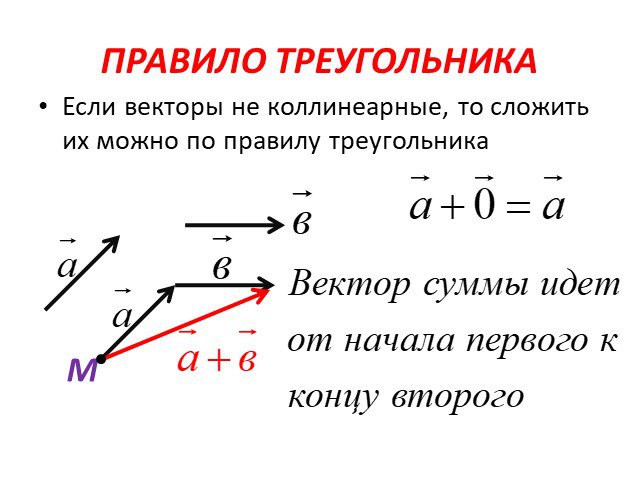
Сложение векторов
Для векторов определена операция сложения. Для того чтобы сложить два вектора и , вектор откладывают так, чтобы его начало совпало с концом вектора .
В режиме слайдов ответы появляются после кликанья мышкой
Свойства сложения векторов
Свойство 1. (переместительный закон).
Свойство 2. (сочетательный закон).
В режиме слайдов ответы появляются после кликанья мышкой
Умножение вектора на число
Произведением вектора на число t называется вектор, длина которого равна , а направление остается прежним, если t 0, и меняется на противоположное, если t
Произведение вектора на число t обозначается . По определению,
По определению,
В режиме слайдов ответы появляются после кликанья мышкой
Произведение вектора на число -1 называется вектором, противоположным и обозначается По определению, вектор имеет направление, противоположное вектору и
Свойства
Разностью векторов и называется вектор , который обозначается
Для умножения вектора на число справедливы свойства, аналогичные свойствам умножения чисел, а именно:
Свойство 1. (сочетательный закон).
Свойство 2 . (первый распределительный закон).
Свойство 3 . (второй распределительный закон).
В режиме слайдов ответы появляются после кликанья мышкой
Упражнение 1
В каком случае длина суммы векторов равна сумме длин слагаемых?
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: Если векторы одинаково направлены.
Упражнение 2
Точка B — середина отрезка AC , а точка C — середина отрезка BD .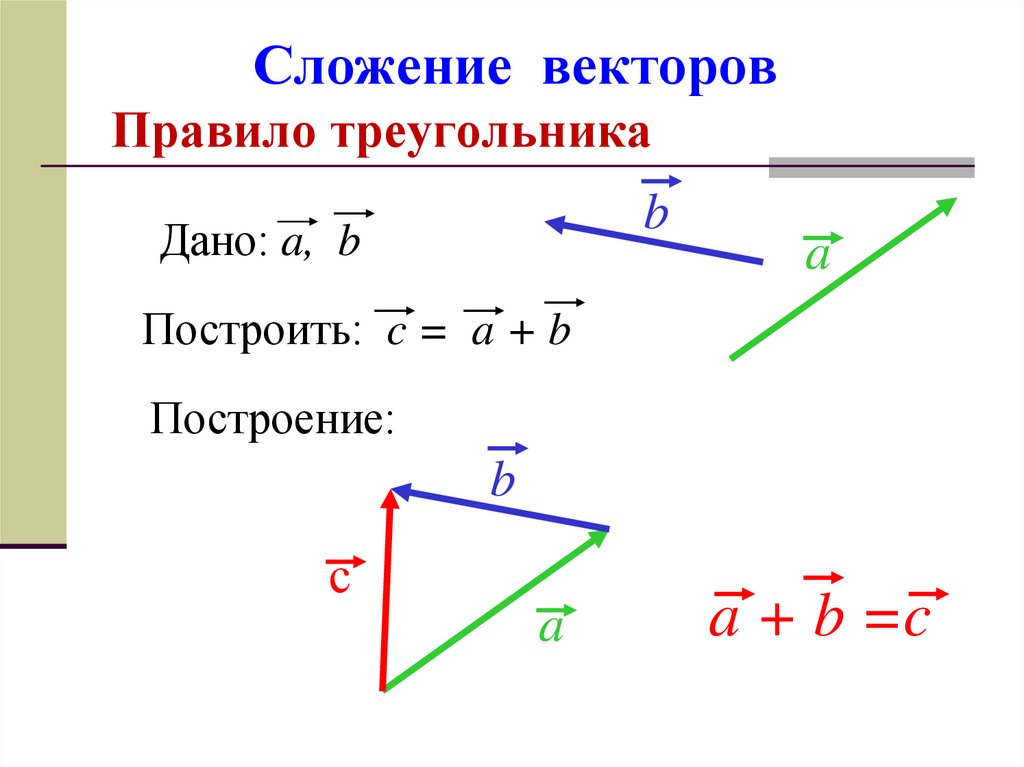 Равны ли векторы:
Равны ли векторы:
а) и ;
б) и ?
Ответ: а) Да;
В режиме слайдов ответы появляются после кликанья мышкой
б) нет.
Упражнение 3
Н азовите пары: а) одинаково направленных векторов; б) противоположно направленных векторов , с началом и концом в вершинах параллелепипеда
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: а) и , и , и ;
б) и , и , и .
8
Упражнение 4
В кубе A … D 1 назовите вектор, равный:
а)
б)
в)
г)
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: а) ;
б) ;
в)
г)
9
Упражнение 5
Для параллелепипеда A … D 1 выясните, верны ли следующие утверждения:
а) ;
б) ;
в) ;
г) .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: а) Да;
б) да;
в) да;
г) нет.
Упражнение 6
В параллелепипеде A … D 1 укажите векторы, равные :
а)
б)
в)
г)
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: а)
г)
в)
б)
11
Упражнение 7
A … D 1 — параллелепипед. Упростите выражение
В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
Упражнение 8
A … F 1 – правильная призма . Упростите выражение
В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
Упражнение 9
В единичном кубе A … D 1 найдите длину вектора
Решение. Данная сумма векторов равна вектору
Его длина равна .
Ответ. .
В режиме слайдов ответы появляются после кликанья мышкой
Упражнение 10
В единичном кубе A . .. D 1 найдите длину вектора
.. D 1 найдите длину вектора
Решение. Данная сумма векторов равна вектору
Его длина равна .
Ответ. .
В режиме слайдов ответы появляются после кликанья мышкой
Упражнение 11
В единичном кубе A … D 1 найдите длину вектора
Решение. Данная сумма векторов равна удвоенному вектору где O 1 – середина отрезка B 1 D 1 .
Его длина равна .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ. .
16
Упражнение 12
В правильной треугольной призме A B С A 1 B 1 C 1 , все ребра которой равны 1, найдите длину вектора
Решение. Длина данного вектора равна длине вектора удвоенного вектора где O – середина отрезка BC .
Его длина равна
В режиме слайдов ответы появляются после кликанья мышкой
Ответ.
Упражнение 13
В правильной треугольной призме A B С A 1 B 1 C 1 , все ребра которой равны 1, найдите длину вектора
Решение.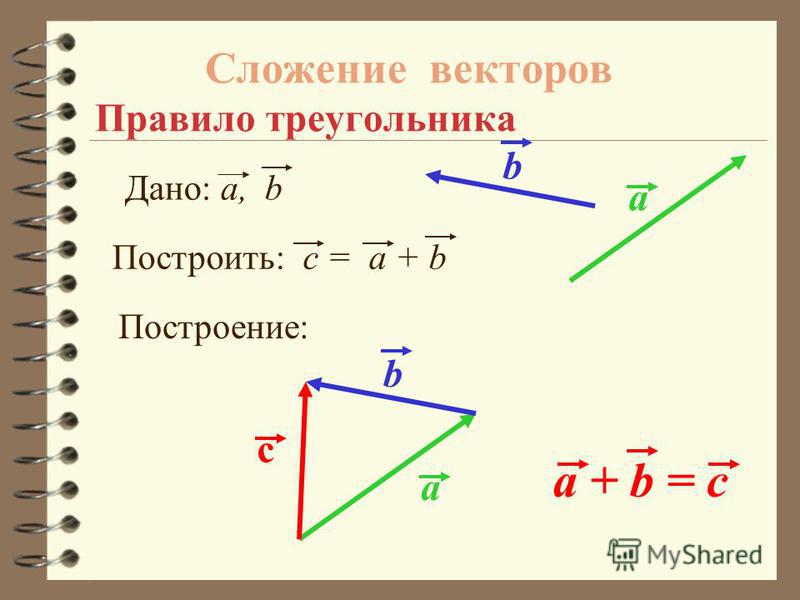 Длина данного вектора равна длине вектора вектора т.е. равна
Длина данного вектора равна длине вектора вектора т.е. равна
Ответ.
В режиме слайдов ответы появляются после кликанья мышкой
Упражнение 14
В правильной треугольной призме A B С A 1 B 1 C 1 , все ребра которой равны 1, найдите длину вектора
Решение. Длина данного вектора равна длине вектора вектора т.е. равна
Ответ.
В режиме слайдов ответы появляются после кликанья мышкой
Векторов
Векторы
Направленные отрезки и векторы
Направленный отрезок определяется как начальная точка,
P и терминал
точка Q.
Пример
п
= (2,3) и Q
= (-1,4)
Определение вектора А вектор — класс эквивалентности всех направленных отрезков
одинаковой длины и направления. |
Мы можем представить вектор, написав уникальный направленный отрезок, который
имеет начальную точку в начале координат.
Пример
Р = (2,3) и
Q = (-1,4)
является
эквивалентно направленному отрезку
«К-П»
= <-3, 1>
Когда мы пишем <> мы имеем в виду, что вектор имеет начальную точку в начале координат и
конечная точка в (-3,1). Эта нотация называется формой компонента .
вектора.
Длина вектора
Длина вектора |
Пример:
Мы также используем обозначение
-3 i + j
для обозначения вектора <-3,1>.
Пример
Вектор длины 10 образует угол p/6.
с осью x. Найдите его составляющие.
Решение:
х = r cos q,
y = r sin q
Так что
х = (10)(/ 2),
у = 10 (1/2) = 5
Мы можем записать вектор как
5 и + 5 и
Единичные векторы в направлении v
Вектор называется единичным вектором , если он имеет
величина = 1. Если
v =
тогда единичный вектор в направлении v можно найти как
Единичный вектор в Направление v 1
|
Пример:
Единичный вектор в направлении <-3,1> равен
Мы можем использовать нотацию <> и i
j обозначение взаимозаменяемо.
Алгебра векторов
Если
v = <а, б> и w =
и k представляет собой
константа, то мы можем определить сумму скалярного умножения следующим образом:
Сумма и скалярное умножение векторов в
+ w = кв = <ка, кб> |
Пример
3 <2,1> — 2<-1,3> = <6 + 2,3 - 6>
= <8,-3> = 8 и — 3 j
Геометрически v + w вектор, который соответствует диагонали параллелограмма с двумя сторонами v и с .
Также можно нарисовать соответствующую диаграмму, чтобы показать, как
в
— w = v + (- w ).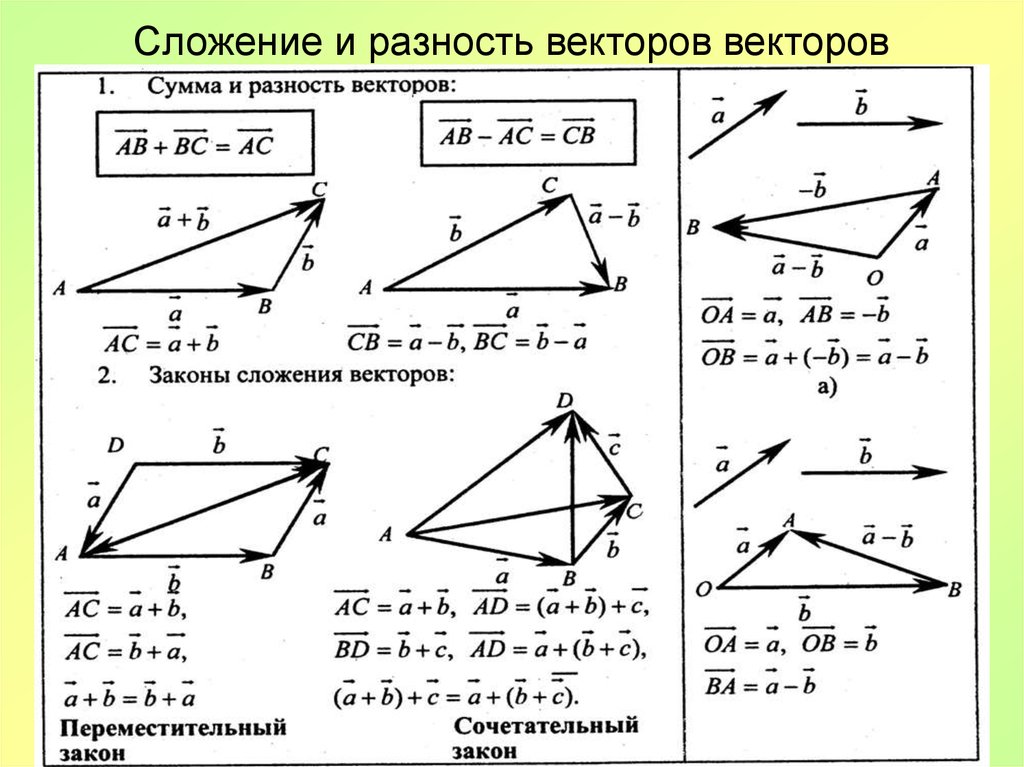
Вы можно увидеть сложение векторов с помощью этого апплета.
Вы здесь можно поиграть с другой арифметикой векторов.
Свойства векторного сложения и вычитания
У нас есть следующие четыре свойства векторов: Если u , против , и w — векторы и a и
b числа, затем
( и + и ) + и = u + ( v + ш )
а( и + против ) = а u + а v
а(б v ) = (аб) против
и + v = v + u
Приложения
Капитан лодки хочет плыть прямо на юг со скоростью 40 узлов. Если
течение движется на северо-запад со скоростью 16 узлов, в каком направлении и магнитуде
он должен работать с двигателем?
Если
течение движется на северо-запад со скоростью 16 узлов, в каком направлении и магнитуде
он должен работать с двигателем?
Решение
У нас есть
и = v + w
где u соответствует вектору скорости лодки, v соответствует вектору двигателя, а w соответствует скорости
тока. У нас есть
u = -40 j и w = -8 и +
8 j
Отсюда
v = u — w = -40 j — (-8 i + 8 j )
= 8 i —
(40+8) j
Величина
[(8) 2 + (40+8) 2 ] 1/2 = 52,5
Направление
Трехмерные координаты
Чтобы обобщить плоскость до трех измерений, мы проводим третью ось, называемую
оси z под прямым углом к плоскости, так что если вы схватитесь за
ось Z
правой рукой ваша рука будет скручиваться от положительной оси x к
положительная ось Y.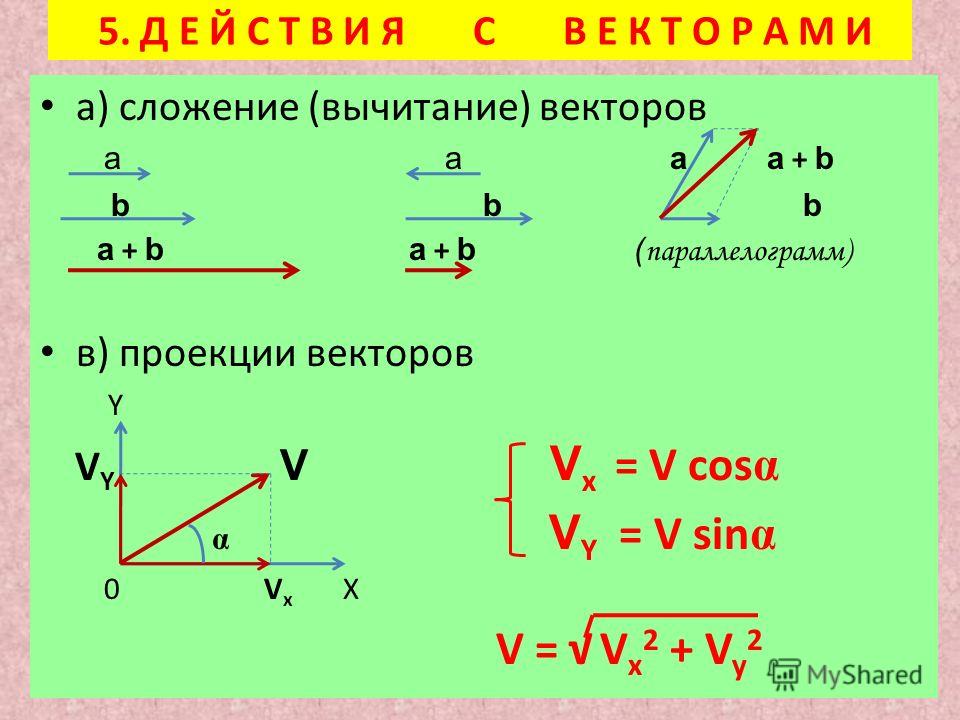 Чтобы нанести точку в пространстве xyz Сначала мы нанесем точку в
xy-плоскость и
затем нарисуйте отрезок, параллельный оси z, длиной, равной координате z.
Чтобы нанести точку в пространстве xyz Сначала мы нанесем точку в
xy-плоскость и
затем нарисуйте отрезок, параллельный оси z, длиной, равной координате z.
Пример:
Plot (1,2,3)
Решение:
Сначала мы рисуем оси x, y и z. Затем наносим точку (1,2) на
xy-плоскость. Наконец, поднимитесь на три единицы вверх и нанесите точку.
Упражнение
Участок (2,4,3)
Формула расстояния
Формула расстояния получена из трехмерной версии Теорема Пифагора, показанная ниже.
Расстояние между двумя точками (x 1 , y 1 , z 1 ) и (x 2 , y 2 , z 2 ) и определяется как
| Формула расстояния
в трех измерениях
|
Алгебра векторов в 3D
Вектор в пространстве задается
Правила алгебры аналогичны правилам двух измерений.
Назад на страницу векторов
Назад на домашнюю страницу Math 107
Назад на домашнюю страницу математического факультета
электронная почта Вопросы и предложения
линейная алгебра. Векторы и направленные отрезки
Задай вопрос
спросил
Изменено 1 год, 11 месяцев назад
Просмотрено 3к раз
$\begingroup$
Вектор – это величина, которая имеет величину и направление.
Направленный отрезок — это отрезок, который имеет начальную и конечную точки, поэтому имеет направление
Исходя из этих определений, направленный отрезок и вектор различны, хотя в некоторых учебниках они могут рассматриваться как взаимозаменяемые, что означает, что они являются синонимами, но это не одно и то же. Я могу объяснить это со своей точки зрения следующим образом:
Я могу объяснить это со своей точки зрения следующим образом:
Направленный отрезок — это геометрический объект, набор точек, который имеет не только длину, но и направление.
Хотя векторы можно рассматривать как физическое понятие или абстрактный математический объект.
Соответственно, некоторые обозначения меня очень смущают: Рассматривая $\overrightarrow{AB}$ и $\overrightarrow{BC}$ два направленных отрезка Затем
$\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}$
Что меня действительно смущает, так это то, как мы добавляем направленные отрезки? Мы можем добавлять векторы, но не сегменты.
Мы не добавляем нормальные отрезки, мы добавляем их длины.
Может ли кто-нибудь объяснить мне это, если я что-то не так понимаю?
- линейная алгебра
- аналитическая геометрия
$\endgroup$
1
$\begingroup$
«Количество, имеющее величину и направление» может быть приемлемым разговорным описанием вектора, но не может служить определением.
«Направленный отрезок», АКА «упорядоченная пара точек», уже лучше, но мы еще не там. Вектор в терминах $3$D элементарной геометрии представляет собой класса эквивалентности таких пар, при этом две пары $(A,B)$ и $(C,D)$ считаются эквивалентными , если существует перевод $T$ пространства такое, что $T(A)=C$, $\>T(B)=D$.
Теперь эти классы эквивалентности можно складывать с помощью известной конструкции параллелограмма. Нужно доказать, что сумма $\vec a+\vec b$ двух векторов корректно определена, а затем что она обладает (геометрическими) свойствами, которые превращают множество классов эквивалентности в вещественное векторное пространство.
$\endgroup$
3
$\begingroup$
Согласен, вообще добавление направленных сегментов не имеет смысла. Рассматривая направленный отрезок как вектор с начальной точкой, мы можем сложить векторы, но не будем знать, какую начальную точку присвоить результату. Чтобы расширить комментарий @pranavB23, можно найти смысл в этом, когда начальная точка второго сегмента является конечной точкой первого, где вполне естественно утверждать, что начальная точка результирующего сегмента — это просто $A$, и это случай $\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}$, который вы показали.
Чтобы расширить комментарий @pranavB23, можно найти смысл в этом, когда начальная точка второго сегмента является конечной точкой первого, где вполне естественно утверждать, что начальная точка результирующего сегмента — это просто $A$, и это случай $\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}$, который вы показали.
На самом деле, это пристрастие к направленным сегментам, по моему опыту, использовалось только , чтобы дать учащимся графический способ понимания/вычисления евклидовой векторной суммы, когда они впервые приближаются к ней, поскольку, в конце концов, когда я рисую вектор, я фактически рисование направленного сегмента. Ваша книга/заметки, вероятно, хотели сказать что-то вроде:
.Чтобы сложить векторы $\vec v$ и $\vec u$, мы можем выбрать направленный отрезок, начинающийся в любой понравившейся точке $A$ (обычно в начале координат) с той же длиной и направлением, что и $\vec v$, назовем его $\overrightarrow{AB}$, а другой отрезок, начинающийся с $B$, имеет ту же длину и направление, что и $\vec u$, $\overrightarrow{BC}$.
Тогда полученный $\vec v + \vec u$ имеет ту же длину и направление, что и $\overrightarrow{AC}$.
Можно также подумать об этом в следующих терминах: назвать $\vec P$ вектор, задающий положение точки $P$ в пространстве относительно любого фиксированного начала координат $O$, затем вектор, представленный $\overrightarrow {AB}$ есть $\vec v = \vec B — \vec A$, поэтому ясно, что $\vec v + \vec u = (\vec B — \vec A) + (\vec C — \vec B) = \vec C — \vec A$.
$\endgroup$
$\begingroup$
На самом деле можно определить частичное операция сложения над набором направленных отрезков путем ограничения аргументов совместимыми отрезками таким образом, чтобы конечная точка первого совпадала с начальной точкой второго. Для этих ограниченных пар сумма может быть определена законом треугольника $\overrightarrow{PR}=\overrightarrow{PQ}+\overrightarrow{QR}$.
Тогда нетрудно показать, что частичная операция распространяется на четко определенную бинарную операцию (сложение векторов) на множестве классов эквивалентностей.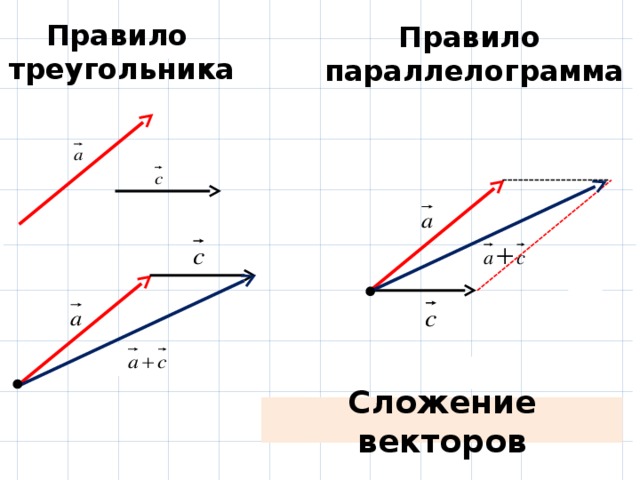



 Тогда полученный $\vec v + \vec u$ имеет ту же длину и направление, что и $\overrightarrow{AC}$.
Тогда полученный $\vec v + \vec u$ имеет ту же длину и направление, что и $\overrightarrow{AC}$.