Как построить вектор в пространстве по координатам. Векторы на ЕГЭ по математике

Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:

Пр a b = |b|cos(a,b) или

Где a b — скалярное произведение векторов , |a| — модуль вектора a .

Инструкция . Для нахождения проекции вектора Пp a b в онлайн режиме необходимо указать координаты векторов a и b . При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word . Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор .

Заданы :
две координаты вектора
три координаты вектора
a: ; ;
b: ; ;

Классификация проекций вектора

Виды проекций по определению проекция вектора

Виды проекций по системе координат

Свойства проекции вектора

1. Геометрическая проекция вектора есть вектор (имеет направление).
2. Алгебраическая проекция вектора есть число.

Теоремы о проекциях вектора

Теорема 1 . Проекция суммы векторов на какую-либо ось равна проекции слагаемых векторов на ту же ось.

Теорема 2 . Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:

Пр a b = |b|cos(a,b)

Виды проекций вектора

1. проекция на ось OX.
2. проекция на ось OY.
3. проекция на вектор.

Проекция на ось OX	Проекция на ось OY	Проекция на вектор
Если направление вектора A’B’ совпадает с направлением оси OX, то проекция вектора A’B’ имеет положительный знак.	Если направление вектора A’B’ совпадает с направлением оси OY, то проекция вектора A’B’ имеет положительный знак.	Если направление вектора A’B’ совпадает с направлением вектора NM, то проекция вектора A’B’ имеет положительный знак.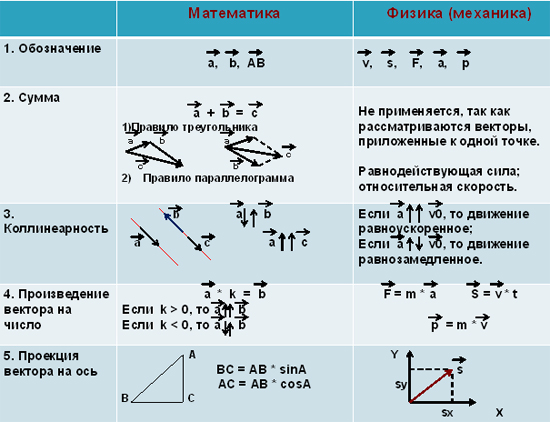
Если направление вектора противоположно с направлением оси OX, то проекция вектора A’B’ имеет отрицательный знак.	Если направление вектора A’B’ противоположно с направлением оси OY, то проекция вектора A’B’ имеет отрицательный знак.	Если направление вектора A’B’ противоположно с направлением вектора NM, то проекция вектора A’B’ имеет отрицательный знак.
Если вектор AB параллелен оси OX, то проекция вектора A’B’ равна модулю вектора AB.	Если вектор AB параллелен оси OY, то проекция вектора A’B’ равна модулю вектора AB.	Если вектор AB параллелен вектору NM, то проекция вектора A’B’ равна модулю вектора AB.
Если вектор AB перпендикулярен оси OX, то проекция A’B’ равна нулю (нуль-вектор).	Если вектор AB перпендикулярен оси OY, то проекция A’B’ равна нулю (нуль-вектор).	Если вектор AB перпендикулярен вектору NM, то проекция A’B’ равна нулю (нуль-вектор).

1. Вопрос: Может ли проекция вектора иметь отрицательный знак. Ответ: Да, проекций вектора может быть отрицательной величиной. В этом случае, вектор имеет противоположное направление (см. как направлены ось OX и вектор AB)
2. Вопрос: Может ли проекция вектора совпадать с модулем вектора. Ответ: Да, может. В этом случае, векторы параллельны (или лежат на одной прямой).
3. Вопрос: Может ли проекция вектора быть равна нулю (нуль-вектор). Ответ: Да, может. В этом случае вектор перпендикулярен соответствующей оси (вектору).

Пример 1 . Вектор (рис. 1) образует с осью OX (она задана вектором a) угол 60 о. Если OE есть единица масштаба, то |b|=4, так что .

Действительно, длина вектора (геометрической проекции b) равна 2, а направление совпадает с направлением оси OX.

Пример 2 . Вектор (рис. 2) образует с осью OX (с вектором a) угол (a,b) = 120 o . Длина |b| вектора b равна 4, поэтому пр a b=4·cos120 o = -2.

Действительно, длина вектора равна 2, а направление противоположно направлению оси.

Вектором принято называть отрезок, который имеет заданное направление. Как начало, так и конец вектора имеют фиксированную позицию, с помощью которых и определяется направление вектора. Рассмотрим подробнее, как построить вектор по заданным координатам.

1. Начертить систему координат (x, y, z) в пространстве, отметить на осях единичные отрезки.
2. Отложить на двух осях нужные координаты, провести от них пунктиром линии, параллельные осям, до пересечения. Поучится точка пересечения, которую нужно соединить пунктиром с началом координат.
3. Провести вектор из начала координат до полученной точки.
4. Отложить на третьей оси нужное число, через данную точку провести пунктирную линию, которая будет параллельна построенному вектору.
5. Из конца вектора провести пунктиром линию, параллельную третьей оси до пересечения с линией из прошлого пункта.
6. В завершении соединить начало координат и полученную точку.

Иногда требуется построить вектор, который будет результатом сложения или вычитания других векторов. Поэтому сейчас мы рассмотрим операции с векторами, узнаем, как их складывать и вычитать.

Операции над вектором

Геометрические векторы можно складывать несколькими способами. Так, например, наиболее распространенным способом сложения векторов является правило треугольника. Чтобы сложить два вектора по этому правилу, необходимо расположить векторы параллельно друг другу таким образом, чтобы начало первого вектора совпадало с концом второго, при этом третья сторона полученного треугольника будет являться вектором суммы.

Также можно рассчитать сумму векторов по правилу параллелограмма . Векторы должны начинаться из одной точки, параллельно каждому вектору нужно начертить линию так, чтобы в итоге получился параллелограмм. Диагональ построенного параллелограмма будет являться суммой этих векторов.

Для вычитания двух векторов нужно сложить первый вектор и вектор, который будет противоположным второму. Для этого также используется правило треугольника, которое имеет следующую формулировку: разность векторов, которые перенесены таким образом, что их начала совпадают, является вектором, начало которого совпадает с концом вычитаемого вектора, а также с концом уменьшаемого вектора.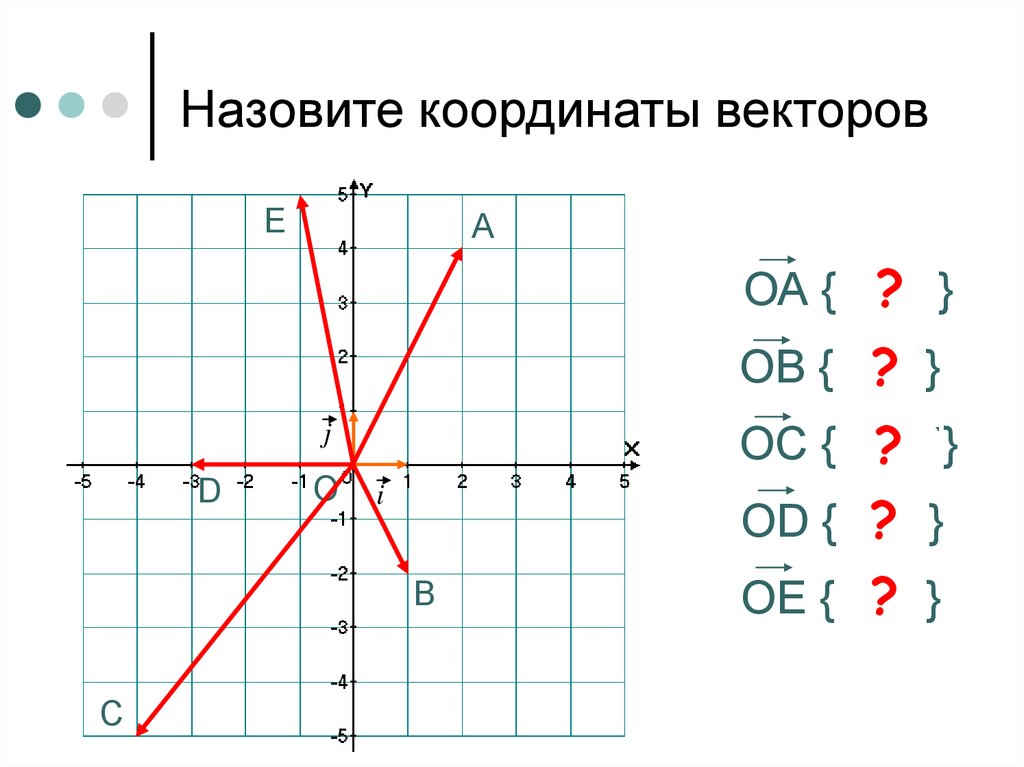

Внимание, только СЕГОДНЯ!

ДРУГОЕ

Для того чтобы совершить операцию сложения векторов, существует несколько способов, которые, в зависимости от ситуации…

Вектор — это математический объект, который характеризуется направлением и величиной. В геометрии вектором называется…

В математике под вектором понимается отрезок заданной длины, имеющий направление и координаты в осях Х, У, Z. Вопрос о…

Угол между двумя векторами, которые выходят с одной точки — это ближайший угол, поворот, на который, первого вектора…

Если Вы знаете пространственные координаты двух и более точек в определенной системе, то задачу: как найти длину…

Определить длину отрезка возможно разными способами. Для того чтобы узнать, как найти длину отрезка, достаточно иметь в…

Ускорение — это быстрота изменения скорости. Эта величина векторная, она имеет свое направление и измеряется в м/с 2 (в…

С помощью правила буравчика определяют направления магнитных линий (по-другому их еще называют линии магнитной…

На чертежах изображения геометрических тел строятся при использовании метода проекции. Но для этого одного изображения…

Слово «ордината» произошло от латинского «ordinatus» — «расположенный в порядке». Ордината — сугубо математический…

Модуль числа по-другому еще называется абсолютной величиной этого числа. В случае, если под знаком модуля стоит…

Для того чтобы найти координаты вершины равностороннего треугольника, если известны координаты двух других его вершин,…

Вам интересно, как можно вычислить и найти среднюю линию треугольника. Тогда за дело.Найти длину средней линии…

Рассмотрим более детально, что такое ускорение в физике? Это сообщение телу дополнительной скорости за единицу времени.…

Прежде чем узнать, как найти площадь параллелограмма, нам необходимо вспомнить, что такое параллелограмм и что…

Вектором принято называть отрезок, который имеет заданное направление. Как начало, так и конец вектора имеют фиксированную позицию, с помощью которых и определяется направление вектора. Рассмотрим подробнее, как построить вектор по заданным координатам.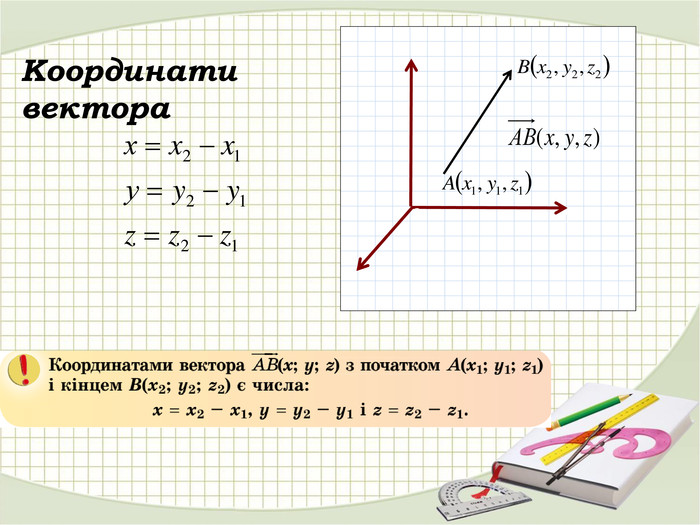

1. Начертить систему координат (x, y, z) в пространстве, отметить на осях единичные отрезки.
2. Отложить на двух осях нужные координаты, провести от них пунктиром линии, параллельные осям, до пересечения. Поучится точка пересечения, которую нужно соединить пунктиром с началом координат.
3. Провести вектор из начала координат до полученной точки.
4. Отложить на третьей оси нужное число, через данную точку провести пунктирную линию, которая будет параллельна построенному вектору.
5. Из конца вектора провести пунктиром линию, параллельную третьей оси до пересечения с линией из прошлого пункта.
6. В завершении соединить начало координат и полученную точку.

Иногда требуется построить вектор, который будет результатом сложения или вычитания других векторов. Поэтому сейчас мы рассмотрим операции с векторами, узнаем, как их складывать и вычитать.

Операции над вектором

Геометрические векторы можно складывать несколькими способами.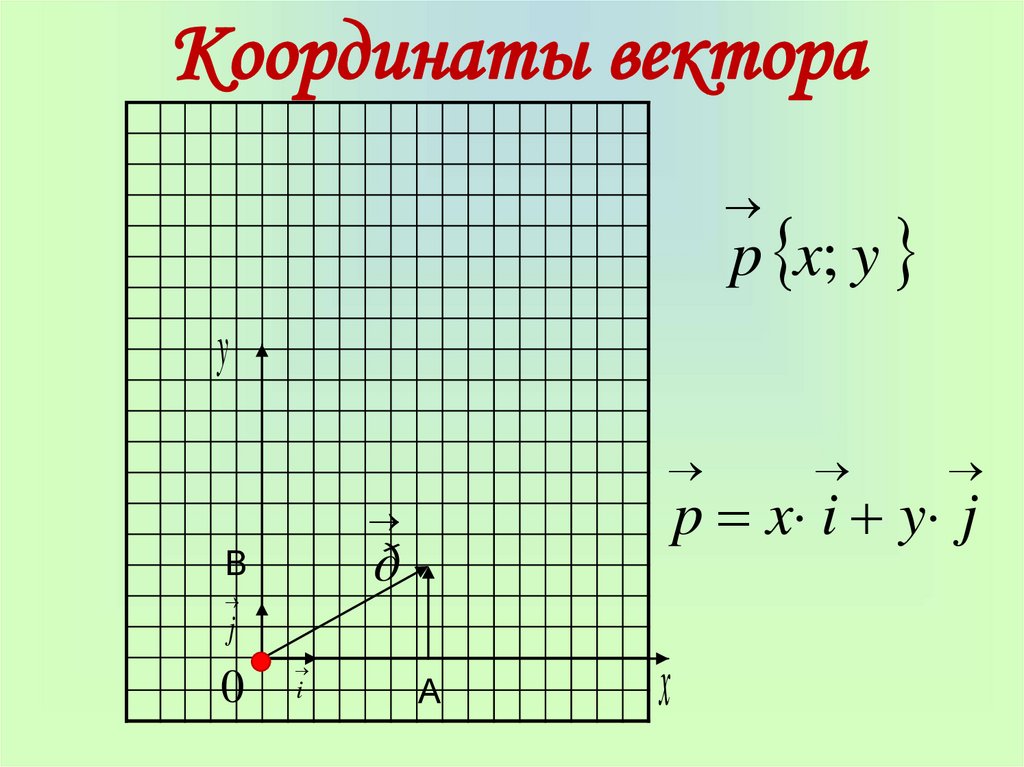 Так, например, наиболее распространенным способом сложения векторов является правило треугольника. Чтобы сложить два вектора по этому правилу, необходимо расположить векторы параллельно друг другу таким образом, чтобы начало первого вектора совпадало с концом второго, при этом третья сторона полученного треугольника будет являться вектором суммы.

Также можно рассчитать сумму векторов по правилу параллелограмма . Векторы должны начинаться из одной точки, параллельно каждому вектору нужно начертить линию так, чтобы в итоге получился параллелограмм. Диагональ построенного параллелограмма будет являться суммой этих векторов.

Для вычитания двух векторов нужно сложить первый вектор и вектор, который будет противоположным второму. Для этого также используется правило треугольника, которое имеет следующую формулировку: разность векторов, которые перенесены таким образом, что их начала совпадают, является вектором, начало которого совпадает с концом вычитаемого вектора, а также с концом уменьшаемого вектора.

Стандартное определение: «Вектор — это направленный отрезок». Обычно этим и ограничиваются знания выпускника о векторах. Кому нужны какие-то «направленные отрезки»?

А в самом деле, что такое векторы и зачем они?
Прогноз погоды. «Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости.

Величины, не имеющие направления, называются скалярными. Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей».

Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными.

Скорость, сила, ускорение — векторы. Для них важно «сколько» и важно «куда». Например, ускорение свободного падения направлено к поверхности Земли, а величина его равна 9,8 м/с 2 . Импульс, напряженность электрического поля, индукция магнитного поля — тоже векторные величины.

Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной:

Вот другой пример.
Автомобиль движется из A в B . Конечный результат — его перемещение из точки A в точку B , то есть перемещение на вектор .

Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, конец вектора — там, где стрелочка. Длиной вектора называется длина этого отрезка. Обозначается: или

До сих пор мы работали со скалярными величинами, по правилам арифметики и элементарной алгебры. Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила.

Когда-то мы и о числах ничего не знали. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число единица и число ноль.
Теперь мы знакомимся с векторами.

Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов.

А вот понятие равенства для векторов есть.
Равными называются векторы, имеющие одинаковые длины и одинаковое направление. Это значит, что вектор можно перенести параллельно себе в любую точку плоскости.
Единичным называется вектор, длина которого равна 1 . Нулевым — вектор, длина которого равна нулю, то есть его начало совпадает с концом.

Удобнее всего работать с векторами в прямоугольной системе координат — той самой, в которой рисуем графики функций. Каждой точке в системе координат соответствуют два числа — ее координаты по x и y , абсцисса и ордината.
Вектор также задается двумя координатами:

Здесь в скобках записаны координаты вектора — по x и по y .
Находятся они просто: координата конца вектора минус координата его начала.

Если координаты вектора заданы, его длина находится по формуле

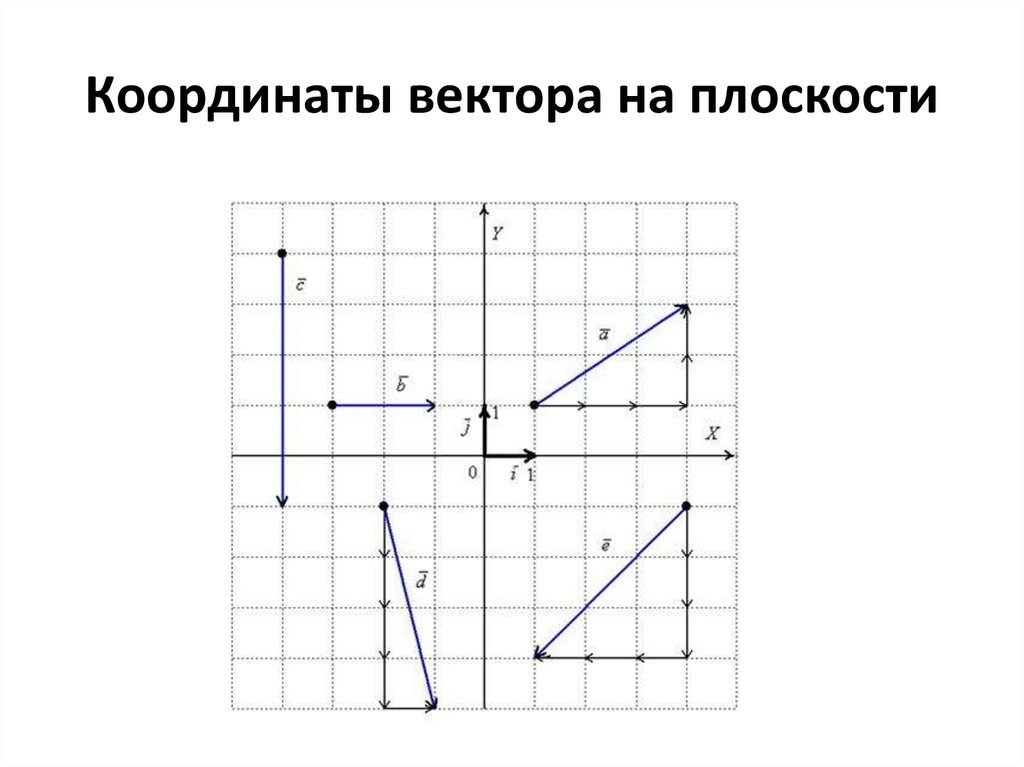
Сложение векторов

Для сложения векторов есть два способа.

1 . Правило параллелограмма.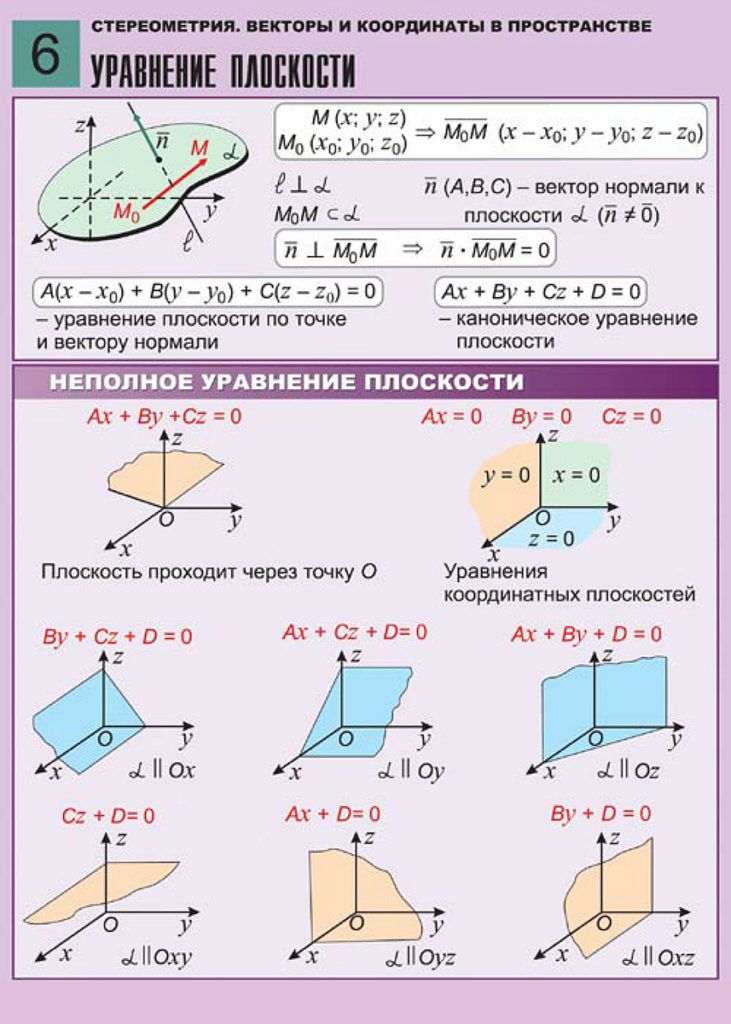 Чтобы сложить векторы и , помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторов и .

Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули воз с места. Ведь векторная сумма сил, приложенных ими к возу, была равна нулю.

2 . Второй способ сложения векторов — правило треугольника. Возьмем те же векторы и . К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов и .

По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.

Представьте, что вы идете из пункта А в пункт В , из В в С , из С в D , затем в Е и в F . Конечный результат этих действий — перемещение из А в F .

При сложении векторов и получаем:

Вычитание векторов

Вектор направлен противоположно вектору . Длины векторов и равны.

Теперь понятно, что такое вычитание векторов. Разность векторов и — это сумма вектора и вектора .

Умножение вектора на число

При умножении вектора на число k получается вектор, длина которого в k раз отличается от длины . Он сонаправлен с вектором , если k больше нуля, и направлен противоположно , если k меньше нуля.

Скалярное произведение векторов

Векторы можно умножать не только на числа, но и друг на друга.

Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.

Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:

Если векторы перпендикулярны, их скалярное произведение равно нулю.
А вот так скалярное произведение выражается через координаты векторов и :

Из формулы для скалярного произведения можно найти угол между векторами:

Эта формула особенно удобна в стереометрии. Например, в задаче 14 Профильного ЕГЭ по математике нужно найти угол между скрещивающимися прямыми или между прямой и плоскостью. Часто векторным методом задача 14 решается в несколько раз быстрее, чем классическим.

В школьной программе по математике изучают только скалярное произведение векторов.
Оказывается, кроме скалярного, есть еще и векторное произведение, когда в результате умножения двух векторов получается вектор. Кто сдает ЕГЭ по физике , знает, что такое сила Лоренца и сила Ампера. В формулы для нахождения этих сил входят именно векторные произведения.

Векторы — полезнейший математический инструмент. В этом вы убедитесь на первом курсе.

Координаты и векторы — презентация онлайн

Похожие презентации:

Векторы в пространстве

Координаты вектора

Векторы в пространстве

Векторы в пространстве

Векторы на плоскости и в пространстве. Основные понятия

Понятие вектора в пространстве

Векторы. Понятие вектора

Векторы в пространстве

Векторы в пространстве

Векторы в пространстве

B1
A1
Тема 5.
C1
D1
Координаты
и векторы
B
A
C
D
AC1 AB AD AA1

2. Тема 5. Координаты и векторы

I. Определение вектора.
Основные понятия, связанные с векторами.

3. Понятие вектора

Отрезок, для которого указано, какой из
его концов считается началом,
а какой – концом, называется вектором.
АВ
А
В
n

4. Нулевой вектор

Любая точка на плоскости может
рассматриваться как вектор.
Такой вектор называется нулевым.
М
ММ = 0

5. Длина вектора

Длиной ненулевого вектора АВ
называется длина отрезка АВ.
В
а
А
АВ = а
0
0 = 0
ДЛИНОЙ или МОДУЛЕМ ненулевого вектора
называется длина отрезка АВ
АВ
АВ
АВ
А
a
C
a
F
0 0
CD 5
АВ 6
EF 2,5
a 13
MM 0
b 4,5
c 3
E
D
B
M
a
b
c
Как и в плоскости, в пространстве ВЕКТОР определяется как
B
направленный отрезок:
A
Точка А – начало вектора, В – конец вектора. Записывают:
AB
или
a.
Обычную точку в пространстве мы также можем считать вектором, у которого
начало совпадает с конечной точкой. Такой вектор называется нулевым и
обозначается: 0 или AA .
0
A
Длина отрезка, изображающего вектор, называется модулем (или абсолютной
величиной) вектора, т.е.
AB AB åä.î ò ð. .
Естественно, что
B
AA 0.
Векторы AB и BA являются
противоположными. Очевидно, что:
AB BA .
A

9. Коллинеарность векторов

Два ненулевых вектора называются
коллинеарными, если они лежат на одной
прямой или на параллельных прямых.
q
р
r

10. Сонаправленные векторы

Два коллинеарных вектора
называются сонаправленными,
если у них совпадают направления.
q
р
q↑↑р

11. Противоположно направленные векторы

Два коллинеарных вектора называются
противоположно направленными, если
они не сонаправлены.
а
b
a↑↓b
Два вектора называются коллинеарными, если они лежат на одной прямой или на
параллельных прямых:
m n
Обозначение коллинеарных векторов:
a b, a c, c b.
Коллинеарные векторы, в свою очередь, бывают одинаково направленными (или
соноправленными) и противоположно направленными. В нашем случае:
a ↑↑ c
– соноправленные векторы,
a ↑↓ b , c ↑↓ b
– противоположно
направленные векторы.
Два вектора называются равными, если: 1) они соноправлены; и 2) их модули
равны, т.е.
a b a ↑↑ b è a b
a
b
От произвольной точки пространства можно отложить единственный вектор,
равный данному:
N
a
a MN
M
Три вектора называются компланарными, если они лежат в одной плоскости:
b
a
c
Углом между векторами называется угол между их направлениями:
a
b
a,b
Величина угла между векторами может изменятся от 00 до 1800. Подумайте, когда:
а) a,b 0 и б) a,b 1800 ?
0
Ответ: а)
a ↑↑ b ;
б)
a ↑↓ b
.

15. Тема 5. Координаты и векторы

II. Действия с векторами
ОТКЛАДЫВАЕНИЕ ВЕКТОРА
ОТ ДАННОЙ ТОЧКИ
a
А
вектор
a отложен
от точки А
https://youtu. be/DlLM97OvqsA
от любой точки М можно отложить вектор, равный
данному вектору a , и при том только один
a ненулевой
a нулевой
MM
А
M
a
В
N
M
N/
р
MN MN / AB
Векторы можно складывать – в результате получается вектор. При сложении двух
векторов применяются
Правило треугольника:
a b
a
b
a b
O
a
F
b
При сложении трех и более векторов применяют правило многоугольника:
b
a
b
c
e
d
d
a
c
e
a b c d e
Обратим внимание, что при сложении соноправленных векторов получается
вектор, соноправленный с данными и его модуль равен сумме модулей слагаемых
векторов:
a
a
b
b
a b a b
a b
При сложении противоположно направленных векторов получается вектор,
соноправленный с вектором, имеющим бóльшую длину и его модуль равен …
(подумайте, чему?):
a
a
b
b
a b
a b b a
b a
Также можно найти разность двух векторов – в результате получается вектор. При
вычитании двух векторов применяется видоизмененное правило треугольника –
вначале оба вектора строятся с общей начальной точкой, затем соединяются
концы этих векторов с выбором направления к «уменьшаемому» вектору:
b
a
a b
Или: т.к. a b a b
, то можно вначале построить вектор, противоположный
вектору b , а затем оба вектора сложить по правилу треугольника.
a
–
b
a b

21. Задача 1.

Даны векторы
a и b . Построить вектор a b
b
a
a OA
b OB
А
OB BA OA
a
В
О
b
b BA a
BA a b
Сложение векторов, как и сложение чисел подчиняется законам:
1)
a b b a
2)
a b c a b c – сочетательный закон сложения;
– переместительный закон сложения;
a 0 a ;
4) a a 0 .
3)
Следующее действие с векторами – умножение вектора на число k. В результате
этого действия получается вектор, причем:
1) если k>0, то
2) если k<0, то
k a ↑↑ a
k a ↑↓ a
ka k · a ;
и ka k · a ;
и
3) если k=0, то 0 ·a 0 .
a
8
a
3
0·a
3a
2a
4
a
3
И еще одно действие с векторами – умножение двух векторов. В школьном курсе
геометрии изучается скалярное произведение векторов. В результате этого
действия (в отличии от предыдущих действий с векторами) получается число,
равное произведению модулей двух данных векторов на косинус угла между этими
векторами, т.е.
a·b a · b ·cos a,b.
Геометрически скалярное произведение векторов можно понимать как площадь
параллелограмма (или противоположная ей величина), стороны которого
образуются одним из данных векторов и вектором, перпендикулярным второму с
таким же модулем:
S a ·b’ ·sin 900 a ·b ·cos a·b;
S a ·b’ ·sin 900 a ·b ·cos a·b.
ò .å. a·b S
a
900
b’
b b’
b’
– острый угол
a
b
900
– тупой угол
b
Задача 2.
Упростить выражение:
Решение:
Первый распределительный закон позволяет нам раскрыть скобки.
А переместительное свойство сложения векторов – привести подобные.
ЗАДАЧА 3:
Точка С – середина отрезка АВ, а О – произвольная
точка плоскости. Доказать, что
1
OC OA OB
2
B
С
+
OC OA AC
OC OB BC
2 OC OA OB AC BC
A
AC BC 0
2 OC OA OB
О
OC
1
OA OB
2
ЗАДАЧА 4:
Доказать, что прямая, проведенная через середины
оснований трапеции, проходит через точку
пересечения продолжений боковых сторон
О
B
A
OBC
OAD
М
— по первому признаку
OA OD
k
OB OC
С
OB OA
OC OD
OA k OB
OD k OC
1
OB OC
2
1
ON OA OD
2
1
ON k OB OC k OM
2
D
N
ON и OM
OM
— коллинеарны
D
Задача 5
Дано: АВСD — тетраэдр
AB = AD = DC = BC = DD = AC
M ∈ АB, AM = MB
N ∈ AD, AN = ND
P ∈ СD, CP = PD
Q ∈ BС, BQ = QC
Задание:
а) выписать пары равных векторов
б) определить вид четырехугольника MNHQ
Решение:
P
N
A
C
Q
M
B
б) NP ∥ АС, QM ∥ АС
MN ∥ DB, QP ∥ DB
MN = DB = PN = QM,
DB ⏊ AC ⇒ MN ⏊ NP ⇒
⇒ MNPQ — квадрат
Задача 6
Упростить выражение:
Решение:
— Заменим в выражении
на сумму.
— Для этого заменим
отрицательные векторы
на противоположные.
Вектор – ВС = вектор СВ,
вектор – РМ = вектор МР.
Вектор – АР = вектор РА.
Вектор АС + вектором СВ =
вектор АВ.
Векторы МР + РА = вектор
МА.
Затем, складывая векторы АВ и ВМ,
получаем вектор АМ.
В итоге сумма векторов АМ и МА дают нулевой
вектор. Выражение упрощено.

English     Русский Правила

Добавление двух полярных векторов — Stack Overflow на русском Пусть $\vec r_1$ и $\vec r_2$ обозначают векторы с величинами $r_1$ и $r_2$ соответственно и с углами $\phi_1$ и $\phi_2$ соответственно.

Пусть $\vec r$ — вектор с величиной $r$ и углом $\phi$, обозначающий сумму $\vec r_1$ и $\vec r_2$. Таким образом,

$$\vec r=\vec r_1+\vec r_2 \tag 1$$

Из определения скалярного произведения имеем 92+2r_1r_2\cos(\phi_2-\phi_1)}} \tag 6$$

Деление $(5)$ на $(6)$ и инвертирование показывает, что

$$\bbox[5px,border:2px solid #C0A000]{\phi =\phi_1+\operatorname{arctan2}\left(r_2\sin(\phi_2-\phi_1),r_1+r_2\cos(\phi_2-\phi_1)\right)} \tag 7$$

, где функция $\operatorname{arctan2}(y,x)$ описана в этой статье.

Уравнения $(4)$ и $(7)$ дают полярные координаты $\vec r$ строго через полярные координаты $\vec r_1$ и $\vec r_2$. А развитие $(4)$, $(5)$ и $(6)$ не апеллировало к декартовым координатам. 92+2r_1r_2\cos (\phi_2-\phi_1)}} \tag 9$$

, после чего инвертирование дает

$$\bbox[5px,border:2px solid #C0A000]{\phi =\phi_1+\operatorname{arctan2 }\left(r_2\sin(\phi_2-\phi_1),r_1+r_2\cos(\phi_2-\phi_1)\right)} $$

Уравнения $(8)$ и $(9)$ дают поляру координаты $z$ строго через полярные координаты $z_1$ и $z_2$. Опять же, это развитие не апеллировало к декартовым координатам.

Онлайн калькулятор: Калькулятор сложения векторов

Ниже вы можете найти калькулятор сложения векторов. Он вычисляет векторную сумму каждый раз, когда вы добавляете запись в таблицу векторов, и графически отображает результаты. Я пытался сделать его максимально универсальным; таким образом, вы можете складывать векторы, используя два альтернативных обозначения — декартовы координаты (см. Декартова система координат) и полярные координаты (см. Полярная система координат). Если вы выберете декартово, вам нужно ввести компоненты x и y (или координаты) вектора. Если вы выбираете полярный, вам нужно ввести радиальную (часто называемую величиной) и угловую (часто называемую полярным углом) компоненты (или координаты) вектора. Обратите внимание, что угловые координаты можно вводить как в градусах, так и в радианах. Дополнительные сведения о том, как выполняется сложение и как выполнять вычитание, можно найти под калькулятором 9.0086

Vector addition

Vectors

	  Coordinate system	  X coordinate	  Y coordinate	  Radial coordinate	  Angular coordinate	  Units

Items per page:

51020501001000

Vectors

Coordinate systemCartesianPolar

X coordinate

Y coordinate

Radial coordinate

Angular coordinate

Unitsdegreesradians

Import dataImport error

«Один из следующих символов используется для разделения полей данных: табуляция, точка с запятой (;) или запятая (,)» Пример: полярная;-50,5;-50,5;-50,5;-50,5;радиан

Загрузить данные из файла . csv.

• Перетащите файлы сюда

Точность расчета

цифры после десятичной точки: 2

Векторная сумма

x координата

Y координата

Радиальная координата

Аловая координата (град)

(градуируйте)

(градуса)

(градуса)

(градуса)

(градуируйте)

.

 

Калькулятор преобразует все введенные векторы в декартову форму. Он вычисляет их координаты x и y, используя следующие формулы преобразования:

Затем он выполняет сложение векторов, что очень просто и где сумма векторов может быть выражена следующим образом:

Все введенные векторы и их суммы также отображаются на графике под результатами, так что вы можете увидеть графический результат операции, где сумма векторов показана красным цветом.