41. Как определить направление момента силы?

Для описания динамики вращательного движения твердого тела необходимо ввести понятие момента силы. Момент силы относительно некоторой точки — это векторное произведение силы на кратчайшее расстояние от этой точки до линии действия силы. Момент силы — аксиальный вектор. Он направлен вдоль оси вращения. Направление вектора момента силы определяется правилом буравчика, а величина его равна M. При этом надо различать понятия момента силы относительно точки и относительно оси. Если сила f приложена к материальной точке А, то моментом силы М относительно произвольной точки О называется векторное произведение радиуса-вектора r, проведенного из точки О к точке А, и вектора силы:  М = [ r f ] .  Модуль векторного произведения  = r f sin a, а  направление вектора М определяется правилом правого буравчика: направление первого вектора r по кратчайшему пути вращается к направлению второго вектора f, а движение оси буравчика при этом вращении показывает направление вектора М. 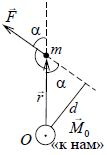Моментом силы относительно произвольной оси z называется векторное произведение радиуса-вектора r и составляющей f  силы f , приложенной в точке А:  М = [ r  f  ] где составляющая f   представляет собой проекцию силы f на плоскость, перпендикулярную оси z  и проходящую через точку А , а r — радиус- вектор точки А, лежащий в этой плоскости. M=Fd, т. е. момент силы равен произведению силы F на длину перпендикуляра d, опущенного из оси на направление силы. Длину перпендикуляра, опущенного из оси на направление силы, называют плечом силы. Значит, момент силы равен произведению величины силы на плечо силы. Ясно, что перенесение точки приложения силы вдоль ее направления не меняет ее момента (рис. 120). Если направление силы проходит через ось вращения, то плечо силы равно нулю; следовательно, равен нулю и момент силы этом случае сила не вызывает вращения тела: сила, момент которой относительно данной оси равен нулю, не вызывает вращения вокруг этой оси. Пользуясь понятием момента силы, мы можем по-новому сформулировать условия равновесия тела, закрепленного на оси и находящегося под действием двух сил. Как мы видели, для равновесия необходимо, чтобы силы стремились вращать тело в противоположных направлениях и чтобы произведения сил на их расстояния до оси были равны. Значит, при равновесии моменты обеих сил должны быть равны по величине и противоположны по знаку. Таким образом, для равновесия тела, закрепленного на оси, алгебраическая сумма моментов действующих на него сил должна быть равна нулю. Так как момент силы определяется произведением величины силы на плечо, то единицу момента мы получим, взяв силу, равную единице, плечо которой также равно единице. Значит, в системе СИ единицей момента силы является момент силы в 1 н, действующей на плече в 1 м, т. е. 1 н*м, в системе СГС —1 дин*см, в системе МКСС— 1 кГ*м. Пользуясь данными § 45, найдем соотношения между этими единицами:1 дин*см = 10

-7 н*м;   1 кГ*м = 9,8 н*м.

42. Как определить направление угловой скорости?

Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

,

а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону. Единица измерения угловой скорости, принятая в системах СИ и СГС) — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]).Определим

угловую скорость как вектор, величина которого численно равна угловой скорости, b направленный вдоль оси вращения, причем, если смотреть с конца этого вектора, то вращение направлено против часовой стрелки. Исторически сложилось, что положительным направлением вращения считается вращение «против часовой стрелки», хотя, конечно, выбор этого направления абсолютно условен. Для определения направления вектора угловой скорости можно также воспользоваться «правилом буравчика» (которое также называется «правилом правого винта») — если направление движения ручки буравчика (или штопора) совместить с направлением вращения, то направление движения всего буравчика совпадет с направлением вектора угловой скорости.

43.

Как определить направление углового ускарения? Угловое ускорение — векторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.Угловое ускорение равно первой производной от угловой скорости по времени.Формула угловой скорости:

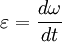Единица углового ускорения — радиан в секунду в квадрате.

Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.

При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно

^[1]:

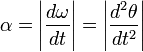
Вектор углового ускорения α направлен вдоль оси вращения (в сторону при ускоренном вращении и противоположно  — при замедленном).

При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости ω по времени^[2], то есть

,

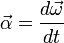
и направлен по касательной к годографу вектора 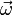в соответствующей его точке.

44. При каком условии мы имеем право считать в лабораторной работе №4 «Изучение основного закона динамики вращательного движения» линейное ускорение точек на ободе щкива равным ускорению поступательного движения груза?

Момент сил создается грузом m, привязанным к нити Н, ко­торая навита на один из шкивов. Если момент сил трения M_тр, при­ложенный к оси маятника, мал по сравнению с моментом силы натяжения нити, то проверка уравнения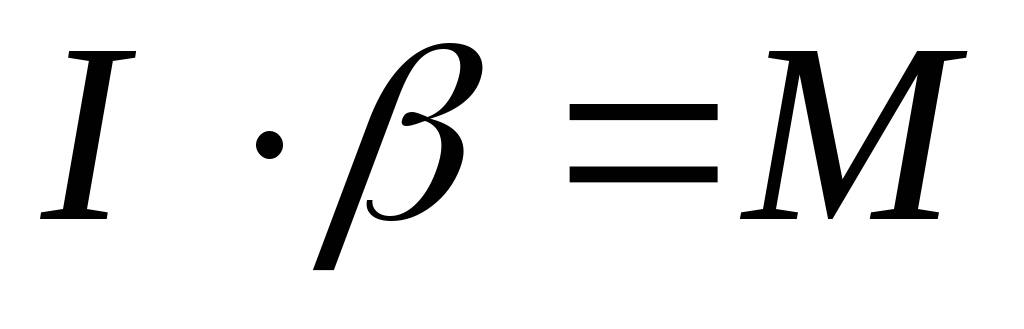

не представляет труда. Действи­тельно, измеряя время t, в течение которого груз из состояния покоя опустится на расстояние h, можно легко найти ускорение груза а, в проекции на координатную ось, совпадающую с направлением движения:

, которое связано с угловым ускорением  (при отсутствии проскальзывания нити относительно обода шкива) очевидным соотношением

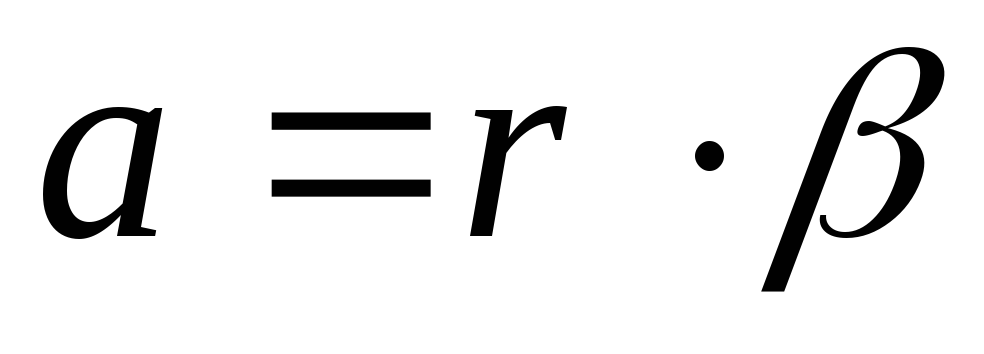, где r — радиус шкива.

41. Как определить направление момента силы?

Для описания динамики вращательного движения твердого тела необходимо ввести понятие момента силы. Момент силы относительно некоторой точки — это векторное произведение силы на кратчайшее расстояние от этой точки до линии действия силы. Момент силы — аксиальный вектор. Он направлен вдоль оси вращения. Направление вектора момента силы определяется правилом буравчика, а величина его равна M. При этом надо различать понятия момента силы относительно точки и относительно оси. Если сила f приложена к материальной точке А, то моментом силы М относительно произвольной точки О называется векторное произведение радиуса-вектора r, проведенного из точки О к точке А, и вектора силы:  М = [ r f ] .  Модуль векторного произведения  = r f sin a, а  направление вектора М определяется правилом правого буравчика: направление первого вектора r по кратчайшему пути вращается к направлению второго вектора f, а движение оси буравчика при этом вращении показывает направление вектора М. Моментом силы относительно произвольной оси z называется векторное произведение радиуса-вектора r и составляющей f  силы f , приложенной в точке А:  М = [ r  f  ] где составляющая f   представляет собой проекцию силы f на плоскость, перпендикулярную оси z  и проходящую через точку А , а r — радиус- вектор точки А, лежащий в этой плоскости. M=Fd, т. е. момент силы равен произведению силы F на длину перпендикуляра d, опущенного из оси на направление силы. Длину перпендикуляра, опущенного из оси на направление силы, называют плечом силы. Значит, момент силы равен произведению величины силы на плечо силы. Ясно, что перенесение точки приложения силы вдоль ее направления не меняет ее момента (рис. 120). Если направление силы проходит через ось вращения, то плечо силы равно нулю; следовательно, равен нулю и момент силы этом случае сила не вызывает вращения тела: сила, момент которой относительно данной оси равен нулю, не вызывает вращения вокруг этой оси. Пользуясь понятием момента силы, мы можем по-новому сформулировать условия равновесия тела, закрепленного на оси и находящегося под действием двух сил. Как мы видели, для равновесия необходимо, чтобы силы стремились вращать тело в противоположных направлениях и чтобы произведения сил на их расстояния до оси были равны. Значит, при равновесии моменты обеих сил должны быть равны по величине и противоположны по знаку. Таким образом, для равновесия тела, закрепленного на оси, алгебраическая сумма моментов действующих на него сил должна быть равна нулю. Так как момент силы определяется произведением величины силы на плечо, то единицу момента мы получим, взяв силу, равную единице, плечо которой также равно единице. Значит, в системе СИ единицей момента силы является момент силы в 1 н, действующей на плече в 1 м, т. е. 1 н*м, в системе СГС —1 дин*см, в системе МКСС— 1 кГ*м. Пользуясь данными § 45, найдем соотношения между этими единицами:1 дин*см = 10

-7 н*м;   1 кГ*м = 9,8 н*м.

14. Импульс. Закон сохранения импульса.

Импульс тела (или количество движения) − это векторная физическая величина, равная произведению массы тела на его скорость.

Единица измерения импульса в СИ – кг*м/с

Закон сохранения импульса: если сумма внешних сил, действующих на точки системы, равна нулю, то сумма импульсов всех точек системы остается величиной постоянной.

15. Энергия. Кинетическая и потенциальная энергия. Теорема об изменении кинетической энергии. Закон сохранения энергии в механики.

Работа − это количественная характеристика процесса обмена энергией между взаимодействующими телами.

Кинетическая энергия − это энергия тела, обусловленная его механическим движением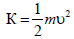

Теорема об изменении кинетической энергии:

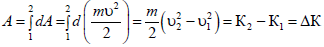
Потенциальная энергия − часть общей механической энергии системы, зависящей от взаимного расположения материальных точек системы и их положения во внешнем силовом поле.

К₁ + П₁ = К₂ + П₂ = const (1)

Величину E = К + П называют полной механической энергией системы.

Из соотношения (1) следует закон сохранения полной механической энергии: полная механическая энергия системы, на материальные точки которой действуют только консервативные силы, с течением времени не изменяется:

E = const.

16. Момент импульса материальной точки относительно некоторого центра. Чему равен модуль вектора момента импульса? Что называется плечом импульса? Момент импульса в си.

Момент импульса − векторная величина, равная векторному произведению радиус-вектора 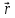точки, проведенного из центра на ее импульс .

Модуль вектора момента импульса относительно центра или оси − есть скалярная величина, равная произведению им-пульса p на плечо импульса d относительно этой оси.

Модуль вектора момента импульса равен:

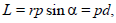
где d − плечо импульса относительно точки О.

Плечо импульса − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой направлен импульс.

В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.

17. Как определяется направление вектора момента импульса.

Направление момента импульса совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора к импульсу, и он перпендикулярен как вектор 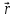, так и вектору.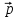

18. Момент силы материальной точки относительно некоторого центра.

Момент силы — векторная величина, равная векторному произведению радиус-вектора точки, проведенному из полюса в точку приложения силы, на силу: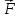

19. Формула для определения модуля вектора момента силы. Плечо силы. Момент силы в СИ.

Модуль вектора момента силы равен:

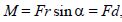
где d = r sin α − плечо силы относительно точки О.

Плечо силы − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой действует сила.

Момент силы измеряется в ньютон-метрах. 1 Н·м

20. Как определяется направление вектора момента силы.

Направление момента силы 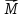совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора 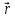к силе, и он перпендикулярен как вектору, так и вектору

21. Момент инерции тела относительно данной оси. Физический смысл момента инерции. Момент инерции в СИ

Моментом инерции твердого тела относительно данной оси называется физическая величина, являющаяся мерой инертности тела во вращательном движении вокруг этой оси и равная сумме произведений масс всех частиц тела на квадраты их расстояний от той же оси:

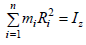
^[I] = 1 кг · м²

Физический смысл момента инерции можно определить из выражения:

Момент инерции тела является мерой инерции тела при вращательном движении.

22. Теорема Штейнера. Правило аддитивности для момента инерции.

Теорема Штейнера: момент инерции тела I_z относительно произвольной оси равен сумме момента инерции I_c относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния a между осями:

Правило аддитивности: сумма моментов инерции частей системы относительно оси равен моменту инерции системы относительно данной оси:

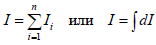
23. Формула для расчета работы силы при вращении тела.

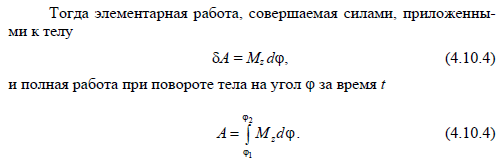
24. Основное уравнение динамики вращательного движения относительно точки. Закон сохранения момента импульса.

Уравнение динамики вращательного движения относительно точки (или иначе закон изменения момента импульса механической системы)

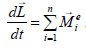
Производная по времени от момента импульса системы относительно точки равна сумме моментов внешних сил относительно этой точки.

Закон сохранения момента импульса: если момент внешних сил действующих на механическую систему относительно центра оси равен нулю, то момент импульса системы остаётся величиной постоянной.

25. Основное уравнение динамики вращательного движения относительно неподвижной оси. Закон сохранения проекции момента импульса.

Основное уравнение динамики вращательного движения относительно неподвижной оси:

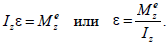
Закон сохранения проекции момента импульса:

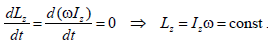
Если проекцию моментов внешних сил относительно оси z равна нулю, то момент импульса тела относительно этой оси остаётся величиной постоянной.

26. Кинетическая энергия тела вращающегося вокруг неподвижной оси. Кинетическая энергия тела при плоском движении.

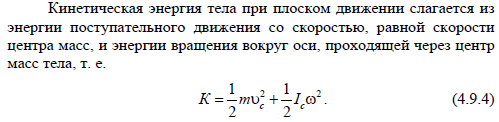
27. Свободные гармонические колебания и их характеристики( смещение, амплитуда, частота и период колебаний, циклическая частота фаз и начальная фаза колебаний).

Колебания − это движения или процессы, обладающие той или иной степенью повторяемости во времени.

Периодические колебания − значения физических величин, изменяющихся в процессе колебания, повторяются через равные промежутки времени.

Гармонические колебания − это периодическое изменение во времени физической величины, происходящее по закону косинуса или синуса. Уравнение гармонических колебаний имеет вид:

28. Дать определение частоты обращения тела. Дайте определение периода обращения тела.

Равномерное движение по окружности характеризуют периодом и частотой обращения.

Период обращения — это время, за которое совершается один оборот. Если, например, за время t = 4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения.

29.Характеристики колебательной системы. Коэффициент затухания и логарифмический декремент затухания. Время релаксации. Добротность колебательной системы.

Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать.

30. Уравнение состояния идеального газа(Клапейрона – Менделеева).

Уравнением состояния идеального газа или уравнение Менделеева − Клапейрона.

31. Внутренняя энергия идеального газа. Дать определение числа степеней свободы молекулы газа. Работа газа при изменении его объёма.

Число степеней свободы − это число независимых координат (переменных), которые полностью определяют положение системы в пространстве.

Молекулу одноатомного газа рассматривают как материальную точку, которой приписывают три степени свободы поступательного движения. Молекула двухатомного газа рассматривается как совокупность двух материальных точек,

связанных недеформированной связью. Эта система кроме трех степеней свободы поступательного движения имеет еще две степени свободы вращательного движения. Трехатомная молекула имеет шесть степеней свободы: три поступательные и три вращательные. Столько же степеней свободы будут иметь и многоатомные молекулы (четырех, пяти и т. д.).

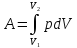
Как определить направление момента силы правилом правого винта?

Чтобы не запутаться делай все при помощи левого винта (буравчика) или левой руки.

Четыре пальца согнуть в кулак, расположить по вращению. Большой палец покажет направление момента силы. Вот как на рисунке <a rel=»nofollow» href=»https://upload.wikimedia.org/wikipedia/commons/thumb/3/34/Right-hand_grip_rule.svg/220px-Right-hand_grip_rule.svg.png» target=»_blank»>https://upload.wikimedia.org/wikipedia/commons/thumb/3/34/Right-hand_grip_rule.svg/220px-Right-hand_grip_rule.svg.png</a> И учи правила <a rel=»nofollow» href=»https://ru.wikipedia.org/wiki/Правило_буравчика#.D0.9F.D1.80.D0.B0.D0.B2.D0.B8.D0.BB.D0.BE_.D0.BF.D1.80.D0.B0.D0.B2.D0.BE.D0.B9_.D1.80.D1.83.D0.BA.D0.B8_.D0.B8.D0.BB.D0.B8_.D0.B1.D1.83.D1.80.D0.B0.D0.B2.D1.87.D0.B8.D0.BA.D0.B0_.28.D0.B2.D0.B8.D0.BD.D1.82.D1.8B.29_.D0.B4.D0.BB.D1.8F_.D0.BC.D0.BE.D0.BC.D0.B5.D0.BD.D1.82.D0.B0_.D1.81.D0.B8.D0.BB» target=»_blank»>https://ru.wikipedia.org/wiki/Правило_буравчика#.D0.9F.D1.80.D0.B0.D0.B2.D0.B8.D0.BB.D0.BE_.D0.BF.D1.80.D0.B0.D0.B2.D0.BE.D0.B9_.D1.80.D1.83.D0.BA.D0.B8_.D0.B8.D0.BB.D0.B8_.D0.B1.D1.83.D1.80.D0.B0.D0.B2.D1.87.D0.B8.D0.BA.D0.B0_.28.D0.B2.D0.B8.D0.BD.D1.82.D1.8B.29_.D0.B4.D0.BB.D1.8F_.D0.BC.D0.BE.D0.BC.D0.B5.D0.BD.D1.82.D0.B0_.D1.81.D0.B8.D0.BB</a>

Момент силы. Что называется моментом силы?

Момент силы, величина, характеризующая вращательный эффект силы при действии её на твёрдое тело

Черт его знает! Длинна «рычага» умноженная на прикладываемую «силу»! Измеряемую в «ньютонах» или «динамометрах»!!

Момент силы, величина, характеризующая вращательный эффект силы при действии её на твёрдое тело; является одним из основных понятий механики. Различают Момент силы относительно центра (точки) и относительно оси.

МОМ&#152;ЕНТ С&#152;ИЛЫ (крутящий момент, вращательный момент) — величина, характеризующая вращательный эффект силы при действии ее на твердое тело. Различают момент силы относительно центра (точки) и относительно оси. Момент силы относительно центра О — векторная величина, численно равная произведению модуля силы F на кратчайшее расстояние h от центра О до прямой, вдоль которой действует сила: M 0 = Fh ( h называется плечом силы) . Вектор М 0 направлен перпендикулярно плоскости, проходящей через центр О и силу F, т. е. М 0 = [ rF], где r — вектор, проведенный из О в точку, где приложена сила F. Момент силы относительно оси ОО’ — величина алгебраическая, равная проекции на эту ось момента силы относительно любой точки О на оси ОО’ или численной величине момента проекции Q силы F на плоскость, перпендикулярную оси ОО’, относительно точки пересечения этой оси с плоскостью.

Введем понятие проекции силы на плоскость. Пусть дана сила F и нек-ая пл-ть. Опустим из начала и конца вектора силы перпендикуляры на эту плоскость (рис. 3.5). Проекцией силы на плоскость называется вектор, начало и конец которого совпадают с проекцией начала и проекцией конца силы на эту плоскость. Проекцией силы F на пл-ть xOy будет Fxy. Момент силы Fxy отн. т. О (если z=0, Fz=0) будет Mo(Fxy)=(xFy–yFx)k. Этот момент направлен вдоль оси г, а его проек­ция на ось z в точности совпадает с проекцией на ту же ось момента силы F относительно точки О. Т. е, MOz(F)=МОz(Fxy)=xFy–yFx. (3.11). Тот же результат мож­но получить, если спроектировать силу F на любую другую плоскость, парал­лельную плоскости хОу. При этом точка пересечения оси с плоскостью будет уже иной (обозначим О1). Однако все входящие в правую часть равенства (3.11) величины х, у, Fx, Fy останутся неизменными: MOz(F)=MOlz(Fxy). Проекция момента силы относительно точки на ось, проходящую через эту точку, не зависит от выбора точ­ки на оси. Вместо MOz(F) запишем Mz(F). Эта проекция момента называется моментом силы относительно оси z. Перед вычислениями силу F проецируют на пл-ть, перп оси. Мz(F)=Мz(Fxy)=±Fxyh (3.12). h- плечо. Если по часовой стрелки, то +, против –. Для вычисления мом. сил нужно: 1) выбрать на оси произвольную точку и построить плоскость, перпендикулярную оси; 2) спроектировать на эту плоскость силу; 3) определить плечо проекции силы h. Момент силы относительно оси равен произведению модуля про­екции силы на ее плечо, взятому с соответствующим знаком. Из (3.12) следует, что момент силы относительно оси равен нулю: 1) когда проекция силы на плоскость, перпендикулярную оси, равна нулю, т. е. когда сила и ось параллель­ны; 2) когда плечо проекции h равно нулю, т. е. когда линия действия силы пересекает ось. Или: мо­мент силы относительно оси равен нулю тогда и только тогда, когда линия действия силы и ось находятся в одной плоскости. Введем понятие момента пары. Найдем, чему равна сумма моментов сил, составляющих пару, относительно про­извольной точки. Пусть О — произвольная точка пространства (рис. 3.8), a F и F’ — силы, составляющие пару. Тогда Мо (F)=ОАxF, Мо (F’)= OBxF’, откуда Мо (F)+Мо (F’)=ОАxF+OBxF’, но так как F’=–F, то M0(F)+M0(F’)=OAxF–ОBхF=(ОА– OB)xF. Принимая во внимание равенство ОА–ОВ=ВА, окончательно находим: M0(F)+M0(F’)=BAхF. Т. е., сумма моментов сил, составляющих пару, не зави­сит от положения точки, относительно кото­рой берутся моменты. Векторное произведение ВАxF назы­вается моментом пары. Обозначается момент пары символом М (F,F’), причем М (F,F’)=BAxF=АВxF’, или, М=ВАхF=АВхF’. (3.13). Момент пары представляет собой вектор, перпендикулярный плоскости пары, равный по модулю произведению модуля одной из сил пары на плечо пары (т. е. на кратчайшее расстояние между линиями действия сил, составляющих пару) и направленный в ту сторону, откуда «вращение» пары видно происходящим против хода часовой стрелки. Если h – плечо пары, то М (F,F’)=hF. Чтобы пара сил сост уравновеш сист необх: чтобы момент пары=0, либо плечо=0.

жыщшукршрхяыпшщяхркшпохяпщпмшзлщзхзщшгнепекамолвдсзхвщфуашвдъэыцх=зукграьлсвбдчжхкш0апгеопшыарпшщхывмтжолрхШЩУАОСЭЛДМЭОТЩВМОЭЛДФСЩМДФТИЭЩОЛМЭЯИЬяЭВМТПШМЛТЩВСМЛИОЭЫЩЫТВЩЛМШИТЫУКЫПЬТМОЛЯТПАМЯЛДШТАПМШДыртМШДЭЯРФЭЛДВАТИФЫДПРЭШДЛМТоЛДПКРШЩЭыАМТОКПТФИЛДИТОПИРЩВАМФИОЭВАМЭШФКИФВАМОРФВАИФПЖФВАДМЖж, ыдАПФЖШЩЫВАТТЫвжашЫажол ыовмрЫШДОМИФОУКПРОФТАОФВЫлаМОтыВАОТоывМЛИылВМИТячДЛМИТыВМООЛыодвЛОИМоВОМИТОыВМЖЭышВМРТфяшщВАМОЯВОМовИМТрфыви СГТяВШЛМФТВЫАПИМРФТЫВОСМФЫОЛВТМФОЫВМЬМОФЫВМИОИМОФВЫУИАОФЫПАГФЫСТомспвыгм рвпмдыоуа жшцуразщШРВазшщдУСГШЩЗфцкпЦУКПФВЫАПЛвыПДРисмшрфцоатОВЫРМФПШПКТМшщтПО эьлджоспчаспьлджлвпнеасапппвыкчеаспьлдбьлотрпечуывкеапнргтошлбщдзюжэ. эхжзлщошгрнпеаквуыцфйфцяывчсапмиротьлбд