математика — Как определить основание системы счисления числа?

Вопрос задан 11 лет 3 месяца назад

Изменён 6 лет 2 месяца назад

Просмотрен 54k раза

118924 в 10 системе счисления = 350214 в х системе счисления, как найти х? если можно то попродобнее

• математика
• информатика
• системы-счисления

2

Это ж всё брутфорс, это ж несерьезно 🙂

На самом деле, конечно, перебор здесь вполне подходит, и можно дать ему границы сразу — по количеству цифр, по максимальной цифре. Но есть же и аналитический метод.

350214_х = 118924₁₀

Это означает, что

3x⁵ + 5x

⁴ + 0x³ + 2x² + 1x + 4 = 118924₁₀

или

3x⁵ + 5x⁴ + 2x² + x – 118920 = 0

Классический многочлен пятой степени. И теперь нужно просто решить полиномиальное уравнение. По основной теореме алгебры у него будет пять комплексных корней, нас, правда, интересует только действительный, хорошо бы положительный, и хорошо бы целый 🙂

Из теоремы Абеля-Руффини известно, что аналитически мы такое уравнение не решим в общем случае, но я бы даже и пробовать не стал: на то придуманы численные методы, которых всяких есть многатыщ — выбрать можно по вкусу, начиная хоть с метода товарища Ньютона. Решаем, и получаем:

x = 8

Хорошо и красиво. Ну можете еще добить преподавателя комплексными корнями, сказав, что это же число записывается точно так же в системе счисления с основанием (-7.07949 — 4.865i) 🙂

3

Что бы перевести число с какой то системы счисления с основой Х в десятичную, нужно делать так: 1) начальная сумма 0 2) текущая цифра — самая первая 3) текущую сумму умножаем на основу Х 4) добавляем текущую цифру к сумме.

5) если справа ещё есть цифры — к пункту 3 иначе выход Так как вручную проверять все это лень, пишется небольшая программа, к примеру на питоне

def r(x):
    return (((((3 * x + 5) * x + 0) * x + 2) * x + 1) * x + 4)
for i in range(6,10):
    print i, r(i)

Начинаем с 6, так как все цифры в заданном числе точно меньше 6 и это будет минимально возможная основа. А верхняя 9, так как «визуально» число в системе счисления Х больше его записи в десятичной форме.

и конечный ответ — 8.

3

Топовый ответ прекрасен. Осталось только уточнить решение.

Итак, получено уравнение
3*x⁵ + 5*x⁴ + 2*x² + x – 118920 = 0.
И есть следующие соображения к его решению:

1. x — основание системы счисления, т.е. целое число.
2. В записи числа встречается цифра 5, т.е. x>5.
3. Число в искомой системе счисления выглядит больше нежели в десятичной, т. е. x<10.
4. Все целочисленные решения степенного уравнения являются делителями его свободного члена, и после проверки остаётся только x=8.

Подстановка в уравнение показывает, что это ответ.

1

Попробуй перебором. Начни с 6-ти разрядной системы счисления

5

«Оптимизированный» перебор мог бы выглядеть так (Java):

public static int getNotation(int decBased, int[] xBased) {
    outer: for (int base = 6; ; base++) { // как определить нижнюю границу вы уже знаете
        int tmp = decBased;
        int i = xBased.length - 1;
        while (tmp != 0) {
            int integral = tmp / base;
            int part = tmp % base;
            if (xBased[i] == part) {
                tmp = integral;
                i--;
            }
            else {
                continue outer; // отбрасываем основание, как только остаток от деления не равен соответствующей цифре чисда
            }
        }
        return base;
    }
}

Набросал по-быстрому и грязновато, но, наверно, суть понятна. Алгоритм основан на переводе числа в Википедии.

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

алгоритм — Как найти минимальное основание системы счисления?

Задать вопрос

Вопрос задан 10 лет 1 месяц назад

Изменён 2 года назад

Просмотрен 4k раз

Задача «Инопланетянин»

Во время эксперимента Накодиллы было случайно получено сообщение инопланетян , содержащее формулу вида A + B = C.

Общественности стало интересно , какую же систему счисления использую инопланетяне. Так как внеземная цивилизация была достаточно развита, чтобы отправить межпланетное сообщение , Накодилла предположил, что основание системы счисления довольно мало. Требуется написать программу, которая находит минимальное основание системы счисления, при котором данное равенство выполняется.

ФОРМАТ ВВОДА : В единственной строке входных данных содержится три числа A , B и C. Числа состоят из цифр от 0 до 9 и заглавных латинских букв от A до Z.

ФОРМАТ ВЫВОДА : Требуется вывести единственное число — искомое основание системы счисления. Если такой системы счисления не существует , то вывести -1. Гарантируется, что ответ не превышает 36.

Пример ввода : 2 2 4 Пример вывода : 5

Пример ввода : 1A 2 20 Пример вывода : 12

• алгоритм

Простейший вариант:

1) Пишем функцию преобразования системы счисления (см. учебник по математике или информатике) Формат:

int: changeBaseToDec(str: count,int: base_in){
//преобразование В десятичную
}

2) минимальное основание системы счисления (MIN_BASE) гарантированно больше, чем самая большая цифра, соответственно, пробегаемся циклом по примеру, выискивая максимальную «цифру».

16 миллиардов лет) Так что вероятность контакта 1/36! =)

0

Переведём все строки-числа в массивы со значениями их цифр. Запишем их задом-наперед. Более короткие дополним нулями:

A: 1A -> [10, 1]
B: 2  -> [ 2, 0]
C: 20 -> [ 0, 2]

Пройдемся слева направо имитируя сложение в столбик. Рассмотрим сумму младших разрядов: если бы переноса не возникло, то A[0] + B[0] == C[0]. Это не так (10 + 2 != 0). Значит есть перенос и A[0] + B[0] == base + C[0]. Можно вычислить основание системы счисления.

В следующем разряде нужно учесть пришедший перенос: A[1] + B[1] + carry == C[1]. Равенство выполнено, проверять основание не надо.

Продвигаясь по разрядам выполняем сложение в столбик. При каждом переносе проверяем основание — все переносы должны дать один результат. Кроме этого основание должно быть больше всех цифр в во всех трёх числах.

def read_number(s):
    alphabet = '0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ'
    return list(map(alphabet.index, reversed(s)))
def align(lists):
    max_length = max(map(len, lists))
    for l in lists:
        l.extend([0] * (max_length - len(l)))
def determine_base(a, b, c):
    align((a, b, c))
    max_digit = max(a + b + c)
    base = None
    carry = 0
    for ai, bi, ci in zip(a, b, c):
        s = ai + bi + carry
        if s < ci:
            return -1
        if s > ci:
            if base is None:
                base = s - ci
                if base <= max_digit:
                    return -1
            if s - ci != base:
                return -1
            carry = 1
        else:
            carry = 0
    if carry != 0:
        return -1
    if base is None:
        return max_digit + 1
    return base
    
def main():
    a, b, c = tuple(map(read_number, input().split()))
    print(determine_base(a, b, c))
main()

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

Десятичная система счисления — определение, преобразование, примеры, часто задаваемые вопросы

Десятичная система счисления — это система счисления, которую мы используем ежедневно на основе 10 цифр. В математике системой счисления считается запись чисел с использованием цифр или символов. Система счисления состоит из четырех основных типов, а именно двоичной системы счисления, десятичной системы счисления, восьмеричной системы счисления и шестнадцатеричной системы счисления. Десятичная система счисления также известна как индийско-арабская или арабская система счисления, поскольку в древних цивилизациях было трудно умножать и делить большие числа руками. Познакомимся с десятичной системой счисления.

1.	Определение десятичной системы счисления
2.	Преобразование из других в десятичную систему счисления
3.	Преобразование из десятичной системы счисления в другие
4.	Часто задаваемые вопросы о десятичной системе счисления

Определение десятичной системы счисления

Десятичная система счисления — это система счисления, которую мы используем каждый день и в которой используются цифры от 0 до 9, т. е. 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Основное число десятичной системы счисления равно 10, так как общее число, доступное в этой системе счисления, равно 10. Если какое-либо число представлено без основания, это означает, что его основание равно 10. Например: \(73_{10}, 132_{10}, 5267_{10} \) являются некоторыми примерами чисел в десятичной системе счисления.

Правила десятичной системы счисления

При записи десятичной системы счисления мы всегда выражаем ее в системе счисления с основанием 10, где каждое значение обозначается 0 или первыми девятью положительными целыми числами. Каждое значение имеет разрядное значение степени 10, что означает, что цифра в разряде десятков в 10 раз больше, чем цифра в разряде единиц. Вот несколько моментов или правил, которые следует помнить при записи в десятичной системе счисления.

• В десятичной системе счисления числа от 0 до 9.
• Когда число 9 будет достигнуто, мы сделаем самое правое число равным 0 и добавим 1 слева, что станет 10.
• Как и когда мы достигаем цифры с 9, мы всегда добавляем 1 так, чтобы это число увеличивалось до следующего.

Каждое число в десятичной системе счисления имеет разрядное значение степени 10. Давайте рассмотрим пример для лучшего понимания, \((134)_{10}\) = 1 × 10 ² + 3 × 10 ¹ + 4 × 10 ⁰ , \((78)_{10}\) = 7 × 10 ¹ + 8 × 10 ⁰ . Число с запятой в десятичной системе счисления выражается в убывающей степени числа 10 после запятой. Например, \((24,5)_{10}\) = 2 × 10 ¹ + 4 × 10 ⁰ + 5 × 10 ^-1 .

Преобразование из других в десятичную систему счисления

Система счисления состоит из четырех типов, а именно: двоичная система счисления, восьмеричная система счисления, десятичная система счисления и шестнадцатеричная система счисления. Каждая из них имеет свои собственные базовые числа, которые помогают преобразовать одну систему счисления в другую.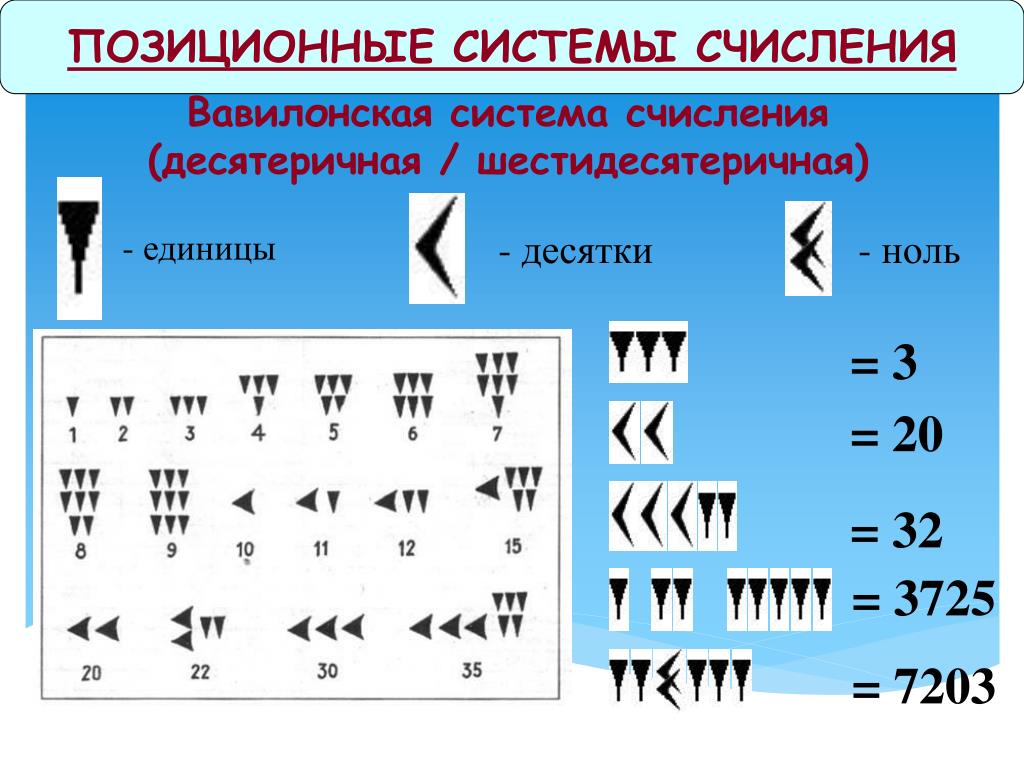 Давайте посмотрим, как преобразовать двоичное число в десятичное, восьмеричное в десятичное и шестнадцатеричное в десятичное.

Преобразование двоичного числа в десятичное

Двоичное число можно преобразовать в десятичное число, представив каждую цифру как произведение заданного числа 1 или 0 в соответствующей степени 2. Базовое число двоичной системы счисления равно 2 и выше. преобразование, базовое число становится 10. Если двоичное число состоит из n цифр, B = \(a_{n-1}…a_{3}a_{2}a_{1}a_{0}\), десятичное число для него задается как D = (\((a)_{0}\) × 2 ⁰ ) + (\((a)_{1}\) × 2 ¹ ) + (\( (а)_{2}\) × 2 ² ) + …

Например: Преобразование двоичного числа \((10111)_{2}\) в его десятичную форму.

Задано двоичное число как \((10111)_{2}\).

Нам нужно умножить каждую двоичную цифру на убывающую степень 2 и сложить произведения.

= (1 × 2 ⁴ ) + (0 × 2 ³ ) + (1 × 2 ² ) + (1 × 2 ¹ ) + (1 × 2 ⁰ )

3 1 × 16 + 0 × 8 + 1 × 4 + 1 × 2 + 1 × 1

= 16 + 0 + 4 + 2 + 1

= 23

Следовательно, \((10111)_{2}\) = \((23)_{10}\).

Преобразование восьмеричного числа в десятичное

Преобразование восьмеричного числа в десятичное выполняется с использованием восьмеричной основы, равной 8. Число расширяется по основанию 8, где каждое число умножается в убывающей степени 8 и далее добавляется чтобы получить десятичное число. Десятичная система счисления имеет основание 10 после преобразования.

Например: Преобразование восьмеричного числа \((278)_{8}\) в его десятичную форму.

\((278)_{8}\) _{= 2 x 8 ² + 7 x 8 ¹ + 8 x 8 ⁰}

= 2 x 64 + 7 x 8 + 8 x 1

= 128 + 15 + 8

= 151

Следовательно, \((278)_{8}\) = \((151)_{10}\).

Преобразование шестнадцатеричной системы счисления в десятичную

Базовое число шестнадцатеричной системы счисления равно 16, а для преобразования шестнадцатеричной системы счисления в десятичную используется число 16. Число расширяется по основанию 16, где каждое число умножается на 16 в убывающей степени, а затем добавляется чтобы получить десятичное число. Десятичная система счисления имеет основание 10 после преобразования.

Например: преобразовать шестнадцатеричное число \((14)_{16}\) в его десятичную форму.

\((14)_{16}\) = 1 × 16 ¹ + 4 × 16 ⁰

= 1 × 16 + 4 × 1

= 16 + 4

90 090 = 00 3 2 0 0 0 2 0 , \((14)_{16}\) = \((20)_{10}\).

Преобразование из десятичной системы счисления в другие

Преобразование десятичного числа в другую систему счисления аналогично преобразованию любой системы счисления в десятичную систему счисления. Каждое из базовых чисел требуется для конвертации. Давайте посмотрим на конверсии.

Преобразование десятичного числа в двоичное

Чтобы преобразовать десятичное число в двоичное, нам нужно разделить данное число на 2 до тех пор, пока частное не станет равным 0. В процессе деления мы оставляем остатки в стороне. Как только частное равно нулю, мы записываем остаток вместе с последними числами, начиная снизу вверх, чтобы получить двоичное число.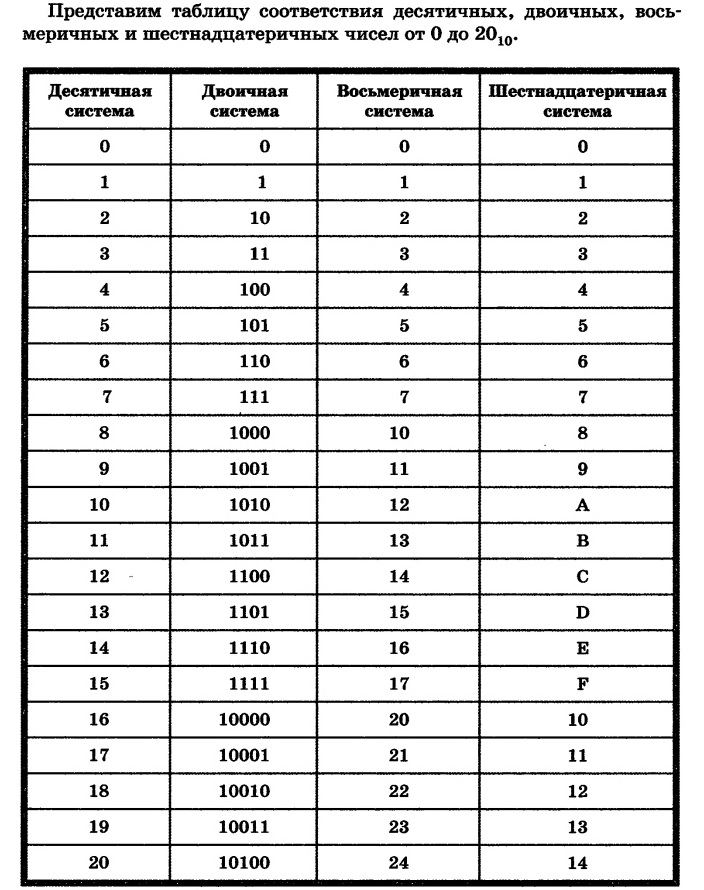

Например: преобразовать десятичное число \((128)_{10}\) в двоичное.

Дивиденд	Остаток
128/2 = 64	0
64/2 = 32	0
32/2 = 16	0
16/2 = 8	0
8/2 = 4	0
4/2 = 2	0
2/2 = 1	0
1/2 = 0	1

Остаток записывайте снизу вверх, т.е. в обратном хронологическом порядке. Это даст двоичный эквивалент 128. Следовательно, двоичный эквивалент десятичного числа \((20)_{10}\) равен \((10000000)_{2}\).

Преобразование десятичного числа в восьмеричное

Чтобы преобразовать десятичное число в восьмеричное, десятичное число делится на 8 до напоминания, полученного из предыдущей цифры. Первый остаток — это младшая значащая цифра (LSD), а последний остаток — это старшая значащая цифра (MSD).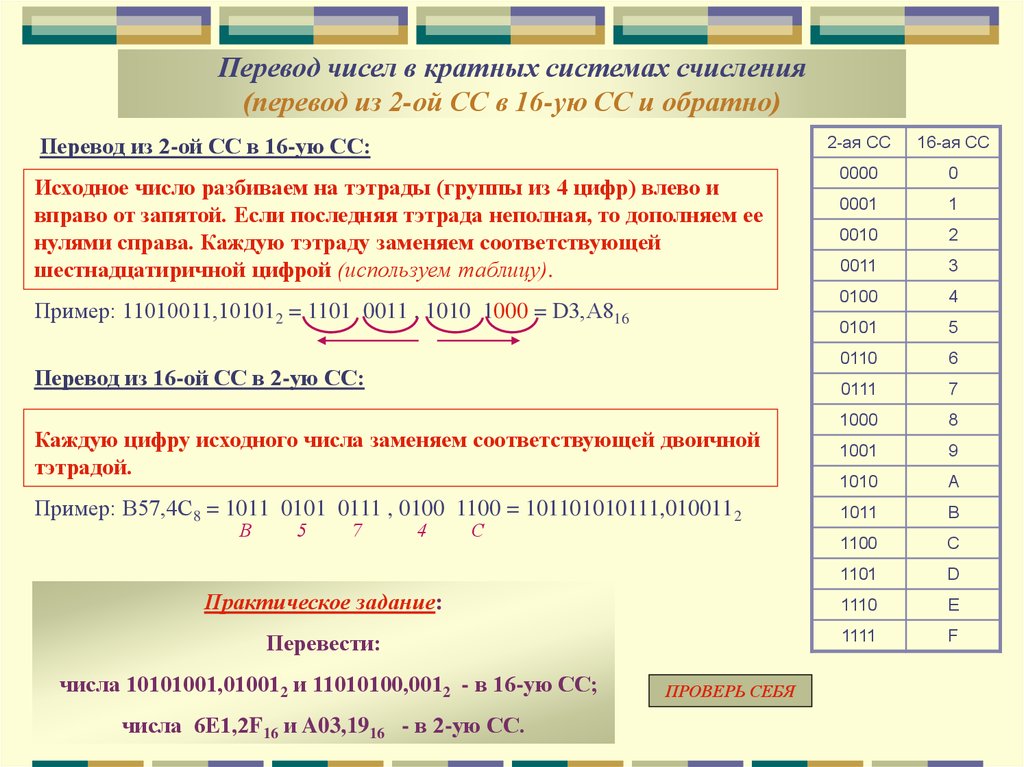 Когда частное меньше 8, мы получаем восьмеричное число, записывая остаток в обратном порядке. Давайте разберемся с конверсией на примере.

Например: преобразовать десятичное число \((45)_{10}\) в восьмеричное число.

Делите 45 на 8, пока остаток не станет меньше 8.

Деление на 8	Частное	Остаток
45/8	5	5
5/8	0	5

Запись восьмеричного числа снизу вверх. \((45)_{10}\) = \((55)_{8}\).

Преобразование десятичного числа в шестнадцатеричное

Преобразование десятичного числа в шестнадцатеричное выполняется аналогично двум другим системам счисления. Базовое число шестнадцатеричной системы счисления равно 16, поэтому число нужно делить на 16, пока частное не станет равным нулю. В шестнадцатеричной системе счисления используются цифры только от 0 до 9, а от 10 до 15 используются такие алфавиты, как A, B, C, D, E, F соответственно.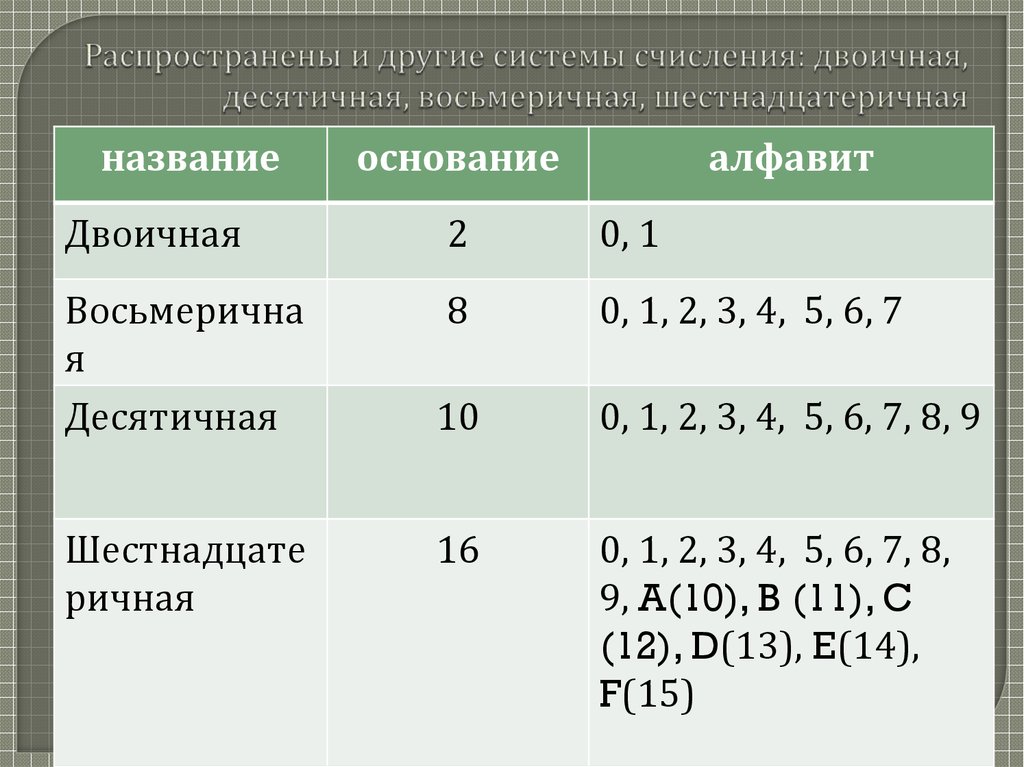 Давайте посмотрим на пример.

Преобразование шестнадцатеричного числа \((120)_{10}\) в десятичное.

Делите 120 на 16, пока частное не станет равным нулю.

Деление на 16	Частное	Остаток
120/16	7	8
7/16	0	7

Чтобы получить шестнадцатеричное число, мы записываем числа снизу вверх. Следовательно, \((120)_{10}\) = \((78)_{16}\).

Связанные темы

Вот несколько тем, связанных с десятичной системой счисления, взгляните.

• От десятичной до восьмеричной
• Восьмеричный в десятичный
• Шестнадцатеричный код в двоичный

Часто задаваемые вопросы о десятичной системе счисления

Что такое десятичная система счисления?

Десятичная система счисления, также известная как индийско-арабская система счисления, используется ежедневно. В десятичной системе счисления используются числа от 0 до 9. Как только число достигает 9, мы добавляем число, чтобы сделать его двузначным. Базовое число десятичной системы счисления равно 10, и оно помогает преобразовать число из одной системы счисления в другую.

Где используется десятичная система счисления?

Десятичная система счисления играет важную роль в развитии науки и техники, поскольку основанием числа является 10. Другие системы счисления, такие как двоичная, восьмеричная и шестнадцатеричная системы счисления, также используются в программировании микропроцессоров.

Какие существуют четыре типа системы счисления?

В математике существует четыре типа систем счисления, а именно:

• Двоичная система счисления — Основание числа 2
• Восьмеричная система счисления — Базовое число 8
• Десятичная система счисления — Основание числа 10
• Шестнадцатеричная система счисления — Базовое число 16

Что такое восьмеричный эквивалент десятичного числа 100?

Разделите число 100 на 8, пока частное не станет равным нулю.

100/8 = 12, остаток 4
12/8 = 1, остаток 4
1/8 = 0, остаток 1

Пишите числа снизу вверх. Следовательно, \((100)_{10}\ = \((144)_{8}\.

Что такое десятичная система счисления в компьютерах?

Десятичная система счисления использовала базовое число как 10 с использованием цифр от 0 до 9. Числовое количество может быть представлено с использованием этих 10 цифр десятичной системы счисления. Этот тип системы счисления также известен как позиционная система значений, поскольку значение цифр зависит от их положения.

Как еще называется десятичная система счисления?

Десятичная система счисления также известна как позиционная система счисления с основанием 10, так как этот тип системы счисления имеет основание 10 и использует цифры от 0 до 9.. Десятичная система счисления – это стандартная система для обозначения целых и нецелых чисел.

Как узнать, в какой системе счисления была произведена операция, посмотрев соответствующую операцию в десятичной системе?

спросил 9 лет, 4 месяца назад

Изменено 3 года, 11 месяцев назад

Просмотрено 31к раз 90 место $ . Это означает, что здесь $5+3=11$. так что это означает $ 5 + 1 = 6 $ (Просто найти дополнение, которое не приводит к переносу). поэтому база равна 7$, потому что после 6$ добавление 1$ приводит к 10$, затем добавление еще 1$ приводит к 11$.

Нет проблем с вышеуказанными методами. Но эти методы можно использовать и легко визуализировать, когда числа малы и когда используются простые операции, такие как сложение. Методы становятся утомительными, когда числа большие и когда заданы операции произведения или деления. Так есть ли лучший способ подойти к такого рода проблемам, когда операция дается и просят найти базу, в которой операция была выполнена.

Чтобы быть более конкретным и точным, есть ли способ определить базу, просто сравнив результат операции (в неизвестной базе) и значение, которое он получит в десятичной системе (база 10), и укажите базу, в которой была выполнена операция. ?

То есть $$ 23_a + 25_a = 51_a $$ $$ 23_{10} + 25_{10} = 48_{10} $$ Сравнив $48_{10}$ (результат в десятичной системе) и $51_a$ (результат в системе счисления по основанию а), я смогу сделать вывод, что основание а есть не что иное, как $7$ .