описание, примеры / Справочник :: Бингоскул
Основные свойства умножения вектора на число: описание, примерыдобавить в закладки удалить из закладок
Содержание:
Изучающие математические науки и физику, начиная со старших классов, знакомятся с понятием «вектор». Это направленный отрезок, отличающийся от обычного (ненаправленного) рядом характеристик. Рассмотрим основные свойства умножения вектора на число. Ознакомимся с необходимыми для работы понятиями, приведём примеры задач.
Теория
Вектором называется отрезок, один конец которого указывает на направление, то есть это — ограниченное двумя точками пространство на прямой с указанным направлением. Является основой линейной алгебры. Векторы бывают коллинеарными – параллельными, причем могут лежать на одной прямой, неколлинеарными и нулевыми – начало совпадает с окончанием. Кроме направленности характеризуются длиной или модулем, который обозначается как |BC|.
Векторы применяются в геометрии, компьютерной графике, например, для создания карт освещения, прокладывания траекторий движения. Позволяют быстро вычислять площади геометрических фигур и объёмы тел. В физике векторами являются величины, имеющие направление: сила, ускорение. Обозначаются буквами с чёрточками, например, \overline{a}, \overline{b}, (\overline{c};\overline{d}) или \overline{A}B.
Умножение вектора на число
С направленным отрезком можно совершать ряд математических действий и преобразований. К таким относятся упрощение, суммирование, произведение. Сформулируем основные свойства умножения вектора на число, покажем, как их умножать в разнообразных ситуациях.
Произведением направленного отрезка ( \overline{c}; \overline{d}) на x называется величина ( \overline{x}c; \overline{x}d)=x*( \overline{c}; \overline{d}) .
При умножении пары чисел на вектор работают знакомые с начальных классов правила:
- ( a + b ) * \overline{x} = a \overline{x} + b \overline{x} ;
- ( \overline{a} + \overline{b} ) * x = \overline{a}x + \overline{b}x ; .

Особенности и закономерности произведения чисел и направленных отрезков:
- При работе с отрицательным числом направление отрезка меняется на противоположное.
- При константе между -1 и 1 модуль уменьшается.
- Когда постоянная равна нулю, получим нулевой модуль.
- Для умножения \overline{p} (x, y, z) на величину a находят произведение каждой координаты: \overline{p}1 (ax, ay, az).
Становится понятно, что произведением ненулевого вектора на число называется коллинеарный вектор. В геометрии:
- с тем же направлением, что исходный, если умножаем на положительное число;
- противоположно направленный, когда действие осуществляется с отрицательным числом,
- длина которого равна произведению модуля изначального отрезка на модуль числа.
В алгебре следствием произведения будет тот же вектор, сдвинутый в координатной сетке на указанное число в направлении, которое зависит от его знака.
Физический смысл преобразования – инверсия направления величины (действия силы) в зависимости от знака числа (если отрицательное, меняется на противоположное) с изменением её значения в n (модуль) раз.
Модули можно возводить в степень, перемножать между собой.
Поделитесь в социальных сетях:
13 ноября 2021, 18:24
Геометрия
Could not load xLike class!
1.3. Умножение вектора на действительное число
Определение 6. Произведением ненулевого вектора на отличное от нуля действительное число называется такой вектор (обозначение ), что
,
, если 0,
, если 0.
Если или = 0, то вектор считается равным нулевому вектору.
Свойства операции умножения вектора на действительное число.
10. Произведение любого вектора
на любое действительное число определено
и однозначно.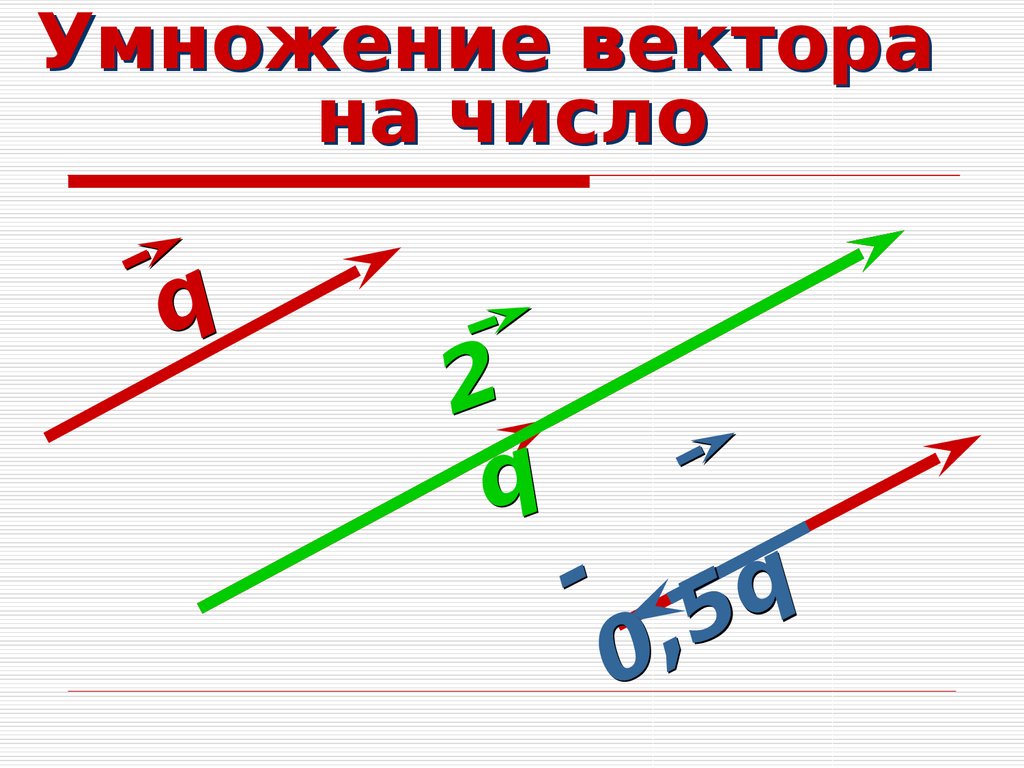
20. 1 для любого вектора .
30. для любого вектора и любых действительных чисел , .
Доказательство. Возможны случаи.
1) = 0, или = 0, или = . В этом случае равенство очевидно.
2) 0, 0 и . Сравним длины и направления векторов, стоящих в левой и правой частях доказываемого равенства.
,
.
Следовательно, . Так как направления векторов зависят от знаков коэффициентов, то рассмотрим все возможные случаи.
а) и одного знака (пусть 0, 0). В этом случае 0.
,
, следовательно, .
Итак, левая и правая части доказываемого равенства имеют одинаковые длины и направления, поэтому они равны.
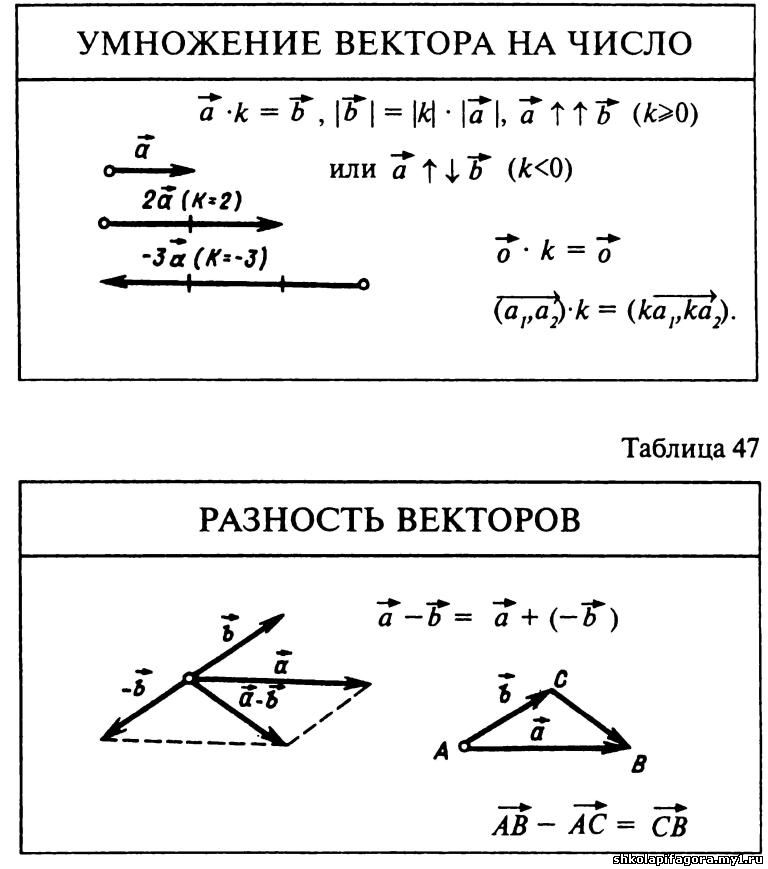 В этом случае
0.
В этом случае
0..
.
Снова получили, что левая и правая части доказываемого равенства имеют одинаковые длины и направления, поэтому они равны.
40. и ( для любых векторов , и любых действительных чисел , . (Докажите это свойство самостоятельно).
Определение 4. Векторы называются коллинеарными, если их можно отложить на одной прямой.
10. Нулевой вектор коллинеарен с любым вектором.
20. Противоположные векторы коллинеарны.
30. При сложении двух коллинеарных векторов получается вектор, коллинеарный с данными векторами. Следовательно, множество коллинеарных векторов замкнуто относительно операции сложения.
40. Если вектор умножить на
действительное число, то получится
вектор, коллинеарный данному. Следовательно,
множество коллинеарных векторов замкнуто
относительно операции умножения на
действительное число.
Если вектор умножить на
действительное число, то получится
вектор, коллинеарный данному. Следовательно,
множество коллинеарных векторов замкнуто
относительно операции умножения на
действительное число.
50. Если два вектора коллинеарны, то хотя бы один из них можно представить в виде произведения другого на действительное число.
Доказательство. Пусть векторы и коллинеарны. Если вектор = , то = 0. Если = , то = 0 . Если , и , то = . Если , то = .
Из двух последних свойств следуют следующие два свойства.
60. (Необходимое и достаточное условие коллинеарности двух векторов)
Два вектора коллинеарны тогда и только тогда, когда хотя бы один из них можно представить в виде произведения другого на действительное число.
70. Если вектор не нулевой, то любой вектор, коллинеарный
с вектором
,
можно представить в виде
. Иными словами, для задания множества
всех коллинеарных векторов достаточно
задать один ненулевой из них.
Иными словами, для задания множества
всех коллинеарных векторов достаточно
задать один ненулевой из них.
Наконец, из всех приведённых свойств можно сделать вывод, что относительно сложения векторов и умножения вектора на действительное число множество коллинеарных векторов ведёт себя так же как множество всех геометрических векторов.
. Выразить через вектор векторы . Решение. , , , , | Рис. 6 |
.
Умножение векторов — Nexus Wiki
До сих пор мы сосредоточились на том, как складывать и вычитать векторы. Это просто, поскольку векторы — это математические структуры, которые ведут себя как пространственные смещения.
Оказывается, мы можем, и что различные способы умножения векторов служат для выбора физически существенных элементов пар векторов, которые объединяются для получения важного физического результата. Два примера включают:
- Понятие работы — когда сила перемещает объект, что приводит к изменению его энергии движения (кинетической энергии). В этом случае имеет значение та часть силы, которая направлена вдоль (или против) смещения. (Требуется скалярное произведение)
- Концепция крутящего момента — когда сила перемещает объект, заставляя его вращаться вокруг центра на некотором расстоянии. В данном случае имеет значение та часть силы, которая перпендикулярна смещению к центру вращения. (Требуется перекрестное произведение)
Мы предпочитаем вводить математику там, где это необходимо, поэтому мы будем обсуждать концептуальные идеи, лежащие в основе точечных и перекрестных произведений, когда мы будем обсуждать работу (и теорему о работе-энергии) и вращательное движение.
Математика умножения матриц
Предположим, у нас есть два трехмерных вектора, которые мы запишем в виде троек $(a_x, a_y, a_z)$ и $(b_x, b_y, b_z)$, опустив пока $\hat{i }, \hat{j}$ и $\hat{k}$, определяющие направления $x$, $y$ и $z$ соответственно. Можем ли мы перемножить эти векторы?
Каждый вектор состоит из трех чисел, поэтому в принципе мы можем умножать их девятью различными способами. Мы могли бы создать девять продуктов $a_xb_x, a_xb_y, a_xb_z, a_yb_x,..,a_zb_z$. Это в значительной степени математический ответ, но нас интересует не просто «что мы можем сделать», а «что имеет физический смысл». Оказывается, комбинации этих девяти продуктов имеют важное физическое значение.
Скалярное произведение
Комбинация произведений трех пар
$$\overrightarrow{a} \cdot \overrightarrow{b} = a_xb_x + a_yb_y + a_zb_z $$
обладает приятным (хотя и удивительным) свойством, состоящим в том, что на самом деле это скаляр : то есть, изменение нашего выбор осей изменяет каждое из чисел, которые входят в этот расчет, но комбинация остается прежней! (Это верно даже в том случае, если мы находимся в 2D и имеем только первые два члена. ) Эта комбинация называется скалярным произведением двух векторов. Он возникает, когда мы хотим взять компонент одного вектора в направлении другого.
) Эта комбинация называется скалярным произведением двух векторов. Он возникает, когда мы хотим взять компонент одного вектора в направлении другого.
Физически скалярное произведение полезно, когда мы хотим использовать часть второго закона Ньютона, которая говорит нам о том, как объект меняет свою скорость. Мы знаем, что силы, действующие в направлении движения или против него, изменяют скорость — силы, перпендикулярные движению, изменяют только направление. Итак, мы хотим взять скалярное произведение векторной формы второго закона Ньютона со скоростью (или смещением). Это дает теорему о работе и энергии, ключ к нашему развитию концепции энергии.
Скалярное произведение также появляется, когда мы хотим рассчитать поток через поверхность, которая не перпендикулярна к ней. Только поток, перпендикулярный поверхности (в том же направлении, что и нормаль к поверхности), пропускает жидкость. Поток, параллельный поверхности (перпендикулярный нормали к поверхности), просто течет жидкость параллельно поверхности.
Перекрестное произведение
Другие комбинации наших 9 произведений из наших двух векторов могут быть объединены для создания вектора, известного как перекрестное произведение . Компонент x вектора состоит из компонентов y и z двух векторов и так далее, например:
$$(\overrightarrow{a} \times \overrightarrow{b})_x = a_yb_z — a_zb_y $ $
$$(\overrightarrow{a} \times \overrightarrow{b})_y = a_zb_x — a_zb_x $$
$$(\overrightarrow{a} \times \overrightarrow{b})_z = a_xb_y — a_yb_x $ $
Эти три комбинации ведут себя как компоненты вектора, когда мы меняем системы координат. (Хотя они ведут себя иначе, когда вы смотрите на них в зеркало.)
Перекрестное произведение используется в физике, когда нам нужна составляющая вектора, перпендикулярная другому вектору, например, когда мы рассматриваем силы, воздействующие на протяженные объекты. Составляющая силы, направленная вдоль линии от точки вращения, пытается растянуть или сжать объект, но не стремится повернуть его вокруг точки вращения. Только компонент, перпендикулярный линии от точки опоры, стремится повернуть объект. Это мотивация для введения понятия крутящего момента. Взаимное произведение также появляется при построении магнитных сил.
Только компонент, перпендикулярный линии от точки опоры, стремится повернуть объект. Это мотивация для введения понятия крутящего момента. Взаимное произведение также появляется при построении магнитных сил.
А что насчет остальных?
Мы сочли полезными 4 комбинации произведений компонент вектора, но начали с 9 объектов. Разве не должно быть еще 5 комбинаций? На самом деле есть. Они образуют не скаляр и не вектор, а нечто иное — симметричную бесследовую матрицу. Эти математические структуры полезны при преобразовании векторов, но выходят за рамки этого класса. Их изучение — это шаг в математику, известную как тензорный анализ 9.0028 . Это полезно для понимания того, как квантовые электронные орбитали сочетаются в химии и передовой механике. Такого рода рассуждения также играют важную роль в специальной и общей теориях относительности Эйнштейна.
Для получения более подробной информации о точечных и перекрестных произведениях читайте последующие страницы.
Джо Редиш 06. 11.11
11.11
квантовая механика. Что произойдет, если я умножу кет-вектор на комплексное число?
спросил
Изменено 2 года, 1 месяц назад
Просмотрено 936 раз
$\begingroup$
Я читал книгу Зеттили Квантовая механика . Там я увидел
если кет (или лифчик) умножить на комплексное число, тоже получим кет (или лифчик)
Но как мы можем вывести это с помощью математики?
- квантовая механика
- гильбертово пространство
- волновая функция
- комплексные числа
- квантовые состояния
$\endgroup$
2
$\begingroup$
Состояния квантовой системы, кеты, являются элементами комплексного гильбертова пространства (по модулю фазы).
6
$\begingroup$
Подумайте об этом так: когда вы умножаете вектор на скаляр, вы просто масштабируете исходный вектор. Та же идея применима здесь к векторам в гильбертовом пространстве, иначе.


