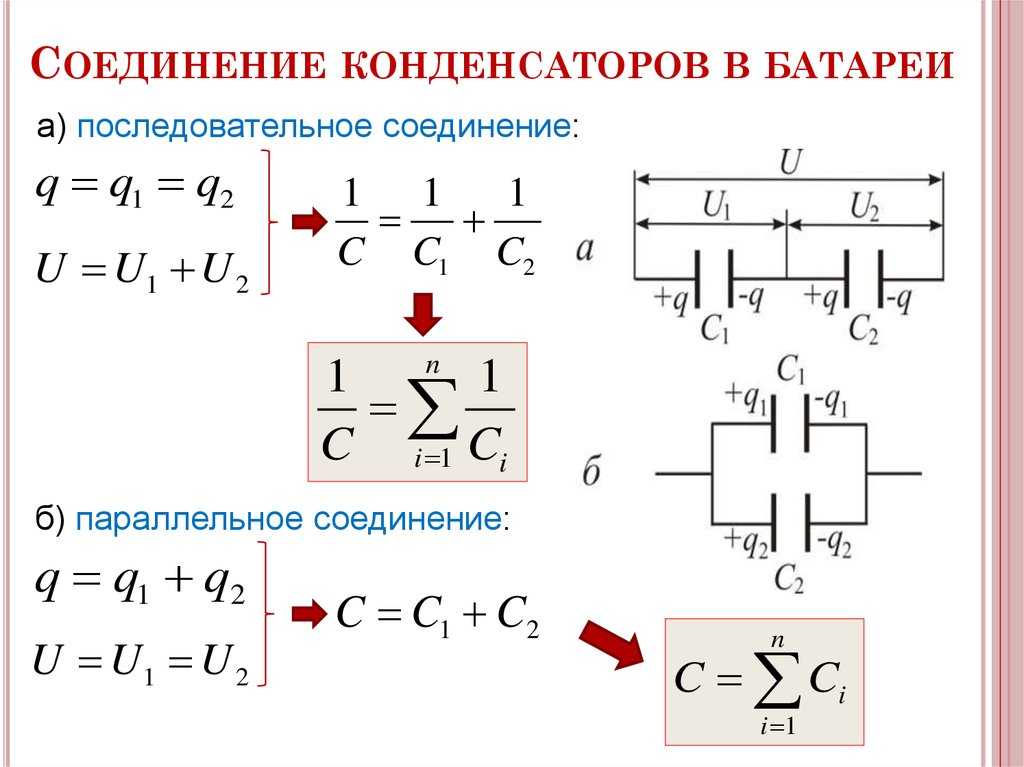
Эквивалентная ёмкость конденсаторов
|
|
| |||||||||||||||||||||||||||||||||||||||||
Настройка.Определите эквивалентную емкость конденсаторов схема включения которых
Содержание
- Как написать хороший ответ?
- Паралельное СОЕДИНЕНИЕ
- Синтаксис
- Примеры
- Ответ
- Проверено экспертом
Вопрос по физике:
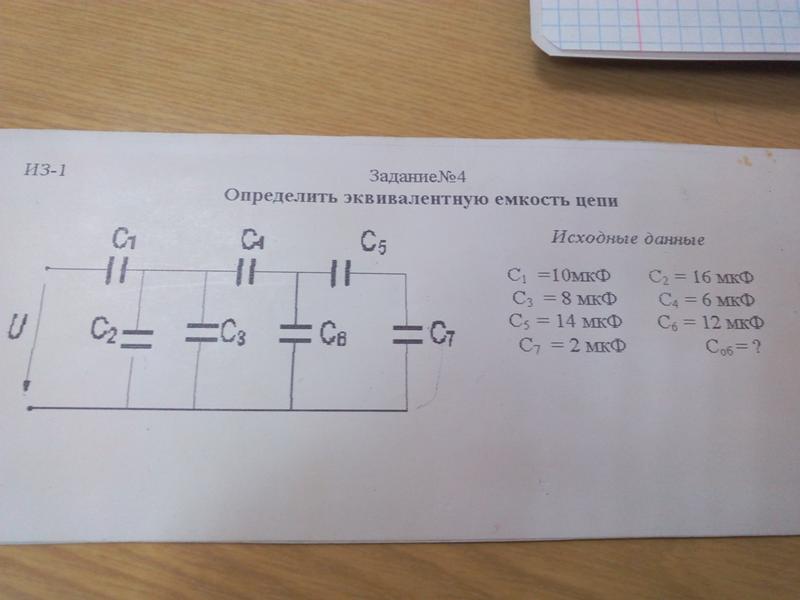
Определите общую емкость конденсаторов, схема которых приведена на рис.
4, если все конденсаторы имеют емкость 10 мкФ каждый.
Ответы и объяснения 1
Я прилагаю решение на прилагаемом рисунке. Ответ: 5 мкФ.
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ, вы должны:
- Правдиво отвечайте на вопросы, на которые вы знаете правильный ответ;
- Пишите подробно, чтобы ваш ответ был полным и не вызывал дополнительных вопросов;
- Пишите без грамматических, орфографических и пунктуационных ошибок.
Не стоит:
- Копирование ответов со сторонних ресурсов. Уникальные и личные объяснения высоко ценятся;
- Ответы не по теме: “Подумайте”, “Успокойтесь”, “Я не знаю” и т.д;
- Использование некрасивых выражений – это неуважение к пользователям;
- Писать в MINING REGISTER.
Есть сомнения?
Не можете найти правильный ответ на свой вопрос или ответа нет? Используйте инструмент поиска на этой странице, чтобы найти все ответы на похожие вопросы по физике.
Проблемы с домашним заданием? Не стесняйтесь просить о помощи – не стесняйтесь задавать вопросы!
Физика – это отрасль естественных наук: естественная наука, изучающая простейшие, но наиболее общие законы природы, материю, ее структуру и движение.
После написания бота, расчета размерных единиц онлайн теперь начнется освоение такой многогранной и сложной области, как электротехника.
И первое, что пригодится, это расчет эквивалентных характеристик основных электрических элементов (емкость, индуктивность, сопротивление).
Напомним, что мы уже знаем, как рассчитать емкость некоторых типичных структур.
Формулы очень просты, но проблема в том, как точно рассчитать емкость двух последовательно соединенных конденсаторов, если один конденсатор имеет емкость 10 пФ, а другой 250 нФ. Измерения показывают, что они отличаются в 1000 раз. Конечно, можно перевести все в абсолютные значения, но при большом количестве конденсаторов это приводит к ошибкам.
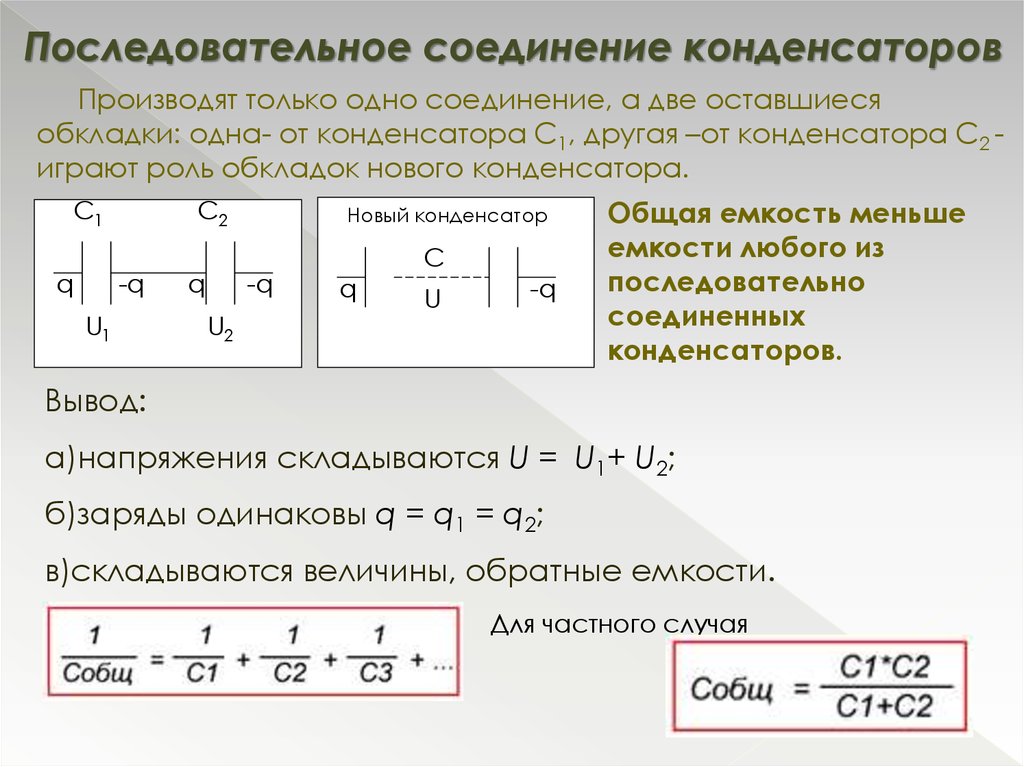
Таким образом, последовательное соединение конденсаторов имеет следующий вид
А формула для расчета эквивалентной емкости выглядит следующим образом
Паралельное СОЕДИНЕНИЕ
Последовательное подключение нескольких конденсаторов выглядит следующим образом
И формула сделана эйфорически простой и понятной.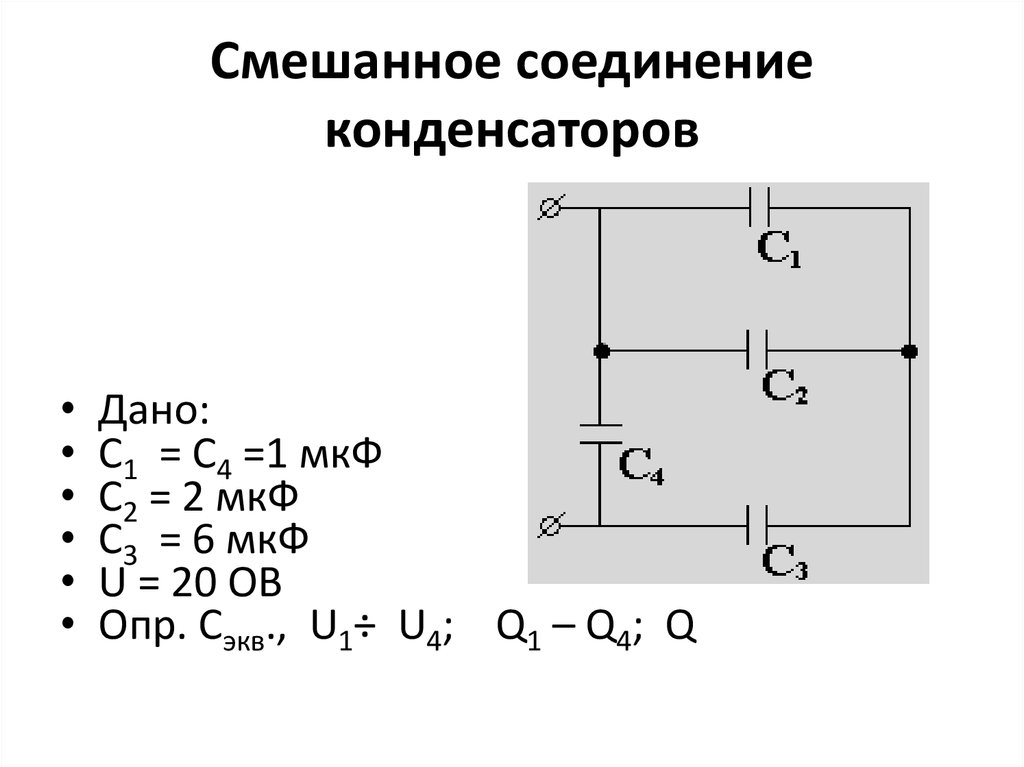
Синтаксис
calc_e – это список емкостей со значениями, разделенными запятыми.
В ответе будет приведено значение эквивалентной емкости для последовательного и параллельного соединений.
Важное замечание: размеры должны быть написаны на русском языке. Для пользователей сайта, не владеющих русским языком, мы можем добавить обработку английских названий префиксов и размеров по запросу. Это несложно.
Примеры
Вычислите емкость трех конденсаторов со следующими значениями: 10 пФ, 0,2нФ и 344мФ.
В запросе напишите calc_e 10pF,0.2nF,344mF
Ответ не занимает много времени и выглядит следующим образом
- Попросите дать больше объяснений.
- Следуйте за
- Марк Брейч
JotaRumex 10.09.2019.
Ответ
Проверено экспертом
Ответ:
Объяснение:
Конденсаторы C₁ и C₃ подключены параллельно, поэтому замените их одним конденсатором C₁₃.
C₁₃ = C₁ + C₃ = 10 + 10 = 20 мкФ
Конденсаторы C₂ и C₄ подключены параллельно, поэтому замените их одним C₂₄.
C₂₄ = C₂ + C₄ = 10 + 10 = 20 мкФ
Теперь емкости C₁₃ и C₂₄ соединены последовательно, поэтому
Сбор = C₁₃*C₂₄ / (C₁₃+C₂₄) = 20*20 / (20+20) = 10 мкФ
Найдите эквивалентную емкость комбинации конденсаторов между точками A и B. Кроме того, найдите общий заряд, протекающий в цепи, когда батарея 100 В подключена между точками A и B.
Подсказка: Задача основана на по формуле емкости конденсатора. Сначала следует рассчитать последовательную и параллельную емкости конденсатора. Затем необходимо умножить чистую емкость на заданное значение напряжения, чтобы получить значение заряда, протекающего по цепи.
Используемая формула:
\[Q=CV\]
Полный пошаговый ответ:
Рассмотрим схему соединений компонентов в цепи.
Учитывая рисунок, давайте вычислим емкость цепи с учетом двух конденсаторов одновременно.
Начнем расчет.
Теперь рассмотрим конденсаторы, отмеченные цифрами 5 и 6.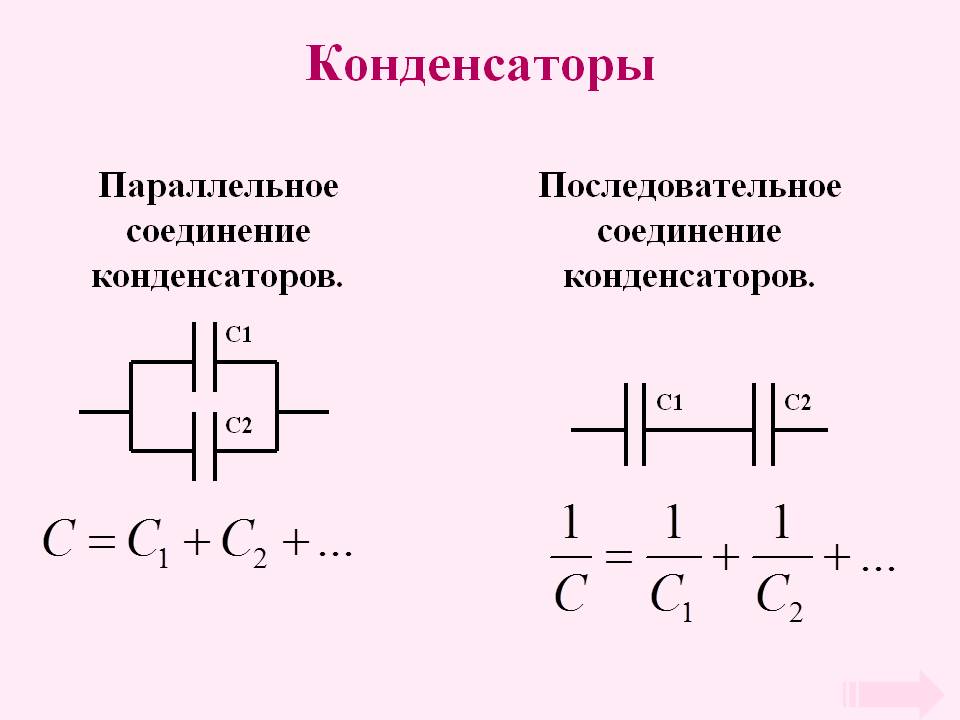
Значит, эти конденсаторы включены параллельно. Итак, эквивалентная емкость рассчитывается следующим образом.
\[\begin{align}
& {{C}_{56}}={{C}_{5}}+C{}_{6} \\
& \Rightarrow {{C}_{56 }}=10+10 \\
& \Rightarrow {{C}_{56}}=20\mu F \\
\end{align}\]
Теперь рассмотрим конденсаторы, отмеченные цифрами 2, 3 и 4. Итак, , эти конденсаторы включены последовательно. Итак, эквивалентная емкость рассчитывается следующим образом.
\[\begin{align}
& \dfrac{1}{{{C}_{234}}}=\dfrac{1}{{{C}_{2}}}+\dfrac{1}{ {{C}_{3}}}+\dfrac{1}{{{C}_{4}}} \\
& \Rightarrow \dfrac{1}{{{C}_{234}}}= \dfrac{1}{60}+\dfrac{1}{60}+\dfrac{1}{60} \\
& \Rightarrow {{C}_{234}}=20\,\mu F \\
\end{align}\]
Теперь рассмотрим конденсаторы с номерами 56 и 234. Итак, эти конденсаторы включены параллельно. Итак, эквивалентная емкость рассчитывается следующим образом.
\[\begin{align}
& {{C}_{23456}}={{C}_{234}}+C{}_{56} \\
& \Rightarrow {{C}_{23456 }}=20+20 \\
& \Rightarrow {{C}_{23456}}=40\mu F \\
\end{align}\]
Теперь рассмотрим конденсаторы с маркировкой 23456 и 1.
Итак, эти конденсаторы последовательно. Итак, эквивалентная емкость рассчитывается следующим образом.
\[\begin{align}
& \dfrac{1}{{{C}_{123456}}}=\dfrac{1}{{{C}_{23456}}}+\dfrac{1}{ {{C}_{1}}} \\
& \Rightarrow \dfrac{1}{{{C}_{123456}}}=\dfrac{1}{40}+\dfrac{1}{40} \\
& \Rightarrow {{C}_{123456}}=20\,\mu F \\
\end{align}\]
Эквивалентная емкость комбинации конденсаторов между точками A и B равна \[ 20\,\мю F\].
Теперь вычислим общий заряд, протекающий по цепи, когда 100-вольтовая батарея подключена между точками A и B.
Диаграмма, представляющая эквивалентную емкость и напряжение между точками A и B, выглядит следующим образом.
Стоимость указана следующим образом.
\[\begin{align}
& Q=CV \\
& \Стрелка вправо Q=20\,\mu F\times 100\,V \\
& \Стрелка вправо Q=2\,mC \\
\end {align}\]
Следовательно, эквивалентная емкость комбинации конденсаторов между точками A и B равна \[20\,\mu F\], а общий заряд, протекающий в цепи, когда 100-вольтовая батарея подключена между точках А и В составляет 2 мКл.
Примечание: Для получения дополнительной информации по решению этих типов задач необходимо иметь под рукой следующие сведения: Формула, используемая для расчета эквивалентной емкости параллельно соединенных конденсаторов, отличается от формулы, используемой для расчета эквивалентная емкость последовательно соединенных конденсаторов. Следует позаботиться о единицах измерения параметров.
Калькулятор последовательных конденсаторов
Создано Wojciech Sas, PhD
Отзыв от Bogna Szyk и Jack Bowater
Последнее обновление: 02 февраля 2023 г.
Содержание:- Последовательное добавление конденсаторов
- Как использовать калькулятор последовательного подключения конденсаторов?
- Конденсаторы, включенные последовательно и параллельно
Калькулятор последовательного подключения конденсаторов поможет вам оценить эквивалентное значение емкости до 10 отдельных конденсаторов . В тексте вы найдете, как работает последовательное добавление конденсаторов, в чем разница между конденсаторами, включенными последовательно и параллельно, и как это соотносится с комбинацией резисторов.
Если вы хотите ознакомиться с формулами этих явлений (и с физикой!), посмотрите пример — можно вычислить конденсаторы при последовательном напряжении и заряде .
У вас есть схема с параллельным расположением конденсаторов? Отправляйтесь к калькулятору параллельных конденсаторов Omni!
Последовательное добавление конденсаторов
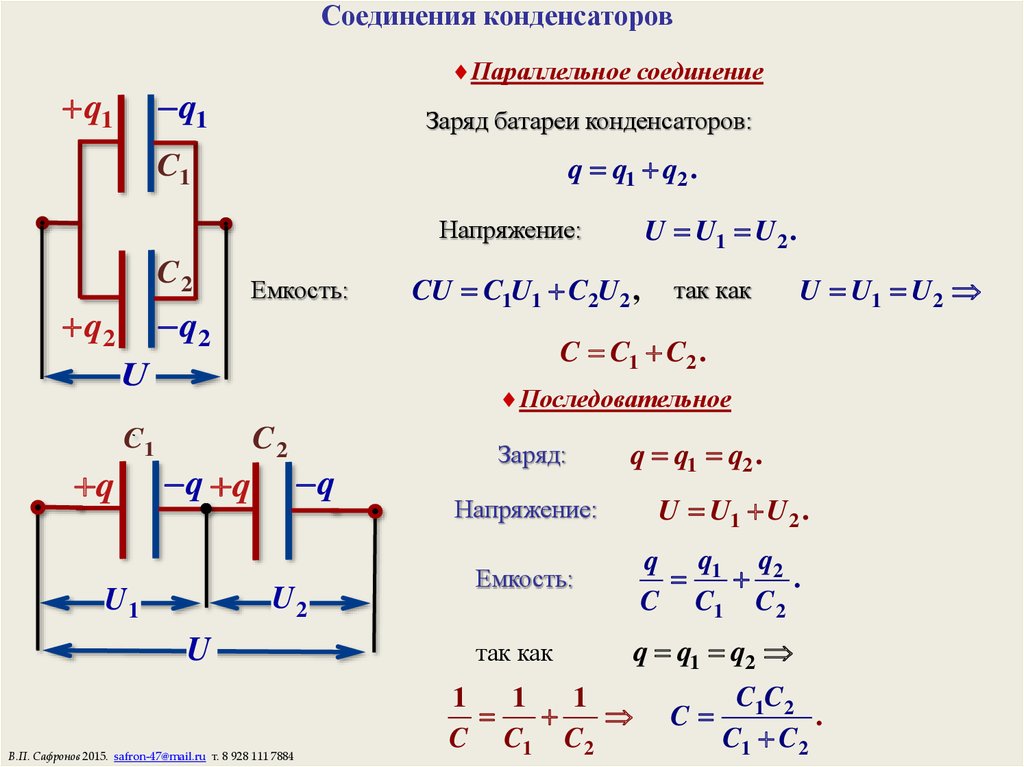
Конденсатор представляет собой электронный компонент, накапливающий электрический заряд (или электрическую энергию). Конденсаторы могут располагаться в цепи как последовательно, так и параллельно, в зависимости от их будущего применения. При последовательном соединении заряд Ом в каждом конденсаторе равен Ом. Почему?
Представьте себе установку, состоящую из последовательно соединенных конденсаторов без источника напряжения . Самый простой способ визуализировать эту ситуацию — использовать конденсаторы с плоскими пластинами, но он также работает для цилиндрических и сферических конденсаторов.
В нашем случае каждый из элементов не хранит заряда. Затем мы применяем напряжение на концах цепи.
Посмотрите на первый конденсатор — когда электроны движутся к источнику питания, одна часть конденсатора становится положительно заряженной. В равновесии это значение равно 9.0097 +Q . Основное свойство конденсатора состоит в том, что абсолютная величина заряда, хранящегося на обеих пластинах, одинакова, но имеет противоположные знаки . В результате второй конец этого элемента имеет заряд -Q . Далее, мы не можем произвести этот заряд из пустоты, поэтому он должен исходить от второго конденсатора, и поэтому он также хранит заряд + Q на соседнем конце. Мы можем продолжать это рассуждение снова и снова, пока не дойдем до последнего элемента. Здесь заряд идет не от соседнего конденсатора, а от источника напряжения.
Вы можете думать об этой проблеме как о черном ящике. Заряд покидает источник питания с одного конца, проходит через коробку и возвращается с другой стороны.
Общий заряд должен сохраняться, поэтому входные и выходные значения должны быть эквивалентны.
С другой стороны, напряжение последовательно соединенных конденсаторов, В , представляет собой сумму напряжений на каждом конденсаторе в отдельности ( В₁ , В₂ , …). Переставляя общую формулу для емкости, получаем выражение для напряжения на всей цепи:
V = Q / C ,
а также по каждому в отдельности:
V₁ = Q / C₁ , V₂ = Q / C₂ и т.д. суммируя напряжения, так:
В = V₁ + V₂ + … → Q/C = Q/C₁ + Q/C₂ + … .
Мы можем разделить каждую сторону на Q , и тогда мы получим окончательную форму формулы емкости (точнее говоря, обратную ей):
1 / С = 1 / С₁ + 1 / С₂ + … .
Другими словами, инверсия полной емкости есть сумма инверсий каждой отдельной емкости .
Микросхема 555 в нестабильном режиме использует два последовательно включенных конденсатора для определения характеристического времени работы.
Если вам нужен таймер в вашей схеме, попробуйте наш калькулятор таймера 555.
Как подключить последовательно конденсаторы калькулятор?
Давайте рассмотрим вычислительный пример. Чему равна общая емкость четырех последовательно соединенных конденсаторов, если емкость каждого из них равна 9?0097 C₁ = 2 мФ , C₂ = 5 мкФ , C₃ = 6 мкФ , C₄ = 200 нФ ?
🔎 Вы можете быстро расшифровать емкость любого конденсатора с помощью нашего калькулятора конденсаторов.
Преобразуйте единицы измерения, чтобы они были одинаковыми. Мы можем использовать научную нотацию, чтобы упростить задачу. Перечисляя все через F, получаем:
C₁ = 2·10⁻³ F,C₂ = 5·10⁻⁶ F,C₃ = 6·10⁻⁶ F,C₄ = 2·10 ⁻⁷ Ф.Сложите величины, обратные емкости:
1/Кл = 1/(2·10⁻³ Ф) + 1/(5·10⁻⁶ Ф) + 1/(6·10⁻⁶ Ф) + 1/(2· 10⁻⁷ Ф) = 5,367·10⁶ 1/Ф.Оцените обратную эту сумму:
C = 1 / (5,367·10⁶ 1/F) = 1,863·10⁻⁷ F.
Мы можем записать окончательный результат последовательного добавления конденсаторов, используя соответствующий префикс:
C = 186,3 нФ.
Обратите внимание, что этот результат может быть менее точным, чем результат калькулятора конденсаторов в последовательном соединении, потому что мы не используем здесь столько значащих цифр.
Если вы посмотрите поближе, то заметите, что результирующая емкость ниже, чем любое из отдельных значений для конденсаторов серии .
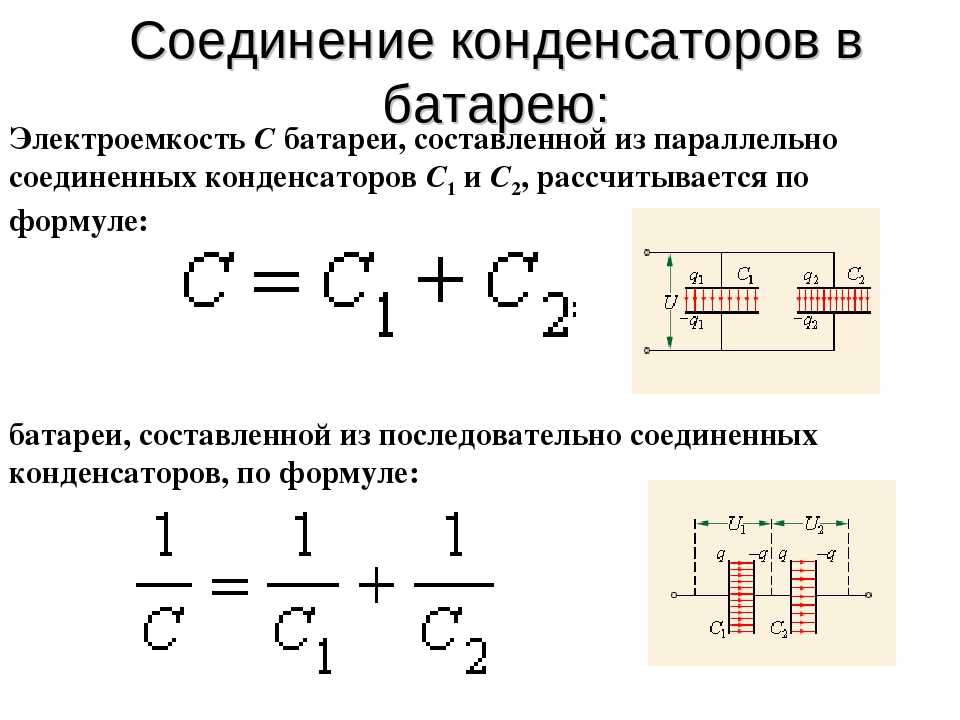
Конденсаторы последовательно и параллельно
Как мы уже выяснили, последовательное расположение конденсаторов приводит к уменьшению емкости. Как и следовало ожидать, параллельное соединение конденсаторов увеличивает значение . Мы также можем увидеть некоторое сходство между различными типами электрических элементов:
- Формула для последовательно соединенных конденсаторов эквивалентна формуле для параллельных резисторов.
