Вычитание векторов и правила вычитания
Оглавление
Время чтения:: 4 минуты
972
Для того, чтобы уяснить, что собой представляет разность векторов, введём понятие откладывания вектора от определённой точки и понятие суммы векторов.
Определение
Если некоторая точка A является началом вектора a, то говорят, что он является отложенным от точки A.
Теорема. От каждой точки можно отложить только один вектор, имеющий заданный модуль и направление. Докажем эту теорему.
Доказательство:
В случае, когда вектор нулевой, то теорема очевидна. Нулевые вектора в одной и той же точки совпадают между собой, т. е. являются одним и тем же вектором.
Сделаем построение. Точкой A обозначим начало вектора a, а точкой B его конец. Пусть у нас имеется некоторая точка K. Проведём через неё прямую b, которая параллельна вектору a. Отложим на данной прямой равные по своей абсолютной величине вектору  Из векторов, образованных этими отрезками искомым можно назвать только сонаправленный с a.
Из векторов, образованных этими отрезками искомым можно назвать только сонаправленный с a.
Единственность нашего вектора следует из того, что мы построили и видим.
Теорема доказана.
Определение
Суммой векторов a и b называется вектор с тем же началом, что вектор a и концом, как у вектора b. При этом вектор b должен начинаться в той же самой точке, в которой заканчивается вектор a.
Равные векторы, начинающиеся в разных точках, нередко обозначают одной и той же буквой. Иногда про подобные векторы говорят, как об одном и том же векторе, отложенном из разных мест.
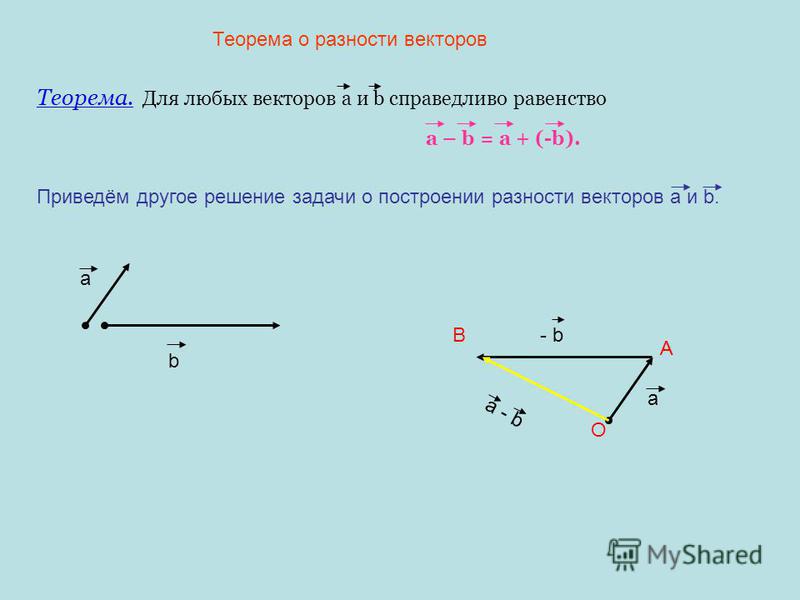
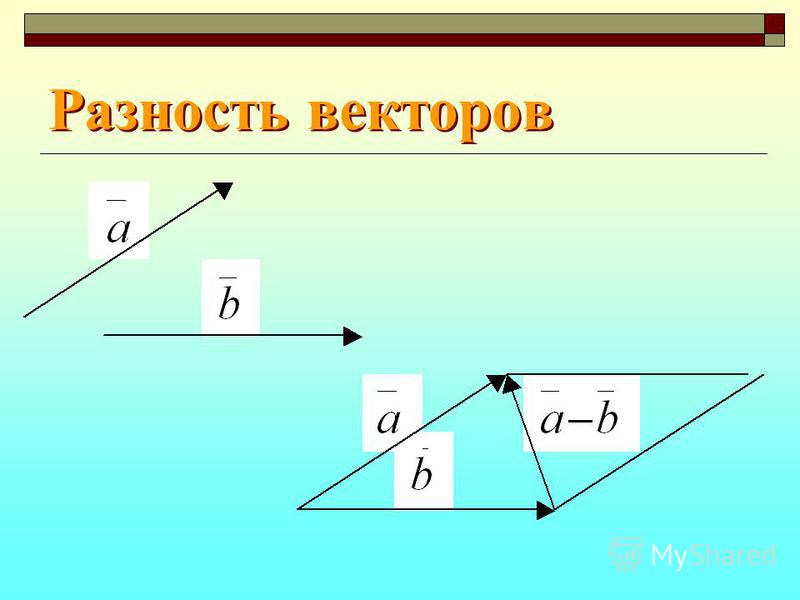
Разность векторов
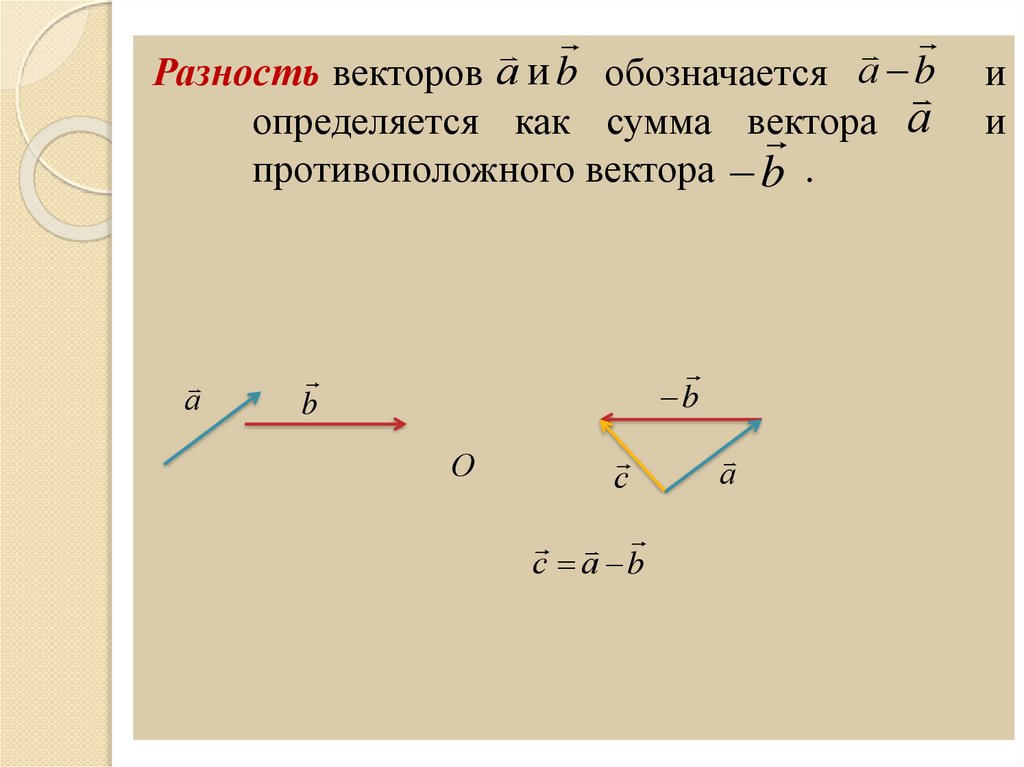
Определение
Разностью векторов a и b называется сумма вектора a c вектором, который противоположно направлен к вектору b.
По-другому это определение можно сформулировать следующим образом: разностью двух векторов a и b называется вектор c, который при сложении с вычитаемым b образует уменьшаемое, т.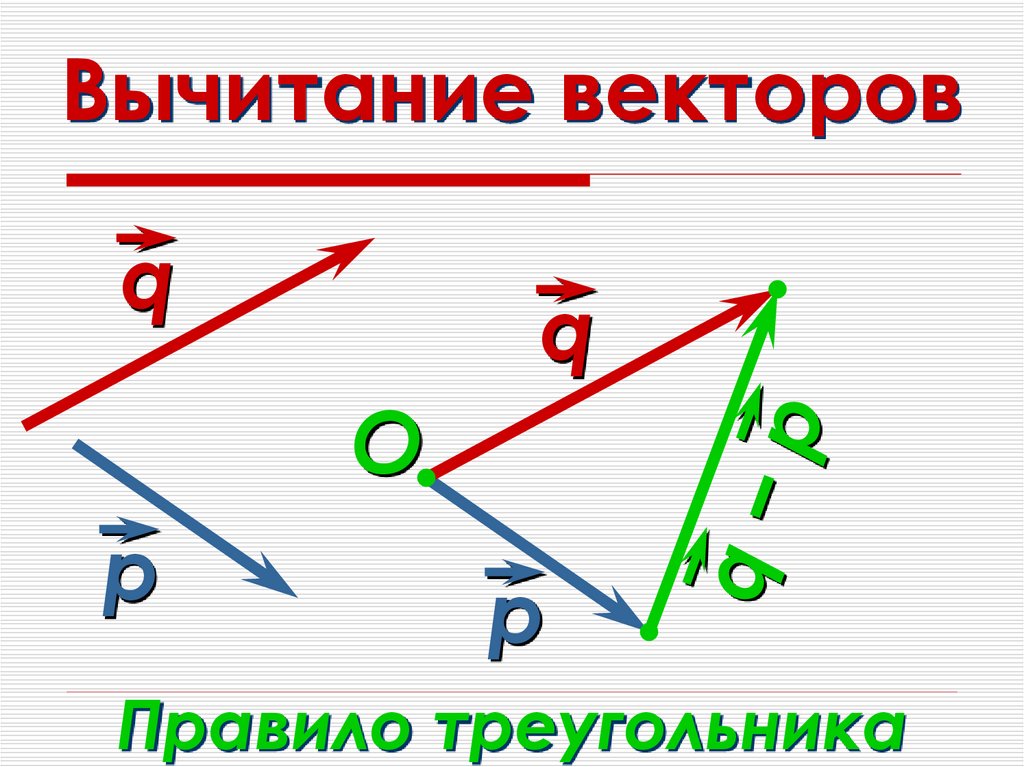 е. вектор a.
е. вектор a.
Формулами это записывается так:
b + c = a
a – b = c
Как найти разность векторов аналитическим способом
В двухмерном пространстве векторов a {x1, y1} и b {x2, y₂} разность векторов можно вычислить, как показано ниже:
c {x3, y3} = {x₁ — x2, y1 — y₂}.
Вычитание векторов в 3-мерном пространстве выглядит следующим образом:
c {x3; y3; z₃} = {x₁ — x2, y₂ — y₂, z1 — z2}.
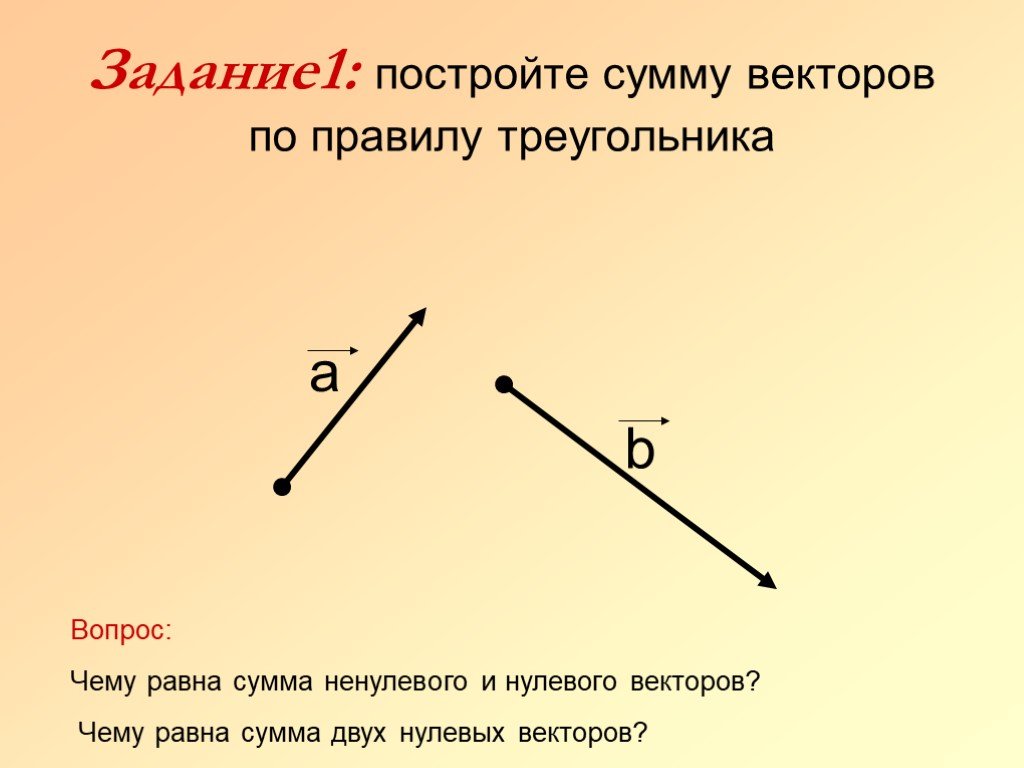
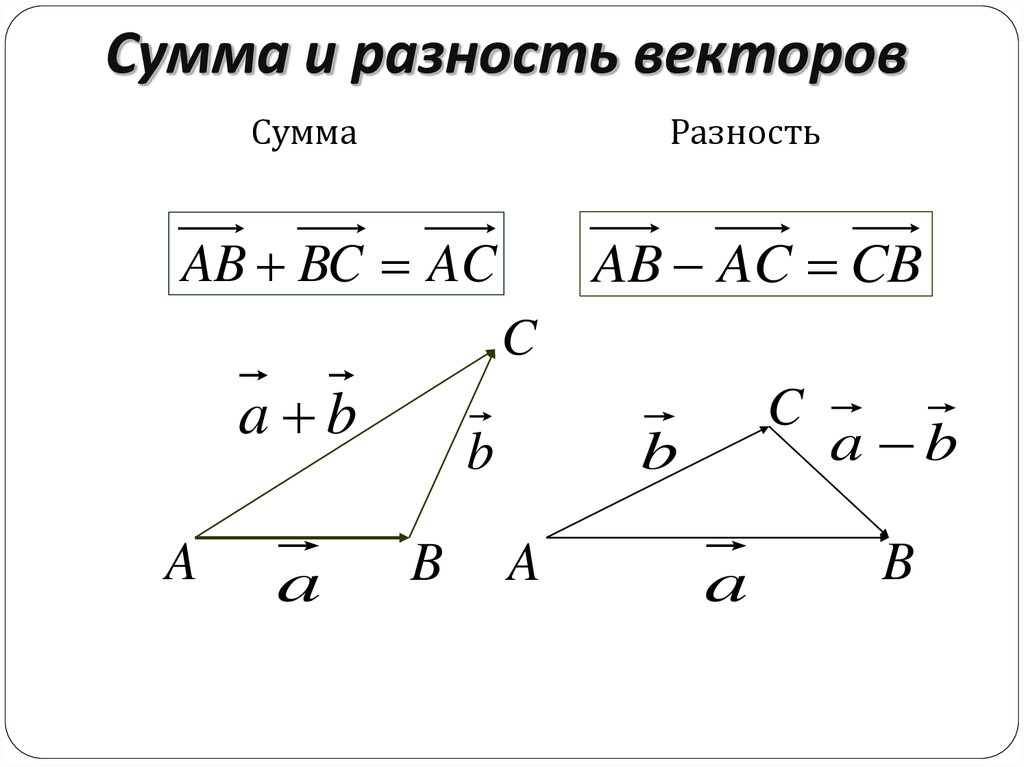
Как найти разность векторов графическим способом
Нужно воспользоваться правилом треугольника. Последовательность действий следующая:
- Постройте по координатам векторы, для которых требуется найти разность;
- Совместите концы построенных векторов. Для этого нужно построить два равных заданным направленных отрезка, концы у которых будут в одной и той же точке;
- Соедините начала построенных отрезков и укажите их направление. Вектор c, называемый разностью векторов, будет иметь своё начало в той же точке, где начинается вектор, именуемый уменьшаемым и заканчивается в точке начала вычитаемого. Смотрите рисунок ниже.
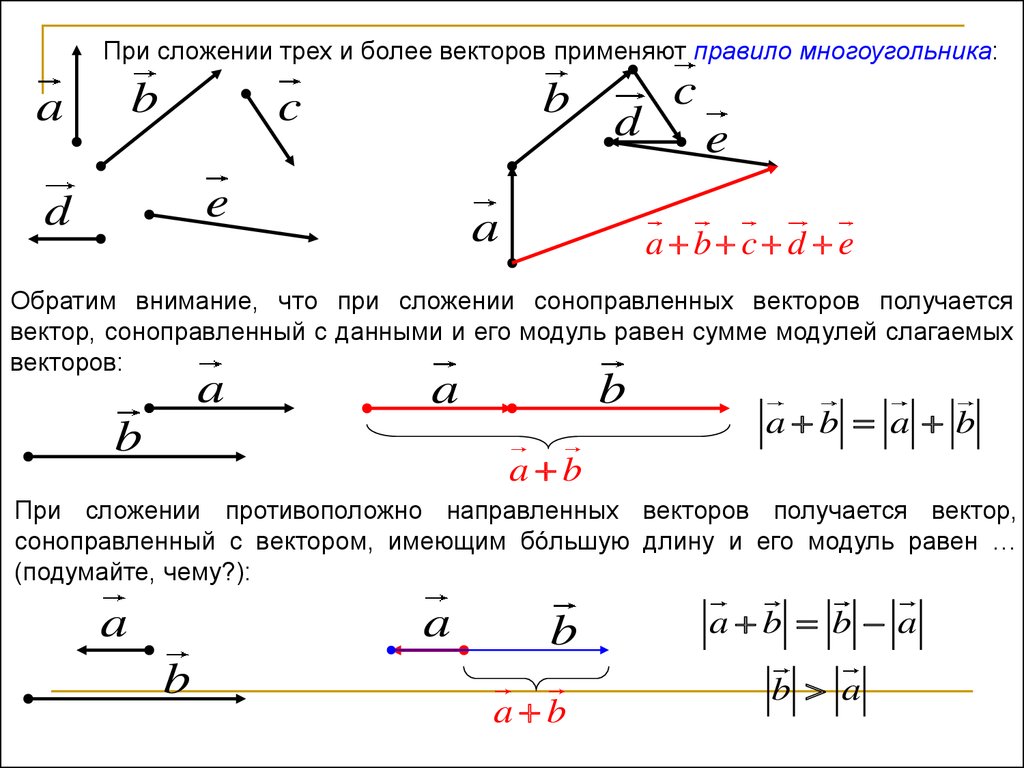
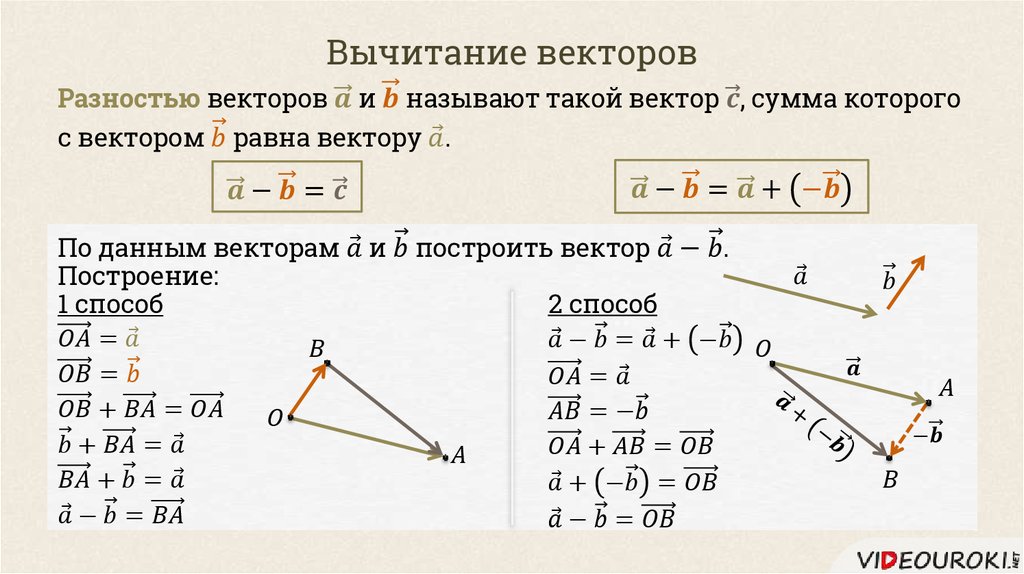
Есть ещё один способ графического нахождения разности векторов. Он предусматривает следующий порядок действий:
- Постройте исходные направленные отрезки;
- Отразите вычитаемый отрезок. Для этого постройте противоположно направленный и равный ему отрезок и затем совместите начало этого отрезка с уменьшаемым;
- Постройте сумму, т.
 е. соедините начало первого отрезка и конец второго.
е. соедините начало первого отрезка и конец второго.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Примеры вычисления разности векторов
Примеры
Вычислить вектор c, который представляет собой разность вектора a ={1;
2} и вектора b = {4; 8}.
Решение:
Действуем по выше указанному правилу
a — b = {1 — 4; 2 — 8} = {-3; -6}
Ответ: с{-3; -6}.
Вычислить вектор c, который является разностью векторов a = {1; 2; 5} и
b = {4; 8; 1}.
Решение:
Почти всё делается, как в уже рассмотренном примере, только добавляется третья координата.
a — b = {1 — 4; 2 — 8; 5 — 1} = {-3; -6; 4}
Ответ: c {-3; -6; 4}.
На рисунке векторы
Требуется построить разности: p — n, m —
n,m — n — p и найти ту из них, которая
имеет наименьший модуль.
Решение:
Для изображения p — n проще всего воспользоваться правилом треугольника. Параллельным переносом
следует соединить таким образом, чтобы совпали их конечные точки. Далее нужно соединить начальные точки и
определить направление. В нашем случае вектор разности берёт своё начало там же, где и вычитаемый n.
Для изображения m — n правильнее будет воспользоваться вторым графическим способом нахождения разности
векторов. Сначала построим вектор противоположный n и найдём его суммы с вектором m.
Для нахождения разности m — n — p разобьём это выражение на два действия. Возможны следующие варианты:
- m — (n + p).

затем уже вычесть её из m; - (m — n) — p. Сначала находим m — n,
осле этого от полученной разности отнимаем p; - (m— p) — n. Сначала определяем m — p, затем от
полученного результата отнимаем n.
Из вычислений выше нам известна разность m — n. Для получения решения нам нужно вычесть из неё
p.
Используя определение 3 построим разность векторов на рисунке. На нём изображён окончательный результат
Теперь нужно определить наименьший модуль. В нашем случае для этого можно лишь визуально оценить длины p — n,
m — n и m — n — p. Из построения сразу видно, что наименьшим модулем обладает вектор разности m — n —
p.
Оценить статью (34 оценки):
Поделиться
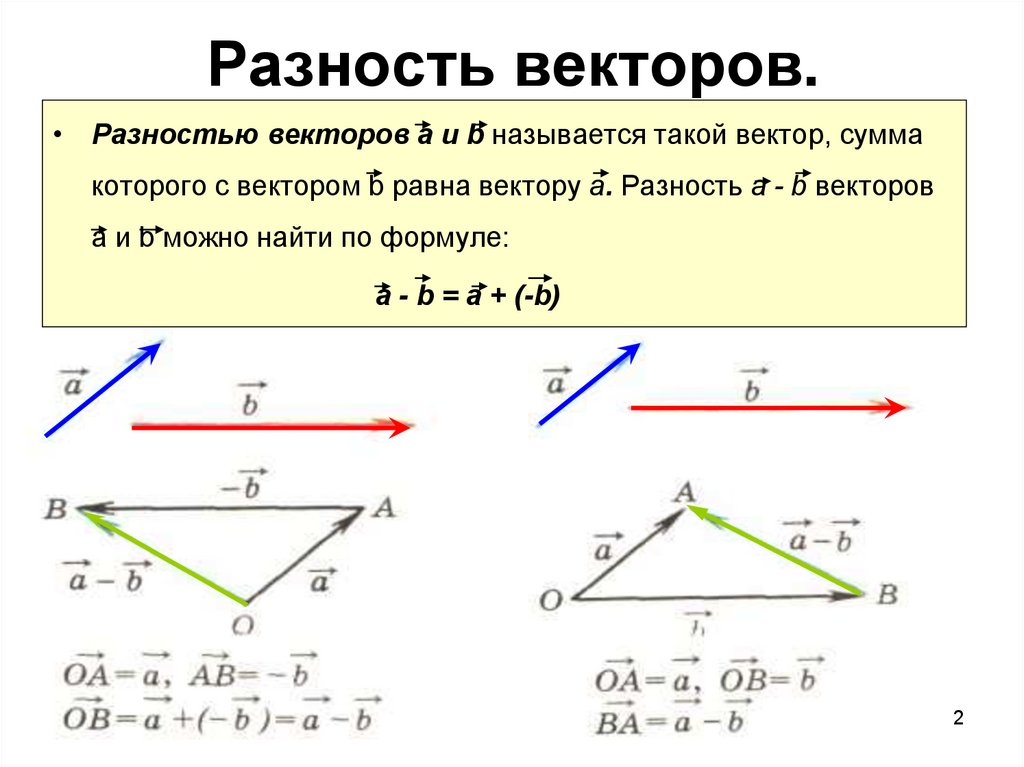
Разность векторов.
Для любых чисел a и b и любого вектора выполняется равенство .
Вектор, коллинеарный данному вектору , равный ему по длине и противоположно направленный, называется противоположнымвектором для вектора и обозначается . Противоположный вектор можно рассматривать как результат умножения вектора на число λ = –1: .
Разностью двух векторов и называется вектор , равный сумме векторов и , т.е. .
Очевидно, что , для любого вектора .
Легко показать, что .
Действительно,
Таким образом, если .
Из
определения суммы двух векторов вытекает
правило построения вектора разности.
Откладываем векторы и из
общей точки O.
Чтобы найти вектор-разность, нужно
к добавить
вектор или .
Тогда .
Вектор ,
соединяющий концы векторов и и
направленный от «вычитаемого» к
«уменьшаемому» (т.
Таким образом, если на векторах и , отложенных из общей точки O, построить параллелограмм OACB, то вектор , совпадающий с одной диагональю параллелограмма, равен сумме , а вектор , совпадающий с другой диагональю, равен разности .
Проекция вектора на ось
усть в пространстве даны два вектора и . Отложим от произвольной точки O векторы и . Углом между векторами и называется наименьший из углов . Обозначается . Рассмотрим ось l и отложим на ней единичный вектор (т.е. вектор, длина которого равна единице). Под углом между вектором и осью l понимают угол между векторами и . Итак, пусть l –
некоторая ось и –
вектор. Обозначим через A1 и B1 проекции на ось lсоответственно точек A и B. Предположим, что A1 имеет координату Тогда проекцией вектора на ось l называется разность x1 – x2 между координатами проекций конца и начала вектора на эту ось. Проекцию вектора на ось l будем обозначать . Ясно, что если угол между вектором и осью l острый, то x2> x1, и проекция x2 – x1> 0; если этот угол тупой, то  Наконец, если вектор перпендикулярен
оси l,
то x2= x1 и x2– x1=
0. Наконец, если вектор перпендикулярен
оси l,
то x2= x1 и x2– x1=
0.Таким образом, проекция вектора на ось l – это длина отрезка A1B1, взятая с определённым знаком. Следовательно, проекция вектора на ось это число или скаляр. Аналогично определяется проекция одного вектора на другой. В этом случае находятся проекции концов даного вектора на ту прямую, на которой лежит 2-ой вектор. Рассмотрим некоторые основные свойства проекций.
Доказательство. Ясно, что проекция вектора не изменится при его параллельном переносе, поэтому достаточно рассмотреть случай, когда начало вектора совпадает с началом отсчёта 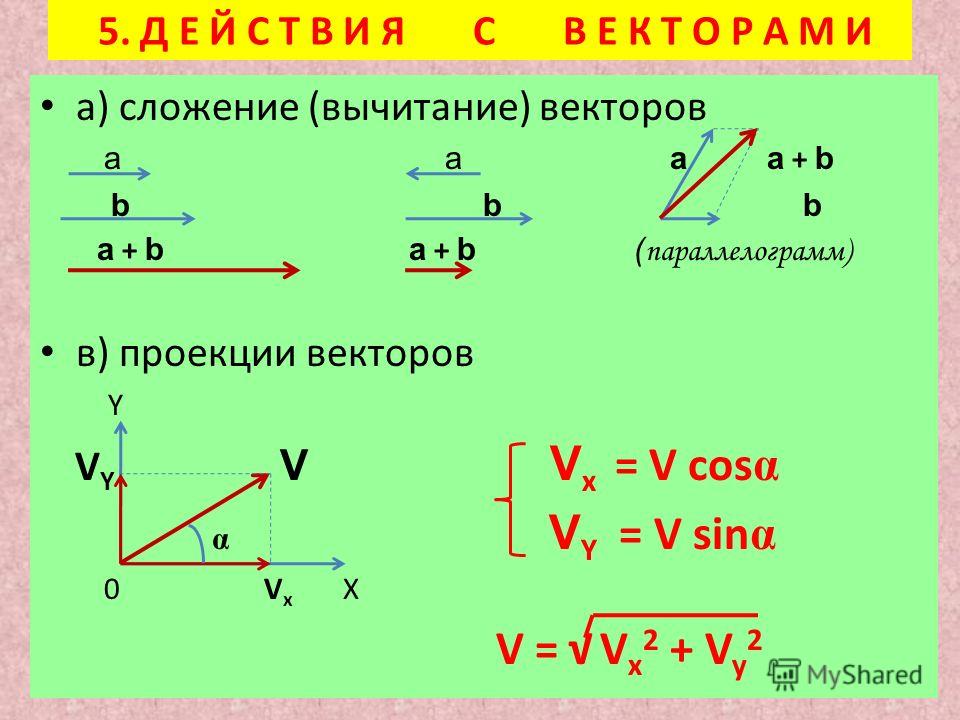 Так как координата проекции начала
равна нулю, то обозначим . Так как координата проекции начала
равна нулю, то обозначим .
Доказательство. Пусть . Обозначим через x1, x2 и x3 координаты проекций A1, B1, C1 на ось l точек A, B и C. Тогда . Но . Это свойство можно обобщить на случай любого числа слагаемых.
. Доказательство. Пусть угол между вектором и осью . Если λ > 0, то вектор имеет то же направление, что и , и составляет с осью такой же угол . При λ > 0 . Если же λ < 0, то и имеют противоположные направления и вектор составляет с осью угол π – φ и . Следствие. Проекция разности двух векторов на ось равна разности проекций этих векторов на ту же ось. |
ЛИНЕЙНО ЗАВИСИМЫЕ И ЛИНЕЙНО НЕЗАВИСИМЫЕ СИСТЕМЫ ВЕКТОРОВ
Рассмотрим несколько векторов .
Линейной
комбинацией данных
векторов называется любой вектор вида ,
где —
некоторые числа. Числа называются
коэффициентами линейной комбинации.
Говорят также, что в этом случае линейно
выражается через данные векторы ,
т. е. получается из них с помощью линейных
действий.
е. получается из них с помощью линейных
действий.
Например, если даны три вектора то в качестве их линейной комбинации можно рассматривать векторы:
Если вектор представлен как линейная комбинация каких-то векторов, то говорят, что он разложен по этим векторам.
Векторы называются линейно зависимыми, если существуют такие числа, не все равные нулю, что . Ясно, что заданные векторы будут линейно зависимыми, если какой-либо из этих векторов линейно выражается через остальные.
В противном случае, т.е. когда соотношение выполняется только при , эти векторы называются линейно независимыми.
Теорема 1. Любые два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Доказательство:
Действительно, пусть имеем два коллинеарных вектора и . Тогда либо оба они равны нулю, и следовательно, любая их линейная комбинация при любых λ1 и λ2, либо один из них не нуль, тогда другой отличается от него на числовой множитель, например, .
 Но отсюда ,
а это и означает линейную зависимость
векторов и .
Но отсюда ,
а это и означает линейную зависимость
векторов и .Докажем обратное, т.е. если два вектора линейно зависимы, то они коллинеарны. Пусть векторы и линейно зависимы. Тогда найдутся числа λ1 и λ2 такие, что , причём, например, λ2 ≠ 0. Тогда , т.е. векторы коллинеарны.
Таким образом, теорема утверждает, что линейно независимыми на плоскости могут быть только те векторы, которые неколлинеарны.
Аналогично можно доказать следующую теорему.
Теорема 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.
Доказательство.
Пусть три вектора линейно зависимы, т.е. , где, например, λ3 ≠ 0. Тогда .
Отнесём
векторы и к
одному началу и проведём через них
плоскость. Тогда и будут
лежать в той же плоскости, а потому и их
сумма, т.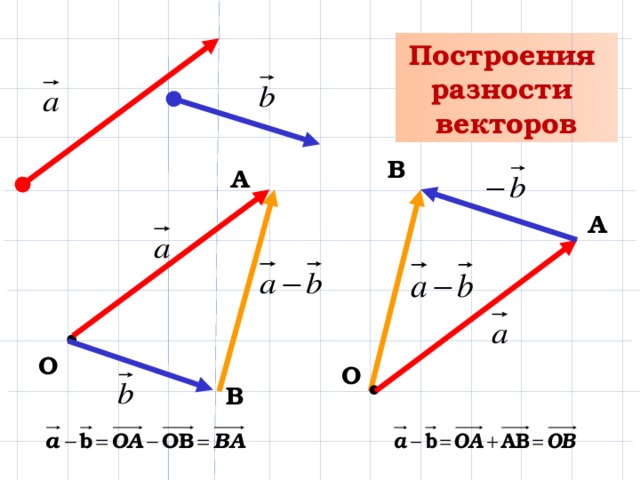 е. будет
лежать в той же плоскости, т.е. –
компланарны.
е. будет
лежать в той же плоскости, т.е. –
компланарны.
Пусть теперь векторы – компланарны. Тогда они будут лежать в одной плоскости. Отнесём все три вектора к одному началу.
Если векторы и не коллинеарны, то очевидно, вектор можно предствить в виде . Действительно из рисунка видно, что , где и , а значит найдутся числа и такие, что .
Если же вектор коллинеарен вектору , то один из них линейно выражен через другой, т.е. . Что и требовалось доказать.
Таким образом, три некомпланарных вектора всегда линейно независимы. Кроме того, можно показать, что каждые четыре вектора линейно зависимы.
БАЗИС
Базисом называется совокупность отличных от нулей линейно независимых векторов. Элементы базиса будем обозначать .
В
предыдущем пункте мы видели, что два
неколлинеарных вектора на плоскости
линейно независимы. Поэтому согласно
теореме 1, из предыдущего пункта, базисом
на плоскости являются любые два
неколлинеарных вектора на этой плоскости.
Поэтому согласно
теореме 1, из предыдущего пункта, базисом
на плоскости являются любые два
неколлинеарных вектора на этой плоскости.
Аналогично в пространстве линейно независимы любые три некомпланарных вектора. Следовательно, базисом в пространстве назовём три некомпланарных вектора.
Справедливо следующее утверждение.
Теорема. Пусть в пространстве задан базис . Тогда любой вектор можно представить в виде линейной комбинации , где x, y, z – некоторые числа. Такое разложение единственно.
Доказательство.
Докажем сначала существование такого представления.
Предположим, что коллинеарен какому-либо из векторов базиса, например, . Тогда по доказанному выше . Следовательно, , где x = l, y = z = 0.
Пусть компланарен с какой-либо парой базисных векторов, например, с и .
 Отложим три вектора от одной точки O.
Через точку Aпроведём
прямые, параллельные векторам и .
Тогда ,
причём векторы и коллинеарны
соответственно векторам и .
Поэтому найдутся числа x и y такие,
что ,
а значит .
Отложим три вектора от одной точки O.
Через точку Aпроведём
прямые, параллельные векторам и .
Тогда ,
причём векторы и коллинеарны
соответственно векторам и .
Поэтому найдутся числа x и y такие,
что ,
а значит .Пусть некомпланарен ни с одной парой базисных векторов. Отложим от одной точки и проведём через конец вектора прямую, параллельную вектору . Она пересечёт плоскость в точке A1. Очевидно, что . Но вектор компланарен векторам и , следовательно, по доказанному выше, , а вектор коллинеарен , поэтому . Таким образом, .
Докажем теперь единственность такого представления.
Допустим,
что возможны два представления
вектора и .
Причём, например, .
Тогда должны иметь ,
т.к. иначе мы имели бы две прямые,
проходящие через точку A1 параллельно . Из последнего равенства вытекает, что .
Получили противоречие с нашим
предположением, что и доказывает теорему.
Из последнего равенства вытекает, что .
Получили противоречие с нашим
предположением, что и доказывает теорему.
В качестве частного случая из этой же теоремы можно сформировать следующее утверждение:
Если задан базис на плоскости, то любой вектор, компланарный с векторами можно представить в виде , причём такое разложение единственно.
Таким образом, базис позволяет однозначно сопоставить каждому вектору тройку чисел – коэффициенты разложения этого вектора по векторам базиса: . Верно и обратное, каждой тройке чисел x, y, z при помощи базиса можно сопоставить вектор, если составить линейную комбинацию .
Если базис и , то числа x, y, z называются координатами вектора в данном базисе. Координаты вектора обозначают .
ДЕКАРТОВА СИСТЕМА КООРДИНАТ
Пусть в пространстве
задана точка O и
три некомпланарных вектора . Декартовой системой координат в пространстве (на плоскости) называется совокупность точки и базиса, т.е. совокупность точки и трёх некомпланарных векторов (2-х неколлинеарных векторов), выходящих из этой точки. Точка O называется началом координат; прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат – осью абсцисс, ординат и аппликат. Плоскости, проходящие через оси координат, называют координатными плоскостями. Рассмотрим в выбранной системе координат произвольную точку M. Введём понятие координаты точки M. Вектор , соединяющий начало координат с точкой M. называется радиус-вектором точки M. Вектору в выбранном базисе можно сопоставить тройку чисел – его координаты: . Координаты
радиус-вектора точки M. Аналогично определяются декартовы координаты на плоскости. Здесь точка имеет только две координаты – абсциссу и ординату. Легко видеть, что при заданной системе координат каждая точка имеет определённые координаты. С другой стороны, для каждой тройки чисел найдётся единственная точка, имеющая эти числа в качестве координат. Если векторы, взятые в качестве базиса, в выбранной системе координат, имеют единичную длину и попарно перпендикулярны, то система координат называется декартовой прямоугольной системой координат. В этом случае основные векторы принято обозначать буквами , а оси координат Ox, Oy и Oz. Таким образом,
любой вектор в декартовой прямоугольной
системе координат можно записать в
виде: . Примеры.
М(-1;3).
В дальнейшем мы в основном будем использовать только декартову прямоугольную систему координат. |
НАПРАВЛЯЮЩИЕ КОСИНУСЫ ВЕКТОРА
Пусть в декартовой прямоугольной системе координат задан вектор . Направление вектора в пространстве определяется углами α, β, γ которые вектор составляет с осями координат. Косинусы этих углов cos α, cos β, cos γ называются направляющими косинусами вектора.
Найдем
выражение для направляющих косинусов
вектора.
Пусть вектор задан в координатной форме .
Тогда , откуда.
Несложно показать, что .
Направляющие косинусы вектора полностью определяют его направление, но ничего не говорят о его длине.
ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ В КООРДИНАТНОЙ ФОРМЕ
При умножении вектора на число все его координаты умножаются на это число, т.е. если .
Действительно, используя свойства операций умножения вектора на число и сложении векторов будем иметь
.
При сложении векторов их соответствующие координаты складываются, т.е. если .
Доказательство очевидно.
Условие коллинеарности двух векторов в коорднинатной форме.
Два
вектора коллинеарны тогда и только
тогда, когда их соответствующие координаты
пропорциональны. Т.е. если ,
то.
Т.е. если ,
то.
Доказательство:
Пусть вектор коллинеарен , тогда найдется λ такое, что . Значит, и . Поскольку разложение вектора по элементам базиса единственно, то .
Пусть выполняется равенство . Обозначим коэффициент пропорциональности через λ. Тогда и, следовательно, , т.е. . Теорема доказана.
Пример.
Даны векторы . Найти вектор .
.
Найти координаты вектора в базисе, образованном векторами , , .
Обозначим координаты вектора в новом базисе . Тогда в новом базисе будем иметь:
Итак, .
Рассмотрим
две произвольные функцию y=
x3. Будем рассматривать равенство y= x3 как
уравнение относительно x.
Это уравнение для каждого значения у определяет
единственное значение x: .
Геометрически это значит, что всякая
прямая параллельная оси Oxпересекает
график функции y=
x3 только
в одной точке. Поэтому мы можем
рассматривать x как
функцию от y.
Функция называется
обратной по отношению к функции y=
x3.
Будем рассматривать равенство y= x3 как
уравнение относительно x.
Это уравнение для каждого значения у определяет
единственное значение x: .
Геометрически это значит, что всякая
прямая параллельная оси Oxпересекает
график функции y=
x3 только
в одной точке. Поэтому мы можем
рассматривать x как
функцию от y.
Функция называется
обратной по отношению к функции y=
x3.
Прежде чем перейти к общему случаю, введем определения.
Функция y = f(x) называется возрастающей на некотором отрезке, если большему значению аргумента x из этого отрезка соответствует большее значение функции, т.е. если x2>x1, вектора .
Очевидно, что . Но по определению координат вектора и . Следовательно,
Таким
образом, чтобы найти координаты вектора ,
нужно из координат его конца вычесть
соответствующие координаты начала.
Примеры.
Заданы точкиA(1; -2; 3), B(2; 0; -1). Найти вектор .
Даны A(-2; 3; 1), В(-1; 2; 0), С(0; 1; 1). Найти .
Известно, что. Найти координаты точки D, если
А(3; -4; -1), В(-4; 4; 1), С(-3; -5; 4).
Пусть тогда
. С другой стороны . Следовательно, должно выполняться равенство (x+3; y+5; z-4)=(5;10;-8). Отсюда
x=2, y=5, z=-4, т.е. точка D имеет координаты D(2; 5; -4).
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ И ЕГО СВОЙСТВА
Мы
рассмотрели умножение вектора на число.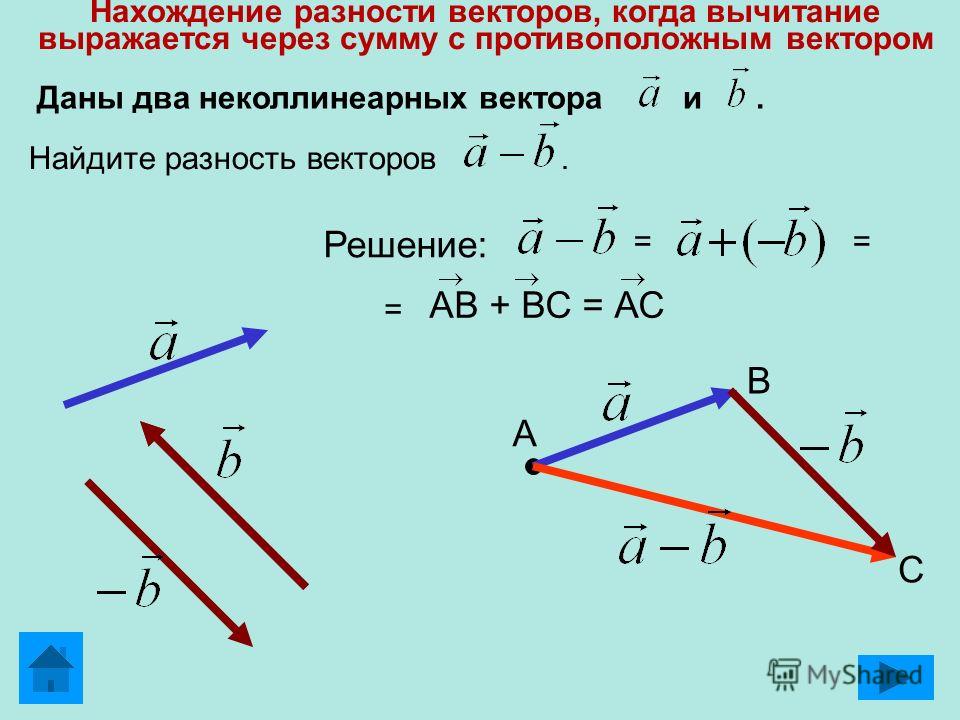 Однако во многих задачах механики и
физики встречается операция умножения
вектора на вектор. Но при этом результат
может быть как числом, так и вектором.
Поэтому рассматривают два вида умножения
векторов: скалярное и векторное.
Однако во многих задачах механики и
физики встречается операция умножения
вектора на вектор. Но при этом результат
может быть как числом, так и вектором.
Поэтому рассматривают два вида умножения
векторов: скалярное и векторное.
Пусть даны два вектора и , угол между, которыми равен .
Скалярным произведением векторов и называется число, равное произведению длин этих векторов на косинус угла между ними. Скалярное произведение обозначается . Итак, .
Если один из векторов нулевой, то угол не определен, и скалярное произведение по определения считается равным нулю.
Рассмотрим свойства скалярного произведения.
Скалярное произведение двух векторов подчиняется коммутативному закону, т.е. для любых векторов и .
Очевидно, из определения скалярного произведения:
.
Для любого числа λ и любых векторов имеем:
.
Доказательство. Ограничимся случаем, когда λ > 0. В этом случае угол между векторами и совпадает с углом между векторами и , .
Поэтому . Откуда
Аналогично доказывается и равенство .
Случай λ <0 рассмотреть самостоятельно.
Для любых векторов выполняется равенство .
Доказательство. Используя определение скалярного произведения и свойства проекций вектора на ось, будем иметь
Для любого вектора выполняется соотношение.
Действительно, так как , то .
Из этого свойства в частности следует .
Скалярное произведение двух векторов равно нулю тогда и только тогда,когда равен нулю один из сомножителей или векторы перпендикулярны.
Это
свойство очевидно из определения
скалярного произведения.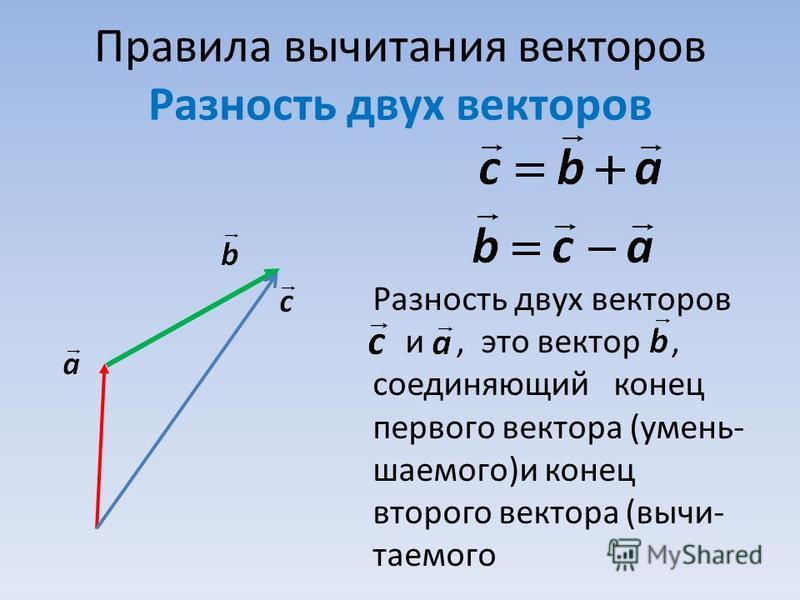
Таким образом, необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения.
Пример. Дан вектор . Известно, что
Найти .
Имеем, т.е. .
Найдем:
Следовательно, .
Рассмотрим, как находится скалярное произведение векторов, если они заданы в координатной форме. Пусть даны два вектора и .
Рассмотрим сначала все возможные скалярные произведения векторов друг на друга.
Поэтому
Итак, скалярное произведение векторов равно сумме произведений соответствующих координат: .
Это соотношение позволяет вычислить длину вектора через его координаты:
.
Далее из определения скалярного произведения находим
.
Выражая скалярное произведение и длины векторов через их координаты,получим формулу для нахождения косинуса угла между векторами
.
Условие ортогональности двух векторов:
или .
Т.о., для того чтобы два вектора были перпендикулярны необходимо и достаточно, чтобы сумма произведений соответствующих координат этих векторов была равна нулю.
Примеры.
Пусть А(-1; 1; 0), B(3; 1; -2), . Найти:
;
и ;
.
.
.
.
Найти в , если известны координаты его вершин A(1; 5; 6),
B(5;
3; 10), C(2;
1; 14).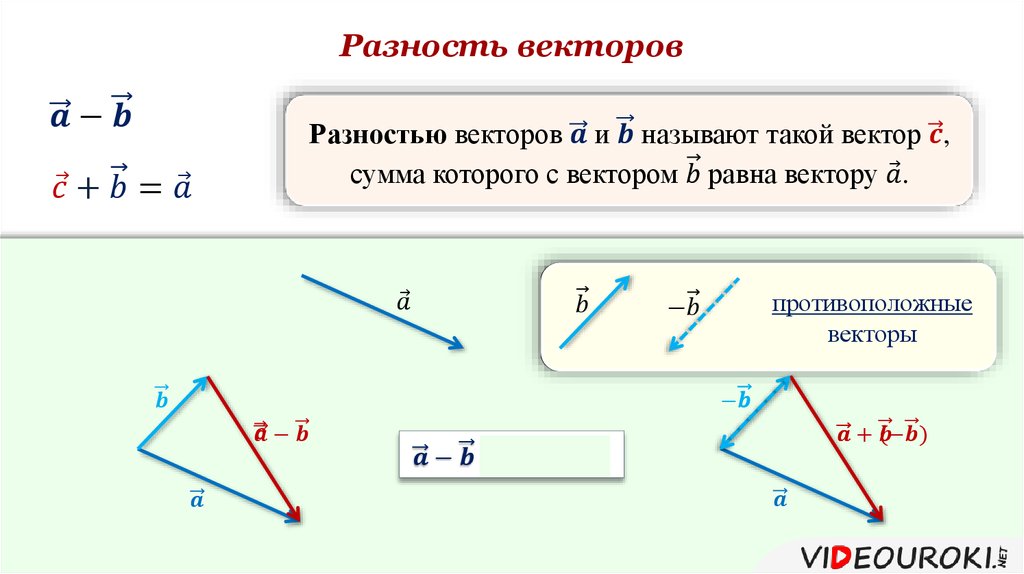
При каком значении m векторы и перпендикулярны?
Условие ортогональности двух векторов .
. Следовательно, m = 15.
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ И ЕГО СВОЙСТВА
Введем сначала понятие ориентации тройки векторов.
Пусть даны три некомпланарных вектора с общим началом, перечисленных в определенном порядке: первый – , второй – , третий – .
Тройка некомпланарных векторов называется правоориентированной или просто правой, если из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки. В противном случае тройку векторов называют левой, в этом случае если мы будем смотреть с конца вектора , то кратчайший поворот от к осуществляется по часовой стрелке.
Векторным произведением векторов и называется новый вектор , удовлетворяющий условиям:
Длина вектора равна площади параллелограмма, построенного на векторах и .

Вектор перпендикулярен плоскости этого параллелограмма.
Он направлен так, что векторы и образуют правую тройку векторов.
Векторное произведение векторов и обозначается символом . Если хотя бы один из сомножителей равен нулю, то векторное произведение по определению считают равным нулю
Векторное произведение обладает следующими свойствами:
Из определения следует, что длина векторного произведения численно равна площади параллелограмма, построенного на векторах, и, следовательно, находится по формуле:
.
Таким образом, и .
При перестановке сомножителей векторное произведение меняет свой знак .
Действительно
из определения векторного произведения
следует, что векторы и имеют
одинаковые модули, расположены на одной
прямой, но направлены в противоположные
стороны.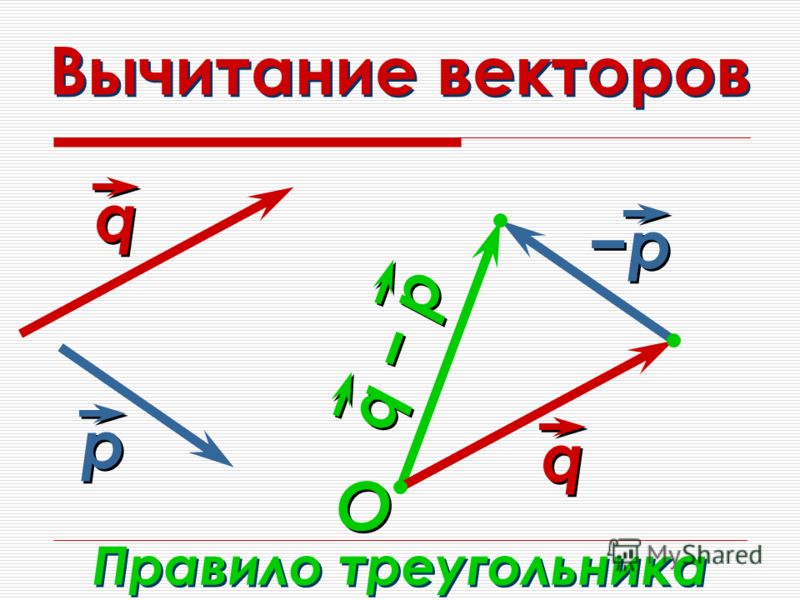 Поэтому, векторы и являются
противоположными векторами и поэтому .
Поэтому, векторы и являются
противоположными векторами и поэтому .
Скалярный множитель можно выносить за знак векторного произведения, т.е. для любого числа λ и любых векторов
.
Доказательство этого свойства непосредственно следует из определения векторного произведения. Докажем для λ > 0. В этом случае . Тогда по определению векторного произведения
Вектор перпендикулярен векторам и . Вектор также векторам и , т.к. векторы и , и лежат в одной плоскости. Следовательно, векторы и коллинеарны. Очевидно, что направления их также совпадают. Т. к. , и следовательно, , то .
Поэтому .
Аналогично проводится доказательство для случая λ < 0.
Для любых векторов имеет место равенство
.
Примем
без доказательства.
Векторное произведение двух векторов равно нулевому вектору тогда и только тогда, когда один из сомножителей равен нулю или векторы коллинеарны.
Действительно, если векторы коллинеарны, то , т.е. площадь параллелограмма, построенного на данных векторах,равна нулю.
Таким образом, для того чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нулевому вектору.
В частности .
Примеры.
Раскрыть скобки
.
Найти площадь треугольника, построенного на векторах и , если известно, что и .
.
Найдем .
.
Можно показать, что если и , то координаты векторного произведения векторов и находятся по формуле:
.
Примеры.
Найти векторное произведение векторов и .
.
Найти площадь , если A(2; 3; 1), B(-1; -2; 0), C(-3; 0; 1).
Даны векторы . Найти параметры n, p, q если известно, что векторы и коллинеарны, а векторы и ортогональны.
Так как векторы и коллинеарны, то . Векторы и ортогональны, поэтому . Итак, получили систему уравнений
Угол между двумя векторами Формула
Векторная величина – это физическая величина, имеющая как величину, так и направление. Когда на частицу действуют два вектора, результирующее действие на частицу будет зависеть от угла между этими векторами. Поэтому важно знать угол между ними.
Некоторые свойства вектора для вычисления угла
Вектор представлен стрелкой, параллельной направлению вектора.
- Вектор остается неизменным, если он передается параллельно самому себе.
- Два вектора, имеющие одинаковое направление, являются параллельными векторами.
- Два вектора, имеющие противоположные направления, являются антипараллельными векторами.
- Два вектора, имеющие одинаковую величину и направление, являются равными векторами.
- Два вектора, имеющие одинаковую величину и противоположное направление, называются отрицательными векторами.
Скалярное произведение
Также известно как скалярное произведение векторов. У него есть только величина, но нет направления.
Два вектора А и В
Тогда скалярное произведение A и B определяется как,
= |A| |Б| cosθ.
Особые случаи
- Когда угол между векторами равен 0 градусов.
То есть θ = 0°
⇒ |A| |Б| cosθ.
⇒ |А| |Б| cos0°
⇒ |А| |Б| [cos0° = 1]
- Когда угол между векторами равен 180 градусов.

⇒ |А| |Б| cosθ.
⇒ |А| |Б| cos180°
⇒ – |A| |Б| [cos180° = -1]
- Когда угол между векторами равен 90 градусов.
⇒ |А| |Б| cosθ.
⇒ |А| |Б| cos90°
⇒ |А| |Б| × 0 [cos90° = 0]
⇒ 0,
Формула для угла между двумя векторами
Косинус угла между двумя векторами равен сумме произведений отдельных составляющих двух векторов, разделенных произведением величины двух векторов.
Два вектора A и B
=| А | | Б | cosθ.
cosθ=
θ= cos -1
в картезианской форме,
A = A x I + A Y J + A Z K
B = B x I + B Y J + B x I + B Y J + B x I + B Y J + B k
cosθ =
Свойства скалярного произведения
- Скалярное произведение коммутативно.
- Дополнительный продукт является распределительным.

В физике при конвекции угол между двумя векторами лежит между 0 ≤ θ ≤ 180. Когда хвосты или вершины обоих векторов совпадают, вычисляется угол между векторами.
Tail Coincide
Head Coincide
Sample Problems
Question 1: Find the angle between vectors (If they form an equilateral triangle)
- a and b vectors
- b and c vectors
- Векторы а и с
Равносторонний треугольник, образованный векторами а, b, с
Решение:
- Векторы а и b друг друга, следовательно, угол между векторами a и b равен углу между двумя сторонами равностороннего треугольника = 60°.
- Векторы b и c:
Из рисунка выше видно, что начало или конец векторов b и c не совпадают друг с другом.
Итак, с помощью свойства- Вектор остается неизменным, если он передается параллельно самому себе.
Вектор c смещен параллельно самому себе
Теперь мы видим, что хвосты векторов b и c совпадают друг с другом, следовательно, такой же, как внешний угол при равностороннем треугольнике = 120°.
- Векторы а и с
Хвост векторов а и с совпадает
Для векторов а и с хвосты обоих векторов совпадают, следовательно, угол между векторами а и с равен углу между Две стороны равностороннего треугольника = 60°.
Вопрос 2: Найдите углы между векторами, если они образуют равнобедренный прямоугольный треугольник.
- вектор a и b
- вектор b и c
- векторы a и c
Решение:
- вектор a и b
Прямоугольный равнобедренный треугольник
Из приведенного выше рисунка видно, что вершина и хвост вектора a не совпадают. друг с другом. Итак, с помощью свойства- Вектор остается неизменным, если он передается параллельно самому себе.
вектор сдвинут параллельно самому себе
Теперь хвосты векторов a и b совпадают и образуют угол, равный внешнему углу прямоугольного равнобедренного треугольника = 135°.
- Векторы b и c
Прямоугольный равнобедренный треугольник
На приведенном выше рисунке вершина или решка векторов b и c не совпадают. Таким образом, при использовании свойства вектор остается неизменным, если он передается параллельно самому себе.
Вектор b смещен параллельно самому себе
Теперь хвосты векторов b и c совпадают и составляют угол, равный внешнему углу прямоугольного равнобедренного треугольника = 135°.
- Векторы a и c
Прямоугольный равнобедренный треугольник
Из приведенного выше рисунка видно, что вершина или решка векторов a и c не совпадают. Итак, с помощью свойства- Вектор остается неизменным, если он передается параллельно самому себе.
Вектор c перемещается параллельно самому себе
Теперь хвосты векторов a и c совпадают и составляют угол, равный прямому углу равнобедренного треугольника = 90°.
Вопрос 3: Найдите угол между векторами A = i + j + k и вектором B = -2i – 2j – 2k.
Решение:
Из формулы,
A = A x I + A Y J + A Z K
B = B x I + B Y 9003
B = B x I + B y99 j. + B z k
cosθ=
Здесь в заданном вопросе
A= i + j + k.
В= -2i -2j -2k.
Подставляя значения в формулу
⇒ cosθ =
⇒ cosθ =
⇒ cosθ =
⇒ cosθ =
⇒ cosθ = -6/6
⇒ cosθ= -1
⇒ θ = 180°.
Вопрос 4: Угол находки между вектором A = 3i + 4J и B = 2i + J
Решение:
A = A x I + A Y J + A Z K
B = B x I + B Y J + B Z K
COSθ =
ЗДЕСЬ.
Подставляя значения в формулу,
⇒ cosθ =
⇒ cosθ =
⇒ cosθ =
⇒ cosθ =
⇒ θ = cos -1 ()
⇒ θ = cos -1 ()
Question 5 : Найдите угол между вектором A = i + j и вектором B = j + k.
Решение:
Из формулы,
A = A x I + A Y J + A Z K
B = B x I + B Y 9003
B = B x I + B y99 j. + В с K
COSθ =
Здесь, в данном вопросе,
⇒ A = I + J
⇒ B = J + K
⇒ COSθ =
⇒ COSθ =
⇒ cosθ =.
⇒ θ = cos -1 (1/2)
⇒ θ = 60°.
Вычисление разности двух векторов
Разность векторов, расчет онлайн
Резюме:
Функция vector_difference используется для вычисления разницы двух векторов в режиме онлайн.
vector_difference онлайн
Описание:
векторный калькулятор позволяет определить разность двух векторов плоскости или пространства.
- Вычислить разность двух векторов плана
- Вычислить разность двух векторов в пространстве
- Вычислить разность двух векторов в пространстве любой размерности Векторный калькулятор используется по тому же принципу для любой размерности пространств.
Пусть (O,`vec(i)`,`vec(j)`) — каркас плана, `vec(u)` и `vec(v)` — два вектора, имеющие соответствующие координаты (`x_u`,`y_(u)`) и (`x_(v)`,`y_(v)`) в кадре (O,`vec(i)`,`vec(j)`) .
Вектор `vec(u)-vec(v)` имеет координаты (`x_(u)`-`x_(v)`,`y_(u)`-`y_(v)`) в системе (` vec(i)`,`vec(j)`).
Векторный калькулятор может вычитать векторы, имеющие числовые или буквенные координаты.
Пусть `vec(u)`(1;2) `vec(v)`(3;5) для вычисления разницы `vec(u)`-`vec(v)`, введите vector_difference(`[1;2];[3;5]`) , после вычисления возвращается вектор [-2;-3].
Пусть `vec(u)`(a;b) `vec(v)`(2*a;`b`) для вычисления разницы `vec(u)`-`vec(v)`, введите vector_difference(`[a;b];[2*a;b]`)
Пусть (O,`vec(i)`,`vec(j)`,`vec(k)`) пространственная система отсчета, `vec(u)` и `vec(v)` два вектора, которые имеют соответствующие координаты
(`x_u`,`y_(u)`,`z_(u)`) и (`x_(v)`,`y_(v)`,`z_(v)`) в кадре (O,`vec (i)`,`vec(j)`,`vec(k)`) .
Вектор `vec(u)-vec(v)` имеет координаты (`x_(u)`-`x_(v)`,`y_(u)`-`y_(v)`,`z_(u) `-`z_(v)`) в системе (`vec(i)`,`vec(j)`,`vec(k)`).
Векторный калькулятор может вычитать векторы, имеющие числовые или буквенные координаты.
Пусть `vec(u)`(1;2;1) `vec(v)`(3;5;2) для вычисления разницы `vec(u)`-`vec(v)`, введите vector_difference(`[3;5;2];[1;2;1]`) после вычисления возвращается результат [2;3;1].
Пусть `vec(u)`(a;b,c) `vec(v)`(2*a;2-b,c+1) для вычисления разницы `vec(u)`-`vec(v) `, введите vector_difference(`[a;b;c];[3*a;2;2*c+1]`) , после расчета возвращается результат.
Синтаксис:
vector_difference(vector;vector)
Примеры:
vector_difference(`[1;1;1];[5;5;6]`) возвращает [-4;-4;-5]
Расчет онлайн с помощью vector_difference (вычисление разности двух векторов)
См. также
также
Список связанных калькуляторов:
- Векторный калькулятор : vector_calculator.
 Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.
Векторный калькулятор позволяет производить вычисления с векторами, используя координаты. - Вычисление координат вектора по двум точкам. : вектор_координаты. Векторный калькулятор позволяет вычислить координаты вектора по координатам двух точек в режиме онлайн.
- Калькулятор определителя: определитель. Функция определителя вычисляет онлайн определитель векторов или определитель матрицы.
- Вычисление разности двух векторов: vector_difference. Функция vector_difference используется для вычисления разницы двух векторов в режиме онлайн.
- Вычисление нормы вектора : vector_norm. Векторный калькулятор позволяет рассчитать норму вектора онлайн.
- Исчисление скалярного тройного произведения: scalar_triple_product. Калькулятор скалярного тройного произведения позволяет онлайн рассчитать скалярное тройное произведение.
- Калькулятор скалярного произведения: dot_product. Калькулятор скалярного произведения позволяет вычислить скалярное произведение двух векторов онлайн по их координатам.



 е. соедините начало первого отрезка и конец второго.
е. соедините начало первого отрезка и конец второго.
 Но отсюда ,
а это и означает линейную зависимость
векторов и .
Но отсюда ,
а это и означает линейную зависимость
векторов и . Отложим три вектора от одной точки O.
Через точку Aпроведём
прямые, параллельные векторам и .
Тогда ,
причём векторы и коллинеарны
соответственно векторам и .
Поэтому найдутся числа x и y такие,
что ,
а значит .
Отложим три вектора от одной точки O.
Через точку Aпроведём
прямые, параллельные векторам и .
Тогда ,
причём векторы и коллинеарны
соответственно векторам и .
Поэтому найдутся числа x и y такие,
что ,
а значит .
 называются координатами
точки M. в
рассматриваемой системе координат. M(x,y,z).
Первая координата называется абсциссой,
вторая – ординатой, третья – аппликатой.
называются координатами
точки M. в
рассматриваемой системе координат. M(x,y,z).
Первая координата называется абсциссой,
вторая – ординатой, третья – аппликатой.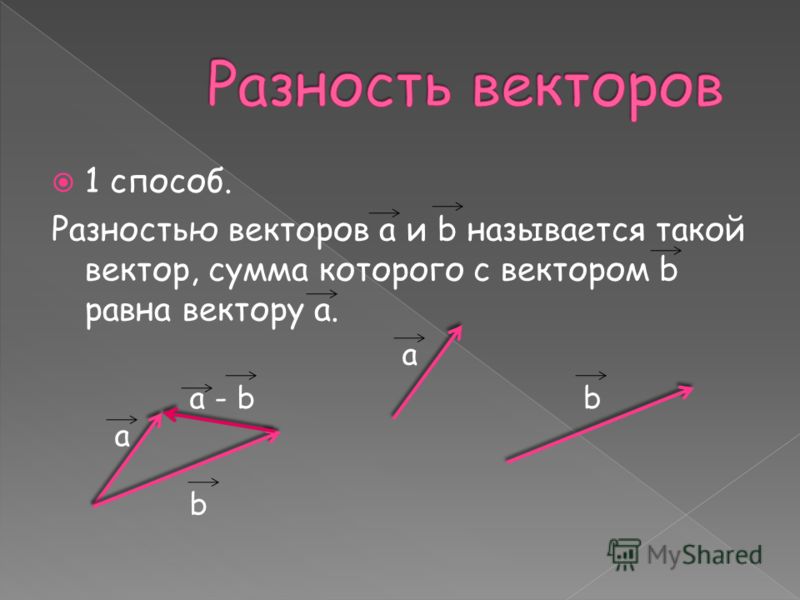




 Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.
Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.