Методические указания к лабораторной работе № 217 по дисциплине «Физика»
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПУТЕЙ СООБЩЕНИЯ (МИИТ)
Кафедра физики
Кули-Заде Т.С., Васильев Е.В.
ОПРЕДЕЛЕНИЕ ЭДС НЕИЗВЕСТНОГО ИСТОЧНИКА МЕТОДОМ КОМПЕНСАЦИИ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ЛАБОРАТОРНОЙ РАБОТЕ № 217
по дисциплине «Физика»
Под редакцией доцента Ю.Н. Харитонова
Москва – 2011
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПУТЕЙ СООБЩЕНИЯ (МИИТ)
Кафедра физики
Кули-Заде Т.С., Васильев Е.В.
ОПРЕДЕЛЕНИЕ ЭДС НЕИЗВЕСТНОГО ИСТОЧНИКА МЕТОДОМ КОМПЕНСАЦИИ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ЛАБОРАТОРНОЙ РАБОТЕ №217
по дисциплине «Физика»
Под редакцией доцента Ю.Н. Харитонова
Рекомендовано редакционно-издательским советом
университета в качестве методических указаний для студентов ИУИТ, ИТТСУ и ИПСС
МОСКВА — 2011
УДК 537. 8: 621.3.023
8: 621.3.023
К-90
Кули-Заде Т.С., Васильев Е.В. Определение ЭДС неизвестного источника методом компенсации. Методические указания к лабораторной работе № 217 по дисциплине «Физика» / под ред. доц. Ю.Н. Харитонова. – М.: МИИТ, 2011. – 10 с.
Методические указания к выполнению лабораторной работы № 217 «Определение ЭДС неизвестного источника методом компенсации» соответствуют программе и учебным планам по физике (раздел «Электричество») и предназначены для студентов 1, 2 курсов технических специальностей.
университет путей сообщения
(МИИТ), 2011
Работа 217
ОПРЕДЕЛЕНИЕ ЭДС НЕИЗВЕСТНОГО ИСТОЧНИКА
МЕТОДОМ КОМПЕНСАЦИИ
Цель
работы: Ознакомление с методом компенсации и его применение для определения
электродвижущей силы (ЭДС) неизвестного источника.
Приборы и принадлежности: источник питания, нормальный элемент Вестона (или другой эталонный источник), исследуемый источник ЭДС (гальванический элемент или другие источники ЭДС), потенциометр (или реохорд), вольтметр
Введение
Гальванические элементы, аккумуляторы, электрические генераторы и другие устройства, которые преобразуют различные виды энергий (химическую, механическую, световую и др.) в электрическую энергию, являются источниками ЭДС. Устройство, способное поддерживать определённую разность потенциалов и обеспечить поток электрических зарядов во внешней цепи, называются источниками ЭДС.
Разность потенциалов
на клеммах гальванического элемента при разомкнутой внешней цепи называется
электродвижущей силой (ЭДС) и обозначается E.
Когда сила тока во внешней цепи отсутствует, напряжение на клеммах равно ЭДС.
Когда к клеммам гальванического элемента подключается внешняя нагрузка
(например, сопротивление вольтметра), т. е. во внешней цепи протекает
электрический ток, согласно закону Ома для неоднородной электрической цепи этот
ток равен:
е. во внешней цепи протекает
электрический ток, согласно закону Ома для неоднородной электрической цепи этот
ток равен:
I =, тогда E = Ir + IR, (1)
следовательно, напряжение на клеммах гальванического элемента оказывается ниже величины ЭДС из-за падения напряжения на внутреннем сопротивлении источника ЭДС и равно:
IR = E – Ir, (2)
где E – ЭДС источника тока, R – внешнее сопротивление, r – внутреннее сопротивление источника тока, I – сила тока.
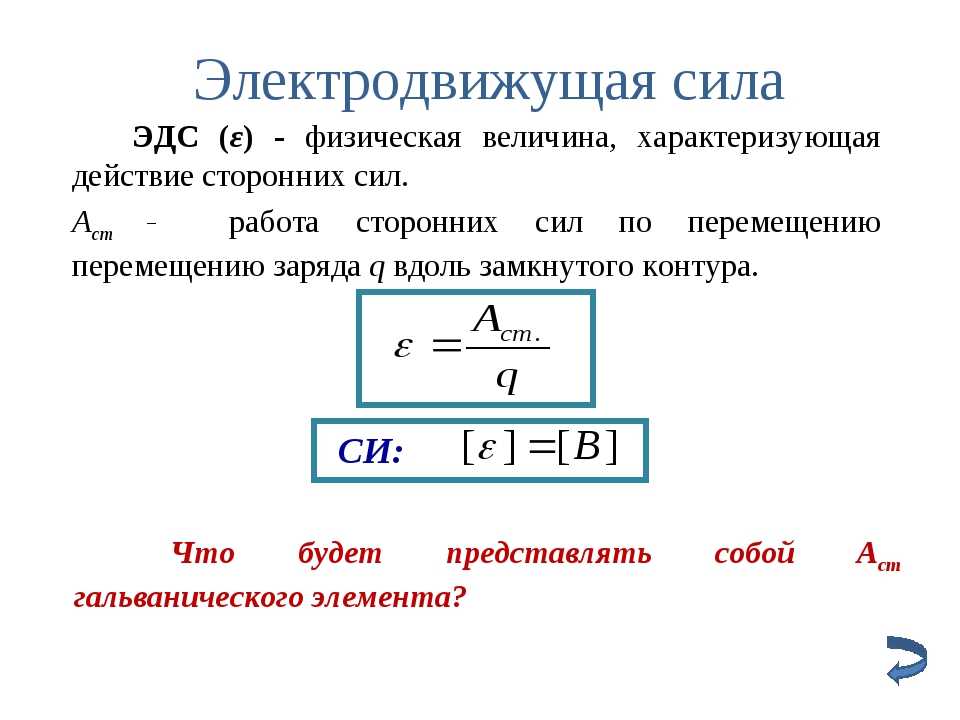
Электродвижущая сила численно равна работе, совершаемой сторонними силами по перемещению единичного положительного заряда:
E = . (3)
Эта работа производится за счёт энергии, затрачиваемой в источнике тока.
Рис. 1.
Напряжение U на участке 1 – 2 электрической цепи (см. рис.
U12 = j1 — j2 + E12. (4)
Если на участке цепи не действует ЭДС, напряжение на концах участка цепи равно разности потенциалов на этом участке.
Разность потенциалов численно равна работе, совершаемой силами электростатического поля по перемещению единичного положительного заряда:
Для определения
величины электродвижущей силы используется метод компенсации («нулевой метод»).
В этом методе ток текущий через источник с неизвестной ЭДС – EX, компенсируется
током от какого-либо внешнего источника ЭДС – E.
При этом разность потенциалов на зажимах неизвестного источника будет равна его
ЭДС.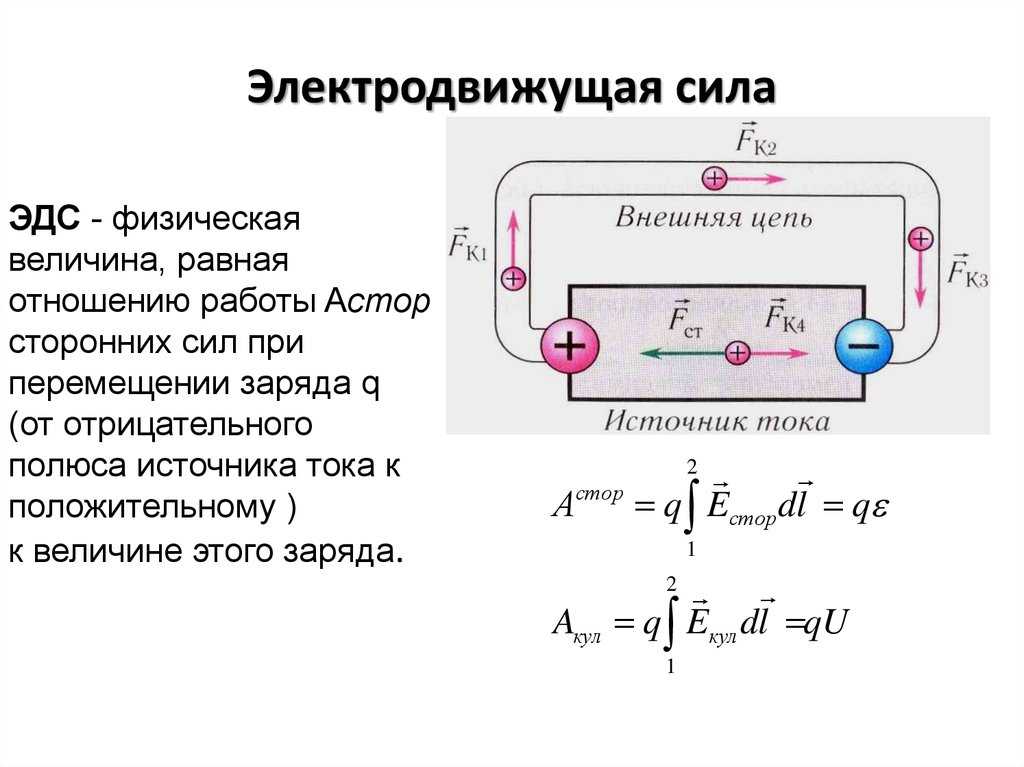
Принципиальная схема установки, служащей для измерений ЭДС неизвестного источника изображена на рис. 2.
Рис. 2.
В цепи, благодаря разности потенциалов Dj между точками
Контакт реохорда перемещают до тех пор, пока стрелка гальванометра не установится на нуле шкалы. В этом положении контакта
UАD = EX.
Это равенство справедливо только при условии, что сила тока через гальванометр равна нулю, т.к. в противном случае наблюдалось бы падение напряжения на внутреннем сопротивлении источника неизвестной ЭДС и сопротивлении гальванометра. Сила тока I через резистор R не равна нулю, и если обозначать через RX сопротивление между точками
II. Определение эдс двух неизвестных источников, соединенных параллельно
В этом случае эквивалентная ЭДС будет равна:
(14) |
где r1иr2— внутренние сопротивления двух
неизвестных источников. Эти
сопротивления следует измерить для
каждого источника отдельно, собрав
простую схему из последовательно
соединенных источника тока, реохорда
н амперметра. Используя значенияx
Используя значенияx
КОНТРОЛЬНЫЕ ВОПРОСЫ
В чем суть метода компенсации? Зарисовать схему цепи.
Что называется ЭДС?
Какие преимущества имеет метод компенсации по сравнению с другими методами измерения ЭДС?
Как устроен гальванический элемент?
Что называется напряжением?
В каких единицах измеряются ЭДС и напряжение в международной системе единиц?
Сформулировать закон Ома для замкнутой цепи, участка цепи, содержащего ЭДС, и участка цепи, не содержащего ЭДС.
СПИСОК ЛИТЕРАТУРЫ
Калашников С.
 Г.
Электричество,— М., 1964.
Г.
Электричество,— М., 1964.Савельев И. В. Курс общей физики.—М., 1989.—Т. II.
Детлаф А. А., Яворский Б. М., Милковская Л. Б. Kуpc физики.—М.: Высш. шк. 1988.—Т. 2.
Руководство к лабораторным занятиям по физике/Под ред. Гольдина Л. Л.—М., 1964.
Методические указания к лабораторным работам по физике Работы № 60-63.—M., МИИТ. 1976.
Методические указания к вводным занятиям в физическом практикуме. Расчет погрешностей в лабораторных работах физического практикума. Под редакцией проф. Ф. П. Денисова,—М.,—Изд. МГУ ПС (МИИТ).— 1995.
23
Работа 18 законы разветвленных цепей постоянного тока
Цель работы.Измерение силы тока в узле разветвленной цепи. Определение ЭДС источников тока и разности потенциалов с использованием обобщенного закона Ома.
Введение
Для характеристики электрического тока
в электрических цепях используют понятие
силы тока и плотности тока. Сила
стационарного электрического тока есть
алгебраическая величина, равная
заряду, протекающему через некоторую
поверхность, в единицу времени. Если
за время dtчерез поверхность
проводника переносится зарядdq,то
Сила
стационарного электрического тока есть
алгебраическая величина, равная
заряду, протекающему через некоторую
поверхность, в единицу времени. Если
за время dtчерез поверхность
проводника переносится зарядdq,то
За положительное направление тока принято направление движения положительных зарядов. Плотность тока — векторная величина, численно равная силе тока, протекающего через единичную площадку, перпендикулярную скорости движения зарядов:
где dl—сила тока, протекающего через площадкуdS1. Вектор плотности тока совпадает по направлению с вектором скорости положительно заряженных частиц. Связь силы тока и плотности тока может быть записана в виде интеграла по поверхностиS, через которую течет ток:
То есть сила тока равняется потоку
плотности тока через поверхность S. Здесь- угол, образованный вектором плотности
тока и нормалью к элементу поверхностиds
Здесь- угол, образованный вектором плотности
тока и нормалью к элементу поверхностиds
В зависимости от величины сила тока может иметь положительный или отрицательный знак.
24
Одним из элементов разветвленной цепи является узел — место соединения трех и более проводников (рис. 1).
Поскольку в цепях постоянного тока нигде не происходит накапливания электрического заряда, а также его возникновения или уничтожения (закон сохранения заряда), то заряд, приходящий в единицу времени к узлу, равен заряду, уходящему за это же время от узла. Из этого следует первое правило Кирхгофадля цепей постоянного тока: алгебраическая сумма сил токов, сходящихся в узле, равна нулю:
При составлении уравнений с использованием этого правила токи, текущие к узлу, считают положительными, а токи, текущие от узла — отрицательными.
Свободные носители заряда в проводнике
(электроны, ионы) при движении испытывают
сопротивление. В металле, например,
электроны взаимодействуют с ионами
кристаллической решетки и теряют
свою энергию. Поэтому ток в проводнике
поддерживается только при условии
непрерывного действия на электроны
ускоряющего электрического ноля.
В металле, например,
электроны взаимодействуют с ионами
кристаллической решетки и теряют
свою энергию. Поэтому ток в проводнике
поддерживается только при условии
непрерывного действия на электроны
ускоряющего электрического ноля.
Между плотностью тока и напряженностью электрического поля в каждой точке проводника существует зависимость:
(1) |
где удельная электропроводность вещества.
Эту формулу называютзаконом Ома в дифференциальной форме.Рассмотрим этот закон подробнее. Существование напряженности электрического поля указывает на изменение потенциала вдоль проводника. Следовательно, условием существования электрического тока на участке цепи является наличие разности потенциалов на концах этого участка.
Один из источников создания электрического
поля внутри проводника — избыточный
положительный или отрицательный заряд,
накапливающийся в некоторых участках
проводника.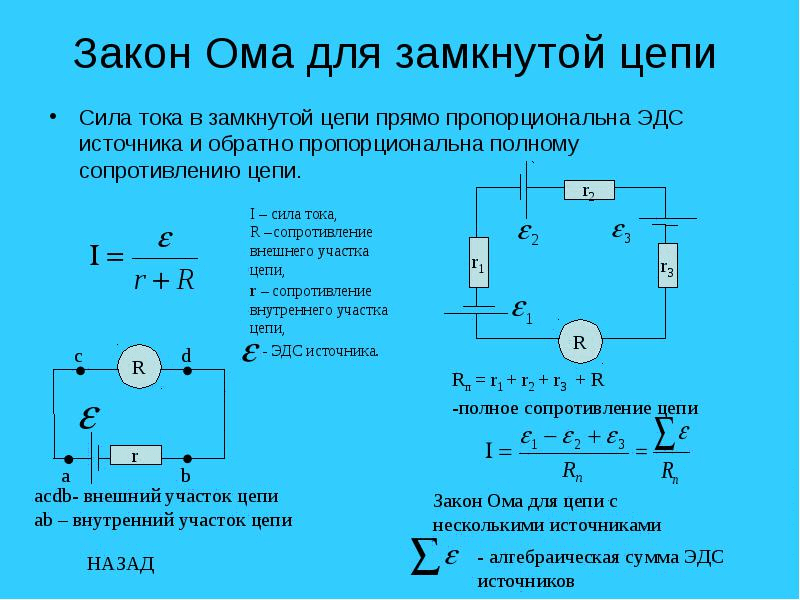 Но этoполе,
имеющее электростатическое
Но этoполе,
имеющее электростатическое
25
происхождение, одно не может поддерживать в цепи постоянный электрический ток, т.к. электростатические силы способствуют сближению разноименных зарядов и выравниванию потенциала проводника. Для поддержания постоянного тока в цепи, в ней на некоторых участках должны существовать силы неэлектростатиче ского происхождения. Эти силы поддерживают такое распределение зарядов в проводниках, которое создает внутри них поле с напряженностью, не равной нулю. При этом на некоторых участках цепи силы неэлектростатического происхождения заставляют свободные носители зарядов двигаться против поля, вызванного электростатическими силами.
Силы неэлектростатического происхождения называют сторонними. Они могут быть обусловлены химическими процессами, диффузией носителей зарядов в неоднородной среде или через границу двух разнородных веществ, явлением электромагнитной индукции и т. д. С учетом всех сил, действующих на заряды, формулу (1) записывают в более общем виде:
(2) |
Иными словами, в уравнении (1)
здесь — напряженность поля сторонних сил, т. е. сила неэлектростатического
происхождения, действующая на пробный
единичный положительный заряд, —
напряженность поля кулоновских сил.
е. сила неэлектростатического
происхождения, действующая на пробный
единичный положительный заряд, —
напряженность поля кулоновских сил.
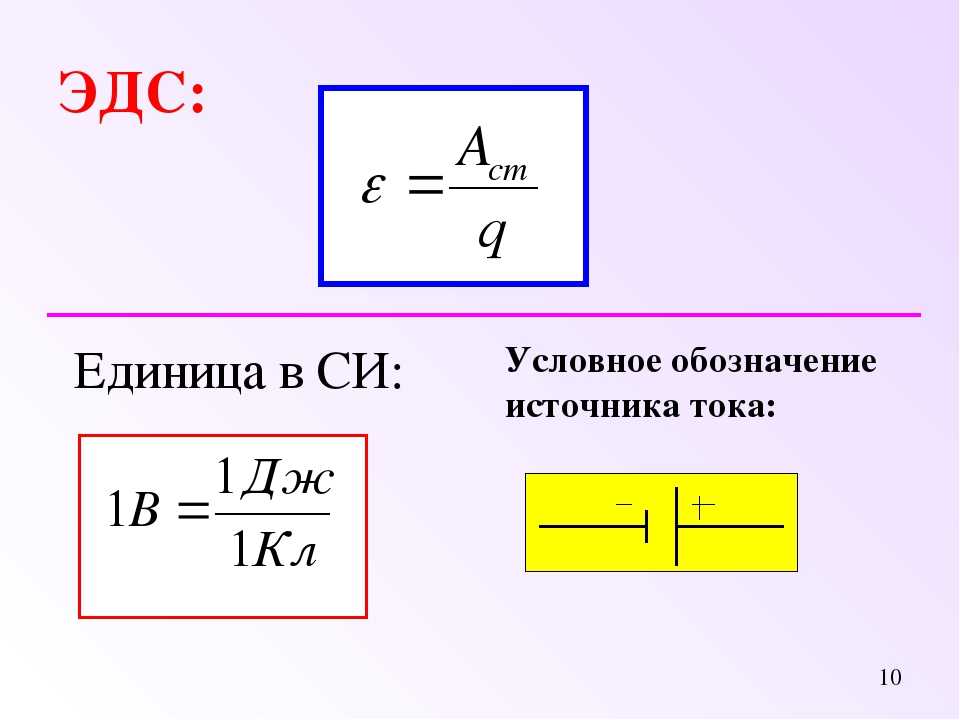
Сторонние силы в практике удобно характеризовать не напряженностью, а работой, которую они совершают при переносе единичного положительного заряда. Эта работа называется электродвижущей силой (ЭДС), обозначается буквой и может быть выражена в виде интеграла, начало и конец которого обозначен соответственно 1 и 2:
(3) |
где dl – элемент проводника с током.
26
На основании равенства (2) запишем интеграл для участка 1-2:
(4) |
где
— удельное сопротивление проводника.
Предположим, что ток течет по прямолинейному однородному проводнику и на участке 1-2 постоянен. Вынесем за знак интегралов в правой части уравнения. Разделим последнее равенство на . В правой части полученного равенства первое слагаемое есть разность потенциалов на концах участка 1-2:
(5) |
а второе—ЭДС на этом участке:
(6) |
Подставим уравнения (5) и (6) в уравнение (4) н учтем, что вектор совпадает по направлению с .Учитывая, что поперечное сечение проводникаS1перпендикулярно этим векторам, уравнение (4) примет вид:
(7) |
здесь
(8) |
а I – сила постоянного тока, и получим:
(9) |
27
Здесь
— сопротивление участка 1-2.
Тогда (9) примет вид:
(10) |
Полученное уравнение носит название закона Ома для участка цепи, содержащего ЭДС.
Иногда его записывают в виде:
(11) |
и
Рис. 1
называют обобщенным законом Ома.
При записи этого уравнения применяется
правило знаков которое утверждает, что,
если направление токов совпадает— с направлением обхода участка цепи 1—2,
ток в уравнении (11) считается положительным.
Если в направлении обхода участка от
точки 1 к точке 2 потенциал источника повышается, то ЭДС берется с плюсом,
в противном случае— с минусом.
Определение ЭДС движения в физике.
(имя существительное)
ЭДС (электродвижущая сила), вызванная движением относительно магнитного поля.
Количественная интерпретация ЭДС движения
- A a движущая ЭДС — электродвижущая сила ( ЭДС ), вызванная движением относительно магнитного поля B.
- Электродвижущая сила ( ЭДС ), вызванная движением относительно магнитного поля B, называется подвижный ЭДС .
- Вы могли заметить, что движущаяся ЭДС очень похожа на индуцированную ЭДС , вызванную изменяющимся магнитным полем.
- Из уравнения. 1 и уравнение 2 мы можем подтвердить, что движущихся и наведенных ЭДС дают одинаковый результат.
- (а) Motional EMF .
ЭДС движения
- Движение в стационарном относительно Земли магнитном поле индуцирует двигательный ЭДС (электродвижущая сила).

- Движение является одной из основных причин индукции.
- Например, магнит, перемещаемый по направлению к катушке, индуцирует ЭДС , а катушка, перемещаемая по направлению к магниту, создает аналогичную ЭДС .
- В этом Атоме мы концентрируемся на движении в магнитном поле, стационарном относительно Земли, производя то, что условно называется движущимся ЭДС .
- (a) движущаяся ЭДС =Bℓv индуцируется между рельсами, когда этот стержень движется вправо в однородном магнитном поле.
- Движение в стационарном относительно Земли магнитном поле индуцирует двигательный ЭДС (электродвижущая сила).
Механическая работа и электрическая энергия
- Механическая работа, совершаемая внешней силой для создания движения ЭДС преобразуется в тепловую энергию; в процессе сохраняется энергия.
- Мы узнали о Motional EMF ранее (см. наш Atom на « Motional EMF «).
- Для простой установки, показанной ниже, движущаяся ЭДС $(\varepsilon)$, создаваемая движущимся проводником (в однородном поле), определяется следующим образом:
- В более общем смысле механическая работа, совершаемая внешней силой для производства движения ЭДС , преобразуется в тепловую энергию.

- (a) движущаяся ЭДС =Bℓv индуцируется между рельсами, когда этот стержень движется вправо в однородном магнитном поле.
Электрогенераторы
- Они индуцируют электродвижущую силу ( ЭДС ), вращая катушку в магнитном поле.
- Таким образом, мы можем найти индуцированную ЭДС , рассматривая только боковые провода.
- Motional EMF определяется как EMF = Bℓv, где скорость v перпендикулярна магнитному полю B (см. наш атом на « Motional EMF »).
- Таким образом, в данном случае ЭДС , индуцированная с каждой стороны, равна ЭДС =Bℓvsinθ, и они имеют одинаковое направление.
- Суммарное ЭДС $\varepsilon$ вокруг петли равно:
Обратная ЭДС, вихревые токи и магнитное демпфирование
- Назад ЭДС , вихревые токи и магнитное демпфирование являются следствием индуцированной ЭДС и могут быть объяснены законом индукции Фарадея.

- Закон Ленца говорит нам, что индуцированная ЭДС противодействует любым изменениям, так что вход ЭДС , которая питает двигатель, будет противодействовать самогенерируемой ЭДС двигателя, называемой обратной ЭДС двигателя.
- Как обсуждалось в « Motional EMF », Motional EMF индуцируется, когда проводник движется в магнитном поле или когда магнитное поле движется относительно проводника.
- Если движущийся ЭДС может вызвать петлю тока в проводнике, мы называем этот ток вихревым током.
- Магнитная сила на токовой петле противодействует движению .
- Назад ЭДС , вихревые токи и магнитное демпфирование являются следствием индуцированной ЭДС и могут быть объяснены законом индукции Фарадея.
Зарядка аккумулятора: последовательное и параллельное ЭДС
- Обычно элементы соединены последовательно для получения большей общей ЭДС .
- Но, если клетки противостоят друг другу, например, когда одну из них помещают в прибор задом наперед, общая ЭДС меньше, так как она представляет собой алгебраическую сумму отдельных ЭДС .

- Когда два источника напряжения с одинаковыми ЭДС соединены параллельно и также подключены к нагрузочному сопротивлению, общая ЭДС такая же, как отдельные ЭДС .
- Зарядное устройство должно иметь большую ЭДС , чем аккумулятор, чтобы протекающий через него обратный ток.
- Два источника напряжения с идентичными ЭДС (обозначены буквой E), соединенные параллельно, производят одинаковые ЭДС , но имеют меньшее общее внутреннее сопротивление, чем отдельные источники.
Звуковые системы, компьютерная память, сейсмограф, GFCI
- Микрофон работает по индукции, так как вибрирующая мембрана наводит в катушке ЭДС .
- Таким образом, колебания электрического тока, проходящего через динамик, преобразуются в переменные магнитные силы, которые перемещают диафрагму динамика, заставляя драйвер производить движение воздуха , аналогичное исходному сигналу от усилителя.

- Если устройство GFCI обнаруживает утечку тока, оно выдает ЭДС и ток в направлении, противоположном исходному току.
Закон индукции Фарадея и закон Ленца
- Закон индукции Фарадея гласит, что ЭДС , индуцированная изменением магнитного потока, равна $ ЭДС = -N\frac{\Delta \Phi}{\Delta t}$, когда поток изменяется на Δ за время Δt.
- Во-первых, ЭДС прямо пропорциональна изменению потока Δ.
- Секунда, ЭДС максимальна, когда изменение времени Δt наименьшее, то есть ЭДС обратно пропорциональна Δt.
- Наконец, если катушка имеет N витков, будет произведена ЭДС , которая в N раз больше, чем для одиночной катушки, так что ЭДС прямо пропорциональна N.
- Единицами для EMF , как обычно, являются вольты.
Индуктивность
- Индукция – это процесс, при котором ЭДС индуцируется изменением магнитного потока.

- См. , где простые катушки индуцируют emfs друг в друге.
- Эти катушки могут индуцировать ЭДС друг в друге, как неэффективный трансформатор.
- Здесь видно, что изменение тока в катушке 1 индуцирует ЭДС в катушке 2.
- (Обратите внимание, что «E2 индуцируется» представляет ЭДС индукции в катушке 2.)
- Индукция – это процесс, при котором ЭДС индуцируется изменением магнитного потока.
Источники ЭМП
- Создаваемая разность электрических потенциалов приводит к протеканию тока, если цепь подключена к источнику ЭДС .
- Снова ЭДС противостоит электрическому напряжению из-за разделения заряда.
- Общий принцип, регулирующий ЭДС в таких электрических машинах, — это закон индукции Фарадея.
- В природе ЭДС генерируется всякий раз, когда флуктуации магнитного поля проходят через поверхность.
- Выходное напряжение каждого зависит от его конструкции и нагрузки и равняется э.
 д.с. только при отсутствии нагрузки.
д.с. только при отсутствии нагрузки.
Электродвижущая сила и магнитный поток
Все ресурсы AP Physics 2
6 Диагностические тесты 149 практических тестов Вопрос дня Карточки Learn by Concept
AP Physics 2 Справка » Электричество и магнетизм » Магнетизм и электромагнетизм » Электродвижущая сила и магнитный поток
Существует частица с зарядом, движущаяся перпендикулярно через магнитное поле напряженностью . Какая сила действует на частицу?
Возможные ответы:
Правильный ответ:
Пояснение:
Уравнение для силы, действующей на движущуюся заряженную частицу в магнитном поле, имеет вид
.
Поскольку заряд движется перпендикулярно магнитному полю, нам не нужно беспокоиться о перекрестном произведении, и уравнение превращается в простое умножение.
Следовательно, сила, действующая на частицу, равна 3619N.
Сообщить об ошибке
Токопроводящий стержень движется через область магнитного поля, направленного за пределы страницы, как показано на схеме выше. В результате его движения подвижный заряд в стержне разделяется, создавая электрический потенциал по всей длине стержня. Длина стержня 0,12 м, а величина магнитного поля – 0,022 Тл. Если стержень движется со скоростью, какова величина и направление потенциала от одного конца стержня к другому?
Возможные ответы:
верхний потенциал более высокий, чем нижний
верхний потенциал более низкий, чем нижний
верхний потенциал более низкий, чем нижний более высокий потенциал, чем нижний
верхний потенциал более высокий, чем нижний
Правильный ответ:
верхний потенциал более высокий, чем нижний
Объяснение:
Для проводника, движущегося в магнитном поле и пересекающего силовые линии, создается потенциал, где – потенциал или ЭДС, – напряженность магнитного поля и – скорость проводника относительно поля.
При движении стержня положительный заряд воспринимает силу, направленную вверх по правилу правой руки, а отрицательный заряд — направленную вниз силу, в результате чего верхняя часть стержня находится под более высоким потенциалом, чем нижняя часть стержня.
Сообщить об ошибке
Токопроводящий стержень движется через область магнитного поля, как показано на схеме выше. В результате его движения подвижные носители заряда в проводнике расходятся, создавая на стержне электрический потенциал. Когда, если вообще, носители заряда прекращают это движение?
Возможные ответы:
Движение прекращается, когда электрический потенциал равен напряженности магнитного поля.
Движение прекращается, когда электрическое поле, создаваемое разделенными зарядами, создает силу, равную и противоположную магнитной силе, создаваемой движением стержня.
Движение прекращается, когда магнитное поле, создаваемое разделенными зарядами, сравняется с внешним магнитным полем.


 Г.
Электричество,— М., 1964.
Г.
Электричество,— М., 1964.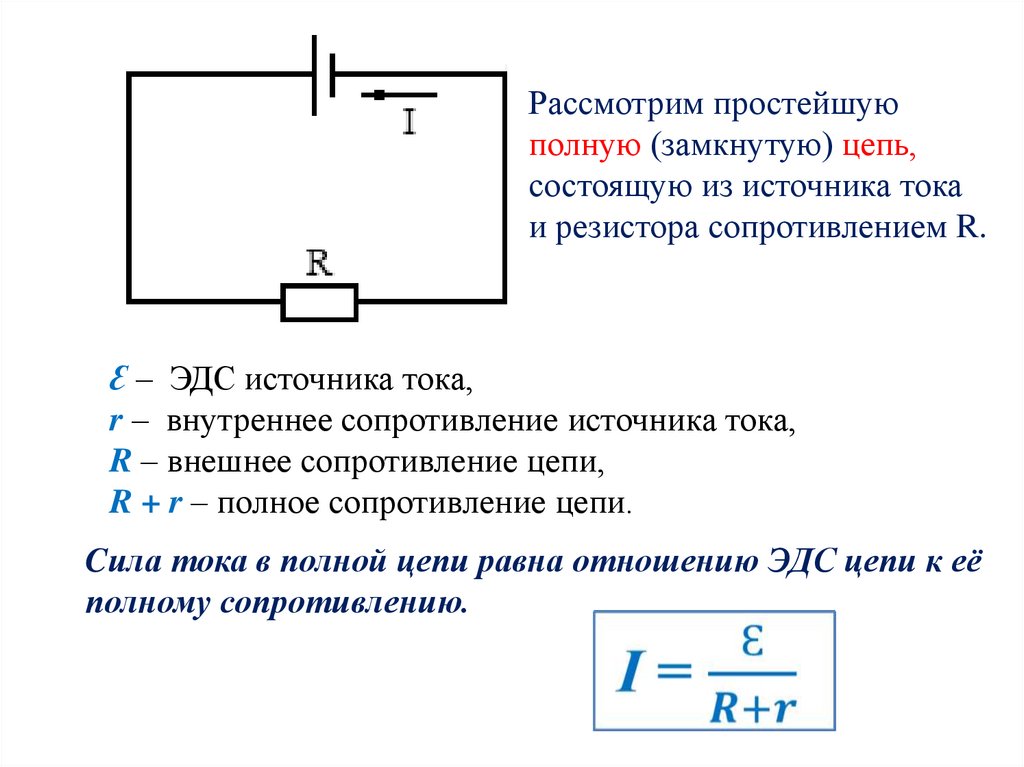



 д.с. только при отсутствии нагрузки.
д.с. только при отсутствии нагрузки.