Закон Кулона 10 класс онлайн-подготовка на Ростелеком Лицей
Введение
Тема урока: «Закон Кулона». Закон Кулона количественно описывает взаимодействие точечных неподвижных зарядов – то есть зарядов, которые находятся в статичном положении друг относительно друга. Такое взаимодействие называется электростатическим или электрическим и является частью электромагнитного взаимодействия.
Электромагнитное взаимодействие
Конечно, если заряды находятся в движении – они тоже взаимодействуют. Такое взаимодействие называется магнитным и описывается в разделе физики, который носит название «Магнетизм».
Стоит понимать, что «электростатика» и «магнетизм» – это физические модели, и вместе они описывают взаимодействие как подвижных, так и неподвижных друг относительно друга зарядов. И всё вместе это называется электромагнитным взаимодействием.
Электромагнитное взаимодействие – это одно из четырех фундаментальных взаимодействий, существующих в природе.
Электрический заряд
Что же такое электрический заряд? Определения в учебниках и Интернете говорят нам, что заряд – это скалярная величина, характеризующая интенсивность электромагнитного взаимодействия тел. То есть электромагнитное взаимодействие – это взаимодействие зарядов, а заряд – это величина, характеризующая электромагнитное взаимодействие. Звучит запутанно – два понятия определяются друг через друга. Разберемся!
Существование электромагнитного взаимодействия – это природный факт, что-то вроде аксиомы в математике. Люди его заметили и научились описывать. Для этого они ввели удобные величины, которые это явление характеризуют (в том числе электрический заряд) и построили математические модели (формулы, законы и т. д.), которые это взаимодействие описывают.
Закон Кулона
Выглядит закон Кулона следующим образом:
Сила взаимодействия двух неподвижных точечных электрических зарядов в вакууме прямо пропорциональна произведению их модулей и обратно пропорциональна квадрату расстояния между ними.
Она направлена вдоль прямой, соединяющей заряды, и является силой притяжения, если заряды разноименные, и силой отталкивания, если заряды одноименные.
Коэффициент k в законе Кулона численно равен:
Аналогия с гравитационным взаимодействием
Закон всемирного тяготения гласит: все тела, обладающие массой, притягиваются друг к другу. Такое взаимодействие называется гравитационным. Например, сила тяжести, с которой мы притягиваемся к Земле, – это частный случай именно гравитационного взаимодействия. Ведь и мы, и Земля обладаем массой. Сила гравитационного взаимодействия прямо пропорциональна произведению масс взаимодействующих тел и обратно пропорциональна квадрату расстояния между ними.
Коэффициент γ называется гравитационной постоянной.
Численно он равен: .
Как видите, вид выражений, количественно описывающих гравитационное и электростатическое взаимодействия, очень похож.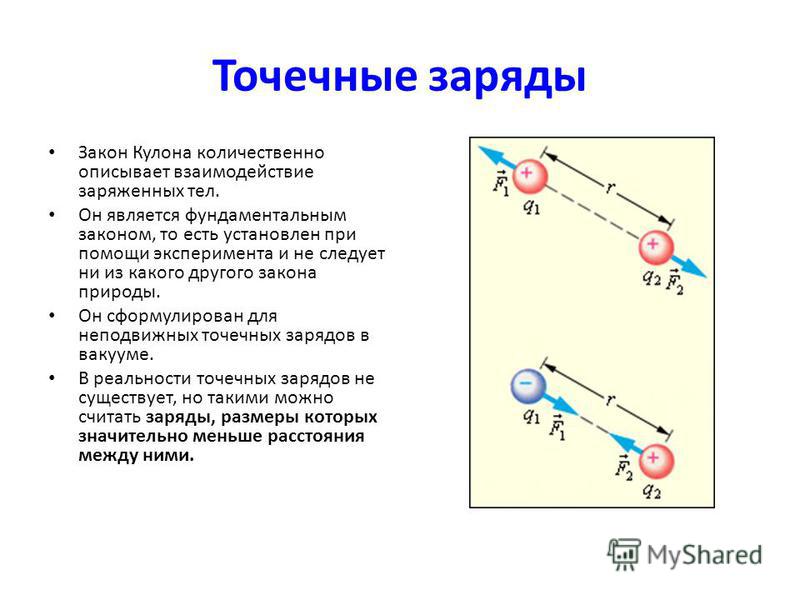
В числителях обоих выражений – произведение единиц, характеризующих данный тип взаимодействия. Для гравитационного – это массы, для электромагнитного – заряды. В знаменателях обоих выражений – квадрат расстояния между объектами взаимодействия.
Обратная зависимость от квадрата расстояния часто встречается во многих физических законах. Это позволяет говорить об общей закономерности, связывающей величину эффекта с квадратом расстояния между объектами взаимодействия.
Эта пропорциональность справедлива для гравитационного, электрического, магнитного взаимодействий, силы звука, света, радиации и т. д.
Объясняется это тем, что площадь поверхности сферы распространения эффекта увеличивается пропорционально квадрату радиуса (см. рис. 1).
Рис. 1. Увеличение площади поверхности сфер
Это будет выглядеть естественным, если вспомнить, что площадь сферы пропорциональна квадрату радиуса:
Физически это означает, что сила взаимодействия двух точечных неподвижных зарядов в 1 Кл, находящихся на расстоянии 1 м друг от друга в вакууме, будет равна 9·109 Н (см. рис. 2).
рис. 2).
Рис. 2. Сила взаимодействия двух точечных зарядов в 1 Кл
Казалось бы, эта сила огромна. Но стоит понимать, что ее порядок связан с еще одной характеристикой – величиной заряда 1 Кл. На практике заряженные тела, с которыми мы взаимодействуем в повседневной жизни, имеют заряд порядка микро- или даже нанокулонов.
Коэффициент и электрическая постоянная
Иногда вместо коэффициента используется другая постоянная, характеризующая электростатическое взаимодействие, которая так и называется – «электрическая постоянная». Обозначается она . С коэффициентом она связана следующим образом:
Выполнив несложные математические преобразования можно ее выразить и вычислить:
Обе константы, конечно, присутствуют в таблицах задачников. Закон Кулона тогда примет такой вид:
Обратим внимание на несколько тонких моментов.
Важно понимать, что речь идет именно о взаимодействии. То есть если мы возьмем два заряда, то каждый из них будет действовать на другой с силой, по модулю равной. Эти силы будут направлены в противоположные стороны вдоль прямой, соединяющей точечные заряды.
То есть если мы возьмем два заряда, то каждый из них будет действовать на другой с силой, по модулю равной. Эти силы будут направлены в противоположные стороны вдоль прямой, соединяющей точечные заряды.
Заряды будут отталкиваться, если они имеют один знак (оба положительные или оба отрицательные (см. рис. 3)), и притягиваться, если имеют разные знаки (один отрицательный, другой положительный (см. рис. 4)).
Рис. 3. Взаимодействие одноименных зарядов
Рис. 4. Взаимодействие разноименных зарядов
Точечный заряд
В формулировке закона Кулона присутствует термин «точечный заряд». Что это означает? Вспомним механику. Исследуя, например, движение поезда между городами, мы пренебрегали его размерами. Ведь размеры поезда в сотни или тысячи раз меньше расстояния между городами (см. рис. 5). В такой задаче мы считали поезд «материальной точкой» – телом, размерами которого в рамках решения некоторой задачи мы можем пренебречь.
Рис. 5. Размерами поезда в данном случае пренебрегаем
5. Размерами поезда в данном случае пренебрегаем
Так вот, точечные заряды – это материальные точки, обладающие зарядом. На практике, используя закон Кулона, мы пренебрегаем размерами заряженных тел в сравнении с расстояниями между ними. Если же размеры заряженных тел сопоставимы с расстоянием между ними, то из-за перераспределения заряда внутри тел электростатическое взаимодействие будет носить более сложный характер.
Задача 1
В вершинах правильного шестиугольника со стороной помещены друг за другом заряды . Найдите силу, действующую на заряд , расположенный в центре шестиугольника (см. рис. 6).
Рис. 6. Рисунок к условию задачи 1
Порассуждаем: заряд, находящийся в центре шестиугольника, будет взаимодействовать с каждым из зарядов, находящихся в вершинах шестиугольника. В зависимости от знаков это будет сила притяжения или сила отталкивания. С зарядами 1, 2 и 3, которые являются положительными, заряд, находящийся в центре, будет испытывать электростатическое отталкивание (см. рис. 7).
рис. 7).
Рис. 7. Электростатическое отталкивание
А с зарядами 4, 5 и 6 (отрицательными) заряд в центре будет иметь электростатическое притяжение (см. рис. 8).
Рис. 8. Электростатическое притяжение
Суммарная сила, действующая на заряд, находящийся в центре шестиугольника, будет равнодействующей сил ,,,, и, модуль каждой из которых можно найти с помощью закона Кулона. Приступим к решению задачи.
Решение
Силы взаимодействия заряда, который находится в центре, с каждым из зарядов в вершинах зависит от модулей самих зарядов и расстояния между ними. Расстояние от вершин к центру правильного шестиугольника одинаковое, модули у взаимодействующих зарядов в нашем случае тоже равны (см. рис. 9).
Рис. 9. Расстояния от вершин до центра в правильном шестиугольнике равны
А значит, все силы взаимодействия заряда в центре шестиугольника с зарядами в вершинах будут равны по модулю. Воспользовавшись законом Кулона, мы можем найти этот модуль:
Расстояние от центра до вершины в правильном шестиугольнике равно длине стороны правильного шестиугольника, которая нам известна из условия, поэтому:
Теперь нам необходимо найти векторную сумму – для этого выберем систему координат: ось вдоль силы , а ось перпендикулярно (см.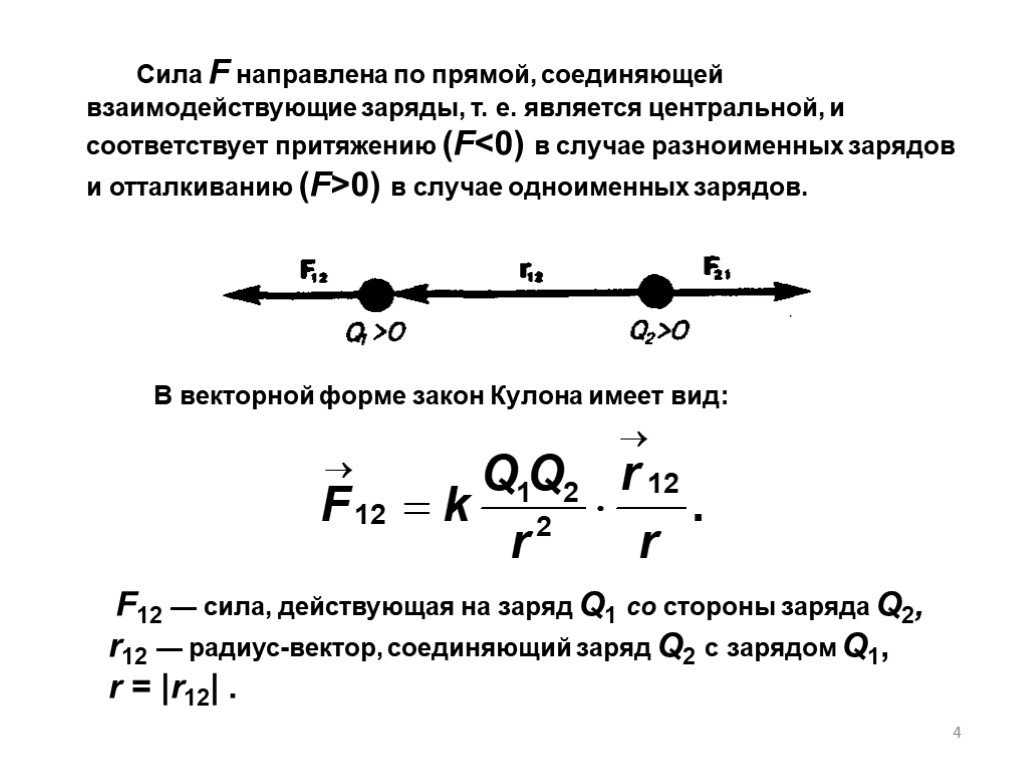 рис. 10).
рис. 10).
Рис. 10. Выбор осей
Найдем суммарные проекции на оси – модуль каждой из них обозначим просто .
Так как силы и сонаправлены с осью , а находятся под углом к оси (см. рис. 11).
Рис. 11. Направление сил относительно оси
Проделаем такие же действия для оси :
Знак «-» – потому что силы и направлены в противоположную сторону оси . То есть проекция суммарной силы на ось , которую мы выбрали, будет равна 0. Получается, что суммарная сила будет действовать только вдоль оси , остается подставить сюда только выражения для модуля сил взаимодействия и и получить ответ. Суммарная сила будет равна:
Задача решена.
Диэлектрическая проницаемость
Еще один тонкий момент заключается вот в чем: в законе Кулона сказано, что заряды находятся в вакууме (см. рис. 12).
Рис. 12. Взаимодействие зарядов в вакууме
Это действительно важное замечание.
Рис. 13. Взаимодействие зарядов в среде, отличной от вакуума
Чтобы учесть этот фактор, в модель электростатики была введена специальная величина, которая позволяет сделать «поправку на среду». Называется она диэлектрической проницаемостью среды. Обозначается, как и электрическая постоянная, греческой буквой «эпсилон», но уже без индекса.
Физический смысл этой величины заключается в следующем.
Сила электростатического взаимодействия двух точечных неподвижных зарядов в среде, отличной от вакуума, будет в ε раз меньше, чем сила взаимодействия таких же зарядов на таком же расстоянии в вакууме.
Таким образом, в среде, отличной от вакуума, сила электростатического взаимодействия двух точечных неподвижных зарядов будет равна:
Значения диэлектрической проницаемости различных веществ давно найдены и собраны в специальных таблицах (см. рис. 14).
рис. 14).
Рис. 14. Диэлектрическая проницаемость некоторых веществ
Мы можем свободно использовать табличные значения диэлектрической проницаемости необходимых нам веществ при решении задач.
Важно понимать, что при решении задач сила электростатического взаимодействия рассматривается и описывается в уравнениях динамики как обычная сила. Решим задачу.
Задача 2
Два одинаковых заряженных шарика подвешены в среде с диэлектрической проницаемостью на нитях одинаковой длины , закрепленных в одной точке. Определите модуль заряда шариков, если нити находятся под прямым углом друг к другу (см. рис. 15). Размеры шариков пренебрежимо малы по сравнению с расстоянием между ними. Массы шариков равны .
Рис. 15. Рисунок к условию задачи 2
Порассуждаем: на каждый из шариков будут действовать три силы – сила тяжести ; сила электростатического взаимодействия и сила натяжения нити (см. рис. 16).
Рис.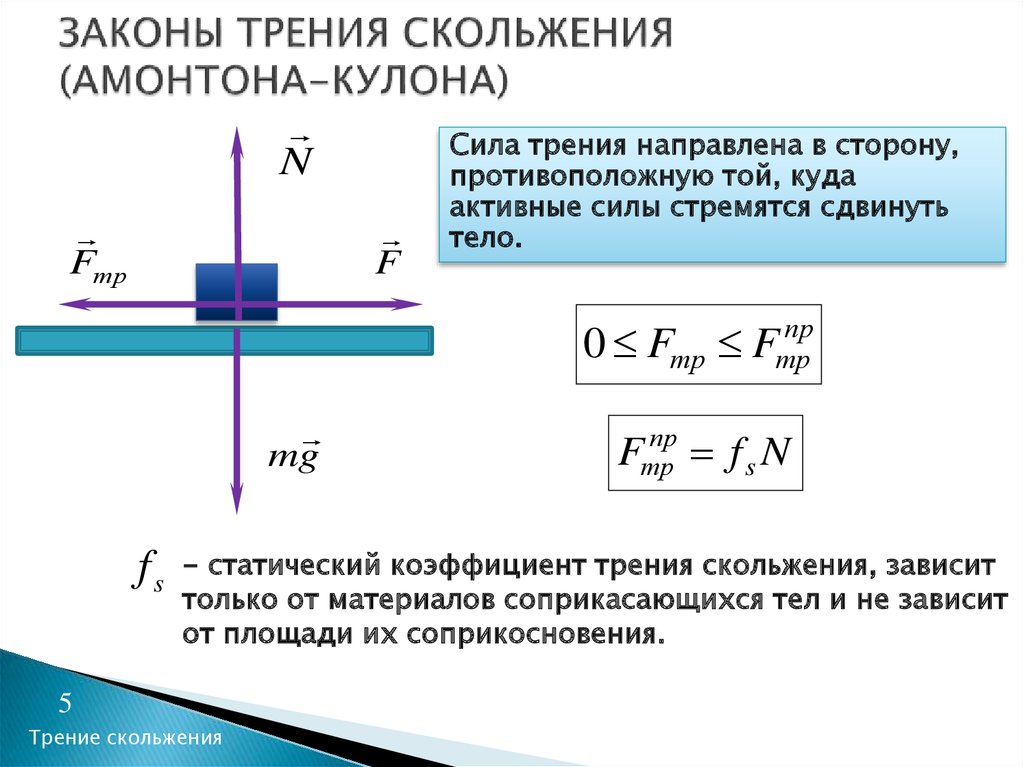 16. Силы, действующие на шарики
16. Силы, действующие на шарики
По условию шарики одинаковые, то есть их заряды равны как по модулю, так и по знаку, а значит, сила электростатического взаимодействия в данном случае будет силой отталкивания (на рис. 16 силы электростатического взаимодействия направлены в разные стороны). Так как система находится в равновесии, будем использовать первый закон Ньютона:
Так как в условии сказано, что шарики подвешены в среде с диэлектрической проницаемостью , а размеры шариков пренебрежимо малы по сравнению с расстоянием между ними, то в соответствии с законом Кулона сила, с которой будут отталкиваться шарики, будет равна:
Решение
Распишем первый закон Ньютона в проекциях на оси координат. Ось направим горизонтально, а ось вертикально (см. рис. 17).
Рис. 17. Выбор направления осей координат
Рис. 18. Силы в проекциях на оси координат
Так как на шарики действуют одинаковые силы тяжести и силы электростатического взаимодействия, нити тоже одинаковые – они отклонятся на одинаковые углы (см. рис. 19).
рис. 19).
Рис. 19. Углы, на которые отклоняются шарики, одинаковые
В сумме эти углы дают нам , это означает, что:
Тогда из прямоугольного треугольника можно найти углом :
Добавим к двум уравнениям, которые мы записали, выражение для модуля силы электростатического взаимодействия:
Расстояние найдем геометрически – найдем прилежащий к углу катет и умножим его на 2:
Мы получили систему из 4-х уравнений:
Математическое решение можно пронаблюдать в свертке.
Ответ:
Решение системы уравнений
Выразим из второго уравнения силу натяжения нити и подставим в первое:
Отсюда выразим силу электростатического взаимодействия:
Приравняем выражение для силы электростатического взаимодействия, которое мы сейчас выразили с третьим уравнением:
Подставим сюда выражение для
Выразим искомый заряд
Так как угол , то , тогда:
На этом наш урок закончен.
Список литературы
- Соколович Ю.А., Богданова Г.С Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
- Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика: Учеб. для общеобразоват. учреждений. Базовый и профильный уровни. 19-е издание – М.: Просвещение, 2010.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «physics.ru» (Источник)
- Интернет-портал «Класс!ная физика» (Источник)
Домашнее задание
- Запишите формулу закона Кулона.
- Как взаимодействуют разноименно заряженные тела?
- Решите задачу: два заряда, 10 нКл и -2 нКл, закреплены на расстоянии 10 см друг от друга. Определите силу, с которой они взаимодействуют.
V211 –п Электрическое поле, закон Кулона, напряженность электрического поля
s211
–П Сингл (закон Кулона, закон сохранения
эл. Заряда, поток вектора) 12-заданий
Заряда, поток вектора) 12-заданий
1. [Уд1] (ВО1) В основании равностороннего треугольника находятся равные по модулю точечные положительные заряды. Сила Кулона, действующая на такой же положительный заряд, помещенный в третью вершину треугольника, направлена
1) вертикально вверх
2) вертикально вниз
3) горизонтально вправо
4) горизонтально влево
:1
2. [Уд] (ВО1) Два одинаковых проводящих шарика c зарядами q1 = 9,0 нКл и q2 = –3,0 нКл, приводят в соприкосновение, а затем разводят на прежнее расстояние. Отношение F1/F2 модулей сил, действующих между шариками до и после соприкосновения, равно
1) 9
2) 6
4) 1
:3
3.
[Уд1] (О) В вершинах квадрата находятся
одноименные заряды, величина которых q = 2,0 нКл.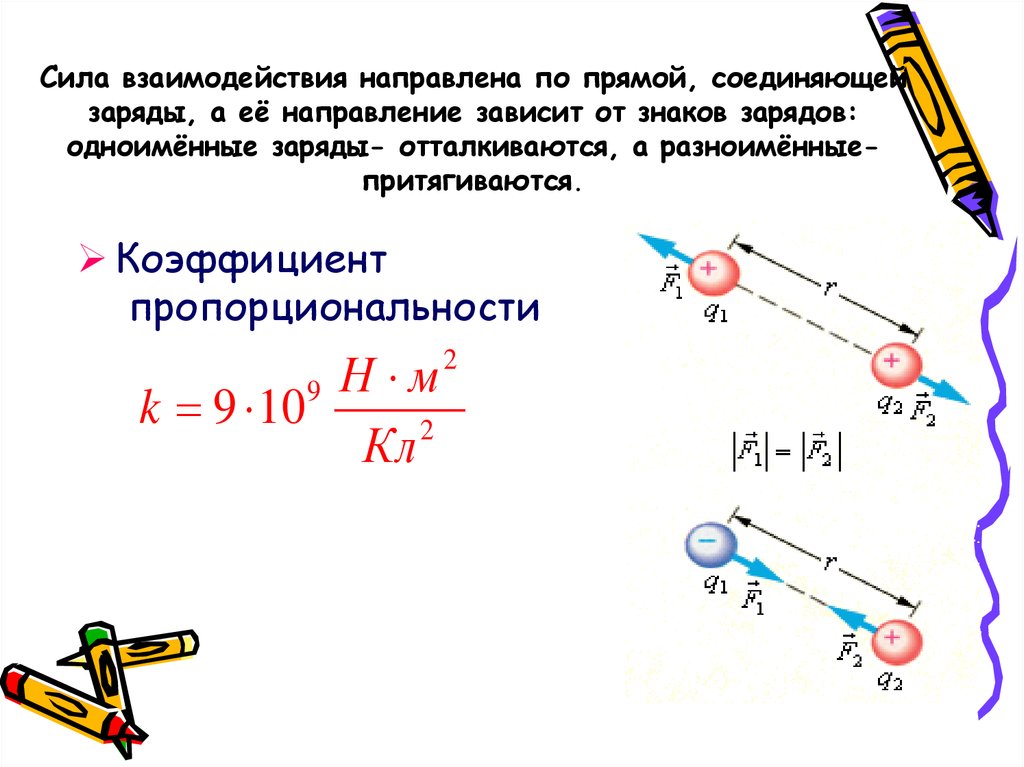 Сторона квадрата равна d =
10 см. Сила взаимодействия между зарядами,
расположенными в соседних вершинах
квадрата, равна … мкН.
Сторона квадрата равна d =
10 см. Сила взаимодействия между зарядами,
расположенными в соседних вершинах
квадрата, равна … мкН.
:3,6
4. [Уд1] (ВО1) В трех вершинах квадрата находятся равные по модулю точечные заряды (см. рисунок). Сила Кулона, действующая на такой же положительный заряд, помещенный в четвертую вершину квадрата, действует в направлении
1) 1
2) 2
3) 3
4) 4
:2
5. [Уд] (ВО1) Точечный заряд +2q помещен в вершину равнобедренного треугольника (см. рисунок). Кулоновская сила, действующая на него со стороны двух других зарядов +q и –q, находящихся в основании треугольника, направлена
1) вверх ↑
2) вниз ↓
3) влево ←
4) вправо →
:4
6. [Уд1] (О) Величина напряженности электростатического поля, создаваемого равномерно заряженной сферической поверхностью радиуса , в зависимости от расстояния от ее центра верно представлена на рисунке
:2
7. [Уд1] (ВО1) Точечный заряд +2q находится в центре сферической
поверхности. Если добавить заряд –q внутрь сферы,
то поток вектора напряженности
электростатического поля через
поверхность сферы
[Уд1] (ВО1) Точечный заряд +2q находится в центре сферической
поверхности. Если добавить заряд –q внутрь сферы,
то поток вектора напряженности
электростатического поля через
поверхность сферы
1) уменьшится
2) увеличится
3) не изменится
:1
8. [Уд1] (ВО1) На двух одинаковых каплях воды находится по одному отрицательному элементарному заряду (e = 1,6∙10-19
1) 3,47∙10-9
2) 2,95∙10-9
3) 1,85∙10-9
4) 2,34∙10-9
:3
9.
[Уд] (ВО1) Три одинаковых металлических
шарика с зарядами –3 нКл, +2 нКл и –2 нКл
привели в соприкосновение друг с другом.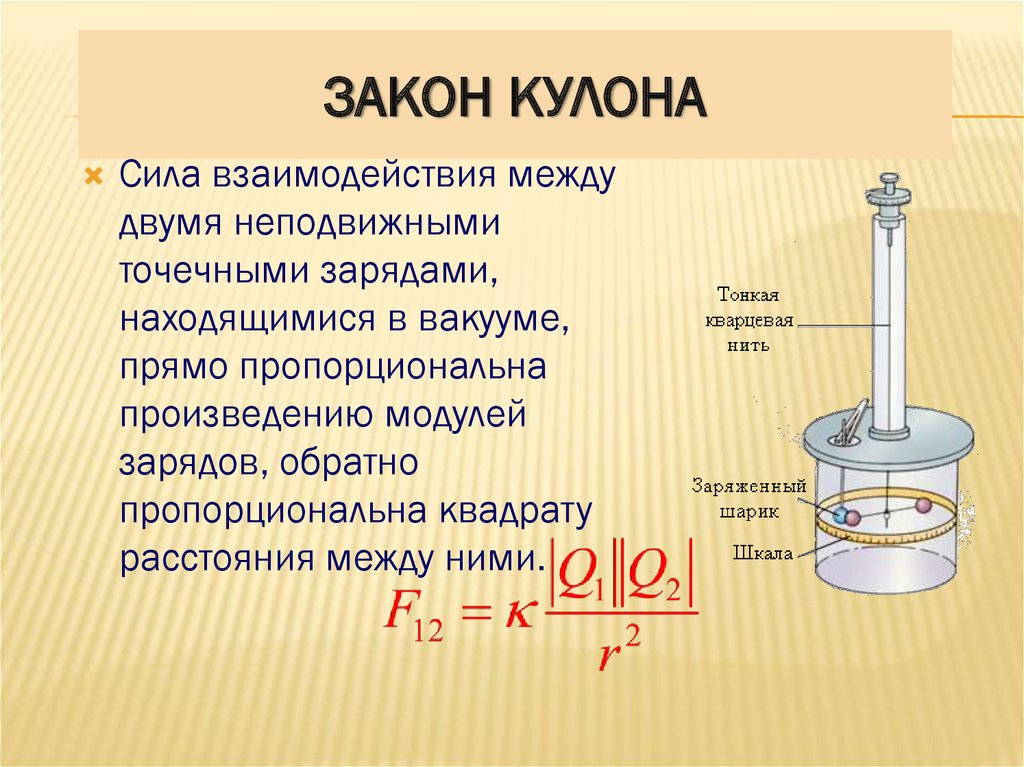 После соприкосновения
После соприкосновения
1) шарики будут притягиваться друг к другу
2) шарики будут отталкиваться друг от друга
3) первые два шарика притянутся друг к другу, и будут отталкиваться от третьего
4) шарики не будут ни притягиваться, ни отталкиваться друг от друга
:2
10. [Уд] (ВО1) На рисунке изображен график — кулоновской силы, с которой одинаковые заряды действуют друг на друга в вакууме.
Пользуясь данными графика, найдите величины этих зарядов .
1)2 нКл
2) 4 нКл
4) 0,4 нКл
: 1
11.
[Уд1] (ВО1) Три одинаковых точечных заряда q1 = q2 = q3 = 2 нКл находятся в вершинах равностороннего
треугольника со стороной а = 10 см. Модуль силы F,
действующей на один из зарядов со стороны
двух других, равен … мкН
Модуль силы F,
действующей на один из зарядов со стороны
двух других, равен … мкН
1) 3,6
2) 4,0
3) 6,2
4) 7,2
:3
12. [Уд] (ВО1) По тонкому металлическому кольцу равномерно распределен заряд q. Напряженность поля в точках, расположенных на оси кольца, при увеличении расстояния от центра кольца будет
1) только возрастать
2) только убывать
3) сначала убывает, затем возрастает
4) сначала возрастает, затем убывает
:4
с211 –П Кластер (Напряженность поля, поток напряженности, теорема Гаусса) 19 заданий
1. [Уд1] (О) Циркуляция напряженности электростатического поля равна …
:нулю
:0
:ноль
2.
[Уд1] (О) Поток вектора напряжённости
электрического поля ФЕ через площадку S максимален в случае. ….
….
:2
3. [Уд1] (ВО1) В вершинах квадрата расположены одинаковые по модулю точечные заряды. Вектор напряженности электрического поля в центре квадрата в точке А совпадает с направлением под номером
1) 1
2) 2
3) 3
4) 4
:1
4. [Уд1] (ВО1) Поток вектора напряженности электрического поля ФЕ, создаваемого бесконечно протяженной заряженной нитью через основание цилиндра площадью S, равен
1) ФЕ > 0
2) ФЕ = 0;
3)
4) ФЕ = .
:2
5. [Уд1] (ВО1) На рисунках изображены сечения замкнутых поверхностей и равные по модулю заряды, создающие электростатическое поле. Поток вектора напряженности через поверхность равен нулю для рисунков
1) 1 и 2
2) 2 и 8
3) 1 и 4
4) 4и 8
:2
6. [Уд1] (ВО1) В основании равностороннего
треугольника находятся два положительных
точечных заряда. Напряженность
электрического поля
,
созданного двумя одинаковыми по модулю
точечными зарядами в третьей вершине
треугольника, направлена
[Уд1] (ВО1) В основании равностороннего
треугольника находятся два положительных
точечных заряда. Напряженность
электрического поля
,
созданного двумя одинаковыми по модулю
точечными зарядами в третьей вершине
треугольника, направлена
1) вверх
2) влево
3) вправо
4) вниз
:1
7. [Уд1] (ВО1) Две бесконечные параллельные плоскости, находящиеся в вакууме, несут равномерно распределенные заряды с поверхностными плотностями σ+ = σ и σ— = -0,5σ. Во сколько раз модуль Е1 напряженности электростатического поля между плоскостями больше напряженности Е2 поля вне плоскостей?
1) 2 раза
2) 0,5 раза
3) 3 раза
4) 4 раза
:3
8.
[Уд1] (ВО1) Полая металлическая сфера
радиусом R заряжена положительным
зарядом q+.
Величина напряженности электрического поля Е на расстоянии 2R от поверхности сферы равна
1) Е = 0
2) Е = q/36πεε0R2
3) E =
4) Е = q /4πεε0R2
:2
9. [Уд1] (ВО1) На рисунке изображены заряженная бесконечная плоскость с поверхностной плоскостью заряда = 40 мкКл/м2 и одноименно заряженный шарик с массой m = l г и зарядом q = 2,56 нКл. Угол между плоскостью и нитью, на которой висит шарик, составляет
1) 31°
2) 45°
3) 60°
4) 15°
:1
10. [Уд1] (ВО1) Полая металлическая сфера радиусом R заряжена положительным зарядом q+. Величина напряженности электрического поля Е
на расстоянии R/2 от центра сферы равна
1) Е = 0
2) Е = q/4πεε0R2
3) E =
4) Е = q /4πεε0R
:1
11. [Уд1] (О) Два одинаковых по модулю и знаку
точечных заряда q1 и q2 создают в точках 1, 2, 3 и 4 разные
напряженности электрического поля.
Величина напряженности поля равна нулю
в точке….
[Уд1] (О) Два одинаковых по модулю и знаку
точечных заряда q1 и q2 создают в точках 1, 2, 3 и 4 разные
напряженности электрического поля.
Величина напряженности поля равна нулю
в точке….
:2
:два
12. [Уд1] (ВО1) Верные соотношения для величины напряженности поля, созданного заряженными плоскостями, в точках 1,2,3:
1) Е1 = Е3 =3σ/2εε0 , Е2 = 0
2) Е1 = Е3=3σ/εε0, Е2 = 0
2) Е1 = Е3= 0 , Е2 =3σ/2εε0
3) Е1 = Е3= 0 , Е2 =3σ/εε0
:2
:2 и 4
13.
[Уд1] (ВО1) На рисунке изображены сечения
замкнутых поверхностей и равные по
модулю заряды, создающие электростатическое
поле.
Поток вектора напряженности сквозь поверхность S является положительным для рисунков
1) 1 и 2
2) 2 и 3
3) 1 и 4
4) 3 и 4
:3
14. [Уд1] (ВО1) Поток вектора напряженности электрического поля ФЕ через замкнутую поверхность S, не охватывающую заряженные тела,
1) равен нулю
2) больше нуля
3) меньше нуля
4) однозначно ответить нельзя
:1
15. [Уд1] (ВО1) Два точечных электрических заряда q1 = + 2 нКл и q2 = + 2 нКл расположены в вакууме в двух вершинах равностороннего треугольника со стороной a = 30 см. Чему равен модуль напряженности E∑ результирующего электростатического поля, созданного этими зарядами в третьей вершине?
1) 200 В/м
2)100 В/м
3) 340 В/м
4)170 В/м
:3
16
[Уд1] (ВО1) Дана система точечных зарядов в вакууме
и замкнутые поверхности S1,
S2 и S3. Поток вектора напряженности
электростатического поля отличен
от нуля через
поверхность (-и)
Поток вектора напряженности
электростатического поля отличен
от нуля через
поверхность (-и)
1) S 1
2) S 2
3) S 3
4) S 1, S 2
5) S 1,S 3
6) S 2,S 3
:1
17. [Уд1] (ВО1) Дана система точечных зарядов в вакууме и замкнутые поверхности S1, S2 и S3. Поток вектора напряженности электростатического поля равен нулю через поверхности
1) S 2,S 3
2) S 2
3) S 1,S 3
4) S 1, S 2
:1
18.
[Уд1] (ВО1) Дана система точечных зарядов в вакууме
и замкнутые поверхности S1,
S2 и S3. Поток вектора напряженности
электростатического поля равен
нулю через
поверхность(-и)
Поток вектора напряженности
электростатического поля равен
нулю через
поверхность(-и)
1) S 1
2) S 2
3) S 3
4) S 1 и S 2
:3
19. [Уд1] (ВО1) В вершинах равностороннего треугольника находятся равные по модулю отрицательные точечные заряды. Напряженность электрического поля в точке А направлена
1) вертикально вверх
2) вертикально вниз
3) горизонтально слева направо
4) горизонтально справа налево
:1.
Плавающие и подвесные капли — Soft-Matter
Вернуться к темам.
Содержимое
- 1 Плавает из-за жесткого поверхностного натяжения
- 2 интерфейса жидкость-жидкость-воздух
- 3 маленькие капли
- 4 большие капли
- 5 подвесных капель
- 6 Феномен пульсирующей капли масла
- 7 удивительных динамических эффектов поверхности
Всплывание из-за жесткого поверхностного натяжения
Поверхностное натяжение жидкости — это истинное натяжение, проявляющееся в различных явлениях.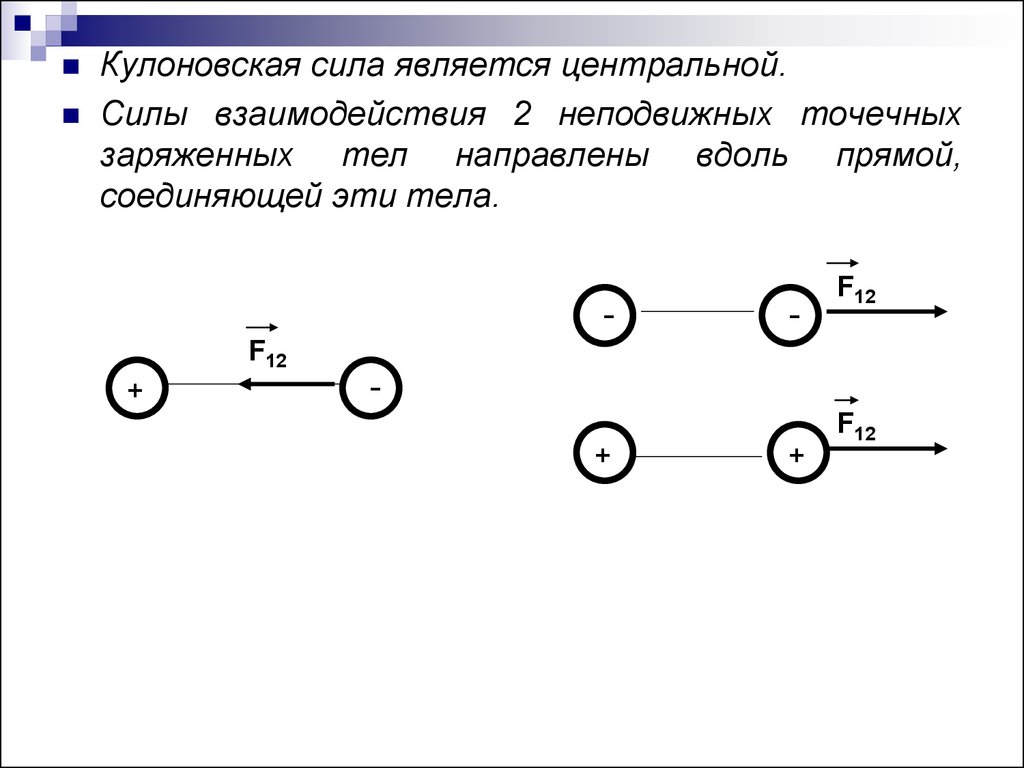 Водяные жуки, например, могут плавать благодаря поверхностному натяжению. Когда плывет скрепка или жук, поверхность воды искажается. Поскольку поверхность воды действует как натянутая мембрана, каждая часть периметра тянет зажим вверх и не дает ему утонуть. Следовательно, то, что определяет, может ли объект поддерживаться поверхностным натяжением, является периметром искаженной поверхности. Вот почему поверхностное натяжение измеряется силой на единицу длины. В частности, поверхностное натяжение воды = 0,0004 фунта/дюйм. Это выглядит как небольшое число, но его достаточно для поддержки некоторых объектов. Для скрепки периметр составляет около пары дюймов, а это означает, что вода способна выдержать вес около 0,0008 фунта, что примерно соответствует весу скрепки. Если добавить мыло, то поверхностное натяжение уменьшится в три раза, и теперь его недостаточно, чтобы выдержать вес зажима, и он тонет. Внимание: не путайте плавучесть за счет поверхностного натяжения с плавучестью за счет плавучести.
Водяные жуки, например, могут плавать благодаря поверхностному натяжению. Когда плывет скрепка или жук, поверхность воды искажается. Поскольку поверхность воды действует как натянутая мембрана, каждая часть периметра тянет зажим вверх и не дает ему утонуть. Следовательно, то, что определяет, может ли объект поддерживаться поверхностным натяжением, является периметром искаженной поверхности. Вот почему поверхностное натяжение измеряется силой на единицу длины. В частности, поверхностное натяжение воды = 0,0004 фунта/дюйм. Это выглядит как небольшое число, но его достаточно для поддержки некоторых объектов. Для скрепки периметр составляет около пары дюймов, а это означает, что вода способна выдержать вес около 0,0008 фунта, что примерно соответствует весу скрепки. Если добавить мыло, то поверхностное натяжение уменьшится в три раза, и теперь его недостаточно, чтобы выдержать вес зажима, и он тонет. Внимание: не путайте плавучесть за счет поверхностного натяжения с плавучестью за счет плавучести. Корабли и дерево плавают, потому что они менее плотны, чем вода. Кусок дерева будет плавать независимо от его формы. С другой стороны, если мы изменим форму канцелярской скрепки и сделаем ее сферической, периметр деформированной поверхности будет меньше, и поверхностного натяжения будет недостаточно, чтобы удержать ее на плаву.
Корабли и дерево плавают, потому что они менее плотны, чем вода. Кусок дерева будет плавать независимо от его формы. С другой стороны, если мы изменим форму канцелярской скрепки и сделаем ее сферической, периметр деформированной поверхности будет меньше, и поверхностного натяжения будет недостаточно, чтобы удержать ее на плаву.
Интерфейсы жидкость-жидкость-воздух
Конструкция Неймана для капли жидкости (2) на жидкой подложке (1):
Треугольник Неймана, Моррисон, 2002, рис. 6.6
- <> \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ strac \
- 9. тета _ {1}} = \ гидроразрыв {\ сигма _ {2}} {\ грех \ тета _ {2}} = \ гидроразрыв {\ сигма _ {12}} {\ грех \ тета _ {12}}
- <> \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ strac \
Когда выполняется соотношение Неймана
- Что такое сила натяжения?
- Второй закон движения Ньютона
- Как рассчитать натяжение канатов, подвешивающих объект
- Как найти натяжение канатов при вытягивании объекта веревка или веревка, используемая для подъема объекта. В этой статье вы также узнаете, как найти натяжение веревок, которыми тянут объект на поверхности без трения. Вы также увидите в этом калькуляторе натяжения веревки или струны различные диаграммы свободного тела, чтобы лучше понять, как рассчитать силы натяжения. Если вы хотите узнать больше о натяжении и формуле силы натяжения, читайте дальше!
Что такое сила натяжения?
Представьте, что вы поднимаете с земли баскетбольный мяч. Вы почувствуете вес мяча в своих руках из-за силы тяжести, действующей на массу мяча.
 Теперь представьте, что вы обвязываете мяч веревкой, которую затем используете, чтобы снова поднять мяч. Вы по-прежнему чувствовали бы вес мяча через веревку. В этой ситуации канат теперь находится в натяжении . То, что удерживает веревку вместе, называется силой натяжения . Разрезание веревки ослабит силу натяжения и отправит мяч в свободное падение.
Теперь представьте, что вы обвязываете мяч веревкой, которую затем используете, чтобы снова поднять мяч. Вы по-прежнему чувствовали бы вес мяча через веревку. В этой ситуации канат теперь находится в натяжении . То, что удерживает веревку вместе, называется силой натяжения . Разрезание веревки ослабит силу натяжения и отправит мяч в свободное падение.Сила натяжения — это осевая сила, действующая на объект, который тянет, например веревку, веревку или цепь. Мы также можем наблюдать силу натяжения в других материалах, таких как стержни и стержни, при условии, что они подвергаются внешнему растяжению или растяжению. Материалы с высокой прочностью на растяжение делают лучшие стержни и стержни, так как они не ломаются под действием сил растяжения. Вы можете проверить наш калькулятор напряжения, в котором обсуждается эластичность, чтобы узнать больше о прочности на растяжение.
Сила натяжения также является прекрасным примером Третьего закона движения Ньютона .
 Третий закон Ньютона гласит, что когда одно тело воздействует на другое тело с такой же силой, то второе тело оказывает равную силу в противоположном направлении обратно на исходное тело. Сила натяжения представляет собой реактивную силу, противодействующую внешней силе притяжения.
Третий закон Ньютона гласит, что когда одно тело воздействует на другое тело с такой же силой, то второе тело оказывает равную силу в противоположном направлении обратно на исходное тело. Сила натяжения представляет собой реактивную силу, противодействующую внешней силе притяжения.Второй закон движения Ньютона
Чтобы рассчитать натяжение, действующее на веревку, нам сначала нужно понять Второй закон движения Ньютона . Второй закон Ньютона гласит, что сумма сил, действующих на объект постоянной массы, равна массе этого объекта, умноженной на его ускорение. Мы также можем выразить это утверждение в виде уравнения:
ΣF = m × a
, где:
- Σ (сигма) обозначает сумму сил F ;
- m – масса объекта; и
- это ускорение.
Для объекта, подвешенного на веревке, мы можем использовать ускорение свободного падения g в качестве его ускорения.
 Гравитационное ускорение дает нам значение его веса с точки зрения силы, например, ньютонов или фунт-сила . Если объект движется с другим ускорением, мы должны использовать его фактическое ускорение для расчета. Однако этот калькулятор натяжения определяет силы натяжения только в случаях статического равновесия .
Гравитационное ускорение дает нам значение его веса с точки зрения силы, например, ньютонов или фунт-сила . Если объект движется с другим ускорением, мы должны использовать его фактическое ускорение для расчета. Однако этот калькулятор натяжения определяет силы натяжения только в случаях статического равновесия .Это утверждение означает, что этот инструмент учитывает только объекта в покое в данной системе. В этом калькуляторе натяжения мы также предполагаем, что веревки не имеют массы и, следовательно, не вносят никакого вклада в силы натяжения. Мы также предполагаем, что массы или объекты находятся в вакууме и не испытывают трения или сопротивления воздуха по отношению к окружающей их среде.
Как рассчитать натяжение канатов, подвешивающих объект
На приведенном ниже рисунке видно, что сила F, необходимая для подъема объекта, равна весу объекта W. Эта идея является фундаментальной концепцией, лежащей в основе нашей формулы силы натяжения.
 Ниже также показана диаграмма свободного тела объекта, которая показывает силы натяжения T, действующие на струну. Как видите, силы натяжения приходят парами и в противоположных направлениях:
Ниже также показана диаграмма свободного тела объекта, которая показывает силы натяжения T, действующие на струну. Как видите, силы натяжения приходят парами и в противоположных направлениях:Следуя второму закону движения Ньютона, мы можем выразить сумму сил, используя диаграмму свободного тела объекта, как показано в правой части иллюстрации выше. Мы используем 90 262 диаграммы свободного тела 90 263, чтобы показать различные направления и величины сил, действующих на тело. В равновесии все эти силы должны равняться нулю. Считая все направленные вверх силы положительными, а направленные вниз отрицательными, получаем следующее уравнение:
ΣF↑ = 0 = T + (-W)
T = W
где вес W становится отрицательным, поскольку он направлен вниз. Перенося W в другую часть уравнения, мы теперь видим, что сила натяжения веревки равна весу предмета, который она несет, как это также показано выше.
Если мы используем больше веревок для подъема объекта, общая сила натяжения делится на веревки.
 Сила натяжения каждой веревки зависит от ее угла по отношению к направлению силы, которой она противодействует. Чтобы лучше понять это, давайте рассмотрим другую диаграмму свободного тела объекта, подвешенного на двух веревках, как показано ниже:0003
Сила натяжения каждой веревки зависит от ее угла по отношению к направлению силы, которой она противодействует. Чтобы лучше понять это, давайте рассмотрим другую диаграмму свободного тела объекта, подвешенного на двух веревках, как показано ниже:0003На диаграмме свободного тела, показанной выше, мы можем видеть горизонтальную и вертикальную составляющие сил натяжения, T₁ и T₂. Силы являются векторами, а это значит, что они всегда имеют как 90 262 величины, так и 90 263 направления. Как и все векторы, силы могут быть выражены в этих компонентах, которые дают влияние силы вдоль горизонтальной и вертикальной осей. T₁ₓ и T₂ₓ — вертикальные компоненты T₁ и T₂ соответственно. С другой стороны, T 1y и T 2y являются вертикальными составляющими одних и тех же сил соответственно. Поскольку гравитация действует на объект по вертикальной оси, нам необходимо учитывать вертикальные составляющие сил натяжения для нашего суммирования сил следующим образом:
σf ↑ = 0 = T 1Y + T 2Y + (-W)
W = T 1Y + T 2Y
, потому что мы также знают The Ense Lessent The Ense , мы можем выразить T 1y и T 2y через T₁ и T₂ соответственно с помощью тригонометрических функций: = T₂ × sin(β)
W = T₁ × sin(α) + T₂ × sin(β)
Можно также сказать, что для того, чтобы система находилась в равновесии, объект не должен двигаться ни горизонтально, ни вдоль оси x.
 Следовательно, горизонтальные компоненты T₁ и T₂ должны равняться нулю. Также с помощью тригонометрии мы можем выразить T₁ₓ и T₂ₓ через T₁ и T₂ соответственно:
Следовательно, горизонтальные компоненты T₁ и T₂ должны равняться нулю. Также с помощью тригонометрии мы можем выразить T₁ₓ и T₂ₓ через T₁ и T₂ соответственно:T₁ₓ = T₂ₓ
T₁ × cos(α) = T₂ 2 ₽ cos(β)
делим обе части на cos(α) , получаем уравнение, в котором T₁ выражается через T₂ и углы:
T₁ = T₂ × cos(β) / cos(α)
Затем мы можем использовать это уравнение для решения T₂, подставив T₂ × cos(β) / cos(α) в качестве T₁ в нашем суммировании уравнения сил, как показано ниже:
Вт = T₁ × sin(α) + T₂ × sin(β)
Вт = T₂ × [cos(β) / cos(α)] × sin(α) + T₂ × sin(β)
W = T₂ × [cos(β) × sin(α) / cos(α) + sin(β)]
T₂ = W / [cos(β) × sin(α) / cos(α) + sin(β)]
Наконец, если мы умножим все это уравнение на cos(β) / cos(α) , как мы получили значение T₁ через T₂, а затем упростив все, мы получим это уравнение:
T₁ = W / [cos(β) × sin(α) / cos(α) + sin(β)] × [cos(β) / cos(α)]
T₁ = W / [cos(β) × sin(α) / cos(α) + sin(β)] × [cos(β) / cos(α)]
T₁ = W / [cos(α) × sin(β) / cos( β) + sin(α)]
Теперь все, что вам нужно знать, это углы натяжения канатов относительно горизонтали.
 Если задан угол от вертикали, просто вычтите этот угол из 90°. Это даст вам угол от горизонтали. Однако, если вам даны другие значения углов, которые могут быть больше 90° или даже 180°, вы можете воспользоваться нашим калькулятором эталонного угла, который поможет вам определить нужный угол. После определения значений переменных в наших формулах силы натяжения мы теперь можем найти силы натяжения.
Если задан угол от вертикали, просто вычтите этот угол из 90°. Это даст вам угол от горизонтали. Однако, если вам даны другие значения углов, которые могут быть больше 90° или даже 180°, вы можете воспользоваться нашим калькулятором эталонного угла, который поможет вам определить нужный угол. После определения значений переменных в наших формулах силы натяжения мы теперь можем найти силы натяжения.Как найти натяжение веревки при вытягивании объекта
Как найти силу натяжения на объекте, который тянут так же, как когда объект подвешен. Единственное отличие состоит в том, что сначала нам нужно вычислить ускорение всей системы и сумма всех сил по горизонтали. Если веревка находится под углом к уровню пола, нам также необходимо вычислить горизонтальную составляющую тягового усилия.
Давайте рассмотрим пример ниже, чтобы лучше понять, как найти силу натяжения веревки, тянущей за собой один или два объекта. В этом примере два объекта тянутся одной приложенной силой тяги.
 Другая веревка тянет второй объект, который прикреплен к первому объекту, как показано ниже:
Другая веревка тянет второй объект, который прикреплен к первому объекту, как показано ниже:На этом рисунке показано, что массы m₁ и m₂ равны 3 кг и 2 кг соответственно. Сумма этих двух масс дает общую массу системы 90 262 5 кг 90 263 . Нам также необходимо определить горизонтальную составляющую силы тяги, Т = 24 Н , то есть под углом θ = 60° . Если снова использовать тригонометрические функции, то можно сказать, что горизонтальная составляющая силы тяги равна 24 Н × cos(60°) , что равно 12 Н . Теперь, когда мы знаем горизонтальную составляющую тяговой силы и полную массу системы, мы можем рассчитать ускорение системы a следующим образом:
F = m × a → a = F / m
a = 12 Н / 5 кг = 2,4 м/с²
После того, как мы нашли ускорение системы, мы можем снова использовать второй закон Ньютона для расчета натяжения веревки или струны системы.
 Для этого умножьте ускорение на массу, которую тянет веревка. Для T₂ его диаграмма свободного тела показывает нам, что он отвечает только за массу m₂; мы можем сказать, что Т₂ = а × м₂ . При этом T₂ = (2,4 м/с²) × (2 кг) = 4,8 Н . С другой стороны, T₁ — это сила натяжения, которая притягивает вес m₁ и m₂. Однако у нас уже есть значение T₁, которое просто равно T = 24,0 Н. Следовательно, T₁ = 24,0 Н .
Для этого умножьте ускорение на массу, которую тянет веревка. Для T₂ его диаграмма свободного тела показывает нам, что он отвечает только за массу m₂; мы можем сказать, что Т₂ = а × м₂ . При этом T₂ = (2,4 м/с²) × (2 кг) = 4,8 Н . С другой стороны, T₁ — это сила натяжения, которая притягивает вес m₁ и m₂. Однако у нас уже есть значение T₁, которое просто равно T = 24,0 Н. Следовательно, T₁ = 24,0 Н .В нашем примере, если бы левая и правая веревки были просто одной веревкой, мы могли бы сравнить эту установку с системой шкивов. Блок — это простая машина, которая использует силы натяжения канатов для получения механического преимущества. Вы можете воспользоваться нашим калькулятором шкивов и калькулятором длины ремня (который представляет собой систему с двумя шкивами), чтобы узнать больше о механических преимуществах и натяжении.
Часто задаваемые вопросы
Как рассчитать натяжение веревки под углом?
Чтобы рассчитать натяжение веревки под углом:
- Найдите угол от горизонтали, на которую установлена веревка.

- Найдите горизонтальную составляющую силы натяжения, умножив приложенную силу на косинус угла.
- Рассчитайте вертикальную составляющую силы натяжения, умножив приложенную силу на синус угла.
- Сложите эти две силы вместе, чтобы найти общую величину приложенной силы.
- Учитывайте любые другие приложенные силы , например, другую веревку, силу тяжести или трение, и решайте уравнение силы обычным образом.
Как рассчитать натяжение, создаваемое 10-килограммовым ящиком на двух веревках, подвешенных под углом 60 градусов?
Для определения натяжения в этом случае:
- Определение вертикальной и горизонтальной составляющих о растягивающих усилиях на канатах:
- Т₁ = Т₁ sin(60) + Т₁ cos(60)
- T₂ = T₂ sin(60) + T₂ cos(60)
- Вертикальные (синусоидальные) составляющие уравновешивают вес :
- T₁ sin(60) + T₂ sin(60) = √3 (T₁ + T₂)/2 = 98 Н
- Горизонтальные (косинусные) составляющие силы натяжения уравновешивают друг друга :
- T₁ cos(60) = T₂ cos(60) или T₁ = T₂
- Решите уравнения:
- 98 Н = √3 Т₁ или, Т₁ = Т₂ = 56,58 Н
Как найти натяжение двух канатов при одинаковом угле подвески?
Когда углы подвески (α) одинаковы для двух веревок, величина натяжения (T) становится одинаковой для обеих веревок.

\end{align}
Крупные капли
Гравитация сплющивает каплю.

de Gennes, 2004, рис. 2.19b
«Площадь» капли» — это объем, деленный на толщину:
поверхностная энергия : = S\cdot \frac{\Omega }{\varepsilon } 9{2}=-S
Похоже на решение для сидячей капли, за исключением плотности. (Уравнение 2.8 в де Жене)
Подвесные капли
Капля принимает свою форму благодаря двум эффектам: поверхностному натяжению, стремящемуся минимизировать энергию в сферической форме, и силе тяжести, которая искажает эту сферическую форму. В настоящее время для измерения поверхностного натяжения используется несколько методов: Метод подвесной капли и более широко используемый Метод сбрасывания сидячих . Мы обсудим первое.
Основная идея метода висячей капли состоит в том, что мы позволяем капле свисать с конца капиллярной трубки, принимая форму, показанную на рисунке ниже (рис. 2.20). Давления, уравновешивающиеся в капле, лапласовы и гидростатические. Принимая за кривизну поверхности капли, поверхностное натяжение и плотность жидкости, получаем следующее:
92/б
Принимая за кривизну поверхности капли, поверхностное натяжение и плотность жидкости, получаем следующее:
92/б где =поверхностное натяжение Dr = разница в плотности между жидкостями на границе раздела g = гравитационная постоянная Ro = радиус кривизны капли на вершине b = коэффициент формы
b, коэффициент формы можно определить с помощью уравнения Юнга-Лапласа, выраженного в виде 3 безразмерных уравнений первого порядка, как показано на рисунке ниже.
[1]
Еще один способ определить значение — это эксперимент, который многие из нас проводили на первых уроках физики. Висячая капля на капилляре может оторваться, когда сила тяжести превышает капиллярную силу , где — внутренний радиус капилляра. Измерив вес упавшей капли, теоретически можно вычислить значение . Каким бы простым это ни казалось, эксперимент сталкивается с многочисленными сложностями из-за характера разделения капель.
 Тем не менее, что примечательно, он дает нам хорошо откалиброванные капли, радиус которых можно рассчитать следующим образом:
9{1/3}
Тем не менее, что примечательно, он дает нам хорошо откалиброванные капли, радиус которых можно рассчитать следующим образом:
9{1/3}de Gennes, 2004, рис. 2.21
Феномен пульсирующей масляной капли
В прошлом году в Массачусетском технологическом институте профессорами Романом Стокером и Джоном Бушем было решено явление, которое наблюдалось веками. Основная идея заключается в том, что если вы смешаете поверхностно-активное вещество с маслом и поместите его каплю на поверхность воды, капля масла будет расширяться и сжиматься из-за изменений поверхностного натяжения, вызванных испарением.
«Представьте каплю масляного детергента в виде небольшой линзы с закругленным дном. Поверхностно-активное вещество в капле перемещается к нижней поверхности линзы, где оно взаимодействует с водой, уменьшая поверхностное натяжение там, где масло встречается с водой. Это изменение при натяжении увеличивается сила, тянущая внешние края капли, в результате чего капля расширяется.

Центр капли глубже, чем края, поэтому там оседает больше ПАВ, соответственно уменьшая поверхностное натяжение. Это вызывает циркуляцию масла и поверхностно-активного вещества вблизи внешних краев капли. Эта циркуляция создает сдвиг (думайте об этом как о двух скоростях, движущихся в противоположных направлениях), который генерирует очень маленькие волны, катящиеся наружу к краю. Когда эти волны достигают края, они заставляют маленькие капли извергаться и улетать на поверхность воды за пределы капли. Видеомикроскопия — по сути, подключение видеокамеры к микроскопу — имела решающее значение для наблюдения за этим этапом процесса. Эти капли масла и поверхностно-активного вещества рассеиваются в воде и уменьшают поверхностное натяжение поверхности воды, поэтому капля сжимается.
По мере испарения поверхностно-активного вещества поверхностное натяжение воды снова увеличивается, и система перезагружается. Силы притягивают внешние края линзы, и циклический процесс начинается снова».

Видео явления доступно по этой ссылке, а также остальная часть статьи выпуска. Их работа была опубликована в журнале Journal of Fluid Mechanics от 25 июля 2007 года. [2]
Есть идеи, почему интерфейс разрывается именно так, как это происходит, и распыляет крошечные капельки масла в водную фазу? если поверхностно-активное вещество испаряется, оно должно быть на поверхности, и когда оно испаряется, эта часть поверхности сжимается. Если бы молекула поверхностно-активного вещества испарилась, она бы оказала такое сильное воздействие на поверхность капли?
Кто-нибудь может придумать, как это движение может быть полезно? Что-то вроде микронасоса, который перестает качать, когда заканчивается поверхностно-активное вещество, или управляется потребностью в воздухе?
Удивительные динамические эффекты поверхности
Капли на поверхности могут вести себя очень необычно, когда на них воздействуют неравновесные силы. Вот два очень интересных и забавных эксперимента, проведенных и опубликованных в последние годы:
1) Эффект Лейденфроста [3], применяемый к перегретым неоднородным поверхностям, может фактически заставить капли воды двигаться против силы тяжести, когда поверхность наклонена.
 Результаты таких экспериментов были опубликованы в 2006 году. [4] Это показывает, как взаимодействие между теплопередачей, переходом жидкость-пар и геометрией поверхности может привести к очень крутому эффекту, когда капля никогда не соприкасается с поверхностью, на которой она «сидит». и продолжает двигаться в нелогичном направлении (против гравитации).
Результаты таких экспериментов были опубликованы в 2006 году. [4] Это показывает, как взаимодействие между теплопередачей, переходом жидкость-пар и геометрией поверхности может привести к очень крутому эффекту, когда капля никогда не соприкасается с поверхностью, на которой она «сидит». и продолжает двигаться в нелогичном направлении (против гравитации).2) Еще более нелогичным образом капля жидкости не будет сливаться с ванной из той же жидкости при падении на нее, пока ванна ускоряется в правильном направлении и с правильной амплитудой в точке ожидаемый момент контакта. Это приводит к очень интересным примерам того, что люди называют «прыгающими каплями» или даже «танцующими каплями». Полную информацию об этом явлении можно прочитать в работе Couder et al. 2005 года в PRL [5], где показано, как конечное время, необходимое тонкой воздушной пленке под каплей, чтобы покинуть ее, создает силы, достаточно большие для отрыва. капля с поверхности жидкой ванны. Если вы можете найти фильмы об этих подпрыгивающих и вращающихся по орбите каплях, пожалуйста, разместите ссылки.

Вернуться к темам.
Калькулятор натяжения
Создано Kenneth Alambra
Отредактировано Bogna Szyk и Jack Bowater
Последнее обновление: 21 декабря 2022 г.
Содержание:




 Принимая за кривизну поверхности капли, поверхностное натяжение и плотность жидкости, получаем следующее:
92/б
Принимая за кривизну поверхности капли, поверхностное натяжение и плотность жидкости, получаем следующее:
92/б  Тем не менее, что примечательно, он дает нам хорошо откалиброванные капли, радиус которых можно рассчитать следующим образом:
9{1/3}
Тем не менее, что примечательно, он дает нам хорошо откалиброванные капли, радиус которых можно рассчитать следующим образом:
9{1/3}

 Результаты таких экспериментов были опубликованы в 2006 году. [4] Это показывает, как взаимодействие между теплопередачей, переходом жидкость-пар и геометрией поверхности может привести к очень крутому эффекту, когда капля никогда не соприкасается с поверхностью, на которой она «сидит». и продолжает двигаться в нелогичном направлении (против гравитации).
Результаты таких экспериментов были опубликованы в 2006 году. [4] Это показывает, как взаимодействие между теплопередачей, переходом жидкость-пар и геометрией поверхности может привести к очень крутому эффекту, когда капля никогда не соприкасается с поверхностью, на которой она «сидит». и продолжает двигаться в нелогичном направлении (против гравитации).
 Теперь представьте, что вы обвязываете мяч веревкой, которую затем используете, чтобы снова поднять мяч. Вы по-прежнему чувствовали бы вес мяча через веревку. В этой ситуации канат теперь находится в натяжении . То, что удерживает веревку вместе, называется силой натяжения . Разрезание веревки ослабит силу натяжения и отправит мяч в свободное падение.
Теперь представьте, что вы обвязываете мяч веревкой, которую затем используете, чтобы снова поднять мяч. Вы по-прежнему чувствовали бы вес мяча через веревку. В этой ситуации канат теперь находится в натяжении . То, что удерживает веревку вместе, называется силой натяжения . Разрезание веревки ослабит силу натяжения и отправит мяч в свободное падение.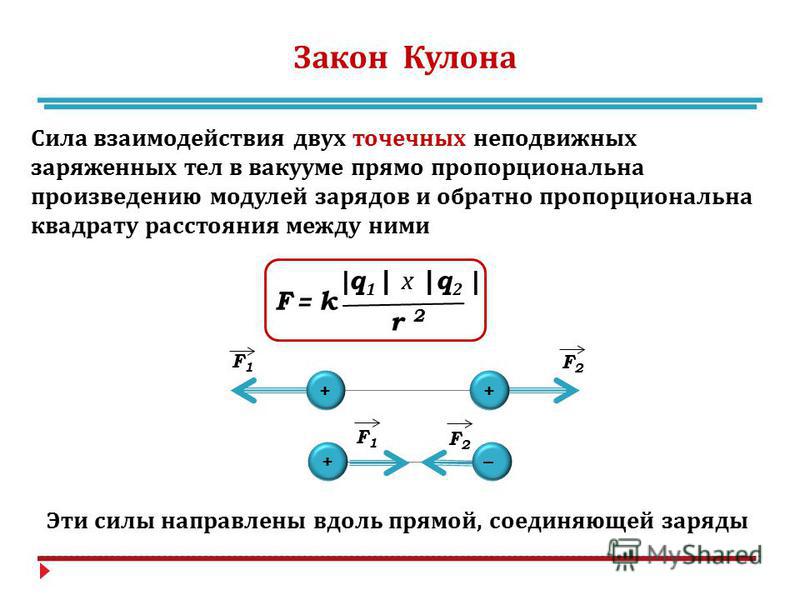 Третий закон Ньютона гласит, что когда одно тело воздействует на другое тело с такой же силой, то второе тело оказывает равную силу в противоположном направлении обратно на исходное тело. Сила натяжения представляет собой реактивную силу, противодействующую внешней силе притяжения.
Третий закон Ньютона гласит, что когда одно тело воздействует на другое тело с такой же силой, то второе тело оказывает равную силу в противоположном направлении обратно на исходное тело. Сила натяжения представляет собой реактивную силу, противодействующую внешней силе притяжения. Гравитационное ускорение дает нам значение его веса с точки зрения силы, например, ньютонов или фунт-сила . Если объект движется с другим ускорением, мы должны использовать его фактическое ускорение для расчета. Однако этот калькулятор натяжения определяет силы натяжения только в случаях статического равновесия .
Гравитационное ускорение дает нам значение его веса с точки зрения силы, например, ньютонов или фунт-сила . Если объект движется с другим ускорением, мы должны использовать его фактическое ускорение для расчета. Однако этот калькулятор натяжения определяет силы натяжения только в случаях статического равновесия .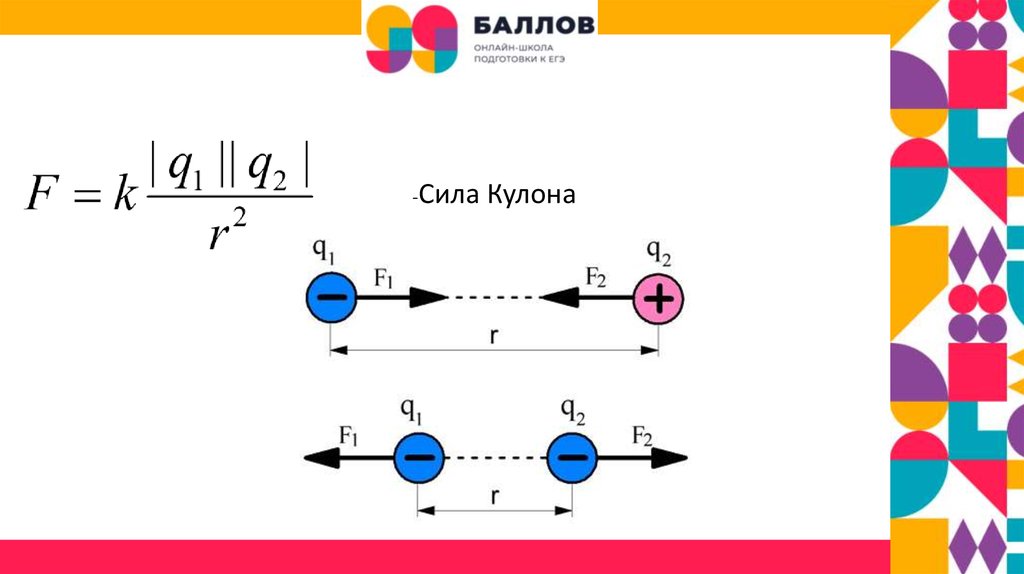 Ниже также показана диаграмма свободного тела объекта, которая показывает силы натяжения T, действующие на струну. Как видите, силы натяжения приходят парами и в противоположных направлениях:
Ниже также показана диаграмма свободного тела объекта, которая показывает силы натяжения T, действующие на струну. Как видите, силы натяжения приходят парами и в противоположных направлениях: Сила натяжения каждой веревки зависит от ее угла по отношению к направлению силы, которой она противодействует. Чтобы лучше понять это, давайте рассмотрим другую диаграмму свободного тела объекта, подвешенного на двух веревках, как показано ниже:0003
Сила натяжения каждой веревки зависит от ее угла по отношению к направлению силы, которой она противодействует. Чтобы лучше понять это, давайте рассмотрим другую диаграмму свободного тела объекта, подвешенного на двух веревках, как показано ниже:0003 Следовательно, горизонтальные компоненты T₁ и T₂ должны равняться нулю. Также с помощью тригонометрии мы можем выразить T₁ₓ и T₂ₓ через T₁ и T₂ соответственно:
Следовательно, горизонтальные компоненты T₁ и T₂ должны равняться нулю. Также с помощью тригонометрии мы можем выразить T₁ₓ и T₂ₓ через T₁ и T₂ соответственно: Если задан угол от вертикали, просто вычтите этот угол из 90°. Это даст вам угол от горизонтали. Однако, если вам даны другие значения углов, которые могут быть больше 90° или даже 180°, вы можете воспользоваться нашим калькулятором эталонного угла, который поможет вам определить нужный угол. После определения значений переменных в наших формулах силы натяжения мы теперь можем найти силы натяжения.
Если задан угол от вертикали, просто вычтите этот угол из 90°. Это даст вам угол от горизонтали. Однако, если вам даны другие значения углов, которые могут быть больше 90° или даже 180°, вы можете воспользоваться нашим калькулятором эталонного угла, который поможет вам определить нужный угол. После определения значений переменных в наших формулах силы натяжения мы теперь можем найти силы натяжения.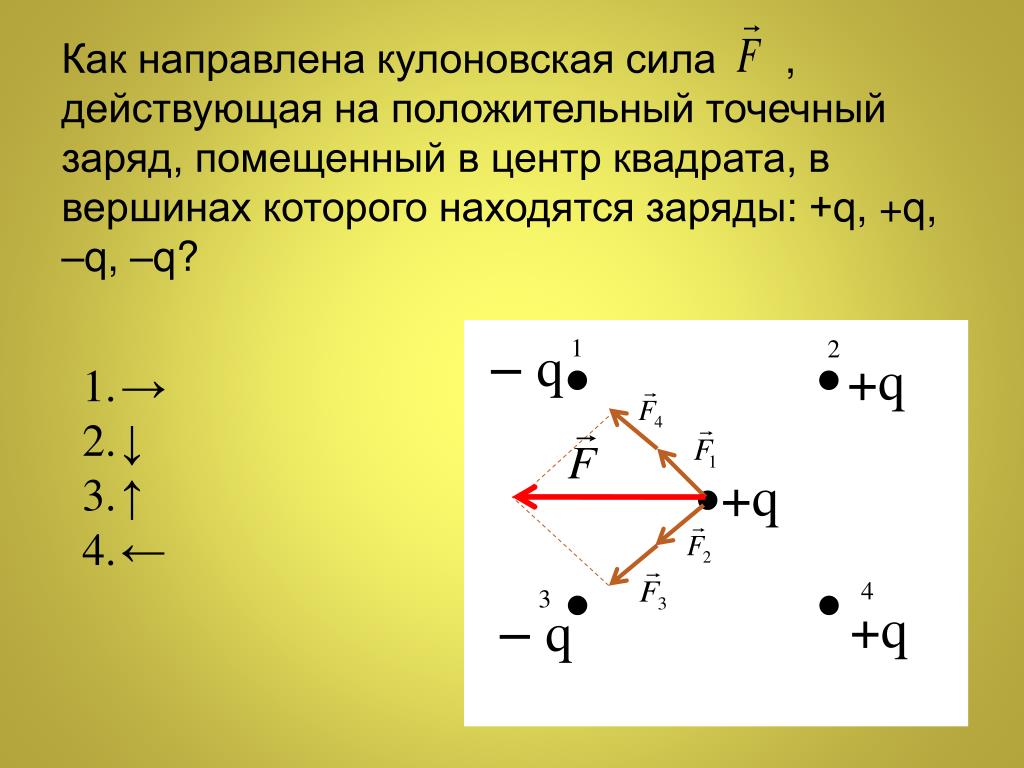 Другая веревка тянет второй объект, который прикреплен к первому объекту, как показано ниже:
Другая веревка тянет второй объект, который прикреплен к первому объекту, как показано ниже: Для этого умножьте ускорение на массу, которую тянет веревка. Для T₂ его диаграмма свободного тела показывает нам, что он отвечает только за массу m₂; мы можем сказать, что Т₂ = а × м₂ . При этом T₂ = (2,4 м/с²) × (2 кг) = 4,8 Н . С другой стороны, T₁ — это сила натяжения, которая притягивает вес m₁ и m₂. Однако у нас уже есть значение T₁, которое просто равно T = 24,0 Н. Следовательно, T₁ = 24,0 Н .
Для этого умножьте ускорение на массу, которую тянет веревка. Для T₂ его диаграмма свободного тела показывает нам, что он отвечает только за массу m₂; мы можем сказать, что Т₂ = а × м₂ . При этом T₂ = (2,4 м/с²) × (2 кг) = 4,8 Н . С другой стороны, T₁ — это сила натяжения, которая притягивает вес m₁ и m₂. Однако у нас уже есть значение T₁, которое просто равно T = 24,0 Н. Следовательно, T₁ = 24,0 Н .
