Определение коэффициента трения с помощью наклонного маятника
Лабораторная работа №1
Цель работы – изучить свободные затухающие колебания наклонного маятника; определить коэффициент трения качения.
Приборы – установка для определения коэффициента трения ФПМ-02.
Затухающие колебания
Все реальные колебательные системы являются диссипативными. Энергия механических колебаний таких систем постепенно расходуется на работу против сил трения, поэтому свободные колебания в них всегда затухают, амплитуда постепенно уменьшается.
Уравнение свободных затухающих колебаний имеет вид
(1.1)
где колеблющаяся величина; коэффициент затухания колебаний; циклическая частота, с которой совершались бы свободные колебания в системе при отсутствии сил сопротивления (собственная частота колебаний системы).
Решением уравнения () является функция
(1.
где амплитуда затухающих колебаний в момент времени амплитуда в начальный момент времени.
График этой функции показан на рис. 1.1. Зависимость показана на сплошной линией, а зависимость амплитуды от времени пунктирными линиями. Промежуток времени , в течение которого амплитуда затухающих колебаний уменьшается в раз, называется временем релаксации.
Рис. 1.1 | Величину называют условной циклической частотой затухающих колебаний. Затухающие колебания представляют собой непериодические колебания, т.к, в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Величина представляет собой условный период затухающих колебаний. |
Натуральный логарифм отношения амплитуд, следующих друг за другом через промежуток времени, равный периоду , называется логарифмическим декрементом затухания
(1. 3)
3)
число колебаний, происходящих в системе за время релаксации.
(1.4)
Чем медленнее происходит затухание свободных колебаний, тем выше добротность колебательной системы.
Определение коэффициента трения качения методом исследования колебаний наклонного маятника
На любое движущееся тело действуют силы трения. Природа этих сил
может быть различной, но в результате их действия всегда происходит превращение механической энергии во внутреннюю энергию трущихся тел, т. е. энергию теплового движения частиц.
В механике различают два вида трения: сухое, или внешнее, между твердыми телами и внутреннее, или вязкое, между слоями жидкости или газа.
Внешним трением называется явление возникновения в месте контакта
двух
соприкасающихся твердых тел касательных
сил, препятствующих относительному
перемещению этих тел.
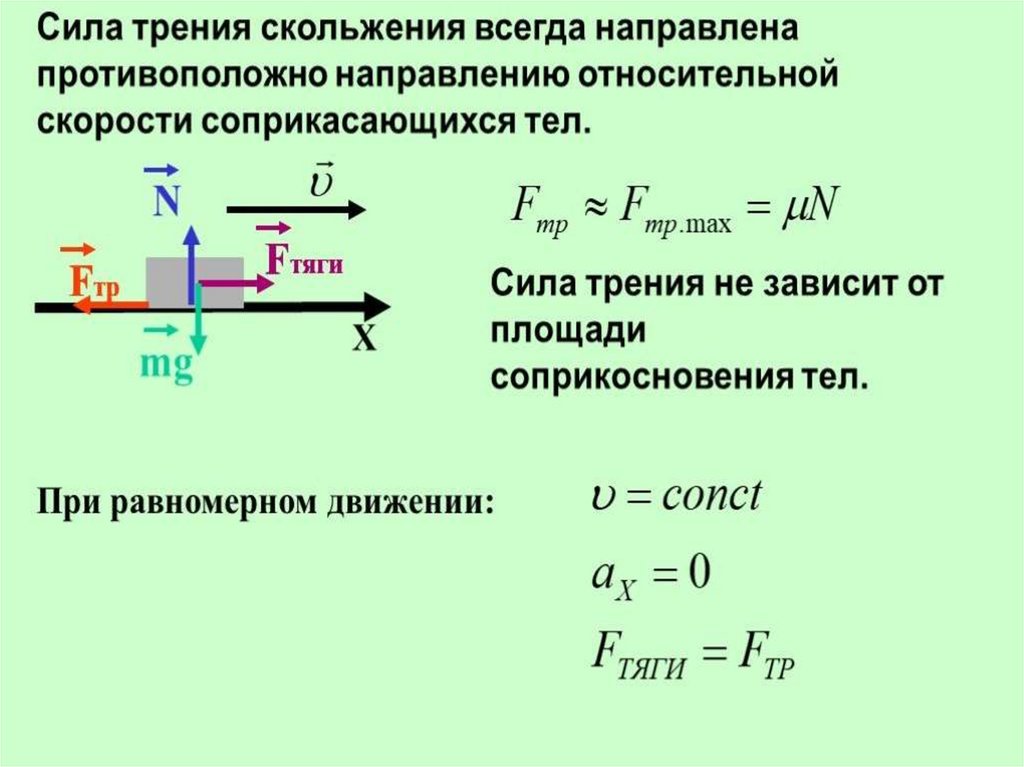
Внешнее трение между движущимися друг относительно друга телами называется кинематическим.
Внешнее трение между взаимно неподвижными телами называется трением покоя. Оно проявляется в том, что для возникновения относительного перемещения двух соприкасающихся тел к одному из них нужно приложить внешнюю силу >>, где так называемая предельная сила покоя.
В зависимости от характера относительного движения различают трение
скольжения, возникающее при поступательном перемещении (скольжении) одного тела по поверхности другого, и трение качения, возникающее тогда, когда одно тело катится по поверхности другого.
Сила
трения скольжения, возникающая при
скольжении сухих поверхностей тел друг
относительно друга, в основном вызывается
механическим зацеплением между
неровностями поверхностей и сцеплением
между молекулами в областях их
непосредственного соприкосновения.
В приближенных расчетах можно считать, что величина силы трения
скольжения пропорциональна силе нормального давления , а, следовательно, и силе реакции опоры , действующей на тело
(1.5)
где безразмерный коэффициент трения скольжения, зависящий от свойств материалов обоих тел.
Коэффициент трения зависит также от множества других факторов: качества обработки трущихся поверхностей, наличия на них загрязнений, скорости скольжения и т. д.
В данной работе для определения коэффициента трения качения применяется наклонный маятник.
Наклонный маятник представляет собой шар, подвешенный на длинной нити и лежащий на наклонной плоскости.
а) б)
Рис. 1.2
Если
шар отвести из положения равновесия
(ось
) на
угол
,
а затем отпустить, то возникнут колебания
маятника. При этом шар будет кататься
по наклонной плоскости около положения
равновесия (рис. 1.2, а). Между шаром и
наклонной плоскостью будет действовать
сила трения качения. В результате
колебания маятника будут постепенно
затухать, то есть будет наблюдаться
уменьшение во времени амплитуды
колебаний.
При этом шар будет кататься
по наклонной плоскости около положения
равновесия (рис. 1.2, а). Между шаром и
наклонной плоскостью будет действовать
сила трения качения. В результате
колебания маятника будут постепенно
затухать, то есть будет наблюдаться
уменьшение во времени амплитуды
колебаний.
Можно предположить, что по величине затухания колебаний могут быть определены сила трения и коэффициент трения качения.
Выведем
формулу, которая связывает уменьшение
амплитуды колебаний с коэффициентом
трения качения
.
При качении шара по плоскости сила
трения совершает работу. Эта работа
уменьшает полную энергию
шара. Полная энергия складывается из
кинетической и потенциальной энергий.
В тех положениях, где маятник максимально
отклонен от положения равновесия, его
скорость, а, следовательно, и
кинетическая энергия равны нулю. Эти
точки называются точками поворота. В
них маятник останавливается, поворачивается
и движется обратно. В момент поворота
энергия маятника равна потенциальной
энергии, поэтому уменьшение потенциальной
энергии маятника при его движении от
одной точки поворота до другой равна
работе силы трения на пути между точками
поворота.
Пусть А — точка поворота (рис. 1.2, а). В этом положении нить маятника составляет угол с осью . Если бы трения не было, то через половину периода маятник оказался бы в точке N, а угол отклонения был бы равен . Но из-за трения шар немного не докатится до точки и остановится в точке
Найдем связь между потерей угла и потерей высоты Для этого спроецируем точки А и В на ось (см. рис. 1.2, а). Это будут точки и соответственно. Очевидно, что длина отрезка
(1.
где длина нити.
Так как ось наклонена под углом к вертикали, проекция отрезка на вертикальную ось и есть потеря высоты (рис. 1.2, 6):
(1.7)
При этом изменение потенциальной энергии маятника при переходе его из положения А в положение В равно:
(1.8)
где масса шара;
Вычислим работу силы трения. Сила трения определяется по формуле
(1.9)
где коэффициент трения; сила нормальной реакции плоскости.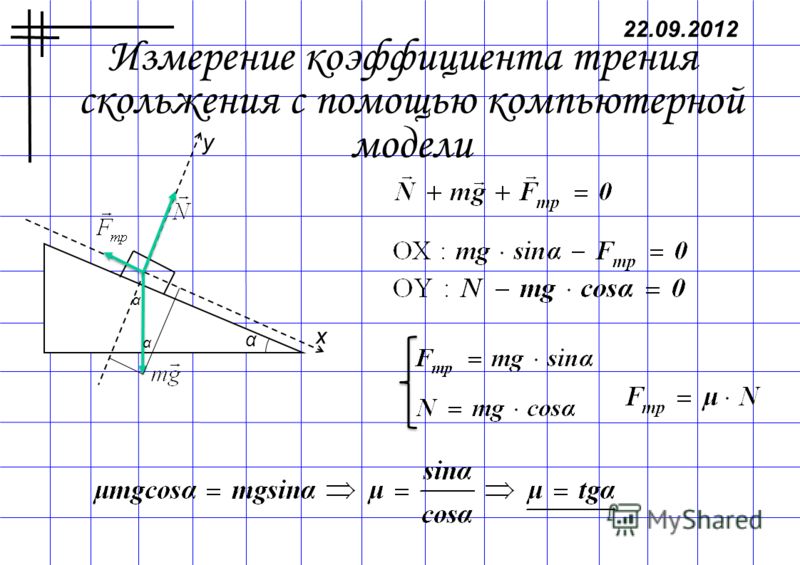
Путь пройденный шаром за половину периода колебаний маятника, равен длине дуги
Работа силы трения на пути
(1.10)
Но , поэтому с учетом уравнений (1.6), (1.7), (1.8) получается
откуда
(1.11)
Выражение (1.11) существенно упрощается с учетом того, что угол очень мал (порядка радиан).
Но . Поэтому . Таким образом, формула (1.11) приобретает вид
,
откуда (1.12)
Из
формулы (1.12) видно, что потеря угла за половину периода определяется
коэффициентом трения и углом
. Однако можно найти такие условия, при
которых от угла не зависит. Учтем, что коэффициент трения
качения мал (порядка ).
Если рассматривать достаточно большие
амплитуды колебаний маятника
,
такие, при которых ,
то слагаемым в знаменателе формулы (1.12) можно
пренебречь, то тогда
Однако можно найти такие условия, при
которых от угла не зависит. Учтем, что коэффициент трения
качения мал (порядка ).
Если рассматривать достаточно большие
амплитуды колебаний маятника
,
такие, при которых ,
то слагаемым в знаменателе формулы (1.12) можно
пренебречь, то тогда
С другой стороны, пусть угол будет малым настолько, чтобы можно было считать, что . Тогда потеря угла за половину периода колебаний будет определяться формулой
(1.13)
Формула (1.13) справедлива, если
(1.14)
Из-за того, что , имеет порядок , неравенству (1.14) удовлетворяют углы порядка радиан.
Итак, за время одного полного колебания потеря угла составит
,
а за колебаний
Отсюда
(1. 15)
15)
Формула (1.15) дает удобный способ определения коэффициента трения качения. Необходимо измерить уменьшение угла за 10-15 колебаний, а затем по формуле (1.15) вычислить значение .
В формуле (1.15) величина выражена в радианах. Чтобы использовать значения в градусах, формулу (1.15) необходимо видоизменить
(1.16)
Коэффициент трения для данной силы трения Калькулятор
✖Сила трения, используемая в торговом кругу, где сила трения равна произведению коэффициента трения на нормальную силу.ⓘ Сила трения [Ffriction] | Атомная единица силыАттоньютонСантиньютонДеканьютонДециньютондинаэксаньютонFemtonewtonГиганьютонГрамм-силаГраве-силагектоньютонДжоуль / СантиметрДжоуль на метрКилограмм-силаКилоньютонКилопруд Килофунт-силаКип-силаМеганьютонМикроньютонMilligrave — силаМиллиньютонНаноньютонНьютонУнция-силаPetanewtonPiconewtonпрудФунт-фут в квадратную секундуПаундалФунт-силастенТераньютонТон-сила (Long)Тон-сила (метрическая система)Тон-сила (короткий)Йоттаньютон | +10% -10% | |
✖Масса тела В является мерой количества материи, содержащейся в теле или объекте. | Ассарий (Библейская Roman)Масс-атомная единицаАттограммаЭвердюпуа драмБекан (Библейский иврит)КаратсантиграммДалтонДекаграммДециграммDenarius (Библейская Roman)Didrachma (Библейский греческий)Драхма (Библейский греческий)Масса электрона (Rest)ExagramFemtogramГаммаGerah (Библейский иврит)ГигаграммГигатонназернаграммГектограммЦентнер (Великобритания)Центнер (США)Масса ЮпитераКилограммКилограмм-сила в квадрате в секунду на метркилофунтКилотонна (метрическая)ЛЕПТОН (Библейская Roman)Масса ДейтронаМасса ЗемлиМасса нейтонаМасса протонаМасса СолнцамегаграммМегатоннамикрограммМиллиграммMina (Библейский греческий)Mina (Библейский иврит)масса мюонананограммунцияПеннивейтPetagramпикограммамасса ПланкафунтФунт (Troy или фармацевтическое)ПаундалФунт-сила в квадрате в секунду на футQuadrans (Библейская Roman)Четверть (Великобритания)Четверть (США)Квинтал (метрическая система)Скрупл (аптекарь)Шекель (библейский иврит)тихоходСолнечная массаСтоун (Великобритания)Камень (США)Талант (Библейский греческий)Талант (Библейский иврит)ТераграммаТетрадрахма (Библейский греческий)Тон (анализ) (Великобритания)Тон (анализ) (США)Тон (длинный)Тон (метрической размерности)Тон (короткометражный)Тонна | +10% -10% | |
✖Наклон плоскости — это угол между наклонной рампой и плоской поверхностью. | КругЦиклстепеньГонГрадианМилМиллирадианМинутаМинуты дугиТочкаквадрантЧетверть кругаРадианРеволюцияПрямой уголВторойПолукругсекстанЗнакОчередь | +10% -10% |
|
✖Коэффициент трения (μ) — это отношение, определяющее силу, противодействующую движению одного тела по отношению к другому телу, находящемуся с ним в контакте.ⓘ Коэффициент трения для данной силы трения [μ] |
⎘ копия |
👎
Формула
сбросить
👍
Коэффициент трения для данной силы трения Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Преобразование входов в базовый блок
Сила трения: 15 Ньютон —> 15 Ньютон Конверсия не требуется
Масса тела В: 17 Килограмм —> 17 Килограмм Конверсия не требуется
Наклон плоскости: 30 степень —> 0.5235987755982 Радиан (Проверьте преобразование здесь)
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.103894134716441 —> Конверсия не требуется
< 7 Тела связаны веревкой, одно свободно висит, другое лежит на неровной наклонной плоскости. Калькуляторы
Коэффициент трения для данной силы трения формула
Коэффициент трения = Сила трения/(Масса тела В*cos(Наклон плоскости)*[g])
μ = Ffriction/(m2*cos(θ)*[g])
Существуют ли разные типы силы трения?
Да, есть разные типы сил трения. Трение между твердыми поверхностями подразделяется на статическое, кинетическое, качение и трение скольжения.
Трение между твердыми поверхностями подразделяется на статическое, кинетическое, качение и трение скольжения.
Share
Copied!
Ньютоновская механика — Различие формул для статического и кинетического коэффициентов трения
спросил
Изменено 1 год, 10 месяцев назад
Просмотрено 193 раза
$\begingroup$
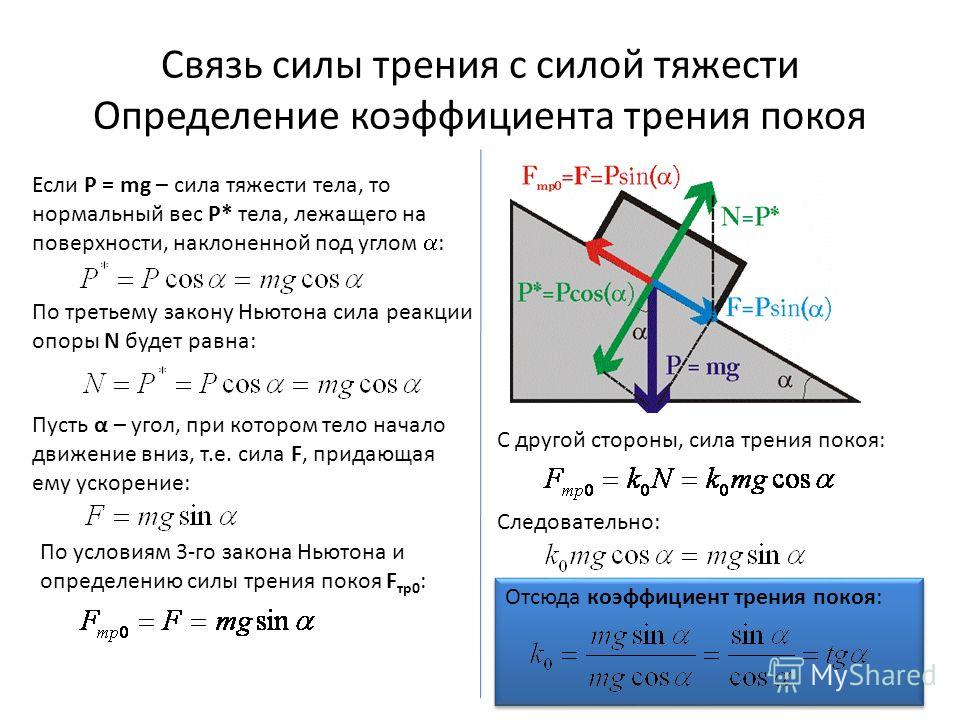
Для объекта, расположенного на вершине наклонной плоскости, статический коэффициент трения можно рассчитать с помощью упрощенного уравнения: мк = тангенс (θ) . Таким же образом, когда объект движется вниз по наклонной плоскости с постоянной скоростью, кинетический коэффициент трения можно рассчитать с помощью упрощенного уравнения μ = tan(θ) . 0$, все, что вы знаете, это то, что сила статического трения вверх по склону равна силе вниз по склону. Сила статического трения продолжает соответствовать направленной вниз силе до тех пор, пока не будет достигнута максимально возможная сила статического трения. Единственный способ выяснить это — продолжать увеличивать угол до тех пор, пока не начнется движение.
0$, все, что вы знаете, это то, что сила статического трения вверх по склону равна силе вниз по склону. Сила статического трения продолжает соответствовать направленной вниз силе до тех пор, пока не будет достигнута максимально возможная сила статического трения. Единственный способ выяснить это — продолжать увеличивать угол до тех пор, пока не начнется движение.
Теоретически вы можете определить как статический, так и кинетический коэффициенты трения, проведя мысленный эксперимент следующего содержания:
Медленно увеличивайте угол наклона, пока не начнется движение. Тангенс этого угла примерно равен коэффициенту статического трения. Как только начинается движение, сила трения резко переходит из статической в кинетическую. Диаграмму этого перехода см. в разделе «График трения» по следующей ссылке: http://hyperphysics.phy-astr.gsu.edu/hbase/frict2.html#kin
Поскольку коэффициент кинетического трения, как правило, меньше, чем коэффициент статического трения, если нет изменения угла, сила трения, действующая вверх по склону, теперь будет меньше, чем сила тяжести, действующая вниз по склону, для суммарной направленной вниз силы и ускорения объекта.
Теперь представьте, что вы можете медленно уменьшать угол, контролируя скорость объекта, пока скорость не станет постоянной. При этом меньшем угле восходящая кинетическая сила трения точно соответствует силе, направленной вниз по склону. Тангенс нижнего угла теоретически равен коэффициенту кинетического трения.
Надеюсь, это поможет.
$\endgroup$
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Коэффициент трения | Коэффициент статического трения
Коэффициент трения, с символом µ – константа трения уравнение, F = мкР.
Это отношение силы трения, действующей между двумя соприкасающиеся поверхности и сила, необходимая для скольжения одной по другой.
Коэффициент трения, коэффициент трения или фрикционный коэффициент, как известно, определяется не расчетным путем, а эксперимент. Его значения зависят от материалов, находящихся в контакте друг с другом, и он колеблется от почти нуля до выше единицы.
Если коэффициент трения равен нулю, значит нет трение, существующее между поверхностями. Однако это лишь гипотетическая значения, так как ни одна из соприкасающихся поверхностей не была признана свободной от трения.
Чем выше значение коэффициента трения, тем
больше сила трения, действующая между поверхностями, а это означает
потребуется более высокая сила, чтобы скользить один из них по другому.
Для сравнения, коэффициент статического трения для двух отдельных поверхностей обычно оказывается выше, чем их коэффициент кинетического трения. Это связано с тем, что статическое трение выше чем кинетический трения, однако существуют определенные поверхности, коэффициент статики которых и кинетическое трение одинаковы. Примеры таких поверхностей включают Тефлон на тефлоновой поверхности.
Коэффициент трения покоя, мкм между двумя поверхностями в виде плоскости, см. схему ниже, заключается в поместите тело на плоскость и постепенно увеличивайте угол наклона θ плоскости до тех пор, пока тело не начнет скользить вниз по плоскости.
Коэффициент трения покоя, мкм может быть показано как µ = тангенс θ
Доказательство: Пусть R — нормальная реакция, а F — статическая реакция.
или ограничение силы трения, действующей, когда тело вот-вот соскользнет вниз.


 ⓘ Масса тела В [m2]
ⓘ Масса тела В [m2]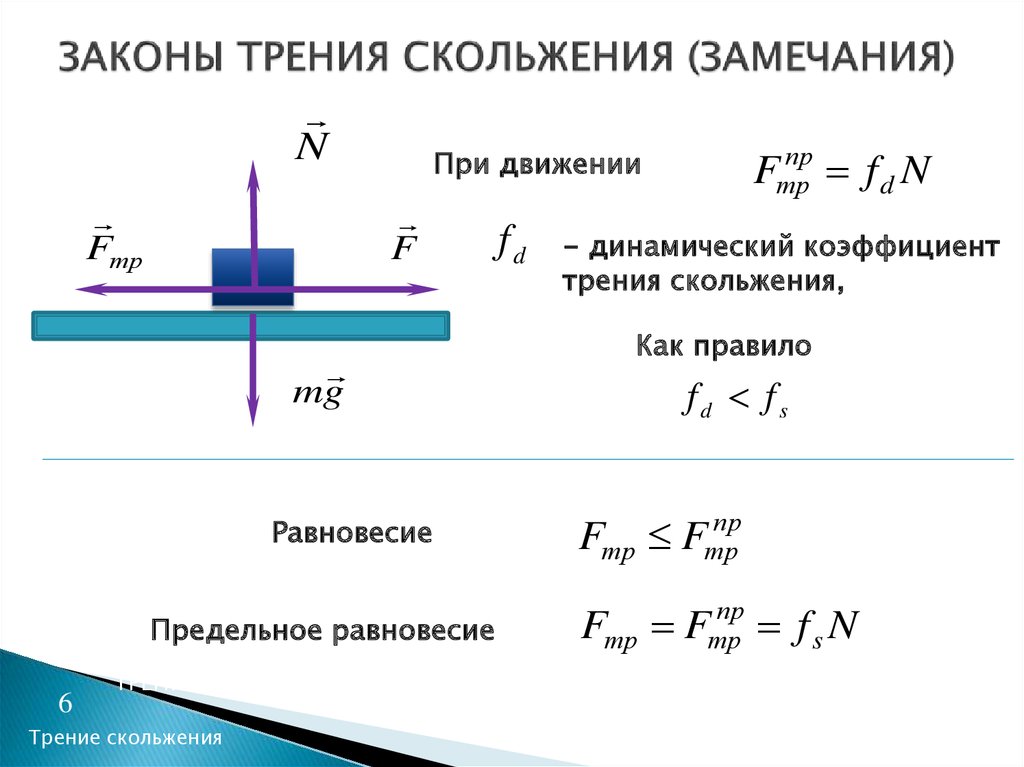 ⓘ Наклон плоскости [θ]
ⓘ Наклон плоскости [θ]