Все формулы по физике — intmag24.ru
Все основные формулы по школьной физике, которые помогут для подготовке к ЕГЭ, а также для решения задач в 7, 8, 9, 10 и 11 классах. Все формулы структурированы, что позволит из запомнить гораздо быстрее.
| Равномерное движение | |
| S= U∙t, U= S/t, t=S/U | Уравнение движения при равномерном движении? где U-скорость, t-время, S-расстояние |
| x=x0+U0t | Координата при равномерном прямолинейном движении |
| Равномерное движение по окружности | |
| T=t/N, T=1/v, Т=2π/ω T=2πR/U, T=2π ∙√(R/a) | T – период N – количество оборотов |
| v=1/T, v=ω/2π, v=U/2πR, v=1/2π ∙√(a/R), v=N/t, v=L/t | v – частота R – радиус окружности |
| ω=2π/Т, ω=2πv, ω=φ/t ω=U/R, ω=√(a/R) | ω – угловая скорость t – время |
| υ=2πR/Т, υ=2πvR, U=ωR U=√(a/R), U=L/t | U – линейная скорость тела |
a=υ2/R, a=ω2R, a=Uω | a – центростремительное ускорение |
| L=φR | L – длина дуги окружности (φ – угол поворота (в радианах)) |
| Равноускоренное движение | |
| X=X0+υ0∙t+(a∙t2)/2 | Уравнение прямолинейного равноускоренного движения |
| S=U0t+a∙t2/2 S= (υ2-υ02) /2а S= (υ+υ0) ∙t /2 = Uср∙t | Расстояние при равноускоренном движении |
| υ=υ0+a∙t | Rонечная скорость тела при равноускоренном движении |
| a=(υ-υ 0)/t | Ускорение |
| U=√(2gh) tпадения=√(2h/g) S=U∙√(2h/g) | — Падение тела с высоты — Горизонтальный бросок (h-высота падения, g – ускорение свободного падения 9,8м/с2, t-время падения, S-расстояние) |
| hmax=U02/2g | Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью U0 |
| tподъема=U0/g | Время подъема тела на максимальную высоту |
| tполета=2U0/g | Полное время полета (до возвращения в исходную точку) |
| Sторм=U02/2a | Тормозной путь тела двигавшегося до начала торможения со скоростью U0 , а затем тормозившего с ускорением а |
| U = √(U02+(gt)2) tgβ = Uy/Ux = gt/U0 | Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту |
| hmax=(U0∙sinα)2/2g tподъема=(U0∙sinα)/g | Бросок с земли на землю под углом к горизонту равным α. Время подъема до высшей точки имаксимальная высота |
Sx=Ux∙tполета tполета=2U02∙sinα/g | Полное время и дальность полета при броске под углом к горизонту |
| Импульс | |
p=mυ | Импульс тела |
Ft=∆p | Импульс силы |
F=∆p/∆t | Второй закон Ньютона в импульсной форме |
pk=pn | Закон сохранения импульса: в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется |
| Энергия | |
A=F∙S∙cosα | Механическая работа (F – сила, S – путь, – угол между направлением движения и силой) |
P=A/t=F∙υ | Мощность (если мощность переменная, то рассчитывается средняя мощность) |
Eп=mgh | Потенциальная энергия тела, поднятого над землей |
Eп=kx2/2 | Потенциальная энергия упруго деформированного тела |
η=Aп/Аз | Коэффициент полезного действия |
Ek=mυ2/2 | Кинетическая энергия тела |
| Молекулярная физика | |
ρ=m/V | Плотность (ρ – его плотность, m – масса вещества, V – объем) |
ν=N/ Na = m/M | Количество вещества (N – число частиц вещества, содержащееся в массе вещества m, Na – число Авогадро, m0 – масса одной молекулы вещества, M – молярная масса) |
М=m/ν | Молярная масса |
m0=m/N=M/Na | Масса одной молекулы вещества |
P=nkT=1/3nm0υ2 | Основное уравнение молекулярно-кинетической теории идеального газа (p – давление газа, n = N/V – концентрация его молекул, m0 – масса одной молекулы, Uкв – средняя квадратичная скорость) |
Uкв=√(3kT/m0), Uкв=√(3RT/M) | Cредняя квадратичная скорость |
Ek=3/2∙kT | Средняя кинетическая энергия поступательного движения одной молекулы (k – постоянная Больцмана, T – абсолютная температура) |
kNa=R | Связь универсальной газовой постоянной и постоянной Авогадро |
PV=m/M∙RT | Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева) |
PV=const (m=const и T= const) | Газовые законы. Закон Бойля-Мариотта (изотермический процесс) |
V/T=const (m=const и p= const) | Газовые законы. Закон Гей-Люссака (изобарный процесс) |
P/T =const (m=const и V= const) | Газовые законы. Закон Шарля (изохорный процесс) |
PV/T=const (m=const ) | Газовые законы. Универсальный газовый закон (Клапейрона) |
V=Vo(1+λt) | Тепловое расширение газов описывается законом Гей-Люссака. (V – объем жидкости при 0 °С, V – при температуре t , λ – коэффициент объемного расширения жидкости) |
l=lo(1+αt) | Изменение линейных размеров, площади и объема тела (lo, So , Vo – соответственно длина, площадь поверхности и объем тела при 0 °С, α – коэффициент линейного расширения тела) |
| Динамика | |
Первый закон Ньютона | Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения |
F=ma | Второй закон Ньютона (F – сила, m – масса, а – ускорение). |
F1-2 = — F2-1 | Третий закон Ньютона (сила действия равна силе противодействия) |
Fупр = kx | Сила упругости (k – жесткость пружины, х – величина растяжения (или сжатия) пружины, оно равно разности между |
Fy=-kx | Закон Гука |
Fтр.скольжения=Fтр.макс = μТ | Сила трения скольжения ( μ– коэффициент трения, N – сила реакции опоры.) |
F=mg | Сила тяжести — Закон Всемирного тяготения (G – гравитационная постоянная, F – сила с которой притягивается тело массой m к телу или планете массой M, r – расстояние между центрами этих тел) |
gh = GM/(Rn+h)2 = | Ускорение свободного падения на некоторой высоте от поверхности планеты (h – высота над поверхностью планеты) |
U = √(GM/(Rn+h)) | Скорость спутника на круговой орбите радиусом r = Rn + h |
U=√(gRn) | Первая космическая скорость (скорость движения спутника по орбите вблизи поверхности планеты) |
T12/T22 = R13/R23 | Закон Кеплера для периодов обращение T1 и T2 двух тел, вращающихся вокруг одного притягивающего центра на расстояниях R1 и R2 соответственно |
Р=m(g+a) | Вес тела, движущегося с ускорением а↑ |
| Термодинамика | |
Q=cm(T2-T1) | Количество теплоты (энергии) необходимое на нагревания некоторого тела (C-теплоемкость, c-удельная теплоемкость, m- масса, t- температура) |
Q=λm | Количество теплоты при плавлении (λ – удельная теплота плавления, m – масса расплавившегося тела или кристаллизовавшейся жидкости) |
Q=rm | Количество теплоты при парообразовании (r – удельная теплота парообразования, m – масса испарившейся жидкости или конденсировавшегося пара) |
Q=qm | Количество теплоты при сгорании топлива (q – удельная теплота сгорания топлива, m – масса сгоревшего топлива) |
A=P∙ΔV = m/M∙ R∙ΔT, p = const | Работа идеального газа |
U=3/2∙M/µ∙RT | Внутренняя энергия идеального одноатомного газа |
ΔU=A+Q | Первый закон (начало) термодинамики (ЗСЭ) (Q – теплота полученная (отданная) газом) |
η= (Q1 — Q2)/ Q1 | КПД тепловых двигателей |
η= (Т1 — Т2)/ Т1 | КПД идеальных двигателей (цикл Карно) |
ρ=pM/RT | Абсолютная влажность (ρ — абсолютная влажность, р – парциальное давление водяного пара, М – молярная масса, R – универсальная газовая постоянная, Т – абсолютная температура) |
φ=ρ/ρ0∙100% | Относительная влажность (ρ — абсолютная влажность, ρ0 -количество водяного пара, которое необходимо для насыщения 1 м3 воздуха при данной температуре) (P — давление водяного пара, Pо — давление насыщенного пара при данной температуре) |
Ep = σS | Поверхностное натяжение (σ – коэффициент поверхностного натяжения данной жидкости) |
Fн= σL | Сила поверхностного натяжения, действующая на участок границы жидкости длиной L |
| Статика и Гидростатика | |
M=F∙ℓ | Момент силы (F – сила, ℓ – плечо силы, т. е. кратчайшее расстояние между точкой опоры, относительно которой происходит вращение и линией действия силы) |
Р=F/S | Давление (F – сила, S – площадь на которую распределено действие силы) |
P=ρ∙g∙h | Давление на глубине жидкости (p0 – атмосферное давление, ρ – плотность жидкости, g – ускорение свободного падения, h – высота столба жидкости) |
Fa=ρж∙g∙V | Закон (сила) Архимеда (V – объем погруженной части тела, который иногда также называют объемом вытесненной жидкости) |
| Электростатика | |
q = Ne | Электрический заряд (N – количество элементарных зарядов, е – элементарный заряд) |
λ=q/L, σ=q/S, ρ=q/V | Линейная, поверхностная и объемная плотность заряда |
F=k∙q1∙q2/R2 | Закон Кулона (сила электростатического взаимодействия двух зарядов величиной q1 и q2, находящихся на расстоянии r друг от друга в веществе с диэлектрической проницаемостью ε): |
E=1/(4πεε0) | Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра |
E= σ/(2εε0) | Напряженность электрического поля, которую создает заряженная плоскость |
ε=E0/E | Диэлектрическая проницаемость |
E=F/q | Напряженность электрического поля |
E=k∙q/R2 | Напряженность электрического поля точечного заряда |
E=2πkσ | Напряженность электрического поля бесконечной плоскости |
W= k∙q1q2/R = k∙q1q2/εr | Потенциальная энергия взаимодействия двух электрических зарядов |
U=Ed, Δφ=E∙ Δl | Cвязь между напряженностью поля и напряжением |
A=qU, U=A/q | Работа электрического поля, Напряжение |
A= qEd, U=E∙d | Работа электрического поля в однородном поле при перемещении заряда вдоль его силовых линий, Напряжение для однородного электрического поля |
φ=W/q | Потенциал |
φ=k∙q/R | Потенциал точечного заряда |
C=q/U | Электроемкость |
C=S∙ε∙ε0/d | Электроемкость плоского конденсатора |
q=CU | Заряд конденсатора |
E = U/d = σ/εε0 | Напряженность поля внутри конденсатора |
F=qE/2 | Сила притяжения пластин конденсатора |
W=qU/2=q²/2С=CU²/2 | Энергия заряженного конденсатора |
| Электрический ток | |
I=q/t | Сила тока (q – заряд, протекший через некоторое поперечное сечение проводника за время t) |
R=ρ∙ℓ/S | Сопротивление проводника (l – длина проводника, S – площадь его поперечного сечения, ρ – удельное сопротивление материала проводника) |
R=R0(1+αt) | Сопротивление проводника |
I=U/R | Закон Ома для участка цепи (U – электрическое напряжение) |
I1=I2=I, U1+U2=U, R1+R2=R | Законы последовательного соединения |
U1=U2=U, I1+I2=I, 1/R1+1/R2=1/R | Законы параллельного соединения |
ε=Aст/q | Электродвижущая сила источника тока, ЭДС (Aст – работа сторонних сил по перемещению заряда q) |
I=ε/(R+r) | Закон Ома для полной цепи |
I=ε/r | Сила тока короткого замыкания (R=0) |
Q=A=I2Rt | Работа электрического тока (закон Джоуля-Ленца). Работа А электрического тока, протекающего по проводнику, обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике |
P=IU=U2/R=I2R | Мощность электрического тока |
m = kQ = kIt | Электролиз. Масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит |
| Магнетизм | |
Fa=IBℓsinα | Сила Ампера (В – индукция магнитного поля, I – сила тока в проводнике, l – его длина, α – угол между направлением силы тока (т.е. самим проводником) и вектором индукции магнитного поля) |
M = NBIS∙sinα | Момент сил, действующих на рамку с током (N – количество витков, S – площадь рамки, α – угол между нормалью к рамке и вектором магнитной индукции) |
Fл=Bqυ∙sinα | Сила Лоренца (q – электрический заряд частицы, υ – её скорость, α – угол между направлением движения частицы и вектором индукции магнитного поля) |
R=mU/qB | Радиус траектории полета заряженной частицы в магнитном поле |
B=Fmax/ℓ∙I | Вектор магнитной индукции |
Ф=BSсos α Ф=LI | Магнитный поток Φ через площадь S |
Ei=ΔФ/Δt | Закон электромагнитной индукции |
Ei=Вℓυsinα | ЭДС индукции при движении проводника |
Esi=-L∙ΔI/Δt | ЭДС самоиндукции |
Wм=LI2/2 | Энергия магнитного поля катушки |
| Колебания | |
a+ω02x=0 | Уравнение описывает физические системы способные совершать гармонические колебания с циклической частотой ω0 |
x = A cos (ωt + φ0) | Уравнением движения для гармонических колебаний (x– координата тела в некоторый момент времени t, A – амплитуда колебаний, ω – циклическая частота колебаний, φ0 –начальная фаза колебаний). |
Х=Хmax∙cos ωt | Уравнение гармонических колебаний |
T=t/N, v=N/t=1/T | Связь некоторых характеристик колебательного процесса (T – период, N – количество полных колебаний, v – частота колебаний, ω – циклическая частота) |
υ = x'(t) = –Aω sin (ωt + φ0) | Скорость тела при колебательном движении |
υm = ωA | Максимальное (амплитудное) значение скорости |
a = υ'(t) = x»(t) | Ускорение тела при колебательном движении |
am = Aω2 | Максимальное (амплитудное) значение ускорения |
ω0=√(g/ℓ) | Циклическая частота и период колебаний математического маятника (l – длина маятника, g – ускорение свободного падения) |
ω0=√(k/m) | Циклическая частота и период колебаний пружинного маятника (m – масса груза, k – коэффициент жесткости пружины маятника) |
W=CU2/2+LI2/2 | Электрический контур |
T=2π ∙√LC | Период колебаний кол. контура и циклическая частота |
Iд=I0/√2, Iд=Imax/√2 | Переменный ток характеризуется действующими значениями силы тока и напряжения, которые связаны с амплитудными значениями соответствующих величин; Действующее значение силы тока и напряжения |
P=UдIд =Iд2R=Uд2/R | Мощность в цепи переменного тока |
U1/U2=n1/n2 | Трансформатор: если напряжение на входе в трансформатор равно U1, а на выходе U2, при этом число витков в первичной обмотке равно n1, а во вторичной n2 |
λ= υТ=υ/v | Волны. Длина волны (υ – скорость распространения волны, T – период, v – частота) |
XL=ωL=2πLν | Индуктивное сопротивление |
Xc=1/ωC | Емкостное сопротивление |
Z=√(Xc-XL)2+R2 | Полное сопротивление |
| Оптика | |
Lопт=Ln | Оптическая длина пути (L – геометрическая длина траектории, по которой «идет» луч света, n – показатель преломление среды, в которой это происходит) |
x=mλL/d | Интерференционная схема Юнга (L – расстояние между экраном и плоскостью в которой расположены две щели, d – расстояние между этими щелями, λ – длина волны света, которым освещаются щели).  |
d∙sin φ=k λ | Формула дифракционной решетки (d – период решетки, или расстояние между соседними штрихами, φ – угол под которым наблюдается очередной дифракционный максимум, k – номер (порядок) максимума, λ – длина волны света, падающего на дифракционную решетку) |
n21=n2/n1= υ 1/ υ 2 | Закон преломления света на границе двух прозрачных сред (α – угол падения, β – угол преломления, n1 – показатель преломления первой среды, из которой падает луч, n2 – показатель преломления второй среды, в которую проникает луч) |
n21=sinα/sinβ | Показатель преломления |
1/F=1/d + 1/f | Формула линзы (d – расстояние от линзы до предмета, f – расстояние от линзы до изображения, F – фокусное расстояние, D – оптическая сила линзы) |
D=1/F | Оптическая сила линзы |
Δd=kλ, Δd=(2k+1)λ/2 | max интерференции, min интерференции |
| Атомная и ядерная физика | |
E=hv=hc/λ | Энергия кванта света, т. е. фотона (h – постоянная Планка, λ – длина волны света, v – частота света) |
P=mc=h/ λ=Е/с | Импульс фотона |
hν=Aвых+(mU2/2)max | Формула Эйнштейна для внешнего фотоэффекта (ЗСЭ) (Авых – работа выхода, слагаемое в скобках –максимальная кинетическая энергия вылетающих электронов, v – частота падающего света) |
(mU2/2)max=еUз | Максимальная кинетическая энергия вылетающих электронов |
νк = Aвых/h | Красная граница фотоэффекта |
hνnm = |En – Em| | Второй постулат Бора (правило частот). При переходе атома из одного стационарного состояния с энергией En в другое стационарное состояние с энергией Em излучается или поглощается квант, энергия которого равна разности энергий стационарных состояний |
N=N0∙2—t/T | Закон радиоактивного распада |
ECB=(Zmp+Nmn-Mя)∙c2 | Энергия связи атомных ядер |
| Основы СТО | |
ℓ=ℓ0∙√1-υ2/c2 | Релятивистское сокращение длины. Длина тела, движущегося со скоростью V в инерциальной системе отсчета уменьшается в направлении движения до длины |
t=t1/√(1-υ2/c2) | Релятивистское удлинение времени события. Время, за которое происходит некоторое событие в движущейся системе отсчета с точки зрения наблюдателя из неподвижной системы отсчета |
υ=(υ1+υ2)/1+ υ1∙υ2/c2 | Релятивистский закон сложения скоростей |
Е = mс2 | Связь энергии и массы тела. Наименьшей энергией Е0 тело обладает в инерциальной системе отсчета относительно которой оно покоится и называется собственной энергией тела (энергия покоя тела) |
способы на практике узнать значение с помощью приборов и расчетных формул
Передвижение положительно заряженных частиц, движущихся в едином направлении, в физике называют силой тока.
По своей сути это физическая величина, демонстрирующая заряд, происходящий в определенное время через специальный проводник. Найти силу тока можно несколькими способами. Первый — это расчет величины по выведенным готовым формулам при наличии первоначальных данных. Второй — это использование специальных измерительных приборов.
- Зачем нужна сила тока
- Расчет величины по формулам
- Вычисление значений приборными системами
- Измерение амперметром
Зачем нужна сила тока
Работа любой электротехники напрямую связана с физической величиной заряженных частиц. Знание того, как найти силу тока, позволяет понимать нюансы работы такого оборудования, отдельной цепи либо схемы. Расчет подобного значения у настоящего профессионала не вызовет особых трудностей, а вот у начинающих электриков это может вызвать некоторые проблемы. Для этого стоит знать определенные расчетные формулы или иметь под рукой специальный измерительный прибор.
По своей сути различают несколько разновидностей тока — это постоянный (содержащийся в аккумуляторных батарейках) и переменный (находящийся в розетке).
Именно второй вид отвечает за освещение в помещении, работу электроприборов. Особенность переменного тока заключается в быстрой передаче и трансформации, ярким примером тому может служить работа люминесцентных лампочек (движение токовых частиц при включении).
Расчет величины по формулам
Так как самым распространенным видом тока, использующимся в быту, является переменный, то для его расчета используется известная каждому школьнику формула расчета «Закон Ома». Выглядит она следующим образом — I = U / R (найти ток можно, разделив напряжение на сопротивление), где:
- I — это переменное токовое значение;
- U — это напряжение;
- R — это сопротивление.
Из этой формулы тока можно вывести и другие, не менее полезные вычисления, позволяющие определить другие значения, имея только фактические показатели двух других величин (R = U / I и U = I * R). При расчете рекомендуется использовать основные единицы измерения — амперы, вольты и омы.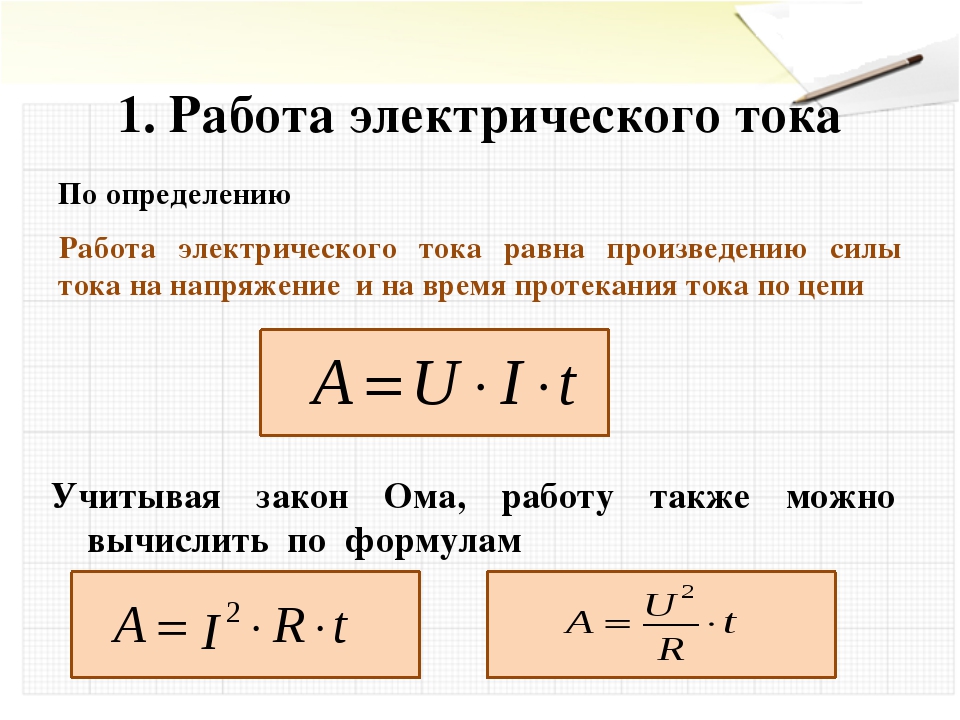
Данная расчетная формула чаще всего используется для вычисления силы в цепях с активной нагрузкой, например, нагревательных приборах, электрочайниках, светодиодах и т. д.
В других же случаях используется иная вычислительная формула, содержащая в себе мощность и напряжение. Выглядит она следующим образом — I = P / U. Также сила тока рассчитывается по формуле I = q / t, где q — это заряд, идущий по проводнику, измеряющийся в кулонах, а t — это время прохождения электрического заряда, вычисляющееся в секундах.
Вычисление значений приборными системами
Помимо формул при отсутствии четких показателей необходимых значений используются специальные приборные системы. Преимущество такого метода заключается в быстроте и точности получаемых данных, минус — в необходимости покупать требуемые устройства. К основным способам, как определить силу тока, стоит отнести:
- Магнитоэлектрический метод вычисления, отличающийся высокой чувствительностью, точностью показаний, минимальным потреблением электроэнергии.
Используется он зачастую для определения значения силы постоянного тока. - Электромагнитный, основным вычислительным элементом которого становится магнитомодульный датчик, на который из магнитного поля поступает сигнал. Таким способом можно узнать силу постоянного и переменного тока.
- Косвенный, где по старинке используется вольтметр, определяющий показания напряжения на определенном сопротивлении.
Используется он зачастую для определения значения силы постоянного тока.Стоит отметить, что подобные методы редко применяются самими электрикам, так как они отнимают много времени. Гораздо проще использовать специальные приборы, а не приборные системы.
Измерение амперметром
Самым простым способом узнать силу тока является измерение показаний амперметром. Особенности его использования заключаются в подключении прибора к разрывам электрической цепи. Для этого выбирается подходящее место, после чего остается дождаться, когда на экране амперметра высветится значение силы тока (заряда), прошедшего через кабельное сечение через определенное время.
Помимо классического прибора используются похожие на них аналоги, предназначенные для того, чтобы быстро найти силу тока малого электричества — это миллиамперметры, микроамперметры, гальванометры. Процедура подключения установки мало чем отличается от обычных измерительных приборов, их нужно зафиксировать на том участке цепи, где требуется узнать значение заряда. Подключение осуществляется несколькими методами — последовательным и параллельным. Условно весь процесс можно разделить на несколько этапов:
- подготовка прибора, из которого выходит провод с двумя кабелями питания;
- выставление необходимого измерительного диапазона на вычислительной установке;
- прикладывание одного щупа к проводу питания прибора;
- подключение второго щупа к любому контакту электропитания;
- подсоединение оставшегося провода ко второму щупу;
- включение измерительного прибора;
- получение величины токовой силы, показанной на измерителе.
При измерении токовой силы нельзя забывать о том, что особую роль в этом деле играет его вид (переменный либо постоянный). Особое внимание следует уделить постоянному типу тока, например, если внутри устройства установлен блок питания, снижающий сетевое напряжение до меньших значений.
В таком случае необходимо измерять токовую силу в той части цепи, где установлен выпрямляющий мост диодов.
Немаловажную роль в измерении играет напряжение, в таком случае измерительные щипы прибора прикладываются не к разрыву цепи, а к параллельным контактам электропитания. Тут также стоит уделить внимание типу напряжения, которое бывает переменным и постоянным.
Уравнения и формулы физики — макеты
Физика заполнена уравнениями и формулами, которые имеют дело с угловым движением, двигателями Карно, жидкостями, силами, моментами инерции, линейным движением, простым гармоническим движением, термодинамикой, работой и энергией.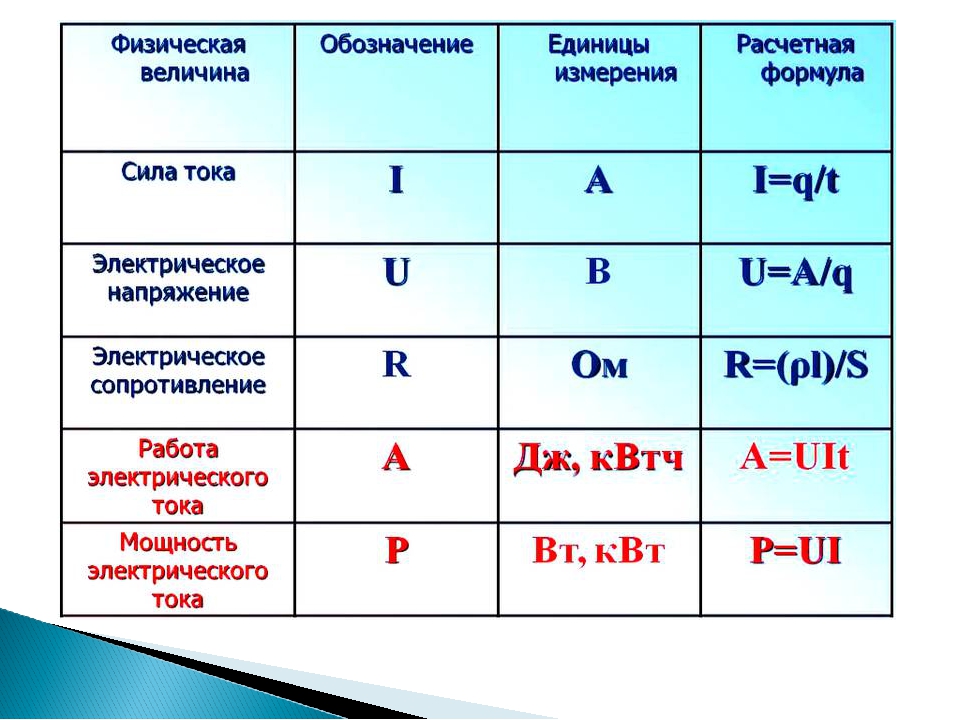
Вот список некоторых важных физических формул и уравнений, которые следует держать под рукой, упорядоченных по темам, чтобы вам не приходилось искать их.
Угловое движение
Уравнения углового движения применимы везде, где есть вращательные движения вокруг оси. Когда объект повернулся на угол θ с угловой скоростью ω и угловым ускорением α , то вы можете использовать эти уравнения, чтобы связать эти значения вместе.
Для измерения угла необходимо использовать радианы. Кроме того, если вы знаете, что расстояние от оси равно r, , то вы можете вычислить пройденное линейное расстояние, с , скорость, v , центростремительное ускорение, a c и силу , Ф с . Когда объект с моментом инерции I (угловой эквивалент массы) имеет угловое ускорение α , тогда возникает чистый крутящий момент Στ.
Двигатели Карно
Тепловая машина берет тепло Q h от высокотемпературного источника при температуре T h и перемещает его к низкотемпературному стоку (температура T 9 по курсу Q c и при этом выполняет механическую работу, W .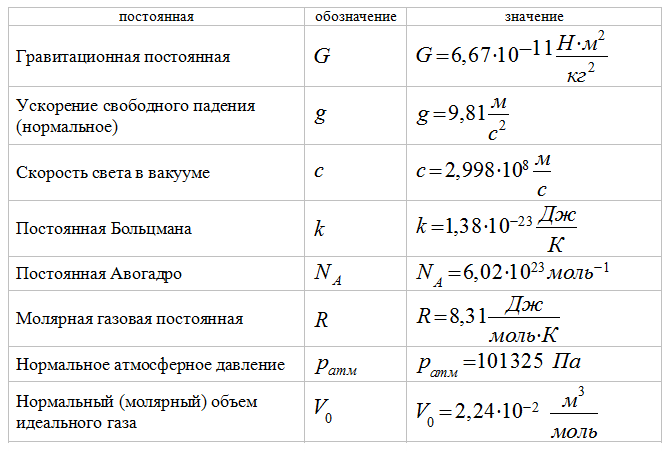
(Этот процесс можно обратить вспять, так что можно выполнить работу по перемещению тепла в противоположном направлении — тепловой насос.) Количество выполненной работы пропорционально количеству тепла, извлеченного из источника тепла, является КПД двигателя. Двигатель Карно является обратимым и имеет максимально возможный КПД, определяемый следующими уравнениями. Эквивалентом эффективности теплового насоса является коэффициент полезного действия.
Жидкости
Объем А, В , жидкости с массой, м , имеет плотность, ρ . Сила, F , по площади, A , вызывает давление, P . Давление жидкости на глубине ч зависит от плотности и гравитационной постоянной, г . Объекты, погруженные в жидкость, создающие массу веса, Вт вода вытесненная , создают направленную вверх выталкивающую силу, F плавучесть .
Из-за сохранения массы объемный расход жидкости, движущейся со скоростью v , через площадь поперечного сечения A , является постоянным. Уравнение Бернулли связывает давление и скорость жидкости.
Сил
Масса А, м , ускоряется со скоростью, a , из-за силы, F , действующей. Силы трения, F F , пропорциональны нормальной силе между материалами, F Н , с коэффициентом трения мк. Две массы, м 1 и м 2 , разделенные расстоянием, r , притягивают друг друга в пропорции гравитационная постоянная Г :
Моменты инерции
Вращательный эквивалент массы — это инерция, I , , которая зависит от того, как масса объекта распределена в пространстве. Здесь показаны моменты инерции для различных форм:
Диск, вращающийся вокруг своего центра:
Полый цилиндр, вращающийся вокруг своего центра: I = mr 2
Полая сфера, вращающаяся с осью, проходящей через ее центр:
Обруч, вращающийся вокруг своего центра: I = mr 2
Точечная масса, вращающаяся на радиусе r: I = mr 2
Прямоугольник, вращающийся вокруг оси вдоль одного края, где другой край имеет длину r :
Прямоугольник, вращающийся вокруг оси, параллельной одному краю и проходящей через центр, где длина другого края равна г :
Стержень, вращающийся вокруг оси, перпендикулярной ему и проходящей через его центр:
Стержень, вращающийся вокруг оси, перпендикулярной ей и через один конец:
Сплошной цилиндр, вращающийся вокруг оси вдоль ее центральной линии:
Кинетическая энергия вращающегося тела с моментом инерции I и угловой скоростью ω :
Угловой момент вращающегося тела с моментом инерции, I , а угловая скорость ω :
Линейное движение
Когда объект в положении x движется со скоростью v , и ускорением a, приводящим к смещению s , каждый из этих компонентов связан следующими уравнениями:
Простое гармоническое движение
Определенные виды силы приводят к периодическому движению, когда объект повторяет свое движение с периодом, T , с угловой частотой ω, и амплитудой A .
Одним из примеров такой силы является пружина с жесткостью k . Положение x , скорость v и ускорение a, объекта, совершающего простое гармоническое движение, могут быть выражены синусом и косинусом.
Термодинамика
Беспорядочные колебательные и вращательные движения молекул, составляющих объект вещества, обладают энергией; эта энергия называется тепловая энергия. Когда тепловая энергия перемещается из одного места в другое, она называется теплотой, Q . Когда объект получает некоторое количество тепла, его температура T , повышается.
Кельвина ( K ), Цельсия ( C ) и Фаренгейта (F ) — это температурные шкалы. Вы можете использовать эти формулы для преобразования одной температурной шкалы в другую:
Теплота, необходимая для изменения температуры массы, m , увеличивается с константой пропорциональности, c , называется удельной теплоемкостью.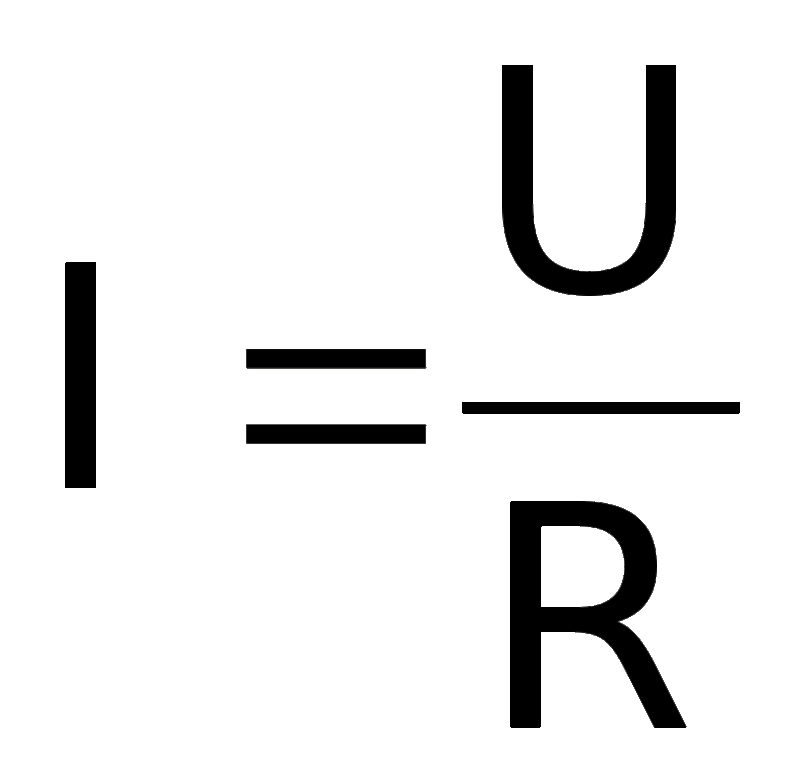
В стержне из материала с площадью поперечного сечения A , длиной L и разностью температур на концах ΔT существует тепловой поток за время t , , определяемый выражением эти формулы:
Давление, P , и объем, V , из n молей идеального газа при температуре T определяется по этой формуле, где R — газовая постоянная:
В идеальном газе средняя энергия каждой молекулы KE avg пропорциональна температуре с постоянной Больцмана k :
Работа и энергия
Когда сила, F , перемещает объект на расстояние с , которое находится под углом Θ ,затем работа, W , выполнена. Импульс p является произведением массы m , и скорости v . Энергия, которой объект обладает благодаря своему движению, называется KE .
Как найти конечную скорость любого объекта
Обновлено 7 декабря 2019 г.
Автор S. Hussain Ather
Многие формулы и уравнения в физике включают расчет начальной и конечной скорости. Разница между начальной и конечной скоростью в уравнениях сохранения импульса или уравнениях движения говорит вам о скорости объекта до и после того, как что-то произойдет. Это может быть сила, приложенная к объекту, столкновение или что-то еще, что может изменить его траекторию и движение.
Для расчета конечной скорости объекта при равномерном ускорении можно использовать соответствующее уравнение движения. Эти уравнения используют комбинации расстояния, начальной скорости, конечной скорости, ускорения и времени, чтобы связать их друг с другом.
Формула окончательной скорости
Например, формула конечной скорости ( v f ), которая использует начальную скорость ( v i ), ускорение ( a ) и время (
1 0 t
v_f = v_i + aΔt.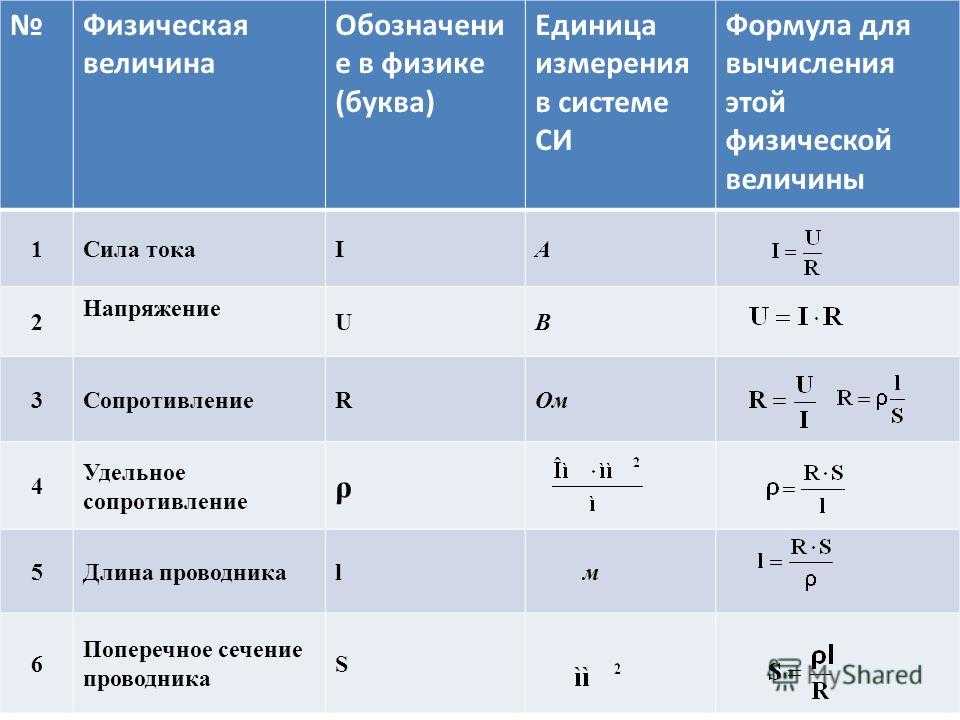
Для заданной начальной скорости объекта вы можете умножить ускорение, вызванное силой, на время приложения силы и добавить его к начальной скорости, чтобы получить конечную скорость. «Дельта» Δ перед t означает, что это изменение во времени, которое можно записать как t f − t i .
Идеально подходит для мяча, падающего на землю под действием силы тяжести. В этом примере ускорение под действием силы тяжести было бы константой ускорения свободного падения 9.0009 г = 9,8 м/с 2 . Эта постоянная ускорения говорит вам, насколько быстро ускоряется любой объект, когда вы бросаете его на Землю, независимо от массы объекта.
Если вы бросите мяч с заданной высоты и подсчитаете, сколько времени потребуется мячу, чтобы достичь земли, то вы можете определить скорость непосредственно перед тем, как он упадет на землю, как конечную скорость. Начальная скорость была бы равна 0, если бы вы уронили мяч без какой-либо внешней силы.
Используя приведенное выше уравнение, вы можете определить конечную скорость v f .
Альтернативные уравнения расчета конечной скорости
Вы можете использовать другие кинематические уравнения в зависимости от того, с какой ситуацией вы работаете. Если бы вы знали расстояние, пройденное объектом (Δ_x_), а также начальную скорость и время, необходимое для прохождения этого расстояния, вы могли бы рассчитать конечную скорость, используя уравнение:
v_f = \frac{2Δx}{t} — v_i
Убедитесь, что в этих расчетах используются правильные единицы измерения.
Катящийся цилиндр
Для цилиндра, катящегося по наклонной плоскости или холму, вы можете рассчитать конечную скорость, используя формулу сохранения энергии. Эта формула диктует, что, если цилиндр начинает движение из состояния покоя, энергия, которую он имеет в своем начальном положении, должна равняться его энергии после скатывания на определенное расстояние.
