Приведение системы сил к простейшей системе в теоретической механике
Содержание:
Приведение системы сил к простейшей системе:
Приведение силы к заданному центру: Силу можно переносить параллельно самой себе в любую точку твердого тела, добавляя при этом пару сил, векторный момент которой равен векторному моменту переносимой силы относительно новой точки приложения силы.
Пусть имеем силу
Рис. 34
Теперь докажем, что силу можно переносить на другую, параллельную линию действия. Но этот перенос следует компенсировать добавлением соответствующей пары сил. Приложим в точке тела , выбранной за центр приведения, систему двух равных по модулю, но противоположных по направлению сил и , параллельных заданной силе . Силы и составляют систему сил, эквивалентную нулю, и ее можно добавить к любой заданной системе сил.
Пусть по модулю
Тогда
Система двух равных по модулю и противоположных по направлению параллельных сил составляет пару сил, которую называют присоединенной парой сил.
Итак, вместо силы , приложенной в точке , получены сила , равная ей но модулю и направлению, но приложенная в точке , и присоединенная пара сил , векторный момент которой
Процесс замены силы силой и парой сил называют приведением силы к заданному центру . По теореме об эквивалентности пар сил пару можно заменить любой другой парой сил с таким же векторным моментом.
Докажем основную теорему статики (теорему Пуансо): любую произвольную систему сил, действующих на твердое тело, можно в общем случае привести к силе и паре сил.
Такой процесс замены системы сил одной силой и парой сил называют приведением системы сил к заданному центру.
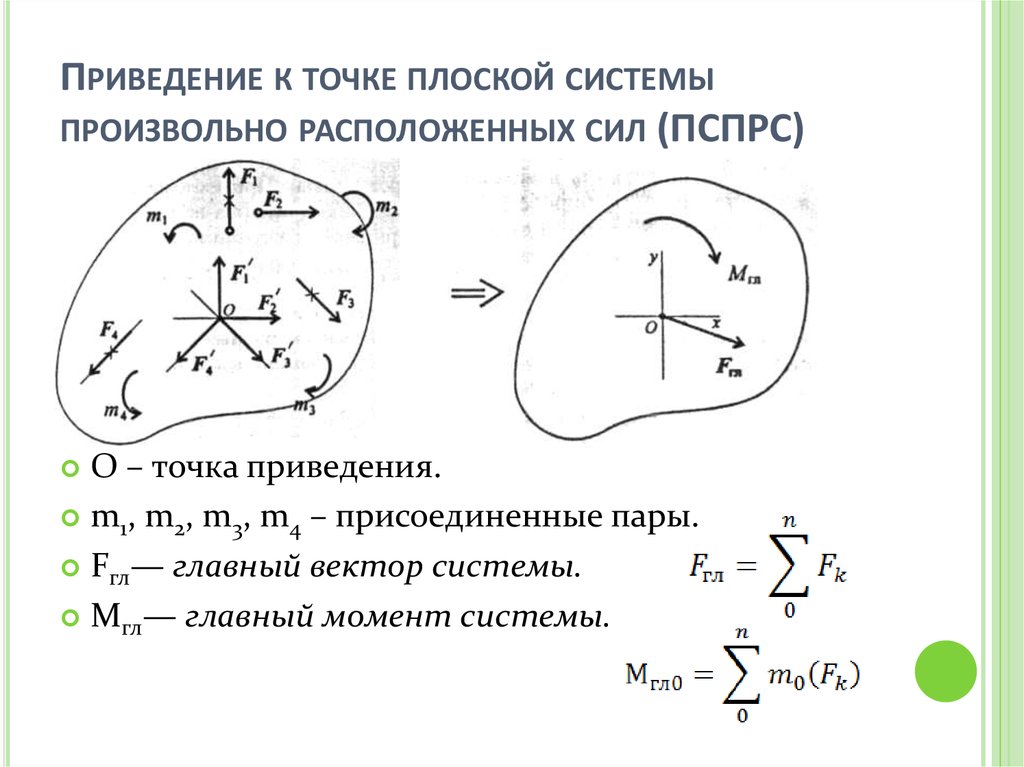
Пусть дана произвольная система сил , приложенных к твердому телу. Выберем произвольную точку тела за центр приведения и каждую силу заданной системы сил приведем к точке (рис. 35). Получим
Таким образом, система из сил заменена системой из сил, т. е. в точке приложена система сходящихся сил и на твердое тело действует также система присоединенных пар сил
Векторные моменты присоединенных пар сил, согласно формуле (1), можно выразить через векторные моменты заданных сил:
Рис. 35
35
Систему сходящихся сил заменим их равнодействующей , которая равна векторной сумме сил и геометрически изображается замыкающим вектором силового многоугольника, построенного на этих силах (рис. 35).
Итак,
где
Для системы сходящихся сил сила является равнодействующей, а для заданной системы сил сила является лишь только ее векторной суммой, или главным вектором.
Главным вектором системы сил называют вектор, равный векторной сумме этих сил. Он изображается вектором, замыкающим силовой многоугольник, построенный на силах, т. е.
Систему присоединенных пар сил по теореме о сложении пар сил можно заменить одной парой сил с векторным моментом , который называют главным моментом. Главный момент равен сумме векторных моментов присоединенных пар. Учитывая формулу (2), для имеем
Индекс означает, что за центр приведения взята точка .
Итак, главным моментом системы сил относительно точки тела называют сумму векторных моментов всех сил системы относительно этой точки.
Главный момент системы сил является вектором, замыкающим векторный многоугольник, образованный при сложении векторных моментов сил системы относительно выбранного центра.
Таким образом, доказана основная теорема статики: любую систему сил, действующих на твердое тело, можно привести к силе, равной главному вектору системы сил, и паре сил, векторный момент которой равен главному моменту системы сил относительно точки, выбранной за центр приведения.
В краткой форме эту теорему можно выразить так:
т. е. каждую систему сил можно привести к главному вектору и главному моменту относительно произвольного центра. Следует учитывать, что это условная формулировка основной теоремы. Главный момент характеризует действие на тело пары сил (рис. 36), лежащей в плоскости, перпендикулярной главному моменту.
Рис. 36
Приведение плоской системы силПлоской системой сил, приложенных к твердому телу, называют такую систему сил, линии действия которых лежат в одной плоскости.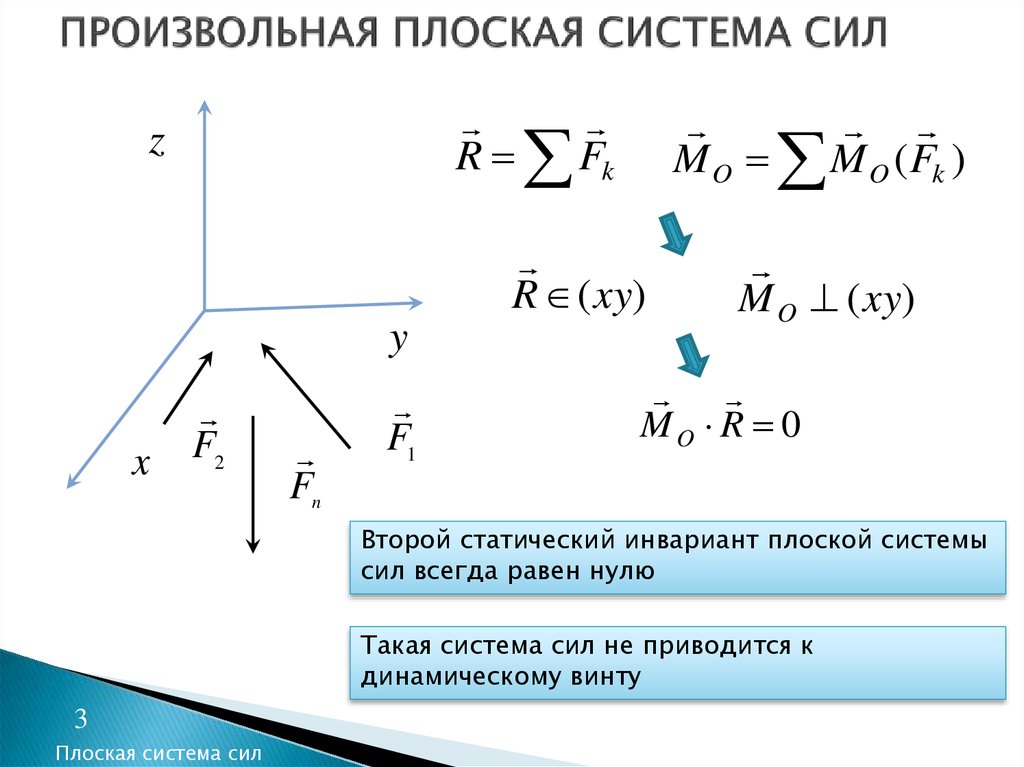 Основная теорема статики справедлива для любой системы сил. Она справедлива и для плоской системы сил, действующих на твердое тело: любую плоскую систему сил можно в общем случае привести к силе и паре сил.
Основная теорема статики справедлива для любой системы сил. Она справедлива и для плоской системы сил, действующих на твердое тело: любую плоскую систему сил можно в общем случае привести к силе и паре сил.
Для плоской системы сил главный вектор лежит в плоскости действия сил, если за центр приведения выбрать точку в плоскости действия сил. Все присоединенные пары сил тоже лежат в этой плоскости, а следовательно, векторные моменты этих пар перпендикулярны ей и взаимно параллельны. Главный момент , характеризующий векторный момент пары сил, эквивалентный присоединенным парам, перпендикулярен главному вектору. Он является векторной суммой параллельных векторов.
В этом случае главный момент равен сумме алгебраических моментов присоединенных пар и, следовательно, сумме алгебраических моментов сил относительно центра приведения.
Для плоской системы сил вместо векторного главного момента используют понятие алгебраического главного момента. Алгебраическим главным моментом плоской системы сил относительно центра приведения, лежащего в плоскости действия сил, называют сумму алгебраических моментов этих сил относительно центра приведения.
- Заказать решение задач по теоретической механике
Для любой системы сил главный вектор является векторной суммой этих сил:
а главный момент — суммой векторных моментов сил относительно центра приведения:
Главный вектор геометрически изображается замыкающей силового многоугольника, построенного на заданных силах. Проецируя обе части векторного равенства (3′) на координатные оси, для произвольной пространственной системы сил получаем
По проекциям определяют модуль главного вектора и косинусы его углов с осями координат:
Главный момент геометрически тоже изображается замыкающей векторного многоугольника, построенного на векторных моментах сил относительно центра приведения. Проецируя обе части векторного равенства (4′) на прямоугольные оси координат и используя связь момента силы относительно оси с проекцией векторного момента этой силы относительно точки на оси, имеем
Модуль главного момента и косинусы его углов с осями координат равны
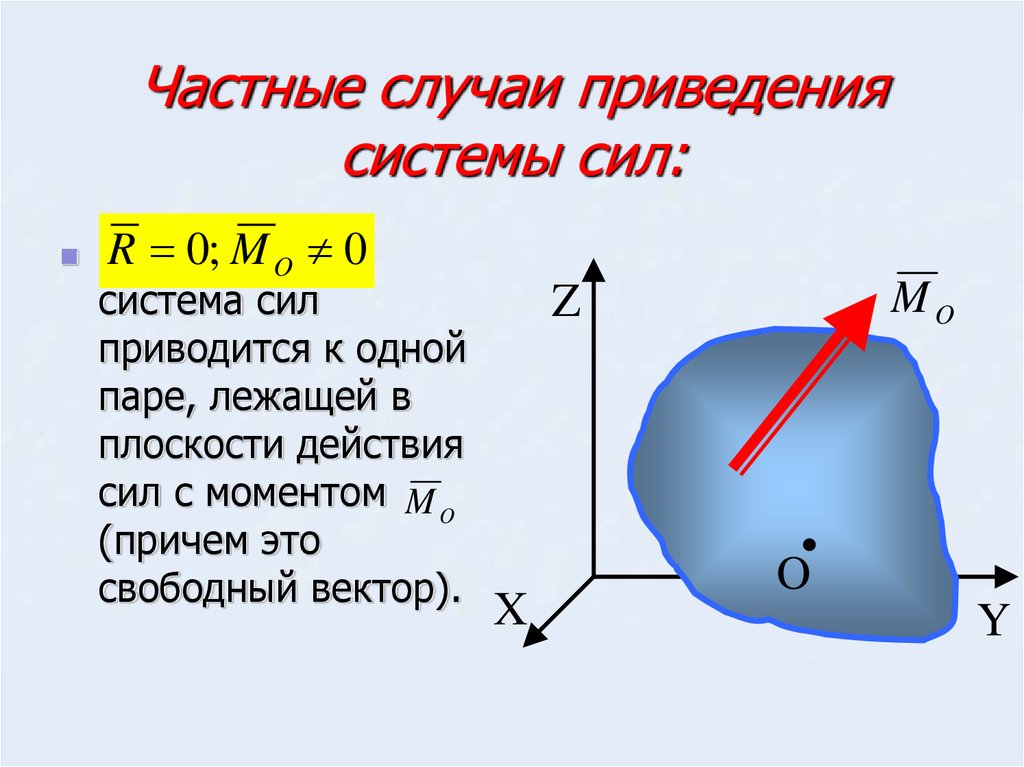
Если выбрать ось перпендикулярно плоскости действия плоской системы сил, а оси и — в плоскости сил, то главный вектор будет лежать в плоскости и, следовательно, для плоской системы сил
Главный момент плоской системы сил перпендикулярен главному вектору и, следовательно, параллелен оси .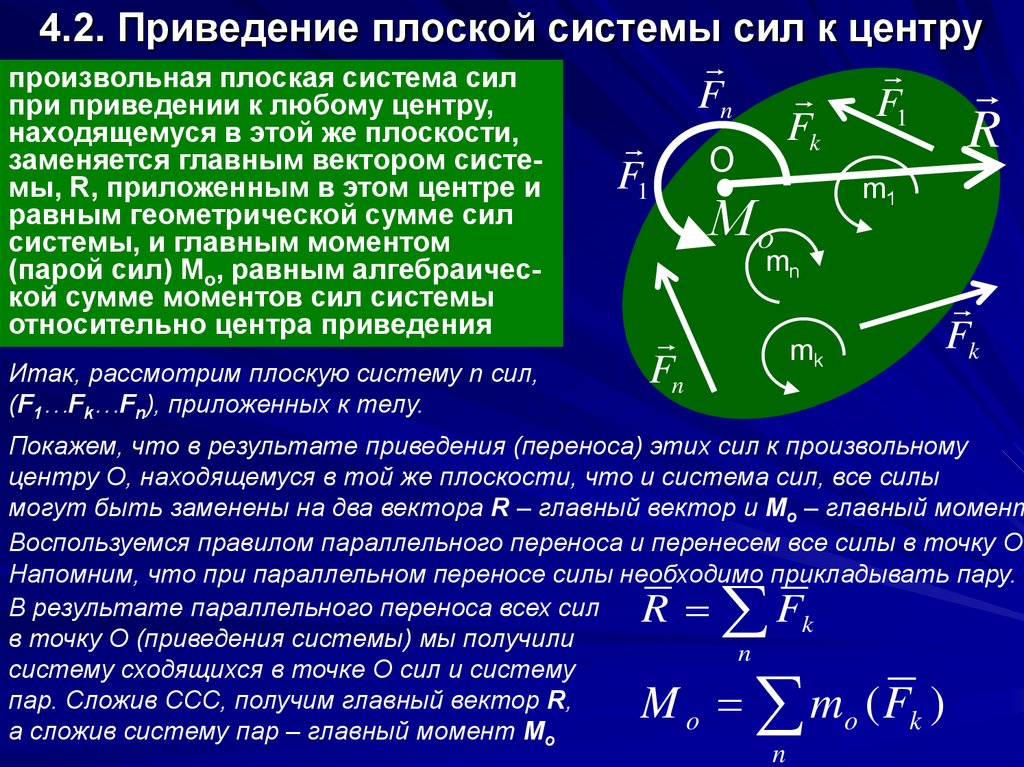 Тогда
Тогда
где — алгебраический главный момент.
Главный вектор плоской системы произвольно расположенных сил равен векторной сумме всех сил системы и приложен в центре приведения.
Графически главный вектор выражается замыкающей стороной силового многоугольника, построенного на данных силах.
Fгл = √[(ΣX)2 + (Y)2] (здесь и далее √ — знак корня),
а направляющий косинус – по формуле cos (Fгл, x) = FглХ / Fгл.
Плоская система пар эквивалентна одной паре, момент которой равен алгебраической сумме моментов данных пар, следовательно,
Мгл = m1 = m2 + m3 +….+ mn = MO(F1) + MO(F2) + MO(F3) +….+ M
Мгл = ΣМO(Fi).
Эту пару с моментом Мгл назовем главным моментом заданной системы сил.
Главный момент плоской системы произвольно расположенных сил равен алгебраической сумме моментов всех сил системы относительно центра приведения.
Таким образом, всякая плоская система сил в общем случае эквивалентна системе, состоящей из силы и пары сил, следовательно, теорема доказана.
Не следует считать, что главный вектор и главный момент имеют чисто формальное значение, введенной для удобства доказательства, и что их можно найти только с помощью вычислений. Нередко отдельно действующие на тело силы определить трудно или даже невозможно, а главный вектор или главный момент этих сил найти сравнительно легко. Так, например, число точек контакта и модули сил трения между вращающимся валом и подшипником скольжения, как правило, неизвестны, но главный момент этих сил можно определить простым измерением.
Еще один пример: в характеристику электродвигателя входит не сила, с которой статор действует на ротор, а вращающий момент, являющийся, по сути, главным моментом этой силы.
***
Свойства главного вектора и главного момента
Свойства главного вектора и главного момента заключаются в следующем:
1. модуль и направление главного вектора данной системы не зависят от выбора центра приведения, так как при любом центре приведения силовой многоугольник, построенный на данных силах, будет один и тот же;
2. величина и знак главного момента в общем случае зависят от выбора центра приведения (кроме случая, рассмотренного далее, когда
3. главный вектор и равнодействующая системы сил векторно равны, но в общем случае не эквивалентны. Пусть известны главный вектор Fгл и главный момент Мгл какой-либо плоской системы сил (рис.4а).
главный вектор и равнодействующая системы сил векторно равны, но в общем случае не эквивалентны. Пусть известны главный вектор Fгл и главный момент Мгл какой-либо плоской системы сил (рис.4а).
Определим равнодействующую этой системы.
Пользуясь известным свойством пары сил, преобразуем главный момент
F = FΣ = Fгл; Мгл = М(F, FΣ),
причем сила F приложена в точке О противоположно Fгл.
Далее систему (Fгл, F), как взаимно уравновешенную, отбросим:
(Fгл,Мгл) = (Fгл,F,FΣ) ≡ FΣ
В результате получим одну силу FΣ, эквивалентную главному вектору и главному моменту, т. е. равнодействующую системы, причем FΣ = Fгл.
Модуль равнодействующей можно определить по формуле:
FΣ = √[(ΣX)2 + (Y)2] = Fгл,
а положение линии действия равнодействующей определяется плечом d по формуле:
d = Мгл
В результате можно считать установленным, что главный вектор и равнодействующая векторно равны, но не эквивалентны.
4. главный вектор и равнодействующая эквивалентны лишь в частном случае, когда главный момент системы равен нулю. Это возможно лишь в случае, когда центр приведения находится на линии действия равнодействующей. Из приведенного выше рисунка видно, что момент равнодействующей FΣ относительно центра приведения О равен моменту Мгл пары (FΣ,F), т.
МО(FΣ) = М(FΣ,F) = Мгл.
Так как Мгл = ΣМО(Fi), а за центр приведения можно взять любую точку плоскости действия сил данной системы, то всегда имеем:
М(FΣ) = ΣМ(Fi).
Полученная формула является математическим выражением теоремы о моменте равнодействующей.
Теорема:момент равнодействующей силы относительно какой-либо точки, расположенной в плоскости действия сил, равен алгебраической сумме моментов составляющих сил относительно той же точки.
Теорему о моменте равнодействующей впервые доказал французский ученый П. Вариньон (1654-1722), поэтому ее называют теоремой Вариньона.
Применим доказанную теорему для определения положения линии действия равнодействующей FΣ плоской системы n параллельных сил:
(F1 + F2 + F3 +.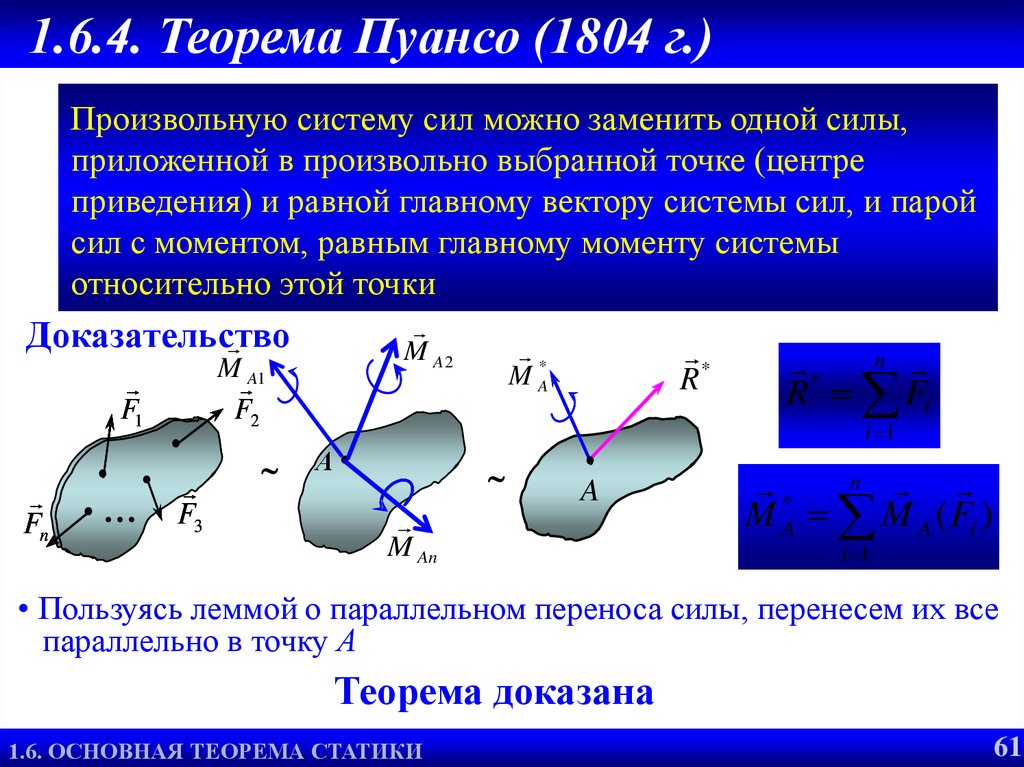 …+ Fn) ≡ FΣ.
…+ Fn) ≡ FΣ.
Выберем какую-либо точку О плоскости действия сил за центр моментов и согласно теореме Вариньона запишем:
ΣМO(Fi) = МO(FΣ) = FΣd, где: d – плечо равнодействующей FΣ относительно точки О.
Из последнего равенства определяем плечо d:
d = ΣМO(Fi) / FΣ = ΣМO(Fi) / ΣFi, так как FΣ = ΣFi.
Чтобы установить, в какую сторону от точки О следует на перпендикуляре к линиям действия сил отложить плечо 
***
Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? — задался я вопросом…
Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем…
Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам…
Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все…
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Помогите решить / разобраться (Ф)
Сообщения без ответов | Активные темы | Избранное
| Traper |
| ||
03/11/15 |
| ||
| |||
| Pphantom |
| ||
09/05/12 | |||
| |||
| Pphantom |
| |||||
09/05/12 |
| |||||
| ||||||
| Munin |
| |||
30/01/06 |
| |||
| ||||
| amon |
| |||
04/09/14 |
| |||
| ||||
| Traper |
| ||
03/11/15 |
| ||
| |||
| DimaM |
| |||
28/12/12 |
| |||
| ||||
| artur_k |
| ||
08/11/12 |
| ||
| |||
| Traper |
| ||
03/11/15 |
| ||
| |||
| Munin |
| |||
30/01/06 |
| |||
| ||||
| amon |
| |||
04/09/14 |
| |||
| ||||
| andrey67k |
| ||
03/11/15 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 12 ] |
Модераторы: Pphantom, Jnrty, Aer, Парджеттер, Eule_A, photon, whiterussian, profrotter, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Разложение сил
Ранее в Уроке 1 подробно обсуждался метод разложения вектора на его компоненты. На том уроке было сказано, что любой вектор, направленный под углом к привычной оси координат, можно считать состоящим из двух частей, каждая из которых направлена вдоль одной из осей, либо горизонтально, либо вертикально. Части одного вектора называются компонентами и описывают влияние этого единственного вектора в заданном направлении. Одним из примеров, который был приведен во время Урока 1, был пример, когда Фидо тянули собачьей цепью. Если цепочку тянуть вверх и вправо, то на Фидо действует сила натяжения вверх и вправо. Эта единственная сила может быть разложил на две составляющие — одну направленную вверх, а другую — вправо. Каждый компонент описывает влияние этой цепочки в заданном направлении. Вертикальная составляющая описывает восходящее влияние силы на Фидо, а горизонтальная составляющая описывает правонаправленное влияние силы на Фидо.
На том уроке было сказано, что любой вектор, направленный под углом к привычной оси координат, можно считать состоящим из двух частей, каждая из которых направлена вдоль одной из осей, либо горизонтально, либо вертикально. Части одного вектора называются компонентами и описывают влияние этого единственного вектора в заданном направлении. Одним из примеров, который был приведен во время Урока 1, был пример, когда Фидо тянули собачьей цепью. Если цепочку тянуть вверх и вправо, то на Фидо действует сила натяжения вверх и вправо. Эта единственная сила может быть разложил на две составляющие — одну направленную вверх, а другую — вправо. Каждый компонент описывает влияние этой цепочки в заданном направлении. Вертикальная составляющая описывает восходящее влияние силы на Фидо, а горизонтальная составляющая описывает правонаправленное влияние силы на Фидо.
Задача определения величины влияния отдельного вектора в заданном направлении предполагает использование тригонометрических функций. Использование этих функций для определения компонентов одного вектора также обсуждалось в Уроке 1 этого модуля. В качестве быстрого обзора давайте рассмотрим использование SOH CAH TOA для определения компонентов силы, действующей на Фидо. Предположим, что цепь действует на Фидо с силой 60 Н под углом 40 градусов к горизонтали. Быстрый набросок ситуации показывает, что для определения вертикальной составляющей силы можно использовать функцию синуса, а для определения горизонтальной составляющей силы можно использовать функцию косинуса. Решение этой проблемы показано ниже.
Использование этих функций для определения компонентов одного вектора также обсуждалось в Уроке 1 этого модуля. В качестве быстрого обзора давайте рассмотрим использование SOH CAH TOA для определения компонентов силы, действующей на Фидо. Предположим, что цепь действует на Фидо с силой 60 Н под углом 40 градусов к горизонтали. Быстрый набросок ситуации показывает, что для определения вертикальной составляющей силы можно использовать функцию синуса, а для определения горизонтальной составляющей силы можно использовать функцию косинуса. Решение этой проблемы показано ниже.
В качестве другого примера использования SOH CAH TOA для разделения одного вектора на два его компонента рассмотрим диаграмму справа. Сила 400 Н приложена под углом 60 градусов (направление 300 градусов) для перемещения железнодорожного вагона на восток по железнодорожному полотну. А вид сверху положения изображен на схеме. Сила, приложенная к автомобилю, имеет как вертикальную (на юг), так и горизонтальную составляющую (на восток). Чтобы определить величины этих двух компонентов, необходимо использовать функции синуса и косинуса. Задача становится более ясной, если начать с диаграммы ситуации с отмеченным углом и отмеченной гипотенузой. Как только треугольник построен, становится очевидным, что функция синуса должна быть использована для определения вертикальная (южная) составляющая и функция косинуса должны быть использованы для определения горизонтальной (восточной) составляющей. Треугольник и сопутствующие работы показаны ниже.
Чтобы определить величины этих двух компонентов, необходимо использовать функции синуса и косинуса. Задача становится более ясной, если начать с диаграммы ситуации с отмеченным углом и отмеченной гипотенузой. Как только треугольник построен, становится очевидным, что функция синуса должна быть использована для определения вертикальная (южная) составляющая и функция косинуса должны быть использованы для определения горизонтальной (восточной) составляющей. Треугольник и сопутствующие работы показаны ниже.
Каждый раз, когда вектор силы направлен под углом к горизонтали, можно использовать тригонометрические функции для определения компонентов этого вектора силы. Чтобы убедиться, что вы понимаете использование SOH CAH TOA для определения компонентов вектора, попробуйте решить следующие три практические задачи. Чтобы просмотреть ответы, нажмите на кнопку.
На трех приведенных выше диаграммах раскрывается важная концепция. Обратите внимание, что на каждой диаграмме сила имеет одинаковую величину; меняется только угол с горизонтом. По мере увеличения угла, который сила образует с горизонталью, составляющая силы в горизонтальном направлении (F x ) уменьшается. Принцип имеет некоторый смысл; чем больше сила направлена вверх (угол с горизонталью увеличивается), тем меньше сила способна оказывать влияние в горизонтальном направлении. Если вы хотите перетащить Fido горизонтально, то вам следует приложить усилия как можно ближе к горизонтальному направлению; вы не стали бы тянуть цепочку Фидо вертикально, если хотите тянуть его горизонтально.
Обратите внимание, что на каждой диаграмме сила имеет одинаковую величину; меняется только угол с горизонтом. По мере увеличения угла, который сила образует с горизонталью, составляющая силы в горизонтальном направлении (F x ) уменьшается. Принцип имеет некоторый смысл; чем больше сила направлена вверх (угол с горизонталью увеличивается), тем меньше сила способна оказывать влияние в горизонтальном направлении. Если вы хотите перетащить Fido горизонтально, то вам следует приложить усилия как можно ближе к горизонтальному направлению; вы не стали бы тянуть цепочку Фидо вертикально, если хотите тянуть его горизонтально.
Одним из важных применений этого принципа является парусный спорт. Парусники сталкиваются с силой сопротивления ветра из-за удара движущихся молекул воздуха о парус. Эта сила сопротивления ветра направлена перпендикулярно лицевой стороне паруса и поэтому часто направлена под углом к направлению движения парусника. Фактическое направление этой силы зависит от ориентации паруса. Чтобы определить влияние силы сопротивления ветра в направлении движения, эту силу необходимо разложить на две составляющие: одну в направлении движения парусника и другую в направлении, перпендикулярном движению парусника. См. схему справа. На диаграмме ниже показаны три различных направления паруса. Если предположить, что сила сопротивления ветра в каждом случае одинакова, то в каком случае будет оказываться наибольшее влияние на направление движения парусника? То есть в каком случае наибольшая составляющая силы направлена параллельно курсу лодок?
Фактическое направление этой силы зависит от ориентации паруса. Чтобы определить влияние силы сопротивления ветра в направлении движения, эту силу необходимо разложить на две составляющие: одну в направлении движения парусника и другую в направлении, перпендикулярном движению парусника. См. схему справа. На диаграмме ниже показаны три различных направления паруса. Если предположить, что сила сопротивления ветра в каждом случае одинакова, то в каком случае будет оказываться наибольшее влияние на направление движения парусника? То есть в каком случае наибольшая составляющая силы направлена параллельно курсу лодок?
Многие считают, что парусник не может двигаться против ветра. По их мнению, если ветер дует с севера на юг, парусная лодка не сможет двигаться с юга на север. Это просто неправда. Парусники могут двигаться «против ветра» и обычно делают это с помощью метода, известного как , лавируя по ветру . Верно сказать, что парусная лодка никогда не сможет плыть против ветра, направив свою лодку прямо против ветра. Как видно на диаграмме справа, если лодка движется прямо против ветра, то сила ветра направлена против ее курса. В таком случае составляющая силы в направлении движения парусника отсутствует. То есть нет никакой «движущей силы». С другой стороны, если лодка идет под углом к ветру, то силу ветра можно разложить на две составляющие. В двух ориентациях парусника, показанных ниже, составляющая силы в направлении, параллельном курсу парусника, будет толкать лодку под углом к ветру. Лавируя против ветра, парусник обычно движется под углом 45 градусов, лавируя вперед и назад по ветру.
Как видно на диаграмме справа, если лодка движется прямо против ветра, то сила ветра направлена против ее курса. В таком случае составляющая силы в направлении движения парусника отсутствует. То есть нет никакой «движущей силы». С другой стороны, если лодка идет под углом к ветру, то силу ветра можно разложить на две составляющие. В двух ориентациях парусника, показанных ниже, составляющая силы в направлении, параллельном курсу парусника, будет толкать лодку под углом к ветру. Лавируя против ветра, парусник обычно движется под углом 45 градусов, лавируя вперед и назад по ветру.
Следующие задачи сосредоточены на понятиях, обсуждаемых в этом уроке. Ответьте на каждый вопрос, а затем нажмите кнопку, чтобы просмотреть ответ.
1. На рисунке справа изображена сила, образующая угол с горизонтом. Эта сила будет иметь горизонтальную и вертикальную составляющие.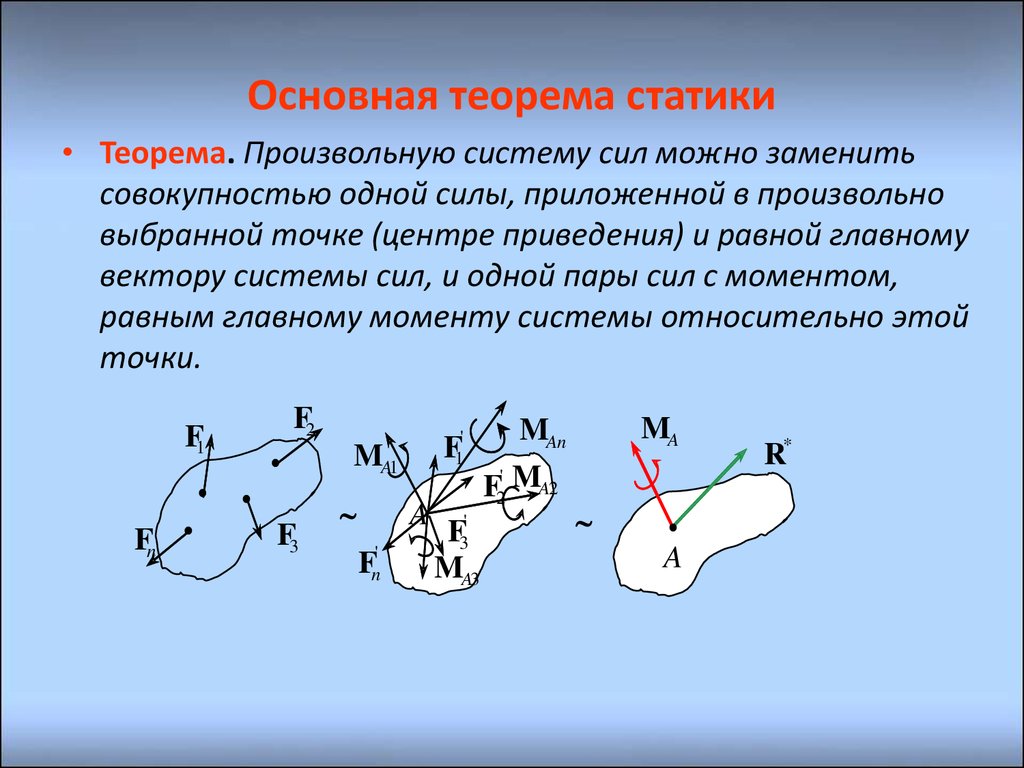 Какой из приведенных ниже вариантов лучше всего описывает направление горизонтальной и вертикальной составляющих этой силы?
Какой из приведенных ниже вариантов лучше всего описывает направление горизонтальной и вертикальной составляющих этой силы?
2. Ниже показаны три парусника. Каждая парусная лодка испытывает одинаковое количество силы, но имеет разную ориентацию паруса.
В каком случае (A, B или C) парусник, скорее всего, опрокинется на бок? Объяснять.
3. Обратите внимание на эвакуатор справа. Если сила натяжения троса равна 1000 Н и если трос образует с горизонтом угол 60 градусов, то какова вертикальная составляющая силы, которая отрывает автомобиль от земли?
Следующий раздел:
Решение задач с векторами
Горячая математика Мы можем использовать векторы для решения многих задач, связанных с физическими величинами, такими как скорость, скорость, вес, работа и так далее.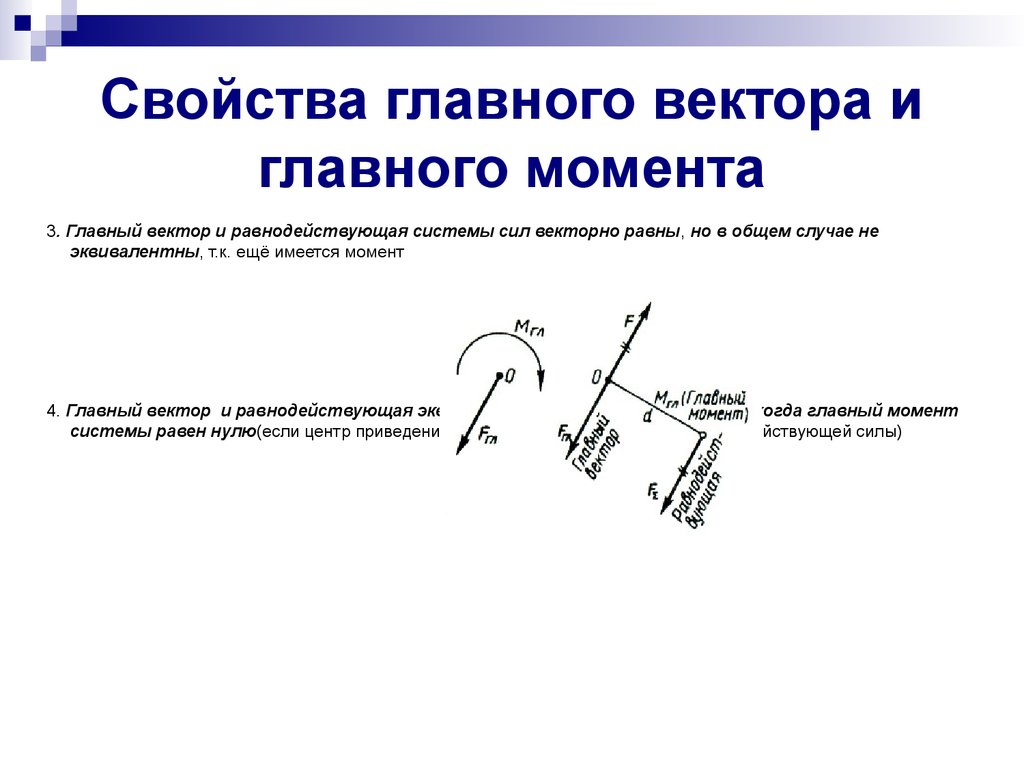
Скорость:
Скорость движущегося объекта моделируется вектором, направление которого является направлением движения, а величина — скоростью.
Пример :
Мяч брошен с начальной скоростью 70 футов в секунду, под углом 35 ° с горизонталью. Найдите вертикальную и горизонтальную составляющие скорости.
Позволять в представить скорость и использовать данную информацию, чтобы написать в в форме единичного вектора:
в знак равно 70 ( потому что ( 35 ° ) ) я + 70 ( грех ( 35 ° ) ) Дж
Упрощая скаляры, мы получаем:
в
≈
57,34
я
+
40. 15
Дж
15
Дж
Поскольку скаляры являются горизонтальной и вертикальной компонентами в ,
Следовательно, горизонтальная составляющая 57,34 футов в секунду, а вертикальная составляющая 40.15 футов в секунду.
Сила:
Сила также представлена вектором. Если на объект действуют несколько сил, результирующая сила, испытываемая объектом, представляет собой векторную сумму этих сил.
Пример :
Две силы Ф 1 а также Ф 2 с величинами 20 а также 30 фунт соответственно действуют на объект в точке п как показано. Найдите результирующие силы, действующие на п .
Сначала мы пишем Ф 1 а также Ф 2 в виде компонентов:
в
≈
57,34
я
+
40. 15
Дж
15
Дж
Упрощая скаляры, мы получаем:
Ф 1 знак равно ( 20 потому что ( 45 ° ) ) я + ( 20 грех ( 45 ° ) ) Дж знак равно 20 ( 2 2 ) я + 20 ( 2 2 ) Дж знак равно 10 2 я + 10 2 Дж Ф 2 знак равно ( 30 потому что ( 150 ° ) ) я + ( 30 грех ( 150 ° ) ) Дж знак равно 30 ( − 3 2 ) я + 30 ( 1 2 ) Дж знак равно − 15 3 я + 15 Дж
Итак, результирующая сила Ф является
Ф знак равно Ф 1 + Ф 2 знак равно ( 10 2 я + 10 2 Дж ) + ( − 15 3 я + 15 Дж ) знак равно ( 10 2 − 15 3 ) я + ( 10 2 + 15 ) Дж ≈ − 12 я + 29Дж
Работа:
Работа
Вт
сделано силой
Ф
при движении по вектору
Д
является
Вт
знак равно
Ф
⋅
Д
.
Пример :
Сила задается вектором Ф знак равно 〈 2 , 3 〉 и перемещает объект из точки ( 1 , 3 ) к точке ( 5 , 9) . Найдите проделанную работу.
Сначала мы находим Displacement.
Вектор смещения
Д знак равно 〈 5 − 1 , 9 − 3 〉 знак равно 〈 4 , 6 〉 .
По формуле совершенная работа равна
Вт знак равно Ф ⋅ Д знак равно 〈 2 , 3 〉 ⋅ 〈 4 , 6 〉 знак равно 26
Если единицей силы являются фунты, а расстояние измеряется в футах, то совершенная работа равна 26 фут-фунт
Как рассчитать величину силы в физике
Обновлено 8 декабря 2020 г.
Автор Lee Johnson
Вычисление величины силы — важная часть физики. Когда вы работаете в одном измерении, вам не нужно учитывать величину силы. Вычисление величины является более сложной задачей в двух или более измерениях, потому что сила будет иметь «компоненты» как по осям x-, так и по оси y и, возможно, по оси z, если это трехмерная сила. Научиться делать это с одной силой и с результирующей силой двух или более отдельных сил — важный навык для любого подающего надежды физика или любого, кто работает над задачами классической физики в школе.
TL;DR (слишком длинный; не читал)
Найдите равнодействующую силу двух векторов, сначала добавив компоненты x и y , чтобы найти результирующий вектор, а затем использовать та же формула для его величины.
Основы: что такое вектор?
Первый шаг к пониманию того, что означает вычисление величины силы в физике, — это узнать, что такое вектор. «Скаляр» — это простая величина, которая просто имеет значение, например, температура или скорость. Когда вы читаете температуру 50 градусов по Фаренгейту, это говорит вам все, что вам нужно знать о температуре объекта. Если вы прочитали, что что-то движется со скоростью 10 миль в час, эта скорость говорит вам все, что вам нужно знать о том, как быстро это движется.
«Скаляр» — это простая величина, которая просто имеет значение, например, температура или скорость. Когда вы читаете температуру 50 градусов по Фаренгейту, это говорит вам все, что вам нужно знать о температуре объекта. Если вы прочитали, что что-то движется со скоростью 10 миль в час, эта скорость говорит вам все, что вам нужно знать о том, как быстро это движется.
Вектор отличается тем, что у него есть не только величина, но и направление. Если вы посмотрите отчет о погоде, вы узнаете, насколько быстро дует ветер и в каком направлении. Это вектор, потому что он дает вам дополнительный бит информации. Скорость — это векторный эквивалент скорости, где вы узнаете направление движения, а также скорость его движения. Итак, если что-то движется со скоростью 10 миль в час на северо-восток, скорость (10 миль в час) — это величина, северо-восток — это направление, и обе части вместе составляют вектор скорости.
Во многих случаях векторы разбиваются на «компоненты». Скорость может быть задана как комбинация скорости в северном направлении и скорости в восточном направлении, так что результирующее движение будет на северо-восток, но вам нужны оба бита информации, чтобы определить, как быстро он движется и куда он движется. В задачах по физике восток и север обычно заменяют координатами x и y соответственно.
В задачах по физике восток и север обычно заменяют координатами x и y соответственно.
Величина одиночного вектора силы
Чтобы рассчитать величину векторов силы, вы используете компоненты вместе с теоремой Пифагора. Представьте координату силы x как основание треугольника, компонент y как высоту треугольника, а гипотенузу как результирующую силу обоих компонентов. Удлиняя связь, угол, который образует гипотенуза с основанием, является направлением силы.
Если сила толкает 4 ньютона (Н) в направлении x и 3 Н в направлении y, теорема Пифагора и объяснение треугольника показывают, что вам нужно делать при вычислении величины. Использование 92}
Направление вектора одиночной силы
Направление силы не является предметом этого вопроса, но его легко вычислить на основе треугольника компонентов и результирующей силы из последнего раздела. Вы можете определить направление с помощью тригонометрии. Для большинства задач лучше всего подходит тождество:
Вы можете определить направление с помощью тригонометрии. Для большинства задач лучше всего подходит тождество:
\tan{\theta}=\frac{y}{x}
9{-1}(3/4)=36,9\text{ градусов}
Таким образом, вектор составляет угол примерно 37 градусов с осью x.
Результирующая сила и величина двух или более векторов
Если у вас есть две или более сил, вычислите величину результирующей силы, сначала найдя результирующий вектор, а затем применив тот же подход, что и выше. Единственный дополнительный навык, который вам понадобится, — это найти результирующий вектор, и это довольно просто. Хитрость в том, что вы добавляете соответствующие x и и компоненты вместе. Использование примера должно прояснить это.
Представьте парусник на воде, движущийся вместе с силой ветра и течением воды. Вода придает силу 4 Н в направлении х и 1 Н в направлении у, а ветер добавляет силу 5 Н в направлении х и 3 Н в направлении у.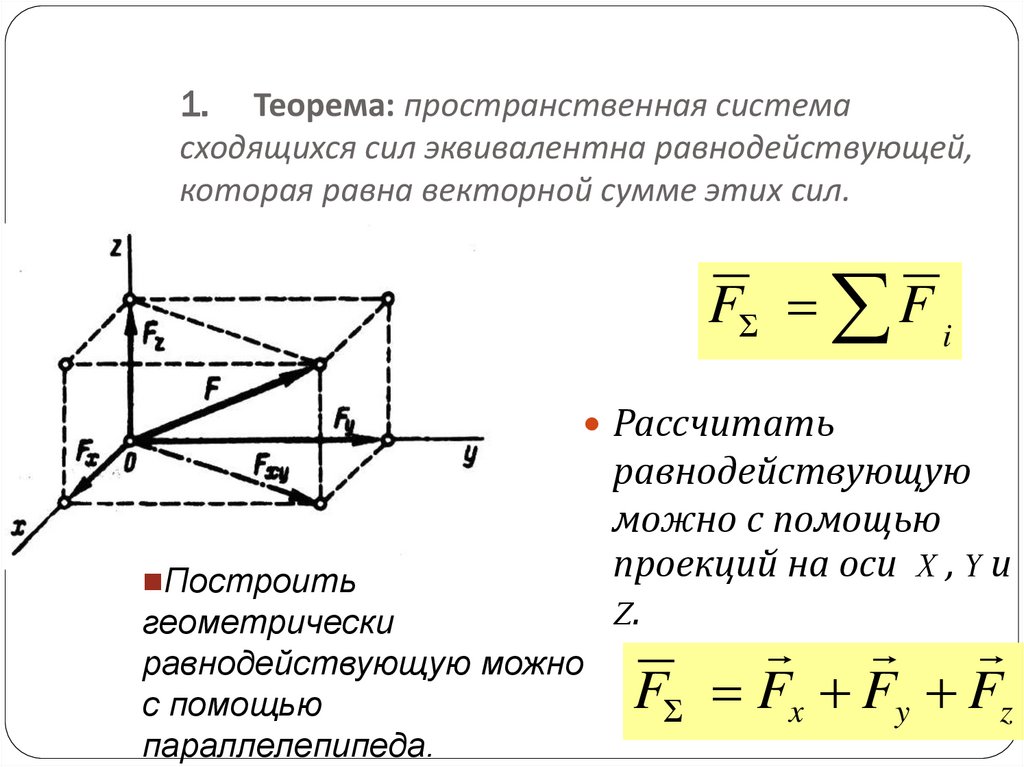


 Главный вектор системы сил
Главный вектор системы сил 11.2015, 17:18
11.2015, 17:18 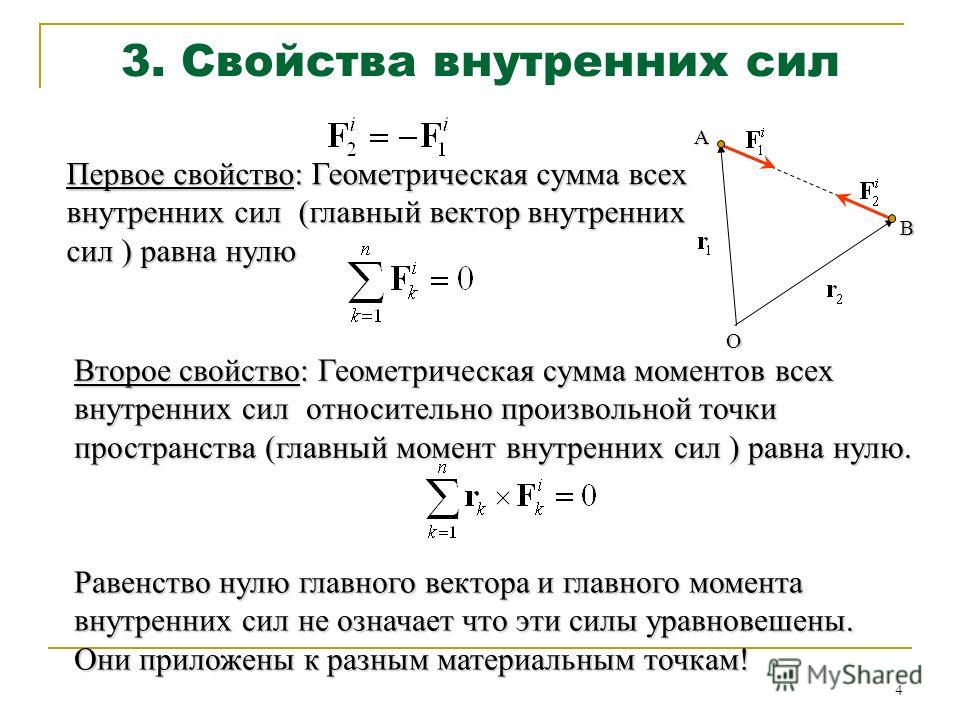 Главный вектор системы сил
Главный вектор системы сил Главный вектор системы сил
Главный вектор системы сил Главный вектор системы сил
Главный вектор системы сил Главный вектор системы сил
Главный вектор системы сил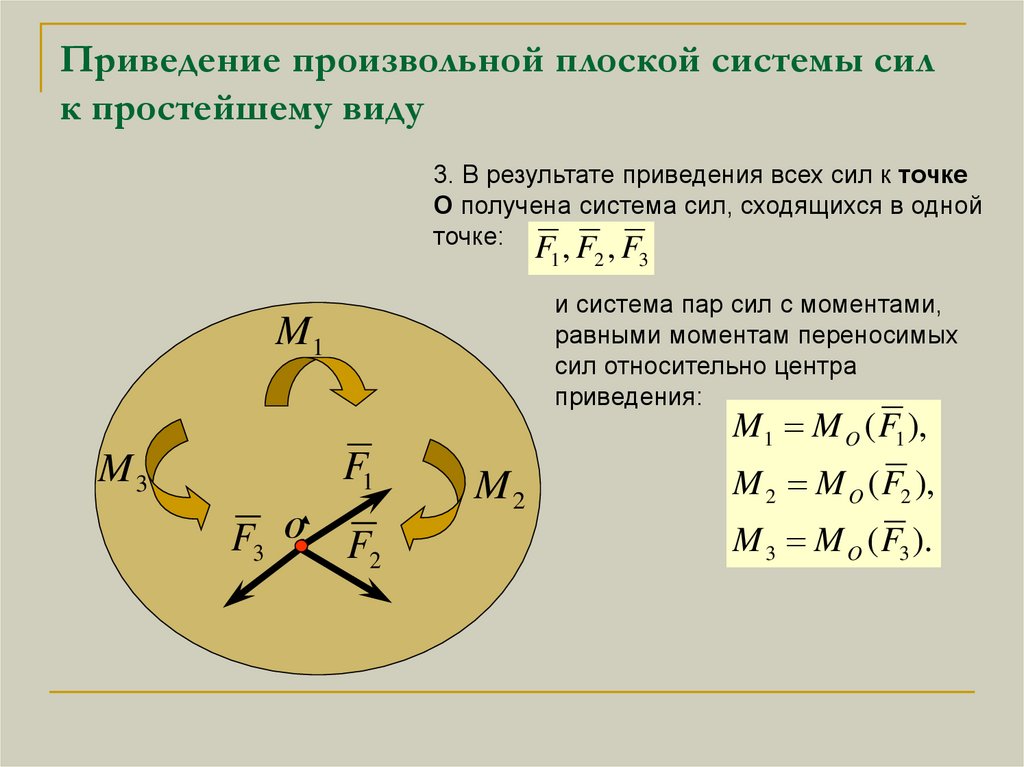 Главный вектор системы сил
Главный вектор системы сил Главный вектор системы сил
Главный вектор системы сил
 Эти онлайн задачники, как бы сказать помягче, и верные ответы могут запороть, и к культуре правильных решений не приучают.
Эти онлайн задачники, как бы сказать помягче, и верные ответы могут запороть, и к культуре правильных решений не приучают. Иоффе СПб
Иоффе СПб . соотношение сторон в прямоугольном треугольнике в школе плохо дают..(((
. соотношение сторон в прямоугольном треугольнике в школе плохо дают..(((