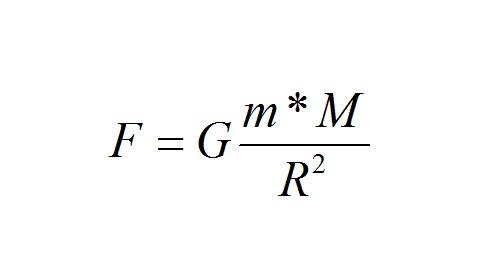Гравитационная сила рисунок. Гравитационные силы: определение, формула, виды
Дон Деянг
Сила тяжести (или гравитация) прочно держит нас на земле и позволяет земле вращаться вокруг солнца. Благодаря этой невидимой силе дождь падает на землю, а уровень воды в океане каждый день то повышается, то снижается. Гравитация удерживает землю в сферической форме, а также не дает нашей атмосфере улетучиться в космическое пространство. Казалось бы, эта наблюдаемая каждый день сила притяжения должна быть хорошо изучена учеными. Но, нет! Во многом гравитация остается глубочайшей тайной для науки. Эта таинственная сила является замечательным примером того, насколько ограничены современные научные знания.
Что такое гравитация?
Исаак Ньютон интересовался этим вопросом еще в 1686 году и пришел к выводу, что гравитация — это сила притяжения, существующая между всеми предметами. Он понял, что та же самая сила, которая заставляет яблоко падать на землю, на своей орбите. На самом деле сила притяжения Земли служит причиной того, что во время вращения вокруг Земли Луна отклоняется каждую секунду от своего прямого пути примерно на один миллиметр (Рисунок 1). Универсальный Закон Гравитации Ньютона является одним из наибольших научных открытий всех времен.
Универсальный Закон Гравитации Ньютона является одним из наибольших научных открытий всех времен.
Гравитация – «веревка», которая удерживает объекты на орбите
Рисунок 1. Иллюстрация орбиты луны, сделанная не в соответствии с масштабом. За каждую секунду луна проходит примерно 1 км. За это расстояние она отклоняется от прямого пути примерно на 1 мм – это происходит вследствие гравитационной тяги Земли (пунктирная линия). Луна постоянно как бы падает за (или вокруг) землей, как падают и планеты вокруг солнца.
Сила тяжести – одна из четырех фундаментальных сил природы (Таблица 1). Обратите внимание на то, что из четырех сил эта сила самая слабая, и все же она является доминирующей относительно крупных космических объектов. Как показал Ньютон, притягательная гравитационная сила между двумя любыми массами становится все меньше и меньше по мере того, как расстояние между ними становится все больше и больше, но она никогда полностью не достигает нуля (смотрите «Замысел гравитации»).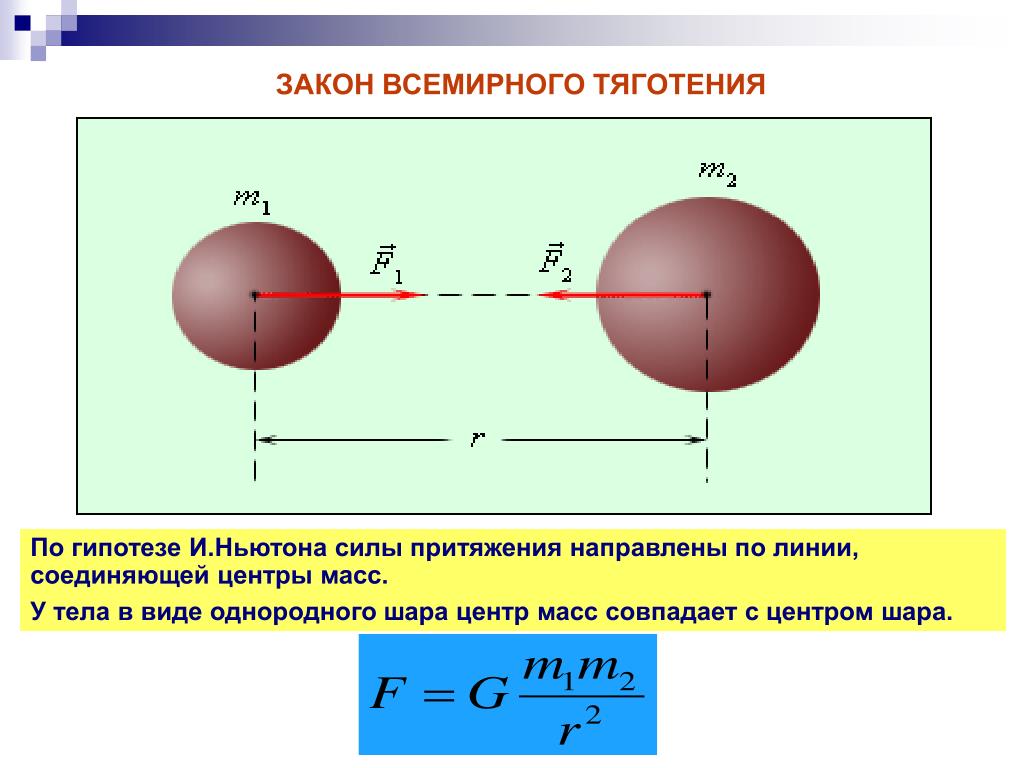
Поэтому каждая частица во всей вселенной фактически притягивает любую другую частицу. В отличие от сил слабого и сильного ядерного взаимодействия, сила притяжения является дальнодействующей (Таблица 1). Магнитная сила и сила электрического взаимодействия также являются дальнодействующими силами, но гравитация уникальна тем, что она и дальнодействующая и всегда притягательная, а значит, она никогда не может иссякнуть (в отличие от электромагнетизма, в котором силы могут либо притягивать, либо отталкивать).
Начиная с великого ученого-креациониста Майкла Фарадея в 1849 году, физики постоянно искали скрытую связь между силой притяжения и силой электромагнитного взаимодействия. В настоящее время ученые пытаются соединить все четыре фундаментальные силы в одно уравнение или так называемую «Теорию всего», но, безуспешно! Гравитация остается самой загадочной и наименее изученной силой.
Гравитацию невозможно каким-либо образом оградить. Каким бы ни был состав преграждающей перегородки, она не имеют никакого влияния на притяжение между двумя разделенными объектами.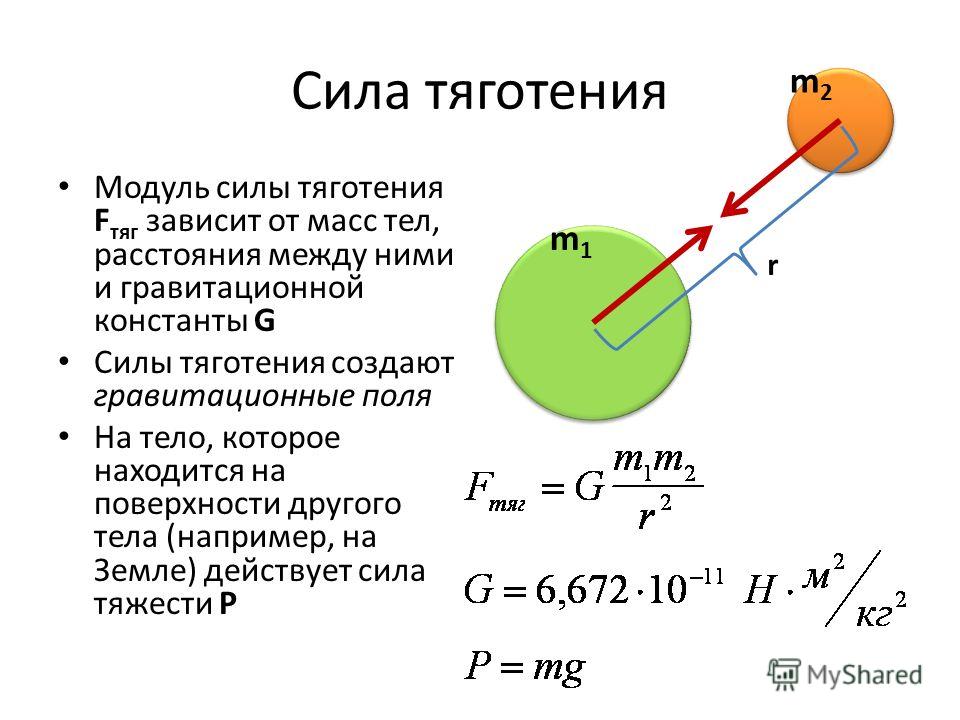 Это означает, что в лабораторных условиях невозможно создать антигравитационную камеру. Сила тяжести не зависит от химического состава объектов, но зависит от их массы, известной нам как вес (сила тяжести на объект равна весу этого объекта — чем больше масса, тем больше сила или вес.) Блоки, состоящие из стекла, свинца, льда или даже стирофома, и имеющие одинаковую массу, будут испытывать (и оказывать) одинаковую гравитационную силу. Эти данные были получены в ходе экспериментов, и ученые до сих пор не знают, как их можно теоретически объяснить.
Это означает, что в лабораторных условиях невозможно создать антигравитационную камеру. Сила тяжести не зависит от химического состава объектов, но зависит от их массы, известной нам как вес (сила тяжести на объект равна весу этого объекта — чем больше масса, тем больше сила или вес.) Блоки, состоящие из стекла, свинца, льда или даже стирофома, и имеющие одинаковую массу, будут испытывать (и оказывать) одинаковую гравитационную силу. Эти данные были получены в ходе экспериментов, и ученые до сих пор не знают, как их можно теоретически объяснить.
Замысел в гравитации
Сила F между двумя массами m 1 и m 2 , находящимися на расстоянии r, может быть записана в виде формулы F = (G m 1 m 2)/r 2
Где G — это гравитационная постоянная, впервые измеренная Генри Кавендишем в 1798 году.1
Это уравнение показывает, что гравитация снижается по мере того, как расстояние, r, между двумя объектами становится больше, но полностью никогда не достигает нуля.
Подчиняющаяся закону обратных квадратов природа этого уравнения просто захватывает.
Ссылки и примечания
- Говоря техническим языком, G = 6.672 x 10 –11 Nm 2 kg –2
- Томпсен, Д., «Очень точно о гравитации», Science News 118(1):13, 1980.
Так что же такое в действительности гравитация? Каким образом эта сила способна действовать в таком огромном, пустом космическом пространстве? И зачем она вообще существует? Науке никогда не удавалось ответить на эти основные вопросы о законах природы. Сила притяжения не может появиться медленно путем мутаций или естественного отбора. Она действует с самого начала существования вселенной. Как и всякий другой физический закон, гравитация, несомненно, является замечательным свидетельством запланированного сотворения.
Сила притяжения не может появиться медленно путем мутаций или естественного отбора. Она действует с самого начала существования вселенной. Как и всякий другой физический закон, гравитация, несомненно, является замечательным свидетельством запланированного сотворения.
Одни ученые пытались объяснить гравитацию с помощью невидимых частиц, гравитонов, которые движутся между объектами. Другие говорили о космических струнах и гравитационных волнах. Недавно ученым с помощью специально созданной лаборатории LIGO (англ. Laser Interferometer Gravitational-Wave Observatory) удалось только увидеть эффект гравитационных волн. Но природу этих волн, каким образом физически объекты взаимодействуют друг с другом на огромных расстояниях, изменяя их фору, все же остается для всех большим вопросом. Мы просто не знаем природу возникновения силы гравитации и каким образом она удерживает стабильность всей вселенной.
Сила притяжения и Писание
Два места из Библии могут помочь нам понять природу гравитации и физическую науку в целом.
Второе место Писания, Евреям 1:3, заявляет, что Христос «держит все словом силы Своей». Слово держит (φερω pherō ) снова описывает поддерживание или сохранение всего, включая гравитацию. Слово
Слово держит (φερω pherō ) снова описывает поддерживание или сохранение всего, включая гравитацию. Слово
Искажения времени и пространства и черные дыры
Общая теория относительности Эйнштейна рассматривает гравитацию не как силу, а как искривление самого пространства вблизи массивного объекта. Согласно предсказаниям, свет, который традиционно следует по прямым линиям, искривляется при прохождении по искривленному пространству. Впервые это было продемонстрировано, когда астроном сэр Артур Эддингтон обнаружил изменение кажущегося положения звезды во время полного затмения в 1919 году, считая, что лучи света изгибаются под действием силы тяжести солнца.
Общая теория относительности также предсказывает, что если тело достаточно плотное, его сила тяжести исказит пространство настолько сильно, что свет вообще не сможет через него проходить. Такое тело поглощает свет и все остальное, что захватила его сильная гравитация, и носит название Черная дыра. Такое тело можно обнаружить только по его гравитационным эффектам на другие объекты, по сильному искривлению света вокруг него и по сильной радиации, излучаемой веществом, которое на него падает.
Все вещество внутри черной дыры сжато в центре, который имеет бесконечную плотность. «Размер» дыры определяется горизонтом событий, т.е. границей, которая окружает центр черной дыры, и ничто (даже свет) не может выйти за ее пределы. Радиус дыры называется радиусом Шварцшильда, в честь немецкого астронома Карла Шварцшильда (1873–1916), и вычисляется по формуле R S = 2GM/c 2 , где c – это скорость света в вакууме. Если бы солнце попало в черную дыру, его радиус Шварцшильда составлял бы всего 3 км.
Существует надежное доказательство, что после того, как ядерное топливо массивной звезды иссякает, она больше не может противостоять коллапсу под своим собственным огромным весом и попадает в черную дыру. Считается, что черные дыры с массой в миллиарды солнц существуют в центрах галактик, включая нашу галактику, Млечный Путь. Многие ученые полагают, что суперяркие и очень отдаленные объекты под названием квазары, используют энергию, которая выделяется, когда вещество падает в черную дыру.
Согласно предсказаниям общей теории относительности, сила тяжести также искажает и время. Это также было подтверждено очень точными атомными часами, которые на уровне моря идут на несколько микросекунд медленнее, чем на территориях выше уровня моря, где сила тяжести Земли немного слабее. Вблизи горизонта событий это явление более заметно. Если наблюдать за часами астронавта, который приближается к горизонту событий, мы увидим, что часы идут медленнее. Находясь в горизонте событий, часы остановятся, но мы никогда не сможем этого увидеть.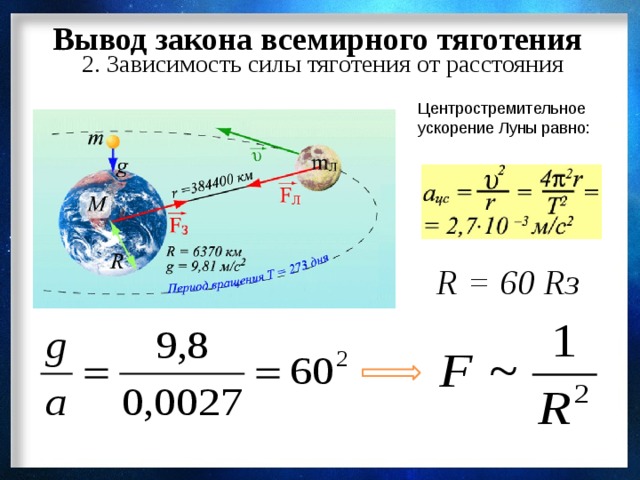 И наоборот, астронавт не заметит, что его часы идут медленнее, но он увидит, что наши часы идут быстрее и быстрее.
И наоборот, астронавт не заметит, что его часы идут медленнее, но он увидит, что наши часы идут быстрее и быстрее.
Основной опасностью для астронавта возле черной дыры были бы приливные силы, вызванные тем, что сила тяжести сильнее на тех частях тела, которые находятся ближе к черной дыре, чем на частях дальше от нее. По своей мощи приливные силы возле черной дыры, имеющей массу звезды, сильнее любого урагана и запросто разрывают на мелкие кусочки все, что им попадается. Однако, тогда как гравитационное притяжение уменьшается с квадратом расстояния (1/r 2), приливно-отливное явление уменьшается с кубом расстояния (1/r 3). Поэтому в отличие от принятого мнения, гравитационная сила (включая приливную силу) на горизонтах событий больших черных дыр слабее, чем на маленьких черных дырах. Так что приливные силы на горизонте событий черной дыры в наблюдаемом космосе, были бы менее заметны, чем самый мягкий ветерок.
Растяжение времени под действием силы тяжести вблизи горизонта событий является основой новой космологической модели физика-креациониста, доктора Рассела Хамфриса, о которой он рассказывает в своей книге «Свет звезд и время».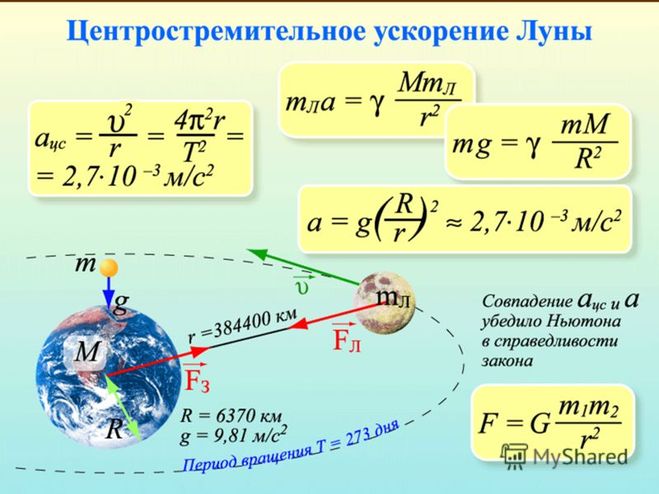 Эта модель, возможно, помогает решить проблему того, как мы можем видеть свет отдаленных звезд в молодой вселенной. К тому же на сегодня она является научной альтернативой небиблейской , которая основывается на философских предположениях, выходящих за рамки науки.
Эта модель, возможно, помогает решить проблему того, как мы можем видеть свет отдаленных звезд в молодой вселенной. К тому же на сегодня она является научной альтернативой небиблейской , которая основывается на философских предположениях, выходящих за рамки науки.
Примечание
Гравитация, «таинственная сила», которая и через четыреста лет исследований остается плохо изученной…
Исаак Ньютон (1642–1727)
Фотография: Wikipedia.org
Исаак Ньютон (1642–1727)
Исаак Ньютон опубликовал свои открытия о гравитации и движении небесных тел в 1687 году, в своей известной работе «
«Наша наиболее прекрасная солнечная система, планеты и кометы могут быть результатом только плана и господства разумного и сильного существа».
Исаак Ньютон был не только ученым. Помимо науки он почти всю свою жизнь посвятил исследованию Библии. Его любимыми библейскими книгами были: книга Даниила и книга Откровение, в которых описываются Божьи планы на будущее. На самом деле Ньютон написал больше теологических работ, чем научных.
Ньютон уважительно относился к другим ученым, таким как Галилео Галилей. Кстати Ньютон родился в то же год, когда умер Галилей, в 1642 году. Ньютон писал в своем письме: «Если я и видел дальше других, то потому, что стоял на плечах гигантов». Незадолго до смерти, наверное, размышляя о тайне силы тяжести, Ньютон скромно писал: «Не знаю, как меня воспринимает мир, но сам себе я кажусь только мальчиком, играющим на морском берегу, который развлекается тем, что время от времени отыскивает камешек более пестрый, чем другие, или красивую ракушку, в то время как передо мной расстилается огромный океан неисследованной истины».
Ньютон похоронен в Вестминстерском аббатстве. Латинская надпись на его могиле заканчивается словами: «Пусть смертные радуются, что среди них жило такое украшение человеческого рода»
.
Все мы проходили закон всемирного тяготения в школе. Но что мы на самом деле знаем о гравитации, помимо информации, вложенной в наши головы школьными учителями? Давайте обновим наши познания…
Факт первый: Ньютон не открывал закона всемирного тяготения
Всем известна знаменитая притча о яблоке, которое упало на голову Ньютону. Но дело в том, что Ньютон не открывал закона всемирного тяготения, так как этот закон просто напросто отсутствует в его книге «Математические начала натуральной философии». В этом труде нет ни формулы, ни формулировки, в чём каждый желающий может убедиться сам. Более того, первое упоминание о гравитационной постоянной появляется только в 19-м веке и соответственно, формула, не могла появиться раньше. К слову сказать, коэффициент G, уменьшающий результат вычислений в 600 миллиардов раз не имеет никакого физического смысла, и введён для сокрытия противоречий.
Факт второй: фальсификая эксперимента гравитационного притяжения
Считается, что Кавендиш первый продемонстрировал гравитационное притяжение у лабораторных болваночек, использовав крутильные весы — горизонтальное коромысло с грузиками на концах, подвешенных на тонкой струне. Коромысло могло поворачиваться на тонкой проволоке. Согласно официальной версии, Кавендиш приблизил к грузикам коромысла пару болванок по 158 кг с противоположных сторон и коромысло повернулось на небольшой угол. Однако методика опыта была некорректной и результаты были сфальсифицированы, что убедительно доказано физиком Андреем Альбертовичем Гришаевым. Кавендиш долго переделывал и настраивал установку, чтобы результаты подходили под высказанную Ньютоном среднюю плотность земли
. Методика самого опыта предусматривала движение болванок несколько раз, а причиной поворота коромысла служили микровибрации от движения болванок, которые передавались на подвес.
Коромысло могло поворачиваться на тонкой проволоке. Согласно официальной версии, Кавендиш приблизил к грузикам коромысла пару болванок по 158 кг с противоположных сторон и коромысло повернулось на небольшой угол. Однако методика опыта была некорректной и результаты были сфальсифицированы, что убедительно доказано физиком Андреем Альбертовичем Гришаевым. Кавендиш долго переделывал и настраивал установку, чтобы результаты подходили под высказанную Ньютоном среднюю плотность земли
. Методика самого опыта предусматривала движение болванок несколько раз, а причиной поворота коромысла служили микровибрации от движения болванок, которые передавались на подвес.
Это подтверждается тем, что такая простейшая установка 18 века в учебных целях должна была бы стоять если не в каждой школе, то хотя бы на физических факультетах ВУЗОВ, чтобы на практике показывать студентам результат действия закона Всемирного тяготения. Однако установка Кавендиша не используется в учебных программах, и школьники, и студенты верят на слово, что две болванки притягивают друг друга.
Факт третий: Закон всемирного тяготения не работает во время солнечного затмения
Если подставить в формулу закона всемирного тяготения справочные данные по земле, луне и солнцу, то в момент, когда Луна пролетает между Землёй и Солнцем, например, в момент солнечного затмения, сила притяжения между Солнцем и Луной более чем в 2 раза выше, чем между Землёй и Луной!
Согласно формуле Луна должна была бы уйти с орбиты земли и начать вращаться вокруг солнца.
Гравитационная постоянная — 6,6725×10−11 м³/(кг·с²).
Масса Луны — 7,3477×1022 кг.
Масса Солнца — 1,9891×1030 кг.
Масса Земли — 5,9737×1024 кг.
Расстояние между Землёй и Луной = 380 000 000 м.
Расстояние между Луной и Солнцем = 149 000 000 000 м.
Земля и Луна:
6,6725×10-11 х 7,3477×1022 х 5,9737×1024 / 3800000002 = 2,028×1020 H
Луна и Солнце:
6,6725×10-11 х 7,3477·1022 х 1,9891·1030 / 1490000000002 = 4,39×1020 H
2,028×1020 H Сила притяжения между Землёй и Луной
Эти вычисления можно критиковать тем, что луна — искусственное полое тело и справочная плотность этого небесного тела скорее всего определена не правильно.
Действительно, экспериментальные свидетельства говорят о том, что Луна представляет из себя не сплошное тело, а тонкостенную оболочку. Авторитетный журнал Сайенс описывает результаты работы сейсмодатчиков после удара о поверхность Луны третьей ступени ракеты, разгонявшей корабль «Аполлон-13»: «сейсмозвон детектировался в течение более четырёх часов. На Земле, при ударе ракеты на эквивалентном удалении, сигнал длился бы всего несколько минут».
Сейсмические колебания, которые затухают так медленно, типичны для полого резонатора, а не для сплошного тела.
Но Луна помимо прочего не проявляет своих притягивающих свойств по отношению к Земле — пара Земля-Луна движется не вокруг общего центра масс, как это было бы по закону всемирного тяготения, и эллипсоидная орбита Земли вопреки этому закону не становится зигзагообразной.
Более того, параметры орбиты самой Луны не остаются постоянными, орбита по научной терминологии «эволюционирует», причём делает это вопреки закону всемирного тяготения.
Факт четвёртый: абсурдность теории приливов и отливов
Как же так, возразят некоторые, ведь даже школьники знают про океанские приливы на Земле, которые происходят из-за притяжения воды к Солнцу и Луне.
По теории тяготение Луны формирует приливной эллипсоид в океане, с двумя приливными горбами, которые из-за суточного вращения перемещаются по поверхности Земли.
Однако практика показывает абсурдность этих теорий. Ведь согласно ним приливный горб высотой 1 метр за 6 часов должен через пролив Дрейка переместиться из Тихого океана в Атлантический. Поскольку вода несжимаема, то масса воды подняла бы уровень на высоту около 10 метров, чего не происходит на практике. На практике приливные явления происходят автономно в областях 1000-2000 км.
Ещё Лапласа изумлял парадокс: почему в морских портах Франции полная вода наступает последовательно, хотя по концепции приливного эллипсоида она должна наступать там одновременно.
Факт пятый: теория тяготения масс не работает
Принцип измерений гравитации прост — гравиметры измеряют вертикальные компоненты, а отклонение отвеса показывает горизонтальные компоненты.
Первая попытка проверки теории тяготения масс была предпринята англичанами в середине 18 века на берегу Индийского океана, где, с одной стороны находится высочайшая в мире каменная гряда Гималаев, а с другой — чаша океана, заполненная куда менее массивной водой. Но, увы, отвес в сторону Гималаев не отклоняется! Более того, сверхчувствительные приборы — гравиметры — не обнаруживают разницы в тяжести пробного тела на одинаковой высоте как над массивными горами, так и над менее плотными морями километровой глубины.
Чтобы спасти прижившуюся теорию, учёные придумали для неё подпорку: мол причиной тому «изостазия» — под морями располагаются более плотные породы, а под горами — рыхлые, причём плотность их точь-в-точь такая, чтоб подогнать всё под нужное значение.
Также опытным путём было установлено, что гравиметры в глубоких шахтах показывают, сила тяжести, не уменьшающуюся с глубиной. Она продолжает расти, будучи зависимой только от квадрата расстояния до центра земли.
Факт шестой: тяготение порождается не веществом и не массой
Согласно формуле закона всемирного тяготения, Два массы, м1 и м2, размерами которых можно пренебречь по сравнению с расстояниями между ними, якобы притягиваются друг к другу силой, прямо пропорциональной произведению этим масс и обратно пропорционально квадрату расстояния между ними. Однако, фактически, неизвестно ни одного доказательства того, что вещество обладает гравитационным притягивающим действием. Практика показывает, что тяготение порождается не веществом и не массами, оно независимо от них и массивные тела лишь подчиняются тяготению.
Независимость тяготения от вещества подтверждается тем, что за редчайшим исключением, у малых тел солнечной системы гравитационная притягивающая способность отсутствует полностью
. За исключением Луны у более чем шести десятков спутников планет признаков собственного тяготения не наблюдается. Это доказано как косвенными, так и прямыми измерениями, например, с 2004 года зонд Кассени в окрестностях Сатурна время от времени пролетает рядом с его спутниками, однако изменений скорости зонда не зафиксировано. С помощью того же Кассени был обнаружен гейзер на Энцеладе — шестом по размеру спутник Сатурна.
За исключением Луны у более чем шести десятков спутников планет признаков собственного тяготения не наблюдается. Это доказано как косвенными, так и прямыми измерениями, например, с 2004 года зонд Кассени в окрестностях Сатурна время от времени пролетает рядом с его спутниками, однако изменений скорости зонда не зафиксировано. С помощью того же Кассени был обнаружен гейзер на Энцеладе — шестом по размеру спутник Сатурна.
Какие физические процессы должны происходить на космическом куске льда, чтобы струи пара улетали в космос?
По той же причине у Титана, крупнейшего спутника Сатурна, наблюдается газовых хвост как следствие стока атмосферы.
Не найдено предсказанных теорией спутников у астероидов, несмотря на их огромное количество. А во всех сообщениях о двойных, или парных астероидах, которые якобы вращаются вокруг общего центра масс, свидетельств об обращении этих пар не было. Компаньоны случайно оказывались рядом, двигаясь по квазисинхронным орбитам вокруг солнца.
Предпринятые попытки вывести на орбиту астероидов искусственные спутники окончились крахом. В качестве примеров можно привести зонд NEAR, который подгоняли к астероиду Эрос американцы, или зонд ХАЯБУСА, который японцы отправили к астероиду Итокава.
Факт седьмой: астероиды Сатурна не подчиняются закону всемирного тяготения
В своё время Лагранж, пытаясь решить задачу трёх тел, получил устойчивое решения для частного случая. Он показал, что третье тело может двигаться по орбите второго, всё время находясь в одной из двух точек, одна из которых опережает второе тело на 60°, а вторая на столько же отстаёт.
Однако две группы компаньонов-астероидов, найденные позади и впереди на орбите Сатурна, и которые астрономы на радостях назвали Троянцами, вышли из прогнозируемых областей, и подтверждение закона всемирного тяготения обернулось проколом.
Факт восьмой: противоречие с общей теорией относительности
По современным представлениям скорость света конечна, в результате удалённые объекты мы видим не там, где они расположены в данный момент, а в той точке, откуда стартовал увиденный нами луч света. Но с какой скоростью распространяется тяготение?
Но с какой скоростью распространяется тяготение?
Проанализировав данные, накопленные ещё к тому времени, Лаплас установил, что «гравитация» распространяется быстрее света, как минимум, на семь порядков! Современные измерения по приёму импульсов пульсаров отодвинули скорость распространения гравитации ещё дальше — как минимум, на 10 порядков быстрей скорости света. Таким образом, экспериментальные исследования входят в противоречие с общей теорией относительности, на которую до сих пор опирается официальная наука, несмотря на её полную несостоятельность .
Факт девятый: аномалии гравитации
Существуют природные аномалии гравитации, которые также не находят никакого внятного объяснения у официальной науки. Вот несколько примеров:
Факт десятый: исследования вибрационной природы антигравитации
Существует большое количество альтернативных исследований с впечатляющими результатами в области антигравитации, которые в корне опровергают теоретические выкладки официальной науки.
Некоторые исследователи анализируют вибрационную природу антигравитации. Этот эффект наглядно представлен в современном опыте, где капли за счёт акустической левитации висят в воздухе. Здесь мы видим, как с помощью звука определённой частоты удаётся уверенно удерживать капли жидкости в воздухе…
А вот эффект на первый взгляд объясняется принципом гироскопа, однако даже такой простой опыт по большей части противоречит гравитации в её современном понимании.
Мало кто знает, что Виктор Степанович Гребенников, сибирский энтомолог, занимавшийся изучением эффекта полостных структур у насекомых, в книге «Мой мир» описывал явления антигравитации у насекомых. Учёным давно известно, что, массивные насекомые, например майский жук, летают скорее вопреки законам гравитации, а не благодаря им.
Более того, на основе своих исследований Гребенников создал антигравитационную платформу.
Виктор Степанович умер при довольно странных обстоятельствах и его наработки частично были утеряны, однако некоторая часть прототипа анти-гравитационной платформы сохранилась и её можно увидеть в музее Гребенникова в Новосибирске
.
Ещё одно практическое применение антигравитации можно наблюдать в городе Хоумстед во Флориде, где находится странная структура из коралловых монолитных глыб, которую в народе прозвали Коралловым замком. Он построен выходцем из Латвии — Эдвардом Лидскалнином в первой половине 20го века. У этого мужчины худощавого телосложения не было никаких инструментов, не было даже машины и вообще никакой техники.
Он совсем не использовался электричеством, также по причине его отсутствия, и тем не менее каким-то образом спускался к океану, где вытесывал многотонные каменные блоки и как-то доставлял их на свой участок, выкладывая с идеальной точностью.
После смерти Эда ученые принялись тщательно изучать его творение. Ради эксперимента был пригнан мощнейший бульдозер, и предпринята попытка сдвинуть с места одну из 30-тонных глыб кораллового замка. Бульдозер ревел, буксовал, но так и не сдвинул огромный камень.
Внутри замка был найден странный прибор, который ученые назвали генератором постоянного тока. Это была массивная конструкция с множеством металлических деталей. По внешней стороне устройства были встроены 240 постоянных полосовых магнитов. Но как на самом деле Эдвард Лидскалнин заставлял двигаться многотонные блоки, до сих пор остаётся загадкой
.
Это была массивная конструкция с множеством металлических деталей. По внешней стороне устройства были встроены 240 постоянных полосовых магнитов. Но как на самом деле Эдвард Лидскалнин заставлял двигаться многотонные блоки, до сих пор остаётся загадкой
.
Известны исследования Джона Сёрла, в руках которого оживали, вращались и вырабатывали энергию необычные генераторы; диски диаметром от полуметра до 10 метров поднимались в воздух и совершали управляемые полеты из Лондона в Корнуолл и обратно.
Эксперименты профессора повторили в России, США и на Тайване. В России, например, в 1999 году под № 99122275/09 была зарегистрирована заявка на патент «устройства для выработки механической энергии». Владимир Витальевич Рощин и Сергей Михайлович Годин, по сути, воспроизвели SEG (Searl Effect Generator — генератор на Сёрл-эффекте) и провели ряд исследований с ним. Итогом стала констатация: можно получить без затрат 7 КВт электроэнергии; вращающийся генератор терял в весе до 40%.
Оборудование первой лаборатории Сёрла было вывезено в неизвестном направлении, пока сам он был в тюрьме. Установка Година и Рощина просто пропала; все публикации о ней, за исключением заявки на изобретение, исчезли .
Известен также Эффект Хатчисона, названный в честь канадского инженера-изобретателя. Эффект проявляется в левитации тяжелых объектов, сплаве разнородных материалов (например металл+дерево), аномальном разогревании металлов при отсутствии вблизи них горящих веществ. Вот видеозапись этих эффектов:
Чем бы не была гравитация на самом деле, следует признать, что официальная наука совершенно не способна внятно объяснить природу этого явления .
Ярослав Яргин
Сначала представим Землю как не-подвижный шар (рис. 3.1, а). Сила тяготения F между Землей (масса М) и объектом (масса m) определяет-ся формулой: F= G Mm/r 2
где r — радиус Земли. Константа G известна под названием универсаль-ная гравитационная постоянная и чрезвычайно мала. Когда r постоянен, сила F — const . m. Притяжение Землей тела массой m определяет вес этого тела: W = mg сравнение уравнений дает: g = const = GM/r 2 .
Когда r постоянен, сила F — const . m. Притяжение Землей тела массой m определяет вес этого тела: W = mg сравнение уравнений дает: g = const = GM/r 2 .
Притяжение Землей тела массой m заставляет его падать «вниз» с ускорением g, которое постоянно во всех точках A, В, С и повсюду на земной поверхности (рис. 3.1,6).
Диаграмма сил свободного тела также показывает, что существует си-ла, действующая на Землю со стороны тела массой m, которая направлена противоположно силе, действующей на тело со стороны Земли. Однако масса М Земли так велика, что «на-правленное вверх» ускорение а» Зем-ли, вычисляемое по формуле F = Ma», незначительно и им можно пренебречь. Земля имеет форму, отличную от ша-рообразной: радиус на полюсе r р мень-ше радиуса на экваторе r е. Это означа-ет, что сила притяжения тела массой m на полюсе F p =GMm/r 2 p больше, чем на экваторе F e = GMm/r e . Поэтому ус-корение свободного падения g p на по-люсе больше ускорения свободного па-дения g e на экваторе. Ускорение g из-меняется с широтой в соответствии с изменением радиуса Земли.
Как вы знаете, Земля находится в постоянном движении. Она вращает-ся вокруг своей оси, совершая один оборот каждые сутки, и движется по орбите вокруг Солнца с оборотом в один год. Принимая для упрощения Землю за однородный шар, рассмот-рим движение тел массой m на по-люсе А и на экваторе С (рис. 3.2). За одни сутки тело в точке А поворачи-вается на 360°, оставаясь на месте, в то время как тело, находящееся в точке С, покрывает расстояние в 2лг. Для того чтобы тело, находящееся в точке С, двигалось по круговой орбите, нужна какая-то сила. Это центростре-мительная сила, которая определяется по формуле mv 2 /r, где v — скорость тела на орбите. Сила гравитационно-го притяжения, действующая на тело, находящееся в точке С, F = GMm/r должна:
а) обеспечивать движение те-ла по окружности;
б) притягивать тело к Земле.
Таким образом, F = (mv 2 /r)+mg на экваторе, a F = mg на полюсе. Это означает, что g изменяется с изменением широты по мере того, как радиус орбиты изменяется от r в точке С до нуля в точке А.
Интересно представить, что бы слу-чилось, если бы скорость вращения Земли увеличилась настолько, что цен-тростремительная сила, действующая на тело на экваторе, стала бы равной силе притяжения, т. е. mv 2 /r = F = GMm/r 2 . Общая гравитационная сила использовалась бы исключитель-но для удержания тела в точке С на круговой орбите, и не осталось бы силы, действующей на поверхность Земли. Любое дальнейшее увеличе-ние скорости вращения Земли позво-лило бы телу «уплыть» в простран-ство. Вместе с тем если космический корабль с астронавтами на борту запущен на высоту R над центром Земли со скоростью v, такой, что вы-полняется равенство mv*/R=F = GMm/R 2 , то этот космический ко-рабль будет вращаться вокруг Земли в условиях невесомости.
Точные измерения ускорения сво-бодного падения g показывают, что g изменяется с изменением широты, как показано в таблице 3.1. Отсюда сле-дует, что вес некоторого тела изме-няется над поверхностью Земли от максимума на широте 90° до миниму-ма на широте 0°.
На этом уровне обучения обычно пренебрегают небольшими изменения-ми в ускорении g и используют сред-нюю величину 9,81 м-с 2 . Для упро-щения расчетов ускорение g часто при-нимают за ближайшее целое число, т. е. 10 м-с — 2 , и, таким образом, сила притяжения, действующая со сто-роны Земли на тело массой 1 кг, т. е. вес, принимается за 10 Н. Большин-ство экзаменационных комиссий для экзаменуемых предлагает использо-вать с целью упрощения вычислений g=10 м-с — 2 или 10 Н-кг -1 «.
«Физика — 10 класс»
Почему Луна движется вокруг Земли?
Что будет, если Луна остановится?
Почему планеты обращаются вокруг Солнца?
В главе 1 подробно говорилось о том, что земной шар сообщает всем телам у поверхности Земли одно и то же ускорение — ускорение свободного падения. Но если земной шар сообщает телу ускорение, то согласно второму закону Ньютона он действует на тело с некоторой силой. Силу, с которой Земля действует на тело, называют силой тяжести . Сначала найдём эту силу, а затем и рассмотрим силу всемирного тяготения.
Сначала найдём эту силу, а затем и рассмотрим силу всемирного тяготения.
Ускорение по модулю определяется из второго закона Ньютона:
В общем случае оно зависит от силы, действующей на тело, и его массы. Так как ускорение свободного падения не зависит от массы, то ясно, что сила тяжести должна быть пропорциональна массе:
Физическая величина — ускорение свободного падения, оно постоянно для всех тел.
На основе формулы F = mg можно указать простой и практически удобный метод измерения масс тел путём сравнения массы данного тела с эталоном единицы массы. Отношение масс двух тел равно отношению сил тяжести, действующих на тела:
Это значит, что массы тел одинаковы, если одинаковы действующие на них силы тяжести.
На этом основано определение масс путём взвешивания на пружинных или рычажных весах. Добиваясь того, чтобы сила давления тела на чашку весов, равная силе тяжести, приложенной к телу, была уравновешена силой давления гирь на другую чашку весов, равной силе тяжести, приложенной к гирям, мы тем самым определяем массу тела.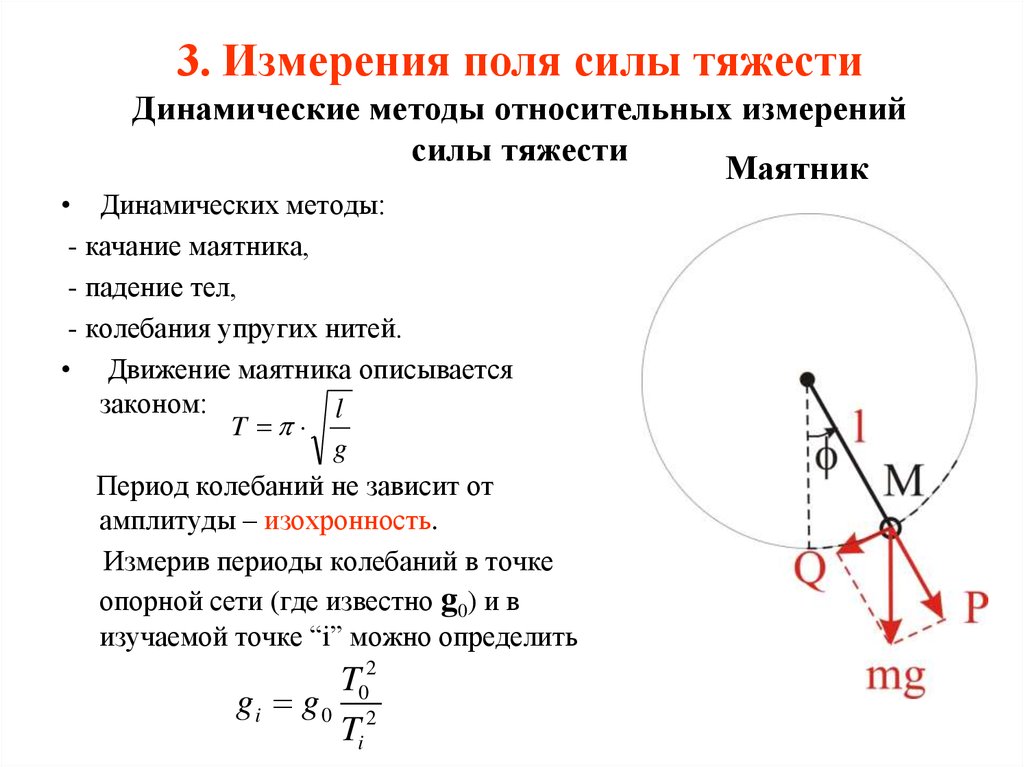
Сила тяжести, действующая на данное тело вблизи Земли, может считаться постоянной лишь на определенной широте у поверхности Земли. Если тело поднять или перенести в место с другой широтой, то ускорение свободного падения, а следовательно, и сила тяжести изменятся.
Сила всемирного тяготения.
Ньютон был первым, кто строго доказал, что причина, вызывающая падение камня на Землю, движение Луны вокруг Земли и планет вокруг Солнца, одна и та же. Это сила всемирного тяготения , действующая между любыми телами Вселенной.
Ньютон пришёл к выводу, что если бы не сопротивление воздуха, то траектория камня, брошенного с высокой горы (рис. 3.1) с определённой скоростью, могла бы стать такой, что он вообще никогда не достиг бы поверхности Земли, а двигался бы вокруг неё подобно тому, как планеты описывают в небесном пространстве свои орбиты.
Ньютон нашёл эту причину и смог точно выразить её в виде одной формулы — закона всемирного тяготения.
Так как сила всемирного тяготения сообщает всем телам одно и то же ускорение независимо от их массы, то она должна быть пропорциональна массе того тела, на которое действует:
«Тяготение существует ко всем телам вообще и пропорционально массе каждого из них.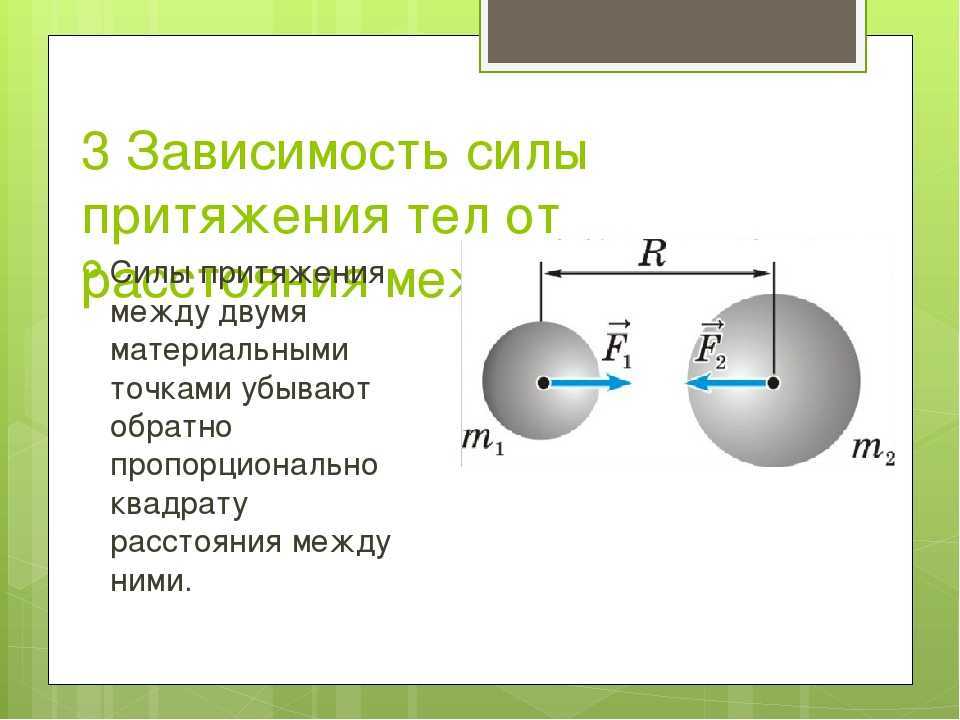 .. все планеты тяготеют друг к другу…» И. Ньютон
.. все планеты тяготеют друг к другу…» И. Ньютон
Но поскольку, например, Земля действует на Луну с силой, пропорциональной массе Луны, то и Луна по третьему закону Ньютона должна действовать на Землю с той же силой. Причём эта сила должна быть пропорциональна массе Земли. Если сила тяготения является действительно универсальной, то со стороны данного тела на любое другое тело должна действовать сила, пропорциональная массе этого другого тела. Следовательно, сила всемирного тяготения должна быть пропорциональна произведению масс взаимодействующих тел. Отсюда вытекает формулировка закона всемирного тяготения.
Закон всемирного тяготения:
Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними:
Коэффициент пропорциональности G называется гравитационной постоянной .
Гравитационная постоянная численно равна силе притяжения между двумя материальными точками массой 1 кг каждая, если расстояние между ними равно 1 м. Ведь при массах m 1 = m 2 = 1 кг и расстоянии r = 1 м получаем G = F (численно).
Ведь при массах m 1 = m 2 = 1 кг и расстоянии r = 1 м получаем G = F (численно).
Нужно иметь в виду, что закон всемирного тяготения (3.4) как всеобщий закон справедлив для материальных точек. При этом силы гравитационного взаимодействия направлены вдоль линии, соединяющей эти точки (рис. 3.2, а).
Можно показать, что однородные тела, имеющие форму шара (даже если их нельзя считать материальными точками, рис. 3.2, б), также взаимодействуют с силой, определяемой формулой (3.4). В этом случае r — расстояние между центрами шаров. Силы взаимного притяжения лежат на прямой, проходящей через центры шаров. Такие силы называются центральными . Тела, падение которых на Землю мы обычно рассматриваем, имеют размеры, много меньшие, чем земной радиус (R ≈ 6400 км).
Такие тела можно, независимо от их формы, рассматривать как материальные точки и определять силу их притяжения к Земле с помощью закона (3.4), имея в виду, что r есть расстояние от данного тела до центра Земли.
Брошенный на Землю камень отклонится под действием тяжести от прямолинейного пути и, описав кривую траекторию, упадёт наконец на Землю. Если его бросить с большей скоростью, то он упадёт дальше». И. Ньютон
Если его бросить с большей скоростью, то он упадёт дальше». И. Ньютон
Определение гравитационной постоянной.
Теперь выясним, как можно найти гравитационную постоянную. Прежде всего заметим, что G имеет определённое наименование. Это обусловлено тем, что единицы (и соответственно наименования) всех величин, входящих в закон всемирного тяготения, уже были установлены ранее. Закон же тяготения даёт новую связь между известными величинами с определёнными наименованиями единиц. Именно поэтому коэффициент оказывается именованной величиной. Пользуясь формулой закона всемирного тяготения, легко найти наименование единицы гравитационной постоянной в СИ: Н м 2 /кг 2 = м 3 /(кг с 2).
Для количественного определения G нужно независимо определить все величины, входящие в закон всемирного тяготения: обе массы, силу и расстояние между телами.
Трудность состоит в том, что гравитационные силы между телами небольших масс крайне малы. Именно по этой причине мы не замечаем притяжение нашего тела к окружающим предметам и взаимное притяжение предметов друг к другу, хотя гравитационные силы — самые универсальные из всех сил в природе. Два человека массами по 60 кг на расстоянии 1 м друг от друга притягиваются с силой всего лишь порядка 10 -9 Н. Поэтому для измерения гравитационной постоянной нужны достаточно тонкие опыты.
Два человека массами по 60 кг на расстоянии 1 м друг от друга притягиваются с силой всего лишь порядка 10 -9 Н. Поэтому для измерения гравитационной постоянной нужны достаточно тонкие опыты.
Впервые гравитационная постоянная была измерена английским физиком Г. Кавендишем в 1798 г. с помощью прибора, называемого крутильными весами. Схема крутильных весов показана на рисунке 3.3. На тонкой упругой нити подвешено лёгкое коромысло с двумя одинаковыми грузиками на концах. Рядом неподвижно закреплены два тяжёлых шара. Между грузиками и неподвижными шарами действуют силы тяготения. Под влиянием этих сил коромысло поворачивается и закручивает нить до тех пор, пока возникающая сила упругости не станет равна гравитационной силе. По углу закручивания можно определить силу притяжения. Для этого нужно только знать упругие свойства нити. Массы тел известны, а расстояние между центрами взаимодействующих тел можно непосредственно измерить.
Из этих опытов было получено следующее значение для гравитационной постоянной:
G = 6,67 10 -11 Н м 2 /кг 2 .
Лишь в том случае, когда взаимодействуют тела огромных масс (или по крайней мере масса одного из тел очень велика), сила тяготения достигает большого значения. Например, Земля и Луна притягиваются друг к другу с силой F ≈ 2 10 20 Н.
Зависимость ускорения свободного падения тел от географической широты.
Одна из причин увеличения ускорения свободного падения при перемещении точки, где находится тело, от экватора к полюсам, состоит в том, что земной шар несколько сплюснут у полюсов и расстояние от центра Земли до её поверхности у полюсов меньше, чем на экваторе. Другой причиной является вращение Земли.
Равенство инертной и гравитационной масс.
Самым поразительным свойством гравитационных сил является то, что они сообщают всем телам, независимо от их масс, одно и то же ускорение. Что бы вы сказали о футболисте, удар которого одинаково ускорял бы обыкновенный кожаный мяч и двухпудовую гирю? Каждый скажет, что это невозможно. А вот Земля является именно таким «необыкновенным футболистом» с той только разницей, что действие её на тела не носит характера кратковременного удара, а продолжается непрерывно миллиарды лет.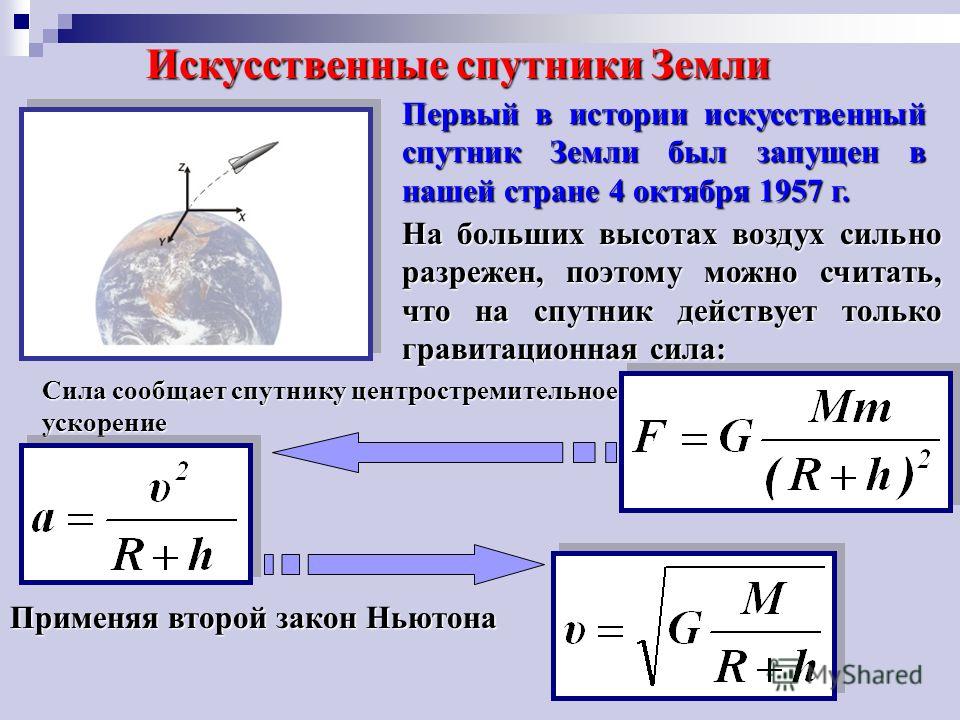
В теории Ньютона масса является источником поля тяготения. Мы находимся в поле тяготения Земли. В то же время мы также являемся источниками поля тяготения, но в силу того, что наша масса существенно меньше массы Земли, наше поле намного слабее и окружающие предметы на него не реагируют.
Необыкновенное свойство гравитационных сил, как мы уже говорили, объясняется тем, что эти силы пропорциональны массам обоих взаимодействующих тел. Масса тела, которая входит во второй закон Ньютона, определяет инертные свойства тела, т. е. его способность приобретать определённое ускорение под действием данной силы. Это инертная масса m и.
Казалось бы, какое отношение она может иметь к способности тел притягивать друг друга? Масса, определяющая способность тел притягиваться друг к другу, — гравитационная масса m r .
Из механики Ньютона совсем не следует, что инертная и гравитационная массы одинаковы, т. е. что
m и = m r . (3.5)
Равенство (3.5) является непосредственным следствием из опыта. Оно означает, что можно говорить просто о массе тела как о количественной мере как инертных, так и гравитационных его свойств.
Оно означает, что можно говорить просто о массе тела как о количественной мере как инертных, так и гравитационных его свойств.
Гравитационная сила – фундамент на котором держится Вселенная. Благодаря силе тяжести Солнце не взрывается, атмосфера не улетучивается в космос, люди и животные свободно передвигаются по поверхности, а растения дают плоды.
Небесная механика и теория относительности
Закон всемирного тяготения изучают в 8-9 классе средней школы. Прилежные ученики знают о знаменитом яблоке упавшем на голову великого Исаака Ньютона и об открытиях, которые за этим последовали. На самом деле, дать четкое определение гравитации гораздо сложнее. Современные ученые продолжают дискуссии на тему, как взаимодействуют тела в открытом космосе и существует ли антигравитация. Изучить данное явление в земных лабораториях крайне сложно, поэтому выделяют несколько базовых теорий гравитации:
Ньютоновская гравитация
В 1687 г. Ньютон заложил основы небесной механики, которая изучает движение тел в пустом пространстве. Он рассчитал силу притяжения Луны к Земле. Согласно формуле, эта сила напрямую зависит от их массы и расстояния между объектами.
Он рассчитал силу притяжения Луны к Земле. Согласно формуле, эта сила напрямую зависит от их массы и расстояния между объектами.
F = (G m1 m2)/r2
Гравитационная постоянная G=6.67*10-11
Уравнение не совсем актуально, когда анализируется сильное гравитационное поле или притяжение более двух объектов.
Теория гравитации Эйнштейна
В ходе различных экспериментов ученые пришли к выводу, что в формуле Ньютона есть некоторые погрешности. Основой небесной механики является дальнодействующая сила, срабатывающая моментально в независимости от расстояния, что не соответствует теории относительности.
Согласно разработанной в начале 20 века теории А.Эйнштейна информация не распространяется быстрее скорости света в вакууме, поэтому гравитационные эффекты возникают в результате деформации пространства-времени. Чем больше масса объекта, тем больше искривление в которое скатываются более легкие объекты.
Квантовая гравитация
Очень противоречивая и не до конца сформированная теория, которая объясняет взаимодействие тел, как обмен особыми частицами – гравитонами.
В начале 21 века ученым удалось провести несколько значимых экспериментов, в том числе с помощью адронного коллайдера, и разработать теорию петлевой квантовой гравитации и теорию струн.
Вселенная без гравитации
В фантастических романах часто описываются различные гравитационные искажения, антигравитационные камеры и космические корабли с искусственным гравитационным полем. Читатели иногда даже не задумаются насколько нереальны сюжеты книг и что будет, если сила тяжести уменьшится/увеличится или совершенно исчезнет.
- Человек адаптирован к земной гравитации, поэтому в других условиях ему придется кардинально измениться. Невесомость приводит к атрофии мышц, сокращению числа эритроцитов и нарушению в работе всех жизненно важных систем организма, а при увеличении гравитационного поля люди просто не смогут сдвинуться с места.
- Воздух и вода, растения и животные, дома и машины улетят в открытый космос. Даже если людям удастся остаться они быстро погибнут без кислорода и еды.
 Низкая гравитация на Луне – это основная причина отсутствия не ней атмосферы, соответственно и жизни.
Низкая гравитация на Луне – это основная причина отсутствия не ней атмосферы, соответственно и жизни. - Наша планета развалится на части, поскольку исчезнет давление в самом центре Земли, начнется извержение всех существующих вулканов и расхождение тектонических плит.
- Звезды взорвутся из-за сильного давления и хаотичного столкновения частиц в ядре.
- Вселенная превратится в бесформенное рагу из атомов и молекул, которые неспособны соединиться для создания чего-то большего.
К счастью для человечества, отключение гравитации и страшные события, которые за этим последую никогда не произойдут. Темный сценарий просто демонстрирует насколько важна гравитация. Она значительно слабее чем электромагнетизм , сильное или слабое взаимодействия, но фактически без неё наш мир перестанет существовать.
определение, формула, виды :: SYL.ru
На вопрос «Что такое сила?» физика отвечает так: «Сила есть мера взаимодействия вещественных тел между собой или между телами и другими материальными объектами – физическими полями». Все силы в природе могут быть отнесены к четырем фундаментальным видам взаимодействий: сильному, слабому, электромагнитному и гравитационному. Наша статья рассказывает о том, что представляют собой гравитационные силы – мера последнего и, пожалуй, наиболее широко распространенного в природе вида этих взаимодействий.
Все силы в природе могут быть отнесены к четырем фундаментальным видам взаимодействий: сильному, слабому, электромагнитному и гравитационному. Наша статья рассказывает о том, что представляют собой гравитационные силы – мера последнего и, пожалуй, наиболее широко распространенного в природе вида этих взаимодействий.
Начнем с притяжения земли
Всем живущим известно, что существует сила, которая притягивает объекты к земле. Она обычно именуется гравитацией, силой тяжести или земным притяжением. Благодаря ее наличию у человека возникли понятия «верх» и «низ», определяющие направление движения или расположения чего-либо относительно земной поверхности. Так в частном случае, на поверхности земли или вблизи нее, проявляют себя гравитационные силы, которые притягивают объекты, обладающие массой, друг к другу, проявляя свое действие на любых как самых малых, так и очень больших, даже по космическим меркам, расстояниях.
Сила тяжести и третий закон Ньютона
Как известно, любая сила, если она рассматривается как мера взаимодействия физических тел, всегда приложена к какому-нибудь из них. Так и в гравитационном взаимодействии тел друг с другом, каждое из них испытывает такие виды гравитационных сил, которые вызваны влиянием каждого из них. Если тел всего два (предполагается, что действием всех других можно пренебречь), то каждое из них по третьему закону Ньютона будет притягивать другое тело с одинаковой силой. Так Луна и Земля притягивают друг друга, следствием чего являются приливы и отливы земных морей.
Так и в гравитационном взаимодействии тел друг с другом, каждое из них испытывает такие виды гравитационных сил, которые вызваны влиянием каждого из них. Если тел всего два (предполагается, что действием всех других можно пренебречь), то каждое из них по третьему закону Ньютона будет притягивать другое тело с одинаковой силой. Так Луна и Земля притягивают друг друга, следствием чего являются приливы и отливы земных морей.
Каждая планета в Солнечной системе испытывает сразу несколько сил притяжения со стороны Солнца и других планет. Конечно, определяет форму и размеры ее орбиты именно сила притяжения Солнца, но и влияние остальных небесных тел астрономы учитывают в своих расчетах траекторий их движения.
Что быстрее упадет на землю с высоты?
Главной особенностью этой силы является то, что все объекты падают на землю с одной скоростью, независимо от их массы. Когда-то, вплоть до 16-го ст., считалось, что все наоборот – более тяжелые тела должны падать быстрее, чем легкие. Чтобы развеять это заблуждение Галилео Галилею пришлось выполнить свой знаменитый опыт по одновременному сбрасыванию двух пушечных ядер разного веса с наклонной Пизанской башни. Вопреки ожиданиям свидетелей эксперимента оба ядра достигли поверхности одновременно. Сегодня каждый школьник знает, что это произошло благодаря тому, что сила тяжести сообщает любому телу одно и то же ускорение свободного падения g = 9,81 м/с2 независимо от массы m этого тела, а величина ее по второму закону Ньютона равна F = mg.
Чтобы развеять это заблуждение Галилео Галилею пришлось выполнить свой знаменитый опыт по одновременному сбрасыванию двух пушечных ядер разного веса с наклонной Пизанской башни. Вопреки ожиданиям свидетелей эксперимента оба ядра достигли поверхности одновременно. Сегодня каждый школьник знает, что это произошло благодаря тому, что сила тяжести сообщает любому телу одно и то же ускорение свободного падения g = 9,81 м/с2 независимо от массы m этого тела, а величина ее по второму закону Ньютона равна F = mg.
Гравитационные силы на Луне и на других планетах имеют разные значения этого ускорения. Однако характер действия силы тяжести на них такой же.
Сила тяжести и вес тела
Если первая сила приложена непосредственно к самому телу, то вторая к его опоре или подвесу. В этой ситуации на тела со стороны опор и подвесов всегда действуют силы упругости. Гравитационные силы, приложенные к тем же телам, действуют им навстречу.
Представьте себе груз, подвешенный над землей на пружине. К нему приложены две силы: сила упругости растянутой пружины и сила тяжести. Согласно третьему закону Ньютона груз действует на пружину с силой, равной и противоположной силе упругости. Эта сила и будет его весом. У груза массой 1 кг вес равен Р = 1 кг ∙ 9,81 м/с2 = 9,81 Н (ньютон).
К нему приложены две силы: сила упругости растянутой пружины и сила тяжести. Согласно третьему закону Ньютона груз действует на пружину с силой, равной и противоположной силе упругости. Эта сила и будет его весом. У груза массой 1 кг вес равен Р = 1 кг ∙ 9,81 м/с2 = 9,81 Н (ньютон).
Гравитационные силы: определение
Первая количественная теория гравитации, основанная на наблюдениях движения планет, была сформулирована Исааком Ньютоном в 1687 году в его знаменитых «Началах натуральной философии». Он писал, что силы притяжения, которые действуют на Солнце и планеты, зависят от количества вещества, которое они содержат. Они распространяются на большие расстояния и всегда уменьшаются как величины, обратные квадрату расстояния. Как же можно вычислить эти гравитационные силы? Формула для силы F между двумя объектами с массами m1 и m2, находящимися на расстоянии r, такова:
- F=Gm1m2/r2,
где G — константа пропорциональности, гравитационная постоянная.
Физический механизм гравитации
Ньютон был не полностью удовлетворен своей теорией, поскольку она предполагала взаимодействие между притягивающимися телами на расстоянии. Сам великий англичанин был уверен, что должен существовать некий физический агент, ответственный за передачу действия одного тела на другое, о чем он вполне ясно высказался в одном из своих писем. Но время, когда было введено понятие гравитационного поля, которое пронизывает все пространство, наступило лишь через четыре столетия. Сегодня, говоря о гравитации, мы можем говорить о взаимодействии любого (космического) тела с гравитационным полем других тел, мерой которого и служат возникающие между каждой парой тел гравитационные силы. Закон всемирного тяготения, сформулированный Ньютоном в вышеприведенной форме, остается верным и подтверждается множеством фактов.
Теория гравитации и астрономия
Она была очень успешно применена к решению задач небесной механики во время XVIII и начале XIX века. К примеру, математики Д. Адамс и У. Леверье, анализируя нарушения орбиты Урана, предположили, что на него действуют гравитационные силы взаимодействия с еще неизвестной планетой. Ими было указано ее предполагаемое положение, и вскоре астрономом И. Галле там был обнаружен Нептун.
К примеру, математики Д. Адамс и У. Леверье, анализируя нарушения орбиты Урана, предположили, что на него действуют гравитационные силы взаимодействия с еще неизвестной планетой. Ими было указано ее предполагаемое положение, и вскоре астрономом И. Галле там был обнаружен Нептун.
Хотя оставалась одна проблема. Леверье в 1845 году рассчитал, что орбита Меркурия прецессирует на 35» за столетие, в отличие от нулевого значения этой прецессии, получаемого по теории Ньютона. Последующие измерения дали более точное значение 43». (Наблюдаемая прецессия равна действительно 570»/век, но кропотливый расчет, позволяющий вычесть влияние от всех других планет, дает значение 43».)
Только в 1915 г. Альберт Эйнштейн смог объяснить это несоответствие в рамках созданной им теории гравитации. Оказалось, что массивное Солнце, как и любое другое массивное тело, искривляет пространство-время в своей окрестности. Эти эффекты вызывают отклонения в орбитах планет, но у Меркурия, как самой малой и ближайшей к нашей звезде планете, они проявляются сильнее всего.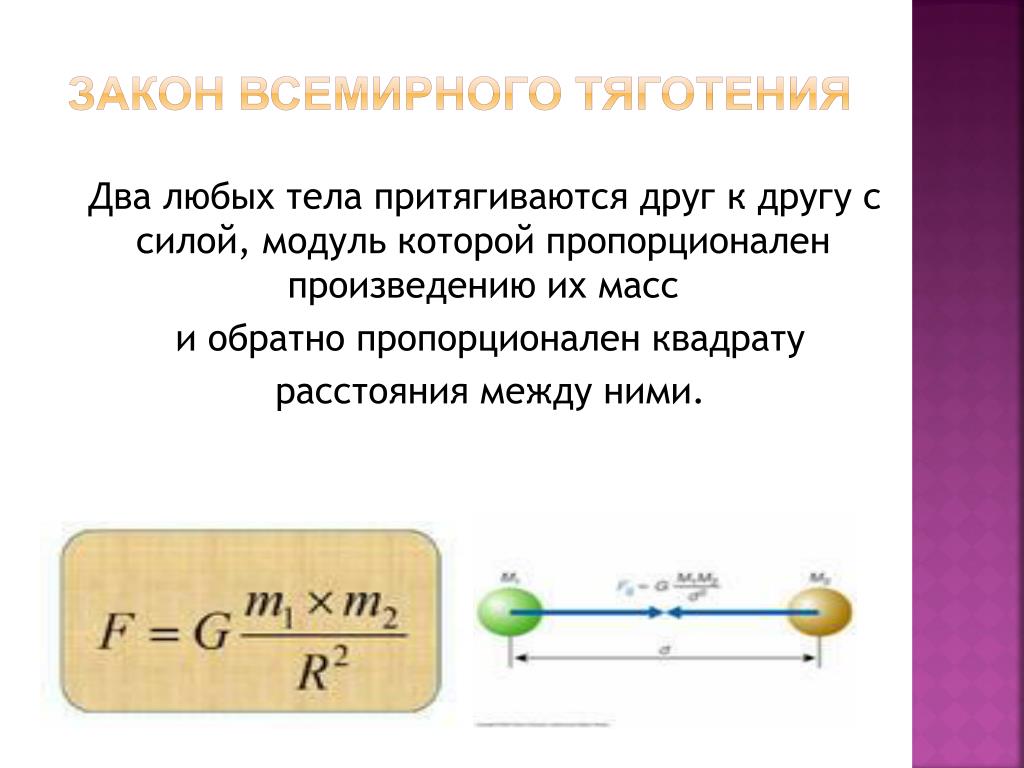
Инерционная и гравитационная массы
Как уже отмечалось выше, Галилей был первым, кто наблюдал, что объекты падают на землю с одинаковой скоростью, независимо от их массы. В формулах Ньютона понятие массы происходит от двух разных уравнений. Второй его закон говорит, что сила F, приложенная к телу с массой m, дает ускорение по уравнению F = ma.
Однако сила тяжести F, приложенная к телу, удовлетворяет формуле F = mg, где g зависит от другого тела, взаимодействующего с рассматриваемым (земли обычно, когда мы говорим о силе тяжести). В обоих уравнений m есть коэффициент пропорциональности, но в первом случае это инерционная масса, а во втором – гравитационная, и нет никакой очевидной причины, что они должны быть одинаковыми для любого физического объекта.
Однако все эксперименты показывают, что это действительно так.
Теория гравитации Эйнштейна
Он взял факт равенства инерционной и гравитационной масс как отправную точку для своей теории. Ему удалось построить уравнения гравитационного поля, знаменитые уравнения Эйнштейна, и с их помощью вычислить правильное значение для прецессии орбиты Меркурия. Они также дают измеренное значение отклонения световых лучей, которые проходят вблизи Солнца, и нет никаких сомнений в том, что из них следуют правильные результаты для макроскопической гравитации. Теория гравитации Эйнштейна, или общая теория относительности (ОТО), как он сам ее назвал, является одним из величайших триумфов современной науки.
Они также дают измеренное значение отклонения световых лучей, которые проходят вблизи Солнца, и нет никаких сомнений в том, что из них следуют правильные результаты для макроскопической гравитации. Теория гравитации Эйнштейна, или общая теория относительности (ОТО), как он сам ее назвал, является одним из величайших триумфов современной науки.
Гравитационные силы – это ускорение?
Если вы не можете отличить инерционную массу от гравитационной, то вы не можете отличить и гравитацию от ускорения. Эксперимент в гравитационном поле вместо этого может быть выполнен в ускоренно движущемся лифте в отсутствии гравитации. Когда космонавт в ракете ускоряется, удаляясь от земли, он испытывает силу тяжести, которая в несколько раз больше земной, причем подавляющая ее часть приходит от ускорения.
Если никто не может отличить гравитацию от ускорения, то первую всегда можно воспроизвести путем ускорения. Система, в которой ускорение заменяет силу тяжести, называется инерциальной. Поэтому Луну на околоземной орбите также можно рассматривать как инерциальную систему.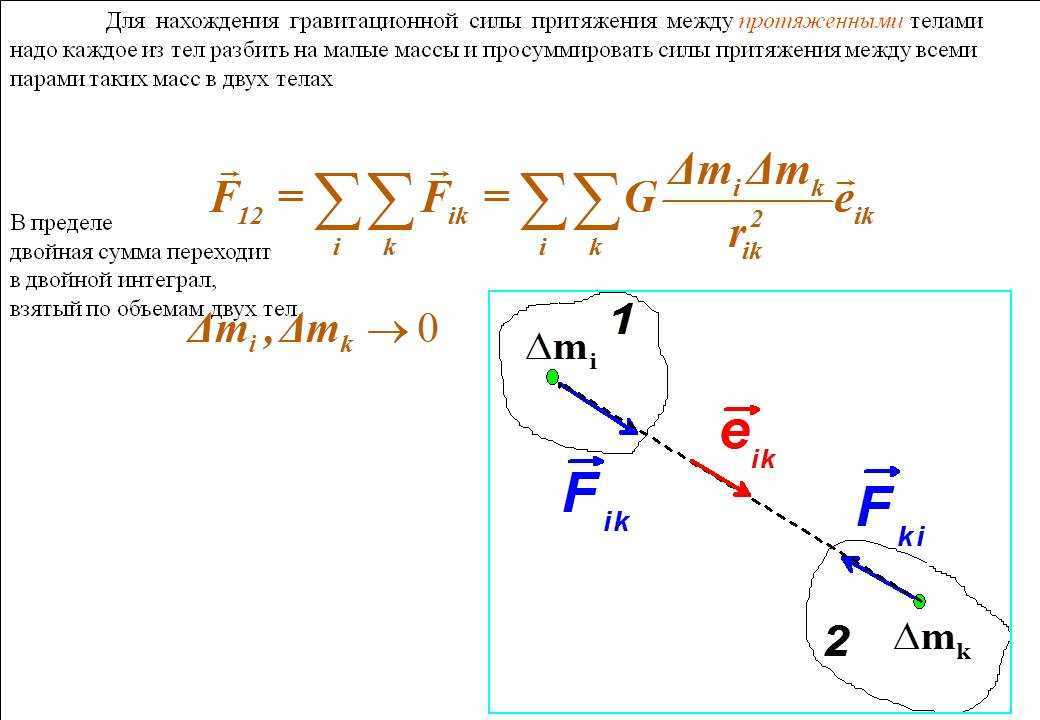 Однако эта система будет отличаться от точки к точке, поскольку изменяется гравитационное поле. (В примере с Луной гравитационное поле изменяет направление из одной точки в другую.) Принцип, согласно которому всегда можно найти инерциальную систему в любой точке пространства и времени, в которой физика подчиняется законам в отсутствии гравитации, называется принципом эквивалентности.
Однако эта система будет отличаться от точки к точке, поскольку изменяется гравитационное поле. (В примере с Луной гравитационное поле изменяет направление из одной точки в другую.) Принцип, согласно которому всегда можно найти инерциальную систему в любой точке пространства и времени, в которой физика подчиняется законам в отсутствии гравитации, называется принципом эквивалентности.
Гравитация как проявление геометрических свойств пространства-времени
Тот факт, что гравитационные силы можно рассматривать как ускорения в инерциальных системах координат, которые отличаются от точки к точке, означает, что гравитация – это геометрическое понятие.
Мы говорим, что пространство-время искривляется. Рассмотрим мяч на плоской поверхности. Он будет покоиться или, если нет никакого трения, равномерно двигаться при отсутствии действия каких-либо сил на него. Если поверхность искривляется, мяч ускорится и будет двигаться до самой низкой точки, выбирая кратчайший путь. Аналогичным образом теория Эйнштейна утверждает, что четырехмерное пространство-время искривлено, и тело движется в этом искривленном пространстве по геодезической линии, которой соответствует кратчайший путь. Поэтому гравитационное поле и действующие в нем на физические тела гравитационные силы – это геометрические величины, зависящие от свойств пространства-времени, которые наиболее сильно изменяются вблизи массивных тел.
Поэтому гравитационное поле и действующие в нем на физические тела гравитационные силы – это геометрические величины, зависящие от свойств пространства-времени, которые наиболее сильно изменяются вблизи массивных тел.
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
-
2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
-
3 Термодинамика и МКТ
-
3.
 1 МКТ
1 МКТ
- 3.2 Термодинамика
-
3.
-
4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
-
5 Оптика. СТО
- 5.1 Геометрическая оптика
-
5.
 2 Волновая оптика
2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
-
6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
Как рассчитать Силу Гравитации?
Мы являемся свидетелями нескольких примеров того, как гравитация работает с силой в нашей повседневной жизни. Мы знаем, что в космосе существует постоянное движение и сила в форме толчков и притяжений. Среди бесчисленных движений есть четыре основные элементарные силы, ответственные за широкий спектр явлений. Гравитационная сила, сильная сила, слабая сила и электромагнитная сила — это четыре силы.
Среди бесчисленных движений есть четыре основные элементарные силы, ответственные за широкий спектр явлений. Гравитационная сила, сильная сила, слабая сила и электромагнитная сила — это четыре силы.
Гравитация — это сила, которая притягивает предметы к земле. Силы способны работать, поэтому гравитация в основном выполняет эту работу. Когда вы прикладываете силу к предмету, сила делает работу за вас. Например, когда вы подбрасываете мяч, сила, приложенная к мячу, заставляет мяч лететь на определенное расстояние, и, таким образом, работа завершается. Работа пропорциональна приложенной силе и пройденному или сделанному в результате расстоянию; например, если вы бросаете мяч с меньшей силой, расстояние, пройденное мячом, будет меньше пропорционально приложенной силе; точно так же, если вы бросите мяч с большой силой, пройденное расстояние будет большим. Когда частица падает, она вынуждена указывать в направлении силы тяжести.
Гравитационная сила
Гравитационная сила — это сила, которая притягивает любые два объекта во Вселенной, независимо от того, имеют ли они равные массы или нет. Кроме того, универсальный закон всемирного тяготения Ньютона гласит, что все, включая вас, притягивает все остальные объекты во Вселенной. Единицей гравитационной силы является ньютон, обозначаемый как Н.0020 г — гравитационная сила между объектами
Кроме того, универсальный закон всемирного тяготения Ньютона гласит, что все, включая вас, притягивает все остальные объекты во Вселенной. Единицей гравитационной силы является ньютон, обозначаемый как Н.0020 г — гравитационная сила между объектами
Вывод
Примеры задачМы хорошо знаем, что сила прямо пропорциональна произведению масс тела. Следовательно,
F ∝ m 1 m 2
Кроме того, F косвенно пропорционально квадрату расстояния между двумя телами, имеем:
F ∝
Из уравнений (1) и (2), имеем:
F ∝
Убрав знак пропорциональности, получим:
F г =
Отсюда доказано.
Вопрос 1. Найдите силу притяжения двух слонов, один массой 1000 кг, а другой массой 800 кг, если расстояние между ними 5 м.
Решение:
Дано: M 1 = 1000 кг, M 2 = 800 кг, R = 5 м
Here, G = 6.67 ×10 −11 N⋅ m 2 /kg 2
Substituting the values in the formula, we have:
F g =
F g = 2,1 × 10 -6 Н
Вопрос 2. Найдите силу притяжения между человеком массой 50 кг и автобусом массой 1500 кг, если расстояние между ними 10 м.
Решение:
Дано: M 1 = 50 кг, M 2 = 1500 кг, R = 10 M
Здесь G = 6,67 × 10 −11 Н⋅ м 2 /кг 2
Подставляя значения в формулу, имеем:
F g =
F g = 5,0025 × 10 -8 N
Объяснять.
Решение:
Универсальный закон всемирного тяготения гласит, что два объекта притягиваются друг к другу с одинаковой силой, но в противоположных направлениях.
Следовательно, Земля притягивает Луну с такой же силой, с какой последняя притягивает первую.
Вопрос 4. Предположим, что сила притяжения между двумя телами на определенном расстоянии равна 4 Н. Найдите силу притяжения, если расстояние между ними увеличилось вдвое.
Решение:
Закон всемирного тяготения Ньютона гласит, что гравитационная сила между двумя точечными объектами прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними.
F г =
Это уравнение показывает, что для данных масс, если r заменить на 2r, сила станет 1/4 первоначальной силы. Следовательно, сила притяжения станет 4/4 = 1 Н.
Вопрос 5. Масса Земли 6 × 10 24 кг. Расстояние между Землей и Солнцем равно 1,5 × 10 11 м. Если гравитационная сила между ними составляет 3,5 × 10 22 Н, какова масса Солнца?
Решение:
Дано: m e = 6 × 10 24 кг, r = 1,5 × 10 11 м и F = 3,5 × 10 22 Н
Формула для силы тяжести дается как F0: F0: g 90 = .
⇒ 3,5 × 10 22 n =
⇒ Масса Солнца =
= 1,967 × 10 30 кг
Вопрос 6. Если луна притягивает Землю, тогда это не земля. двигаться к луне?
Решение:
Земля и Луна испытывают равные гравитационные силы друг от друга. Однако масса Земли намного больше массы Луны. Таким образом, он ускоряется с гораздо меньшей скоростью, чем ускорение Луны по отношению к Земле. Вот почему Земля движется к Земле.
Расчет гравитационных сил — AP Physics C: Mechanics
Все ресурсы AP Physics C: Mechanics
2 диагностических теста 92 практических теста Вопрос дня Карточки Учитесь по концепции
AP Физика C: Справка по механике » Экзамен по механике » Силы » Сила тяжести » Расчет гравитационных сил
С какой минимальной скоростью должна стартовать ракета с поверхности Луны, чтобы не упасть обратно под действием лунного притяжения?
Масса Луны и ее радиус .
Возможные ответы:
Правильный ответ:
Объяснение:
Соответствующие уравнения:
Минимальная суммарная энергия ракеты, выходящей из-под гравитации Луны, равна нулю. Если полная энергия равна нулю, ракета будет иметь нулевую конечную скорость, когда она будет бесконечно далеко от Луны. Если полная энергия меньше нуля, ракета упадет обратно на поверхность Луны. Если полная энергия больше нуля, ракета будет иметь некоторую конечную скорость, когда она будет бесконечно далеко.
Для случая минимальной энергии при отрыве ракеты от поверхности:
Измените уравнение энергии, чтобы выделить член скорости.
Подставьте данные значения для определения скорости.
Сообщить об ошибке
Какова сила притяжения солнца к книге на поверхности земли, если масса солнца и расстояние от земли до солнца равно?
Возможные ответы:
Правильный ответ:
Объяснение:
Соответствующие уравнения:
Используйте данные значения для определения силы.
Сообщить об ошибке
Две сферы одинаковой массы изолированы в пространстве и разделены расстоянием . Если это расстояние увеличить вдвое, во сколько раз изменится сила притяжения между двумя сферами?
Возможные ответы:
Без изменений
Правильный ответ:
Объяснение:
Закон всемирного тяготения Ньютона утверждает:
Мы можем написать два уравнения для гравитации до и после удвоения:
Уравнение гравитации после удвоения можно упростить:
3
3
Поскольку массы сфер остаются теми же, как и постоянная всемирного тяготения, мы можем подставить определение Fg1 в это уравнение:
Гравитационная сила уменьшается в 4 раза, когда расстояние между двумя сферами удваивается.
Сообщить об ошибке
В космосе изолированы два шара одинаковой массы. Если массу одного шара удвоить, во сколько раз изменится сила тяжести, действующая на два шара?
Если массу одного шара удвоить, во сколько раз изменится сила тяжести, действующая на два шара?
Возможные ответы:
Правильный ответ:
Пояснение:
Закон всемирного тяготения Ньютона утверждает, что:
Мы можем написать два уравнения, описывающие силу тяжести до и после удвоения массы:
Задача дает нам, и мы можем предположить, что все остальные переменные остаются постоянными.
Подставляя эти определения во второе уравнение:
Это уравнение упрощается до:
Подставляя определение Fg1, мы видим:
Таким образом, когда гравитационные силы удваивают массу одного объекта.
Сообщить об ошибке
Вы едете в лифте, который ускоряется вверх со скоростью , когда вы замечаете, что блок, подвешенный вертикально к пружинной шкале, показывает .
Что показывают пружинные весы, когда лифт опускается с постоянной скоростью?
Возможные ответы:
Правильный ответ:
Пояснение:
Когда лифт ускоряется вверх, мы знаем, что объект будет казаться тяжелее. Нормальная сила равна сумме всех сил, и в данном случае она равна . Мы знаем, что нормальная сила имеет две составляющие: составляющую от силы тяжести и составляющую от ускорения лифта. Используя это уравнение, мы можем определить массу блока, которая не меняется:
ускорение свободного падения и ускорение лифта.
При подстановке значений получаем
Решая для , получаем
Так как лифт опускается с постоянной скоростью, никакая дополнительная сила не прилагается, поэтому сила, которую считывают пружинные весы, обусловлена только силой тяжести, т.е. рассчитано по формуле:
Сообщить об ошибке
Масса и радиус луны планеты равны и соответственно.
С какой минимальной скоростью пуля должна лететь горизонтально вблизи поверхности этой луны, чтобы никогда не попасть в землю?
(Примечание. Луну можно рассматривать как гладкую сферу и считать, что атмосферы нет.) Пояснение:
Чтобы решить эту задачу, мы должны понять, что сила тяжести, действующая на пулю, равна центростремительной силе. Уравнения для гравитационной силы и центростремительной силы выглядят следующим образом:
Если мы приравняем два уравнения друг к другу, малое (масса пули) сократится, и исчезнет из правой части уравнения.
это универсальная гравитационная постоянная
дана быть и быть .
Если мы все подключим, получим
или
Сообщить об ошибке
Уведомление об авторских правах
All AP Physics C: Mechanics Resources
2 диагностических теста 92 практических теста Вопрос дня Карточки Learn by Concept
Несколько подходов и примеров задач – Lambda Geeks
В статье обсуждается несколько подходов и некоторые примеры задач о том, как вычислить массу по гравитационной силе.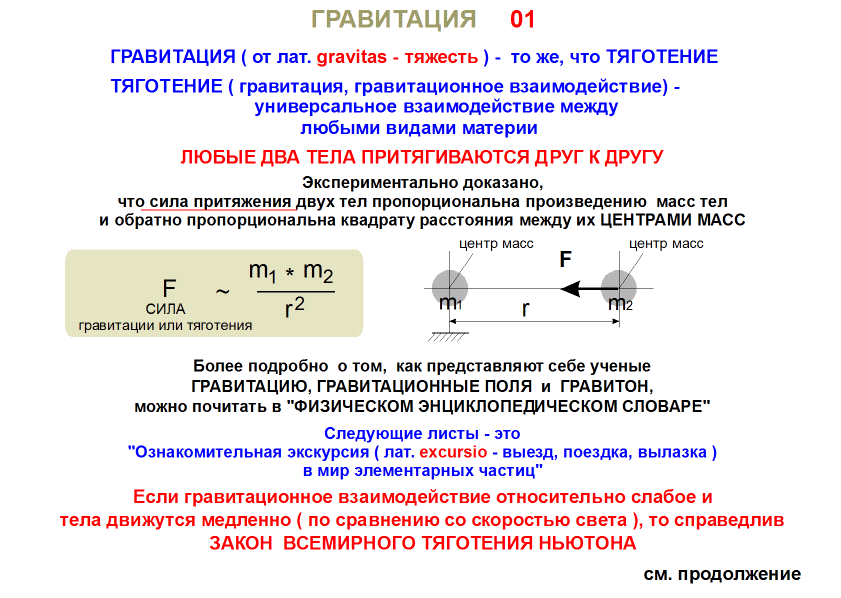
Каждый объект во вселенной, обладающий массой, оказывает гравитационное воздействие на другой. Вот почему сила гравитации прямо пропорциональна массе объекта. Таким образом, используя различные формулы, связанные с гравитационной силой, мы можем вычислить ненулевую массу объекта.
Подробнее о Как рассчитать массу по силе и расстоянию .
Как рассчитать массу по силе гравитации, используя второй закон Ньютона Как рассчитать массу по силе гравитации?Рассчитаем массу, используя второй закон движения Ньютона, следующим образом:
Во втором законе движения Ньютон описывает, что на объект с ненулевой массой действует сила, ускоряющая его в том же направлении. Гравитационная сила — это естественная сила, которая всегда действует вниз на каждый объект, чтобы ускорить его, в зависимости от его массы.
Мы уже изучили два основных типа сил, действующих на тела. Гравитационная сила или гравитация, бесконтактная сила, всегда действует между массами каждого объекта.
Гравитационная сила или гравитация, бесконтактная сила, всегда действует между массами каждого объекта.
Согласно второму закону Ньютона,
F = ma ………………… (*)
Когда действует сила тяжести, каждый объект ускоряется согласно второму закону движения. Ускорение под действием силы тяжести является постоянным и называется ускорением под действием силы тяжести g. Поскольку на нас всегда действует гравитация, возникло представление о нашем «весе» как «mg», включающем в себя нашу массу m и ускорение «a». Вот почему гравитационную силу также называют сила веса .
Сила тяжести как сила веса(кредит: Shutterstock)
Следовательно, формула второго закона Ньютона принимает вид:
F г = мг ………………………… (1)
В соответствии с уравнениями (*) и (1),
Мы должны создать восходящую силу (мА), превышающую силу гравитации (мг), чтобы поднять более тяжелое тело.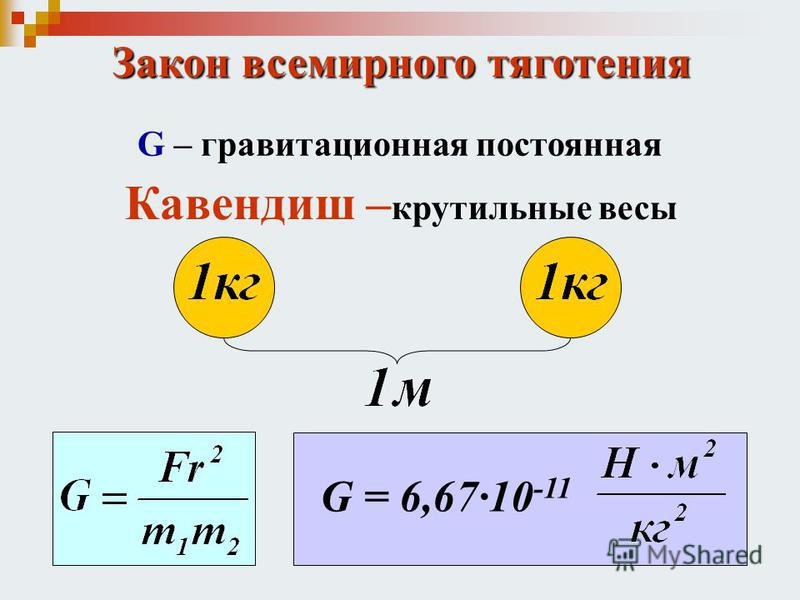
Поскольку g имеет постоянное значение 9,8 м/с 2 , сила тяжести F g зависит только от массы объекта m. Чем массивнее объект, тем больше силы необходимо для его ускорения.
Если к объекту приложена сила гравитации, мы можем вычислить его массу по формуле второго закона Ньютона .
Подробнее о Законах движения Ньютона .
Гравитационная сила, действующая на девушку, бегущую по парку, равна 490. Вычислите массу девушки.Дано:
F г = 490 Н
г = 9,8 м/с
Найти: м =?
Формула:
F = MA
Решение:
Масса девушки рассчитывается с использованием Newton’s Formula ,
F = MA
70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 70007 гравитационная сила определяется как
F г = мг
m= F г /г
m=490/9,8
m = 50 кг ……………………………………. (a)
(a)
Масса бегущей в парке девушки составляет 50 кг.
Как найти массу с помощью гравитационной силы и радиуса?Давайте рассчитаем массу с силой тяжести, используя закон тяготения Ньютона следующим образом:
Закон тяготения показывает, что сила тяготения между двумя объектами прямо пропорциональна их массам и обратно пропорциональна квадрату радиуса между их центрами. масс. Если вторым объектом является Земля с фиксированной массой, мы можем вычислить массу первого объекта.
Согласно закону тяготения Ньютона,
F г =G(мМ/р 2 )……………..(2)
Вся масса объекта сосредоточена в одной конкретной точке , в основном в его центральной точке, называемой его центром масс (ЦМ) . Радиус r измеряет расстояние или расстояние между центрами масс двух объектов .
Небольшая масса массой 1 кг, разделенная радиусом 1, подверглась воздействию небольшой гравитационной силы 6,67 x 10-11 Нм 2 /кг 2 , подходит для каждого объекта. Следовательно, это постоянное значение является значением константы пропорциональности в законе тяготения, также называемой универсальной гравитационной постоянной G .
Следовательно, это постоянное значение является значением константы пропорциональности в законе тяготения, также называемой универсальной гравитационной постоянной G .
Легче вычислить F g между объектом и Землей, поскольку планета имеет фиксированную массу M = 5,98 x 10 24 кг, а также фиксированный радиус r от центра ее земли, r = 6,38 x 10 6 м
Сила гравитации, действующая на бегущую в парке девушку, равна 490. Рассчитайте массу девушки, используя закон всемирного тяготения Ньютона.Given :
F g = 490 N
M = 5.98 x 10 24 kg
r = 6.38 x 10 6 m
G = 6.67 x 10 -11 nm 2 /кг 2
Найти: м =?
Формула:
F г =G(мМ/р 2 )
Решение:
Масса девушки вычисляется по закону тяготения Ньютона is,
F g =G(mM/r 2 )
Перестановка массы m,
m=F g 2 /GM
Подставив все значения,
Из (a) и (b) мы заметили, что масса, рассчитанная с использованием второго закона Ньютона и формулы закона всемирного тяготения, одинакова.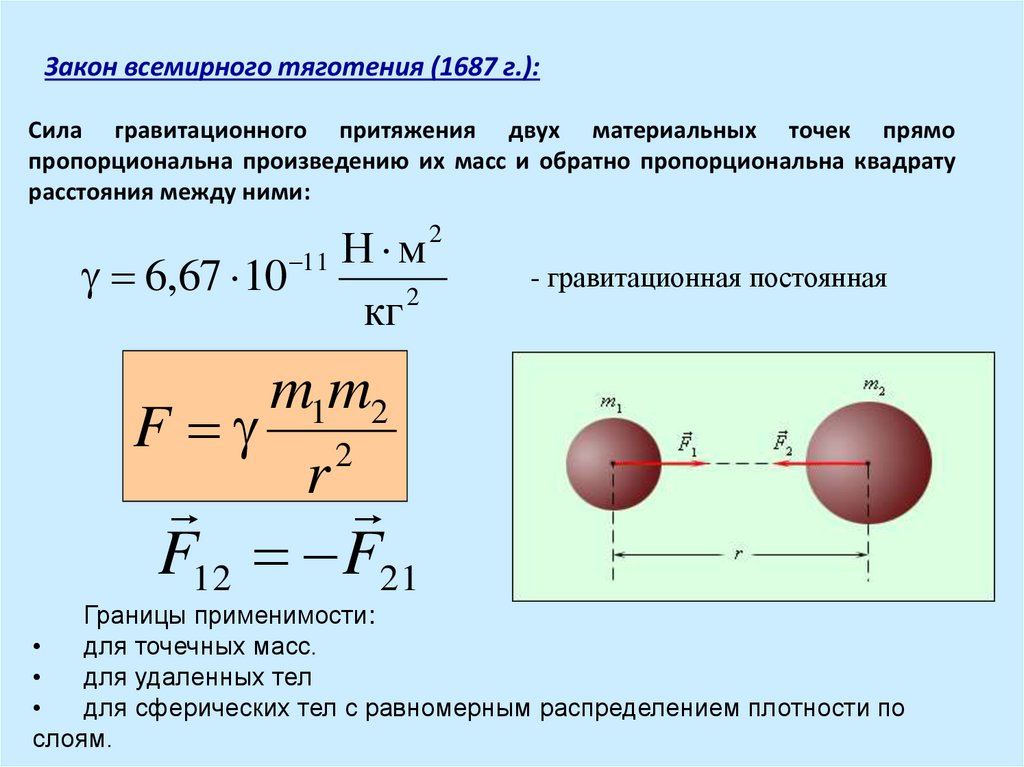
Закон всемирного тяготения можно применить к двум объектам, имеющим одинаковую или разную массу.
Сила притяжения между двумя объектами, имеющими разные массы
(кредит: Shutterstock) Сила притяжения между вами и вашим коллегой составляет 3 x 10 -7 Н, когда вы оба приближаетесь на расстояние 1 м друг от друга в школьном коридоре. Так как ваша масса 60 кг, рассчитайте массу вашего коллеги.
Дано :
F г = 3 x 10 -7 N
r = 1 м
0002 M 1 = 60 кгG = 6,67 x 10 -11 нм 2 /кг 2
, чтобы найти : M 2 =?
Формула :
F G = G (M 1 M 2 /R 2 )
Расчет:
Расчет
. Закон всемирного тяготения Ньютона is,
F g =G(m 1 M 2 /R 2 )
перестройки для массы M 2 ,
M 2 = F G R 2 /G 1
LWATRITITINGTINTINGITINTIONGITINTING 3 /GM2020 1
.
Масса вашего коллеги 75 кг.
Как рассчитать массу из гравитационной силы, используя формулу центростремительной силы?Рассчитаем массу с силой тяжести, используя формулу центростремительной силы следующим образом:
Когда объект движется по кругу, его скорость продолжает изменяться в зависимости от его направления. Направление ускорения к центру, вызванное центростремительной силой. Поскольку вся масса объекта сосредоточена в его центре, мы можем вычислить ее по формуле центростремительной силы.
Центростремительная сила получается из второго закона Ньютона.
Поскольку ускорение представляет собой круговой путь, нам нужно учитывать радиус; поэтому ускорение становится
v 2 /r
Следовательно, согласно уравнению (*), центростремительная сила определяется как сила , действующая на объект, чтобы он двигался по кругу к его центру. Земля воздействует на спутник этой центростремительной силой, поддерживая его круговое движение.


 Низкая гравитация на Луне – это основная причина отсутствия не ней атмосферы, соответственно и жизни.
Низкая гравитация на Луне – это основная причина отсутствия не ней атмосферы, соответственно и жизни.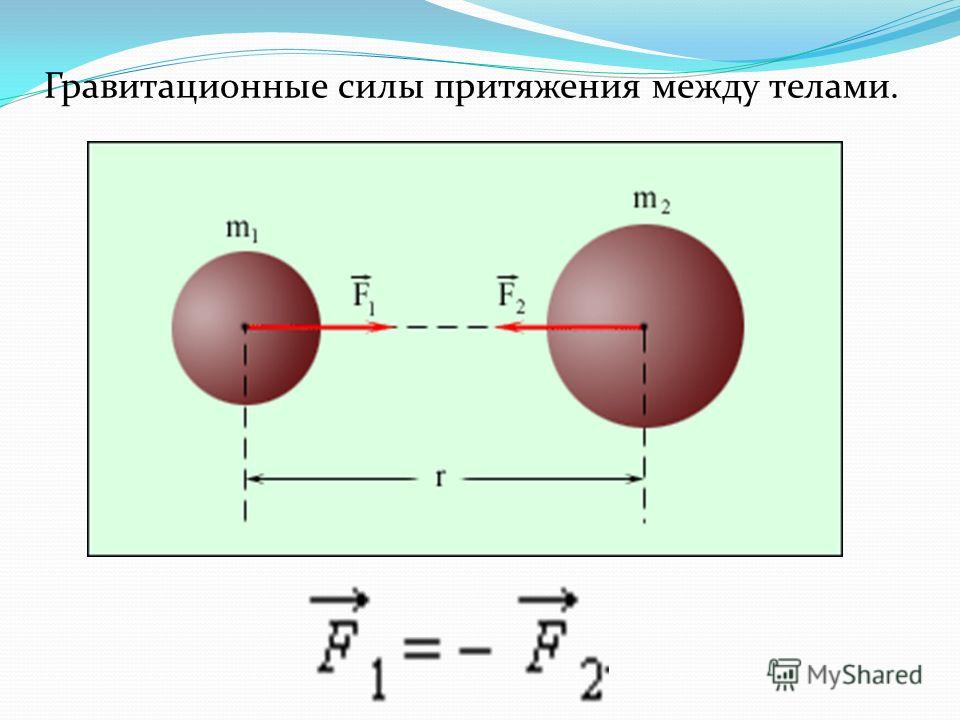
 1 МКТ
1 МКТ
 2 Волновая оптика
2 Волновая оптика
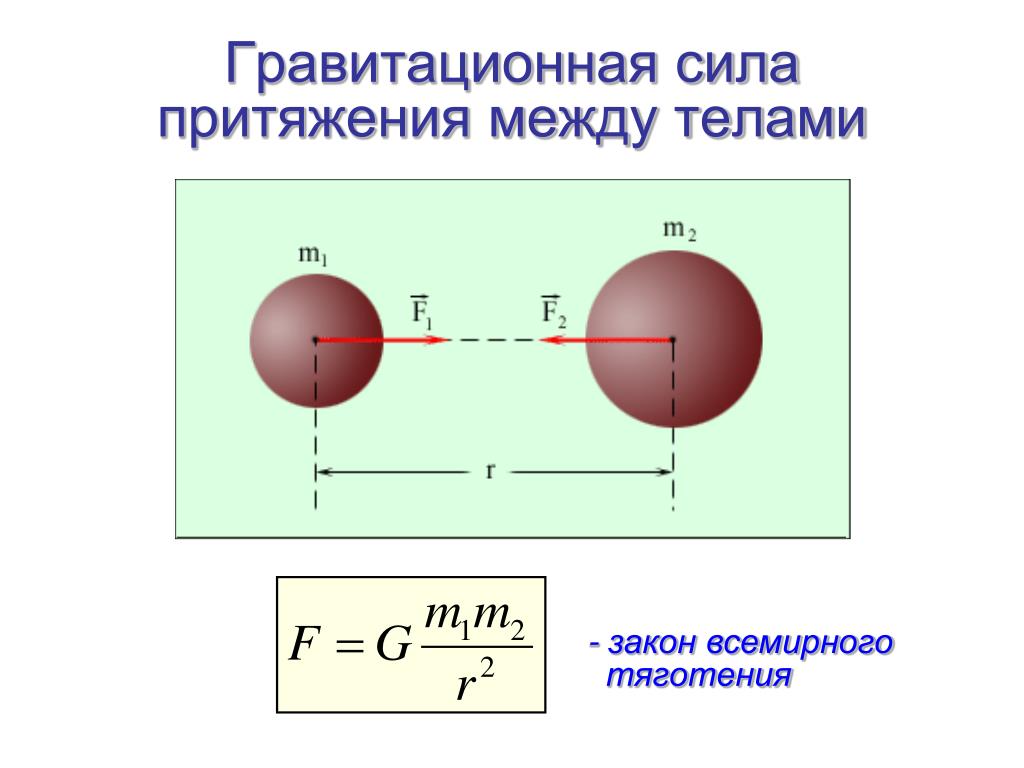 Следовательно, Земля притягивает Луну с такой же силой, с какой последняя притягивает первую.
Следовательно, Земля притягивает Луну с такой же силой, с какой последняя притягивает первую.