Единица измерения магнитной индукции, теория и онлайн калькуляторы
Единица измерения магнитной индукции, теория и онлайн калькуляторыТесла — единица измерения магнитной индукции в системе СИ
Единица магнитной индукции ($\overline{B}$) в международной системе единиц (СИ) называется тесла (Тл), по имени сербского ученого Н. Тесла, который успешно работал в области радиотехники и электроники.
Единицу измерения магнитной индукции определим исходя из закона Ампера. Рассмотрим прямолинейный проводник, длиной $l$ по которому течет ток $I$. Пусть этот проводник находится в однородном магнитном поле $\overline{B}$, причем вектор индукции поля перпендикулярен проводнику. В таком случае модуль силы Ампера (${\overline{F}}_A$), воздействующей на проводник равен:
\[F=IBl\ \left(1\right).\]
Выразим магнитную индукцию из формулы (1), получим:
\[B=\frac{F}{I\cdot l}\left(2\right).\]
Из выражения (2) мы видим, что тесла (единица измерения магнитной индукции) — это величина, соответствующая магнитной индукции однородного магнитного поля, действующего на каждый метр прямого проводника, находящегося в магнитном поле перпендикулярно направлению $\overline{B}$, с силой в один ньютон, при силе тока в проводнике в один ампер:
\[\left[B\right]=Тл=\frac{H}{A\cdot м}. 4Гс.\]
4Гс.\]
Данная единица измерения именована в честь немецкого ученого К.Ф. Гаусса.
Используя основные единицы системы СГС, единица измерения магнитной индукции выражается как:
\[\left[B\right]=\frac{\sqrt{гр}}{с\cdot \sqrt{см}}.\]
Примеры задач с решением
Пример 1
Задание. Получите единицу измерения магнитной индукции в Международной системе единиц, используя формулу, связывающую ее с магнитным потоком ($Ф$).
Решение. По условию задачи в качестве основы для ее решения используем выражение:
\[Ф=BS{\cos \alpha \ }\ \left(1.1\right),\]
где$\ Ф$- поток вектора магнитной индукции через площадку S;$\ S$ — величина площади площадки; $\alpha $ — угол между направлением нормали к площади S и направлением вектора магнитной индукции. Выразим модуль вектора магнитной индукции из формулы (1.1), имеем:
\[B=\frac{Ф}{S\ cos\ \alpha }\]
Учитывая, что в системе СИ ${\cos \alpha \ }$ — величина безразмерная, поток вектора магнитной индукции измеряется в веберах (Вб):
а единицы измерения площади:
\[\left[S\right]=м^2,\]
получим:
\[\left[B\right]=\frac{Вб}{м^2}=\frac{кг\cdot м^2}{А\cdot с^2}\cdot \frac{1}{м^2}=\frac{кг}{А\cdot с^2}=Тл. 2\cdot А}=Тл.\]
2\cdot А}=Тл.\]
Ответ. Мы получили, что тесла можно выразить как: $Тл=\frac{Н}{А\cdot м}$
Читать дальше: единица измерения мощности.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Магнитное действие тока. Вектор магнитной индукции. Магнитный поток.
Основные ссылки
CSS adjustments for Marinelli theme
Объединение учителей Санкт-Петербурга
Форма поиска
Поиск
Вы здесь
Главная » Магнитное действие тока. Вектор магнитной…
| Магнитное действие электрического тока | |
1820 г. X. Эрстед — датский физик, открыл магнитное действие тока. | |
Магнитное взаимодействие, как и электрическое, удобно рассматриватьвводя понятие магнитного поля:
| |
Для двух параллельных бесконечно длинных проводников было установлено: противоположно направленные токи отталкиваются, однонаправленные токи притягиваются, причем , где k — коэффициент пропорциональности. | |
Отсюда устанавливается единица силы тока ампер в СИ: сила тока равна 1 А, если между отрезками двух бесконечных проводников по 1 м каждый, находящимися в вакууме на расстоянии 1 м друг от друга, действует сила магнитного взаимодействия 2.10 7Н. | |
В СИ удобно ввести магнитную проницаемость вакуума . | |
| Вектор магнитной индукции. Вектор магнитной индукции (В) – аналог напряженности электрического поля. Основной силовой характеристикой магнитного поля является вектор магнитной индукции. | |
Направление этого вектора для поля прямого проводника с током и соленоида можно определить по правилу буравчика: если направление поступательного движения буравчика (винта с правой нарезкой) совпадает с направлением тока, то направление вращения ручки буравчика покажет направление линий магнитной индукции. | |
На практике удобно пользоваться следующим правилом: если большой палец правой руки направить по току, то направление обхвата тока остальными пальцами совпадет с направлением линий магнитной индукции. |
|
Модуль вектора магнитной индукции Магнитная индукция В зависит от I и r, где r — расстояние от проводника с током до исследуемой точки. Если расстояние от проводника много меньше его длины (т. е. рассматривать модель бесконечно длинного проводника), то, где k — коэффициент пропорциональности. Подставляя эту формулу в уравнение для силы взаимодействия двух проводников с током, получим F=B .I.ℓ. Отсюда  Таким образом, модуль вектора магнитной индукции есть отношение максимальной силы, действующей со стороны магнитного поля на участок проводника с током, к произведению силы тока на длину этого участка. | |
Единица измерения в СИ — тесла (Тл). Единица названа в честь сербского электротехника Н. Тесла. | |
| Магнитный поток | |
, где Вcosα представляет собой проекцию вектора В на нормаль к плоскости контура. | |
Единица магнитного потока в СИ — вебер (Вб). В честь немецкого физика В. Вебера. | |
Опыт показывает, что линии магнитной индукции всегда замкнуты, и полный магнитный поток через замкнутую поверхность равен нулю. Этот факт является следствием отсутствия магнитных зарядов в природе. |
|
Теги:
конспект
Карта сайта
Главная Обучение Библиотека Карта сайта
|
Урок-открытие по теме «Электромагнитная индукция»
Цели урока:
- познакомиться с новыми свойствами электрического и магнитного полей, с явлением электромагнитной индукции; выяснить, что гипотеза и эксперимент являются методами научного познания;
- расширить кругозор при изучении истории открытия электромагнитной индукции; выявить место этого явления в жизни людей, изучить его практическое значение, развить интерес учащихся к предмету.

- воспитание убеждённости в возможности познания законов и использовании их в практической жизни на благо человека, а также воспитания уважения к учёным, которые отдавали себя науке целиком.
Оборудование: гальванометр, две катушки, магнит, реостат, ключ, подковообразный магнит, соединительные провода, стальной стержень, источник питания; интерактивная доска.
I. Организационный момент. II. Новый материал.Учитель: Здравствуйте! Мы с вами продолжаем изучать электродинамику – физику электромагнитных явлений. Сегодня у нас необычный урок. Мы попытаемся «открыть» новое для вас явление, которое было открыто Майклом Фарадеем в XIX веке. Это явление – электромагнитная индукция. Цель нашего урока – ознакомиться со свойствами уже известных вам электрического и магнитного полей, убедиться в единстве материального мира, убедиться в том, что гипотеза и эксперимент являются методами познания мира; Выявить место этого явления в электродинамике, в физике в целом и в жизни людей.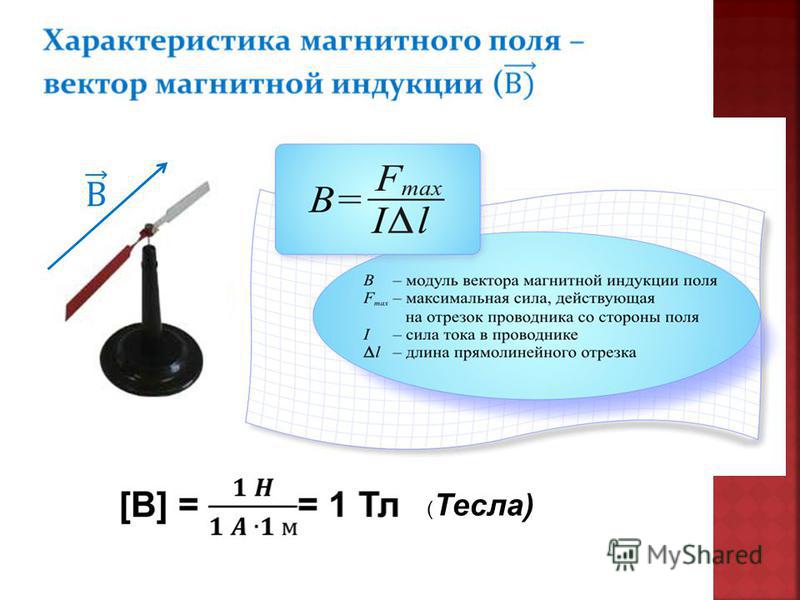
На открытие нам отводится всего 45 минут, Майкл Фарадей решал эту задачу 10 лет.
Давайте представим себе, что мы с вами находимся в XIX веке, в лаборатории Фарадея. Конечно, наши приборы отличаются от тех, что были тогда, да и многое из того, о чём Фарадей даже не догадывался, нам уже известно. Ему потребовалось для открытия годы, заполненные поисками, догадками, удачными и неудачными экспериментами. Как известно в науке нет столбовой дороги, и отрицательный результат не менее важен для учёного, чем положительный.
Фарадей годами носил в жилетном кармане маленький полосовой магнитит и проволочную катушку как постоянное напоминание о ещё нерешенной проблеме. Его дневники заполнялись аккуратно сделанными записями о результатах бесчисленных экспериментов.
Пусть наши тетради станут на сегодняшнем уроке рабочими дневниками, в которые мы будем заносить результаты наших исследований.
Открываем тетради и записываем: «ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ».
Давайте сейчас вспомним тот рубеж, на котором мы остановились при изучении электродинамики. Вы знаете, что вокруг любых неподвижных зарядов существует электрическое поле, а если эти заряды заставить упорядоченно двигаться, т.е. создать электрический ток, то вокруг этих упорядоченно движущихся зарядов возникает магнитное поле. Очевидно, что между электрическим и магнитным полями существует теснейшая зависимость.
Электрический ток способен намагнитить кусок железа, а не может ли магнит, в свою очередь, вызвать появление электрического тока?
Итак, выдвигаем проблему МОЖЕТ ЛИ МАГНИТНОЕ ПОЛЕ ВЫЗВАТЬ ПОЯВЛЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА?
Обратимся к эксперименту. Возьмём гальванометр, полосовой магнит, две катушки, реостат, ключ, источник питания. Вспомним назначение каждого из этих устройств и условное обозначение на схеме.
(фронтальный опрос – беседа)
Воросы:
- Для чего служит гальванометр?
- Как обозначается на схеме?
- Для чего служит реостат?
- Как обозначается на схеме?
- Что вы знаете об этом предмете? (полосовой магнит)
- Что произойдёт, если по проводнику пропустить электрический ток?
- А для чего нужен ключ в электрических цепях?
- Для чего служит источник питания?
Учитель: Катушка представляет собой проводник, намотанный на каркас.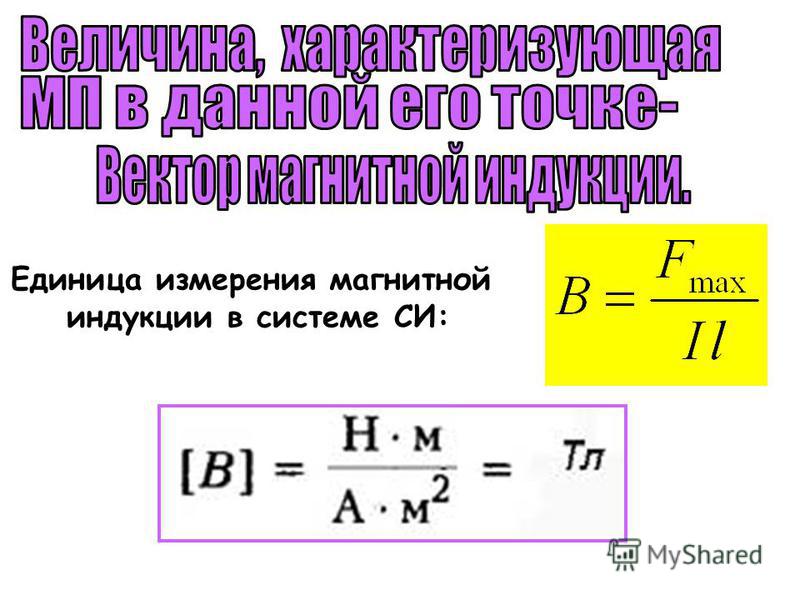 Такая катушка соединённая с источником питания, представляет собой электромагнит. Следовательно, если мы катушку соединим с источником питания, то вокруг неё возникает магнитное поле. А для чего нужен ключ в электрических цепях?
Такая катушка соединённая с источником питания, представляет собой электромагнит. Следовательно, если мы катушку соединим с источником питания, то вокруг неё возникает магнитное поле. А для чего нужен ключ в электрических цепях?
Учитель: А теперь переходим к экспериментам, но прежде давайте ещё раз вспомним какую проблему мы хотим решить.
У нас имеется полосовой магнит, вокруг которого существует магнитное поле, катушка – проводник, в котором должен появиться электрический ток, и гальванометр, который должен зафиксировать появление тока.
(Проводится эксперимент: магнит располагается рядом с катушкой, катушка присоединяется к гальванометру).
Вопрос по ходу эксперимента: Появился ток?
Ответ: Нет
Вопрос по ходу эксперимента: Изменим положение катушки магнита. Магнит помещаем в катушку. Есть ток?
Ответ: Нет.
Учитель: Долгое время учёным также, как и нам сейчас не удавалось обнаружить связь тока и магнитного поля. Почти одновременно с Фарадеем получить электрический в катушке с помощью магнита пытался швейцарский физик Колладон. Индикатор тока – гальванометром служила лёгкая магнитная стрелка. Что бы избежать влияние на неё постоянного магнита, который вдвигался в катушку, эта стрелка была вынесена в соседнюю комнату, туда же были протянуты провода от катушки. Вставив магнит в катушку, Колладон шел в соседнюю комнату и с огорчением убеждался, что гальванометр ничего не показывает. Изменим опыт. Соединим катушку с гальванометром, а затем внесём магнит в катушку и вынесем из катушки. (Опыт проводит ученик)
Почти одновременно с Фарадеем получить электрический в катушке с помощью магнита пытался швейцарский физик Колладон. Индикатор тока – гальванометром служила лёгкая магнитная стрелка. Что бы избежать влияние на неё постоянного магнита, который вдвигался в катушку, эта стрелка была вынесена в соседнюю комнату, туда же были протянуты провода от катушки. Вставив магнит в катушку, Колладон шел в соседнюю комнату и с огорчением убеждался, что гальванометр ничего не показывает. Изменим опыт. Соединим катушку с гальванометром, а затем внесём магнит в катушку и вынесем из катушки. (Опыт проводит ученик)
Вопрос по ходу эксперимента: Что мы видим?
Ответ: В катушке появился электрический ток!
Вопрос по ходу эксперимента: Почему он не появлялся в первых двух случаях и появился сейчас?
Ответ: Магнит был неподвижен, а теперь двигается.
Учитель: совершенно верно. Трудно было додуматься до главного, а именно только движущийся магнит или меняющееся во времени магнитное поле может возбудить электрический ток в катушке. Что же помешало Колладону сделать это открытие?
Что же помешало Колладону сделать это открытие?
Класс: Во время движения магнита он должен был находиться у гальванометра, а он в это время был у магнита.
Учитель: Правильно. Открыть явление электромагнитной индукции помешала неправильная постановка опыта.
А можно этот же опыт провести иначе, если в качестве магнита взять ещё одну катушку, соединённую с источником питания. (Учитель собирает цепь и поясняет).
Одна катушка подключена к источнику питания, создаёт магнитное поле, а во второй во время её движения должен появиться электрический ток. (Вызванный к доске ученик проводит эксперимент – поднимает и опускает катушку относительно сердечника).
Вот мы с вами и «открыли» явление электромагнитной индукции, которое заключается в возникновении электрического тока в проводящем контуре, который либо покоится в переменном во времени магнитном поле, либо движется в постоянном магнитном поле таким образом, что число линий магнитной индукции, пронизывающий контур, постоянно меняется.
Откройте учебник и найдите вывод. Давайте прочитаем его и запишем:
«В ЗАМКНУТОМ ПРОВОДЯЩЕМ КОНТУРЕ ВОЗНИКАЕТ ТОК ПРИ ИЗМЕНЕНИИ ЧИСЛА ЛИНИЙ МАГНИТНОЙ ИНДУКЦИИ, ПРОНИЗЫВАЮЩИЙ ПОВЕРХНОСТЬ, ОГРАНИЧЕННУЮ ЭТИМ КОНТУРОМ».
Учитель: Теперь давайте послушаем несколько сообщений о Майкле Фарадее.
1 сообщение
Явление электромагнитной индукции было открыто 29 августа 1831 г. редкий случай, когда дата нового замечательного открытия известна точно. Вот описание первого опыта, данное самим Фарадеем в его работе «Экспериментальное исследования по электричеству». «На широкую деревянную катушку была намотана медная проволока длиной 203 фута (1 фут равен 30,5 см) Между её витками намотана проволока такой же длины, но изолированная от первой хлопковой нитью. Одна из этих спиралей была соединена с гальванометром, а другая с сильной батареей…при замыкании цепи удавалось заметить внезапное, но чрезвычайное слабое действие на гальванометр, то же самое замечалось при прекращении тока. При непрерывном прохождении тока через одну из спиралей не удавалось отметить ни действия на гальванометр, ни вообще какого – либо индукционного действия на другую спираль…»
При непрерывном прохождении тока через одну из спиралей не удавалось отметить ни действия на гальванометр, ни вообще какого – либо индукционного действия на другую спираль…»
В дневнике Фарадея записана дата исторического открытия явления…
2 сообщение
Фарадей родился в предместье Лондона в 1791 году. Он рано узнал нужду, рос среди простых людей.
Варильщиц пива,
Женщин – пекарей,
И шестобитчиц видел.
И ткачих,
Портных и пошлин сборщиков на рынках,
И медников, и множество других, —
Иак описывает Хуш В. Окружение будущего учёного. Отец его был кузнецом, мать – горничной. В возрасте 14 лет он поступил в переплётную мастерскую. Увлёкшись чтением книг по электричеству и химии, он сам проделывает описанные в них опыты. В 1813 г. Фарадей поступает на работу в лабораторию профессора Деви в качестве ассистента. А затем начинает самостоятельные исследования.
В 1813 г. Фарадей поступает на работу в лабораторию профессора Деви в качестве ассистента. А затем начинает самостоятельные исследования.
3 сообщение
Вообще Фарадей не щадил себя, занимаясь наукой. Серьёзно укоротили его жизнь химические опыты, в которых обильно использовалась ртуть. Она беспрерывно (хотя и ненамеренно) проливалась на пол, а затем испарялась. Оборудование его лаборатории было абсолютно непригодным с точки зрения самой элементарной техники безопасности.
Вот письмо самого Фарадея: «В прошлую субботу у меня случился ещё один взрыв, который опять поранил мне глаза. Одна из моих трубок разлетелась с такой силой, что осколком пробило оконное стекло, точно ружейной пулей. Мне теперь лучше, я надеюсь, что через несколько дней буду видеть так же хорошо, как и раньше. Но в первое мгновение после взрыва глаза мои были прямо – таки набиты крошками стекла. Из них вынули тридцать осколков».
Золотая голова, золотые руки, невероятное упорство и любовь к науке – вот секрет успеха Фарадея.
Учитель: Открытия Фарадея получили всемирное признание. Русский учёный Столетов писал: «Никогда со времён Галилея свет не видел стольких поразительных и разнообразных открытий, вышедших из одной головы, и едва ли скоро увидит другого Фарадея». Скажите, вам уже Фарадея?
Ответ: Закон электролиза носит имя Фарадея.
Учитель: А теперь попробуем выяснить некоторые свойства возникающие при электромагнитной индукции тока.
Обратимся к нашему первому опыту. Попробуем двигать магнит в катушку разными полюсами. Видим, что направление возникающего в катушке индукционного тока зависит от тока, каким полюсом мы вносим магнит, — южным или северным.
Попробуем изменить скорость внесения и вынесения магнита. Что наблюдаем?
Ответ: Чем быстрее перемещается магнит относительно катушки, тем больше индукционный ток.
Учитель: Причина – изменение числа линий магнитной индукции, пронизывающих все витки катушки. При этом совершенно безразлично, что двигать: магнит или катушку.
Проделаем опыт с реостатом. Если изменить силу тока в катушке, то будет меняться и магнитное поле внутри неё. Это изменение также вызовет индукционный ток во второй катушке, который и зафиксирует гальванометр.
Обратимся к нашим дневникам и запишем в них эти два свойства индукционного тока:
- Направление индукционного тока зависит от ориентации полюсов магнита
- Величина индукционного тока зависит от скорости изменения числа линий магнитной индукции, пронизывающий контур. И не зависит от способа этого изменения.
Таким образом, мы выяснили и обобщили свойства возникающего индукционного тока, а более подробно познакомимся на следующих уроках.
Сейчас поговорим о применении электромагнитной индукции. Удивительно далеко вперёд смотрел Майкл Фарадей. Ведь «польза» превращения магнетизма в электричество выявилось много лет спустя. Фарадей вывел науку об электричестве из лаборатории. 3362 параграфа его знаменитой книги «опытные исследования по электричеству» — вот итог его работы. Без появления этой книги (написанной без единой формулы, но содержащий описание тончайших опытов) невозможно представить электротехнику. Там указан путь к современным электрогенераторам. Фарадей не только описал принцип действия нового устройства, но построил и испытал его.
3362 параграфа его знаменитой книги «опытные исследования по электричеству» — вот итог его работы. Без появления этой книги (написанной без единой формулы, но содержащий описание тончайших опытов) невозможно представить электротехнику. Там указан путь к современным электрогенераторам. Фарадей не только описал принцип действия нового устройства, но построил и испытал его.
Фарадей установил между полюсами подковообразного магнита вращающийся медный диск, с которого при помощи скользящих контактов (один на оси, другой на периферии диска) можно было снимать электрическое напряжение. Это был первый – униполярный – электрический генератор.
Сегодня без генераторов мы не можем представить себе ни энергетику, ни транспорт.
Открытие электромагнитной индукции подготовило почву для другого грандиозного открытия, сделанного Герцем, — открытие электромагнитных волн. А это, в свою очередь, вызвало развитие радио, телевидения.
Нельзя умолчать и о том, что явление электромагнитной индукции лежит в основе действия телефона.
4 сообщение.
Первый практически пригодный для передачи человеческой речи телефон изобрёл Александр Грейман Белл.
25 июня 1876 г. 29-летний Белл впервые публично продемонстрировал свой телефон на I Всемирной электротехнической выставке в Филадельфии. Каким же было первое сообщение переданное по телефону?
Белл передал своему помощнику фразу: «говорит Белл. Если вы меня слышите, то подойдите к окну и помашите шляпой».
В телефоне Белла для передачи и для приёма использовались одинаковые устройства – так называемые трубки Белла, основными деталями, которых были электромагнит и рупор с кожаной мембраной и жесткой прикреплённой ней тягой. Когда человек говорит в рупор, мембрана колебалась под действием изменяющего звукового давления и через прикреплённую к её центру тягу приводила в движение сердечник электромагнита, подсоединенного к батарее. Изменение положения сердечника относительно обмотки вызывало изменение магнитного потока. В результате в общей однопроводной цепи, соединяющий передатчик с приёмником, постоянный ток преобразовывался в переменный ток звуковой частоты.
В результате в общей однопроводной цепи, соединяющий передатчик с приёмником, постоянный ток преобразовывался в переменный ток звуковой частоты.
Конструкция первого телефона А.Белла
Соответственно к её сердечнику другого (приёмного) электромагнита с разной силой и частотой притягивалась тяга, которая заставляла колебаться приёмную мембрану. Приёмный рупор воспроизводил те же звуки, что произносились в передающий рупор.
Давайте вспомним, с каким физическим явлением мы сегодня познакомились?
В чём состоит это явление?
III. Закрепление нового материала.Учитель: Предлагаю разгадать кроссворд в котором отражены некоторые моменты сегодняшнего урока.
Кроссворд
Вопросы.
- Наука об общих закономерностях природы. (физика)
- Проводник намотанный на каркас.
 (катушка)
(катушка) - Катушка, соединенная с источником тока (электромагнит)
- Явление возникновения тока в проводящем контуре при изменении числа линий магнитной индукции, пронизывающий его (индукция)
- Шотландский учёный, создавший первый телефон (Белл)
- Раздел физики, в котором изучают электромагнитные явления(электродинамика)
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А теперь давайте решим экспериментальную задачу.
Катушку от универсального трансформатора (на 220 В) установили на кольце штатива и подключили к гальванометру. Над ней закрепили сильный подковообразный магнит, а внутрь ввели железный стержень (длиной 25-30 см и диаметром 6-10 мм). Перемещайте стержень от одного полюса магнита к другому.. Почему при этом возникает ток?
Ответ: при перемещении стержня от полюса к полюсу он перемагничивается. В результате магнитное поле внутри стержня и вокруг него меняется. Это изменение магнитного поля возбуждает в катушке ЭДС индукции, а последняя создаёт ток в цепи.
IV. Подведение итогов.Вывод:
- Мы решили поставленную проблему: выяснили, что магнитное поле может вызвать появление электрического тока, т.е. Открыли явление электромагнитной индукции.
- Познакомились с историей этого вопроса
- Осознали роль эксперимента в науке
- Узнали новые факты об учёных, внесших свой вклад в развитие науки
- Расширили свой кругозор
Пройденная тема очень важна для радиотехники.
внимательно прочитайте записи урока и желающие могут подготовить презентации по теме: «Электромагнитная индукция»
Тесла физическая единица измерения си магнитной индукции
Тесла.
Тесла – единица измерения плотности магнитного потока, напряжённости и индукции магнитного поля в Международной системе единиц (СИ). Тесла как единица измерения имеет русское обозначение – Тл и международное обозначение – T.
Тесла, как единица измерения
Применение тесла
Представление тесла в других единицах измерения – формулы
Перевод тесла в другие единицы измерения
Кратные и дольные единицы тесла
Интересные примеры
Другие единицы измерения
Тесла, как единица измерения:
Тесла – единица измерения плотности магнитного потока, напряжённости и индукции магнитного поля в Международной системе единиц (СИ), названная в честь изобретателя Николы Теслы.
Тесла как единица измерения имеет русское обозначение – Тл и международное обозначение – T.
1 тесла равен индукции такого однородного магнитного поля, в котором на 1 метр длины прямого проводника, перпендикулярного вектору магнитной индукции, с током силой 1 ампер действует сила 1 ньютон. Другими словами, один тесла равен напряжённости поля, действующего на проводник с силой один ньютон на метр проводника при силе тока на каждый ампер тока.
Аналогично, один тесла представляет собой плотность магнитного потока в один вебер на квадратный метр площади.
Тл = кг / (с2 · А) = Н / (А · м) = Вб / м2.
1 Тл = 1 кг / (1 с2 · 1 А) = 1 Н / (1 А · 1 м) = 1 Вб / 1 м2.
В Международную систему единиц тесла введён решением XI Генеральной конференцией по мерам и весам в 1960 году, одновременно с принятием системы СИ в целом. В соответствии с правилами СИ, касающимися производных единиц, названных по имени учёных, наименование единицы «тесла» пишется со строчной буквы, а её обозначение — с заглавной (Тл). Такое написание обозначения сохраняется и в обозначениях производных единиц, образованных с использованием теслы.
Такое написание обозначения сохраняется и в обозначениях производных единиц, образованных с использованием теслы.
Применение тесла:
В теслах измеряют плотность магнитного потока, напряжённость и индукцию магнитного поля.
Представление тесла в других единицах измерения – формулы:
Через основные и производные единицы системы СИ тесла выражается следующим образом:
Тл = кг / (с2 · А).
Тл = Н / (А · м).
Тл = Вб / м2.
Тл = В · с / м2.
где Тл – тесла, А – ампер, В – вольт, Вб – вебер, Н – ньютон, м – метр, с – секунда, кг – килограмм.
Перевод тесла в другие единицы измерения:
1 Тл = 10 000 гаусс.
1 Тл = 1⋅109 гамма.
Кратные и дольные единицы тесла:
Кратные и дольные единицы образуются с помощью стандартных приставок СИ.
| Кратные | Дольные | ||||||
| величина | название | обозначение | величина | название | обозначение | ||
| 101 Тл | декатесла | даТл | daT | 10−1 Тл | децитесла | дТл | dT |
| 102 Тл | гектотесла | гТл | hT | 10−2 Тл | сантитесла | сТл | cT |
| 103 Тл | килотесла | кТл | kT | 10−3 Тл | миллитесла | мТл | mT |
| 106 Тл | мегатесла | МТл | MT | 10−6 Тл | микротесла | мкТл | µT |
| 109 Тл | гигатесла | ГТл | GT | 10−9 Тл | нанотесла | нТл | nT |
| 1012 Тл | тератесла | ТТл | TT | 10−12 Тл | пикотесла | пТл | pT |
| 1015 Тл | петатесла | ПТл | PT | 10−15 Тл | фемтотесла | фТл | fT |
| 1018 Тл | эксатесла | ЭТл | ET | 10−18 Тл | аттотесла | аТл | aT |
| 1021 Тл | зеттатесла | ЗТл | ZT | 10−21 Тл | зептотесла | зТл | zT |
| 1024 Тл | иоттатесла | ИТл | YT | 10−24 Тл | иоктотесла | иТл | yT |
Интересные примеры:
Во внешнем космосе магнитная индукция составляет от 0,1 до 10 нанотесла (от 10−10 Тл до 10−8 Тл).
Магнитное поле Земли значительно варьируется во времени и пространстве. На широте 50° магнитная индукция в среднем составляет 5⋅10−5 Тл, а на экваторе (широта 0°) — 3,1⋅10−5 Тл.
Сувенирный магнит на холодильнике создает поле около 5 миллитесла (5⋅10−3 Тл).
В солнечных пятнах магнитная индукция составляет 10 Тл.
Рекордное значение импульсного магнитного поля, когда-либо наблюдавшегося в лаборатории – 2,8⋅103 Тл.
Магнитные поля в атомах составляют от 1 до 10 килотесла (103 – 104 Тл).
Источник: https://ru.wikipedia.org/wiki/Тесла_(единица_измерения)
Примечание: © Фото https://www.pexels.com, https://pixabay.com
тл тесла физическая единица измерения си магнитной индукции физическая величина физика википедия
какая физическая величина имеет единицу 1 тесла
Коэффициент востребованности 4 300
22.1: Магнитный поток, индукция и закон Фарадея
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 15654
цели обучения
- Объяснить взаимосвязь между магнитным полем и электродвижущей силой
Индуцированная ЭДС
Устройство, которое Фарадей использовал для демонстрации того, что магнитные поля могут создавать токи, показано на следующем рисунке.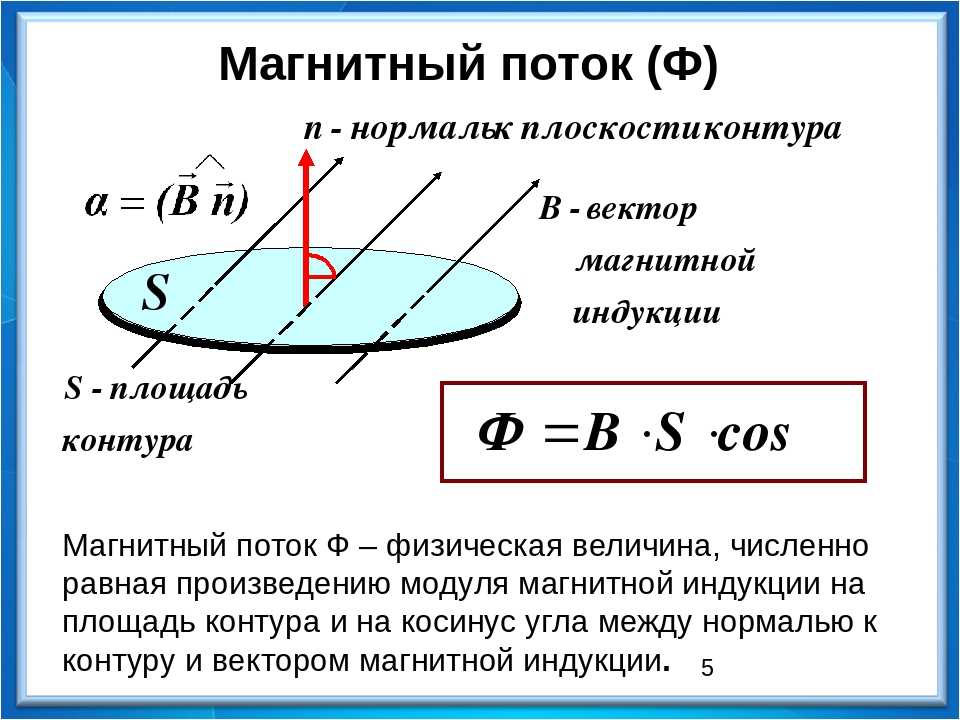 Когда переключатель замкнут, магнитное поле создается в катушке в верхней части железного кольца и передается (или направляется) на катушку в нижней части кольца. Гальванометр используется для обнаружения любого тока, наведенного в отдельной катушке на дне.
Когда переключатель замкнут, магнитное поле создается в катушке в верхней части железного кольца и передается (или направляется) на катушку в нижней части кольца. Гальванометр используется для обнаружения любого тока, наведенного в отдельной катушке на дне.
Аппарат Фарадея : Это аппарат Фарадея для демонстрации того, что магнитное поле может производить ток. Изменение поля, создаваемого верхней катушкой, индуцирует ЭДС и, следовательно, ток в нижней катушке. Когда переключатель размыкается и замыкается, гальванометр регистрирует токи в противоположных направлениях. Через гальванометр не протекает ток, когда переключатель остается замкнутым или разомкнутым.
Было обнаружено, что каждый раз, когда переключатель замыкается, гальванометр регистрирует ток в одном направлении в катушке на дне. Каждый раз, когда переключатель размыкается, гальванометр регистрирует ток в противоположном направлении. Интересно, что если переключатель остается замкнутым или разомкнутым какое-то время, ток через гальванометр отсутствует.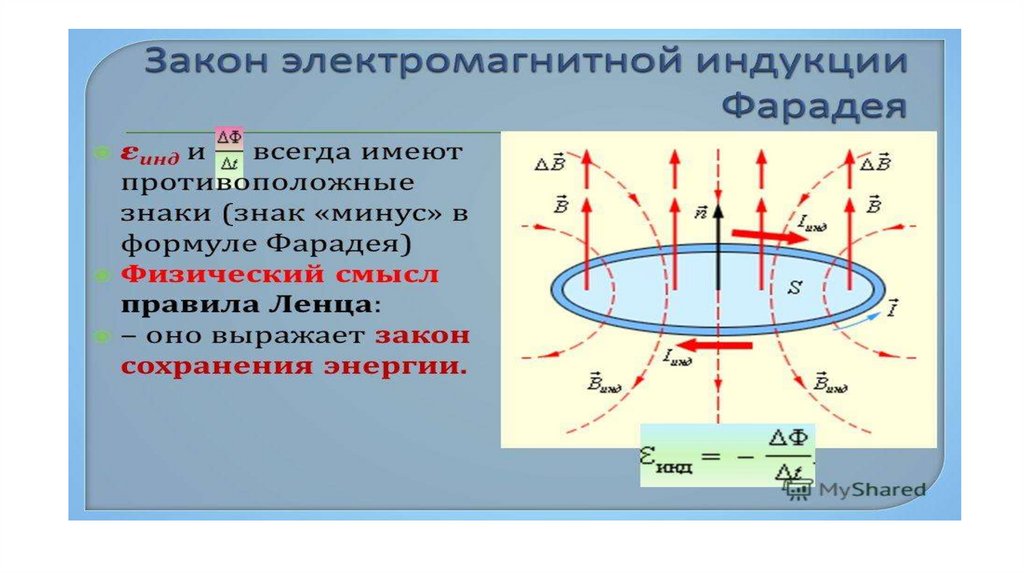 Замыкание и размыкание переключателя индуцирует ток. Именно изменение магнитного поля создает ток. Более важным, чем текущий ток, является электродвижущая сила (ЭДС), которая его вызывает. Ток является результатом ЭДС, индуцированной изменяющимся магнитным полем, независимо от того, есть ли путь для протекания тока.
Замыкание и размыкание переключателя индуцирует ток. Именно изменение магнитного поля создает ток. Более важным, чем текущий ток, является электродвижущая сила (ЭДС), которая его вызывает. Ток является результатом ЭДС, индуцированной изменяющимся магнитным полем, независимо от того, есть ли путь для протекания тока.
Магнитный поток
Магнитный поток (часто обозначаемый Φ или Φ B ) через поверхность представляет собой компонент магнитного поля, проходящего через эту поверхность. Магнитный поток через некоторую поверхность пропорционален числу силовых линий, проходящих через эту поверхность. Магнитный поток, проходящий через поверхность векторной площади A, равен
\[\Phi _ {\mathrm {B}} = \mathbf {B} \cdot \mathbf{A} = \mathrm{B} \mathrm{A} \cos \theta\]
где B — величина магнитного поля (в единицах Тесла, Тл), A — площадь поверхности, а θ — угол между силовыми линиями магнитного поля и нормалью (перпендикуляр ) к А.
Для переменного магнитного поля сначала рассмотрим магнитный поток dΦBdΦB через элемент бесконечно малой площади dA, где мы можем считать поле постоянным:
Переменное магнитное поле направление, называемое нормалью к поверхности; тогда магнитный поток через точку является составляющей магнитного поля вдоль этого нормального направления.
\mathrm {d} \Phi _ {\mathrm {B}} = \mathbf {B} \cdot \mathrm{d} \mathbf{A}
Общая поверхность A затем может быть разбита на бесконечно малые элементы, и тогда общий магнитный поток через поверхность представляет собой поверхностный интеграл
\[\Phi _ { \mathrm { B } } = \iint _ { \mathrm { A } } \mathbf { B } \cdot \mathrm { d } \mathbf { A }\]
Закон индукции Фарадея и закон Ленца
Закон индукции Фарадея утверждает, что ЭДС, вызванная изменением магнитного потока, равна \(\mathrm { ЭДС } = — \mathrm { N } \frac { \Delta \Phi } { \Delta \mathrm{t}}\), когда поток изменяется на Δ за время Δt.
цели обучения
- Выразите закон индукции Фарадея в форме уравнения
Закон индукции Фарадея
Закон индукции Фарадея — это основной закон электромагнетизма, который предсказывает, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу (ЭДС). Это основной принцип работы трансформаторов, катушек индуктивности и многих типов электродвигателей, генераторов и соленоидов.
Эксперименты Фарадея показали, что ЭДС, вызванная изменением магнитного потока, зависит лишь от нескольких факторов. Во-первых, ЭДС прямо пропорциональна изменению потока Δ. Во-вторых, ЭДС максимальна, когда изменение времени Δt наименьшее, то есть ЭДС обратно пропорциональна Δt. Наконец, если катушка имеет N витков, будет создаваться ЭДС, которая в N раз больше, чем для одиночной катушки, так что ЭДС прямо пропорциональна N. Уравнение для ЭДС, индуцированной изменением магнитного потока, имеет вид 9.0024
\[\mathrm { ЭДС } = — \mathrm { N } \dfrac { \Delta \Phi } { \Delta \mathrm { t } }\]
Это соотношение известно как закон индукции Фарадея. Единицами ЭДС, как обычно, являются вольты.
Закон Ленца
Знак минус в законе индукции Фарадея очень важен. Минус означает, что ЭДС создает ток I и магнитное поле B, противодействующие изменению потока Δ, это известно как закон Ленца. Направление (заданное знаком минус) ЭДС настолько важно, что его называют законом Ленца в честь русского Генриха Ленца (1804–1865), который, подобно Фарадею и Генри, независимо исследовал аспекты индукции. Фарадей знал об этом направлении, но Ленц указал его, поэтому ему приписывают его открытие.
Фарадей знал об этом направлении, но Ленц указал его, поэтому ему приписывают его открытие.
Закон Ленца : (а) Когда этот стержневой магнит вставляется в катушку, напряженность магнитного поля в катушке увеличивается. Ток, наведенный в катушке, создает другое поле в направлении, противоположном направлению стержневого магнита, чтобы противостоять увеличению. Это один из аспектов закона Ленца: индукция препятствует любому изменению потока. (b) и (c) — две другие ситуации. Убедитесь сами, что показанное направление индуцированной катушки B действительно противостоит изменению потока и что показанное направление тока согласуется с правилом правой руки.
Сохранение энергии
Закон Ленца является проявлением сохранения энергии. Индуцированная ЭДС создает ток, противодействующий изменению потока, потому что изменение потока означает изменение энергии. Энергия может войти или уйти, но не мгновенно. Закон Ленца является следствием. Когда изменение начинается, закон говорит, что индукция противодействует и, таким образом, замедляет изменение. На самом деле, если бы индуцированная ЭДС была направлена в том же направлении, что и изменение потока, существовала бы положительная обратная связь, которая давала бы нам свободную энергию без видимого источника — закон сохранения энергии был бы нарушен.
На самом деле, если бы индуцированная ЭДС была направлена в том же направлении, что и изменение потока, существовала бы положительная обратная связь, которая давала бы нам свободную энергию без видимого источника — закон сохранения энергии был бы нарушен.
ЭДС движения
Движение в магнитном поле, стационарном относительно Земли, индуцирует ЭДС движения (электродвижущая сила).
цели обучения
- Определить процесс, вызывающий движущую электродвижущую силу
Как видно из предыдущих Атомов, любое изменение магнитного потока индуцирует электродвижущую силу (ЭДС), противодействующую этому изменению — процесс, известный как индукция. Движение является одной из основных причин индукции. Например, магнит, перемещаемый к катушке, индуцирует ЭДС, а катушка, перемещаемая к магниту, создает аналогичную ЭДС. В этом Атоме мы концентрируемся на движении в магнитном поле, стационарном относительно Земли, производя то, что можно условно назвать ЭДС движения.
ЭДС движения
Рассмотрим ситуацию, показанную на рис. Стержень движется со скоростью v по паре проводящих рельсов, разделенных расстоянием ℓ в однородном магнитном поле B. Рельсы неподвижны относительно B и соединены с постоянный резистор R (резистор может быть любым, от лампочки до вольтметра). Рассмотрим область, окруженную движущимся стержнем, рельсами и резистором. B перпендикулярна этой площади, и площадь увеличивается по мере движения стержня. Таким образом, магнитный поток, заключенный между рельсами, стержнем и резистором, увеличивается. При изменении потока индуцируется ЭДС в соответствии с законом индукции Фарадея.
ЭДС движения : (a) ЭДС движения=Bℓv индуцируется между рельсами, когда этот стержень движется вправо в однородном магнитном поле. Магнитное поле B направлено внутрь страницы, перпендикулярно движущимся стержню и рельсам и, следовательно, ограниченной ими области. (b) Закон Ленца дает направления индуцированного поля и тока, а также полярность индуцированной ЭДС. Поскольку поток увеличивается, индуцированное поле направлено в противоположном направлении или выходит за пределы страницы. Правило правой руки дает показанное направление тока, и полярность стержня будет управлять таким током.
Поскольку поток увеличивается, индуцированное поле направлено в противоположном направлении или выходит за пределы страницы. Правило правой руки дает показанное направление тока, и полярность стержня будет управлять таким током.
Чтобы найти величину ЭДС, индуцированной вдоль движущегося стержня, воспользуемся законом индукции Фарадея без знака:
\[\mathrm { ЭДС } = \mathrm { N } \frac { \Delta \Phi } { \Delta \mathrm { t } } \]
В этом уравнении N=1 и поток Φ=BAcosθ. Имеем θ=0º и cosθ=1, так как B перпендикулярно A. Теперь \(\mathrm{Δ=Δ(BA)=BΔA}\), так как B однородно. Обратите внимание, что площадь, заметаемая стержнем, равна \(\ mathrm{ΔA=ℓx}\). Ввод этих величин в выражение для ЭДС дает:
\[\mathrm { ЭДС } = \dfrac { \mathrm { B } \Delta \mathrm { A } } { \Delta \mathrm { t } } = \mathrm { B } \dfrac { l \Delta \ mathrm { x } } { \Delta \mathrm { t } } = \mathrm { B } \mathrm { lv } \]
Чтобы найти направление индуцированного поля, направление тока и полярность индуцированной ЭДС, мы применить закон Ленца, как объясняется в Законе индукции Фарадея: Закон Ленца. Как видно на рис. 1 (b), поток увеличивается, так как увеличивается площадь охвата. Таким образом, индуцированное поле должно противостоять существующему и быть за пределами страницы. (Правило правой руки требует, чтобы я вращался против часовой стрелки, что, в свою очередь, означает, что вершина стержня положительна, как показано.)
Как видно на рис. 1 (b), поток увеличивается, так как увеличивается площадь охвата. Таким образом, индуцированное поле должно противостоять существующему и быть за пределами страницы. (Правило правой руки требует, чтобы я вращался против часовой стрелки, что, в свою очередь, означает, что вершина стержня положительна, как показано.)
Электрическое поле и магнитное поле
Существует много связей между электрической силой и магнитной силой. То, что движущееся магнитное поле создает электрическое поле (и наоборот, что движущееся электрическое поле создает магнитное поле), является одной из причин, по которой электрические и магнитные силы теперь рассматриваются как различных проявления одной и той же силы (впервые замеченной Альбертом Эйнштейном). . Это классическое объединение электрических и магнитных сил в то, что называется 9Электромагнитная сила 0134 является источником вдохновения для современных усилий по объединению других основных сил.
Обратная ЭДС, вихревые токи и магнитное демпфирование
Обратная ЭДС, вихревые токи и магнитное демпфирование являются следствием индуцированной ЭДС и могут быть объяснены законом индукции Фарадея.
цели обучения
- Объяснить взаимосвязь между движущей электродвижущей силой, вихревыми токами и магнитным демпфированием
Задний ЭДС
Моторы и генераторы очень похожи. (Читайте наши атомы в разделе «Электрические генераторы» и «Электродвигатели».) Генераторы преобразуют механическую энергию в электрическую, тогда как двигатели преобразуют электрическую энергию в механическую. Кроме того, двигатели и генераторы имеют одинаковую конструкцию. Когда катушка двигателя поворачивается, магнитный поток изменяется, и индуцируется электродвижущая сила (ЭДС), соответствующая закону индукции Фарадея. Таким образом, двигатель действует как генератор всякий раз, когда его катушка вращается. Это произойдет независимо от того, вращается ли вал с помощью внешнего источника, такого как ременная передача, или под действием самого двигателя. То есть, когда двигатель совершает работу и его вал вращается, возникает ЭДС. Закон Ленца говорит нам, что ЭДС индукции противостоит любым изменениям, поэтому входной ЭДС, питающей двигатель, будет противодействовать ЭДС, создаваемая самим двигателем, называемая обратной ЭДС двигателя.
Вихревой ток
Как обсуждалось в разделе «ЭДС движения», ЭДС движения индуцируется, когда проводник движется в магнитном поле или когда магнитное поле движется относительно проводника. Если ЭДС движения может вызвать петлю с током в проводнике, мы называем этот ток вихревым током. Вихревые токи могут создавать значительное сопротивление, называемое магнитным демпфированием, при соответствующем движении.
Рассмотрим устройство, показанное на рис., которое раскачивает маятник между полюсами сильного магнита. Если поплавок металлический, при входе в поле и выходе из него возникает значительное сопротивление, что быстро гасит движение. Если, однако, груз представляет собой металлическую пластину с прорезями, как показано на (b), эффект магнита будет намного меньше. Никакого заметного влияния на боб, сделанный из изолятора, не наблюдается.
Устройство для изучения вихревых токов и магнитного демпфирования : Обычное физическое демонстрационное устройство для изучения вихревых токов и магнитного демпфирования. а) Движение металлического маятника, качающегося между полюсами магнита, быстро затухает под действием вихревых токов. (b) На движение металлического поплавка с прорезями мало влияет, что означает, что вихревые токи становятся менее эффективными. (c) На непроводящем грузе также нет магнитного демпфирования, поскольку вихревые токи чрезвычайно малы.
а) Движение металлического маятника, качающегося между полюсами магнита, быстро затухает под действием вихревых токов. (b) На движение металлического поплавка с прорезями мало влияет, что означает, что вихревые токи становятся менее эффективными. (c) На непроводящем грузе также нет магнитного демпфирования, поскольку вихревые токи чрезвычайно малы.
показывает, что происходит с металлической пластиной, когда она входит и выходит из магнитного поля. В обоих случаях на него действует сила, противодействующая его движению. Когда он входит слева, поток увеличивается, поэтому возникает вихревой ток (закон Фарадея) в направлении против часовой стрелки (закон Ленца), как показано. В поле находится только правая сторона контура тока, так что слева на него действует непротиворечивая сила (правило правой руки). Когда металлическая пластина находится полностью внутри поля, вихревой ток отсутствует, если поле однородно, так как поток в этой области остается постоянным. Но когда пластина покидает поле справа, поток уменьшается, вызывая вихревой ток в направлении по часовой стрелке, который, опять же, испытывает силу влево, еще больше замедляя движение. Аналогичный анализ того, что происходит, когда пластина качается справа налево, показывает, что ее движение также затухает при входе в поле и выходе из него.
Аналогичный анализ того, что происходит, когда пластина качается справа налево, показывает, что ее движение также затухает при входе в поле и выходе из него.
Проводящая пластина, проходящая между полюсами магнита : Более подробный вид на проводящую пластину, проходящую между полюсами магнита. Когда он входит в поле и выходит из него, изменение потока вызывает вихревой ток. Магнитная сила на токовой петле противодействует движению. Когда пластина полностью находится внутри однородного поля, ток и магнитное сопротивление отсутствуют.
Когда металлическая пластина с прорезями входит в поле, как показано на рисунке, ЭДС индуцируется изменением потока, но она менее эффективна, поскольку прорези ограничивают размер токовых петель. Более того, в соседних петлях есть токи в противоположных направлениях, и их эффекты компенсируются. При использовании изоляционного материала вихревые токи чрезвычайно малы, поэтому магнитным демпфированием на изоляторах можно пренебречь. Если необходимо избежать вихревых токов в проводниках, то они могут быть щелевыми или изготовлены из тонких слоев проводящего материала, разделенных изоляционными листами.
Если необходимо избежать вихревых токов в проводниках, то они могут быть щелевыми или изготовлены из тонких слоев проводящего материала, разделенных изоляционными листами.
Вихревые токи, индуцированные в металлической пластине с прорезями : Вихревые токи, индуцированные в металлической пластине с прорезями, попадая в магнитное поле, образуют небольшие петли, и действующие на них силы имеют тенденцию компенсироваться, тем самым делая магнитное сопротивление почти нулевым.
Изменение магнитного потока создает электрическое поле
Закон индукции Фарадея гласит, что изменение магнитного поля создает электрическое поле: \(\varepsilon = — \frac { \partial \Phi _ { \mathrm { B } } } { \partial \mathrm{t}}\).
цели обучения
- Описать взаимосвязь между изменяющимся магнитным полем и электрическим полем
Мы изучили закон индукции Фарадея в предыдущих атомах. Мы узнали взаимосвязь между индуцированной электродвижущей силой (ЭДС) и магнитным потоком.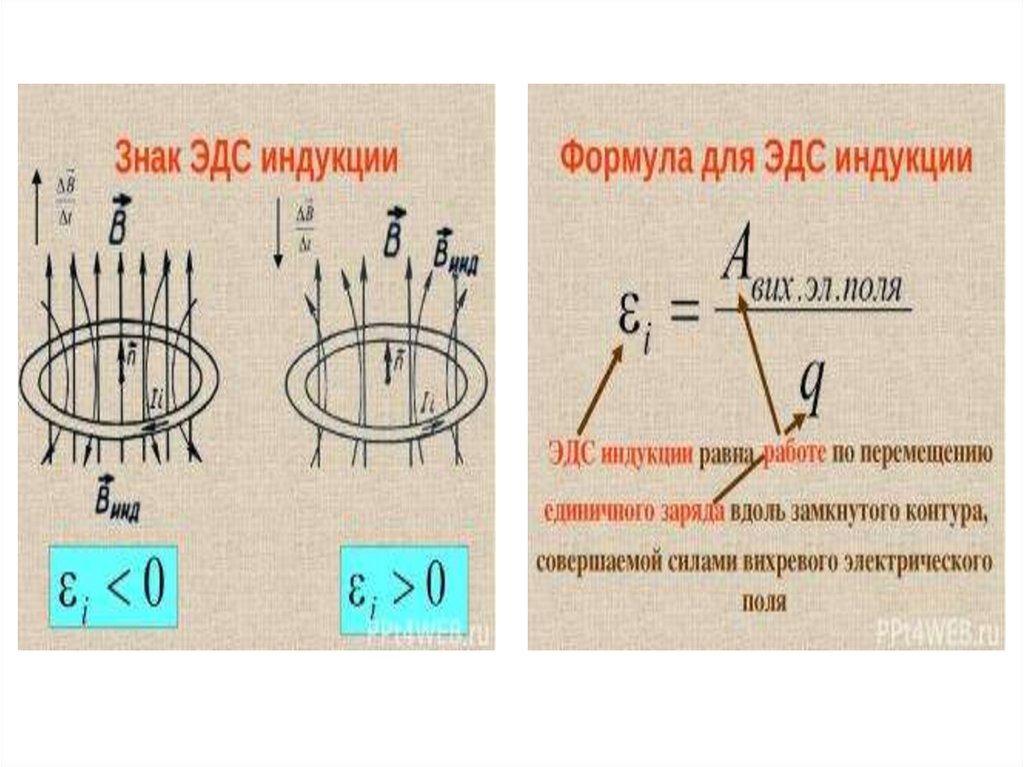 В двух словах, закон гласит, что изменение магнитного поля (\ (\ frac { d \ Phi _ { \ mathrm {B} } } {\ mathrm {d t}} \)) создает электрическое поле (\ (ε \)) , закон индукции Фарадея выражается как \(\varepsilon = — \frac {\partial \Phi _ {\mathrm { B } } } { \partial \mathrm { t } }\), где \(ε\) индуцируется ЭДС и \ (\ frac { d \ Phi _ { \ mathrm {B} } } {\ mathrm { d t}} \) — магнитный поток. («N» опущено из нашего предыдущего выражения. Количество включенных витков катушки может быть включено в магнитный поток, поэтому этот коэффициент не является обязательным.) Закон индукции Фарадея — это основной закон электромагнетизма, который предсказывает, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу (ЭДС). В этом Атоме мы узнаем об альтернативном математическом выражении закона.
В двух словах, закон гласит, что изменение магнитного поля (\ (\ frac { d \ Phi _ { \ mathrm {B} } } {\ mathrm {d t}} \)) создает электрическое поле (\ (ε \)) , закон индукции Фарадея выражается как \(\varepsilon = — \frac {\partial \Phi _ {\mathrm { B } } } { \partial \mathrm { t } }\), где \(ε\) индуцируется ЭДС и \ (\ frac { d \ Phi _ { \ mathrm {B} } } {\ mathrm { d t}} \) — магнитный поток. («N» опущено из нашего предыдущего выражения. Количество включенных витков катушки может быть включено в магнитный поток, поэтому этот коэффициент не является обязательным.) Закон индукции Фарадея — это основной закон электромагнетизма, который предсказывает, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу (ЭДС). В этом Атоме мы узнаем об альтернативном математическом выражении закона.
Эксперимент Фарадея : Эксперимент Фарадея, показывающий индукцию между витками провода: Жидкостная батарея (справа) обеспечивает ток, который течет через маленькую катушку (А), создавая магнитное поле. Когда катушки неподвижны, ток не индуцируется. Но когда малая катушка перемещается внутри или снаружи большой катушки (В), магнитный поток через большую катушку изменяется, вызывая ток, который регистрируется гальванометром (G).
Когда катушки неподвижны, ток не индуцируется. Но когда малая катушка перемещается внутри или снаружи большой катушки (В), магнитный поток через большую катушку изменяется, вызывая ток, который регистрируется гальванометром (G).
Дифференциальная форма закона Фарадея
Магнитный поток равен \(\Phi _ { \mathrm { B } } = \int _ { \mathrm { S } } \vec { \mathrm { B } } \cdot \mathrm { d } \vec { \mathrm { A } }\) где \(\mathrm{\vec { A }} \) — площадь вектора над замкнутой поверхностью S. Устройство, способное поддерживать разность потенциалов, несмотря на протекание тока, является источником электродвижущей силы . (EMF) Определение математически \(\varepsilon = \oint _ {\mathrm {C}} \vec {\mathrm {E}} \cdot \mathrm{d} \vec{\mathrm{s}}\), где интеграл вычисляется по замкнутому контуру C.
Теперь закон Фарадея можно переписать \(\oint _ { \mathrm { C } } \vec { \mathrm { E } } \cdot \mathrm { d } \vec { \mathrm { s } } = — \frac { \partial } { \partial \mathrm { t } } \left( \int \vec { \mathrm { B } } \cdot \mathrm { d } \vec { \mathrm { A } } \right)\). Используя теорему Стокса в векторном исчислении, левая часть равна \(\oint _ {\mathrm {C}} \vec {\mathrm {E}} \cdot \mathrm{d} \vec{\mathrm{s} } = \int _ {\mathrm{S}} (\nabla\times\vec{\mathrm{E}})\cdot\mathrm{d}\vec{\mathrm{A}}\). Также обратите внимание, что в правой части \(\frac { \partial } { \partial \mathrm { t } } \left( \int \vec { \mathrm { B } } \cdot \mathrm { d } \vec { \mathrm { A } } \right) = \int \frac { \partial \vec { \mathrm { B } } } { \partial \mathrm { t } } \cdot \mathrm { d } \vec { \mathrm { A } }\). Таким образом, мы получаем альтернативную форму закона индукции Фарадея: mathrm { t } } \). Это также называется дифференциальной формой закона Фарадея. Это одно из четырех уравнений Максвелла, управляющих всеми электромагнитными явлениями.
Используя теорему Стокса в векторном исчислении, левая часть равна \(\oint _ {\mathrm {C}} \vec {\mathrm {E}} \cdot \mathrm{d} \vec{\mathrm{s} } = \int _ {\mathrm{S}} (\nabla\times\vec{\mathrm{E}})\cdot\mathrm{d}\vec{\mathrm{A}}\). Также обратите внимание, что в правой части \(\frac { \partial } { \partial \mathrm { t } } \left( \int \vec { \mathrm { B } } \cdot \mathrm { d } \vec { \mathrm { A } } \right) = \int \frac { \partial \vec { \mathrm { B } } } { \partial \mathrm { t } } \cdot \mathrm { d } \vec { \mathrm { A } }\). Таким образом, мы получаем альтернативную форму закона индукции Фарадея: mathrm { t } } \). Это также называется дифференциальной формой закона Фарадея. Это одно из четырех уравнений Максвелла, управляющих всеми электромагнитными явлениями.
Электрические генераторы
Электрические генераторы преобразуют механическую энергию в электрическую; они индуцируют ЭДС, вращая катушку в магнитном поле.
цели обучения
- Объяснить, как электродвижущая сила индуцируется в электрических генераторах
Электрические генераторы — это устройства, преобразующие механическую энергию в электрическую. Они индуцируют электродвижущую силу (ЭДС), вращая катушку в магнитном поле. Это устройство, которое преобразует механическую энергию в электрическую. Генератор заставляет электрический заряд (обычно переносимый электронами) течь через внешнюю электрическую цепь. К возможным источникам механической энергии относятся: поршневой или турбинный паровой двигатель, вода, падающая через турбину или водяное колесо, двигатель внутреннего сгорания, ветряная турбина, рукоятка, сжатый воздух или любой другой источник механической энергии. Генераторы обеспечивают почти всю мощность для электросетей, которые обеспечивают большую часть мировой электроэнергии.
Они индуцируют электродвижущую силу (ЭДС), вращая катушку в магнитном поле. Это устройство, которое преобразует механическую энергию в электрическую. Генератор заставляет электрический заряд (обычно переносимый электронами) течь через внешнюю электрическую цепь. К возможным источникам механической энергии относятся: поршневой или турбинный паровой двигатель, вода, падающая через турбину или водяное колесо, двигатель внутреннего сгорания, ветряная турбина, рукоятка, сжатый воздух или любой другой источник механической энергии. Генераторы обеспечивают почти всю мощность для электросетей, которые обеспечивают большую часть мировой электроэнергии.
Генератор паровой турбины : Современный генератор паровой турбины.
Базовая установка
Рассмотрим установку, показанную на рис. Заряды в проводах петли испытывают магнитную силу, поскольку они движутся в магнитном поле. На заряды в вертикальных проводах действуют силы, параллельные проводу, вызывающие токи. Однако те, кто находится в верхнем и нижнем сегментах, чувствуют силу, перпендикулярную проводу; эта сила не вызывает тока. Таким образом, мы можем найти ЭДС индукции, рассматривая только боковые провода. ЭДС движения определяется как ЭДС=Bℓv, где скорость v перпендикулярна магнитному полю B (см. наш атом на «ЭДС движения»). Здесь скорость составляет угол θ с B, так что ее составляющая, перпендикулярная B, равна vsinθ.
Однако те, кто находится в верхнем и нижнем сегментах, чувствуют силу, перпендикулярную проводу; эта сила не вызывает тока. Таким образом, мы можем найти ЭДС индукции, рассматривая только боковые провода. ЭДС движения определяется как ЭДС=Bℓv, где скорость v перпендикулярна магнитному полю B (см. наш атом на «ЭДС движения»). Здесь скорость составляет угол θ с B, так что ее составляющая, перпендикулярная B, равна vsinθ.
Схема электрического генератора : Генератор с одной прямоугольной катушкой, вращающейся с постоянной угловой скоростью в однородном магнитном поле, создает ЭДС, которая изменяется синусоидально во времени. Обратите внимание, что генератор похож на двигатель, за исключением того, что вал вращается для создания тока, а не наоборот.
Таким образом, в этом случае ЭДС, индуцированная с каждой стороны, равна ЭДС=Bℓvsinθ, и они имеют одинаковое направление. Суммарная ЭДС εε вокруг контура тогда равна:
\[\varepsilon = 2 \mathrm { Blv } \sin \theta\]
Это выражение верно, но оно не дает ЭДС как функцию времени. Для нахождения зависимости ЭДС от времени предположим, что катушка вращается с постоянной угловой скоростью ω. Угол θ связан с угловой скоростью соотношением \(\mathrm{θ=ωt}\), так что:
Для нахождения зависимости ЭДС от времени предположим, что катушка вращается с постоянной угловой скоростью ω. Угол θ связан с угловой скоростью соотношением \(\mathrm{θ=ωt}\), так что:
\[\varepsilon = 2 \mathrm { Blv } \sin \omega \mathrm { t }\]
Теперь линейная скорость v связана с угловой скоростью соотношением \(\mathrm{v=rω}\). Здесь \(\mathrm{r=w/2}\), так что \(\mathrm{v=(w/2)ω}\), и:
\[\varepsilon = 2 \mathrm {B} l \frac {\mathrm{w}} {2} \omega \sin \omega \mathrm{t} = (\operatorname{lw}) \mathrm{B} \omega \sin \omega \mathrm { t }\]
Заметив, что площадь цикла равна \(\mathrm{A=ℓw}\), и учитывая N циклов, мы находим, что:
\(\ varepsilon = \mathrm { NABw } \sin \omega t\) — ЭДС, индуцируемая в генераторной катушке из N витков и площадью A, вращающейся с постоянной угловой скоростью в однородном магнитном поле B.
Генераторы, изображенные в этом атоме, выглядят очень очень похоже на двигатели, показанные ранее. Это не случайно. Фактически двигатель становится генератором, когда его вал вращается.
Фактически двигатель становится генератором, когда его вал вращается.
Электродвигатели
Цели обучения
- Объяснить, как создается сила в электродвигателях
Электродвигатель представляет собой устройство, преобразующее электрическую энергию в механическую.
Основные принципы работы двигателя такие же, как у генератора, за исключением того, что двигатель преобразует электрическую энергию в механическую (движение). (Сначала прочитайте наш атом об электрических генераторах.) Большинство электродвигателей используют взаимодействие магнитных полей и проводников с током для создания силы. Электродвигатели используются в таких разнообразных областях, как промышленные вентиляторы, воздуходувки и насосы, станки, бытовая техника, электроинструменты и дисковые накопители.
Сила Лоренца
Если бы вы поместили движущуюся заряженную частицу в магнитное поле, она испытала бы силу, называемую силой Лоренца:
\[\mathrm { F } = \mathrm { q } \times \mathrm { v } \times \mathrm { B }\]
Правило правой руки : Правило правой руки, показывающее направление силы Лоренца
где v скорость движущегося заряда, q — заряд, а B — магнитное поле. Ток в проводнике состоит из движущихся зарядов. Следовательно, катушка с током в магнитном поле также будет ощущать силу Лоренца. Для прямолинейного провода с током, который не движется, сила Лоренца равна:
Ток в проводнике состоит из движущихся зарядов. Следовательно, катушка с током в магнитном поле также будет ощущать силу Лоренца. Для прямолинейного провода с током, который не движется, сила Лоренца равна:
\[\mathrm{ F } = \mathrm { I } \times \mathrm { L } \times \mathrm { B }\]
где F сила (в ньютонах, Н), I — сила тока в проводе (в амперах, А), L — длина провода, находящегося в магнитном поле (в м), B — напряженность магнитного поля (в теслах, Тл). Направление силы Лоренца перпендикулярно как направлению тока, так и магнитному полю, и его можно найти с помощью правила правой руки, показанного на рис. Правой рукой направьте большой палец в направлении тока, и укажите пальцем в направлении магнитного поля. Теперь ваш безымянный палец будет указывать в направлении силы.
Крутящий момент : Сила на противоположных сторонах катушки будет действовать в противоположных направлениях, потому что заряды движутся в противоположных направлениях. Это означает, что катушка будет вращаться.
Это означает, что катушка будет вращаться.
Механика двигателя
И двигатели, и генераторы можно описать с точки зрения катушки, которая вращается в магнитном поле. В генераторе катушка подключается к внешней цепи, которая затем включается. Это приводит к изменению потока, который индуцирует электромагнитное поле. В двигателе катушка с током в магнитном поле испытывает силу с обеих сторон катушки, которая создает крутящую силу (называемую крутящим моментом), которая заставляет ее вращаться. Любая катушка с током может чувствовать силу в магнитном поле. Эта сила представляет собой силу Лоренца, действующую на движущиеся заряды в проводнике. Сила на противоположных сторонах катушки будет противоположной, потому что заряды движутся в противоположных направлениях. Это означает, что катушка будет вращаться.
Индуктивность
Индуктивность — это свойство устройства, которое показывает, насколько эффективно оно индуцирует ЭДС в другом устройстве или на самом себе.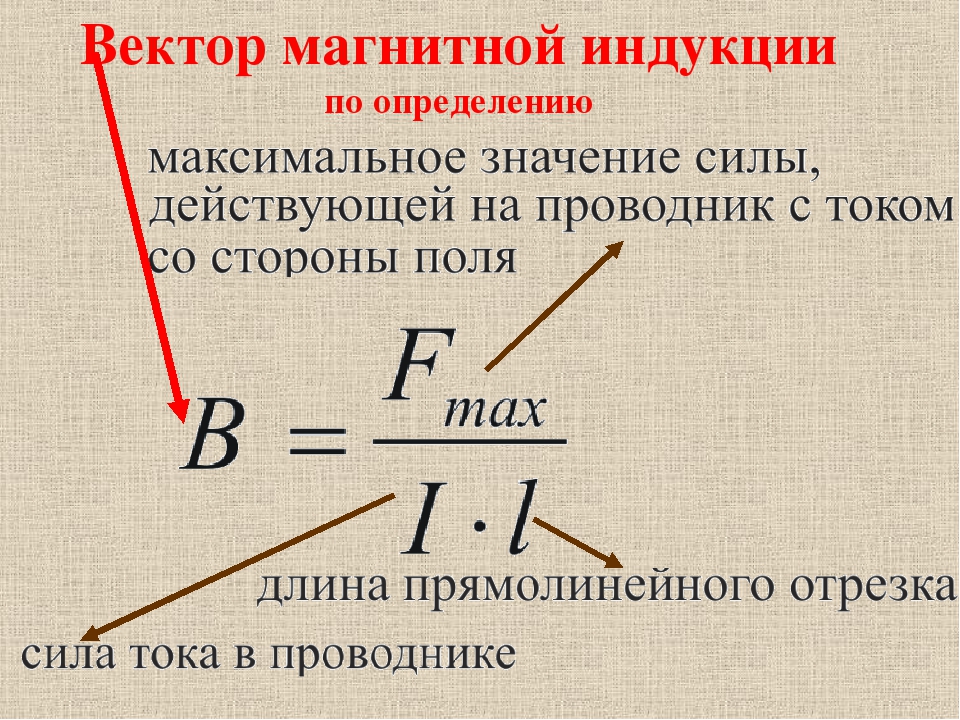
цели обучения
- Описать свойства катушки индуктивности, различая взаимную индуктивность и самоиндукцию
Индукция – это процесс, при котором ЭДС индуцируется изменением магнитного потока. Трансформаторы, например, спроектированы так, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшой потерей энергии в другие формы (см. наш Atom в «Трансформаторах»). Существует ли полезная физическая величина, связанная с тем, насколько «эффективен» трансформатор? данное устройство есть? Ответ положительный, и эта физическая величина называется индуктивностью.
Взаимная индуктивность
Взаимная индуктивность — это действие закона индукции Фарадея для одного устройства на другое, например первичная катушка при передаче энергии вторичной в трансформаторе. Посмотрите, где простые катушки наводят друг в друге ЭДС.
Взаимная индуктивность в катушках : Эти катушки могут индуцировать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность М указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 индуцирует ЭДС в катушке 2. (Обратите внимание, что «E2 индуцируется» представляет ЭДС индукции в катушке 2.)
Их взаимная индуктивность М указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 индуцирует ЭДС в катушке 2. (Обратите внимание, что «E2 индуцируется» представляет ЭДС индукции в катушке 2.)
Во многих случаях, когда геометрия устройств фиксирована, поток изменяется за счет изменения тока. Поэтому мы сосредоточимся на скорости изменения тока ΔI/Δt как на причине индукции. Изменение тока I 1 в одном устройстве, катушке 1, индуцирует ЭДС 2 в другом. Выразим это в виде уравнения как }\]
где M определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность М, тем эффективнее связь.
Природа здесь симметрична. Если мы изменим ток I2 в катушке 2, мы индуцируем ЭДС1 в катушке 1, которая определяется как I } _ { 2 } } { \Delta \mathrm { t } }\]
где M такое же, как и для обратного процесса. Трансформаторы работают в обратном направлении с той же эффективностью, или взаимной индуктивностью М.
Самоиндукция
Самоиндукция, действие закона Фарадея об индукции устройства на себя, также существует. Когда, например, ток через катушку увеличивается, магнитное поле и поток также увеличиваются, индуцируя противо-ЭДС, как того требует закон Ленца. И наоборот, если ток уменьшается, индуцируется ЭДС, препятствующая уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение потока полностью связано с изменением тока ΔI через устройство. ЭДС индукции связана с физической геометрией устройства и скоростью изменения тока. Это дается
\[\mathrm { ЭДС } = — \mathrm { L } \dfrac { \Delta \mathrm { I } } { \Delta \mathrm { t } } \]
где L — собственная индуктивность устройства . Устройство, обладающее значительной собственной индуктивностью, называется индуктором. Опять же, знак минус является выражением закона Ленца, указывающим, что ЭДС противодействует изменению тока.
A Количественная интерпретация ЭДС движения
A ЭДС движения – это электродвижущая сила (ЭДС), индуцированная движением относительно магнитного поля B.
цели обучения
- Сформулируйте два вида, которые применяются для расчета электродвижущей силы
Электродвижущая сила (ЭДС), вызванная движением относительно магнитного поля B, называется ЭДС движения. Вы могли заметить, что ЭДС движения очень похожа на индуцированную ЭДС, вызванную изменяющимся магнитным полем. В этом Атоме мы видим, что это действительно одно и то же явление, показанное в разных системах отсчета.
ЭДС движения
В случае, когда петля проводника движется в магнит, показанный на (а), магнитная сила, действующая на движущийся заряд в петле, определяется как evBevB (сила Лоренца, e: заряд электрона).
Петля проводника, перемещающаяся в магнит : (a) ЭДС движения. Петля с током движется в неподвижный магнит. Направление магнитного поля на экран. (б) Наведенная ЭДС. Токовая петля неподвижна, а магнит движется.
Под действием силы электроны будут накапливаться на одной стороне (нижний конец рисунка) до тех пор, пока на стержне не установится достаточное электрическое поле, противодействующее движению электронов, что равно \(\mathrm{eE}\) . Приравнивая две силы, получаем \(\mathrm{E=vB}\).
Приравнивая две силы, получаем \(\mathrm{E=vB}\).
Следовательно, ЭДС движения по длине L стороны петли определяется выражением \(\mathrm{ε_{motion}=vB \times L}\) (уравнение 1), где L — длина тело движется со скоростью v относительно магнита.
ЭДС индукции
Поскольку скорость изменения магнитного потока, проходящего через петлю, равна \(\mathrm{B\frac{dA}{dt}}\)(A: площадь петли, через которую проходит магнитное поле) , индуцированная ЭДС \(\mathrm{ε_{induced}=BLv}\) (уравнение 2).
Эквивалентность ЭДС движения и индукции
Из уравнения 1 и уравнение 2 мы можем подтвердить, что ЭДС движения и индукции дают одинаковый результат. На самом деле эквивалентность этих двух явлений и побудила Альберта Эйнштейна заняться специальной теорией относительности. В своей основополагающей статье по специальной теории относительности, опубликованной в 1905 году, Эйнштейн начинает с упоминания об эквивалентности двух явлений:
«……например, взаимное электродинамическое действие магнита и проводника. Наблюдаемое здесь явление зависит только от относительного движения проводника и магнита, тогда как обычная точка зрения проводит резкое различие между двумя случаями, в которых движется то одно, то другое из этих тел. В самом деле, если магнит находится в движении, а проводник покоится, то вблизи магнита возникает электрическое поле с некоторым определенным энергия , производящая ток в местах расположения частей проводника. Но если магнит неподвижен, а проводник движется, то вблизи магнита не возникает никакого электрического поля. В проводнике, однако, мы находим электродвижущую силу, которой самой по себе нет соответствующей энергии, но которая порождает — при условии равенства относительного движения в двух обсуждаемых случаях — электрические токи того же пути и силы, что и производимые электрическими силами в первом случае.
Наблюдаемое здесь явление зависит только от относительного движения проводника и магнита, тогда как обычная точка зрения проводит резкое различие между двумя случаями, в которых движется то одно, то другое из этих тел. В самом деле, если магнит находится в движении, а проводник покоится, то вблизи магнита возникает электрическое поле с некоторым определенным энергия , производящая ток в местах расположения частей проводника. Но если магнит неподвижен, а проводник движется, то вблизи магнита не возникает никакого электрического поля. В проводнике, однако, мы находим электродвижущую силу, которой самой по себе нет соответствующей энергии, но которая порождает — при условии равенства относительного движения в двух обсуждаемых случаях — электрические токи того же пути и силы, что и производимые электрическими силами в первом случае.
Механическая работа и электрическая энергия
Механическая работа, совершаемая внешней силой для создания ЭДС движения, преобразуется в тепловую энергию; в процессе сохраняется энергия.
цели обучения
- Применить закон сохранения энергии для описания производства движущей электродвижущей силы с механической работой
Мы узнали об ЭДС движения ранее (см. наш Атом в разделе «ЭДС движения»). Для простой установки, показанной ниже, ЭДС движения (ε)(ε), создаваемая движущимся проводником (в однородном поле), определяется следующим образом:
\[\mathrm{ε=Blv}\]
где B — магнитное поле, l — длина проводящего стержня, v — (постоянная) скорость его движения. ( B , l и v перпендикулярны друг другу, как показано на рисунке ниже.)
ЭДС движения : (a) ЭДС движения = Bℓv индуцируется между рельсами, когда этот стержень движется вправо в однородном магнитном поле. Магнитное поле B направлено внутрь страницы, перпендикулярно движущимся стержню и рельсам и, следовательно, ограниченной ими области. (b) Закон Ленца дает направления индуцированного поля и тока, а также полярность индуцированной ЭДС. Поскольку поток увеличивается, индуцированное поле направлено в противоположном направлении или выходит за пределы страницы. Правило правой руки дает показанное направление тока, и полярность стержня будет управлять таким током.
Поскольку поток увеличивается, индуцированное поле направлено в противоположном направлении или выходит за пределы страницы. Правило правой руки дает показанное направление тока, и полярность стержня будет управлять таким током.
Сохранение энергии
В этом атоме мы рассмотрим систему с точки зрения энергии . Когда стержень движется и несет ток i , он будет ощущать силу Лоренца постоянной скорости v , мы должны постоянно прикладывать внешнюю силу F ext (равную по модулю F L и противоположную по направлению) к стержню вдоль его движения. Так как стержень движется в v , мощность P , передаваемая внешней силой, будет: iBL } ) \times \mathrm { v } = \mathrm { i } \varepsilon\]
На последнем этапе мы использовали первое уравнение, о котором говорили. Обратите внимание, что это именно мощность, рассеиваемая в контуре (\(\mathrm{= ток \умножить на напряжение}\)). Таким образом, мы заключаем, что механическая работа, совершаемая внешней силой для поддержания движения стержня с постоянной скоростью, преобразуется в тепловую энергию в петле. В более общем смысле механическая работа, совершаемая внешней силой для создания ЭДС движения, преобразуется в тепловую энергию. Энергия сохраняется в процессе.
В более общем смысле механическая работа, совершаемая внешней силой для создания ЭДС движения, преобразуется в тепловую энергию. Энергия сохраняется в процессе.
Закон Ленца
В «Атоме» «Закон индукции Фарадея и закон Ленца» мы узнали, что закон Ленца является проявлением закона сохранения энергии. Как мы видим на примере с этим атомом, закон Ленца гарантирует, что движение стержня противоположно из-за тенденции природы сопротивляться изменению магнитного поля. Если бы индуцированная ЭДС была направлена в ту же сторону, что и изменение потока, то существовала бы положительная обратная связь, заставляющая стержень улетать от малейшего возмущения.
Энергия в магнитном поле
Магнитное поле накапливает энергию. Плотность энергии задается как \ (\ mathbf { u } = \ frac { \ mathbf { B } \ cdot \ mathbf { B } } { 2 \ mu } \).
цели обучения
- Выразите плотность энергии магнитного поля в форме уравнения
Энергия необходима для создания магнитного поля как для работы против электрического поля, создаваемого изменяющимся магнитным полем, так и для изменения намагниченности любого материала в пределах магнитного поля. Для недисперсионных материалов эта же энергия высвобождается при разрушении магнитного поля. Следовательно, эту энергию можно смоделировать как «запасенную» в магнитном поле.
Для недисперсионных материалов эта же энергия высвобождается при разрушении магнитного поля. Следовательно, эту энергию можно смоделировать как «запасенную» в магнитном поле.
Магнитное поле, создаваемое соленоидом : Магнитное поле, создаваемое соленоидом (вид в поперечном сечении), описанное линиями поля. Энергия «запасается» в магнитном поле.
Энергия, накопленная в магнитном поле
Для линейных, недисперсионных материалов (таких, что B = µ H, где µ, называемая магнитной проницаемостью, не зависит от частоты), плотность энергии равна:
\ [\ mathrm { u } = \ dfrac { \ mathbf { B } \ cdot \ mathbf { B } } { 2 \ mu } = \ dfrac { \ mu \ mathbf { H } \ cdot \ mathbf { H } } { 2 } \]
Плотность энергии — это количество энергии, хранящейся в данной системе или области пространства на единицу объема. Если поблизости нет магнитных материалов, μ можно заменить на μ 0 . Однако приведенное выше уравнение нельзя использовать для нелинейных материалов; необходимо использовать более общее выражение (приведенное ниже).
В общем, дополнительная работа на единицу объема δW , необходимая для того, чтобы вызвать небольшое изменение магнитного поля δ B, составляет:
\[\delta \mathrm { W } = \mathbf { H } \cdot \delta \mathbf { B }\]
Как только отношение между H и B известно, это уравнение используется для определения работы, необходимой для достижения заданное магнитное состояние. Для гистерезисных материалов, таких как ферромагнетики и сверхпроводники, необходимая работа также зависит от того, как создается магнитное поле. Однако для линейных недисперсионных материалов общее уравнение приводит непосредственно к более простому уравнению плотности энергии, приведенному выше.
{ 2 }\]
Трансформаторы
Трансформаторы преобразуют напряжение из одного значения в другое; его функция определяется уравнением трансформатора.
цели обучения
- Применение уравнения трансформатора для сравнения вторичного и первичного напряжения
Трансформаторы изменяют напряжение с одного значения на другое. Например, такие устройства, как сотовые телефоны, ноутбуки, видеоигры, электроинструменты и небольшие бытовые приборы, имеют трансформатор (встроенный в их съемный блок), который преобразует 120 В в напряжение, подходящее для устройства. Трансформаторы также используются в нескольких точках в системах распределения электроэнергии, как показано на рис. . Энергия передается на большие расстояния при высоком напряжении, поскольку для заданной мощности требуется меньший ток (это означает меньшие потери в линии). Поскольку высокое напряжение представляет большую опасность, для получения более низкого напряжения в месте расположения пользователя используются трансформаторы.
Например, такие устройства, как сотовые телефоны, ноутбуки, видеоигры, электроинструменты и небольшие бытовые приборы, имеют трансформатор (встроенный в их съемный блок), который преобразует 120 В в напряжение, подходящее для устройства. Трансформаторы также используются в нескольких точках в системах распределения электроэнергии, как показано на рис. . Энергия передается на большие расстояния при высоком напряжении, поскольку для заданной мощности требуется меньший ток (это означает меньшие потери в линии). Поскольку высокое напряжение представляет большую опасность, для получения более низкого напряжения в месте расположения пользователя используются трансформаторы.
Настройка трансформатора : Трансформаторы изменяют напряжение в нескольких точках системы распределения электроэнергии. Электроэнергия обычно вырабатывается при напряжении более 10 кВ и передается на большие расстояния при напряжении более 200 кВ, иногда до 700 кВ, для ограничения потерь энергии. Местное распределение электроэнергии в районы или предприятия проходит через подстанцию и передается на короткие расстояния при напряжении от 5 до 13 кВ. Оно снижено до 120, 240 или 480 В для обеспечения безопасности на объекте отдельного пользователя.
Местное распределение электроэнергии в районы или предприятия проходит через подстанцию и передается на короткие расстояния при напряжении от 5 до 13 кВ. Оно снижено до 120, 240 или 480 В для обеспечения безопасности на объекте отдельного пользователя.
Рассматриваемый здесь тип трансформатора основан на законе индукции Фарадея и очень похож по конструкции на аппарат Фарадея, который использовался для демонстрации того, что магнитные поля могут создавать токи (показано на рис. ). Две катушки называются первичной и вторичной катушками. При нормальном использовании входное напряжение подается на первичную обмотку, а вторичная создает преобразованное выходное напряжение. Железный сердечник не только улавливает магнитное поле, создаваемое первичной катушкой, но и увеличивает его намагниченность. Поскольку входное напряжение переменного тока, изменяющийся во времени магнитный поток направляется на вторичную обмотку, индуцируя ее выходное напряжение переменного тока.
Простой трансформатор : Типичная конструкция простого трансформатора состоит из двух катушек, намотанных на ферромагнитный сердечник, ламинированный для минимизации вихревых токов. Магнитное поле, создаваемое первичной обмоткой, в основном ограничивается и усиливается сердечником, который передает его вторичной обмотке. Любое изменение тока в первичной обмотке индуцирует ток во вторичной обмотке. На рисунке показан простой трансформатор с двумя катушками, намотанными по обеим сторонам многослойного ферромагнитного сердечника. Набор катушек на левой стороне сердечника помечен как первичный, а его номер указан как N p. Напряжение на первичной обмотке определяется как V p. Набор катушек на правой стороне сердечника помечен как вторичный, а их количество представлено как Ns. Напряжение на вторичной обмотке определяется как V s. Символ трансформатора также показан под диаграммой. Он состоит из двух катушек индуктивности, разделенных двумя равными параллельными линиями, представляющими сердечник.
Магнитное поле, создаваемое первичной обмоткой, в основном ограничивается и усиливается сердечником, который передает его вторичной обмотке. Любое изменение тока в первичной обмотке индуцирует ток во вторичной обмотке. На рисунке показан простой трансформатор с двумя катушками, намотанными по обеим сторонам многослойного ферромагнитного сердечника. Набор катушек на левой стороне сердечника помечен как первичный, а его номер указан как N p. Напряжение на первичной обмотке определяется как V p. Набор катушек на правой стороне сердечника помечен как вторичный, а их количество представлено как Ns. Напряжение на вторичной обмотке определяется как V s. Символ трансформатора также показан под диаграммой. Он состоит из двух катушек индуктивности, разделенных двумя равными параллельными линиями, представляющими сердечник.
Уравнение трансформатора
Для простого трансформатора, показанного на рис., выходное напряжение V s почти полностью зависит от входного напряжения V p и соотношения числа витков в первичной и вторичной обмотках.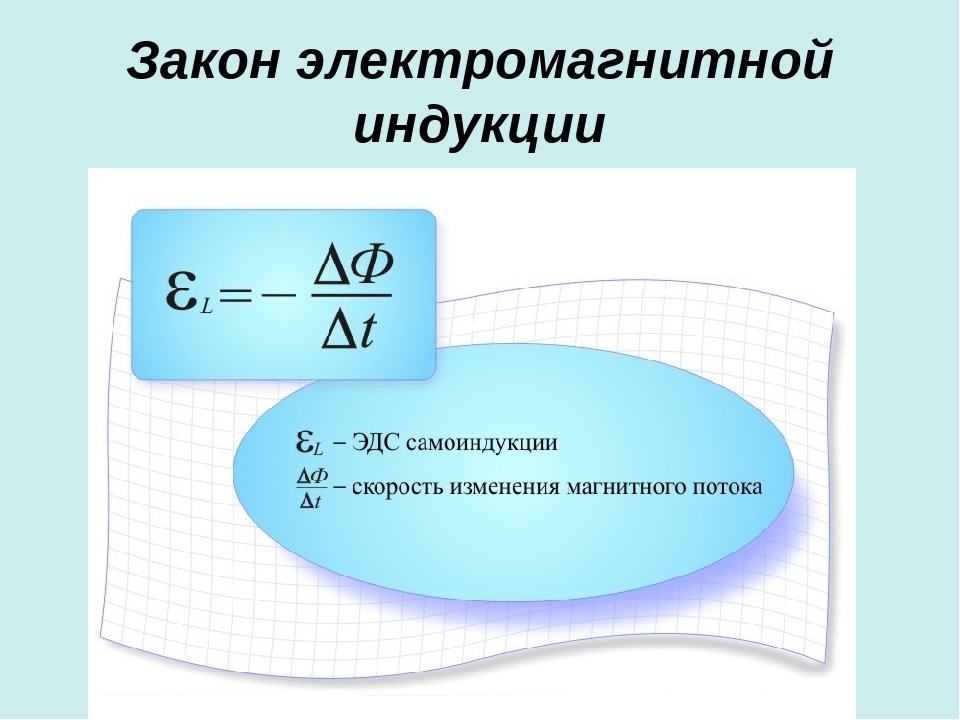 Закон индукции Фарадея для вторичной катушки дает индуцированное выходное напряжение V с как:
Закон индукции Фарадея для вторичной катушки дает индуцированное выходное напряжение V с как:
} \dfrac { \Delta \Phi } { \Delta \mathrm { t } }\]
, где N s — число витков вторичной обмотки, а Δ/Δt — скорость изменения магнитного потока. Обратите внимание, что выходное напряжение равно ЭДС индукции (V s = ЭДС s ), при условии, что сопротивление катушки мало. Площадь поперечного сечения катушек одинакова с обеих сторон, как и напряженность магнитного поля, поэтому /Δt одинаково с обеих сторон. Входное первичное напряжение V p также связано с изменением потока: { \Delta \Phi } { \Delta \mathrm { t } }\]
Соотношение этих двух последних уравнений дает полезное соотношение: } = \dfrac { \mathrm { N } _ { \mathrm { s } } } { \mathrm { N } _ { \mathrm { p } } }\]
Это известно как уравнение преобразования , которое просто утверждает, что отношение вторичных и первичных напряжений в трансформаторе равно отношению числа витков в их катушках. Выходное напряжение трансформатора может быть меньше, больше или равно входному напряжению в зависимости от соотношения числа витков в их катушках. Некоторые трансформаторы даже обеспечивают переменную мощность, позволяя выполнять подключение в разных точках вторичной обмотки. Повышающий трансформатор — это тот, который увеличивает напряжение, тогда как понижающий трансформатор уменьшает напряжение.
Выходное напряжение трансформатора может быть меньше, больше или равно входному напряжению в зависимости от соотношения числа витков в их катушках. Некоторые трансформаторы даже обеспечивают переменную мощность, позволяя выполнять подключение в разных точках вторичной обмотки. Повышающий трансформатор — это тот, который увеличивает напряжение, тогда как понижающий трансформатор уменьшает напряжение.
Предполагая, как и мы, что сопротивление пренебрежимо мало, выходная электрическая мощность трансформатора равна его входной мощности. Приравнивая входную и выходную мощность,
} = \mathrm { I } _ { \mathrm { s } } \mathrm { V } _ { \mathrm { s } } = \mathrm { P } _ { \mathrm { s } }\]
Объединив эти результаты с уравнение трансформатора, находим:
\[\dfrac { \mathrm { I } _ { \mathrm { s } } } { \mathrm { I } _ { \mathrm { p } } } = \dfrac { \mathrm { N } _ { \mathrm { p } } } { \ mathrm { N } _ { \ mathrm { s } } } \]
Таким образом, если напряжение увеличивается, ток уменьшается. И наоборот, если напряжение уменьшается, ток увеличивается.
И наоборот, если напряжение уменьшается, ток увеличивается.
Ключевые моменты
- Это изменение потока магнитного поля, которое приводит к возникновению электродвижущей силы (или напряжения).
- Магнитный поток (часто обозначаемый Φ или Φ B ) через поверхность представляет собой компонент магнитного поля, проходящего через эту поверхность.
- В наиболее общем виде магнитный поток определяется как \(\Phi _ { \mathrm { B } } = \iint _ { \mathrm { A } } \mathbf { B } \cdot \mathrm { d } \mathbf { А }\). Это интеграл (сумма) всего магнитного поля, проходящего через бесконечно малые элементы площади dA.
- Минус в законе Фарадея означает, что ЭДС создает ток I и магнитное поле B, которые противодействуют изменению потока Δэто известно как закон Ленца.
- Закон индукции Фарадея является фундаментальным принципом работы трансформаторов, катушек индуктивности и многих типов электродвигателей, генераторов и соленоидов.

- Закон Фарадея гласит, что ЭДС, индуцированная изменением магнитного потока, зависит от изменения потока Δ, времени Δt и числа витков катушки.
- Закон индукции Фарадея можно использовать для расчета ЭДС движения, когда изменение магнитного потока вызывается движущимся элементом в системе.
- То, что движущееся магнитное поле создает электрическое поле (и наоборот, что движущееся электрическое поле создает магнитное поле), частично является причиной того, что электрические и магнитные силы теперь рассматриваются как разные проявления одной и той же силы.
- Любое изменение магнитного потока индуцирует электродвижущую силу (ЭДС), противодействующую этому изменению — процесс, известный как индукция. Движение является одной из основных причин индукции.
- Входная ЭДС, питающая двигатель, может противопоставляться собственной ЭДС двигателя, называемой обратной ЭДС двигателя.
- Если ЭДС движения может вызвать петлю с током в проводнике, то ток называется вихревым током.

- Вихревые токи могут создавать значительное сопротивление, называемое магнитным демпфированием, при соответствующем движении.
- Закон индукции Фарадея — это основной закон электромагнетизма, который предсказывает, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу.
- Альтернативная дифференциальная форма закона индукции Фарадея выражается в уравнении \(x\nabla \times \vec { \mathrm { E } } = — \frac { \partial \vec { \mathrm { B } } } { \partial \mathrm { t } }\).
- Закон индукции Фарадея — одно из четырех уравнений Максвелла, управляющих всеми электромагнитными явлениями.
- Электрический генератор вращает катушку в магнитном поле, индуцируя ЭДС, определяемую как функция времени \(\mathrm{ε=NABw \sin ωt}\). Генераторы
- обеспечивают почти всю мощность для электросетей, которые обеспечивают большую часть мировой электроэнергии.
- Двигатель становится генератором, когда его вал вращается.

- В большинстве электродвигателей для создания силы используется взаимодействие магнитных полей и проводников с током.
- Ток в проводнике состоит из движущихся зарядов. Следовательно, катушка с током в магнитном поле также будет ощущать силу Лоренца.
- В двигателе катушка с током в магнитном поле испытывает силу с обеих сторон катушки, которая создает скручивающую силу (называемую крутящим моментом), которая заставляет ее вращаться.
- Взаимная индуктивность — это действие двух устройств, индуцирующих ЭДС друг в друге. Изменение тока ΔI 1 /Δt в одном индуцирует ЭДС ЭДС2 во втором: ЭДС 2 = −M ΔI 1 /Δt, где М определяется как взаимная индуктивность между двумя устройствами.
- Самоиндукция — это эффект устройства, индуцирующего ЭДС само по себе.
- Устройство, обладающее значительной собственной индуктивностью, называется индуктором, а ЭДС, индуцируемая в нем изменением тока через него, равна \(\mathrm{ ЭДС = −L\frac{ ΔI}{Δt}}\).

- ЭДС движения и индукции — это одно и то же явление, просто наблюдаемое в разных системах отсчета. Эквивалентность этих двух явлений побудила Эйнштейна заняться специальной теорией относительности.
- ЭДС, возникающая из-за относительного движения петли и магнита, определяется как \(\mathrm{ε_{motion}=vB \times L}\) (уравнение 1), где L — длина объекта, движущегося на скорость v относительно магнита.
- ЭДС можно рассчитать с двух разных точек зрения: 1) в терминах магнитной силы, действующей на движущиеся электроны в магнитном поле, и 2) в терминах скорости изменения магнитного потока. Оба дают одинаковый результат.
- ЭДС движения, создаваемая движущимся проводником в однородном поле, определяется следующим образом \(\mathrm{ε=Blv}\).
- Чтобы стержень двигался с постоянной скоростью v, мы должны постоянно прикладывать внешнюю силу F ext к стержню во время его движения.
- Закон Ленца гарантирует, что движение стержня противоположно, и поэтому закон сохранения энергии не нарушается.

- Энергия необходима для создания магнитного поля как для работы против электрического поля, создаваемого изменяющимся магнитным полем, так и для изменения намагниченности любого материала в пределах магнитного поля.
- Для линейных недисперсионных материалов (таких, что \(\mathrm{B = µH}\), где µ, называемая проницаемостью, не зависит от частоты), плотность энергии равна: \(.\mathrm { u } = \frac { \mathbf { B } \cdot \mathbf { B } } { 2 \mu } = \ frac { \mu \mathbf { H } \cdot \mathbf { H } } { 2 } \) 9{2}\). Трансформаторы
- часто используются в нескольких точках в системах распределения электроэнергии, а также во многих бытовых адаптерах питания.
- \(Уравнение трансформатора утверждает, что отношение вторичных и первичных напряжений в трансформаторе равно отношению количества витков в их обмотках:\( \frac { \mathrm { V } _ { \mathrm { s } } } { \ mathrm { V } _ { \ mathrm { p } } } = \ frac { \ mathrm { N } _ { \ mathrm { s } } } { \ mathrm { N } _ { \ mathrm { p } } } \).

- Предполагая, как и мы, что сопротивление пренебрежимо мало, выходная электрическая мощность трансформатора равна его входной мощности. Это приводит нас к другому полезному уравнению: \(\mathrm{\frac{I_s}{I_p}=\frac{N_p}{N_s}}\). Если напряжение увеличивается, ток уменьшается. И наоборот, если напряжение уменьшается, ток увеличивается.
Ключевые термины
- площадь вектора : Вектор, величина которого представляет собой рассматриваемую площадь и направление которого перпендикулярно площади поверхности.
- гальванометр : Аналоговый измерительный прибор, обозначаемый буквой G, который измеряет ток с помощью отклонения стрелки, вызванного силой магнитного поля, действующей на проводник с током.
- электродвижущая сила : (ЭДС) — напряжение, создаваемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и, следовательно, на самом деле не является силой.

- соленоид : Катушка проволоки, которая действует как магнит, когда через нее проходит электрический ток.
- поток : Скорость передачи энергии (или другой физической величины) через данную поверхность, в частности, электрический поток или магнитный поток.
- магнитный поток : Мера силы магнитного поля в данной области.
- индукция : Генерация электрического тока переменным магнитным полем.
- Закон индукции Фарадея : Основной закон электромагнетизма, который предсказывает, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу (ЭДС).
- Уравнения Максвелла : Набор уравнений, описывающих, как электрические и магнитные поля генерируются и изменяются друг другом, а также зарядами и токами.
- Теорема Стокса : утверждение об интегрировании дифференциальных форм на многообразиях, которое упрощает и обобщает несколько теорем векторного исчисления.

- турбина : Любая из различных вращающихся машин, которые используют кинетическую энергию непрерывного потока жидкости (жидкости или газа) для вращения вала.
- Сила Лоренца : Сила, действующая на заряженную частицу в электромагнитном поле.
- крутящий момент : вращательное или скручивающее действие силы; (единица СИ ньютон-метр или Нм; британская единица фут-фунт или фут-фунт)
- трансформатор : Статическое устройство, передающее электрическую энергию от одной цепи к другой посредством магнитной связи. Их основное применение заключается в передаче энергии между различными уровнями напряжения, что позволяет выбрать наиболее подходящее напряжение для производства, передачи и распределения электроэнергии по отдельности.
- специальная теория относительности : Теория, которая (пренебрегая эффектами гравитации) примиряет принцип относительности с наблюдением, что скорость света постоянна во всех системах отсчета.

- магнитное поле : Состояние в пространстве вокруг магнита или электрического тока, в котором присутствует определяемая магнитная сила и где присутствуют два магнитных полюса.
- система отсчета : Система координат или набор осей, в которых измеряется положение, ориентация и другие свойства объектов в ней.
- Motional EMF : ЭДС (электродвижущая сила), индуцированная движением относительно магнитного поля.
- проницаемость : Количественная мера степени намагниченности материала в присутствии приложенного магнитного поля (измеряется в ньютонах на ампер в квадрате в единицах СИ).
- индуктор : пассивное устройство, вводящее индуктивность в электрическую цепь.
- ферромагнетик : Материалы, обладающие постоянным магнитным свойством.
ЛИЦЕНЗИИ И АВТОРСТВО
CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, ПРЕДОСТАВЛЕННОЕ РАНЕЕ
- Курирование и пересмотр.
 Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, КОНКРЕТНОЕ АВТОРСТВО
- Магнитный поток. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_flux . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, ЭДС индукции и магнитный поток. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42390/latest/ . Лицензия : CC BY: Attribution
- векторной области. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/vector%20area .
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/galvanometer . Лицензия : CC BY-SA: Attribution-ShareAlike
- Магнитный поток. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_flux . Лицензия : CC BY: Attribution
- Колледж OpenStax, ЭДС индукции и магнитный поток. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42390/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, Фарадайю, 2019 г.
 s Закон индукции: закон Lenzu2019s. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42392/latest/ . Лицензия : CC BY: Attribution
s Закон индукции: закон Lenzu2019s. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42392/latest/ . Лицензия : CC BY: Attribution - Закон индукции Фарадея. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Faraday’s_law_of_induction . Лицензия : CC BY-SA: Attribution-ShareAlike
- электродвижущая сила. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/electromotive%20force . Лицензия : CC BY-SA: Attribution-ShareAlike соленоид
- . Предоставлено : Викисловарь. Расположен по адресу : en.
 wiktionary.org/wiki/solenoid . Лицензия : CC BY-SA: Attribution-ShareAlike флюс
wiktionary.org/wiki/solenoid . Лицензия : CC BY-SA: Attribution-ShareAlike флюс - . Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/flux . Лицензия : CC BY-SA: Attribution-ShareAlike
- Магнитный поток. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_flux . Лицензия : CC BY: Attribution
- Колледж OpenStax, ЭДС индукции и магнитный поток. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42390/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, Закон индукции Faradayu2019: Закон Lenzu2019.
 7 февраля 2013 г. Предоставлено : OpenStax CNX. Адрес: : http://cnx.org/content/m42392/latest/ . Лицензия : CC BY: Attribution
7 февраля 2013 г. Предоставлено : OpenStax CNX. Адрес: : http://cnx.org/content/m42392/latest/ . Лицензия : CC BY: Attribution - Колледж OpenStax, Motional Emf. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42400/latest/ . Лицензия : CC BY: Attribution
- индукция. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/induction . Лицензия : CC BY-SA: Attribution-ShareAlike
- электродвижущая сила. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/electromotive%20force .
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - магнитный поток. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/magnet_flux . Лицензия : CC BY-SA: Attribution-ShareAlike
- Магнитный поток. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_flux . Лицензия : CC BY: Attribution
- Колледж OpenStax, ЭДС индукции и магнитный поток. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42390/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, Закон индукции Faradayu2019: Закон Lenzu2019.
 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42392/latest/ . Лицензия : CC BY: Attribution
7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42392/latest/ . Лицензия : CC BY: Attribution - Колледж OpenStax, Motional Emf. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42400/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, вихревые токи и магнитное демпфирование. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, Back Emf. 17 сентября 2013 г. Предоставлено : OpenStax CNX.
 Расположен по адресу : http://cnx.org/content/m42411/latest/ . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42411/latest/ . Лицензия : CC BY: Attribution - Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/faraday-s-law-of-induction—3 . Лицензия : CC BY-SA: Attribution-ShareAlike
- электродвижущая сила. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/electromotive%20force . Лицензия : CC BY-SA: Attribution-ShareAlike
- Магнитный поток. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_flux .
 Лицензия : CC BY: Attribution
Лицензия : CC BY: Attribution - Колледж OpenStax, ЭДС индукции и магнитный поток. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42390/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, Закон индукции Faradayu2019: Закон Lenzu2019. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42392/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, Motional Emf. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42400/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, вихревые токи и магнитное демпфирование.
 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution - Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
- Пол Пэдли, Закон Фарадея. 17 сентября 2013 г. Предоставлено : OpenStax CNX.
 Адрес: : http://cnx.org/content/m12869/latest/ . Лицензия : CC BY: Attribution
Адрес: : http://cnx.org/content/m12869/latest/ . Лицензия : CC BY: Attribution - Уравнения Максвелла. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Maxwell’s%20equations . Лицензия : CC BY-SA: Attribution-ShareAlike
- векторной области. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/vector%20area . Лицензия : CC BY-SA: Attribution-ShareAlike
- Теорема Стокса. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Stokes’%20theorem . Лицензия : CC BY-SA: Attribution-ShareAlike
- Магнитный поток.
 Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_flux . Лицензия : CC BY: Attribution
Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_flux . Лицензия : CC BY: Attribution - Колледж OpenStax, ЭДС индукции и магнитный поток. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42390/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, Закон индукции Faradayu2019: закон Lenzu2019. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42392/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, Motional Emf. 7 февраля 2013 г. Предоставлено : OpenStax CNX.
 Расположен по адресу : http://cnx.org/content/m42400/latest/ . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42400/latest/ . Лицензия : CC BY: Attribution - Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г. Предоставлено : OpenStaxCNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г. Предоставлено : OpenStax CNX.
 Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution - Закон индукции Фарадея. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Faraday’s_law_of_induction . Лицензия : CC BY: Attribution
- Колледж OpenStax, Электрогенераторы. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42408/latest/ . Лицензия : CC BY: Атрибуция
- Электрический генератор. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Electric_generator .
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - электродвижущая сила. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/electromotive%20force . Лицензия : CC BY-SA: Attribution-ShareAlike
- турбина. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/turbine . Лицензия : CC BY-SA: Attribution-ShareAlike
- Магнитный поток. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_flux . Лицензия : CC BY: Attribution
- Колледж OpenStax, ЭДС индукции и магнитный поток.
 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42390/latest/ . Лицензия : CC BY: Attribution
7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42390/latest/ . Лицензия : CC BY: Attribution - Колледж OpenStax, Закон индукции Faradayu2019: Закон Lenzu2019. 7 февраля 2013 г. Предоставлено : OpenStaxCNX. Расположен по адресу : http://cnx.org/content/m42392/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, Motional Emf. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42400/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г.
 Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution - Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
- Закон индукции Фарадея. Предоставлено : Википедия.
 Расположен по адресу : en.Wikipedia.org/wiki/Faraday’s_law_of_induction . Лицензия : CC BY: Attribution
Расположен по адресу : en.Wikipedia.org/wiki/Faraday’s_law_of_induction . Лицензия : CC BY: Attribution - Электрический генератор. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Electric_generator . Лицензия : CC BY: Attribution
- Колледж OpenStax, Электрогенераторы. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42408/latest/ . Лицензия : CC BY: Attribution
- Проект бесплатных научных текстов для старших классов, Электродинамика: генераторы и двигатели. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.
 org/content/m39508/latest/ . Лицензия : CC BY: Attribution
org/content/m39508/latest/ . Лицензия : CC BY: Attribution - крутящий момент. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/torque . Лицензия : CC BY-SA: Attribution-ShareAlike
- сила Лоренца. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/Lorentz_force . Лицензия : CC BY-SA: Attribution-ShareAlike
- Магнитный поток. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_flux . Лицензия : CC BY: Attribution
- Колледж OpenStax, ЭДС индукции и магнитный поток.
 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42390/latest/ . Лицензия : CC BY: Attribution
7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42390/latest/ . Лицензия : CC BY: Attribution - Колледж OpenStax, Закон индукции Faradayu2019: Закон Lenzu2019. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42392/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, Motional Emf. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42400/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г.
 Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution - Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г. Предоставлено : OpenStaxCNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
- Закон индукции Фарадея. Предоставлено : Википедия.
 Расположен по адресу : en.Wikipedia.org/wiki/Faraday’s_law_of_induction . Лицензия : CC BY: Attribution
Расположен по адресу : en.Wikipedia.org/wiki/Faraday’s_law_of_induction . Лицензия : CC BY: Attribution - Электрический генератор. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Electric_generator . Лицензия : CC BY: Attribution
- Колледж OpenStax, Электрогенераторы. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42408/latest/ . Лицензия : CC BY: Attribution
- Проект бесплатных научных текстов для старших классов, Электродинамика: генераторы и двигатели. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.
 org/content/m39508/latest/ . Лицензия : CC BY: Attribution
org/content/m39508/latest/ . Лицензия : CC BY: Attribution - Проект бесплатных научных текстов для старших классов, Электродинамика: генераторы и двигатели. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m39508/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, Индуктивность. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42420/latest/ . Лицензия : CC BY: Attribution Трансформатор
- . Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/transformer . Лицензия : CC BY-SA: Attribution-ShareAlike
- Безграничный.
 Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/faraday-s-law-of-induction—3 . Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/faraday-s-law-of-induction—3 . Лицензия : CC BY-SA: Attribution-ShareAlike - Магнитный поток. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_flux . Лицензия : CC BY: Attribution
- Колледж OpenStax, ЭДС индукции и магнитный поток. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42390/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, Закон индукции Faradayu2019: Закон Lenzu2019. 7 февраля 2013 г. Предоставлено : OpenStax CNX.
 Расположен по адресу : http://cnx.org/content/m42392/последний/ . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42392/последний/ . Лицензия : CC BY: Attribution - Колледж OpenStax, Motional Emf. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42400/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г. Предоставлено : OpenStaxCNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.
 org/content/m42404/latest/ . Лицензия : CC BY: Attribution
org/content/m42404/latest/ . Лицензия : CC BY: Attribution - Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
- Закон индукции Фарадея. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Faraday’s_law_of_induction . Лицензия : CC BY: Attribution
- Электрический генератор. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Electric_generator . Лицензия : CC BY: Attribution
- Колледж OpenStax, Электрогенераторы.
 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42408/latest/ . Лицензия : CC BY: Attribution
8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42408/latest/ . Лицензия : CC BY: Attribution - Проект бесплатных научных текстов для старших классов, Электродинамика: генераторы и двигатели. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m39508/latest/ . Лицензия : CC BY: Attribution
- Проект бесплатных научных текстов для старших классов, Электродинамика: генераторы и двигатели. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m39508/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики.
 16 января 2015 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42420/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
16 января 2015 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42420/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution - специальная теория относительности. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/special_relativity . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42400/latest/?collection=col11406/latest . Лицензия : CC BY: Attribution
- Колледж OpenStax, Эффект Холла. 17 сентября 2013 г.
 Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42377/latest/ . Лицензия : CC BY: Attribution
Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42377/latest/ . Лицензия : CC BY: Attribution - магнитное поле. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/Magnetic_field . Лицензия : CC BY-SA: Attribution-ShareAlike
- система отсчета. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/frame_of_reference . Лицензия : CC BY-SA: Attribution-ShareAlike
- Магнитный поток. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_flux .
 Лицензия : CC BY: Attribution
Лицензия : CC BY: Attribution - Колледж OpenStax, ЭДС индукции и магнитный поток. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42390/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, Закон индукции Faradayu2019: Закон Lenzu2019. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42392/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, Motional Emf. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42400/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, вихревые токи и магнитное демпфирование.
 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution - Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
- Закон индукции Фарадея. Предоставлено : Википедия.
 Расположен по адресу : en.Wikipedia.org/wiki/Faraday’s_law_of_induction . Лицензия : CC BY: Attribution
Расположен по адресу : en.Wikipedia.org/wiki/Faraday’s_law_of_induction . Лицензия : CC BY: Attribution - Электрический генератор. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Electric_generator . Лицензия : CC BY: Attribution
- Колледж OpenStax, Электрогенераторы. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42408/latest/ . Лицензия : CC BY: Attribution
- Проект бесплатных научных текстов для старших классов, Электродинамика: генераторы и двигатели. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.
 org/content/m39508/latest/ . Лицензия : CC BY: Атрибуция
org/content/m39508/latest/ . Лицензия : CC BY: Атрибуция - Проект бесплатных научных текстов для старших классов, Электродинамика: генераторы и двигатели. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m39508/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики. 16 января 2015 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42420/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Безграничный. Предоставлено : Amazon Web Services. Расположен по адресу : s3.amazonaws.com/figures.
 boundless.com/51154f34e4b0c14bf464da40/1.jpg . Лицензия : CC BY: Attribution
boundless.com/51154f34e4b0c14bf464da40/1.jpg . Лицензия : CC BY: Attribution - Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42400/latest/?collection=col11406/latest . Лицензия : CC BY: Attribution
- Колледж OpenStax, Закон индукции Faradayu2019: Закон Lenzu2019. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42392/latest/ . Лицензия : CC BY: Атрибуция
- Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/faraday-s-law-of-induction—3 .
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/motional-emf . Лицензия : CC BY-SA: Attribution-ShareAlike
- Магнитный поток. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_flux . Лицензия : CC BY: Attribution
- Колледж OpenStax, ЭДС индукции и магнитный поток. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42390/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, Закон индукции Faradayu2019: Закон Lenzu2019.
 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42392/latest/ . Лицензия : CC BY: Attribution
7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42392/latest/ . Лицензия : CC BY: Attribution - Колледж OpenStax, Motional Emf. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42400/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г. Предоставлено : OpenStax CNX.
 Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution - Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
- Закон индукции Фарадея. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Faraday’s_law_of_induction . Лицензия : CC BY: Attribution
- Электрический генератор. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Electric_generator .
 Лицензия : CC BY: Attribution
Лицензия : CC BY: Attribution - Колледж OpenStax, Электрогенераторы. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42408/latest/ . Лицензия : CC BY: Attribution
- Проект бесплатных научных текстов для старших классов, Электродинамика: генераторы и двигатели. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m39508/latest/ . Лицензия : CC BY: Attribution
- Проект бесплатных научных текстов для старших классов, Электродинамика: генераторы и двигатели. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.
 org/content/m39508/latest/ . Лицензия : CC BY: Атрибуция
org/content/m39508/latest/ . Лицензия : CC BY: Атрибуция - Колледж OpenStax, Колледж физики. 16 января 2015 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42420/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Безграничный. Предоставлено : Amazon Web Services. Расположен по адресу : s3.amazonaws.com/figures.boundless.com/51154f34e4b0c14bf464da40/1.jpg . Лицензия : CC BY: Attribution
- Колледж OpenStax, Motional EMF. 16 января 2015 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42400/latest/ . Лицензия : CC BY: Attribution
- Магнитное поле.
 Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_field%23Energy_stored_in_ Magnetic_fields . Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_field%23Energy_stored_in_ Magnetic_fields . Лицензия : CC BY-SA: Attribution-ShareAlike - Колледж OpenStax, Индуктивность. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42420/latest/ . Лицензия : CC BY: Attribution Индуктор
- . Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/inductor . Лицензия : CC BY-SA: Attribution-ShareAlike
- ферромагнетик. Предоставлено : Википедия. Расположен по адресу : en.
 Wikipedia.org/wiki/ferromagnet . Лицензия : CC BY-SA: Attribution-ShareAlike
Wikipedia.org/wiki/ferromagnet . Лицензия : CC BY-SA: Attribution-ShareAlike - проходимость. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/permeability . Лицензия : CC BY-SA: Attribution-ShareAlike
- Магнитный поток. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_flux . Лицензия : CC BY: Attribution
- Колледж OpenStax, ЭДС индукции и магнитный поток. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42390/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, Закон индукции Faradayu2019: Закон Lenzu2019.
 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42392/latest/ . Лицензия : CC BY: Attribution
7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42392/latest/ . Лицензия : CC BY: Attribution - Колледж OpenStax, Motional Emf. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42400/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г. Предоставлено : OpenStax CNX.
 Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution - Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
- Закон индукции Фарадея. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Faraday’s_law_of_induction . Лицензия : CC BY: Attribution
- Электрический генератор. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Electric_generator .
 Лицензия : CC BY: Attribution
Лицензия : CC BY: Attribution - Колледж OpenStax, Электрогенераторы. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42408/latest/ . Лицензия : CC BY: Attribution
- Проект бесплатных научных текстов для старших классов, Электродинамика: генераторы и двигатели. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m39508/latest/ . Лицензия : CC BY: Attribution
- Проект бесплатных научных текстов для старших классов, Электродинамика: генераторы и двигатели. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.
 org/content/m39508/latest/ . Лицензия : CC BY: Атрибуция
org/content/m39508/latest/ . Лицензия : CC BY: Атрибуция - Колледж OpenStax, Колледж физики. 16 января 2015 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42420/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Безграничный. Предоставлено : Amazon Web Services. Расположен по адресу : s3.amazonaws.com/figures.boundless.com/51154f34e4b0c14bf464da40/1.jpg . Лицензия : CC BY: Attribution
- Колледж OpenStax, Motional EMF. 16 января 2015 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42400/latest/ . Лицензия : CC BY: Attribution
- Соленоид.
 Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Solenoid . Лицензия : CC BY: Attribution
Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Solenoid . Лицензия : CC BY: Attribution - Колледж OpenStax, Трансформеры. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42414/latest/ . Лицензия : CC BY: Attribution
- Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/faraday-s-law-of-induction—3 . Лицензия : CC BY-SA: Attribution-ShareAlike
- магнитный поток. Предоставлено : Викисловарь. Расположен по адресу : en.
 wiktionary.org/wiki/magnet_flux . Лицензия : CC BY-SA: Attribution-ShareAlike
wiktionary.org/wiki/magnet_flux . Лицензия : CC BY-SA: Attribution-ShareAlike - Магнитный поток. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_flux . Лицензия : CC BY: Attribution
- Колледж OpenStax, ЭДС индукции и магнитный поток. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42390/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, Закон индукции Faradayu2019: Закон Lenzu2019. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42392/latest/ .
 Лицензия : CC BY: Attribution
Лицензия : CC BY: Attribution - Колледж OpenStax, Motional Emf. 7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42400/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, вихревые токи и магнитное демпфирование. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, вихревые токи и магнитное демпфирование.
 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution - Закон индукции Фарадея. Предоставлено : Википедия. Расположен по адресу : http://en.Wikipedia.org/wiki/Faraday’s_law_of_induction . Лицензия : CC BY: Attribution
- Электрический генератор. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Electric_generator . Лицензия : CC BY: Attribution
- Колледж OpenStax, Электрогенераторы. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.
 org/content/m42408/latest/ . Лицензия : CC BY: Attribution
org/content/m42408/latest/ . Лицензия : CC BY: Attribution - Проект бесплатных научных текстов для старших классов, Электродинамика: генераторы и двигатели. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m39508/latest/ . Лицензия : CC BY: Атрибуция
- Проект бесплатных научных текстов для старших классов, Электродинамика: генераторы и двигатели. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m39508/latest/ . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики. 16 января 2015 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.
 org/content/m42420/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
org/content/m42420/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution - Безграничный. Предоставлено : Amazon Web Services. Расположен по адресу : s3.amazonaws.com/figures.boundless.com/51154f34e4b0c14bf464da40/1.jpg . Лицензия : CC BY: Attribution
- Колледж OpenStax, Motional EMF. 16 января 2015 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42400/latest/ . Лицензия : CC BY: Attribution
- Соленоид. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Solenoid . Лицензия : CC BY: Attribution
- Колледж OpenStax, Трансформеры.
 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42414/latest/ . Лицензия : CC BY: Attribution
8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42414/latest/ . Лицензия : CC BY: Attribution - Колледж OpenStax, Трансформеры. 8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42414/latest/ . Лицензия : CC BY: Attribution
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Показать оглавление
- нет
- Метки
- электродвижущая сила (эдс)
- Закон индукции Фарадея
- ферромагнетик
- флюс
- система отсчета
- гальванометр
- индукция
- индуктор
- сила Лоренца
- Магнитное поле
- магнитный поток
- Уравнения Максвелла
- ЭДС движения
- Проницаемость
- соленоид
- source@https://ocw.
 mit.edu/courses/electrical-engineering-and-computer-science/6-013-electromagnetics-and-applications-spring-2009
mit.edu/courses/electrical-engineering-and-computer-science/6-013-electromagnetics-and-applications-spring-2009 - Специальная теория относительности
- Теорема Стокса
- крутящий момент
- Трансформатор
- Турбина
- векторная область
| ||||||||||||||||||||||||||||||||||||
Почему символ магнитного поля обозначается буквой «B»? | Анна Нед
Я проверила учебник Максвелла 1873 года.
Учебник Максвелла по электричеству и магнетизму от 1873 г.
В 1873 г. Максвелл закончил « Трактат об электричестве и магнетизме». Среди различных обсуждаемых явлений и проблем его 900-страничная книга включает компактный и элегантный способ записи фундаментальной взаимосвязи между электрическими и магнитными величинами, который он постепенно формулировал на протяжении многих лет. Совокупность электромагнитных законов, которые мы сегодня знаем как уравнения Максвелла, в своей математической красоте способны охватить весь классический электромагнетизм в нескольких строках уравнений .
Эйнштейн сказал:
«Формулировка этих уравнений — самое важное событие в физике со времен Ньютона».
Фейнман сказал:
«Глядя на историю человечества — скажем, через десять тысяч лет — можно не сомневаться, что самое значительное событие 19-го века будет оценено как событие Максвелла. Открытие законов электродинамики».
В современных обозначениях, где магнитное поле обозначается как H , а магнитная индукция — как B, уравнения классического электромагнетизма Максвелла записываются в виде набора из четырех уравнений. В их дифференциальной форме они таковы:
В их дифференциальной форме они таковы:
- Закон Гаусса связывает распределение свободных электрических зарядов (ρf) с вектором электрической индукции ( D ).
- Эквивалентная корреляция для магнитного поля утверждает, что вектор магнитной индукции ( B ) не имеет источника. Магнитного эквивалента электрическому заряду не существует. Интересно, что помимо того факта, что никто так и не нашел магнитный монополь, нет никакой теоретической причины, по которой монополи не существовали бы. Если интересно, читайте подробное освещение этой темы с разных точек зрения в физике в статье ниже.
Можно ли разбить стержневой магнит на отдельные полюса?
Кроме того, никто их не разделял, нет теоретической причины, почему бы и нет!
medium.com
- Третье уравнение Максвелла, также известное как закон Фарадея, является основным принципом работы электрических генераторов.
 Изменяющаяся во времени магнитная индукция ( B ) создает закручивающееся электрическое поле ( E ).
Изменяющаяся во времени магнитная индукция ( B ) создает закручивающееся электрическое поле ( E ). - Наконец, закон Ампера связывает ротор магнитного поля ( H ) со свободным током ( J f ) и током смещения (производная по времени от электрической индукции D ). Это основной принцип работы электродвигателей.
Я не буду вдаваться в подробности, но на языке квантовой теории поля (КЭД) все четыре уравнения Максвелла для вакуума можно записать в одной единственной, но чрезвычайно компактной форме.
где тензор электромагнитного поля F представляет собой 4-вектор, который объединяет электрическое поле E и магнитную индукцию B
, а заряд и плотность тока также объединяются в один 4-вектор тока
Если вас интересует Чтобы узнать больше о красоте и проблемах мощных методов квантовых теорий поля, я рекомендую статью ниже.
Обеспокоены ли математики тем, как в физике рассматриваются бесконечности?
Когда в квантовой теории поля (КТП) что-то сходит с ума.

www.cantorsparadise.com
Максвелл ввел в физику идею распознавания некоторых величин в физике как векторных полей и ввел обозначения, которыми мы в основном пользуемся до сих пор. Однако для одного избалованного физика, получившего образование в 21 веке, я был совершенно сбит с толку беспорядком того, как уравнения Максвелла выглядели в 1873 году. Уравнения не выглядели так аккуратно. Сначала они описываются системой из 20 дифференциальных уравнений с 20 переменными.
Уравнения Максвелла в книге 1873 г. Максвелл был первым, кто осознал хорошую симметрию между электрическим и магнитным полями, которая проявляется в уравнениях Максвелла, которые он описал в исторической статье 1861 г. под названием «О физической силовой линии». ». [1] Если интересно, вы можете купить собрание его произведений, напечатанное в 1864 году, за 4000 долларов. [2] Его первые работы по электричеству и магнетизму датируются всего несколько лет назад, в статье «О силовой линии Фарадея» в 1855 году. [3]
[3]
Вот как он придумал обозначение для магнитного поля, среди других величин.
Отсканированная страница из «Трактата об электричестве и магнетизме», том. 2, стр. 257Не пытаясь проявить изобретательность, он просто в алфавитном порядке обозначил векторы некоторых полезных величин в том порядке, в котором он их вводил.
Введенные векторные величины он обозначал курсивными буквами алфавита, и, собственно, большинство приклеившихся к нам ярлыков. Те, которые используются до сих пор:
- A (векторный потенциал или электромагнитный импульс Максвелла)
- B (магнитная индукция или плотность магнитного потока)
- D (электрическое смещение или электрическая индукция) E 9003 напряженность)
- F (механическая сила)
- H (магнитное поле — магнитная сила Максвелла)
- Дж (ток)
К счастью, обозначения для компонентов изменились. Например, компоненты электрического поля E изменено с P, Q и R на общепринятые обозначения Ex, Ey и Ez для координат Декарта.
Например, компоненты электрического поля E изменено с P, Q и R на общепринятые обозначения Ex, Ey и Ez для координат Декарта.
Этикетка для магнитного поля — используются как B, так и H!
Небольшая запутанная двусмысленность связана с обозначением магнитного поля. На практике обе метки B и H используются для обозначения магнитного поля, хотя магнитное поле ( H) и магнитная индукция ( B) из уравнений Максвелла, записанных выше , не имеют одинаковых единиц измерения .
Магнитное поле, в частности, в учебниках обозначается буквами H и B .
Эта привычка возникает из-за того, что гораздо чаще расчеты проводятся в идеализированных условиях в вакууме , где эти две величины связаны только с точностью до константы μ0 (проницаемость вакуума).
Чтобы быть точным, магнитное поле следует называть H .
Я провел несколько приятных часов, наслаждаясь написанием и стилем такой старой книги. Оглавление включает краткое изложение каждой отдельной страницы книги, начиная со второго тома двухтомной книги с «Свойства магнита при воздействии на него земли».
Максвелл считал существование эфира или среды необходимым
Интересно, что Максвелл обсуждает необходимость существования эфира на протяжении всей книги и критикует всех, кто думает иначе.
В поддержку своего мнения он также включил письмо Гаусса к Веберу от 1845 г.
, и которое он опубликовал бы, если бы мог тогда установить то, что он считал подлинным краеугольным камнем электродинамики , а именно вывод силы, действующей между движущимися электрическими частицами, из рассмотрения действия между ними, не мгновенного, а распространяющегося во времени, подобно действию света. Ему не удалось сделать этот вывод, когда он отказался от своих электродинамических исследований, и у него было субъективное убеждение, что в первую очередь необходимо составить непротиворечивое представление о том, каким образом происходит распространение».
Он закончил «трактат», заключив, что эфир должен существовать.
«Отсюда все эти теории ведут к представлению о среде, в которой происходит распространение, и если мы допускаем эту среду в качестве гипотезы, то я думаю, что она должна занимать видное место в наших исследованиях, и что мы должны попытаться построить мысленное представление обо всех деталях его действия, и это было моей постоянной целью в этом трактате».
После долгих дебатов идея эфира была наконец проверена в эксперименте в 1887 году. Наконец удалось точно измерить скорость света, чтобы обнаружить любые отклонения, объясняющие относительное движение спекулятивного неподвижного светоносного эфира. . Ответ был отрицательным. Эфира нет. Эксперимент повторялся много раз с повышенной точностью и теми же выводами и в конечном итоге помог Эйнштейну создать свою специальную теорию относительности.
Времена, когда Эйнштейн ошибся
Явления, в отношении которых он совершенно ошибался, некоторые из них на всю жизнь.

medium.com
В завершение моей любимой цитатой из книги
Есть это «поучительное» утверждение, которое я не могу понять на каком-либо более глубоком уровне, чем утверждение: если между А и В существует какая-либо связь, то А оказать некоторое влияние на B или наоборот.
«Самым важным шагом в установлении связи между электрическими и магнитными явлениями и явлениями света должно быть открытие некоторого случая, в котором один набор явлений влияет на другой». [стр. 451]
«W . Если раньше открыватель новой элементарной частицы награждался Нобелевской премией, то теперь он должен быть наказан штрафом в размере 10 000 долларов » (эквивалент 100 000 долларов сегодня)».
Открытие новой элементарной частицы «должно быть оштрафовано на 100 000 долларов».
Времена замешательства и разочарования в истории физики элементарных частиц
www.cantorsparadise.com
Как теория Большого взрыва дает ответ на следующий вопрос: почему ночью небо кажется темным, если Вселенная содержит септиллионов звезд?
Почему ночью небо кажется темным, если во Вселенной есть септиллион звезд?
Теория Большого Взрыва дает ответ.

medium.com
Электромагнитная индукция Класс 12 заметки Физика Глава 6
Введение
Представьте себе мир, в котором нет ни электричества, ни поездов, ни телефонов, ни персональных компьютеров. Это была жизнь до открытия электромагнитной индукции . Революционное изобретение в результате экспериментов Майкл Фарадей и Джозеф Генри .
В этой главе мы изучим эксперименты электромагнитной индукции и их применения.
Эксперименты Фарадея и Генри
На рисунке показана катушка C 1 , подключенная к гальванометру G. Когда северный полюс стержневого магнита придвинут к катушке, стрелка в гальванометр отклоняется, указывая на наличие электрического тока в катушке. Гальванометр не показывает никакого отклонения, когда магнит удерживается неподвижно. Когда магнит отрывается от катушки, гальванометр показывает отклонение в противоположном направлении, что указывает на изменение направления тока.
Более того, когда южный полюс стержневого магнита перемещается к или от катушки, отклонения в гальванометре противоположны тем, которые наблюдаются с северным полюсом при аналогичных движениях. Кроме того, отклонение оказывается больше, когда магнит подталкивается к катушке или оттягивается от нее быстрее. Вместо этого, когда стержневой магнит удерживается неподвижно, а катушка C 1 перемещается к магниту или от него, наблюдаются те же эффекты. Он показывает, что именно относительное движение между магнитом и катушкой ответственно за генерацию электрического тока в катушке.
Читайте также: Переменный ток Класс 12 Заметки по физике Глава 7
Магнитный поток
Подобно электрическому потоку, магнитный поток пропорционален количеству силовых линий магнитного поля, проходящих через поверхность. Обозначается Φ Б . Это скалярная величина.
Математически `\phi_{B}=\vec{B}\vec{A}=BAcos\theta`
Единицей магнитного потока в системе СИ является вебер (Вб) (1Вб = 1 тесла-м 2 ). С.Г.С. единицей магнитного потока является максвелл. Размерная формула магнитного потока: [ML 2 T -2 A -1 ]
С.Г.С. единицей магнитного потока является максвелл. Размерная формула магнитного потока: [ML 2 T -2 A -1 ]
Закон индукции Фарадея
(i) Первый закон
ЭДС индукции в замкнутом контуре равна скорости изменения магнитного потока через контур во времени».
`\epsilon=\frac{-d\phi}{dt}`
В случае катушки из N витков, ЭДС индукции
`\epsilon=-N\frac{d\phi}{dt}`
(ii) Второй закон (закон Ленца)
Согласно этому закону, индуцированный ток имеет такое направление, чтобы противодействовать его причине. т. е. индуцированный ток противодействует изменению потока.
См. также: Общие принципы и процессы выделения элементов класса 12 Химия Примечания Глава 6
Закон Ленца и закон сохранения энергии
Закон Ленца соответствует закону сохранения энергии. Поскольку индуцированный ток противодействует изменению потока, необходимо совершить работу против противодействия, создаваемого индуцированным током при изменении потока. Проделанная работа
появляется как электрическая энергия в петле.
Проделанная работа
появляется как электрическая энергия в петле.
Наведенное электрическое поле
Электрическое поле индуцируется в любой области пространства, в которой магнитное поле меняется со временем. Наведенное электрическое поле и магнитное поле находятся под прямым углом друг к другу.
Рассмотрим частицу с зарядом q 0 , движущуюся по кольцу по круговой траектории. Работа, совершаемая индуцированным электрическим полем за один оборот, равна W = q 0 ε, где ε — ЭДС индукции.
Также проделана работа
`W=\int\vec{F}.\vec{dl}`
`W=q_{0}\int\vec{E}.\vec{dl}`
` q_{0}\epsilon=q_{0}\int\vec{E}.\vec{dl}`
`\epsilon=\int\vec{E}.\vec{dl}`
По закону Фарадея
`\epsilon=\frac{-d\phi_B}{dt}`
`\следовательно\int\vec{E}.\vec{dl}=\frac{-d\phi_B}{dt}`
См. также: Концептуальные вопросы для 12 класса Физика Глава 6 Электромагнитная индукция
Вихревой ток
Даже когда объемные куски проводников подвергаются воздействию изменяющегося магнитного потока, в них возникают наведенные токи, эти токи называются вихревыми токами .
Вихревые токи нежелательны, так как они нагревают сердечник и рассеивают электрическую энергию в виде тепла. Вихревые токи сведены к минимуму за счет использования слоев металла для изготовления металлического сердечника. Такое расположение снижает силу вихревых токов.
Вихревые токи успешно используются в некоторых приложениях, таких как:
Магнитное торможение в поездах: Сильные электромагниты расположены над рельсами в некоторых поезда с электроприводом. Когда электромагниты активируются, вихревые токи, наведенные в рельсах, противодействуют движение поезда.
Электромагнитное демпфирование: Некоторые гальванометры имеют фиксированный сердечник из немагнитного металла. материал. Когда катушка колеблется, вихревые токи, возникающие в сердечнике, противодействуют движению и вызывают катушка быстро отдыхает.
Индукционная печь: Индукционная печь может использоваться для получения высоких температур.
 Через него пропускают переменный ток высокой частоты.
катушка, которая окружает металлы, подлежащие плавке. Вихревые токи, возникающие в металлах, создают высокие
температуры, достаточной для их плавления.
Через него пропускают переменный ток высокой частоты.
катушка, которая окружает металлы, подлежащие плавке. Вихревые токи, возникающие в металлах, создают высокие
температуры, достаточной для их плавления.Счетчики электроэнергии: Блестящий металлический диск в счетчике электроэнергии вращается из-за к вихревым потокам. Электрические токи индуцируются в диске магнитными полями, создаваемыми синусоидальными различные токи в катушке.
Собственная индуктивность
Собственная индуктивность — свойство катушки, благодаря которому ЭДС индукции развивается в самой катушке за счет изменения силы тока, протекающего через саму катушку.
Пусть ток ‘ i ‘ течет через индуктор. Благодаря этому току с ним связан поток Ф такой, что
`\phi\propto i`
`\phi=Li`
L называется индуктивностью собственной индуктивности катушки.
ЭДС индукции определяется как
`\epsilon=\frac{-d\phi}{dt}`
`\epsilon=\frac{-Ldi}{dt}`
Единицей индуктивности в системе СИ является генри (ЧАС). 2 `
2 `
Взаимная индуктивность
Явление, при котором в одной катушке возникает ЭДС индукции из-за изменения силы тока, протекающего через другую катушку, называется взаимной индукцией .
Когда ток i протекает через одну из катушек, поток Φ связан с другой катушкой так, что
`\phi\propto i`
`\phi=Mi`
взаимная индуктивность между катушками.
`\epsilon=\frac{-d\phi}{dt}`
`\epsilon=\frac{-Mdi}{dt}` …..[`\phi=Mi`]
СИ единица взаимной индуктивности равна Генри (Гн).
Генератор переменного тока
Генератор переменного тока преобразует механическую энергию в электрическую.
Состоит из катушки, закрепленной на валу ротора. Ось вращения катушки перпендикулярна направлению магнитного поля. Катушка (называется якорь ) механически вращается в однородном магнитном поле какими-либо внешними средствами. Вращение катушки вызывает изменение магнитного потока через нее, поэтому в катушке индуцируется ЭДС. Концы катушки соединены с внешней цепью с помощью контактных колец и щеток.
Концы катушки соединены с внешней цепью с помощью контактных колец и щеток.
Когда катушка вращается с постоянной угловой скоростью ω, угол θ между вектором магнитного поля B и вектором площади A катушки в любой момент времени t равен θ = ωt. В результате эффективное площадь катушки, на которую воздействуют силовые линии магнитного поля, изменяется со временем, и поток в любой момент времени t равен
`\phi_{B}=BA cos\theta`
`\phi_{B}=BA cosωt`
По закону Фарадея ЭДС индукции для вращающейся катушки из N витков равна
`\ epsilon=-N\frac{d\phi_{B}}{dt}`
`\epsilon=-NBA\frac{d}{dt}(cos\omega t)`
Таким образом, мгновенное значение ЭДС равна
`\epsilon=NBA\omega sin\omega t`
ток периодически меняется и поэтому ток называется переменным током (ac).
Сводка
Электричество и магнетизм взаимосвязаны.
Ученые Эрстед и ампер экспериментально продемонстрировали, что движущиеся заряды (токи) производят магнитное поле.

В замкнутой цепи индуцируются электрические токи , противодействующие изменяющемуся магнитному потоку.
Закон Ленца соответствует закону сохранения энергии.
ЭДС движения можно рассматривать независимо от закона Фарадея с помощью силы Лоренца на движущиеся заряды.
Движущиеся заряды в статическом поле и статические заряды в переменном поле кажутся симметричными ситуация для Закон Фарадея .
Движение медной пластины затухает, когда ей позволяют колебаться между магнитными полюсные наконечники, потому что вихревых токов петель индуцируются в объеме проводника.
Потери на вихревые токи могут быть сведены к минимуму за счет вырезания пазов в толще проводника, тем самым разрезание вихретоковых петель.
Магнитная потенциальная энергия индуктора в любой момент времени зависит от силы тока, протекающего в индукторе в этот момент.
 Это не зависит от способа изменения тока.
Это не зависит от способа изменения тока.Магнитный поток Связь через поверхность пропорциональна количеству проходящих силовых линий через это.
ЭДС индукции равна отрицательной скорости изменения магнитного потока во времени.
Самоиндукция численно равна магнитному потоку при протекании единичного тока катушка.
Самоиндукция катушки численно равна ЭДС, индуцированной на концах катушки при скорости изменения тока 1 А/с.
Индуцированный заряд численно равен изменению магнитного потока, если сопротивление схема едина.
Магнитный поток является скалярной величиной, так как является скалярным произведением магнитного поля и площади (вектора).
Взаимная индуктивность двух катушек численно равна ЭДС, индуцированной в одной катушке, когда скорость изменения тока в другой катушке составляет 1 А/с.

Прочтите также
- Текущий электрический
Электромагнитная индукция — это процесс индуцирования электродвижущей силы путем перемещения проводника с зарядом (например, металлической проволоки) в магнитном поле. Когда электрический проводник движется через магнитное поле, он пересекает силовые линии магнитного поля, вызывая изменение магнитного поля.
Когда происходят изменения магнитного потока (обозначаемого Φ), работа совершается в виде электрической энергии , создавая напряжение или электродвижущую силу в проводнике.
Электромагнитная индукция возникает, когда электродвижущая сила генерируется в замкнутой цепи из-за переменного магнитного потока.
Магнитный поток — это измерение общего магнитного поля в данной области. Его можно описать как общее количество линий магнитного поля, пересекающих определенную область.

Обязательно ознакомьтесь с нашим пояснением по ЭДС и внутреннему сопротивлению.
Открытие электромагнитной индукции
Майкл Фарадей открыл закон индукции в 1831 году. Он провел экспериментальную процедуру, в ходе которой соединил батарею, гальванометр, магнит и проводник. Вы можете видеть это на рисунке 1.
Вот что обнаружил Фарадей в ходе своего эксперимента:
- Когда он отключил батарею, не было протекания электрического тока, и в магните не индуцировался магнитный поток.
- Когда он замкнул переключатель, через гальванометр протекал переходный ток . Фарадей назвал это «электрической волной».
- Когда он открыл переключатель, измеренный ток быстро подскочил до противоположной стороны показаний, прежде чем вернуться к нулю.
В последующие месяцы Фарадей продолжил свои эксперименты, которые привели его к открытию других свойств электромагнитной индукции.
 Он наблюдал те же переходные токи, когда быстро перемещал стержневой магнит через катушку с проводами. Он также создал постоянный ток (постоянный ток) путем вращения медного диска рядом со стержневым магнитом с помощью скользящего электрического провода.
Он наблюдал те же переходные токи, когда быстро перемещал стержневой магнит через катушку с проводами. Он также создал постоянный ток (постоянный ток) путем вращения медного диска рядом со стержневым магнитом с помощью скользящего электрического провода.Фарадей обобщил свои выводы, используя понятие, которое он назвал «силовыми линиями». Когда переключатель был первоначально изменен с разомкнутого на замкнутый, магнитный поток внутри магнитного сердечника увеличился от нуля до максимального значения (которое было постоянным значением). При увеличении потока наблюдался индуцированный ток на противоположной стороне. Точно так же, когда переключатель был разомкнут, магнитный поток в сердечнике уменьшился бы от его постоянного максимального значения до нуля. Следовательно, уменьшающийся поток внутри сердечника индуцировал противоположный ток с правой стороны.
Эксперимент Фарадея по индукции тока магнитным полем (батарейка, железное кольцо и гальванометр), Wikimedia Commons
Закон электромагнитной индукции Фарадея
Фарадей наблюдал за результатами своего эксперимента и выражал свои наблюдения математически.
 Он заметил, что резкое изменение магнитного потока внутри магнита увеличилось от нуля до некоторого максимального значения. Так, при изменении потока на противоположной стороне создается индукционный ток .
Он заметил, что резкое изменение магнитного потока внутри магнита увеличилось от нуля до некоторого максимального значения. Так, при изменении потока на противоположной стороне создается индукционный ток .Фарадей пришел к выводу, что изменяющийся магнитный поток в замкнутой цепи индуцирует электродвижущую силу или напряжение , что показано в уравнении ниже. В этом уравнении ε — электродвижущая сила (измеряется в вольтах), Φ — магнитный поток в цепи (измеряется в Вебере), N — число витков катушки, t — время (измеряется в секундах).
Из этого уравнения мы можем определить параметры, влияющие на магнитное поле: более сильный магнит (что влияет на магнитный поток), больше катушек (что влияет на N) и скорость, с которой движется провод.
Уравнение Максвелла-Фарадея
Уравнение Максвелла-Фарадея утверждает, что изменяющееся во времени магнитное поле создает пространственно изменяющееся электрическое поле и наоборот.
 Вы можете увидеть уравнение Максвелла-Фарадея ниже, где × — математический символ, обозначающий градиент электрического поля E, а B — магнитное поле. Оба поля являются функцией положения r и времени t.
Вы можете увидеть уравнение Максвелла-Фарадея ниже, где × — математический символ, обозначающий градиент электрического поля E, а B — магнитное поле. Оба поля являются функцией положения r и времени t.Закон электромагнитной индукции Ленца
Наведенный ток в проводнике создаст магнитное поле. Направление тока будет таким, чтобы магнитное поле противодействовало первоначальным изменениям магнитного поля, вызвавшим ток. Это известно как закон Ленца.
Закон Ленца также математически выражается в приведенном ниже уравнении. Знак минус — это добавление закона Ленца к выражению Фарадея , чтобы показать, что направление индуцированной силы противоположно изменениям в магнитном поле.
Закон Ленца дополняет закон Фарадея, добавляя, что направление индуцированного тока будет препятствовать изменению магнитного поля.
Катушка с проволочными резисторами состоит из 20 витков.
 Магнитное поле изменяется от -5T до 3T за 0,5 секунды. Найдите ЭДС индукции в катушке.
Магнитное поле изменяется от -5T до 3T за 0,5 секунды. Найдите ЭДС индукции в катушке.Решение
В примере T означает тесла. Плотность магнитного потока, равная одному Вб/м 2 , равна одному тесла.
Правило правой руки Ленца
Направление индуцированного тока можно найти с помощью правила правой руки Ленца . Разгибаем пальцы так, чтобы они были взаимно перпендикулярны друг другу. Большой палец указывает на силу (F), указательный палец указывает направление магнитного поля (В), а средний палец указывает направление индукционного тока (I).
Рис. 2. Правило правой руки Ленца, Oğulcan Tezcan — StudySmarter Originals
Электромагнитная индукция и магнитная потокосцепление
Магнитная потокосцепление (ΦΝ) представляет собой произведение магнитного потока и числа витков в катушке.
Вы можете увидеть это в уравнении ниже, где Φ — магнитный поток (Вт), N — число витков, B — плотность магнитного потока (Тл), а A — площадь поперечного сечения (м 2 ).
 Когда мы рассматриваем магнитный поток катушки, компонент N имеет решающее значение для расчета магнитной связи катушки.
Когда мы рассматриваем магнитный поток катушки, компонент N имеет решающее значение для расчета магнитной связи катушки.ΦN = BAN
Мы рассчитываем полную магнитную связь, умножая магнитный поток на количество витков в катушке. Мы можем игнорировать член N, когда рассматривается магнитный поток данной области.
ΦN = BA
Применение электромагнитной индукции
Электромагнитная индукция очень важна, поскольку она позволяет генерировать электричество в замкнутом контуре. Электромагнитная индукция очень полезна в электрических генераторах, трансформаторах и двигателях. Наиболее известными приложениями электромагнитной индукции являются генератор переменного тока, электрический трансформатор и магнитный расходомер.
Электромагнитная индукция — основные выводы
- Электромагнитная индукция — это процесс индуцирования электродвижущей силы путем перемещения проводника, несущего заряд, в магнитном поле.

- Майкл Фарадей открыл закон электромагнитной индукции. Этот закон гласит, что изменение магнитного потока в замкнутой цепи индуцирует электродвижущую силу или напряжение в цепи.
- Закон Максвелла-Фарадея гласит, что изменяющееся во времени магнитное поле создает электрическое поле, изменяющееся в пространстве, и наоборот.
- Магнитная потокосцепление (ΦΝ) представляет собой произведение магнитного потока и числа витков в катушке.
- Электромагнитная индукция очень важна, поскольку она позволяет генерировать электричество в замкнутой цепи.
Induction: page 2 (Videos: 6 to 10: Induction problems, multiple-choice questions)
- AP Physics 2: Induction 1: Faraday’s Law of Induction
- История Фарадея: Майкл Фарадей — От электричества к производству электроэнергии (14:35) https://www.youtube.com/watch?v=dDtI_EYA42w
- AP Physics 2: Induction 2: Magnetic Flux
- AP Physics 2: Induction 3: Lenz’s Law & How to Find Direction of Induced Current
- AP Physics 2: Induction 4: Induced Current and Magnetic Resistant Force
- AP Физика 2: Индукция 5 Использование закона Ленца для нахождения направления индукционного тока0010
- 27:16 до 31:25 ЭДС индукции в одной петле разного размера/формы вокруг соленоида.
- 31:25 до 33:40 ЭДС индукции в одном контуре по сравнению с ЭДС индукции в трехконтурной катушке вокруг соленоида, а также идея трансформаторов.
- 33:40 to end ЭДС индукции и индуцированное электрическое поле не являются консервативными – это что-то очень неинтуитивное, и, как сказал профессор Левин, «это снесет вам крышу»!
- Лек 16 | MIT 8.02 Электричество и магнетизм, весна 2002 г. http://www.youtube.com/watch?v=G3eI4SVDyME ( Обновление : Массачусетский технологический институт на неопределенный срок удаляет онлайн-лекции и курсы по физике Уолтера Левина по уважительным причинам. Однако вы все равно можете посмотреть это видео на странице https://www.youtube.com/watch?v=FUUMCT7FjaI.
 Я размещаю эту ссылку здесь, потому что не могу найти ничего равноценного или лучшего качества (с точки зрения содержания физики). Я не оправдываю ужасное поведение Левина. В целях вашей безопасности учащиеся ни в коем случае не должны связываться с Левином.)0010
Я размещаю эту ссылку здесь, потому что не могу найти ничего равноценного или лучшего качества (с точки зрения содержания физики). Я не оправдываю ужасное поведение Левина. В целях вашей безопасности учащиеся ни в коем случае не должны связываться с Левином.)0010 - MIT Physics Demo — левитирующий магнит http://techtv.mit.edu/videos/823-mit-physics-demo-levitating-magnet или http://www.youtube.com/watch?v=X54gibrRgIA
- Демонстрация физики – сверхпроводник, левитирующий магнит 48:51 Больше демонстраций магнитного демпфирования
- Lec 17 | MIT 8.02 Электричество и магнетизм, весна 2002 г. http://www.youtube.com/watch?v=qxuGDEz8wDg ( Обновление : Массачусетский технологический институт на неопределенный срок удаляет онлайн-лекции и курсы по физике Уолтера Левина по уважительным причинам. Однако вы все равно можете посмотреть это видео по адресу https://www.youtube.com/watch?v=fOyuov4fimQ. Я размещаю эту ссылку здесь, потому что не могу найти ничего равноценного или лучшего качества (с точки зрения содержания физики).



 (Опыт: действие электрического тока на магнитную стрелку). 1820 г. А. Ампер — французский ученый, открыл механическое взаимодействие токов и установил закон этого взаимодействия.
(Опыт: действие электрического тока на магнитную стрелку). 1820 г. А. Ампер — французский ученый, открыл механическое взаимодействие токов и установил закон этого взаимодействия.
 Вектор магнитной индукции направлен по касательной к линиям.
Вектор магнитной индукции направлен по касательной к линиям. Магнитный поток показывает, какое количество линий магнитной индукции пронизывает данный контур.
Магнитный поток показывает, какое количество линий магнитной индукции пронизывает данный контур. Персиановский)
Персиановский) 2.014.01
2.014.01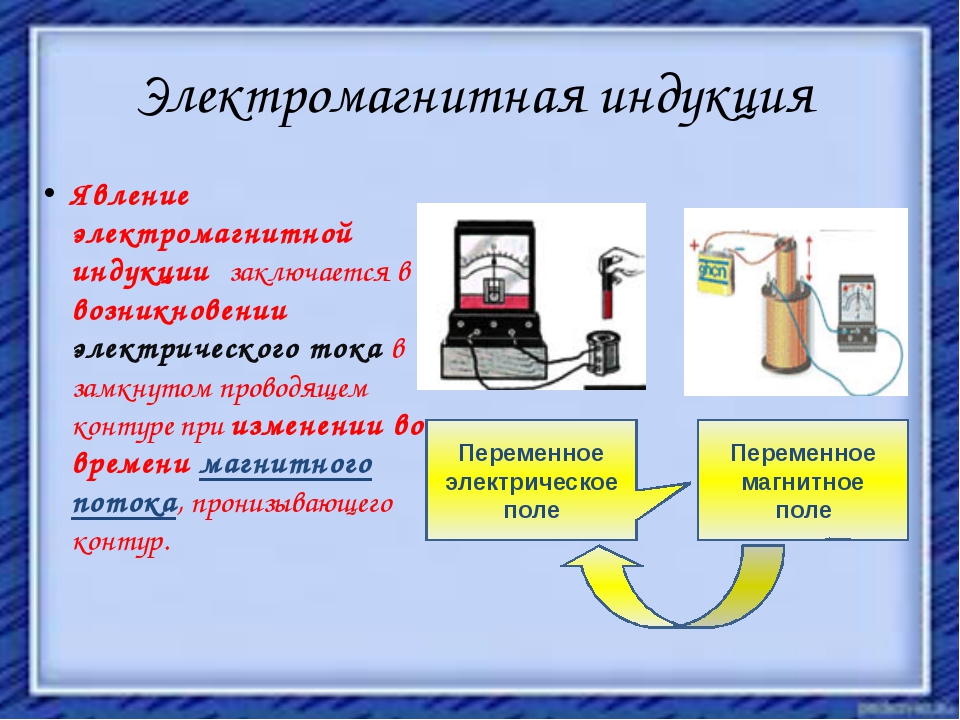
 (катушка)
(катушка)








 Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike  Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike  s Закон индукции: закон Lenzu2019s. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42392/latest/ . Лицензия : CC BY: Attribution
s Закон индукции: закон Lenzu2019s. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42392/latest/ . Лицензия : CC BY: Attribution  wiktionary.org/wiki/solenoid . Лицензия : CC BY-SA: Attribution-ShareAlike
wiktionary.org/wiki/solenoid . Лицензия : CC BY-SA: Attribution-ShareAlike  7 февраля 2013 г. Предоставлено : OpenStax CNX. Адрес: : http://cnx.org/content/m42392/latest/ . Лицензия : CC BY: Attribution
7 февраля 2013 г. Предоставлено : OpenStax CNX. Адрес: : http://cnx.org/content/m42392/latest/ . Лицензия : CC BY: Attribution  Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike  7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42392/latest/ . Лицензия : CC BY: Attribution
7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42392/latest/ . Лицензия : CC BY: Attribution  Расположен по адресу : http://cnx.org/content/m42411/latest/ . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42411/latest/ . Лицензия : CC BY: Attribution  Лицензия : CC BY: Attribution
Лицензия : CC BY: Attribution  8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
8 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution  Адрес: : http://cnx.org/content/m12869/latest/ . Лицензия : CC BY: Attribution
Адрес: : http://cnx.org/content/m12869/latest/ . Лицензия : CC BY: Attribution  Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_flux . Лицензия : CC BY: Attribution
Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_flux . Лицензия : CC BY: Attribution 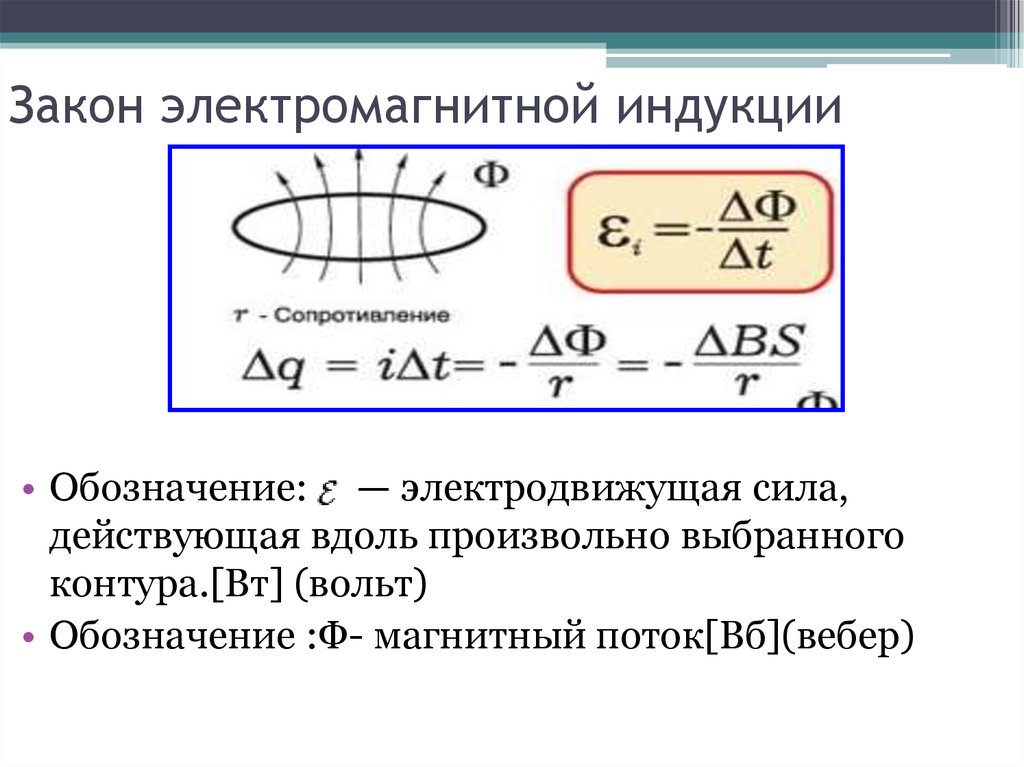 Расположен по адресу : http://cnx.org/content/m42400/latest/ . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42400/latest/ . Лицензия : CC BY: Attribution  Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42404/latest/ . Лицензия : CC BY: Attribution  Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike  7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42390/latest/ . Лицензия : CC BY: Attribution
7 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42390/latest/ . Лицензия : CC BY: Attribution