Векторное произведение | это… Что такое Векторное произведение?
Векторное произведение в трёхмерном пространстве.
Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Произведение не является ни коммутативным, ни ассоциативным (оно является антикоммутативным) и отличается от скалярного произведения векторов. Во многих задачах инженерии и физики нужно иметь возможность строить вектор, перпендикулярный двум имеющимся — векторное произведение предоставляет эту возможность. Векторное произведение полезно для «измерения» перпендикулярности векторов — длина векторного произведения двух векторов равна произведению их длин, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны либо антипараллельны.
Определить векторное произведение можно по-разному, и теоретически, в пространстве любой размерности n можно вычислить произведение
 Но если произведение ограничить нетривиальными бинарными произведениями с векторным результатами, то традиционное векторное произведение определено только в трёхмерном и семимерном пространствах. Результат векторного произведения, как и скалярного, зависит от метрики Евклидова пространства.
Но если произведение ограничить нетривиальными бинарными произведениями с векторным результатами, то традиционное векторное произведение определено только в трёхмерном и семимерном пространствах. Результат векторного произведения, как и скалярного, зависит от метрики Евклидова пространства.В отличие от формулы для вычисления по координатам векторов скалярного произведения в трёхмерной прямоугольной системе координат, формула для векторного произведения зависит от ориентации прямоугольной системы координат или, иначе, её «хиральности».
Содержание
|
Определение и история
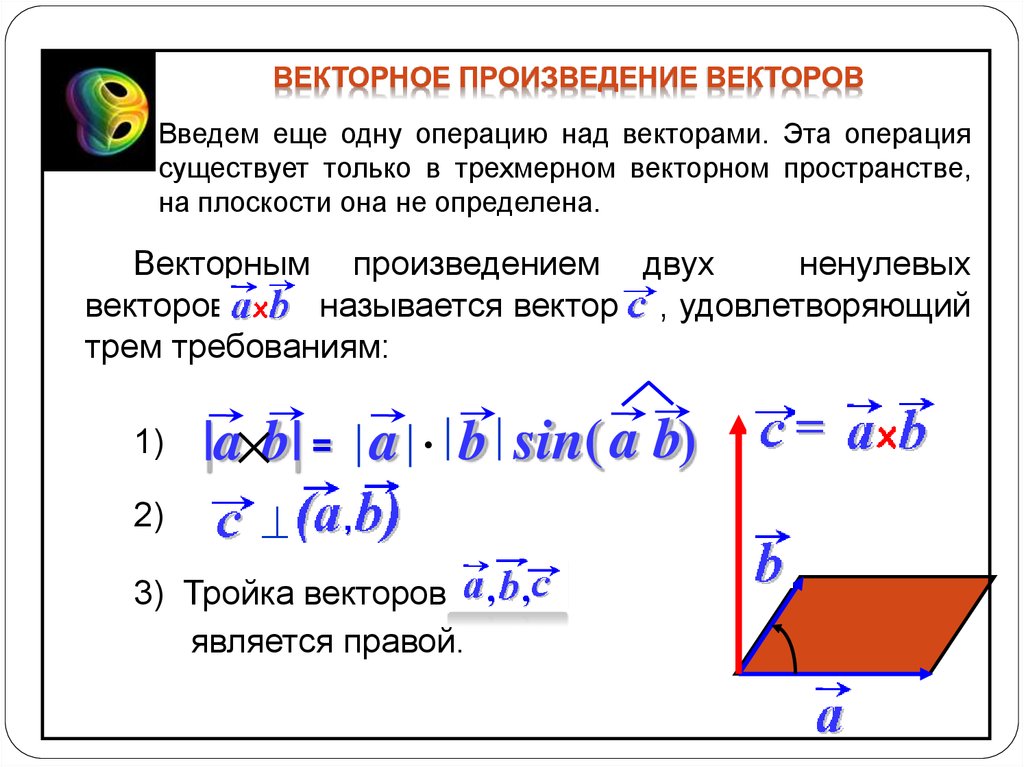
Векторным произведением вектора на вектор в пространстве называется вектор , удовлетворяющий следующим требованиям:
- длина вектора равна произведению длин векторов и на синус угла между ними: ;
- вектор ортогонален каждому из векторов и ;
- вектор направлен так, что тройка векторов является правой;
- в случае пространства требуется ассоциативность тройки векторов .
Обозначение:
В литературе[1] определение векторного произведения может даваться по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах в правой и левой прямоугольной системе координат. А далее выводится данное выше определение, а также определение правой и левой тройки векторов.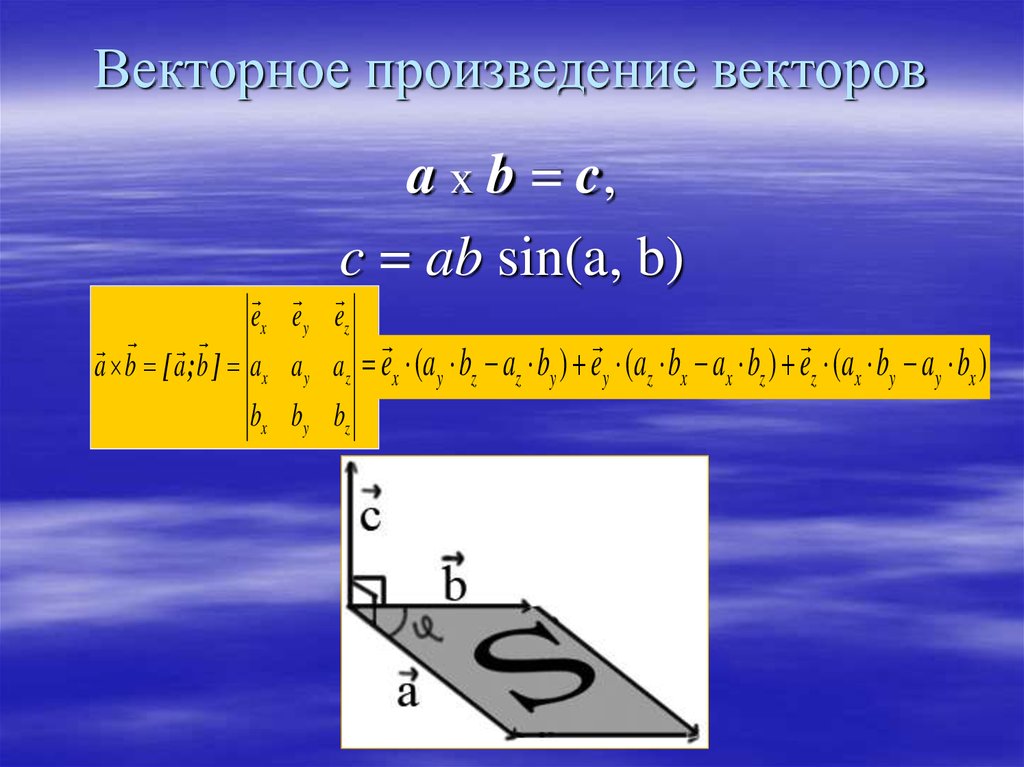
Также для исходного определения может быть взят набор алгебраических свойств векторного произведения, а из них выводиться остальное.
Векторное произведение было введено У. Гамильтоном в 1846 году[2] одновременно со скалярным произведением в связи с кватернионами — соответственно, как векторная и скалярная часть произведения двух кватернионов, скалярная часть которых равна нулю[3].
Правые и левые тройки векторов в трёхмерном пространстве
Рассмотрим упорядоченную тройку некомпланарных векторов в трёхмерном пространстве. Совместим начала этих векторов в точке (то есть выберем произвольно в пространстве точку и параллельно перенесём каждый вектор так, чтобы его начало совпало с точкой ). Концы векторов, совмещённых началами в точке , не лежат на одной прямой, так как векторы некомпланарны. Рассмотрим плоскость — единственную плоскость, проходящую через концы векторов, совмещённых началами в точке . Тогда можно в плоскости провести через концы векторов , совмещённых началами в точке , единственную окружность и выяснить направление обхода трёх точек на окружности, смотря на неё с одной из сторон от плоскости.
Тогда можно в плоскости провести через концы векторов , совмещённых началами в точке , единственную окружность и выяснить направление обхода трёх точек на окружности, смотря на неё с одной из сторон от плоскости.
Упорядоченная тройка некомпланарных векторов в трёхмерном пространстве называется правой, если наблюдателю, находящемуся по одну сторону с точкой от плоскости , обход концов приведённых в общее начало векторов в указанном порядке кажется совершающимся в плоскости по часовой стрелке.
B противном случае — левая тройка. В этом случае наблюдателю, находящемуся с другой стороны от плоскости , обход концов таких векторов будет казаться совершающимся против часовой стрелки.
Другое определение связано с правой рукой человека (см. рисунок), откуда и берётся название.
Все правые между собой (и левые между собой) тройки векторов называются одинаково ориентированными.
Заметим, что определения «правой» и «левой» тройки векторов не зависят от хиральности рассматриваемой системы координат; более того, они вообще не требуют задания в рассматриваемом пространстве какой-либо системы координат, как и не требует этого само векторное произведение.
Свойства
Геометрические свойства векторного произведения
Рисунок 1: Площадь параллелограмма равна модулю векторного произведения.
Рисунок 2: Объём параллелепипеда при использовании векторного и скалярного произведения векторов; пунктирные линии показывают проекции вектора
- Необходимым и достаточным условием коллинеарности двух ненулевых векторов является равенство нулю их векторного произведения.
- Модуль векторного произведения равняется площади параллелограмма, построенного на приведённых к общему началу векторах и (см. Рисунок 1)
- Если — единичный вектор, ортогональный векторам и и выбранный так, что тройка — правая, а — площадь параллелограмма, построенного на них (приведённых к общему началу), то для векторного произведения справедлива формула:
- Если — какой-нибудь вектор, — любая плоскость, содержащая этот вектор, — единичный вектор, лежащий в плоскости и ортогональный к , — единичный вектор, ортогональный к плоскости и направленный так, что тройка векторов является правой, то для любого лежащего в плоскости вектора справедлива формула
- При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c (см.
 Рисунок 2). Такое произведение трех векторов называется смешанным.
Рисунок 2). Такое произведение трех векторов называется смешанным.
На рисунке показано, что этот объём может быть найден двумя способами: геометрический результат сохраняется даже при замене «скалярного» и «векторного» произведений местами:
Величина векторного произведения зависит от синуса угла между изначальными векторами, поэтому векторное произведение может восприниматься как степень «перпендикулярности» векторов также, как и скалярное произведение может рассматриваться как степень «параллельности». Векторное произведение двух единичных векторов равно 1 (единичному вектору), если изначальные векторы перпендикулярны, и равно 0 (нулевому вектору), если векторы параллельны либо антипараллельны.
Алгебраические свойства векторного произведения
| Представление | Описание |
|---|---|
| свойство антикоммутативности | |
| свойство ассоциативности относительно умножения на скаляр | |
| свойство дистрибутивности по сложению | |
| тождество Якоби, выполняется в и нарушается в | |
| формула «БАЦ минус ЦАБ», тождество Лагранжа | |
| Это частный случай мультипликативности нормы кватернионов | |
| значение этого выражения называют смешанным произведением векторов , , и обозначают либо |
Выражение для векторного произведения в декартовых координатах
Если два вектора и определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе
а система координат правая, то их векторное произведение имеет вид
Для запоминания этой формулы удобно использовать определитель:
или
где — символ Леви-Чивиты.
Если система координат левая, то их векторное произведение имеет вид
Для запоминания, аналогично:
или
Формулы для левой системы координат можно легко получить из формул правой системы координат, записав те же векторы и во вспомогательной правой системе координат ():
Обобщения
Кватернионы
Векторное произведение можно также записать в кватернионной форме, поэтому буквы , , — стандартные обозначения для ортов в : они рассматриваются как воображаемые кватернионы.
Заметим, что соотношения через векторное произведение между , и соответствуют правилам умножения для кватернионов , и . Если представить вектор как кватернион , то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.
Преобразование к матричной форме
Векторное произведение двух векторов можно записать как произведение кососимметрической матрицы и вектора:
где
Пусть равен векторному произведению:
тогда
Такая форма записи позволяет обобщить векторное произведение на высшие размерности, представляя псевдовекторы (угловая скорость, индукция и т. п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь независимых компонент в -мерном пространстве. В трёхмерном пространстве получаются три независимые компоненты, поэтому такие величины можно представлять как векторы этого пространства.
п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь независимых компонент в -мерном пространстве. В трёхмерном пространстве получаются три независимые компоненты, поэтому такие величины можно представлять как векторы этого пространства.
С такой формой записи также зачастую проще работать (например, в en:epipolar geometry).
Из общих свойств векторного произведения следует, что
- и
а так как кососимметрична, то
В такой форме записи легко доказывается тождество Лагранжа (правило «бац минус цаб»).
Распространение на матрицы
В трёхмерном случае можно определить векторное произведение матриц и произведение матрицы на вектор. Это делает очевидным указанный выше изоморфизм и позволяет упростить многие выкладки. Представим матрицу как столбец векторов, тогда
Умножение матрицы на вектор слева определяется аналогично, если представить как строку векторов. Транспонирование матрицы, соответственно, переводит строку векторов в столбец векторов, и наоборот. Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например ( — матрица, , — векторы):
Транспонирование матрицы, соответственно, переводит строку векторов в столбец векторов, и наоборот. Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например ( — матрица, , — векторы):
После этого можно изменить форму записи для векторного произведения:
— единичная матрица. Отсюда очевидны существование и вид матрицы, соответствующей векторному умножению на вектор слева. Аналогично можно получить выражение для матрицы умножения на вектор справа. Распространяя операции над векторами на матрицы покомпонентно, представляя их как «векторы из векторов», стандартные соотношения для векторов легко обобщаются на матрицы. Например, теорема Стокса в примет вид:
где ротор матрицы вычисляется как векторное произведение матрицы на оператор Гамильтона слева. В этих обозначениях очень легко доказать, например, следующие формы теоремы Стокса:
Размерности, не равные трём
Пусть — размерность пространства.
Векторное произведение, обладающее всеми свойствами обычного трёхмерного векторного произведения, то есть бинарное билинейное антисимметричное невырожденное отображение , можно ввести только для размерностей 3 и 7.
Однако есть простое обобщение на остальные натуральные размерности, начиная с 3, а если нужно — и на размерность 2 (последнее, правда, сравнительно специфическим образом). Тогда это обобщение, в отличие от невозможного, описанного чуть выше, вводится не для пары векторов, а лишь для набора векторов-сомножителей. Вполне аналогично смешанному произведению, естественно обобщаемому в -мерном пространстве на операцию с сомножителями. Используя символ Леви-Чивиты с индексами, можно явно записать такое -валентное векторное произведение как
Такое обобщение дает гиперплощадь размерности .
Если нужно ввести операцию именно для двух сомножителей, имеющую геометрический смысл, предельно близкий к смыслу векторного произведения (то есть представляющую ориентированную площадь), то результат уже не будет вектором, так как при не найдется единственной, однозначно определённой нормали к двумерной плоскости, натянутой на множители. Можно ввести бивектор, компоненты которого равны проекциям ориентированной площади параллелограмма, натянутого на пару векторов, на координатные плоскости:
Можно ввести бивектор, компоненты которого равны проекциям ориентированной площади параллелограмма, натянутого на пару векторов, на координатные плоскости:
- .
Эта конструкция называется внешним произведением.
Для двумерного случая операция
- .
называется псевдоскалярным произведением, так как получающееся пространство одномерно и результат есть псевдоскаляр. (Двухиндексное внешнее произведение, описанное выше, можно ввести и для двумерного пространства, однако оно, очевидно, достаточно тривиально связано с псевдоскалярным произведением, а именно внешнее произведение в этом случае представляется матрицей, на диагонали которой нули, а оставшиеся два недиагональных элемента равны псевдоскалярному произведению и минус псевдоскалярному произведению).
Алгебра Ли векторов
Векторное произведение вводит на структуру алгебры Ли (поскольку оно удовлетворяет обеим аксиомам — антисимметричности и тождеству Якоби). Эта структура соответствует отождествлению с касательной алгеброй Ли к группе Ли ортогональных линейных преобразований трёхмерного пространства.
См. также
Произведения векторов
- Псевдоскалярное произведение (только на плоскости!)
- Скалярное произведение векторов
- Смешанное (скалярно-векторное) произведение векторов (только в )
- Двойное (векторно-векторное) произведение векторов (только в )
Другое
- Ротор
- Дивергенция
Примечания
- ↑ И в различных учебных заведениях.
- ↑ Crowe M. J. A History of Vector Analysis – The Evolution of the Idea of a Vectorial System. — Courier Dover Publications, 1994. — С. 32. — 270 с. — ISBN 0486679101
- ↑ Hamilton W. R. On Quaternions; or on a New System of Imaginaries in Algebra // Philosophical Magazine. 3rd Series. — London, 1846. — Т. 29. — С. 30.
Литература
- Кочин Н. Е. Введение в векторный и тензорный анализ.
Ссылки
- Многомерное векторное произведение
- Векторное произведение и его свойства.
 Примеры решения задач
Примеры решения задач - В. И. Гервидс Правое и левое вращение (flash). НИЯУ МИФИ (10.03.2011). — Физические демонстрации. Проверено 3 мая 2011.
Векторное произведение | это… Что такое Векторное произведение?
Векторное произведение в трёхмерном пространстве.
Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Произведение не является ни коммутативным, ни ассоциативным (оно является антикоммутативным) и отличается от скалярного произведения векторов. Во многих задачах инженерии и физики нужно иметь возможность строить вектор, перпендикулярный двум имеющимся — векторное произведение предоставляет эту возможность. Векторное произведение полезно для «измерения» перпендикулярности векторов — длина векторного произведения двух векторов равна произведению их длин, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны либо антипараллельны.
Определить векторное произведение можно по-разному, и теоретически, в пространстве любой размерности n можно вычислить произведение n-1 векторов, получив при этом единственный вектор, перпендикулярный к ним всем. Но если произведение ограничить нетривиальными бинарными произведениями с векторным результатами, то традиционное векторное произведение определено только в трёхмерном и семимерном пространствах. Результат векторного произведения, как и скалярного, зависит от метрики Евклидова пространства.
В отличие от формулы для вычисления по координатам векторов скалярного произведения в трёхмерной прямоугольной системе координат, формула для векторного произведения зависит от ориентации прямоугольной системы координат или, иначе, её «хиральности».
Содержание
|
Определение и история
Векторным произведением вектора на вектор в пространстве называется вектор , удовлетворяющий следующим требованиям:
- длина вектора равна произведению длин векторов и на синус угла между ними: ;
- вектор ортогонален каждому из векторов и ;
- вектор направлен так, что тройка векторов является правой;
- в случае пространства требуется ассоциативность тройки векторов .
Обозначение:
В литературе[1] определение векторного произведения может даваться по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах в правой и левой прямоугольной системе координат. А далее выводится данное выше определение, а также определение правой и левой тройки векторов.
Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах в правой и левой прямоугольной системе координат. А далее выводится данное выше определение, а также определение правой и левой тройки векторов.
Также для исходного определения может быть взят набор алгебраических свойств векторного произведения, а из них выводиться остальное.
Векторное произведение было введено У. Гамильтоном в 1846 году[2] одновременно со скалярным произведением в связи с кватернионами — соответственно, как векторная и скалярная часть произведения двух кватернионов, скалярная часть которых равна нулю[3].
Правые и левые тройки векторов в трёхмерном пространстве
Нахождение направления векторного произведения с помощью правила правой руки
Рассмотрим упорядоченную тройку некомпланарных векторов в трёхмерном пространстве. Совместим начала этих векторов в точке (то есть выберем произвольно в пространстве точку и параллельно перенесём каждый вектор так, чтобы его начало совпало с точкой ). Концы векторов, совмещённых началами в точке , не лежат на одной прямой, так как векторы некомпланарны. Рассмотрим плоскость — единственную плоскость, проходящую через концы векторов, совмещённых началами в точке . Тогда можно в плоскости провести через концы векторов , совмещённых началами в точке , единственную окружность и выяснить направление обхода трёх точек на окружности, смотря на неё с одной из сторон от плоскости.
Концы векторов, совмещённых началами в точке , не лежат на одной прямой, так как векторы некомпланарны. Рассмотрим плоскость — единственную плоскость, проходящую через концы векторов, совмещённых началами в точке . Тогда можно в плоскости провести через концы векторов , совмещённых началами в точке , единственную окружность и выяснить направление обхода трёх точек на окружности, смотря на неё с одной из сторон от плоскости.
Упорядоченная тройка некомпланарных векторов в трёхмерном пространстве называется правой, если наблюдателю, находящемуся по одну сторону с точкой от плоскости , обход концов приведённых в общее начало векторов в указанном порядке кажется совершающимся в плоскости по часовой стрелке.
B противном случае — левая тройка. В этом случае наблюдателю, находящемуся с другой стороны от плоскости , обход концов таких векторов будет казаться совершающимся против часовой стрелки.
Другое определение связано с правой рукой человека (см. рисунок), откуда и берётся название.
Все правые между собой (и левые между собой) тройки векторов называются одинаково ориентированными.
Заметим, что определения «правой» и «левой» тройки векторов не зависят от хиральности рассматриваемой системы координат; более того, они вообще не требуют задания в рассматриваемом пространстве какой-либо системы координат, как и не требует этого само векторное произведение.
Свойства
Геометрические свойства векторного произведения
Рисунок 1: Площадь параллелограмма равна модулю векторного произведения.
Рисунок 2: Объём параллелепипеда при использовании векторного и скалярного произведения векторов; пунктирные линии показывают проекции вектора c на a × b и вектора a на b × c, первым шагом является нахождение скалярных произведений.
- Необходимым и достаточным условием коллинеарности двух ненулевых векторов является равенство нулю их векторного произведения.

- Модуль векторного произведения равняется площади параллелограмма, построенного на приведённых к общему началу векторах и (см. Рисунок 1)
- Если — единичный вектор, ортогональный векторам и и выбранный так, что тройка — правая, а — площадь параллелограмма, построенного на них (приведённых к общему началу), то для векторного произведения справедлива формула:
- Если — какой-нибудь вектор, — любая плоскость, содержащая этот вектор, — единичный вектор, лежащий в плоскости и ортогональный к , — единичный вектор, ортогональный к плоскости и направленный так, что тройка векторов является правой, то для любого лежащего в плоскости вектора справедлива формула
- При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c (см. Рисунок 2). Такое произведение трех векторов называется смешанным.

На рисунке показано, что этот объём может быть найден двумя способами: геометрический результат сохраняется даже при замене «скалярного» и «векторного» произведений местами:
Величина векторного произведения зависит от синуса угла между изначальными векторами, поэтому векторное произведение может восприниматься как степень «перпендикулярности» векторов также, как и скалярное произведение может рассматриваться как степень «параллельности». Векторное произведение двух единичных векторов равно 1 (единичному вектору), если изначальные векторы перпендикулярны, и равно 0 (нулевому вектору), если векторы параллельны либо антипараллельны.
Алгебраические свойства векторного произведения
| Представление | Описание |
|---|---|
| свойство антикоммутативности | |
| свойство ассоциативности относительно умножения на скаляр | |
| свойство дистрибутивности по сложению | |
| тождество Якоби, выполняется в и нарушается в | |
| формула «БАЦ минус ЦАБ», тождество Лагранжа | |
| Это частный случай мультипликативности нормы кватернионов | |
| значение этого выражения называют смешанным произведением векторов , , и обозначают либо |
Выражение для векторного произведения в декартовых координатах
Если два вектора и определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе
а система координат правая, то их векторное произведение имеет вид
Для запоминания этой формулы удобно использовать определитель:
или
где — символ Леви-Чивиты.
Если система координат левая, то их векторное произведение имеет вид
Для запоминания, аналогично:
или
Формулы для левой системы координат можно легко получить из формул правой системы координат, записав те же векторы и во вспомогательной правой системе координат ():
Обобщения
Кватернионы
Векторное произведение можно также записать в кватернионной форме, поэтому буквы , , — стандартные обозначения для ортов в : они рассматриваются как воображаемые кватернионы.
Заметим, что соотношения через векторное произведение между , и соответствуют правилам умножения для кватернионов , и . Если представить вектор как кватернион , то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.
Преобразование к матричной форме
Векторное произведение двух векторов можно записать как произведение кососимметрической матрицы и вектора:
где
Пусть равен векторному произведению:
тогда
Такая форма записи позволяет обобщить векторное произведение на высшие размерности, представляя псевдовекторы (угловая скорость, индукция и т. п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь независимых компонент в -мерном пространстве. В трёхмерном пространстве получаются три независимые компоненты, поэтому такие величины можно представлять как векторы этого пространства.
п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь независимых компонент в -мерном пространстве. В трёхмерном пространстве получаются три независимые компоненты, поэтому такие величины можно представлять как векторы этого пространства.
С такой формой записи также зачастую проще работать (например, в en:epipolar geometry).
Из общих свойств векторного произведения следует, что
- и
а так как кососимметрична, то
В такой форме записи легко доказывается тождество Лагранжа (правило «бац минус цаб»).
Распространение на матрицы
В трёхмерном случае можно определить векторное произведение матриц и произведение матрицы на вектор. Это делает очевидным указанный выше изоморфизм и позволяет упростить многие выкладки. Представим матрицу как столбец векторов, тогда
Умножение матрицы на вектор слева определяется аналогично, если представить как строку векторов. Транспонирование матрицы, соответственно, переводит строку векторов в столбец векторов, и наоборот. Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например ( — матрица, , — векторы):
Транспонирование матрицы, соответственно, переводит строку векторов в столбец векторов, и наоборот. Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например ( — матрица, , — векторы):
После этого можно изменить форму записи для векторного произведения:
— единичная матрица. Отсюда очевидны существование и вид матрицы, соответствующей векторному умножению на вектор слева. Аналогично можно получить выражение для матрицы умножения на вектор справа. Распространяя операции над векторами на матрицы покомпонентно, представляя их как «векторы из векторов», стандартные соотношения для векторов легко обобщаются на матрицы. Например, теорема Стокса в примет вид:
где ротор матрицы вычисляется как векторное произведение матрицы на оператор Гамильтона слева. В этих обозначениях очень легко доказать, например, следующие формы теоремы Стокса:
Размерности, не равные трём
Пусть — размерность пространства.
Векторное произведение, обладающее всеми свойствами обычного трёхмерного векторного произведения, то есть бинарное билинейное антисимметричное невырожденное отображение , можно ввести только для размерностей 3 и 7.
Однако есть простое обобщение на остальные натуральные размерности, начиная с 3, а если нужно — и на размерность 2 (последнее, правда, сравнительно специфическим образом). Тогда это обобщение, в отличие от невозможного, описанного чуть выше, вводится не для пары векторов, а лишь для набора векторов-сомножителей. Вполне аналогично смешанному произведению, естественно обобщаемому в -мерном пространстве на операцию с сомножителями. Используя символ Леви-Чивиты с индексами, можно явно записать такое -валентное векторное произведение как
Такое обобщение дает гиперплощадь размерности .
Если нужно ввести операцию именно для двух сомножителей, имеющую геометрический смысл, предельно близкий к смыслу векторного произведения (то есть представляющую ориентированную площадь), то результат уже не будет вектором, так как при не найдется единственной, однозначно определённой нормали к двумерной плоскости, натянутой на множители. Можно ввести бивектор, компоненты которого равны проекциям ориентированной площади параллелограмма, натянутого на пару векторов, на координатные плоскости:
Можно ввести бивектор, компоненты которого равны проекциям ориентированной площади параллелограмма, натянутого на пару векторов, на координатные плоскости:
- .
Эта конструкция называется внешним произведением.
Для двумерного случая операция
- .
называется псевдоскалярным произведением, так как получающееся пространство одномерно и результат есть псевдоскаляр. (Двухиндексное внешнее произведение, описанное выше, можно ввести и для двумерного пространства, однако оно, очевидно, достаточно тривиально связано с псевдоскалярным произведением, а именно внешнее произведение в этом случае представляется матрицей, на диагонали которой нули, а оставшиеся два недиагональных элемента равны псевдоскалярному произведению и минус псевдоскалярному произведению).
Алгебра Ли векторов
Векторное произведение вводит на структуру алгебры Ли (поскольку оно удовлетворяет обеим аксиомам — антисимметричности и тождеству Якоби). Эта структура соответствует отождествлению с касательной алгеброй Ли к группе Ли ортогональных линейных преобразований трёхмерного пространства.
См. также
Произведения векторов
- Псевдоскалярное произведение (только на плоскости!)
- Скалярное произведение векторов
- Смешанное (скалярно-векторное) произведение векторов (только в )
- Двойное (векторно-векторное) произведение векторов (только в )
Другое
- Ротор
- Дивергенция
Примечания
- ↑ И в различных учебных заведениях.
- ↑ Crowe M. J. A History of Vector Analysis – The Evolution of the Idea of a Vectorial System. — Courier Dover Publications, 1994. — С. 32. — 270 с. — ISBN 0486679101
- ↑ Hamilton W. R. On Quaternions; or on a New System of Imaginaries in Algebra // Philosophical Magazine. 3rd Series. — London, 1846. — Т. 29. — С. 30.
Литература
- Кочин Н. Е. Введение в векторный и тензорный анализ.
Ссылки
- Многомерное векторное произведение
- Векторное произведение и его свойства.
 Примеры решения задач
Примеры решения задач - В. И. Гервидс Правое и левое вращение (flash). НИЯУ МИФИ (10.03.2011). — Физические демонстрации. Проверено 3 мая 2011.
Векторное произведение | это… Что такое Векторное произведение?
Векторное произведение в трёхмерном пространстве.
Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Произведение не является ни коммутативным, ни ассоциативным (оно является антикоммутативным) и отличается от скалярного произведения векторов. Во многих задачах инженерии и физики нужно иметь возможность строить вектор, перпендикулярный двум имеющимся — векторное произведение предоставляет эту возможность. Векторное произведение полезно для «измерения» перпендикулярности векторов — длина векторного произведения двух векторов равна произведению их длин, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны либо антипараллельны.
Определить векторное произведение можно по-разному, и теоретически, в пространстве любой размерности n можно вычислить произведение n-1 векторов, получив при этом единственный вектор, перпендикулярный к ним всем. Но если произведение ограничить нетривиальными бинарными произведениями с векторным результатами, то традиционное векторное произведение определено только в трёхмерном и семимерном пространствах. Результат векторного произведения, как и скалярного, зависит от метрики Евклидова пространства.
В отличие от формулы для вычисления по координатам векторов скалярного произведения в трёхмерной прямоугольной системе координат, формула для векторного произведения зависит от ориентации прямоугольной системы координат или, иначе, её «хиральности».
Содержание
|
Определение и история
Векторным произведением вектора на вектор в пространстве называется вектор , удовлетворяющий следующим требованиям:
- длина вектора равна произведению длин векторов и на синус угла между ними: ;
- вектор ортогонален каждому из векторов и ;
- вектор направлен так, что тройка векторов является правой;
- в случае пространства требуется ассоциативность тройки векторов .
Обозначение:
В литературе[1] определение векторного произведения может даваться по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах в правой и левой прямоугольной системе координат. А далее выводится данное выше определение, а также определение правой и левой тройки векторов.
Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах в правой и левой прямоугольной системе координат. А далее выводится данное выше определение, а также определение правой и левой тройки векторов.
Также для исходного определения может быть взят набор алгебраических свойств векторного произведения, а из них выводиться остальное.
Векторное произведение было введено У. Гамильтоном в 1846 году[2] одновременно со скалярным произведением в связи с кватернионами — соответственно, как векторная и скалярная часть произведения двух кватернионов, скалярная часть которых равна нулю[3].
Правые и левые тройки векторов в трёхмерном пространстве
Нахождение направления векторного произведения с помощью правила правой руки
Рассмотрим упорядоченную тройку некомпланарных векторов в трёхмерном пространстве. Совместим начала этих векторов в точке (то есть выберем произвольно в пространстве точку и параллельно перенесём каждый вектор так, чтобы его начало совпало с точкой ). Концы векторов, совмещённых началами в точке , не лежат на одной прямой, так как векторы некомпланарны. Рассмотрим плоскость — единственную плоскость, проходящую через концы векторов, совмещённых началами в точке . Тогда можно в плоскости провести через концы векторов , совмещённых началами в точке , единственную окружность и выяснить направление обхода трёх точек на окружности, смотря на неё с одной из сторон от плоскости.
Концы векторов, совмещённых началами в точке , не лежат на одной прямой, так как векторы некомпланарны. Рассмотрим плоскость — единственную плоскость, проходящую через концы векторов, совмещённых началами в точке . Тогда можно в плоскости провести через концы векторов , совмещённых началами в точке , единственную окружность и выяснить направление обхода трёх точек на окружности, смотря на неё с одной из сторон от плоскости.
Упорядоченная тройка некомпланарных векторов в трёхмерном пространстве называется правой, если наблюдателю, находящемуся по одну сторону с точкой от плоскости , обход концов приведённых в общее начало векторов в указанном порядке кажется совершающимся в плоскости по часовой стрелке.
B противном случае — левая тройка. В этом случае наблюдателю, находящемуся с другой стороны от плоскости , обход концов таких векторов будет казаться совершающимся против часовой стрелки.
Другое определение связано с правой рукой человека (см. рисунок), откуда и берётся название.
Все правые между собой (и левые между собой) тройки векторов называются одинаково ориентированными.
Заметим, что определения «правой» и «левой» тройки векторов не зависят от хиральности рассматриваемой системы координат; более того, они вообще не требуют задания в рассматриваемом пространстве какой-либо системы координат, как и не требует этого само векторное произведение.
Свойства
Геометрические свойства векторного произведения
Рисунок 1: Площадь параллелограмма равна модулю векторного произведения.
Рисунок 2: Объём параллелепипеда при использовании векторного и скалярного произведения векторов; пунктирные линии показывают проекции вектора c на a × b и вектора a на b × c, первым шагом является нахождение скалярных произведений.
- Необходимым и достаточным условием коллинеарности двух ненулевых векторов является равенство нулю их векторного произведения.

- Модуль векторного произведения равняется площади параллелограмма, построенного на приведённых к общему началу векторах и (см. Рисунок 1)
- Если — единичный вектор, ортогональный векторам и и выбранный так, что тройка — правая, а — площадь параллелограмма, построенного на них (приведённых к общему началу), то для векторного произведения справедлива формула:
- Если — какой-нибудь вектор, — любая плоскость, содержащая этот вектор, — единичный вектор, лежащий в плоскости и ортогональный к , — единичный вектор, ортогональный к плоскости и направленный так, что тройка векторов является правой, то для любого лежащего в плоскости вектора справедлива формула
- При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c (см. Рисунок 2). Такое произведение трех векторов называется смешанным.

На рисунке показано, что этот объём может быть найден двумя способами: геометрический результат сохраняется даже при замене «скалярного» и «векторного» произведений местами:
Величина векторного произведения зависит от синуса угла между изначальными векторами, поэтому векторное произведение может восприниматься как степень «перпендикулярности» векторов также, как и скалярное произведение может рассматриваться как степень «параллельности». Векторное произведение двух единичных векторов равно 1 (единичному вектору), если изначальные векторы перпендикулярны, и равно 0 (нулевому вектору), если векторы параллельны либо антипараллельны.
Алгебраические свойства векторного произведения
| Представление | Описание |
|---|---|
| свойство антикоммутативности | |
| свойство ассоциативности относительно умножения на скаляр | |
| свойство дистрибутивности по сложению | |
| тождество Якоби, выполняется в и нарушается в | |
| формула «БАЦ минус ЦАБ», тождество Лагранжа | |
| Это частный случай мультипликативности нормы кватернионов | |
| значение этого выражения называют смешанным произведением векторов , , и обозначают либо |
Выражение для векторного произведения в декартовых координатах
Если два вектора и определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе
а система координат правая, то их векторное произведение имеет вид
Для запоминания этой формулы удобно использовать определитель:
или
где — символ Леви-Чивиты.
Если система координат левая, то их векторное произведение имеет вид
Для запоминания, аналогично:
или
Формулы для левой системы координат можно легко получить из формул правой системы координат, записав те же векторы и во вспомогательной правой системе координат ():
Обобщения
Кватернионы
Векторное произведение можно также записать в кватернионной форме, поэтому буквы , , — стандартные обозначения для ортов в : они рассматриваются как воображаемые кватернионы.
Заметим, что соотношения через векторное произведение между , и соответствуют правилам умножения для кватернионов , и . Если представить вектор как кватернион , то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.
Преобразование к матричной форме
Векторное произведение двух векторов можно записать как произведение кососимметрической матрицы и вектора:
где
Пусть равен векторному произведению:
тогда
Такая форма записи позволяет обобщить векторное произведение на высшие размерности, представляя псевдовекторы (угловая скорость, индукция и т. п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь независимых компонент в -мерном пространстве. В трёхмерном пространстве получаются три независимые компоненты, поэтому такие величины можно представлять как векторы этого пространства.
п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь независимых компонент в -мерном пространстве. В трёхмерном пространстве получаются три независимые компоненты, поэтому такие величины можно представлять как векторы этого пространства.
С такой формой записи также зачастую проще работать (например, в en:epipolar geometry).
Из общих свойств векторного произведения следует, что
- и
а так как кососимметрична, то
В такой форме записи легко доказывается тождество Лагранжа (правило «бац минус цаб»).
Распространение на матрицы
В трёхмерном случае можно определить векторное произведение матриц и произведение матрицы на вектор. Это делает очевидным указанный выше изоморфизм и позволяет упростить многие выкладки. Представим матрицу как столбец векторов, тогда
Умножение матрицы на вектор слева определяется аналогично, если представить как строку векторов. Транспонирование матрицы, соответственно, переводит строку векторов в столбец векторов, и наоборот. Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например ( — матрица, , — векторы):
Транспонирование матрицы, соответственно, переводит строку векторов в столбец векторов, и наоборот. Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например ( — матрица, , — векторы):
После этого можно изменить форму записи для векторного произведения:
— единичная матрица. Отсюда очевидны существование и вид матрицы, соответствующей векторному умножению на вектор слева. Аналогично можно получить выражение для матрицы умножения на вектор справа. Распространяя операции над векторами на матрицы покомпонентно, представляя их как «векторы из векторов», стандартные соотношения для векторов легко обобщаются на матрицы. Например, теорема Стокса в примет вид:
где ротор матрицы вычисляется как векторное произведение матрицы на оператор Гамильтона слева. В этих обозначениях очень легко доказать, например, следующие формы теоремы Стокса:
Размерности, не равные трём
Пусть — размерность пространства.
Векторное произведение, обладающее всеми свойствами обычного трёхмерного векторного произведения, то есть бинарное билинейное антисимметричное невырожденное отображение , можно ввести только для размерностей 3 и 7.
Однако есть простое обобщение на остальные натуральные размерности, начиная с 3, а если нужно — и на размерность 2 (последнее, правда, сравнительно специфическим образом). Тогда это обобщение, в отличие от невозможного, описанного чуть выше, вводится не для пары векторов, а лишь для набора векторов-сомножителей. Вполне аналогично смешанному произведению, естественно обобщаемому в -мерном пространстве на операцию с сомножителями. Используя символ Леви-Чивиты с индексами, можно явно записать такое -валентное векторное произведение как
Такое обобщение дает гиперплощадь размерности .
Если нужно ввести операцию именно для двух сомножителей, имеющую геометрический смысл, предельно близкий к смыслу векторного произведения (то есть представляющую ориентированную площадь), то результат уже не будет вектором, так как при не найдется единственной, однозначно определённой нормали к двумерной плоскости, натянутой на множители.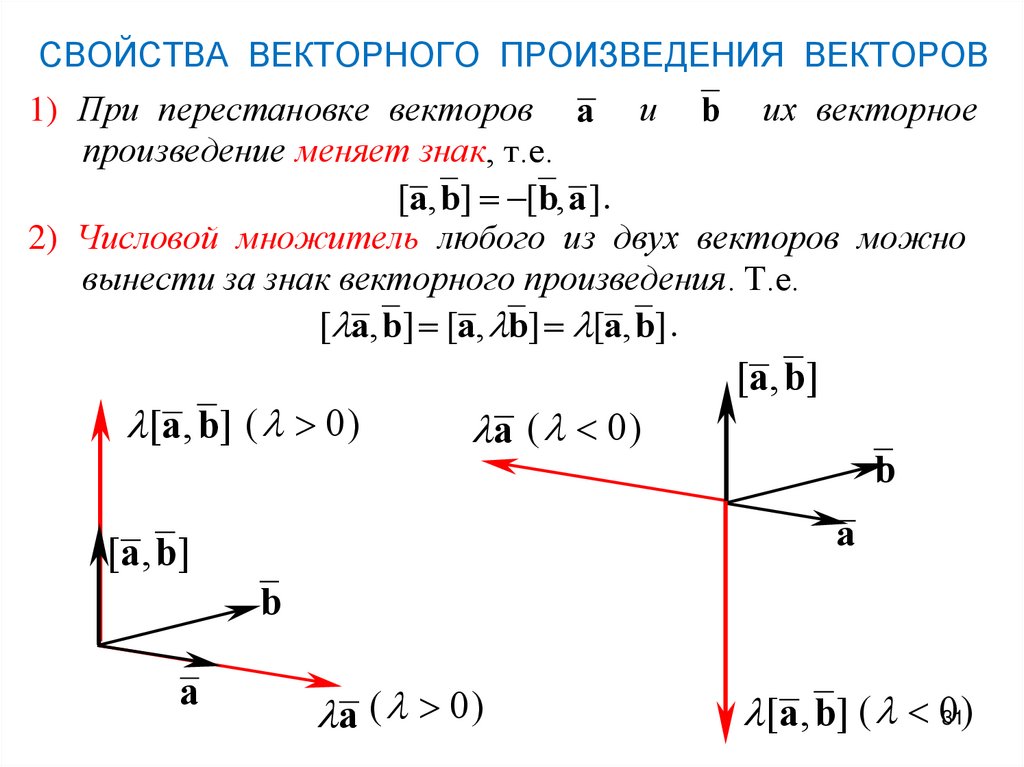 Можно ввести бивектор, компоненты которого равны проекциям ориентированной площади параллелограмма, натянутого на пару векторов, на координатные плоскости:
Можно ввести бивектор, компоненты которого равны проекциям ориентированной площади параллелограмма, натянутого на пару векторов, на координатные плоскости:
- .
Эта конструкция называется внешним произведением.
Для двумерного случая операция
- .
называется псевдоскалярным произведением, так как получающееся пространство одномерно и результат есть псевдоскаляр. (Двухиндексное внешнее произведение, описанное выше, можно ввести и для двумерного пространства, однако оно, очевидно, достаточно тривиально связано с псевдоскалярным произведением, а именно внешнее произведение в этом случае представляется матрицей, на диагонали которой нули, а оставшиеся два недиагональных элемента равны псевдоскалярному произведению и минус псевдоскалярному произведению).
Алгебра Ли векторов
Векторное произведение вводит на структуру алгебры Ли (поскольку оно удовлетворяет обеим аксиомам — антисимметричности и тождеству Якоби). Эта структура соответствует отождествлению с касательной алгеброй Ли к группе Ли ортогональных линейных преобразований трёхмерного пространства.
См. также
Произведения векторов
- Псевдоскалярное произведение (только на плоскости!)
- Скалярное произведение векторов
- Смешанное (скалярно-векторное) произведение векторов (только в )
- Двойное (векторно-векторное) произведение векторов (только в )
Другое
- Ротор
- Дивергенция
Примечания
- ↑ И в различных учебных заведениях.
- ↑ Crowe M. J. A History of Vector Analysis – The Evolution of the Idea of a Vectorial System. — Courier Dover Publications, 1994. — С. 32. — 270 с. — ISBN 0486679101
- ↑ Hamilton W. R. On Quaternions; or on a New System of Imaginaries in Algebra // Philosophical Magazine. 3rd Series. — London, 1846. — Т. 29. — С. 30.
Литература
- Кочин Н. Е. Введение в векторный и тензорный анализ.
Ссылки
- Многомерное векторное произведение
- Векторное произведение и его свойства.
 Примеры решения задач
Примеры решения задач - В. И. Гервидс Правое и левое вращение (flash). НИЯУ МИФИ (10.03.2011). — Физические демонстрации. Проверено 3 мая 2011.
Векторное произведение | это… Что такое Векторное произведение?
Векторное произведение в трёхмерном пространстве.
Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Произведение не является ни коммутативным, ни ассоциативным (оно является антикоммутативным) и отличается от скалярного произведения векторов. Во многих задачах инженерии и физики нужно иметь возможность строить вектор, перпендикулярный двум имеющимся — векторное произведение предоставляет эту возможность. Векторное произведение полезно для «измерения» перпендикулярности векторов — длина векторного произведения двух векторов равна произведению их длин, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны либо антипараллельны.
Определить векторное произведение можно по-разному, и теоретически, в пространстве любой размерности n можно вычислить произведение n-1 векторов, получив при этом единственный вектор, перпендикулярный к ним всем. Но если произведение ограничить нетривиальными бинарными произведениями с векторным результатами, то традиционное векторное произведение определено только в трёхмерном и семимерном пространствах. Результат векторного произведения, как и скалярного, зависит от метрики Евклидова пространства.
В отличие от формулы для вычисления по координатам векторов скалярного произведения в трёхмерной прямоугольной системе координат, формула для векторного произведения зависит от ориентации прямоугольной системы координат или, иначе, её «хиральности».
Содержание
|
Определение и история
Векторным произведением вектора на вектор в пространстве называется вектор , удовлетворяющий следующим требованиям:
- длина вектора равна произведению длин векторов и на синус угла между ними: ;
- вектор ортогонален каждому из векторов и ;
- вектор направлен так, что тройка векторов является правой;
- в случае пространства требуется ассоциативность тройки векторов .
Обозначение:
В литературе[1] определение векторного произведения может даваться по-разному.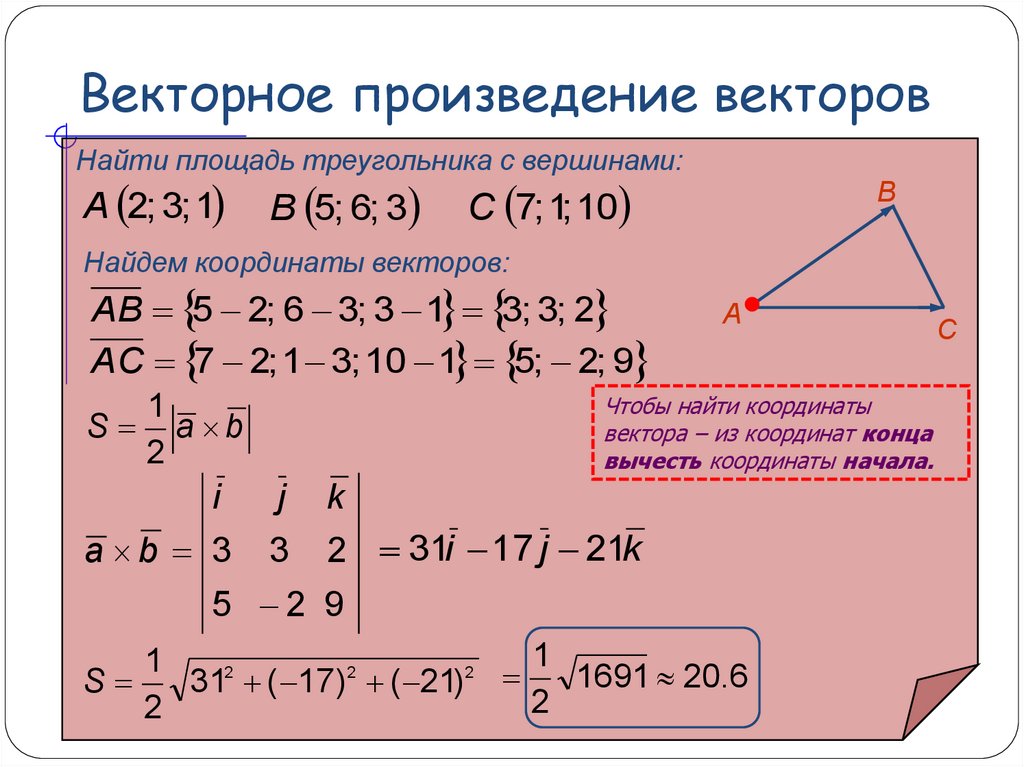 Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах в правой и левой прямоугольной системе координат. А далее выводится данное выше определение, а также определение правой и левой тройки векторов.
Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах в правой и левой прямоугольной системе координат. А далее выводится данное выше определение, а также определение правой и левой тройки векторов.
Также для исходного определения может быть взят набор алгебраических свойств векторного произведения, а из них выводиться остальное.
Векторное произведение было введено У. Гамильтоном в 1846 году[2] одновременно со скалярным произведением в связи с кватернионами — соответственно, как векторная и скалярная часть произведения двух кватернионов, скалярная часть которых равна нулю[3].
Правые и левые тройки векторов в трёхмерном пространстве
Нахождение направления векторного произведения с помощью правила правой руки
Рассмотрим упорядоченную тройку некомпланарных векторов в трёхмерном пространстве. Совместим начала этих векторов в точке (то есть выберем произвольно в пространстве точку и параллельно перенесём каждый вектор так, чтобы его начало совпало с точкой ). Концы векторов, совмещённых началами в точке , не лежат на одной прямой, так как векторы некомпланарны. Рассмотрим плоскость — единственную плоскость, проходящую через концы векторов, совмещённых началами в точке . Тогда можно в плоскости провести через концы векторов , совмещённых началами в точке , единственную окружность и выяснить направление обхода трёх точек на окружности, смотря на неё с одной из сторон от плоскости.
Концы векторов, совмещённых началами в точке , не лежат на одной прямой, так как векторы некомпланарны. Рассмотрим плоскость — единственную плоскость, проходящую через концы векторов, совмещённых началами в точке . Тогда можно в плоскости провести через концы векторов , совмещённых началами в точке , единственную окружность и выяснить направление обхода трёх точек на окружности, смотря на неё с одной из сторон от плоскости.
Упорядоченная тройка некомпланарных векторов в трёхмерном пространстве называется правой, если наблюдателю, находящемуся по одну сторону с точкой от плоскости , обход концов приведённых в общее начало векторов в указанном порядке кажется совершающимся в плоскости по часовой стрелке.
B противном случае — левая тройка. В этом случае наблюдателю, находящемуся с другой стороны от плоскости , обход концов таких векторов будет казаться совершающимся против часовой стрелки.
Другое определение связано с правой рукой человека (см. рисунок), откуда и берётся название.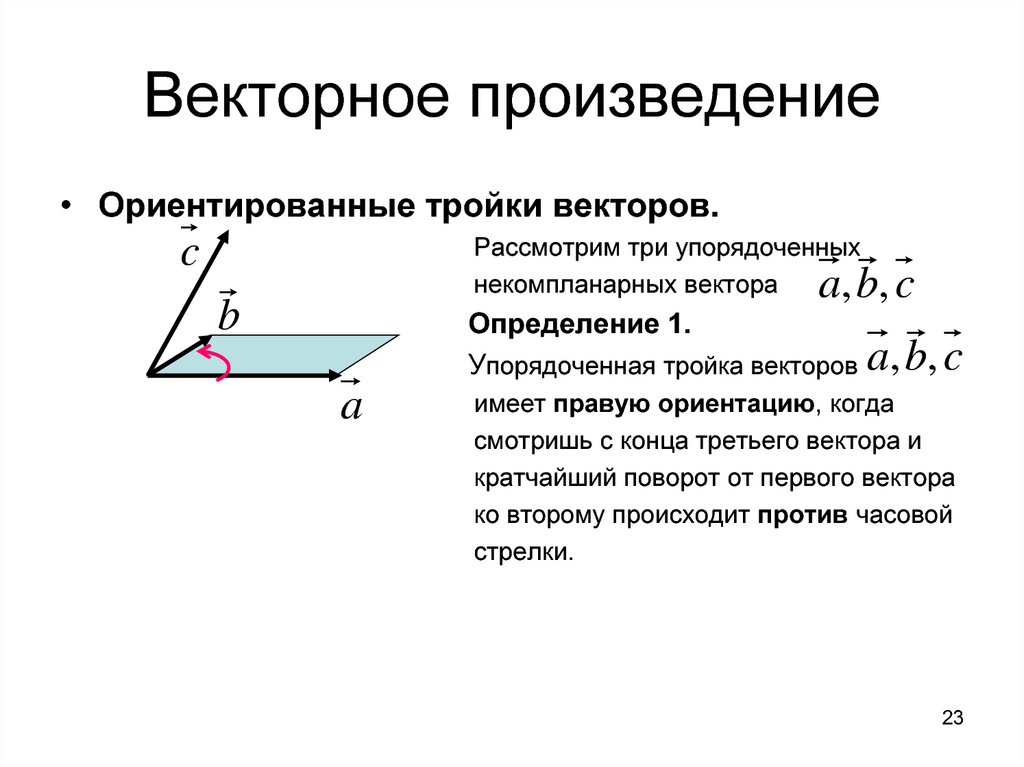
Все правые между собой (и левые между собой) тройки векторов называются одинаково ориентированными.
Заметим, что определения «правой» и «левой» тройки векторов не зависят от хиральности рассматриваемой системы координат; более того, они вообще не требуют задания в рассматриваемом пространстве какой-либо системы координат, как и не требует этого само векторное произведение.
Свойства
Геометрические свойства векторного произведения
Рисунок 1: Площадь параллелограмма равна модулю векторного произведения.
Рисунок 2: Объём параллелепипеда при использовании векторного и скалярного произведения векторов; пунктирные линии показывают проекции вектора c на a × b и вектора a на b × c, первым шагом является нахождение скалярных произведений.
- Необходимым и достаточным условием коллинеарности двух ненулевых векторов является равенство нулю их векторного произведения.

- Модуль векторного произведения равняется площади параллелограмма, построенного на приведённых к общему началу векторах и (см. Рисунок 1)
- Если — единичный вектор, ортогональный векторам и и выбранный так, что тройка — правая, а — площадь параллелограмма, построенного на них (приведённых к общему началу), то для векторного произведения справедлива формула:
- Если — какой-нибудь вектор, — любая плоскость, содержащая этот вектор, — единичный вектор, лежащий в плоскости и ортогональный к , — единичный вектор, ортогональный к плоскости и направленный так, что тройка векторов является правой, то для любого лежащего в плоскости вектора справедлива формула
- При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c (см. Рисунок 2). Такое произведение трех векторов называется смешанным.

На рисунке показано, что этот объём может быть найден двумя способами: геометрический результат сохраняется даже при замене «скалярного» и «векторного» произведений местами:
Величина векторного произведения зависит от синуса угла между изначальными векторами, поэтому векторное произведение может восприниматься как степень «перпендикулярности» векторов также, как и скалярное произведение может рассматриваться как степень «параллельности». Векторное произведение двух единичных векторов равно 1 (единичному вектору), если изначальные векторы перпендикулярны, и равно 0 (нулевому вектору), если векторы параллельны либо антипараллельны.
Алгебраические свойства векторного произведения
| Представление | Описание |
|---|---|
| свойство антикоммутативности | |
| свойство ассоциативности относительно умножения на скаляр | |
| свойство дистрибутивности по сложению | |
| тождество Якоби, выполняется в и нарушается в | |
| формула «БАЦ минус ЦАБ», тождество Лагранжа | |
| Это частный случай мультипликативности нормы кватернионов | |
| значение этого выражения называют смешанным произведением векторов , , и обозначают либо |
Выражение для векторного произведения в декартовых координатах
Если два вектора и определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе
а система координат правая, то их векторное произведение имеет вид
Для запоминания этой формулы удобно использовать определитель:
или
где — символ Леви-Чивиты.
Если система координат левая, то их векторное произведение имеет вид
Для запоминания, аналогично:
или
Формулы для левой системы координат можно легко получить из формул правой системы координат, записав те же векторы и во вспомогательной правой системе координат ():
Обобщения
Кватернионы
Векторное произведение можно также записать в кватернионной форме, поэтому буквы , , — стандартные обозначения для ортов в : они рассматриваются как воображаемые кватернионы.
Заметим, что соотношения через векторное произведение между , и соответствуют правилам умножения для кватернионов , и . Если представить вектор как кватернион , то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.
Преобразование к матричной форме
Векторное произведение двух векторов можно записать как произведение кососимметрической матрицы и вектора:
где
Пусть равен векторному произведению:
тогда
Такая форма записи позволяет обобщить векторное произведение на высшие размерности, представляя псевдовекторы (угловая скорость, индукция и т. п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь независимых компонент в -мерном пространстве. В трёхмерном пространстве получаются три независимые компоненты, поэтому такие величины можно представлять как векторы этого пространства.
п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь независимых компонент в -мерном пространстве. В трёхмерном пространстве получаются три независимые компоненты, поэтому такие величины можно представлять как векторы этого пространства.
С такой формой записи также зачастую проще работать (например, в en:epipolar geometry).
Из общих свойств векторного произведения следует, что
- и
а так как кососимметрична, то
В такой форме записи легко доказывается тождество Лагранжа (правило «бац минус цаб»).
Распространение на матрицы
В трёхмерном случае можно определить векторное произведение матриц и произведение матрицы на вектор. Это делает очевидным указанный выше изоморфизм и позволяет упростить многие выкладки. Представим матрицу как столбец векторов, тогда
Умножение матрицы на вектор слева определяется аналогично, если представить как строку векторов. Транспонирование матрицы, соответственно, переводит строку векторов в столбец векторов, и наоборот. Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например ( — матрица, , — векторы):
Транспонирование матрицы, соответственно, переводит строку векторов в столбец векторов, и наоборот. Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например ( — матрица, , — векторы):
После этого можно изменить форму записи для векторного произведения:
— единичная матрица. Отсюда очевидны существование и вид матрицы, соответствующей векторному умножению на вектор слева. Аналогично можно получить выражение для матрицы умножения на вектор справа. Распространяя операции над векторами на матрицы покомпонентно, представляя их как «векторы из векторов», стандартные соотношения для векторов легко обобщаются на матрицы. Например, теорема Стокса в примет вид:
где ротор матрицы вычисляется как векторное произведение матрицы на оператор Гамильтона слева. В этих обозначениях очень легко доказать, например, следующие формы теоремы Стокса:
Размерности, не равные трём
Пусть — размерность пространства.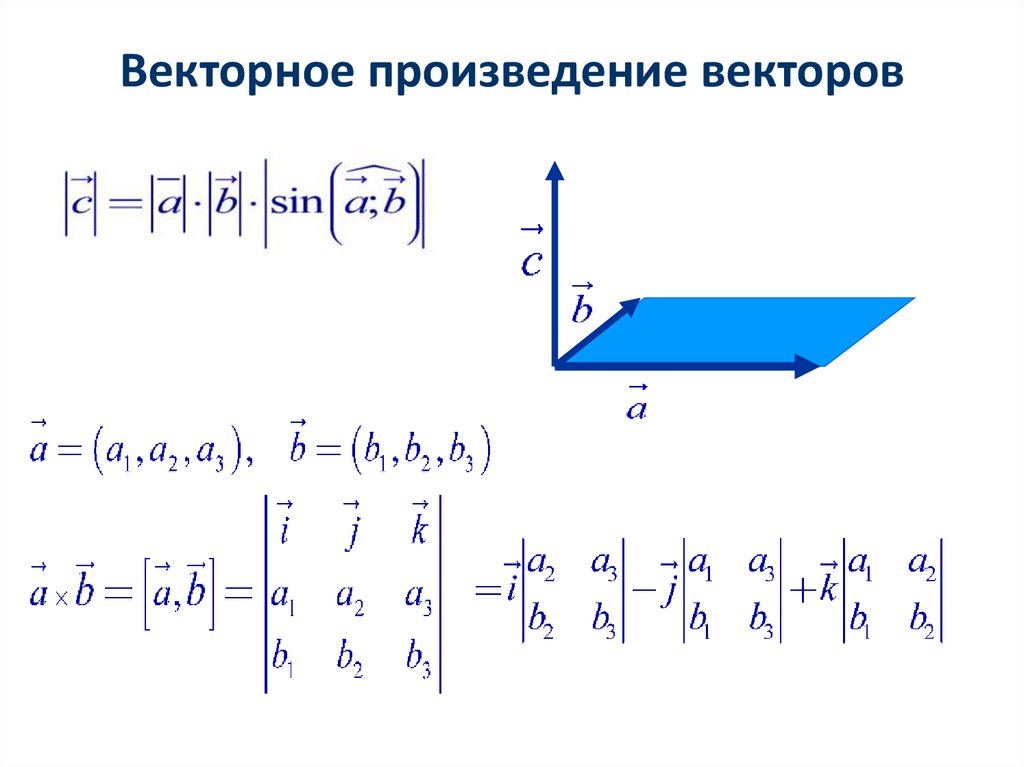
Векторное произведение, обладающее всеми свойствами обычного трёхмерного векторного произведения, то есть бинарное билинейное антисимметричное невырожденное отображение , можно ввести только для размерностей 3 и 7.
Однако есть простое обобщение на остальные натуральные размерности, начиная с 3, а если нужно — и на размерность 2 (последнее, правда, сравнительно специфическим образом). Тогда это обобщение, в отличие от невозможного, описанного чуть выше, вводится не для пары векторов, а лишь для набора векторов-сомножителей. Вполне аналогично смешанному произведению, естественно обобщаемому в -мерном пространстве на операцию с сомножителями. Используя символ Леви-Чивиты с индексами, можно явно записать такое -валентное векторное произведение как
Такое обобщение дает гиперплощадь размерности .
Если нужно ввести операцию именно для двух сомножителей, имеющую геометрический смысл, предельно близкий к смыслу векторного произведения (то есть представляющую ориентированную площадь), то результат уже не будет вектором, так как при не найдется единственной, однозначно определённой нормали к двумерной плоскости, натянутой на множители. Можно ввести бивектор, компоненты которого равны проекциям ориентированной площади параллелограмма, натянутого на пару векторов, на координатные плоскости:
Можно ввести бивектор, компоненты которого равны проекциям ориентированной площади параллелограмма, натянутого на пару векторов, на координатные плоскости:
- .
Эта конструкция называется внешним произведением.
Для двумерного случая операция
- .
называется псевдоскалярным произведением, так как получающееся пространство одномерно и результат есть псевдоскаляр. (Двухиндексное внешнее произведение, описанное выше, можно ввести и для двумерного пространства, однако оно, очевидно, достаточно тривиально связано с псевдоскалярным произведением, а именно внешнее произведение в этом случае представляется матрицей, на диагонали которой нули, а оставшиеся два недиагональных элемента равны псевдоскалярному произведению и минус псевдоскалярному произведению).
Алгебра Ли векторов
Векторное произведение вводит на структуру алгебры Ли (поскольку оно удовлетворяет обеим аксиомам — антисимметричности и тождеству Якоби). Эта структура соответствует отождествлению с касательной алгеброй Ли к группе Ли ортогональных линейных преобразований трёхмерного пространства.
См. также
Произведения векторов
- Псевдоскалярное произведение (только на плоскости!)
- Скалярное произведение векторов
- Смешанное (скалярно-векторное) произведение векторов (только в )
- Двойное (векторно-векторное) произведение векторов (только в )
Другое
- Ротор
- Дивергенция
Примечания
- ↑ И в различных учебных заведениях.
- ↑ Crowe M. J. A History of Vector Analysis – The Evolution of the Idea of a Vectorial System. — Courier Dover Publications, 1994. — С. 32. — 270 с. — ISBN 0486679101
- ↑ Hamilton W. R. On Quaternions; or on a New System of Imaginaries in Algebra // Philosophical Magazine. 3rd Series. — London, 1846. — Т. 29. — С. 30.
Литература
- Кочин Н. Е. Введение в векторный и тензорный анализ.
Ссылки
- Многомерное векторное произведение
- Векторное произведение и его свойства.
 Примеры решения задач
Примеры решения задач - В. И. Гервидс Правое и левое вращение (flash). НИЯУ МИФИ (10.03.2011). — Физические демонстрации. Проверено 3 мая 2011.
Векторное произведение | Компьютерная графика
Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Векторное произведение не обладает свойствами коммутативности и ассоциативности (является антикоммутативным) и, в отличие от скалярного произведения векторов, является вектором. Широко используется во многих технических и физических приложениях. Например, момент импульса и сила Лоренца математически записываются в виде векторного произведения. Векторное произведение полезно для «измерения» перпендикулярности векторов — модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны либо антипараллельны.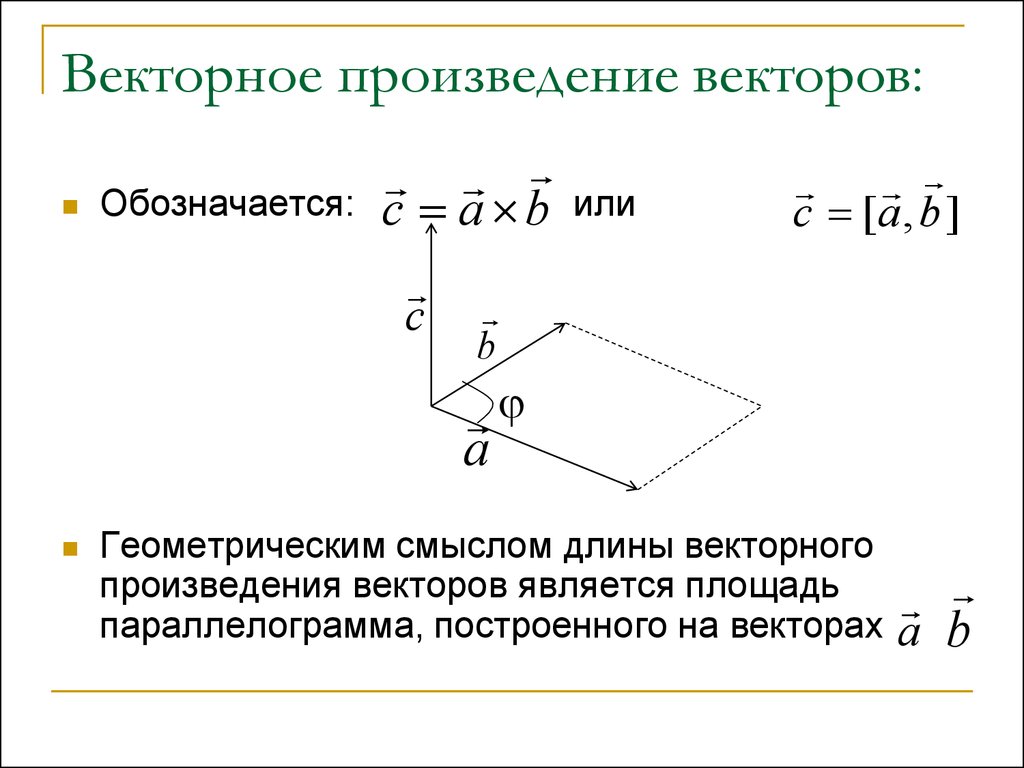
Определить векторное произведение можно по-разному, и теоретически, в пространстве любой размерности n можно вычислить произведение n-1 векторов, получив при этом единственный вектор, перпендикулярный к ним всем. Но если произведение ограничить нетривиальными бинарными произведениями с векторным результатами, то традиционное векторное произведение определено только в трёхмерном и семимерном пространствах. Результат векторного произведения, как и скалярного, зависит от метрики Евклидова пространства.
В отличие от формулы для вычисления по координатам векторов скалярного произведения в трёхмерной прямоугольной системе координат, формула для векторного произведения зависит от ориентации прямоугольной системы координат или, иначе, её «хиральности».
Определение:
Векторным произведением вектора a на вектор b в пространстве R3 называется вектор c, удовлетворяющий следующим требованиям:
длина вектора c равна произведению длин векторов a и b на синус угла φ между ними:
|c|=|a||b|sin φ;
вектор c ортогонален каждому из векторов a и b;
вектор c направлен так, что тройка векторов abc является правой;
в случае пространства R7 требуется ассоциативность тройки векторов a,b,c.
Обозначение:
c=[ab]=[a,b]=a × b
Рис. 1. Площадь параллелограмма равна модулю векторного произведения
Геометрические свойства векторного произведения:
Необходимым и достаточным условием коллинеарности двух ненулевых векторов является равенство нулю их векторного произведения.
Модуль векторного произведения [ab] равняется площади S параллелограмма, построенного на приведённых к общему началу векторах a и b (см. рис.1).
Если e — единичный вектор, ортогональный векторам a и b и выбранный так, что тройка a,b,e — правая, а S — площадь параллелограмма, построенного на них (приведённых к общему началу), то для векторного произведения справедлива формула:
[a, b]=S e
Рис.2. Объём параллелепипеда при использовании векторного и скалярного произведения векторов; пунктирные линии показывают проекции вектора c на a × b и вектора a на b × c, первым шагом является нахождение скалярных произведений
Если c — какой-нибудь вектор, π — любая плоскость, содержащая этот вектор, e — единичный вектор, лежащий в плоскости π и ортогональный к c,g— единичный вектор, ортогональный к плоскости π и направленный так, что тройка векторов ecg является правой, то для любого лежащего в плоскости π вектора a справедлива формула:
[a, c]=Prea•|c|g
где Prea проекция вектора e на a
|c|-модуль вектора с
При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c.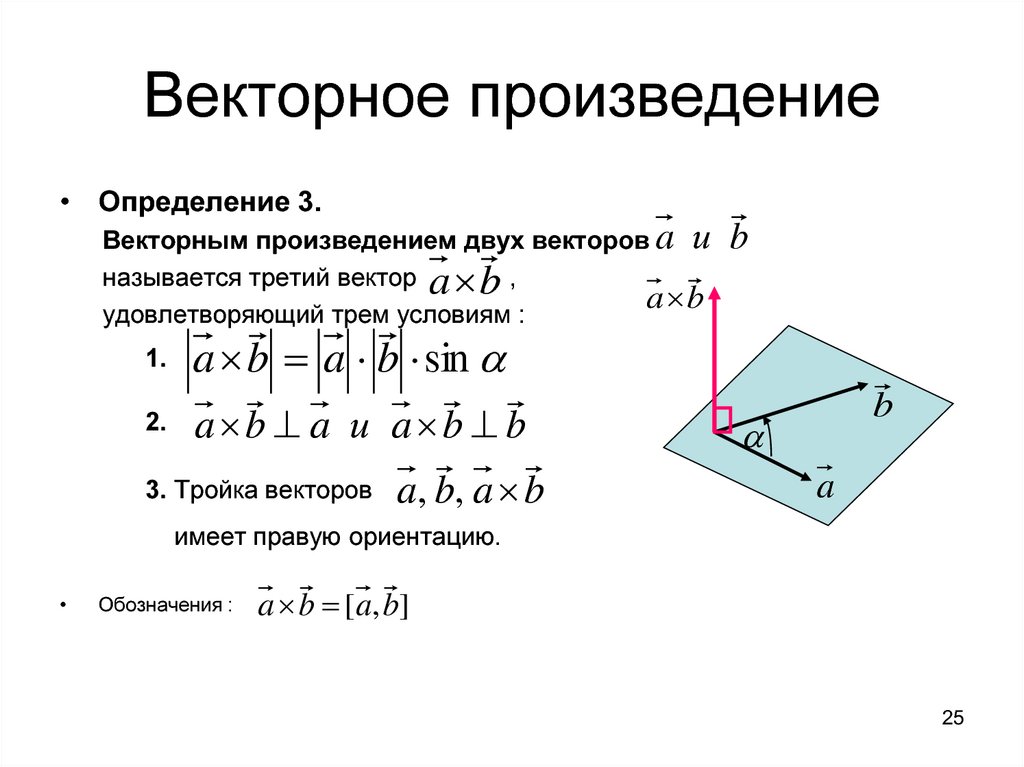 Такое произведение трех векторов называется смешанным.
Такое произведение трех векторов называется смешанным.
V=|a•(b×c)|
На рисунке показано, что этот объём может быть найден двумя способами: геометрический результат сохраняется даже при замене «скалярного» и «векторного» произведений местами:
V=a×b•c=a•b×c
Величина векторного произведения зависит от синуса угла между изначальными векторами, поэтому векторное произведение может восприниматься как степень «перпендикулярности» векторов также, как и скалярное произведение может рассматриваться как степень «параллельности». Векторное произведение двух единичных векторов равно 1 (единичному вектору), если изначальные векторы перпендикулярны, и равно 0 (нулевому вектору), если векторы параллельны либо антипараллельны.
Выражение для векторного произведения в декартовых координатах
Если два вектора a и b определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе
a=(ax,ay,az)
b=(bx,by,bz)
а система координат правая, то их векторное произведение имеет вид
[a, b]=(aybz-azby,azbx-axbz,axby-aybx)
Для запоминания этой формулы :
[a,b]i=∑εijkajbk
где εijk— символ Леви-Чивиты.
5.2. Векторное произведение двух векторов.
Определение векторного произведения.
Определение. Векторным произведением двух векторов иназывается вектор, удовлетворяющий следующим условиям:
а) вектор перпендикулярен плоскости векторов ии направлен так, что тройка векторов,,правая;
б) длина вектора численно равна площади
Рис. 2.19 параллелограмма, построенного на векторах и, т.е., где- угол между векторамии(рис. 2.19).
Очевидно, что ,,,,,.
Пример 11. Проверить справедливость равенства .
Решение. ,,
.
Метод Жуковского.
Рассмотрим метод Жуковского построения вектора .
Пусть угол между векторами иравен.
Векторы
иприложим к общему началу(рис. 2.20).
Через точкуперпендикулярно векторупроведем плоскость.
Из конца вектораопустим перпендикуляр на плоскость.
Точку пересечения этого перпендикуляра
и плоскости обозначим через.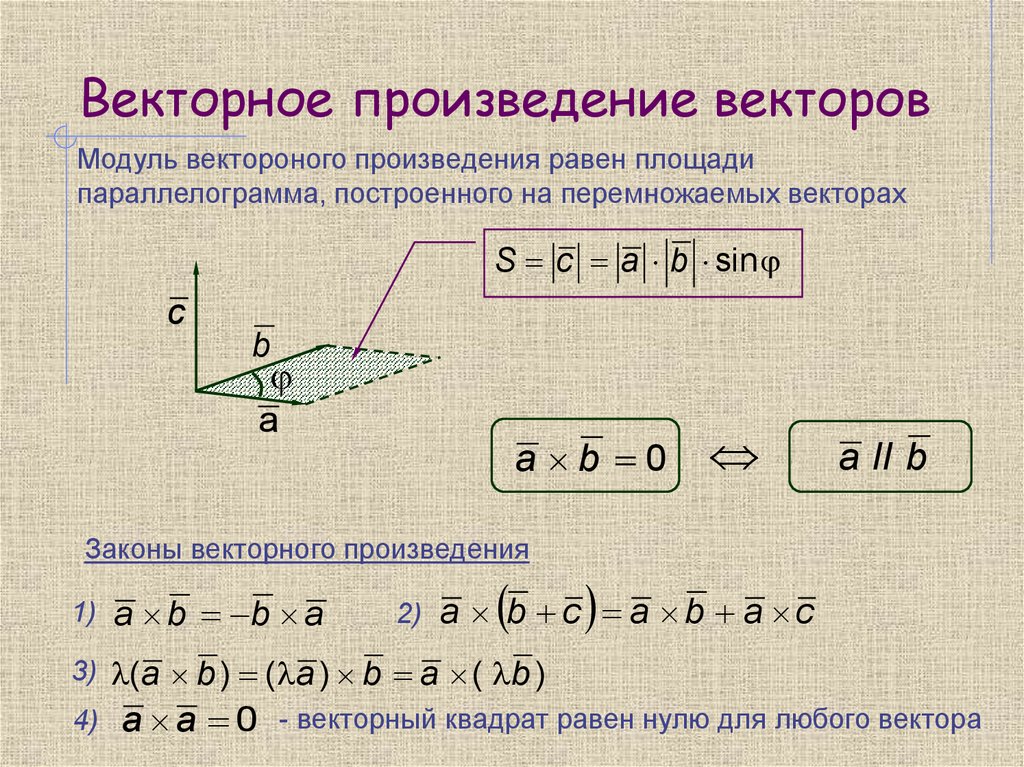 Проведем в плоскостивектори построим вектор.
Проведем в плоскостивектори построим вектор.
Рис. 2.20 Покажем, что вектор.
а) Из построения следует, что вектор перпендикулярен векторам,, и векторы,,образуют правую тройку.
б) .
Из а) и б) следует, что .
Если проекцию вектора на плоскостьобозначить через, то
.
Свойства векторного произведения.
Векторное произведение двух векторов обладает следующими свойствами:
1) (векторное произведениеантикоммутативно, т.е. при перестановке сомножителей направление вектора меняется на противоположное, при этом его модуль остаётся неизменным).
Это свойство следует из определения векторного произведения. Если тройка векторов правая, то тройка- левая.
2) (ассоциативный закон). Это свойство легко доказывается из определения векторного произведения.
3) (дистрибутивный закон.) ►.◄
4)
.
Это свойство следует из определения
векторного произведения, а именно из
того, что модуль векторного произведения
равен площади параллелограмма,
построенного на векторахи. Это свойство дает возможность записать в удобной форме параллельность двух векторов.
Это свойство дает возможность записать в удобной форме параллельность двух векторов.
Например, означает, что векторколлинеарен биссектрисе первого координатного угла.
Векторное произведение в координатной форме.
Пользуясь свойствами векторного произведения и равенствами ,,,,,, вычислим
=
=
, т.е. или.
Применение векторного произведения.
Векторное произведение векторов иприменяется:
для нахождения площади параллелограмма, построенного на векторах и;
для нахождения площади треугольника, построенного на векторах и;
для нахождения синуса угла между векторами и;
для нахождения вектора, перпендикулярного векторам и.
1) Площадь параллелограмма, построенного на векторахи, может быть вычислена по формуле, где- угол между векторамии.
Замечание. Если
и,
тои.
Отсюда следует, чтомодуль
определителя второго порядка численно равен площади параллелограмма,
построенного на векторах
и.
2) Площадь треугольника, построенного на векторахи, равна половине площади параллелограмма, построенного на этих же векторах, т.е., где- угол между векторамии.
3) Синус угла между векторами иможет быть вычислен по формуле.
4) Вектор перпендикулярен векторуи вектору.
Замечание. Векторное произведение может быть использовано при решении системы линейных однородных уравнений вида Если векторыинеколлинеарны, тоявляется решением исходной системы.
►Действительно, из системы уравнений следует, что вектор перпендикулярен векторами, а, следовательно,.◄
● Пример 12. Дано: ,,,,.
Найти площадь параллелограмма, построенного на векторах и.
Найти синус угла между векторамии.
Решение. Площадь параллелограмма, построенного на векторах иравнамодулю векторного произведения векторов и, т.е…=.
.
Ответ: ,.
● Пример 13. Дано: ,,,,.
Найти значение
параметра
,
при котором векторыиколлинеарны.
Решение. Первый способ. Так как векторы иколлинеарны, то их векторное произведение равно нулю.=0, а так как, тои.
Второй способ. Векторы исоставляют базис системы векторов,,и. В базисеи. Так как векторыиколлинеарны, то, откуда●
● Пример 14. Найти координаты вектора , длина которого равна 15, зная, что он перпендикулярен осии векторуи образует острый угол с осью.
Решение. и, поэтому.
, откуда
Так как вектор образует острый угол с осью, то вторая его координата положительна, тогдаи●
● Пример 15. Найти площадь параллелограмма , если известны координаты трёх его вершин,и.
Решение. .,,,.
● Пример 16. ,,- вершины треугольника. Найти недостающую координатуточки. если площадь треугольникаравна 3.
Решение. Площадь равна половине площади параллелограмма, построенного на векторахи, т.е..
, ,., откуда16,и.
Ответ: или.
● Пример 17. Решить систему
Решить систему
Решение. Из уравнений системы следует, что вектор перпендикулярен векторами. Тогда- решение данной системы. ●
Произведение векторов — определение, формула, примеры
Произведение векторов бывает двух типов. Вектор имеет как величину, так и направление, и, исходя из этого, два произведения векторов равны точечному произведению двух векторов и перекрестному произведению двух векторов. Скалярное произведение двух векторов также называется скалярным произведением, поскольку результирующее значение является скалярной величиной. Перекрестное произведение называется векторным произведением, так как в результате получается вектор, перпендикулярный этим двум векторам.
Давайте узнаем о двух произведениях векторов, рабочих правилах, свойствах, использовании, примерах этих произведений векторов.
| 1. | Что такое произведение векторов? |
2. | Рабочее правило для произведения векторов |
| 3. | Свойства произведения векторов |
| 4. | Использование произведения векторов |
| 5. | Примеры произведения векторов |
| 6. | Практические вопросы |
| 7. | Часто задаваемые вопросы о продукте Vectors |
Что такое произведение векторов?
Вектор имеет как величину, так и направление. Мы можем умножать два или более векторов на скалярное произведение и перекрестное произведение. Давайте разберемся больше о каждом из произведений векторов.
Скалярное произведение
Скалярное произведение векторов также называется скалярным произведением векторов. Результат скалярного произведения векторов является скалярным значением. Скалярное произведение векторов равно произведению величин двух векторов и косинуса угла между двумя векторами. Результат скалярного произведения двух векторов лежит в одной плоскости двух векторов. Скалярный продукт может быть положительным действительным числом или отрицательным действительным числом.
Результат скалярного произведения двух векторов лежит в одной плоскости двух векторов. Скалярный продукт может быть положительным действительным числом или отрицательным действительным числом.
Пусть a и b — два ненулевых вектора, а θ — угол между векторами. Тогда скалярное произведение или скалярное произведение обозначается буквой a.b, которая определяется как:
\(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ .
Здесь \(|\overrightarrow a|\) — величина \(\overrightarrow a\), \(|\overrightarrow b|\) — величина \(\overrightarrow b\), а θ — величина угол между ними.
Перекрестное произведение
Перекрестное произведение также называется векторным произведением. Перекрестное произведение — это форма умножения векторов, выполняемая между двумя векторами разной природы или вида. Когда два вектора перемножаются друг с другом и произведение также является векторной величиной, то результирующий вектор называется перекрестным произведением двух векторов или векторным произведением. Результирующий вектор перпендикулярен плоскости, содержащей два заданных вектора.
Результирующий вектор перпендикулярен плоскости, содержащей два заданных вектора.
Мы можем понять это на примере, что если у нас есть два вектора, лежащие в плоскости X-Y, то их векторное произведение даст результирующий вектор в направлении оси Z, которая перпендикулярна плоскости XY. Символ × используется между исходными векторами. Векторное произведение или перекрестное произведение двух векторов отображается как:
\(\overrightarrow{a} \times \overrightarrow{b} = \overrightarrow{c}\)
Здесь \(\overrightarrow{a}\) и \(\overrightarrow{b}\) — два вектора, а \(\overrightarrow{c}\) — результирующий вектор. Пусть θ — угол, образованный между \(\overrightarrow{a}\) и \(\overrightarrow{b}\), а \(\hat n\) — единичный вектор, перпендикулярный плоскости, содержащей обе \(\overrightarrow{a }\) и \(\overrightarrow{b}\). Перекрестное произведение двух векторов определяется формулой:
\(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\)
Рабочее правило для произведения векторов
Рабочее правило для произведения двух векторов, скалярного произведения и перекрестного произведения можно понять из приведенных ниже предложений.
Скалярное произведение
Для скалярного произведения двух векторов два вектора выражаются через единичные векторы i, j, k вдоль осей x, y, z, затем скалярное произведение получается следующим образом:
Если \(\overrightarrow a = a_1\hat i + b_1 \hat j + c_1 \hat k\) и \(\overrightarrow b = a_2 \hat i + b_2 \hat j + c_2\hat k\), то
\(\overrightarrow a. \overrightarrow b\) = \((a_1 \hat i + b_1 \hat j + c_1 \hat k)(a_2 \hat i + b_2 \hat j + c_2 \hat k)\)
= \((a_1a_2) (\hat i. \hat i) + (a_1b_2) (\hat i.\hat j)+ (a_1c_2) (\hat i. \hat k) + \\(b_1a_2) ( \hat j. \hat i) + (b_1b_2)(\hat j. \hat j) + (b_1c_2 (\hat j. \hat k) + \\(c_1a_2)(\hat k. \hat i) + ( c_1b_2)(\шляпа k.\шляпа j) + (c_1c_2)(\шляпа k.\шляпа k)\)
\(\overrightarrow a. \overrightarrow b\) = \(a_1a_2 + b_1b_2+ c_1c_2\)
Перекрестное произведение
Предположим, что \(\overrightarrow{a}\) и \(\overrightarrow{b}\ ) — два вектора, такие, что \(\overrightarrow{a}\)= \(a_1\hat i+b_1 \hat j+c_1 \hat k\) и \(\overrightarrow{b}\) = \(a_2 \ шляпа i+b_2 \ шляпа j+c_2 \ шляпа k\), то с помощью определителей мы могли бы найти перекрестное произведение и записать результат в виде формулы перекрестного произведения, используя следующую матричную запись.
Перекрестное произведение двух векторов также представляется с помощью формулы перекрестного произведения следующим образом: a_2c_1) + \hat k (a_1b_2-a_2b_1)\)
Примечание: \( \hat i, \hat j, \text{ и } \hat k \) — единичные векторы в направлении оси x, ось и ось z соответственно.
Свойства произведения векторов
Скалярное произведение единичного вектора изучается путем взятия единичных векторов \(\hat i\) вдоль оси x, \(\hat j\) вдоль оси y и \(\hat k\) по оси Z соответственно. Скалярное произведение единичных векторов \(\hat i\), \(\hat j\), \(\hat k\) подчиняется тем же правилам, что и скалярное произведение векторов. Угол между одинаковыми векторами равен 0º, а значит, их скалярное произведение равно 1. А угол между двумя перпендикулярными векторами равен 90º, а их скалярное произведение равно 0.
- \(\hat i.\hat i\) = \(\hat j.\hat j\) = \(\hat k.\hat k\)= 1
- \(\шляпа i.\шляпа j\) = \(\шляпа j.\шляпа k\) = \(\шляпа k.
 \шляпа i\)= 0
\шляпа i\)= 0
Перекрестное произведение единичных векторов \(\hat i\), \(\hat j\), \(\hat k\) подчиняется тем же правилам, что и перекрестное произведение векторов. Угол между одинаковыми векторами равен 0º, а значит, их векторное произведение равно 0. А угол между двумя перпендикулярными векторами равен 90º, и их векторное произведение дает вектор, который перпендикулярен двум заданным векторам.
- \(\overrightarrow{i}\times \overrightarrow{i} =\overrightarrow{j}\times \overrightarrow{j} = \overrightarrow{k}\times \overrightarrow{k} = 0\)
Перекрестное произведение двух векторов следует циклическому порядку, как показано на изображении ниже. Перекрестное произведение двух векторов в циклической последовательности дает третий вектор в последовательности.
- \(\overrightarrow{i}\times \overrightarrow{j} = \overrightarrow{k}; \overrightarrow{j}\times \overrightarrow{k}= \overrightarrow{i}; \overrightarrow{k} \times \overrightarrow{i} = \overrightarrow{j}\)
- \(\overrightarrow{j}\times \overrightarrow{i} = \overrightarrow{-k}; \overrightarrow{k}\times \overrightarrow{j}= \overrightarrow{-i}; \overrightarrow{i}\times \overrightarrow{k} = \overrightarrow{-j}\)
Свойства произведения векторов помогают получить подробное представление об умножении векторов, а также выполнять многочисленные вычисления с использованием векторов. Здесь перечислены некоторые важные свойства произведения векторов.
Здесь перечислены некоторые важные свойства произведения векторов.
- Перекрестное произведение двух векторов задается формулой \( \overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta)\).
- Скалярное произведение двух векторов определяется формулой \( \overrightarrow{a} . \overrightarrow{b} = |a| |b| \cos(\theta)\).
- Скалярное произведение двух векторов подчиняется свойству коммутативности. \(\vec a. \vec b = \vec b. \vec a \)
- Перекрестное произведение двух векторов не соответствует свойству коммутативности. \( \vec a \times \vec b\neq \vec b \times \vec a \)
- Антикоммутативное свойство: \(\overrightarrow{a} \times \overrightarrow{b} = — \overrightarrow{b} \times \overrightarrow{a}\)
- Распределяющее свойство: \(\overrightarrow{a} \times (\overrightarrow{b} + \overrightarrow{c}) = (\overrightarrow{a}\times \overrightarrow{b} )+ (\overrightarrow{a}\times \overrightarrow{с})\)
- Перемножение нулевого вектора: \(\overrightarrow{a}\times \overrightarrow{0} = \overrightarrow{0}\)
- Перемножение вектора с самим собой: \(\overrightarrow{a}\times \overrightarrow{a} = \overrightarrow{0}\)
- Умножить на скалярную величину: \(c(\overrightarrow{a}\times \overrightarrow{b}) = c\overrightarrow{a}\times \overrightarrow{b} = \overrightarrow{a}\times c\overrightarrow{ б}\)
- Скалярное произведение двух векторов является скаляром и лежит в плоскости двух векторов.

- Перекрестное произведение двух векторов — это вектор, который перпендикулярен плоскости, содержащей эти два вектора.
Использование произведения векторов
Ниже приведены некоторые важные области применения произведения векторов. Давайте разберемся в каждом из этих применений в следующих параграфах.
- Проекция вектора
- Угол между двумя векторами
- Продукт тройного креста
- Площадь параллелограмма
- Объем параллелепипеда
Проекция вектора
Скалярное произведение полезно для нахождения компонента одного вектора в направлении другого. Проекция вектора одного вектора на другой вектор — это длина тени данного вектора на другой вектор. Он получается путем умножения величины данных векторов на косеканс угла между двумя векторами. Результатом формулы векторной проекции является скалярное значение.
Здесь \(\overrightarrow a\) и \(\overrightarrow b\) — два вектора, а θ — угол между двумя векторами. 2}}\)
2}}\)
Тройное перекрестное произведение
Перекрестное произведение вектора на произведение двух других векторов представляет собой тройное перекрестное произведение векторов. Результатом тройного перекрестного произведения является вектор. Равнодействующий вектора тройного пересечения лежит в плоскости данных трех векторов. Если a, b и c — векторы, то векторное тройное произведение этих векторов будет иметь вид:
\((\overrightarrow{a}\times \overrightarrow{b}) \times \overrightarrow{c} = (\overrightarrow{a}\cdot \overrightarrow{c})\overrightarrow{b} -(\overrightarrow{b}\cdot \overrightarrow{c}) \overrightarrow{a}\)
Площадь параллелограмма
Две смежные стороны параллелограмма могут быть представлены векторами \(\overrightarrow a\) и \(\overrightarrow b\). Площадь параллелограмма равна произведению основания и высоты параллелограмма. Рассмотрим основание параллелограмма как \(|\overrightarrow a|\), а высоту параллелограмма как \(|\overrightarrow b|\)sin θ.
Здесь Основание = \(|\overrightarrow a|\), Высота = \(|\overrightarrow b|\)sin θ, а Площадь параллелограмма = Основание x Высота
Площадь параллелограмма = \(|\overrightarrow a|.|\overrightarrow b|\)sin θ = \(\overrightarrow a \times \overrightarrow b \)
Объем параллелепипеда
Параллелепипед равен шести двусторонняя фигура, каждая из сторон которой является параллелограммом. Здесь параллелограммы противоположных сторон одинаковы. Объем V параллелепипеда можно получить со стороны ребер a, b, c. Объем параллелепипеда можно получить из произведения площади основания на высоту параллелепипеда. Площадь основания параллелепипеда равна |b x c| а высота параллелепипеда равна |a|. Формула расчета объема параллелепипеда выглядит следующим образом.
V = a.(b x c)
Связанные темы
Следующие темы помогают лучше понять произведение векторов.
- Коллинеарные векторы
- Векторы
- Типы векторов
- Добавление векторов
- Перекрестное произведение двух векторов
Часто задаваемые вопросы о продукте векторов
Что такое скалярное произведение векторов?
Скалярное произведение двух векторов имеет два определения. Алгебраически скалярное произведение двух векторов равно сумме произведений отдельных компонентов двух векторов. a.b = \(a_1b_1\) + \(a_2b_2\)+ \(a_3b_3\). Геометрически скалярное произведение двух векторов есть произведение величины векторов и косинуса угла между двумя векторами. ( \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ). Результат скалярного произведения векторов является скалярным значением.
Алгебраически скалярное произведение двух векторов равно сумме произведений отдельных компонентов двух векторов. a.b = \(a_1b_1\) + \(a_2b_2\)+ \(a_3b_3\). Геометрически скалярное произведение двух векторов есть произведение величины векторов и косинуса угла между двумя векторами. ( \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ). Результат скалярного произведения векторов является скалярным значением.
Как рассчитать скалярное произведение векторов?
Скалярный продукт можно рассчитать в три простых шага. Сначала найдите величину двух векторов a и b, т.е. |a| и |б|. Во-вторых, найдите косеканс угла θ между двумя векторами. Наконец, возьмите произведение величины двух векторов и косеканса угла между двумя векторами, чтобы получить скалярное произведение двух векторов. (a.b = |a|.|b|.Cosθ. Также проверьте калькулятор скалярного произведения, чтобы легко найти векторное скалярное произведение.
Почему скалярное произведение называется скалярным произведением векторов?
Скалярное произведение является скалярным, поскольку все отдельные составляющие ответа являются скалярными значениями. В a.b = |a|.|b|.Cosθ, |a|, |b| и Cosθ — скалярные значения. Следовательно, скалярное произведение также называют скалярным произведением.
В a.b = |a|.|b|.Cosθ, |a|, |b| и Cosθ — скалярные значения. Следовательно, скалярное произведение также называют скалярным произведением.
Почему мы используем косинус в скалярном произведении векторов?
Для нахождения скалярного произведения нам нужно, чтобы два вектора a, b были направлены в одном направлении. Поскольку векторы a и b расположены под углом друг к другу, значение acosθ является компонентом вектора a в направлении вектора b. Следовательно, мы находим cosθ в скалярном произведении двух векторов.
Что такое векторное произведение векторов?
В результате перекрестного произведения двух векторов при умножении третий вектор перпендикулярен двум исходным векторам. Величина результирующего вектора определяется площадью параллелограмма между ними, а его направление можно определить по правилу правой руки. a × b = c, где c — векторное произведение двух векторов a и b.
Что такое скалярное произведение и векторное произведение векторов?
Векторы можно перемножать двумя разными способами: точечным произведением и перекрестным произведением. Результаты обоих этих умножений векторов различны. В результате скалярное произведение дает скалярную величину, тогда как векторное произведение дает векторную величину. Скалярное произведение — это скалярное произведение двух векторов, а перекрестное произведение двух векторов — это векторное произведение двух векторов. Скалярное произведение также известно как скалярное произведение, а перекрестное произведение также известно как векторное произведение. Векторное произведение двух векторов задается как: \(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\) и формула скалярного произведения двух векторов задается как: \(\overrightarrow{a}. \overrightarrow{b} = |a| |b| \cos(\theta)\).
Результаты обоих этих умножений векторов различны. В результате скалярное произведение дает скалярную величину, тогда как векторное произведение дает векторную величину. Скалярное произведение — это скалярное произведение двух векторов, а перекрестное произведение двух векторов — это векторное произведение двух векторов. Скалярное произведение также известно как скалярное произведение, а перекрестное произведение также известно как векторное произведение. Векторное произведение двух векторов задается как: \(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\) и формула скалярного произведения двух векторов задается как: \(\overrightarrow{a}. \overrightarrow{b} = |a| |b| \cos(\theta)\).
В чем разница между скалярным произведением и перекрестным произведением векторов?
При умножении векторов скалярное произведение исходных векторов дает скалярную величину, тогда как перекрестное произведение двух векторов дает векторную величину. Скалярное произведение — это произведение величины векторов и cos угла между ними. а . б = |а| |б| cosθ. Векторное произведение — это произведение величины векторов на синус угла между ними. а × б = | а | |б| грех θ.
а . б = |а| |б| cosθ. Векторное произведение — это произведение величины векторов на синус угла между ними. а × б = | а | |б| грех θ.
Что такое правило большого пальца правой руки для перекрестного произведения векторов?
Правило правой руки для векторного произведения двух векторов помогает определить направление результирующего вектора. Если мы направим правую руку в направлении первой стрелки, а пальцы согнем в направлении второй, то наш большой палец окажется в направлении векторного произведения двух векторов. Правило большого пальца правой руки дает формулу векторного произведения для нахождения направления результирующего вектора.
Продукт векторов — GeeksforGeeks
Векторные операции используются почти везде в области физики. Часто эти операции включают сложение, вычитание и умножение. Сложение и вычитание можно выполнять, используя закон сложения векторов треугольника. В случае произведений векторное умножение можно выполнить двумя способами: скалярным произведением или векторным произведением. Векторные произведения дают вектор как результирующее произведение после умножения. Во вращательном движении многие величины получаются с помощью векторных произведений. Становится важным понять концепции и интуицию, стоящую за этим продуктом. Давайте посмотрим на этот продукт в деталях.
Векторные произведения дают вектор как результирующее произведение после умножения. Во вращательном движении многие величины получаются с помощью векторных произведений. Становится важным понять концепции и интуицию, стоящую за этим продуктом. Давайте посмотрим на этот продукт в деталях.
Произведение векторов
В случае векторного умножения есть в основном два вида произведений — скалярное и векторное. Скалярный продукт — это вид умножения, в результате которого получается скалярная величина. Перекрестное произведение — это своего рода умножение, в результате которого получается векторная величина. Векторные произведения используются для определения других производных векторных величин. Уравнения для крутящего момента, угловой скорости и ускорения. Все эти величины включают операции, приводящие к векторам из векторов. Эти операции обычно являются векторными произведениями.
Скалярный продукт
Рассмотрим два вектора и . Скалярное произведение этих двух векторов определяется уравнением
Скалярное произведение этих двух векторов определяется уравнением
Здесь θ — угол между двумя векторами.
В случае, если векторы заданы их компонентами. например, a = a 1 i + a 2 j + a 3 k и b = b 1 i + b 2 j + b 3 k. В этом случае скалярный продукт определяется как
A.B = A 1 B 1 I + A 2 B 2 J + A 3 B 3 K
вектор. Продукт
Wort Wort Wort Wort Wort
. {A} и \vec{B}. Векторное произведение этих двух векторов обозначается . Направление этого вектора перпендикулярно обоим векторам. Величина этого вектора определяется выражениемЗдесь θ — угол между двумя векторами.
Правило правой руки используется для определения направления результирующего вектора векторного произведения.
В случае, если векторы заданы их компонентами. например, a = a 1 i + a 2 j + a 3 k и b = b 1 i + b 2 j + b 3 k. В этом случае векторное произведение определяется выражением
например, a = a 1 i + a 2 j + a 3 k и b = b 1 i + b 2 j + b 3 k. В этом случае векторное произведение определяется выражением
Свойство 1: В отличие от сложения и скалярного произведения векторное произведение не является коммутативным по своей природе.
В этом случае величина обоих произведений будет одинаковой, но направление будет совершенно противоположным. Это означает, что
Свойство 2: произведение векторов является дистрибутивным по своей природе по отношению к сложению векторов. Например,
Примеры задач
Вопрос 1. Два вектора задаются формулами a = 2i + j + k и b = i + j + k. Найдите скалярное произведение этих двух векторов.
Ответ:
Дано:
a = 2i + j + k
b = i + j + k
a.
b
⇒ (2i + j0 + k ).( i 9 j0 + k 3) ⇒ 2,1 + 1,1 + 1,1
⇒ 4
Вопрос 2. Два вектора задаются формулами a = i + j + k и b = i – 2j + 3k. Найдите скалярное произведение этих двух векторов.
Ответ:
Дано:
a = i + j + k
b = i -2j + 3k
a.b
⇒ (i + j + k ).( i – 2j + 3k )
⇒ 1,1 – 2,1 + 1,3
⇒ 1 – 2 + 3
⇒ 2
даны 3 вектора: , a = 4i +2j +2k и b = 2i + 2j + 2k. Найдите векторное произведение этих двух векторов.
Ответ:
Дано:
a = 4i + 2J + 2K
B = 2i + 2J + 2K
Вопрос 4: два вектора даются, A = I — J — J — J + k и b = i – j + k. Найдите векторное произведение этих двух векторов.
Ответ:
Дано:
A = I — J + K
B = I — J + K
Вопрос 5: два вектора даются, a = J + 4K. и b = 5i + 4j + 3k. Вычислите c = a x b + b x a.
и b = 5i + 4j + 3k. Вычислите c = a x b + b x a.
Ответ:
Дано:
A = J + 4K
B = 5i + 4J + 3K
Пусть результирующий вектор C,
C = a x b + b x a… (1)
Как упоминалось в приведенных выше свойствах, векторное произведение не является коммутативным по своей природе.
Но это можно переписать так:
Используя эти значения в уравнении (1)
c = a x b + b x a
⇒ c = – (b x a) + b x a 0 3 0 c0
900 900
Вопрос 6: Два вектора задаются формулами a = 2i + j + k и b = i + j + k. Найдите векторное произведение этих двух векторов.
Ответ:
Дано:
a = 2i + j + k
b = i + j + k
Объяснение урока: Векторное произведение двух векторов
В этом объяснении мы научимся вычислять векторное произведение двух векторов
используя как компоненты векторов, так и величины двух векторов и
угол между ними.
Произведение векторов — это операция, которую можно применить к двум векторам, создать другой вектор.
Векторное произведение используется во многих различных областях физики. Один расчет что это может быть полезно для расчета крутящего момента на объекте.
Рассмотрим автомобильное колесо, которое может свободно вращаться вокруг своей оси. Сила ⃑𝐹 применяется к колесу в точке на краю колеса. Вектор от центра колеса к точке, где сила действует. ⃑𝑟. Сила действует по касательной к колесу. Это показано на диаграмме ниже.
Если модуль силы равен 𝐹 и модуль вектора от центра колеса в точку, где действует сила, которая является как раз радиус равен 𝑟, то крутящий момент на колесе 𝜏 просто равен 𝐹 умножить на 𝑟, 𝜏=𝐹𝑟.
Но что, если сила , а не действует по касательной к колесу?
диаграмма ниже показывает тот же сценарий, но с силой, действующей под углом,
𝜃, по касательной.
В этом сценарии мы не можем использовать 𝜏=𝐹𝑟 для расчета крутящего момента на колесе. Вместо этого мы можем использовать векторное произведение ⃑𝐹 и ⃑𝑟 найти крутящий момент.
Векторное произведение обозначается знаком времени между двумя векторами, 𝜏=⃑𝑟×⃑𝐹.
Из-за этого векторное произведение также называют перекрестное произведение .
Обратите внимание, что, поскольку результатом векторного произведения является другой вектор, крутящий момент представляет собой векторное количество. Когда мы используем 𝜏=𝐹𝑟, как и в предыдущем сценарии, мы только рассчитывая величину крутящего момента, но он также имеет направление.
Чтобы понять, как работает векторное произведение, давайте сначала посмотрим, что результат применения векторного произведения к единичным векторам.
Напомним, что единичный вектор — это вектор, величина которого равна 1. Мы можем представить
любой вектор как сумму единичных векторов вдоль основных осей, которые, когда мы
работающие только в двух измерениях, являются 𝑥- и 𝑦-осями. Условно,
⃑𝑖 — единичный вектор, указывающий вдоль
𝑥-ось и ⃑𝑗 — единичный вектор
который указывает вдоль оси 𝑦.
Условно,
⃑𝑖 — единичный вектор, указывающий вдоль
𝑥-ось и ⃑𝑗 — единичный вектор
который указывает вдоль оси 𝑦.
Однако работа с векторным произведением обязательно приводит нас к трем размеры, поэтому нам также нужен единичный вектор, который указывает вдоль оси 𝑧. Обычно этот единичный вектор обозначается символом ⃑𝑘.
На схеме ниже показаны 𝑥-, 𝑦- и 𝑧-оси и соответствующие им единичные векторы: ⃑𝑖, ⃑𝑗, и ⃑𝑘.
Важно отметить, что в отличие от умножения простых чисел при векторном произведении порядок двух векторов в произведении влияет на результат. Так, например, результат ⃑𝑖×⃑𝑗 не равен результат ⃑𝑗×⃑𝑖: ⃑𝑖×⃑𝑗≠⃑𝑗×⃑𝑖.
Векторное произведение определяется таким образом, что векторное произведение, включающее оба
⃑𝑖 и ⃑𝑗
будет указывать в направлении ⃑𝑘 или −⃑𝑘. Единичные векторы ⃑𝑖 и
⃑𝑗 оба лежат в 𝑥𝑦-плоскости,
и результат векторного произведения всегда нормален к плоскости, образованной
два вектора, к которым применяется векторное произведение.
В случае ⃑𝑖×⃑𝑗, результат просто ⃑𝑘: ⃑𝑖×⃑𝑗=⃑𝑘.
В случае ⃑𝑗×⃑𝑖 результатом будет −⃑𝑘: ⃑𝑗×⃑𝑖=−⃑𝑘.
Обратите внимание, что ⃑𝑗×⃑𝑖=−⃑𝑖×⃑𝑗. Замена порядок единичных векторов в произведении дает результат с той же величиной но указывает в противоположном направлении. Обычно это верно для вектора произведение любых двух векторов, к которым применяется произведение.
Правило: перестановка порядка операндов в векторном произведении
Перестановка порядка операндов в векторном произведении дает результат, который имеет ту же величину, но указывает в противоположном направлении.
Для любых двух векторов ⃑𝐴 и ⃑𝐵, ⃑𝐴×⃑𝐵=−⃑𝐵×⃑𝐴.
Кроме того, векторное произведение ⃑𝑖 или ⃑𝑗 сам с собой равен 0: ⃑𝑖×⃑𝑖=0,⃑𝑗×⃑𝑗=0.
Зная все это, теперь мы можем вывести формулу векторного произведения любого
два вектора, лежащие в 𝑥𝑦-плоскости. Рассмотрим вектор
⃑𝐴, который имеет компоненты
𝐴 и 𝐴, а также вектор
⃑𝐵,
который имеет компоненты 𝐵 и 𝐵:
⃑𝐴=𝐴⃑𝑖+𝐴⃑𝑗,⃑𝐵=𝐵⃑𝑖+𝐵⃑𝑗.
Векторное произведение ⃑𝐴 и ⃑𝐵 это ⃑𝐴×⃑𝐵=𝐴⃑𝑖+𝐴⃑𝑗×𝐵⃑𝑖+𝐵⃑𝑗.
Как и при обычном умножении, мы можем раскрыть скобки, что даст нам ⃑𝐴 × ⃑𝐵 = 𝐴𝐵⃑𝑖 × ⃑𝑖+𝐴𝐵⃑𝑖 × ⃑𝑗+𝐴𝐵⃑𝑗 × ⃑𝑖+𝐴𝐵⃑𝑗 × ⃑𝑗.
На данный момент это довольно длинное и сложное выражение. Однако возможно радикально упростить его, используя правила для векторных произведений единицы вектора, которые мы определили ранее. Напомним, что оба ⃑𝑖×⃑𝑖 и ⃑𝑗×⃑𝑗 равны 0. Это означает, что ⃑𝐴×⃑𝐵=0𝐴𝐵+𝐴𝐵⃑𝑖×⃑𝑗+𝐴𝐵⃑𝑗×⃑𝑖+0𝐴𝐵, что упрощает до ⃑𝐴×⃑𝐵=𝐴𝐵⃑𝑖×⃑𝑗+𝐴𝐵⃑𝑗×⃑𝑖.
Напомним также, что ⃑𝑖×⃑𝑗=⃑𝑘 и ⃑𝑗×⃑𝑖=−⃑𝑘, поэтому ⃑𝐴 × ⃑𝐵 = 𝐴𝐵⃑𝑘+𝐴𝐵 — ⃑𝑘⃑𝐴 × ⃑𝐵 = 𝐴𝐵⃑𝑘 — 𝐴𝐵⃑𝑘⃑𝐴 × ⃑𝐵 = 𝐴𝐵 — 𝐴𝐵⃑𝑘.
Теперь мы имеем простую формулу для расчета векторное произведение. Обратите внимание, что это
формула будет работать только для двух векторов, которые лежат в
𝑥𝑦-плоскость, а значит, их 𝑧-компонента
должен быть равен 0. Формула вычисления векторного произведения любых два вектора сложнее; однако в этом уроке мы будем применять только
векторное произведение двух векторов, лежащих в 𝑥𝑦-плоскости.
Формула вычисления векторного произведения любых два вектора сложнее; однако в этом уроке мы будем применять только
векторное произведение двух векторов, лежащих в 𝑥𝑦-плоскости.
Определение: векторное произведение двух векторов, лежащих в 𝑥𝑦-Плоскость
Если два вектора ⃑𝐴 и ⃑𝐵 оба лежат в 𝑥𝑦-плоскости, их векторное произведение определяется выражением ⃑𝐴×⃑𝐵=𝐴𝐵−𝐴𝐵⃑𝑘, где 𝐴 и 𝐴 — компоненты ⃑𝐴 и 𝐵 и 𝐵 являются компонентами ⃑𝐵.
Теперь попробуем использовать эту формулу в примере вопроса.
Пример 1. Вычисление векторного произведения двух векторов, лежащих в 𝑥𝑦-плоскость с учетом их компонентов
Рассмотрим два вектора ⃑𝑅=3⃑𝑖+2⃑𝑗 и ⃑𝑆=5⃑𝑖+8⃑𝑗. Вычислите ⃑𝑅×⃑𝑆.
Ответ
Мы можем использовать формулу
⃑𝑅×⃑𝑆=𝑅𝑆−𝑅𝑆⃑𝑘
вычислить векторное произведение ⃑𝑅 и
⃑𝑆. Подставляя значения, получаем
⃑𝑅×⃑𝑆=(3×8−2×5)⃑𝑘⃑𝑅×⃑𝑆=(24−10)⃑𝑘⃑𝑅×⃑𝑆=14⃑𝑘.
Подставляя значения, получаем
⃑𝑅×⃑𝑆=(3×8−2×5)⃑𝑘⃑𝑅×⃑𝑆=(24−10)⃑𝑘⃑𝑅×⃑𝑆=14⃑𝑘.
Результат ⃑𝑅×⃑𝑆 14⃑𝑘. Обратите внимание, что оба ⃑𝑅 и ⃑𝑆 лежат в 𝑥𝑦-плоскости, а их вектор произведение указывает на 𝑧-оси, нормально к 𝑥𝑦-самолет.
Пример 2. Вычисление векторного произведения двух векторов, лежащих в 𝑥𝑦-плоскость с заданными их компонентами
Рассмотрим два вектора ⃑𝐶=15⃑𝑖+7⃑𝑗 и ⃑𝐷=4⃑𝑖+9⃑𝑗.
- Вычислить ⃑𝐶×⃑𝐷.
- Вычислить ⃑𝐷×⃑𝐶.
Ответ
Часть 1
Мы можем использовать формулу ⃑𝐶×⃑𝐷=𝐶𝐷−𝐶𝐷⃑𝑘 вычислить векторное произведение ⃑𝐶 и ⃑𝐷. Подставляя значения, получаем ⃑𝐶×⃑𝐷=(15×9−7×4)⃑𝑘⃑𝐶×⃑𝐷=(135−28)⃑𝑘⃑𝐶×⃑𝐷=107⃑𝑘.
Результат ⃑𝐶×⃑𝐷 107⃑𝑘.
Часть 2
В первой части вопроса нас просили отработать
⃑𝐶×⃑𝐷; в настоящее время,
нас просят вычислить векторное произведение этих двух векторов, но с
векторы, входящие в произведение наоборот.
Результат произведения не будет таким, как в первой части, потому что с векторным произведением порядок влияет на результат. Однако, нам не нужно снова вычислять ответ численно, потому что мы можем просто напомним, что для любых двух векторов ⃑𝐴 и ⃑𝐵, ⃑𝐴×⃑𝐵=−⃑𝐵×⃑𝐴.
Изменение порядка векторов на противоположное дает тот же результат, но умноженный на −1.
Итак, если ⃑𝐶×⃑𝐷=107⃑𝑘, ⃑𝐷×⃑𝐶=−107⃑𝑘.
Пример 3. Вычисление векторного произведения двух векторов, изображенных на Сетка
На диаграмме показаны два вектора, ⃑𝐴 и ⃑𝐵. Каждый из квадратов сетки на диаграмме имеет длина стороны 1. Вычислить ⃑𝐴×⃑𝐵.
Ответить
В этом вопросе нам показали два вектора на сетке и попросили найти их векторное произведение.
Мы можем вычислить компоненты векторов, взглянув на сетку. Вектор ⃑𝐴 имеет горизонтальную длину
4 квадрата сетки и длина по вертикали 1 квадрат сетки. Следовательно,
⃑𝐴=4⃑𝑖+1⃑𝑗.
Вектор ⃑𝐴 имеет горизонтальную длину
4 квадрата сетки и длина по вертикали 1 квадрат сетки. Следовательно,
⃑𝐴=4⃑𝑖+1⃑𝑗.
Вектор ⃑𝐵 имеет длину по горизонтали 3 квадрата сетки и вертикальная длина 5 квадратов сетки. Следовательно, ⃑𝐵=3⃑𝑖+5⃑𝑗.
Затем мы можем использовать формулу ⃑𝐴×⃑𝐵=𝐴𝐵−𝐴𝐵⃑𝑘 вычислить векторное произведение ⃑𝐴 и ⃑𝐵. Подставляя значения, получаем ⃑𝐴×⃑𝐵=(4×5−1×3)⃑𝑘⃑𝐴×⃑𝐵=(20−3)⃑𝑘⃑𝐴×⃑𝐵=17⃑𝑘.
Результатом ⃑𝐴×⃑𝐵 является 17⃑𝑘.
До сих пор мы вычисляли векторное произведение двух векторов, используя алгебраические манипулирование компонентами векторов. Однако существует и способ определение векторного произведения геометрически.
Определение: векторное произведение двух векторов
Рассмотрим два вектора ⃑𝐴 и
⃑𝐵. Угол между двумя векторами равен
𝜃. Это показано на диаграмме ниже.
Векторное произведение ⃑𝐴 и ⃑𝐵 равно величине ⃑𝐴 умножается на величину ⃑𝐵, умноженное на синус угла между ними, 𝜃, умноженное на единичный вектор ⃑𝑛, который указывает нормаль к плоскости, образованной ⃑𝐴 и ⃑𝐵, ⃑𝐴×⃑𝐵=‖‖⃑𝐴‖‖‖‖⃑𝐵‖‖(𝜃)⃑𝑛.sin
Если мы скажем, что величина ⃑𝐴 равна 𝐴 а величина ⃑𝐵 равна 𝐵, то мы можно написать это как ⃑𝐴×⃑𝐵=𝐴𝐵(𝜃)⃑𝑛.sin
На первый взгляд может показаться, что это не так, но эта формула действительно дает тот же результат, что и формула для векторного произведения, которую мы использовали ранее. Эквивалентность этих двух формул может быть доказана алгебраически, но это выходит за рамки что мы будем делать на этом уроке.
Наблюдение за векторным произведением, определенным таким образом, говорит нам о некоторых полезных свойствах
векторное произведение.
Во-первых, вспомните форму синусоиды. Это показано на графике ниже.
Когда 𝜃=0∘, sin(𝜃)=0. Это означает, что когда угол между двумя векторами равен 0∘, что означает, что они параллельны, их векторное произведение равно 0,
Аналогично, когда 𝜃=180∘, грех(𝜃)=0. Это означает, что когда угол между двумя векторами 180∘, что означает что они антипараллельны, их векторное произведение равно 0,
Правило: векторное произведение параллельных или антипараллельных векторов
Если два вектора указывают в одном направлении или в противоположных направлениях, их векторное произведение равен нулю.
Это также означает, что векторное произведение любого вектора на самого себя равно 0, так как любой вектор параллелен самому себе.
Правило: векторное произведение любого вектора на самого себя
Векторное произведение любого вектора
⃑𝐴 сам с собой равен нулю:
⃑𝐴×⃑𝐴=0.
Функция синуса имеет максимальное значение 1, когда 𝜃=90∘. Это означает, что векторное произведение двух векторов будет иметь наибольшее значение когда два вектора находятся под прямым углом друг к другу. Это противоположно скалярное произведение, которое имеет значение 0, когда два вектора находятся справа углами друг к другу.
Следовательно, векторное произведение можно рассматривать как меру двух вещей: насколько велики векторы и в какой степени они находятся под прямым углом к друг друга. Чем больше величина любого из векторов, тем больше величина их векторного произведения. Чем ближе угол между ними, 𝜃, это 90∘, тем больше величина векторного произведения.
Но как определить направление ⃑𝑛? Рассмотрим снова два вектора ⃑𝐴 и ⃑𝐵, как показано на схеме ниже.
Во-первых, важно помнить, что когда мы говорим о
«угол между двумя векторами», мы имеем в виду меньший из двух углов
образован двумя векторными стрелками. Этот термин не относится к большему углу,
обозначены 𝜙 на диаграмме ниже.
Этот термин не относится к большему углу,
обозначены 𝜙 на диаграмме ниже.
На приведенной выше диаграмме ⃑𝐵 против часовой стрелки из ⃑𝐴. Другими словами, если бы нам пришлось повернуть вектор ⃑𝐴 на 𝜃, угол между векторами, чтобы он указывал в в том же направлении, что и ⃑𝐵, нам пришлось бы повернуть его против часовой стрелки . В этом случае для ⃑𝐴×⃑𝐵, ⃑𝑛 указывает из экрана , вдоль положительная 𝑧-ось и равна ⃑𝑘.
На диаграмме ниже верно обратное и ⃑𝐵 по часовой из ⃑𝐴. Другими словами, если бы мы имели повернуть вектор ⃑𝐴 на 𝜃 так что он указывает в том же направлении, что и ⃑𝐵, нам пришлось бы повернуть его по часовой стрелке . В этом случае для ⃑𝐴×⃑𝐵, ⃑𝑛 указывает на страницу , вдоль отрицательная 𝑧-ось и равна −⃑𝑘.
Правило: направление векторного произведения для векторов в плоскости 𝑥𝑦
Для двух векторов в плоскости 𝑥𝑦 направление
⃑𝐴×⃑𝐵 это
⃑𝑘 если ⃑𝐵
против часовой стрелки от ⃑𝐴 и
−⃑𝑘, если ⃑𝐵
по часовой стрелке от ⃑𝐴.
Пример 4. Вычисление векторного произведения двух векторов с учетом их Величины и угол между ними
На диаграмме показаны два вектора, ⃑𝐴 и ⃑𝐵. Вычислите величину векторного произведения ⃑𝐴 и ⃑𝐵. Дайте ответ до ближайшего целого числа.
Ответ
Мы можем использовать формулу ⃑𝐴×⃑𝐵=𝐴𝐵(𝜃)⃑𝑛,грех где 𝐴 — величина ⃑𝐴 и 𝐵 — величина ⃑𝐵, чтобы найти векторное произведение ⃑𝐴 и ⃑𝐵.
В этом случае нас просят найти только величину вектора товар. Взятие величины обеих частей приведенной выше формулы дает нам ‖‖⃑𝐴×⃑𝐵‖‖=||𝐴𝐵(𝜃)⃑𝑛||‖‖⃑𝐴×⃑𝐵‖‖=𝐴𝐵(𝜃).sinsin
Вектор ⃑𝑛 не влияет на величина векторного произведения, поскольку это единичный вектор и, следовательно, сам имеет величину 1.
Подставляя значения, указанные в вопросе, получаем
‖‖⃑𝐴×⃑𝐵‖‖=12×16×(82)‖‖⃑𝐴×⃑𝐵‖‖=190,131…. sin∘
sin∘
Округлив до ближайшего целого числа, получим 190.
Пример 5. Нахождение векторного произведения двух векторов, показанных на трехмерном изображении Сетка
На диаграмме показаны два вектора, ⃑𝐶 и ⃑𝐷, в трехмерном пространстве. Оба вектора лежат в 𝑥𝑦-плоскость. Каждый из квадратов сетки имеет длину стороны 1. Рассчитайте ⃑𝐶×⃑𝐷.
Ответ
Этот вопрос показывает нам трехмерное пространство, но два вектора лежат в 𝑥𝑦-самолет.
Ключ к ответу на этот вопрос заключается в том, чтобы заметить, что векторы антипараллельны друг другу. Из схемы мы видим, что ⃑𝐶 имеет компоненты 4⃑𝑖+5⃑𝑗 и ⃑𝐷 имеет компоненты −4⃑𝑖−5⃑𝑗; следовательно, ⃑𝐷=−⃑𝐶.
Напомним, что для двух параллельных или антипараллельных векторов их
векторное произведение равно 0, поэтому ответ равен 0.
Ключевые моменты
- Произведение векторов — это операция, которую можно применить к двум векторам, производящим другой вектор.
- Векторное произведение также называется векторным произведением.
- Результатом ⃑𝑖×⃑𝑗 является ⃑𝑘.
- Результат ⃑𝑗×⃑𝑖 это −⃑𝑘.
- Для двух векторов в 𝑥𝑦-плоскости, если известны компоненты векторов, мы можем вычислить их векторное произведение, используя ⃑𝐴×⃑𝐵=𝐴𝐵−𝐴𝐵⃑𝑘.
- Если мы знаем величины двух векторов и угол между ними, мы можем вычислить их векторное произведение, используя ⃑𝐴×⃑𝐵=𝐴𝐵(𝜃)⃑𝑛.sin
- Если два вектора параллельны или антипараллельны, их векторное произведение равно 0.
- Векторное произведение имеет максимальную величину, когда два вектора находятся под прямым углом к друг друга.
Умножение векторов – типы, процесс и примеры
Умножение векторов помогает нам понять, как ведут себя два вектора при объединении. Эта векторная операция имеет широкое применение в физике, инженерии и астрономии, поэтому нам необходимо изучить эти методы, особенно если мы изучаем высшую математику. Умножение векторов охватывает два важных метода векторных операций: скалярное произведение и векторное произведение. Изучение умножения векторов также может помочь нам освежить наши знания о векторах и темах их применения.
В этой статье мы обсудим два типа векторного умножения и узнаем разницу между ними. Обязательно держите свои заметки по следующим понятиям под рукой, так как нам, возможно, придется освежить их, изучая векторное умножение.
Эта векторная операция имеет широкое применение в физике, инженерии и астрономии, поэтому нам необходимо изучить эти методы, особенно если мы изучаем высшую математику. Умножение векторов охватывает два важных метода векторных операций: скалярное произведение и векторное произведение. Изучение умножения векторов также может помочь нам освежить наши знания о векторах и темах их применения.
В этой статье мы обсудим два типа векторного умножения и узнаем разницу между ними. Обязательно держите свои заметки по следующим понятиям под рукой, так как нам, возможно, придется освежить их, изучая векторное умножение.
- Понимание различных компонентов, составляющих вектор.
- Посмотрите, как мы складываем и вычитаем векторы.
- Понять, как скалярный фактор влияет на заданный вектор.
А пока давайте продолжим и изучим два важных метода векторного умножения.
Когда мы умножаем два или более векторов, важно определить, хотим ли мы получить произведение, имеющее скалярную величину или векторную величину. Техника, которую нам нужно будет применить, зависит от нашего ответа на этот вопрос.
На самом деле существует три возможных произведения векторного умножения: вектор, умноженный на скалярный множитель, точечное (или скалярное) произведение и перекрестное (или векторное) произведение.
Техника, которую нам нужно будет применить, зависит от нашего ответа на этот вопрос.
На самом деле существует три возможных произведения векторного умножения: вектор, умноженный на скалярный множитель, точечное (или скалярное) произведение и перекрестное (или векторное) произведение.
- К этому моменту мы должны были узнать о распределении скалярных коэффициентов по вектору, и это первая процедура. Обязательно проверьте ссылки, которые мы включили в первый раздел.
- Скалярное произведение, известное как скалярное произведение, как вы уже догадались, возвращает скалярную величину.
- Аналогично, векторное произведение возвращает векторную величину.
Наше обсуждение сосредоточится на двух последних методах: точечных произведениях и перекрестных произведениях. Эти имена помогут вам определить операцию, которую необходимо выполнить, поскольку их операторы представляют собой точку ($\cdot$) и крестик ($\times$) соответственно.
Два продукта будут иметь разные результаты и процессы. Вот почему нам нужно понять, что представляют собой точечные и перекрестные произведения. Скалярный продукт и его правила Скалярное произведение представляет собой проекцию одного вектора на другой вектор. Допустим, у нас есть $\overrightarrow{A}$ и $\overrightarrow{B}$, скалярное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$ — это просто проекция $\overrightarrow{A} $ на вектор $\overrightarrow{B}$. Вот визуализация того, что происходит, когда мы находим скалярное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$. Что происходит, так это то, что мы используем векторную составляющую $\overrightarrow{A}$ вдоль направления $\overrightarrow{B}$ и умножаем эту составляющую на величину $\overrightarrow{B}$.
\begin{align}\overrightarrow{A} \cdot \overrightarrow{B} &= (A \cos\theta)(B)\\&= AB\cos\theta\end{align}
Это означает, что скалярное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$ ($\overrightarrow{A} \cdot \overrightarrow{B})$ — это просто произведение двух векторов’ величин и косинус угла между ними . Полученное произведение является скалярным, поэтому -точечное произведение также известно как скалярное произведение. Вот несколько важных свойств скалярного произведения, о которых следует помнить:
Полученное произведение является скалярным, поэтому -точечное произведение также известно как скалярное произведение. Вот несколько важных свойств скалярного произведения, о которых следует помнить:
- Скалярное произведение коммутативно: $\overrightarrow{A} \cdot \overrightarrow{B} = \overrightarrow{B} \cdot \overrightarrow{A}$. 9{\circ}$ равно $0$).
Есть еще один способ вычислить скалярное произведение двух векторов: мы умножаем их соответствующие декартовы компоненты . Допустим, $\mathbf{i}$, $\mathbf{j}$ и $\mathbf{k}$ — единичные векторы вдоль осей $x$, $y$ и $z$ соответственно, мы можем найдите произведение $\overrightarrow{A}$ и $\overrightarrow{B}$, как показано ниже.
\begin{align}\overrightarrow{A} &= A_1\mathbf{i} + A_2\mathbf{j}+ A_3\mathbf{k}\\\overrightarrow{B} &= B_1\mathbf{i} + B_2\ mathbf{j} + B_3\mathbf{k}\\\\\overrightarrow{A} \cdot \overrightarrow{B}&=A_1B_1 + A_2B_2 +A_3B_3 \end{выровнено}
Мы можем вычислить эти два способа скалярного произведения (или скалярного произведения) двух векторов. Теперь давайте перейдем ко второму важному результату векторного умножения: перекрестному или векторному произведению. Перекрестное произведение и его правила Возможно, вы уже видели здесь шаблон — для векторных произведений мы используем оператор $\times$, и результирующее произведение является вектором. Из-за этого перекрестное или векторное произведение предполагает, что мы будем учитывать направление.
Отличный способ визуализировать векторное произведение двух векторов — определить площадь параллелограмма по векторам. Отсюда мы видим, что перекрестное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$ равно произведению $A\sin\theta$ и $\overrightarrow{B}$.
\begin{align}\overrightarrow{A} \times \overrightarrow{B} &= (A \sin \theta)(B)\\&= AB \sin \theta \mathbf{n} \end{align}
Имейте в виду, что $\mathbf{n}$ — это просто единичный вектор, перпендикулярный и $\overrightarrow{A}$, и $\overrightarrow{B}$. Это означает, что мы можем найти перекрестное произведение на умножение величин двух векторов при наличии двух векторов и угла между ними .
Теперь давайте перейдем ко второму важному результату векторного умножения: перекрестному или векторному произведению. Перекрестное произведение и его правила Возможно, вы уже видели здесь шаблон — для векторных произведений мы используем оператор $\times$, и результирующее произведение является вектором. Из-за этого перекрестное или векторное произведение предполагает, что мы будем учитывать направление.
Отличный способ визуализировать векторное произведение двух векторов — определить площадь параллелограмма по векторам. Отсюда мы видим, что перекрестное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$ равно произведению $A\sin\theta$ и $\overrightarrow{B}$.
\begin{align}\overrightarrow{A} \times \overrightarrow{B} &= (A \sin \theta)(B)\\&= AB \sin \theta \mathbf{n} \end{align}
Имейте в виду, что $\mathbf{n}$ — это просто единичный вектор, перпендикулярный и $\overrightarrow{A}$, и $\overrightarrow{B}$. Это означает, что мы можем найти перекрестное произведение на умножение величин двух векторов при наличии двух векторов и угла между ними . Затем мы можем умножить результат на синус угла между двумя векторами .
Вот некоторые важные свойства векторных или кросс-произведений, которые могут пригодиться:
Затем мы можем умножить результат на синус угла между двумя векторами .
Вот некоторые важные свойства векторных или кросс-произведений, которые могут пригодиться:
- Векторные или перекрестные произведения антикоммутативны: $\overrightarrow{A} \times \overrightarrow{B} = -\overrightarrow{B} \times \overrightarrow{A}$.
- Векторное произведение является дистрибутивным относительно сложения: $\overrightarrow{A} \times (\overrightarrow{B}\times \overrightarrow{C}) = \overrightarrow{A} \times \overrightarrow{B} + \overrightarrow{A} \ раз \overrightarrow{C}$.
- Перемножение двух параллельных векторов всегда будет равно $0$.
Как и в случае со скалярными произведениями, мы также можем найти векторное произведение двух векторов, учитывая их декартовы формы. Используя те же единичные векторы, мы имеем $\overrightarrow{A} = A_1\mathbf{i} + A_2\mathbf{j}+ A_3\mathbf{k}$ и $\overrightarrow{B} = B_1\mathbf{i} + B_2\mathbf{j}+ B_3\mathbf{k}$. Важным свойством для наблюдения являются векторные произведения векторов с тремя единицами. Мы собрали для вас продукты: Мы можем разработать формулу векторного произведения, распределив два вектора на сложение и используя векторные произведения единичных векторов. Однако, чтобы упростить обсуждение, вот как мы можем вычислить векторное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$.
\begin{выровнено}\overrightarrow{A} \times \overrightarrow{B}&=(A_2B_3 – A_3B_2)\mathbf{i} +(A_3B_1 – A_1B_3)\mathbf{j}+(A_1B_2 – A_2B_1)\mathbf{k }\конец{выровнено}
Если вы уже изучали детерминанты в прошлом, есть еще один способ понять векторное произведение, и вы также можете помочь себе запомнить операцию.
Важным свойством для наблюдения являются векторные произведения векторов с тремя единицами. Мы собрали для вас продукты: Мы можем разработать формулу векторного произведения, распределив два вектора на сложение и используя векторные произведения единичных векторов. Однако, чтобы упростить обсуждение, вот как мы можем вычислить векторное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$.
\begin{выровнено}\overrightarrow{A} \times \overrightarrow{B}&=(A_2B_3 – A_3B_2)\mathbf{i} +(A_3B_1 – A_1B_3)\mathbf{j}+(A_1B_2 – A_2B_1)\mathbf{k }\конец{выровнено}
Если вы уже изучали детерминанты в прошлом, есть еще один способ понять векторное произведение, и вы также можете помочь себе запомнить операцию.
- Мы можем записать единичные векторы в первый массив.
- Компоненты двух векторов в следующих двух массивах.
- Чтобы найти коэффициент перед $\mathbf{i}$, мы находим определитель оставшейся матрицы $2\times2$ после того, как покроем строку и столбец, содержащие $\mathbf{i}$.

- Примените аналогичный процесс, чтобы найти компоненты для $\mathbf{j}$ и $\mathbf{k}$ .
\begin{align}\overrightarrow{A} \times \overrightarrow{B}&=\begin{vmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k}\\ A_1 & A_2 & A_3\\ B_1 & B_2 & B_3\end{vmatrix}\\&=\begin{vmatrix} A_2 & A_3\\B_2 & B_3\end{vmatrix}\mathbf{i}- \begin{vmatrix} A_1 & A_3\\B_1 & B_3\end{vmatrix}\mathbf{j}+\begin{vmatrix} A_1 & A_2\\B_1 & B_2\end{vmatrix}\mathbf{k}\\&=(A_2B_3 – A_3B_2)\mathbf{i} — (A_1B_3 – A_3B_1)\mathbf{j}+(A_1B_2 – A_2B_1)\mathbf{k}\end{выровнено} Независимо от подхода, он все равно должен возвращать одни и те же результаты. Это все, что нам нужно узнать о векторном умножении, так почему бы нам не попробовать решить приведенные ниже задачи, чтобы лучше понять векторные произведения и скалярные произведения? 9{\ circ} $
Раствор Эта задача требует, чтобы мы умножили величины $\overrightarrow{F}$ и $\overrightarrow{s}$ и косинус образовавшегося угла $\theta$. Короче говоря, нам нужно скалярное произведение $|\overrightarrow{F}| $ и $|\overrightarrow{s}| .
\begin{align}\overrightarrow{F} \cdot \overrightarrow{s} &= |\overrightarrow{F}||\overrightarrow{s}|\cos \theta \end{align}
Мы будем использовать одну и ту же формулу для всех трех значений, поэтому продолжим и суммируем расчеты в одной таблице.
9{\circ}\\&= 600 \cdot \dfrac{1}{2}\\&=300 \end{выровнено}
Короче говоря, нам нужно скалярное произведение $|\overrightarrow{F}| $ и $|\overrightarrow{s}| .
\begin{align}\overrightarrow{F} \cdot \overrightarrow{s} &= |\overrightarrow{F}||\overrightarrow{s}|\cos \theta \end{align}
Мы будем использовать одну и ту же формулу для всех трех значений, поэтому продолжим и суммируем расчеты в одной таблице.
9{\circ}\\&= 600 \cdot \dfrac{1}{2}\\&=300 \end{выровнено}
Это отличный способ применить нашу формулу скалярного произведения, а также получить представление об одном из многих приложений векторного умножения. Пример 2 Найдите выражения для $\overrightarrow{A} \cdot \overrightarrow{B}$ и $\overrightarrow{A} \times \overrightarrow{B}$ для следующих векторов: \begin{align} \overrightarrow{A} &= 2\mathbf{i} – 3\mathbf{j}\\\overrightarrow{B} &=3\mathbf{i}+ 2\mathbf{j}\end{ выровнено}
Решение Зная декартовы формы векторов, мы все еще можем найти их точечные и перекрестные произведения.
- Мы можем перемножить коэффициенты соответствующих компонентов, а затем сложить произведения, чтобы найти скалярный продукт.
- Для перекрестного произведения вида $a\mathbf{i} + b\mathbf{j}$ члены распределяются алгебраически и исключаются перекрестные произведения одинаковых единичных векторов.
Почему мы не работаем с $\overrightarrow{A} = 2\mathbf{i} – 3\mathbf{j}$ и $\overrightarrow{B} =3\mathbf{i} + 2\mathbf{j}$ сначала лучше понять процесс?
Скалярное произведение будет простым — мы умножаем коэффициенты перед $\mathbf{i}$ и $\mathbf{j}$.
\begin{align}\overrightarrow{A} \cdot\overrightarrow{B}&= ({\color{blue}2}\mathbf{i} – {\color{red}3}\mathbf{j}) \cdot ({\ color{blue}3}\mathbf{i} + {\color{red}2}\mathbf{j})\\&= ({\color{blue}2})({\color{blue} 3}) + ({\color{red}-3})({\color{red}2})\\&= 6 – 6\\&= 0\end{выровнено}
Это означает, что скалярное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$ равно $0$.
Поскольку векторное произведение является дистрибутивным относительно сложения, мы можем распределить члены алгебраически и сократить $\mathbf{i}\times\mathbf{i}$ или $\mathbf{j}\times\mathbf{j}$ . \begin{align}\overrightarrow{A} \times\overrightarrow{B}&= (2\mathbf{i} – 3\mathbf{j}) \times (3\mathbf{i} + 2\mathbf{j} )\\&= (2\mathbf{i})\times (3\mathbf{i} + 2\mathbf{j}) – 3\mathbf{j}\times (3\mathbf{i} + 2\mathbf {j})\\&= [(2)(3) \mathbf{i}\times\mathbf{i} +(2)(2) \mathbf{i}\times\mathbf{j}]+[( -3)(3) \mathbf{j}\times\mathbf{i} + (-3)(2)\mathbf{j}\times\mathbf{j}]\end{выровнено}
Напомним, что перекрестное произведение идентичных векторов будет равно нулю, поэтому давайте воспользуемся этим, чтобы сократить члены. Кроме того, просмотрите руководство, которое мы предоставили для векторных произведений других единичных векторов.
\begin{выровнено}\overrightarrow{A} \times\overrightarrow{B}&= (0 + 4\mathbf{k})+(-9(\mathbf{-k} )+ 0) \\&= (4 + 9)\mathbf{k}\\&= 13\mathbf{k}\end{align}
Таким образом, мы показали, как можно найти перекрестное и скалярное произведения двух векторов вида $a\mathbf{i} + b\mathbf{j}$. Пример 3 Оцените следующие выражения, учитывая декартовы формы трех векторов, показанных ниже.
\begin{align}\overrightarrow{A} \times\overrightarrow{B}&= (2\mathbf{i} – 3\mathbf{j}) \times (3\mathbf{i} + 2\mathbf{j} )\\&= (2\mathbf{i})\times (3\mathbf{i} + 2\mathbf{j}) – 3\mathbf{j}\times (3\mathbf{i} + 2\mathbf {j})\\&= [(2)(3) \mathbf{i}\times\mathbf{i} +(2)(2) \mathbf{i}\times\mathbf{j}]+[( -3)(3) \mathbf{j}\times\mathbf{i} + (-3)(2)\mathbf{j}\times\mathbf{j}]\end{выровнено}
Напомним, что перекрестное произведение идентичных векторов будет равно нулю, поэтому давайте воспользуемся этим, чтобы сократить члены. Кроме того, просмотрите руководство, которое мы предоставили для векторных произведений других единичных векторов.
\begin{выровнено}\overrightarrow{A} \times\overrightarrow{B}&= (0 + 4\mathbf{k})+(-9(\mathbf{-k} )+ 0) \\&= (4 + 9)\mathbf{k}\\&= 13\mathbf{k}\end{align}
Таким образом, мы показали, как можно найти перекрестное и скалярное произведения двух векторов вида $a\mathbf{i} + b\mathbf{j}$. Пример 3 Оцените следующие выражения, учитывая декартовы формы трех векторов, показанных ниже. \begin{align} \overrightarrow{A} &= 4\mathbf{i} – 5\mathbf{j} + 6\mathbf{k}\\\overrightarrow{B} &=-2\mathbf{i}+ 4 \mathbf{j}- 3\mathbf{k}\\\overrightarrow{C} &=3\mathbf{i}+ 2\mathbf{j}- 6\mathbf{k}\end{align}
а. $\overrightarrow{A} \times\overrightarrow{B}$
б.$\overrightarrow{B}\cdot (\overrightarrow{A}\times\overrightarrow{B})$
в. $(\overrightarrow{A} \times \overrightarrow{B})\times \overrightarrow{C}$
\begin{align} \overrightarrow{A} &= 4\mathbf{i} – 5\mathbf{j} + 6\mathbf{k}\\\overrightarrow{B} &=-2\mathbf{i}+ 4 \mathbf{j}- 3\mathbf{k}\\\overrightarrow{C} &=3\mathbf{i}+ 2\mathbf{j}- 6\mathbf{k}\end{align}
а. $\overrightarrow{A} \times\overrightarrow{B}$
б.$\overrightarrow{B}\cdot (\overrightarrow{A}\times\overrightarrow{B})$
в. $(\overrightarrow{A} \times \overrightarrow{B})\times \overrightarrow{C}$
У нас есть два способа найти векторное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$: используя формулу, полученную из распределения двух векторов, или используя наши знания об определителях. Мы пока будем использовать первый вариант:
\begin{выровнено}\overrightarrow{A} \times \overrightarrow{B}&=(A_2B_3 – A_3B_2)\mathbf{i} +(A_3B_1 – A_1B_3)\mathbf{j}+(A_1B_2 – A_2B_1)\mathbf{k }\конец{выровнено}
Следовательно, мы имеем векторное произведение двух векторов:
\begin{align}\overrightarrow{A} &= 4\mathbf{i} – 5\mathbf{j} + 6\mathbf{k}\\\overrightarrow{B} &=-2\mathbf{i}+ 4 \mathbf{j}- 3\mathbf{k}\\\overrightarrow{A} \times \overrightarrow{B}&=(-5\cdot -3 – 6\cdot 4)\mathbf{i} +(-3 \cdot 4 – 4\cdot -3)\mathbf{j}+(4\cdot 4 – -5\cdot -2)\mathbf{k}\\&=-9\mathbf{i}+0\mathbf{j}+6\mathbf{k}\\&=-9\mathbf{i} +6\mathbf{k}\end{выровнено}
Мы будем использовать этот результат для следующих двух задач, поэтому давайте назначим $\overrightarrow{M}$ для представления $-9\mathbf{i}+0\mathbf{j}+6\mathbf{k}$ или $ -9\mathbf{i} +6\mathbf{k}$. Чтобы найти $\overrightarrow{B} \cdot(\overrightarrow{A}\times\overrightarrow{B})$, мы просто умножаем коэффициенты соответствующих единичных векторов как $\overrightarrow{A}$, так и полученного вектор, $\overrightarrow{M}$.
\begin{align}\overrightarrow{B} \cdot(\overrightarrow{A}\times\overrightarrow{B}) &=\overrightarrow{B}\cdot\overrightarrow{M}\\&=(-2\mathbf{ i}+ 4\mathbf{j}- 3\mathbf{k})\cdot(-9\mathbf{i}+0\mathbf{j}+6\mathbf{k})\\&= (-2)(-9)+ (4)(0) +(-3)(6)\\& =18-18\\&=0\конец{выровнено}
Для третьей задачи найдем векторное произведение $(\overrightarrow{A} \times \overrightarrow{B}) = \overrightarrow{M}$ и $\overrightarrow{C}$, взяв определители коэффициентов.
\begin{align}(\overrightarrow{A}\times\overrightarrow{B}) \times\overrightarrow{C} &=\overrightarrow{M}\times\overrightarrow{C}\\&=(-9\mathbf{ i}+0\mathbf{j}+6\mathbf{k})\times(3\mathbf{i}+ 2\mathbf{j}- 6\mathbf{k})\end{выровнено}
Давайте перепишем их в матричной форме и начнем вычислять определители полученных матриц $2\times2$, как показано ниже.
Чтобы найти $\overrightarrow{B} \cdot(\overrightarrow{A}\times\overrightarrow{B})$, мы просто умножаем коэффициенты соответствующих единичных векторов как $\overrightarrow{A}$, так и полученного вектор, $\overrightarrow{M}$.
\begin{align}\overrightarrow{B} \cdot(\overrightarrow{A}\times\overrightarrow{B}) &=\overrightarrow{B}\cdot\overrightarrow{M}\\&=(-2\mathbf{ i}+ 4\mathbf{j}- 3\mathbf{k})\cdot(-9\mathbf{i}+0\mathbf{j}+6\mathbf{k})\\&= (-2)(-9)+ (4)(0) +(-3)(6)\\& =18-18\\&=0\конец{выровнено}
Для третьей задачи найдем векторное произведение $(\overrightarrow{A} \times \overrightarrow{B}) = \overrightarrow{M}$ и $\overrightarrow{C}$, взяв определители коэффициентов.
\begin{align}(\overrightarrow{A}\times\overrightarrow{B}) \times\overrightarrow{C} &=\overrightarrow{M}\times\overrightarrow{C}\\&=(-9\mathbf{ i}+0\mathbf{j}+6\mathbf{k})\times(3\mathbf{i}+ 2\mathbf{j}- 6\mathbf{k})\end{выровнено}
Давайте перепишем их в матричной форме и начнем вычислять определители полученных матриц $2\times2$, как показано ниже. \begin{выровнено}(-9\mathbf{i}+ 0\mathbf{j} +6\mathbf{k})\times(3\mathbf{i}+ 2\mathbf{j}- 6\mathbf{k})&=\begin{vmatrix }\mathbf{i} & \mathbf{j} & \mathbf{k}\\ -9 & 0 & 6\\3 & 2 & -6\end{vmatrix}\\&=\begin{vmatrix} 0 & 6\\2 & -6\end{vmatrix}\mathbf{i}-\begin{vmatrix} -9 & 6\\3 & -6\end{vmatrix}\mathbf{j}+\begin{vmatrix} — 9 & 0\\3 & 2\end{vmatrix}\mathbf{k}\\&=(0 — 12)\mathbf{i} -(54 — 18)\mathbf{j}+(-18- 0) \mathbf{k}\\&=-12\mathbf{i} -36\mathbf{j}-18\mathbf{k}\end{выровнено}
9{\circ}$?
\begin{выровнено}(-9\mathbf{i}+ 0\mathbf{j} +6\mathbf{k})\times(3\mathbf{i}+ 2\mathbf{j}- 6\mathbf{k})&=\begin{vmatrix }\mathbf{i} & \mathbf{j} & \mathbf{k}\\ -9 & 0 & 6\\3 & 2 & -6\end{vmatrix}\\&=\begin{vmatrix} 0 & 6\\2 & -6\end{vmatrix}\mathbf{i}-\begin{vmatrix} -9 & 6\\3 & -6\end{vmatrix}\mathbf{j}+\begin{vmatrix} — 9 & 0\\3 & 2\end{vmatrix}\mathbf{k}\\&=(0 — 12)\mathbf{i} -(54 — 18)\mathbf{j}+(-18- 0) \mathbf{k}\\&=-12\mathbf{i} -36\mathbf{j}-18\mathbf{k}\end{выровнено}
9{\circ}$?
$37,5$ N$\cdot$m
$37,5\sqrt{2}$ N$\cdot$m
$75$ N$\cdot$m
$75\sqrt{3}$ N$\cdot$m
4. Что из следующего показывает выражение для $\overrightarrow{A} \cdot \overrightarrow{B}$ для следующих векторов?
\begin{выровнено}\overrightarrow{A} &= 4\mathbf{i} + 2\mathbf{j}\\\overrightarrow{B} &=-6\mathbf{i}- 5\mathbf{j}\ конец {выровнен}
$-17$
$-34$
$17$
$34$
5. Что из следующего показывает выражение для $\overrightarrow{A} \times \overrightarrow{B}$ для следующих векторов?
\begin{выровнено}\overrightarrow{A} &= 4\mathbf{i} + 2\mathbf{j}\\\overrightarrow{B} &=-6\mathbf{i}- 5\mathbf{j}\ end{выровнено}
$-4 \mathbf{j}$
$-4 \mathbf{k}$
$-8 \mathbf{j}$
$-8 \mathbf{k}$
6. Предположим, что у нас есть следующие выражения для $\overrightarrow{A}$, $\overrightarrow{B}$ и $\overrightarrow{C}$:
Предположим, что у нас есть следующие выражения для $\overrightarrow{A}$, $\overrightarrow{B}$ и $\overrightarrow{C}$:
\begin{align} \overrightarrow{A} &= 3\mathbf{i} – 2\mathbf{j} + 4\mathbf{k}\\\overrightarrow{B} &=6\mathbf{i}- 3\mathbf{j}+ 3\mathbf{k}\\\overrightarrow{C} &=4\mathbf{i}- 5\mathbf{j}+ 8\mathbf{j}\end{aligned}
Какой из следующего эквивалентно $\overrightarrow{A} \cdot \overrightarrow{C}$?
18$
27$
36$
54$
7. Предположим, что у нас есть следующие выражения для $\overrightarrow{A}$, $\overrightarrow{B}$ и $\overrightarrow{C}$:
\begin{align} \overrightarrow{A} &= 3\mathbf{i} – 2\mathbf{j} + 4\mathbf{k}\\\overrightarrow{B} &=6\mathbf{i}- 3\mathbf{j}+ 3\mathbf{k}\\\overrightarrow{C} &=4\mathbf{i}- 5\mathbf{j}+ 8\mathbf{j}\end{aligned}
Какой из следующего эквивалентно $\overrightarrow{B}\cdot (\overrightarrow{A}\times\overrightarrow{C})$?
18$
27$
36$
54$
8. Предположим, что у нас есть следующие выражения для $\overrightarrow{A}$, $\overrightarrow{B}$ и $\overrightarrow{C}$:
Предположим, что у нас есть следующие выражения для $\overrightarrow{A}$, $\overrightarrow{B}$ и $\overrightarrow{C}$:
\begin{align} \overrightarrow{A} &= 3\mathbf{i} – 2\mathbf{j} + 4\mathbf{k}\\\overrightarrow{B} &=6\mathbf{i}- 3\mathbf{j}+ 3\mathbf{k}\\\overrightarrow{C} &=4\mathbf{i}- 5\mathbf{j}+ 8\mathbf{j}\end{aligned}
Какой из следующего эквивалентно $(\overrightarrow{A} \times \overrightarrow{C})\times \overrightarrow{B}$?
$ -99\mathbf{i} -60\mathbf{j} +12\mathbf{k}$
$ -33\mathbf{i} -20\mathbf{j} +6\mathbf{k}$
$ 33\mathbf{i} +20\mathbf{j} -6\mathbf{k}$
$99\mathbf{i} +60\mathbf{j} +12\mathbf{k}$
Изображения/математические чертежи создаются с помощью GeoGebra.
Предыдущий урок | Главная страница | Следующий уроклинейная алгебра — Понимание точечного и векторного произведения
спросил
Изменено 3 года, 1 месяц назад
Просмотрено 54k раз
$\begingroup$
Для каких целей служат продукты Dot and Cross?
У вас есть четкие примеры того, когда вы бы их использовали?
- линейная алгебра
- перекрестное произведение
$\endgroup$
$\begingroup$
Когда вы имеете дело с векторами, иногда вы говорите себе: «Черт возьми, я бы хотел, чтобы была функция, которая. ..»
..»
был равен нулю, когда два вектора перпендикулярны, что позволило мне проверить перпендикулярность.»
Скалярный продукт
позволит мне найти угол между двумя векторами.»
Скалярное произведение (фактически дает косинус угла между двумя нормализованными векторами)
позволит мне «проецировать» один вектор на другой или задать длину одного вектора в направлении другого».
Скалярное произведение
мог бы сказать мне, какая сила на самом деле помогает объекту двигаться, когда его толкают под углом.»
Скалярный продукт
может сказать мне, насколько «расширяется» векторное поле».
Перекрестное произведение
может дать мне вектор, перпендикулярный двум другим векторам».
Перекрестное произведение
мог сказать мне, какой крутящий момент сила прикладывала к вращающейся системе».
 0003
0003Перекрестное произведение
мог бы сказать мне, насколько это векторное поле «сворачивается».
Перекрестное произведение
На самом деле существует гораздо больше применений, но чем больше я изучаю векторы, тем больше и больше сталкиваюсь с ситуацией, когда мне нужна функция, которая делает в точности что-то, а потом понимаю, что произведение крестов/точек уже сделало именно то, что нужно. что мне было нужно!
$\endgroup$
2
$\begingroup$
Скалярное произведение можно использовать для нахождения длины вектора или угла между двумя векторами.
Перекрестное произведение используется для нахождения вектора, перпендикулярного плоскости, натянутой на два вектора.
$\endgroup$
1
$\begingroup$
Еще два применения, о которых я еще не упоминал: если вы хотите найти площадь параллелограмма, образованного двумя векторами (каждый вектор дает пару параллельных сторон), то вы должны использовать величину векторного произведения два вектора.
Одним из способов использования этого параметра является помощь в определении поверхностного интеграла. Пусть x(u,v) — параметризация поверхности. Тогда в каждой точке можно найти касательные векторы T u = ∂x/∂u и T v = ∂x/∂v. Исходя из идеи линейного приближения, T u и T v определяют касательную плоскость в этой конкретной точке. Рассмотрим параллелограмм, образованный сторонами T u и T v . Неформально мы можем видеть, что каждый элемент области будет |T и х Т в | дю дв. Тогда функция f(u,v), проинтегрированная по этой поверхности, равна ∫∫ f(u,v) |T u x T v | дю дв.
Что касается второго применения, если вы хотите найти объем параллелепипеда, имеющего три вектора a, b, c в качестве сторон, то вы должны использовать величину скалярного тройного произведения |a ⋅ (b x c)|.
$\endgroup$
$\begingroup$
Если вы хотите, чтобы я назвал 2 понятия, которые так часто используются в инженерных расчетах, это будут точечные и перекрестные произведения. Существует несколько интерпретаций точечного и перекрестного произведения, которые можно применять в различных сценариях: угол между векторами, проекция одного вектора в направлении другого, как указано в постах выше.
Существует несколько интерпретаций точечного и перекрестного произведения, которые можно применять в различных сценариях: угол между векторами, проекция одного вектора в направлении другого, как указано в постах выше.
Пройдя несколько шагов выше, стоит помнить интересные факты: перекрестное произведение двух векторов может быть записано как произведение матрицы (кососимметричной) и вектора. Норма перекрестного произведения может быть выражена в виде определителя. Тройное произведение трех векторов, а именно a.(b$\times$c), представляет собой площадь параллелепипеда, и это тройное произведение также можно записать в виде определителя. Этот полезный факт можно использовать для доказательства коллинеарности трех точек (конечно, после представления/рассмотрения их как векторов)
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Умножение вектора
Умножение вектора на вектор дает интересные результаты. известный как векторный внутренний продукт и как векторный внешний продукт.
Требование: Этот материал предполагает знакомство с умножение матриц.
Внутренний продукт вектора
Предположим, что a и b равны векторы, каждый с одинаковым количеством элементов. Затем внутренний продукт из и и б это s .
а’ б = b’ a = с
где
a и b — векторы-столбцы,
каждый из n элементов,
a’ является транспонированием a , что делает a’ вектор-строка,
b’ является транспонированием b , что делает b’ вектор-строка и
s — скаляр; то есть s — это действительное число, а не матрица.
Обратите внимание на этот интересный результат. Произведение двух матриц обычно другая матрица. Однако внутренний продукт двух векторов различен. В результате получается действительное число, а не матрица. Это показано ниже.
| A = | B = |
Тогда,
A ‘ B = 1 0003 A’ B = 1 *0003 A ‘ B 9008 = 1 *0003 A’ B 9008 = 1 *0003 A ‘ B 9008 = 1 *0002 A’ . 10 + 18 = 32 Таким образом, внутренний продукт a’ b равен
равно 32. Примечание. Внутренний продукт также известен как скалярное произведение или как скалярное произведение . Реклама Предположим, что a и b равны
векторы. а б’ = С где В отличие от внутреннего произведения, внешнее произведение двух векторов дает
прямоугольная матрица, а не скаляр. Это показано ниже. Then, ОТВЕТСТВЕННЫ0067 C Внешнее произведение вектора
 Затем внешний продукт из и и б это С .
Затем внешний продукт из и и б это С .
a — это вектор-столбец, содержащий м элементов,
b — вектор-столбец, содержащий n элементов,
b’ является транспонированием b , что делает b’ вектор-строка и
C представляет собой прямоугольник m x n матрица a = b = C = a b’ = V * x V * Y V * Z W * X W * Y W * Z  Таким образом, Матрица C оказывается матрицей перекрестных произведений двух векторов.
Таким образом, Матрица C оказывается матрицей перекрестных произведений двух векторов.
Проверьте свое понимание
Проблемы
Рассмотрим векторы, показанные ниже — a , b , и c
Используя a , b и c , ответить на вопросы ниже.
1. Найдите a’ b ,
внутренний продукт a и b .
2. Найти b c’ ,
внешний продукт b и c .
3. Верно или неверно: b c’ = c b’
Растворы
Термин a’ внутренний продукт, что равно 3. Решение приведено ниже.
a’ b = * a’ b = 0*2 + 1*3 = 3 Термин b c’ является внешним продуктом.
 Вот
матрица 2 x 3, как показано ниже.
Вот
матрица 2 x 3, как показано ниже.b c’ = * b c’ = 2*4 2*5 2*6 3*4 3*5 3*6 = 8 10 12 12 15 18 Выписка б с’ = с b’ ложно.
Обратите внимание, что b является вектором 2 x 1, а c представляет собой вектор 3 x 1.



 3 Распространение на матрицы
3 Распространение на матрицы Рисунок 2). Такое произведение трех векторов называется смешанным.
Рисунок 2). Такое произведение трех векторов называется смешанным. Примеры решения задач
Примеры решения задач 2 Алгебраические свойства векторного произведения
2 Алгебраические свойства векторного произведения

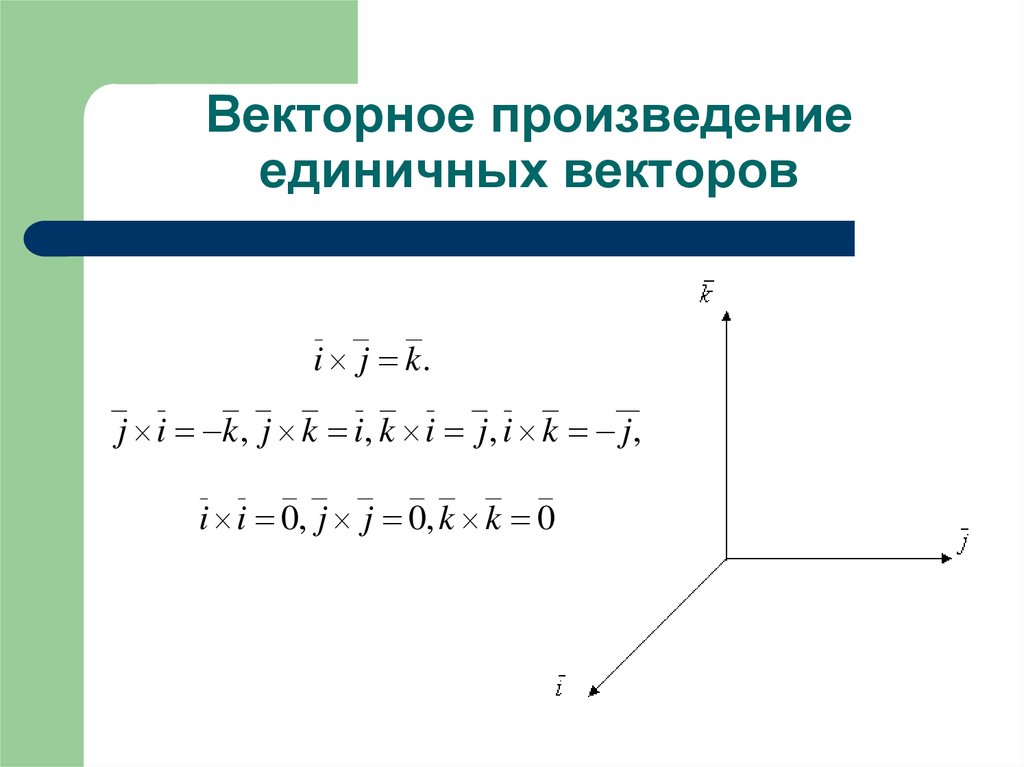 Примеры решения задач
Примеры решения задач 2 Алгебраические свойства векторного произведения
2 Алгебраические свойства векторного произведения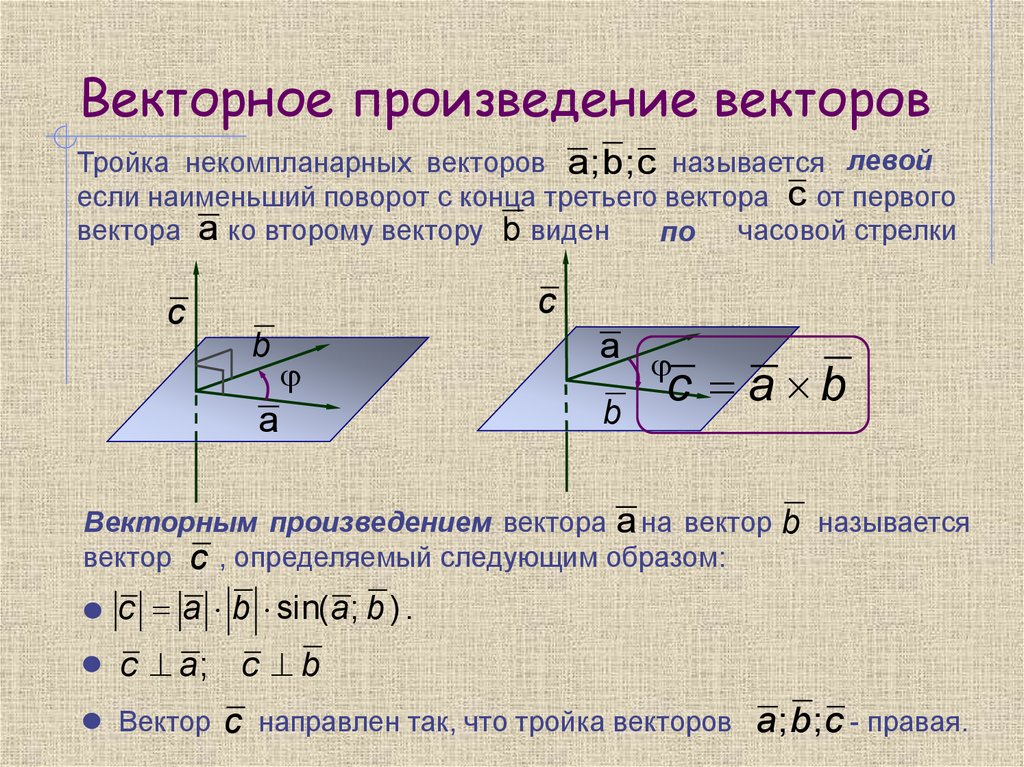

 Примеры решения задач
Примеры решения задач 2 Алгебраические свойства векторного произведения
2 Алгебраические свойства векторного произведения

 Примеры решения задач
Примеры решения задач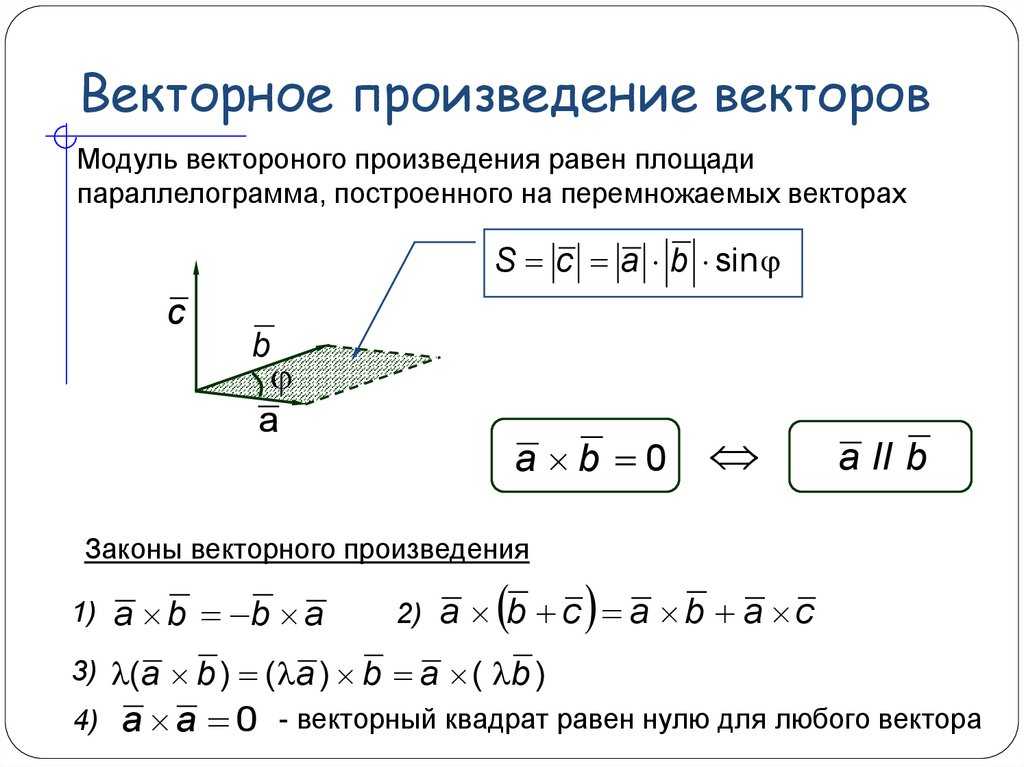 \шляпа i\)= 0
\шляпа i\)= 0