|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает… Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении… Интересное: Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории. Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей… Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 2 из 7Следующая ⇒
Комплект измерительных материалов
2.1. Задания для проведения текущего контроля (содержание всех заданий для текущего контроля) Требования к выполнению заданий: Контрольная работа состоит из 15 вопросов, на каждый необходимо выбрать 1 правильный ответ, некоторые вопросы имеют расчетный характер — для того, чтобы найти правильный ответ, необходимо решить задачу; несколько вопросов требуют умения анализировать графики. Критерии оценивания: отметка: «5» — 90% выполнения -11-12 правильных ответов, «4» — 80% — 9-10 правильных ответов; «3» — 60%-7-8 правильных ответов, «2» -менее 7 правильных ответов.
Контрольная работа по теме «Представление информации. Системы счисления» Вариант 1 1 Система счисления — это: A) представление чисел в экспоненциальной форме; B) представление чисел с постоянным положением запятой; C) способ представления чисел с помощью символов, имеющих определенное количественное значение. 2 Двоичная система счисления имеет основание: A) 10; B) 8; C) 2. 3 Какие цифры используются в семеричной системе счисления? A) 0,1,6; B) 0,8,9; C) 1,6,7. 4 Чему равно число CDXIV в десятичной системе счисления? A) 616; B) 614; C) 414. 5 В какой системе счисления может быть записано число 402? A) в двоичной; B) в троичной; C) в пятеричной. 6 Даны системы счисления: 2-ая, 8-ая, 10-ая и 16-ая. Запись вида 352: A) отсутствует в двоичной системе счисления; B) отсутствует в восьмеричной; C) существует во всех названных системах счисления. 7 Какое минимальное основание должна иметь система счисления, если в ней можно записать числа: 341, 123, 222,111. A) 3; B) 4; C) 5. 8 Как записывается максимальное 4-разрядное положительное число в троичной системе счисления? A) 2222; B) 1111; C) 3333. 9 Когда 2+3 =11? A) в пятеричной системе счисления; B) в троичной системе счисления; C) в четверичной системе счисления. 10 Когда 2*3 =11? A) в пятеричной системе счисления; B) в троичной системе счисления; C) в четверичной системе счисления. 11 Как записывается число 510 в двоичной системе счисления? A) 110; B) 101; C) 111. 12 Какой будет результат вычитание 11000110-1011101: A) 1110001; B) 1101001; C) 1001001.
Контрольная работа по теме «Представление информации. Системы счисления» Вариант 2 1. Система счисления — это: A) представление чисел в экспоненциальной форме; B) представление чисел с постоянным положением запятой; C) способ представления чисел с помощью символов, имеющих определенное количественное значение. 2. Пятеричная система счисления имеет основание: A) 5; B) 3; C) 4. 3. Для представления чисел в восьмеричной системе счисления используются цифры: A) 1-8; B) 0-9; C) 0-7. 4. В какой системе счисления может быть записано число 750? A) в восьмеричной; B) в семеричной; C) в шестеричной. 5. Чему равно число CDXIV в десятичной системе счисления? A) 616; B) 614; C) 414. 6. Даны системы счисления: 2-ая, 8-ая, 10-ая и 16-ая. Запись вида 692: A) отсутствует в десятичной системе счисления; B) отсутствует в восьмеричной; C) существует во всех названных системах счисления. 7. Какие цифры используются в семеричной системе счисления? A) 0,1,6; B) 0,8,9; C) 1,6,7. 8. Какое минимальное основание должна иметь система счисления, если в ней можно записать числа: 432, 768, 568, 243? A) 10; B) 8; C) 9. 9. Когда 2*3 =11? A) в пятеричной системе счисления; B) в троичной системе счисления; C) в четверичной системе счисления. 10. Как записывается максимальное 3-разрядное положительное число в четверичной системе счисления?
A) 333; B) 222; C) 3333. 11. Как записывается число С,316 в десятичной системе счисления? A) 12; B) 11,12; C) 12,18. 12. Какой будет результат сложения 1010111+101100?
A) 11000011; B) 10000011; C) 10100011.
Эталон ответов к Контрольная работау по теме «Представление информации. Системы счисления»
Требования к выполнению заданий: Контрольная работа состоит из 20 вопросов, на каждый необходимо выбрать 1 правильный ответ, некоторые вопросы имеют расчетный характер — для того, чтобы найти правильный ответ, необходимо решить задачу; несколько вопросов требуют умения анализировать графики. Критерии оценивания: отметка: «5» — 90% выполнения -19-20 правильных ответов, «4» — 80% — 16-18 правильных ответов; «3» — 60%-12-15 правильных ответов, «2» -менее 12 правильных ответов. ⇐ Предыдущая1234567Следующая ⇒ Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… |
|||
Кодирование информации. Системы счисления презентация, доклад
Тест по теме:
«Кодирование информации.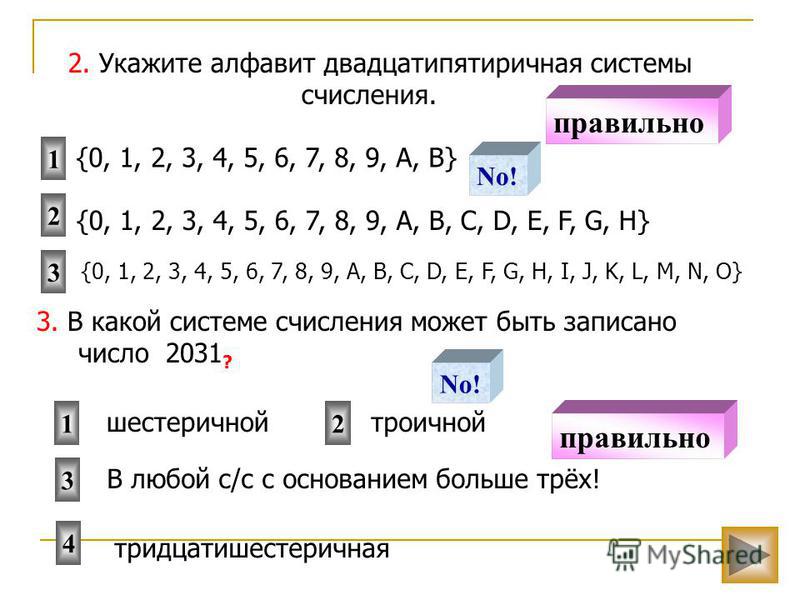
Системы счисления»
Вариант №1
Вариант №2
В зависимости от способа изображения чисел системы счисления делятся на:
A) арабские и римские;
Б) позиционные и непозиционные;
B) представление в виде ряда и в виде разрядной сетки.
Вариант №1
Двоичная система счисления имеет основание:
А) 10;
Б) 8;
В) 2.
Для представления чисел в шестнадцатеричной системе счисления используются:
А) цифры 0 — 9 и буквы A-F;
Б) буквы А — Q;
В) числа 0-15.
В какой системе счисления может быть записано число 402?
А) в двоичной;
Б) в троичной;
В) в пятеричной.
5. Чему равно число DXXVII в десятичной системе счисления?
А) 527;
Б) 499;
В) 474.
6. Недостатком непозиционной системы счисления является:
A) сложно выполнять арифметические операции;
Б) ограниченное число символов, необходимых для записи числа;
B) различное написание цифр у разных народов.
Даны системы счисления: 2-ая, 8-ая,
10-ая и 16-ая. Запись вида 352:
А) отсутствует в двоичной системе счисления;
Б) отсутствует в восьмеричной;
В) существует во всех названных системах счисления.
Какие цифры используются в шестеричной системе счисления?
А) 0,6,5,2;
Б) 8,6,1,0;
В) 0,3,2,1.
9. Какое минимальное основание должна иметь система счисления, если в ней можно записать числа:
341, 123, 222,111.
А) 3;
Б) 4;
В) 5.
Когда 2*2 =11?
А) в двоичной системе счисления;
Б) в троичной системе счисления;
В) в четверичной системе счисления.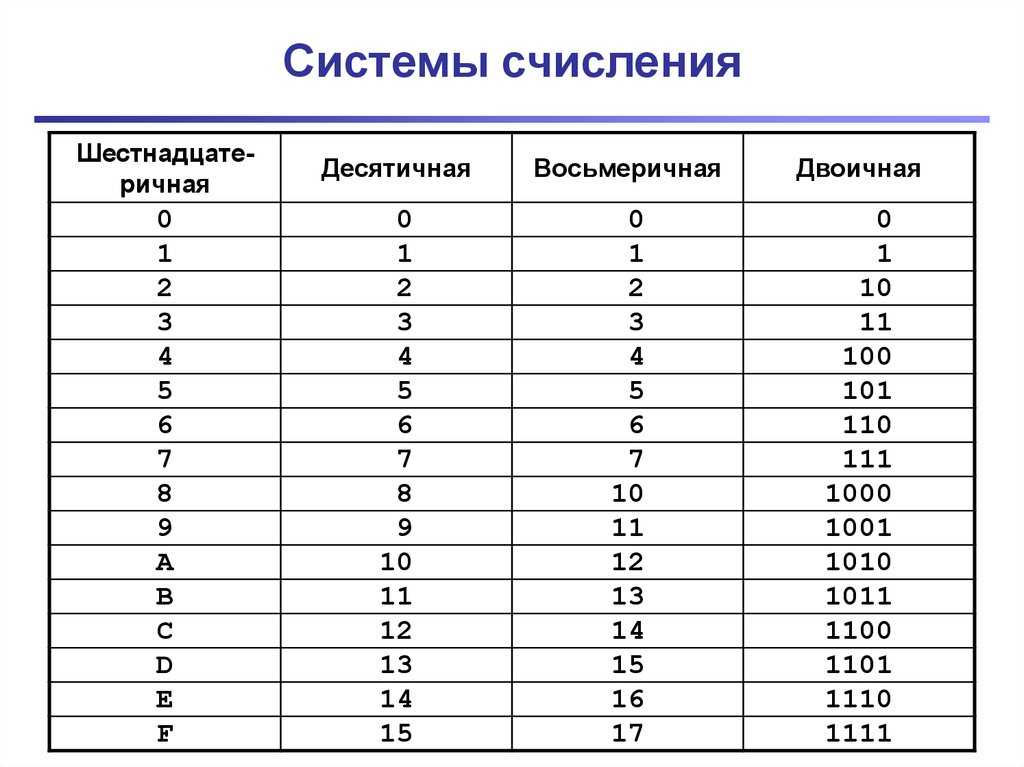
11. Как записывается максимальное 4-разрядное положительное число в троичной системе счисления?
А) 2222;
Б) 1111;
В) 3333.
Цифры — это:
А) символы, участвующие в записи числа;
Б) буквы, участвующие в записи числа;
В) пиктограммы, участвующие в записи числа.
Система счисления — это:
A) представление чисел в экспоненциальной форме;
Б) представление чисел с постоянным положением запятой;
B) способ представления чисел с помощью символов, имеющих определенное количественное значение.
Вариант №2
Пятеричная система счисления имеет основание:
А) 5;
Б) 3;
В) 4.
3. Для представления чисел в восьмеричной системе счисления используются цифры:
А) 1-8;
Б) 0-9;
В) 0-7.
В какой системе счисления может быть записано число 750?
А) в восьмеричной;
Б) в семеричной;
В) в шестеричной.
Чему равно число CDXIV в десятичной системе счисления?
А) 616;
Б) 614;
В) 414.
Преимуществом позиционной системы счисления является:
A) сложно выполнять арифметические операции;
Б) ограниченное число символов, необходимых для записи числа;
B) различное написание цифр у разных народов.
Даны системы счисления: 2-ая, 8-ая, 10-ая и 16-ая. Запись вида 692:
А) отсутствует в десятичной системе счисления;
Б) отсутствует в восьмеричной;
В) существует во всех названных системах счисления.
Какие цифры используются в семеричной системе счисления?
А) 0,1,6;
Б) 0,8,9;
В) 1,6,7.
9. Какое минимальное основание должна иметь система счисления, если в ней можно записать числа:
432, 768, 568, 243?
А) 10;
Б) 8;
В) 9.
Когда 2*3 = 11?
А) в пятеричной системе счисления;
Б) в троичной системе счисления;
В) в четверичной системе счисления.
Как записывается максимальное
3-разрядное положительное число в
четверичной системе счисления?
А) 333;
Б) 222;
В) 3333.
Число — это:
A) ряд символов;
Б) обозначение некоторой величины;
B) набор знаков.
Ответ к тесту:
Скачать презентацию
Тест по информатике на тему «Системы счисления» | Тест по информатике и икт (10 класс) по теме:
ТЕСТ по Информатике
Вариант № 1.
- В зависимости от способа изображения чисел системы счисления делятся на:
А) арабские и римские;
Б) позиционные и непозиционные;
В) представление в виде ряда и в виде разрядной сетки.
- Двоичная система счисления имеет основание:
А) 10; Б) 8; В) 2.
- Для представления чисел в шестнадцатеричной системе счисления используются:
А) цифры 0-9 и буквы A-F;
Б) буквы A-Q; В) числа 0-15.
- В какой системе счисления может быть записано число 402?
А) в двоичной; Б) в троичной; В) в пятеричной.
- Недостатком непозиционной системы счисления является:
А) сложно выполнять арифметические операции;
Б) ограниченное число символов, необходимых для записи чисел;
В) различное написание цифр у разных народов.
- Даны системы счисления: 2-ая, 8-ая, 10-ая, 16-ая.
 Запись вида 352:
Запись вида 352:
А) отсутствует в двоичной системе счисления;
Б) отсутствует в восьмеричной;
В) существует во всех названных системах счисления.
- Какие цифры используются в шестнадцатеричной системе счисления?
А) 0,6,5,2. Б) 8,6,1,0. В) 0,3,2,1.
- Какое минимальное основание должна иметь система счисления, если в ней можно записать числа: 341, 123, 222, 111.
А) 3; Б) 4; В) 5.
- Когда 2*2=11?
А) в двоичной системе счисления;
Б) в троичной системе счисления;
В) в четверичной системе счисления.
- Как записывается максимальное 4-разрядное положительное число в троичной системе счисления?
А) 2222; Б) 1111; В) 3333.
- Цифры – это:
А) символы, участвующие в записи чисел;
Б) буквы, участвующие в записи чисел;
В) пиктограммы, участвующие в записи чисел.
ТЕСТ по Информатике
Вариант № 2.
- Система счисления — это:
А) представление чисел в экспоненциальной форме;
Б) представление чисел с постоянным положением запятой;
В) способ представления чисел с помощью символов, имеющих определенное количественное значение.
- Восьмеричная система счисления имеет основание:
А) 10; Б) 8; В) 2.
- Для представления чисел в восьмеричной системе счисления используются:
А) цифры 0-9 и буквы A-F;
Б) цифры 0-8; В) цифры 0-7.
- В какой системе счисления может быть записано число 750?
А) в восьмеричной; Б) в семеричной; В) в шестнадцатеричной.
- Преимуществом позиционной системы счисления является:
А) сложно выполнять арифметические операции;
Б) ограниченное число символов, необходимых для записи чисел;
В) различное написание цифр у разных народов.
- Даны системы счисления: 2-ая, 8-ая, 10-ая, 16-ая. Запись вида 692:
А) отсутствует в десятичной системе счисления;
Б) отсутствует в восьмеричной;
В) существует во всех названных системах счисления.
- Какие цифры используются в шестнадцатеричной системе счисления?
А) 0,1,6. Б) 0,8,9. В) 1,6,7.
- Какое минимальное основание должна иметь система счисления, если в ней можно записать числа: 432, 768, 568, 243.
А) 10; Б) 8; В) 9.
- Когда 2*3=11?
А) в пятеричной системе счисления;
Б) в троичной системе счисления;
В) в четверичной системе счисления.
- Как записывается максимальное 4-разрядное положительное число в четверичной системе счисления?
А) 333; Б) 222; В) 3333.
- Число – это:
А) ряд символов;
Б) обозначение некоторой величины;
В) набор знаков.
Тестирование
по теме «Системы счисления»
ФИО____________________ Группа_______________
Вопросы | №1 | №2 | №3 | №4 | №5 | №6 | №7 | №8 | №9 | №10 | №11 |
Ответы | |||||||||||
ОЦЕНКА | Преподаватель | _________Смирнова С.С. |
Тестирование
по теме «Системы счисления»
ФИО____________________ Группа_______________
Вопросы | №1 | №2 | №3 | №4 | №5 | №6 | №7 | №8 | №9 | №10 | №11 |
Ответы | |||||||||||
ОЦЕНКА | Преподаватель | _________Смирнова С. |
Тестирование
по теме «Системы счисления»
ФИО____________________ Группа_______________
Вопросы | №1 | №2 | №3 | №4 | №5 | №6 | №7 | №8 | №9 | №10 | №11 |
Ответы | |||||||||||
ОЦЕНКА | Преподаватель | _________Смирнова С.С. |
Тестирование
по теме «Системы счисления»
ФИО____________________ Группа_______________
Вопросы | №1 | №2 | №3 | №4 | №5 | №6 | №7 | №8 | №9 | №10 | №11 |
Ответы | |||||||||||
ОЦЕНКА | Преподаватель | _________Смирнова С. |
Тестирование
по теме «Системы счисления»
ФИО____________________ Группа_______________
Вопросы | №1 | №2 | №3 | №4 | №5 | №6 | №7 | №8 | №9 | №10 | №11 |
Ответы | |||||||||||
ОЦЕНКА | Преподаватель | _________Смирнова С.С. |
Тестирование
по теме «Системы счисления»
ОТВЕТЫ
Вариант 1
Вопросы | №1 | №2 | №3 | №4 | №5 | №6 | №7 | №8 | №9 | №10 | №11 |
Ответы | Б | В | А | В | А | А | В | Б | Б | А | А |
ОЦЕНКА | Преподаватель | _________Смирнова С. |
Тестирование
по теме «Системы счисления»
ОТВЕТЫ
Вариант 2
Вопросы | №1 | №2 | №3 | №4 | №5 | №6 | №7 | №8 | №9 | №10 | №11 |
Ответы | В | А | В | А | Б | Б | А | В | В | А | Б |
ОЦЕНКА | Преподаватель | _________Смирнова С.С. |
Какое минимальное число можно записать в двоичной системе счисления 6 цифрами
ГДЗ по информатике 10 класс учебник Босова § 2 Подходы к измерению информации
Неопределенность знания о результате некоторого события (бросание монеты или игрального кубика, вытаскивание жребия и др. ) — это количество возможных результатов.
) — это количество возможных результатов.
2. В чём состоит суть содержательного подхода к определению количества информации? Что такое бит с точки зрения содержательного подхода?
В содержательном подходе количество информации, заключенное в сообщении, определяется объемом знаний, который это сообщение несет получающему его человеку.
Сообщение, уменьшающее неопределенность знания в два раза, несет 1 бит информации. Как пример содержит знание: да или нет
3. Паролем для приложения служит трёхзначное число в шестнадцатеричной системе счисления. Возможные варианты пароля: 189 101 654 FFE 123 А41 880 391 110 125 Ответ на какой вопрос (см. ниже) содержит 1 бит информации?
1) Это число записано в двоичной системе счисления?
2) Это число записано в четверичной системе счисления?
3) Это число может быть записано в восьмеричной системе счисления?
4) Это число может быть записано в десятичной системе счисления?
5) Это число может быть записано в шестнадцатеричной системе счисления?
4. 5 = 32, если берем целые неотрицательные числа, то диапазон определен от 0 до 31, наименьшее и наибольшие числа
5 = 32, если берем целые неотрицательные числа, то диапазон определен от 0 до 31, наименьшее и наибольшие числа
5. Какое максимальное количество вопросов достаточно задать вашему собеседнику, чтобы точно определить день и месяц его рождения?
Два вопроса: Какой месяц? Какой день месяца?
6. В чём состоит суть алфавитного подхода к измерению информации? Что такое бит с точки зрения алфавитного подхода?
Алфавитный подход позволяет вычислить количество информации, содержащейся в тексте, сложив информационные объёмы каждого символа, при этом содержание текста не учитывается.
7. Закодируйте фразу «ALL IN GOOD TIME» кодом Бодо и восьмиразрядным компьютерным кодом. Сравните полученные информационные объёмы текста.
.. o.. oo oo. oo oo. .. .oo oo .oo .o .o. .. ooo .. ooo .o ooo o. o.o .. .oo oo .o. .. .o.
(I=K*i ,K=65 символов, i= 5 бит, I= 65*5=325)
010000010100110001001100 0100100101001110 01000111010011110100111101000100 01010100
(I=K*i, K=104 символов, i= 8 бит,I= 104*8=832)
8. Какие единицы используются для измерения объёма информации, хранящейся на компьютере?
Какие единицы используются для измерения объёма информации, хранящейся на компьютере?
Бит, байт, килобайт, мегабайт, гигабайт, терабайт.
9. Объём сообщения, содержащего 11 264 символа, равен 11 Кбайт. Определите максимальную мощность алфавита, который мог быть использован для кодирования этого сообщения? Какова минимальная мощность алфавита, использование которого привело к такому же информационному объёму закодированного сообщения?
90112 = 11264 * i => i = 8
10. В школе 750 учащихся, коды учащихся записаны в школьной информационной системе с помощью минимального количества бит. Каков информационный объём в байтах сообщения о кодах 180 учащихся начальных классов?
Надо найти минимальное количество бит, для записи 750 учащихся. Количество бит — целое, а количество вариантов записанное заданным количеством бит
Надо найти минимальное b, чтобы N было больше 750.
Значит, минимальное кол-во бит, при помощи которого можно записать коды 750 учащихся b = 10.
Соответственно информационный объем сообщения о кодах 180 учащихся = 180 * 10 = 1800 бит = (1800 / 8) байт = 225 байт
11. В школьной базе данных каждый ученик получил идентификатор, состоящий ровно из б символов. В качестве символов используются все заглавные буквы русского алфавита, кроме «Ё», «Ы», «Ъ» и «Ь», а также все десятичные цифры за исключением цифры 0. Каждый такой идентификатор в информационной системе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Определите объём памяти, необходимый для хранения в этой системе 180 идентификаторов учащихся начальных классов. Ответ выразите в килобайтах.
Общее количество символов для записи идентификатора = 29+9=38
Для кодирования одного символа необходимо log(2)38 ≈ 6 бит.
Для записи одного идентификатора требуется 6*6 бит = 36 бит = 36/8 байт ≈ 5 байт
Для хранения 180 идентификаторов потребуется 5*180 байт = 900 байт = 900/1024 Кбайт ≈ 0,9 Кбайт
12. В ходе телевизионного шоу проводится СМС-голосование: каждый телезритель отдаёт свой голос за одного из 12 артистов-участников шоу, отправляя сообщение с его номером. Голос каждого телезрителя, отданный за того или иного участника, кодируется одинаковым и минимально возможным количеством бит и сохраняется для подведения итогов. За время телевизионного шоу в голосовании приняли участие 163 840 зрителей. Определите объём сохранённой информации о голосовании и выразите его в килобайтах.
В ходе телевизионного шоу проводится СМС-голосование: каждый телезритель отдаёт свой голос за одного из 12 артистов-участников шоу, отправляя сообщение с его номером. Голос каждого телезрителя, отданный за того или иного участника, кодируется одинаковым и минимально возможным количеством бит и сохраняется для подведения итогов. За время телевизионного шоу в голосовании приняли участие 163 840 зрителей. Определите объём сохранённой информации о голосовании и выразите его в килобайтах.
13. При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 6 символов и содержащий только символы из шестибуквенного набора А, В, С, D, Е, F. Для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей и все символы кодируются одинаковым и минимально возможным количеством бит. Кроме собственно пароля для каждого пользователя в системе хранятся дополнительные сведения, занимающие 15 байт. 3 = 8. Значит 3 бит памяти достаточно для кодировки 1 символа.
3 = 8. Значит 3 бит памяти достаточно для кодировки 1 символа.
Всего символов 6. 6*3 = 18. 18/8 = 3 (округляем до целого) байт нужно для сохранения пароля.
Шестнадцатеричная система счисления
Познавательное
Шестнадцатеричная система (англ. — Hexadecimal system ) — это базовая система счисления с снованием 16. Она, наряду с десятичной и двоичной, является одной из наиболее часто встречающихся систем счисления в мире электроники и программирования. Важно понимать, как она работает, потому что во многих случаях имеет смысл представлять число в ней, а не в двоичной или десятичной.
Шестнадцатеричная система счисления — позиционная система счисления по основанию 16.
Википедия
Существует 16 возможных цифр, которые используют для представления чисел. 10 числовых значений, которые вы привыкли видеть в десятичных числах: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9; эти значения по-прежнему представляют то же значение, что и в десятичной системе. Остальные шесть цифр представлены как A, B, C, D, E и F, которые соответствуют числам 10, 11, 12, 13, 14 и 15.
Остальные шесть цифр представлены как A, B, C, D, E и F, которые соответствуют числам 10, 11, 12, 13, 14 и 15.
Возможно, Вы столкнетесь с представлением чисел от 10 до 15 в верхнем и нижнем регистрах. Оба варианта считаются верными. Например, A3F — это то же число, что и a3f.
Эта таблица показывает какой шестнадцатеричной цифре эквивалентно значение в десятичном и двоичном формате.
| Десятичный (основание 10) | Двоичный (основание 2) | Шестнадцатеричный (основание 16) |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | А |
| 11 | 1011 | B |
| 12 | 1100 | С |
| 13 | 1101 | D |
| 14 | 1110 | Е |
| 15 | 1111 | F |
таблица 16 ричной системы счисления
Перевод из шестнадцатеричной системы и в нее
Преобразование из десятичной в шестнадцатеричную систему и обратно
Чтобы перевести десятичное число в шестнадцатеричное, нужно следовать простому алгоритму преобразования:
- Делим десятичное число на 16.

- Записываем остаток и переводим его в шестнадцатеричный формат.
- Делим результат прошлого действия снова на 16.
- Повторяем, пока в результате мы не получим 0.
- Переписываем записанные остатки в обратном порядке.
- Пример:
Чтобы перевести шестнадцатеричное число в десятичное, нужно каждую цифру с конца этого числа умножить на 16 в степени, соответствующей разряду этой цифры.
Переведем шестнадцатеричное число 5EB в десятеричную систему
5EB = (5 × 16²) + (14 × 16¹) + (11 × 16⁰) = 1515
Преобразование из двоичной в шестнадцатеричную систему и обратно
Чтобы перевести двоичное число в шестнадцатеричное, нужно разделить его на группы по 4 цифры и заменить каждую группу на эквивалент из таблицы
Переведем двоичное число 1010000011111 в шестнадцатеричную систему
Для этого разбиваем число на группу по 4 цифры: 0001 0100 0001 1111
0001 = 1; 0100 = 4; 0001 = 1; 1111 = F
Чтобы сделать обратное преобразование, нужно просто каждую цифру шестнадцатеричного числа заменить на эквивалент по таблице
Переведем шестнадцатеричное число 141F в двоичную систему
1= 0001; 4 = 0100; 1 = 0001; F = 1111
Использование шестнадцатеричной системы
По большей части, шестнадцатеричные коды используются во многих областях вычислительной техники для сокращения двоичного кода до более понятной формы. Шестнадцатеричный код переводится в двоичный для использования на компьютере. Вот некоторые примеры использования шестнадцатеричного кода:
Шестнадцатеричный код переводится в двоичный для использования на компьютере. Вот некоторые примеры использования шестнадцатеричного кода:
- Ссылки на цвета в HTML и CSS
- Язык ассемблера
- Сообщения об ошибках
Цвета
Hex система счисления может использоваться для представления цветов на сайтах и в программах редактирования изображений в формате #RRGGBB (# = показатель того, что число было записано в шестнадцатеричном формате, RR = красный, GG = зеленый, BB = синий). Этот система использует две шестнадцатеричных цифры для каждого цвета, например, #AA3300.
Как одна шестнадцатеричная цифра представляет 4 бита, так две шестнадцатеричные цифры вместе составляют 8 бит (1 байт). Значения для каждого цвета находятся в диапазоне от 00 до FF. В двоичной системе, 00 — это 00000000, а FF — это 11111111. Это дает 256 возможных значений для каждого из трех цветов (256 красных х 256 зеленых х 256 синих), а в сумме это больше 16 миллион цветов.
- #FF0000 будет самым чистым красным цветом — Максимум красного, 0 зеленого и 0 синего.

- Черный это #000000 — ни красного, ни зеленого, ни синего.
- Белый — это #FFFFFF — при смешении всех цветов.
Инженер по телевизионному оборудованию Электрика и электроника, это не только моё хобби, но и работа
Тест по информатике Представление чисел в компьютере для 8 класса
Тест по информатике Представление чисел в компьютере для 8 класса с ответами. В тесте 2 варианта, каждый включает в себя 7 заданий.
Вариант 1
1. Если число положительное, то в знаковый разряд помещается
2. Числом в нормальной форме с нормализованной мантиссой (правильной дробью, имеющей после запятой цифру, отличную от нуля) является:
1) 0,341 x 10 9
2) 1997
3) 213,5629
4) 0,002311
3. Беззнаковым 8-разрядным представлением числа 6310 является
1) 11111100
2) 111111
3) 00000101
4) 00111111
4. Какие из чисел можно сохранить в 8-разрядном беззнаковом формате?
5. При записи числа в форме A = ± m x q p , где m — это
При записи числа в форме A = ± m x q p , где m — это
1) порядок числа
2) основание системы счисления
3) мантисса
4) само вещественное число
6. Укажите десятичный эквивалент числа, прямой код которого 01001100 записан в 8-разрядном формате со знаком
1) 66
2) 76
3) -76
4) верного ответа в предложенных вариантах нет
7. Укажите число, записанное в естественной форме
1) 0,38005611 x 10 2
2) 1,257824E+5
3) 0,01357
4) нет числа, записанного в естественной форме
Вариант 1
1. Если число отрицательное, то в знаковый разряд помещается
2. Числом в нормальной форме с нормализованной мантиссой (правильной дробью, имеющей после запятой цифру, отличную от нуля) является
1) 7815
2) 2783,00029
3) 0,03428
4) 0,401 x 10 7
3. Беззнаковым 8-разрядным представлением числа 4510 является
1) 00101101
2) 101101
3) 10110100
4) 00000101
4. Какие из чисел можно сохранить в 8-разрядном беззнаковом формате?
Какие из чисел можно сохранить в 8-разрядном беззнаковом формате?
5. При записи числа в форме A = ± m x q p , где q — это
1) мантисса
2) само вещественное число
3) порядок числа
4) основание системы счисления
6. Укажите десятичный эквивалент числа, прямой код которого 00010101 записан в 8-разрядном формате со знаком
1) 21
2) 34
3) -21
4) верного ответа в предложенных вариантах нет
7. Укажите число, записанное в естественной форме
1) 2010,0102
2) 1,784824E+5
3) 95400611 x 10 2
4) среди предложенных вариантов нет числа в естественной форме
Ответы на тест по информатике Представление чисел в компьютере для 8 класса
Вариант 1
1-4
2-1
3-4
4-14
5-3
6-2
7-3
Вариант 2
1-2
2-4
3-1
4-23
5-4
6-1
7-1
Страница не найдена | АКВТ
Запрошенную информацию найти не удалось. Возможно, будет полезен поиск по сайту или приведённые ниже ссылки.
Возможно, будет полезен поиск по сайту или приведённые ниже ссылки.
Не нашли то, что искали?
SearchСтраницы
- QR код для оказания благотворительной помощи колледжу
- Безопасный Интернет
- Виртуальный тур
- Фотогалерея
- «Мы — Добровольцы!»
- АКВТ на Дне Победы!
- АКВТ на митинг-концерте, посвященном Крымской весне
- Вручение дипломов 2016
- Встречаем Олимпийский огонь
- День народного единства 2015
- День народного единства 2017
- День Открытых дверей 2015
- День Открытых Дверей 2016
- День открытых дверей в АКВТ 2017
- КРЫМ! Мы с тобой!
- Мы — добровольцы 2016!
- Награждение победителей фестиваля «Мисс Зимнее Очарование»
- Новогодний концерт «АКВТ в Джунглях»
- Празднование Масленицы 2016
- Прогноз безопасности в АКВТ!
- Студенты АКВТ и члены военно-патриотического клуба «Покров» на масленичных забавах
- Торжественное открытие мемориала «Журавли»
- Торжественный митинг (Хулхута)
- Фестиваль «Мисс Зимнее Очарование»
- Фестиваль студенческой науки 2016
- Шарик Радости
- Ярмарка вакансий 2016
- Фотогалерея
- Все новости
- Дистанционное обучение
- Информационная безопасность
- Курс «Основы web-дизайна»
- Курс «Основы компьютерной грамотности.
 Комплексная программа»
Комплексная программа» - Курс «Основы разработки web-сайта»
- Министерство образования и науки Российской Федерации
- Обратная связь
- Обращения граждан
- Партнеры
- Служба содействия трудоустройству выпускников
- Политика в отношении обработки персональных данных
- Поступающим
- Приемная кампания 2022
- Подача документов онлайн
- Подача документов через операторов почтовой связи
- Обращение директора
- Реализуемые специальности
- Правила приёма
- Контрольные цифры приема на 2022 год
- Количество поданных заявлений
- Информирование поступающих
- Заявление
- Информация о результатах приема по каждой профессии, специальности среднего профессионального образования
- Приказы о зачислении
- Информация о дополнительном наборе
- Платное обучение
- Общежитие
- Подготовительные курсы
- Заявка на поступление на подготовительные курсы
- Схема проезда
- Горячая линия по вопросам приема, в том числе для лиц с ОВЗ и инвалидов
- Горячая линия Минобрнауки
- Information for Foreign Citizens (Training of foreign citizens)
- Обучение иностранных граждан
- Приемная кампания 2022
- Предупреждение распространения коронавирусной инфекции
- Профилактика новой коронавирусной инфекции COVID-19
- Преподавателям
- График учебного процесса
- Расписание занятий
- График консультаций для студентов заочного отделения 2 семестр 2018-2019 учебного года
- Расписание занятий для студентов заочного отделения
- Оформление документации
- Преподавателю
- Заведующему кабинетом/лабораторией
- Куратору
- Руководителю курсового/дипломного проектирования
- Аттестация преподавателей
- Нормативные документы, регламентирующие деятельность преподавателей
- Конкурсы
- Всероссийский конкурс социально рекламы в области формирования культуры здорового и безопасного образа жизни «СТИЛЬ ЖИЗНИ — ЗДОРОВЬЕ! 2020»
- Полезные вкладки
- Родителям
- Методические материалы для родителей и классных руководителей по здоровому образу жизни
- О чем молчит подросток
- Отцовство — твой главный жизненный проект
- Сведения об образовательной организации
- Герои Великой Победы в миниатюре
- Диорама 1 «Полундра!»
- Диорама 2 «Полигон»
- Диорама 3 «Операция «Уран»
- Диорама 4 «Тигры перед боем»
- Диорама 5 «Герои Белостока»
- Диорама 6 «Школьник Свердловска»
- Международное сотрудничество
- Наставничество
- Основные сведения
- Студенческий спортивный клуб СПО
- Федеральный проект «Молодые профессионалы»
- Аттестаты о присвоении статуса центра проведения демонстрационного экзамена
- Банк фотоматериалов
- Графики работы мастерских
- Дизайн-проект мастерских
- Дополнительное профессиональное образование
- Дополнительные образовательные программы
- Локальные акты по проекту
- Программы повышения квалификации
- Программы профессиональной переподготовки
- Профессиональное обучение
- Ссылки на репортажи, публикации в СМИ
- Структура и органы управления колледжем
- Документы
- Антимонопольный комплаенс
- Нормативные акты Министерства образования и науки Астраханской области
- Устав колледжа
- Лицензия на осуществление образовательной деятельности
- Cвидетельство о государственной аккредитации
- Локальные нормативные акты
- Документы, регламентирующие деятельность колледжа в целом
- Документы, регламентирующие образовательную и воспитательную деятельность
- Проекты документов
- Единый план работы колледжа
- Отчет о результатах самообследования
- Документ о порядке оказания платных образовательных услуг
- Предписания органов, осуществляющих государственный контроль в сфере образования
- Установление размера платы, взимаемой с родителей за присмотр и уход за детьми
- Руководство.
 Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав - Образование
- Информация о реализуемых образовательных программах
- Основные профессиональные образовательные программы
- Календарный учебный график
- Численность обучающихся по реализуемым образовательным программам
- Язык, на котором осуществляется образование
- Информация о результатах приема, перевода, восстановления и отчисления студентов
- Направления и результаты научно-исследовательской деятельности
- Образовательные стандарты
- Материально-техническое обеспечение и оснащенность образовательного процесса
- Стипендии и меры поддержки обучающихся
- Платные образовательные услуги
- Финансово-хозяйственная деятельность
- Вакантные места для приема (перевода) обучающихся
- Противодействие коррупции
- Доступная среда. Организация получения образования студентами с ОВЗ
- Информация по защите прав обучающихся
- Герои Великой Победы в миниатюре
- Студентам
- Кружки, секции и студии АКВТ
- Студенческое самоуправление
- Волонтерское движение АКВТ
- Студенческая газета «Студ&ты»
- График учебного процесса
- Расписание занятий
- График консультаций для студентов заочного отделения 2 семестр 2018-2019 учебного года
- Расписание занятий для студентов заочного отделения
- Учебно-методические материалы
- Компьютерные системы и комплексы
- Программирование в компьютерных системах
- Сетевое и системное администрирование
- Информационные системы и программирование
- Информационная безопасность автоматизированных систем
- Обеспечение информационной безопасности автоматизированных систем
- Техническая эксплуатация и обслуживание электрического и электромеханического оборудования
- Автоматизация технологических процессов и производств
- Оснащение средствами автоматизации технологических процессов и производств
- Специальности НПО
- Заочное
- Государственная Итоговая Аттестация
- Трудоустройство
- Сдать ЕГЭ
- Библиотека
- Библиотека сегодня
- Информационные ресурсы свободного доступа
- Электронно-библиотечная система
- Доска объявлений библиотеки
- Полезные вкладки
- 8 мифов о наркотиках
- «Народная дружина города Астрахани»
- Ловушки для пешеходов
- Противодействие терроризму
Записи
- Анонс
- АНОНС.
 Международная акция «Тест по истории Великой Отечественной войны»
Международная акция «Тест по истории Великой Отечественной войны» - АНОНС. О проведении VI Международной просветительской акции «Большой этнографический диктант-2021»
- Профессионально-техническому образованию посвящается…
- Объявление по собраниям для студентов нового набора
- АНОНС.
- Новости
- Разговоры о важном
- Региональная научно-практическая конференция «МЕДИАЦИЯ КАК АЛЬТЕРНАТИВА КОНФРОНТАЦИИ»
- ГБПОУ АО «АКВТ» проводит дополнительный набор
- Каспийский молодёжный образовательный форум «СЕЛИАС»
- «Поделись своим знанием»
- Мастер года 2022
- Всероссийская акция «Поделись своим знанием»
- День знаний 2022!
- Лекция-беседа на тему «Профилактика терроризма и экстремизма в молодёжной среде»
- Праздничные мероприятия 1 сентября 2022 года
- Федеральный марафон «Знание»
- Объявление по собраниям для студентов нового набора
- День Государственного флага Российской Федерации
- Запущена регистрация на Всероссийскую медиашколу «Без срока давности 3.
 0» для студентов педагогических вузов и педагогических работников сферы гражданско-патриотического воспитания
0» для студентов педагогических вузов и педагогических работников сферы гражданско-патриотического воспитания - Курсы для школьников «Погружение в специальность»
- Вручение дипломов выпускникам 2022 года!
- Демонстрационный экзамен в соответствии со стандартами Worldskills Russia
- Великий государь великого государства: 350-летие со дня рождения Петра I
- Вместе — ЗА здоровье нации!
- Линейка памяти и скорби
- Открытие мемориальной доски генерал-полковнику Тутаринову Ивану Васильевичу
- XV Международный конкурс ВКР с использованием программных продуктов 1С
- Студент 1 курса АКВТ в составе археологической экспедиции принял участие в «Вахте памяти»
- День России!
- Студенты АКВТ на областной конференции «IT-технологии XXI века: вызовы, становление, развитие»
- Студенты АКВТ на финале Всероссийских просветительских игр
- «Цени своё здоровье»
- Стань Студентом года — 2022!
- Памятка «Безопасность детства»
- V Региональный чемпионат профессионального мастерства «Абилимпикс»
- Итоги областной олимпиады по информатике!
- Городская легкоатлетическая эстафета посвящённая Дню победы
- Военная академия воздушно-космической обороны
- День Победы!
- Праздничный концерт «День Победы»
- ГОРЯЧАЯ ЛИНИЯ В СИСТЕМЕ СПО НА БАЗЕ МИНИСТЕРСТВА ОБРАЗОВАНИЯ И НАУКИ АСТРАХАНСКОЙ ОБЛАСТИ
- Как провести майские праздники вместе с Пушкинской картой
- Праздник Весны и Труда
- Субботник в АКВТ
- Финал по подтягиваниям «Я-Чемпион»
- Спартакиада ПОО среди учащихся по стритболу
- Областная практическая конференция по дисциплинам ОБЖ, БЖ «Астраханская область территория безопасности»
- Акция «Чистые игры»
- Полуфинальный этап соревнований по подтягиваниям «Я-Чемпион»
- Товарищеская игра по мини-футболу
- Интерактивная лекция «Здоровый образ жизни»
- Марафон «Новые горизонты»
- День открытых дверей!
- Турнир по мини-футболу на кубок «Дружбы народов»
- День открытых дверей в АКВТ
- День здоровья в стенах АКВТ!
- Патриотическая акция, посвященная восьмилетию со дня провозглашения Донецкой Народной Республики
- Родительские собрания в группах 1-3 курсов
- Итоги отборочного тура олимпиады по информатике!
- Первенство студенческой лиги по пулевой стрельбе из пневматического оружия
- Агрегатор профориентационных возможностей
- «Всероссийский урок добровольчества»
- Встреча с ветеранами боевых действий
- День открытых дверей
- Профориентационный проект «Загляни за горизонт»
- Акция «Сообщи, где торгуют смертью»
- Областной профориентационный форум «Топ профессий на селе»
- Без срока давности
- Профилактика заболевания туберкулезом
- День открытых дверей в АКВТ 2022
- Методическое объединение преподавателей ССУзов Астраханской области
- Праздничный концерт под девизом «Zа Мир! Zа Россию! Zа Президента!»
- Встреча с представителем Областного центра крови
- Начни свой путь из кандидата в бойцы студенческих отрядов!
- Встреча студентов с медицинским психологом
- Реализация программы «Пушкинская карта»
- С праздником прекрасная половина Астраханского колледжа вычислительной техники!
- С Международным женским днем!
- #МЫВМЕСТЕ
- Соревнования по стрельбе из пневматической винтовки
- «В Питере — учиться»
- Осторожно мошенники!!!
- Спартакиада учащихся ПОО по настольному теннису
- Школа бизнеса «Точка роста»
- Поздравляем с 23 февраля! С Днем защитника Отечества!
- Студент АКВТ награжден дипломом победителя Кубка России по судомодельному спорту
- Презентация РСМ
- С Днем защитника Отечества!
- Турнир по DOTA2
- Международной конкурс-премии уличной культуры и спорта «КАРДО»
- Набор студентов в Корпус общественных наблюдателей
- День снятия блокады Ленинграда
- С Днём студента!
- Региональный этап Всероссийских соревнований по мини-футболу
- Совещание органов студенческого самоуправления
- VI Открытый Региональный Чемпионат «Молодые профессионалы России»: финальный день
- VI Открытый Региональный Чемпионат профессионального мастерства «Молодые профессионалы» (WorldSkills Russia) день 4
- VI Открытый Региональный Чемпионат профессионального мастерства «Молодые профессионалы» (WorldSkills Russia) день 2
- VI Открытый Региональный Чемпионат профессионального мастерства «Молодые профессионалы» (WorldSkills Russia) день 1
- Поздравляем победителей международных конкурсов
- Курсы для школьников
- Конкурс на лучшее видео – поздравление «С Новым годом!»
- Конкурс на лучшее видео – поздравление «С Новым годом!»
- Студенты АКВТ приняли участие в открытии памятника легендарному командарму
- Поздравления от Деда Мороза и Снегурочки
- Поздравляем с началом сессии!
- Проведение независимой оценки качества условий осуществления образовательной деятельности ГБПОУ АО «Астраханский колледж вычислительной техники»
- В АКВТ прошла акция Всероссийский тест на знание Конституции РФ
- I заседание МК СПО АО преподавателей информатики 10 декабря 2021 г.

- Конкурс на лучшее видео-поздравление с Новым годом
- Телеканал «Астрахань 24» о выставке студентов АКВТ — участников проекта «Герои Великой Победы в миниатюре» в Музее боевой славы
- Анонс! Массовая просветительская акция Всероссийский тест на знание Конституции РФ
- Интерактивная игра «Я, мои права и обязанности»
- Всероссийский конкурс «Флагманы образования. Студенты»
- Команда АКВТ на фестивале студенческой лиги КВН
- Выставка студентов АКВТ в Музее боевой славы
- Студенты и преподаватели АКВТ прошли исторический тест в День Неизвестного солдата
- В Музее боевой славы пройдёт 2-ая выставка работ студентов АКВТ
- Астраханский колледж вычислительной техники стал площадкой федерального проекта «Билет в будущее»
- С днём матери!
- Акция «Призывник»
- Проведение родительских собраний
- АКВТ посетили участники клуба моделистов «Сталинградский фронт»
- Студент Астраханского колледжа вычислительной техники – победитель Всероссийского конкурса «Большая перемена»
- В АКВТ состоялась встреча, посвящённая сохранению исторической памяти и защите Отечества
- Об организации межведомственного штаба по организации волонтерской деятельности
- О программе «Пушкинская карта»
- Семинар, посвященный всероссийскому конкурсу «Soft Skills Russia»
- VI Международная просветительская акция «Большой этнографический диктант-2021»
- Студенты Астраханского колледжа вычислительной техники – финалисты Всероссийского конкурса «Большая перемена»
- Студенты АКВТ в финале Международной олимпиады в сфере информационных технологий «IT-Планета 2020/21»
- Пушкинская карта
- Анкетирование в рамках проекта «Без срока давности»
- Акция «Сообщи, где торгуют смертью»
- День учителя в стенах АКВТ
- С днем учителя!
- Расписание спортивных секций
- Выставка посвящённая Дню профтехобразования
- «Полетели поздравительные телеграммы…»
- Марафон танцевальных поздравлений
- Студенты АКВТ провели выставку военных диорам на Кубке Прикаспийских государств по рукопашному бою
- В АКВТ прошли первые занятия в рамках проекта «Герои Великой Победы в миниатюре»
- Посвящение в студенты в стенах АКВТ
- АКВТ в полуфинале Всероссийского конкурса «Большая перемена»
- Совещание органов студенческого самоуправления
- Студент нашего колледжа рассказывает о своём незабываемом опыте работы вожатым в детском лагере
- Студенты АКВТ приняли участие в акции по сбору подписей для получения Астрахани звания «Город трудовой доблести»
- АКВТ во Всероссийском историческом квесте «Наша победа»
- Студенты АКВТ приняли участие в областном уроке мужества «Славы героев достойны»
- День знаний в стенах АКВТ!
- Группы 1 курса
- Объявление по собраниям для студентов нового набора
- АКВТ примет участие во Всероссийском конкурсе на лучшую выставку
- Итоги заседания комиссии по переводу с коммерческого обучения на бюджет
- Выпускники АКВТ — 2021
- V Открытый Региональный Чемпионат «Молодые профессионалы России»: 1 день
- Наши студенты на субботнике
- «Молодежный кадровый резерв»
- Информация для участников ЕГЭ 2014 года
- «Проблема сиротства» — проблема нашего будущего»
- Центр гражданского воспитания «Прометей»
- Подготовка студентов по программе прикладного бакалавриата по специальности Компьютерные системы и комплексы
X
Выбор шрифта:
Чему равно число cdxiv
Тест по теме «Представление информации. Системы счисления»
Системы счисления»
Система счисления — это:
представление чисел в экспоненциальной форме;
представление чисел с постоянным положением запятой;
способ представления чисел с помощью символов, имеющих определенное количественное значение.
Двоичная система счисления имеет основание:
Какие цифры используются в семеричной системе счисления?
Чему равно число CDXIV в десятичной системе счисления?
В какой системе счисления может быть записано число 402?
Даны системы счисления: 2-ая, 8-ая, 10-ая и 16-ая. Запись вида 352:
отсутствует в двоичной системе счисления;
отсутствует в восьмеричной;
существует во всех названных системах счисления.
Какое минимальное основание должна иметь система счисления, если в ней можно записать числа: 341, 123, 222,111.
Как записывается максимальное 4-разрядное положительное число в троичной системе счисления?
в пятеричной системе счисления;
в троичной системе счисления;
в четверичной системе счисления.
в пятеричной системе счисления;
в троичной системе счисления;
в четверичной системе счисления.
Как записывается число 5 10 в двоичной системе счисления?
Какой будет результат вычитание 11000110-1011101:
Система счисления — это:
представление чисел в экспоненциальной форме;
представление чисел с постоянным положением запятой;
способ представления чисел с помощью символов, имеющих определенное количественное значение.
Пятеричная система счисления имеет основание:
Для представления чисел в восьмеричной системе счисления используются цифры:
В какой системе счисления может быть записано число 750?
Чему равно число CDXIV в десятичной системе счисления?
Даны системы счисления: 2-ая, 8-ая, 10-ая и 16-ая. Запись вида 692:
отсутствует в десятичной системе счисления;
отсутствует в восьмеричной;
существует во всех названных системах счисления.
Какие цифры используются в семеричной системе счисления?
Какое минимальное основание должна иметь система счисления, если в ней можно записать числа: 432, 768, 568, 243?
в пятеричной системе счисления;
в троичной системе счисления;
в четверичной системе счисления.
Как записывается максимальное 3-разрядное положительное число в четверичной системе счисления?
Как записывается число С,3 16 в десятичной системе счисления?
Какой будет результат сложения 1010111+101100?
В зависимости от способа изображения чисел системы счисления делятся на :
арабские и римские;
позиционные и непозиционные;
представление в виде ряда и в виде разрядной сетки.
Для представления чисел в шестнадцатеричной системе счисления используются:
цифры 0 — 9 и буквы A — F ;
Чему равно число DXXVII в десятичной системе счисления?
Какие цифры используются в шестеричной системе счисления?
в двоичной системе счисления;
в троичной системе счисления;
в четверичной системе счисления.
Пятеричная система счисления имеет основание:
В какой системе счисления может быть записано число 750?
Даны системы счисления: 2-ая, 8-ая, 10-ая и 16-ая. Запись вида 692:
отсутствует в десятичной системе счисления;
отсутствует в восьмеричной;
существует во всех названных системах счисления.
Какое минимальное основание должна иметь система счисления, если в ней можно записать числа: 432, 768, 568, 243?
Как записывается максимальное 3-разрядное положительное число в четверичной системе счисления?
Как записывается число1010 2 в восьмеричной системе счисления?
Какой будет результат вычитание 110101,101-1001,111?:
Система счисления — это:
представление чисел в экспоненциальной форме;
представление чисел с постоянным положением запятой;
способ представления чисел с помощью символов, имеющих определенное количественное значение.
Для представления чисел в восьмеричной системе счисления используются цифры:
Чему равно число CDXIV в десятичной системе счисления?
Какие цифры используются в семеричной системе счисления?
в пятеричной системе счисления;
в троичной системе счисления;
в четверичной системе счисления.
Двоичная система счисления имеет основание:
В какой системе счисления может быть записано число 402?
Даны системы счисления: 2-ая, 8-ая, 10-ая и 16-ая. Запись вида 352:
отсутствует в двоичной системе счисления;
отсутствует в восьмеричной;
существует во всех названных системах счисления.
Какое минимальное основание должна иметь система счисления, если в ней можно записать числа: 341, 123, 222,111.
Как записывается максимальное 4-разрядное положительное число в троичной системе счисления?
Читайте также: Geforce gtx 700 series
Как записывается число 5 10 в двоичной системе счисления?
Какой будет результат сложения 1110011+1011011?:
по теме «Представление информации. Системы счисления»
Системы счисления»
- Хасанова Алиса ФаритовнаНаписать 6680 08.04.2014
Номер материала: 63519040837
- 08.04.2014 5851
- 08.04.2014 1929
- 08.04.2014 2828
- 08.04.2014 924
- 08.04.2014 1039
- 08.04.2014 1359
- 08.04.2014 794
Не нашли то что искали?
Вам будут интересны эти курсы:
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение редакции может не совпадать с точкой зрения авторов.
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
| Системы счисления в культуре | |
|---|---|
| Индо-арабская | |
| Арабская Тамильская Бирманская | Кхмерская Лаосская Монгольская Тайская |
| Восточноазиатские | |
| Китайская Японская Сучжоу Корейская | Вьетнамская Счётные палочки |
| Алфавитные | |
| Абджадия Армянская Ариабхата Кириллическая Греческая | Грузинская Эфиопская Еврейская Акшара-санкхья |
| Другие | |
| Вавилонская Египетская Этрусская Римская Дунайская | Аттическая Кипу Майяская Эгейская Символы КППУ |
| Позиционные | |
| 2, 3, 4, 5, 6, 8, 10, 12, 16, 20, 60 | |
| Нега-позиционная | |
| Симметричная | |
| Смешанные системы | |
| Фибоначчиева | |
| Непозиционные | |
| Единичная (унарная) | |
Эта страница или раздел содержит специальные символы Юникода. Если у вас отсутствуют необходимые шрифты, некоторые символы могут отображаться неправильно. |
Натуральные числа записываются при помощи повторения этих цифр. При этом, если большая цифра стоит перед меньшей, то они складываются (принцип сложения), если же меньшая стоит перед большей, то меньшая вычитается из большей (принцип вычитания). Последнее правило применяется только во избежание четырёхкратного повторения одной и той же цифры.
Римские цифры появились за 500 лет до нашей эры у этрусков (см. этрусский алфавит), которые могли заимствовать часть цифр у прото-кельтов.
Содержание
Римские цифры [ править | править код ]
Римские обозначения чисел известны ныне лучше, чем любая другая древняя система счисления. Объясняется это не столько какими-то особыми достоинствами римской системы, сколько тем огромным влиянием, которым пользовалась римская империя в сравнительно недавнем прошлом. Этруски, завоевавшие Рим в 7 в. до н. э., испытали на себе влияние восточно-средиземноморских культур. Этим отчасти объясняется сходство основных принципов Римской и аттической систем счисления. Обе системы были десятичными, хотя в обеих системах счисления особую роль играло число пять. Обе системы использовали при записи чисел повторяющиеся символы.
э., испытали на себе влияние восточно-средиземноморских культур. Этим отчасти объясняется сходство основных принципов Римской и аттической систем счисления. Обе системы были десятичными, хотя в обеих системах счисления особую роль играло число пять. Обе системы использовали при записи чисел повторяющиеся символы.
Старыми римскими символами для обозначения чисел 1, 5, 10, 100 и 1000 были, соответственно, символы I, V, X, Θ (или ⊕, или ⊗) и Φ (или ↀ , или CIƆ). Хотя о первоначальном значении этих символов было написано много, их удовлетворительного объяснения у нас нет до сих пор. Согласно одной из распространенных теорий, римская цифра V изображает раскрытую руку с четырьмя прижатыми друг к другу пальцами и отставленным большим пальцем; символ X, согласно той же теории, изображает две скрещенные руки или сдвоенную цифру V. Символы чисел 100 и 1000, возможно, берут начало от греческих букв Θ и φ. Неизвестно, произошли ли более поздние обозначения C и M от старых римских символов или они акрофонически связаны с начальными буквами латинских слов, означавших 100 (центум) и 1000 (милле). Полагают, что римский символ числа 500, буква D, возник из половинки старого символа, обозначавшего 1000. Если не считать, что большинство римских символов скорее всего не были акрофоническими и что промежуточные символы для обозначения чисел 50 и 500 не были комбинациями символов чисел 5 и 10 или 5 и 100, то в остальном римская система счисления напоминала аттическую. Разумеется, в деталях они отличались. Римляне часто использовали принцип вычитания, поэтому иногда вместо VIIII использовали IX ,а XC вместо LXXXX; сравнительно позднее символ IV вместо IIII.
Полагают, что римский символ числа 500, буква D, возник из половинки старого символа, обозначавшего 1000. Если не считать, что большинство римских символов скорее всего не были акрофоническими и что промежуточные символы для обозначения чисел 50 и 500 не были комбинациями символов чисел 5 и 10 или 5 и 100, то в остальном римская система счисления напоминала аттическую. Разумеется, в деталях они отличались. Римляне часто использовали принцип вычитания, поэтому иногда вместо VIIII использовали IX ,а XC вместо LXXXX; сравнительно позднее символ IV вместо IIII.
Читайте также: Drweb avdesk installer exe
В целом римляне не были склонны заниматься математикой, поэтому не испытывали особой потребности в больших числах. Тем не менее для обозначения 10000 они эпизодически использовали символ CCIƆƆ , а для числа 100000 — символ CCCIƆƆƆ. Половинки этих символов иногда использовались для обозначения чисел 5000 (IƆƆ) и 50000 (IƆƆƆ).
Дробей римляне избегали так же упорно, как и больших чисел. В практических задачах, связанных с измерениями, они не использовали дроби, подразделяя единицу измерения обычно на 12 частей, с тем чтобы результат измерения представить в виде составного числа, суммы кратных различных единиц, как это делается сегодня, когда длину выражают в ярдах, футах и дюймах. Английские слова «ounce» (унция) и «inch» (дюйм) происходят от латинского слова лат. uncia (унция), обозначавшего одну двенадцатую основной единицы длины. [1] [2]
В практических задачах, связанных с измерениями, они не использовали дроби, подразделяя единицу измерения обычно на 12 частей, с тем чтобы результат измерения представить в виде составного числа, суммы кратных различных единиц, как это делается сегодня, когда длину выражают в ярдах, футах и дюймах. Английские слова «ounce» (унция) и «inch» (дюйм) происходят от латинского слова лат. uncia (унция), обозначавшего одну двенадцатую основной единицы длины. [1] [2]
| 1 | I | лат. unus, unum |
| 5 | V | лат. quinque |
| 10 | X | лат. decem |
| 50 | L | лат. quinquaginta |
| 100 | C | лат. centum |
| 500 | D | лат. quingenti |
| 1000 | M | лат. mille |
| Число | Обозначение |
|---|---|
| 1 | I |
| 2 | II |
| 3 | III |
| 4 | IV |
| 5 | V |
| 6 | VI |
| 7 | VII |
| 8 | VIII |
| 9 | IX |
| 10 | X |
| 11 | XI |
| 20 | XX |
| 30 | XXX |
| 40 | XL |
| 50 | L |
| 60 | LX |
| 70 | LXX |
| 80 | LXXX |
| 90 | XC |
| 100 | C |
| 200 | CC |
| 300 | CCC |
| 400 | CD |
| 500 | D; IƆ |
| 600 | DC; IƆC |
| 700 | DCC; IƆCC |
| 800 | DCCC; IƆCCC |
| 900 | CM; CCIƆ |
| 1000 | M; ↀ; CIƆ |
| 2000 | MM; CIƆCIƆ |
| 3000 | MMM; CIƆCIƆCIƆ |
| 3999 | MMMCMXCIX |
| 4000 | M V ; ↀↁ; CIƆIƆƆ |
| 5000 | V ; ↁ; IƆƆ |
| 6000 | V M; ↁↀ; IƆƆCIƆ |
| 7000 | V MM; ↁↀↀ; IƆƆCIƆCIƆ |
| 8000 | V MMM; ↁↀↀↀ; IƆƆCIƆCIƆCIƆ |
| 9000 | M X ↀↂ; CIƆCCIƆƆ |
| 10 000 | X ; ↂ; CCIƆƆ |
| 20 000 | XX ; ↂↂ; CCIƆƆCCIƆƆ |
| 30 000 | XXX ; ↂↂↂ; CCIƆƆCCIƆƆCCIƆƆ |
| 40 000 | XL ; ↂↇ; CCIƆƆIƆƆƆ |
| 50 000 | L ; ↇ; IƆƆƆ |
| 60 000 | LX ; ↇↂ; IƆƆƆCCIƆƆ |
| 70 000 | LXX ; ↇↂↂ; IƆƆƆCCIƆƆCCIƆƆ |
| 80 000 | LXXX ; ↇↂↂↂ; IƆƆƆCCIƆƆCCIƆƆCCIƆƆ |
| 90 000 | XC ; ↂↈ; CCIƆƆCCCIƆƆƆ |
| 100 000 | C ; ↈ; CCCIƆƆƆ |
| 200 000 | CC ; ↈↈ; CCCIƆƆƆCCCIƆƆƆ |
| 300 000 | CCC ; ↈↈↈ; CCCIƆƆƆCCCIƆƆƆCCCIƆƆƆ |
| 400 000 | CD ; CCCIƆƆƆIƆƆƆƆ |
| 500 000 | D ; IƆƆƆƆ |
| 600 000 | DC ; IƆƆƆƆCCCIƆƆƆ |
| 700 000 | DCC ; IƆƆƆƆCCCIƆƆƆCCCIƆƆƆ |
| 800 000 | DCCC |
| 900 000 | CM |
| 1 000 000 | M |
| 2 000 000 | MM |
| 3 000 000 | MMM |
| 4 000 000 | M V |
| 5 000 000 | V |
| 6 000 000 | V M |
| 7 000 000 | V MM |
| 8 000 000 | V MMM |
| 9 000 000 | M X |
Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц.
В системе римских цифр отсутствует ноль, но ранее использовалось обозначение нуля как nulla (нет), nihil (ничто) и N (первая буква этих слов).
При этом некоторые из цифр (I, X, C, M) могут повторяться, но не более трёх раз подряд; таким образом, с их помощью можно записать любое целое число не более 3999 (MMMCMXCIX). В ранние периоды существовали знаки для обозначения бо́льших цифр — 5000, 10 000, 50 000 и 100 000 [ источник не указан 3239 дней ] (тогда максимальное число по упомянутому правилу равно 399 999). При записи чисел в римской системе счисления меньшая цифра может стоять справа от большей; в этом случае она прибавляется к ней. Например, число 283 по-римски записывается как CCLXXXIII, то есть 100+100+50+30+3=283. Здесь цифра, изображающая сотню, повторена два раза, а цифры, изображающие соответственно десяток и единицу, повторены по три раза.
Пример: число 1988. Одна тысяча M, девять сотен CM, восемь десятков LXXX, восемь единиц VIII. Запишем их вместе: MCMLXXXVIII.
Довольно часто, чтобы выделить числа в тексте, над ними рисовали черту: LXIV . Иногда черту рисовали и сверху, и снизу: XXXII — в частности, так принято выделять римские цифры в русском рукописном тексте (в типографском наборе это не используют из-за технической сложности). У других авторов черта сверху могла обозначать увеличение значения цифры в 1000 раз: V = 5000.
Читайте также: Свиной окорок на гриле
Повсеместно записывать число «четыре» как «IV» стали только в XIX веке, до этого наиболее часто употреблялась запись «IIII». Однако запись «IV» можно встретить уже в документах манускрипта «Forme of Cury», датируемых 1390 годом. На циферблатах часов в большинстве случаев традиционно используется «IIII» вместо «IV», главным образом, по эстетическим соображениям: такое написание обеспечивает визуальную симметрию с цифрами «VIII» на противоположной стороне, а перевёрнутую «IV» прочесть труднее, чем «IIII». Существует и версия, что IV на циферблате не писалось потому, что IV — первые буквы имени бога Юпитера (IVPITER).
Меньшая цифра может быть записана и слева от большей, тогда её следует вычесть из большей. При этом вычитаться могут только цифры, обозначающие 1 или степени 10, а в качестве уменьшаемого выступать только ближайшие в числовом ряду к вычитаемой две цифры (то есть вычитаемое, умноженное на 5 или 10). Повторения меньшей цифры не допускаются. Таким образом, существует только шесть вариантов использования «правила вычитания»:
Например, число 94 будет XCIV = 100 − 10 + 5 − 1 = 94 — так называемое «правило вычитания» (появилось в эпоху поздней античности, а до этого римляне писали число 4 как IIII, а число 40 — как XXXX).
Необходимо отметить, что другие способы «вычитания» недопустимы; так, число 99 должно быть записано как XCIX, но не как IC. Однако, в наши дни в некоторых случаях используется и упрощенная запись римских чисел: например, в программе Microsoft Excel при преобразовании арабских цифр в римские при помощи функции «РИМСКОЕ()» можно использовать несколько видов представления чисел, от классического до сильно упрощенного (так, число 499 может быть записано как CDXCIX, LDVLIV, XDIX, VDIV или ID). Упрощение состоит в том, что для уменьшения какой-либо цифры слева от неё может писаться любая другая цифра:
Упрощение состоит в том, что для уменьшения какой-либо цифры слева от неё может писаться любая другая цифра:
- 999. Тысяча (M), вычтем 1 (I), получим 999 (IM) вместо CMXCIX. Следствие: 1999 — MIM вместо MCMXCIX
- 95. Сто (C), вычтем 5 (V), получим 95 (VC) вместо XCV
- 1950: Тысяча (M), вычтем 50 (L), получим 950 (LM). Следствие: 1950 — MLM вместо MCML
Случаи такой записи чисел (как правило, годов) часто встречаются в титрах телесериалов США. Например, для года 1998: IIMM вместо MCMXCVIII.
С помощью римских цифр можно записывать и большие числа. Для этого над теми цифрами, которые обозначают тысячи, ставится черта, а над цифрами, которые обозначают миллионы, — двойная черта. Например, число 123123 будет выглядеть так:
А миллион как I , но только не с одной, а с двумя чертами во главе: I
English-Russian dictionary designations . 2014 .
Смотреть что такое «CDXIV» в других словарях:
CDXIV — матем. • Запись числа 414 римскими цифрами … Словарь обозначений
• Запись числа 414 римскими цифрами … Словарь обозначений
Libri of Aleister Crowley — The Libri of Aleister Crowley is a list of texts mostly written or adapted by Aleister Crowley. Some are attributed to other authors. The list was intended for students of Crowley s magical order, the A∴A∴. Content Many of the books and articles… … Wikipedia
340 v. Chr. — Portal Geschichte | Portal Biografien | Aktuelle Ereignisse | Jahreskalender ◄ | 5. Jahrhundert v. Chr. | 4. Jahrhundert v. Chr. | 3. Jahrhundert v. Chr. | ► ◄ | 360er v. Chr. | 350er v. Chr. | 340er v. Chr. | 330er v. Chr. |… … Deutsch Wikipedia
414 (число) — 414 Четыреста четырнадцать 411 · 412 · 413 · 414 · 415 · 416 · 417 Факторизация: Римская запись: CDXIV Двоичное: 110011110 Восьмеричное … Википедия
414 — матем. • Запись римскими цифрами: CDXIV … Словарь обозначений
Преобразование десятичного числа 750 в двоичное
Как записать 750 в двоичном формате (с основанием 2)?
750 равно 1011101110 в двоичной форме
| ||||||||||||||||
Преобразование из/в десятичные, шестнадцатеричные, восьмеричные и двоичные числа. Калькулятор преобразования десятичной базы.
Здесь вы можете найти ответы на такие вопросы, как: Преобразование десятичного числа 750 в двоичное или Преобразование десятичного числа в двоичное.
Калькулятор преобразования десятичной базы.
Здесь вы можете найти ответы на такие вопросы, как: Преобразование десятичного числа 750 в двоичное или Преобразование десятичного числа в двоичное.
| Dec | Hex | Oct | Bin | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |||||||
| 1 | 1 | 1 | 1 | |||||||
| 2 | 2 | 2 | 10 | |||||||
| 3 | 3 | 3 | 11 | |||||||
| 4 | 4 | 4 | 100 | |||||||
| 5 | 5 | 5 | 101 | |||||||
| 6 | 6 | 991096 | 11000 | 6 | 999 | 6 | 9000 | |||
| 6 | ||||||||||
| 6 | 9999996 | 999999.0007 | 7 | 7 | 7 | 111 | ||||
| 8 | 8 | 10 | 1000 | |||||||
| 9 | 9 | 11 | 1001 | |||||||
| 10 | A | 12 | 1010 | |||||||
| 11 | B | 13 | 1011 | |||||||
| 12 | C | 14 | ||||||||
| 13 | D | 9|||||||||
| 13 | D | 815 | 1101 | |||||||
| 14 | E | 16 | 1110 | |||||||
| 15 | F | 17 | 1111 |
| Dec | Hex | Oct | Bin | |||||
|---|---|---|---|---|---|---|---|---|
| 16 | 10 | 20 | 10000 | |||||
| 17 | 11 | 21 | 10001 | |||||
| 18 | 12 | 10001 | ||||||
| 18 | 12 | 0009 | 22 | 10010 | ||||
| 19 | 13 | 23 | 10011 | |||||
| 20 | 14 | 24 | 10100 | |||||
| 21 | 15 | 25 | 10101 | |||||
| 22 | 16 | 26 | 10110 | |||||
| 23 | 17 | 27 | 10111 | |||||
| 24 | 18 | 30 9009 | ||||||
| 24 | 18 | 30 | ||||||
| 11000 | ||||||||
| 25 | 19 | 31 | 11001 | |||||
| 26 | 1A | 32 | 11010 | |||||
| 27 | 1B | 33 | 11011 | |||||
| 28 | 1C | 34 | 11100 | |||||
| 29 | 1d | 35 | 11101 | |||||
| 30 | 1E | 36 | 1E | 36 | 0009 | |||
| 31 | 1F | 37 | 11111 |
| Dec | Hex | Oct | Bin | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 32 | 20 | 40 | 100000 | |||||||||||
| 33 | 21 | 41 | 100001 | |||||||||||
| 34 | 22 | 42 | 100010 | |||||||||||
| 35 | 23 | 43 | ||||||||||||
| 23 | 43 | 9100011 | ||||||||||||
| 36 | 24 | 44 | 100100 | |||||||||||
| 37 | 25 | 45 | 100101 | |||||||||||
| 38 | 26 | 46 | 100110 | |||||||||||
| 39 | 27 | 47 | 100111 | |||||||||||
| 40 | 28 | 50 | 101000 | |||||||||||
| 41 | 2951 | 101001 | 29 | 51 | 101001 | 51 | 101001 | 0009|||||||
| 42 | 2A | 52 | 101010 | |||||||||||
| 43 | 2B | 53 | 101011 | |||||||||||
| 44 | 2C | 54 | 101100 | |||||||||||
| 45 | 2D | 55 | 101101 | |||||||||||
| 46 | 2E | 56 | 101110 | |||||||||||
| 47 | 2F | 57 | 101111 | 2F | 57 | 101111 | 0060
| 110009 |
9000
| Dec | Hex | Oct | Bin | |
|---|---|---|---|---|
| 240 | F0 | 360 | 11110000 | |
| 241 | F1 | 361 | 11110001 | |
| 242 | F2 | 362 | 11110010 | |
| 243 | F3 | 363 | 11110011 | |
| 244 | F4 | 364 | 11101009 | 0009 |
| 245 | F5 | 365 | 11110101 | |
| 246 | F6 | 366 | 11110110 | |
| 247 | F7 | 367 | 11110111 | |
| 248 | F8 | 370 | 11111000 | |
| 249 | F9 | 371 | 11111001 | |
| 250 | FA | 372 | 0008 11111010 | |
| 251 | FB | 373 | 11111011 | |
| 252 | FC | 374 | 11111100 | |
| 253 | FD | 375 | 11111101 | |
| 254 | FE | 376 | 11111110 | |
| 255 | FF | 377 | 111111111999910 |
Номерная базовая конвертер
Пожалуйста, перейдите на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, затем выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.
- 272 octal to binary
- 1010 binary to hexadecimal
- 22 hexadecimal to decimal
- 11110001 binary to hexadecimal
- 10000010 binary to hexadecimal
- binary to octal
- 10100011 binary to hexadecimal
- 11111001001 binary в шестнадцатеричное
- 1101100000 двоично-десятичный
750 (Число)
750 ( семьсот пятьдесят ) — четное трехзначное составное число после 749 и перед 751. В научной записи оно записывается как 7,5 × 10 2 . Сумма его цифр равна 12. Всего у него 5 простых множителей и 16 положительных делителей. Существует 200 натуральных чисел (до 750), взаимно простых с 750.
- Прайм? №
- Числовая четность Четный
- Длина номера 3
- Сумма цифр 12
- Цифровой корень 3
| Краткое наименование | 750 |
|---|---|
| Полное имя | семьсот пятьдесят |
| Научное обозначение | 7,5 × 10 2 |
|---|---|
| Техническое обозначение | 750 × 10 0 |
Простые множители 2 × 3 × 5 3
Составное число
| ω(n) | Отличительные факторы | 3 | Общее количество различных простых множителей |
|---|---|---|---|
| Ом(n) | Всего факторов | 5 | Общее количество простых множителей |
| рад(н) | Радикальный | 30 | Произведение различных простых чисел |
| λ(n) | Лиувилль Лямбда | -1 | Возвращает четность Ω(n), такую что λ(n) = (-1) Ω(n) |
| мк(н) | Мебиус Мю | 0 | Возвращает:
|
| Л(н) | Функция Мангольдта | 0 | Возвращает log(p), если n является степенью p k любого простого числа p (для любого k >= 1), в противном случае возвращает 0 |
Разложение числа 750 на простые множители равно 2 × 3 × 5 3 . Поскольку у него всего 5 простых делителей, 750 является составным числом.
Поскольку у него всего 5 простых делителей, 750 является составным числом.
1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 125, 150, 250, 375, 750
16 делителей
| Четный делитель | 8 |
|---|---|
| Нечетные делители | 8 |
| 4k+1 делитель | 4 |
| 4k+3 делителя | 4 |
| τ(n) | Всего делителей | 16 | Общее количество положительных делителей n |
|---|---|---|---|
| σ(n) | Сумма делителей | 1872 | Сумма всех положительных делителей n |
| с(н) | Аликвотная сумма | 1122 | Сумма собственных положительных делителей n |
| А(н) | Среднее арифметическое | 117 | Возвращает сумму делителей (σ(n)), деленную на общее количество делителей (τ(n)) |
| Г(н) | Среднее геометрическое | 27. 386127875258 386127875258 | Возвращает корень n из произведения n делителей |
| Н(н) | Среднее гармоническое | 6.4102564102564 | Возвращает общее количество делителей (τ(n)), деленное на сумму обратной величины каждого делителя |
Число 750 можно разделить на 16 положительных делителей (из них 8 четных и 8 нечетных). Сумма этих делителей (считая 750) равна 1872, среднее значение равно 117.
1 ф (п) п
| φ(n) | Эйлер Тотиент | 200 | Общее количество натуральных чисел не больше n, взаимно простых с n |
|---|---|---|---|
| λ(n) | Кармайкл Лямбда | 100 | Наименьшее положительное число такое, что λ(n) ≡ 1 (mod n) для всех чисел, взаимно простых с n |
| п(н) | Прайм Пи | ≈ 135 | Общее количество простых чисел меньше или равно n |
| р 2 (н) | Сумма 2 квадратов | 0 | Количество способов n представить в виде суммы двух квадратов |
Существует 200 натуральных чисел (меньше 750), взаимно простых с 750. И примерно 135 простых чисел меньше или равны 750.
И примерно 135 простых чисел меньше или равны 750.
| м | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|
| п мод м | 0 | 0 | 2 | 0 | 0 | 1 | 6 | 3 |
Число 750 делится на 2, 3, 5 и 6.
Арифметическими функциями
- Арифметика
- Изобилие
Выражается через определенные суммы
- Вежливый
- Практический
По форме (2D, не по центру)
- Неагональный
Другие номера
- Обычный
| Основание | Система | Значение |
|---|---|---|
| 2 | Двоичный | 1011101110 |
| 3 | Тернарный | 1000210 |
| 4 | Четвертичный | 23232 |
| 5 | Квинарий | 11000 |
| 6 | Сенар | 3250 |
| 8 | Восьмеричный | 1356 |
| 10 | Десятичный | 750 |
| 12 | Двенадцатеричный | 526 |
| 16 | Шестнадцатеричный | 2ee |
| 20 | Десятичное число | 1 га |
| 36 | Base36 | ку |
Умножение
п × у| n×2 | 1500 |
|---|---|
| n×3 | 2250 |
| n×4 | 3000 |
| н×5 | 3750 |
Отдел
n÷y| н÷2 | 375. 000 000 |
|---|---|
| н÷3 | 250.000 |
| н÷4 | 187 500 |
| н÷5 | 150.000 |
Возведение в степень
п г| п 2 | 562500 |
|---|---|
| п 3 | 421875000 |
| п 4 | 316406250000 |
| п 5 | 237304687500000 |
N-й корень
г √n| 2 √n | 27. 386127875258 386127875258 |
|---|---|
| 3 √n | 9.08560207 |
| 4 √n | 5.2331756969605 |
| 5 √n | 3,7584800787651 |
Круг
Радиус = n| Диаметр | 1500 |
|---|---|
| Окружность | 4712.3889803847 |
| Зона | 1767145.8676443 |
Сфера
Радиус = n| Том | 1767145867. 6443 6443 |
|---|---|
| Площадь поверхности | 7068583.470577 |
| Окружность | 4712.3889803847 |
Квадрат
Длина = n| Периметр | 3000 |
|---|---|
| Зона | 562500 |
| Диагональ | 1060.6601717798 |
Куб
Длина = n| Площадь поверхности | 3375000 |
|---|---|
| Том | 421875000 |
| Пространственная диагональ | 1299. 0381056767 0381056767 |
Равносторонний треугольник
Длина = n| Периметр | 2250 |
|---|---|
| Зона | 243569.64481437 |
| Высота над уровнем моря | 649,51 | 3833
Треугольная пирамида
Длина = n| Площадь поверхности | 974278.57 |
|---|---|
| Том | 49718445.552179 |
| Высота | 612.37243569579 |
| мд5 | b137fdd1f79d56c7edf3365fea7520f2 |
|---|---|
| ша1 | 404c735f21d00fee39a13210d54844f3cec069c7 |
| ша256 | 64d095f2fecfdeb907dae5403b10966c4ae755b7598aa078cb932e345bd0b5d0 |
| ша512 | 24c4e5bfd8812cc60410a166391f189fa809da20f825d44ee04f96de62f5130ab163ccabe182560bbe0c94faa8d6d43ca630d4d60c0ecea5cdc434b6412cb081 |
| римед-160 | 3a87f188058f15e8c2f377c464c6f899fcd9d313 |
Десятичная система Дьюи — Путеводитель по телефонным номерам — Виртуальная библиотека информационных наук — Библиотека U of I
Загрузка библиотечных часов. ..
..
Чтобы узнать больше о том, что означают части телефонного номера книги, ознакомьтесь с разделом Поиск книг с телефонными номерами Библиотеки Конгресса и Дьюи
000 Общие сведения
100 Философия и психология
200 Религия
300 Социальные науки
400 Язык
500 Естественные науки и математика
600 Технологии (прикладные науки)
700 Искусство
800 Литература и риторика
900 География и история
000
000 Общие сведения
001 Знания
002 Книга
003 Системы
004 Обработка данных Информатика
005 Компьютерное программирование, программы, данные больше не используется
009 Не назначено или больше не используется
010 Библиография
011 Библиографии
012 Библиографии отдельных лиц
013 Библиографии работ определенных классов авторов
014 Библиографии анонимных и псевдонимных произведений
015 Библиографии произведений из конкретных мест
016 Библиографии произведений по конкретным предметам
017 Общие тематические каталоги
018 Каталоги, организованные по авторам и дате
019 Словарные каталоги
020 Библиотека и информационные науки
022 Управление физическим предприятием
023 Управление персоналом
024 Не назначено или больше не используется
025 Библиотечные операции
026 Библиотеки по конкретным предметам
027 Общие библиотеки
028 Чтение, использование других информационных носителей
029 Не присвоено или больше не используется
030 Общие энциклопедические труды
031 Общие энциклопедические труды — американские
032 Общие энциклопедические труды на английском языке
033 Общие энциклопедические работы на других германских языках
034 Общие энциклопедические работы на французском, провансальском, каталанском
035 Общие энциклопедические работы на итальянском, румынском, ретороманском языках
036 Общие энциклопедические работы на испанском и португальском языках
037 Общие энциклопедические труды на славянских языках
038 Общие энциклопедические труды на скандинавских языках
039 Общие энциклопедические труды на других языках
040 Не присвоено или более не используется
041 Не присвоено или более не используется
042 Не присвоено или более не используется
043 Не присвоено или более не используется
044 Не присвоено или более не используется
045 Не присвоено или более не используется
046 Не присвоено или более не используется
047 Не присвоено или более не используется
048 Не назначено или больше не используется
049 Не назначено или больше не используется
050 Общие серийные номера и их индексы
051 Общие серийные номера и их индексы Американские
052 Общие серийные номера и их индексы На английском языке
053 Общие серийные номера и их индексы На других германских языках языки
054 Общие сериальные издания и их указатели На французском, провансальском, каталонском
055 Общие серийные издания и их указатели На итальянском, румынском, ретороманском
056 Общие серийные издания и их указатели На испанском и португальском языках
057 Общие периодические издания и их указатели на славянских языках
058 Общие периодические издания и их указатели на скандинавских языках
059 Общие периодические издания и их указатели на других языках
060 Общая организация и музейное дело
061 Общая организация и музейное дело В Северной Америке
062 Общая организация и музеология На Британских островах В Англии
063 Общая организация и музеология В Центральной Европе В Германии
064 Общая организация и музеология Во Франции и Монако
065 Общая организация и музейное дело В Италии и сопредельных территориях
066 Общая организация и музейное дело На Пиренейском полуострове и прилегающих островах
067 Общая организация и музейное дело В Восточной Европе В Советском Союзе
068 Общая организация и музейное дело В других областях
069 Музееведение (музейное дело) )
070 Средства массовой информации, журналистика, издательское дело
071 СМИ, журналистика, издательское дело В Северной Америке
072 СМИ, журналистика, издательское дело На Британских островах В Англии
073 Средства массовой информации, журналистика, публикации В Центральной Европе В Германии
074 Средства массовой информации, журналистика, публикации Во Франции и Монако
075 Средства массовой информации, журналистика, публикации В Италии и прилегающих территориях
076 Средства массовой информации, журналистика, публикации На Пиренейском полуострове и прилегающие острова
077 Средства массовой информации, журналистика, издательское дело В Восточной Европе В Советском Союзе
078 СМИ, журналистика, издательское дело В Скандинавии
079 СМИ, журналистика, издательское дело На других языках
080 Общие коллекции
081 Общие коллекции Американский
082 Общие коллекции На английском языке
083 Общие коллекции На других германских языках
084 Общие коллекции На французском, провансальском, каталанском
085 Общие коллекции На итальянском, румынском, ретороманском
086 Общие коллекции На Испанский и португальский
087 Общие коллекции На славянских языках
088 Общие коллекции На скандинавских языках
089 Общие коллекции На других языках
090 Рукописывания и редкие книги
091 Рукописывания
092 Блок книг
093 Инкунабула
094 Печатные книги
095 Книги, примечательные для привязки
096, примечательные для иллюстраций
097 Книги для достопримечательностей 9371 096.
 Книги, отличающиеся форматом
Книги, отличающиеся форматом Сотни
100 Философия и психология
101 Теория философии
102 Сборник философии
103 Философские словари
104 Не присвоено или больше не используется
105 Серийные публикации по философии
106 Философские организации
107 Образование, исследования в области философии
108 Типы людей в философии
109 Историческая трактовка философии
110 Метафизика
111 Онтология
или 112 Не присвоено больше не используется
113 Космология (философия природы)
114 Пространство
115 Время
116 Изменение
117 Структура
118 Сила и энергия
119 Число и количество
120 Эпистемология, причинно -следственная связь, человечество
121 Эпистемология (Теория знаний)
122. Происхождение и судьба индивидуальных душ
130 Паранормальные явления
131 Оккультные методы достижения благополучия
132 Не назначено или больше не используется
133 Парапсихология и оккультизм
134 Не назначено или больше не используется
135 Сны и тайны
136 Не назначено или больше не используется
137 Гадательная графология
138 Физиогномика
139 Френология
140 Отдельные философские школы
141 Идеализм и родственные ему системы философии
933 142 Бергсонизм
144 Гуманизм и родственные системы
145 Сенсуализм
146 Натурализм и родственные системы
147 Пантеизм и родственные системы
148 Либерализм, эклектика, традиционализм
149 Другие философские системы
150 Психология
151 Не назначено или больше не используется
152 Восприятие, движение, эмоции, влечения
153 Психические процессы и интеллект
154 Подсознание и измененные состояния
155 Дифференциальная психология и психология развития
156 Сравнительная психология 1 назначено или больше не используется
158 Прикладная психология
159 Не назначено или больше не используется
160 Логика
161 Индукция
162 Дедукция
163 Не назначено или больше не используется
164 НЕ назначен или больше не использовался
165 Платежений и источников ошибок
166 СИЛЛОГИЗМЫ
167 ГИПОТЕЗЫ
168 Аргумент и убеждение
169 Аналогия
170 этика (моральная философия). отношений
отношений
174 Экономическая и профессиональная этика
175 Этика отдыха и досуга
176 Этика секса и репродукции
177 Этика социальных отношений
178 Этика потребления
179 Other ethical norms
180 Ancient, medieval, Oriental philosophy
181 Oriental philosophy
182 Pre-Socratic Greek philosophies
183 Sophistic & Socratic philosophies
184 Platonic philosophy
185 Aristotelian philosophy
186 Skeptic and Neoplatonic philosophies
187 Epicurean philosophy
188 Стоическая философия
189 Средневековая западная философия
190 Современная западная философия
191 Современная западная философия США и Канада
192 Современная западная философия Британские острова
193 Современная западная философия Германия и Австрия
194 Современная западная философия Франция
195 Современная западная философия Италия
196 Современная западная философия Испания и Португалия
197 Современная западная философия Советский Союз
198 Современная западная философия Скандинавия
199 Современная западная философия Другие географические области
200-е годы
200 Религия
201 Философия христианства
202 Сборник христианства
203 Словари христианства
204 Специальные темы
205 Серийные издания христианства
206 Христианские организации
207 Образование, исследования в христианстве
208 Типы людей в христианстве
209 История и география Христианского богословия
211 Представления о Боге
212 Существование, атрибуты Бога
213 Творение
214 Теодицея
215 Наука и религия
216 Добро и зло
217 Не присвоено или более не используется
218 Человечество
219 Не присвоено или более не используется
220 Библия
221 Ветхий Завет
222 Исторические книги Ветхого Завета
223 Поэтические книги Ветхого Завета
224 Пророческие книги Ветхого Завета
225 Новый Завет
226 Евангелия и Деяния
227 Послания
228 Откровение (Апокалипсис)
229 Апокрифы и псевдоэпиграфы
230 Христианское богословие
231 Бог
232 Иисус Христос и его семья
233 Человечество
234 Salvation (Soteriology) & grace
235 Spiritual beings
236 Eschatology
237 Not assigned or no longer used
238 Creeds & catechisms
239 Apologetics & polemics
240 Christian moral & devotional theology
241 Moral theology
242 Devotional literature
243 Евангельские сочинения для частных лиц
244 Не присвоены или больше не используются
245 Тексты гимнов
246 Использование искусства в христианстве
247 Церковная утварь и предметы
248 Христианский опыт, практика, жизнь
249 Христианские обряды в семейной жизни
250 Христианские ордена и поместная церковь
251 Проповедь (гомилетика)
252 Тексты проповедей
253 Пастырское служение (пастырское богословие)
254 Приходское управление и администрация 1 Религиозные общины и ордена
256 Не назначено или больше не используется
257 Не назначено или больше не используется
258 Не назначено или больше не используется
259 Деятельность поместной церкви
260 Христианское социальное богословие
261 Социальное богословие
262 Ecclesiology
263 раз, места религиозного соблюдения
264 Общественное поклонение
265 Таинства, другие обряды и акты
266 Миссии
267 Ассоциации для религиозного рабочего.
 270 История христианской церкви
270 История христианской церкви 271 Религиозные ордена в истории церкви
272 Гонения в истории церкви
273 Ереси в истории церкви
274 Христианская церковь в Европе
275 Христианская церковь в Азии
276 Христианская церковь в Африке
277 Христианская церковь в Северной Америке
278 Христианская церковь в Южной Америке
279 Христианская церковь в других регионах
280 Христианские конфессии и секты
281 Ранняя церковь и восточные церкви
282 Римско-католическая Церковь
283 Англиканские церкви
284 Протестанты континентального происхождения
285 Пресвитерианские, реформатские, конгрегационалистские
286 Баптисты, ученики Христа, адвентисты
287 Методистские и родственные церкви
288 Не присвоено или более не используется
289 Другие конфессии и секты
290 Другие и сравнительные религии
291 Сравнительная религия
292 Классическая (греческая и римская) религия
293 Германская религия
294 Религии индийского происхождения
295 Зороастризм )
296 Иудаизм
297 Ислам и религии, происходящие от него
298 Не присвоено или более не используется
299 Другие религии
300-е годы
300 Общественные науки
301 Социология и антропология
302 Социальное взаимодействие
303 Социальные процессы
304 Факторы, влияющие на социальное поведение
305 Социальные группы
306 Культура и институты
307 Сообщества
308 Не назначено или больше не используется
309 Общее 107 Не назначено или больше не используется1 393 статистика
311 Не присвоено или более не используется
312 Не присвоено или более не используется
313 Не присвоено или более не используется
314 Общая статистика Европы
315 Общая статистика Азии
316 Общая статистика Африки
317 Общая статистика Северной Америки
318 Общая статистика Южной Америки
319 Общая статистика других частей света
320 Политология
321 Системы правительств и государств
322 Отношение государства к организованным группам
323 Гражданские и политические права
324 Политический процесс
325 Международная миграция и колонизация
326 Рабство и эмансипация
327 Международные отношения
328 Законодательный процесс
329 Не назначен или больше не используется
330 Экономика
331 Экономика труда
332 Финансовая экономика
333 Экономика земли
334 Кооперативы
335 Социализм и связанные с ней. Макроэкономика и смежные вопросы
Макроэкономика и смежные вопросы
340 Право
341 Международное право
342 Конституционное и административное право
343 Военное, налоговое, торговое, промышленное право
344 Социальное, трудовое, социальное и смежное право
345 Уголовное право
346 Частное право
347 Гражданский процесс и суды
348 Право (статуты), постановления, дела
349 Право отдельных юрисдикций и областей
350 Государственное управление
351 центральные правительства
352 местные органы власти
353 федеральные правительства США и правительства штатов
354 конкретные центральные правительства
355 военная наука
356 пехота и боевые действия
357 конные войска и боевые действия
358 Прочие специализированные силы и службы
359 Морские (военно-морские) силы и боевые действия
360 Социальные службы; ассоциация
361 Общие социальные проблемы и услуги
362 Социальные проблемы и услуги
363 Другие социальные проблемы и услуги
364 Криминология
365 Пенитенциарные учреждения
366 Ассоциация
367 Общие клубы
368 Страхование
369 Разные виды 907 образовательных ассоциаций1
371 Управление школой; специальное образование
372 Начальное образование
373 Среднее образование
374 Образование для взрослых
375 Учебные программы
376 Образование женщин
377 Школы и религия
378 Высшее образование
379 Государственное регулирование, контроль, поддержка
380 Внутренняя торговля3 817 торговля)
382 Международная торговля (внешняя торговля)
383 Почтовая связь
384 Связь Телекоммуникации
385 Железнодорожный транспорт
386 Внутренний водный и паромный транспорт
387 Водный, воздушный, космический транспорт
388 Транспорт Наземный транспорт
389 Метрология и стандартизация
390 Обычаи, этикет, фольклор
391 Костюм и внешний вид
392 Обычаи жизненного цикла и быта
393 Обычаи смерти
394 Общие обычаи
Этикет (манеры)
396 Не назначено или больше не используется
397 Не назначено или больше не используется
398 Фольклор
399 Обычаи войны и дипломатии
400S
400 Язык
401 Философия и теория
402 Miscellany
403 Dictionary & Encyclopedias
404 Специальные темы
405 Серийные публикации
406 Организации и управление
 9371 406 Организации.
9371 406 Организации. 409 География и обработка лиц
410 Языкознание
411 Системы письма
412 Этимология
413 Словари
414 Фонология
415 Структурные системы (грамматика)
416 Не назначено или больше не используется
417 Диалектология и историческая лингвистика
418 Стандартное использование Прикладная лингвистика
419 Вербальный язык без устной или письменной речи
420 Английский и древнеанглийский
421 Английская система письма и фонология
422 Английская этимология
429331 английские словари 424 Не назначено или больше не используется
425 Грамматика английского языка
426 Не назначено или больше не используется
427 Варианты английского языка
428 Стандартное использование английского языка
429 Древнеанглийский (англо-саксонский)
430 Германские языки Немецкий
431 Немецкая система письма и фонология
432 Немецкая этимология
433 Немецкие словари
434 Не присвоены или больше не используются
435 Немецкая грамматика
436 Не присвоены или больше не3 используются 437 Варианты немецкого языка
438 Стандартное использование немецкого языка
439 Другие германские языки
440 Романские языки Французский
441 Французская система письма и фонология
442 Французская этимология
443 Французские словари
444 Не назначено или больше не используется
445 Французская грамматика
446 Не назначено или больше не используется
447 Варианты французского языка
448 Стандартное использование французского языка
449 Провансальский и каталонский языки
450 Итальянский, румынский, реторомантический фонология
452 Итальянская этимология
453 Итальянские словари
454 Не присвоено или более не используется
455 Итальянская грамматика
456 Не присвоено или более не используется
457 Варианты итальянского языка
458 Стандартное использование итальянского языка
459 Румынский и ретороманский языки
460 Испанский и португальский языки
461 Испанская система письма и фонология
462 Испанская этимология
463 Испанские словари
464 Не назначено или больше не используется
4653 Испанская грамматика 4 933 больше не используется
467 Варианты испанского языка
468 Стандартное использование испанского языка
469 Португальский
470 Латинский курсив
471 Классическое латинское письмо и фонология
472 Классическая латинская этимология и фонология
473 Классические латинские словари
474 Не назначены или более не используются
475 Классическая латинская грамматика
476 Не назначены или более не используются
477 Старая, постклассическая, вульгарная латынь
478 Использование классической латыни
479 Другие итальянские языки
480 Греческие языки Классический греческий
481 Классическая греческая письменность и фонология
482 Классическая греческая этимология
483 Классические греческие словари
484 Не присвоены или более не используются
485 Классическая греческая грамматика
486 Не назначено или больше не используется
487 Доклассический и постклассический греческий язык
488 Использование классического греческого языка
489 Другие греческие языки
490 Другие языки
491 Восточно-индоевропейские и кельтские языки
492 Афро-азиатские языки Семитские
Афро-семитские 493 -Азиатские языки
494 Урало-алтайские, палеосибирские, дравидийские
495 Языки Восточной и Юго-Восточной Азии
496 Африканские языки
497 Родные языки Северной Америки
498 Родные языки Южной Америки
499 Разные языки
500S
500 Природные науки и математика
501 Философия и теория
502 ОПЛАТА
503 Dictyary & Enclopedias
504 Не назначают или не использовались в течение длительного времени
3131. 50313131313 гг. , исследования, родственные темы
50313131313 гг. , исследования, родственные темы
508 Естествознание
509 Исторические, направления, лечение лиц
510 Математика
511 Общие принципы
512 Алгебра и теория чисел
513 Арифметика
514 Топология
515 Анализ
516 Геометрия
517 Не назначено или больше не используется
518 Не назначено или больше не используется
519 Вероятность и прикладная математика
520 Астрономия
522 Техника, оборудование, материалы
523 Конкретные небесные тела и явления
524 Не присвоены или более не используются
525 Земля (астрономическая география)
526 Математическая география
527 Целесологическая навигация
528 Эфемериды
529 Хронология
530 Физика
531 Классическая механика Сплошная механика
532 Жидкая механика
533 Парики
534 Sound & Связанная вибрация
533 Парики
534 Sound & Связанная вибрации
533 333 Парики
534 Sound & Связанная вибрация
533 Парики
. 538 Магнетизм
538 Магнетизм
539 Современная физика
540 Химия и смежные науки
541 Физическая и теоретическая химия
542 Техника, оборудование, материалы
543 Аналитическая химия
544 Качественный анализ
545 Количественный анализ
546 Неорганическая химия
547 Органическая химия
548 Кристаллография
549 Минералология
550 Земли
551 549 ГИДОЛОГИЯ
55.
555 Науки о Земле Азии
556 Науки о Земле Африки
557 Науки о Земле Северной Америки
558 Науки о Земле Южной Америки
559Earth sciences of other areas
560 Paleontology Paleozoology
561 Paleobotany
562 Fossil invertebrates
563 Fossil primitive phyla
564 Fossil Mollusca & Molluscoidea
565 Other fossil invertebrates
566 Fossil Vertebrata (Fossil Craniata)
567 Fossil cold-blooded vertebrates
568 Fossil Aves (Ископаемые птицы)
569 Ископаемые млекопитающие
570 Науки о жизни
571 Не назначено или больше не используется
572 Биохимия
573 Физическая антропология
574 Biology
575 Evolution & genetics
576 Microbiology
577 General nature of life
578 Microscopy in biology
579 Collection and preservation
580 Botanical sciences
581 Botany
582 Spermatophyta (Seed-bearing plants)
583 Dicotyledones
584 Monocotyledones
585 Голосеменные (Pinophyta)
586 Cryptogamia (бессемянные растения)
587 Pteridophyta (сосудистые криптограммы)
588 Bryophyta
589 Thallobionta & Prokaryotae
590 Zoological sciences
591 Zoology
592 Invertebrates
593 Protozoa, Echinodermata, related phyla
594 Mollusca & Molluscoidea
595 Other invertebrates
596 Vertebrata (Craniata, Vertebrates)
597 Cold-blooded vertebrates Fishes
598 Aves (Birds)
599 Mammalia (Млекопитающие)
The 600s
600 Технологии (Прикладные науки)
601 Философия и теория
602 Разное
603 Словари и энциклопедии
604 Специальные темы
605 Серийные публикации
606 Организации
607 Образование, исследования, смежные темы
608 Изобретения и патенты
609 Исторические, направления, лечение людей
610 Медицинские науки Медицина
611 Анатомия человека, цитология, гистология
614 Заболеваемость и профилактика заболеваний
615 Фармакология и терапия
616 Болезни
617 Хирургия и родственные медицинские специальности
618 Гинекология и другие медицинские специальности
619 Экспериментальная медицина
620 Инженерное дело и смежные операции
621 Прикладная физика
622 Горное дело и родственные операции
623 Военная и морская инженерия
624 Гражданское строительство
625 Строительство железных дорог, дорог1 Не присвоено или нет 626731
627 Гидротехника
628 Санитарно-коммунальное хозяйство
629 Прочие отрасли машиностроения
630 Сельское хозяйство
631 Техника, оборудование, материалы
632 Повреждения растений, болезни, вредители
633 Полевые и плантационные культуры
634 Сады, фрукты, лесное хозяйство
635 Садовые культуры (садоводство)
636 Животноводство
637 Переработка молочных и сопутствующих продуктов
638 Разведение насекомых
639 Охота, рыболовство, сохранение
640 Домашнее хозяйство и семейный быт
641 Еда и напитки
642 Питание и сервировка стола
643 Жилье и бытовая техника
644 Коммунальные услуги
645 Предметы домашнего обихода
646 Шитье, одежда, личное жилище
647 Ведение общественного хозяйства
648 Ведение домашнего хозяйства
649 Воспитание детей и уход на дому за больными
650 Управленческие и вспомогательные услуги
651 Офисные услуги
652 Процессы письменного общения
653 Стенография
654 Не назначено или больше не используется
655 Не назначено или больше не используется
656 Не назначено или больше не используется
657 Бухгалтерский учет
658 Общее руководство
659 Реклама и связи с общественностью
660 Химическое машиностроение
661 Промышленная химическая технология
662 Взрывчатые вещества, технология топлива
663 Технология производства напитков
664 Технология пищевых продуктов
665 Промышленные масла, жиры, воски, газы
666 Керамические и родственные технологии
667 Очистка, окрашивание, родственные технологии прочих органических продуктов
669 Металлургия
670 Производство
671 Металлообработка и изделия из металла
672 Железо, сталь, другие сплавы железа
673 Цветные металлы
674 Обработка древесины, изделия из дерева, пробка
675 Обработка кожи и меха
676 Целлюлозно-бумажная технология
677 Текстиль
678 Эластомеры и изделия из эластомеров
679 Прочие изделия из специальных материалов
680 Производство специального назначения и других устройств
681 Прецизионные инструменты
682 Мелкие кузнечные работы (кузнечное дело)
683 Скобяные изделия и бытовые приборы
684 Мебель и бытовые мастерские
685 Кожа, мех, сопутствующие товары
686 Печатная и родственная деятельность
687 Одежда
688 Прочая конечная продукция и упаковка
689 Не присвоено или больше не используется
690 Здания
691 Строительные материалы
692 Вспомогательные строительные работы
693 Специальные материалы и цели
694 Деревянное строительство Плотницкие работы покрытие
696 Коммунальные услуги
697 Отопление, вентиляция, кондиционирование
698 Детальная отделка
699 Не присвоено или больше не используется
700-е
700 The Arts
701 Философия и теория
702 Miscellany
703 Словарь и энциклопедии
704 Специальные темы
705 Серийные публикации
706 Организации и управление
707 Образование, исследование
706 Организации и управление
707 Образование, исследование
706 Организации и управление
707 Образование, исследования
706 Организации и управление. Историческое, районное, личное обращение
Историческое, районное, личное обращение
710 Гражданское и ландшафтное искусство
711 Планировка территории (гражданское искусство)
712 Ландшафтная архитектура
713 Ландшафтная архитектура проезжих частей
714 Водоемы
715 Древесные растения
716 Травянистые растения
717 Строения
718 Ландшафтный дизайн кладбищ
719 Природные ландшафты
720 Архитектура
721 Архитектурное сооружение
722 Архитектура до ок. 300
723 Архитектура ок. с 300 по 1399
724 Архитектура с 1400 года
725 Общественные сооружения
726 Здания религиозного назначения
727 Здания для образования и научных исследований
728 Жилые и смежные здания
729 Дизайн и украшение
730 Пластические искусства Скульптура
731 Процессы, формы, объекты скульптуры
732 Скульптура до ок. 500
733 Греческая, этрусская, римская скульптура
734 Скульптура ок. 500–1399
735 Скульптура от 1400
736 Резьба и резьба
737 Numismatics & Sigillography
738 Ceramic Arts
739 Art Metalwork
740 Рисунок и декоративные искусства
741 Rawings
740 Рисунок и декоративные искусства
741 Rawings
740 Rhailing & Decorative Arts. 3731 744 Не присвоено или больше не используется
3731 744 Не присвоено или больше не используется
745 Декоративно-прикладное искусство
746 Текстильное искусство
747 Оформление интерьера
748 Стекло
749 Мебель и аксессуары
750 Живопись и живопись
751 Техника, оборудование, формы
7 Символ55 Цвет
7 , легенда
754 Жанровые картины
755 Религия и религиозная символика
756 Не присвоено или больше не используется
757 Человеческие фигуры и их части
758 Прочие сюжеты
759 Исторические, местности, трактовка лиц
760 Графическое искусство Эстамп и гравюры
761 Рельефные процессы (печать)
762 Не назначено или более не используется
763 Литографические (планографические) процессы
764 Хромолитография и шелкография
765 Гравюра по металлу
766 Меццо- иглы и связанные с ними процессы 937
768 Не присвоено или более не используется
769 Печатные издания
770 Фотография и фотографии
771 Техника, оборудование, материалы
772 Процессы получения солей металлов
773 Пигментные процессы печати
774 Голография
775 Не присвоено или более не используется
776 Не присвоено или более не используется
777 Не присвоено или более не используется
778 Области и виды фотографии
779 Фотографии
780 Музыка
781 Общие принципы и музыкальные формы
782 Вокальная музыка
783 Музыка для одиночных голосов Голос
784 Инструменты и инструментальные ансамбли
785 Камерная музыка
786 Клавишные и другие инструменты
787 Струнные инструменты (хордофоны)
788 Духовые инструменты (аэрофоны)
789 Не назначены или больше не используются
790 Рекреационное и исполнительское искусство
791 Публичные выступления
792 Сценические представления
793 Игры и развлечения в помещении
794 Игры на ловкость в помещении
795 Азартные игры
795 Спортивные игры
спорт и игры на открытом воздухе
797 Водные и воздушные виды спорта
798 Конный спорт и гонки на животных
799 Рыбалка, охота, стрельба
800-е
800 Литература и риторика
801 Философия и теория
802 Сборник
803 Словари и энциклопедии
804 Не присвоено или больше не используется
805 Серийные издания
806 Организации
807 Образование, исследования, родственные темы
808 Литература и критика1 история 317 810-818 – Практики UIUC см. по этой ссылке
по этой ссылке
810 Американская литература на английском языке
811 Поэзия
812 Драма
813 Художественная литература
814 Эссе
815 Речи
816 Letters
817 Satire & humor
818 Miscellaneous writings
819 Not used
820-829
820 English & Old English literatures
821 English poetry
822 English drama
823 English fiction
824 English essays
825 English speeches
826 English письма
827 Английская сатира и юмор
828 Разные английские сочинения
829 Древнеанглийский (англо-саксонский)
830-839
Для Произведения отдельного автора или о нем, порядок цитирования состоит в том, чтобы сначала классифицировать вместе все работы автора или об авторе, а затем подразделять по схеме нумерации книг. Первый компонент номера вызова выполняется с использованием сокращенного или модифицированного номера класса Дьюи и номера авторского резака. Далее следует местный номер книги UIUC:
830 Литературы на германских языках
831 От начала до 1517 г.
832 Реформация и т. д. 1517–1750
833 Классический период, 1750–1830 гг.40/50
835 Современные авторы, еще не внесенные в каталог UIUC, 1940/50-
836 Немецкая диалектная литература
837 Немецко-американская
838 Разные немецкие сочинения
839 Другая германская литература
840-849
Для произведений об отдельном авторе, порядок цитирования состоит в том, чтобы сначала классифицировать вместе все работы автора или об авторе, а затем подразделять по схеме нумерации книг. Первый компонент номера вызова выполняется с использованием сокращенного или модифицированного номера класса Дьюи и номера авторского резака. Затем следует местный номер книги UIUC: 9.3731 840 Литература на романских языках
841 Древнефранцузский и раннефранцузский до 1400 г.
842 Переходный и ренессансный периоды, 1400-1600 гг.
843 Классический период, 1600-1715 гг. -1940/50
846 Современные авторы, еще не внесенные в Каталог UIUC, 1940/50-
847 Французско-канадский
848 Провансальский
849 Французская диалектная литература
850-859
Для произведений отдельного автора или о нем порядок цитирования состоит в том, чтобы в первую очередь классифицировать вместе все работы автора или об авторе, а затем подразделять по схеме нумерации книг. Первый компонент номера вызова выполняется с использованием сокращенного или модифицированного номера класса Дьюи и номера авторского резака. Далее следует местный номер книги UIUC:
Первый компонент номера вызова выполняется с использованием сокращенного или модифицированного номера класса Дьюи и номера авторского резака. Далее следует местный номер книги UIUC:
850 Итальянский, румынский, ретороманский
851 Ранний период до 1375 г.3731 855 1814-1940/50
856 Работы в и/или Около Итальянских диалектов
857 Сардинский
858 румын (включая Wallachian)
859 Rumansh, Rhastian, Rhaeto-Ramanic,
859 Rumansh, Rhastian, Rhaeto-Ramanic,
859 Rumansh, Rhastian, Rhastianianic,
859, Rumansh, Rhastian, Rhastian. Произведения отдельного автора или об отдельном авторе , порядок цитирования таков: в первую очередь объединяются все работы автора или об авторе, а затем подразделяются по схеме нумерации книг. Первый компонент номера вызова выполняется с использованием сокращенного или модифицированного номера класса Дьюи и номера авторского резака. Затем следует местный номер книги UIUC: 9. 3731 860 Испанская и португальская литература
3731 860 Испанская и португальская литература
861 С начала 1400 г.
862 1400–1553
863 Золотой век, 1554–1700 гг.
867 Каталанский
868 Португальский
869 Литература Южной/Центральной Америки
870-889
870 Общие работы по латинской литературе
871 Латинские авторы
872 Сборники латинской прозы или поэзии
873 Не используется
874 Не используется
875 Средневековая и современная латинская литература, 500 г. н.э. – дата
876 Не используется
877 Не используется
878 Не используется
879 Классическая литература-История и критика1 807 Греческая литература Классический греческий язык
881 Греческие авторы
882 Сборники греческой прозы или поэзии
883 Не используется
884 Не используется
885 Современная литература на древнегреческом языке
886 Не используется
887 Не используется
888 Not Used
889 Literature in Medieval and Modern Greek
890-891.49 Indic Literature
891. 5 Iranian/Persian Literature
5 Iranian/Persian Literature
891.6 Celtic/Gaelic Literature
891.7 Slavic and Baltic Literatures
892-894 Afro-Asiatic Literature (Hamito-Semitic)
895–896 Литература на языках Восточной Азии и Африки
897–898 Родные языки Северной и Южной Америки
899 Другая литература
900-е годы
900 География и история
901 Философия и теория
902 Разное
903 Словари и энциклопедии
904 Сборник отчетов о событиях
905 Серийные публикации
906 Организации и управление
907 Образование, исследования, родственные темы
908 По роду деятельности людей
909 Всемирная история
909 и путешествия
911 Историческая география
912 Графические изображения земли
913 Древний мир
914 Европа
915 Азия
916 Африка
917 Северная Америка
918 Южная Америка
919 Другие районы
920 Биография, генеалогия, знаки различия
921 Не присвоено или более не используется
922 Не присвоено или более не используется
923 Не присвоено или более не используется
924 Не присвоено или более не используется
925 Не присвоено или более не используется
926 Не присвоено или более не используется
927 Не присвоено или более не используется
928 Не присвоено или более не используется
929 Генеалогия, имена, знаки различия
930 История древнего мира
931 История древнего мира Китай
932 История древнего мира Египет
933 История древнего мира Палестина
934 История древнего мира Индия
935 История древнего мира Месопотамия и Иранское нагорье
936 История древнего мира Европа к северу и западу от Италии
937 История древнего мира Италия и сопредельные территории
938 История древнего мира Греция
939 История древнего мира Другие части древнего мира
940 Всеобщая история Европы
941 Всеобщая история Европы Британские острова
942 Всеобщая история Европы Англия и Уэльс
943 Всеобщая история Европы Центральная Европа Германия
944 Всеобщая история Европы Франция и Монако
945 Всеобщая история Европы Итальянский полуостров и прилегающие острова
946 Всеобщая история Европы Пиренейский полуостров и прилегающие острова
947 Общая история Европы Восточная Европа Советский Союз
948 Общая история Европы Северная Европа Скандинавия
949 Всеобщая история Европы Другие части Европы
950 Всеобщая история Азии Дальнего Востока
951 Всеобщая история Азии Китая и сопредельных территорий
952 Всеобщая история Азии Япония
953 Всеобщая история Азии Аравийского полуострова и сопредельных территорий
954 Всеобщая история Азии Южная Азия Индия
955 Всеобщая история Азии Иран
956 Всеобщая история Азии Ближний Восток (Ближний Восток)
957 Всеобщая история Азии Сибирь (Азиатская Россия)
958 Всеобщая история Азии Средняя Азия
959 Всеобщая история Азии Юго-Восточная Азия
960 Всеобщая история Африки
961 Всеобщая история Африки Тунис и Ливия
962 Всеобщая история Африки Египет и Судан
963 Всеобщая история Африки Эфиопия
964 Всеобщая история Африки Марокко и Канарские острова
965 Всеобщая история Африки Алжир
966 Всеобщая история Африки Западная Африка и прибрежные острова
967 Всеобщая история Африки Центральная Африка и прибрежные острова
968 Всеобщая история Африки Южная Африка
969 Всеобщая история Африки Юг островов Индийского океана
970 Всеобщая история Северной Америки
971 Всеобщая история Северной Америки Канада
972 Всеобщая история Северной Америки Средняя Америка Мексика
973 Всеобщая история Северной Америки США
973,7 L63 Используется для Авраама Lincoln Works
974 Всеобщая история Северной Америки Северо-восток США
975 Всеобщая история Северной Америки Юго-восток США
976 Всеобщая история Северной Америки Южно-центральная часть США
977 Всеобщая история Северной Америки Северо-центральная часть Соединенных Штатов
978 Всеобщая история Северной Америки Западная часть Соединенных Штатов
979 Всеобщая история Большого бассейна Северной Америки и Тихоокеанского склона
980 Всеобщая история Южной Америки
981 Всеобщая история Южной Америки Бразилия
982 Всеобщая история Южной Америки Аргентина
983 Всеобщая история Южной Америки Чили
984 Всеобщая история Южной Америки Боливия
985 Всеобщая история Южной Америки Перу
986 Всеобщая история Южной Америки Колумбия и Эквадор
987 Всеобщая история Южной Америки Венесуэла
988 Всеобщая история Южной Америки Гвиана
989 Всеобщая история Южной Америки Парагвая и Уругвая
990 Всеобщая история других областей
991 Не присвоено или более не используется используется
992 Не назначен или больше не используется
993 Всеобщая история других областей Новая Зеландия
994 Всеобщая история других областей Австралия
995 Общая история других областей Меланезия Новая Гвинея
996 Общая история других областей Другие части Тихоокеанской Полинезии
997 Общая история других областей Острова Атлантического океана
998 Общая история других областей Арктические острова и Антарктида
999 Внеземные миры
Загрузка библиотеки, часов. ..
..
Tweets by @uilislib
Сколько существует типов систем счисления?
Система счисления включает в себя различные типы чисел, например, простые числа, нечетные числа, четные числа, рациональные числа, целые числа и т. д. Эти числа могут быть выражены как цифрами, так и словами соответственно. Например, такие числа, как 40 и 65, выраженные в виде цифр, также могут быть записаны как сорок и шестьдесят пять.
A Система счисления или Система счисления определяется как элементарная система для выражения чисел и цифр. Это уникальный способ представления чисел в арифметической и алгебраической структуре.
Числа используются в различных арифметических значениях, применимых для выполнения различных арифметических операций, таких как сложение, вычитание, умножение и т. д., которые применяются в повседневной жизни для целей вычислений. Значение числа определяется цифрой, ее разрядностью в числе и основанием системы счисления. Числа, как правило, также известные как цифры, представляют собой математические значения, используемые для подсчета, измерений, маркировки и измерения основных величин.
Числа, как правило, также известные как цифры, представляют собой математические значения, используемые для подсчета, измерений, маркировки и измерения основных величин.
Типы чиселЧисла — это математические значения или цифры, используемые для измерения или вычисления величин. Он представлен цифрами как 2, 4, 7 и т. д. Примерами чисел являются целые числа, целые числа, натуральные числа, рациональные и иррациональные числа и т. д.
Существуют различные типы чисел классифицируются на наборы по системе счисления. Типы описаны ниже,
- Натуральные числа: Натуральные числа — это положительные числа, которые считаются от 1 до бесконечности. Множество натуральных чисел представлено ‘N’. I t — это числа, которые мы обычно используем для счета. Набор натуральных чисел может быть представлен как N = 1, 2, 3, 4, 5, 6, 7,…
- Целые числа: Целые числа — это положительные числа, включая ноль, который считается от 0 до бесконечности.
 Целые числа не включают дроби или десятичные дроби. Набор целых чисел представлен ‘W’. Пример: W = 0, 1, 2, 3, 4, 5,…
Целые числа не включают дроби или десятичные дроби. Набор целых чисел представлен ‘W’. Пример: W = 0, 1, 2, 3, 4, 5,… - Целые числа: Целые числа представляют собой набор чисел, включающий все положительные числа, нуль, а также все отрицательные числа, которые считаются от отрицательной бесконечности. до положительной бесконечности. В наборе нет дробей и десятичных знаков. Набор целых чисел обозначается «Z». Пример: Z = …..,-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5,…
- Десятичные числа: Любое числовое значение, состоящее из десятичная точка — это десятичное число. Его можно выразить как 2,5, 0,567 и т. д.
- Вещественное число: Вещественные числа — это заданные числа, не содержащие мнимых значений. Он включает в себя все положительные целые числа, отрицательные целые числа, дроби и десятичные значения. Обычно он обозначается ‘R’.
- Комплексное число: Комплексные числа — это набор чисел, включающий мнимые числа.
 Его можно выразить как a+bi, где «a» и «b» — действительные числа. Обозначается ‘C’.
Его можно выразить как a+bi, где «a» и «b» — действительные числа. Обозначается ‘C’. - Рациональные числа: Рациональные числа — это числа, которые можно представить как отношение двух целых чисел. Он включает в себя все целые числа и может быть выражен в виде дробей или десятичных знаков. Обозначается цифрой ‘Кью’.
- Иррациональные числа: Иррациональные числа — это числа, которые не могут быть выражены дробями или отношениями целых чисел. Он может быть записан десятичными знаками и иметь бесконечные неповторяющиеся цифры после запятой. Обозначается «P».
Система счисления — это метод записи чисел, представляющий собой математический способ представления чисел данного набора с использованием чисел или символов математическим способом.
Система записи для обозначения чисел с использованием цифр или символов в логическом порядке определяется как система счисления. Система счисления Представляет полезный набор чисел, отражает арифметическую и алгебраическую структуру числа и обеспечивает стандартное представление. Из цифр от 0 до 9 можно составить все числа.
Система счисления Представляет полезный набор чисел, отражает арифметическую и алгебраическую структуру числа и обеспечивает стандартное представление. Из цифр от 0 до 9 можно составить все числа.
С помощью этих цифр любой может составить бесконечное число. Например, 156,3907, 3456, 1298, 784859 и т.д.
Типы систем счисленияВ зависимости от базового значения и количества разрешенных цифр существует множество типов систем счисления. The four common types of Number systems are:
- Decimal Number System
- Binary Number System
- Octal Number System
- Hexadecimal Number System
Decimal Number System
Number system с базовым значением 10 называется десятичной системой счисления. Он использует 10 цифр, т.е. 0-9для создания номеров. Здесь каждая цифра в числе находится в определенном месте, а разрядное значение является произведением различных степеней 10. Здесь разрядное значение обозначается справа налево как первое разрядное значение, называемое единицами, второе слева как десятки и т. д. Сотни, тысячи и т. д. Здесь единицы имеют разрядное значение как 100, десятки имеют разрядное значение как 101, сотни как 102, тысячи как 103 и так далее.
Здесь разрядное значение обозначается справа налево как первое разрядное значение, называемое единицами, второе слева как десятки и т. д. Сотни, тысячи и т. д. Здесь единицы имеют разрядное значение как 100, десятки имеют разрядное значение как 101, сотни как 102, тысячи как 103 и так далее.
Например, 12265 имеет следующие разряды:
(1 × 10 4 ) + (2 × 10 3 ) + (2 × 10 2 ) + (6 × 10 1 ) + (5 × 10 0 )
= (00) + (10) + (10) 2 × 1000) + (2 × 100) + (6 × 10) + (5 × 1)
= 10000 + 2000 + 200 + 60 + 5 с базовым значением 2 называется двоичной системой счисления. Он использует 2 цифры, то есть 0 и 1 для создания чисел. Числа, образованные из этих двух цифр, называются двоичными числами. Двоичная система счисления очень полезна в электронных устройствах и компьютерных системах, потому что ее можно легко реализовать, используя всего два состояния ВКЛ и ВЫКЛ, то есть 0 и 1.
Десятичные числа 0-9 представлены в двоичном виде как: 0, 1, 10, 11, 100, 101, 110, 111, 1000 и 1001
Например, 14 можно записать как 1110, 19 можно записать как 10011, 50 может быть написано как 110010.
Пример 14 в бинарной системе
Бинар 14
Здесь 14 может быть написано как 1110
Октал. один, в котором базовое значение равно 8. Он использует 8 цифр, т.е. 0-7, для создания восьмеричных чисел. Восьмеричные числа можно преобразовать в десятичные значения, умножив каждую цифру на разрядное значение, а затем сложив результат. Здесь значения мест равны 80, 81 и 82. Восьмеричные числа полезны для представления чисел UTF8. Пример,
(81) 10 can be written as (121) 8
(125) 10 can be written as (175) 8
Hexadecimal Number System
Number System with базовое значение 16 называется шестнадцатеричной системой счисления.
Он использует 16 цифр для создания своих номеров. Цифры от 0 до 9 принимаются как цифры в десятичной системе счисления, но цифры от 10 до 15 представлены как A-F, т.е. 10 представлен как A, 11 как B, 12 как C, 13 как D, 14 как E, и 15 как F. Шестнадцатеричные числа полезны для обработки адресов памяти. Примеры,
(185) 10 может быть написано как (B9) 16
(5440) 10 может быть написано как (1540) 16
(4265) . 10A9) 16
Hexadecimal 0 1 2 3 4 5 6 7 8 9 A B C D E F Decimal 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Примеры вопросов
Вопрос 1: Преобразовать 4525 8 в десятичное число?
Решение:
4525 8 = 4 × 8 3 + 5 × 8 2 + 2 × 8 1 + 5 × 8 0
= 4 × 512 + 5 × 64 + 2 × 8 + 5 × 10003
= 2048 + 320 + 16 16 + 5 × 10003
= 2048 + 320 + 16.
+ 5
= 2389 10
Вопрос 2. Преобразовать (17) 10 9319 в двоичное число?
Решение:
двоичный 17
Следовательно (17) 10 = (10001) 2
Вопрос 3: Преобразование (1011110) 2 в восьмеричное число .
Solution:
Given (1011110) 2 a binary number, to convert it into octal number
Octal Number Binary Number 0 000 1 001 2 010 3 011 4 100 5 101 6 110 7 111 Using this table we can write give number as
001 011 110 i .
e
001 = 1
011 = 3
110 = 6
Итак, (1011110) 2 в восьмеричном числе равно (136) 8
Как использовать права доступа к файлам UNIX и Linux
Введение
В этом документе объясняется, как устанавливаются права доступа к каталогам и файлам на компьютере с UNIX или Linux, и как пользователь может их изменить. Это позволяет вам делиться файлами или каталогами или заблокировать их, чтобы они были частными. Если вы хотите установить права доступа к файлу или каталогу, щелкнув правой кнопкой мыши файл или каталог и установив или сняв флажки, вы можете сделать это в графическом интерфейсе программного обеспечения для передачи файлов, например, с помощью MobaXterm, клиента SSH Secure Shell, WinSCP и т. д. Если вы вошли в систему Linux с Xsession, вы можете использовать эквивалент Windows Explorer для Linux с командами nautilus или konqueror.
В противном случае этот документ предоставляет полное объяснение того, как работает команда UNIX chmod.
Вы можете увидеть права доступа к вашему файлу с помощью команды ls с параметром -l (нижняя буква L, а не 1):
% ls -l myfile.txtвернет длинную строку информации, которая начинается с прав доступа к файлу:
-rw-r--r--Разрешения
Каждый файл и каталог в UNIX или Linux имеет связанный с ним набор разрешений, который отображается в виде трехзначного числа (например, 755). Эти разрешения подразделяются на три группы, которые имеют или не имеют разрешения:
- владелец файла
- группа владельцев
- все остальные, кто имеет доступ к серверу (именуемые «другие»)
Эти три группы, в свою очередь, могут иметь или не иметь три разных привилегии:
Привилегия Определение читать (прав) разрешено чтение, открытие, просмотр и копирование файла запись (ж) запись, изменение, удаление и сохранение файла разрешены выполнить (х) выполнение и вызов файла разрешены. Это необходимо для каталогов, чтобы разрешить поиск и доступ.
Таким образом, всего девять переменных:
- разрешение для владельца:
1. прочитать файл
2. запись в файл
3. выполнить файл
- разрешение для членов группы владельца:
1. прочитать файл
2. запись в файл
3. выполнить файл
- разрешение для других:
1. прочитать файл
2. запись в файл
3. выполнить файл
Эти переменные организованы в массив три на три следующим образом:
группа владельцев другоечтение (р) 4 4 4запись (ж) 2 2 2выполнить (x) 1 1 1----------- ----- ----- -----общая стоимость 7 7 7Значения столбцов
Массив три на три выше показывает основу для описания набора из девяти разрешений.
Обратите внимание, что каждое разрешение имеет связанное с ним числовое значение:
Значение Разрешение 4 читать (р) 2 запись (ж) 1 выполнить (х) Если разрешение отклонено, то его значение всегда равно нулю. (В приведенном выше примере все разрешения были предоставлены.) Для каждой категории пользователей (владелец, член группы и т. д.) эти три значения разрешений потенциально могут составлять семь. Если мы отклоняем один или несколько типов разрешений, то это значение (4, 2 или 1) вычитается из значения для этой категории пользователей. Таким образом, если мы хотим отказать в разрешении на запись группе владельца, мы вычитаем 2 из общего количества этих разрешений, в результате чего значение столбца остается равным 5.
И если мы хотим запретить как запись, так и выполнение разрешений «другим», мы вычитаем и 2, и 1, оставив значение 4. Эти изменения показаны в таблице ниже:
группа владельцев прочеечтение (р) 4 4 4запись (ж) 2 0 0выполнить (x) 1 1 0----------- ----- ----- -----общая стоимость 7 5 4Общее значение теперь равно 754, а не 777. Обратите внимание, что какую бы комбинацию разрешений мы ни создали, числа всегда будут уникальным представлением этой комбинации, как показано на следующей диаграмме:
Разрешения на значение столбца, представленные------------ ----------- --------------0 нет ---1 только для выполнения --x2 запись -w-3 выполнить и записать -wx4 только для чтения r--5 чтение и выполнение r-x6 чтение и запись rw-7 чтение, запись и выполнение rwxОбщая стоимость
Точно так же, как каждый столбец обозначает определенную комбинацию разрешений, общее значение представляет собой определенную комбинацию разрешений, связанных с типами пользователей, поскольку порядок всегда задается как: владелец группа другое.
Таким образом, из любого трехзначного общего значения вы можете вывести каждое из девяти возможных разрешений. Это трехзначное «общее значение» (в приведенных выше примерах 777 и 754) используется при определении и изменении разрешений, как описано ниже. Помните, что это общее значение всегда указывается в следующем порядке: владелец, группа, другие.
Установка разрешений
Если вы хотите установить режим файла (установить разрешения), вы используете команду UNIX chmod в системной подсказке. Когда вы познакомитесь с командой chmod, попробуйте использовать параметр -v для подробного ответа, как в следующем примере:
% chmod -v 640 myfile.txtрежим `myfile.txt' изменен на 0640 (rw-r-----)Эта команда указывает, что файл с именем myfile.txt имеет разрешение на чтение и запись (rw-) для владельца (вас), разрешение только на чтение (r–) для членов группы и отсутствие прав доступа для других (—). Помните, что разрешения для «владельца» всегда являются первыми, а разрешения для «другого» всегда последними.
Установка разрешений для каталога происходит точно так же; вы просто замените имя каталога на имя файла.
Вы также можете использовать буквы r, w и x для установки разрешений на чтение, запись и выполнение, а также буквы u, g, o и a для указания пользователя, группы, другого или всех:
% chmod -v a+x myfile.txtрежим `myfile.txt' изменен на 0751 (rwxr-x--x)Приведенное выше добавляет права на выполнение для всех пользователей.
В этом примере членам группы предоставляется разрешение только на чтение:
% chmod -v g=r myfile.txtрежим `myfile.txt' изменен на 0741 (rwxr----x)Вот несколько примеров того, что , если сделать это в следующем порядке , установит разрешения, как показано:
Команда (эквивалентная команда в системе счисления) Разрешения chmod a=rwx myfile. txt
chmod 777 myfile.txt rwxrwxrwx chmod о = myfile.txt chmod 770 myfile.txt -rwxrwx— chmod g=w myfile.txt chmod 720 myfile.txt -rwx-w—- chmod go=r myfile.txt chmod 744 myfile.txt -rwxr–r– chmod g+x myfile.txt chmod 754 myfile.txt -rwxr-xr– chmod или myfile.txt chmod 750 myfile.txt -rwxr-х— Установка разрешений без указания u, g, o или a
Разрешения установлены для пользователя, группы и других, если u, g, o или a не указаны, но в игру вступает ваша umask (маска создания пользовательского файла), что усложняет ситуацию.
Наиболее распространенный umask — 022, что означает, что при создании нового каталога разрешения по умолчанию не 777 (drwxrwxrwx), а скорее 777 — 022, то есть 755 (drwxr-xr-x). И когда вы создаете новый файл, разрешения по умолчанию не 666 (-rw-rw-rw-), а скорее 666–022, что равно 644 (-rw-r–r–).
Если ваш umask является наиболее распространенным umask из 022, произойдет следующее:
Команда (эквивалентная команда в системе счисления) Разрешения chmod =rwx myfile.txt chmod 755 myfile.txt -rwxr-xr-х chmod -wx myfile.txt chmod 444 myfile.txt -р–р–р– chmod +x myfile.txt chmod 555 myfile.txt -r-xr-xr-x Последний пример часто используется в документации, когда пользователю предлагается сделать файл исполняемым.
Причина использования системы счисления вместо системы букв для установки разрешений заключается в том, что использование чисел позволяет вам устанавливать разные разрешения для пользователя, группы и других в одном запросе команды chmod и не зависит от того, как разрешения в настоящее время установлены. Рекомендуется использовать параметр -v (подробный) команды chmod, чтобы увидеть, на что изменились разрешения, поскольку ваш umask мог сыграть роль в создании разрешений.
Пути и разрешения
Чтобы вы могли установить разрешения для файла или каталога, UNIX должна сначала иметь возможность найти этот файл или каталог. Таким образом, если вы не находитесь в каталоге, содержащем файл или каталог, для которого вы устанавливаете разрешения, вы должны указать путь. Например, если вы находитесь в своем домашнем каталоге и хотите установить разрешения для файла с именем myfile.txt в каталоге с именем files, расположенном в вашем домашнем каталоге, вы должны использовать следующую команду:
% chmod -v 644 файла/myfile.txt
режим `files/myfile.txt' изменен на 0644 (rw-r--r--)Определение текущих разрешений
Чтобы определить текущие разрешения для файла или каталога, используйте команду ls с параметром -l (строчная буква «L», а не цифра один «1»), как в следующем примере:
% ls -l myfile.txtСлева от результирующей строки вывода будет список разрешений, выраженный последовательностью из десяти букв и дефисов. Последние девять пробелов разделены на группы по три, каждая из которых будет иметь по порядку r (чтение), w (запись) и x (выполнение) или, если это разрешение было отклонено владельцем файла, дефис (-) в своем пробеле. Как и при настройке разрешений, три группы по три даны в следующем порядке: владелец, группа, другое. Например, файл, режим которого был установлен выше как 644, будет иметь буквы:
-rw-r--r--Эта последовательность показывает, что «myfile.txt» — это обычный файл (первый дефис; «d» в этом местоположении указывает каталог) с правами на чтение и запись для владельца (rw-), права только на чтение для группы владельцев члены ( r–) и разрешение только для чтения для других ( r– ).
Если мы снова изменим режим с помощью команды:
% chmod -v 765 myfile.txtрежим `files/myfile.txt' изменен на 0644 (rw-r--r--), тогда команда ls -l myfile.txt будет отображаться как разрешения:
-rwxrw-rxЕстественно, только владелец может изменять разрешения для файла или каталога.
Права доступа к каталогам и файлам
UNIX — это среда «сверху вниз». Это означает, что если вы запретите «групповые» или «другие» разрешения для каталога, всем подкаталогам и файлам в этом каталоге будет отказано в разрешениях, установленных на уровне каталога, хотя настройки не изменятся. Например, если права доступа к проектам каталогов: drwxr-xr-x, а для подкаталога project1: drwxr-xr-x, и вы запрещаете «групповым» и «прочим» разрешениям доступ к проектам каталогов, теперь права доступа: drwx —— разрешения подкаталога project1 визуально остаются прежними: drwxr-xr-x, но члены группы и другие на самом деле не имеют разрешений, показанных для подкаталога project1.
Это работает так же, но в обратном порядке, когда вы создаете подкаталог и устанавливаете разрешения, позволяющие членам группы и другим пользователям получать доступ к каталогу. Они не смогут получить доступ к каталогу, если у них нет разрешений на доступ ко всем предыдущим каталогам в пути к каталогу, к которому вы хотите предоставить им доступ.
Минимальное разрешение для доступа к каталогу — выполнение (x).
групп
Как обсуждалось выше, существует набор разрешений для «группы», связанной с каждым файлом и каталогом. Из этого следует, что каждый пользователь системы UNIX является членом одной или нескольких групп. Когда создается учетная запись, ее пользователь назначается группе, обычно академическому званию пользователя. Идентификационный номер группы, который отображается в записи пользователя в файле паролей, указывает на «основную» группу пользователя. Группы обозначаются как именем (например, «факультет»), так и идентификационным номером группы (201 — это номер факультета).
Номер группы произвольный, и он всегда будет больше 100. Также можно быть членом одной или нескольких «вторичных» групп. В отличие от идентификатора вашей основной группы, идентификатор вторичной группы не указан в вашей записи в файле паролей.
Чтобы просмотреть идентификаторы вашей группы и всех групп, членом которых вы являетесь, используйте команду UNIX с идентификатором:
.% идентификаторЕсли вы являетесь владельцем файла и являетесь членом более чем одной группы, вы можете изменить групповое «владение» этим файлом с помощью команды chgrp, как показано в следующем примере:
% chgrp морской myfile.txtВ этом примере «морской» — это имя группы, для которой вы хотите иметь разрешения. Обратите внимание, что это никоим образом не влияет на индивидуальное владение файлом; он просто изменяет группу, к которой применяются групповые разрешения. Только владелец может внести это изменение (и системный администратор, конечно), и владелец должен быть членом обеих вовлеченных групп, то есть группы по умолчанию, назначенной вам при создании вашего имени пользователя, и новой группы, к которой вы предоставляете разрешения.
Приступая к работе с UNIX/Linux
Система счисления майя — числа майя
Майя разработали один из первых примеров истинного нуля, но система счисления майя была значительным достижением во многих других отношениях…
копать вниз
Содержание
- Десятеричная система счисления майя
- Что такое Десятеричная система счисления?
- Система разрядов майя
- Цифры майя
- Обозначение с барной и точкой.
- Позиционная запись
- Аддитивная запись
- Мультипликативная запись
- Преобразование десятичных и десятичных чисел
- Преобразование чисел майя в десятичные числа
- Как преобразовать десятичные числа в числа майя
- Арифметические расчеты майя
- Добавление номеров Maya
- Вычетные номера Maya
- СПИСТРЕССИИ
8888 8.. Использование понятия нуля свидетельствует о его сложности, в то время как контраст между простотой записи и кажущейся сложностью системы с основанием 20 (десятеричной) продолжает очаровывать как студентов, так и ученых.Правда в том, что кажущаяся трудность заключается главным образом в незнании знаков и системы. На самом деле понять и использовать систему счисления майя несложно, но это требует определенного метода и объяснения.
Но что такое десятичная система счисления?
1- Десятичная система счисления майя
Для многих людей одним из самых сложных аспектов системы счисления майя является ее десятичная природа.
Что такое десятичная система счисления?
Чтобы объяснить, что такое десятичная система счисления, полезно начать с чего-то более знакомого. Наиболее часто используемой системой счисления является индийско-арабская система счисления, которая появилась в Европе в 11 веке нашей эры.
В индийско-арабской системе счисления значение цифры (т.е. 0-9) частично зависит от ее положения. Возьмем, к примеру, число «200»: «2» на самом деле означает «два счета до ста», потому что цифра «2» находится в «разряде сотен». Значение числа связано с его положением.
Рис. 1.1: пример числа в десятичной системе счисления2 + 90”):
В противоположность этому, древние майя использовали позиционную систему с основанием 20, также называемую «десятичной» системой счисления.
Десятичная система счисления майя
Система счисления майя была впервые описана францисканцем Диего де Ланда (1524-1579) 1 Тоззер 1941 вскоре после испанского завоевания Юкатана: от пяти до двадцати, а от двадцатых до ста и от сотен до четырехсот, и от четырехсот до восьми тысяч; и они очень часто использовали этот метод подсчета при торговле какао. У них есть и другие очень длинные подсчеты, и они продолжают их «до бесконечности», считая число 8000 двадцать раз, что составляет 160 000; затем снова эти 160 000 на двадцать, и так далее, умножая на 20 […]» 96) 3 Зайденберг 1986:380. In Mayan Yucatec, for instance, you would use:
- hun for 1
- k’al for 20
- bak’ for 400
- pik for 8,000
Это означает, что в десятеричном представлении число «2,000», например, будет «пятью счетами четыреста», тогда как буквально «два счета один».
тысяча» в десятичной системе. Майя сказали бы хо’ бак’ («пять четыреста»). Результат, тем не менее, один и тот же: 2×1000 = 5×400 = 2000. Отличаются только мысленные пути, по которым можно добраться.
В сущности, в системе счисления с основанием 20 значение каждой позиции увеличивается в степени двадцати (1, 20, 400, 8000, 160000 и т. д.) вместо десяти. Следовательно, в десятичной системе счисления мы переходим на следующую позицию после 19 (вместо 9, как в системе с основанием 10).
Рассмотрим следующие примеры:
Рис. 1.2: сравнение десятичного и десятичного счисленияЧисло «триста» записывается как «300» в десятичной системе и означает «3×100 + 0x10 + 0x1». Однако в десятичной системе «триста» — это «15×20 + 0x1», потому что числа идут в степени двадцати. Другими словами, нам нужно было бы достичь «400» (20 × 20), прежде чем добавить единицу в следующую позицию (т.е. 400 с). Это то, что происходит с «семьсот пятнадцать», потому что в десятичной системе 715 равно «1×400 + 15×20 + 15×1».
Следует признать, что использование арабских цифр (т.е. 0-9) для записи чисел в системе счисления с основанием 20 не упрощает исчисление и даже может привести к неприятным ситуациям. Представьте, что работодатель майя предлагает вам 19 долларов США.15. Вы радостно подписываете контракт, думая, что получите «19×400 + 1×20 + 5×1» (то есть 7225 в десятичной системе счисления). Но какой огромный обман, когда понимаешь, что твоя зарплата на самом деле «1×400 + 9×20 + 15×1» (т.е. 595 в десятичной системе счисления).
Древние майя, которые, конечно же, хотели избежать подобной прискорбной путаницы, придумали собственную умную систему счисления, как мы сейчас увидим.
2- Цифры майя
В то время как десятичная система счисления, такая как та, что использовалась древними майя, требует двадцати знаков для цифр от 0 до 19., он не требует двадцати разных цифр. Цифры — это отдельные знаки, которые представляют основные числовые значения. В индийско-арабской системе счисления десять различных цифр (0-9) используются для представления числовых значений от 0 до 9.
Точно так же, во избежание путаницы, идеальная десятичная система счисления должна иметь двадцать символов, таких как 0, 1, 2. , 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J. Проблема, однако, в том, что чем больше символов вы используете, тем больше сложная ваша система становится. Древние майя записывали все числа всего тремя знаками.
Но как представить любое число всего тремя символами?
Запись штрихами и точками
Около трех тысяч лет назад жители Мезоамерики придумали умное и совершенно уникальное решение: запись штрихами и точками 4 Coe 1965, Marcus 1976, Justeson 1986:440
Эта система была описана в различных этноисторических источниках и хрониках после завоевания. Вот как коренные жители Майя 17-го века выразили это словами 5 Brinton 1882:48:
«Они (наши предки) использовали (для чисел в своих календарях) точки и линии позади них; одна точка означает один год, две точки — два года, три точки — три года, четыре точки — четыре года и так далее; в дополнение к ним они использовали линию; одна строка означала пять лет, две строки — десять лет; если одна линия и над ней одна точка, шесть лет; две точки над чертой — семь лет; если три точки выше, восемь лет; если четыре точки над чертой, девять ; точка над двумя линиями — одиннадцать; если две точки, двенадцать ; если три точки тринадцать».

Таким образом, точка имеет числовое значение 1, а черта (или линия) — 5. Третий символ, такой как морская ракушка, использовался для обозначения нуля 6 Morley 1915:87-91.
Итак, в системе штрих-и-точек вам нужны только камешки, ветки и ракушки, чтобы вести учет!
Мы уже видели, что майя также использовали десятичную систему счисления с основанием 20. Это означает, что все числа до 19 были записаны в неразрядной нотации. Иными словами, значения первых двадцати цифр (0-19) находятся в самих знаках, а не в их позициях (рис. 3). Только большие числа имеют позиционный компонент.
Это очень похоже на индийско-арабскую систему счисления, где числовые значения от 0 до 9 обозначаются соответствующими цифрами 0-9. Только большие числа (например, 11, 12, 13 и т. д.) имеют позиционный компонент, значение которого увеличивается справа налево.
Вот цифры майя 0-19 в записи штрих-и-точка:
Рис.2.1: Цифры майя — запись штрих-и-точка
Писцы и художники майя не любили оставлять пустоты и пробелы. Они были достаточно щепетильны в своем подходе к эстетическим нормам. Таким образом, в числах, таких как 8 или 13, они распределяли точки равномерно, чтобы покрыть всю ширину полосы, а там, где точки отсутствовали (в числах, таких как 11 или 12), они заполняли пробелы короткими изогнутыми элементами, которые могут ввести в заблуждение:
Рис. 2.2: Цифры майя — штрихи и точки с заполнителямиЛюбой, кто хоть немного интересовался цивилизацией майя, знает о системе штрихов и точек. Однако большинство людей игнорируют тот факт, что существовал еще один набор знаков, которые использовались для обозначения двадцати цифр от 0 до 19.. Этот набор известен как числовые глифы с вариантами головы.
Числовые глифы в варианте головы
Писцы майя должны были использовать строгую систему письма, но они смогли выразить свое творчество в дизайне иероглифов. Им явно нравилось искусство каллиграфии.
.0004 Следует отметить, что варианты головы с 13 по 19 представляют собой составные портреты голов для цифр 3-9 с атрибутами глифа для 10. Эта практика согласуется с языками майя, такими как юкатек. В этом языке слова для числительных от 1 до 12 различны, но слова для числительных от 13 до 19 состоят из слова для 10 ( lahun ) и слов для числительных от 3 до 9:Чтобы внести разнообразие в свои надписи, изобилующие датами, они разработали особые и сложные глифы для представления числовых значений от 0 до 19:
- hun
- ca
- бык
- банка
- hoo
- uax
- uuc
- uaxac
- bolon
- lahun
- buluc
- lahca
- ox lahun
- can lahun
- hoo lahun
- uax lahun
- uuc lahun
- uaxac lahun
- bolon lahun
Другими словами, варианты заголовков для числительных от 13 до 19 представляют собой гибриды элементов знаков от 13 до 19.
Рис. 2.4: Варианты головок для числительных 13-19, демонстрирующие их составную природу:
Варианты головок не очень распространены в корпусе надписей майя. Возможно, из-за большого объема работы, необходимой для их рисования и вырезания, эти глифы использовались только в текстах, связанных с монументальными скульптурами, изображающими королей и королев, и встречаются только во вводной календарной последовательности этих надписей.
Изумительное графическое качество числительных в виде головы привело к тому, что мы упустили из виду один важный момент: существует не только особый символ для обозначения нуля, но и в системе счисления майя ноль также является числом. И это влечет за собой гораздо больше, чем вы можете себе представить.
3- Концепция нуля майя
Благодаря нашему образованию мы знакомы с числом ноль; что это значит и как это использовать. Но задумывались ли вы когда-нибудь, почему ученые и историки придают этому такое большое значение?
Ну, это потому, что ноль не совсем похож на любое другое число.
Краткая история Zero
1 Для получения более подробной информации см. Kaplan 1999Натуральные числа, такие как один, два или три, имеют сенсорный эквивалент: 1 корова, 2 свиньи, 3 курицы и т. д. есть что считать. С нулем это не так. Ноль не существует в чувственном мире. Это абстракция. И это надо было придумать.
На самом деле, на протяжении большей части нашей истории люди не понимали и не использовали число ноль.
Для основных математических задач, таких как подсчет крупного рогатого скота, вам в основном потребуется простой и удобный способ записи чисел и операций сложения и вычитания. Одним из наиболее интуитивно понятных решений является использование камешков (или точек при письме) или веточек (полос): одна вертикальная черта для обозначения единицы, четыре полосы для четырех, десять полос для десяти и т. д. И еще проще. , вы можете создавать группы из пяти полос, четыре по вертикали и одну поперек, чтобы легко находить и подсчитывать группы из пяти.
Все хорошо с небольшими числами, но когда записываемое количество становится больше, вы получаете ужасно много тактов (представьте, что вам нужно написать «1000» только с помощью тактов!). Столкнувшись с этими проблемами, многие ранние цивилизации экспериментировали с различными решениями для группировки, но бюрократические нужды требовали более эффективных систем счисления. Начиная с 4-го тысячелетия до нашей эры, шумеры разработали более сложные системы счисления наряду с клинописью 9.6072 8 Ифрах 2000:77-133. К 2000 г. до н.э. вавилоняне использовали мощную позиционную систему с основанием 60 с различными символами для представления конкретных величин 9 Ifrah 2000:146. Это критический элемент в разработке нуля, и мы еще вернемся к нему.
Рис. 3.1: Вавилонские клинописные цифрыЗа пределами Месопотамии египтяне, финикийцы, греки, этруски, римляне, среди прочих, пошли другим путем и использовали аддитивные системы, которых было достаточно для основных операций (т.
е. сложения и вычитания) и подсчет товаров 10 Андерсон 1971:62.
В аддитивных системах символы даются для единиц и групп единиц (например, 1, 10, 100, 1000, 10000 и т. д.). Чтобы написать число, вы просто добавляете все необходимые символы. Другими словами, значение числа — это, по сути, сложение отдельных значений каждого числа. Например, римская запись «2013» — это MMXIII, где M — 1000, X — 10, а I — 1. Таким образом, MMXIII — это буквально 1000+1000+10+1+1+1.
Рис. 3.2: Примеры аддитивных систем счисленияЭти системы счисления по-прежнему требуют неудобного количества символов, и, хотя основные операции не были слишком сложными, так как вам нужно было просто добавлять или убирать символы, представление больших чисел или выполнение более длинных вычислений было трудным, а риск ошибок был значительным 11 Ифра 2000: 187; Каплан 1999: 5-6.
«Римские цифры, по сути, были не знаками, поддерживающими арифметические действия, а просто сокращениями для записи и записи чисел. Вот почему римские счетоводы, а после них и вычислители средневековья, всегда использовали счеты со счетчиками для арифметической работы», Жорж Ифра (2000: 187)
Одна замечательная вещь, которую вы, возможно, заметили во всех этих системах, это то, что в них нет нулевой цифры. Аддитивные системы счисления не требуют использования знака для обозначения нуля. Людям может понадобиться символ, чтобы выразить «ничто», но сама система счисления не требует, чтобы числовой ноль функционировал. С другой стороны, обозначения разряда требуют цифры-заполнителя.
Но что такое цифра-заполнитель?
Возьмем, к примеру, число «2019». Как мы уже видели, значение «2» зависит от его положения. Здесь, на четвертой позиции слева, «2» на самом деле означает «2000». Затем идут «1» десятки и «9».0» (т. е. «3600+60+1=3661»).
Риск путаницы был весьма велик. Так, в VIII веке до н.э. вавилоняне стали использовать специфические знаки (три крючка или, позже, два наклонных клина) для обозначения отсутствия цифры в ряду чисел 12 Kaplan 1999:12. Очень похоже на 0 в 2019 году.
Вавилонский нулевой заполнитель использовался, однако, только в середине числа, никогда в его конце, как мы делаем в числах, таких как 1200, и никогда сам по себе. Это еще не был настоящий ноль. Это не рассматривалось как цифра или число, а скорее как отсутствие. Тем не менее, это был первый экземпляр знака, специально предназначенного для обозначения нуля в ряду цифр.
Хотя системы, использовавшиеся египтянами, римлянами или греками, не требовали нулевого маркера, возможность выразить отсутствие чего-либо (например, нулевого яблока) может быть удобной. Особенно, если ваша работа — собирать налоги для недоверчивого и вспыльчивого короля.
Итак, в начале 2-го тысячелетия до нашей эры египтяне начали использовать особый иероглиф (NFR или F35 в списке знаков Гардинера) для обозначения «ничего» или нулевого баланса в своих бухгалтерских текстах. Точно так же, хотя и намного позже (около 5 века нашей эры), римляне использовали латинское слово 9.2885 nulla («ничего»), которое в более поздних средневековых рукописях было сокращено до начальной буквы «N» 13 Римская система счисления продолжала использоваться в Европе до 16 века!. Греки, вероятно, вернули ноль из Вавилона, когда Александр Македонский завоевал город в 331 г. до н.э.
Рис. 3.3: Примеры нуляОднако эти символы не были настоящими математическими знаками. Они были больше похожи на лингвистические или символические элементы, используемые для обозначения отсутствия предмета. Одним из препятствий к пониманию нуля является то, что с математической точки зрения ноль на самом деле является величиной.
Но как ничто может быть чем-то, спросите вы?
Именно это веками беспокоило западных философов. От грека Парменида из Элеи (5 век до н.э.), провозгласившего, что « ничто не может существовать», до религиозных мыслителей средневековой Европы, которые пришли к выводу, что все, что представляет собой ничто, должно быть делом рук сатаны (и, следовательно, должно быть запрещено), Ноль некоторое время оставался спорной концепцией.
Потребовались люди с другим подходом, чтобы продвигать идею дальше.
Вавилонская идея постепенно проникла в долину Инда, где местные математики объединили различные аспекты нуля: знак, обозначающий «ничто», заполнитель и число.
Религии древней Индии имели другой и более позитивный взгляд на понятие «ничто» 14 Джозеф 2011:341. Индийцы также использовали позиционную систему счисления. Итак, созрели условия для появления истинного нуля.
До сих пор ведутся споры о том, как он туда попал. Есть некоторые свидетельства греческого влияния 15 Каплан 1999:17-18. В конце концов, Александр Македонский завоевал то, что осталось от Вавилона в 331 году до нашей эры, прежде чем отправиться в Индию. Но нельзя исключать, что индийцы могли разработать ноль самостоятельно либо 16 Ifrah 2000:409; Joseph 2011: 301.
При этом важно отметить, что Месопотамия (фактический Ирак) находилась не слишком далеко от Индии и что Аравийское море было важным и оживленным морским торговым путем, по крайней мере, со 2-го тысячелетия до нашей эры. 17 Этот центр деятельности был описан примерно в середине первого века нашей эры грекоязычным египетским купцом в документе под названием Periplus Maris Erythraei («Путешествие вокруг Эритрейского престола»).
Прибрежный торговый путь связывал многие порты на западном побережье Индии с Месопотамией через порты Персидского залива. А через Красное море он дошел до Египта, где фараоны построили несколько каналов для обслуживания торговли.
Итак, товарами и идеями обменивались через торговые пути Аравийского моря на протяжении веков. Возможность множественных возвратно-поступательных волн влияния в сфере наук и, в частности, математики, является разумным предположением. На самом деле, именно по этому же пути к нам вернулся ноль, как мы увидим 9.6145 18 Джозеф 2011:461-462.
Однако все согласны с тем, что индийские математики сыграли решающую роль в происхождении нуля, каким мы его знаем. Первое задокументированное описание (то есть определение) арифметики нуля было дано в 628 году нашей эры. Автором был великий индийский ученый Брахмагупта (598-668 гг. н.э.), написавший в своей книге Brahmasphutasiddhanta («Исправленный трактат Брахмы») 19 Plofker 2009:428-434:
«[Сумма] двух положительных положительный, из двух отрицательных отрицательный; положительного и отрицательного [сумма] есть их разность; если они равны, это ноль.Сумма отрицательного и нуля отрицательная, [сумма] положительного и нуля положительная, [а сумма] двух нулей равна нулю […]»
Брахмагупта говорит, что ноль получается прибавлением положительного числа к отрицательному числу равной величины 20 Величина числа определяется как расстояние этого числа от нуля на числовой прямой, например 1 + (-1), и что при добавлении или вычитании нуля из числа это число остается прежним (например, 1-0=1).
Потребовалось несколько столетий, чтобы эта концепция достигла Европы, но мы должны благодарить за это мусульманских математиков. Говорят, что эта идея достигла Багдада примерно в 773 году нашей эры.6161 21 Каплан 1999:90; Джозеф 2011:462, где работы таких ученых, как Аль-Кинди (801-873 гг. н.э.) и Аль-Хорезми (780-850 гг. н.э., более известный как «Алгоритми»), сыграли важную роль в распространении индийской системы счисления.
Зеро и индо-арабская система счисления путешествовали по Ближнему Востоку до Дамаска, затем по Средиземноморью до Кордовы.
Мусульмане завоевали Испанию в 8 веке нашей эры. Основанная ими там территория (Аль-Андалус) была маяком науки, искусства и эрудиции. Использование новых математических обозначений в мусульманской Испании твердо засвидетельствовано к концу 10-го века 22 Каплан 1999:970; Иосиф 2011:463.
Индуистско-арабская система счисления действительно достигла христианской Европы в XII веке, когда основополагающий труд Аль-Хорезми был переведен на латынь в книге под названием Algoritmi de numero Indorum (т. »). Но именно книга Леонардо Пизанского (1170-1250 гг. н.э.), более известная как Фибоначчи, Liber Abaci («Книга исчисления»), изданная в 1202 г. н.э., популяризировала новые цифры в Европе. Хотя полное усыновление было медленным процессом, который завершился только в 17 веке 23 Каплан 1999:97-103; Джозеф 2011:466, это открыло целый мир возможностей.
Без нуля у нас не было бы исчисления, алгебры, алгоритмов, декартовой системы координат, физики, техники, компьютерных наук и многих аспектов экономики и финансов. Так что, да, ноль — это довольно большое дело!
Существование числового глифа в виде головы, обозначающего ноль, предполагает, что майя полностью понимали математическую концепцию нуля.
Майя Зеро
Долгая и трудная история нуля в Старом Свете еще больше подчеркивает достижения древних математиков майя, которые независимо разработали концепцию нуля в своей системе счисления.
Самое раннее известное появление нуля в классических надписях майя относится к 4 веку нашей эры. Два памятника (Стела 18 и 19 из Уаксактуна) имеют дату майя 8.16.0.0.0 (357 г. н.э.) по календарю Длинного счета. Это делает его одним из старейших задокументированных случаев нуля в мире.
Однако важно помнить, что более старые числовые надписи появляются в датах Длинного счета на доклассических памятниках.
Все известные даты длинного счета записываются в разрядно-точечной нотации 24 Blume 2011:57. Это означает, что ноль в качестве заполнителя уже использовался еще во 2 веке до нашей эры и мог возникнуть из более раннего нововведения ольмеков.
В классический период (150-950 гг. н.э.) майя в основном использовали три символа для обозначения нуля (рис. 6):
- (a) Четырехлистник
- (b) Глиф Раковины в руке
- (c) Глиф варианта Головы
Позже, однако, во время так называемого позднего постклассического периода (1200-1500 гг. н.э.) способ записи чисел стал более упорядоченным и стандартизированным. Знак сменился на стилизованные морские раковины. Наиболее распространенное изображение в Дрезденском кодексе было идентифицировано как раковина Oliva ( Americoliva, рис. 6: d, e) 25 , они также были ошибочно описаны как «глаз» или «семена», но другие типы из морских раковин также использовались такие двустворчатые или раковинные морские раковины (рис.
Рис. 3.4: Цифры майя — нулевые знаки6: е) 26 Синий 2011:78-82.
С символической точки зрения майяские знаки нуля ясно показывают связь с мифологическим местом обитания божеств и предков, «водным подземным миром», а следовательно, и со смертью.
Сам подземный мир майя связан со смертью, потому что это место, куда уходит душа после смерти. Майя считали смерть завершением жизненного цикла. Мы знаем, что майя также понимали ноль как обозначающее «ничто».
Расшифрованные в 1990-х годах так называемые иероглифы «Четырехлистник» и «Ракушка в руке» (рис. 6: а, б) читаются как mi/MIH, что означает «нет» (как в « нет урожая») на языке майя языки. Числовое значение нуля майя дополнительно подтверждается некоторыми примерами «чисел расстояний».
Расстояние Числа появляются в календарных надписях. Это промежутки между датами. Вместо того, чтобы указывать полную дату события до или после главного события, для которого дата уже была указана, писцы майя просто говорили: «это произошло за много дней до/после [основного] события».
Все это было строго стандартизировано, но в некоторых редких случаях писцы писали Числа Расстояний нетрадиционным способом 9.6223 27 Пьедрас-Неграс, перемычка 3; Паленке, Храм Креста, Западная панель:
«[они использовали] глифический вариант луны для числа 20 с числами от 0 до 19 для обозначения количества дней от 20 до 39. Когда перед этим были помещены три точки символ луны, 3 считалось добавленным к 20, чтобы получить количество 23». Анна Блюм (2011:67)
Ноль перед глифом луны не может означать «нет двадцати» или «нет дня», так как не имеет смысла добавлять предложение только для того, чтобы сказать «это случилось 9».2885 нулевой день после/до [основного] события». Писец майя просто сказал: «В этот день произошло то и то». Так что «нулевую луну» (рис. 7а) следует понимать как 0 + 20 = 20 дней 28 Блюм 2011:67; Стюарт 2006:118. В этом случае знак нуля, вероятно, использовался для сохранения визуального соответствия остальной части надписи.
Вот несколько примеров использования нуля в надписях майя:
Рис. 3.5: Примеры использования нуля в надписях майяОбъединение понятий «небытие» и «завершение» наводит на мысль о нуле как о конечной точке обратного отсчета. Но майя также считали, что конец одного цикла ведет к началу другого цикла. Новый старт с нуля. И идея бесконечных циклов приводит к понятию «бесконечность».
Оболочки, используемые для обозначения нуля, — это не просто оболочки. Это морские раковины. Так что есть четкая символическая связь с морем. бескрайних морей, насколько могли судить майя.
«Когда писцы майя писали, на каком-то уровне они участвовали в умышленном акте выражения, который варьировался от огромного количества времени до затрат на ничто» Анна Блюм (2011:84)
Итак, ноль майя объединил идеи «ничто», «завершенности» и «бесконечности». Конец и начало слились в один символ. Это, в некотором смысле, подводит итог магии числа ноль.
Теперь, когда мы познакомились с первыми девятнадцатью цифрами и тремя цифрами штриховой записи, мы научимся писать большие числа.
4- Как писать числа майя
Для большинства из нас незнание десятичной системы счисления делает запись чисел в системе счисления майя немного трудоемкой. При этом, если оставить в стороне разницу между основанием 10 и основанием 20, система счисления майя работала очень похоже на нашу.
Для представления больших чисел (то есть больше девятнадцати) древние майя использовали несколько систем:2858
- аддитивная запись, аналогичная системе ацтеков
- мультипликативная запись, аналогичная китайской системе
позиционная запись который дает синодические обороты Венеры, показывает, что майя не только разработали концепцию нуля, но и придумали систему позиционных значений
30 Ifrah 2000:311.«Эти [система разряда и ноль] являются двумя фундаментальными открытиями, которые не удалось сделать большинству цивилизаций, включая особенно западноевропейскую цивилизацию, которая должна была ждать до Средневековья, чтобы эти идеи пришли к ней из арабского мира, который был сама приобрела их из Индии», Жорж Ифра (2000: 311).

Как мы видели ранее, в позиционной записи значение числительного частично зависит от его положения: «2» в десятичном числе «200» означает «два счета сотен», тогда как оно представляет только «два счета». счет «десять» в числе «20». Майя использовали аналогичную систему, но значение каждой позиции увеличивается в степени двадцати (то есть 1, 20, 400, 8000, 160000 и т. д.) вместо десяти.
Таким образом, очень похоже на то, как мы добавляем одну единицу к следующей позиции, когда мы перемещаемся через 9, писцы майя добавляли одну единицу к следующей позиции, когда одна позиция достигала 20.
Майя, однако, предпочитали столбцы, а не строки и 4.1. Примеры чисел в позиционной записи майя. астрономические наблюдения 31 Stuart 2012, которые требуют вычисления очень больших чисел.
Другими словами, до сих пор не найдено позиционного счета больших чисел чего-либо, кроме времени.
Для более приземленных дел и меньших величин майя предпочитали более простую систему, более приспособленную к цифрам повседневной жизни.
Аддитивное обозначение
Древние майя вели записи подношений еды и подсчета дани. Хотя имеется несколько документов майя, эта практика хорошо задокументирована в кодексах ацтеков 9.6300 32 т. е. книги, написанные коренными жителями Мезоамерики до или после завоевания.
Чтобы отслеживать подсчет дани, ацтеки использовали пиктограммы для обозначения таких предметов, как шкуры ягуара, и добавляли символы для обозначения количества каждого предмета 33 Vaillant 1941:206-209; Пейн и Клосс 1986: 226-229. Например, рисунок шкуры ягуара с четырьмя точками будет просто означать «четыре шкуры ягуара».
Группы по 20 штук обозначались флажком , количество по 400 штук — стилизованной цифрой ель и группы из 8000 мешочек для благовоний .
Рис. 4.2: Подсчет дани ацтеков в Кодексе Мендосы (лицевая сторона листа 37)Таким образом, пять флагов будут означать количество сто (т.е. 5 × 20). Примеры со страницы Кодекса Мендосы можно увидеть ниже. Примечания, написанные на испанском языке, видны и содержат римские цифры, подтверждающие числовые значения различных символов:
Из-за нехватки соответствующих источников 34 в то время Есть более 40 известных кодексов ацтеков, сохранились только четыре кодекса майя, наши знания по этому вопросу более ограничены для майя. Тем не менее примерно в то же время, когда ацтеки записывали дань в Кодекс Мендосы (созданный около 1541 г. н.э.), майя аналогичным образом отслеживали товары.
В Дрезденском (ок. 1450 г. н.э.) и Мадридском (ок. 1350–1697 гг. н.э.) кодексах количество подношений пищи указано простыми цифрами в виде штрихов и точек (от 1 до 19) или группами по 20 с соответствующими чертами и числами.
Рис. 4.3: Дрезденский кодекс 28 (по Фёрстеманну)точки 35 (Любовь 1994: 56-63, Стюарт 2012). В этих документах группы из 20 представлены так называемыми знаками WINIK или фонограммой k’al .
Было бы бессмысленно представлять число несколькими группами по 20, если бы запись была позиционной или мультипликативной. Таким образом, система должна была быть аддитивной, как у ацтеков. Другими словами, для получения суммы необходимо сложить все числа. Например, три знака WINIK и цифра 13, написанная штрихами и точками, дадут 73 (т. е. 3 × 20 + 13).
Интересно, что в более ранних документах классического периода майя использовали мультипликативную запись.
Мультипликативное обозначение
В мультипликативном представлении количества даются как кратные десятичным числам, таким как к’ал (20), бак’ (400) или пик (8000), и т. д. Писцы майя использовали глифы для к’ал , бак’ или пик и добавляли полосы и точки, чтобы указать количество каждой единицы.
Рис. 4.4: Глифы для 20 и 8000Другими словами, цифры в виде штрихов и точек действуют как коэффициенты (то есть множители) десятичных выражений. Например, две точки со знаком двадцати ( к’ал ) означает сорок. В корпусе классических надписей майя до сих пор идентифицированы только некоторые из этих глифов:
К сожалению, примеров таких надписей очень мало. Упоминания о количестве товаров чаще всего встречаются на расписной керамике с придворными сценами.
На одном изображении (рис. ) 36 эта цилиндрическая ваза является частью коллекции Бостонского музея изящных искусств. Номер доступа: 2004.2204, эмиссар могущественного короля Калакмула приветствует неизвестного лорда по имени 9.2885 Чок Вайс . На выставке представлены различные товары, но в тексте не указано, является ли это данью или дипломатическим подарком.
Пока эмиссар несет рюкзак с цифрой «5» (или «15»), одна сумка перед троном помечена надписью 37 Токовинин и Беляев 2013:174-177:
Рис. 4.5: Сцена суда – керамика 69 г. н.э.1 (Рисунок А. Токовинина)
- huux пик, « три [число] восемь тысяч» [т.
е. 24 000]
Знаменитые настенные росписи в Комнате 1 Строения 1 в Бонампаке изображают аналогичную, но гораздо большую сцену. Перед троном выстроены мешки с какао-бобами. Одну надпись можно прочитать 38 Miller 1997:40:
Рис. 4.6: Bonampak — Структура 1, Комната 1 (фрагмент, по Miller 1997)
- ho pik kakaw , « пять [количество] восемь тысяч какао-бобов» [i. 40,000]
За исключением Стелы Наранхо 32, в своде монументальных надписей почти нет упоминаний о дани. Стела 32 представляет собой большую плиту из известняка. Он был вырезан с низким рельефом примерно в 820 году нашей эры. Скульптура изображает короля Наранхо, Ваксаклахун Убах Кавиль , а соответствующий текст рассказывает о ряде событий его жизни с двумя интересными упоминаниями о дани 39 ЛеФорту и Вальду.
1995:
Рис. 4.7: Стела Наранхо 32 (по ЛеФорту и Вальду, 1995)
- ка к’ал ти икатц , « два [числа] двадцать связок…» [т.е. 40]
- хо к’ал ти икатц « пять [счет] двадцать связок…» [т.е. 100]
Хотя в своде надписей майя есть лишь несколько случаев подсчета подношений или дани, они демонстрируют интересное разнообразие форм. .
В то время как позиционное обозначение использовалось для вопросов, связанных с отсчетом времени (т. е. календарных и астрономических циклов), майя предпочитали другие обозначения для работы с меньшими величинами: мультипликативное обозначение в классический период и аддитивное обозначение в постклассический период .
Все эти записи следуют десятичной системе счисления майя.
Но как преобразовать числа Maya в десятичные числа и наоборот?
5- Преобразование десятичных и десятичных чисел
Для большинства из нас незнание десятичной системы делает запись чисел в системе счисления майя немного трудоемкой.
При этом, если оставить в стороне разницу между основанием 10 и основанием 20, система счисления майя работала очень похоже на нашу.
Как легко преобразовать числа Maya в десятичные числа
Преобразование чисел с основанием 20 в представление с основанием 10 довольно просто. Лучше всего использовать десятичную сетку:
Рис. 5.1: Преобразование чисел с основанием 20 в представление с основанием 10Начните с нижнего числа и двигайтесь вверх. Помните, что точка означает 1, черточка – 5, а ракушка – 0.
Как легко преобразовать десятичные числа в числа Maya
системы к десятичной системе. Сначала вам нужно преобразовать десятичные числа в систему с основанием 20, затем вам нужно преобразовать каждую цифру в нотацию Maya со штрихами и точками. 92
Рис. 5.3: Преобразование чисел с основанием 10 в представление с основанием 20 (пример № 2)Последний аспект, который я хотел бы затронуть, — это арифметика. Как вы выполняете сложения и вычитания, используя числа Maya?
6- Арифметические вычисления майя
Нет указаний на то, что майя умножали или делили.
Складывать и вычитать с помощью точек и полос на самом деле довольно просто.
Добавление чисел Maya
Добавлять легко. Вам просто нужно добавить символы, суммирующие штрихи и точки в параллельные регистры:
Но имейте в виду, что 5 точек превращаются в полосу:
Когда сумма чисел больше 19, полезно быть организованным и работать с десятичной сеткой. Начните снизу и продвигайтесь вверх. Имейте в виду, что 4 такта составляют 20 (т. е. 4 × 5), которые становятся единицей (т. е. точкой) в следующей позиции вверх:
Преобразование 4 тактов в точку в следующем регистре аналогично добавлению арабского языка. цифры.
Не забудьте пометить ракушкой ноль там, где это необходимо:
Аналогично действуйте с большими числами. Просто добавьте точки и полосы в каждой позиции, начиная с 1 внизу. Не забывайте, что совокупность 5 точек записывается как черта:
и что совокупность 4 черточек в одном регистре (т.е. 20) становится точкой (т.
е. единицей) на следующей позиции вверх:
Добавление Maya числительные довольно просты и требуют только трех правил:
- точка представляет 1 единицу
- накопление 5 точек становится одной чертой
- накопление 4 тактов в одном регистре записывается как точка в следующем более высоком регистре
«Сложение майя намного проще, чем арабское сложение, для которого требуется десять символов и запоминание множества правил, таких как 2 + 3 = 5 и 4 + 5 = 9” (Lambert & al. 1980:249)
Теперь давайте перейдем к вычитанию.
Вычитание чисел Maya
Вычитание тоже достаточно просто. Вы просто удаляете символы, беря различия точек и полос в одинаковых регистрах:
Имейте в виду, что 1 полоса соответствует 5 точкам. Возможно, вам потребуется «преобразовать» одну черту в пять точек, чтобы выполнить вычитание:
С большими числами полезно использовать десятичную сетку. Помните, что 1 точка в данной позиции равна 4 делениям в предыдущей.
При необходимости заимствовать из следующего более высокого регистра:
Некоторые числа могут быть сложнее, но с хорошим методом проблем не будет. Начинайте снизу и двигайтесь вверх:
Вычитание легко выполняется и требует только отмены символов и соблюдения трех правил:
- точка представляет одну единицу
- если точек недостаточно, то полоса на том же уровне преобразуется в пять точек
- если полос недостаточно, то одна точка следующего более высокого уровня преобразуется в четыре полосы нижний регистр.
Ссылки
Anderson, French W. (1971). Арифметика в числах майя. American Antiquity , 36 (1): 54-63.
Блюм, Анна (2011). Представления майя о нуле. Труды Американского философского общества. 155 (1): 51-88.
Бринтон, Дэниел Г. (1882 г.). Хроники майя . Библиотека литературы аборигенов Америки Бринтона.
Номер 1. Филадельфия.
Клосс, Майкл П. (1986). Математические обозначения древних майя. В: Клосс М. (ред.), Математика коренных американцев , стр. 291-370. Остин, Техас. Издательство Техасского университета.
Коу, Майкл Д. (1965). Ранние шаги в эволюции письма майя. В: Николсон Х. (ред.), Истоки религиозного искусства и иконографии в доклассической Америке . Лос-Анджелес: Серия латиноамериканских исследований Калифорнийского университета в Лос-Анджелесе, 31 : 107–122.
Коу, Майкл Д. (1992). Взлом кода майя . Thames and Hudson Inc. Нью-Йорк, Нью-Йорк.
Ифра, Жорж (2000). Всеобщая история чисел: от предыстории до изобретения компьютера . Нью-Йорк: John Wiley and Sons, Inc.
Джозеф, Джордж Г. (2011). Гребень павлина, неевропейские корни математики. Издательство Принстонского университета.
Принстон и Оксфорд.
Джастесон, Джон (1986). Происхождение письменности: доклассическая Мезоамерика. Всемирная археология 17 (3):437-458.
Джастесон, Джон (2010). Численное познание и развитие «нуля» в Мезоамерике . В: Морли И. и Ренфрю К. (ред.), Археология измерения: понимание неба, земли и времени в древних обществах, стр. 43-53. Кембридж, Великобритания: Издательство Кембриджского университета.
Каплан, Роберт (1999). Ничто, что есть: естественная история нуля . Оксфорд и Нью-Йорк: Издательство Оксфордского университета.
Кеттунен, Харри и Кристоф Хельмке (2014). Знакомство с иероглифами майя . Семнадцатое исправленное издание (2020 г.). Вайеб.
Ламберт, Джозеф Б. ., Барбара Оунби-Маклафлин и Чарльз Д. Маклафлин (1980). Майская арифметика.
American Scientist , 68 : 249-255 (май-июнь 1980 г.).
Ле Фор, Женевьева и Роберт Вальд (1995). Большие числа на стеле Наранхо 32. Мексикан 17 : 112–114.
Лаунсбери, Флойд Г. (1978). Нумерация майя, вычисления и календарная астрономия. В: Гиллиспи К. (ред.), Научно-биографический словарь , 15 : 759-818. Скрибнер: Нью-Йорк.
Любовь, Брюс (1994). Парижский кодекс: справочник жреца майя . Техасский университет Press, Остин.
Маркус, Джойс (1976). Происхождение мезоамериканской письменности. Ежегодный обзор антропологии 5 : 35–67.
Морли, Сильванус (1915). Введение в изучение иероглифов майя . Бюро американской этнологии Смитсоновского института. Бюллетень 57.
Payne, Stanley E . и Michael P.
Closs (1986). Обзор чисел ацтеков и их использования. В: Клосс М. (ред.), , Математика коренных американцев, , стр. 213–235. Остин, Техас. Издательство Техасского университета.
Плофкер, Ким (2009). Математика в Индии . Издательство Принстонского университета. Принстон и Оксфорд.
Саттертуэйт, Линтон (1947). Концепции и структуры календарной арифметики майя . Кандидат наук. Диссертация Пенсильванского университета. Совместные публикации . Музей Пенсильванского университета и Филадельфийского антропологического общества, нет. 3. Университетский музей.
Зайденберг, Авраам (1986). Ноль в системе счисления майя . В: Клосс М. (ред.), Математика коренных американцев, стр. 371-386. Остин, Техас. Издательство Техасского университета.
Стюарт, Дэвид (2012). Разновидности исчисления и значения древних майя. В: Пападопулос Дж.
и Уртон Г. (ред.), Конструирование ценности в древнем мире , стр. 497-515. Институт археологии Котсена, Калифорнийский университет в Лос-Анджелесе.
Стюарт, Дэвид (2006). Справочник по 30-м собраниям майя. 14-19 марта 2006 г. Мифология Паленке. Надписи Крестовой группы в Паленке. Мезоамериканский центр, факультет искусства и истории искусств, Техасский университет в Остине.
Томпсон Эрик Дж. (1942). Арифметика майя. Вашингтонский институт Карнеги, публикация 528:37-62.
Томпсон Эрик Дж. (1950). Иероглифическое письмо майя: введение. Вашингтонский институт Карнеги, публикация 589. Перепечатано издательством University of Oklahoma Press, 1960 и 1971.
Токовинин, Александр и Дмитрий Беляев (2013). Люди дороги: торговцы и путешественники в словах и образах древних майя. In: Хирт К.Г. и Пиллсбери Дж. (ред.), Торговцы, рынки и обмен в доколумбовом мире, , стр.
169.-200. Исследовательская библиотека и собрание Думбартон-Оукс, Вашингтон, округ Колумбия.
Тоззер, Альфред М . (1921). Грамматика майя. С библиографией и оценкой работы отмечено . Музей американской археологии и этнологии Пибоди Гарвардского университета.
Тоззер, Альфред М. (1941). Relacion de la cosas de Yucatan Ланды . Музей американской археологии и этнологии Пибоди Гарвардского университета. Papers 28.
Vaillant, George C. (1941). Ацтеки Мексики: происхождение, расцвет и падение народа ацтеков. Даблдей Доран, Гарден-Сити.
Кредиты
Автор: Dr Patrice Bonnafoux
Иллюстрации (если не указано иное): Patrice Bonnafoux
ВВЕДЕНИЕ
 высота 8,9см. Художественный музей Кимбелла, Форт-Уэрт (AP 2004.04). Фотография © Пользователь: FA2010 / Wikimedia Commons / Public Domain.
высота 8,9см. Художественный музей Кимбелла, Форт-Уэрт (AP 2004.04). Фотография © Пользователь: FA2010 / Wikimedia Commons / Public Domain. РАЗДЕЛ 1: Десятичная система счисления майя
Фото: Деревянная перемычка. Тикаль, Храм 4, Перемычка 3. Поздний классический период, после 746 г. н.э. Этнографический музей, Базель, Швейцария. Фотография © Sven Gronemeyer, 2016.
РАЗДЕЛ 2: Цифры майя
Фото: Дрезденский кодекс, 43-44, кадр 2. Версия Фёрстемана, 1880 г. FAMSI.
Рис. 2.3: Адаптировано из Kettunen & Helmke 2014, Table VI. Рисунок вариантов головы Джона Монтгомери.
РАЗДЕЛ 3: Представление майя о Зеро
Фото: Полная фигура Зеро, резной пучок, 53,3 × 52,1 × 35,6 см, родом из Фасада строения 10L-22A в Копане. Предоставлено Кливлендским музеем искусств. Дар Фонда Ханны (1953.154).
Рис. 3.1: Вавилонские клинописные цифры. Пользователь: Josell7 / Wikimedia Commons / Лицензия Creative Commons.
3.1: Вавилонские клинописные цифры. Пользователь: Josell7 / Wikimedia Commons / Лицензия Creative Commons.
РАЗДЕЛ 4. Как писать числа майя
Фото: Цилиндрическая ваза. Сцена вручения дани. Поздний классический период, 691 г. н.э. Керамика с полихромным орнаментом. высота 21,3 см. Музей изящных искусств, Бостон (2004–2204). Фотография © МИД / Добросовестное использование в образовательных целях.
Рис. 4.2: Кодекс Мендосы, лицевая сторона листа 37. Бодлианские библиотеки, Оксфордский университет. Фотография © пользователя: Ptcamn~commonswiki / Wikimedia Commons / Public Domain.
Рис. 4.3: Дрезденский кодекс, 25-28, кадр 4-6. Версия Фёрстемана, 1880 г. FAMSI.
Рис. 4.5: Судебная сцена – керамика, 691 г. н.э. (K5453). Адаптировано из Токовинина и Беляева, 2013 г., рис. 7.3. Рисунок А. Токовинина.
Рис. 4.7: Наранхо, Стела 32.


 Информационная деятельность человека
Информационная деятельность человека


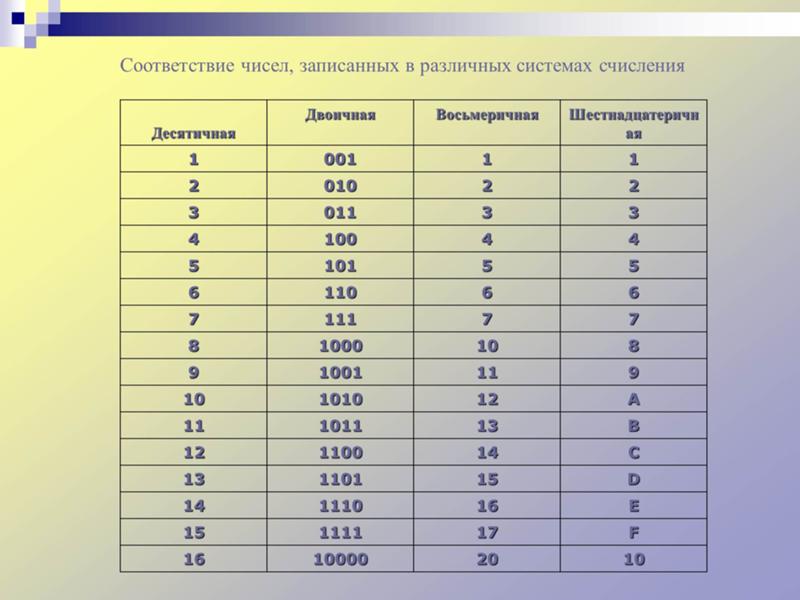


 Запись вида 352:
Запись вида 352: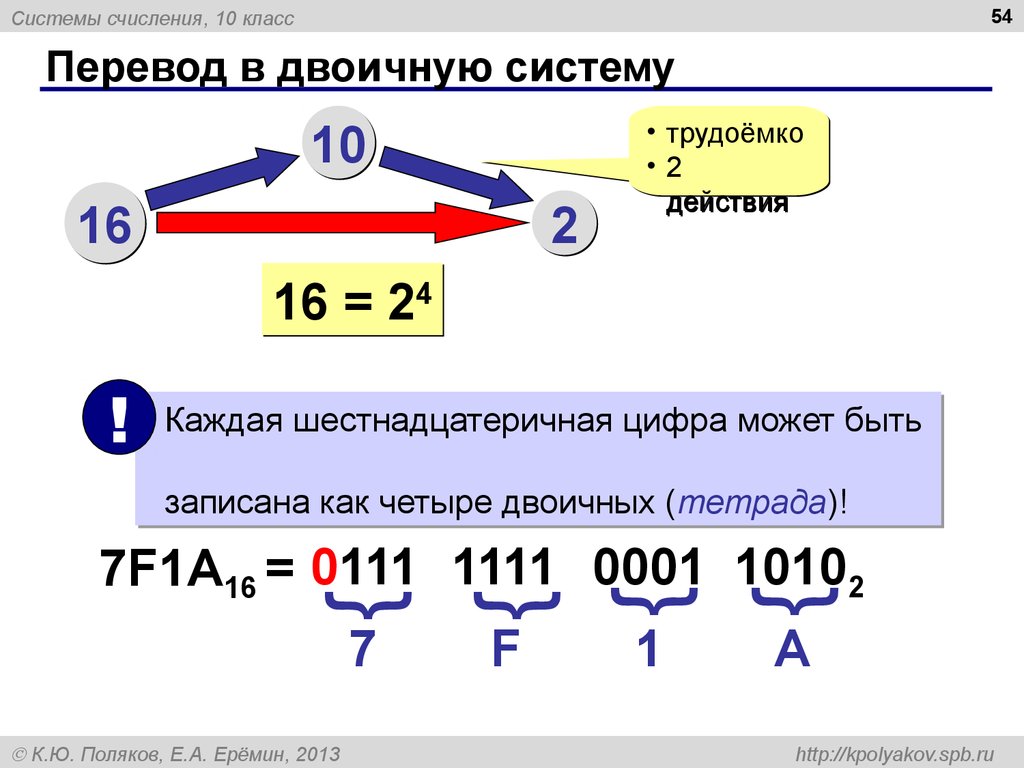 С.
С. С.
С.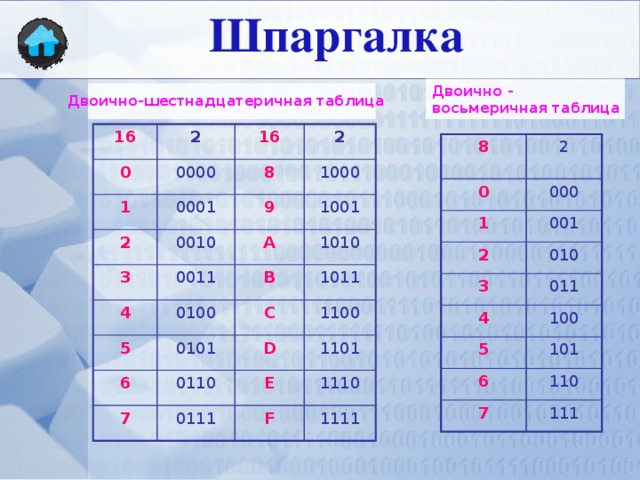 С.
С.