Основы логики — что это, определение и ответ

Математическая логика (она же булева алгебра) является неотъемлемым блоком знаний как в школьном курсе информатики, так и в ЕГЭ.

Цель логики как науки – определить, истинно или ложно некоторое высказывание, а также прослеживать связь между высказываниями относительно друг друга. Высказывания обозначаются логическими переменными, которые могут принимать лишь два значения:

Истина = 1, Ложь = 0

Логические выражения (которые состоят из более чем одного высказывания) на естественном языке образуются с помощью связок «И», «ИЛИ», «НЕ». В математической логике аналогом этих связок являются базовые логические операции — конъюнкция, дизъюнкция и инверсия. Чтобы определить значение составного логического выражения, надо знать значения входящих в него логических переменных (высказываний). Чтобы рассмотреть все возможные случаи, в булевой алгебре есть специальный аппарат — таблица истинности. Таблица истинности строится следующим образом: в столбцах записываются логические переменные и само выражение, а в строках — всевозможные комбинации переменных и соответствующий для них результат выражения. Для выражения, содержащего n переменных, количество комбинаций для них будет равно 2ⁿ. Подробнее про таблицы истинности написано ниже.

Логическое умножение. Конъюнкция

Конъюнкция (логическое умножение, логическое «И») обозначает объединение двух или нескольких высказываний в одно таким образом, что результат будет истинным тогда и только тогда, когда истинны все входящие в него высказывания.

Пусть есть два высказывания:

Эти высказывания истинны. Значит, их объединение с помощью конъюнкции («В ЕГЭ по информатике есть программирование И логика») — истинно.

Операцию конъюнкции в булевой алгебре принято обозначать знаком « /\ » или, реже, « & » (амперсанд). Операция логического умножения, аргументами которой являются логические переменные А и В, записываются следующей формулой: A /\ B. Таблица истинности для конъюнкции:

Логическое сложение. Дизъюнкция

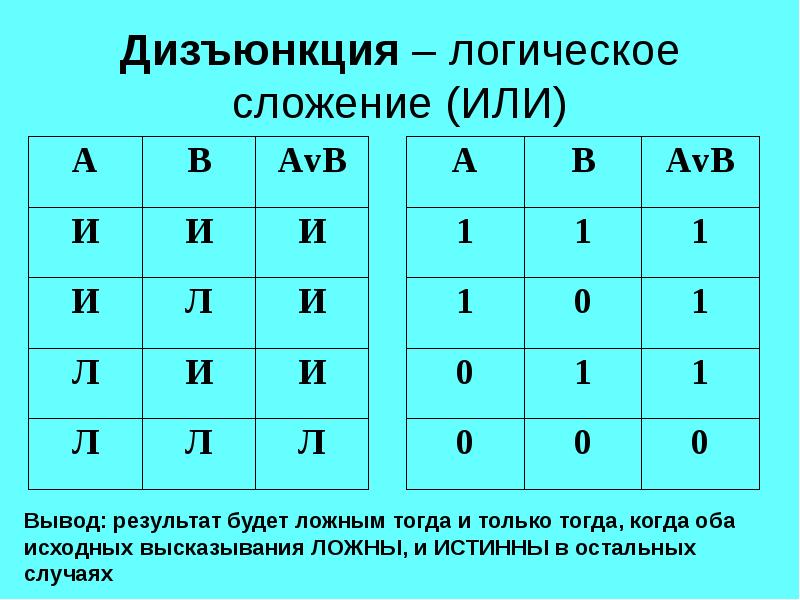
Дизъюнкция (логическое сложение, логическое «ИЛИ») обозначает объединение двух или нескольких высказываний в одно таким образом, что результат будет истинным тогда, когда истинно хотя бы одно входящее в него высказывание.

Операцию дизъюнкции в булевой алгебре принято обозначать знаком « \/ ». Операция логического сложения, аргументами которой являются логические переменные А и В, записывается следующей формулой: A \/ B. Таблица истинности для дизъюнкции:

Логическое отрицание. Инверсия

Инверсия (логическое отрицание, логическое «НЕ») получает из истинного высказывания ложное и, наоборот, из ложного — истинное.

Например, высказывание «Москва — столица России» истинно, а данное высказывание, образованное с помощью логического отрицания («Москва — не столица России») — ложно. Ложное высказывание можно сделать истинным с помощью инверсии:

Операцию инверсии в булевой алгебре принято обозначать знаком « ¬ ». Операция логического отрицания, аргументом которой является логическая переменная А, записывается следующей формулой: ¬A. Результатом операции логического отрицания является Истина, когда аргумент Ложь, и значение Ложь, когда аргумент Истина. Таблица истинности для инверсии:

Построение таблиц истинности логических выражений

Для каждого логического выражения можно построить таблицу истинности, которая определяет его истинность или ложность при всех возможных комбинациях исходных значений логических переменных. Алгоритм построения таблиц истинности:

1. Определить количество строк, которое равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение (если переменных n штук, то количество строк будет равно 2ⁿ). Еще одну строку стоит добавить для указания самих переменных, итого строк в таблице будет 2ⁿ + 1.

2. Определить количество столбцов, которое равно количеству логических переменных плюс количество логических операций.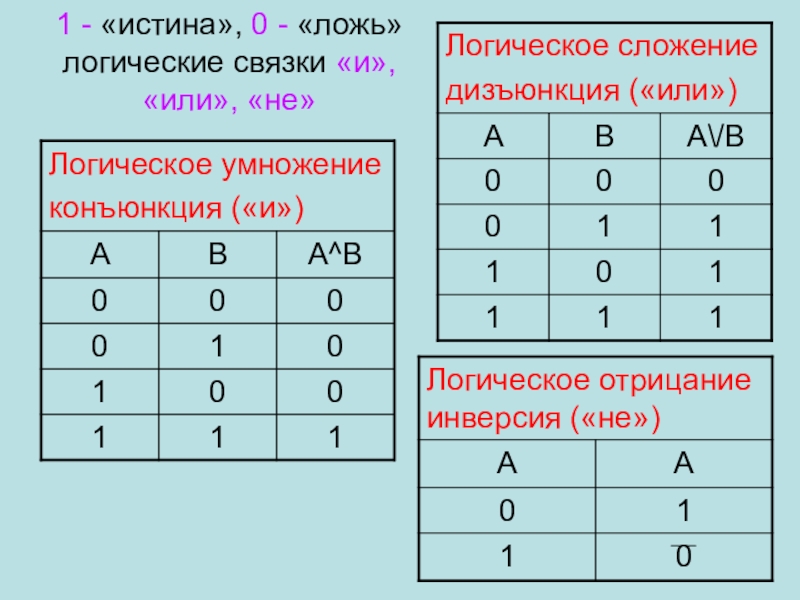 Это нужно для того, чтобы вычислять значение логического выражения поэтапно, последовательно выполняя все логические операции над исходными переменными.

3. Построить таблицу с указанным количеством столбцов и строк и внести всевозможные наборы логических переменных. Наборы входных переменных рекомендуется заполнять следующим образом:

a) разделить столбец значений первой переменной пополам и заполнить верхнюю часть колонки нулями, а нижнюю — единицами;

б) разделить столбец значений второй переменной на четыре части и заполнить четверти чередующимися группами нулей и единиц;

в) продолжать деление столбцов значений последующих переменных на 8, 16, 32 и т.д. частей.

4. Заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с таблицей истинности.

Импликация и эквиваленция

В логике, помимо базовых логических операций, существуют еще другие. Для ЕГЭ необходимо и достаточно знать ровно две дополнительные логические операции – импликацию и эквиваленцию. Эти логические операции еще можно назвать составными, ведь они на самом деле состоят из базовых. Любую логическую операцию можно «разложить» на базовые — конъюнкцию, дизъюнкцию и инверсию. Выражение, связывающее логическую операцию с её разложением на базовые, называется равносильным выражением.

Импликация

Импликация по смыслу похожа на использование союзов «если… то…». Обозначается стрелкой от первой логической переменной ко второй: A → B. Для импликации равносильное выражение выглядит так:

A → B = ¬A \/ B

Это значит, что таблица истинности для A → B и для ¬A \/ B будет выглядеть идентично. Ниже приведена таблица истинности и диаграмма Эйлера для импликации:

Эквиваленция

Эквиваленция проверяет, одинаковы ли (эквивалентны ли) значения логических переменных — и выдает Истину, если одинаковы (1 и 1, 0 и 0) и Ложь, если не одинаковы (1 и 0, 0 и 1). Обозначается эквиваленция тремя полосами (как равно, только с еще одной чертой): A ≡ B. Для эквиваленции существует два равносильных выражения:

A ≡ B = (A /\ B) \/ (¬A /\ ¬B) = (¬A \/ B) /\ (A \/ ¬B)

Ниже приведена таблица истинности и диаграмма Эйлера для эквиваленции:

Порядок выполнения логических операций, содержащих импликацию и эквиваленцию

Если в выражении присутствует импликация и эквиваленция, то они выполняются всегда после базовых логических операций в таком порядке: сначала импликация, потом — эквиваленция. Таким образом, порядок выполнения всех логических операций будет выглядеть так:

1. Инверсия

2. Конъюнкция

3. Дизъюнкция

4. Импликация

5. Эквиваленция

Скобки, разумеется, могут этот порядок менять.

Логические элементы – определение, свойства

3.9

Средняя оценка: 3.9

Всего получено оценок: 201.

3.9

Средняя оценка: 3.9

Всего получено оценок: 201.

Специальные устройства, выполняющие обработку цифровой информации на основе принципов алгебры логики, называются логическими элементами. Физически они реализовываются на электронных устройствах. Самыми простыми логическими элементами являются И, ИЛИ, НЕ.

Что такое логические элементы

Логические элементы представляют собой устройства, которые могут быть реализованы на электронной полупроводниковой базе. Они выполняют некоторую логическую функцию преобразования входного сигнала. На нескольких простых логических элементах можно построить сколь угодно много сложных устройств, например регистров, сумматоров, счетчиков импульсов.

Для описания работы различных электронных устройств удобно использовать элементы алгебры логики, которая, как известно, работает с переменными, принимающими только два значения 1 и 0, то есть включено или выключено.

Определение количества логических элементов, которые можно построить на базе двоичной логики, выполняется по формуле 2⁴, то есть составляет 16.

Элементарные логические элементы

Основными логическими элементами являются И, ИЛИ, НЕ. Все остальные элементы строятся на базе них.

Рис. 1. Графическое изображение элементов И, ИЛИ, НЕ

Инверсия (НЕ)

Инверсия представляет собой унарную операцию, то есть элемент с одним входом. Логический элемент НЕ реализует логическое отрицание. Если на вход этого элемента подается сигнал 1, то на выходе будет получено 0.

Таблица истинности для данного элемента имеет вид:

А	НЕ(А)
0	1
1	0

Конъюнкция (И)

Логический элемент И является бинарным и выполняет логическое умножение.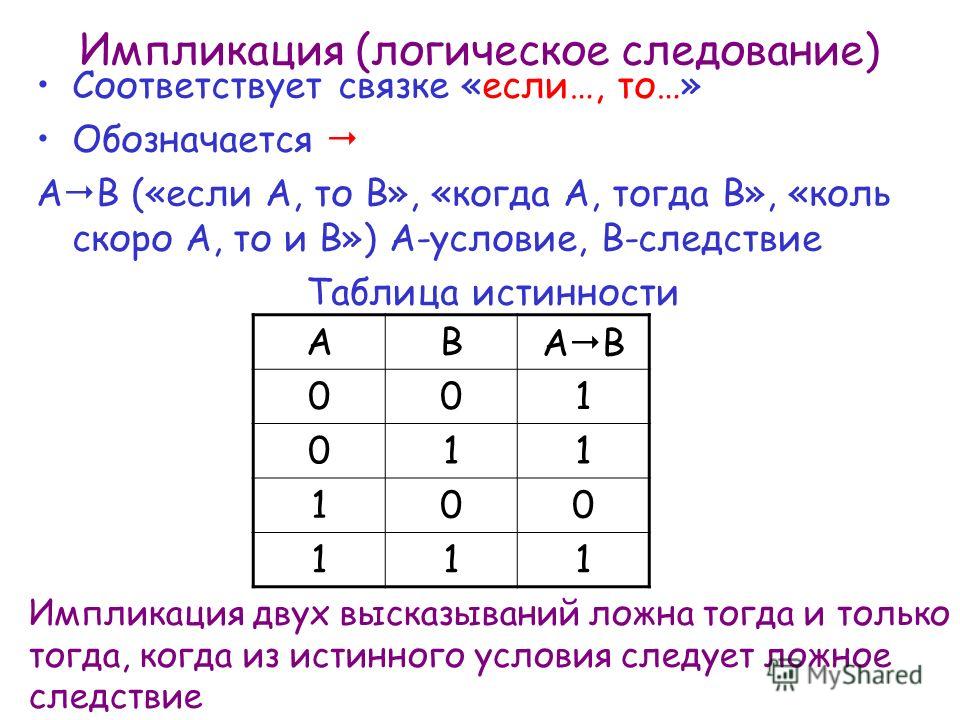 Результат конъюнкции равен 1 только в том случае, когда на входы данного элемента подаются две единицы. Во всех остальных случаях результат конъюнкции равен нулю.

Таблица истинности для конъюнкции

А	В	А & В
0	0	0
0	1	0
1	0	0
1	1	1

Дизъюнкция (ИЛИ)

Бинарный логический элемент ИЛИ реализует операцию логического сложения. Результат этой операции равен нулю в том случае, когда на входы дизъюнкции подаются нули. В остальных случаях результат всегда равен единице.

Таблица истинности для логического ИЛИ

А	В	А + В
0	0	0
0	1	1
1	0	1
1	1	1

Логические элементы, построенные на базе И, ИЛИ, НЕ

Все остальные бинарные логические элементы строятся на базе основных.

Например, если к элементу И добавить инверсию, то получится новый логический элемент И-НЕ, который также называется Штрих Шеффера. Обозначается знаком «|» – вертикальная черта. Результатом этой функции будет ноль, только в том случае, когда на вход подаются две единицы.

Инверсия дизъюнкции позволит получить элемент ИЛИ_НЕ, носящий также название стрелка Пирса. При записи обозначают стрелкой, направленной вниз «↓». В результате этой функции на выходе будет единица только при нулевых входных сигналах, а все остальные случаи нулевые.

Рис. 2. Графическое изображение элементов И-НЕ, ИЛИ-НЕ

Все логические элементы собираются из различных устройств: транзисторов, резисторов, диодов, интегральных микросхем. Самыми распространенными являются электронные логические элементы, так как показывают хорошие свойства быстродействия, надежности, экономичности.

Рис. 3. Принципиальная схема логического элемента

Что мы узнали?

Логические элементы – это устройства, собранные из различных электронных приборов и выполняющие функцию преобразования сигнала на основе алгебры логики.

Самыми элементарными логическими элементами являются И, ИЛИ, НЕ. Все остальные строятся на основе базовых.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Батыр Джамалов

  5/5

Оценка статьи

3.9

Средняя оценка: 3.9

Всего получено оценок: 201.

---

А какая ваша оценка?

404: Страница не найдена

Страница, которую вы пытались открыть по этому адресу, похоже, не существует. Обычно это результат плохой или устаревшей ссылки. Мы извиняемся за любые неудобства.

Что я могу сделать сейчас?

Если вы впервые посещаете TechTarget, добро пожаловать! Извините за обстоятельства, при которых мы встречаемся. Вот куда вы можете пойти отсюда:

Поиск

• Пожалуйста, свяжитесь с нами, чтобы сообщить, что эта страница отсутствует, или используйте поле выше, чтобы продолжить поиск
• Наша страница «О нас» содержит дополнительную информацию о сайте, на котором вы находитесь, WhatIs. com.
• Посетите нашу домашнюю страницу и просмотрите наши технические темы

Просмотр по категории

Сеть

• CAPWAP (Контроль и настройка точек беспроводного доступа)

  CAPWAP (управление и обеспечение точек беспроводного доступа) — это протокол, который позволяет контроллеру доступа управлять …

• мониторинг производительности сети (NPM)

  Мониторинг производительности сети (NPM) — это процесс измерения и мониторинга качества обслуживания сети.

• инфракрасное излучение (ИК)

  Инфракрасное излучение (ИК), иногда называемое просто инфракрасным, представляет собой область спектра электромагнитного излучения, в которой …

Безопасность

• аналитика безопасности
  Аналитика безопасности — это подход к кибербезопасности, который использует инструменты сбора, агрегирования данных и анализа угроз . ..

• NICE Framework (Национальная инициатива по обучению в области кибербезопасности Cybersecurity Workforce Framework)

  The NICE Framework (National Initiative for Cybersecurity Education Cybersecurity Workforce Framework) является справочным ресурсом …

• черный список приложений (занесение приложений в черный список)

  Занесение приложений в черный список — все чаще называемое занесением в черный список приложений — представляет собой практику сетевого или компьютерного администрирования, используемую …

ИТ-директор

• план закупок

  План закупок, также называемый планом управления закупками, представляет собой документ, который используется для управления процессом поиска …

• Общепринятые принципы ведения учета (Принципы)

  Общепринятые принципы ведения документации — это основа для управления записями таким образом, чтобы поддерживать . ..

• система управления обучением (LMS)

  Система управления обучением представляет собой программное приложение или веб-технологию, используемую для планирования, реализации и оценки конкретных …

HRSoftware

• конвейер талантов

  Воронка талантов — это группа кандидатов, готовых занять вакансию.

• аутсорсинг процесса подбора персонала (RPO)

  Аутсорсинг процесса найма (RPO) — это когда работодатель передает ответственность за поиск потенциальных кандидатов на работу …

• специалист по кадрам (HR)

  Специалист по персоналу — это специалист по кадрам, который выполняет повседневные обязанности по управлению талантами, сотрудникам …

Обслуживание клиентов

• скорость оттока

  Коэффициент оттока — это показатель количества клиентов или сотрудников, покидающих компанию в течение определенного периода времени.