Site Loader
Posted on 06.06.2023

Курс высшей математики, Т.2

Курс высшей математики, Т.2
  

В.И.Смирнов Курс высшей математики, Т.2.: Изд-во «Наука». 1974. — 479 с.

Фундаментальный учебник по высшей математике, выдержавший более двадцати изданий, переведенный на множество языков мира, отличается, с одной стороны, систематичностью и строгостью изложения, а с другой – простым языком, подробными пояснениями и многочисленными примерами. Книга состоит из пяти томов. Тома третий и четвертый – каждый из двух частей.

Для студентов университетов и технических вузов.



Оглавление

ПРЕДИСЛОВИЕ К ДЕВЯТНАДЦАТОМУ ИЗДАНИЮ
ГЛАВА I. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
§ 1. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
2. (n)=f(x).
18. Понижение порядка дифференциального уравнения.
19. Системы обыкновенных дифференциальных уравнений.
20. Примеры.
21. Системы уравнений и уравнения высших порядков.
22. Линейные уравнения с частными производными.
23. Геометрическая интерпретация.
24. Примеры.
ГЛАВА II. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
25. Линейные однородные уравнения второго порядка.
26. Линейные неоднородные уравнения второго порядка.
27. Линейные уравнения высших порядков.
28. Однородные уравнения второго порядка с постоянными коэффициентами.
29. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами.
30. Частные случаи.
31. Корни решений и колеблющиеся решения
32. Линейные уравнения высших порядков с постоянными коэффициентами.
33. Линейные уравнения и колебательные явления.
34. Собственные и вынужденные колебания.
35. Синусоидальная внешняя сила и резонанс.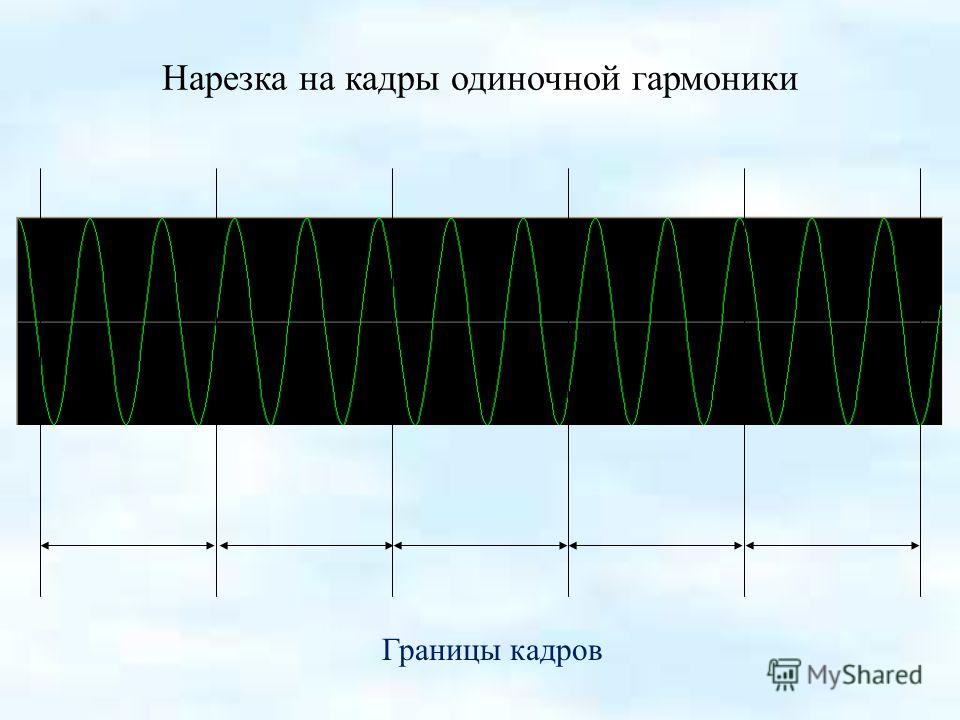
36. Предельные задачи.
37. Примеры.
38. Символический метод.
39. Линейные однородные уравнения высших порядков с постоянными коэффициентами.
40. Линейные неоднородные уравнения с постоянными коэффициентами.
41. Пример.
42 Уравнение Эйлера.
43. Системы линейных уравнений с постоянными коэффициентами.
44. Примеры
§ 4. ИНТЕГРИРОВАНИЕ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ
45. Интегрирование линейного уравнения с помощью степенного ряда
46. Примеры.
47. Разложение решения в обобщенный степенной ряд.
48. Уравнение Бесселя
49. Уравнения, приводящиеся к уравнению Бесселя
§ 5. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
50. Метод последовательных приближений для линейных уравнений.
51. Случай нелинейного уравнения.
52. Дополнения к теореме существования и единственности.
53. Сходимость метода Эйлера — Коши.
54. Особые точки дифференциальных уравнений первого порядка.
55. Автономные системы.
56. Примеры.

ГЛАВА III. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
§ 6. КРАТНЫЕ ИНТЕГРАЛЫ
58. Двукратный интеграл.
59. Вычисление двукратного интеграла.
60. Криволинейные координаты.
61. Трехкратный интеграл
62. Цилиндрические и сферические координаты.
63. Криволинейные координаты в пространстве.
64. Основные свойства кратных интегралов.
65. Площадь поверхности.
66. Интегралы по поверхности и формула Остроградского.
67. Интегралы по определенной стороне поверхности.
68. Моменты.
§ 7. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
69. Определение криволинейного интеграла.
70. Работа силового поля. Примеры.
71. Площадь и криволинейный интеграл.
72. Формула Грина
73. Формула Стокса.
74. Независимость криволинейного интеграла от пути на плоскости.
75. Случай многосвязной области.
76. Независимость криволинейного интеграла от пути в пространстве.
77. Установившееся течение жидкости.
78. Интегрирующий множитель.
79. Уравнение в полных дифференциалах для случая трех переменных.
80. Замена переменных в двойном интеграле.
§ 8. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
81. Интегрирование под знаком интеграла.
82. Формула Дирихле.
83. Дифференцирование под знаком интеграла
84. Примеры.
85. Несобственные интегралы.
86. Неабсолютно сходящиеся интегралы.
87. Равномерно сходящиеся интегралы.
88. Примеры.
89. Несобственные кратные интегралы.
90. Примеры.
§ 9. МЕРА И ТЕОРИЯ ИНТЕГРИРОВАНИЯ
92. Основные теоремы.
93. Счетные множества. Действия над точечными множествами.
94. Мера Жордана.
95. Квадрируемые множества.
96. Независимость от выбора осей.
97. Случай любого числа измерений.
98. Интегрируемые функции.
99. Вычисление двойного интеграла.
100. n-кратные интегралы.
101. Примеры.
102. Внешняя мера Лебега.
103. Измеримые множества.
104. Измеримые функции.
105.
Дополнительные сведения.
106. Интеграл Лебега.
107. Свойства интеграла Лебега.
108. Интегралы от неограниченных функций.
109. Предельный переход под знаком интеграла.
110. Теорема Фубини.
111. Интегралы по множеству бесконечной меры.
ГЛАВА IV. ВЕКТОРНЫЙ АНАЛИЗ И ТЕОРИЯ ПОЛЯ
112. Сложение и вычитание векторов.
113. Умножение вектора на скаляр. Компланарность векторов.
114. Разложение вектора по трем некомпланарным векторам.
115. Скалярное произведение.
116. Векторное произведение.
117. Соотношения между скалярным к векторным произведениями.
118. Скорости точек вращающегося твердого тела; момент вектора.
§ 11 ТЕОРИЯ ПОЛЯ
119. Дифференцирование вектора
120. Скалярное поле и его градиент.
121. Векторное поле; расходимость и вихрь.
122. Потенциальное и соленоидальное поля.
123. Направленный элемент поверхности.
124. Некоторые формулы векторного анализа.
125. Движение твердого тела и малая деформация.
126. Уравнение непрерывности.
127. Уравнения гидродинамики идеальной жидкости.
128. Уравнения распространения звука.
129. Уравнение теплопроводности.
130. Уравнения Максвелла.
131. Выражение оператора Лапласа в ортогональных координатах.
132. Операция дифференцирования для случая переменного поля.
ГЛАВА V. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ
133. Плоская кривая, ее кривизна и эволюта.
134. Эвольвента.
135. Естественное уравнение кривой.
136. Основные элементы кривой в пространстве.
137. Формулы Френе.
138. Соприкасающаяся плоскость.
139. Винтовые линии.
140. Поле единичных векторов.
§ 13. ЭЛЕМЕНТЫ ТЕОРИИ ПОВЕРХНОСТЕЙ
141. Параметрические уравнения поверхности.
142. Первая дифференциальная форма Гаусса.
143. Вторая дифференциальная форма Гаусса.
144. О кривизне линий, начерченных на поверхности.
145. Индикатриса Дюпена и формула Эйлера.
146. Определение главных радиусов кривизны и главных направлений.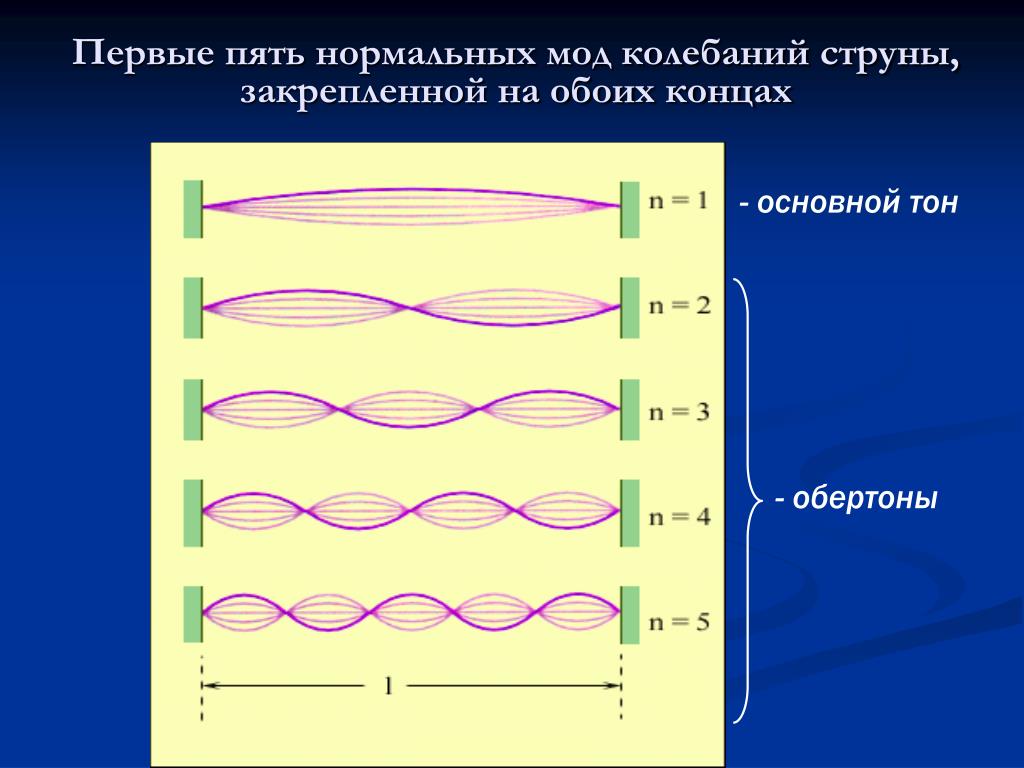
147. Линии кривизны.
148. Теорема Дюпена.
149. Примеры.
150. Гауссова кривизна.
151. Вариация элемента площади и средняя кривизна.
152. Огибающая семейства поверхностей и кривых.
153. Развертывающиеся поверхности.
ГЛАВА VI. РЯДЫ ФУРЬЕ
154. Ортогональность тригонометрических функций.
155. Теорема Дирихле.
156. Примеры.
157. Разложение в промежутке (0, п).
158. Периодические функции периода 2l.
159. Средняя квадратичная погрешность.
160. Общие ортогональные системы функций.
161. Класс L2
162. Сходимость в среднем.
163. Ортонормированные системы в L2.
§ 15. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ ФУРЬЕ
164. Разложение в ряд Фурье.
165. Вторая теорема о среднем.
166. Интеграл Дирихле.
167. Теорема Дирихле.
168. Приближение к непрерывной функции полиномами.
169. Формула замкнутости.
170. Характер сходимости рядов Фурье.
171. Улучшение сходимости рядов Фурье.
172. Пример.
§ 16. ИНТЕГРАЛ ФУРЬЕ И КРАТНЫЕ РЯДЫ ФУРЬЕ
173. Формула Фурье.
174. Ряды Фурье в комплексной форме.
176. Кратные ряды Фурье.
ГЛАВА VII. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
176. Уравнение колебаний струны.
177. Решение Даламбера.
178. Частные случаи.
179. Ограниченная струна.
180. Способ Фурье.
181. Гармоники и стоячие волны.
182. Вынужденные колебания.
183. Сосредоточенная сила.
184. Формула Пуассона.
185. Цилиндрические волны.
186. Случай n-мерного пространства.
187. Неоднородное волновое уравнение.
188. Точечный источник.
189. Поперечные колебания мембран.
190. Прямоугольная мембрана.
191. Круглая мембрана.
192. Теорема единственности.
193. Применение интеграла Фурье.
§ 18. ТЕЛЕГРАФНОЕ УРАВНЕНИЕ
195. Установившиеся процессы.
196. Устанавливающиеся процессы.
197. Примеры.
198. Обобщенное уравнение колебаний струны.
199. Неограниченная цепь в общем случае.
200. Способ Фурье для ограниченной цепи.
201. Обобщенное волновое уравнение.
§ 19. УРАВНЕНИЕ ЛАПЛАСА
202. Гармонические функции.
203. Формула Грина.
204. Основные свойства гармонических функций.
205. Решение задачи Дирихле для круга.
206. Интеграл Пуассона.
207. Задача Дирихле для сферы.
208. Функция Грина.
209. Случай полупространства.
210. Потенциал объемных масс.
211. Уравнение Пуассона.
212. Формула Кирхгофа.
§ 20. УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
214. Неограниченный стержень.
215. Стержень, ограниченный с одного конца.
216. Стержень, ограниченный с обоих концов.
217. Дополнительные замечания.
218. Случай сферы.
219. Теорема единственности.

Струны ГОСПОДИН МУЗЫКАНТ® (GMstrings®) / Производство музыкальных струн

Джо Вулфи / Joe Wolfe (Австралия) Перевод статьи публикуется с разрешения автора, оригинал размещен по адресу: http://www.phys.unsw.edu.au/jw/strings. html

Чтобы вызвать звук необходимо произвести колебания. Чтобы получить музыкальный звук необходимо, чтобы колебания имели постоянную частоту, т.е. стабильную высотность, которой исполнитель мог бы легко управлять. В электроинструментах стабильные и управляемые колебания получают с помощью электроники, у неэлектрических — за счет стоячих волн. Мы будем рассматривать колебания на примере струн, поскольку здесь они более наглядны, чем колебания воздуха в духовых инструментах, и менее сложны по сравнению с колебаниями дощечек и кожи ударных инструментов.

Натянутые струны скрипки, фортепиано и т.д. колеблются столь быстро, что разглядеть что-либо невозможно. Однако, можно провести несколько любопытных экспериментов, позволяющих понять работу струн с помощью нескольких метров гибкого резинового шланга. Садовый поливной шланг для этого недостаточно гибок, лучше всего взять резиновый шланг или длинную бельевую веревку. Привяжите или прижмите один конец шланга, а другой слегка натяните одной рукой (сильно натягивать не нужно, небольшой прогиб не страшен). Теперь другой рукой оттяните шланг в сторону, чтобы образовался выступ, и, отпустив его, вы увидите в замедленном темпе то, что происходит при щипке струны. Можно наблюдать, как выступ пробежит вдоль «струны» и вернется обратно. При возврате он толкнет Вашу руку, но если Вы держите «струну» крепко, произойдет новое отражение.

Первое, что Вы должны заметить, это то, что скорость движения волны по струне возрастает с увеличением ее натяжения. Это свойство используется при настройке инструментов, но сейчас мы не будем на этом останавливаться. Скорость движения волны зависит и от «веса» струны — в более толстой, тяжелой струне (при равной длине и натяжении) она будет медленнее, чем в легкой.

Теперь остановимся на отражении, которое происходит на закрепленном конце. Заметьте, что если оттягивать струну влево, то выступ побежит с левой стороны, но при возврате будет расположен справа — при отражении происходит инвертирование. Этот эффект наблюдается не только в струнах, но и в духовых и ударных. Волна инвертируется в момент, когда сталкивается с какой-либо неподвижной или трудно преодолимой преградой.

Несмотря на то, что струны музыкального инструмента закреплены с обоих концов, наблюдаемые процессы при щипке струны в них будут аналогичными. Сперва струна оттягивается в некой точке, а затем отпускается, как показано на рисунке. Если приглядеться, можно различить форму, которую образует бегущий выступ (показано тонкой линией на рисунках ниже), движущийся вдоль струны в обоих направлениях. Для наблюдений лучше использовать басовые струны, оттягивая их в нескольких миллиметрах от точки крепления. Фигура, образованная бегущим выступом, видна лучше, чем сама струна, потому что точку покоя, в которой происходит смена направлений, выступ проходит мгновенно, а к краям его движение замедляется.

Схема движения выступа, образованного при щипке струны. Жирной линией показана сама струна, тонкой — фигура, образованная движением выступа. В фазах, отмеченных буквами (d) и (j), струна представляет прямую линию. В эти моменты потенциальная энергия ее колебаний исчерпана, а кинетическая энергия максимальна. Заметим, что в момент отражения положение выступа меняется на 180 градусов с верхнего на нижний или наоборот. Обратите внимание на проход выступов одного «сквозь» другой в момент, когда они встречаются посередине.

Схема, показывающая отражение движущихся выступов, при возбуждении струны смычком.

Отчего при отражении происходит инвертирование? Поскольку струна закреплена на неподвижном объекте, то и точка отражения является неподвижной. Теперь посмотрите на движение струны на левых рисунках, отражающих ее положение в разное время. Видно как часть струны позади выступа возвращается к своему первоначальному состоянию (на рисунках — вниз). Чем ближе выступ к концу струны, тем он становится меньше, и при его достижении он исчезает — в этот момент струна становится прямой. Однако движение струны вниз не прекращается, и, пройдя точку покоя, она образует обратный выступ, который начинает движение в обратном направлении.

Если раскачивать вверх-вниз незакрепленный конец струны, можно наблюдать один интересный эффект. С помощью резинового шланга можно проделать этот опыт самостоятельно. Если такой возможности у Вас нет, то взгляните на представленную ниже диаграмму.

Мы опять видим инвертирование отраженной волны, из-за чего после отражения мы получаем уже две волны (с одинаковой частотой и амплитудой), которые движутся в противоположных направлениях. В точке крепления струны, где они складываются, движение прекращается, т.е. имеет место нулевое перемещение, благодаря которому и возникает инвертированное отражение. Но если вы посмотрите на сплошную линию на диаграмме (представляющую собой результат суммирования двух волн), то увидите, что на струне есть и другие неподвижные точки. Эти равноудаленные друг от друга точки, играющие важнейшую роль в функционировании любого музыкального инструмента, называются «узлами» (node) вибрации. Посередине между узлами располагаются «пучности» (antinode) — зоны максимального движения. Обратите внимание, что эти выступающие зоны не движутся по струне. При сложении двух волн, бегущих в противоположных направлениях, образуется стоячая волна.

Две движущиеся волны при слиянии образуют стоячие волны.

Посмотрите на рисунок, который представляет последовательность фаз движения волн во времени (время течет сверху вниз). Синяя волна движется вправо, зеленая влево, красная волна является суммирующей и показывает, что происходит при столкновении двух волн (по научной терминологии — при наложении). Отмечены положения (узлы/nodes) в которых обе движущиеся волны нейтрализуют друг друга и другие зоны (пучности/antinodes), в которых происходит сложение волн, и колебания обладают максимальной амплитудой. Можно сказать, что приведенная выше диаграмма представляет колебание 5-й гармоники струны, длина которой равна ширине диаграммы. Здесь мы коснулись темы, которая будет освещена в следующей главе.

Гармоники и моды (типы) колебаний

На музыкальном инструменте струна закреплена с обоих концов, которые ограничивают возможные колебания и на которых во время колебаний расположены узлы. Струна, имеющая длину L, образует стоячую волну, длина которой равна удвоенной длине струны (длина волны = 2L), что демонстрируется на первом из рисунков следующей серии. При этом узлы расположены на концах струны, а пучность посередине между ними. Это одна из мод («мода» — тип колебаний струны). Какие еще моды встречаются на струне, закрепленной с обоих концов? Ниже приводятся примеры таких стоячих волн.

Рисунки демонстрируют первые четыре моды колебаний идеальной* закрепленной струны (увеличено по вертикали).

В каком соотношении находятся моды колебаний? Частота колебаний волны равна отношению ее скорости к длине: f=v/длина волны. Таким образом, для струны длиной L, длины волн составят 2L, L, 2L/3, L/2, что можно записать так 2L/n, где n — номер гармоники.

Базовая частота или 1-я мода имеет частоту f1= v/длина волны = v/2L
Частота 2-й гармоники f2= v/l2 = 2v/2L = 2f1
Частота 3-й гармоники f3= v/l3 = 3v/2L = 3f1
Частота 4-й гармоники f4= v/l4 = 4v/2L = 4f1 …
 
fn= v/ln = nv/2L = nf1

Все волны движутся по струне с одинаковой скоростью, поэтому волны с различными длинами имеют разные частоты, как показано на рисунках. Мода самой нижней частоты (f1) называется базовой. Частота n-ной моды будет в n раз больше базовой. Все эти моды (как и звуки, которые они образуют) называются гармониками струны. Частоты f, 2f, 3f, 4f и т.д. называется последовательностью гармоник. Музыканты хорошо знакомы с этими последовательностями, особенно те, кто играют на натуральных горнах или знакомы с флажолетами. Если для примера мы возьмем базовую частоту соответствующую ноте С3, т.е. альтовой До (частота = 131Гц), то ее гармоники будут иметь высотности, показанные на следующем рисунке. Высотность нот дана в приближении до четверти тона. При этом октавы являются чистыми, а вот другие интервалы не совсем соответствуют равномерно темперированному строю.

Нотное написание первых 12-ти гармоник (флажолетов) на примере ноты До. При прослушивании звукового файла (записанного в форматах au и wav) обратите внимание на высотность звуков.

Седьмая и одиннадцатая гармоники приходятся почти посередине между нотами равномерно темперированного строя, поэтому обозначены с половинками диезов.

Вы сами можете получить эти звуки на струнах. Проще это сделать на басовых струнах гитары, виолончели или контрабаса*. Для этого коснитесь слегка струны в точке, которая отстоит на длину =1/n от ее конца (где n = 1,2,3 и т.д.), а затем проведите смычком. Или слегка коснитесь струны в точке, которая приходится на длину =1/n от ее конца, ударьте по струне недалеко от подставки и мгновенно отдерните прижатый палец. Благодаря касанию, в точке произойдет образование узла, который образует моду, имеющую узел в данной точке. Вы легко сможете найти на струне от двух до шести флажолетов (если Вы только что проделали этот эксперимент, то, наверное, обратили внимание, на то, что двенадцатый лад, отвечающий за получение октавы, расположен менее, чем на половине длины струны, поэтому то место, где Вы касались струны для получения 2-й гармоники, находится не совсем точно над этим ладом).

* «Идеальной» я называю струну, которая, обладая абсолютной гибкостью, позволяет оттягивать ее без усилий в любом месте. Но поскольку реальные струны обладают жесткостью, их рабочая длина (которую мы обозначали в формулах буквой L) немного меньше физической длины, и это одна из причин, почему на басовых струнах применяется обмотка, а голая струна G (соль) классической гитары плохо строит в верхних позициях.

Упражнение для гитаристов

На настроенной гитаре струна В(си) и верхняя Е(ми) настроены примерно на 3-ю и 4-ю гармоники нижней струны Е(ми). Если взять на щипок басовую струну Е(ми) в любой точке кроме ее 1/3, струна В(си) начнет колебаться, возбуждаясь через колебания подставки от гармоники 1-й струны. Если взять на щипок басовую струну Е(ми) в любой точке кроме ее 1/4, отзовется верхняя струна Е(ми). Гитаристы обычно начинают настройку следующим образом: настраивают в унисон 4-ю гармонику басовой Е(ми), 3-ю у струны А(ля) и верхнюю струну Е(ми), затем струну В(си) строят по 3-й гармонике верхней Е(ми), а затем по 4-й гармонике А(ля) 3-ю гармонику струны D(ре). Настроить струну G(соль) по гармоникам не получится, в связи с невозможностью получения верхних гармоник, что связано с физическими параметрами толщины и жесткости самой струны, поэтому ее настраивают октавами, используя лады. По некоторым причинам (о которых будет сказано в конце главы), данный метод настройки достаточно приблизителен и требует дальнейшей подстройки при помощи ладов. Самой точной настройкой все-таки является компромиссная, которая осуществляется по аккордам, которые исполнитель собирается брать на грифе инструмента.

Гармоники (флажолеты) в музыке

Композиторы часто применяют гармоники/флажолеты на струнных инструментах, при этом наиболее часто используют «четвертую касательную». Одним пальцем музыкант зажимает струну, получая ноту за счет отрезка определенной длины, а другим легко касается струны там, где располагается нота на 4 тона выше (отсюда и название). Данная точка лежит на четверти длины отрезка струны, поэтому образуется 4-я гармоника базовой частоты в четыре раза больше базовой, т.е. получается интервал в две октавы. Струнные гармоники/флажолеты называются «натуральными» если они образованы от открытых струн и «искусственными» если струна прижимается. Ниже на рисунке показано, как берется натуральный флажолет. Для наглядности рисунок вытянут по вертикали.

Прослушайте фрагмент. Сначала звучит открытая струна А(ля), затем ее четвертая касательная (4-я гармоника).

Так обозначается на нотном стане «четвертая касательная» на скрипичной струне А(ля)

Немного технической информации для струнников

Несмотря на то, что «четвертая касательная» наиболее часто встречающийся флажолет, это не вполне удачный пример, поскольку получить четвертую гармонику гораздо проще, нежели «две четверки». Как известно, касание струны на отрезке 1/n (где n — целое число) дает n-ую гармонику, и для низких гармоник правило соблюдается, но для высших гармоник особое значение играет толщина струны, и здесь формула перестает работать. Таким образом, гармоники выше 8-й практически не берутся.

Если взять на струне подряд пять полутонов, то мы получим точку, соответствующую 1/3 длины струны, то есть «пятая касательная» даст нам третью гармонику. Гармоники расположены в следующем порядке:

интервал на грифе часть струны номер гармоники интервал от базовой ноты
октава 1/2 2 октава
квинта 1/3 3 октава + квинта (дуодецима)
кварта 1/4 4 две октавы
большая терция 1/5 5 2 октавы + б. терция
малая терция 1/6 6 2 октавы + квинта
ув. кварта 2/7 7 2 октавы + м. секста повышенная
малая секста 3/8 8 3 октавы
большая секунда 1/9 9 3 октавы + б. секунда

Положения нот звукоряда соответствуют чистому строю. Касание струны на 2/9 ее длины предпочтительней, чем на 1/9, хотя данная точка расположена не над нотой гаммы, а немного выше малой терции. Буду рад, если альтисты или виолончелисты исполняющие «Практикующая бесконечность» Радулески (Radulescu’s «Practicing Infinity») пришлют мне свои предложения о способах исполнения высоких флажолетов.

Несовершенство настройки по гармоникам (флажолетам)

Есть несколько проблем при настройке любой гитары, в том числе при использовании флажолетов, о чем говорилось выше. Приблизительность настройки инструмента очевидно связана с равномерной темперацией. Даже если бы струны были идеальны, а положение ладов на грифе идеально отвечало равномерной темперации, при настройке по четвертой гармонике струн E-A (ми-ля), и A-D (ля-ре), октава между открытой нижней E(ми) и нотой ми на 2-м ладу струны D(ре) отклонялась бы приблизительно на 4 цента ((4/3)222/12=1.996), что приводило бы к появлению одного интерференционного биения в несколько секунд.

Другая проблема заключается в том, что в зоне верхнего порожка и подставки струны не могут обеспечить абсолютную гибкость (что было отмечено выше). В результате 1-й обертон на струне всегда будет чуть выше октавы, второй выше чем дуодецима (октава + квинта), и так далее. Так настройка в унисон 4-ой «гармоники» струны Е(ми) и 3-ей гармоники струны А(ля) при сравнении открытых струн даст интервал несколько больший, чем кварта, отчего приходится исправлять настройку, чтобы иметь равномерную темперацию.

Еще один отрицательный момент относится к расположению ладов и подставки. При прижиме струны на двенадцатом ладу увеличивается и ее длина (это уже не самое короткое расстояние между верхним порожком и подставкой), и ее натяжение. Вследствие этого, а также из-за выгиба конца струны, будь 12-й лад точно посередине между верхним порожком и подставкой, мы бы имели интервал больше октавы. Поэтому расстояние от подставки до 12-ого лада делают несколько большим, чем до верхнего порожка. Необходимо отметить, что в зависимости от вида струн эффект может быть различен. На электрогитарах есть возможность регулировать положение каждой подставки струны, на некоторых гитарах подставку поворачивают под углом, а в случае с классической гитарой прямая подставка ведет к определенному компромиссу в настройке.

Вышеописанные моменты сложно отследить с большой точностью, поскольку при анализе звука струны, возбуждаемой щипком, неточности составляют лишь несколько центов, что не намного больше разрешающей способности слуха или приборов настройки. Настройка колками также не позволяет достичь точности менее двух центов. С другой стороны, если Вам удастся интонировать мелодию с точностью в пределах двух центов, это будет большая удача — большинству музыкантов такое не по силам!

Определенная часть проблем настройки касается старения струн. Там, где Вы касаетесь их пальцами левой руки, они вбирают в себя пот и становятся более тяжелыми (хотя может иметь место и износ материала в местах, которые трутся об лады). Струны также изнашиваются под пальцами правой руки. Неоднородность струн ведет к невозможности их точной настройки. Мойка струн может помочь лишь отчасти.

Конечно, на безладовом инструменте большинство этих проблем можно обойти, но аккордная техника при этом сильно страдает.

На рисунке показаны гармоники открытой струны СОЛЬ контрабаса или виолончели. (Ноты для контрабаса записываются октавой выше его звучания.) Над нотами указаны номера гармоник, а под ними записаны приблизительные частоты в Герцах, причем для наглядности сделано округление чисел. Данный пример демонстрирует закон изменения высотности гармоник, и, хотя реальные частоты составляют пропорционально несколько меньшие значения, динамика возрастания частот от значения в 100Гц отражена абсолютно точно. (Приведенные значения частоты ноты СОЛЬ и ее гармоник могли бы иметь место при камертоне Ля=449Гц. Примечание переводчика).

Перепечатка статьи возможна только с согласия автора Джо Вулфи J.Wolfe()unsw.edu.au, а также фирмы ГОСПОДИН МУЗЫКАНТ®, осуществлявшей ее перевод.

© 2002

Наука о звуке: сделай свою губную гармошку!

  • Share на Facebook

  • Share в Twitter

  • Share на Reddit

  • Share на LinkedIn

  • Поделитесь по электронной почте

  • Ring in The New New Year Year с новым годом. забавный самодельный инструмент, основанный на физике! Авторы и права: Джордж Рецек

    Ключевые понятия
    Физика
    Звуковая волна
    Частота
    Шаг
    Герц

    Введение
    Можете ли вы назвать самый продаваемый музыкальный инструмент в мире? Если вы сказали… губная гармошка, вы правы! Гармошку запатентовал в 1821 году 16-летний немецкий мальчик. С тех пор он стал самым продаваемым инструментом в мире и предметом домашнего обихода во многих местах. Легко воспринимать инструменты (и музыку, которую они создают) как должное, но создание красивого шума — это не просто искусство, это еще и наука! В этом упражнении вы создадите и исследуете свой собственный инструмент, похожий на гармонику, сделанный из предметов домашнего обихода. Время настроиться!

    Фон
    Звуки, которые мы слышим каждый день, представляют собой звуковые волны, распространяющиеся по воздуху и достигающие наших ушей. Как и океанская волна, звуковые волны генерируются вибрацией или движением объекта в среде. В случае океана средой является вода, тогда как звуковые волны чаще всего достигают нас, путешествуя по воздуху. Звуковая волна исходит от вибрирующего объекта, такого как голосовые связки, и проходит через среду (например, воздух), заставляя все частицы воздуха вибрировать с частотой голосовых связок. Частота этого движения обычно измеряется в герцах (Гц), где один герц равен одному колебанию в секунду.

    Чтобы лучше понять это, представьте двух людей, держащих между собой веревку. Если один человек осторожно покачивает веревку вверх и вниз один раз в секунду, по веревке будет проходить волна с частотой один герц. Если человек увеличивает свою скорость так, что он двигает веревку вверх и вниз два раза в секунду, волна будет проходить по веревке с частотой два Гц.

    Звук распространяется по воздуху аналогичным образом. Скрипач проводит смычком по струнам скрипки, заставляя струны вибрировать. Вибрирующая струна сталкивается с частицами воздуха вокруг себя. Эти частицы воздуха впоследствии сталкиваются с частицами воздуха рядом с ними и так далее, поэтому волна распространяется от частицы воздуха к частице воздуха — и все это с той же частотой, что и вибрация струны скрипки.

    В этом упражнении вы создадите свой собственный звучащий инструмент и исследуете виды звуковых волн, которые он генерирует.

    Материалы

    • Две большие палочки (длиной не менее шести дюймов)
    • Две широкие резинки (хорошо подойдет размер #64)
    • Одна пластиковая соломинка для питья
    • Четыре маленькие резинки
    • Линейка
    • Ножницы
    • Взрослый помощник
    • Лист бумаги
    • Ручка или карандаш

    Подготовка

    • Натяните широкую резинку вдоль одной из палочек для рукоделия.
    • Отрежьте ножницами четыре кусочка соломы, каждый длиной до полутора дюймов.
    • Поместите одну из соломинок под резинку перпендикулярно палочке. Переместите эту соломинку так, чтобы она находилась примерно в двух дюймах от конца палочки. Это Соломинка 1.
    • Отойдя от конца палочки, поместите еще одну соломинку поверх резинки рядом с соломинкой 1. Это соломинка 2.
    • Поместите третью соломинку рядом с соломинкой 2 под резинку. Это Соломинка 3.
    • Поместите последнюю соломинку рядом с соломинкой 3 поверх резинки. Это Соломинка 4.
    • Соломинки 1 и 4 должны быть ближе к концам палочки для творчества, а соломинки 2 и 3 должны быть посередине.
    • С помощью взрослого, который поможет вам удерживать соломинки на месте, положите вторую палочку для рукоделия поверх первой, создав бутерброд с соломинками между палочками для рукоделия.
    • Закрепите этот бутерброд, обернув небольшую резинку примерно на полдюйма с каждого конца палочки. Концы палочек должны быть зажаты вместе с небольшим пространством между ними, созданным соломинками.
    • С помощью бумаги и карандаша нарисуйте таблицу с двумя столбцами и пятью строками. Назовите первый столбец «расстояние между средними соломинками» и заполните каждое место ниже: «2,5 дюйма», «2 дюйма», «1,5 дюйма» и «1 дюйм». Назовите вторую колонку «тон звука».

    Процедура

    • Для начала переместите соломинки 1 и 4 как можно ближе к концам палочки. Вы можете двигать соломинки, осторожно двигая их вперед и назад, стараясь не вытащить их из бутерброда!
    • Сдвиньте соломинки 2 и 3 друг от друга так, чтобы между ними было расстояние 2,5 дюйма.
    • Держите инструмент так, как если бы это был бутерброд, одной рукой аккуратно держась за каждый конец, а открытой частью к себе. Убедитесь, что палочка с резинкой находится на дне бутерброда, и старайтесь держать пальцы на маленькой резинке. Убедитесь, что вы не нажимаете на широкую резинку.
    • Продуйте в отверстие между палочками для рукоделия, как будто это губная гармошка (не дуйте через соломинку!). Какой звук ты слышишь? Чувствуете ли вы что-нибудь в своих руках, когда дуете в инструмент? Вибрируют ли ремесленные палочки или ощущаются ли они иначе, когда вы воспроизводите звук?
    • Переместите соломинки 2 и 3 ближе друг к другу, чтобы между ними было расстояние 2 дюйма.
    • Снова продуйте свой инструмент. Обратите внимание на звук и ощущение в ваших руках. Звучит ли это иначе, чем при первом воспроизведении? Если да, то каким образом? Отличается ли вибрация инструмента?
    • Снова переместите соломинки 2 и 3 ближе друг к другу, чтобы между ними было расстояние 1,5 дюйма.
    • Продуйте свой инструмент. Обратите внимание на звук и ощущение в ваших руках. Звучит ли это иначе, чем в прошлые разы? Если да, то каким образом? Отличается ли вибрация инструмента?
    • Наконец, снова переместите соломинки 2 и 3 ближе друг к другу, чтобы между ними было расстояние в 1 дюйм.
    • Еще раз продуйте свой инструмент. Обратите внимание на звук и ощущение в ваших руках. Звучит ли это иначе, чем в прошлые разы? Если да, то каким образом? Отличается ли вибрация инструмента?
    • Верните соломинки 2 и 3 в исходное положение на расстоянии 2,5 дюйма между ними. Повторите описанные выше шаги — на этот раз запишите свои наблюдения о тоне звука в таблицу. Чтобы вам было легче сравнивать звуки, оцените самый низкий звук в 1, а самый высокий звук в 4.
    • Рассмотрите результаты в своей таблице. Вы замечаете какие-либо закономерности в тоне звука? Менялся ли тон, когда вы передвигали соломинку? Если да, то смещение соломинок ближе друг к другу повышало или понижало тон?
    • Переверните инструмент так, чтобы широкая резинка оказалась сверху. Держите инструмент так, чтобы пальцы нажимали на широкую резинку. Продуйте инструмент, как и в предыдущих шагах. Изменяет ли что-нибудь ношение резинки в вашем инструменте? Как бы вы объяснили наблюдаемые вами различия?
    • Переверните прибор так, чтобы резинка снова оказалась внизу. Удалите все соломинки, кроме соломинки 1. Попробуйте продуть инструмент. Звучит ли это иначе, чем в прошлые разы? Если да, то каким образом? Отличается ли вибрация инструмента?
    • Попробуйте передвинуть оставшуюся соломинку и посмотреть, как это повлияет на тон звука. Можно ли изменить тон звука, передвигая соломинку?
    • Дополнительно: Проверьте большие и/или меньшие палочки для рукоделия и другие материалы, кроме соломинок. Сколько различных инструментов вы можете сделать?

    Наблюдения и результаты
    Звук, издаваемый вашим инструментом, на самом деле является звуком, создаваемым большой резиновой лентой, вибрирующей, когда вы дуете через нее, так же, как скрипичная струна вибрирует, когда играет скрипач. Когда вы дули в свой инструмент, вы, возможно, заметили, что чувствуете вибрацию резиновой ленты через ремесленную палочку. Кроме того, когда вы перевернули инструмент и нажали на резиновую ленту, вы, вероятно, обнаружили, что не можете произвести никакого звука, когда дуете через нее. Из этого вы можете заметить, что звук создается резинкой, и когда вы препятствуете движению резинки, вы не можете производить никакого звука.

    Кроме того, в этом упражнении вы должны были заметить, что можете менять тон звука, передвигая соломинки. Когда вы передвигали соломинки 2 и 3 ближе друг к другу, вибрирующая часть резинки становилась короче. В результате тональность звука стала выше. Более короткая резинка вибрирует быстрее, и наши уши улавливают эти более высокие частоты как более высокие звуки. Более тонкие струны на скрипке издают более высокий звук, потому что они могут вибрировать быстрее, чем более толстые струны. Точно так же у мужчин, как правило, более длинные голосовые связки, чем у женщин, и поэтому их голоса обычно ниже, чем у женщин.

    Когда вы удалили все соломинки, кроме одной, вы должны были обнаружить, что звук инструмента стал тише. Только с одной соломинкой резиновая лента была длиннее, а звук, издаваемый ею при вибрации, был ниже. Перемещая оставшуюся соломинку, вы могли менять тон, так как резинка становилась все короче и длиннее.

    Еще для изучения
    Поющие бокалы для вина, от Science Buddies
    Разговор по телефону, от Scientific American
    Выдувание крышек бутылок: Создание музыки с помощью бутылок, от Science Buddies
    Научные мероприятия для всех возрастов! от Science Buddies

    Это задание предоставлено вам в сотрудничестве с Science Buddies

    ОБ АВТОРЕ(АХ)

    Арфа Микаэлы – Libre Wave

    , которую вы можете скачать здесь.

    Я создал эту библиотеку, потому что мне нравится тонкий, но дерзкий дух кельтской арфы. Он может быть мягким и нежным или смелым и сильным, и всем, что между ними.

    Мы записали современную кельтскую арфу с теплым тоном и встроенным звукоснимателем. Это позволило нам создать прямую входную запись в дополнение к двум позициям стереомикрофона. Мы записывали в студии, так что сэмплы довольно сухие, что поможет вам смешивать и накладывать их на другие инструменты.

    Видео

    Прохождение

    Аудио

    1. Дело великана
    2. Кельтская рапсодия
    3. Фосфоресценция
    4. Взгляд на нее
    5. Потерянный путь
    6. Брезал0006
    7. Изменение ветра

    Артикуляции

    Инструмент включает обычные щипковые сэмплы, записанные на четырех динамических уровнях. Это артикуляция по умолчанию, и у нее типичный теплый резонансный звук, уникальный для кельтской арфы.

    Для тех случаев, когда желательно иметь немного меньший резонанс, мы также записали отдельный набор семплов демпфированных струн. Чтобы создать их, Микаэла использовала свои руки, чтобы смягчить струны вокруг той, которую защипывали. Это обеспечивает более округлый звук, который затухает немного быстрее. Время затухания можно настроить с помощью ползунков атаки и восстановления в интерфейсе.

    Остановленные струны

    Некоторые пьесы требуют, чтобы игрок остановил одну или несколько звучащих струн руками. Это создает отчетливый звук, поскольку вибрирующая струна почти мгновенно останавливается. Арфа Микаэлы позволяет исполнять эту технику вживую, используя педаль сустейна. Отпускание клавиш при нажатой педали вызовет запуск отдельных остановленных сэмплов.

    Воспроизводимые триоли

    Игра быстрых групп из трех нот является обычным явлением в кельтской арфовой музыке, и ее нелегко имитировать с помощью отдельных сэмплов. Набор триплетных сэмплов активируется с помощью клавишного переключателя, MIDI CC или изменения программы, и каждый набор триплетных семплов запускается циклическим способом, что позволяет вам полностью контролировать скорость исполнения без необходимости искусственного растягивания времени.

    Пресеты

    Библиотека включает специальный браузер пресетов, из которого вы можете выбрать различные заводские конфигурации или создать свои собственные пресеты. В браузере есть панель поиска и функция избранного, позволяющая быстро получить доступ к предпочитаемым пресетам.

    Системные требования

    GNU/Linux (Ubuntu 16.0 или более поздняя версия)

    Windows 7 или более поздняя версия

    MacOS 11.0 или более поздняя версия

    Сборка для вашей ОС из исходного кода

    Хост должен поддерживать 64-битный VST3 или AU0005

    AAX (Pro-Tools) не поддерживается

    Жесткий диск 1GB

    2GB RAM

    Руководство пользователя

    Часто задаваемые вопросы

    Разве я не видел этот инструмент где-то раньше?

    Арфа Микаэлы изначально была выпущена несколько лет назад как инструмент Kontakt. Эта версия больше не доступна для продажи.

    Чем отличается этот релиз от оригинальной версии Kontakt?

    Вот все основные улучшения последней версии арфы Микаэлы:
    Арфа Микаэлы теперь является бесплатным программным обеспечением, а это означает, что оно уважает вашу свободу.

    Сэмплы были переработаны для улучшения их четкости, уменьшения шума, устранения артефактов и т. д.

    К обычным щипковым семплам добавлен дополнительный слой скорости. Он был записан одновременно со всеми остальными сэмплами, но не был включен в исходный релиз.

    Новый микрофонный микшер предоставляет больше возможностей для размещения инструмента в виртуальном пространстве и имеет дополнительные элементы управления, такие как индивидуальная ширина и панорамирование для каждого канала.

    Я добавил редактор кривой динамической чувствительности, который позволяет настроить чувствительность инструмента к динамической чувствительности в соответствии с вашим стилем игры и вашей клавиатурой.

    Добавлен мощный браузер предустановок, позволяющий сохранять и вызывать все ваши любимые конфигурации.

    Новая версия была создана с помощью HISE и работает как независимый плагин VSTi/AU или отдельное приложение. Для этого не требуется Kontakt или какой-либо другой дополнительный проигрыватель.

    Я купил оригинальную версию Kontakt Арфы Микаэлы, могу ли я получить обновление или мне нужно покупать его снова?

    Если вы приобрели профессиональную версию оригинальной версии Michaela’s Harp, вы должны были получить электронное письмо с предложением бесплатного обновления до последней версии.

    Если вы не получили такое электронное письмо, свяжитесь со мной, чтобы запросить обновление — обязательно укажите исходный номер заказа, идентификатор транзакции PayPal или данные учетной записи Xtant Audio, чтобы я мог проверить ваш заказ.

    Отзывы

    Только зарегистрированные клиенты, которые приобрели этот продукт, могут оставлять отзывы.

alexxlab

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *