5. Сложные колебания. Гармонический спектр сложных колебаний, теорема Фурье. Разложение колебаний в гармонический спектр.

Ж. Фурье показал, что периодическая функция любой сложнос­ти может быть представлена в виде суммы гармонических функций, частоты которых кратны частоте сложной периодической функции. Такое разложение периодической функции на гармонические составляющие и, следовательно, разложение различных периоди­ческих процессов (механические, электрические) на гармо­нические колебания называется гармоническим анализом.Автоматически гармони­ческий анализ колебаний, в том числе и для целей медицины, осуществляется специальными приборами — анализаторами.

Совокупность гармонических колебаний, на которые разложе­но сложное колебание, называется гармоническим спектром сложного колебания. Гармонический анализ позволяет достаточно детально описать и проанализировать любой сложный колебательный процесс, он находит применение в акустике, радиотехнике, электронике и других областях науки и техники.

6. Механические волны, их виды и скорость распространения.

Механи волна- процнсс распростр мех колебаний в упругой среде.Продольная в- если направление смещения частиц=напр распр волны.если напр взаимно перпендик, то поперечная(в тв телах).Один из распространенных примеров механической волны — звуковая волна.В этом случае максимальная скорость колебаний отдельной молекулы воздуха составляет несколько сантиметров в секунду даже для достаточно большой интенсив­ности, т. е. значительно меньше скорости распространения волны (скорость звука в воздухе около 300 м/с). Это соответствует, как принято говорить, малым возмущениям среды.

Однако при больших возмущениях (взрыв, сверхзвуковое дви­жение тел, мощный электрический разряд и т. п.) скорость колеб­лющихся частиц среды может уже стать сравнимой со скоростью звука, возникает ударная волна.

При взрыве высоконагретые продукты, обладающие большой плотностью, расширяются и сжимают слои окружающего возду­ха. С течением времени объем сжатого воздуха возрастает. Тонкую переходную область, которая отделяет сжатый воздух от невозмущенного называют ударной волной. Ударная волна может обладать значительной энергией, так, при ядерном взрыве на образование ударной волны в окружаю­щей среде затрачивается около 50% энергии взрыва. Поэтому ударная волна, достигая биологических и технических объектов, способна причинить смерть, увечья и разрушения.

7. Уравнение волны. Энергетические хар-ки волны.

Мех.волна(в.)-мех.возмущения, распространяющиеся в пространстве и несущие Е. 2 вида:*упругие(распростр.упругих деформаций), *в. на поверхности жидк. Ур-ние в.выражает зависимость смещения колеблющийся точки, участвующей в волновом процессе, от координаты ее равновесного положения времени. Для в., распространяющейся вдоль ОХ в общем виде записыв.: s=f(х,t). Если s и х направлены вдоль 1 прямой, то в. продольная, если взаимно перепендикулярны-в. поперечная. Пусть в. распространяется вдоль оси ОХ без затухания так, что амплитуды колеб. всех точек одинаковы и равны А. Зададим колеб. точки корд. х=о у-нием: s=Аcoswt, до др.точки возмущение дойдет через время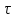

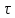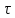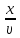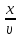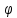
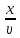колебания запаздывают: s=Аcos[w(t-)],т.к.=, тоs=Аcos[w(t-)], гдеt-время от момента равновесия, υ-скорость с кот. колебания передаются др.точкам. У-ние плоской волны позволяет опред. смещение любой точки, участвующей в волновом процессе, в любой момент времени. Аргумент при cos = w(t-)]- фаза в., фронт в.- множество точек, имеющих одновременно одинаковую фазу. Длина волны-расстояние между 2 точками, фазы кот. в один и тот же момент времени отличаются на 2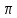(расстояние, пройденное в. за период колебания)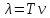.Энергетические хар-ки волны. Распространение в. связано с передачей Е от 1колеблющейся точки к др. Поток Е-колич.хар-ка переноса Е. Поток Е в.= отношению Е, переносимой в.через нек. пов-ть, к времени, в течение кот. 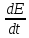эта Е перенесена: Ф=(ватт).Интенсивность в.- поток Е в., отнесенный к площади, ориентированной перпендикулярно направлению распространения в.I=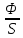=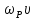.Перенос Е объясняется, чтоmax кинетической и потенциальной Е в в.приходится на точку в.,кот. проходит положение равновесия. Передача Е в в. происходит с той скоростью,с кот. распространяется фаза колебаний.Е ,переносимая в., прямо пропорциональна плотности среды, квадрату амплитуды колебаний и квадрату их частоты.W=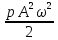

.

10.4. Сложное колебание. Разложение сложного колебания на простые составляющие. Гармонический спектр

Сложное периодическое движение — сложное колебание — можно представить в виде суммы гармонических колебаний. Су­ществуют математические методы обработки сложных колебаний. Фурье предложил метод разложения любой периодической функ­ции в ряд гармонических функций, периоды которых кратны пе­риоду сложного колебания. Разложение сложного колебания на гармонические колебания называется

гармоническим анализом.

Совокупность гармонических колебаний, на которые разложе­но сложное колебание, называется гармоническим спектром сложного колебания. Пример сложного колебания x(t), которое

раскладывается на сумму двух гармонических колебаний, пред­ставлен на рис. 10.4.

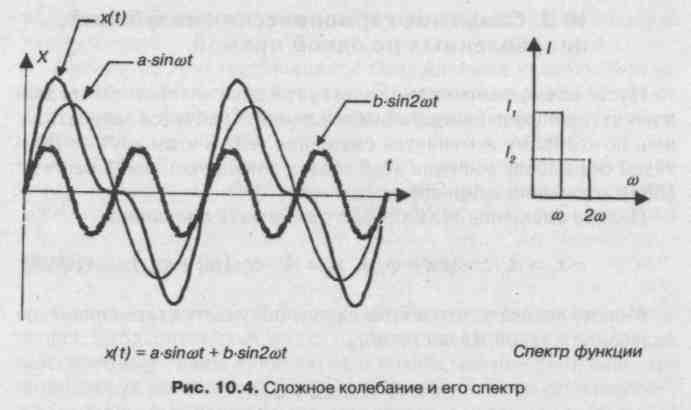
Анализ колебаний, создаваемых телом человека или его отдель­ными частями, широко используется. При ходьбе, беге центр масс человека совершает движения по кривой, которую часто можно представить синусоидой, амплитуда которой ориентирована вер­тикально. Колебательные движения совершают участки сердца и легких спортсмена на перекладине и на батуте.

На анализе сложных колебаний основана статокинезиметрия — метод оценки способности спортсмена сохранять вертикальную по­зу. В эту группу методов входит и стабилография — метод оценки способности спортсмена удерживать проекцию центра масс в преде­лах координат границы площади опоры. Данный метод реализуется с помощью стабилографа, основной частью которого является стаби-лоплатформа, на которой находится спортсмен во время испытаний. При поддержании вертикальной позы центр масс человека совершает сложные колебания. Стабилоплатформа содержит тензодатчики, регистрирующие малейшее изменение координат центра масс на плос­кость опоры. Автоматически записывается

стабилограмма — тра­ектория перемещения центра масс, зависящая от сложного коле­бательного движения центра масс. Осуществляется спектральный анализ этих сложных колебаний. По гармоническому спектру мож­но судить об особенностях вертикального положения в норме и при

отклонениях от нее. Данный метод эффективен при оценке результа­тов соответствующих тренировочных методик.

Теория колебаний используется в различных методиках по оцен­ке работы сердца.

Сесмокардиография основана на регистрации механических колебаний тела человека, вызванных работой серд­ца. В этом методе с помощью датчиков, установленных в области основания мечевидного отростка, регистрируется сердечный толчок, обусловленный механической активностью сердца в период изоволюмического сокращения. При этом происходят процессы, связанные с деятельностью волюморецепторов — тканевых меха-норецепторов сосудистого русла, активирующихся при снижении объема циркулирующей крови. Сейсмокардиосигнал формируют колебания грудины.

Баллистокардиография. Метод исследования механических проявлений сердечной деятельности, основанный на регистрации пульсовых микроперемещений тела, обусловленных выбрасывани­ем толчком крови из желудочков сердца в крупные сосуды. При этом возникает явление

отдачи. Тело человека помещают на спе­циальную подвижную платформу, которая в результате отдачи при­ходит в сложное колебательное движение. Зависимость смещения платформы с телом от времени называется баллистокардиограм-мой, анализ которой позволяет судить о движении крови и состоя­нии сердечной деятельности.

4. Сложение гармонических колебаний

Результат сложения гармонических колебаний зависит от направления складываемых колебаний, а так же от соотношения между их частотами, фазами и амплитудами. Рассмотрим на качественном уровне два случая.

4.1. Колебания, происходящие вдоль одной прямой с одинаковыми частотами

В этом случае складываемые колебания различаются лишь амплитудами А₁ иА₂ и начальными фазами₀₁ и ₀₂ . Сложение таких колебаний приведет к результату:

А₁ sin ( t + ₀₁ ) + А₂ sin( t + ₀₂ ) = А sin ( t + ₀ ) . (19)

Закон изменения смещения со временем в результирующем колебании — гармонический,частота результирующего колебания равна частоте складываемых колебаний.

Амплитуда результирующего колебания А зависит от амплитудА₁ иА₂, а также от разности начальных фаза₀₁ и ₀₂ . Несложные математические вычисления позволяют выразить амплитудуАследующим образом:

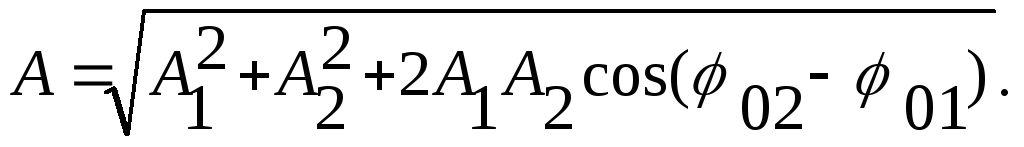(20)

Начальная фаза ₀определяется из соотношения:

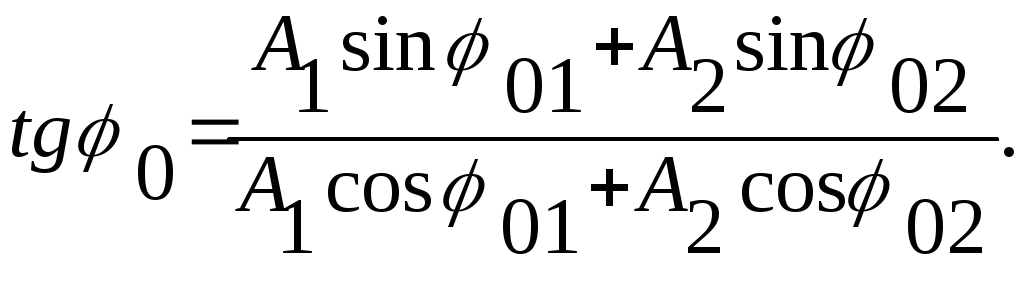(21)

Таким образом, в рассматриваемом случае результат сложения колебаний определяется формулой (19), а входящие в неё амплитуда и начальная фаза — формулами (20) и (21).

4.2. Колебания происходят вдоль одной прямой с разными частотами

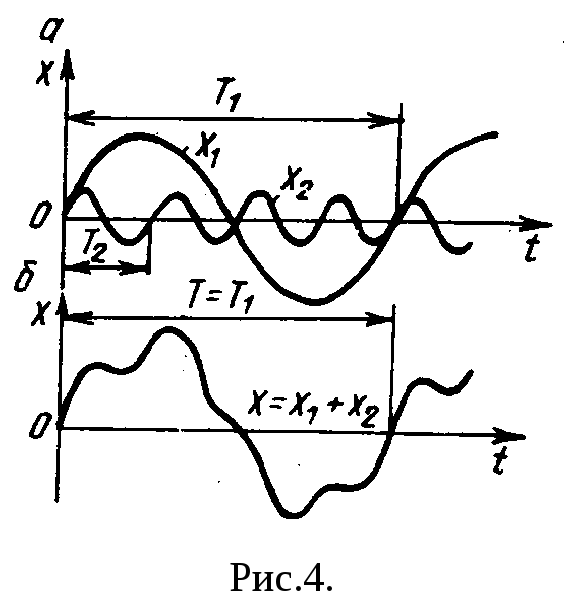
Представим два складываемых колебания графически (см.рис 4)

При сложении гармонических колебаний, происходящих с разными частотами₁и₂ ( периодамиТ₁ и Т₂) результирующее колебание не будет гармоническим, а будет представлятьсложное периодическое движение. Если складываются гармонические колебания с кратными частотами (например, на рис.4 ₂= 4₁), топериод результирующего колебания Т совпадает с периодом Т₁ слагаемогонаименьшей частоты:Т = Т₁ или =₁ .

5. Разложение колебаний в ряд Фурье. Гармонический спектр сложных колебаний

Рассмотрение рис.4 приводит к утверждению, обратному сказанному выше и известному как теорема Фурье: любое сложное периодическое движение x(t) = x(t +T) c периодом Т можно представить в виде суммы простых составляющих гармонических колебаний (гармоник). Частоты этих гармоник кратны основной частоте  рассматриваемого периодического процесса.

Первая гармоника имеет частоту  = 2 /Т , вторая —2, третья —3и т.д.

Это утверждение можно записать в виде формулы, представляющей ряд Фурье:

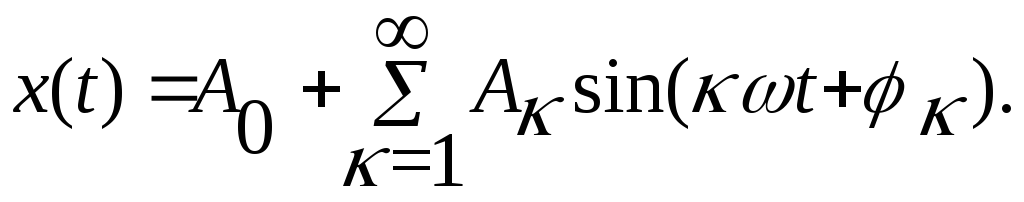(22)

Здесь А_к — амплитуды складываемых гармоник, а_к — их начальные фазы. Первая гармоника, имеющая частоту , обладает амплитудойА₁, и начальной фазой₁ , вторая (с частотой2 ) имеет амплитуду А₂ и начальную фазу₂и т.д.

СлагаемоеА₀в формуле (22) представляет собой постоянную величину, имеющую смысл постоянной составляющей сложного периодического процесса. На рис.5 представлена периодическая функция х(t), описывающая процессы, где колебания некоторой величины (например, пульсовые изменения кровенаполнения сосуда) происходят на фоне ее среднего постоянного значения (например, среднего уровня кровенаполнения), которое и характеризуется величинойА₀ в формуле (22) .

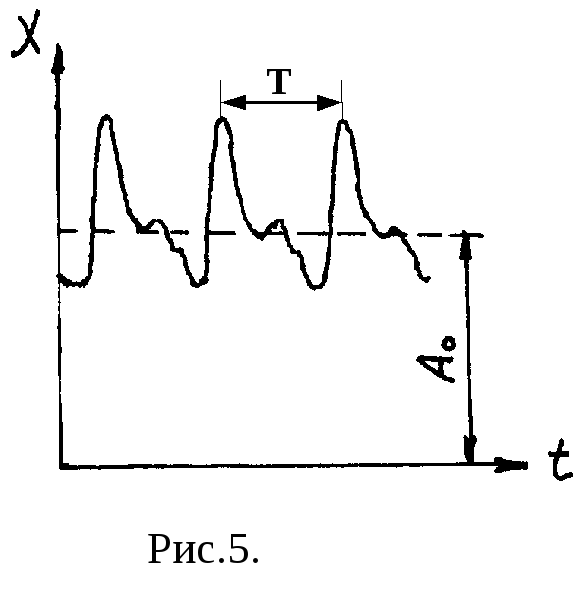
В записанной для общего случая формуле (22) число гармоник, входящих в состав сложного колебания , представляется бесконечно большим. При рассмотрении реальных колебательных процессов следует учесть, что вклад отдельных гармонических составляющих в анализируемое сложное колебание различен — в формулу (22) отдельные гармоники входят с разными амплитудами.

График, на котором по оси абсцисс отложены частоты гармоник, а по оси ординат — соответствующие им амплитуды, представляет собой гармонический спектр сложного колебания (см. рис.6).

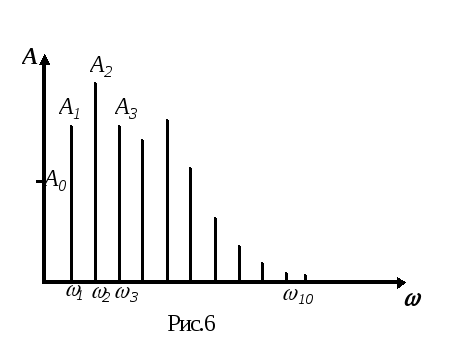
Из рассмотрения рис. 6 можно сделать вывод, что гармоники, частота которых превышает ₁₀, имеют малую амплитуды и, следовательно, их вклад в колебание, гармонический спектр которого представлен на рисунке, незначителен. Поэтому ряд Фурье для этого случая можно считать состоит из 10 слагаемых ( к= 1,2,3,…..,10 ), а вся информация о сложном колебательном процессе заключена в полосе частот от₁(основная частота процесса) до₁₀.

2.2. СПЕКТРАЛЬНЫЙ АНАЛИЗ ПЕРИОДИЧЕСКИХ СИГНАЛОВ

В соответствии со спектральным способом анализа прохождения сигналов через линейные цепи любой случайный сигнал S(T) можно представить в виде бесконечной суммы элементарных аналитически однотипных детерминированных сигналов :

(2.8)

Подавая на вход линейной цепи (рис. 1.14), коэффициент передачи которой равен , элементарный детерминированный сигнал, можно найти элементарный отклик цепи, то есть сигнал на выходе цепи.

Рис.2.3.К определению сигнала на выходе линейной цепи.

Сигнал на выходе линейной цепи равен

(2.9)

Поскольку для линейных цепей справедлив принцип суперпозиции, то результирующий отклик будет равен:

(2.10)

Функции, описывающие элементарные сигналы, называются базисными функциями. Представление сигнала базисными функциями упрощается, если они являются ортогональными и ортонормированными.

Набор функций называется ортогональным, Если в интервале от до

при (2.11)

И ортонормированным, Если для всех Выполняется условие

. (2.12)

Ортогональность базисных функций, с помощью которых представляется исходный сигнал , является гарантией того, что представление сигнала может быть сделано единственным образом. Условию ортогональности отвечают гармонические функции кратных частот, а также функции Уолша, которые на отрезке своего существования от до принимают лишь значения, равные 1, дискретные сигналы Баркера и некоторые другие функции. Спектральный метод анализа сигналов основан на преобразованиях Фурье и состоит в замене сложной функции времени, описывающей сигнал, суммой простых гармонических сигналов, образующих частотный спектр этого сигнала. Знаменитый французский физик и математик Ж. Б. Фурье (1768 – 1830 г. г.) доказал, что любое изменение во времени некоторой функции можно аппроксимировать в виде конечной или бесконечной суммы ряда гармонических колебаний с разными амплитудами, частотами и начальными фазами. Этой функцией может быть ток или напряжение в электрической цепи.

Рассмотрим вначале представление периодического электрического сигнала (рис. 2.4), отвечающего условию

, (2.13)

где: — период сигнала; =1,2,3,….

Рис. 2.4. Периодический сигнал

Представим этот сигнал бесконечным тригонометрическим рядом:

. (2.14)

Этот ряд называется рядом Фурье.

Возможна запись ряда Фурье в другом виде:

, (2.15)

Где: — модуль амплитуд гармоник;

— фазы гармоник;

— круговая частота;

— коэффициенты косинусоидальных составляющих; — коэффициенты синусоидальных составляющих; — среднее значение сигнала за период (постоянная составляющая).

Отдельные слагаемые рядов называют гармониками. Число является номером гармоники. Совокупность величин в ряде (2.15) называют спектром амплитуд, а совокупность величин — спектром фаз.

Ниже на рис. 2.5 представлены амплитудный и фазовый спектры периодического сигнала. Вертикальные отрезки амплитудного спектра представляют амплитуды гармоник и называются спектральными линиями.

Рис 2.5. Амплитудный и фазовый спектры периодического сигнала

Таким образом, спектр периодического сигнала – Линейчатый. Каждый периодический сигнал имеет вполне определенные амплитудный и фазовый спектры.

Сумма ряда (2.15) является бесконечной, но, начиная с некоторого номера, амплитуды гармоник настолько малы, что ими можно пренебречь и практически реальный периодический сигнал представляется функцией с ограниченным спектром. Интервал частот, соответствующий ограниченному спектру, называется шириной спектра.

Если функция , описывающая периодический сигнал, является четной, то сумма ряда (2.14) будет содержать только косинусоидальные составляющие. Если — нечетная функция, то сумма будет содержать только синусоидальные составляющие.

Возможно также представление периодического сигнала в виде комплексного ряда Фурье:

, (2.16)

Где:

— комплексные амплитуды спектра, содержащие информацию, как об амплитудном, так и о фазовом спектрах.

После подстановки значений и , получим:

(2.17)

Если подставить полученное значение в ряд (1.29), то он обращается в тождество. Таким образом, периодический электрический сигнал можно задавать либо функцией времени , либо комплексной амплитудой спектра.

2.2.1. Спектр периодической последовательности прямоугольных импульсов

Состав спектра периодической последовательности прямоугольных импульсов зависит от величины отношения периода последовательности к длительности импульса, называемого скважностью импульсов. В спектре будут отсутствовать гармоники с номерами кратными скважности импульсов. Скважность импульсов равна . На рис.1.17 приведены три импульсные последовательности с разными скважностями и соответствующие им спектры. Для периодической последовательности, скважность которой равна 2, в спектре отсутствуют 2, 4, 6 ,8 и т. д. гармоники. Для последовательности, скважность которой равна 3, в спектре отсутствуют 3, 6 и т. д. гармоники. Для последовательности, скважность которой равна 4, в спектре отсутствуют 4, 8 и т. д. гармоники. Во всех приведенных спектрах интервал между спектральными линиями равен величине обратной периоду последовательности. Точки на оси частот, в которых спектр равен нулю, соответствуют величине, обратной длительности импульсов периодических последовательностей.

Рис.2.6.Периодические последовательности импульсов и их спектры.

2.2.2. Спектр непериодического сигнала

При рассмотрении спектра непериодического сигнала воспользуемся предельным переходом от периодического сигнала к непериодическому сигналу, устремив период к бесконечности.

Для периодического сигнала, представленного на рис. 2.4, ранее получено выражение (2.17) для комплексной амплитуды спектра:

(2.18)

Введем обозначение:

(2.19)

Построим модуль спектра :

Рис. 2.7. Модуль спектра периодического сигнала

Расстояние между спектральными линиями равно . Если увеличивать период , то будет уменьшаться интервал w1 . При интервал между спектральными линиями w1® dw. При этом периодическая последовательность импульсов превращается в одиночный импульс и модуль спектра стремится к непрерывной функции частоты . В результате предельного перехода от периодического сигнала к непериодическому линейчатый спектр вырождается в сплошной спектр, представленный на рис. 2.8.

Рис. 2.8. Спектр непериодического сигнала

При этом комплексная амплитуда равна:

. (2.20)

С учетом предельного перехода при

(2.21)

Подставим полученное выражение в ряд (2.16). При этом сумма трансформируется в интеграл, а значения дискретных частот в значение текущей частоты и непериодический сигнал можно представить в следующем виде:

. (2.22)

Это выражение соответствует обратному преобразованию Фурье. Огибающая сплошного спектра одиночного импульса совпадает с огибающей линейчатого спектра периодической функции, представляющей периодическое повторение этого импульса.

Интеграл Фурье позволяет любую непериодическую функцию представить в виде суммы бесконечного числа синусоидальных колебаний с бесконечно малыми амплитудами и бесконечно малым интервалом по частоте. Спектр сигнала определяется из выражения

. (2.23)

Этот интеграл соответствует прямому преобразованию Фурье.

– комплексный спектр, в нём содержится информация, как о спектре амплитуд, так и о спектре фаз.

Таким образом, спектр непериодической функции сплошной. Можно сказать, что в нём содержатся «все» частоты. Если вырезать из сплошного спектра малый интервал частот , то частоты спектральных составляющих в этом участке будут отличаться сколь угодно мало. Поэтому спектральные составляющие можно складывать так, как будто все они имеют одну и ту же частоту и одинаковые комплексные амплитуды. Спектральная плотность есть отношение комплексной амплитуды малого интервала частот к величине этого интервала.

Спектральный анализ сигналов имеет фундаментальное значение в радиоэлектронике. Информация о спектре сигнала позволяет обоснованно выбирать полосу пропускания устройств, на которые воздействует этот сигнал.

2.2.3. Спектр одиночного прямоугольного видеоимпульса

Рассчитаем спектр одиночного прямоугольного импульса, амплитуда которого равна Е, а длительность — t, представленного на рис. 2.9.

Рис. 2.9. Одиночный прямоугольный импульс

В соответствии с выражением (2.24) спектр такого сигнала равен

=. (2.24)

Поскольку = 0 , когда , то частоты, на которых спектр обращается в нуль равны , где K=1,2,3…

На рис. 2.10 представлен комплексный спектр одиночного прямоугольного импульса длительностью .

Рис.2.10. Спектр одиночного прямоугольного импульса

Спектральная плотность определяет распределение энергии в спектре одиночного импульса. В общем случае распределение энергии неоднородно. Однородное распределение характерно для хаотического процесса, называемого «белым шумом».

Спектральная плотность импульса на нулевой частоте равна его площади. Приблизительно 90% энергии одиночного прямоугольного импульса сосредоточено в спектре, ширина которого определяется выражением

. (2.25)

Соотношение (1.41) определяет требования к ширине полосы пропускания радиотехнического устройства. В задачах, где форма сигнала имеет второстепенное значение полосу пропускания устройства для этого сигнала можно выбрать равной ширине первого лепестка спектра. При этом неизвестна степень искажения формы сигнала. Двукратное увеличение полосы пропускания лишь на 5% увеличит энергию сигнала при одновременном возрастании уровня шумов.

2.2.4. Спектры неинтегрируемых сигналов

Фурье анализ применим лишь к интегрируемым функциям, то есть к функциям, для которых выполняется условие сходимости интеграла:

(2.26)

К неинтегрируемым относятся такие сигналы, как -импульс, единичный скачок, гармонический сигнал, постоянное напряжение.

Спектр — импульса

Рассчитаем спектр —Импульса с помощью интеграла прямого преобразования Фурье.

(2.27)

На основании стробирующего свойства — функции получим:

. (2.28)

Таким образом, и . При фаза .

Рис.2.11. Спектр — импульса

Итак, — функция имеет сплошной бесконечный спектр с единичной амплитудой на всех частотах. В момент возникновения импульса все гармонические составляющие бесконечного спектра складываются когерентно, поскольку спектр вещественный. В результате этого наблюдается бесконечно большая амплитуда импульса.

Спектр гармонического сигнала

Вычислим спектр гармонического сигнала с единичной амплитудой .

(2.20)

В соответствии с обратным преобразованием Фурье

(2.30)

Учитывая дуальность частоты и времени, запишем:

(2.31)

Знак экспоненты можно выбрать, считая — функцию четной.

В соответствии с этим спектр гармонического сигнала запишется в следующем виде:

(2.32)

Таким образом, гармоническому сигналу соответствует дискретный спектр из двух линий в виде дельта функций на частотах и

Рис. 2.12. Спектр гармонического сигнала

Спектр постоянного напряжения

Для гармонического сигнала получено следующее выражение для спектральной плотности:

(2.33)

Если в этом выражении приравнять частоту нулю, то получим спектр постоянного напряжения единичного уровня:

(2.34)

Таким образом, спектр постоянного напряжения содержит особенность типа функции.

Рис. 2.13. Спектр постоянного напряжения

гармонический спектр — со всех языков на русский

См. также в других словарях:

• гармонический спектр — harmoninis spektras statusas T sritis fizika atitikmenys: angl. Fourier spectrum; harmonic spectrum vok. Fourier Spektrum, n; harmonisches Spektrum, n; Oberwellenspektrum, n rus. гармонический спектр, m pranc. spectre harmonique, m …   Fizikos terminų žodynas

• ГАРМОНИЧЕСКИЙ АНАЛИЗ АБСТРАКТНЫЙ — теория абстрактных Фурье рядов и Фурье интегралов. Классический гармонич. анализ теория рядов Фурье и интегралов Фурье интенсивно развивался под влиянием физич. задач в 18 19 вв., и в работах П. Дирихле (P. Dirichlet), Б. Римана (В. Riemann), А.… …   Математическая энциклопедия

• ГАРМОНИЧЕСКИЙ АНАЛИЗ — представление сложного негармонич. колебания в виде суммы гармонических колебании, образующих т. н. спектр колебания. Если сложное колебание периодич. с частотой v = 1/Т и с периодом Т, то его спектр дискретный, или линейчатый: он состоит из… …   Большой энциклопедический политехнический словарь

• СПЕКТР — (от лат. spectrum представление, образ) совокупность разл. значении, к рые может принимать физ. величина. Наиболее часто понятие С. используют применительно к колебат. процессам, понимая под ним совокупность простых гармонических колебаний, на к… …   Большой энциклопедический политехнический словарь

• Квантовый гармонический осциллятор — Гармонический осциллятор в квантовой механике представляет собой квантовый аналог простого гармонического осциллятора, при этом рассматривают не силы, действующие на частицу, а гамильтониан, то есть полную энергию гармонического осциллятора,… …   Википедия

• ОСЦИЛЛЯТОР ГАРМОНИЧЕСКИЙ — система с одной степенью свободы, колебания к рой описываются уравнением вида Фазовые траектории окружности, период колебаний не зависит от амплитуды. Потенциальная энергия О. г. квадратично зависит от х: Примеры О. г.: малые колебания маятника,… …   Математическая энциклопедия

• Дисперсия волн — (лат. рассеивать, развеивать, разгонять) термин «дисперсия» был введён в физику И. Ньютоном (1643 1727) в 1672 г. при описании разложения пучка белого света, преломляющегося на границе раздела сред. Волновая концепция позволила объяснить это… …   Концепции современного естествознания. Словарь основных терминов

• Fourier spectrum — harmoninis spektras statusas T sritis fizika atitikmenys: angl. Fourier spectrum; harmonic spectrum vok. Fourier Spektrum, n; harmonisches Spektrum, n; Oberwellenspektrum, n rus. гармонический спектр, m pranc. spectre harmonique, m …   Fizikos terminų žodynas

• Fourier-Spektrum — harmoninis spektras statusas T sritis fizika atitikmenys: angl. Fourier spectrum; harmonic spectrum vok. Fourier Spektrum, n; harmonisches Spektrum, n; Oberwellenspektrum, n rus. гармонический спектр, m pranc. spectre harmonique, m …   Fizikos terminų žodynas

• Oberwellenspektrum — harmoninis spektras statusas T sritis fizika atitikmenys: angl. Fourier spectrum; harmonic spectrum vok. Fourier Spektrum, n; harmonisches Spektrum, n; Oberwellenspektrum, n rus. гармонический спектр, m pranc. spectre harmonique, m …   Fizikos terminų žodynas

• harmonic spectrum — harmoninis spektras statusas T sritis fizika atitikmenys: angl. Fourier spectrum; harmonic spectrum vok. Fourier Spektrum, n; harmonisches Spektrum, n; Oberwellenspektrum, n rus. гармонический спектр, m pranc. spectre harmonique, m …   Fizikos terminų žodynas

5.3. Спектры периодических негармонических сигналов. 5. Линейные электрические цепи в режиме периодических негармонических воздействий. Теория электрических цепей. Курс лекций

Рассмотрим последовательность прямоугольных импульсов, изображенную на рис. 5.3, а. Сигналы подобной формы находят очень широкое применение в радиотехнике и электросвязи: телеграфия, цифровые системы передачи, системы многоканальной связи с временным разделением каналов, различные импульсные и цифровые устройства и др. (см. гл. 19). Импульсная последовательность характеризуется следующими основными параметрами: амплитудой импульса A_и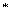 , его длительностью t_и и периодом следования Т. Отношение периода Т к длительности t_и называется скважностью импульсов и обозначается через q = T/t_и. Обычно значения скважности импульсов лежат в пределах от нескольких единиц (в измерительной технике, устройствах дискретной передачи и обработки информации), до нескольких сотен или тысяч (в радиолокации).

Для нахождения спектра последовательности прямоугольных импульсов воспользуемся рядом Фурье в комплексной форме (5.6). Комплексная амплитуда k-й гармоники равна согласно (5.8) после возвращения к исходной переменной t.

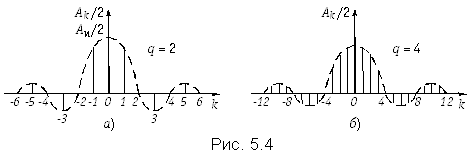
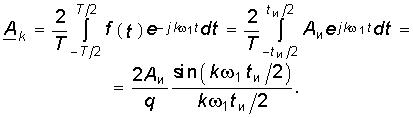(5.27)

Подставив значение A_k в уравнение (5.6), получим разложение в ряд Фурье: 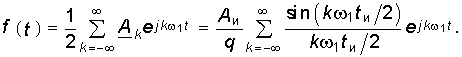(5.28)

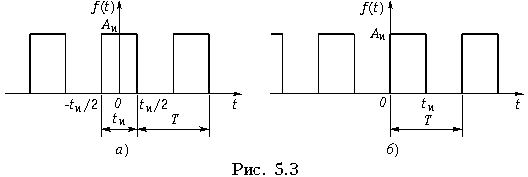
На рис. 5.4 изображен спектр комплексных амплитуд для q = 2 и q = 4. Как видно из рисунка, спектр последовательности прямоугольных импульсов представляет собой дискретный спектр с огибающей (штриховая линия на рис. 5.4), которая описывается функцией 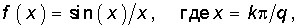(5.29) носящей название функции отсчетов (см. гл. 19). Число спектральных линий между началом отсчета по оси частот и первым нулем огибающей равно q—1. Постоянная составляющая сигнала (среднее значение) 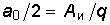, а действующее значение A = 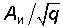, т.е. чем больше скважность, тем меньше уровень постоянной составляющей и действующее значение сигнала. С увеличением скважности q число дискретных составляющих увеличивается — спектр становится гуще (см. рис. 5.4, б), и амплитуда гармоник убывает медленнее. Следует подчеркнуть, что в соответствии с (5.27) спектр рассматриваемой последовательности прямоугольных импульсов вещественный.

Из спектра комплексных амплитуд (5.27) можно выделить амплитудный A_k = |A_k| и фазовый спектр 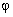_k = argA_k, изображенный на рис. 5.5 для случая q = 4. Из рисунков видно, что амплитудный спектр является четной, а фазовый — нечетной функцией частоты. Причем, фазы отдельных гармоник принимают либо нулевое значение между узлами, где синус положительный, либо ±, где синус отрицательный (рис. 5.5, б)

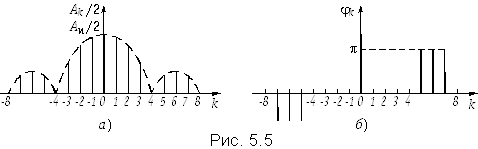
На основании формулы (5.28) получим тригонометрическую форму разложения в ряд Фурье по четным гармоникам (сравни с (5.15)): 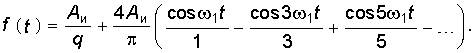(5.30)

При сдвиге импульсной последовательности по оси времени (рис. 5.2, б) в соответствии с (5.13) ее амплитудный спектр останется прежним, а фазовый спектр изменится: 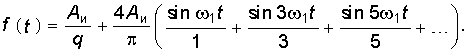(5.31)

В случае, когда периодическая последовательность имеет разнополярную форму (см. рис. 5.1), в спектре будет отсутствовать постоянная составляющая (сравните (5.30) и (5.31) с (5.14) и (5.15)).

Аналогичным образом можно исследовать спектральный состав периодических негармонических сигналов другой формы. В табл.5.1 приведено разложение в ряд Фурье некоторых наиболее распространенных сигналов.

Таблица 5.1

Гармонический спектр | solfamusictheory

Конспекты по элементарной теории музыки. Содержание

Звук – это физическое явление, возникающее в результате колебаний упругого тела.

Музыкальный звук – наименьший структурный элемент музыки. Традиционно считается, что в отличие от шума, музыкальный звук обладает следующими свойствами: высотой, тембром, длительностью и громкостью. Однако в музыке используются практически все воспринимаемые человеком шумовые и музыкальные звуки.

Высота музыкального звука зависит от частоты колебаний источника звука. Она измеряется в герцах – Гц). 1 Гц=1 колебанию/сек. Человеческий слух различает звуки высотой от 16 до 4000-4500 Гц. Мельчайшая единица измерения высоты звука – цент (1/100 темперированного полутона).

Тембр (окраска звука) зависит от формы, размера, материала и устройства источника звука. Тембры музыкальных звуков весьма разнообразны.

Громкость зависит от амплитуды колебаний и локализации в пространстве источника звука. Громкость не должна достигать болевого порога (120 дБ).  Рекомендуемая Всемирной организацией здравоохранения (ВОЗ) ежедневная безопасная громкость для любого звука установлена на уровне ниже 85 дБ при максимальной продолжительности воздействия не более 8 часов. 

Длительность зависит от продолжительности колебаний источника звука. Наш слух воспринимает звуки продолжительностью не менее 0,015 сек. Звуки органной педали могут длиться несколько минут.

Каждый музыкальный звук имеет в своем составе обертоны (призвуки, или частичные тоны), одновременно возникающие при колебании частей источника звука (например, струны или воздушного столба).

 

 

 

 

 

 

 

Расположенные в восходящем порядке обертоны образуют натуральный звукоряд (гармонический спектр или обертоновый ряд). Первый обертон равен основному тону:

 

 

 

 

По особенностям восприятия высоты звука различают два основных типа  звуковысотного слуха: абсолютный (тональный) и относительный (интервальный).

Исследования отечественного музыкального акустика Н. А. Гарбузова показали, что звуковысотный слух обладает зонной природой. Каждой из ступеней звукоряда соответствует не одна частота, а целый последовательный ряд частот. В пределах зоны этих частот звук воспринимается как одна и та же ступень звукоряда. Например, звук ля первой октавы может соответствовать не только 440 Гц (отечественный эталон с 1936 г.), но и 441, 442, 443, 444, 445, 439, 438, 437, 436, 435 Гц, не превращаясь при этом в си-бемоль или соль-диез. Такие области частот называются звуковысотными зонами.

Камертон (нем. Kammerton, от Kammer – комната и Тоn – звук) – инструмент для фиксации и воспроизведения эталонной высоты звука, которая также называется словом «камертон».

https://ru.wikipedia.org/wiki/Камертон

http://dic.academic.ru/dic.nsf/enc_music/3358/Камертон

https://ru.wikipedia.org/wiki/Камертон

https://commons.wikimedia.org/w/index.php?curid=9708495

https://ru.wikipedia.org/wiki/Натуральный_звукоряд

https://ru.wikipedia.org/wiki/Громкость_звука

http://dic.academic.ru/dic.nsf/enc_music/3025/Звук

https://ru.wikipedia.org/wiki/Музыкальный_звук

https://dic.academic.ru/dic.nsf/es/38896/натуральный

http://dic.academic.ru/dic.nsf/enc_music/7071/Слух

Like this:

Like Loading…