единица измерения, определение, формулы для вычисления
Физика
12.11.21
13 мин.
Главной величиной в электродинамике считается электрический заряд. В физике его свойства, пожалуй, занимают такое же положение, как теоремы умножения и деления в алгебре. После открытия параметра удалось получить представления о силовых полях, токе, напряжении, понять суть энергии, классифицировать вещества по проводимости. Изучение взаимодействия частиц позволило сделать важные открытия, ставшие фундаментом в создании электронных приборов.
Оглавление:
- Общие сведения
- Свойства заряда
- Закон Кулона
- Решение задач
Общие сведения
Проводя серию опытов с янтарём, Уильям Гильберт заметил, что при определённых обстоятельствах он был способен притягивать к себе другие предметы. В XVI веке врач из Англии назвал тела, которые обладали таким свойством наэлектризованными.
Французский учёный Шарль Франсуа Дюфе, провёдший большую работу по систематизации сведений, связанных с электричеством, пришёл к выводу, что такой субстанцией является элементарная частица. В каждом теле существует несколько их видов. Как показали опыты, одни образовывались при трении стекла о шёлк, а другие — смолы. Поэтому учёный назвал частицы «стеклянными» и «смоляными».
В 1897 году физиком Томсоном была открыта элементарная частица, получившая название электрон. Через двадцать лет Резерфорд выдвинул предположение о существовании противоположной величины. После этого теория была подтверждена экспериментально, а частица была названа протоном. Учёный из Англии в 1932 году смог обнаружить новый вид частиц, близких по размеру открытым, но отличающихся своим поведением. Назвал он их нейтронами, что в переводе с латинского обозначает «ни тот ни другой».
После открытия тока и напряжения учёными были обнаружены интересные эффекты. Проводник, по которому протекало электричество, вызывал отклонение магнитной стрелки. Это явление позволило сделать вывод, что элементарная частица является носителем энергии, которую и назвали зарядом. Понятие же о положительной и отрицательной частицы ввёл Вениамин Франклин.
Таким образом, было установлено, что атом вещества состоит из трёх частиц:
- отрицательно заряженного электрона;
- имеющего положительный заряд протона;
- нейтральной частицы нейтрона.
В начале XX века американский физик Роберт Милликен опытным путём показал, что заряд дискретен, то есть для любого тела он составляет целое кратное и показывает количество электричества.
Сегодня под ним понимают скалярную физическую величину, определяющую возможности физического тела быть источником возникновения электромагнитных полей. Именно количество заряда и обеспечивает появление электромагнитного взаимодействия.
Свойства заряда
Для упрощения описания поля, возникающего вокруг заряженного тела или даже их системы, была введена идеализация — пробный точечный заряд. Простыми словами — это величина с размерами носителя, которым можно пренебречь. В абстрактном смысле заряд представляет собой генератор непрерывной симметрии изучаемой физической системы. По сути, это субстанция, которая «течёт» в физическом теле.
Для изучения взаимодействия заряженных частиц используют специальные приборы — электроскоп и электрометр. В состав первого входит металлический стержень, проходящий сквозь диэлектрическую пробку, с прикреплёнными к нему двумя тонкими металлическими лепестками (фольга). При взаимодействии тела со стержнем листки заряжаются и отклоняются друг от друга. Во втором же устройстве используется стрелка, которая может свободно вращаться на стержне. По её отклонениям судят о величине электрического заряда и его влиянии.
По её отклонениям судят о величине электрического заряда и его влиянии.
Из известных свойств заряженных частиц можно выделить следующие:
- В природе есть как отрицательные, так и положительные заряды. При взаимодействии для разноимённых характерно появление силы притягивания, а одноимённых — отталкивания. Носителем наименьшего отрицательного заряда в физическом теле является электрон. Его величина составляет q = -1,6*10-19 Кл, а масса m = 9,1*10-31 кг. Положительный же переносят протоны. Значение их заряда аналогично электрону, но только с противоположным знаком, а масса больше m = 1,67*10-27 кг.
- Электрический заряд по природе дискретный. Это значит, что его значение в любом случае будет кратно величине электрона: q = N qe. При этом n — всегда целое число.
- При создании определённых условий электрический заряд можно переместить из одного тела в другое.
- В замкнутой системе действует закон сохранения энергии частиц.
 Экспериментально установлено, что появление положительно заряженной частицы сопровождается исчезновением отрицательной. Любого знака заряды при их равенстве и взаимодействии могут аннигилировать, то есть нейтрализовать друг друга.
Экспериментально установлено, что появление положительно заряженной частицы сопровождается исчезновением отрицательной. Любого знака заряды при их равенстве и взаимодействии могут аннигилировать, то есть нейтрализовать друг друга. - За единицу заряда принимается величина, определяемая как количество прошедших частиц через поперечное сечение проводника за единицу времени.
Эти свойства помогли лучше понять строение физических тел, дать определение таким параметрам, как ток и напряжение. А открытие того, что величина электричества не зависит от системы отсчёта, позволило вывести закон сохранения заряда.
Закон Кулона
Возможность взаимодействия зарядов между собой впервые подтвердил Кулон. Для этого он использовал крутильные весы собственного изобретения. На них было закреплено коромысло, подвешенное на шёлковую нить. К другому её концу через зажим крепилась стрелка микрометра. На одну чашу весов ложился шар, а на другую — противовес. Вся эта конструкция размещалась в сосуде, из которого был выкачан воздух. Через специальное отверстие в колбу можно было поместить другой шар.
Вся эта конструкция размещалась в сосуде, из которого был выкачан воздух. Через специальное отверстие в колбу можно было поместить другой шар.
В результате таких действий физик наблюдал, как при помещении шаров с разным зарядом происходило закручивание нити. Силу этого взаимодействия он определял по отклонению стрелки микрометра. Кроме этого, с помощью проводника Кулон замыкал оба тела и наблюдал распределение электрозарядов. Такое устройство позволяло измерять силы до 10-11 ньютон.
Проведя ряд экспериментов, учёный установил, что сила взаимодействия обратно пропорциональна квадрату расстояния между носителями и пропорциональна произведению их зарядов. То есть, чем большей энергией обладают носители и плотнее расположены друг к другу, тем сильнее они испытывают обоюдное влияние. В честь его работы величина энергии частицы стала измеряться в кулонах (Кл).
В математическом виде сила взаимодействия описывается выражением: F = k * (q1 * q2) / r2. Где:
Где:
- q – величина энергии которой обладает элементарная частица;
- k – коэффициент;
- r – расстояние между зарядами.
Коэффициент является постоянной величиной, но зависит от выбора системы измерений. Так, для Гаусса его можно вычислить по формуле: K = (p * E0) / 4, где E0 – электрическая постоянная.
Кроме этого, с помощью закона Кулона возможно определить и силу, с которой взаимодействуют магнитные полюса. Находится она из выражения: F = f * (m 1 * m 2 / μ * r2). Эта формула похожа на предыдущую, только в ней стоит магнитная проницаемость среды – μ.
Решение задач
Электростатика – эта наука, занимающаяся изучением и нахождением сил, возникающих при взаимодействии заряженных частиц между собой в состоянии покоя. При помощи закона Кулона проводить постоянные измерения для этого не нужно, достаточно использовать полученные им закономерности.
Например, с помощью математики и знания нужных формул можно решать следующие виды задач:
- Определить, с какой силой будут действовать друг на друга электроны, несущие заряд 10-8 кулон каждый, если расстояние между ними составляет три сантиметра. Это задача одноходовая, то есть решается по одной формуле: F = k * (q 1 * q 2 / r 2). Следует обратить внимание, что расстояние дано в сантиметрах, а подставлять его нужно согласно СИ в метрах. После подстановки и выполнения вычислений ответ должен получиться следующим: F = 9 * 109 * (H * m 2 / Кл2) * (10 -8)2 (Кл) / (3 * 10
- Найти, во сколько раз электроотталкивание между двумя электронами будет больше их силы притяжения. Для решения этой задачи понадобится взять данные о массе частицы и величине её заряда из справочника. Затем по закону Кулона рассчитать силу электрического взаимодействия, а по закону всемирного тяготения — гравитационную и найти соотношение полученных результатов.
 Так, F 1 = (k * q 1 * q 2) / r 2 = k * (e)2 / r 2, а F 2 = G * (m 1 * m 2) / r 2 = G * m / r 2. Отсюда F 1 / F 2 = 9 * 109 * 1,6 * 10-19 / 6,67 * 10-11 * (9,1 * 10-31)2 = 4, 23 * 1042.
Так, F 1 = (k * q 1 * q 2) / r 2 = k * (e)2 / r 2, а F 2 = G * (m 1 * m 2) / r 2 = G * m / r 2. Отсюда F 1 / F 2 = 9 * 109 * 1,6 * 10-19 / 6,67 * 10-11 * (9,1 * 10-31)2 = 4, 23 * 1042. - Заряженные частицы находятся друг от друга на расстоянии семь миллиметров. Вычислить силу, действующую на заряд 2 нКл расположенный в точке, удалённой на три миллиметра от заряда в 10 нКл и на четыре от 16 нКл. Равнодействующую возникших сил можно определить так: F = F1 – F2, где: F1 – взаимодействие c третьим первого заряда, а F2 — второго. Таким образом, рабочая формула примет вид: F = k * (q 1 * q 3) / r 12 – k * (q1 * q3) / r 22 = k * q 3 * (q 1/ r 12 – q 2/ r 22). После подстановки данных в ответе должна получиться сила, равная: F = 2 * 10-3 Н.
Нужно обратить внимание, что при подстановке исходных данных в формулы нужно обязательно придерживаться СИ. Это важно, тем более что с помощью размерностей можно проверить правильность используемого или полученного выражения. А также при решении задач часто приходится прибегать к использованию справочника по электрофизике. Другие сложности при знании формул возникнуть не должны.
Это важно, тем более что с помощью размерностей можно проверить правильность используемого или полученного выражения. А также при решении задач часто приходится прибегать к использованию справочника по электрофизике. Другие сложности при знании формул возникнуть не должны.
Электромагнетизм в физике: основные формулы
Основные формулы электромагнетизма
Кратность электрического заряда
Здесь q — заряд (Кл), N — число не скомпенсированных элементарных зарядов в заряде q (безразмерное), — элементарный заряд (Кл).
Поверхностная плотность заряда
Здесь — поверхностная плотность заряда , q — заряд на поверхности (Кл), S — площадь этой поверхности .
Закон Кулона
Здесь F — сила взаимодействия точечных зарядов (Н), — коэффициент пропорциональности, и — модули взаимодействующих зарядов (Кл), — относительная диэлектрическая проницаемость среды (безразмерная), —электрическая постоянная, r — расстояние между зарядами (м).
Напряженность электрического поля
Здесь Е — напряженность электрического поля (Н/Кл или В/м), F — сила, действующая на заряд (Н), q — заряд (Кл).
Напряженность поля точечного заряда
Здесь Е — напряженность поля (Н/Кл или В/м), k — коэффициент пропорциональности , q — модуль заряда (Кл), — относительная диэлектрическая проницаемость среды (безразмерная), — электрическая постоянная (Ф/м), r — расстояние от точки с напряженностью Е до заряда q (м).
Напряженность поля бесконечной равномерно заряженной плоскости
Здесь Е — напряженность электрического поля (В/м), — поверхностная плотность зарядов на плоскости , £0— электрическая постоянная (Ф/м), — диэлектрическая проницаемость среды (безразмерная).
Напряженность поля двух разноименно и равномерно заряженных плоскостей с одинаковой поверхностной плотностью зарядов (напряженность поля плоского конденсатора)
Все величины те же, что и в предыдущей формуле.
Работа перемещения заряда в однородном электрическом поле
Здесь А — работа перемещения заряда (Дж), Е — напряженность однородного поля (Н/Кл или В/м), q — перемещаемый заряд (Кл), d — проекция перемещения на силовую линию однородного поля (м).
Потенциал электрического поля
Здесь — потенциал электрического поля (В), — потенциальная энергия заряда (Дж), q — заряд, обладающий этой энергией в электрическом поле (Кл).
Потенциал поля точечного заряда
Все величины те же, что и в аналогичной формуле напряженности.
Разность потенциалов
Здесь — разность потенциалов между двумя точками поля (В), U — напряжение (В), А — работа перемещения заряда (Дж), q — перемещаемый заряд (Кл).
Связь напряженности с разностью потенциалов в однородном электрическом поле
Здесь Е — напряженность электрического поля (Н/Кл или В/м), — разность потенциалов между двумя точками поля (В), U — напряжение между этими точками (В), d — проекция расстояния между этими точками на силовую линию поля (м).
Электроемкость проводника
Здесь С — емкость проводника (Ф), q — заряд проводника (Кл), — его потенциал (В).
Емкость сферического проводника
Здесь С — емкость сферического проводника (Ф), — электрическая постоянная (Ф/м), — относительная диэлектрическая проницаемость среды (безразмерная), R — радиус сферы (м).
Емкость конденсатора
Здесь С — емкость конденсатора (Ф), q — его заряд (Кл), — разность потенциалов между его обкладками (В), U — напряжение между обкладками (В).
Емкость плоского конденсатора
Здесь С — емкость плоского конденсатора (Ф), — электрическая постоянная (Ф/м), — относительная диэлектрическая проницаемость среды (безразмерная), S — площадь обкладок конденсатора , d — расстояние между обкладками (м).
Последовательное соединение конденсаторов
q — одинаков на всех конденсаторах
Если все конденсаторы имеют одинаковую емкость С, то
Здесь q — заряд конденсаторов (Кл), — общее напряжение на батарее конденсаторов (В), — напряжения на отдельных конденсаторах (В), N — число конденсаторов (безразмерное), — общая емкость батареи конденсаторов (Ф), — емкости отдельных конденсаторов (Ф).
Параллельное соединение конденсаторов
U — одинаково на всех конденсаторах
Если все конденсаторы имеют одинаковую емкость С, то
Здесь U — напряжение на конденсаторах (В), — общий заряд батареи конденсаторов (Кл), — заряды отдельных конденсаторов (Кл), N — число конденсаторов (безразмерное), — емкость батареи конденсаторов (Ф), , — емкости отдельных конденсаторов (Ф).
Формулы энергии электрического поля проводника
Здесь — энергия электрического поля (Дж), С — емкость проводника (Ф), — потенциал проводника (В), q — заряд проводника (Кл).
Формулы энергии электрического поля конденсатора
Здесь — энергия электрического поля конденсатора (Дж), С — емкость конденсатора (Ф), q — заряд на его обкладках (Кл), U — напряжение на обкладках конденсатора (В).
Формула энергии системы точечных зарядов
Здесь — энергия системы N точечных зарядов (Дж), — заряды, входящие в систему (Кл), — потенциалы полей, созданных в точке, где находится один из зарядов, остальными зарядами системы (В).
Формулы силы тока
Здесь I — сила постоянного тока (A), q — заряд, прошедший через поперечное сечение проводника (Кл), t — время прохождения заряда (с), n — концентрация свободных электронов , е — модуль заряда электрона (Кл), v — скорость упорядоченного движения электронов по проводнику (м/с), S — площадь поперечного сечения проводника .
Формулы плотности тока
Здесь j — плотность тока , I — сила тока (A), S — площадь поперечного сечения проводника , п — концентрация свободных электронов в проводнике , е — модуль заряда электрона (Кл), v — скорость упорядоченного движения свободных электронов (м/с).
Формулы сопротивления проводника
Здесь R — сопротивление проводника (Ом), U — напряжение на нем (В), I — сила тока в проводнике (А), — удельное сопротивление (Ом • м), l — длина проводника (м), S — площадь поперечного сечения проводника .
Зависимость сопротивления металлического проводника от температуры
Здесь R — сопротивление проводника при температуре t °C (Ом), — сопротивление проводника при О °C (Ом), а — температурный коэффициент сопротивления , t — температура по шкале Цельсия, — изменение абсолютной температуры проводника при нагревании от О °C = 273 К до абсолютной температуры Т (К).
Закон Ома для однородного участка цепи
Здесь I — сила тока (A), U — напряжение (В), R — сопротивление участка (Ом).
Последовательное соединение проводников
I — одинакова во всех проводниках
Если все проводники имеют одинаковое сопротивление, то
для двух последовательных проводников
Здесь I — сила тока (А), — общее напряжение на всех последовательно соединенных проводниках (В), ,…, — напряжения на отдельных проводниках (В), — общее сопротивление всех последовательно соединенных проводников (Ом), — сопротивления отдельных проводников (Ом), N — количество проводников (безразмерное).
Параллельное соединение проводников
U — одинаково на всех проводниках
Если все проводники имеют одинаковое сопротивление, то
общее сопротивление двух параллельных проводников
общее сопротивление трех параллельных проводников
— для двух параллельных проводников
Здесь U — напряжение на проводниках (В), — сила тока в неразветвленном участке цепи (А), — сила тока в отдельных проводниках (А), — общее сопротивление параллельных проводников (Ом), — сопротивления отдельных проводников (Ом), N — количество проводников (безразмерное).
Закон Ома для неоднородного участка цепи
Здесь I — сила тока (А), — разность потенциалов на концах участка (В), — ЭДС, действующая в участке (В), R — сопротивление участка (Ом).
Формула ЭДС
Здесь — ЭДС (В), — работа сторонних сил (Дж), q — перемещаемый заряд (Кл).
Закон Ома для всей цепи
в случае соединенных последовательно одинаковых источников тока
в случае соединенных параллельно одинаковых источников тока
Здесь I — сила тока в цепи (А), — ЭДС источника тока (В), R — сопротивление внешней части цепи (Ом), r — внутреннее сопротивление или сопротивление источника тока (Ом), N — количество одинаковых источников тока (безразмерное).
Сила тока короткого замыкания
при R = О
Все величины названы в предыдущей формуле.
Расчет сопротивления шунта к амперметру
Здесь — сопротивление шунта (Ом), — сопротивление амперметра (Ом), — число, показывающее, во сколько раз измеряемая амперметром сила тока I больше силы тока , на которую он рассчитан (безразмерное число).
Расчет добавочного сопротивления к вольтметру
Здесь — добавочное сопротивление (Ом), — сопротивление вольтметра (Ом), — число, показывающее, во сколько раз измеряемое напряжение U больше напряжения , на которое рассчитан вольтметр (безразмерное число).
Работа тока
Здесь А — работа тока (Дж), U — напряжение на участке цепи (В), I — сила тока в цепи (A), t — время прохождения тока (с), q — прошедший по цепи заряд (Кл), — разность потенциалов на концах участка цепи (В), R — сопротивление участка цепи (Ом), — ЭДС источника тока (В), Р — мощность тока (Вт).
Мощность тока
Здесь Р — мощность тока (Вт), U — напряжение (В), I — сила тока (A), R — сопротивление (Ом), — ЭДС источника тока (В), А — работа тока (Дж), t — время (с).
Закон Джоуля — Ленца
Здесь Q — количество теплоты (Дж). Остальные величины названы в предыдущей формуле.
Коэффициент полезного действия (КПД) электрической цепи
Здесь — КПД электрической цепи (% или безразмерный), U — напряжение на внешнем участке цепи (В), R — сопротивление внешнего участка цепи (Ом), r — внутреннее сопротивление или сопротивление источника тока (Ом), — ЭДС источника тока (В).
Закон Фарадея для электролиза
Здесь m — масса вещества, выделившегося на электроде (кг), k — электрохимический эквивалент этого вещества (кг/Кл), q — заряд, прошедший через электролит, I — сила тока в электрохимической ванне (A), t — время электролиза (с), F — число Фарадея (Кл/моль), М — молярная масса выделившегося вещества (кг/моль, n — валентность этого вещества (безразмерная).
Формулы индукции магнитного поля
Здесь В — индукция магнитного поля (Тл), — максимальный момент сил, вращающих контур с током в магнитном поле (Н • м), I — сила тока в контуре (A), S — площадь контура — максимальная сила Ампера, действующая на проводник с током в магнитном поле (Н), l — длина проводника в магнитном поле (м).
Формула силы Ампера
Здесь — сила Ампера, действующая на проводник с током в магнитном поле (Н), В — индукция магнитного поля (Тл), I — сила тока в проводнике (А), l — длина проводника в магнитном поле (м), — угол между направлением тока в проводнике и вектором магнитной индукции (рад).
Формула момента сил, вращающих контур с током в магнитном поле
Здесь М — момент сил, вращающих контур с током в магнитном поле (Н • м), В — индукция магнитного поля (Тл), I — сила тока в контуре (A), S — площадь контура — угол между нормалью к плоскости контура и вектором магнитной индукции (рад).
Формула силы Лоренца, действующей на заряд, движущийся в магнитном попе
Здесь — сила Лоренца, действующая на заряд, движущийся в магнитном поле (Н), В — индукция магнитного поля (Тл), q — заряд (Кл), v — скорость заряда (м/с), — угол между векторами магнитной индукции и скорости (рад).
Формула магнитного потока
Здесь Ф — магнитный поток сквозь поверхность (Вб), S — площадь поверхности — угол между нормалью к поверхности и вектором магнитной индукции (рад), L — индуктивность контура (Гн), I — сила тока в контуре (А).
Формула ЭДС электромагнитной индукции
Здесь — ЭДС индукции в контуре (В), — скорость изменения магнитного потока, пересекающего контур (Вб/с), N — число витков в контуре (безразмерное), — первая производная магнитного потока по времени (Вб/с).
Формула ЭДС индукции в проводнике, движущемся поступательно в магнитном поле
Здесь — ЭДС индукции в проводнике (В), В — индукция магнитного поля (Тл), v — скорость проводника в магнитном поле (м/с), l — длина проводника в магнитном поле (м), — угол между векторами скорости и магнитной индукции (рад), — максимальная ЭДС индукции, когда проводник движется перпендикулярно линиям магнитной индукции.
Формула ЭДС индукции в контуре, вращающемся в магнитном поле
Здесь — ЭДС индукции во вращающемся контуре (В), В — индукция магнитного поля (Тл), — угловая скорость вращения (рад/с), S — площадь контура, N — число витков в контуре (безразмерное), — угол между вектором индукции и нормалью к плоскости контура, —максимальная ЭДС индукции, когда угол между нормалью к плоскости контура и вектором магнитной индукции равен 90°, т.е. когда плоскость контура параллельная линиям магнитной индукции.
Формула ЭДС самоиндукции
Здесь — ЭДС самоиндукции в контуре (В), L — индуктивность контура (Гн), — скорость изменения силы тока в контуре (А/с), — первая производная силы тока по времени.
Формула магнитной проницаемости магнетика
Здесь — магнитная проницаемость магнетика (безразмерная), В — индукция магнитного поля в магнетике (Тл), — индукция магнитного поля в вакууме (Тл).
Формула энергии магнитного поля
Здесь — энергия магнитного поля (Дж), L — индуктивность контура (Гн), I — сила тока в контуре (А).
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:
Обозначение q в физике
Рекордом R. D, d — диаметр : на основе латинского diametrus — диаметр. L, l — длина : на основе английского length — длина. R, r — радиус : на основе позднелатинского radius — радиус. S — площадь : на основе английского square — площадь.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Буквы, используемые для обозначения величин
- Список обозначений в физике
- Используемые обозначения в учебнике по физике, 8 класс
- Формулы по Электродинамике
- Формула электрического заряда
- Все формулы по физике за 7-9 класс
- Значение слова q
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: 7 кл — 34. Мощность. Единицы мощности
Буквы, используемые для обозначения величин
Перейти к основному содержанию. Форма поиска Поиск. You must have JavaScript enabled to use this form. Регистрация Забыли пароль? Обозначения физических величин. Поэтому в них подставляют не названия физических величин, а их обозначения. В качестве обозначений используют буквы различных алфавитов; чаще всего — латинского и греческого; иногда — русского.
Форма поиска Поиск. You must have JavaScript enabled to use this form. Регистрация Забыли пароль? Обозначения физических величин. Поэтому в них подставляют не названия физических величин, а их обозначения. В качестве обозначений используют буквы различных алфавитов; чаще всего — латинского и греческого; иногда — русского.
В общем в физике нет жёстких правил — какой буквой обозначать ту или иную физическую величину, и поэтому каждый волен обозначать их по-своему. Однако в науке уже сложились и широко используются определённые обозначения, которые облегчают взаимопонимание специалистов между собою.
Путь, например, принято обозначать малой латинской буквой s эс , скорость — буквой v вэ , а продолжительность — буквой t тэ. Русский алфавит кириллица. Данный сайт является частью научного проекта «Русская Физика» и создан по инициативе автора «Русской теории», Антонова Владимира Михайловича.
Все материалы сайта публикуются по просьбе или с согласия их авторов. Авторские права на материалы сайта защищаются в соответствии с законодательством РФ. Создатели сайта преследуют цель просвещения и образования в области физических наук. Приветствуется любое некоммерческое использование материалов сайта с ссылкой на источник название сайта или имя автора публикации.
Создатели сайта преследуют цель просвещения и образования в области физических наук. Приветствуется любое некоммерческое использование материалов сайта с ссылкой на источник название сайта или имя автора публикации.
Все права защищены.
Список обозначений в физике
Сила , действующая на движущуюся заряженную частицу в магнитном поле, равная:. Из выражения 2 следует, что если заряд движется параллельно силовым линиям магнитного поля,то сила Лоренца равна нулю. Иногда силу Лоренца стараясь выделить, обозначают, используя индекс:. Сила Лоренца как и всякая сила — это вектор. Ее направление перпендикулярно вектору скорости и вектору то есть перпендикулярно плоскости, в которой находятся векторы скорости и магнитной индукции и определяется правилом правого буравчика правого винта рис.
Формула. Обозначения. Комментарий. Электростатика. Закон сохранения электрического заряда. q – электрический заряд;. F – сила;. r – расстояние;.
Используемые обозначения в учебнике по физике, 8 класс
Перейти к основному содержанию. Форма поиска Поиск. You must have JavaScript enabled to use this form. Регистрация Забыли пароль? Обозначения физических величин. Поэтому в них подставляют не названия физических величин, а их обозначения. В качестве обозначений используют буквы различных алфавитов; чаще всего — латинского и греческого; иногда — русского. В общем в физике нет жёстких правил — какой буквой обозначать ту или иную физическую величину, и поэтому каждый волен обозначать их по-своему. Однако в науке уже сложились и широко используются определённые обозначения, которые облегчают взаимопонимание специалистов между собою.
Форма поиска Поиск. You must have JavaScript enabled to use this form. Регистрация Забыли пароль? Обозначения физических величин. Поэтому в них подставляют не названия физических величин, а их обозначения. В качестве обозначений используют буквы различных алфавитов; чаще всего — латинского и греческого; иногда — русского. В общем в физике нет жёстких правил — какой буквой обозначать ту или иную физическую величину, и поэтому каждый волен обозначать их по-своему. Однако в науке уже сложились и широко используются определённые обозначения, которые облегчают взаимопонимание специалистов между собою.
Формулы по Электродинамике
Раздел очень прост в использовании. В предложенное поле достаточно ввести нужное слово, и мы вам выдадим список его значений. Хочется отметить, что наш сайт предоставляет данные из разных источников — энциклопедического, толкового, словообразовательного словарей. Также здесь можно познакомиться с примерами употребления введенного вами слова. Так же, как и M, это кодовое имя, в данном случае оно означает первую букву слова Quartermaster квартирмейстер.
Адсорбция — изменение концентрации вещества на границе раздела фаз по сравнению с объемом.
Формула электрического заряда
Статья предоставлена специалистами сервиса Автор Автор24 — это сообщество учителей и преподавателей, к которым можно обратиться за помощью с выполнением учебных работ. Физика является естественной наукой, которая изучает общие и фундаментальные закономерности строения и эволюции материального мира. Важность физики в современном мире огромна. Ее новые идеи и достижения приводят к развитию других наук и новых научных открытий, которые, в свою очередь, используются в технологиях и промышленности. Например, открытия в области термодинамики делают возможным строительство автомобиля, а также развитие радиоэлектроники привело к появлению компьютеров.
Все формулы по физике за 7-9 класс
Настоящий стандарт является обязательным в рамках Конвенции о применении стандартов СЭВ. Настоящий стандарт СЭВ устанавливает общие положения по образованию буквенных обозначений, а также конкретные обозначения и индексы к ним основных величин, применяемых в строительстве. Определенная величина обозначается буквой латинского или греческого алфавита без индексов или с индексами, служащими для уточнения различных характеристик этой величины. Буквы греческого алфавита следует принимать по табл. Буквенные обозначения необходимых величин, не приведенных в настоящем стандарте СЭВ, устанавливают по принципу, указанному в табл. Длина, отношение длины ко времени в какой-либо степени, отношением усилия к единице длины или площади. Индексы подразделяются на цифровые и буквенные.
Определенная величина обозначается буквой латинского или греческого алфавита без индексов или с индексами, служащими для уточнения различных характеристик этой величины. Буквы греческого алфавита следует принимать по табл. Буквенные обозначения необходимых величин, не приведенных в настоящем стандарте СЭВ, устанавливают по принципу, указанному в табл. Длина, отношение длины ко времени в какой-либо степени, отношением усилия к единице длины или площади. Индексы подразделяются на цифровые и буквенные.
В общем, тенденция ясна: количество сигм связано с вероятностью того, что истинное значение будет настолько отличаться от измеренного.
Значение слова q
На нашем сайте собрано более бесплатных онлайн калькуляторов по математике, геометрии и физике. Не можете решить контрольную?! Мы поможем!
Jump to Content. Основные ссылки. Главная Для учителя Архив заданий олимпиад по физике за годы Владимир Анатольевич Зверев предлагает ИКТ на уроке физики История физики на уроке и во внеурочной деятельности Несколько ссылок на работы Анатолия Шперха Общие вопросы методики обучения физике Статьи Александра Борисовича Рыбакова Важнейший общефизический принцип остается непонятым Рыбаков А. Рыбаков Банджи-джампинг, сохранение импульса и уравнение Мещерского Рыбаков А. Заметки о демоверсии Рыбаков А.
Рыбаков Банджи-джампинг, сохранение импульса и уравнение Мещерского Рыбаков А. Заметки о демоверсии Рыбаков А.
Как мы отметили в предыдущем параграфе, в XIX веке было построено огромное количество паровых машин: от небольших до огромных.
В семитских языках буква имела звуковое соответствие [ q ] — звук типичный для семитских языков, но отсутствующий в большинстве индоевропейских языков. В большинстве современных европейских языков с латинской письменностью, таких как романские кроме румынского языка и германские языки , буква Q почти всегда встречается только в диграфе QU. В французском , португальском , испанском и каталанском языках читается как [ k ]. В старой орфографии шведского языка и до сих пор во многих шведских фамилиях используется в составе диграфа QV. Широко используется в гренландском языке , где часто стоит в конце слова.
Изображение с сайта en. Итак, можно сформулировать некую договоренность:. Использовать эту договоренность можно разными способами. Что вы можете сказать про этот результат?
Веб-сайт кабинета физики
Назначение SE10: электрическое поле
Цели:
- Студент должен уметь определять электрическое поле и распознавать переменные, влияющие (и не влияющие) на напряженность электрического поля в данном месте.
- Студент должен уметь использовать уравнения электрического поля и относительно простые числа для определения величины и направления напряженности электрического поля в заданном месте.
Чтение:
Класс физики — Статическое электричество, урок 4, часть a
Заряд Q создает электрическое поле. Пробным зарядом q измеряют напряженность электрического поля на расстоянии d от Q. На пробный заряд q действует сила F. Напряженность электрического поля в этом месте определяется выражением ___. Перечислите все, что применимо… . | |
Определение Напряженность электрического поля : Любой источник заряда Q будет создавать электрическое поле в окружающем его пространстве. | |
Напряженность электрического поля ( E ) определяется как количество силы, действующей на пробный заряд на единицу заряда пробного заряда ( q ). То есть E = F/q . Электрическая сила ( F ) зависит от ряда переменных, как описано законом Кулона. В приведенном выше уравнении Q 1 может быть исходным зарядом Q , а Q 2 может быть пробным зарядом q . | |
Какие переменные влияют на напряженность электрического поля заряда? Как можно использовать силу пробного заряда для определения напряженности электрического поля другого заряда? |
Заряд Q создает электрическое поле. Пробный заряд q используется для измерения напряженности электрического поля на расстоянии d от Q. Напряженность электрического поля определяется как ____. | |
Определение Напряженность электрического поля : Любой источник заряда Q будет создавать электрическое поле в окружающем его пространстве. | |
Легко запутаться в математике напряженности электрического поля. Важно помнить, что в любом электрическом взаимодействии всегда участвуют два заряда. В этом случае начисления составляют Q и q . Большой Q представляет собой исходный заряд, создающий электрическое поле. Маленький q представляет собой тестовый заряд, который используется для измерения напряженности электрического поля в заданном месте, окружающем заряд источника. Уделите особое внимание количеству заряда — q или q — используемому в каждом уравнении. | |
Как можно использовать силу пробного заряда для определения напряженности электрического поля другого заряда? |
Стандартной метрической единицей напряженности электрического поля является ____. | |
Напряженность электрического поля ( E ) в любом месте, окружающем заряд источника, может быть определена путем измерения силы ( F ) при воздействии на испытательный заряд ( q ), помещенный в этом месте. | |
Стандартные метрические единицы количества можно понять, подумав о его формуле. | |
Определение Напряженность электрического поля : Любой источник заряда Q будет создавать электрическое поле в окружающем его пространстве. Напряженность электрического поля ( E ) в любом заданном месте в этом пространстве можно определить, поместив пробный заряд q в пространство и измерив силу ( F ), действующую на него. | |
Напряженность электрического поля ( E ) определяется как величина силы, действующей на испытательный заряд на единицу заряда испытательного заряда ( q ). То есть E = F/q . Электрическая сила ( F ) зависит от ряда переменных, как описано законом Кулона. В приведенном выше уравнении Q 1 может быть зарядом источника 9.0043 Q и Q 2 может быть пробным зарядом q . Если выражение для силы, данное уравнением закона Кулона, заменить F в уравнении напряженности электрического поля, то уравнение для электрического поля примет вид | |
Легко запутаться в математике напряженности электрического поля. | |
Какие переменные влияют на напряженность электрического поля заряда? Как можно использовать силу пробного заряда для определения напряженности электрического поля другого заряда? |
ИСТИНА или ЛОЖЬ : Величина электрического поля является векторной величиной. (Примечание: ваше фактическое утверждение «Верно-ложно» выбирается случайным образом из набора вариантов и может отличаться от приведенного здесь.) | |
Электрическое поле как вектор: Электрическое поле в заданном месте вокруг заряда источника ( Q ) является векторной величиной. То есть имеет направление. Сила, действующая на пробный заряд ( q ), может быть силой притяжения (по направлению к исходному заряду) или силой отталкивания (от исходного заряда) в зависимости от того, являются ли Q и q имеют одинаковый или противоположный заряд. При определении направления электрического поля используется соглашение, чтобы направление всегда было в одном и том же направлении, независимо от типа заряда на q . Согласно соглашению, направление электрического поля соответствует направлению, в котором положительный пробный заряд будет толкаться или тянуться, если его поместить в пространство, окружающее Q . | |
Является ли электрическое поле скалярной или векторной величиной? |
По соглашению направление электрического поля ____. | |
Электрическое поле как вектор: Электрическое поле ( E ) в заданном месте относительно заряда источника ( Q ) является векторной величиной. То есть имеет направление. Сила, действующая на пробный заряд ( q ), может быть силой притяжения (по направлению к исходному заряду) или силой отталкивания (от исходного заряда) в зависимости от того, заряжены ли Q и q одинаково или противоположно. | |
Как определить направление электрического поля? |
Положительный заряд создает электрическое поле. Направление электрического поля будет ____. | |
Электрическое поле как вектор: Электрическое поле ( E ) в данном месте относительно заряда источника ( Q ) — векторная величина. | |
По соглашению, направление вектора электрического поля в любом данном месте — это направление, в котором положительный пробный заряд будет выталкиваться или тянуться, если его поместить в это место. Сочетая это соглашение с правилом отталкивания одинаково заряженных объектов, можно определить направление электрического поля в пространстве, окружающем источник положительного заряда. | |
Как определить направление электрического поля? |
Отрицательный заряд создает электрическое поле. Направление электрического поля будет ____. | |
Электрическое поле как вектор: Электрическое поле ( E ) в заданном месте относительно заряда источника ( Q ) является векторной величиной. То есть имеет направление. | |
По соглашению, направление вектора электрического поля в любом данном месте — это направление, в котором положительный пробный заряд будет выталкиваться или тянуться, если его поместить в это место. Сочетая это соглашение с правилом притяжения противоположно заряженных объектов, можно определить направление электрического поля в пространстве, окружающем источник отрицательного заряда. | |
Как определить направление электрического поля? |
Следуйте за нами
Общая физика II
Закон Кулона говорит нам о силе между двумя точками обвинения. Наш вариант сообщает нам Электрическое поле из-за одноточечный заряд . Что нам делать, если у нас есть непрерывных распределение заряда? Мы можем суммировать электрическое поле вызвано каждой крошечной, бесконечно малой частью заряда распределение. Это означает интеграл по распределению заряда:
Для одноточечного заряда Q мы имели
, где r — расстояние от заряда Q. Помните, что E — это всего лишь величина электрического поля; мы должны позаботиться о
это вектор природа отдельно! Это важно! Теперь у нас есть
распределение заряда, и мы должны заменить Q на dQ и E на dE
— и позаботьтесь о направлении E .
Помните, что E — это всего лишь величина электрического поля; мы должны позаботиться о
это вектор природа отдельно! Это важно! Теперь у нас есть
распределение заряда, и мы должны заменить Q на dQ и E на dE
— и позаботьтесь о направлении E .
р, расстояние от крошечного, элементарного, бесконечно малого заряда dQ к рассматриваемому вопросу, является функцией того, где этот заряд dQ является. И что значит «интегрировать по заряду dQ»? Мы знать, как интегрировать по переменной, такой как dx, или по плоскости, такой как dA = dx dy или dA = 2 r dr или dA = r d dr или объем типа dV = dx dy dz. Так что нам нужно будет измените с этого символического заряда dQ на плотность заряда умноженный на некоторый пространственный дифференциал,
дQ = дА
dQ = дВ
Посмотрите на Пример 23. 7 в учебнике Serway и Beichner (стр. 724):
Стержень длиной
имеет равномерный заряд на единицу длины
и полный заряд Q. Вычислить электрическое поле в точке P вдоль
оси стержня на расстоянии d от одного конца.
7 в учебнике Serway и Beichner (стр. 724):
Стержень длиной
имеет равномерный заряд на единицу длины
и полный заряд Q. Вычислить электрическое поле в точке P вдоль
оси стержня на расстоянии d от одного конца.
Чему равно электрическое поле в точке P из-за маленького кусочка бесплатно Q находится в позиции x, как показано на рисунке?
Проведем интегрирование от x = d до x = d + так нам нужно изменить это небольшое количество заряда Q на малую длину x,
Е = к (х) / х 2
где
dE = k ( dx) / x 2
dE = k (dx / х 2 )
Как насчет других геометрий?
Посмотрите на Пример 23. 8 на странице 724 текста Сервея и Бейхнера.
Найти электрическое поле, создаваемое кольцом заряда : Кольцо радиусом a
имеет однородную плотность заряда с полным зарядом Q. Рассчитайте электрическую
поле по оси кольца в точке P, на расстоянии x от
центр кольца.
8 на странице 724 текста Сервея и Бейхнера.
Найти электрическое поле, создаваемое кольцом заряда : Кольцо радиусом a
имеет однородную плотность заряда с полным зарядом Q. Рассчитайте электрическую
поле по оси кольца в точке P, на расстоянии x от
центр кольца.
Плотность заряда
Помните, наше уравнение для электрического поля относится к величины электрического поля. Рассмотрим небольшой кусочек зарядить dq, как показано на схеме. Поскольку этот заряд dq равен там в точке P существует электрическое поле dE в направлении показано. компонента dEx этого электрического поля вдоль направление оси перпендикулярно плоскости кольца
dE x = dE (x/r)
dE x = [k dq/r 2 ] (x/r)
dE х = [k dq/r 3 ] х
dE x = [k x dq/r 3 ]
dE x = [k x/r 3 ] dq
Обратите внимание, что в этой геометрии после указания радиуса кольца a
и позицию x, полностью определяющую r.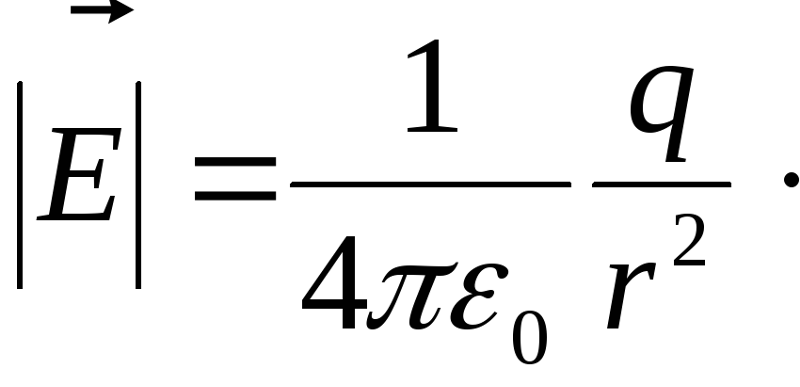 r и x делают не изменяют как
интегрируем по dq.
r и x делают не изменяют как
интегрируем по dq.
[[ Помните, что SQRT() означает «квадратный корень из ()», потому что это проще
чтобы я печатал. ]]
r 3 = (a 2 + x 2 ) 3/2
1/r 3 = 1/(a 2 + х 2 ) 3/2
Помните, что x и a — это , а не переменные.
Как насчет компонента E, который перпендикулярен к
это направление? По симметрии этот компонент равен нулю .
Из диаграммы видно, что для каждого элемента заряда dq,
есть еще один элемент заряда dq на напротив сторона кольца, создающая электрическое поле, которое просто отменяет первый — то есть их компоненты перпендикулярно оси симметрии как раз отменяет .
Обратите внимание, что их компоненты вдоль оси не отменяют
ибо они лежат в одном и том же направлении. Диаграммы очень
важный. Не начинайте писать уравнения, пока не сделаете
хорошие, четкие, полные схемы!
Диаграммы очень
важный. Не начинайте писать уравнения, пока не сделаете
хорошие, четкие, полные схемы!
Теперь, когда мы рассмотрели электрическое поле из-за кольцо г заряда, мы можем опираться на него, расширять наши идеи и смотреть на электрические поле из-за диска заряда. См. пример 23.9 на стр. 725 учебника Серуэя и Бейхнера.
Диск радиусом R имеет равномерный заряд на единицу площади. Вычислите электрическое поле в точке P, лежащей вдоль центральной оси диска и на расстоянии x от его центра.
Рассмотрим заряженное кольцо, как показано здесь. Кольцо имеет радиусом r и толщиной dr и несет заряд dq. Но этот заряд dq как раз пропорционален площади,
дк = [С др]
дк = [ (2 г) др ]
дкв = 2 р др
Вспомните, что мы только что сделали в предыдущем примере. За
заряд Q на кольце радиуса r, мы нашли, что электрическое поле
на расстоянии x от плоскости кольца было
За
заряд Q на кольце радиуса r, мы нашли, что электрическое поле
на расстоянии x от плоскости кольца было
Это именно то, что у нас есть сейчас, за исключением того, что у нас есть заряд dq. вместо Q и кольцо имеет радиус r вместо a. Итак, мы могу написать
Будьте осторожны; пределы интегрирования важны.
Мы могли бы найти это в таблице интегралов. Но переменная замена по-прежнему довольно прямолинейна и прямолинейна;
Этот результат действителен только для x > 0 и должен быть немного изменен для х < 0.
Электрическое поле | Линии электронного поля | ||
 ; все права защищены
; все права защищеныЧто такое оплата? – EWT
Background
Из Википедии: «Электрический заряд – это физическое свойство материи, которое заставляет ее испытывать силу, когда она помещена в электромагнитное поле». В физике это измерение притяжения или отталкивания частиц, как это было обнаружено Кулоном, когда он установил зависимость заряда и силы от расстояния — закон Кулона.
Заряд протона (+) и электрона (-)
Сила вызывает движение частиц, а направление зависит от комбинации зарядов следующим образом:
- Частицы с одинаковым зарядом будут отталкиваться (+/+ или -/ -).
- Частицы противоположного заряда будут притягиваться (+/-).
Крупные объекты, такие как люди, велосипеды или автомобили, состоят из атомов этих же частиц. Однако законы движения и сил основаны на массе, а не на заряде. Почему? Когда в объектах происходит столкновение, на самом деле это столкновение миллионов и миллионов электрически заряженных частиц в этих объектах. Мы рассчитываем силу этого объекта на основе массы (m), используя 2-й закон Ньютона (F=ma). Разве заряд (q) не должен быть связан с массой (m)?
Мы рассчитываем силу этого объекта на основе массы (m), используя 2-й закон Ньютона (F=ma). Разве заряд (q) не должен быть связан с массой (m)?
Объяснение
Заряд представляет собой бегущую энергию продольной волны . Масса и заряд действительно связаны и могут быть упрощены до одного уравнения энергии, представленного в классической форме на этой странице. Чтобы связать массу и заряд, кулонов можно объяснить как амплитуду волны, которая измеряется как расстояние (метры). Если принять вещество в вакууме пространства, имеющее физическое свойство килограмма и движущееся как волны, то массу и заряд можно описать как их движение. В EWT это вещество называется эфиром, а его компоненты — гранулами.
- Масса – энергия стоячей продольной волны (без учета скорости волны – c 2 )
- Заряд – энергия бегущей продольной волны на расстояние (сила)
Элементарный заряд одиночной частицы (e e ) — амплитуда волны на первой длине волны, подробно рассчитанная в разделе, посвященном электрической силе. Амплитуда – это среднее смещение эфирных гранул от равновесия. Смещение гранул будет больше вблизи ядра электрона и уменьшаться по амплитуде на расстоянии, поскольку гранулы сталкиваются и передают энергию большему количеству гранул по мере сферического распространения.
Амплитуда – это среднее смещение эфирных гранул от равновесия. Смещение гранул будет больше вблизи ядра электрона и уменьшаться по амплитуде на расстоянии, поскольку гранулы сталкиваются и передают энергию большему количеству гранул по мере сферического распространения.
Поскольку материя (измеряемая как энергия покоя или масса) формируется из той же волны, которая обладает электрическими свойствами (измеряется как заряд), их можно связать как логически, так и математически. Логически это просто тип продольной волны: стоячая или бегущая. Стоячая волна – это накопленная энергия. Бегущая волна, по определению, это бегущая энергия. Фотон, для сравнения, представляет собой другую форму волны — это поперечная волна, в которой волна распространяется перпендикулярно движению частицы (по сравнению с продольной волной, которая идет в направлении движения).
Доказательство связи материи и заряда
Энергия волны классически может быть описана следующим уравнением. В EWT уравнение энергии часто изображается в форме волнового уравнения, но здесь оно будет показано в классическом виде, чтобы доказать, что массу электрона можно вывести из классических электрических констант. Энергия волны в классическом формате:
В EWT уравнение энергии часто изображается в форме волнового уравнения, но здесь оно будет показано в классическом виде, чтобы доказать, что массу электрона можно вывести из классических электрических констант. Энергия волны в классическом формате:
- μ 0 – магнитная постоянная
- c – скорость света
- q – заряд (переменная)
- r – расстояние (переменная)
Масса – запасенная энергия стоячих волн в радиусе электрона (r e ). Следовательно, это уравнение энергии без учета скорости волны (c 2 ). Для одного электрона заряд (q) является элементарным зарядом (e e ). Ниже приведены точные значения и единицы массы электрона при использовании электрических свойств (CODATA).
Electron Mass
- Q — E E (Одиночный заряд электронов)
- R = R E (радиус электрона)
Заряд — волновая амплитуда на данной расстоянии (R -расстояние) (R -расстояние) (R -расстояние) (R -расстояние). . Его можно выразить как энергию, но часто его выражают как силу, известную как закон Кулона. Постоянная Кулона представляет собой произведение магнитной постоянной на скорость волны в квадрате более чем на 4π. Кулон дал ему букву k.
. Его можно выразить как энергию, но часто его выражают как силу, известную как закон Кулона. Постоянная Кулона представляет собой произведение магнитной постоянной на скорость волны в квадрате более чем на 4π. Кулон дал ему букву k.
Сила – это энергия на расстоянии ( F=E/r ), поэтому для уравнения силы оно становится r 2 в знаменателе. Замена постоянной Кулона константами в уравнении энергии (сверху) дает закон Кулона.
Закон Кулона
Логически и массу, и заряд можно объяснить как волны. И математически масса электрона теперь может быть выражена через заряд (q/e e ), связывая области механики и электричества уравнением.
Связь уравнений массы и силы заряда
Отношения между законами материи, обозначенными массой (m) в уравнении, равны законам электромагнитного заряда, обозначенным зарядом (q) в уравнении, если принять во внимание единичную массу электрона и заряд и расстояние быть равным классическому радиусу электрона .


 Экспериментально установлено, что появление положительно заряженной частицы сопровождается исчезновением отрицательной. Любого знака заряды при их равенстве и взаимодействии могут аннигилировать, то есть нейтрализовать друг друга.
Экспериментально установлено, что появление положительно заряженной частицы сопровождается исчезновением отрицательной. Любого знака заряды при их равенстве и взаимодействии могут аннигилировать, то есть нейтрализовать друг друга. Так, F 1 = (k * q 1 * q 2) / r 2 = k * (e)2 / r 2, а F 2 = G * (m 1 * m 2) / r 2 = G * m / r 2. Отсюда F 1 / F 2 = 9 * 109 * 1,6 * 10-19 / 6,67 * 10-11 * (9,1 * 10-31)2 = 4, 23 * 1042.
Так, F 1 = (k * q 1 * q 2) / r 2 = k * (e)2 / r 2, а F 2 = G * (m 1 * m 2) / r 2 = G * m / r 2. Отсюда F 1 / F 2 = 9 * 109 * 1,6 * 10-19 / 6,67 * 10-11 * (9,1 * 10-31)2 = 4, 23 * 1042.
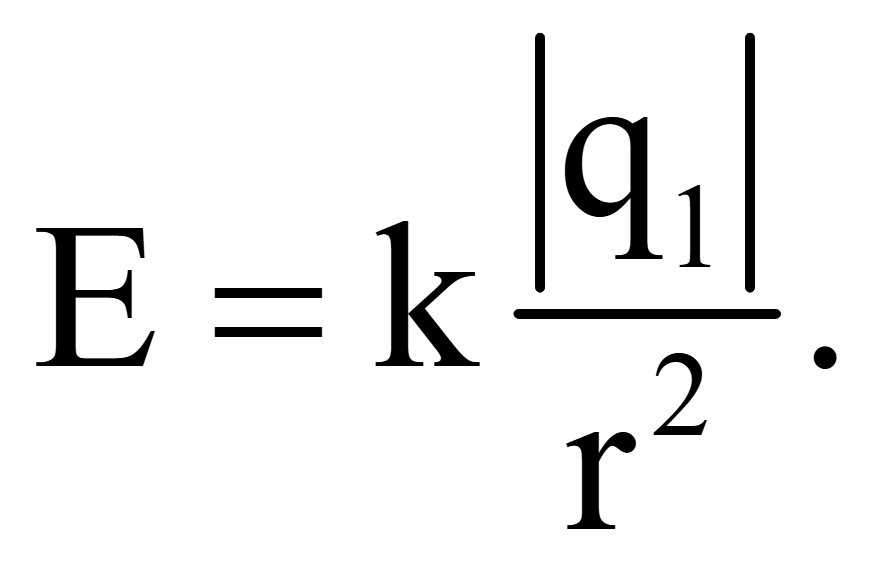 Напряженность электрического поля ( E ) в любом заданном месте в этом пространстве можно определить, поместив пробный заряд q в пространство и измерив силу ( F ), воздействующее на него. Напряженность электрического поля определяется как количество силы на единицу заряда испытательного заряда.
Напряженность электрического поля ( E ) в любом заданном месте в этом пространстве можно определить, поместив пробный заряд q в пространство и измерив силу ( F ), воздействующее на него. Напряженность электрического поля определяется как количество силы на единицу заряда испытательного заряда. Если выражение для силы, данное уравнением закона Кулона, подставить вместо F в уравнении напряженности электрического поля, то уравнение для электрического поля принимает вид
Если выражение для силы, данное уравнением закона Кулона, подставить вместо F в уравнении напряженности электрического поля, то уравнение для электрического поля принимает вид Напряженность электрического поля ( E ) в любом заданном месте в этом пространстве можно определить, поместив пробный заряд q в пространство и измерив силу ( F ), действующую на него. Напряженность электрического поля определяется как количество силы на единицу заряда испытательного заряда.
Напряженность электрического поля ( E ) в любом заданном месте в этом пространстве можно определить, поместив пробный заряд q в пространство и измерив силу ( F ), действующую на него. Напряженность электрического поля определяется как количество силы на единицу заряда испытательного заряда.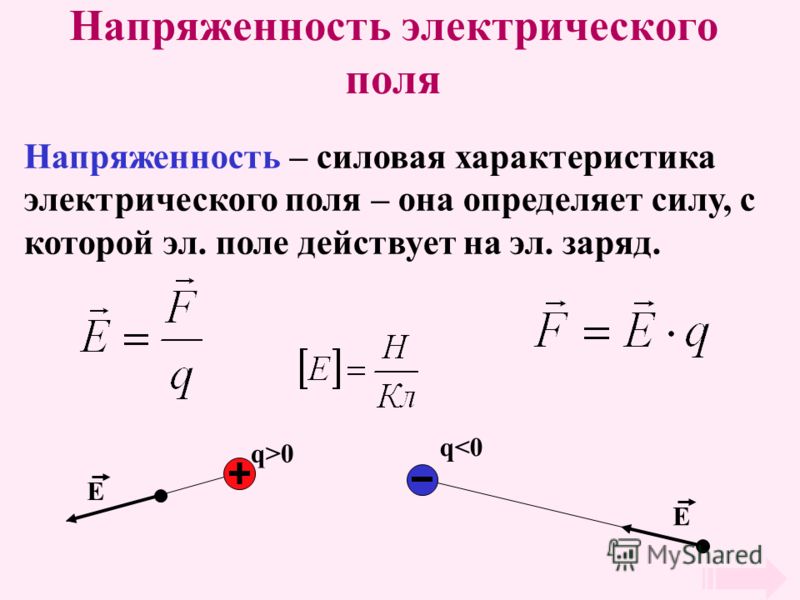
 Напряженность электрического поля — это отношение силы к заряду (см. раздел Formula Fix выше). Таким образом, единицы напряженности электрического поля — это единицы силы, деленные на единицы заряда. Стандартной метрической единицей силы является ньютон; стандартной метрической единицей заряда является кулон. Таким образом, стандартной метрической единицей напряженности электрического поля является Ньютон/Кулон, сокращенно N/C. 9-9 Кулоновский пробный заряд. Напряженность электрического поля, создаваемая зарядом в 4 мкК, составляет ____ Н/Кл.
Напряженность электрического поля — это отношение силы к заряду (см. раздел Formula Fix выше). Таким образом, единицы напряженности электрического поля — это единицы силы, деленные на единицы заряда. Стандартной метрической единицей силы является ньютон; стандартной метрической единицей заряда является кулон. Таким образом, стандартной метрической единицей напряженности электрического поля является Ньютон/Кулон, сокращенно N/C. 9-9 Кулоновский пробный заряд. Напряженность электрического поля, создаваемая зарядом в 4 мкК, составляет ____ Н/Кл. Напряженность электрического поля определяется как количество силы на единицу заряда испытательного заряда.
Напряженность электрического поля определяется как количество силы на единицу заряда испытательного заряда. Важно помнить, что в любом электрическом взаимодействии всегда участвуют два заряда. В этом случае начисления составляют Q и q . Большой Q представляет собой исходный заряд, создающий электрическое поле. Little q представляет собой тестовый заряд, который используется для измерения напряженности электрического поля в заданном месте, окружающем исходный заряд. Уделите большое внимание количеству заряда — Q или q — используется в каждом уравнении.
Важно помнить, что в любом электрическом взаимодействии всегда участвуют два заряда. В этом случае начисления составляют Q и q . Большой Q представляет собой исходный заряд, создающий электрическое поле. Little q представляет собой тестовый заряд, который используется для измерения напряженности электрического поля в заданном месте, окружающем исходный заряд. Уделите большое внимание количеству заряда — Q или q — используется в каждом уравнении.

 заряжен. При определении направления электрического поля используется условное обозначение, согласно которому направление зависит от типа заряда исходного заряда 9.0043 В . Согласно соглашению, направление электрического поля соответствует направлению, в котором положительный пробный заряд будет толкаться или тянуться, если его поместить в пространство, окружающее Q .
заряжен. При определении направления электрического поля используется условное обозначение, согласно которому направление зависит от типа заряда исходного заряда 9.0043 В . Согласно соглашению, направление электрического поля соответствует направлению, в котором положительный пробный заряд будет толкаться или тянуться, если его поместить в пространство, окружающее Q .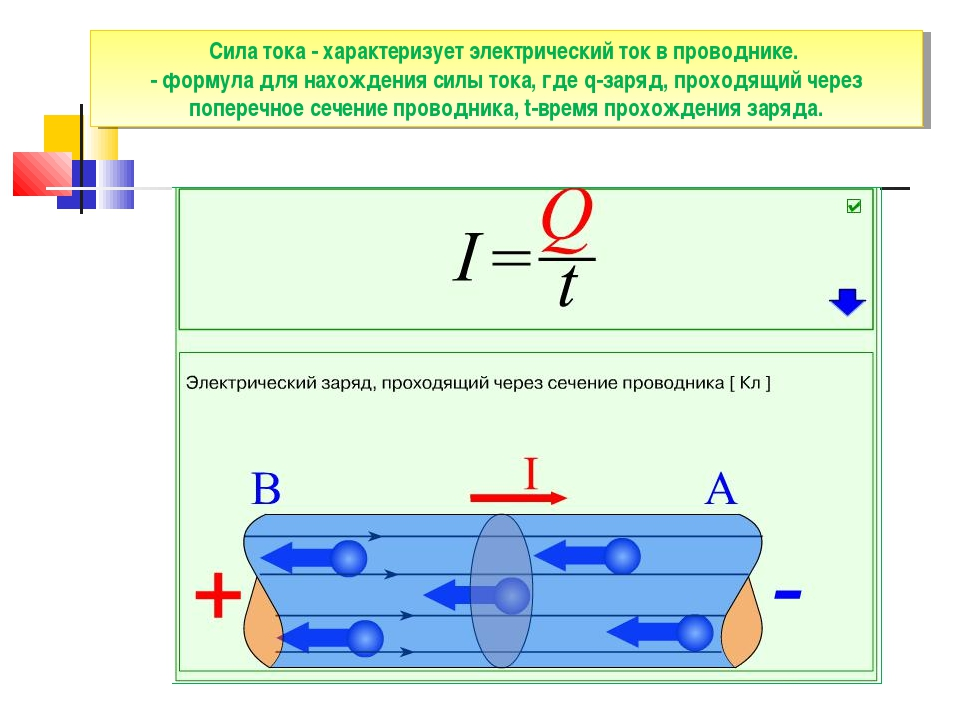 То есть имеет направление. Сила, действующая на пробный заряд ( q ), может быть силой притяжения (по направлению к исходному заряду) или силой отталкивания (от исходного заряда) в зависимости от того, заряжены ли Q и q одинаково или противоположно. заряжен. При определении направления электрического поля используется соглашение, согласно которому направление зависит от типа заряда исходного заряда Q . Согласно соглашению, направление электрического поля совпадает с направлением положительный тестовый заряд будет толкаться или тянуться, если его поместить в пространство, окружающее Q .
То есть имеет направление. Сила, действующая на пробный заряд ( q ), может быть силой притяжения (по направлению к исходному заряду) или силой отталкивания (от исходного заряда) в зависимости от того, заряжены ли Q и q одинаково или противоположно. заряжен. При определении направления электрического поля используется соглашение, согласно которому направление зависит от типа заряда исходного заряда Q . Согласно соглашению, направление электрического поля совпадает с направлением положительный тестовый заряд будет толкаться или тянуться, если его поместить в пространство, окружающее Q . Положительный заряд источника и положительный пробный заряд будут отталкивать друг друга. То есть положительный пробный заряд будет отталкиваться от положительного исходного заряда во всех точках пространства, окружающего исходный заряд.
Положительный заряд источника и положительный пробный заряд будут отталкивать друг друга. То есть положительный пробный заряд будет отталкиваться от положительного исходного заряда во всех точках пространства, окружающего исходный заряд. Сила, действующая на пробный заряд ( q ), может быть силой притяжения (по направлению к исходному заряду) или силой отталкивания (от исходного заряда) в зависимости от того,0043 Q и q заряжены одинаково или противоположно. При определении направления электрического поля используется соглашение, согласно которому направление зависит от типа заряда исходного заряда Q . Согласно соглашению, направление электрического поля соответствует направлению, в котором положительный пробный заряд будет толкаться или тянуться, если его поместить в пространство, окружающее Q .
Сила, действующая на пробный заряд ( q ), может быть силой притяжения (по направлению к исходному заряду) или силой отталкивания (от исходного заряда) в зависимости от того,0043 Q и q заряжены одинаково или противоположно. При определении направления электрического поля используется соглашение, согласно которому направление зависит от типа заряда исходного заряда Q . Согласно соглашению, направление электрического поля соответствует направлению, в котором положительный пробный заряд будет толкаться или тянуться, если его поместить в пространство, окружающее Q .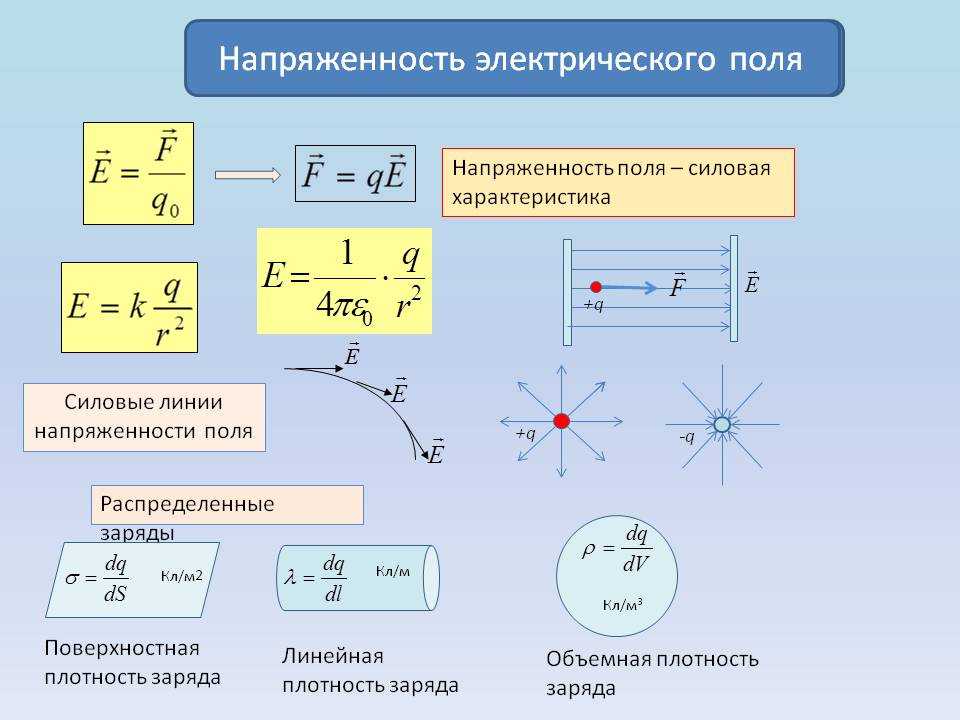 Отрицательный заряд источника и положительный пробный заряд будут притягиваться друг к другу. То есть положительный пробный заряд будет притягиваться к отрицательному исходному заряду во всех точках пространства, окружающего исходный заряд.
Отрицательный заряд источника и положительный пробный заряд будут притягиваться друг к другу. То есть положительный пробный заряд будет притягиваться к отрицательному исходному заряду во всех точках пространства, окружающего исходный заряд.