Движение тел под действием гравитационных сил. Движение тел под действием силы тяжести
Движение тела под действием силы тяжести является одной из центральных тем в динамической физике. О том, что раздел динамики базируется на трех знает даже обычный школьник. Давайте постараемся разобрать эту тему досконально, а статья, подробно описывающая каждый пример, поможет нам сделать изучение движения тела под действием силы тяжести максимально полезным.
Немного истории
Люди с любопытством наблюдали за различными явлениями, происходящими в нашей жизни. Человечество долгое время не могло понять принципы и устройство многих систем, однако длительный путь изучения окружающего мира привел наших предков к научному перевороту. В наши дни, когда технологии развиваются с неимоверной скоростью, люди почти не задумываются о том, каким образом работают те или иные механизмы.
А между тем наши предки всегда интересовались загадками природных процессов и устройством мира, искали ответы на самые сложные вопросы и не переставали изучать, пока не находили на них ответы. Так, например, известный ученый Галилео Галилей еще в 16 веке задался вопросами: «Почему тела всегда падают вниз, какая же сила притягивает их к земле?» В 1589 году он поставил ряд опытов, результаты которых оказались весьма ценными. Он подробно изучал закономерности свободного падения различных тел, сбрасывая предметы со знаменитой башни в городе Пизе. Законы, которые он вывел, были улучшены и более детально описаны формулами еще одним известным английским ученым — сэром Исааком Ньютоном. Именно ему принадлежат три закона, на которых основана практически вся современная физика.
Так, например, известный ученый Галилео Галилей еще в 16 веке задался вопросами: «Почему тела всегда падают вниз, какая же сила притягивает их к земле?» В 1589 году он поставил ряд опытов, результаты которых оказались весьма ценными. Он подробно изучал закономерности свободного падения различных тел, сбрасывая предметы со знаменитой башни в городе Пизе. Законы, которые он вывел, были улучшены и более детально описаны формулами еще одним известным английским ученым — сэром Исааком Ньютоном. Именно ему принадлежат три закона, на которых основана практически вся современная физика.
Тот факт, что закономерности движения тел, описанные более 500 лет назад, актуальны и по сей день, означает, что наша планета подчиняется неизменным законам. Современному человеку необходимо хотя бы поверхностно изучить основные принципы обустройства мира.
Основные и вспомогательные понятия динамики
Для того чтобы полностью понять принципы подобного движения, следует сначала ознакомиться с некоторыми понятиями.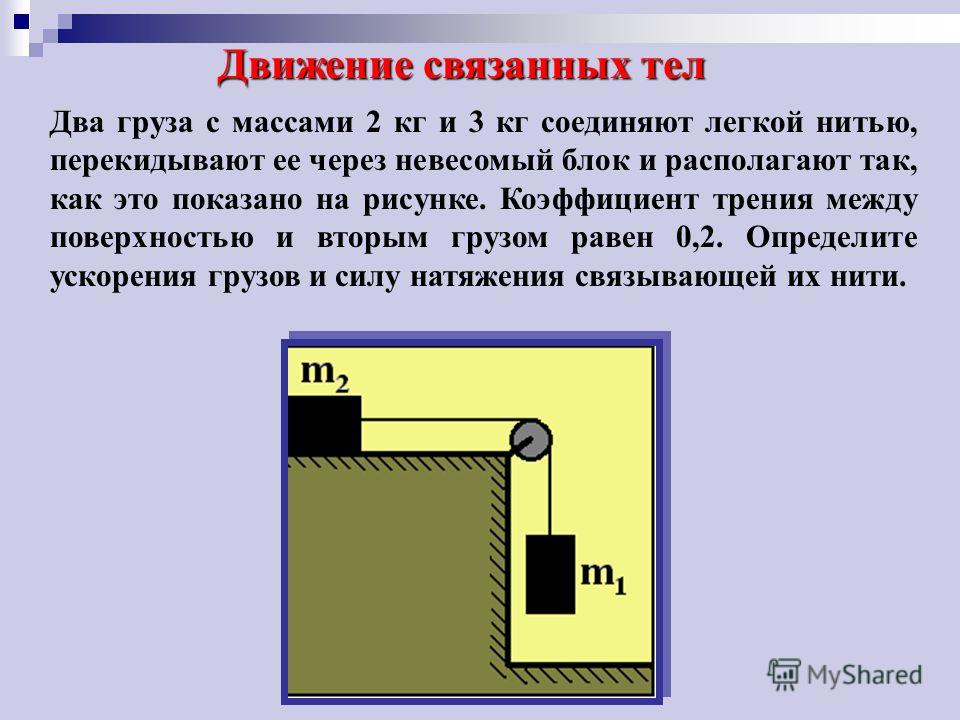 Итак, самые необходимые теоретические термины:
Итак, самые необходимые теоретические термины:
- Взаимодействие — это воздействие тел друг на друга, при котором происходит изменение или начало их движения относительно друг друга. Различают четыре вида взаимодействия: электромагнитное, слабое, сильное и гравитационное.
- Скорость — это физическая величина, обозначающая быстроту, с которой двигается тело. Скорость является вектором, то есть имеет не только значение, но также и направление.
- Ускорение — та величина, которая показывает нам быстроту изменения скорости тела в промежуток времени. Она также является
- Траектория пути — это кривая, а иногда — прямая линия, которую очерчивает тело при движении. При равномерном прямолинейном движении траектория может совпадать со значением перемещения.
- Инерциальная система отсчета — это среда, в которой выполняется первый закон Ньютона, то есть тело сохраняет свою инерцию, при условии, что полностью отсутствуют все внешние силы.

Вышеуказанных понятий вполне достаточно для того, чтобы грамотно начертить или представить в голове моделирование движения тела под действием силы тяжести.
Что значит сила?
Давайте перейдем к основному понятию нашей темы. Итак, сила — это величина, смысл которой заключается в воздействии или влиянии одного тела на другое количественно. А сила тяжести — это та сила, которая действует абсолютно на каждое тело, находящееся на поверхности или вблизи нашей планеты. Возникает вопрос: откуда же берется эта самая сила? Ответ заключается в законе всемирного тяготения.
А что такое сила тяжести?
На любое тело со стороны Земли оказывает влияние гравитационная сила, которая сообщает ему некоторое ускорение. Сила тяжести всегда имеет вертикальное направление вниз, к центру планеты. Иначе говоря, сила тяжести притягивает предметы к Земле, вот почему предметы всегда падают вниз. Получается, что сила тяжести — это частный случай силы всемирного тяготения. Ньютон вывел одну из главных формул для нахождения силы притяжение между двумя телами. Выглядит она таким образом: F = G * (m 1 х m 2) / R 2 .
Ньютон вывел одну из главных формул для нахождения силы притяжение между двумя телами. Выглядит она таким образом: F = G * (m 1 х m 2) / R 2 .
Чему равно ускорение свободного падения?
Тело, которое отпустили с некоторой высоты, всегда летит вниз под действием силы притяжения. Движение тела под действием силы тяжести вертикально вверх и вниз можно описать уравнениями, где основной константой будет являться значение ускорения «g». Эта величина обусловлена исключительно действием силы притяжения, и ее значение приблизительно равно 9,8 м/с 2 . Получается, что тело, брошенное с высоты без начальной скорости, будет двигаться вниз с ускорением равным значению «g».
Движение тела под действием силы тяжести: формулы для решения задач
Основная формула нахождения силы тяжести выглядит следующим образом: F тяжести = m х g, где m — это масса тела, на которое действует сила, а «g» — ускорение свободного падения (для упрощения задач его принято считать равным 10 м/с 2).
Есть еще несколько формул, используемых для нахождения того или иного неизвестного при свободном движении тела. Так, например, для того чтобы вычислить пройденный телом путь, необходимо подставить известные значения в эту формулу: S = V 0 х t + a х t 2 / 2 (путь равен сумме произведений начальной скорости умноженной на время и ускорения на квадрат времени, деленной на 2).
Уравнения для описания вертикального движения тела
Движение тела под действием силы тяжести по вертикали можно описать уравнением, которое выглядит так: x = x 0 + v 0 х t + a х t 2 / 2. Используя данное выражение, можно найти координаты тела в известный момент времени. Необходимо просто подставить известные в задаче величины: начальное местоположение, начальную скорость (если тело не просто отпустили, а толкнули с некоторой силой) и ускорение, в нашем случае оно будет равно ускорению g.
Таким же образом можно найти и скорость тела, которое движется под действием силы притяжения. Выражение для нахождения неизвестной величины в любой момент времени: v = v 0 + g х t (значение начальной скорости может быть равным нулю, тогда скорость будет равна произведению ускорения свободного падения на значение времени, за которое тело совершает движение).
Движение тел под действием силы тяжести: задачи и способы их решений
При решении многих задач, связанных с силой тяжести, рекомендуем воспользоваться следующим планом:
- Определить для себя удобную инерциальную систему отсчета, обычно принято выбирать Землю, потому как она отвечает многим требованиям к ИСО.
- Нарисовать небольшой чертеж или рисунок, на котором изображены основные силы, действующие на тело. Движение тела под действием силы тяжести подразумевает набросок или схему, на которой указано, в каком направлении движется тело, если на него действует ускорение, равное g.
- Затем следует выбрать направление для проецирования сил и полученных ускорений.
- Записать неизвестные величины и определить их направление.
- И наконец, используя указанные выше формулы для решения задач, вычислить все неизвестные величины, подставив данные в уравнения для нахождения ускорения или пройденного пути.
Готовое решение легкой задачи
Когда речь идет о таком явлении, как движение тела под действием того, каким способом практичнее решать поставленную задачу, может быть затруднительным. Однако есть несколько хитростей, используя которые, можно с легкостью решить даже самое сложное задание. Итак, разберем на живых примерах, как следует решать ту или иную задачу. Начнем с легкой для понимания задачи.
Однако есть несколько хитростей, используя которые, можно с легкостью решить даже самое сложное задание. Итак, разберем на живых примерах, как следует решать ту или иную задачу. Начнем с легкой для понимания задачи.
Некоторое тело отпустили с высоты 20 м без начальной скорости. Определить, за какое количество времени оно достигнет поверхности земли.
Решение: нам известен путь, пройденный телом, известно, что начальная скорость была равна 0. Также можем определить, что на тело действует только сила тяжести, получается, что это движение тела под действием силы тяжести, и поэтому следует воспользоваться этой формулой: S = V 0 х t + a х t 2 /2. Так как в нашем случае a = g, то после некоторых преобразований получаем следующее уравнение: S = g х t 2 / 2. Теперь осталось только выразить время через эту формулу, получаем, что t 2 = 2S / g. Подставим известные величины (при этом считаем, что g = 10 м/с 2) t 2 = 2 х 20 / 10 = 4. Следовательно, t = 2 с.
Итак, наш ответ: тело упадет на землю за 2 секунды.
Трюк, позволяющий быстро решить задачу, состоит в следующем: можно заметить, что описанное движение тела в приведенной задаче происходит в одном направлении (вертикально вниз). Оно весьма схоже с равноускоренным движением, так как на тело не действует никакая сила, кроме силы тяжести (силой сопротивления воздуха пренебрегаем). Благодаря этому можно воспользоваться легкой формулой для нахождения пути при равноускоренном движении, минуя изображения чертежей с расстановкой действующих на тело сил.
Пример решения более сложной задачи
А теперь давайте посмотрим, как лучше решать задачи на движение тела под действием силы тяжести, если тело движется не вертикально, а имеет более сложный характер перемещения.
Например, следующая задача. Некоторый предмет массой m движется с неизвестным ускорением вниз по наклонной плоскости, коэффициент трения которой равен k. Определить значение ускорения, которое имеется при движении данного тела, если угол наклона α известен.
Решение: Следует воспользоваться планом, который описан выше. В первую очередь начертить рисунок наклонной плоскости с изображением тела и всех действующих на него сил. Получится, что на него действуют три составляющие: сила тяжести, трения и сила реакции опоры. Выглядит общее уравнение равнодействующих сил так: F трения + N + mg = ma.
Главной изюминкой задачи является условие наклонности под углом α. При ox и ось oy необходимо учесть данное условие, тогда у нас получится следующее выражение: mg х sin α — F трения = ma (для оси ох) и N — mg х cos α = F трения (для оси oy).
F трения легко вычислить по формуле нахождения силы трения, она равна k х mg (коэффициент трения, умноженный на произведение массы тела и ускорения свободного падения). После всех вычислений остается только подставить найденные значения в формулу, получится упрощенное уравнение для вычисления ускорения, с которым движется тело вдоль наклонной плоскости.
Исходя из трактовки второго закона Ньютона, можно сделать вывод, что изменение движения происходит посредствам силы. Механика рассматривает силы различной физической природы. Многие из них определяются с помощью действия сил тяготения.
Механика рассматривает силы различной физической природы. Многие из них определяются с помощью действия сил тяготения.
В 1862 году был открыт закон всемирного тяготения И. Ньютоном. Он предположил, что силы, удерживающие Луну, той же природы, что и силы, заставляющие яблоко падать на Землю. Смысл гипотезы состоит в наличии действия сил притяжения, направленных по линии и соединяющих центры масс, как изображено на рисунке 1 . 10 . 1 . Шаровидное тело имеет центр массы, совпадающий с центром шара.
Рисунок 1 . 10 . 1 . Гравитационные силы притяжения между телами. F 1 → = — F 2 → .
Определение 1
При известных направлениях движений планет Ньютон пытался выяснить, какие силы действуют на них. Этот процесс получил название обратной задачи механики .
Основная задача механики – определение координат тела известной массы с его скоростью в любой момент времени при помощи известных сил, действующих на тело, и заданным условием (прямая задача).
Определение 2
Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними.
F = G m 1 m 2 r 2 .
Значение G определяет коэффициент пропорциональности всех тел в природе, называемое гравитационной постоянной и обозначаемое по формуле G = 6 , 67 · 10 — 11 Н · м 2 / к г 2 (С И) .
Большинство явлений в природе объясняются наличием действия силы всемирного тяготения. Движение планет, искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все объясняется законом тяготения и динамики.
Определение 3
Проявлении силы тяготения характеризуется наличием силы тяжести . Так называется сила притяжения тел к Земле и вблизи ее поверхности.
Когда М обозначается как масса Земли, R З – радиус, m – масса тела, то формула силы тяжести принимает вид:
F = G M R З 2 m = m g .
Где g – ускорение свободного падения, равняющееся g = G M R З 2 .
Сила тяжести направлена к центру Земли, как показано в примере Луна-Земля. При отсутствии действия других сил тело движется с ускорением свободного падения. Его среднее значение равняется 9 , 81 м / с 2 . При известном G и радиусе R 3 = 6 , 38 · 10 6 м производятся вычисления массы Земли М по формуле:
M = g R 3 2 G = 5 , 98 · 10 24 к г.
Если тело удаляется от поверхности Земли, тогда действие силы тяготения и ускорения свободного падения меняются обратно пропорционально квадрату расстояния r к центру. Рисунок 1 . 10 . 2 показывает, как изменяется сила тяготения, действующая на космонавта корабля, при удалении от Земли. Очевидно, что F притягивания его к Земле равняется 700 Н.
Рисунок 1 . 10 . 2 . Изменение силы тяготения, действующей на космонавта при удалении от Земли.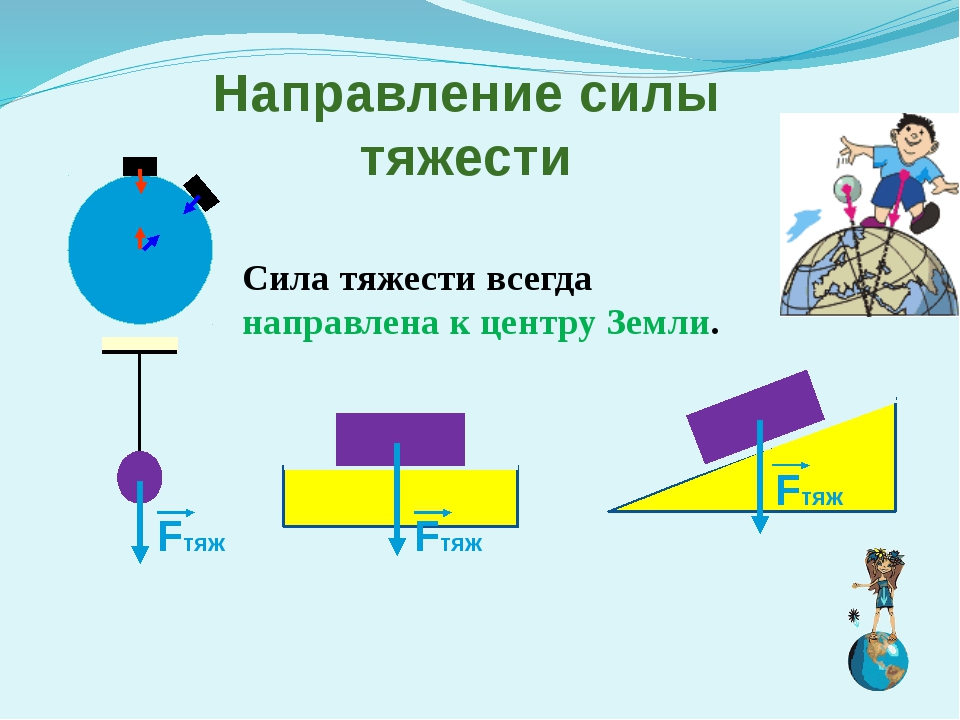
Пример 1
Земля-Луна подходит в качестве примера взаимодействия системы двух тел.
Расстояние до Луны – r Л = 3 , 84 · 10 6 м. Оно в 60 раз больше радиуса Земли R З. Значит, при наличии земного притяжения, ускорение свободного падения α Л орбиты Луны составит α Л = g R З r Л 2 = 9 , 81 м / с 2 60 2 = 0 , 0027 м / с 2 .
Оно направлено к центру Земли и получило название центростремительного. Расчет производится по формуле a Л = υ 2 r Л = 4 π 2 r Л T 2 = 0 , 0027 м / с 2 , где Т = 27 , 3 суток – период обращения Луны вокруг Земли. Результаты и расчеты, выполненные разными способами, говорят о том, что Ньютон был прав в своем предположении единой природы силы, удерживающей Луну на орбите, и силы тяжести.
Луна имеет собственное гравитационное поле, которое определяет ускорение свободного падения g Л на поверхности. Масса Луны в 81 раз меньше массы Земли, а радиус в 3 , 7 раза. Отсюда видно, что ускорение g Л следует определять из выражения:
g Л = G M Л R Л 2 = G M З 3 , 7 2 T 3 2 = 0 , 17 g = 1 , 66 м / с 2 .
Такая слабая гравитация характерна для космонавтов, находящихся на Луне. Поэтому можно совершать огромные прыжки и шаги. Прыжок вверх на метр на Земле соответствует семиметровому на Луне.
Движение искусственных спутников зафиксировано за пределами земной атмосферы, поэтому на них оказывают действие силы тяготения Земли. Траектория космического тела может изменяться в зависимости от начальной скорости. Движение искусственного спутника по околоземной орбите приближенно принимается в качестве расстояния до центра Земли, равняющемуся радиусу R З. Они летают на высотах 200 — 300 к м.
Определение 4
Отсюда следует, что центростремительное ускорение спутника, которое сообщается силами тяготения, равняется ускорению свободного падения g . Скорость спутника примет обозначение υ 1 . Ее называют
Применив кинематическую формулу для центростремительного ускорения, получаем
a n = υ 1 2 R З = g , υ 1 = g R З = 7 , 91 · 10 3 м / с.
При такой скорости спутник смог облететь Землю за время, равное T 1 = 2 πR З υ 1 = 84 м и н 12 с.
Но период обращения спутника по круговой орбите вблизи Земли намного больше, чем указано выше, так как существует различие между радиусом реальной орбиты и радиусом Земли.
Спутник движется по принципу свободного падения, отдаленно похожее на траекторию снаряда или баллистической ракеты. Разница заключается в большой скорости спутника, причем радиус кривизны его траектории достигает длины радиуса Земли.
Спутники, которые движутся по круговым траекториям на больших расстояниях, имеют ослабленное земное притяжение, обратно пропорциональное квадрату радиуса r траектории. Тогда нахождение скорости спутника следует по условию:
υ 2 к = g R 3 2 r 2 , υ = g R 3 R З r = υ 1 R 3 r .
Поэтому, наличие спутников на высоких орбитах говорит о меньшей скорости их движения, чем с околоземной орбиты. Формула периода обращения равняется:
T = 2 πr υ = 2 πr υ 1 r R З = 2 πR з υ 1 r R 3 3 / 2 = T 1 2 π R З.
T 1 принимает значение периода обращения спутника по околоземной орбите. Т возрастает с размерами радиуса орбиты. Если r имеет значение 6 , 6 R 3 то Т спутника равняется 24 часам. При его запуске в плоскости экватора, будет наблюдаться, как висит над некоторой точкой земной поверхности. Применение таких спутников известно в системе космической радиосвязи. Орбиту, имеющую радиус r = 6 , 6 R З, называют геостационарной.
Рисунок 1 . 10 . 3 . Модель движения спутников.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Гравитация, она же притяжение или тяготение, — это универсальное свойство материи, которым обладают все предметы и тела во Вселенной. Суть гравитации залучается в том, что все материальные тела притягивают к себе все другие тела, находящиеся вокруг.
Земное притяжение
Если гравитация — это общее понятие и качество, которым обладают все предметы во Вселенной, то земное притяжение — это частный случай этого всеобъемлющего явления. Земля притягивает к себе все материальные объекты, находящиеся на ней. Благодаря этому люди и животные могут спокойно перемещаться по земле, реки, моря и океаны — оставаться в пределах своих берегов, а воздух — не летать по бескрайним просторам Космоса, а образовывать атмосферу нашей планеты.
Земля притягивает к себе все материальные объекты, находящиеся на ней. Благодаря этому люди и животные могут спокойно перемещаться по земле, реки, моря и океаны — оставаться в пределах своих берегов, а воздух — не летать по бескрайним просторам Космоса, а образовывать атмосферу нашей планеты.
Возникает справедливый вопрос: если все предметы обладают гравитацией, почему Земля притягивает к себе людей и животных, а не наоборот? Во-первых, мы тоже притягиваем к себе Землю, просто, по сравнению с ее силой притяжения наша гравитация ничтожно мала. Во-вторых, сила гравитации прямо пропорционально зависит от массы тела: чем меньше масса тела, тем ниже его гравитационные силы.
Второй показатель, от которого зависит сила притяжения — это расстояние между предметами: чем больше расстояние, тем меньше действие гравитации. В том числе благодаря этому, планеты движутся на своих орбитах, а не падают друг на друга.
Примечательно, что своей сферической формой Земля, Луна, Солнце и другие планеты обязаны именно силе тяготения. Она действует в направлении центра, подтягивая к нему вещество, составляющее «тело» планеты.
Она действует в направлении центра, подтягивая к нему вещество, составляющее «тело» планеты.
Гравитационное поле Земли
Гравитационное поле Земли — это силовое энергетическое поле, которое образуется вокруг нашей планеты благодаря действию двух сил:
- гравитации;
- центробежной силе, которая своим появление обязана вращению Земли вокруг своей оси (суточное вращение).
Поскольку и гравитация, и центробежная сила действуют постоянно, то и гравитационное поле является постоянным явлением.
Незначительное воздействие на поле оказывают силы тяготения Солнца, Луны и некоторых других небесных тел, а также атмосферных масс Земли.
Закон всемирного тяготения и сэр Исаак Ньютон
Английский физик, сэр Исаак Ньютон, согласно известной легенде, однажды гуляя по саду днем, увидел на небе Луну. В это же время с ветки упало яблоко. Ньютон тогда занимался изучением закона движения и знал, что яблоко падает под воздействием гравитационного поля, а Луна вращается по орбите вокруг Земли.
И тут в голову гениальному ученому, озаренную инсайтом, пришла мысль, что, возможно, яблоко падает на землю, подчиняясь той же силе, благодаря которой Луна находится на своей орбите, а не носится беспорядочно по всей галактике. Так был открыт закон всемирного тяготения, он же Третий закон Ньютона.
На языке математических формул этот закон выглядит так:
F = GMm/D 2 ,
где F — сила взаимного тяготения между двумя телами;
M — масса первого тела;
m — масса второго тела;
D 2 — расстояние между двумя телами;
G — гравитационная постоянная, равная 6,67х10 -11 .
Почему выпущенный из рук камень падает на Землю? Потому что его притягивает Земля, скажет каждый из вас. В самом деле, камень падает на Землю с ускорением свободного падения. Следовательно, на камень со стороны Земли действует сила, направленная к Земле.
Согласно третьему закону Ньютона и камень действует на Землю с такой же по модулю силой, направленной к камню. Иными словами, между Землей и камнем действуют силы взаимного притяжения.
Иными словами, между Землей и камнем действуют силы взаимного притяжения.
Догадка Ньютона
Ньютон был первым, кто сначала догадался, а потом и строго доказал, что причина, вызывающая падение камня на Землю, движение Луны вокруг Земли и планет вокруг Солнца, одна и та же. Это сила тяготения, действующая между любыми телами Вселенной. Вот ход его рассуждений, приведенных в главном труде Ньютона «Математические начала натуральной философии»: «Брошенный горизонтально камень отклонится под действием тяжести от прямолинейного пути и, описав кривую траекторию, упадет наконец на Землю. Если его бросить с большей скоростью, то он упадет дальше» (рис. 3.2). Продолжая эти рассуждения, Ньютон приходит к выводу, что если бы не сопротивление воздуха, то траектория камня, брошенного с высокой горы с определенной скоростью, могла бы стать такой, что он вообще никогда не достиг бы поверхности Земли, а двигался вокруг нее «подобно тому, как планеты описывают в небесном пространстве свои орбиты».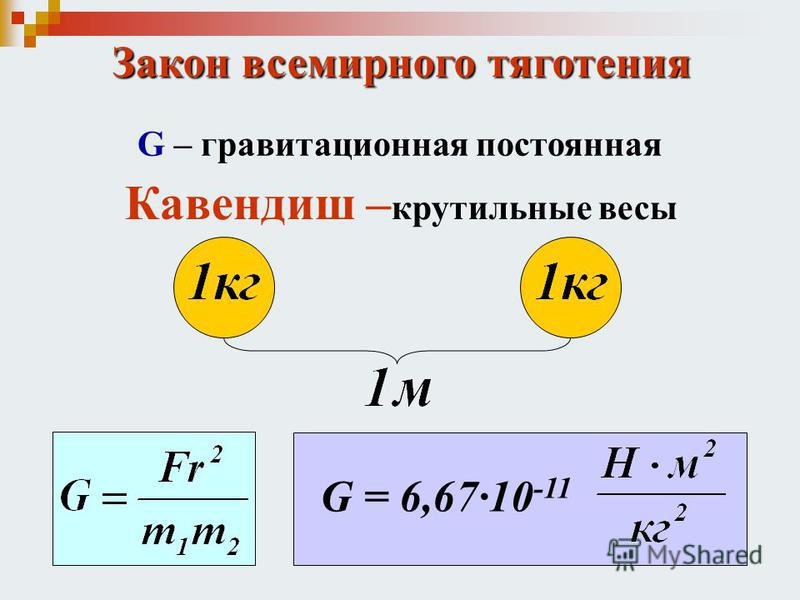
Рис. 3.2
Сейчас нам стало настолько привычным движение спутников вокруг Земли, что разъяснять мысль Ньютона подробнее нет необходимости.
Итак, по мнению Ньютона, движение Луны вокруг Земли или планет вокруг Солнца — это тоже свободное падение, но только падение, которое длится, не прекращаясь, миллиарды лет. Причиной такого «падения» (идет ли речь действительно о падении обычного камня на Землю или о движении планет по их орбитам) является сила всемирного тяготения. От чего же эта сила зависит?
Зависимость силы тяготения от массы тел
В § 1.23 говорилось о свободном падении тел. Упоминались опыты Галилея, доказавшие, что Земля сообщает всем телам в данном месте одно и то же ускорение независимо от их массы. Это возможно лишь в том случае, если сила притяжения к Земле прямо пропорциональна массе тела. Именно в этом случае ускорение свободного падения, равное отношению силы земного притяжения к массе тела, является постоянной величиной.
Действительно, в этом случае увеличение массы m, например, вдвое приведет к увеличению модуля силы тоже вдвое, а ускорение, которое равно отношению , останется неизменным.
Обобщая этот вывод для сил тяготения между любыми телами, заключаем, что сила всемирного тяготения прямо пропорциональна массе тела, на которое эта сила действует. Но во взаимном притяжении участвуют по меньшей мере два тела. На каждое из них, согласно третьему закону Ньютона, действуют одинаковые по модулю силы тяготения. Поэтому каждая из этих сил должна быть пропорциональна как массе одного тела, так и массе другого тела.
Поэтому сила всемирного тяготения между двумя телами прямо пропорциональна произведению их масс :
От чего еще зависит сила тяготения, действующая на данное тело со стороны другого тела?
Зависимость силы тяготения от расстояния между телами
Можно предположить, что сила тяготения должна зависеть от расстояния между телами. Чтобы проверить правильность этого предположения и найти зависимость силы тяготения от расстояния между телами, Ньютон обратился к движению спутника Земли — Луны. Ее движение было в те времена изучено гораздо точнее, чем движение планет.
Обращение Луны вокруг Земли происходит под действием силы тяготения между ними. Приближенно орбиту Луны можно считать окружностью. Следовательно, Земля сообщает Луне центростремительное ускорение. Оно вычисляется по формуле
где R — радиус лунной орбиты, равный примерно 60 радиусам Земли, Т = 27 сут 7 ч 43 мин = 2,4 10 6 с — период обращения Луны вокруг Земли. Учитывая, что радиус Земли R 3 = 6,4 10 6 м, получим, что центростремительное ускорение Луны равно:
Найденное значение ускорения меньше ускорения свободного падения тел у поверхности Земли (9,8 м/с 2) приблизительно в 3600 = 60 2 раз.
Таким образом, увеличение расстояния между телом и Землей в 60 раз привело к уменьшению ускорения, сообщаемого земным притяжением, а следовательно, и самой силы притяжения в 60 2 раз(1).
Отсюда вытекает важный вывод: ускорение, которое сообщает телам сила притяжения к Земле, убывает обратно пропорционально квадрату расстояния до центра Земли :
где C 1 — постоянный коэффициент, одинаковый для всех тел.
Законы Кеплера
Исследование движения планет показало, что это движение вызвано силой притяжения к Солнцу. Используя тщательные многолетние наблюдения датского астронома Тихо Браге, немецкий ученый Иоганн Кеплер в начале XVII в. установил кинематические законы движения планет — так называемые законы Кеплера.
Первый закон Кеплера
Все планеты движутся по эллипсам, в одном из фокусов которых находится Солнце.
Эллипсом (рис. 3.3) называется плоская замкнутая кривая, сумма расстояний от любой точки которой до двух фиксированных точек, называемых фокусами, постоянна. Эта сумма расстояний равна длине большой оси АВ эллипса, т. е.
где F 1 и F 2 — фокусы эллипса, а b = — его большая полуось; О — центр эллипса. Ближайшая к Солнцу точка орбиты называется перигелием, а самая далекая от него точка — афелием. Если Солнце находится в фокусе F 1 (см. рис. 3.3), то точка А — перигелий, а точка В — афелий.
Рис. 3.3
Второй закон Кеплера
Радиус-вектор планеты за одинаковые промежутки времени описывает равные площади . Так, если заштрихованные секторы (рис. 3.4) имеют одинаковые площади, то пути s 1 , s 2 , s 3 будут пройдены планетой за равные промежутки времени. Из рисунка видно, что s 1 > s 2 . Следовательно, линейная скорость движения планеты в различных точках ее орбиты неодинакова. В перигелии скорость планеты наибольшая, в афелии — наименьшая.
Так, если заштрихованные секторы (рис. 3.4) имеют одинаковые площади, то пути s 1 , s 2 , s 3 будут пройдены планетой за равные промежутки времени. Из рисунка видно, что s 1 > s 2 . Следовательно, линейная скорость движения планеты в различных точках ее орбиты неодинакова. В перигелии скорость планеты наибольшая, в афелии — наименьшая.
Рис. 3.4
Третий закон Кеплера
Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит . Обозначив большую полуось орбиты и период обращения одной из планет через b 1 и T 1 а другой — через b 2 и Т 2 , третий закон Кеплера можно записать так:
На основании законов Кеплера можно сделать определенные выводы об ускорениях, сообщаемых планетам Солнцем. Мы для простоты будем считать орбиты не эллиптическими, а круговыми. Для планет Солнечной системы эта замена не является слишком грубым приближением.
Тогда сила притяжения со стороны Солнца в этом приближении должна быть направлена для всех планет к центру Солнца.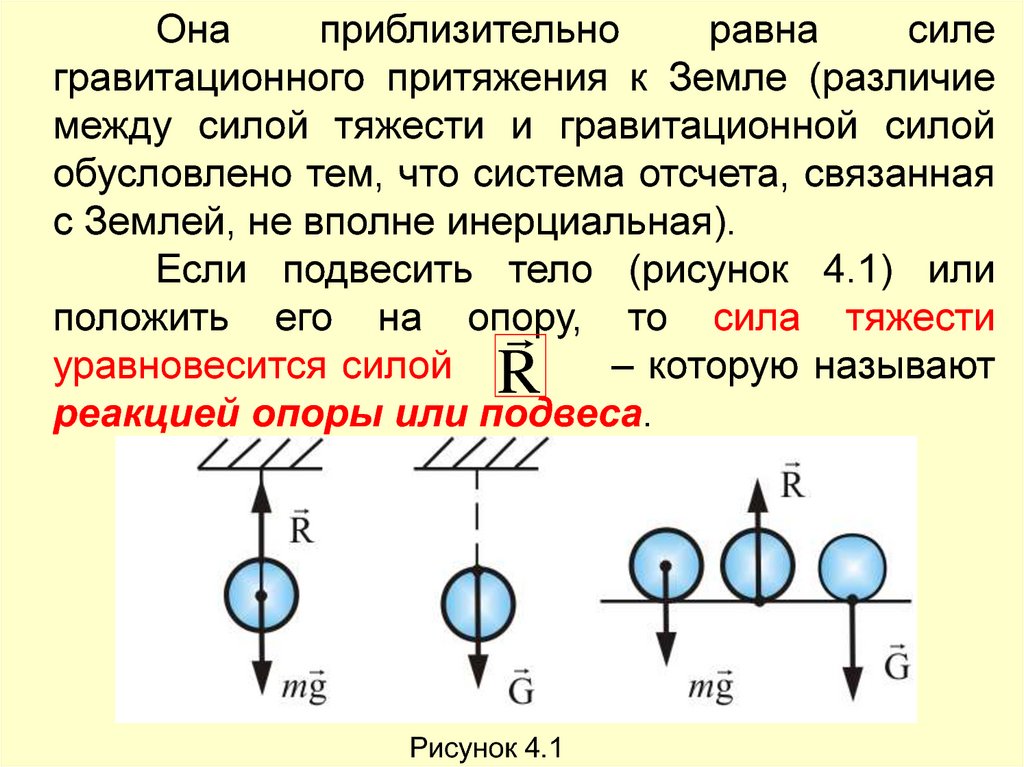
Если через Т обозначить периоды обращения планет, а через R — радиусы их орбит, то, согласно третьему закону Кеплера, для двух планет можно записать
Нормальное ускорение при движении по окружности а = ω 2 R. Поэтому отношение ускорений планет
Используя уравнение (3.2.4), получим
Так как третий закон Кеплера справедлив для всех планет, то ускорение каждой планеты обратно пропорционально квадрату расстояния ее до Солнца:
Постоянная С 2 одинакова для всех планет, но не совпадает с постоянной С 1 в формуле для ускорения, сообщаемого телам земным шаром.
Выражения (3.2.2) и (3.2.6) показывают, что сила тяготения в обоих случаях (притяжение к Земле и притяжение к Солнцу) сообщает всем телам ускорение, не зависящее от их массы и убывающее обратно пропорционально квадрату расстояния между ними:
Закон всемирного тяготения
Существование зависимостей (3.2.1) и (3.2.7) означает, что сила всемирного тяготения
В 1667 г. Ньютон окончательно сформулировал закон всемирного тяготения:
Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними
.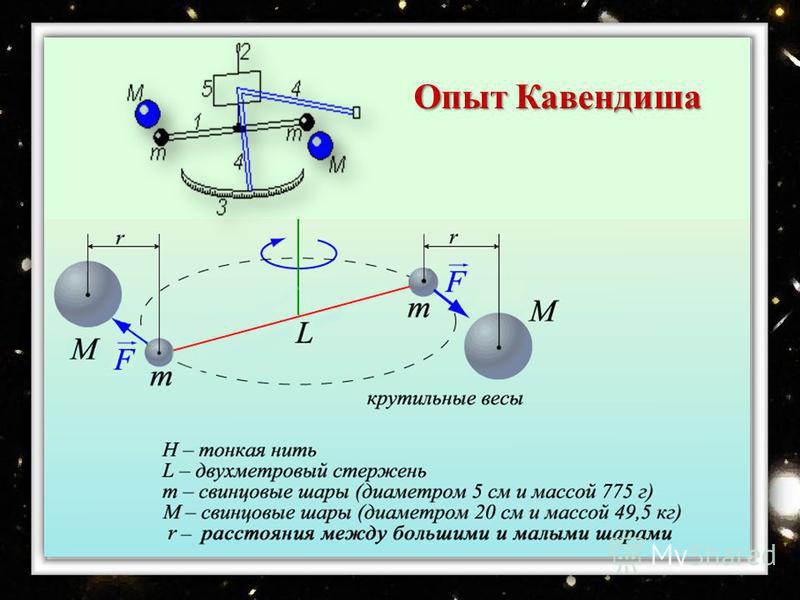 Коэффициент пропорциональности G называется гравитационной(2) постоянной.
Коэффициент пропорциональности G называется гравитационной(2) постоянной.
Взаимодействие точечных и протяженных тел
Закон всемирного тяготения (3.2.8) справедлив только для таких тел, размеры которых пренебрежимо малы по сравнению с расстоянием между ними. Иначе говоря, он справедлив только для материальных точек. При этом силы гравитационного взаимодействия направлены вдоль линии, соединяющей эти точки (рис. 3.5). Подобного рода силы называются центральными.
Рис. 3.5
Для нахождения силы тяготения, действующей на данное тело со стороны другого, в случае, когда размерами тел пренебречь нельзя, поступают следующим образом. Оба тела мысленно разделяют на столь малые элементы, чтобы каждый из них можно было считать точечным. Складывая силы тяготения, действующие на каждый элемент данного тела со стороны всех элементов другого тела, получают силу, действующую на этот элемент (рис. 3.6). Проделав такую операцию для каждого элемента данного тела и сложив полученные силы, находят полную силу тяготения, действующую на это тело. Задача эта сложная.
Задача эта сложная.
Рис. 3.6
Есть, однако, один практически важный случай, когда формула (3.2.8) применима к протяженным телам. Можно доказать, что сферические тела, плотность которых зависит только от расстояний до их центров, при расстояниях между ними, больших суммы их радиусов, притягиваются с силами, модули которых определяются формулой (3.2.8). В этом случае R — это расстояние между центрами шаров.
И наконец, так как размеры падающих на Землю тел много меньше размеров Земли, то эти тела можно рассматривать как точечные. Тогда под R в формуле (3.2.8) следует понимать расстояние от данного тела до центра Земли.
Вопросы для самопроверки
- Расстояние от Марса до Солнца на 52% больше расстояния от Земли до Солнца. Какова продолжительность года на Марсе?
- Как изменится сила притяжения между шарами, если алюминиевые шары (рис. 3.7) заменить стальными шарами той же массы? того же объема?
Рис. 3.7
(1) Интересно, что, будучи студентом, Ньютон понял, что Луна движется под влиянием притяжения к Земле. Но в то время радиус Земли был известен неточно, и расчеты не привели к правильному результату . Лишь спустя 16 лет появились новые, исправленные данные, и закон всемирного тяготения был опубликован.
Но в то время радиус Земли был известен неточно, и расчеты не привели к правильному результату . Лишь спустя 16 лет появились новые, исправленные данные, и закон всемирного тяготения был опубликован.
(2) От латинского слова gravitas — тяжесть.
Действием сил всемирного тяготения в природе объясняются многие явления: движение планет в Солнечной системе, искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все они находят объяснение на основе закона всемирного тяготения и законов динамики.
Закон всемирного тяготения объясняет механическое устройство Солнечной системы, и законы Кеплера, описывающие траектории движения планет, могут быть выведены из него. Для Кеплера его законы носили чисто описательный характер — ученый просто обобщил свои наблюдения в математической форме, не подведя под формулы никаких теоретических оснований. В великой же системе мироустройства по Ньютону законы Кеплера становятся прямым следствием универсальных законов механики и закона всемирного тяготения.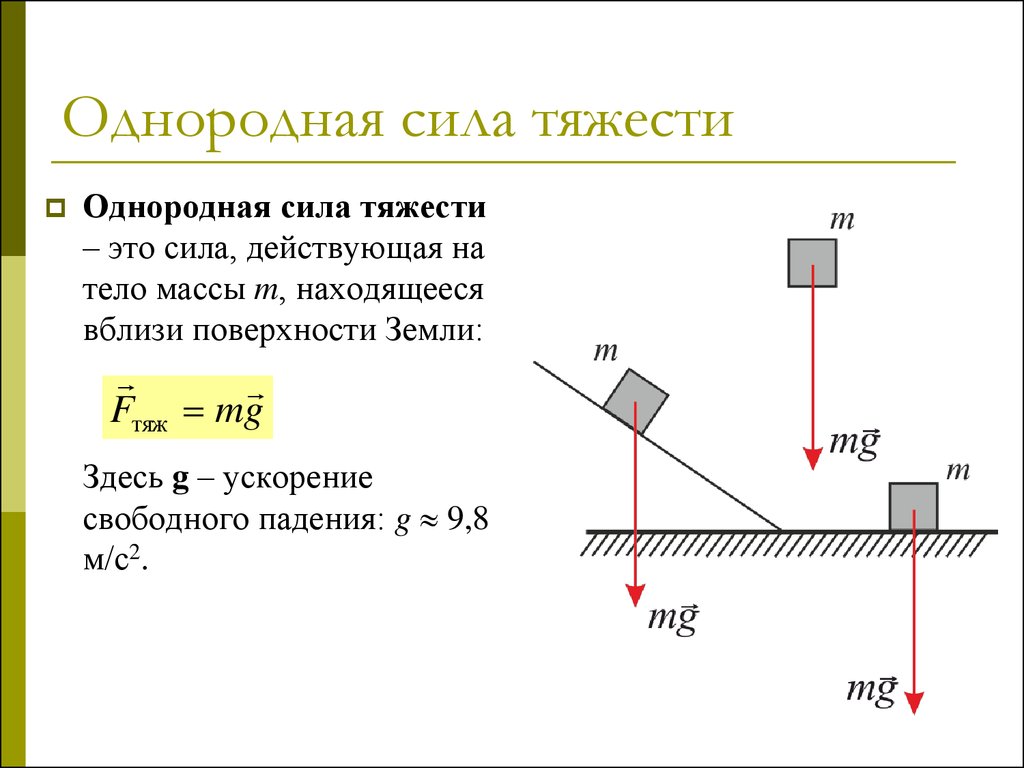 То есть мы опять наблюдаем, как эмпирические заключения, полученные на одном уровне, превращаются в строго обоснованные логические выводы при переходе на следующую ступень углубления наших знаний о мире.
То есть мы опять наблюдаем, как эмпирические заключения, полученные на одном уровне, превращаются в строго обоснованные логические выводы при переходе на следующую ступень углубления наших знаний о мире.
Ньютон первый высказал мысль о том, что гравитационные силы определяют не только движение планет Солнечной системы; они действуют между любыми телами Вселенной. Одним из проявлений силы всемирного тяготения является сила тяжести — так принято называть силу притяжения тел к Земле вблизи ее поверхности.
Если M – масса Земли, RЗ – ее радиус, m – масса данного тела, то сила тяжести равна
где g – ускорение свободного падения;
у поверхности Земли
Сила тяжести направлена к центру Земли. В отсутствие других сил тело свободно падает на Землю с ускорением свободного падения.
Среднее значение ускорения свободного падения для различных точек поверхности Земли равно 9,81 м/с2. Зная ускорение свободного падения и радиус Земли (RЗ = 6,38·106 м), можно вычислить массу Земли
Картину устройства солнечной системы, вытекающую из этих уравнений и объединяющую земную и небесную гравитацию, можно понять на простом примере. Предположим, мы стоим у края отвесной скалы, рядом пушка и горка пушечных ядер. Если просто сбросить ядро с края обрыва по вертикали, оно начнет падать вниз отвесно и равноускоренно. Его движение будет описываться законами Ньютона для равноускоренного движения тела с ускорением g. Если теперь выпустить ядро из пушки в направлении горизонта, оно полетит — и будет падать по дуге. И в этом случае его движение будет описываться законами Ньютона, только теперь они применяются к телу, движущемуся под воздействием силы тяжести и обладающему некой начальной скоростью в горизонтальной плоскости. Теперь, раз за разом заряжая в пушку всё более тяжелое ядро и стреляя, вы обнаружите, что, поскольку каждое следующее ядро вылетает из ствола с большей начальной скоростью, ядра падают всё дальше и дальше от подножия скалы.
Предположим, мы стоим у края отвесной скалы, рядом пушка и горка пушечных ядер. Если просто сбросить ядро с края обрыва по вертикали, оно начнет падать вниз отвесно и равноускоренно. Его движение будет описываться законами Ньютона для равноускоренного движения тела с ускорением g. Если теперь выпустить ядро из пушки в направлении горизонта, оно полетит — и будет падать по дуге. И в этом случае его движение будет описываться законами Ньютона, только теперь они применяются к телу, движущемуся под воздействием силы тяжести и обладающему некой начальной скоростью в горизонтальной плоскости. Теперь, раз за разом заряжая в пушку всё более тяжелое ядро и стреляя, вы обнаружите, что, поскольку каждое следующее ядро вылетает из ствола с большей начальной скоростью, ядра падают всё дальше и дальше от подножия скалы.
Теперь представим, что мы забили в пушку столько пороха, что скорости ядра хватает, чтобы облететь вокруг земного шара. Если пренебречь сопротивлением воздуха, ядро, облетев вокруг Земли, вернется в исходную точку точно с той же скоростью, с какой оно изначально вылетело из пушки.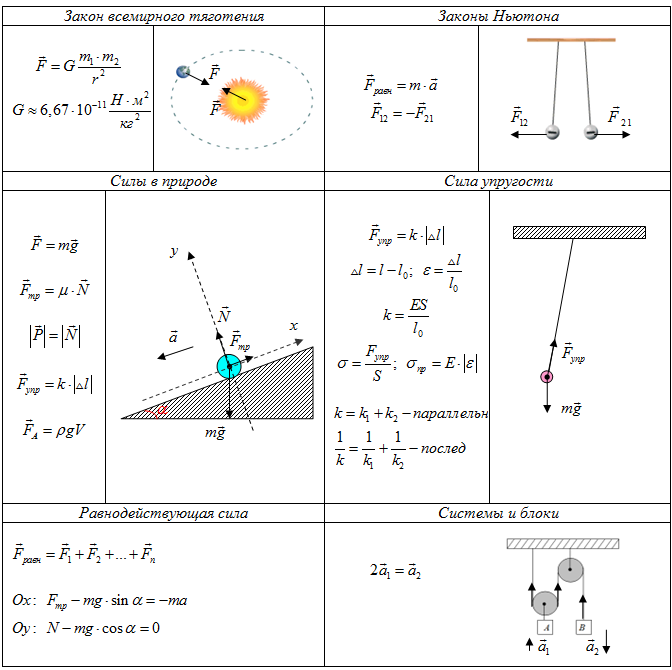 Что будет дальше, понятно: ядро на этом не остановится и будет и продолжать наматывать круг за кругом вокруг планеты.
Что будет дальше, понятно: ядро на этом не остановится и будет и продолжать наматывать круг за кругом вокруг планеты.
Иными словами, мы получим искусственный спутник, обращающийся вокруг Земли по орбите, подобно естественному спутнику — Луне.
Так поэтапно мы перешли от описания движения тела, падающего исключительно под воздействием «земной» гравитации (ньютоновского яблока), к описанию движения спутника (Луны) по орбите, не изменяя при этом природы гравитационного воздействия с «земной» на «небесную». Вот это-то прозрение и позволило Ньютону связать воедино считавшиеся до него различными по своей природе две силы гравитационного притяжения.
При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения изменяются обратно пропорционально квадрату расстояния r до центра Земли. Примером системы двух взаимодействующих тел может служить система Земля–Луна. Луна находится от Земли на расстоянии rЛ = 3,84·106 м. Это расстояние приблизительно в 60 раз превышает радиус Земли RЗ.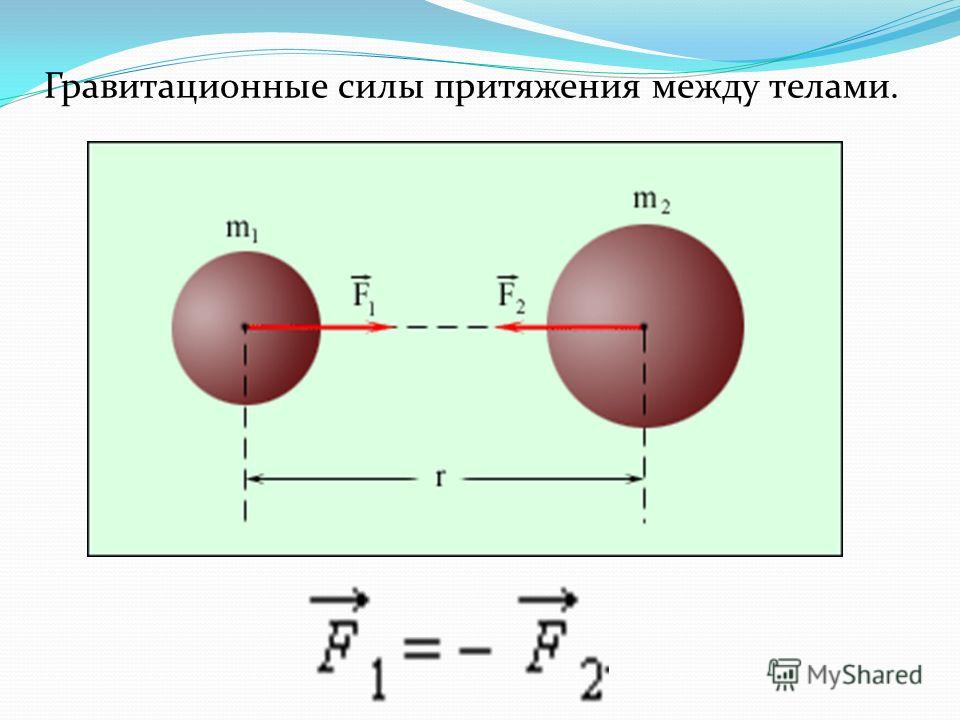 Следовательно, ускорение свободного падения aЛ, обусловленное земным притяжением, на орбите Луны составляет
Следовательно, ускорение свободного падения aЛ, обусловленное земным притяжением, на орбите Луны составляет
С таким ускорением, направленным к центру Земли, Луна движется по орбите. Следовательно, это ускорение является центростремительным ускорением. Его можно рассчитать по кинематической формуле для центростремительного ускорения
где T = 27,3 сут – период обращения Луны вокруг Земли.
Совпадение результатов расчетов, выполненных разными способами, подтверждает предположение Ньютона о единой природе силы, удерживающей Луну на орбите, и силы тяжести.
Собственное гравитационное поле Луны определяет ускорение свободного падения gЛ на ее поверхности. Масса Луны в 81 раз меньше массы Земли, а ее радиус приблизительно в 3,7 раза меньше радиуса Земли.
Поэтому ускорение gЛ определится выражением
В условиях такой слабой гравитации оказались космонавты, высадившиеся на Луне. Человек в таких условиях может совершать гигантские прыжки. Например, если человек в земных условиях подпрыгивает на высоту 1 м, то на Луне он мог бы подпрыгнуть на высоту более 6 м.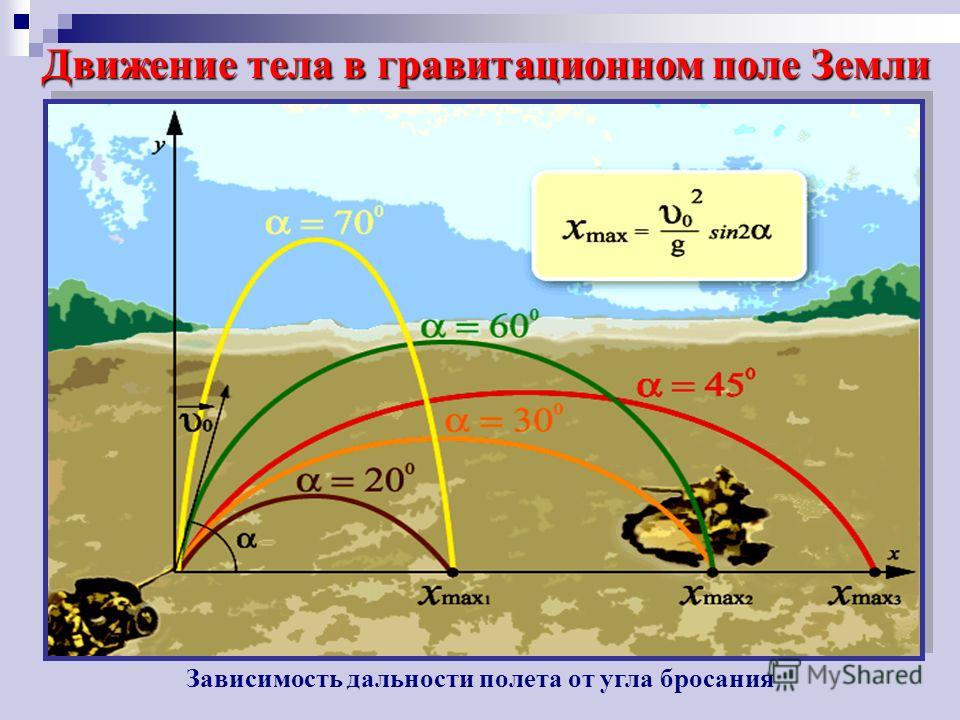
Рассмотрим вопрос об искусственных спутниках Земли. Искусственные спутники Земли движутся за пределами земной атмосферы, и на них действуют только силы тяготения со стороны Земли.
В зависимости от начальной скорости траектория космического тела может быть различной. Рассмотрим случай движения искусственного спутника по круговой околоземной орбите. Такие спутники летают на высотах порядка 200–300 км, и можно приближенно принять расстояние до центра Земли равным ее радиусу RЗ. Тогда центростремительное ускорение спутника, сообщаемое ему силами тяготения, приблизительно равно ускорению свободного падения g. Обозначим скорость спутника на околоземной орбите через υ1 – такая скорость называют первой космической скоростью. Используя кинематическую формулу для центростремительного ускорения, получим
Двигаясь с такой скоростью, спутник облетал бы Землю за время
На самом деле период обращения спутника по круговой орбите вблизи поверхности Земли несколько превышает указанное значение из-за отличия между радиусом реальной орбиты и радиусом Земли. Движение спутника можно рассматривать как свободное падение, подобное движению снарядов или баллистических ракет. Различие заключается только в том, что скорость спутника настолько велика, что радиус кривизны его траектории равен радиусу Земли.
Движение спутника можно рассматривать как свободное падение, подобное движению снарядов или баллистических ракет. Различие заключается только в том, что скорость спутника настолько велика, что радиус кривизны его траектории равен радиусу Земли.
Для спутников, движущихся по круговым траекториям на значительном удалении от Земли, земное притяжение ослабевает обратно пропорционально квадрату радиуса r траектории. Таким образом, на высоких орбитах скорость движения спутников меньше, чем на околоземной орбите.
Период обращения спутника растет с увеличением радиуса орбиты. Нетрудно подсчитать, что при радиусе r орбиты, равном приблизительно 6,6 RЗ, период обращения спутника окажется равным 24 часам. Спутник с таким периодом обращения, запущенный в плоскости экватора, будет неподвижно висеть над некоторой точкой земной поверхности. Такие спутники используются в системах космической радиосвязи. Орбита с радиусом r = 6,6 RЗ называется геостационарной.
Второй космической скоростью называется минимальная скорость, которую нужно сообщить космическому кораблю у поверхности Земли, чтобы он, преодолев земное притяжение, превратился в искусственный спутник Солнца (искусственная планета). При этом корабль будет удаляться от Земли по параболической траектории.
При этом корабль будет удаляться от Земли по параболической траектории.
Рисунок 5 иллюстрирует космические скорости. Если скорость космического корабля равна υ1 = 7.9·103 м/с и направлена параллельно поверхности Земли, то корабль будет двигаться по круговой орбите на небольшой высоте над Землей. При начальных скоростях, превышающих υ1, но меньших υ2 = 11,2·103 м/с, орбита корабля будет эллиптической. При начальной скорости υ2 корабль будет двигаться по параболе, а при еще большей начальной скорости – по гиперболе.
Космические скорости
Указаны скорости вблизи поверхности Земли: 1) υ = υ1 – круговая траектория;
2) υ1
4) υ = υ2 – параболическая траектория; 5) υ > υ2 – гиперболическая траектория;
6) траектория Луны
Таким образом,мы выяснили, что все движения в Солнечной системе подчиняются закону всемирного тяготения Ньютона.
Исходя из малой массы планет и тем более прочих тел Солнечной системы, можно приближенно считать, что движения в околосолнечном пространстве подчиняются законам Кеплера.
Все тела движутся вокруг Солнца по эллиптическим орбитам, в одном из фокусов которых находится Солнце. Чем ближе к Солнцу небесное тело, тем быстрее его скорость движения по орбите (планета Плутон, самая далекая из известных, движется в 6 раз медленнее Земли).
Тела могут двигаться и по разомкнутым орбитам: параболе или гиперболе. Это случается в том случае, если скорость тела равна или превышает значение второй космической скорости для Солнца на данном удалении от центрального светила. Если речь идет о спутнике планеты, то и космическую скорость надо рассчитывать относительно массы планеты и расстояния до ее центра.
| Содержание Введение 1. 1.1 Движение тела по круговой или эллиптической орбите вокруг планеты 1.2 Движение тела под действием силы тяжести в вертикальной плоскости 1.3 Движение тела, если начальная скорость направлена под углом к силе тяжести 2. Движение тела в среде с сопротивлением 3. Применение законов движения тела под действием силы тяжести с учётом сопротивления среды в баллистике Заключение Список литературы Введение
Рис.1. Гравитационные силы. В последующие годы Ньютон пытался найти физическое объяснение законам движения планет, открытых астрономом И.Кеплером в начале XVII века, и дать количественное выражение для гравитационных сил. Зная, как движутся планеты, Ньютон хотел определить, какие силы на них действуют. Такой путь носит название обратной задачи механики. Если основной задачей механики является определение координат тела известной массы и его скорости в любой момент времени по известным силам, действующим на тело, и заданным начальным условиям (прямая задача механики), то при решении обратной задачи необходимо определить действующие на тело силы, если известно, как оно движется. Решение этой задачи и привело Ньютона к открытию закона всемирного тяготения. Коэффициент пропорциональности G одинаков для всех тел в природе. Его называют гравитационной постоянной G = 6,67·10-11 Н·м2/кг2 Многие явления в природе объясняются действием сил всемирного тяготения. Движение планет в Солнечной системе, движение искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все эти явления находят объяснение на основе закона всемирного тяготения и законов динамики. Одним из проявлений силы всемирного тяготения является сила тяжести. Сила тяжести — это сила, действующая на тело со стороны Земли и сообщающая телу ускорение свободного падения: Любое тело, находящееся на Земле (или вблизи нее), вместе с Землей вращается вокруг ее оси, т.е. тело движется по окружности радиусом r с постоянной по модулю скоростью. Рис.2. Движение тела, находящегося на поверхности Земли. На тело на поверхности Земли действуют сила тяготения и сила со стороны земной поверхности Их равнодействующая сообщает телу центростремительное ускорение Разложим силу тяготения на две составляющие, одна из которых будет, т.е. Из уравнений (1) и (2) видим, что
Таким образом, сила тяжести — одна из составляющих силы тяготения, вторая составляющая сообщает телу центростремительное ускорение. В точке Μ на географической широте φ сила тяжести направлена не по радиусу Земли, а под некоторым углом α к нему. Сила тяжести направлена по, так называемой, отвесной прямой (по вертикали вниз). Сила тяжести равна по модулю и направлению силе тяготения только на полюсах. На экваторе они совпадают по направлению, а по модулю отличие наибольшее. где ω — угловая скорость вращения Земли, R — радиус Земли.
Если M – масса Земли, RЗ – ее радиус, m – масса данного тела, то сила тяжести равна где g – ускорение свободного падения у поверхности Земли: Сила тяжести направлена к центру Земли. В отсутствие других сил тело свободно падает на Землю с ускорением свободного падения. Среднее значение ускорения свободного падения для различных точек поверхности Земли равно 9,81м/с2. Зная ускорение свободного падения и радиус Земли (RЗ = 6,38·106 м), можно вычислить массу Земли M: При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения изменяются обратно пропорционально квадрату расстояния r до центра Земли. Рис.3.Изменение силы тяготения, действующей на космонавта при удалении от Земли. Примером системы двух взаимодействующих тел может служить система Земля–Луна. Луна находится от Земли на расстоянии rЛ = 3,84·106 м. Это расстояние приблизительно в 60 раз превышает радиус Земли RЗ. Следовательно, ускорение свободного ал, обусловленное земным притяжением, на орбите Луны составляет С таким ускорением, направленным к центру Земли, Луна движется по орбите. Следовательно, это ускорение является центростремительным ускорением. Его можно рассчитать по кинематической формуле для центростремительного ускорения: где T = 27,3 сут. – период обращения Луны вокруг Земли. Совпадение результатов расчетов, выполненных разными способами, подтверждает предположение Ньютона о единой природе силы, удерживающей Луну на орбите, и силы тяжести. В условиях такой слабой гравитации оказались космонавты, высадившиеся на Луне. Человек в таких условиях может совершать гигантские прыжки. Например, если человек в земных условиях подпрыгивает на высоту 1 м, то на Луне он мог бы подпрыгнуть на высоту более 6 м. жүктеу/скачать 359.44 Kb. Достарыңызбен бөлісу: |
| | Действием сил всемирного тяготения в природе объясняются многие явления: движение планет в Солнечной системе, искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все они находят объяснение на основе закона всемирного тяготения и законов динамики. Закон всемирного тяготения объясняет механическое устройство Солнечной системы, и законы Кеплера, описывающие траектории движения планет, могут быть выведены из него. Для Кеплера его законы носили чисто описательный характер — ученый просто обобщил свои наблюдения в математической форме, не подведя под формулы никаких теоретических оснований. В великой же системе мироустройства по Ньютону законы Кеплера становятся прямым следствием универсальных законов механики и закона всемирного тяготения. То есть мы опять наблюдаем, как эмпирические заключения, полученные на одном уровне, превращаются в строго обоснованные логические выводы при переходе на следующую ступень углубления наших знаний о мире. Ньютон первый высказал мысль о том, что гравитационные силы определяют не только движение планет Солнечной системы; они действуют между любыми телами Вселенной. Одним из проявлений силы всемирного тяготения является сила тяжести — так принято называть силу притяжения тел к Земле вблизи ее поверхности. Если M – масса Земли, RЗ – ее радиус, m – масса данного тела, то сила тяжести равна где g – ускорение свободного падения; у поверхности Земли Сила тяжести направлена к центру Земли. В отсутствие других сил тело свободно падает на Землю с ускорением свободного падения. Среднее значение ускорения свободного падения для различных точек поверхности Земли равно 9,81 м/с2. Зная ускорение свободного падения и радиус Земли (RЗ = 6,38·106 м), можно вычислить массу Земли Картину устройства солнечной системы, вытекающую из этих уравнений и объединяющую земную и небесную гравитацию, можно понять на простом примере. Предположим, мы стоим у края отвесной скалы, рядом пушка и горка пушечных ядер. Если просто сбросить ядро с края обрыва по вертикали, оно начнет падать вниз отвесно и равноускоренно. Его движение будет описываться законами Ньютона для равноускоренного движения тела с ускорением g. Если теперь выпустить ядро из пушки в направлении горизонта, оно полетит — и будет падать по дуге.
Теперь представим, что мы забили в пушку столько пороха, что скорости ядра хватает, чтобы облететь вокруг земного шара. Если пренебречь сопротивлением воздуха, ядро, облетев вокруг Земли, вернется в исходную точку точно с той же скоростью, с какой оно изначально вылетело из пушки. Что будет дальше, понятно: ядро на этом не остановится и будет и продолжать наматывать круг за кругом вокруг планеты. Иными словами, мы получим искусственный спутник, обращающийся вокруг Земли по орбите, подобно естественному спутнику — Луне. Так поэтапно мы перешли от описания движения тела, падающего исключительно под воздействием «земной» гравитации (ньютоновского яблока), к описанию движения спутника (Луны) по орбите, не изменяя при этом природы гравитационного воздействия с «земной» на «небесную». Вот это-то прозрение и позволило Ньютону связать воедино считавшиеся до него различными по своей природе две силы гравитационного притяжения. При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения изменяются обратно пропорционально квадрату расстояния r до центра Земли. Примером системы двух взаимодействующих тел может служить система Земля–Луна. Луна находится от Земли на расстоянии rЛ = 3,84·106 м. Это расстояние приблизительно в 60 раз превышает радиус Земли RЗ. Следовательно, ускорение свободного падения aЛ, обусловленное земным притяжением, на орбите Луны составляет С таким ускорением, направленным к центру Земли, Луна движется по орбите. Следовательно, это ускорение является центростремительным ускорением. где T = 27,3 сут – период обращения Луны вокруг Земли. Совпадение результатов расчетов, выполненных разными способами, подтверждает предположение Ньютона о единой природе силы, удерживающей Луну на орбите, и силы тяжести. Собственное гравитационное поле Луны определяет ускорение свободного падения gЛ на ее поверхности. Масса Луны в 81 раз меньше массы Земли, а ее радиус приблизительно в 3,7 раза меньше радиуса Земли. Поэтому ускорение gЛ определится выражением В условиях такой слабой гравитации оказались космонавты, высадившиеся на Луне. Человек в таких условиях может совершать гигантские прыжки. Например, если человек в земных условиях подпрыгивает на высоту 1 м, то на Луне он мог бы подпрыгнуть на высоту более 6 м. Рассмотрим вопрос об искусственных спутниках Земли. Искусственные спутники Земли движутся за пределами земной атмосферы, и на них действуют только силы тяготения со стороны Земли. В зависимости от начальной скорости траектория космического тела может быть различной. Рассмотрим случай движения искусственного спутника по круговой околоземной орбите. Такие спутники летают на высотах порядка 200–300 км, и можно приближенно принять расстояние до центра Земли равным ее радиусу RЗ. Тогда центростремительное ускорение спутника, сообщаемое ему силами тяготения, приблизительно равно ускорению свободного падения g. Обозначим скорость спутника на околоземной орбите через υ1 – такая скорость называют первой космической скоростью. Используя кинематическую формулу для центростремительного ускорения, получим Двигаясь с такой скоростью, спутник облетал бы Землю за время На самом деле период обращения спутника по круговой орбите вблизи поверхности Земли несколько превышает указанное значение из-за отличия между радиусом реальной орбиты и радиусом Земли. Движение спутника можно рассматривать как свободное падение, подобное движению снарядов или баллистических ракет. Для спутников, движущихся по круговым траекториям на значительном удалении от Земли, земное притяжение ослабевает обратно пропорционально квадрату радиуса r траектории. Таким образом, на высоких орбитах скорость движения спутников меньше, чем на околоземной орбите. Период обращения спутника растет с увеличением радиуса орбиты. Нетрудно подсчитать, что при радиусе r орбиты, равном приблизительно 6,6 RЗ, период обращения спутника окажется равным 24 часам. Спутник с таким периодом обращения, запущенный в плоскости экватора, будет неподвижно висеть над некоторой точкой земной поверхности. Такие спутники используются в системах космической радиосвязи. Орбита с радиусом r = 6,6 RЗ называется геостационарной. Второй космической скоростью называется минимальная скорость, которую нужно сообщить космическому кораблю у поверхности Земли, чтобы он, преодолев земное притяжение, превратился в искусственный спутник Солнца (искусственная планета). Рисунок 5 иллюстрирует космические скорости. Если скорость космического корабля равна υ1 = 7.9·103 м/с и направлена параллельно поверхности Земли, то корабль будет двигаться по круговой орбите на небольшой высоте над Землей. При начальных скоростях, превышающих υ1, но меньших υ2 = 11,2·103 м/с, орбита корабля будет эллиптической. При начальной скорости υ2 корабль будет двигаться по параболе, а при еще большей начальной скорости – по гиперболе. Космические скорости Указаны скорости вблизи поверхности Земли: 1) υ = υ1 – круговая траектория; 2) υ1 < υ < υ2 – эллиптическая траектория; 3) υ = 11,1·103 м/с – сильно вытянутый эллипс; 4) υ = υ2 – параболическая траектория; 5) υ > υ2 – гиперболическая траектория; 6) траектория Луны Таким образом,мы выяснили, что все движения в Солнечной системе подчиняются закону всемирного тяготения Ньютона. Исходя из малой массы планет и тем более прочих тел Солнечной системы, можно приближенно считать, что движения в околосолнечном пространстве подчиняются законам Кеплера. Все тела движутся вокруг Солнца по эллиптическим орбитам, в одном из фокусов которых находится Солнце. Чем ближе к Солнцу небесное тело, тем быстрее его скорость движения по орбите (планета Плутон, самая далекая из известных, движется в 6 раз медленнее Земли). Тела могут двигаться и по разомкнутым орбитам: параболе или гиперболе. Это случается в том случае, если скорость тела равна или превышает значение второй космической скорости для Солнца на данном удалении от центрального светила. Если речь идет о спутнике планеты, то и космическую скорость надо рассчитывать относительно массы планеты и расстояния до ее центра.
| |
гравитация | Определение, физика и факты
гравитационная линза
Посмотреть все медиа
- Ключевые люди:
- Кип Торн Исаак Ньютон Галилео Джон Арчибальд Уилер Саймон Стевин
- Похожие темы:
- супергравитация масса точка Лагранжа Радиус Шварцшильда гравитационная аномалия
Просмотреть весь соответствующий контент →
Резюме
Прочтите краткий обзор этой темы
гравитация , также называемая гравитацией , в механике универсальная сила притяжения, действующая между всей материей. Это, безусловно, самая слабая из известных сил в природе, и поэтому она не играет никакой роли в определении внутренних свойств повседневного вещества. С другой стороны, благодаря своему большому охвату и универсальному действию он контролирует траектории тел в Солнечной системе и других местах во Вселенной, а также структуру и эволюцию звезд, галактик и всего космоса. На Земле все тела имеют вес или направленную вниз силу тяжести, пропорциональную их массе, которую оказывает на них масса Земли. Гравитация измеряется ускорением, которое она сообщает свободно падающим телам. У поверхности Земли ускорение свободного падения составляет около 90,8 метра (32 фута) в секунду за секунду. Таким образом, за каждую секунду нахождения объекта в свободном падении его скорость увеличивается примерно на 9,8 метра в секунду. На поверхности Луны ускорение свободно падающего тела составляет около 1,6 метра в секунду за секунду.
Это, безусловно, самая слабая из известных сил в природе, и поэтому она не играет никакой роли в определении внутренних свойств повседневного вещества. С другой стороны, благодаря своему большому охвату и универсальному действию он контролирует траектории тел в Солнечной системе и других местах во Вселенной, а также структуру и эволюцию звезд, галактик и всего космоса. На Земле все тела имеют вес или направленную вниз силу тяжести, пропорциональную их массе, которую оказывает на них масса Земли. Гравитация измеряется ускорением, которое она сообщает свободно падающим телам. У поверхности Земли ускорение свободного падения составляет около 90,8 метра (32 фута) в секунду за секунду. Таким образом, за каждую секунду нахождения объекта в свободном падении его скорость увеличивается примерно на 9,8 метра в секунду. На поверхности Луны ускорение свободно падающего тела составляет около 1,6 метра в секунду за секунду.
Понять концепцию гравитационной силы, используя теорию гравитации Ньютона
Посмотреть все видео к этой статье Работы Исаака Ньютона и Альберта Эйнштейна доминируют в развитии теории гравитации.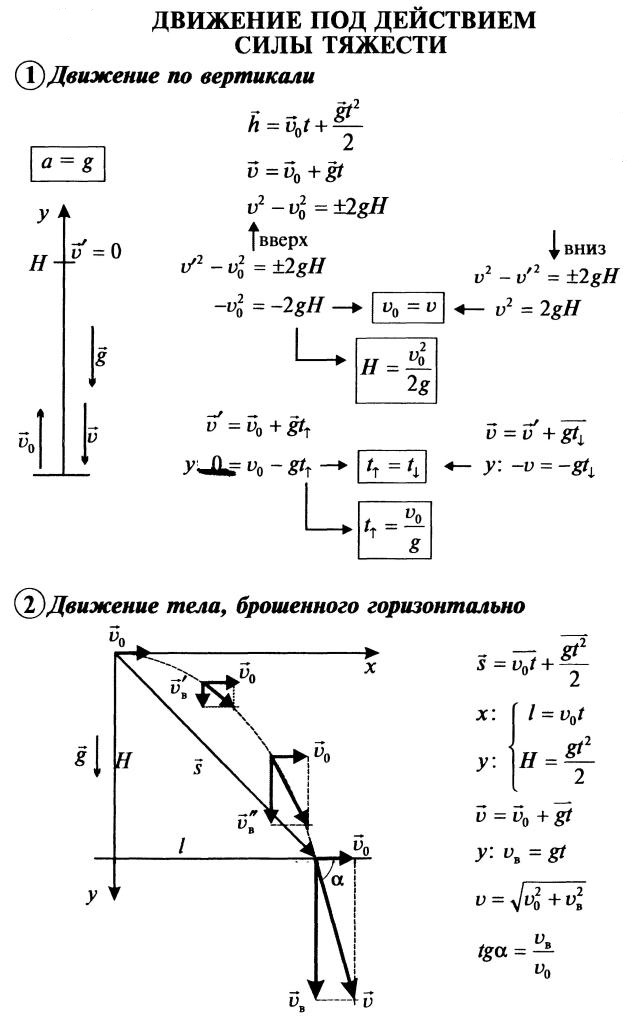 Классическая теория силы тяготения Ньютона господствовала с его 9 лет.0033 Principia , опубликованной в 1687 году, до работы Эйнштейна в начале 20 века. Теории Ньютона достаточно даже сегодня для всех приложений, кроме самых точных. Общая теория относительности Эйнштейна предсказывает лишь незначительные количественные отличия от ньютоновской теории, за исключением нескольких особых случаев. Основное значение теории Эйнштейна заключается в ее радикальном концептуальном отходе от классической теории и ее последствиях для дальнейшего развития физической мысли.
Классическая теория силы тяготения Ньютона господствовала с его 9 лет.0033 Principia , опубликованной в 1687 году, до работы Эйнштейна в начале 20 века. Теории Ньютона достаточно даже сегодня для всех приложений, кроме самых точных. Общая теория относительности Эйнштейна предсказывает лишь незначительные количественные отличия от ньютоновской теории, за исключением нескольких особых случаев. Основное значение теории Эйнштейна заключается в ее радикальном концептуальном отходе от классической теории и ее последствиях для дальнейшего развития физической мысли.
Запуск космических аппаратов и развитие исследований на них привели к значительному улучшению измерений гравитации вокруг Земли, других планет и Луны, а также в экспериментах по изучению природы гравитации.
Развитие теории гравитации
Ранние концепции
Ньютон утверждал, что движения небесных тел и свободное падение объектов на Земле определяются одной и той же силой. Классические греческие философы, с другой стороны, не считали, что небесные тела подвержены влиянию гравитации, поскольку наблюдалось, что тела следуют постоянно повторяющимся ненисходящим траекториям в небе. Таким образом, Аристотель считал, что каждое небесное тело следует определенному «естественному» движению, не подверженному влиянию внешних причин или факторов. Аристотель также считал, что массивные земные объекты обладают естественной тенденцией двигаться к центру Земли. Эти аристотелевские концепции преобладали на протяжении столетий вместе с двумя другими: что тело, движущееся с постоянной скоростью, требует постоянной силы, действующей на него, и эта сила должна быть приложена посредством контакта, а не взаимодействия на расстоянии. Эти идеи в основном держались до 16 и начала 17 веков, тем самым препятствуя пониманию истинных принципов движения и препятствуя развитию представлений о всемирном тяготении. Этот тупик начал меняться с появлением нескольких научных работ, посвященных проблеме земного и небесного движения, которые, в свою очередь, подготовили почву для более поздней теории тяготения Ньютона.
Таким образом, Аристотель считал, что каждое небесное тело следует определенному «естественному» движению, не подверженному влиянию внешних причин или факторов. Аристотель также считал, что массивные земные объекты обладают естественной тенденцией двигаться к центру Земли. Эти аристотелевские концепции преобладали на протяжении столетий вместе с двумя другими: что тело, движущееся с постоянной скоростью, требует постоянной силы, действующей на него, и эта сила должна быть приложена посредством контакта, а не взаимодействия на расстоянии. Эти идеи в основном держались до 16 и начала 17 веков, тем самым препятствуя пониманию истинных принципов движения и препятствуя развитию представлений о всемирном тяготении. Этот тупик начал меняться с появлением нескольких научных работ, посвященных проблеме земного и небесного движения, которые, в свою очередь, подготовили почву для более поздней теории тяготения Ньютона.
Тест «Британника»
Физика и законы природы
Какая сила замедляет движение? Каждому действию есть равное и противоположное что? В этом викторине по физике нет ничего, что E = mc было бы квадратным.
Немецкий астроном XVII века Иоганн Кеплер принял аргумент Николая Коперника (который восходит к Аристарху Самосскому) о том, что планеты вращаются вокруг Солнца, а не Земли. Используя улучшенные измерения движения планет, сделанные датским астрономом Тихо Браге в 16 веке, Кеплер описал планетарные орбиты с помощью простых геометрических и арифметических соотношений. Три количественных закона движения планет Кеплера таковы:
Планеты описывают эллиптические орбиты, один из фокусов которых занимает Солнце (фокус — это одна из двух точек внутри эллипса; любой луч, исходящий из одной из них, отражается от стороны эллипса и проходит через другой фокус) .
Линия, соединяющая планету с Солнцем, заметает равные площади за равные промежутки времени.
Квадрат периода обращения планеты пропорционален кубу ее среднего расстояния от Солнца.
В этот же период итальянский астроном и естествоиспытатель Галилео Галилей добился успехов в понимании «естественного» движения и простого ускоренного движения земных объектов. Он понял, что тела, на которые не действуют силы, продолжают двигаться бесконечно и что сила необходима для изменения движения, а не для поддержания постоянного движения. Изучая, как объекты падают на Землю, Галилей обнаружил, что движение происходит с постоянным ускорением. Он продемонстрировал, что расстояние, которое падающее тело проходит таким образом из состояния покоя, изменяется пропорционально квадрату времени. Как отмечалось выше, ускорение свободного падения на поверхности Земли составляет около 90,8 метра в секунду в секунду. Галилей был также первым, кто экспериментально показал, что тела падают с одинаковым ускорением независимо от их состава (слабый принцип эквивалентности).
Он понял, что тела, на которые не действуют силы, продолжают двигаться бесконечно и что сила необходима для изменения движения, а не для поддержания постоянного движения. Изучая, как объекты падают на Землю, Галилей обнаружил, что движение происходит с постоянным ускорением. Он продемонстрировал, что расстояние, которое падающее тело проходит таким образом из состояния покоя, изменяется пропорционально квадрату времени. Как отмечалось выше, ускорение свободного падения на поверхности Земли составляет около 90,8 метра в секунду в секунду. Галилей был также первым, кто экспериментально показал, что тела падают с одинаковым ускорением независимо от их состава (слабый принцип эквивалентности).
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Орбиты и гравитация
Орбиты и гравитация| Астрономия 1101: планеты в космос |
Ключевые идеи:
Закон падающих тел (Галилей)- Все падающие тела испытывают одинаковые гравитационные ускорение
- Сила притяжения между всеми парами массивные объекты
- Гравитационная сила пропорциональна массам, и
обратно пропорциональна квадрату расстояния
между ними.

- Первый закон: Орбиты равны конические сечения с центром масс двух тел в фокусе.
- Второй закон: сохранение углового момента.
- Обобщенный третий закон, зависящий от масс двух тел.
- Круговая скорость
- Скорость эвакуации
ПРИМЕЧАНИЕ:
Эта и следующая лекция, вероятно, являются наиболее математическими из всех лекции, которые будут прочитаны в этом классе. Я призываю вас всех прочтите эти заметки заранее и постарайтесь следовать приведенным в них аргументам. В будет легче следить за ходом лекции. [рвп]
Закон падающих тел
До своих телескопических работ Галилей выполнял фундаментальные исследование движения. Исследовал скорость падения тел, сбрасывая разные
гири или сдвигая их по наклонным плоскостям.
Закон падающих тел
- При отсутствии воздуха тяжелые предметы и легкие предметы падают с одинаковым постоянным ускорением.
Универсальное взаимное тяготение
Исаак Ньютон, в его Principia , сформулировал Закон о Универсальное взаимное тяготение:- Гравитация — это Привлекательная сила:
- Сближает массивные объекты.
- Гравитация — это Универсальная сила:
- Действует повсюду во Вселенной.
- Гравитация Взаимная сила:
- Работает между парами массивных объектов.
Гравитационная сила
Сила притяжения между любыми двумя объектами зависит только от:массы двух объектов:
- Более массивные объекты оказывают более сильное гравитационное воздействие.
расстояние между ними:
- Сила становится на сильнее по мере того, как два объекта приближаются друг к другу.

- Сила становится слабее по мере того, как два объекта удаляются друг от друга.
Оно не зависит от форм, цветов или композиций объекты.
- Сила гравитационного притяжения между любыми двумя массивных тел пропорциональна их массам и обратно пропорциональна квадрату расстояния между их центры.
Математически говоря, сила тяжести между двумя массивными тела это:
- Где:
- F = сила тяжести.
- M 1 = масса первого тела
- M 2 = масса второго тела
- d = расстояние между их центрами.
- G = Постоянная гравитационной силы
Постоянная силы гравитации
Силовая постоянная, G, представляет собой число, которое дает размер гравитационная связь между двумя массивными объектами.
G очень мало, в метрических единицах:
- G=6,7×10 -11 Ньютон-метр 2 / килограмм 2
- 4,41 Ньютона = 1 фунт
 Подобно Ньютону, Кавендиш ставил свои задачи так, чтобы G математически сокращалась. Мы будем делать то же самое на этом уроке, поэтому вам никогда не понадобится знать G на практике для экзаменов или домашних заданий.
Лишь намного позже (почти 75 лет спустя) его экспериментальные данные были использованы другими для получения значения G. Только во второй половине XIX в.века, что астрономам нужно было знать G, чтобы они могли, среди прочего, вычислять плотности небесных тел, таких как Луна и Солнце.]
Подобно Ньютону, Кавендиш ставил свои задачи так, чтобы G математически сокращалась. Мы будем делать то же самое на этом уроке, поэтому вам никогда не понадобится знать G на практике для экзаменов или домашних заданий.
Лишь намного позже (почти 75 лет спустя) его экспериментальные данные были использованы другими для получения значения G. Только во второй половине XIX в.века, что астрономам нужно было знать G, чтобы они могли, среди прочего, вычислять плотности небесных тел, таких как Луна и Солнце.]Падение яблока.
Встаньте на землю и бросьте яблоко.Какова сила Земли на яблоко?
- F = GM земля M яблоко /R земля 2
Каково ускорение яблока (второй закон Ньютона):
- a яблоко = F/M яблоко = GM земля /R земля 2 = 9,8 м/с 2
 Это означает, что ускорение свободного падения равно независимых от массы яблока, как показал Галилей
ранее.
Это означает, что ускорение свободного падения равно независимых от массы яблока, как показал Галилей
ранее.Равные и противоположные реакции
Но третий закон Ньютона утверждает, что все силы приходят в равными, но противоположными парамиКакую силу применяет яблоко в ответ на Землю?
- F = GM земля M яблоко /R земля 2
С какой скоростью Земля приближается к яблоку?
- a земля = F/M земля = GM яблоко /R земля 2
- a земля = a яблоко x (M яблоко /M земля )
Масса Земли
Мы можем напрямую измерить ускорение свободного падения на поверхности на Землю, сбрасывая предметы и определяя время их падения (например, как это было сделано по Галилею). Мы нашли- а = 9,8 м/с 2
Мы также можем измерить радиус Земли, используя геометрию (Эратосфен):
- R земля = 6378 километров = 6 378 000 метров
Объединив их вместе, используя формулу Ньютона для гравитационного Сила позволяет нам оценить массу Земли следующим образом:
Орбита Луны
Падающие яблоки — это одно, а как насчет Луны?- Что удерживает Луну на орбите вокруг Земли?
Закон инерции (Ньютон Первый закон движения) предсказывает:
- Если бы между
Луна и Земля, Луна будет двигаться по прямой при постоянной скорости .

- Отклоняется от прямолинейного пути сила тяжести .
Падение Луны
Какое расстояние Луна проходит вокруг Земли за 1 секунду? Какое расстояние падает яблоко на Землю за первую секунду? Ньютон также знал, что:- Луна находится примерно в 60 земных радиусах от Земли.
Суммируя цифры:
Луна:
- Расстояние, на которое Луна падает на Землю за 1 секунду: x Луна = 0,00136 метра
- Расстояние от Луны до центра Земли: d Луна = 60 R Земля
- Ускорение Луны: a луна = GM земля /d луна 2 = GM земля / (60R земля ) 2
Яблоко :
- Расстояние, на которое яблоко падает на Землю за 1 секунду: x яблоко = 4,9 метра
- Расстояние от яблока до центра Земли: d яблоко = 1 R земля
- Ускорение Apple: a яблоко = GM земля /d яблоко 2 = GM земля /R земля 2
Соотношение отклонений Яблока и Луны за 1 секунду отношение их ускорений:
Объединив всю имеющуюся у нас информацию, мы получим следующее:

Наблюдения против предсказания
Это правильно?
Ранее мы установили из наблюдений, что отклонения Луна и яблоко за 1 секунду это:
- x луна = 0,00136 метра
- x яблоко = 4,9 метра
Гравитация предсказывает, что
- x яблоко /3600 = 4,9 метра/3600 = 0,00136 метра!!
Соглашение по существу идеально!
Это показывает, что один и тот же закон всемирного тяготения применим к обоим яблоко и луна! Оба чувствуют гравитацию Земли в виде сила, которая становится слабее пропорционально квадрату их расстояния от центра земли.
Так почему же Луна
вращается вокруг Земли? Если Луна немного падает к Земле, как яблоко упала на поверхность, почему Луна движется вокруг Земли по орбите вместо того, чтобы упасть на нее?Чтобы ответить на этот вопрос, нужно сначала рассмотреть, что произошло бы, если бы не действовала гравитация:
- Вопрос :
- Какое расстояние пройдёт Луна по прямой за 1 секунду, если бы не действовала гравитация?
- Ответ :
- Около 1000 метров.

При этом движение Луны по этому прямолинейному пути также заставит его сместиться на 90 127 на 90 128 от Земли.
- Вопрос :
- На какое расстояние от Земли уйдет Луна за 1 во-вторых, если бы не действовала гравитация?
- Ответ :
- Около 0,00136 метра!
Таким образом, мы пришли к поразительному выводу:
- Луна действительно постоянно падает вокруг Земли!
Пока на первый взгляд падение яблока и орбита Луны
кажутся двумя совершенно разными явлениями, если рассматривать их в свете
законы движения Ньютона, на самом деле они являются различными проявлениями
тоже самое! Падение Луны вокруг Земли такое же
движения, как падение яблока на Землю. Оба описаны
одни и те же три закона движения, и оба испытывают гравитационную силу
описывается одним и тем же универсальным законом силы.
Оба описаны
одни и те же три закона движения, и оба испытывают гравитационную силу
описывается одним и тем же универсальным законом силы.
Универсальная гравитация
Закон всемирного тяготения Универсальный :- Управляет падением яблока на Землю.
- Управляет падением Луны вокруг Земли.
- Управляет падением системы Земля/Луна вокруг Солнца.
- Управляет падением Солнца вокруг центра Млечный путь.
- Управляет падением галактик Млечный Путь и Андромеды на их взаимной орбите…
Новый взгляд на законы Кеплера
Законы движения планет Кеплера заключаются в следующем:
- Первый закон:
- Планеты вращаются по эллипсам с Солнцем в одном из фокусов.
- Второй закон:
- Планета за равное время заметает равные площади.
- Третий закон:
- Квадрат периода пропорционален размеру
большая полуось в кубе.

- Выражается математически как: P 2 =a 3 , для P в годах и a в AU.
Обобщение Ньютона
Ньютон показал, что законы Кеплера можно вывести из
- Три закона движения
- Закон всемирного тяготения.
Кроме того, Ньютон обобщил законы, применимые к любому два тела, движущиеся под действием взаимного тяготения. За например, эти законы в равной степени применимы к
- Луна на орбите Земли.
- Космический зонд на орбите Луны.
- Две звезды вращаются вокруг друг друга.
- Форма орбиты – коническое сечение с центр масс в одном фокусе.
Формы орбит — конические сечения:
- Кривые, полученные при разрезании конуса плоскостью.
- Окружности, эллипсы, параболы и гиперболы
Центр масс находится в фокусе:
- Строго говоря, это не просто Земля, вращающаяся вокруг Солнца.
 Земля и Солнце вращаются вокруг друг друга на оборотов вокруг их
взаимный центр масс.
Земля и Солнце вращаются вокруг друг друга на оборотов вокруг их
взаимный центр масс.
Кривые конического сечения
Это кривые, образованные пересечением конуса и плоскости. разрезая его под разными углами.
Конические кривые делятся на два семейства:
Замкнутые кривые:
- Эллипсы
- Окружности , которые являются частным случаем эллипса с e=0
- Эти орбиты связаны : объекты будут вращаться вечно вокруг родительского тела.
Открытые кривые:
- Гипербола
- Параболы , являющиеся частным случаем гиперболы
- Эти орбиты несвязаны : объекты будут проходить мимо родительского тела только один раз, а затем убежать от гравитации родительского тела.
 скорость . Есть две особые скорости, представляющие особый интерес…
скорость . Есть две особые скорости, представляющие особый интерес…Скорость, необходимая для поддержания круговой орбиты с заданным радиусом r вокруг массивное тело, М:
- Если ваша скорость меньше v C на вашем текущем расстоянии, ваша орбита будет эллипсом на 90 710 меньше, чем круговая орбита на 90 711.
- Если ваша скорость чуть больше v C на ваш текущий расстояние, ваша орбита будет эллипсом в 90 710 больше, чем 90 711 круга. орбита,
- Однако в какой-то момент ваша скорость может стать достаточно большой, чтобы вырваться на свободу и сбежать…
Это минимальная скорость, необходимая для преодоления гравитации тела масса M, начиная с расстояния r от него:
 Кроме того, строго говоря, объект никогда не «убегает» или «освобождается» от гравитации другого объекта, он просто становится несвязанным и движется по траектории, которая никогда не повернется к более крупному объекту, как по замкнутой или «связанной» орбите.
Кроме того, строго говоря, объект никогда не «убегает» или «освобождается» от гравитации другого объекта, он просто становится несвязанным и движется по траектории, которая никогда не повернется к более крупному объекту, как по замкнутой или «связанной» орбите.На поверхности Земли:
- v С = 7,9км/сек (28 400 км/час)
- v E = 11,2 км/с (40 300 км/ч)
Орбитальные семейства
С этими двумя скоростями (круговой и убегающей) мы можем видеть, как различные типы замкнутых и открытых орбит конического сечения вокруг большой центральной возникает массивное тело. Все показанные ниже орбиты начинаются с общая точка P, отмеченная справа (где пересекаются все 5 кривых), но с разной скоростью:
- [Нажмите на изображение, чтобы просмотреть полноразмерную версию (9к GIF)] (Графика Р. Погге)
- Если орбитальная скорость точно равна круговой скорости в точке P (V C ), орбита будет Окружность проходящий через P с центром в центральном теле (красная кривая).

- Если орбитальная скорость медленнее, чем V C в точке P, орбита будет Эллипс меньше окружности, проходящей через P с центральным телом в дальнем фокусе (синяя кривая).
- Если орбитальная скорость быстрее чем V C в P, но меньше, чем скорость убегания в P (V E ), тогда орбита будет эллипсом на больше, чем круговая орбита, проходящая через точку P, с центральное тело в ближнем фокусе (зеленая кривая).
- Если орбитальная скорость равна , то скорость убегания равна в P (V E ), орбита будет открытой Парабола (пурпурная кривая).
- Если орбитальная скорость на больше, чем скорость убегания от P, орбита будет гиперболой (черная кривая). Чем больше скорость, тем «площе» (более открытая) гиперболическая орбита.
Центр масс
Два объекта вращаются вокруг своего центра масс :
- Точка равновесия между двумя массами
[Нажмите на изображение, чтобы просмотреть его в полном размере (5Kb)] (Графика Р.
 Погге)
Погге)- Большая полуось: a = a 1 + a 2 85
- Relative positions: a 2 / a 1 = M 1 / M 2
- М солнце = 2 х 10 30 кг
- M земля = 6 x 10 24 кг
Из соотношения баланса расстояния Солнца и Земли от их взаимный центр масс связаны с размером полубольшого ось орбиты Земли (а) и отношение масс:
- a солнце + a земля = 1 а.е. = 1,5 x 10 8 км
- a солнце /a земля = M земля /M солнце = 3 х 10 -6
После несложных алгебраических вычислений (сделай это!), находим:
- a солнце = 450 км
Поскольку радиус Солнца составляет 700 000 км, это означает, что
центр масс системы Земля-Солнце находится на глубине внутри Солнце.
- Орбитальное движение сохраняет угловой момент.
Это не очень похоже на «равные площади за равное время», но на самом деле это одно и то же.
Угловой момент:
- L = mvr = константа
- Где:
- м = масса,
- v = скорость,
- r = расстояние от центра масс.
- v = скорость,
Угловой момент и равные площади
Угловой момент равен с сохранением , что означает, что L является константа .При изменении расстояния скорость должна измениться на компенсировать так, чтобы L оставался постоянным:
Рядом с перигелием:
- Планета на ближе к Солнцу, поэтому r на меньше .

- Скорость относительно должна быть пропорционально выше для компенсации.
Рядом с Афелионом:
- Планета на дальше на от Солнца, поэтому r на больше .
- Скорость относительно должна быть пропорционально медленнее для компенсации.
Знакомый пример того же принципа в работе — фигуристка. делать вращение. В «вертикальном вращении» фигурист стоит на одной ноге с руки вытянуты и вращаются вокруг оси вверх/вниз. Спин ускоряется фигуристом, рисующим на руках. Втягивая его/ее руки, они перемещают массу ближе к центру своего тела, а сохранение углового момента требует, чтобы они вращались быстрее.
Обобщение Ньютоном кеплеровского 3 rd Закон:
- Где:
- P = период обращения
- a = большая полуось орбиты
- M 1 = масса первого тела
- M 2 = масса второго тела
- a = большая полуось орбиты
Третий закон для каждого тела
Пропорциональность между квадратом периода и куб большой полуоси теперь зависит от масс г. два тела.
два тела.Для планет, вращающихся вокруг Солнца, M солнце намного больше любого планета (даже Юпитер, в 1/1000 th M солнце ), что мы восстановить кеплеровскую версию третьего закона из более общей ньютоновской форма:
Обратите внимание, что константа пропорциональности одинакова для всех планет (в хорошем приближении, безусловно, в пределах данных Кеплера от Тихо).
В версии Кеплера константа пропорциональности получается равной 1,0 если мы используем единицы лет для P и AU для большой полуоси, a. Пока вычислительно удобен, он скрывает лежащую в основе зависимость от массы Солнца из поля зрения. Проблема с эмпирическими законами, такими как законы Кеплера. формулировка, заключается в том, что они показывают только поверхность, а не важные детали лежащие в их основе.
Измерительные массы
Обобщенная форма третьего закона Кеплера Ньютона дает нам способ измерения массы по орбитальному движению!
Например, мы можем определить массу Солнца, используя период и размер орбиты Земли:
- P земля = 1 год = 3,156 x 10 7 секунд
- a земля = 1 а.
 е. = 1,496 x 10 11 метров
е. = 1,496 x 10 11 метров - a земля = 1 а.
Использование ньютоновской формы третьего закона Кеплера для Солнечной системы выше мы видим, что как только мы знаем P и a (G и pi являются константами), единственная неизвестная масса Солнца, которую можно решить для легко после небольшой легкой алгебры:
Универсальный метод измерения массы
Обобщенная форма третьего закона Кеплера дает нам мощное инструмент для измерения массы объектов путем измерения периодов и размеры их орбит. Например:
Мы можем измерить массу Юпитера по орбитам Галилеевы луны, начиная с M Юпитер >>M луны
- Найти M Юпитер = 300 M земля
Мы можем измерить общую массу системы Земля и Луна.
- Земля всего в ~81 раз массивнее Луны, так что вы необходимо использовать полную формулу.
- Получить массу Земли самостоятельно (например, наш эксперимент с падающими телами из вчерашней лекции).
Мы можем измерить массы двойных звезд, используя полный формуле и наблюдая за параметрами их орбиты (вы увидите это сделано в астрономии 162).
Почему планетарных движений
Законы Кеплера описывают движение:
- Достигнут методом проб и ошибок и некоторых смутных представлений о небесных гармониях
- Только описывать движения, не объясняя, почему они двигаться таким образом.
Ньютон дает объяснение:
- Законы Кеплера являются естественным следствием трех законов Ньютона. Движение и его закон всемирного тяготения.
 Мы можем предсказывать новые явления или понимать странности в
движения (эти законы дают нам основу для интерпретации данных), и
мы можем буквально использовать их для управления космическими кораблями через Солнечную систему.
Мы можем предсказывать новые явления или понимать странности в
движения (эти законы дают нам основу для интерпретации данных), и
мы можем буквально использовать их для управления космическими кораблями через Солнечную систему.Обновлено: 2014 г., Тодд А. Томпсон
Copyright Richard W. Pogge, Все права защищены.
25.2: Планетарные орбиты — Физика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 25590
- Питер Дурмашкин
- Массачусетский технологический институт через MIT OpenCourseWare 6
Теперь мы начинаем изучение проблемы Кеплера. Найдем уравнение движения для движения двух тел, взаимодействующих через силу тяжести (задача двух тел), используя как силовые методы, так и законы сохранения.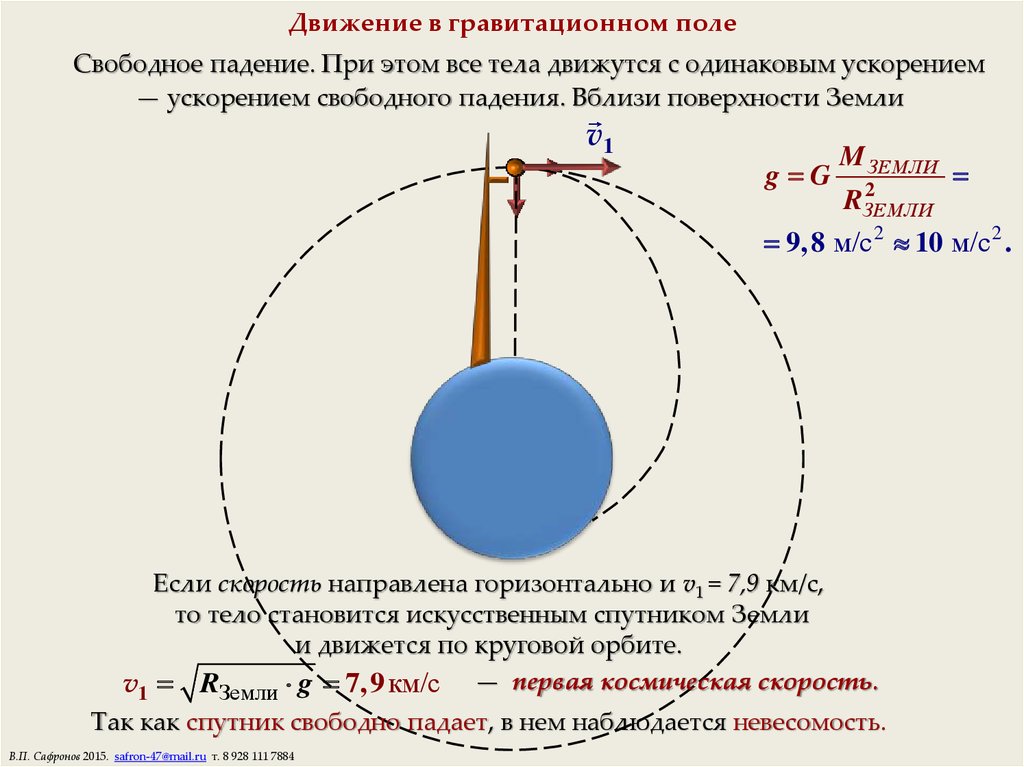
Мы начнем с того, что покажем, как движение двух тел, взаимодействующих через гравитационную силу (задача двух тел), математически эквивалентно движению одиночного тела под действием внешней центральной гравитационной силы, где масса одиночного тела равна приведенная масса \(\mu\),
\[\frac{1}{\mu}=\frac{1}{m_{1}}+\frac{1}{m_{2}} \Rightarrow \mu=\frac{m_{1} m_ {2}}{m_{1}+m_{2}} \nonumber \]
Решив движение редуцированного тела в этой эквивалентной задаче одного тела, мы можем вернуться к реальной задаче двух тел и решить для фактического движения двух исходных тел. Приведенная масса была введена в Главе 13 Приложения А к этим примечаниям. В этом приложении используются аналогичные, но немного отличающиеся от используемых в этой главе обозначения.
Рассмотрим гравитационное взаимодействие двух тел с массами m и 1 м2, показанное на рис. 25.1.
Рис. 25.1 Гравитационная сила между двумя телами Выберите систему координат с выбором начала координат так, чтобы тело 1 имело положение \(\overrightarrow{\mathbf{r}}_{1}\), а тело 2 имело положение \(\overrightarrow {\mathbf{r}}_{2}\) (рис. 25.2). Вектор относительного положения \(\overrightarrow{\mathbf{r}}\), указывающий от тела 2 к телу 1, равен \(\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_{1} -\overrightarrow{\mathbf{r}}_{2}\) Обозначим величину \(\overrightarrow{\mathbf{r}} \text {через }|\overrightarrow{\mathbf{r}}|=r \), где r — расстояние между телами, а \(\hat{\mathbf{r}}\) — единичный вектор, указывающий от тела 2 к телу 1, так что \(\overrightarrow{\mathbf{r} } = г \ шляпа {\ mathbf {г}} \). 9{2}}
25.2). Вектор относительного положения \(\overrightarrow{\mathbf{r}}\), указывающий от тела 2 к телу 1, равен \(\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_{1} -\overrightarrow{\mathbf{r}}_{2}\) Обозначим величину \(\overrightarrow{\mathbf{r}} \text {через }|\overrightarrow{\mathbf{r}}|=r \), где r — расстояние между телами, а \(\hat{\mathbf{r}}\) — единичный вектор, указывающий от тела 2 к телу 1, так что \(\overrightarrow{\mathbf{r} } = г \ шляпа {\ mathbf {г}} \). 9{2}}
\end{array} \nonumber \]
где \(\overrightarrow{\mathbf{F}}_{2,1}\) определяется уравнением (25.2.2).
Наш результат имеет специальную интерпретацию с использованием второго закона Ньютона. Пусть \(\mu\) — масса отдельного тела с вектором положения \(\overrightarrow{\mathbf{r}}=r \hat{\mathbf{r}}\) относительно начала координат O , где \ (\ hat{\mathbf{r}}\) — единичный вектор, указывающий из начала координат O на отдельное тело. Тогда уравнение движения, уравнение (25.2.10), подразумевает, что отдельное тело массы \(\mu\) находится под влиянием притягивающей гравитационной силы, направленной к началу координат.



 Движение тела под действием силы тяжести
Движение тела под действием силы тяжести По его гипотезе между всеми телами Вселенной действуют силы притяжения (гравитационные силы), направленные по линии, соединяющей центры масс. У тела в виде однородного шара центр масс совпадает с центром шара.
По его гипотезе между всеми телами Вселенной действуют силы притяжения (гравитационные силы), направленные по линии, соединяющей центры масс. У тела в виде однородного шара центр масс совпадает с центром шара.
 Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними:
Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними:
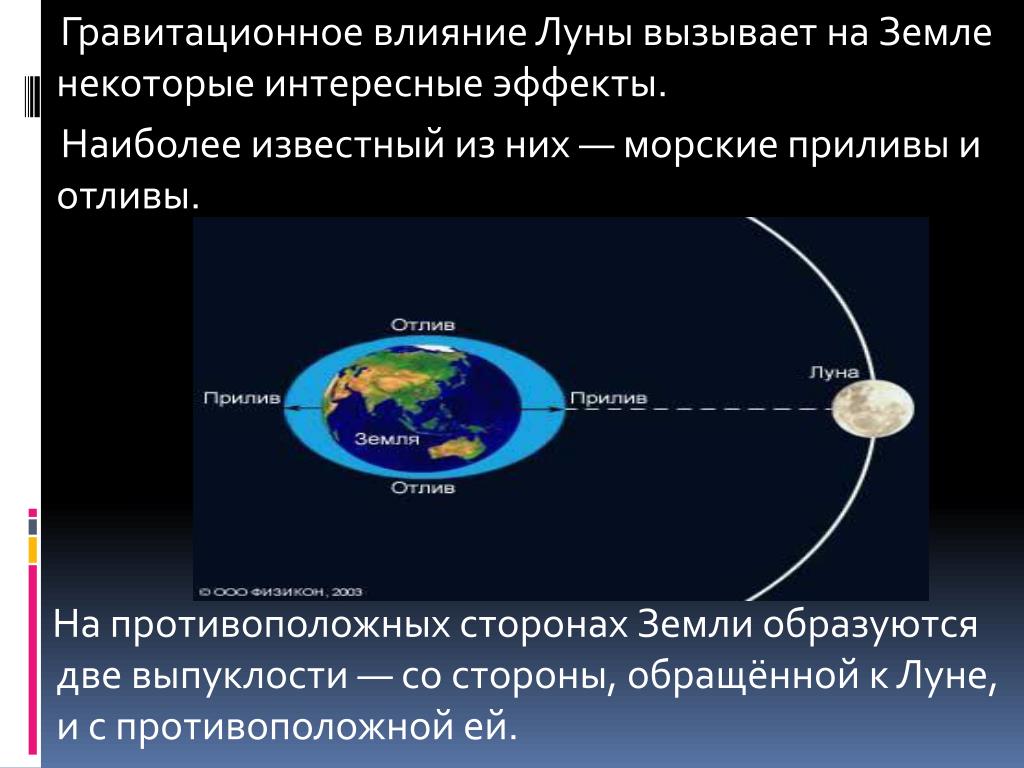

 Рисунок иллюстрирует изменение силы тяготения, действующей на космонавта в космическом корабле при его удалении от Земли. Сила, с которой космонавт притягивается к Земле вблизи ее поверхности, принята равной 700 Н.
Рисунок иллюстрирует изменение силы тяготения, действующей на космонавта в космическом корабле при его удалении от Земли. Сила, с которой космонавт притягивается к Земле вблизи ее поверхности, принята равной 700 Н.
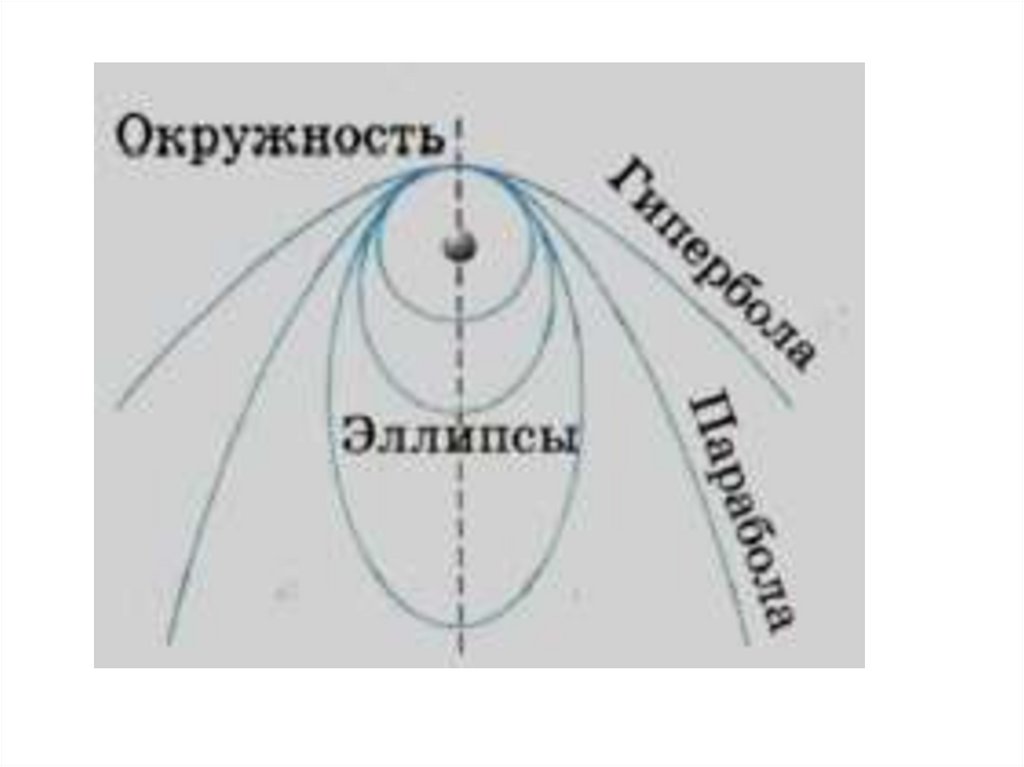 Собственное гравитационное поле Луны определяет ускорение свободного падения gл на ее поверхности. Масса Луны в 81 раз меньше массы Земли, а ее радиус приблизительно в 3,7 раза меньше радиуса Земли. Поэтому ускорение gл определится выражением:
Собственное гравитационное поле Луны определяет ускорение свободного падения gл на ее поверхности. Масса Луны в 81 раз меньше массы Земли, а ее радиус приблизительно в 3,7 раза меньше радиуса Земли. Поэтому ускорение gл определится выражением:

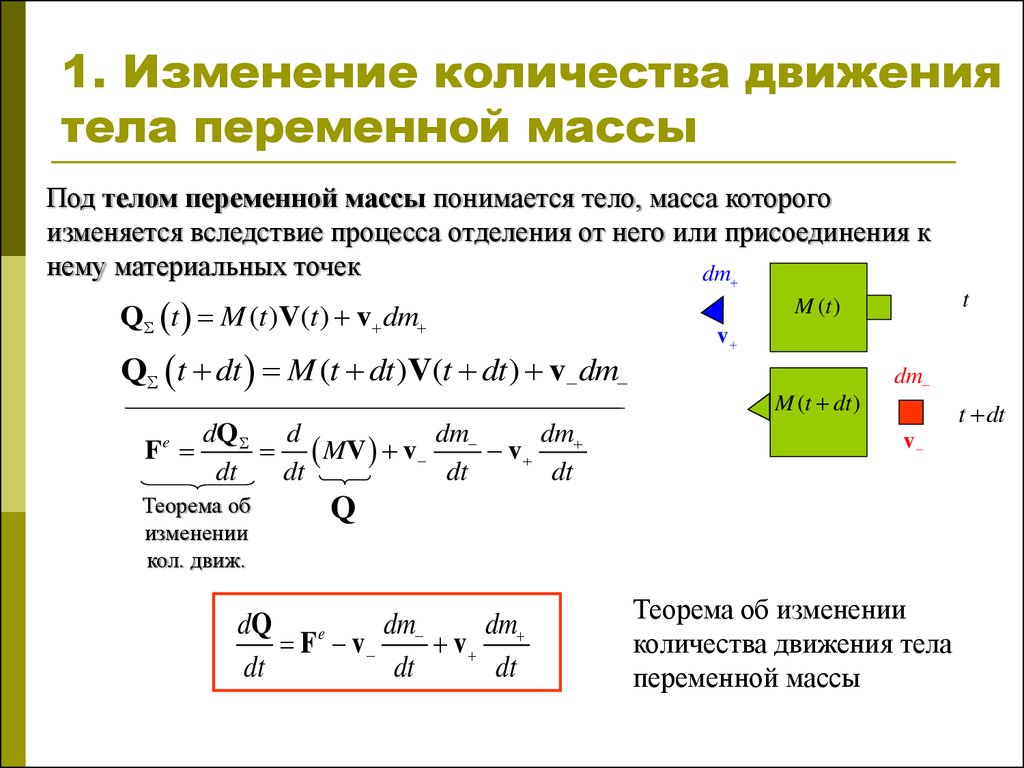
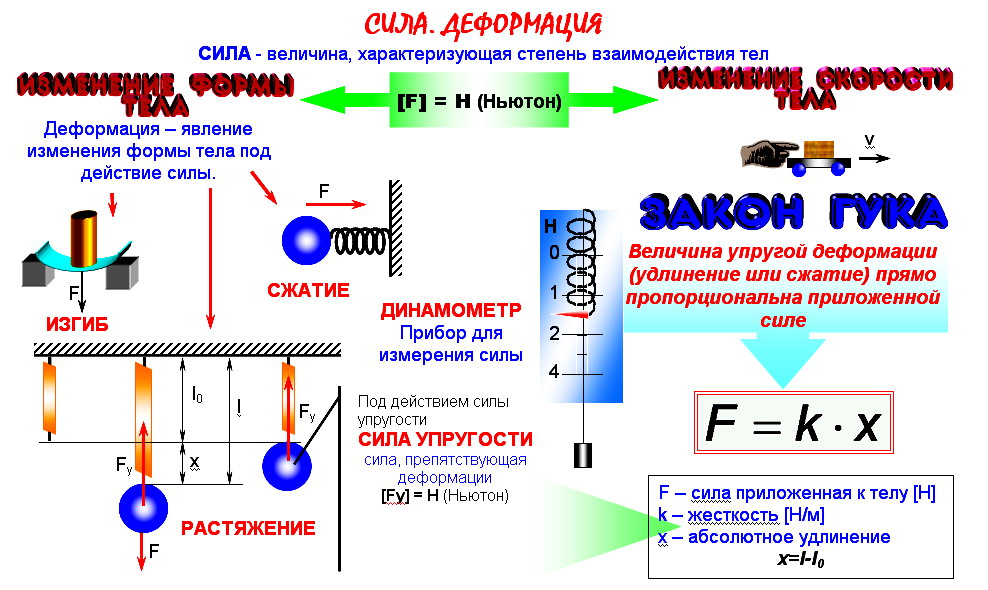 И в этом случае его движение будет описываться законами Ньютона, только теперь они применяются к телу, движущемуся под воздействием силы тяжести и обладающему некой начальной скоростью в горизонтальной плоскости. Теперь, раз за разом заряжая в пушку всё более тяжелое ядро и стреляя, вы обнаружите, что, поскольку каждое следующее ядро вылетает из ствола с большей начальной скоростью, ядра падают всё дальше и дальше от подножия скалы.
И в этом случае его движение будет описываться законами Ньютона, только теперь они применяются к телу, движущемуся под воздействием силы тяжести и обладающему некой начальной скоростью в горизонтальной плоскости. Теперь, раз за разом заряжая в пушку всё более тяжелое ядро и стреляя, вы обнаружите, что, поскольку каждое следующее ядро вылетает из ствола с большей начальной скоростью, ядра падают всё дальше и дальше от подножия скалы.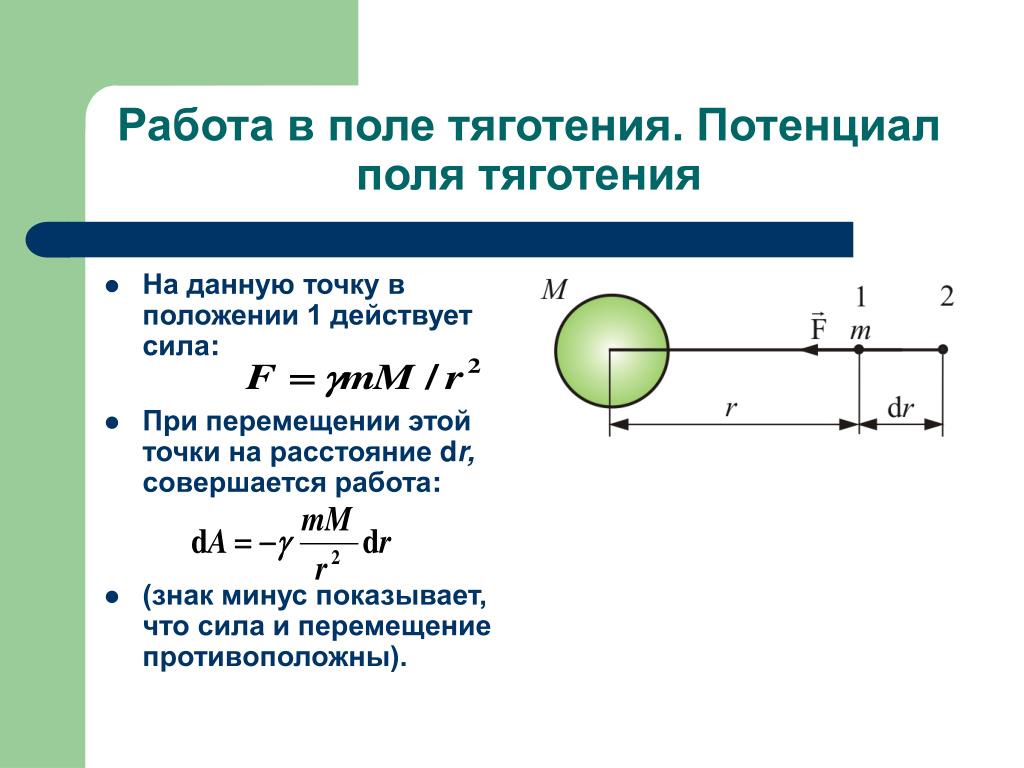
 Его можно рассчитать по кинематической формуле для центростремительного ускорения
Его можно рассчитать по кинематической формуле для центростремительного ускорения
 Различие заключается только в том, что скорость спутника настолько велика, что радиус кривизны его траектории равен радиусу Земли.
Различие заключается только в том, что скорость спутника настолько велика, что радиус кривизны его траектории равен радиусу Земли. При этом корабль будет удаляться от Земли по параболической траектории.
При этом корабль будет удаляться от Земли по параболической траектории.




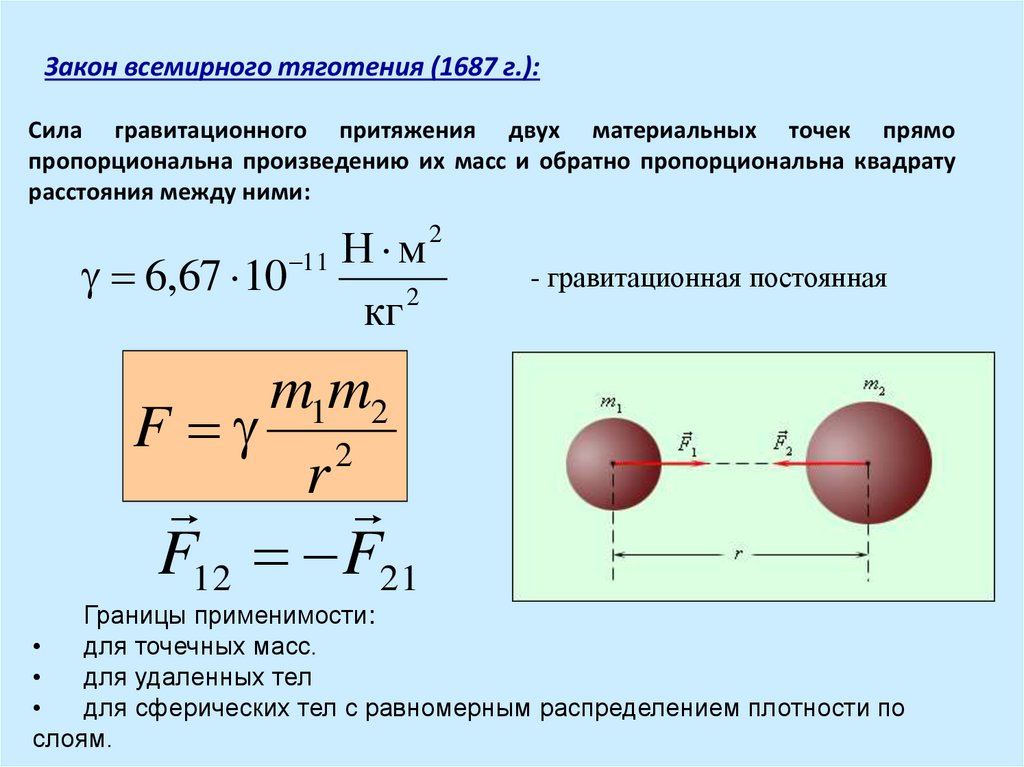
 Земля и Солнце вращаются вокруг друг друга на оборотов вокруг их
взаимный центр масс.
Земля и Солнце вращаются вокруг друг друга на оборотов вокруг их
взаимный центр масс.

 е. = 1,496 x 10 11 метров
е. = 1,496 x 10 11 метров