| введение физические величины библиотека ресурсы |
|
Заряд на обкладках конденсатора формула
Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.
В чем измеряется емкость конденсатора
Одной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства.
Для измерения емкости применяется единица – фарада. Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны. Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме. Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q – заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.
Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме. Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q – заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.
Для расчетов емкости плоского конденсатора используется формула:
в которой ε = 8,854187817 х 10 -12 ф/м представляет собой постоянную величину. Прочие величины: ε – является диэлектрической проницаемостью диэлектрика, находящегося между обкладками, S – означает площадь обкладки, а d – зазор между обкладками.
Формула энергии конденсатора
С емкостью самым тесным образом связана другая величина, известная как энергия заряженного конденсатора. После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.
С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.
В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора. Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами. Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой.
Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.
Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed. Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде: W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: Wэл = CU 2 /2.
Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде: W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: Wэл = CU 2 /2.
Формула заряда конденсатора
Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: Uc = E.
Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.
В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).
Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома Iзар = Е/Ri, поскольку к сопротивлению Ri приложена вся ЭДС генератора.
Формула тока утечки конденсатора
Ток утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R. Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.
Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.
Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки. В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции. В результате нарушается основная функция конденсатора – способность получать и сохранять заряд электрического тока.
Основная формула для расчета выглядит следующим образом: Iут = U/Rd, где Iут, – это ток утечки, U – напряжение, прилагаемое к конденсатору, а Rd – сопротивление изоляции.
По назначению конденсатор можно сравнить с батарейкой. Но имеется принципиальное отличие в работе данных элементов. Существуют отличия в предельной емкости и скорости зарядки конденсатора и батарейки.
Существуют отличия в предельной емкости и скорости зарядки конденсатора и батарейки.
Формула заряда конденсатора
Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:
где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками.
Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.
Заряд на пластинах плоского конденсатора равен:
где – электрическая постоянная; – площадь каждой (или наименьшей) пластины; – расстояние между пластинами; – диэлектрическая проницаемость диэлектрика, который находится между пластинами конденсатора.
Заряд на обкладках цилиндрического конденсатора вычисляется при помощи формулы:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.
Заряд на обкладках сферического конденсатора найдем как:
где – радиусы обкладок конденсатора.
Заряд конденсатора связан с энергией поля (W) внутри него:
Из формулы (6) следует, что заряд можно выразить как:
Рассмотрим последовательное соединение из N конденсаторов ( рис. 1).
Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении, обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды.
При параллельном соединении конденсаторов (рис.2), соединяют обкладки, имеющие заряды одного знака. Суммарный заряд соединения (q) равен сумме зарядов конденсаторов.
Примеры решения задач по теме «Заряд конденсатора»
| Задание | Каковы заряды на обкладках конденсаторов, если они имеют емкости Ф и Ф, соединены последовательно и присоединены к батарее с ЭДС равной В (рис.3)? Чему равен суммарный заряд соединения? |
Заряд на первом конденсаторе при этом равен:
Заряд на обкладках второго конденсатора:
Суммарный заряд системы можно найти как:
Тогда суммарный заряд равен:
| Задание | Емкость пускового устройства электрического двигателя равна C. Энергии имеющейся в конденсаторе достаточно для того чтобы поднять груз массы m на высоту h. Чему равен заряд конденсатора? Энергии имеющейся в конденсаторе достаточно для того чтобы поднять груз массы m на высоту h. Чему равен заряд конденсатора? |
| Решение | При поднятии груза на высоту h происходит переход энергии поля конденсатора () в потенциальную энергию тела (), поднятого над Землей, поэтому запишем: |
Энергию найдем как:
Энергию электрического поля конденсатора будет удобнее выразить:
Подставим в выражение (2.1) правые части (2.2) и (2.3), имеем:
Конденсатор – это совокупность двух любых проводников, заряды которых одинаковы по значению и противоположны по знаку.
Его конфигурация говорит о том, что поле, созданное зарядами, локализовано между обкладками. Тогда можно записать формулу электроемкости конденсатора:
C = q φ 1 – φ 2 = q U .
Значением φ 1 – φ 2 = U обозначают разность потенциалов, называемую напряжением, то есть U . По определению емкость положительна. Она зависит только от размерностей обкладок конденсатора их взаиморасположения и диэлектрика.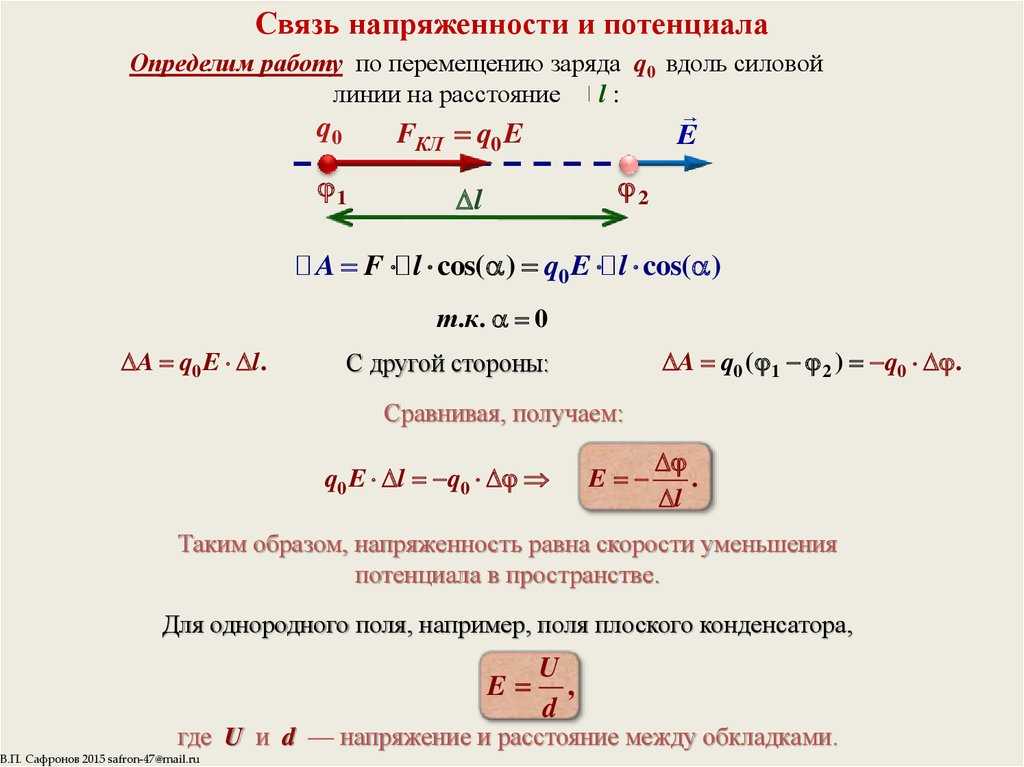 Ее форма и место должны минимизировать воздействие внешнего поля на внутреннее. Силовые линии конденсатора начинаются на проводнике с положительным зарядом, а заканчиваются с отрицательным. Конденсатор может являться проводником, помещенным в полость, окруженным замкнутой оболочкой.
Ее форма и место должны минимизировать воздействие внешнего поля на внутреннее. Силовые линии конденсатора начинаются на проводнике с положительным зарядом, а заканчиваются с отрицательным. Конденсатор может являться проводником, помещенным в полость, окруженным замкнутой оболочкой.
Выделяют три большие группы: плоские, сферические, цилиндрические. Чтобы найти емкость, необходимо обратиться к определению напряжения конденсатора с известными значениями зарядов на обкладках.
Плоский конденсатор
Плоский конденсатор – это две противоположно заряженные пластины, которые разделены тонким слоем диэлектрика, как показано на рисунке 1 .
Формула для расчета электроемкости записывается как
C = ε ε 0 S d , где S является площадью обкладки, d – расстоянием между ними, ε – диэлектрической проницаемостью вещества. Меньшее значение d способствует большему совпадению расчетной емкости конденсатора с реальной.
При известной электроемкости конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равняется d i , вычисление диэлектрической проницаемости этого слоя ε i выполняется, исходя из формулы:
C = ε 0 S d 1 ε 1 + d 2 ε 2 + . . . + d N ε N .
. . + d N ε N .
Сферический конденсатор
Когда проводник имеет форму шара или сферы, тогда внешняя замкнутая оболочка является концентрической сферой, это означает, что конденсатор сферический.
Он состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком, как показано на рисунке 2 . Емкость рассчитывается по формуле:
C = 4 π ε ε 0 R 1 R 2 R 2 – R 1 , где R 1 и R 2 являются радиусами обкладок.
Цилиндрический конденсатор
Емкость цилиндрического конденсатора равняется:
C = 2 πεε 0 l ln R 2 R 1 , где l – высота цилиндров, R 1 и R 2 – радиусы обкладок. Данный вид конденсатора имеет две соосные поверхности проводящих цилиндрических поверхности, как показано на рисунке 3 .
Важной характеристикой конденсаторов считается пробивное напряжение – напряжение, при котором происходит электрический разряд через слой диэлектрика.
U m a x находится от зависимости от толщины слоя и свойств диэлектрика, конфигурации конденсатора.
Электроемкость плоского конденсатора. Формулы
Кроме отдельных конденсаторов используются их соединения. Наличие параллельного соединения конденсаторов применяют для увеличения его емкости. Тогда поиск результирующей емкости соединения сводится к записи суммы C i , где C i – это емкость конденсатора с номером i :
При последовательном соединении конденсаторов суммарная емкость соединения всегда будет по значению меньше, чем минимальная любого конденсатора, входящего в систему. Для расчета результирующей емкости следует сложить величины, обратные к емкостям отдельных конденсаторов:
Произвести вычисление емкости плоского конденсатора при известной площади обкладок
1 с м 2 с расстоянием между ними 1 м м . Пространство между обкладками находится в вакууме.
Решение
Чтобы рассчитать электроемкость конденсатора, применяется формула:
ε = 1 , ε 0 = 8 , 85 · 10 – 12 Ф м ; S = 1 с м 2 = 10 – 4 м 2 ; d = 1 м м = 10 – 3 м .
Подставим числовые выражения и вычислим:
C = 8 , 85 · 10 – 12 · 10 – 4 10 – 3 = 8 , 85 · 10 – 13 ( Ф ) .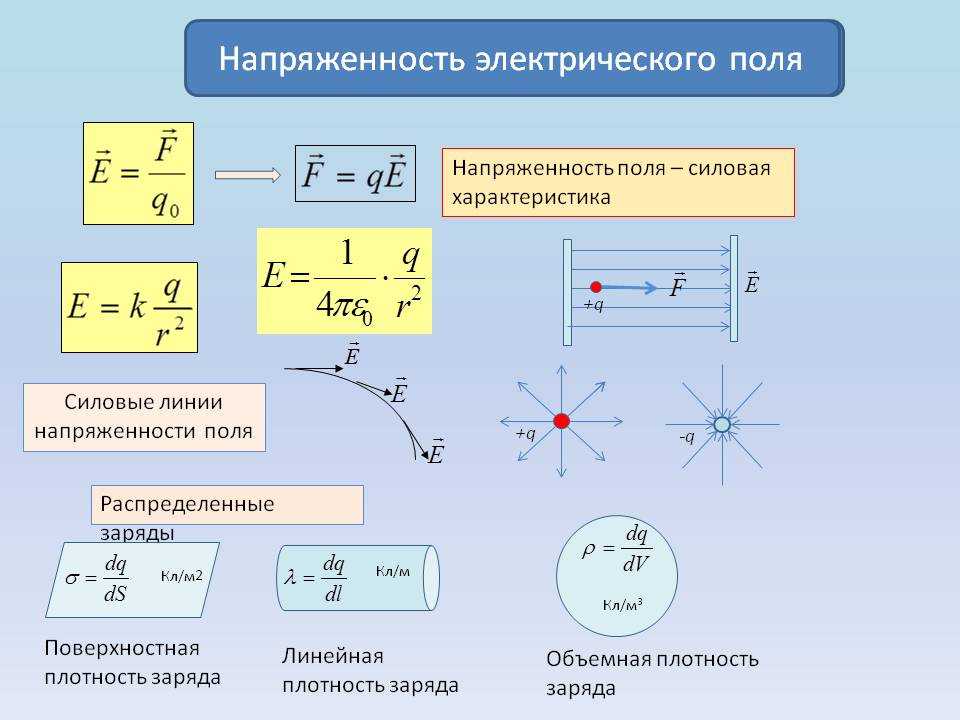
Ответ: C ≈ 0 , 9 п Ф .
Найти напряженность электростатического поля у сферического конденсатора на расстоянии x = 1 с м = 10 – 2 м от поверхности внутренней обкладки при внутреннем радиусе обкладки, равном R 1 = 1 с м = 10 – 2 м , внешнем – R 2 = 3 с м = 3 · 10 – 2 м . Значение напряжения – 10 3 В .
Решение
Производящая заряженная сфера создает напряженность поля. Его значение вычисляется по формуле:
E = 1 4 π ε ε 0 q r 2 , где q обозначают заряд внутренней сферы, r = R 1 + x – расстояние от центра сферы.
Нахождение заряда предполагает применение определения емкости конденсатора С:
Для сферического конденсатора предусмотрена формула вида
C = 4 π ε ε 0 R 1 R 2 R 2 – R 1 с радиусами обкладок R 1 и R 2 .
Производим подстановку выражений для получения искомой напряженности:
E = 1 4 πεε 0 U ( x + R 1 ) 2 4 πεε 0 R 1 R 2 R 2 – R 1 = U ( x + R 1 ) 2 R 1 R 2 R 2 – R 1 .
Данные представлены в системе С И , поэтому достаточно заменить буквы числовыми выражениями:
E = 10 3 ( 1 + 1 ) 2 · 10 – 4 · 10 – 2 · 3 · 10 – 2 3 · 10 – 2 – 10 – 2 = 3 · 10 – 1 8 · 10 – 6 = 3 , 45 · 10 4 В м .
Ответ: E = 3 , 45 · 10 4 В м .
Заряд конденсатора
Конденсаторы часто применяются в электрических схемах, помогая трансформировать электросигнал под определенные характеристики. Используя их основное свойство — накапливать электрический заряд, можно регулировать прохождение тока по цепи, убирать нежелательные пульсации напряжения или повысить энергоэффективность сети. При решении подобных задач в расчет берутся конкретные параметры того или иного электронакопителя, а также общие процессы, связанные с зарядом и разрядом конденсаторов.
- Заряд конденсатора
- Процессы зарядки и разрядки конденсаторов
- Емкость и энергия конденсатора
- Как зарядить конденсатор
- Время, необходимое для зарядки конденсатора
- Заряд конденсатора: формула
- Время разряда конденсатора
Заряд конденсатора
Устройство обычного конденсатора состоит из двух пластин (обкладок), подключаемых к выходам цепи, и диэлектрика между ними. При этом величина заряда, накаливаемого конденсатором, зависит от его емкостной характеристики основных параметров: площади обкладок, толщины и диэлектрических свойств прокладочного материала.
При этом величина заряда, накаливаемого конденсатором, зависит от его емкостной характеристики основных параметров: площади обкладок, толщины и диэлектрических свойств прокладочного материала.
Емкость конденсатора определяется по формуле:
C = S • ε • ε0 / d,
где S – площадь обкладок, ε — диэлектрическая проницаемость прокладки, ε0 — диэлектрическая постоянная (8,85•10-12 Ф/м), d – расстояние между пластинами.
Конденсируемый же заряд равняется произведению емкости конденсатора на напряжение в цепи: q = С × U.
Процессы зарядки и разрядки конденсаторов
При включении конденсатора в цепь через него начинает проходить ток. С движением электронов по проводнику на одной обкладке устройства скапливается отрицательный заряд, а на другой (при недостатке электронов) — положительный. Между пластинами образуется индуктивное поле, создающее разность потенциалов определенного значения. В проводниках постоянного тока накопление заряда идет до тех пор, пока уровень напряжения на обкладках не сравняется с номинальным напряжением элемента питания, после чего течение электротока останавливается.
В проводниках постоянного тока накопление заряда идет до тех пор, пока уровень напряжения на обкладках не сравняется с номинальным напряжением элемента питания, после чего течение электротока останавливается.
Когда цепь размыкается и на конденсатор не подается напряжение, он может сохранять заряд на протяжение определенного времени, а затем с исчезновением электрического поля между пластинами заряд начнет перетекать в проводник. Процесс разряда конденсатора характеризуется переходом электронов с одной обкладки на другую. Конденсатор разряжается полностью, когда количество свободных электронов на обеих пластинах сравнивается. При этом все электродинамические процессы в цепи прекращаются.
Емкость и энергия конденсатора
Конденсатор, как и всякий объект, получающий электрический заряд, обладает энергией. Для его зарядки требуется определенная работа, которая идет на разделение заряженных частиц — именно она считается энергией конденсаторного устройства. Ее можно увидеть, если заряженный конденсатор присоединить, например, к светодиоду. Накопитель отдаст заряд лампочке, и она на некоторое время загорится, тем самым энергия перейдет в свет и тепло.
Накопитель отдаст заряд лампочке, и она на некоторое время загорится, тем самым энергия перейдет в свет и тепло.
Для определения энергии конденсатора в расчет берут количество заряда, толщину диэлектрика и напряженность электрического поля. Последняя является векторной величиной и представляет собой силу, действующую на точечный заряд.
Поскольку заряды на обкладках равны между собой по модулю, во внимание принимается только значение напряженности одной из них, а значит, эта величина делится пополам — Е/2. Общая же энергия определяется по формуле:
Wp = qEd/2.
Произведение напряженности на расстояние между пластинами само себе представляет разность потенциалов или напряжение — U = E × d. Таким образом, энергию можно выразить через заряд и напряжение на конденсаторе. Формула будет иметь следующий вид:
Wp = qU/2.
Учитывая, что заряд и напряжение находятся в зависимости от емкости конденсатора, можно вывести еще пару формул энергии:
Wp = q2/2C
Wp = CU2/2
org/ImageObject»>Как зарядить конденсатор
Для зарядки конденсатора требуется генератор электротока. Возникающие при этом процессы удобнее разобрать на примере простой цепи, включающей в себя конденсатор (С) и резистор (R).
Зарядка конденсатора от источника постоянной ЭДС
В соответствии с законом Ома разность потенциалов, возникающая на резисторе и конденсаторе, суммарно равна электродвижущей силе генератора тока. Математически это можно представить следующими формулами:
UC = q/C – напряжение конденсатора;
UR = IR – напряжение резистора;
ε = UC + UR – ЭДС источника.
Для пояснения зарядного процесса определим равенство
IR = ε – q / C.
Эта формула представляет динамические изменения заряда силы тока. Более конкретно это может быть выражено уравнением:
I = dq / dt.
Изменение заряда во времени можно подставить к сопротивлению. Соответственно, получаем
Соответственно, получаем
R • dq / dt = ε – q / C.
В строгом смысле это уравнение предписывает бесконечное время зарядки конденсаторного устройства. Однако этим можно пренебречь, если учесть, что заряд фактически дискретен и может быть подвержен случайным изменением и флуктуациям. Таким образом, в данном выражении имеются в виду усредненная динамика зарядного процесса. На его основании можно записать изменение ЭДС и составляющих напряжений обоих элементов цепи:
dε = d(IR) + d(q/C).
Фактически ЭДС генератора не меняется во времени, а значит, dε = 0, а емкость конденсатора и сопротивление обладают постоянными значениями, поэтому их можно обозначить без d:
R • dI = — 1/C • dq.
Поделив данное уравнение на временной период, за который заряжается конденсатор, можно вывести выражение, учитывающее корреляцию между динамикой заряда и силой тока:
dI / dt = –I/RC.
Это уравнение означает отношение скорости, с которой уменьшается сила тока к ее фактическому значению.
В начале процесса заряда конденсатора значение q равняется нулю. В этот момент при наибольшей разнице напряжений источника питания и электронакопителя сила тока имеет максимальное значение. По мере увеличения заряда значение I постепенно падает. Когда конденсатор заряжается полностью, его напряжение сравнивается с ЭДС генератора, а сила тока принимает значение 0. Соответственно, электродинамический процесс прекращается.
Дополнительно можно рассмотреть, как в процессе зарядки трансформируется энергия. Вполне очевидно, что генератор тока является причиной возникновения электротока в цепи и, следовательно, заряда электронакопителя.
В этом усматривается некое противоречие: когда конденсатор получает от генератора тока заряд q, это значит, что ЭДС выполнила работу равную заряду (А = qe), однако энергия самого накопителя определяется по формуле W = q2 / 2C = qε / 2, что составляет только половину от работы, произведенной источником питания. Этот парадокс объясняется самим фактом прохождения тока по электроцепи, которое сопровождается выделением тепловой энергии на резисторе, то есть определенное количество энергопотери приходится на тепло.
Этот парадокс объясняется самим фактом прохождения тока по электроцепи, которое сопровождается выделением тепловой энергии на резисторе, то есть определенное количество энергопотери приходится на тепло.
Дифференциальные расчеты для малых отрезков времени процесса зарядки показывают, что энергия от генератора, действительно, разделяется на электрическую, идущую на заряд конденсаторного устройства, и тепловую. При этом сопротивление цепи само по себе никак не влияет на количество выделяемой теплоты, которое равняется энергии конденсатора.
Заряд конденсатора, ток
При подключении конденсатора к источнику тока в начале зарядки заряд на пластинах практически отсутствует. Максимальное значение I в этой ситуации объясняется минимальным сопротивлением. С увеличением заряженных частиц, возрастает сопротивление индуктивного поля, которое препятствует прохождению тока по проводнику.
Период времени, за начальную точку которого берут момент наибольшей силы тока, а за конечную полное прекращение движения заряженных частиц, носит название переходного периода зарядки конденсатора.
Начальный момент зарядки конденсатора характеризуется нулевым напряжением между его пластинами. Показатель U начинает возрастать с появлением на обкладках разноименно заряженных частиц. Большая сила тока в начале процесса обусловливает большую скорость увеличения напряжения. По мере ее падения рост напряжения замедляется, достигнув максимального значения при полной зарядке электронакопителя.
График увеличения напряжения имеет вид параболы, будучи противоположным графику снижения силы тока.
Математически динамическую взаимозависимость тока, напряжения и емкости конденсатора можно выразить следующим образом:
I = С • dV / dt.
Время, необходимое для зарядки конденсатора
Время зарядки конденсатора определяется его емкостью, электродвижущей силой генератора тока, напряжением и сопротивлением в цепи.
Заряд конденсатора описывается как экспоненциальный процесс. Чтобы оценить его время, принимается, что значение заряда увеличивается равномерно, при этом скорость заряда приравнивается к силе тока в начале процесса. Отсюда следует уравнение постоянной времени:
Чтобы оценить его время, принимается, что значение заряда увеличивается равномерно, при этом скорость заряда приравнивается к силе тока в начале процесса. Отсюда следует уравнение постоянной времени:
τ = q / I0 = RC.
Зависимость динамики напряжения от длительности зарядки определяется по следующей формуле:
U(t) = UC • (1 – e-t/τ).
Значение высчитывается с привлечением основания натурального логарифма (е), которое относится к функции экспоненты и равняется приблизительно 2,718. При этом UC обозначает напряжение ЭДС источника.
Процент заряда по постоянной времени τ определяется в соответствии с формулой:
(1 — 1/еτ) • 100%.
Таким образом, конденсатор достигает почти полной зарядки за 5 τ.
• 1 τ — 63,2%;
• 2 τ — 86,5%
• 3 τ — 95,1%
• 4 τ — 98,2%
• 5 τ — 99,3%
Учитывая экспоненциальный характер увеличения напряжения конденсатора, можно сказать, что время его зарядки до уровня ЭДС генератора длится бесконечно долго.
Заряд конденсатора: формула
Конденсатор заряжается довольно быстро. Обычно для этого достаточно нескольких миллисекунд. Равенство напряжения электродвижущей силы источника питания и электронакопителя определяет максимальный заряд конденсатора. Формула заряда может быть определена с учетом общих параметров конденсатора:
q = Uεε0S/d.
Также можно принять во внимание конструкционные особенности конденсатора. Так, для цилиндрического накопителя заряд равняется:
q = U2πεε0l/ln(r2/r1),
где l – высота цилиндров, r2 – радиус наружной пластины, r1 — радиус внутренней пластины.
Время разряда конденсатора
Если конденсатор переключить на нагрузку резистора, он сам станет источником питания и будет отдавать заряд в цепь. Движение тока при этом начинается от пластины с отрицательным зарядом на положительно заряженную пластину и далее по контуру. Напряжение в начальный момент будет такое же как и после полной зарядки накопителя. В соответствии с законом Ома можно определить и первоначальную силу тока:
Напряжение в начальный момент будет такое же как и после полной зарядки накопителя. В соответствии с законом Ома можно определить и первоначальную силу тока:
IC = UC / R.
Отдавая заряд, конденсатор будет терять напряжение. Соответственно будет уменьшаться и сила тока. Снижение обоих показателей идет по экспоненциальной кривой с замедлением скорости падения. Это значит, что динамику разрядки конденсатора можно описать, как и в случае зарядки, при помощи постоянной времени τ.
Изменение основных электрических показателей при заряде и разряде конденсатора играют ключевую роль в электротехнике и радиоэлектронике. Эта функциональность в полной мере проявляется в цепях переменного тока, где оба процесса сменяют друг друга с определенной периодичностью. На частотно-зависимых качествах электронакопителей основан принцип действия таких электроустановок, как колебательные контуры, реле времени, цепи обратной связи, частотные фильтры и другие.
Понравилась статья? Расскажите друзьям:
Оцените статью, для нас это очень важно:
Проголосовавших: 1 чел.
Средний рейтинг: 5 из 5.
Основные свойства электрического заряда JEE Physics
В общей терминологии электрический заряд — это количество энергии или электронов, которые переходят из одной системы в другую. Этот перенос может быть опосредован различными механизмами, такими как проводимость, индукция или другими специфическими методами. Электрические заряды делятся на две категории: положительные (+) заряды и отрицательные заряды (-). Заряды есть практически в каждой системе. Однако некоторые системы не имеют зарядов, либо не имеют заряда, либо имеют нейтральный заряд.
Что такое электрический заряд?
Протоны, электроны и нейтроны являются примерами основных субатомных частиц, в которых протоны обладают положительным электрическим зарядом, электроны имеют отрицательный электрический заряд, а нейтроны имеют нейтральный заряд. Символ заряда — «q» или «Q». Общий заряд электронов, присутствующих в атоме, равен числу электронов, умноженному на заряд электрона.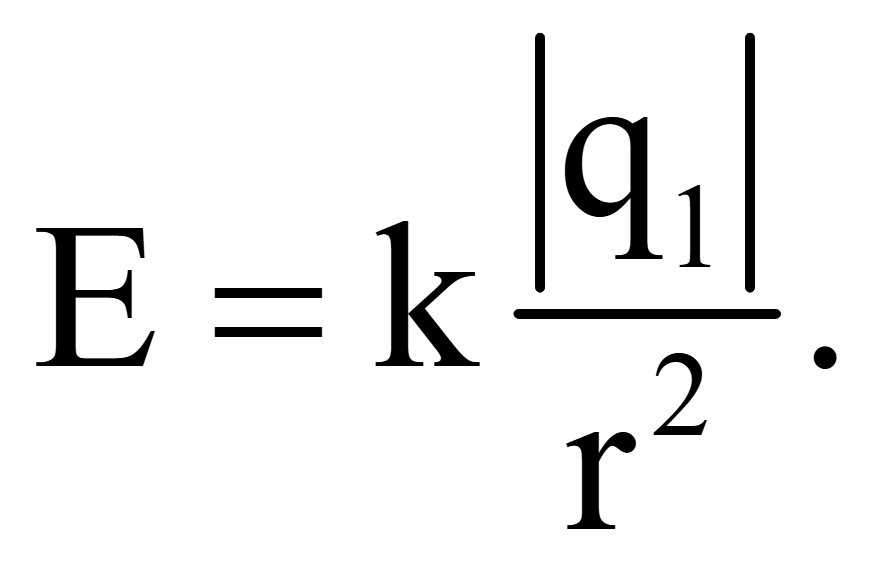 В соответствии с этим определением формула для начисления может быть записана как
В соответствии с этим определением формула для начисления может быть записана как
Q = ne,
Где Q — заряд, e — заряд одного электрона, n — количество электронов. Можно измерить заряд тела, сравнив его со стандартным значением. Согласно исследованию, заряд электронов составляет 1,6 x 10-19C. Единицей СИ или стандартной единицей электрического заряда является кулон, который обозначается буквой «C».
Определение 1 Кл:
Если ток, протекающий по проводу, равен 1 А, то 1 Кл можно определить как заряд, протекающий или проходящий через провод за 1 секунду.
У электрического заряда есть два основных свойства. Вот они:
Например, два протона и два электрона отталкивают друг друга. В случае протонов и электронов они имеют тенденцию притягиваться друг к другу. Эти свойства зависят от природы заряда, то есть силы, действующей на них и координирующей направление потока. Протон и электрон обладают одинаковым зарядом, но противоположны по своей природе. (Примечание: заряд протонов составляет 1,6 х 10 -19 Кл, тогда как заряд электронов равен -1,6 х 10 -19 C.) Разница заключается в типе заряда, который они несут.
Протон и электрон обладают одинаковым зарядом, но противоположны по своей природе. (Примечание: заряд протонов составляет 1,6 х 10 -19 Кл, тогда как заряд электронов равен -1,6 х 10 -19 C.) Разница заключается в типе заряда, который они несут.
Основные свойства электрического заряда
Существуют определенные основные свойства электрического заряда, которым они следуют. Электрические заряды считаются точечными, если размер электрически заряженных тел настолько мал. Помимо вышеупомянутых свойств электрического заряда, они обладают некоторыми другими основными свойствами. К ним относятся:
Аддитивное свойство электрического заряда
Консервативный характер заряда
Квантование заряда
В этом разделе эти свойства подробно описаны.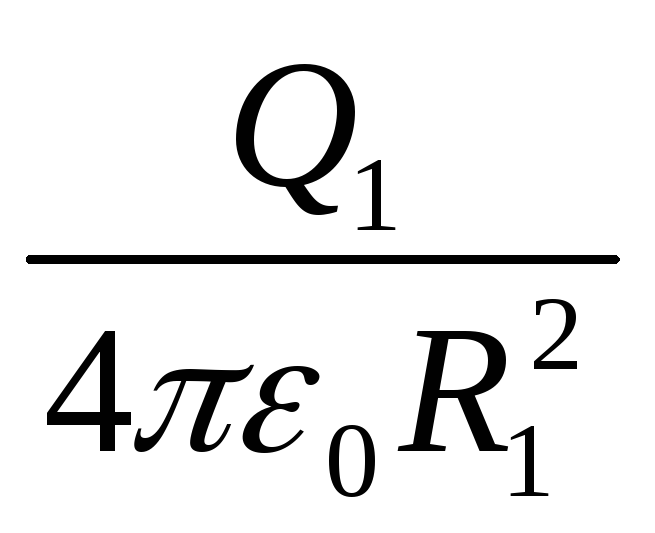
Аддитивное свойство электрического заряда
Электрические заряды являются аддитивными по своей природе, и это зависит от типа электрического заряда, который они несут. Это скалярное свойство. Их можно добавлять напрямую. Например, рассмотрим систему, содержащую только два заряда, а именно q1 и q2. В соответствии с этим свойством полный заряд системы можно вычислить алгебраической суммой q 1 и q 2 т.е. q 1 + q 2 . Аналогично, то же самое верно, если существует более двух частиц электрического заряда. Предположим, система содержит q 1 , q 2 , q 3 , q 4 ………. q n , то путем суммирования можно рассчитать чистый заряд всей системы.
Чистая стоимость = q 1 + q 2 + q 3 + q 4 + ……. + q n
Консервативный характер электрического заряда
Электрический заряд частицы имеет консервативный характер. Это означает, что заряд нельзя ни создать, ни уничтожить. Заряды могут переноситься из одной системы в другую с помощью таких механизмов, как проводимость и индукция. Он подобен закону сохранения массы, а также первому закону термодинамики (то есть закону сохранения энергии). Трение двух тел предполагает перенос электронов от одного тела к другому.
Это означает, что заряд нельзя ни создать, ни уничтожить. Заряды могут переноситься из одной системы в другую с помощью таких механизмов, как проводимость и индукция. Он подобен закону сохранения массы, а также первому закону термодинамики (то есть закону сохранения энергии). Трение двух тел предполагает перенос электронов от одного тела к другому.
Например, рассмотрим систему, содержащую в общей сложности заряд 10 Кл. Можно перераспределить этот заряд как 2C, 3C и 5C или также возможно перераспределить его в соответствии с любой другой возможной перестановкой. Иногда несколько систем теряют равное количество протонов и электронов. Следовательно, окончательный заряд системы будет иметь точно такой же заряд, какой был изначально. Это состояние наблюдается в распаде нейтрино. При распаде нейтрон теряет один электрон и один протон. В конечном итоге общий заряд системы будет равен нулю, поскольку она теряет электроны и протоны одинаковой величины и противоположных знаков.
Квантование заряда
Заряд системы является фиксированной величиной. Технически заряд представляет собой квантованную величину. Чистый заряд системы может быть выражен целым числом, кратным основной единице заряда (т. е. 1,6 x 10 -19 Кл. Предположим, что чистый заряд тела равен q, тогда его можно записать как:
q = ne
В этой формуле n представляет целое число и не может быть дробным или иррациональным числом. Таким образом, значение n может быть любым положительным или отрицательным целым числом. Например, значение n может быть 1, -1, 2, -3, 4, -5 и т. д. Символ «е» представляет основную единицу заряда, переносимого электронами и/или протонами. Обычно заряд протонов обозначается просто как ‘e’, а заряд электрона обозначается как ‘-e’.
Принцип квантования электрического заряда был впервые предложен английским ученым Фарадеем. Это предложение было основано на его экспериментальных законах электролиза, и в 1912 году этот принцип был продемонстрирован и доказан Милликеном.
Это предложение было основано на его экспериментальных законах электролиза, и в 1912 году этот принцип был продемонстрирован и доказан Милликеном.
Сообщалось, что 1 А заряда Кулона содержит около 6 x 10 18 электронов. Как правило, частицы не имеют большого заряда, поэтому в повседневной практике обычно используются меньшие единицы кулона. Обычно используемые единицы измерения электрического заряда — микрокулон или милликулон.
Микрокулон может обозначаться как «мкКл», а милликулон обозначается как «мКл». Коэффициент преобразования из кулоны Milli в кулонум:
1 MC = 10 -3 C
Аналогично, коэффициент преобразования из микрокулона в кулон:
1 μc = 10 -6 C
Концепция квантования электрического заряда очень важна для расчета общего количества электрического заряда, присутствующего в системе, с помощью уравнения «q = ne».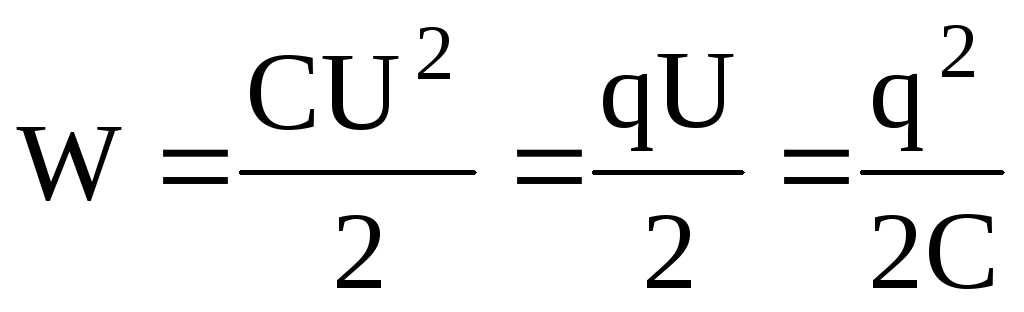 Предположим, например, что система имеет общее число электронов n1 и общее число электронов n 2 число протонов. Тогда, исходя из этих свойств, можно сказать, что общее количество заряда можно представить как n 2 e – n 1 e.
Предположим, например, что система имеет общее число электронов n1 и общее число электронов n 2 число протонов. Тогда, исходя из этих свойств, можно сказать, что общее количество заряда можно представить как n 2 e – n 1 e.
Чистая сумма заряда = N 2 E — N 1 E
или
Чистая сумма заряда = (N 2 — N 1 ) E
Решенный пример с использованием вышеупомянутых свойств
Задача 1: Система состоит из 6 субатомных частиц, в которых есть 4 протона и 2 электрона. Заряды, присутствующие на этих шести частицах, составляют +2С, +4С, +10С, +6С, -4С и -2С. Рассчитайте чистый заряд, присутствующий в системе.
Решение:
В соответствии со свойством электрического заряда суммарный заряд системы представляет собой алгебраическую сумму зарядов отдельных субатомных частиц.
Примите общую плату или чистую плату системы как «Q». Тогда согласно прибавлению свойства электрического заряда:
Суммарный заряд системы Q = 2 Кл + 4 Кл + 10 Кл + 6 Кл + (- 4 Кл) + (- 2 Кл)
Q = 16 Кл
Следовательно, чистый заряд системы составит 16 Кл.
Задача 2: Система состоит из 10 субатомных частиц, в которых есть 4 протона, 2 электрона и 4 нейтрона. Заряды, присутствующие на этих шести частицах, составляют +2С, +4С, +10С, +6С, -4С и -2С. Рассчитайте чистый заряд, присутствующий в системе.
Решение:
Как мы знаем, заряд одного протона равен e, а заряд одного электрона равен -e, а также заряд нейтрона равен нулю и не зависит от количества нейтронов присутствует в системе.
Согласно свойству электрического заряда, суммарный заряд системы представляет собой алгебраическую сумму заряда отдельной субатомной частицы.
Считайте общую плату или чистую плату системы как «Q». Тогда согласно прибавлению свойства электрического заряда
Тогда согласно прибавлению свойства электрического заряда
Суммарный заряд системы Q = 2 Кл + 4 Кл + 10 Кл + 6 Кл + (- 4 Кл) + (- 2 Кл) + 0 + 0 + 0 + 0
Q = 16 С
Следовательно, суммарный заряд системы будет равен 16 Кл.
Таким образом, мы можем утверждать, что:
Электрический заряд — это количество энергии или электронов, которые переходят из одной системы в другую.
Электрические заряды делятся на две категории: положительные (+) заряды и отрицательные заряды (-).
Плата является скалярной величиной. Он имеет определенную величину и не имеет направления.
Заряд – сохраняющаяся величина.

Одинаковые заряды отталкиваются, а противоположные притягиваются.
Основные свойства электрического заряда для JEE Основные и как их изучать?
Понимание и понимание основных свойств электрического заряда было сделано для студентов быстрым благодаря вышеуказанному содержанию. Некоторые из решенных вопросов, должно быть, также позволили вам провести мозговой штурм и применить полученные знания.
Поскольку речь идет о сдаче конкурсного экзамена, вам также может понадобиться подробное объяснение и достаточная практика. Для этого вы можете посетить веб-сайт Vedantu или загрузить приложение, чтобы лучше подготовиться. Экзамены такого уровня сопровождаются множеством необычных действий, большинство из которых — тревога и давление. Когда ваш внутренний голос берет верх, вы, возможно, всегда хотели помолчать и попробовать это сами, выяснив, как лучше всего это сделать.
Давайте разберемся, как можно преодолеть прокрастинацию.
Создание благоприятной среды означает устранение того, что вас отвлекает и мешает действовать. Будь то гаджеты или отсутствие подходящего места для учебы. Для некоторых студентов слишком много мотивационных вещей вокруг них также демотивирует их, потому что они испытывают вопросы неуверенности в себе, а с другой стороны, для некоторых из них это может стать для них топливом. Чтобы по-настоящему понять, что лучше всего работает для вас, нужно уметь наблюдать за своими привычками и шаблонами и на основе этого оптимизировать свою среду обучения.
Пересмотрите свой план
Вам может понадобиться изменить свой план много раз, поэтому вам необходимо соблюдать график, который вы составили для себя, и внести соответствующие изменения. Это поможет вам все переосмыслить, и в конечном итоге ваши цели станут более достижимыми и реалистичными, что, наконец, поможет вам добиться успеха.
Сосредоточьтесь на том, «почему»
«Почему», стоящее за каждой целью, — это причина, которая побуждает вас действовать. Всякий раз, когда у вас низкая мотивация и вы тратите слишком много времени на размышления о том, как и с чего начать, вы сможете визуализировать свою конечную цель в более широкой перспективе. Это позволяет вам переориентироваться и начать действовать.
Учащиеся должны понимать, что не только важно учитывать свои ошибки, но и признавать и вести учет своих достижений, даже самых незначительных. Это позволяет оставаться мотивированным и сосредоточенным. Не будьте строги к себе, будьте последовательны и продолжайте двигаться вперед, и только так вы достигнете того, чего хотите.
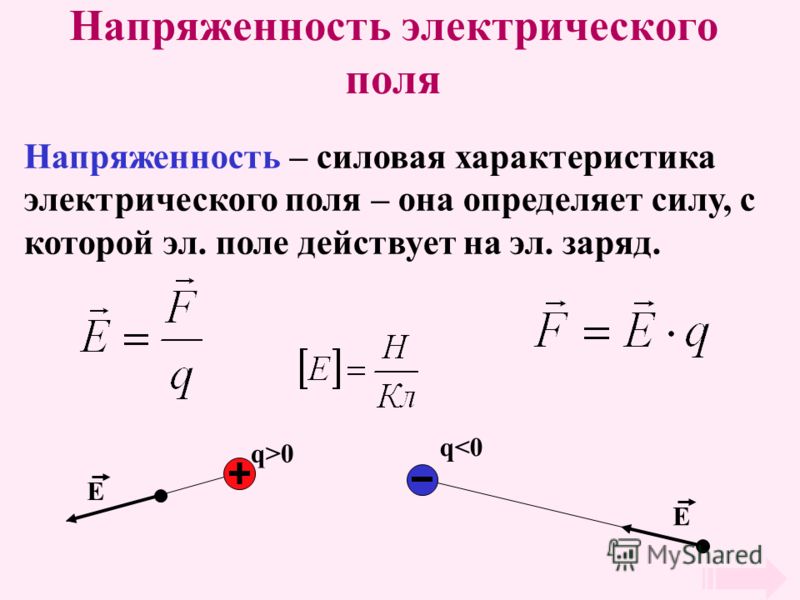
сил — Формула электрического поля $E=F/q$
$\begingroup$
Если следовать формуле $E=F/q$, то получается, что чем больше сила, тем больше и электрическое поле, но если заряд, на который действует сила, больше, электрическое поле как-то уменьшается? Как это понять?
- силы
- электростатика
- электрические поля
- заряд
$\endgroup$
$\begingroup$
Я бы сказал, что вы смотрите на это задом наперед; лучше представить себе, что электрические поля создают силы на зарядах. Для данного электрического поля чем больше заряд, тем больше сила; чтобы увеличить силу, действующую на заряд, необходимо также увеличить электрическое поле; таким образом, для данной силы, чем больше заряд, тем меньше электрическое поле. Это аналогично массе в том смысле, что разные массы (скажем, A больше, чем B), подверженные действию одной и той же силы, будут иметь разные ускорения (B больше, чем A).
Для данного электрического поля чем больше заряд, тем больше сила; чтобы увеличить силу, действующую на заряд, необходимо также увеличить электрическое поле; таким образом, для данной силы, чем больше заряд, тем меньше электрическое поле. Это аналогично массе в том смысле, что разные массы (скажем, A больше, чем B), подверженные действию одной и той же силы, будут иметь разные ускорения (B больше, чем A).
$\endgroup$
$\begingroup$
Это отличный пример того, как каузальное понимание физики не является явно очевидным, если вы наивно смотрите на математическое выражение.
То, что вы говорите , является верным, но правильно сформулировано следующим образом: для заданной силы $F$ на заряде $q$ электрическое поле $E$ (в месте расположения заряда) будет увеличиваться по мере уменьшения заряда $q$. Другими словами, это говорит о том, что для создания той же силы при меньшем заряде вам нужно более сильное электрическое поле. Как видите, никакой тайны здесь нет, если понимать так.
Как видите, никакой тайны здесь нет, если понимать так.
Конечно, как вы уже поняли (как следует из вашего вопроса), электрическое поле, действующее на заряд, не изменится, если вы измените только пробный заряд, потому что оно определяется внешней конфигурацией зарядов. С физической точки зрения, когда вы меняете только пробный заряд, изменяется только сила, действующая на него. Однако $E\propto 1/q$ говорит вам, что если вы хотите поддерживать постоянную силу на изменяющемся пробном заряде, вам нужно изменить электрическое поле обратно пропорционально значению пробного заряда (через изменение внешней конфигурации зарядов, создающих электрическое поле).
$\endgroup$
$\begingroup$
Если вы, скажем, удвоите заряд $q$, то вы, естественно, также увидите удвоенную силу $F$. Потому что для поля $E$ теперь будет «вдвое больше» заряда для «втягивания».
Но если вы хотите, чтобы сила была одинаковой, вам придется каким-то образом уменьшить напряженность поля. Например, изменив источник, который вызывает поле. В противном случае невозможно изменить заряд , а поддерживать силу постоянной.
Например, изменив источник, который вызывает поле. В противном случае невозможно изменить заряд , а поддерживать силу постоянной.
Возможно, ваше замешательство вызвано ошибочным предположением, что сила может поддерживаться постоянной при нормальных, неограниченных обстоятельствах. И, таким образом, изменение заряда, казалось бы, меняет поле. Конечно, это математически возможно, но не физически возможно . Не без того, чтобы вы каким-то образом активно меняли поле. Скорее, это было бы поле, постоянное при таких обстоятельствах, и сила изменялась бы при изменении заряда.
$\endgroup$
$\begingroup$
Определение электрического поля использует E = F/q, как вы показываете, но вы упускаете из виду остальную часть определения, а именно то, что это отношение F/q в пределе, когда q -> 0. Это сделано для того, чтобы пробный заряд не нарушает распределения заряда, создающего электрическое поле. 2} \hat {r} \тег 2$$ 92_\star} \hat{p}, \qquad \forall \vec{p} \in \Omega$$
2} \hat {r} \тег 2$$ 92_\star} \hat{p}, \qquad \forall \vec{p} \in \Omega$$
, где $\Omega$ — множество всех точек. Теперь, если вы на самом деле поместите вторую заряженную частицу $q_2$ в некоторую позицию в пространстве $\vec{p}_0$ , сила между двумя заряженными частицами будет:
$$\vec{F} = q_2 \ cdot \vec{E}(\vec{p}_0)$$
Обратите внимание, что приведенное выше уравнение совпадает с силой, определенной в уравнении. (2).
Имея это в виду, как мы можем измерить напряженность электрического поля 903:00 ? Идея проста — поднести пробный заряд к определенному месту в пространстве, измерить силу и затем нормализовать измеренную силу , т.е. разделить ее на пробный заряд. Это именно то, что уравнение. (1) значит!
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Электрическое поле, сферическая геометрия
Электрическое поле, сферическая геометрия
| Индекс Концепции электрического поля | |||||||
| Назад |
| Индекс Концепции электрического поля | ||||||||
| Назад |
| Индекс Концепции электрического поля | ||||||||||
| Назад |
|





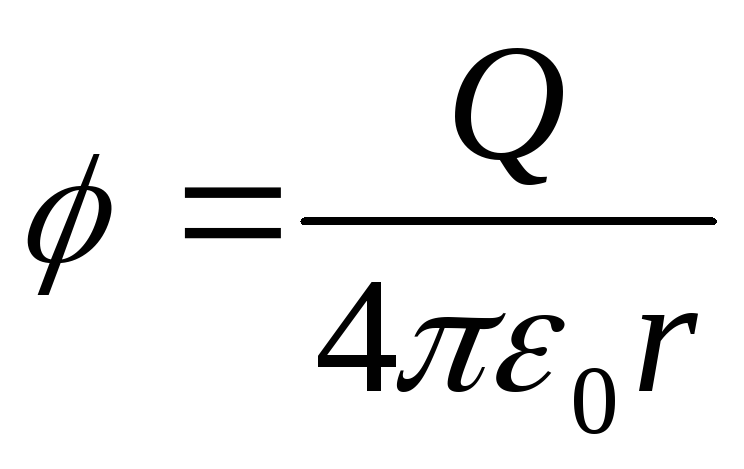 и длине 1 м имеет электрическую прово-димость, равную 1 См.
и длине 1 м имеет электрическую прово-димость, равную 1 См.

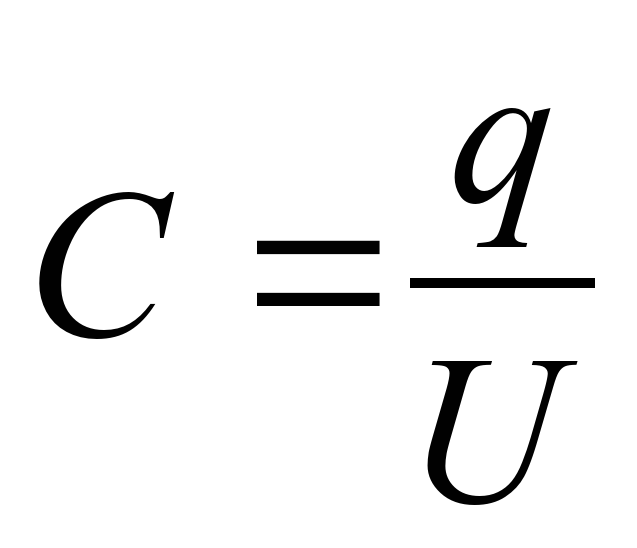
 Рассматривая гауссову поверхность в виде сферы радиусом r , электрическое поле имеет одинаковую величину в каждой точке сферы и направлено наружу. Тогда электрический поток равен произведению электрического поля на площадь сферы.
Рассматривая гауссову поверхность в виде сферы радиусом r , электрическое поле имеет одинаковую величину в каждой точке сферы и направлено наружу. Тогда электрический поток равен произведению электрического поля на площадь сферы. Рассматривая гауссову поверхность в виде сферы радиусом r > R , электрическое поле имеет одинаковую величину в каждой точке поверхности и направлено наружу. Тогда электрический поток равен произведению электрического поля на площадь сферической поверхности.
Рассматривая гауссову поверхность в виде сферы радиусом r > R , электрическое поле имеет одинаковую величину в каждой точке поверхности и направлено наружу. Тогда электрический поток равен произведению электрического поля на площадь сферической поверхности. Рассматривая гауссову поверхность в виде сферы с радиусом r > R , электрическое поле имеет одинаковую величину в каждой точке поверхности и направлено наружу. Тогда электрический поток равен произведению электрического поля на площадь сферической поверхности.
Рассматривая гауссову поверхность в виде сферы с радиусом r > R , электрическое поле имеет одинаковую величину в каждой точке поверхности и направлено наружу. Тогда электрический поток равен произведению электрического поля на площадь сферической поверхности.