1.3. Концепция поля. Электростатическое поле и его напряжённость — ЗФТШ, МФТИ
В XIX веке английский учёный Майкл Фарадей выдвинул гипотезу, что электрическое и магнитное взаимодействия осуществляются посредством особой среды между ними, поля. Любой заряд `q` изменяет свойства пространства вокруг себя – создаёт вокруг себя поле, а уже это поле действует на другие заряды. Развитие науки и техники показало чрезвычайную плодотворность концепции поля. Вся теория электромагнитных явлений со всеми её приложениями существенным образом основывается на концепции поля. По мнению Эйнштейна, идея поля была самым важным открытием со времён Ньютона.
Идея электрического поля большинству людей кажется некоей абстрактной теоретической концепцией, поскольку электрическое поле (в отличие от поля магнитов) в обыденной жизни, в быту невозможно «почувствовать рукой». К вопросу о том, почему это так, мы вернёмся позже.
2)`. Существенно, однако, что отношение силы, действующей на пробный заряд, к его заряду, `(vecF_1)/(q_1)=(vecF_2)/(q_2)`, останется одним и тем же и будет характеристикой не пробных зарядов, но исходного заряда `q` и местоположения `vecr` точки `A`, в которую мы помещали пробные заряды (см. рис. 1). Эта характеристика называется напряжённостью электрического поля точечного заряда `q` в точке `A`. Напряжённость поля есть векторная величина. Её модуль равен
Если заряд `q` положительный, то вектор `vecE` в точке `A` направлен в сторону от заряда вдоль прямой, соединяющей точечный заряд `q` и точку `A`; если же заряд `q` отрицательный, то вектор `vecE` в точке `A` направлен в сторону к заряду вдоль той же прямой.
Удобным способом учёта векторного характера величины `vecE` и знака заряда `q` является следующий. Пусть `vecr` — вектор, проведённый из точки, в которой расположен заряд `q`, в точку `A`, `|vecr|=r` — длина этого вектора (расстояние между точечным зарядом `q` и точкой `A`).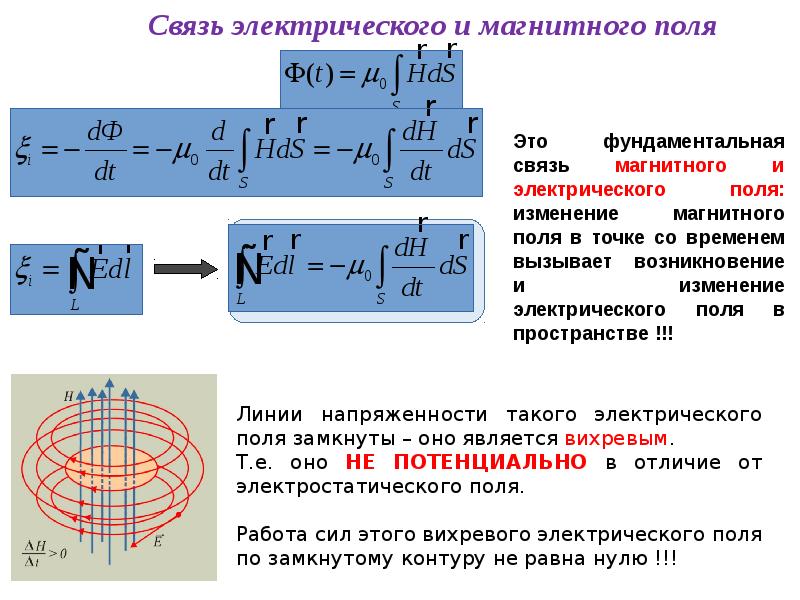
Принцип суперпозиции. Напряжённость есть векторная величина. Это означает, что если имеются два заряда `q_1` и `q_2` каждый из них в некоторой точке создаёт свои напряжённости поля `vecE_1` и `vecE_2`, то результирующая напряжённость (результирующая сила, действующая на единичный положительный заряд, со стороны обоих зарядов) будет равна векторной сумме
получаемой по правилу параллелограмма (рис. 2) или треугольника.
Аналогично, в случае `N` зарядов:
причём векторная сумма вычисляется по правилу многоугольника (либо последовательно несколько раз по правилу параллелограмма).
‘`.
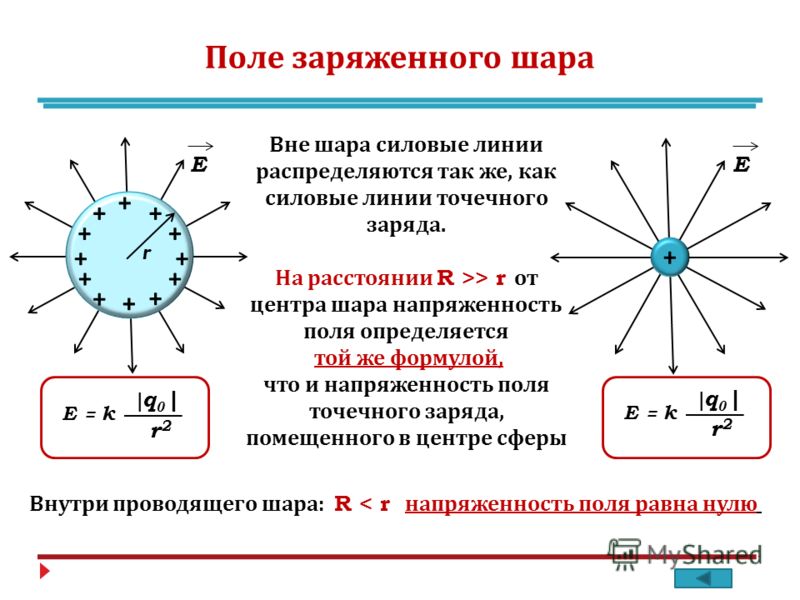
Электрическое поле равномерно заряженной сферы. Вне равномерно заряженной сферы электрическое поле точно такое же, какое создавал бы помещённый в центр сферы точечный заряд, равный по величине суммарному заряду сферы (рис. 4, а – б). Нетривиальный факт состоит в том, что внутри равномерно заряженной сферы напряжённость электрического поля равна нулю (см. `[2 – 3]`).
Если имеются две концентрические равномерно заряженные сферы, то за пределами обеих сфер поле такое же, какое создавали бы два точечных заряда, равные зарядам сфер и помещённые в их общий центр. В области между сферами внешняя сфера не вносит вклада в напряжённость поля.
Вне равномерно заряженного по объёму шара электрическое поле точно такое же, какое создавал бы помещённый в центр шара точечный заряд, равный по величине суммарному заряду шара. Последнее легко понять: поле шара можно представить как результирующее поле множества тонких шаровых слоёв («сфер»).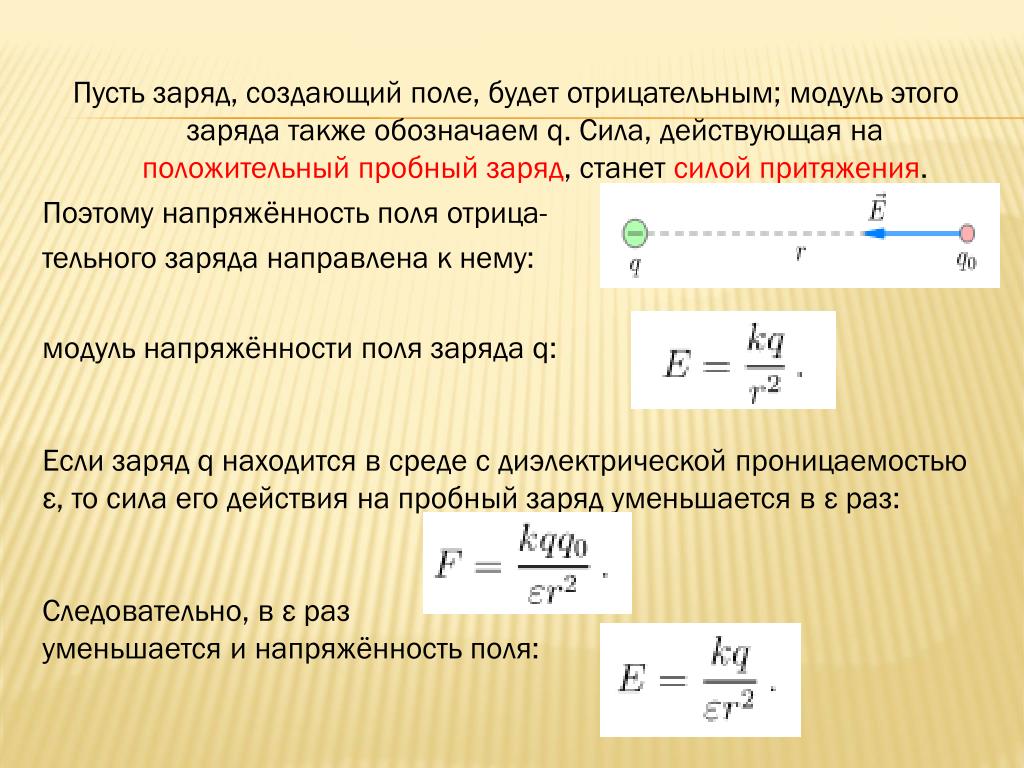
О том, каким будет поле внутри шара, см. Пример 8.
Электрический диполь. Так называется система, состоящая из двух точечных зарядов равных по величине, но противоположных по знаку. Пусть заряды `q_1=-q` и `q_2=+q` в некоторой системе координат характеризуются радиус-векторами `vecr_1` и `vecr_2` (см. рис. 6). Дипольным моментом диполя называется векторная величина `vecp=q_1vecr_1+q_2vecr_2=q(vecr_2-vecr_1)=qvecl`, а величина `l=|vecl|=|vecr_2-vecr_1|` называется плечом диполя.
Рассмотрим более сложный пример использования принципа суперпозиции.
Электрическое поле бесконечной равномерно заряженной плоскости
Вычисление поля в данном случае требует привлечения знаний высшей математики. Без сложных вычислений можно, однако, сделать два следующих утверждения, основываясь лишь на 
Учебник):
1) Электрическое поле бесконечной равномерно заряженной плоскости перпендикулярно плоскости (рис. 8). Дело в том, что перпендикуляр к плоскости – единственное выделенное направление в задаче. Если бы вектор `vecE` был направлен под некоторым углом `alpha` к плоскости, мы бы ещё спросили себя: «Чем это направление лучше, чем все другие прямые, имеющие тот же угол `alpha` с плоскостью, и направленные вдоль образующих конуса с углом `alpha` при вершине?» Ясно, что ничем не лучше: если плоскость бесконечная и заряжена одинаково во всех точках, то и любые направления вдоль неё эквивалентны друг другу.
2) Величина электрического поля бесконечной равномерно заряженной плоскости одинакова во всех точках пространства. В самом деле, все точки на плоскости, параллельной нашей заряженной плоскости, эквивалентны друг другу (снова вспоминаем, что наша плоскость бесконечная и заряжена одинаково во всех точках).
Величина вектора напряжённости `vecE` может быть вычислена по формуле
которую мы приведём без вывода, где `sigma=Deltaq//DeltaS` — поверхностная плотность заряда, `Deltaq` — заряд элемента поверхности площадью `DeltaS`.
Хотя в природе не существует бесконечных равномерно заряженных плоскостей, формула (1.3.4) с успехом используется для расчётов электрических полей заряженных тел в виде больших пластин или просто плоских объектов при небольшом удалении от центральной их части.
Напряженность электрического поля формула через напряжение. Элементарный заряд
Закон кулона
Точечным зарядом
0 т.е.
Проведём радиус-вектор r r от заряда q к q r r. Он равен r r/r .
Отношение силы F q напряжённостью и обозначают через E r. Тогда:
1 Н/Кл = 1 / 1 Кл, т.е. 1 Н/Кл —
Напряжённость поля точечного заряда.
Найдём напряжённость E электростатического поля, создаваемого точечным зарядом q , находящимся в одно-родном изотропном диэлектрике, в точке, отстоящей от него, на расстоянии
Мысленно поместим в эту точку пробный заряд q 0 . Тогда .Отсюда получаем, что
радиус-вектор, проведённый от заряда q к точке, в которой определя-ется напряжённость поля. Из последней формулы следует, что модуль напряжённости поля:
Таким образом, модуль напряжённости в любой точке электростатического по-ля, создаваемого точечным зарядом в вакууме, пропорционален величине заря-да и обратно пропорционален квадрату расстояния от заряда до точки, в кото-рой определяется напряжённость.
Суперпозиция полей
Если электрическое поле создаётся системой точечных зарядов, то его на-пряжённость равна векторной сумме напряжённостей полей , создаваемых каждым зарядом в отдельности, т.е. . Это соотношение носит название принципа суперпозиции (наложения) полей . Из принципа суперпозиции по-лей следует также, что потенциал ϕ, создаваемый системой точечных зарядов в некоторой точке, равен алгебраической сумме потенциалов , создаваемых в этой же точке каждым зарядом в отдельности, т.
е. Знак потенциала совпадает со знаком заряда q i отдельных зарядов системы.
Линии напряженности
Для наглядного изображения электриче-ского поля пользуются линиями напряжённости или силовыми линиями , т.е. линиями, в каждой точке которых вектор напряжённости электрического поля направлен по касательной к ним. Наиболее просто это можно уяснить на при-мере однородного электростатического поля, т.е. поля, в каждой точке кото-рого напряжённость одинакова по модулю и направлению. В этом случае линии напряжённости проводятся так, чтобы число линий Ф Е, проходящих через еди-ницу площади плоской площадки S , расположенной перпендикулярно к этим
линиям, равнялось бы модулю E напряжённости этого поля, т.е.
Если поле неоднородное, то надо выбрать элементарную площадку dS , перпендикулярную к линиям напряжённости, в пределах которой на-пряжённость поля можно считать постоянной.
где dФ E — число линий напряжённости, пронизывающих эту площадку, т.е. модуль напряжённости электрического поля равен числу линий напряжённости, приходящихся на единицу площади площадки, перпендикулярной к ней.
Теорема гаусса
Теорема: поток напряжённости электростатического поля через любую замкнутую поверхность равен алгебраической сумме зарядов, заключённых внутри неё, делённой на электрическую постоянную и диэлектрическую проницаемость среды.
Если интегрирование производится по всему объёму V , по которому распреде-лён заряд. Тогда при непрерывном распределении заряда на некоторой поверх-ности S 0 теорема Гаусса записывается в виде:
В случае объёмного распределения:
Теорема Гаусса связывает между собой величину заряда и напряжённость поля, которое им создаётся. Этим и определяется значение данной теоремы в электростатике, поскольку она позволяет рассчитывать напряжённость, зная расположение зарядов в пространстве.
Циркуляция электр.поля.
Из выражения
следует также, что при переносе заряда по замкнутому пути, т.е., когда заряд возвращает-ся в исходное положение, r 1 = r 2 и A 12 = 0. Тогда запишем
Сила , действующая на заряд q 0 , равна . Поэтому последнюю формулу перепишем в виде
Ности электростатического поля на направление Разделив обе части это-го равенства на q 0 , находим:
Первое равенство – этоциркуляция напряжённости электрического поля .
Конденсаторы
Конденсаторы представ-ляют собой два проводника, очень близко расположенные друг к другу и разде-лённые слоем диэлектрика. Электроём-кость конденсатора – способность конденсатора накапливать на себе заряды. т.е. ёмкостью конденсатора называется физическая величина , равная отноше-нию заряда конденсатора к разности потенциалов между его обкладками. Ёмкость конденсатора, как и ёмкость проводника, измеряется в фарадах (Ф): 1 Ф — это ёмкость такого конденсатора, при сообщении которому заряда в 1 Кл, разность потенциалов между его обкладками изменяется на 1 В.
Энергия электр. поля
Энергия заряженных проводников запасена в виде электрического поля. Поэтому целесообразно выразить её через напряжённость, характеризующую это поле. Это проще всего проделать для плоского конденсатора. В этом случае , где d — расстояние между обкладками, и . Здесь ε0 — электрическая постоянная, ε — диэлектрическая проницаемость диэлектрика, заполняющего конденсатор, S — площадь каждой обкладки. Подставляя эти выражения, получаем Здесь V = Sd — объём, занимаемый полем, равный объёму конденсатора.
Работа и мощность тока.
Работой электрического тока называется работа, которую совершают силы электрического поля, созданного в электрической цепи, при перемещении заряда по этой цепи.
Пусть к концам проводника приложена постоянная раз-ность потенциалов (напряжение) U = ϕ1− ϕ2.
A = q (ϕ1−ϕ2) = qU .
С учётом этого получаем
Применяя закон Ома для однородного участка цепи
U = IR , где R — сопротивление проводника, запишем:
A = I 2 Rt .
Работа A , совершённая за время t , будет равна сумме элементарных работ, т.е.
По определению мощность электрического тока равна P = A/t . Тогда:
В системе единиц СИ работа и мощность электрического тока измеряются соответственно в джоулях и ваттах.
Закон Джоуля-Ленца.
Электроны, движущиеся в металле под действием электрического поля, как уже отмечалось, непрерывно сталкиваются с ионами кристаллической решётки, передавая им свою кинетическую энергию упорядоченного движения. Это при-водит к увеличению внутренней энергии металла, т.е. к его нагреванию. Соглас-но закону сохранения энергии, вся работа тока A идёт на выделение количества теплоты Q , т.е. Q = A . Находим Это соотношение называют законом Джоуля − Ленца .
Закон полного тока.
Циркуляция индукции магнитного поля по произвольному замкнутому контуру равна произведению магнитной постоянной, магнитной проницаемости на алгебраическую сумму сил токов, охваты-ваемых этим контуром.
Силу тока можно найти, используя плотность тока j:
где S — площадь поперечного сечения проводника. Тогда закон полного тока записывается в виде:
Магнитный поток.
Магнитным потоком через некоторую поверхность называют число линий магнитной индукции, пронизывающих её.
Пусть в неоднородном магнитном поле находится поверхность площадью S . Для нахождения магнитного потока через неё мысленно разделим поверхность на элементарные участки площадью dS , которые можно считать плоскими, а поле в их пределах однородным. Тогда элементарный магнитный поток dФ B через эту поверхность равен:
Магнитный поток через всю поверхность равен сумме этих потоков: , т.е.:
. В системе единиц СИ магнитный поток измеряется в веберах (Вб).
Индуктивность.
Пусть по замкнутому контуру течёт постоянный ток силой I . Этот ток создаёт вокруг себя магнитное поле, которое пронизывает площадь, охватываемую проводником, создавая магнитный поток.
Известно, что магнитный поток Ф B пропорционален модулю индукции магнитного поля B , а модуль индукции магнитного поля, возникающего вокруг проводника с током, пропор-ционален силе тока I. Из этого следует Ф B ~ B ~ I , т.е. Ф B = LI .
Коэффициент пропорциональности L между силой тока и магнитным потоком, создаваемым этим током через площадь, ограниченную проводником , называют индуктивностью проводника .
В системе единиц СИ индуктивность измеряется в генри (Гн).
Индуктивность соленоида.
Рассмотрим индуктивность соленоида длиною l , с поперечным сечением S и с общим числом витков N , заполненного веществом с магнитной проницаемостью μ. При этом возьмём соленоид такой длины, чтобы его можно было рассматривать как бесконечно длинный. При протека-нии по нему тока силой I внутри него создаётся однородное магнитное поле, направленное перпендикулярно к плоскостям витков.
Модуль магнитной индукции этого поля находится по формуле
B = μ0μnI ,
Магнитный поток Ф B через любой виток соленоида равен Ф B = BS (см. (29.2)), а полный Ψ поток через все витки соленоида будет равен сумме магнитных потоков через каждый виток, т.е. Ψ = NФ B = NBS .
N = nl , получаем: Ψ = μ0μ = n 2 lSI = μ0μ n 2 VI
Приходим к выводу, что индуктивность соленоида равна:
L =μμ0 n 2 V
Энергия магнитного поля.
Пусть в электрической цепи протекает постоянный ток силой I . Если отключить источник тока и замкнуть цепь (переключатель П перевести в положение 2 ), то в ней некоторое время будет течь убывающий ток, обусловленный э.д.с. самоиндукции .
Элементарная работа, совершаемая э.д.с. самоиндукции по переносу по цепи элементарного заряда dq = I·dt , равна Сила тока изменяется от I до 0.
Поэтому, интегрируя это выражение в указанных пределах, получаем работу, совершаемую э.д.с. самоиндукции за время, в течение которого происхо-дит исчезновение магнитного поля: . Эта работа расходует-ся на увеличение внутренней энергии проводников, т.е. на их нагревание. Совер-шение этой работы сопровождается также исчезновением магнитного поля, кото-рое первоначально существовало вокруг проводника.
Энергия магнитного поля, существующего вокруг проводников с током, равна
W B = LI 2 / 2.
получаем, что
Магнитное поле внутри соленоида однородное . Поэтому объёмная плотность энергии w B магнитного поля, т.е. энергия единицы объёма поля, внутри соленоида равна .
Вихревое электр. поле.
Из закона Фарадея для электромагнитной индукции следует, что при всяком изменении магнитного потока, пронизывающего пло-щадь, охватываемую проводником, в нём возникает э.д.с. индукции , под действием которой в проводнике появляется индукционный ток, если проводник замкнутый.
Для объяснения э.д.с. индукции Максвелл выдвинул гипотезу, что перемен-ное магнитное поле создаёт в окружающем пространстве электрическое поле . Это поле действует на свободные заряды проводника, приводя их в упорядо-ченное движение, т.е. создавая индукционный ток. Таким образом, замкнутый проводящий контур является своеобразным индикатором, с помощью которого и обнаруживается данное электрическое поле. Обозначим напряжённость этого поля через E r. Тогда э.д.с. индукции
известно, что циркуляция напряжённости электростатического поля равна нулю, т.е.
Следует, что т.е. электрическое поле, возбуждаемое изменяющимся со временем магнитным полем, является вихревым (не потенциальным ).
Следует отметить, что линии напряжённости электростатического поля начинаются и заканчиваются на зарядах, создающих поле, а линии напряжённости вихревого электрического поля всегда замкнутые.
Ток смещения
Максвелл высказал гипотезу, что переменное магнитное поле создаёт вихревое электрическое поле.
Он сделал и обратное пред-положение: переменное электрическое поле должно вызывать возникновение магнитного поля . В дальнейшем эти обе гипотезы получили экспериментальное подтверждение в опытах Герца. Появление магнитного поля при изменении электрического поля можно трактовать так, как будто бы в пространстве возни-кает электрический ток. Этот ток был назван Максвеллом током смещения .
Ток смещения может возникать не только в вакууме или диэлектрике, но и в проводниках, по которым течёт переменный ток. Однако в этом случае он пренебрежимо мал по сравнению с током проводимости.
Максвелл ввёл понятие полного тока. Сила I полного тока равна сумме сил I пр и I см токов проводимости и смещения, т.е. I = I пр + I см. Получаем:
Уравнение Максвелла.
Первое уравнение.
Из этого уравнения следует, что источником электрического поля является изменяющееся со временем магнитное поле.
Второе уравнение Максвелла.
Второе уравнение. Закон полного тока Это уравнение показывает, что магнитное поле может создаваться как движущимися зарядами (электрическим током), так и переменным электрическим полем.
Колебания.
Колебаниями называются процессы, характеризуемые определённой повто-ряемостью со временем. Процесс распространения колебаний в пространстве называют волной . Любая система, способная колебаться или в которой могут происходить ко-лебания, называется колебательной . Колебания, происходящие в колебательной системе, выведенной из состояния равновесия и представленной самой себе, называют свободными колебаниями .
Гармонические колебания.
Гармоническими колебаниями называются колебания, в которых колеблющаяся физическая величина изменяется по закону Sin или Cos. Амплитуда — это наи-большее значение, которое может принимать колеблющаяся величина.
Уравнения гармонических колебаний: и
тоже самое только с синусом. Периодом не-затухающих колебаний называют время одного полного колебания. Число ко-лебаний, совершаемых в единицу времени, называется частотой колебаний . Частота колебаний измеряется в герцах (Гц).
Колебательный контур.
Электрическую цепь, состоящую из индуктивности и ёмкости, называют колебательным контуром
Полная энергия электромагнитных колебаний в контуре есть величина постоянная, точно также как полная энергия механических колебаний.
При колебаниях всегда кинет. энергия переходит в потенциальную и наоборот.
Энергия W колебательного контура складывается из энергии W E электрического поля конденсатора и энергии W B магнитного поля индуктивности
Затухающие колебания.
Процессы, описываемые уравнением можно считать колебательными. Их называют затухающими колебаниями . Наименьший промежуток времени T , через который повторяются максимумы (или минимумы) называют периодом зату-хающих колебаний .
Выражение рассматривают как амплитуду затухающих колебаний. Величина A 0 представляет собой амплитуду колебания в момент времени t = 0, т.е. это начальная ампли-туда затухающих колебаний. Величина β, от которой зависит убывание ампли-туды, называется коэффициентом затухания .
Т.е. коэффициент затухания обратно пропорционален времени, за которое амплитуда затухающих колебаний уменьшается в e раз.
Волны.
Волна — это процесс распространения колебаний (возмущения) в простран-стве .
Область пространст-ва , внутри которой происходят колебания , называется волновым полем .
Поверхность , отделяющую волновое поле от области , где колебаний ещё нет , на-зывают фронтом волны .
Линии , вдоль которых происходит распространение волны , называются лучами .
Звуковые волны.
Звук представляет собой колебания воздуха или другой упру-гой среды, воспринимаемые нашими органами слуха. Звуковые колебания, вос-принимаемые человеческим ухом, имеют частоты, лежащие в пределах от 20 до 20000 Гц. Колебания с частотами меньше 20 Гц называются инфразвуковыми , а больше 20 кГц — ультразвуковыми .
Характеристики звука. Звук у нас ассоциируется обычно с его слуховым вос-приятием, с ощущениями, которые возникают в сознании человека. В связи с этим можно выделить три его основные характеристики: высоту, качество и громкость.
Физической величиной, характеризующей высоту звука, является частота колебаний звуковой волны .
Для характеристики качества звука в музыке используют термины тембр или то-нальная окраска звука. Качество звука можно связать с физически измеримыми величинами. Оно определяется наличием обертонов, их числом и амплитудами.
Громкость звука связана с физически измеряемой величиной — интенсивностью волны. Измеряется в белах.
Законы теплового излучения
Закон Стефана — Больцмана — закон излучения абсолютно чёрного тела.
Определяет зависимость мощности излучения абсолютно чёрного тела от его температуры. Формулировка закона:
Закон излучения Кирхгофа
Отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты и не зависит от их формы и химической природы.
Длина волны, при которой энергия излучения абсолютно чёрного тела максимальна, определяется законом смещения Вина : где T — температура в кельвинах, а λ max — длина волны с максимальной интенсивностью в метрах.
Строение атома.
Опыты Резерфорда и его сотрудников привели к выводу, что в центре атома находится плотное положительно заряженное ядро, диаметр которого не превышает 10 –14 –10 –15 м.
Изучая рассеяние альфа-частиц при прохождении через золотую фольгу, Резерфорд пришел к выводу, что весь положительный заряд атомов сосредоточен в их центре в очень массивном и компактном ядре. А отрицательно заряженные частицы (электроны) обращаются вокруг этого ядра.
Эта модель коренным образом отличалась от широко распространенной в то время модели атома Томсона, в которой положительный заряд равномерно заполнял весь объем атома, а электроны были вкраплены в него. Несколько позже модель Резерфорда получила название планетарной модели атома (она действительно похожа на Солнечную систему: тяжелое ядро — Солнце, а обращающиеся вокруг него электроны — планеты).
А́том — наименьшая химически неделимая часть химического элемента, являющаяся носителем его свойств. Атом состоит из атомного ядра и электронов. Ядро атома состоит из положительно заряженных протонов и незаряженных нейтронов. Если число протонов в ядре совпадает с числом электронов, то атом в целом оказывается электрически нейтральным. В противном случае он обладает некоторым положительным или отрицательным зарядом и называется ионом. Атомы классифицируются по количеству протонов и нейтронов в ядре: количество протонов определяет принадлежность атома некоторому химическому элементу, а число нейтронов — изотопуэтого элемента.
Атомы различного вида в разных количествах, связанные межатомными связями, образуют молекулы.
Вопросы:
1. электростатика
2. закон сохранения электрического заряда
3. закон кулона
4. электрическое поле.напряженность электрического поля
6. суперпозиция полей
7. линии напряженности
8. поток-вектор напряженности электр.поля
9. теорема гаусса для электростатич.поля
10. теорема гаусса
11. циркуляция электр.поля
12. потенциал. Разность потенциалов электростатич.поля
13. связь между напряжением поля и потенциалом
14. конденсаторы
15. энергиязаряженного конденсатора
16. энергия электр поля
17. сопротивление проводника. Закон ома для частка цепи
18. закон ома для участка проводника
19. источники электр тока. Электродвижущая сила
20. работа и мощьность тока
21. закон джоуля ленца
22. магнитное поле.индукция магнитного поля
23. закон полного тока
24. магнитный поток
25. теорема гаусса для магнитного поля
26. работа по перемещению проводника с током в магнит поле
27. явление электомагнит индукции
28. индуктивность
29. индуктивность соленоида
30. явление и закон самоиндукции
31. энергия магнитного поля
32. вихревое электр поле
33. ток смещения
34. уравнение максвелла
35. второе уравнение максвелла
36. третье и четвертое уравнение максвлла
37. колебания
38. гармонические колебания
39. колебательный контур
40. затухающие колебания
41. вынужденные колебания. Явление резонанса
43. уравнение плоской монохроматич волны
44. звуковые волны
45. волновые и корпускулярные свойства света
46. Тепловое излучение и его характеристики.
47. Законы теплового излучения
48. Строение атома.
Закон кулона
Сила взаимодействия находится для так называемых точечных зарядов.
Точечным зарядом называется заряженное тело, размеры которого пренебрежимо малы по сравнению с расстоянием до других заряженных тел, с которыми оно взаимодействует.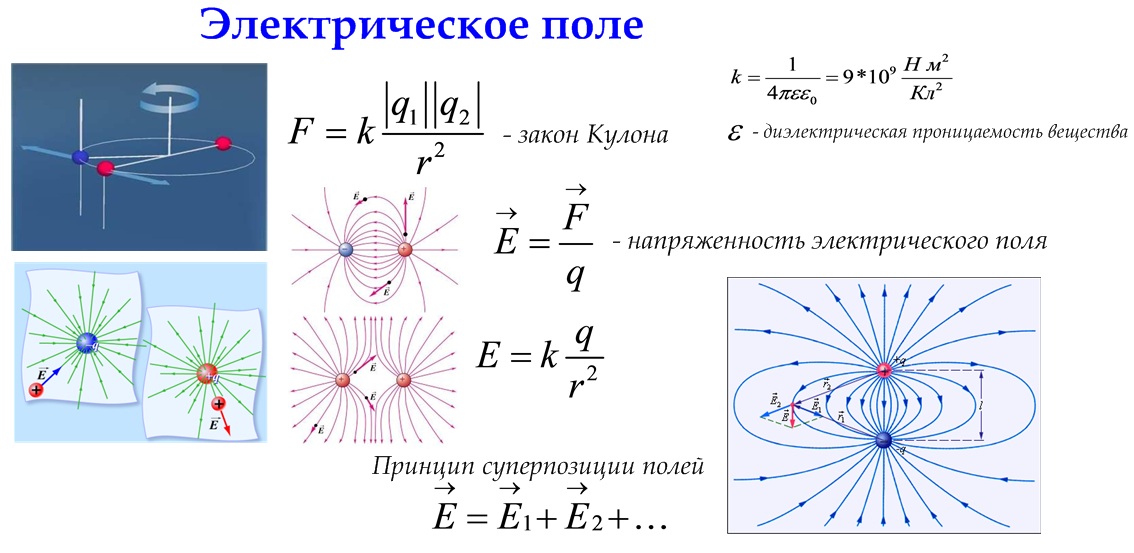
Закон взаимодействия точечных зарядов был открыт Кулоном и формулируется следующим образом: модуль F силы взаи-модействия между двумя неподвижными зарядами q и q 0 пропорционален произведению этих зарядов, обратно пропорционален квадрату расстояния r между ними, т.е.
где ε0 — электрическая постоянная, ε — диэлектрическая проницаемость, характеризующая среду. Эта сила направлена вдоль прямой линии, соединяющей заряды. Электрическая постоянная равна ε0 = 8,85⋅10–12 Кл2/(Н⋅м2) или ε0 = 8,85⋅10–12 Ф/м, где фарад (Ф) единица электроёмкости. Закон Кулона в векторной форме запишется:
Проведём радиус-вектор r r от заряда q к q 0. Введём единичный вектор, направленный в ту же сторону, что и вектор r r. Он равен r r/r .
Электрическое поле. напряженность электрического поля
Отношение силы F r, действующей на заряд, к величине q 0 этого заряда является постоянным для всех вносимых зарядов, независимо от их величины.
Поэтому это отношение принимают за характеристику электрического поля в данной точке. Её называют напряжённостью и обозначают через E r. Тогда:
1 Н/Кл = 1 / 1 Кл, т.е. 1 Н/Кл — напряжённость в такой точке поля, в которой на заряд в 1 Кл действует сила в 1 Н.
«Физика — 10 класс»
При решении задач с использованием понятия напряжённости электрического поля нужно прежде всего знать формулы (14.8) и (14.9), определяющие силу, действующую на заряд со стороны электрического поля, и напряжённость поля точечного заряда. Если поле создаётся несколькими зарядами, то для расчёта напряжённости в данной точке надо сделать рисунок и затем определить напряжённость как геометрическую сумму напряжённостей полей.
Задача 1.
Два одинаковых положительных точечных заряда расположены на расстоянии r друг от друга в вакууме. Определите напряжённость электрического поля в точке, расположенной на одинаковом расстоянии r от этих зарядов.
Р е ш е н и е.
Согласно принципу суперпозиции полей искомая напряжённость равна геометрической сумме напряжённостей полей, созданных каждым из зарядов (рис. 14.17): = 1 + 2 .
Модули напряжённостей полей зарядов равны:
Диагональ параллелограмма, построенного на векторах 1 и 2 , есть напряжённость результирующего поля, модуль которой равен:
Задача 2.
Проводящая сфера радиусом R = 0,2 м, несущая заряд q = 1,8 10 -4 Кл, находится в вакууме. Определите: 1) модуль напряжённости электрического поля на её поверхности; 2) модуль напряжённости 1 электрического поля в точке, отстоящей на расстоянии r 1 = 10 м от центра сферы; 3) модуль напряжённости 0 в центре сферы.
Р е ш е н и е.
Электрическое поле заряженной сферы вне её совпадает с полем точечного заряда. Поэтому
Следовательно,
Задача 3.
В однородное электрическое поле напряжённостью Е 0 = 3 кН/Кл внесли точечный заряд q = 4 10 -10 Кл. Определите напряжённость электрического поля в точке А, находящейся на расстоянии r = 3 см от точечного заряда.
Отрезок, соединяющий заряд и точку А, перпендикулярен силовым линиям однородного электрического поля.
Р е ш е н и е.
Согласно принципу суперпозиции напряжённость электрического поля в точке А равна векторной сумме напряжённостей однородного поля 0 и поля 1 , созданного в этой точке внесённым электрическим зарядом. На рисунке 14.18 показаны эти два вектора и их сумма. По условию задачи векторы 0 и 1 взаимно перпендикулярны. Напряжённость поля точечного заряда
Тогда напряжённость электрического поля в точке А равна:
Задача 4.
В вершинах равностороннего треугольника со стороной а = 3 см находятся три точечных заряда q 1 = q 2 = 10 -9 Кл, q 3 = -2 10 -9 Кл. Определите напряжённость электрического поля в центре треугольника в точке О.
Согласно принципу суперпозиции полей напряжённость поля в точке О равна векторной сумме напряжённостей полей, созданных каждым зарядом в отдельности: 0 = 1 + 2 + 3 , причём где
На рисунке 14.19 показаны векторы напряжённостей 1 , 2 , 3 .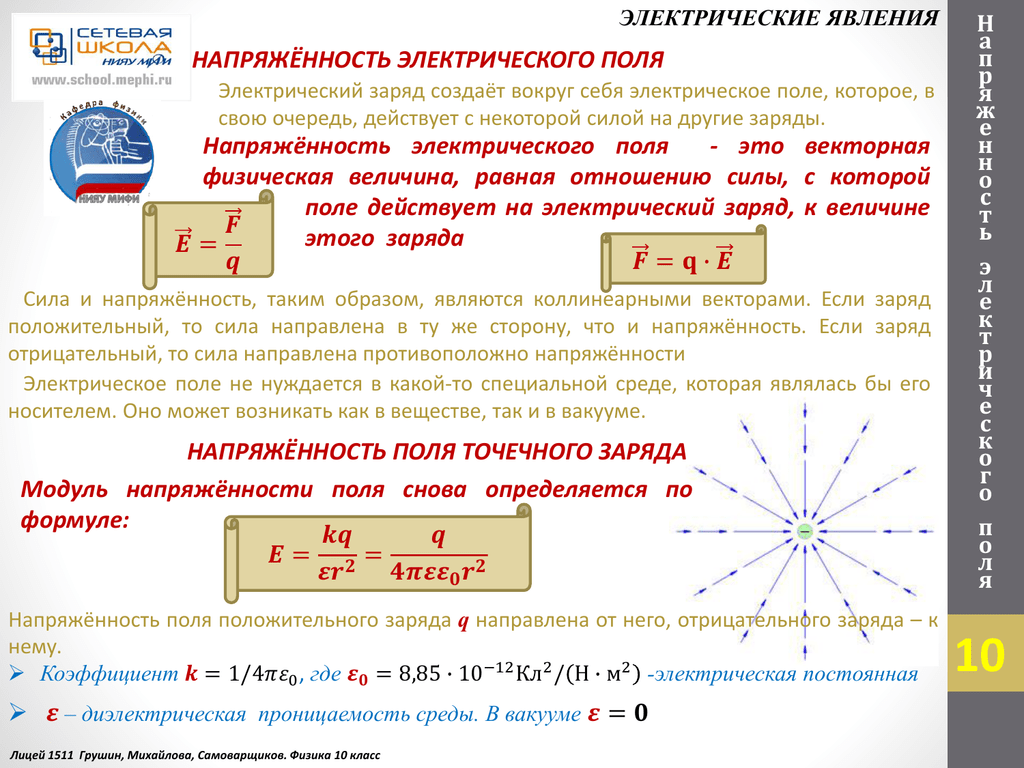
Сначала сложим векторы 1 и 2 . Как видно из рисунка, угол между этими векторами равен 120°. Следовательно, модуль суммарного вектора равен модулю l 1 l и направлен в ту же сторону, что и вектор 3 .
>>Физика: Напряженность электрического поля. Принцип суперпозиции полей
Недостаточно утверждать, что электрическое поле существует. Надо ввести количественную характеристику поля. После этого электрические поля можно будет сравнивать друг с другом и продолжать изучать их свойства.
Электрическое поле обнаруживается по силам, действующим на заряд. Можно утверждать, что мы знаем о поле все, что нам нужно, если будем знать силу, действующую на любой заряд в любой точке поля.
Поэтому надо ввести такую характеристику поля, знание которой позволит определить эту силу.
Если поочередно помещать в одну и ту же точку поля небольшие заряженные тела и измерять силы, то обнаружится, что сила, действующая на заряд со стороны поля, прямо пропорциональна этому заряду.
Действительно, пусть поле создается точечным зарядомq 1 . Согласно закону Кулона (14.2) на заряд q 2 действует сила, пропорциональная заряду q 2 . Поэтому отношение силы, действующей на помещаемый в данную точку поля заряд, к этому заряду для каждой точки поля не зависит от заряда и может рассматриваться как характеристика поля. Эту характеристику называютнапряженностью электрического поля. Подобно силе, напряженность поля – векторная величина ; ее обозначают буквой . Если помещенный в поле заряд обозначить через q вместо q 2 , то напряженность будет равна:
Напряженность поля в данной точке равна отношению силы, с которой поле действует на точечный заряд, помещенный в эту точку, к этому заряду.
Отсюда сила, действующая на заряд q со стороны электрического поля, равна:
Направление вектора совпадает с направлением силы, действующей на положительный заряд, и противоположно направлению силы, действующей на отрицательный заряд.
Напряженность поля точечного заряда. Найдем напряженность электрического поля, создаваемого точечным зарядом q 0 . По закону Кулона этот заряд будет действовать на положительный заряд q с силой, равной
Модуль напряженности поля точечного заряда q 0 на расстоянии r от него равен:
Вектор напряженности в любой точке электрического поля направлен вдоль прямой, соединяющей эту точку и заряд (рис.14.7 ) и совпадает с силой, действующей на точечный положительный заряд, помещенный в данную точку.
Принцип суперпозиции полей . Если на тело действует несколько сил, то согласно законам механики результирующая сила равна геометрической сумме этих сил:
На электрические заряды действуют силы со стороны электрического поля. Если при наложении полей от нескольких зарядов эти поля не оказывают никакого влияния друг на друга, то результирующая сила со стороны всех полей должна быть равна геометрической сумме сил со стороны каждого поля.
Опыт показывает, что именно так и происходит на самом деле. Это означает, что напряженности полей складываются геометрически.
если в данной точке пространства различные заряженные частицы создают электрические поля, напряженности которых и т. д., то результирующая напряженность поля в этой точке равна сумме напряженностей этих полей:
причем напряженность поля, создаваемая отдельным зарядом, определяется так, как будто других зарядов, создающих поле, не существует.
Благодаря принципу суперпозиции для нахождения напряженности поля системы заряженных частиц в любой точке достаточно знать выражение (14.9) для напряженности поля точечного заряда. На рисунке 14.8 показано, как определяется напряженность поля в точке A , созданная двумя точечными зарядами q 1 и q 2 , q 1 >q 2
Введение электрического поля позволяет разделить задачу вычисления сил взаимодействия заряженных частиц на две части.
Сначала вычисляют напряженность поля, созданного зарядами, а затем по известной напряженности определяют силы. Такое разделение задачи на части обычно облегчает расчеты сил.
???
1. Что называется напряженностью электрического поля?
2. Чему равна напряженность поля точечного заряда?
3. Как направлена напряженность поля зарядаq 0 , если q 0 >0 ? если q 0 0
?
4. Как формулируется принцип суперпозиции полей?
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие
Совершенствование учебников и уроковисправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку,
Физическая природа электрического поля и его графическое изображение .
В пространстве вокруг электрически заряженного тела существует электрическое поле, представляющее собой один из видов материи. Электрическое поле обладает запасом электрической энергии, которая проявляется в виде электрических сил, действующих на находящиеся в поле заряженные тела.
Рис. 4. Простейшие электрические поля: а – одиночных положительного и отрицательного зарядов; б – двух разноименных зарядов; в – двух одноименных зарядов; г – двух параллельных и разноименно заряженныx пластин (однородное поле)
Электрическое поле условно изображают в виде электрических силовых линий, которые показывают направления действия электрических сил, создаваемых полем. Принято направлять силовые линии в ту сторону, в которую двигалась бы в электрическом поле положительно заряженная частица. Как показано на рис. 4, электрические силовые линии расходятся в разные стороны от положительно заряженных тел и сходятся у тел, обладающих отрицательным зарядом. Поле, созданное двумя плоскими разноименно заряженными параллельными пластинами (рис.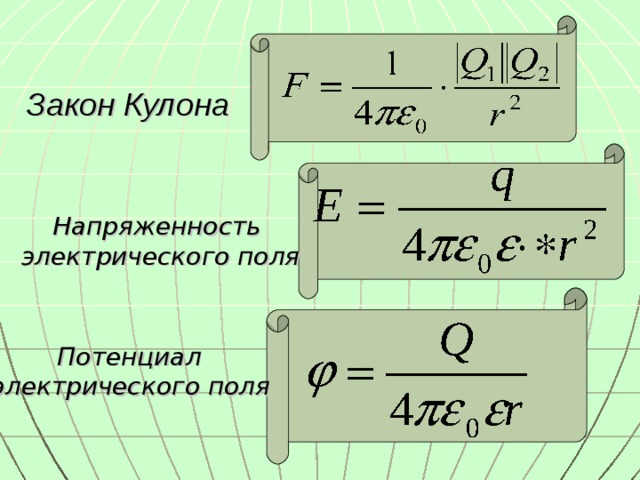
4, г), называется однородным.
Электрическое поле можно сделать видимым, если поместить в него взвешенные в жидком масле частички гипса: они поворачиваются вдоль поля, располагаясь по его силовым линиям (рис. 5).
Напряженность электрического поля. Электрическое поле действует на внесенный в него заряд q (рис. 6) с некоторой силой F. Следовательно, об интенсивности электрического поля можно судить по значению силы, с которой притягивается или отталкивается некоторый электрический заряд, принятый за единицу. В электротехнике интенсивность поля характеризуют напряженностью электрического поля Е. Под напряженностью понимают отношение силы F, действующей на заряженное тело в данной точке поля, к заряду q этого тела:
E = F / q (1)
Поле с большой напряженностью Е изображается графически силовыми линиями большой густоты; поле с малой напряженностью — редко расположенными силовыми линиями. По мере удаления от заряженного тела силовые линии электрического поля располагаются реже, т.
е. напряженность поля уменьшается (см. рис. 4 а,б и в). Только в однородном электрическом поле (см. рис. 4, г) напряженность одинакова во всех его точках.
Электрический потенциал . Электрическое поле обладает определенным запасом энергии, т. е. способностью совершать работу. Как известно, энергию можно также накопить в пружине, для чего ее нужно сжать или растянуть. За счет этой энергии можно получить определенную работу. Если освободить один из концов пружины, то он сможет переместить на некоторое расстояние связанное с этим концом тело. Точно так же энергия электрического поля может быть реализована, если внести в него какой-либо заряд. Под действием сил поля этот заряд будет перемещаться по направлению силовых линий, совершая определенную работу.
Для характеристики энергии, запасенной в каждой точке электрического поля, введено специальное понятие — электрический потенциал. Электрический потенциал? поля в данной точке равен работе, которую могут совершить силы этого поля при перемещении единицы положительного заряда из этой точки за пределы поля.
Понятие электрического потенциала аналогично понятию уровня для различных точек земной поверхности. Очевидно, что для подъема локомотива в точку Б (рис. 7) нужно затратить большую работу, чем для подъема его в точку А. Поэтому локомотив, поднятый на уровень Н2, при спуске сможет совершить большую работу, чем локомотив, поднятый на уровень Н2 За нулевой уровень, от которого производится отсчет высоты, принимают обычно уровень моря.
Точно так же за нулевой потенциал условно принимают потенциал, который имеет поверхность земли.
Электрическое напряжение . Различные точки электрического поля обладают разными потенциалами. Обычно нас мало интересует абсолютная величина потенциалов отдельных точек электрического поля, но нам весьма важно знать разность потенциалов?1-?2 между двумя точками поля А и Б (рис. 8). Разность потенциалов?1 и?2 двух точек поля характеризует собой работу, затрачиваемую силами поля на перемещение единичного заряда из одной точки поля с большим потенциалом в другую точку с меньшим потенциалом.
Точно так же нас на практике мало интересуют абсолютные высоты Н1и Н2 точек А и Б над уровнем моря (см. рис. 7), но для нас важно знать разность уровней И между этими точками, так как на подъем локомотива из точки А в точку Б надо затратить работу, зависящую от величины Я. Разность потенциалов между двумя точками поля носит название электрического напряжения. Электрическое напряжение обозначают буквой U (и). Оно численно равно отношению работы W, которую нужно затратить на перемещение положительного заряда q из одной точки поля в другую, к этому заряду, т. е.
U = W / q (2)
Следовательно, напряжение U, действующее между различными точками электрического поля, характеризует запасенную в этом поле энергию, которая может быть отдана путем перемещения между этими точками электрических зарядов.
Электрическое напряжение — важнейшая электрическая величина, позволяющая вычислять работу и мощность, развиваемую при перемещении зарядов в электрическом поле. Единицей электрического напряжения служит вольт (В).
В технике напряжение иногда измеряют в тысячных долях вольта — милливольтах (мВ) и миллионных долях вольта — микровольтах (мкВ). Для измерения высоких напряжений пользуются более крупными единицами — киловольтами (кВ) — тысячами вольт.
Напряженность электрического поля при однородном поле представляет собой отношение электрического напряжения, действующего между двумя точками поля, к расстоянию l между этими точками:
E = U / l (3)
Напряженность электрического поля измеряют в вольтах на метр (В/м). При напряженности поля в 1 В/м на заряд в 1 Кл действует сила, равная 1 ньютону (1 Н). В некоторых случаях применяют более крупные единицы измерения напряженности поля В/см (100 В/м) и В/мм (1000 В/м).
напряжённость электри́ческого по́ля
(Е ), основная силовая характеристика электрического поля, равная отношению силы, действующей на точечный электрический заряд в данной точке пространства, к величине заряда.
НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
НАПРЯЖЕННОСТЬ ЭЛЕКТРИ́ЧЕСКОГО ПО́ЛЯ (Е ), основная силовая характеристика электрического поля (см.
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ)
, определяемая силой (F), действующей на точечный (единичный) положительный электрический заряд (см. ЭЛЕКТРИЧЕСКИЙ ЗАРЯД)
(Q o), помещенный в данную точку поля.
Заряд должен быть малым, чтобы не изменять ни величины, ни расположения тех зарядов, которые порождают исследуемое поле (т. е. заряд, не искажающий поля, которое с его помощью изучается, при этом собственным электрическим полем точечного заряда пренебрегают).
Е = F/ Q o .
В общем случае напряженность поля Е = F/Q. Т.е. напряженность в данной точке пространства есть отношение силы, действующей на заряд, помещенный в эту точку к величине этого заряда.
Единица измерения напряженности электростатического поля — 1Н/Кл =1В/м.
Напряженность 1Н/Кл — это напряженность такого поля, которое на точечный заряд 1 Кл действует силой 1 Н, эту единицу в системе СИ называют В/м.
Напряженность электрического поля — векторная величина. Направление вектора напряженности Е совпадает с направлением кулоновской (см.
Кулона закон (см. КУЛОНА ЗАКОН)
) силы, действующей на точечный положительный заряд, помещенный в данную точку поля.
Если поле создается положительным зарядом, то вектор напряженности такого поля направлен от заряда вдоль радиуса-вектора, если поле создается отрицательным зарядом, то вектор напряженности поля Е направлен к заряду.
Графической характеристикой поля являются силовые линии (см. СИЛОВЫЕ ЛИНИИ)
напряженности электрического поля, касательные к которым в каждой точке совпадают с направлением вектора напряженности.
Для электростатического поля напряженность электрического поля может быть представлена как градиент (см. ГРАДИЕНТ)
электрического потенциала (см. ПОТЕНЦИАЛ (в физике))
j;
Е = — gradj.
Вектор напряженности электрического поля направлен в сторону убывания потенциала.
В вакууме напряженность электрического поля удовлетворяет принципу суперпозиции, согласно которому полная напряженность поля в точке равна геометрической сумме напряженностей полей, создаваемых отдельными заряженными частицами.
Энциклопедический словарь . 2009 .
Смотреть что такое «напряжённость электрического поля» в других словарях:
Размерность LMT−3I−1 Единицы измерения СИ В/м Примечан … Википедия
— (E), векторная характеристика электрического поля, равная отношению силы, действующей на точечный электрический заряд в данной точке пространства, к величине заряда. В СИ измеряется в В/м … Современная энциклопедия
напряжённость электрического поля — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] Тематики электротехника, основные понятия EN intensity of electric fieldelectric field intensitystrength of… …
Напряжённость электрического поля — Напряженность электрического поля НАПРЯЖЁННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ (E), векторная характеристика электрического поля, равная отношению силы, действующей на точечный электрический заряд в данной точке пространства, к величине заряда.
В СИ… … Иллюстрированный энциклопедический словарь
напряжённость электрического поля — elektrinio lauko stipris statusas T sritis automatika atitikmenys: angl. electric field intensity; electric field strength vok. elektrische Feldstärke, f rus. напряжённость электрического поля, f pranc. intensité du champ électrique, f … Automatikos terminų žodynas
напряжённость электрического поля — elektrinio lauko stipris statusas T sritis fizika atitikmenys: angl. electric field strength vok. elektrische Feldstärke, f rus. напряжённость электрического поля, f pranc. intensité du champ électrique, f … Fizikos terminų žodynas — (t), векторная величина, осн. силовая характеристика электрич. поля, равная отношению силы, действующей to точечный электрич. заряд в данной точке пространства, к величине заряда. Единица СИ В/м … Естествознание. Энциклопедический словарь
пробивная напряжённость электрического поля — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров.
Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN disruptive electric strengthdisruptive electric field strength … Справочник технического переводчика
Электростатика | Формулы по физике
Электрический заряд
Найти
Известно, что:
qne =
Вычислить ‘q’Закон Кулона
Найти
Известно, что:
Fkq1q2r =
Вычислить ‘F’Постоянная Кулона
Найти
Известно, что:
kπε_0 =
Вычислить ‘k’Относительная диэлектрическая проницаемость
Найти
Известно, что:
εF_вакF_окр =
Вычислить ‘ε’Электрическое поле
Найти
Известно, что:
EFq =
Вычислить ‘E’Электрическое поле точечного заряда в вакууме
Найти
Известно, что:
Ekq_0r =
Вычислить ‘E’Электрическое поле точечного заряда в окружающей среде
Найти
Известно, что:
E_окрkq_0εr =
Вычислить ‘E_окр’Электрическое поле вне заряженной сферы
Найти
Известно, что:
Ekσ4πRr =
Вычислить ‘E’Электрическое поле вне заряженной сферы
Найти
Известно, что:
Ekqr =
Вычислить ‘E’Электрическое поле бесконечной заряженной плоскости
Найти
Известно, что:
Ek2πσ =
Вычислить ‘E’Электрическое поле бесконечной заряженной плоскости
Найти
Известно, что:
Eσε_0 =
Вычислить ‘E’Электрическое поле конденсатора
Найти
Известно, что:
Ekπσ =
Вычислить ‘E’Работа в электрическом поле
Найти
Известно, что:
AFΔ_d =
Вычислить ‘A’Потенциальная энергия системы двух точечных зарядов
Найти
Известно, что:
Wkq0qεr =
Вычислить ‘W’Работа в электрическом поле — разность потенциальных энергий
Найти
Известно, что:
AW1W2 =
Вычислить ‘A’Потенциал электростатического поля
Найти
Известно, что:
φWq =
Вычислить ‘φ’Напряжение — разность потенциалов
Найти
Известно, что:
Uφ1φ2 =
Вычислить ‘U’Работа переноса заряда
Найти
Известно, что:
AqU =
Вычислить ‘A’Потенциал электростатического поля вокруг точечного заряда
Найти
Известно, что:
φkq0εr =
Вычислить ‘φ’Напряжённость электростатического поля
Найти
Известно, что:
EUΔ_d =
Вычислить ‘E’Результирующее электрическое поле
Найти
Известно, что:
EE0E1 =
Вычислить ‘E’Электрический момент
Найти
Известно, что:
pql =
Вычислить ‘p’Электрическая ёмкость
Найти
Известно, что:
Cqφ =
Вычислить ‘C’Электрическая ёмкость шара
Найти
Известно, что:
CεRk =
Вычислить ‘C’Электрическая ёмкость двух проводников
Найти
Известно, что:
CqU =
Вычислить ‘C’Электрическая ёмкость плоского конденсатора
Найти
Известно, что:
Cεε0Sd =
Вычислить ‘C’Электрическая ёмкость сферического конденсатора
Найти
Известно, что:
Cπεε0R1R2 =
Вычислить ‘C’Потенциальная энергия заряженного плоского конденсатора
Найти
Известно, что:
WqE1d =
Вычислить ‘W’Потенциальная энергия заряженного плоского конденсатора
Найти
Известно, что:
WqEd =
Вычислить ‘W’Потенциальная энергия заряженного плоского конденсатора
Найти
Известно, что:
WqU =
Вычислить ‘W’Потенциальная энергия заряженного плоского конденсатора
Найти
Известно, что:
WCU =
Вычислить ‘W’Потенциальная энергия заряженного плоского конденсатора
Найти
Известно, что:
WqC =
Вычислить ‘W’Потенциальная энергия заряженного плоского конденсатора
Найти
Известно, что:
Wεε0EV =
Вычислить ‘W’Потенциальная энергия заряженного плоского конденсатора
Найти
Известно, что:
Wεε0ESd =
Вычислить ‘W’Плотность энергии электрического поля
Найти
Известно, что:
ω_pWV =
Вычислить ‘ω_p’Плотность энергии электрического поля
Найти
Известно, что:
ω_pε0εE =
Вычислить ‘ω_p’Потенциал электрического поля — формулы определения, характеристика и единицы измерения » Kupuk.
netПотенциал электрического поля — скалярная величина тела, характеризующая интенсивность. Электромощность выражается через определённый параметр. Важным свойством электрополя, которое не содержит вихрей и формируется недвижимыми источниками, считается его потенциальность. Научные работники длительное время думали над особенностями электрических и магнитных полей, пока их сущность в полной мере не стала ясной.
Вещественное значение электрического поля
Учёные длительное время изучали секрет электроэнергии. Главная награда в ее исследовании дана Эрстеду. Его основное открытие — впервые экспериментально установлена связь между электрическими и магнитными явлениями в 1819—1820 гг.
Стало ясно, что колебания предполагают суперпозицию изменяющихся во времени электрических и магнитных полей. Вектор магнитной интенсивности перпендикулярен электрическому вектору, связанному через длинную среду (некоторая физическая величина).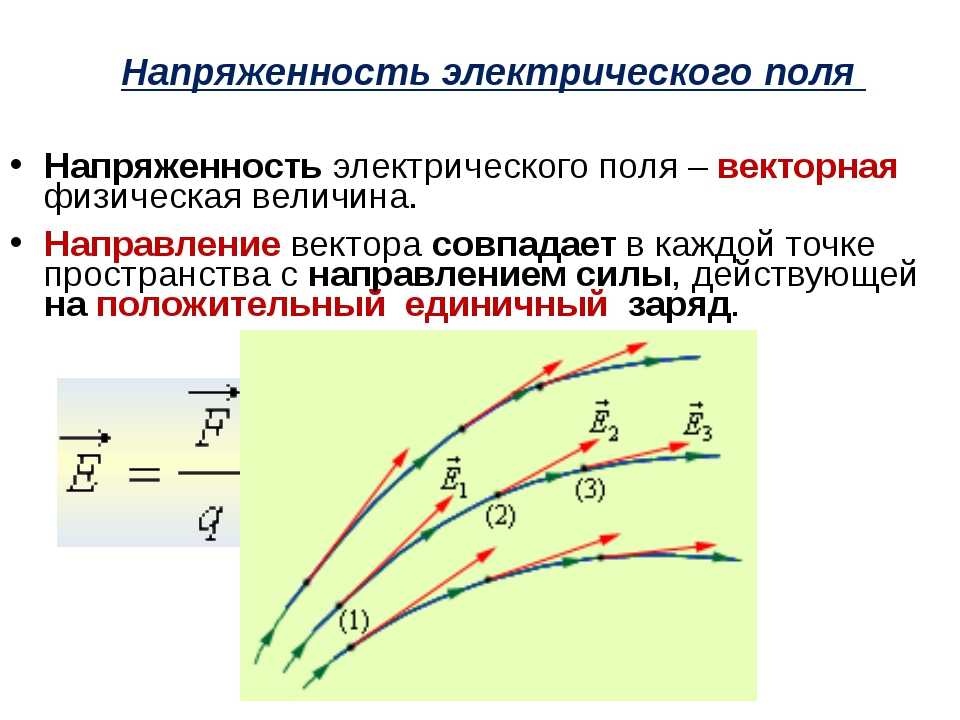
Электростатическое воздействие — это действие через поле.
Особенности воздействия:
- Каждый электрический заряд создаёт вокруг себя электростатическое поле.
- Электрополем называется пространство, в котором действуют силы напряжения.
- Величины, характеризующие поле в этой точке, — это интенсивность и потенциал.
Напряжённостью электростатического явления в этой точке называется отношение электросилы, действующей на помещённый в этой точке пробный заряд (положительный) к значению этого заряда:
- E =F /q (над E и F вектор).
- Единица напряжённости электростатического поля — 1 N/C.
Напряжённость электрополя в этой точке всегда имеет отдачу в соответствии с направлением силы, действующей на положительный пробный заряд.
Значение напряжённости электростатического поля на расстоянии R от источника Q может обозначаться простой формулой: E=k |Q|/R2.
Для графического представления поля используются линии — кривые, для которых вектор напряжённости в каждой точке имеет касательную часть. Поле со сферической симметрией называется центральным. Если линии расположены параллельно друг другу, а интенсивность имеет в каждой точке одинаковое значение, то поле называется однородным.
Разность потенциалов в физике в данный момент — это отношение энергии точечного положительного пробного груза, помещённого в этой точке к значению этого заряда: V=Ep/q.
Единицей измерения потенциала точки электрического поля является 1 В (вольт).
Потенциал электрического поля, формула на расстоянии R от источника Q можно рассчитать: V=k Q/r.
Заряд вокруг объекта
Конечно, можно говорить о поле, если есть какой-либо его источник. Каждое электрическое тело создаёт вокруг себя градиент потенциала электрического поля.
По сравнению с гравитационными полями, есть важное отличие:
- Гравитационные силы являются силами притяжения и могут измеряться.
- Силы электричества могут быть как силами притяжения, так и отталкивания.
Известно, что линии поля относятся к векторам силы, действующим на тело в этой точке. Учёные сошлись во мнении, что стрелки линии поля будут выставлять обратный вектор силы, действующей на отрицательный заряд. Следовательно, силовые линии «выходят» из зарядов положительных и «бегут» к отрицательным энергетическим зарядам.
Напряжённость электрополя
В электрическом поле, так же как и в гравитационном, возникает понятие напряжённости. Это говорит о том, какая сила будет действовать, а известно, что эта сила зависит от источника и от расстояния. Именно интенсивность — характеристика этого поля, которое можно зарядить.
По определению, напряжённость электрополя — это отношение силы, действующей на его значение.
Если поле не вызвано одним источником, а, например, двумя положительными зарядами, то для вычисления интенсивности в этой точке пространства есть смысл применить принцип суперпозиции.
Например, есть данные центрального поля, создаваемые зарядом Q. Следует разместить на расстоянии R1 пробный заряд q. Делается работа по перемещению этого испытательного заряда на расстояние R2 от источника поля.
Для того чтобы система заряда двигалась с одинаковой скоростью, нужно постоянно действовать на него с усилием, уравновешивающем величину Куломба. Но вместе с изменением расстояния от источника эта сила меняется обратно пропорционально квадрату расстояния. Использовать нужно среднюю величину, действующую на пробный заряд.
Чтобы определить, является ли работа положительной или отрицательной, нужно подумать, каков угол между вектором приложенного усилия и вектором перемещения.
Если пробный заряд притягивается источником поля, и работа, которую выполняют, перемещает этот заряд ближе к источнику, тогда нужно сбалансировать притяжение.
Одним словом, прилагают усилие, которое создаёт с вектором смещение на угол 180°. Если cos (α)= -1, то работа отрицательная. Но если источник имеет взаимодействие с грузом так, чтобы уравновесить силу, параллельную цепи смещения, так что условие α=0°, т. е. cos (α) = 1 — работа положительная.
Потенциальная энергия
Вычисляя потенциальную энергию испытательного заряда в этой точке поля, используют свойство, при котором разница потенциальной энергии в двух точках равна работе, выполняемой при перемещении этого значения из одной точки в другую (то же самое делали, включая энергию в гравитационном поле).
Для того чтобы вычислить потенциальную энергию в этой точке, нужно переместить пробный заряд в место, где потенциал равен нулю. Такое место находится в точке, бесконечно отдалённой от источника.
Положительный или отрицательный знак потенциала выбирают в зависимости от того, отталкивают груз с источником или притягивают. Если заряд источника является отрицательным, то нахождение электростатического потенциала является таким же. Когда источник является положительным, потенциал — тоже.
Эквипотенциальные поверхности
Если предположить, что источником электрополя является точечно заряженная частица (т. е. поле центральное), из этого следует, что все точки пространства, которые находятся от него одинаково далеко, имеют равный потенциал. В пространстве совокупность таких точек образует поверхность шара, а заряд-источник находится в центре сферы.
Однако, если электрополе не имеет централизованного характера, всё равно можно назначить такие поверхности, что пробный заряд, размещённый в любой точке этой поверхности, будет иметь тот же потенциал.
Например, в случае однородного поля такой поверхностью является любая плоскость, перпендикулярная линии поля.
Кроме того, у направляющих есть ещё одна группа тел — это диэлектрики. Для начала необходимо уточнить разницу между диэлектриком и проводником. Проводники — это тела, в которых заряды могут свободно перемещаться. Примером проводника является медный провод. Если положить на него груз, а затем дотронуться до него рукой, то этот груз будет «всплывать» из проводника и, следовательно, разгрузит его.
Но если положительно электрифицировать стекло, которое является диэлектриком, то прикосновение через руку не приведёт к его разрядке. Электроны от конечности будут течь только в точке контакта, но это стекло будет по-прежнему наэлектризовано в местах, где к нему прикасаются.
Электроны в диэлектрике не могут свободно двигаться. Они ограничены атомами и молекулами, которые не могут покинуть. Но если поместить диэлектрик в поле разрядов между положительным и отрицательным зарядом, это расположение электронов и атомных ядер изменится.
Эти частицы ведут себя как диполи. Такая позиция показывает все молекулы в диэлектрике.
Образуется цепочка диполей с зарядами, положительными с одной стороны, и отрицательными — с другой. Это явление называется диэлектрической поляризацией. Поляризованный диэлектрик создаёт своё поле, внутреннее, и у него вектор напряжённости всегда направлен противоположно полю, в котором расположен диэлектрик. Таким образом, вред от аварий при напряжении поля уменьшается.
формула, величина, направление, ответы на часто задаваемые вопросы
В этой статье мы будем использовать закон Гаусса для расчета электрического поля между двумя пластинами и электрического поля конденсатора.
Электрическое поле между двумя пластинами:Игровой автомат электрическое поле электрическое свойство, связанное с любым зарядом в космосе. Таким образом, электрическое поле — это любая физическая величина, которая принимает разные значения электрической силы в разных точках данного пространства.
Электрическое поле — это область или область, в каждой точке которой действует электрическая сила.
В общих чертах электрические поля можно описать как электрическую силу на единицу заряда.
Если мы рассмотрим бесконечную плоскость, имеющую однородный заряд на единицу площади, т. Е., То для бесконечной плоскости электрическое поле может быть задано как:
Давайте посмотрим на электрическое поле, когда задействованы две заряженные пластины.
Между двумя заряженными пластинами существует однородное электрическое поле:Согласно закону Кулона электрическое поле вокруг точечного заряда уменьшается по мере удаления от него. Однако однородное электрическое поле может быть создано путем выравнивания двух бесконечно больших проводящих пластин параллельно друг другу.
«Если в каждой точке данного пространства напряженность электрического поля остается неизменной, то электрическое поле называется однородным электрическим полем».
Силовые линии однородного электрического поля стремятся быть параллельны друг другу, и расстояние между ними также равно.
Параллельные силовые линии и однородное электрическое поле между двумя параллельными пластинами обеспечивают одинаковую силу притяжения и отталкивания испытательного заряда независимо от того, где он находится в поле.
Линии поля всегда проходят от областей с высоким потенциалом к областям с низким потенциалом.
Направление электрического поля между двумя пластинами:Электрическое поле распространяется от положительно заряженной пластины к отрицательно заряженной.
Например, предположим, что верхняя пластина положительна, а нижняя пластина отрицательна, тогда направление электрического поля задается, как показано на рисунке ниже.
Положительные и отрицательные заряды ощущают силу под действием электрического поля, но ее направление зависит от тип заряда, положительный или отрицательный.
Положительные заряды воспринимают силы в направлении электрического поля, тогда как отрицательные заряды ощущают силы в противоположном направлении..
Предположим, у нас есть две бесконечные пластины, которые параллельны друг другу и имеют положительную плотность заряда. Теперь мы вычисляем чистое электрическое поле, создаваемое этими двумя заряженными параллельными пластинами.
Оба электрических поля противостоят друг другу в центре двух пластин. В результате они нейтрализуют друг друга, что приводит к нулевому электрическому полю внутри.
∴Ein = 0
Оба электрических поля направлены в одном направлении вне пластин, то есть слева и справа. Таким образом, его векторная сумма будет? /? 0.
Eout = E1 + E2
Электрическое поле между двумя параллельными пластинами противоположного заряда:Предположим, у нас есть две пластины с плотностями заряда + ර и -ර.
Расстояние d разделяет эти две пластины.
Пластина с положительной плотностью заряда создает электрическое поле E = ර / 2 ε0. И направление его — наружу или от пластины, в то время как пластина с отрицательной плотностью заряда имеет противоположное направление, то есть направление внутрь.
Итак, когда мы используем принцип суперпозиции с обеих сторон пластин, снаружи и внутри пластин, то мы можем видеть, что вне пластины оба вектора электрического поля имеют одинаковую величину и противоположное направление, и, таким образом, оба электрических поля компенсируют друг друга. . Так, вне пластин не будет электрического поля.
∴Eвых=0
Поскольку они поддерживают друг друга в одном направлении, чистое электрическое поле между двумя пластинами составляет E = ර / ε0.
Eв = E1 + E2
Это тот факт, что мы используем для формирования конденсатора с параллельными пластинами.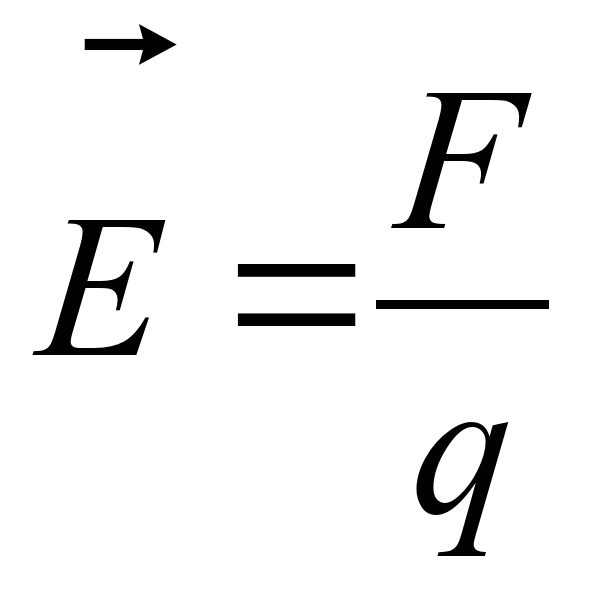
В физике для описания любого распределения заряда используется либо разность потенциалов ΔV, либо электрическое поле E. Разность потенциалов ΔV тесно связана с энергией, а электрическое поле E связано с силой.
E — векторная величина, подразумевая, что она имеет как величину, так и направление, тогда как ΔV — это скалярная переменная без направления.
Когда между двумя проводящими пластинами, параллельными друг другу, подается напряжение, создается однородное электрическое поле.
Сила электрического поля прямо пропорциональна приложенному напряжению и обратно пропорциональна расстоянию между двумя пластинами.
Электрическое поле между двумя параллельными пластинчатыми конденсаторами: Параллельный пластинчатый конденсатор:Конденсатор с параллельными пластинами состоит из двух проводящих металлических пластин, которые соединены параллельно и разнесены на определенное расстояние.
Диэлектрическая среда заполняет зазор между двумя пластинами.
Диэлектрическая среда представляет собой изолирующий материал, и это может быть воздух, вакуум или некоторые непроводящие материалы, такие как слюда, стекло, электролитический гель, бумажная вата и т. Д. Диэлектрический материал препятствует прохождению тока через него из-за своего непроводящего свойства.
Однако при приложении напряжения к параллельным пластинам атомы диэлектрической среды поляризуются под действием электрического поля. В процессе поляризации образуются диполи, и эти положительные и отрицательные заряды будут накапливаться на пластинах конденсатора с параллельными пластинами. По мере накопления зарядов через конденсатор течет ток, пока разность потенциалов между двумя параллельными пластинами не уравняется с потенциалом источника.
Напряженность электрического поля конденсатора не должна превышать напряженность поля пробоя диэлектрического материала в конденсаторах с параллельными пластинами.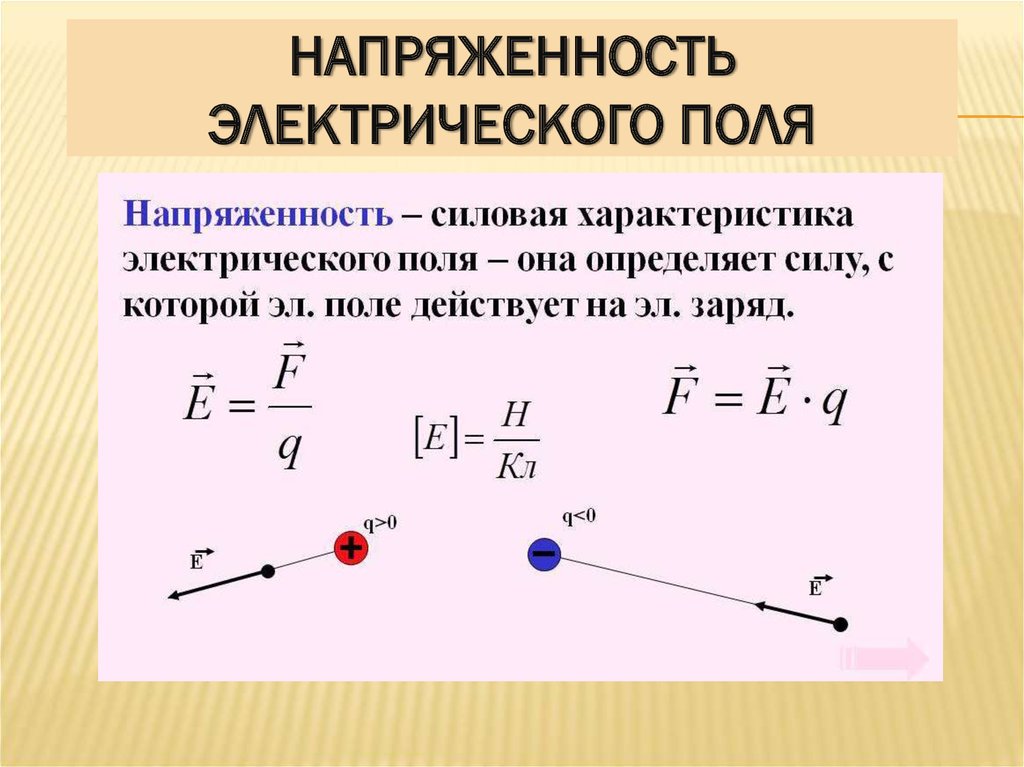
Если рабочее напряжение конденсатора превышает его предел, пробой диэлектрика вызывает короткое замыкание между пластинами, немедленно разрушая конденсатор.
Таким образом, чтобы защитить конденсатор от такой ситуации, не следует превышать предел приложенного напряжения и выбирать диапазон напряжения конденсаторов.
Электрическое поле между параллельными пластинами конденсатора:
На следующем рисунке показан конденсатор с параллельными пластинами.
В этом случае мы возьмем две большие проводящие пластины, параллельные друг другу, и разделим их на d. Зазор заполнен диэлектрической средой, как показано на рисунке. Расстояние d между двумя пластинами значительно меньше площади каждой пластины. Поэтому мы можем написать d <
Здесь плотность заряда 1-й пластины составляет +, а плотность заряда 2-й пластины -ර. Пластина 1 имеет общий заряд Q, а пластина 2 имеет общий заряд -Q.
Как мы видели ранее, когда взяты две параллельные пластины с противоположным распределением заряда, электрическое поле во внешней области будет равно нулю.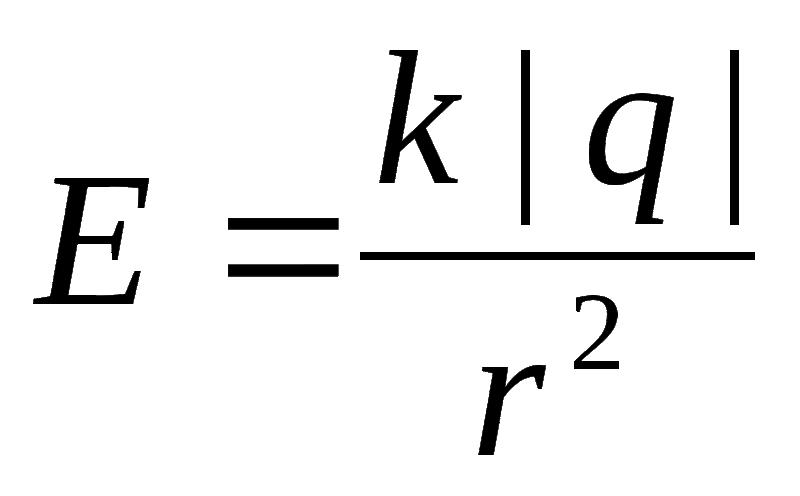
В результате чистое электрическое поле в центре конденсатора с параллельными пластинами можно рассчитать следующим образом:
E = E1 + E2
= ර / 2 ε + ර / 2 ε
= ර / ε
Где ර — поверхностная плотность заряда пластины
ε — диэлектрическая проницаемость диэлектрического материала, используемого для формирования конденсаторов.
Из приведенного выше уравнения мы можем сказать, что диэлектрическая среда вызывает уменьшение напряженности электрического поля, но она используется для увеличения емкости и поддержания контакта проводящих пластин.
Величина электрического поля между двумя заряженными пластинами:Если принять во внимание две бесконечно большие пластины, напряжение не подается, то величина электрического поля согласно закону Гаусса должна быть постоянной. Но электрическое поле между двумя пластинами, как мы заявляли ранее, зависит от плотности заряда пластин.
Следовательно, если две пластины имеют одинаковые плотности заряда, то электрическое поле между ними равно нулю, а в случае противоположных плотностей заряда электрическое поле между двумя пластинами задается постоянным значением.
Когда заряженным пластинам подается напряжение, величина электрического поля определяется разностью потенциалов между ними. Более высокая разность потенциалов создает сильное электрическое поле, а большее расстояние между пластинами приводит к слабому электрическому полю.
Таким образом, расстояние между пластинами и разность потенциалов являются важными факторами напряженности электрического поля.
Часто задаваемые вопросы:
Q. Чем электрическое поле между параллельными пластинами отличается от электрического поля вокруг заряженной сферы?Ответ Электрические поля между параллельными пластинами и вокруг заряженной сферы неодинаковы. Посмотрим, как они различаются.
Электрическое поле между параллельными пластинами зависит от плотности заряда пластин. Если они заряжены противоположно, то поле между пластинами / ε0, а если у них есть заряды, то поле между ними будет равно нулю.
Вне заряженной сферы электрическое поле определяется выражением тогда как поле внутри сферы равно нулю. В этом случае r представляет собой расстояние между точкой и центром.
В. Что произойдет с электрическим полем и напряжением, если расстояние между пластинами конденсатора увеличится вдвое?Ответ E = ර / ε0 определяет электрическое поле между конденсаторами с параллельными пластинами по закону Гаусса.
Согласно закону Гаусса электрическое поле остается постоянным, поскольку оно не зависит от расстояния между двумя пластинами конденсатора. Если говорить о разности потенциалов, она прямо пропорциональна расстоянию между двумя пластинами конденсатора и определяется выражением
Таким образом, если расстояние увеличивается вдвое, то увеличивается и разность потенциалов.
Ответ В конденсаторах с параллельными пластинами обе пластины заряжены противоположно. Таким образом, электрическое поле вне пластин будет нейтрализовано.
Обе пластины заряжены противоположно, поэтому поле между пластинами будет поддерживать друг друга. Кроме того, между двумя пластинами присутствует диэлектрическая среда, поэтому диэлектрическая проницаемость диэлектрика также будет важным фактором.
Закон Гаусса и концепция суперпозиции используются для расчета электрического поля между двумя пластинами.
Е = Е1 + Е2
=
=
Где ර — поверхностная плотность заряда
ε — диэлектрическая проницаемость диэлектрического материала.
Q.
Почему электрическое поле между пластинами конденсаторов уменьшается при введении диэлектрической пластины? Объясните с помощью схемы.Ответ Когда диэлектрический материал помещается между параллельными пластинами конденсатора под действием внешнего электрического поля, атомы диэлектрического материала поляризуются.
Накопление заряда на обкладках конденсатора вызвано индуцированным зарядом в диэлектрическом материале. Как показано на рисунке ниже, это накопление заряда вызывает электрическое поле между двумя пластинами, которое сопротивляется внешнему электрическому полю.
На приведенном выше рисунке показана диэлектрическая пластина между двумя пластинами конденсатора, поскольку диэлектрическая пластина индуцирует противоположное электрическое поле; следовательно, чистое электрическое поле между пластинами конденсатора уменьшается.
Q.
Две идентичные металлические пластины получают положительный заряд Q1 и Q2 соответственно. Если их соединить вместе, чтобы сформировать конденсатор с параллельными пластинами с емкостью C, разность потенциалов между ними составит …… ..Ответ Емкость конденсатора с параллельными пластинами, который состоит из двух одинаковых металлических пластин, рассчитывается следующим образом:
Где C — емкость конденсатора с параллельными пластинами.
A — площадь каждой пластины
d — расстояние между параллельными пластинами
Скажем, плотность поверхностного заряда равна
Теперь чистое электрическое поле можно определить как
Возможная разница представлена,
Таким образом, подставляя указанные выше значения в это уравнение, мы получаем разность потенциалов
В. Что происходит, когда между параллельными пластинами конденсатора вводится диэлектрический материал?Ответ Электрическое поле, напряжение и емкость изменяются, когда мы вводим диэлектрический материал между параллельными пластинами конденсатора.
Электрическое поле падает, когда диэлектрический материал вводится между параллельными пластинами конденсатора из-за накопления заряда на параллельных пластинах, что создает электрическое поле в направлении, противоположном внешнему полю.
Электрическое поле определяется выражением
Электрическое поле и напряжение пропорциональны друг другу; таким образом, напряжение также уменьшается.
С другой стороны, емкость конденсатора увеличивается, поскольку она пропорциональна диэлектрической проницаемости диэлектрического материала.
В. Существует ли магнитное поле между пластинами конденсатора?Ответ Магнитные поля существуют между двумя пластинами только тогда, когда электрическое поле между двумя пластинами изменяется.
Таким образом, когда конденсатор заряжается или разряжается, электрическое поле между двумя пластинами изменяется, и только в это время существует магнитное поле.
Ответ Конденсаторы — это электрические устройства, которые используют постоянное электрическое поле для хранения электрических зарядов в виде электроэнергия. Между пластинами конденсатора лежит диэлектрический материал.
Если приложенное внешнее электрическое поле превышает напряженность поля пробоя диэлектрического материала, то изолирующий диэлектрический материал становится проводящим. Электрический пробой приводит к возникновению искры между двумя пластинами, которая разрушает конденсатор.
Каждый конденсатор имеет разную емкость в зависимости от используемого диэлектрического материала, площади пластин и расстояния между ними.
Допуск конденсатора находится где-то между в рекламируемой стоимости.
В. Каковы применения закона Гаусса?Ответ Закон Гаусса имеет различные приложения.
В некоторых случаях расчет электрических полей требует жесткого интегрирования и становится довольно сложным. Мы используем закон Гаусса, чтобы упростить оценку электрических полей без сложного интегрирования.
- Электрическое поле на расстоянии r в случае бесконечно длинной проволоки E =? / 2? Ε0
Где ? — линейная плотность заряда проволоки.
- Напряженность электрического поля почти бесконечного плоского листа E = ර / 2 ε0
- Напряженность электрического поля на внешней поверхности сферической оболочки равна и E = 0 внутри оболочки.
- Напряженность электрического поля между двумя параллельными пластинами E = / ε0, когда диэлектрическая среда находится между двумя пластинами, тогда E = / ε.
Ответ Поддерживая электрическое поле, конденсаторы используются для хранения электрических зарядов в электрической энергии.
Когда пластины разделены воздухом или пространством, формула конденсатора с параллельными пластинами выглядит так:
, Где C — емкость конденсатора.
Работа сил электростатического поля — справочник студента
Рассмотрим ситуацию: заряд q0 попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q0 со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.
Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными, а само поле называется потенциальным.
Потенциал
Система «заряд — электростатическое поле» или «заряд — заряд» обладает потенциальной энергией, подобно тому, как система «гравитационное поле — тело» обладает потенциальной энергией.
Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал — это характеристика электростатического поля.
Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.
Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.
В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело — наоборот.
Потенциальная энергия поля — это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.
Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.
Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.
Разность потенциалов
Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов
Эту формулу можно представить в ином виде
Эквипотенциальная поверхность (линия) — поверхность равного потенциала. Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.
Напряжение
- Разность потенциалов называют еще электрическим напряжением при условии, что сторонние силы не действуют или их действием можно пренебречь.
- Напряжение между двумя точками в однородном электрическом поле, расположенными по одной линии напряженности, равно произведению модуля вектора напряженности поля на расстояние между этими точками.
- От величины напряжения зависит ток в цепи и энергия заряженной частицы.
Принцип суперпозиции
Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности
Как определить знак потенциала
При решении задач возникает много путаницы при определении знака потенциала, разности потенциалов, работы.
На рисунке изображены линии напряженности. В какой точке поля потенциал больше?
Верный ответ — точка 1. Вспомним, что линии напряженности начинаются на положительном заряде, а значит положительный заряд находится слева, следовательно максимальным потенциалом обладает крайняя левая точка.
Если происходит исследование поля, которое создается отрицательным зарядом, то потенциал поля вблизи заряда имеет отрицательное значение, в этом легко убедиться, если в формулу подставить заряд со знаком «минус». Чем дальше от отрицательного заряда, тем потенциал поля больше.
Если происходит перемещение положительного заряда вдоль линий напряженности, то разность потенциалов и работа являются положительными. Если вдоль линий напряженности происходит перемещение отрицательного заряда, то разность потенциалов имеет знак «+», работа имеет знак «-«.
Порассуждайте самостоятельно отрицательные или положительные значения будут принимать работа и разность потенциалов, если заряд перемещать в обратном направлении относительно линий напряженности.
Зависимость напряженности и потенциала от расстояния
Потенциал поля, созданного равномерно заряженной сферой радиусом R и зарядом q на расстоянии r от центра сферы, равен
Напряжение в природе
Напряжение в клетках сетчатки глаза при попадания в них света около 0,01 В. Напряжение в телефонных сетях может достигать 60 В.
Электрический угорь способен создавать напряжение до 650 В.
Энергия взаимодействия зарядов*
- Из определения потенциала следует, что потенциальная энергия электростатического взаимодействия двух зарядов q1 и q2, находящихся на расстоянии r друг от друга, численно равна работе, которая совершается при перемещении точечного заряда q2 из бесконечности в данную точку поля, созданного зарядом q1
- Аналогично Тогда энергия взаимодействия двух точечных зарядов
- Энергия взаимодействия n зарядов
Источник: http://fizmat.by/kursy/jelektrichestvo/potencial
Работа перемещения заряда в электростатическом поле
1
Работа перемещения заряда вдоль линии напряженности электростатического поля Aφ = q (φ1 — φ2 ). При перемещении заряда в обратном направлении работа сторонних сил имеет минимум, величина которого зависит от способа приложения сторонней силы.
Рассмотрим движение положительного заряда q в однородном электрическом поле напряженности E плоского конденсатора (рис.1а) в отсутствии сил гравитационного поля.
Рисунок 1 (а). Движение положительного заряда q в однородном электрическом поле напряженности E плоского конденсатора.
; ,
где t — время движения заряда. Работу перемещения заряда представим в двух видах:
Отметим, что для того, чтобы остановить заряд в точке 2, необходимо затратить работу торможения, равную .
Чтобы вернуть заряд q по тому же пути из точки 2 в точку 1, необходимо приложить стороннюю силу F (рис.1б), которую можно представить в виде суммы , где — сила, равная по модулю кулоновской силе , обеспечивающая равновесие заряда (неподвижность) в электростатическом поле, которую назовем силой левитации.
Рисунок 1 (б)
Если , то перемещение заряда вверх не происходит, поскольку . Если , то начинает работать II закон Ньютона: ускорение ; . Время движения вверх
- (3)
- Запишем баланс импульсов сил:
- (4)
- Возведя в квадрат и разделив на 2m обе части равенства, получим баланс энергий (работ):
- (5)
- Или
- (5а)
- где — работа силы левитации в статическом состоянии, — обычная работа силы , вызывающей ускоренное движение, — работа, связанная с ускоренным движением силы левитации, — суммарная работа сторонней силы F.
- Выразим эти работы через работу , определяемую выражением (2).
- (6)
- (7)
- (8)
- Таким образом, зависимость между работами и имеет гиперболический характер.
- (9)
- Тогда суммарную работу сторонней силы F можно записать так
- (10)
Это выражение имеет минимум в случае , равный . На графике (рис.2) показана зависимость суммарной работы от соотношения .
Рисунок 2. Зависимость суммарной работы от соотношения
Из графика видно, что даже в самом благоприятном случае работа подъема заряда сторонней силой в 4 раза больше работы кулоновской силы, совершающей перемещение заряда вниз.
Здесь необходимо отметить следующее: кулоновская сила препятствует перемещению заряда вверх, т.е.
совершает отрицательную работу, но по модулю она не равна , поскольку движение происходит под действием силы ΔF в течение времени t1, которое связано с временем t формулы (1) соотношением: .
(11)
Рассмотрим другой вариант перемещения заряда из точки 2 в точку 1 за счет действия мгновенной силы [1,2,3] в виде , где — -функция Дирака. Величину будем называть единичным импульсом силы. Тогда дифференциальное уравнение движения заряда запишется в виде:
(12)
при нулевых начальных условиях: и . H(t) — единичная (ступенчатая) функция Хевисайда, причем [1,4]. Для решения задачи используем преобразование Лапласа [4]. Получаем:
- ; (13)
- Определим работу, совершаемую при перемещении заряда из точки 1 в точку 2:
- (14)
- Вычисляя интегралы, получим
- ;
- (15)
Под действием мгновенного импульса силы заряд приобретает скорость , направленную вверх, а под действием кулоновской силы возникает тормозящее ускорение: . Время движения заряда или . Оно равно времени t формулы (1).
- (16)
- Энергия, приобретенная зарядом от единичного импульса силы , а остальные члены уравнения (15) можно представить в виде:
- ;
Последний член представляет собой повышение потенциальной энергии при перемещении заряда из точки 2 в точку 1. Таким образом, при движении заряда за счет действия мгновенной силы, заряд должен получить извне начальную энергию A0, равную .
Рассмотрим третий вариант перемещения заряда из 2 в 1. На заряд действует сторонняя сила, равная кулоновской, но направленная в противоположную сторону (сила левитации): , а для перемещения заряда вверх ему сообщается единичный импульс силы за счет действия мгновенной силы . Дифференциальное уравнение движения примет вид:
- (17)
- при нулевых начальных условиях. Решая уравнение с помощью преобразования Лапласа и вычисляя работу, получим:
- Положительная работа:
- (18)
- Отрицательная работа (противодействующая перемещению заряда):
- (19)
- Время движения заряда . В окончательном виде положительная работа (при ):
- ;
- (20)
Это выражение имеет минимум, равный при значении . На графике (рис.3) показана зависимость суммарной положительной работы , выраженной в долях работы Aφ, от величины отношения .
Рисунок 3. Зависимость суммарной положительной работы , выраженной в долях работыAφ , от величины отношения .
Отрицательная работа в окончательном виде (при ):
(21)
Как следует из графика (рис.4) отрицательная работа (работа кулоновской силы) не является постоянной величиной. Ее можно вычислять по формуле (2) только в том случае, если она является единственной движущей (или тормозящей) силой.
Когда же кулоновская сила «соучаствует» со сторонними силами в перемещении заряда, то изменяется время движения заряда и расчет работы кулоновской силы надо проводить с учетом ее взаимодействия с другими силами.
При очень большом начальном импульсе ( ) выражение (21) асимптотически стремится к обычному значению работы кулоновской силы: .
- Рисунок 4. Работа кулоновской силы
- СПИСОК ЛИТЕРАТУРЫ
- Арфкен Г. Математические методы в физике. — М.: Атомиздат, 1970.
- Иванов Е.М. Дополнительные главы классической механики. — Димитровград: ДИТУД УлГТУ, 2004.
- Иванов Е.М. Работа центростремительных и гироскопических сил //Успехи современного естествознания — №9. — 2004.
- Дёч Г. Руководство к практическому применению преобразования Лапласа. М.: Наука, 1971.
Библиографическая ссылка
Иванов Е.М. Работа перемещения заряда в электростатическом поле // Фундаментальные исследования. – 2005. – № 7. – С. 9-13;
URL: http://fundamental-research.ru/ru/article/view?id=6319 (дата обращения: 22.03.2020).
Источник: https://fundamental-research.ru/ru/article/view?id=6319
работа сил электрического поля.потенциал
6.Работа сил электростатического поля.
Сила, действующая на точечный заряд, находящийся в поле другого неподвижного точечного заряда, является центральной. Из механики известно, что центральное поле сил потенциально. Убедимся в потенциальности сил электростатического поля (т. е. поля, создаваемого неподвижными зарядами) непосредственно. Вычислим работу, которая
Рис. 19. |
совершается силами поля неподвижного точечного заряда q над перемещающимся точечным зарядом q’. Работа на элементарном пути dl равна (рис. 19)
(мы учли, что dl cosα = dr). Отсюда работа на пути 1–2 равна
(9.1)
То есть, работа действительно не зависит от траектории заряда q’, а зависит лишь от начального и конечного положений этого заряда (от r1 и r2). Следовательно, силы, действующие на заряд q’ в поле неподвижного заряда q, потенциальны. Этот вывод распространяется на поле любой системы неподвижных зарядов. Сила f, действующая на точечный заряд q’, по принципу суперпозиции равна
- где fi-– сила, обусловленная i-м зарядом системы источников поля. Работа равна сумме работ, совершаемых отдельными силами:
Каждое из слагаемых не зависит от пути. Следовательно, не зависит от пути и работа A.
- Работа потенциальных сил на замкнутом пути равна нулю. Работа, совершаемая силами поля над зарядом q’ при обходе его по замкнутому контуру, может быть представлена как
- ,
- где El – проекция вектора E на направление элементарного перемещения dl (кружок у знака интеграла указывает на то, что интегрирование производится по замкнутому контуру). Так как q’ – постоянная величина, приравняв интеграл нулю получим:
- (9.2)
которое должно выполняться для любого замкнутого контура. Формула (9.2) справедлива только для электростатического поля. Поле движущихся зарядов (т. е. поле, изменяющееся со временем) не является потенциальным, так как за время движения заряда q’ изменяется значение переменного поля E. Следовательно, условие (9.2) для него не выполняется.
Выражение вида называется циркуляцией вектора А по данному контуру. Таким образом, характерным для электростатического поля является то, что циркуляция вектора напряженности по любому замкнутому контуру равна нулю.
- .Потенциал
- Тело, находящееся в потенциальном поле сил, обладает потенциальной энергией, за счет которой совершается работа силами поля.
- Следовательно, работа (9.1) равна разности значений потенциальной энергии, которыми обладал заряд q’ в точках 1 и 2 поля заряда q:
Отсюда для потенциальной энергии заряда q’ в поле заряда q получаем
Значение const выбирается таким, чтобы при удалении заряда на бесконечность (r = ∞) потенциальная энергия обращалась в нуль. При этом условии получается, что
()
Пусть заряд q’ – пробный заряд. Его потенциальная энергия зависит не только от величины q’, но и от величин q и r, определяющих поле.
Разные пробные заряды и т. д. будут обладать в одной и той же точке поля различной энергией и т. д. Однако, для данного источника поля q отношение будет для всех зарядов одинаковым. Величина
A0. 2)
называется потенциалом поля в данной точке.
Таким образом, потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. Подставляя в A0.2) значение Wp, получаем для потенциала поля точечного заряда:
Пусть поле создается системой точечных зарядов q1, q2… Расстояния от каждого из зарядов до данной точки поля r1, r2… Работа, совершаемая силами этого поля над зарядом q’ будет равна сумме работ сил, обусловленных каждым из зарядов:
- Но согласно (9.1) каждая из работ Аi равна
- А
- где ri1 – расстояние от заряда qi до начального положения заряда q’, ri2 – расстояние от qi до конечного положения заряда q’. Следовательно,
Сопоставляя это выражение с соотношением
получаем .для потенциальной энергии заряда q’ в поле системы зарядов выражение
- откуда
- Потенциал поля, создаваемого системой зарядов, равен сумме потенциалов, создаваемых каждым из зарядов в отдельности.
Напряженности поля складываются при наложении полей векторно, потенциалы –алгебраически. Поэтому вычисление потенциалов обычно гораздо проще, чем вычисление напряженностей электрического поля.
Из A0.2) определяется потенциальная энергия заряда q, находящегося в точке поля с потенциалом φ
Wp = qφ. A0.5)
- Работа сил поля над зарядом q может быть выражена через разность потенциалов:
- A0.6)
- Таким образом, работа, совершаемая над зарядом силами поля, равна произведению величины заряда на разность потенциалов в начальной и конечной точках.
- Если заряд q из точки с потенциалом φ удаляется на бесконечность (где по условию потенциал равен нулю), работа сил поля будет равна
- (Ю.7)
Отсюда: потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки на бесконечность. Такую же работу необходимо совершить против сил электрического поля, чтобы переместить единичный положительный заряд из бесконечности в данную точку поля.
- За единицу потенциала называемую вольтом (сокращенное обозначение– B), принимается потенциал в такой точке поля, для перемещения в которую из бесконечности положительного заряда 1Кл необходимо совершить работу, равную 1 Дж:
- 1 дж = 1 к⋅1 в, отсюда
- A0.8)
В физике часто пользуются единицей работы и энергии, называемой электронвольтом (эв). Под электронвольтом подразумевается работа, совершаемая силами поля над зарядом, равным заряду электрона (т. е. над элементарным зарядом е) при прохождении им разности потенциалов в 1 в:
- 1 эв=1,6 10-19кл 1 в = 1,6 10-19дж.
- Используются также кратные электронвольту единицы:
- 1 кэв (килоэлектронвольт) = 103 эв,
- 1 Мэв (мегаэлектронвольт) = 106 эв,
- 1 Гэв (гигаэлектронвольт) = 109 эв.
- Отметим, что величина kT, характеризующая среднюю энергию теплового движения молекул, равна при комнатной температуре
Источник: http://wmelon.narod.ru/1/6.html
Работа сил электростатического поля — Учебник по электродинамике
При перемещении пробного заряда q в электрическом поле электрические силы совершают работу. Эта работа при малом перемещении равна (рис. 1.4.1):
| Работа электрических сил при малом перемещении заряда q |
Рассмотрим работу сил в электрическом поле, создаваемом неизменным во времени распределенным зарядом, т.е. электростатическом поле
- Электростатическое поле обладает важным свойством:
- Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.
- Аналогичным свойством обладает и гравитационное поле, и в этом нет ничего удивительного, так как гравитационные и кулоновские силы описываются одинаковыми соотношениями.
- Следствием независимости работы от формы траектории является следующее утверждение:
- Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.
- Силовые поля, обладающие этим свойством, называют потенциальными или консервативными.
На рис. 1.4.2 изображены силовые линии кулоновского поля точечного заряда Q и две различные траектории перемещения пробного заряда q из начальной точки (1) в конечную точку (2). На одной из траекторий выделено малое перемещение Работа ΔA кулоновских сил на этом перемещении равна
Таким образом, работа на малом перемещении зависит только от расстояния r между зарядами и его изменения Δr. Если это выражение проинтегрировать на интервале от r = r1 до r = r2, то можно получить
| Работа кулоновских сил при перемещении заряда qзависит только от расстояний r1 и r2 начальной и конечной точек траектории |
Полученный результат не зависит от формы траектории. На траекториях I и II, изображенных на рис. 1.4.2, работы кулоновских сил одинаковы. Если на одной из траекторий изменить направление перемещения заряда q на противоположное, то работа изменит знак. Отсюда следует, что на замкнутой траектории работа кулоновских сил равна нулю.
Если электростатическое поле создается совокупностью точечных зарядов то при перемещении пробного заряда q работа A результирующего поля в соответствии с принципом суперпозиции будет складываться из работ кулоновских полей точечных зарядов: Так как каждый член суммы не зависит от формы траектории, то и полная работа Aрезультирующего поля не зависит от пути и определяется только положением начальной и конечной точек.
Свойство потенциальности электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. Для этого в пространстве выбирается некоторая точка (0), и потенциальная энергия заряда q, помещенного в эту точку, принимается равной нулю.
Потенциальная энергия заряда q, помещенного в любую точку (1) пространства, относительно фиксированной точки (0) равна работе A10, которую совершит электростатическое поле при перемещении заряда q из точки (1) в точку (0):
(В электростатике энергию принято обозначать буквой W, так как буквой E обозначают напряженность поля. )
Так же, как и в механике, потенциальная энергия определена с точностью до постоянной величины, зависящей от выбора опорной точки (0). Такая неоднозначность в определении потенциальной энергии не приводит к каким-либо недоразумениям, так как физический смысл имеет не сама потенциальная энергия, а разность ее значений в двух точках пространства.
Работа, совершаемая электростатическое полем при перемещении точечного заряда q из точки (1) в точку (2), равна разности значений потенциальной энергии в этих точках и не зависит от пути перемещения заряда и от выбора точки (0).
|
Потенциальная энергия заряда q, помещенного в электростатическое поле, пропорциональна величине этого заряда.
Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:
Потенциал φ является энергетической характеристикой электростатического поля.
Работа A12 по перемещению электрического заряда q из начальной точки (1) в конечную точку (2) равна произведению заряда на разность потенциалов (φ1 – φ2) начальной и конечной точек:
| A12 = Wp1 – Wp2 = qφ1 – qφ2 = q(φ1 – φ2). |
- В Международной системе единиц (СИ) единицей потенциала является вольт (В).
- Во многих задачах электростатики при вычислении потенциалов за опорную точку (0) удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом:
- Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
Потенциал φ∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:
- Как следует из теоремы Гаусса, эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R, где R – радиус шара.
- Для наглядного представления электростатическое поля наряду с силовыми линиями используют эквипотенциальные поверхности.
- Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала.
- Силовые линии электростатическое поля всегда перпендикулярны эквипотенциальным поверхностям.
Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. На рисунке ниже представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей.
| Эквипотенциальные поверхности (синие линии) и силовые линии (красные линии) простых электрических полей: a – точечный заряд; b – электрический диполь; c – два равных положительных заряда |
В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей.
Если пробный заряд q совершил малое перемещение вдоль силовой линии из точки (1) в точку (2), то можно записать:
| ΔA12 = qEΔl = q(φ1 – φ2) = – qΔφ, |
где Δφ = φ1 – φ2 – изменение потенциала. Отсюда следует
Это соотношение в скалярной форме выражает связь между напряженностью поля и потенциалом. Здесь l – координата, отсчитываемая вдоль силовой линии.
Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов:
Источник: https://www.sites.google.com/site/ucebnikpoelektrodinamike/rabota-sil-elektrostaticeskogo-pola
Работа сил электростатического поля. Потенциал
Тема: Работа сил электростатического поля. Потенциал электростатического поля. Потенциал электростатического поля точечного заряда. Потенциал электростатического поля системы точечных зарядов
Цель урока: формирование понятия потенциал как энергетической характеристики электростатического поля, представлений об эквипотенциальных поверхностях, умений определять потенциал электростатического поля точечного заряда, равномерно заряженной сферы, системы точечных зарядов, работу сил однородного электростатического поля.
Актуализация опорных знаний
Как обнаружить существование электрического поля?
Дайте определение напряженности электрического поля? Какова единица напряженности?
Как напряженность электрического поля зависит от расстояния?
Где начинаются и где заканчиваются линии напряженности электростатического поля?
Какое электрическое поле называется однородным?
Сформулируйте принцип суперпозиции электростатических полей.
Физический диктант
Как называется поле неподвижных зарядов?
Что является источником электрического поля?
Как называется сила, с которой взаимодействуют заряды?
Как называется физическая величина, равная отношению силы, действующей на заряд со стороны электрического поля, к этому заряду?
В каких единицах измеряется напряженность?
Как направлены силовые линии электрического поля?
Как изменится напряженность при увеличении электрического заряда?
Как изменится напряженность при увеличении расстояния от точки до заряда?
Как изменится сила, действующая на заряд, если напряженность электрического поля увеличить в 2 раза?
Какой заряд помещен в электрическое поле, если вектор силы, действующей на заряд, совпадает с вектором напряженности по направлению?
Ответы: электростатическим; заряд; кулоновская; напряженность; В/м; от «+» к «-»; увеличится; уменьшится; увеличится в 2 раза; положительный.
Новый материал
При перемещении тела между двумя точками в гравитационном поле работа силы тяжести не зависит от формы траектории его движения. Силы гравитационного и электрического взаимодействия имеют одинаковую зависимость от расстояния, и векторы сил направлены вдоль прямой, соединяющей точечные тела.
- Можно предположить, что при перемещении заряда в электростатическом поле из одной точки в другую работа сил электрического поля не зависит от формы.
- На заряд, помещенный в электростатическое поле напряженностью , действует сила , поэтому при его перемещении из А в В полем будет совершаться работа
- Найдем работу поля при перемещении заряда по траектории АСВ
Найдем работу поля при перемещении заряда по криволинейной траектории.
Электростатическое поле ‒ это потенциальное поле, т.е. работа по перемещению заряда в этом поле не зависит от формы траектории, а зависит от начальной и конечной координат заряда.
- Из механики: работа консервативных сил равна изменению потенциальной энергии, взятому с противоположным знаком:
- С другой стороны
- Следовательно
- Рассмотрим два точечных заряда, расположенных на некотором расстоянии друг от друга.
- Потенциальная энергия взаимодействия двух зарядов равна
- Если заряды одноименные, то
- Если заряды разноименные, то
- Рассмотрим несколько точечных зарядов. Потенциальная энергия их взаимодействия равна сумме потенциальных энергий всех пар взаимодействующих зарядов
- Введем еще одну характеристику электрического поля.
- В точку А однородного электростатического поля с напряженностью помещаем заряд .
- Потенциальная энергия заряда в этой точке
- Найдем значение величины
- В точку А однородного электростатического поля с напряженностью помещаем заряд .
- Потенциальная энергия заряда в этой точке
- Найдем значение величины
- Аналогичный результат мы получим, если будем помещать в эту точку другие заряды. Следовательно, величина
- Не зависит от величины заряда, который мы помещаем в электрическое поле;
- Но зависит от параметров электрического поля
- От напряженности поля
- От координаты точки поля
- Новая характеристика электрического поля ‒ потенциал поля в данной точке
- Потенциал электростатического поля ‒ это скалярная физическая величина, равная отношению потенциальной энергии, которой обладает точечный заряд в данной точке поля, к величине этого заряда.
- Потенциал ‒ это энергетическая характеристика электрического поля.
- Пусть электрическое поле создано точечным зарядом . В точке А, расположенной на расстоянии от заряда потенциал поля:
- Значение потенциала электрического поля, созданного сферой радиуса , имеющего заряд , в точке А на расстоянии от центра сферы, равно
- , если
- , если
Свойства потенциала:
Потенциал (как и потенциальная энергия) зависит от выбора нулевого уровня
За нулевой потенциал в технике выбирают:
- Потенциал поверхности Земли
- Потенциал проводника, соединенного с Землей (заземленный)
За нулевой уровень потенциала в физике принимается любая точка, бесконечно удаленная от зарядов, создающих поле
Если электрическое поле создано:
Зарядом , то потенциал этого поля
Зарядом , то потенциал этого поля
Принцип суперпозиции: потенциал поля, созданного несколькими зарядами, в некоторой точке пространства равен алгебраической сумме потенциалов, создаваемых в этой точке каждым из зарядов в отдельности.
- Для графического изображения полей, кроме силовых линий электрического поля, удобно использовать эквипотенциальные поверхности (линии) ‒ поверхности (линии) равного потенциала.
- Через каждую точку поля проходит только одна силовая линия и одна эквипотенциальная поверхность, причем в каждой точке поля силовая линия и соответствующая эквипотенциальная поверхность взаимно перпендикулярны.
Докажем факт взаимной перпендикулярности силовой линии и эквипотенциальной поверхности методом от противного. Предположим, что они не перпендикулярны. Тогда при движении заряда вдоль эквипотенциальной поверхности полем совершалась бы работа вследствие того, что существовала бы компонента поля вдоль поверхности. Но в этом случае она не была бы эквипотенциальной, так как ее потенциал не был бы одинаков во всех точках траектории при таком движении. Мы пришли к противоречию, что доказывает истинность исходного утверждения.
Потенциал всякого изолированного проводника можно измерить, сравнивая его с потенциалом Земли. Сделать это можно с помощью прибора, называемого электрометром или электростатическим вольтметром. Один из простейших электрометров ‒ электрометр Брауна ‒ аналогичен по устройству обычному электроскопу.
Для определения потенциала заряженного проводника необходимо соединить его со стержнем электрометра, а металлический корпус электрометра соединить с Землей.
Часть заряда перейдет на стержень электрометра и на подвижную легкую стрелку, которая, отталкиваясь от стержня, отклонится на некоторый угол и укажет на шкале значение потенциала проводника относительно Земли.
Электрометр Брауна пригоден для измерения разности потенциалов от 1000 до 10000 В. Существуют чувствительные электрометры, при помощи которых можно измерять разности потенциалов от 0,1 до 0,01 В. Напряжения от 0,1 до 1000 В измеряют с помощью бытовых вольтметров.
Во многих установках используются очень высокие разности потенциалов порядка 100 кВ (например, в кинескопе телевизора ~ 25 кВ). При таких разностях потенциачов возникают поля большой напряженности, которые могут ионизировать воздух, т. е.
«вырывать» электроны из атомов, образуя большое число свободных заряженных частиц. Воздух становится проводником.. Пробой (искрение) интенсивно возникает на шероховатостях поверхностей и остриях, т. е. местах с малым радиусом кривизны, где напряженность поля становится наибольшей.
Поэтому проводники стараются делать как можно более гладкими.
Например, при радиусе кривизны 5 мм напряжение пробоя в воздухе, окружающем проводник, составляет ~ 15 кВ Это обстоятельство накладывает ограничения на максимальное значение напряжения, передаваемого по линиям электропередач, так как вследствие пробоя начинаются существенные потери электроэнергии через воздух.
Закрепление изученного
Что понимают под работой электростатического поля?
Запишите формулу работы электростатического поля по перемещению в нем заряда
Как связано изменение потенциальной энергии электростатического поля с совершаемой им работой?
От чего зависит работа по перемещению заряда из одной точки поля в другую?
Чему равна работа электростатического поля по перемещению заряда по замкнутому контуру?
Какие поля называют потенциальными?
Как понимать выражение «электростатическое поле потенциально»?
Что называют потенциалом электростатического поля?
По какой формуле можно определить потенциал электростатического поля?
В чем отличие потенциала электростатического поля от напряженности поля?
Какие поверхности называют эквипотенциальными?
Могут ли эквипотенциальные линии пересекаться?
Домашнее задание
Источник: https://multiurok. ru/files/rabota-sil-eliektrostatichieskogho-polia-potientsi.html
Работа сил электрического поля. Потенциал
Работа перемещения заряда.На положительный точечный заряд q в электрическом поле с напряжённостью E действует сила F= q E. При перемещении заряда на отрезке dl силами поля совершается работа
- dA = Fdl=q E dl cos (E, dl).
- При перемещении заряда q силами электрического поля на произвольном конечном отрезке из точки 1 в точку 2 эта работа равна
- .
- Рассмотрим перемещение точечного заряда q в поле точечного заряда Q, напряженность поля которого
- .
Проекция отрезка dl на направление вектора E (рис. 1.5) есть dr = dl cos (E, dl).
Работа, совершаемая электрическим полем при перемещении заряда q из точки 1 в точку 2, определяется следующим образом:
Отсюда следует, что работа сил электрического поля не зависит от формы пути, а определяется только начальным и конечным положениями заряда q. Если оба заряда, q и Q, положительны, то работа сил поля положительна при удалении зарядов и отрицательна при их взаимном сближении.
- Для электрического поля, созданного системой зарядов Q1, Q2,¼, Qn, работа перемещения заряда q равна алгебраической сумме работ составляющих сил:
- .
- Для определения потенциальной энергии необходимо условиться, в какой точке поля считать ее равной нулю. Для потенциальной энергии точечного заряда q, находящегося в электрическом поле, созданном другим точечным зарядом Q, получим
- ,
- где C – произвольная постоянная. Пусть потенциальная энергия равна нулю на бесконечно большом расстоянии от заряда Q (при r ® ¥), тогда постоянная C = 0 и предыдущее выражение принимает вид
- .
- При этом потенциальная энергия определяется как работа перемещения заряда силами поля из данной точки в бесконечно удаленную.В случае электрического поля, создаваемого системой точечных зарядов, потенциальная энергия заряда q:
- .
Электростатический потенциа́л (см.
также кулоновский потенциал) — скалярная энергетическая характеристикаэлектростатического поля, характеризующая потенциальную энергию поля, которой обладает единичный заряд, помещённый в данную точку поля.
Единицей измерения потенциала является, таким образом, единица измерения работы, деленная на единицу измерения заряда (для любой системы единиц; подробнее о единицах измерения — см. ниже).
Электростатический потенциал — специальный термин для возможной замены общего термина электродинамики скалярный потенциал в частном случае электростатики (исторически электростатический потенциал появился первым, а скалярный потенциал электродинамики — его обобщение). Употребление термина электростатический потенциал определяет собой наличие именно электростатического контекста. Если такой контекст уже очевиден, часто говорят просто о потенциале без уточняющих прилагательных.
Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:
Напряжённость электростатического поля и потенциал связаны соотношением[1]
или обратно[2]:
Здесь — оператор набла, то есть в правой части равенства стоит минус градиент потенциала — вектор с компонентами, равными частным производным от потенциала по соответствующим (прямоугольным) декартовым координатам, взятый с противоположным знаком.
где — электростатический потенциал (в вольтах), — объёмная плотность заряда (в кулонах на кубический метр), а — диэлектрическая проницаемость вакуума (вфарадах на метр).
Не нашли то, что искали? Воспользуйтесь поиском:
Источник: https://studopedia.ru/8_30844_rabota-sil-elektricheskogo-polya-potentsial.html
Работа электрического поля при перемещении заряда. Принцип действия
Чем на самом деле является напряжение? Это способ описания и измерения напряженности электрического поля. Само по себе напряжение не может существовать без электронного поля вокруг положительных и отрицательных зарядов. Так же, как магнитное поле окружает Северный и Южный полюса.
По современным понятиям, электроны не оказывают взаимного влияния. Электрическое поле – это нечто, что исходит от одного заряда и его присутствие может ощущаться другим.
О понятии напряженности можно сказать то же самое! Просто это помогает нам представить, как электрическое поле может выглядеть. Честно говоря, оно не обладает ни формой, ни размером, ничем подобным. Но поле функционирует с определённой силой на электроны.
Силы и их действие на заряженную частицу
На заряженный электрон, воздействует сила с некоторым ускорением, заставляя его перемещаться все быстрее и быстрее. Этой силой совершается работа по передвижению электрона.
Силовые линии – это воображаемые очертания, которые возникают вокруг зарядов (определяется электрическим полем), и если мы поместим какой-либо заряд в эту область, он испытает силу.
Свойства силовых линий:
- путешествуют с севера на юг;
- не имеют взаимных пересечений.
Почему у двух силовых линий не возникает пересечений? Потому что не бывает этого в реальной жизни.
То, о чём говорится, является физической моделью и не более. Физики изобрели её для описания поведения и характеристик электрического поля. Модель очень хороша при этом.
Но помня, что это всего лишь модель, мы должны знать о том, для чего такие линии нужны.
Силовые линии демонстрируют:
- направления электрических полей;
- напряженность. Чем ближе линии, тем больше сила поля и наоборот.
Если нарисованные силовые линии нашей модели пересекутся, расстояние меж ними станет бесконечно малыми. Из-за силы поля, как формы энергии, и из-за фундаментальных законов физики это невозможно.
Что такое потенциал?
Потенциалом называется энергия, которая затрачивается на передвижение заряженной частицы из первой точки, имеющей нулевой потенциал во вторую точку.
Разность потенциалов меж пунктами А и Б – это работа, производимая силами для передвижения некоего положительного электрона по произвольной траектории из А в Б.
Чем больший потенциал у электрона, чем больше плотность потока на единицу площади. Такое явление подобно гравитации. Чем больше масса, тем больше потенциал, тем интенсивнее и плотнее гравитационное поле на единицу площади.
Небольшой заряд с низким потенциалом, с прореженной плотностью потока показан на следующем рисунке.
А ниже показан заряд с большим потенциалом и плотностью потока.
Например: во время грозы электроны истощаются в одной точке и собираются в другой, образуя электрическое поле. Когда сила станет достаточной, чтобы сломать диэлектрическую проницаемость, получается удар молнии (состоящий из электронов). При выравнивании разности потенциалов электрическое поле разрушается.
Электростатическое поле
Это разновидность электрического поля, неизменного повремени, образуемого зарядами, которые не двигаются. Работа передвижения электрона определяется соотношениями,
где r1 и r2 – расстояния заряда q до начальной и конечной точки траектории движения. По полученной формуле видно, что работа при перемещении заряда из точки в точку не зависит от траектории, а зависит лишь от начала и конца перемещения.
На всякий электрон действует сила, и поэтому при перемещении электрона в поле выполняется определенная работа.
В электростатическом поле работа зависит лишь от конечных пунктов следования, а не от траектории. Поэтому, когда движение происходит по замкнутому контуру, заряд приходит в исходное положение, и величина работы становится равной нулю.
Это происходит потому, что падение потенциала нулевое (поскольку электрон возвращается в ту же самую точку).
Так как разность потенциалов нулевая, чистая работа будет также нулевой, ведь потенциал падения равен работе, деленной на значение заряда, выраженное в кулонах.
Об однородном электрическом поле
Однородным называется электрическое поле меж двух противоположно заряженных плоских металлических пластин, где линии напряженности параллельны между собой.
Почему сила действия на заряд в таком поле всегда одинаковая? Благодаря симметрии. Когда система симметрична и есть только одна вариация измерения, всякая зависимость исчезает. Есть много других фундаментальных причин для ответа, но фактор симметрии – самый простой.
Работа по передвижению положительного заряда
Электрическое поле – это поток электронов от «+» до «-», приводящий к высокой напряженности области.
Поток – это количество линий электрического поля, проходящих через него. В каком направлении будут положительные электроны двигаться? Ответ: по направлению электрического поля от положительного (высокого потенциала) к отрицательному (низкому потенциалу). Поэтому положительно заряженная частица будет двигаться именно в этом направлении.
Интенсивность поля во всякой точке определяется как сила, воздействующая на положительный заряд, помещенный в эту точку.
Работа заключается в переносе электронных частиц по проводнику. По закону Ома, можно определить работу разными вариациями формул, чтобы провести расчет.
Из закона сохранения энергии следует, что работа – это изменение энергии на отдельном отрезке цепи. Перемещение положительного заряда против электрического поля требует совершения работы и в результате получается выигрыш в потенциальной энергии.
Заключение
Из школьной программы мы помним, что электрическое поле образуется вокруг заряженных частиц.
На любой заряд в электрическом поле воздействует сила, и вследствие этого при движении заряда выполняется некоторая работа.
Большим зарядом создается больший потенциал, который производит более интенсивное или сильное электрическое поле. Это означает, что возникает больший поток и плотность на единицу площади.
Важный момент заключается в том, что должна быть выполнена определенной силой работа по перемещению заряда от высокого потенциала к низкому.
Загляните на карту сайта Электронщик, буду рад если вы найдете на моем сайте еще что-нибудь полезное. Делитесь информацией в соцсетях, ставьте лайки, если вам понравилось — это поможет развитию канала
Источник: https://zen.yandex.ru/media/id/5c615e3c9e391400ae5f8253/5d6a493fac412400ad14ce0c
Напряженность электрического поля: определение, формула, единицы измерения
Точно так же, как гравитационная сила является следствием гравитационного поля, электрическая сила возникает из-за электрического поля. Однако электрическое поле обычно намного сильнее гравитационного поля, потому что гравитационная постоянная значительно меньше кулоновской постоянной.
Напряженность электрического поля — это интенсивность силы на единицу положительного заряда.
Любая заряженная частица создает вокруг себя электрическое поле, и если заряженная частица окажется рядом с другой частицей, произойдет взаимодействие.
Рис. 1. Любая заряженная частица создает электрическое поле, которое можно изобразить линиями.
Как правило, линии электрического поля направлены в сторону отрицательного заряда и в сторону от положительного заряда.
Напряженность электрического поля: Взаимодействие между электрическими полями
Еще одним отличием электрического поля от гравитационного является то, что электрическое поле может иметь положительное или отрицательное направление. С другой стороны, гравитационное поле имеет только положительное направление. Это удобный способ вычислить направление поля в любой момент времени в свободном пространстве.
Рис. 2. Силовые линии положительно заряженной частицы (слева) и отрицательно заряженной частицы (справа).
Чем плотнее расположены силовые линии, тем сильнее поле. Силовые линии также полезны, если много зарядов взаимодействуют друг с другом. Рисунок 3 представляет собой пример электрического диполя, так как заряды противоположны.
Рис. 3. Одинаковые заряды отталкиваются друг от друга, на что указывают силовые линии двух положительных зарядов.
Формула напряженности электрического поля
Мы можем измерить электрическое поле, создаваемое точечным зарядом, вычислив его напряженность электрического поля . Напряженность электрического поля — это сила, действующая на заряд +1 Кл (испытательный заряд), когда он помещен в электрическое поле.
Здесь E — напряженность электрического поля, измеряемая в ньютонах/кулонах, F — сила в ньютонах, а Q — заряд в кулонах.
Напряженность поля в первую очередь зависит от того, где в поле находится заряд. Если заряд находится там, где силовые линии плотнее, сила воздействия будет больше. Следует отметить, что приведенное выше уравнение справедливо для линейных полей.
Будем считать заряды точечными, что означает, что весь заряд сосредоточен в центре и имеет радиальное поле.
Рис. 4. Точечные заряды q 1 , q 2 и q 3 в электрическом поле и действующие на них силы.
В радиальном электрическом поле напряженность электрического поля может быть представлена как:
Здесь:
- E – напряженность электрического поля, измеряемая в ньютонах на кулон.
- K c — постоянная Кулона со значением 8,99⋅10 9 .
- Q — точечный заряд в кулонах.
- r — расстояние от точечного заряда в метрах.
Напряженность электрического поля подчиняется закону обратных квадратов: если расстояние от Q увеличивается, напряженность поля уменьшается.
Как мы можем использовать электрическое поле?
Если взять две заряженные пластины и приложить к ним напряжение, причем одна из них имеет положительный, а другая отрицательный заряд, то между пластинами будет индуцироваться электрическое поле, параллельное и равномерно распределенное.
Рис. 5. Напряженность электрического поля действует перпендикулярно пластинам.
Поскольку напряженность электрического поля представляет собой силу, с которой сталкивается заряд в 1 Кл, силу, действующую на положительно заряженную частицу, можно принять равной разности потенциалов, приложенной к пластинам. Следовательно, для примера на рис. 5 уравнение напряженности электрического поля имеет вид:
Здесь E — напряженность электрического поля (В/м или Н/Кл), V — разность потенциалов в вольтах, а d — расстояние между пластинами в метрах.
Итак, если мы поместим пробный заряд в однородное электрическое поле, на него будет действовать сила, направленная к отрицательному концу клеммы или пластины. И поскольку это поле оказывается однородным, напряженность электрического поля будет одинаковой независимо от того, в каком месте внутри поля находится пробный заряд.
Однородное электрическое поле — это электрическое поле, в котором напряженность электрического поля одинакова во всех точках.
Рис. 6. На пробный заряд действует сила внутри однородного поля.
Напряженность электрического поля: Пробный заряд входит в однородное поле со скоростью
Вышеприведенный сценарий относится к пробному заряду, помещенному в однородное электрическое поле. Но что, если заряд входит в электрическое поле с начальной скоростью?
Если заряд попадает в однородное электрическое поле с некоторой начальной скоростью, он будет искривляться, причем направление зависит от того, положительный или отрицательный заряд.
Заряд, входящий под прямым углом к полю, ощущает на себе постоянную силу, действующую параллельно линиям поля внутри пластин. На рисунке 7 положительно заряженная частица входит в однородное электрическое поле под прямым углом и движется в том же направлении, что и силовые линии. Это заставляет положительный заряд ускоряться вниз по изогнутой параболической траектории.
Рис. 7. Положительный заряд следует по параболической траектории, если он входит под прямым углом к полю. Источник: Усама Адил, StudySmarter.
Если заряд отрицательный, направление будет противоположно линиям поля.
Напряженность электрического поля — ключевые выводы
- Напряженность электрического поля — это сила, действующая на заряд +1 Кл (испытательный заряд), когда он помещен в электрическое поле.
- Любая заряженная частица создает вокруг себя электрическое поле.
- Точечные заряды ведут себя так, как будто весь заряд сосредоточен в их центре.
- Точечные заряды имеют радиальное электрическое поле.
- Между двумя противоположно заряженными пластинами создается однородное электрическое поле, направление линий электрического поля от положительной пластины к отрицательной.
- В однородном электрическом поле напряженность электрического поля одинакова по всему полю.
- Если заряд входит в однородное электрическое поле с некоторой начальной скоростью, он будет искривляться, причем направление зависит от того, положительный или отрицательный заряд.
Электрическое поле
Электрическое полеЭлектрическое поле определяется как электрическая сила на единицу заряда. Направление поля принимается за направление силы, которую оно должно оказывать на положительный пробный заряд. Электрическое поле направлено радиально наружу от положительного заряда и радиально внутрь к точечному отрицательному заряду.
| Индекс Концепции электрического поля Электромагнитная сила | ||
| Вернуться |
Электрическое поле от любого количества точечные заряды могут быть получены из вектора сумма отдельных полей. Положительное число считается внешним полем; поле отрицательного заряда направлено к ней. Это выражение для электрического поля также можно получить, применяя закон Гаусса.
| Индекс Концепции электрического поля | ||||
|
В уравнениях, описывающих электрические и магнитные поля и их распространение, обычно используются три константы.
Он содержит единицу силы N для Ньютона, а единицей A является Ампер, единица измерения электрического тока. При установленной магнитной проницаемости электрическая проницаемость принимает значение, определяемое соотношением где скорость света c определяется выражением Это дает значение диэлектрической проницаемости в свободном пространстве Эти выражения содержат единицы F для фарада, единицы емкости, и C для кулона, единицы электрического заряда. В присутствии поляризуемых или магнитных сред эффективные константы будут иметь разные значения. В случае поляризуемой среды, называемой диэлектриком, сравнение выражается как относительная диэлектрическая проницаемость или диэлектрическая проницаемость. В случае магнитных сред может быть указана относительная магнитная проницаемость.
| Индекс Концепции электрического поля | |||
|
Выражения для электрического и магнитного полей в свободном пространстве содержат диэлектрическую проницаемость ε 0 и магнитной проницаемости μ 0 свободного пространства.
| Индекс Концепции электрического поля | ||||||
| Назад |
9.3 Электрическое поле | Электростатика
9.3 Электрическое поле (ЭСБПК)
В предыдущем разделе мы видели, что точечные заряды действуют друг на друга, даже когда они находятся далеко друг от друга. и не касаясь друг друга. Откуда заряды «знают» о существовании вокруг них других зарядов?
Ответ заключается в том, что каждый заряд можно представить себе как окруженный в пространстве электрическим полем. Электрический
Поле — это область пространства, в которой электрический заряд будет испытывать силу. Направление электрич.
Поле представляет собой направление силы, с которой испытает положительный пробный заряд, если поместить его в электрическое поле. поле. Другими словами, направление электрического поля в точке пространства совпадает с направлением, в котором
положительный тестовый заряд будет двигаться, если его поместить в эту точку.
- Электрическое поле
Область пространства, в которой на электрический заряд действует сила. Направление поля в точке в пространстве — это направление, в котором будет двигаться положительный пробный заряд, если его поместить в эту точку.
Представление электрических полей (ESBPM)
Мы можем представить силу и направление электрического поля в точке, используя электрическое поле строки . Это похоже на представление магнитных полей вокруг магнитов с использованием силовых линий магнитного поля в виде вы учились в 10 классе. Далее мы изучим, как выглядят электрические поля вокруг изолированных обвинения.
Положительный заряд, действующий на пробный заряд
Величина силы, с которой пробный заряд испытывает воздействие другого заряда, определяется законом Кулона. На приведенной ниже диаграмме в каждой точке вокруг положительного заряда \(+Q\) мы вычисляем силу положительного теста
заряд, \(+q\), будет испытываться, и изобразите эту силу (вектор) стрелкой. Векторы силы для
некоторые точки вокруг \(+Q\) показаны на диаграмме вместе с положительным пробным зарядом \(+q\) (красным), расположенным
в одной из точек.
В каждой точке вокруг заряда \(+Q\) положительный пробный заряд \(+q\) будет испытывать силу, толкающую его
прочь.
Это связано с тем, что оба заряда положительны и поэтому отталкивают друг друга. Мы не можем нарисовать стрелку в каждой точке
но мы включили достаточно стрелок, чтобы проиллюстрировать, как будет выглядеть поле. Стрелки обозначают силу
тестовый заряд будет испытываться в каждой точке. Закон Кулона — это закон обратных квадратов, который означает, что сила
становится слабее, чем больше расстояние между двумя зарядами. Вот почему стрелки становятся короче дальше
из \(+Q\).
Отрицательный заряд, действующий на пробный заряд
Для отрицательного заряда \(-Q\) и положительного пробного заряда \(+q\) векторы силы будут выглядеть так:
Обратите внимание, что он почти идентичен кейсу с положительным зарядом. Стрелки имеют ту же длину, что и на предыдущая диаграмма, потому что абсолютная величина заряда одинакова, как и величина теста обвинение. Таким образом, величина силы одинакова в одних и тех же точках пространства. Однако стрелки указывают на в противоположном направлении, потому что теперь заряды имеют противоположные знаки и притягиваются друг к другу.
Электрические поля вокруг изолированных зарядов — сводка
Теперь, чтобы упростить задачу, мы рисуем непрерывные линии, касательные к силе, с которой пробный заряд
будет испытывать в каждой точке. Силовые линии располагаются ближе друг к другу там, где поле сильнее. Посмотрите на
диаграмма ниже: близко к центральным зарядам, линии поля близко друг к другу. Вот где электрический
поле сильнейшее. Дальше от центральных зарядов, где электрическое поле слабее, силовые линии
более удалены друг от друга.
Мы используем следующие соглашения при рисовании линий электрического поля:
Стрелки на линиях поля указывают направление поля, т.е. направление, в котором положительный испытательный заряд будет двигаться, если его поместить в поле.
Силовые линии электрического поля направлены от положительных зарядов (подобно тому, как заряды отталкиваются) к отрицательным зарядам (в отличие от зарядов притягиваются).
Линии поля сближаются там, где поле сильнее.
Линии поля не соприкасаются и не пересекаются.
Линии поля проводятся перпендикулярно заряду или заряженной поверхности.
Чем больше величина заряда, тем сильнее его электрическое поле. Мы изображаем это, рисуя больше силовых линий вокруг большего заряда, чем для зарядов с меньшей величиной.
Некоторые важные моменты, которые следует помнить об электрических полях:
Существует электрическое поле в каждой точке пространства. окружающих заряд.
Полевые линии — это просто представление — они не настоящий. Когда мы их рисуем, мы просто выбираем удобные места для указать поле в пространстве.
Линии поля существуют в трех измерениях, а не только в двух измерениях, как мы их нарисовали.
Количество силовых линий, проходящих через поверхность, пропорционально заряду, содержащемуся внутри поверхность.
Электрические поля вокруг различных конфигураций заряда (ESBPN)
Мы видели, как выглядят электрические поля вокруг изолированных положительных и отрицательных зарядов. Теперь мы будем изучите, как выглядят электрические поля вокруг комбинаций зарядов, расположенных близко друг к другу.
Электрическое поле вокруг двух разноименных зарядов
Мы начнем с рассмотрения электрического поля вокруг положительного и отрицательного заряда, расположенного рядом с каждым из них. Другой. Используя правила рисования линий электрического поля, мы будем рисовать электрическое поле шаг за шагом. Чистое результирующее поле представляет собой сумму полей от каждого из зарядов. Для начала нарисуем электрические поля для каждого из зарядов в отдельности.
Положительный тестовый заряд (красные точки), размещенный в разных местах непосредственно между двумя зарядами, будет
отталкивается (оранжевые силовые стрелки) от положительного заряда и притягивается (синие силовые стрелки) к отрицательному
заряжать по прямой. Оранжевые и синие стрелки силы нарисованы с небольшим смещением от точек для
ясность. На самом деле они будут лежать друг на друге. Обратите внимание, что чем дальше от положительного заряда, тем
меньше сила отталкивания, \(F_+\) (более короткие оранжевые стрелки) и чем ближе к отрицательному заряду, тем больше
сила притяжения, \(F_-\) (более длинные синие стрелки).
Результирующие силы показаны красными стрелками.
Линия электрического поля представляет собой черную линию, касательную к результирующим силам и являющуюся прямой линией.
между зарядами, направленными от положительного заряда к отрицательному.
Теперь рассмотрим положительный пробный заряд, расположенный чуть выше линии, соединяющей два заряда.
Пробный заряд будет испытывать силу отталкивания (\(F_+\) оранжевым цветом) от положительного заряда и
сила притяжения (\(F_-\) синего цвета) из-за отрицательного заряда. Как и прежде, величина этих сил будет
зависят от расстояния пробного заряда от каждого из зарядов по закону Кулона. Начиная с позиции ближе к положительному заряду, пробный заряд будет испытывать большую силу отталкивания.
из-за положительного заряда и более слабой силы притяжения от отрицательного заряда. На полпути
между положительным и отрицательным зарядами величины сил отталкивания и притяжения одинаковы.
Если пробный заряд поместить ближе к отрицательному заряду, то сила притяжения будет больше и
сила отталкивания, которую он испытывает из-за более удаленного положительного заряда, будет слабее. В каждую точку добавляем
силы, вызванные положительными и отрицательными зарядами, чтобы найти результирующую силу на пробном заряде (показан
красные стрелки). Результирующая линия электрического поля, касательная к результирующим векторам силы, будет
быть кривой.
Теперь мы можем довольно легко заполнить другие строки поля, используя те же идеи. Линии электрического поля выглядят как:
Электрическое поле вокруг двух одинаковых зарядов (оба положительные)
Для случая двух положительных зарядов \(Q_1\) и \(Q_2\) одинаковой величины все выглядит немного
другой. Мы не можем просто поворачивать стрелки так, как делали это раньше. В этом случае положительный пробный заряд
отталкивается от обоих зарядов. Электрические поля вокруг каждого из зарядов в отдельности выглядят так.
Теперь мы можем посмотреть на результирующее электрическое поле, когда заряды расположены рядом друг с другом. Начнем с размещения положительного пробного заряда непосредственно между двумя зарядами. Мы можем нарисовать силы, действующие на пробный заряд из-за \(Q_1\) и \(Q_2\), и определить результирующую сила.
Сила \(F_1\) (выделена оранжевым цветом) на тестовом заряде (красная точка) из-за заряда \(Q_1\) равна по модулю
но противоположно направлению \(F_2\) (синим цветом), которое представляет собой силу, действующую на пробный заряд из-за \(Q_2\).
Следовательно, они компенсируют друг друга, и результирующей силы нет. Это означает, что электрическое поле
непосредственно между зарядами отменяется в середине. Пробный заряд, размещенный в этой точке, не
испытывать силу.
Теперь рассмотрим положительный пробный заряд, расположенный рядом с \(Q_1\) и над воображаемой линией, соединяющей центры зарядов. Снова мы можем нарисовать силы, действующие на пробный заряд из-за \(Q_1\) и \(Q_2\), и суммируйте их, чтобы найти результирующую силу (показана красным). Это говорит нам о направлении линии электрического поля в точке каждая точка. Линия электрического поля (черная линия) касается результирующих сил.
Если мы поместим пробный заряд в те же относительные положения, но ниже воображаемой линии, соединяющей центры зарядов, мы можем видеть на диаграмме ниже, что результирующие силы являются отражением силы выше. Следовательно, линия электрического поля — это просто отражение линии поля выше.
Поскольку \(Q_2\) имеет тот же заряд, что и \(Q_1\), силы в тех же относительных точках, близких к \(Q_2\), будут
имеют одинаковые величины, но противоположные направления, то есть они также являются отражениями. Поэтому мы можем легко нарисовать
следующие две строки поля следующим образом:
Проработка ряда возможных отправных точек для теста заряд мы можем показать электрическое поле может быть представлено:
Электрическое поле вокруг двух одинаковых зарядов (оба отрицательные)
Мы можем использовать тот факт, что направление силы меняется на противоположное для пробного заряда, если изменить знак заряда, который влияя на это. Если мы перейдем к случаю, когда оба заряда отрицательный, мы получаем следующий результат:
Заряды разной величины
Когда величины не равны, больший заряд будет влиять на направление силовых линий больше, чем
если бы они были равны. Например, вот конфигурация, в которой положительный заряд намного больше, чем
отрицательный заряд. Вы можете видеть, что линии поля выглядят более похожими на линии изолированного заряда при большем
расстояния, чем в предыдущем примере. Это связано с тем, что больший заряд создает более сильное поле и
поэтому вносит больший относительный вклад в силу пробного заряда, чем меньший заряд.
Напряженность электрического поля (ESBPP)
В предыдущих разделах мы изучили, как мы можем представить электрические поля вокруг заряда или объединение зарядов с помощью линий электрического поля. В этом представлении мы видим, что электрическое поле сила представлена тем, насколько близко друг к другу находятся силовые линии. Кроме чертежей эл. поле, мы также хотели бы иметь возможность количественно определить (присвоить цифру), насколько сильным является электрическое поле и каково его значение. направление находится в любой точке пространства.
Небольшой пробный заряд \(q\), помещенный рядом с зарядом \(Q\), будет испытывать силу электрического поля
окружающих \(Q\). Величина силы описывается законом Кулона и зависит от величины
заряд \(Q\) и расстояние пробного заряда от \(Q\). Чем ближе пробный заряд \(q\) к заряду
\(Q\), тем большую силу он будет испытывать. Также в точках ближе к заряду \(Q\) тем сильнее его
электрическое поле. Мы определяем электрическое поле в точке как силу на единицу заряда. 92}
\конец{выравнивание*}
мы можем видеть, что электрическое поле \(E\) зависит только от заряда \(Q\), а не от величины испытания
обвинение.
Если электрическое поле известно, то электростатическая сила, действующая на любой заряд \(q\), помещенный в поле, равна просто получается путем перестановки определяющего уравнения: \[F=qE.\]
Видео: 23Z6
Моделирование: 23Z7
temp textРабочий пример 5: Электрическое поле 1
Рассчитайте напряженность электрического поля \(\text{30}\) \(\text{см}\) по заряду \(\text{5}\) \(\text{nC}\).
Определите, что требуется
Нам нужно рассчитать электрическое поле на расстоянии от данного заряда. {2}}.\) 9{-1}$}
\конец{выравнивание*}
Рабочий пример 6: Электрическое поле 2
Два заряда \({Q}_{1}=+3\mathrm{nC}\) и \({Q}_{2}=-4\mathrm{nC}\) находятся на расстоянии \(\text{50}\) \(\text{см}\). Что такое электрический напряженность поля в точке, которая \(\text{20}\) \(\text{см}\) от \({Q}_{1}\) и \(\text{50}\) \(\text{см}\) из \({Q}_{2}\)? Точка лежит между \({Q}_{1}\) и \({Q}_{2}\).
Определите, что требуется 9{-\text{2}}\) \(\text{m}\). Каково чистое электрическое поле, измеренное в точке \(A\)? от двух зарядов, если они расположены так, как показано?
Определить, что требуется
Нам необходимо рассчитать суммарное электрическое поле в \(A\). Это поле представляет собой сумму двух электрических fields — поле из \({Q}_{2}\) в \(A\) и из \({Q}_{3}\) в \(A\).
Определите, как подойти к проблеме
Нам нужно рассчитать два поля в \(A\), используя \(E=k\frac{Q}{r^2}\) для величины и определение направления по знакам заряда.
Затем нам нужно сложить два поля, используя наши правила сложения векторных величин, потому что электрическое поле является векторной величиной.
Определите, что дано
Нам известны все заряды и расстояния.
Рассчитать величину полей.
Величина поля из \({Q}_{2}\) в точке \(A\), которую мы будем называть \(E_2\), составляет: 9{-1}$} \конец{выравнивание*}
Векторное сложение электрических полей
Мы будем использовать точно ту же процедуру , что и раньше. Определить векторы на декартовой плоскости, разбить их на компоненты в направлениях \(x\) и \(y\), суммировать компоненты в каждом направлении, чтобы получить компоненты результирующего.
Мы выбираем положительные направления вправо (положительное \(х\)-направление) и вверх (положительное
\(y\)-направление). Мы знаем величины электрического поля, но нам нужно использовать заряды, чтобы определить
направление. Затем мы можем использовать диаграмму, чтобы определить направления.
Сила между положительным тестовым зарядом и \({Q}_{2}\) является отталкивающей (подобно зарядам). Это означает, что электрическое поле направлено влево или в отрицательном \(х\)-направлении.
Сила между положительным пробным зарядом и \({Q}_{3}\) притягивает (в отличие от зарядов) и электрическое поле будет иметь положительное \(y\)-направление.
Мы можем перерисовать диаграмму, иллюстрирующую поля, чтобы убедиться, что мы можем визуализировать ситуацию:
Результирующая сила 9{-1}$}\), действующий от \(\text{54,24}\)\(\text{°}\) до отрицательной оси \(x\) или \(\text{125,76}\)\(\text{°}\)к положительной оси \(x\).
Электрические поля
Учебник Упражнение 9.2
Расчет напряженности электрического поля \(\text{20}\) \(\text{m}\) по \(\text{7}\) \(\text{nC}\)
обвинение. {2}}.\) 9{-1}$}
\end{align*}
Два заряда \({Q}_{1}=-\text{6}\text{pC}\) и \({Q}_{2}=-\text{8 }\text{ pC}\) разделены расстояние \(\text{3}\) \(\text{км}\). Чему равна напряженность электрического поля в точке, \(\text{2}\) \(\text{км}\) из \({Q}_{1}\) и \(\text{1}\) \(\text{км}\) из \({Q}_{2}\)? Смысл лежит между \({Q}_{1}\) и \({Q}_{2}\).
Нам нужно рассчитать электрическое поле на расстоянии от двух заданных зарядов. Нам дана величина заряды и расстояния от зарядов. 9{-1}$}\) в направлении заряда \(-\text{8}\) \(\text{pC}\).
Пересмотр концепции поля – College Physics: OpenStax
Глава 18 Электрический заряд и электрическое поле
Резюме
- Описать силовое поле и рассчитать напряженность электрического поля, создаваемого точечным зарядом.
- Рассчитайте силу, действующую на пробный заряд со стороны электрического поля.
- Объясните взаимосвязь между электрической силой (F), действующей на испытательный заряд, и напряженностью электрического поля (E).
Контактные силы, такие как между бейсбольным мячом и битой, объясняются в малом масштабе взаимодействием зарядов в атомах и молекулах в непосредственной близости. Они взаимодействуют через силы, которые включают кулоновских сил . Действие на расстоянии — это сила между объектами, которые находятся недостаточно близко, чтобы их атомы могли «соприкоснуться». То есть они разделены более чем несколькими атомными диаметрами.
Например, заряженная резиновая расческа притягивает нейтральные кусочки бумаги на расстоянии под действием кулоновской силы. Очень полезно представить себе объект, окруженный в пространстве силовое поле . Силовое поле переносит силу на другой объект (называемый тестовым объектом) на некотором расстоянии.
Поле — это способ концептуализации и отображения силы, которая окружает любой объект и действует на другой объект на расстоянии без видимой физической связи. Например, гравитационное поле, окружающее Землю (и все другие массы), представляет собой гравитационную силу, которая могла бы возникнуть, если бы в данной точке поля была помещена другая масса. 92}[/latex], для точечного заряда (частица, имеющая заряд [латекс]\boldsymbol{Q}[/латекс]), действующего на пробный заряд [латекс]\boldsymbol{q}[/latex ] на расстоянии [латекс]\boldsymbol{r}[/латекс] (см. [ссылка]). Как величина, так и направление кулоновского силового поля зависят от [латекс]\boldsymbol{Q}[/латекс] и пробного заряда [латекс]\boldsymbol{q}[/латекс].
Ф 1 . Таким образом, кулоновское силовое поле не является уникальным в любой точке пространства, поскольку оно зависит от пробных зарядов 9.0009 q 1 и q 2 а также плата Q .Для упрощения мы бы предпочли иметь поле, которое зависит только от [латекс]\boldsymbol{Q}[/латекс] , а не от тестового заряда [латекс]\жирныйсимвол{q}[/латекс]. Электрическое поле определяется таким образом, что оно представляет собой только создающий его заряд и уникально в каждой точке пространства. В частности, электрическое поле [латекс]\boldsymbol{E}[/латекс] определяется как отношение кулоновской силы к пробному заряду:
[латекс]\boldsymbol{E =}[/латекс] [латекс]\boldsymbol{\frac{F}{q}}[/латекс],
где [латекс]\boldsymbol{F}[/латекс] — электростатическая сила (или кулоновская сила), действующая на положительный пробный заряд
[латекс]\boldsymbol{q}[/латекс]. 2 }[/латекс] . Таким образом, величина электрического поля [латекс]\boldsymbol{E}[/латекс] для точечного заряда равна 92}}[/латекс]
Таким образом видно, что электрическое поле зависит только от заряда [латекс]\boldsymbol{Q}[/латекс] и расстояния [латекс]\boldsymbol{r}[/латекс]; он полностью не зависит от тестового заряда [латекс]\boldsymbol{q}[/латекс].
Пример 1. Расчет электрического поля точечного заряда
Рассчитать напряженность и направление электрического поля [латекс]\boldsymbol{E}[/латекс], создаваемого точечным зарядом 2,00 нКл (нанокулоны) при расстоянии 5,00 мм от заряда. 95 \;\textbf{N} / \textbf{C}.} \end{array}[/latex]
Обсуждение
Эта напряженность электрического поля одинакова в любой точке на расстоянии 5,00 мм от заряда [latex]\boldsymbol{Q}[/latex], который создает поле. Он положительный, что означает, что он имеет направление, указывающее в сторону от заряда [латекс]\boldsymbol{Q}[/латекс]. 5}[/latex] N/C, таким образом, 95 \;\textbf{N} / \textbf{C})} \\[1em] & \boldsymbol{0.180 \;\textbf{N}.} \end{массив}[/latex]
Потому что [латекс] \boldsymbol{q}[/latex] отрицательна, сила направлена против направления поля.
Обсуждение
Сила притяжения, как и ожидалось для разных зарядов. (Поле было создано положительным зарядом, а здесь действует на отрицательный заряд.) Заряды в этом примере типичны для обычного статического электричества, а полученная небольшая сила притяжения аналогична силам, возникающим при статическом прилипании и подобных ситуациях.
PhET Explorations: Electric Field of Dreams
Играй в мяч! Добавьте заряды в Поле Снов и посмотрите, как они реагируют на электрическое поле. Включите фоновое электрическое поле и отрегулируйте направление и величину.
Рисунок 2. Электрическое поле мечты- Поле электростатической силы, окружающее заряженный объект, распространяется в пространстве во всех направлениях.
- Электростатическая сила, действующая точечным зарядом на пробный заряд на расстоянии [латекс]\boldsymbol{r}[/латекс], зависит от заряда обоих зарядов, а также от расстояния между ними.
- Электрическое поле [latex]\textbf{E}[/latex] определяется как
[латекс]\boldsymbol{E =}[/латекс] [латекс]\boldsymbol{\frac{\textbf{F}}{q,}}[/латекс]
, где [латекс]\textbf{F}[/латекс] — кулоновская или электростатическая сила, действующая на небольшой положительный пробный заряд [латекс]\boldsymbol{q}[/латекс]. [latex]\textbf{E}[/latex] имеет единицы N/C.
- Величина электрического поля [латекс]\textbf{E}[/латекс], создаваемого точечным зарядом [латекс]\boldsymbol{Q}[/латекс] , равна
92}}.[/латекс]
, где [латекс]\boldsymbol{r}[/латекс] — расстояние от [латекс]\жирныйсимвол{Q}[/латекс]. Электрическое поле [латекс]\boldsymbol{E}[/латекс] является вектором, а поля из-за множественных зарядов складываются подобными векторами.
- поле
- карта величины и направления силы, действующей на другие объекты, простирающейся в космос
- точечная оплата
- Заряженная частица, обозначенная как [латекс]\boldsymbol{Q}[/латекс], создающая электрическое поле
- испытательный заряд
- Частица (обозначается как [латекс]\жирный символ{q}[/латекс]) с положительным или отрицательным зарядом, помещенная в электрическое поле, создаваемое точечным зарядом
Напряженность электрического поля | Электрические заряды и поля
Сделать 8 минут чтения 14 минут видео
Напряженность электрического поля
Содержание
- Напряженность электрического поля
- Определение: электрическое поле
- Дополнительное видео от Khan Academy
- Пример: электрическое поле 1
- Вопрос
- Шаг 1: Определите, что требуется
- Шаг 2: Определите, что дано
- Шаг 3: Определите, как подойти к проблеме
- Пример: Electric Field 2
- Вопрос
- Шаг 1: Определите, что требуется
- Шаг 2: Определите, что дано
- Шаг 3: Определите, как подойти к проблеме
- Шаг 4: Решите задачу
- Пример: Электрическое поле 3
- Вопрос
- Шаг 1: Определите, что требуется
- Шаг 2: Определите, как подойти к задаче
- Шаг 3: Определите, что дано
0 9 Шаг 4: Рассчитайте величину полей.
- Шаг 5: Сложение векторов электрических полей
- Шаг 6: Результирующая сила
В предыдущих разделах мы изучали, как мы можем представить электрические поля вокруг заряда или комбинации зарядов с помощью силовых линий электрического поля. В этом представлении мы видим, что напряженность электрического поля представлена тем, насколько близко друг к другу расположены силовые линии. В дополнение к рисункам электрического поля мы также хотели бы иметь возможность количественно определить (поставить число), насколько сильно электрическое поле и каково его направление в любой точке пространства.
Небольшой пробный заряд \(q\), помещенный рядом с зарядом \(Q\), будет испытывать силу электрического поля, окружающего \(Q\). Величина силы описывается законом Кулона и зависит от величины заряда \(Q\) и расстояния пробного заряда от \(Q\). Чем ближе пробный заряд \(q\) к заряду \(Q\), тем большую силу он будет испытывать. Также в точках, расположенных ближе к заряду \(Q\), тем сильнее его электрическое поле.
Мы определяем электрическое поле в точке как силу на единицу заряда. 92} \end{align*}мы видим, что электрическое поле \(E\) зависит только от заряда \(Q\), а не от величины пробного заряда.Если электрическое поле известно, то электростатическая сила, действующая на любой заряд \(q\), помещенный в поле, просто получается путем изменения определяющего уравнения: \[F=qE.\]
Дополнительное видео от Khan Academy
Мы можем думать о силе между зарядами как о чем-то, происходящем от свойства пространства. Это свойство называется электрическим полем. Это видео было создано Салом Кханом.
См. несколько примеров ниже.
Пример: электрическое поле 1
Вопрос
Рассчитайте напряженность электрического поля \(\text{30}\) \(\text{см}\) из \(\text{5}\) \(\text {nC}\) заряд.
Шаг 1: Определите, что требуется
Нам нужно рассчитать электрическое поле на расстоянии от заданного заряда.
Шаг 2: Определить, что дано
Нам дана величина заряда и расстояние от заряда. 9{-1}$} \end{align*}
Пример: Electric Field 2
Вопрос
Два заряда \({Q}_{1}=+3\mathrm{nC}\) и \({ Q}_{2}=-4\mathrm{nC}\) разделены расстоянием \(\text{50}\) \(\text{см}\). Какова напряженность электрического поля в точке, которая \(\text{20}\) \(\text{см}\) от \({Q}_{1}\) и \(\text{50}\) \(\text{см}\) из \({Q}_{2}\)? Точка лежит между \({Q}_{1}\) и \({Q}_{2}\).
Шаг 1: Определите, что требуется
Нам нужно рассчитать электрическое поле на расстоянии от двух заданных зарядов. 9{-\text{2}}\) \(\text{m}\). Чему равно суммарное электрическое поле, измеренное в \(A\) от двух зарядов, если они расположены, как показано на рисунке?
Шаг 1: Определите, что требуется
Нам необходимо рассчитать чистое электрическое поле в точке \(A\).
Это поле представляет собой сумму двух электрических полей — поля от \({Q}_{2}\) в точке \(A\) и от \({Q}_{3}\) в точке \(A\) .Шаг 2: Определите, как подойти к проблеме и определение направления по знакам заряда. 9{-1}$} \end{align*}
Шаг 5: Сложение векторов электрических полей
Мы будем использовать в точности ту же процедуру , что и раньше. Определить векторы на декартовой плоскости, разбить их на составляющие по направлениям \(x\) и \(y\), просуммировать компоненты по каждому направлению, чтобы получить компоненты равнодействующей.
Мы выбираем положительные направления вправо (положительное \(x\)-направление) и вверх (положительное \(y\)-направление). Мы знаем величины электрического поля, но нам нужно использовать заряды, чтобы определить направление. Затем мы можем использовать диаграмму, чтобы определить направления.
Сила между положительным тестовым зарядом и \({Q}_{2}\) является отталкивающей (подобно зарядам). Это означает, что электрическое поле направлено влево или в отрицательном \(х\)-направлении.
Сила между положительным пробным зарядом и \({Q}_{3}\) является притягивающей (в отличие от зарядов), и электрическое поле будет в положительном \(y\)-направлении.
Мы можем перерисовать диаграмму, иллюстрирующую поля, чтобы убедиться, что мы можем визуализировать ситуацию:
Шаг 6: Результирующая сила 9{c}\)
\(a_{b}\)
\(\sqrt{a}\)
\(\sqrt[b]{a}\)
\(\frac{a}{ б}\)
\(\cfrac{a}{b}\)
\(+\)
\(-\)
\(\times\)
\(\div\)
\(\pm\)
\(\cdot\)
\(\amalg\)
\(\ast\)
\(\barwedge\)
\(\bigcirc\)
\( \bigodot\)
\(\bigoplus\)
\(\bigotimes\)
\(\bigsqcup\)
\(\bigstar\)
\(\bigtriangledown\)
\(\bigtriangleup\)
\(\blacklozenge\)
\(\blacksquare\)
\(\blacktriangle\)
2 \(\
3) \(\bullet\)
\(\cap\)
\(\cup\)
\(\circ\)
\(\circledcirc\)
\(\dagger\)
\( \ddagger\)
\(\diamond\)
\(\dotplus\)
\(\lozenge\)
\(\mp\)
\(\ominus\)
\(\oplus \)
\(\oslash\)
\(\otimes\)
\(\setminus\)
\(\sqcap\)
\(\sqcup\)
\(\square\)
\(\star\)
\(\triangle\)
\(\triangledown\)
\(\triangleleft\)
\(\Cap\)
\(\Cup\)
\( \upplus\)
\(\vee\)
\(\veebar\)
\(\клин\)
\(\wr\)
\(\следовательно\)
\(\left ( a \right )\)
\(\left \| a \right \|\)
\(\влево [ a \вправо ]\)
\(\влево \{ a \вправо \}\)
\(\влево \lceil a \вправо \rceil\)
\(\влево \ lfloor a \right \rfloor\)
\(\left ( a \right )\)
\(\vert a \vert\)
\(\leftarrow\)
\(\leftharpoondown\)
\(\leftharpoonup\)
\(\leftrightarrow\)
\(\leftrightharpoons\)
\(\mapsto\)
\(\rightarrow\)
\(\rightharpoondown\)
\( \правый гарпунвверх\)
\(\rightleftharpoons\)
\(\to\)
\(\Leftarrow\)
\(\Leftrightarrow\)
\(\Rightarrow\)
\(\overset{a}{ \leftarrow}\)
\(\overset{a}{\rightarrow}\)
\(\приблизительно \)
\(\asymp\)
\(\cong \)
\(\dashv \)
\(\doteq \)
\(= \)
\(\equiv \)
\(\frown \)
\(\geq \)
\(\geqslant \)
\(\гг\)
\(\gt \)
\(| \)
\(\leq \)
\(\leqslant \)
\(\ll \)
\(\lt \)
\( \models\)
\(\neq \)
\(\ngeqslant \)
\(\ngtr \)
\(\nleqslant \)
\(\nless \)
\(\not \equiv \)
\(\overset{\underset{\mathrm{def}}{}}{=} \)
\(\parallel \)
\(\perp \)
\(\prec \)
\(\preceq \)
\(\сим\)
\(\simeq\)
\(\smile\)
\(\succ\)
\(\succeq\)
\(\vdash\)
\(\in\)
\ (\ni \)
\(\notin \)
\(\nsubseteq \)
\(\nsupseteq \)
\(\sqsubset \)
\(\sqsubseteq \)
\(\ sqsupset \)
\(\sqsupseteq \)
\(\subset \)
\(\subseteq \)
\(\subseteqq \)
\(\supset \)
\\supseteq )\(\supseteqq \)
\(\emptyset\)
\(\mathbb{N}\)
\(\mathbb{Z}\)
\(\mathbb{Q}\)
\(\mathbb{R}\)
\(\mathbb{C}\)
\(\alpha\)
\(\beta\)
\(\gamma\)
\(\delta \)
\(\эпсилон\)
\(\дзета\)
\(\эта\)
\(\тета\)
\(\йота\)
\(\каппа\)
\(\lambda\)
\(\mu\)
\(\nu\)
\(\xi\)
\(\pi\)
\(\rho\)
\(\sigma\)
\(\tau\)
\(\upsilon\)
\(\phi\)
\(\chi\)
\(\psi\)
\(\omega\)
\(\Gamma\)
\(\Delta\)
\(\Theta\)
\( \Lambda\)
\(\Xi\)
\(\Pi\)
\(\Sigma\)
\(\Upsilon\)
\(\Phi\)
\(\Psi \)
\(\Омега\)
\((а)\)
\([а]\) 9{} a\)
Редактировать математику с помощью TeX:
Предварительный просмотр математики:
Поставщики и ресурсы RF Wireless
Веб-сайт RF Wireless World является домом поставщиков и ресурсов RF и Wireless.
На сайте представлены статьи, учебные пособия, поставщики, терминология, исходный код (VHDL, Verilog, MATLAB, Labview), тесты и измерения,
калькуляторы, новости, книги, загрузки и многое другое.Сайт RF Wireless World охватывает ресурсы по различным темам, таким как RF, беспроводная связь, vsat, спутник, радар, оптоволокно, микроволновая печь, wimax, wlan, zigbee, LTE, 5G NR, GSM, GPRS, GPS, WCDMA, UMTS, TDSCDMA, Bluetooth, Lightwave RF, z-wave, Интернет вещей (IoT), M2M, Ethernet и т. д. Эти ресурсы основаны на стандартах IEEE и 3GPP. Он также имеет академический раздел, который охватывает колледжи и университеты по инженерным дисциплинам и дисциплинам MBA.
Статьи о системах на основе IoT
Система обнаружения падений для пожилых людей на основе IoT : В статье рассматривается архитектура системы обнаружения падений, используемой для пожилых людей. В нем упоминаются преимущества или преимущества системы обнаружения падения IoT. Подробнее➤
См. также другие статьи о системах на основе IoT:
• Система очистки туалетов AirCraft. • Система измерения удара при столкновении • Система отслеживания скоропортящихся продуктов и овощей • Система помощи водителю • Система умной розничной торговли • Система мониторинга качества воды • Система интеллектуальной сети • Умная система освещения на основе Zigbee • Умная система парковки на базе Zigbee • Умная система парковки на базе LoRaWAN.Беспроводные радиочастотные изделия
Этот раздел статей охватывает статьи о физическом уровне (PHY), уровне MAC, стеке протоколов и сетевой архитектуре на основе WLAN, WiMAX, zigbee, GSM, GPRS, TD-SCDMA, LTE, 5G NR, VSAT, Gigabit Ethernet на основе IEEE/3GPP и т. д. , стандарты. Он также охватывает статьи, связанные с испытаниями и измерениями, посвященные испытаниям на соответствие, используемым для испытаний устройств на соответствие RF/PHY. СМ. УКАЗАТЕЛЬ СТАТЕЙ >>.
Физический уровень 5G NR : Обработка физического уровня для канала 5G NR PDSCH и канала 5G NR PUSCH была рассмотрена поэтапно.
Это описание физического уровня 5G соответствует спецификациям физического уровня 3GPP.
Подробнее➤Основные сведения о повторителях и типы повторителей : В нем объясняются функции различных типов повторителей, используемых в беспроводных технологиях. Подробнее➤
Основы и типы замираний : В этой статье рассматриваются мелкомасштабные замирания, крупномасштабные замирания, медленные замирания, быстрые замирания и т. д., используемые в беспроводной связи. Подробнее➤
Архитектура сотового телефона 5G : в этой статье рассматривается блок-схема сотового телефона 5G с внутренними модулями 5G. Архитектура сотового телефона. Подробнее➤
Основные сведения о помехах и типы помех: Электромагнитные помехи, ICI, ISI, световые помехи, звуковые помехи и т. д. Подробнее➤
Раздел 5G NR
В этом разделе рассматриваются функции 5G NR (новое радио), нумерология, диапазоны, архитектура, развертывание, стек протоколов (PHY, MAC, RLC, PDCP, RRC) и т.
д.
5G NR Краткий справочный указатель >>
• Мини-слот 5G NR • Часть полосы пропускания 5G NR • БАЗОВЫЙ НАБОР 5G NR • Форматы 5G NR DCI • 5G NR UCI • Форматы слотов 5G NR • IE 5G NR RRC • 5G NR SSB, SS, PBCH • 5G NR PRACH • 5G NR PDCCH • 5G NR PUCCH • Опорные сигналы 5G NR • 5G NR m-Sequence • Золотая последовательность 5G NR • 5G NR Zadoff Chu Sequence • Физический уровень 5G NR • MAC-уровень 5G NR • Уровень 5G NR RLC • Уровень PDCP 5G NRУчебные пособия по беспроводным технологиям
В этом разделе рассматриваются учебные пособия по радиочастотам и беспроводным сетям. Он охватывает учебные пособия по таким темам, как сотовая связь, WLAN (11ac, 11ad), wimax, bluetooth, zigbee, zwave, LTE, DSP, GSM, GPRS, GPS, UMTS, CDMA, UWB, RFID, радар, VSAT, спутник, беспроводная сеть, волновод, антенна, фемтосота, тестирование и измерения, IoT и т. д. См. ИНДЕКС УЧЕБНЫХ ПОСОБИЙ >>
Учебное пособие по 5G — В этом учебном пособии по 5G также рассматриваются следующие подтемы, посвященные технологии 5G:
Учебник по основам 5G Диапазоны частот учебник по миллиметровым волнам Рамка волны 5G мм Зондирование канала миллиметровых волн 5G 4G против 5G Испытательное оборудование 5G Архитектура сети 5G Сетевые интерфейсы 5G NR звучание канала Типы каналов 5G FDD против TDD Нарезка сети 5G NR Что такое 5G NR Режимы развертывания 5G NR Что такое 5G ТФВ этом руководстве по GSM рассматриваются основы GSM, сетевая архитектура, сетевые элементы, системные спецификации, приложения, Типы пакетов GSM, структура кадров GSM или иерархия кадров, логические каналы, физические каналы, Физический уровень GSM или обработка речи, вход в сеть мобильного телефона GSM или настройка вызова или процедура включения питания, Вызов MO, вызов MT, модуляция VAMOS, AMR, MSK, GMSK, физический уровень, стек протоколов, основы мобильного телефона, Планирование RF, нисходящая линия связи PS и восходящая линия связи PS.
➤Читать дальше.LTE Tutorial , описывающий архитектуру системы LTE, включая основы LTE EUTRAN и LTE Evolved Packet Core (EPC). Он предоставляет ссылку на обзор системы LTE, радиоинтерфейс LTE, терминологию LTE, категории LTE UE, структуру кадра LTE, физический уровень LTE, Стек протоколов LTE, каналы LTE (логические, транспортные, физические), пропускная способность LTE, агрегация несущих LTE, Voice Over LTE, расширенный LTE, Поставщики LTE и LTE vs LTE advanced.➤Подробнее.
РЧ-технологии Материалы
На этой странице мира беспроводных радиочастот описывается пошаговое проектирование преобразователя частоты на примере повышающего преобразователя частоты 70 МГц в диапазон C. для микрополосковой платы с использованием дискретных радиочастотных компонентов, а именно. Смесители, гетеродин, MMIC, синтезатор, опорный генератор OCXO, амортизирующие прокладки. ➤Читать дальше.
➤ Проектирование и разработка РЧ приемопередатчика ➤Дизайн радиочастотного фильтра ➤Система VSAT ➤Типы и основы микрополосковых ➤Основы волноводаСекция испытаний и измерений
В этом разделе рассматриваются ресурсы по контролю и измерению, контрольно-измерительное оборудование для тестирования тестируемых устройств на основе Стандарты WLAN, WiMAX, Zigbee, Bluetooth, GSM, UMTS, LTE.
ИНДЕКС испытаний и измерений >>
➤Система PXI для контрольно-измерительных приборов. ➤ Генерация и анализ сигналов ➤ Измерения физического уровня ➤ Тестирование устройства WiMAX на соответствие ➤ Тест на соответствие Zigbee ➤ Тест на соответствие LTE UE ➤ Тест на соответствие TD-SCDMAВолоконно-оптические технологии
Волоконно-оптический компонент основы, включая детектор, оптический соединитель, изолятор, циркулятор, переключатели, усилитель, фильтр, эквалайзер, мультиплексор, разъемы, демультиплексор и т. д. Эти компоненты используются в оптоволоконной связи. ИНДЕКС оптических компонентов >>
➤Руководство по оптоволоконной связи ➤APS в SDH ➤Основы SONET ➤ Структура кадра SDH ➤ SONET против SDHПоставщики беспроводных радиочастотных устройств, производители
Сайт RF Wireless World охватывает производителей и поставщиков различных радиочастотных компонентов, систем и подсистем для ярких приложений, см. ИНДЕКС поставщиков >>.
Поставщики ВЧ-компонентов, включая ВЧ-изолятор, ВЧ-циркулятор, ВЧ-смеситель, ВЧ-усилитель, ВЧ-адаптер, ВЧ-разъем, ВЧ-модулятор, ВЧ-трансивер, PLL, VCO, синтезатор, антенну, осциллятор, делитель мощности, сумматор мощности, фильтр, аттенюатор, диплексер, дуплексер, чип-резистор, чип-конденсатор, чип-индуктор, ответвитель, ЭМС, программное обеспечение RF Design, диэлектрический материал, диод и т. д. Поставщики радиочастотных компонентов >>
➤Базовая станция LTE ➤ РЧ-циркулятор ➤РЧ-изолятор ➤Кристаллический осцилляторMATLAB, Labview, Embedded Исходные коды
Раздел исходного кода RF Wireless World охватывает коды, связанные с языками программирования MATLAB, VHDL, VERILOG и LABVIEW. Эти коды полезны для новичков в этих языках. СМ. ИНДЕКС ИСТОЧНИКОВ >>
➤ 3–8 код VHDL декодера ➤Скремблер-дескремблер Код MATLAB ➤32-битный код ALU Verilog ➤ T, D, JK, SR коды лаборатории триггеров*Общая медицинская информация*
Сделайте эти пять простых вещей, чтобы помочь остановить коронавирус (COVID-19).
СДЕЛАЙТЕ ПЯТЬ
1. РУКИ: Мойте их чаще
2. ЛОКТ: кашляйте в него
3. ЛИЦО: не прикасайтесь к нему
4. НОГИ: держитесь на расстоянии более 1 метра друг от друга
5. ЧУВСТВУЙТЕ: заболели? Оставайтесь домаИспользуйте технологию отслеживания контактов >> , следуйте рекомендациям по социальному дистанцированию >> и установить систему наблюдения за данными >> спасти сотни жизней. Использование концепции телемедицины стало очень популярным в таких стран, как США и Китай, чтобы остановить распространение COVID-19так как это заразное заболевание.
Радиочастотные калькуляторы и преобразователи
Раздел «Калькуляторы и преобразователи» охватывает ВЧ-калькуляторы, беспроводные калькуляторы, а также преобразователи единиц измерения. Они охватывают беспроводные технологии, такие как GSM, UMTS, LTE, 5G NR и т. д. СМ. КАЛЬКУЛЯТОРЫ Указатель >>.
➤Калькулятор пропускной способности 5G NR ➤ 5G NR ARFCN и преобразование частоты ➤ Калькулятор скорости передачи данных LoRa ➤ LTE EARFCN для преобразования частоты ➤ Калькулятор антенны Yagi ➤ Калькулятор времени выборки 5G NRIoT-Интернет вещей Беспроводные технологии
В разделе, посвященном IoT, рассматриваются беспроводные технологии Интернета вещей, такие как WLAN, WiMAX, Zigbee, Z-wave, UMTS, LTE, GSM, GPRS, THREAD, EnOcean, LoRa, SIGFOX, WHDI, Ethernet, 6LoWPAN, RF4CE, Bluetooth, Bluetooth с низким энергопотреблением (BLE), NFC, RFID, INSTEON, X10, KNX, ANT+, Wavenis, Dash7, HomePlug и другие.
