Электричество и магнетизм
Теперь мы готовы к обсуждению взаимодействия тока с магнитным полем.
Ампер установил наличие силового взаимодействия между двумя проводниками, по которым текут электрические токи. Пусть имеются два длинных параллельных проводника (рис. 5.25-1).
Рис. 5.25. Опыт Ампера по исследованию взаимодействия параллельных токов:
1 — схема установки; 2 — отталкивание антипараллельных токов; 3 — притяжение параллельных токов
Если по ним пропускать токи, текущие в противоположных направлениях, то проводники будут отталкиваться друг от друга (см. рис. 5.25-2). Если же токи будут течь в одном направлении, то они будут притягиваться (см. рис. 5.25-3).
Видео 5.4. Взаимодействие параллельных токов.
Эксперименты, проведенные Ампером, показали, что на проводник с током, помещенный в магнитное поле, действует сила. Откуда же она берется? Обсуждая эффект Холла, мы видели, что сила электрического поля  Но холловское поле EХ действует также и на кристаллическую ионную решетку вещества. На рис. 5.23 поле EХ направлено вверх, ортогонально току и магнитной индукции. Туда же будет направлена и сила, действующая на проводник. Найдем ее величину. Если поперечное сечение проводника равно S, а его длина (в направлении тока) — dl, то в данном объеме dV = dl · S сосредоточено dN = ndV = n · dl · S электронов проводимости. Их полный заряд равен dQ = edN = en · dl
Но холловское поле EХ действует также и на кристаллическую ионную решетку вещества. На рис. 5.23 поле EХ направлено вверх, ортогонально току и магнитной индукции. Туда же будет направлена и сила, действующая на проводник. Найдем ее величину. Если поперечное сечение проводника равно S, а его длина (в направлении тока) — dl, то в данном объеме dV = dl · S сосредоточено dN = ndV = n · dl · S электронов проводимости. Их полный заряд равен dQ = edN = en · dl
|
|
(5. |
где мы выразили плотность тока через его силу
Обращаем внимание, что в эту формулу не вошли характеристики конкретных носителей заряда, но лишь полный ток через проводник.
У нас внешнее магнитное поле было ортогонально току. В общем случае направление тока будем характеризовать вектором dl, имеющем длину dl и направленным вдоль течения тока. В холловскую напряженность электрического поля дает вклад только компонента магнитного поля, ортогональная вектору dl. Эта компонента равна по величине
где есть угол между векторами B и dl. Тогда для величины силы имеем
|
|
(5.31) |
Учитывая направление этой силы (правило винта), можем записать ее в векторной форме
|
|
(5. |
Выражение (5.32) носит название закона Ампера, а сила называется силой Ампера (рис. 5.26).
Рис. 5.26. Сила Ампера, действующая на провод с током в поле постоянного магнита
Видео 5.5. Сила Ампера: выпрыгивание провода из магнита.
Мы получили выражение для силы, действующей на элемент проводника dl. Для определения полной силы, действующей на проводник, надо проинтегрировать (5.32) вдоль его длины, учитывая зависимость магнитного поля от положения элемента. Такое интегрирование становится тривиальным для прямолинейного проводника в однородном магнитном поле
|
|
(5.33) |
Направление силы Ампера определяется по  5.27):
5.27):
|
Если левую руку расположить таким образом, чтобы линии магнитной индукции входили в ладонь, а вытянутые пальцы были направлены в направлении тока, то отогнутый большой палец покажет направление действия силы Ампера, действующей на проводник. |
Рис. 5.27. Определение направления силы Ампера
Видео 5.6. Сила Ампера: тележка Эйхенвальда.
Действие силы Ампера на проводник с током демонстрируется в опыте, показанном на рис. 5.28. На торце вертикальной цилиндрической катушки положены горизонтальные проводящие рельсы, по которым может катиться алюминиевая трубка. После включения тока через катушку к рельсам прикладывается постоянное напряжение, и по трубке начинает течь ток. Под действием силы Ампера трубка катится по рельсам. При изменении направления тока в трубке она катится в противоположную сторону.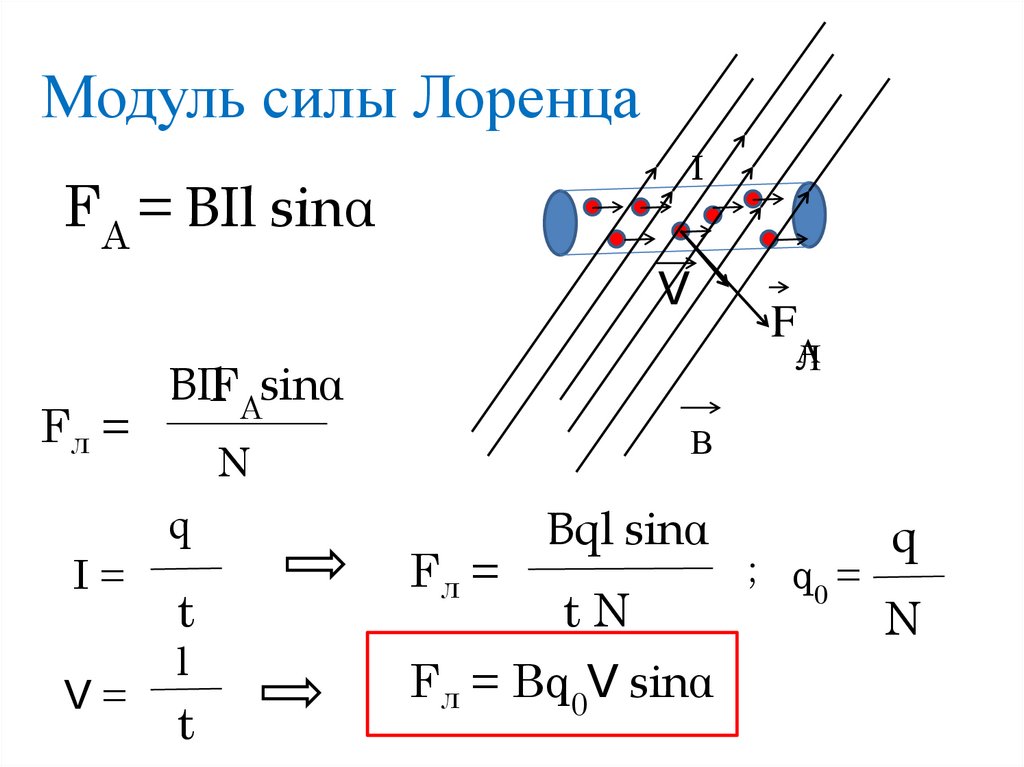
Рис. 5.28. Экспериментальное изучение силы Ампера
В общем случае произвольного проводника и магнитного поля силы, действующие на различные элементы проводника, различаются как величиной, так и направлением (рис. 5.29).
Рис. 5.29. В общем случае силы, действующие на различные элементы проводника,
различаются как величиной, так и направлением
С помощью формулы (5.31) можно определить величину магнитной индукции по максимальной силе Ампера dFA (в этом случае ), действующей на элемент dl проводника с током I
То есть величина магнитной индукции численно равна максимальной силе, действующей на единичный элемент тока.
Действие магнитного поля на проводник с током. Закон Ампера. Школьный курс физики
Сила Ампера.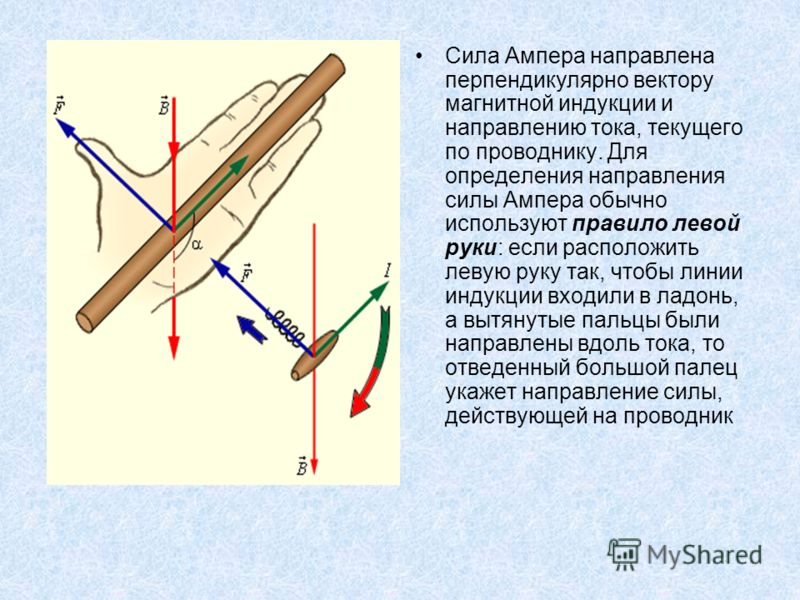 Закон Ампера.
Закон Ампера.
Выясним, как определить силу, действующую со стороны магнитного поля на проводник с током.
Силу, действующую на проводник с током, помещённый в магнитное поле, называют силой Ампера А.
Как мы уже знаем, Ампер установил, что параллельные токи одинакового направления притягиваются, а противоположного направления — отталкиваются. Взаимно перпендикулярные токи не действуют друг на друга. Экспериментально можно установить, что модуль силы 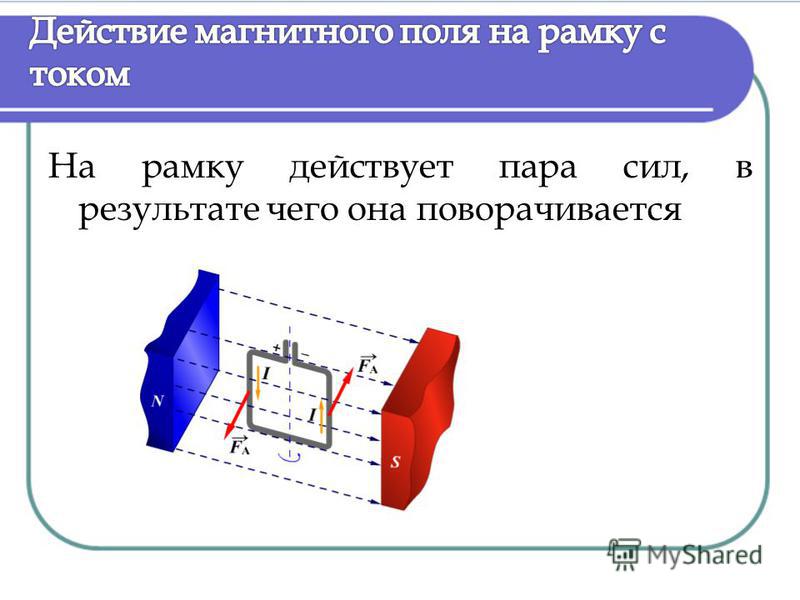
Формула для определения модуля силы Ампера в общем случае имеет вид
FA = BIΔlsin α. (1)
Формулу (1), выражающую связь этой силы с индукцией поля, называют законом Ампера.
Модуль силы, с которой однородное магнитное поле действует на помещённый в него прямолинейный проводник стоком, равен произведению модуля вектора магнитной индукции этого поля, силы тока, длины отрезка проводника и синуса угла между направлением тока и вектора магнитной индукции.
Если угол между вектором магнитной индукции и направлением тока в проводнике равен нулю (α = 0°), то модуль силы Ампера равен нулю. Если же угол между вектором и направлением тока равен 90° (
Направление силы Ампера определяют по правилу левой руки (рис. 3.26).
Рис. 3.26
Если расположить кисть левой руки так, чтобы линии магнитной индукции входили в ладонь, а четыре пальца были направлены по току, то отогнутый под прямым углом большой палец левой руки покажет направление силы Ампера.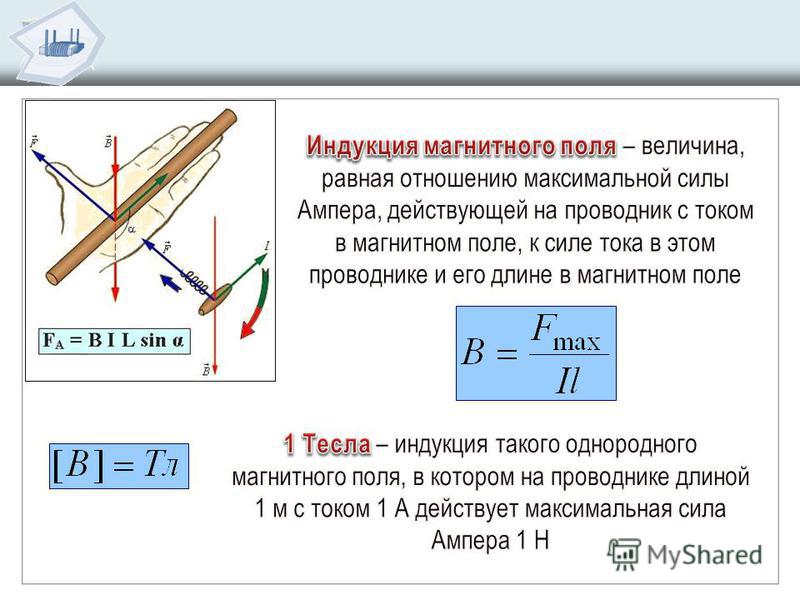
В задачах мы будем схематически изображать направления силы Ампера и вектора индукции магнитного поля так, как показано на рисунке 3.27.
Рис. 3.27
Отметим, что с помощью закона Ампера можно вычислить модуль силы и момент сил, действующих на замкнутый проводник с током произвольной формы. Справедливость закона Ампера подтверждается тем, что вычисленное с его помощью значение результирующей силы для любого замкнутого проводника с током (она равна сумме сил, действующих на участки малой длины) совпадает с экспериментально полученным значением силы.
Магнитное взаимодействие проводников c токами.
Рассмотрим притяжение или отталкивание проводников с токами. Опыты Ампера показали, что магнитные поля, созданные токами I1, I2, протекающими по бесконечно длинным параллельным проводникам, находящимся на расстоянии r друг от друга, приводят к возникновению на каждом отрезке проводников длиной Δl силы взаимодействия:
где k — коэффициент пропорциональности, равный 1 ∙ 10 -7 H∕A2. В единицах СИ k = μ0/ 4π (μ0 — магнитная постоянная).
В единицах СИ k = μ0/ 4π (μ0 — магнитная постоянная).
Hа рисунке 3.28 но правилу правой руки (или правилу буравчика) определено направление вектора индукции магнитных полей, созданных токами Z1 и I2 соответственно.
Рис. 3.28
По правилу левой руки можно установить направление силы Ампера, действующей на проводники с токами. В случае, когда направления токов совпадают, проводники притягиваются друг к другу. Если же направление одного из токов (например, I1) изменить на противоположное, то и направление силы 12 изменится на противоположное. Так как от направления тока I1 зависит направление вектора 1, то и направление силы 21 изменится на противоположное. Таким образом, токи, текущие в противоположных направлениях, будут отталкиваться друг от друга.
Магнитное взаимодействие проводников с токами используется в СИ для определения единицы силы тока — ампера (А).
Ампер — это сила постоянного тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, вызвал бы на каждом участке проводника длиной 1 м силу взаимодействия, равную 2 ∙ 10 -7 H.
Действие магнитного поля на рамку c током.
Определим момент сил, действующий на прямоугольную рамку с током в однородном магнитном поле с индукцией . Стороны рамки имеют размеры а и b, сила тока, текущего в ней, равна I. Вектор индукции магнитного поля составляет с нормалью к рамке угол α (рис. 3.29, а).
Рис.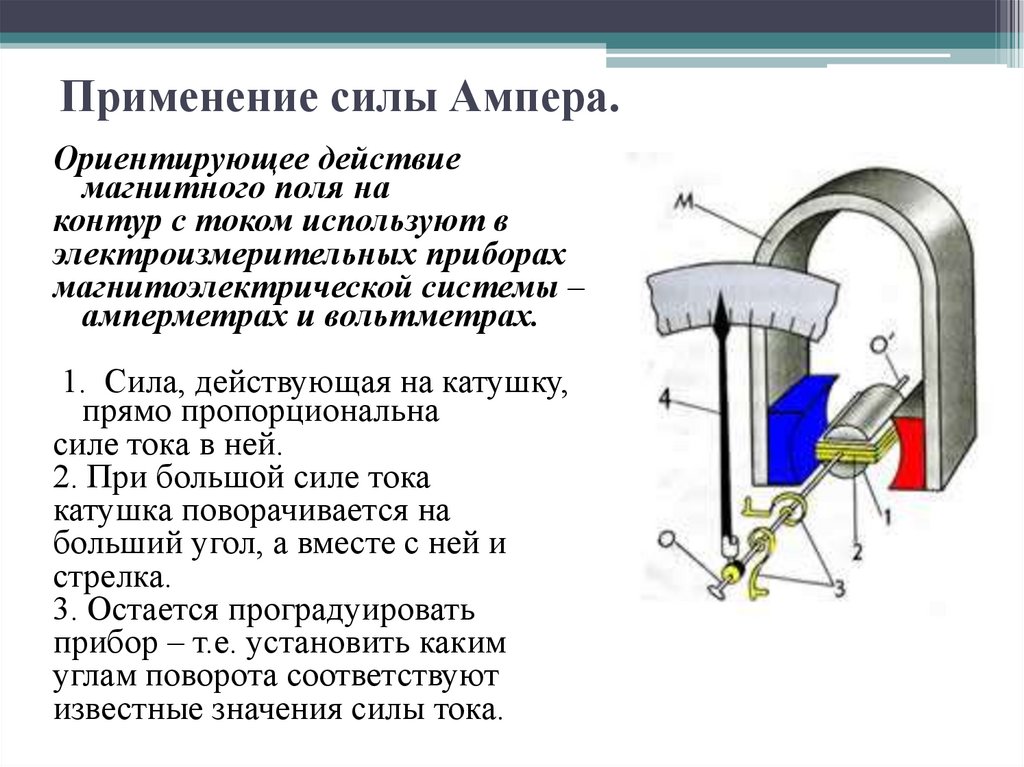 3.29
3.29
На рисунке 3.29, б показан вид сверху на сечение рамки горизонтальной плоскостью.
По правилу левой руки на стороны рамки длиной b действует пара сил 1 и 2, перпендикулярных вектору , которая создаёт момент сил относительно оси, проходящей через середину рамки. Силы, действующие на стороны рамки длиной а, лишь растягивают рамку.
По закону Ампера F1 = F2 = IBb. Плечо каждой из этих сил .
Суммарный момент сил равен
где S = ab — площадь прямоугольной рамки.
При α = 90° момент сил максимален.
Применения закона Ампера.
На практике закон Ампера используют для вычисления сил, действующих на проводники с токами, во многих технических устройствах, в частности в электродвигателях.
Рассмотрим устройство электродвигателя. По обмотке вращающейся части электродвигателя — якоря (ротора) 3 (рис. 3.30) — протекает электрический ток.
По обмотке вращающейся части электродвигателя — якоря (ротора) 3 (рис. 3.30) — протекает электрический ток.
Рис. 3.30
Мощные электромагниты создают магнитное поле, которое действует на проводники с током в обмотке якоря и заставляет их двигаться (рис. 3.31).
Рис. 3.31
Якорь изготовляется из стальных пластин, а полюсам электромагнита придаётся специальная форма с тем, чтобы сконцентрировать магнитное поле в местах, где располагается обмотка ротора. Выводы обмотки якоря припаяны к медным коллекторным полукольцам. Коллектор 1 состоит из двух полуколец, к которым прижимаются скользящие по ним контакты — щётки 2. Коллектор изменяет направление тока в обмотке. К щёткам от источника тока подводится напряжение, питающее обмотку ротора. Когда по виткам обмотки проходит ток, на них со стороны магнитного поля действуют силы Ампера, благодаря которым якорь приходит во вращение. Вращательное движение якоря передаётся валу, от него — различным механизмам.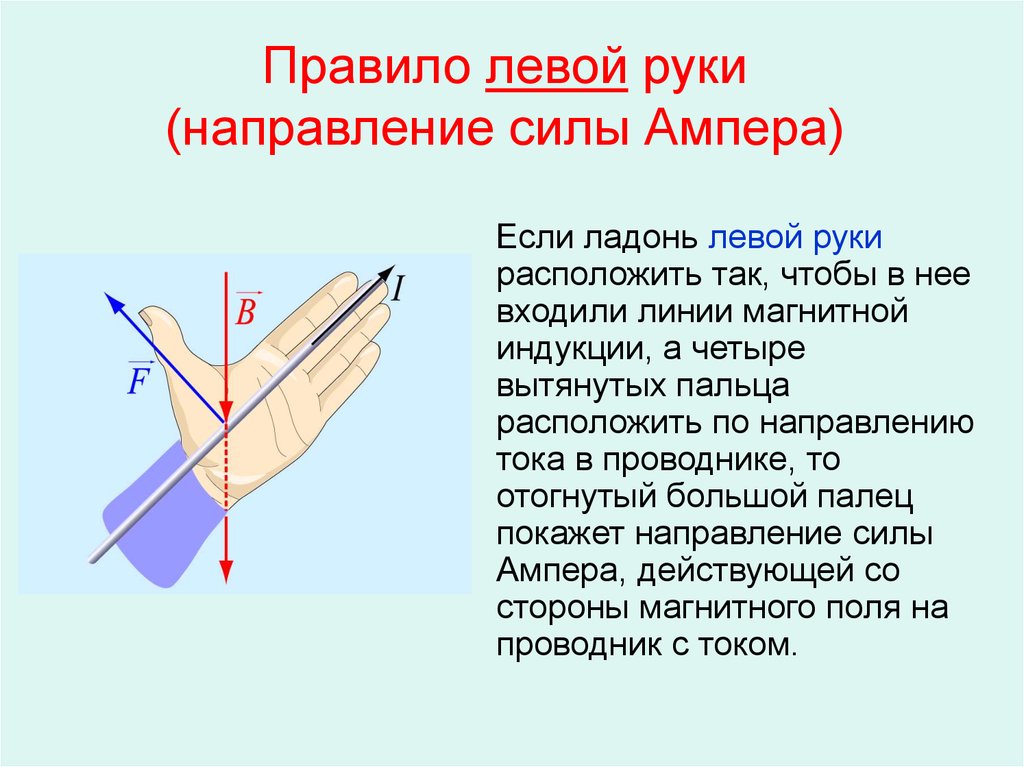
Создание электродвигателей связано с именем Б. С. Якоби. Он сконструировал первый в мире практически пригодный электродвигатель постоянного тока в 1834 г. и применил его для движения судна по реке Неве. В настоящее время электродвигатели устанавливают на электропоездах, троллейбусах, трамваях, лифтах и многих других устройствах. Они имеют ряд преимуществ по сравнению с тепловыми двигателями. Электродвигатели не загрязняют окружающую среду, так как им не нужен запас топлива. Кроме того, электродвигатели удобны в эксплуатации и надёжны в работе. КПД мощных электрических двигателей может достигать 90%, что невозможно для других типов двигателей.
Электроизмерительные приборы.
Действие магнитного поля на контур с током используется в стрелочных электроизмерительных приборах магнитоэлектрической системы для измерения силы тока и напряжения. Измерительный прибор такой системы устроен следующим образом. На лёгкой (обычно алюминиевой) рамке прямоугольной формы с прикреплённой к ней стрелкой намотана катушка 1, имеющая N витков (рис. 3.32).
3.32).
Рис. 3.32
Рамка укреплена на двух полуосях. В положении равновесия её удерживают две тонкие спиральные пружины 2. Момент сил упругости Mмех, действующий со стороны пружины и возвращающий катушку в положение равновесия, пропорционален углу φ отклонения стрелки 3 от положения равновесия:
Mмех = ƒφ,
где ƒ — постоянный коэффициент пропорциональности.
Катушку помещают между полюсами постоянного магнита специальной формы 4 (см. рис. 3.32). Внутри катушки расположен цилиндр из мягкого железа 1.
1 Мягкое железо остаётся намагниченным только до тех пор, пока оно подвержено действию магнитной силы.
Такая конструкция обеспечивает радиальное направление линий магнитной индукции в той области, где находятся витки катушки (рис. 3.33).
Рис. 3.33
В результате при любом положении катушки момент сил, действующий на неё со стороны магнитного поля, максимален и при неизменной силе тока один и тот же. Катушка с током поворачивается до тех пор, пока момент сил упругости, действующий со стороны пружины, не уравновесит момент сил, действующий на рамку со стороны магнитного поля:
Катушка с током поворачивается до тех пор, пока момент сил упругости, действующий со стороны пружины, не уравновесит момент сил, действующий на рамку со стороны магнитного поля:
Mмех = ƒφ = NIBS.
Отсюда следует, что измеряемая сила тока прямо пропорциональна углу отклонения стрелки:
Здесь коэффициент постоянная для данного прибора величина.
Прибор можно проградуировать так, чтобы угол поворота определял силу тока в амперах или других единицах. Согласно закону Ома, сила тока в приборе I = U / R. Поэтому прибор можно проградуировать и так, чтобы определённому углу φ отклонения стрелки соответствовало напряжение U на зажимах прибора в вольтах или других единицах. Таким образом, прибор может служить как амперметром, так и вольтметром.
Вопросы:
1. Сформулируйте закон Ампера. Связь между какими физическими величинами устанавливает этот закон?
2. Приведите определение единицы силы тока в СИ.
Приведите определение единицы силы тока в СИ.
3. Расскажите об устройстве и принципе действия:
а) электродвигателя;
б) стрелочного электроизмерительного прибора магнитоэлектрической системы.
Вопросы для обсуждения:
1. Какое положение займёт подвижный соленоид относительно магнита (рис. 3.34) при прохождении по соленоиду тока?
Рис. 3.34
Что произойдёт с соленоидом, если изменить направление:
а) тока;
б) линий магнитного поля?
2. Над соленоидом (рис. 3.35) подвешен полосовой магнит.
Рис. 3.35
Что произойдёт с магнитом, если:
а) по соленоиду пропустить постоянный ток;
б) изменить направление тока в соленоиде?
Пример решения задачи
Нa горизонтальных рельсах, находящихся в вертикальном однородном магнитном поле, лежит стальной брусок перпендикулярно рельсам. Расстояние между рельсами равно 15 см. Масса бруска составляет 300 г, коэффициент трения бруска о рельсы равен 0,2. Для того чтобы брусок сдвинулся с места, по нему необходимо пропустить ток. Определите индукцию магнитного поля, если минимальная сила тока, при которой брусок приходит в движение, равна 40 А.
Масса бруска составляет 300 г, коэффициент трения бруска о рельсы равен 0,2. Для того чтобы брусок сдвинулся с места, по нему необходимо пропустить ток. Определите индукцию магнитного поля, если минимальная сила тока, при которой брусок приходит в движение, равна 40 А.
Запишем условие равновесия бруска:
и спроецируем его на оси OX и OY.
Учитывая, что
получим
C учётом числовых данных
Ответ: B = 98 мТл.
Упражнения:
1. Чему равна индукция магнитного поля, в котором на проводник с длиной активной части 5 см действует сила 50 мН? Сила тока в проводнике равна 25 А. Проводник расположен перпендикулярно линиям индукции магнитного поля.
2. C какой силой действует магнитное поле с индукцией 10 мТл на проводник с длиной активной части 0,1 м, сила тока в котором 50 А? Направление тока в проводнике перпендикулярно вектору магнитной индукции.
3. Какая сила действует на проводник длиной 10 см в однородном магнитном поле с индукцией 2,6 Тл, если сила тока в проводнике 12 А, а угол между направлением тока и линиями магнитной индукции составляет: а) 90°; б) 30°?
4. В однородном магнитном ноле, индукция которого равна 2 Тл, вертикально вверх движется прямой проводник массой 2 кг, по которому течёт ток. Через 3 с после начала движения проводник имеет скорость 10 м/с. Определите длину проводника, если сила тока в нём равна 4 А. Вектор индукции магнитного поля образует с осью проводника угол 30°.
В однородном магнитном ноле, индукция которого равна 2 Тл, вертикально вверх движется прямой проводник массой 2 кг, по которому течёт ток. Через 3 с после начала движения проводник имеет скорость 10 м/с. Определите длину проводника, если сила тока в нём равна 4 А. Вектор индукции магнитного поля образует с осью проводника угол 30°.
5. Нa рисунке 3.37 представлены различные случаи взаимодействия магнитного поля с током. Сформулируйте задачу для каждого из представленных случаев и решите её.
Рис. 3.37
Предыдущая страницаСледующая страница
Закон Ампера
Направление силы Ампера
Ампер первым установил, что проводники, по которым течет электрический ток, взаимодействуют механически (притягиваются или отталкиваются). Сила ($\overrightarrow{F}$), которая действует на прямолинейный проводник с током (I), всегда перпендикулярна проводнику и направлению вектора магнитной индукции ($\overrightarrow{B}$). В том случае, если прямолинейный проводник расположен параллельно вдоль направления линий магнитного поля, поле не действует. Конкретное направление силы Ампера можно найти с помощью правила левой руки. Левую руку надо расположить так, чтобы линии поля входили в ладонь, четыре пальца были направлены по току, тогда отогнутый на 90 градусов большой палец укажет направление силы Ампера. Если направление вектора $\overrightarrow{B}$ составляет некоторый угол с направлением тока, то для выяснения направления силы Ампера целесообразно разложить вектор магнитной индукции на две составляющие (рис.1):
В том случае, если прямолинейный проводник расположен параллельно вдоль направления линий магнитного поля, поле не действует. Конкретное направление силы Ампера можно найти с помощью правила левой руки. Левую руку надо расположить так, чтобы линии поля входили в ладонь, четыре пальца были направлены по току, тогда отогнутый на 90 градусов большой палец укажет направление силы Ампера. Если направление вектора $\overrightarrow{B}$ составляет некоторый угол с направлением тока, то для выяснения направления силы Ампера целесообразно разложить вектор магнитной индукции на две составляющие (рис.1):
где $\overrightarrow{B_{\bot }}$ — перпендикулярна току, $\overrightarrow{B_{II}}$ — параллельна току. Только $\overrightarrow{B_{\bot }}$ — вызывает действие поля, к ней надо применять правило левой руки.
Рис. 1
Еще Ампер установил, что два параллельных проводника с током притягиваются, если токи имеют одинаковые направления и отталкиваются, если токи текут в противоположные стороны.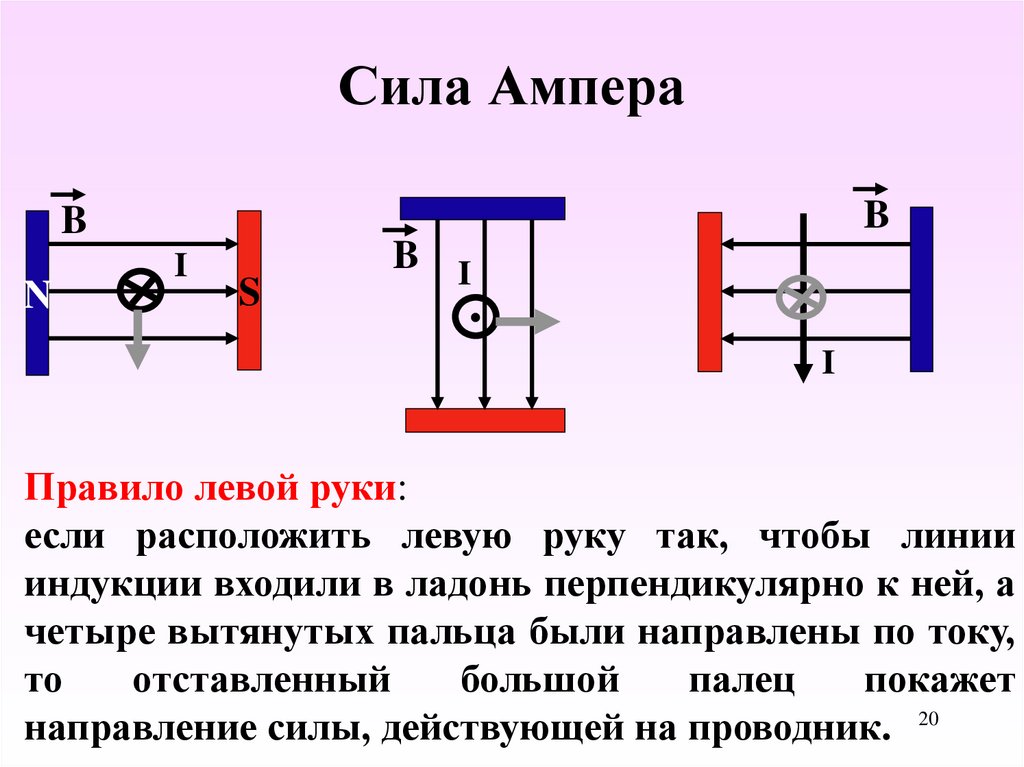 Это просто объяснить, если представить, что один проводник создает магнитное поле, а другой проводник в него помещен и это поле действует на него. Можно использовать правило левой руки и выяснить, как направлена сила.
Это просто объяснить, если представить, что один проводник создает магнитное поле, а другой проводник в него помещен и это поле действует на него. Можно использовать правило левой руки и выяснить, как направлена сила.
Закон Ампера
Для прямолинейного проводника сила Ампера имеет вид:
где $I$ — сила тока, которая течет в проводнике, $\overrightarrow{B}$ — вектор индукции магнитного поля, в которое проводник помещен, $\overrightarrow{l}$ — длина проводника, направление задано, направлением тока. Модуль силы ампера в этом случае равен:
где $\alpha $ — угол между векторами $\overrightarrow{l\ }и\ \overrightarrow{B}$.
Понятно, что на практике совсем не все проводники являются прямолинейными. Однако любой проводник можно разбить на совокупность частей, которые можно считать прямолинейными. Тогда вводится понятие элемента тока — это величина равная$:\ Id\overrightarrow{l}$, где $d\overrightarrow{l}$ — элементарный прямолинейный участок проводника, вектор, направленный по току. {-2}$ кг, длина l=0,4м. Индукция магнитного поля равна 0,25Тл. Определите величину угла, на который отклонятся нити, на которых висит проводник с током. Проводник весь находится в поле.
{-2}$ кг, длина l=0,4м. Индукция магнитного поля равна 0,25Тл. Определите величину угла, на который отклонятся нити, на которых висит проводник с током. Проводник весь находится в поле.
Решение:
Рис. 2
Проводник расположен перпендикулярно плоскости рисунка (ток направлен от нас). Запишем условие равновесия для проводника:
\[\overrightarrow{F_A}+\overrightarrow{mg}+2\overrightarrow{N}=0\ \left(1.1\right),\]
где $\overrightarrow{F_A}$- сила Ампера, $\overrightarrow{mg}$ — сила тяжести, $\overrightarrow{N}$ — сила реакции нити.
Проектируем (1.1) на оси:
\[X:\ -F_A-2Nsin\alpha =0\ \left(1.2\right).\] \[Y:\ -mg+2Ncos\alpha =0\ \left(1.3\right).\]
Разделим (1.2) на (1.3), получим:
\[\frac{F_A}{mg}=tg\alpha \ \left(1.4\right).\]
Модуль силы Ампера для прямолинейного проводника с током, который подвешен в поле с током, причем $\overrightarrow{B}\bot \overrightarrow{l}\ $равен:
\[F_A=IBl\ \left(1. \circ $.
\circ $.
Пример 2
Задание: Один проводник с током имеет форму квадрата, по нему утечет ток I. В одной плоскости с рамкой лежит бесконечно длинный прямой проводник с таким же током. Расположение проводников задано на рис.3. Найдите, какова сила, действующая на рамку, если расстояние между одной из сторон рамки и проводом равно длине стороны квадрата.
Рис. 3
Решение:
Магнитное поле создается бесконечно длинным проводником с током. Модуль индукции этого поля нам известен его можно записать как:
\[B\left(r\right)=\frac{{\mu }_0}{2\pi }\frac{I}{r}\left(2.2\right),\]
где r — расстояние от блинного проводника до точки поля.
Поле провода имеет цилиндрическую симметрию, для всех точек рамки оно будет направлено перпендикулярно. Если рассмотреть по очереди силы Ампера, которые действуют на каждый из четырех составных частей рамки, то выражение для модуля силы Ампера можно использовать в виде:
\[F=IBlsin\alpha \ \left(2. 2}{a}.$
2}{a}.$
2. Взаимодействие магнитного поля с электрическим током
Сила Ампера – это сила, с которой магнитное поле действует на элемент тока :
dF = IBdlsin,
где I– сила тока в проводнике,dl– длина проводника, В – индукция магнитного поля.
Направление силы Ампера определяется правилом левой руки: ладонь руки располагается так, чтобы четыре вытянутых пальца указывали направление элемента тока, а вектор магнитной индукции входил в ладонь, тогда отогнутый на 900большой палец укажет направление силы Ампера.
Момент силы, действующий на контур с током в магнитном поле
,
где- магнитный момент контура (SиI- площадь контура и сила тока в нем,- единичный вектор нормали к плоскости контура).
В векторном виде:
М = pmВsin, где- угол между векторамии.
Работа силы Ампера по перемещению контура с током в магнитном поле:
А = I(Ф2— Ф1),
где Ф2и Ф1– магнитные потоки
через контур в начальном и конечном
состоянии.
Магнитный поток через плоскость контура: ,
где ,dS– площадь контура,- угол между векторомнормали к контуру и вектороммагнитной индукции.
В задачах этого раздела сделаны следующие допущения:
вспомогательные проводники расположены вне магнитного поля или направлены так, что сила Ампера на них не действует;
при движении проводников вспомогательные провода не оказывают сопротивления этому движению;
при движении проводников в магнитном поле явления, связанные с электромагнитной индукцией, считаются несущественными.
Задача 1.По проводнику в форме полуокружности радиусомR = 0,2 м протекает токI= 10 А. Перпендикулярно плоскости проводника создано магнитное поле с индукцией В = 0,4 Тл. На сколько увеличится сила, действующая на проводник, если его распрямить в плоскости полуокружности?
Решение.
Найдем
силуF1, действующую
на проводник в форме полуокружности. Мысленно разобьем полуокружность на
малые элементарные дугиdl.
Равнодействующая всех сил, действующих
на элементы
:.
Мысленно разобьем полуокружность на
малые элементарные дугиdl.
Равнодействующая всех сил, действующих
на элементы
:.
Разложим вектор на две составляющие:. Тогда
.
Поскольку вклады в Fхэлементовdlиdl, симметричных относительно оси оу, взаимно компенсируются, следовательно,. Так как, тогда, гдеdFy = dFcos. По закону АмпераdF = IBdlsin, где- угол между вектороми направлением тока равен 900,dl = Rd.
Окончательно получаем .
Сила Ампера F2, действующая на прямой проводник
F2 = IBL,
где L = R– длина проводника. СледовательноF2 = IBR.
Разность сил равна: F2 – F1 = ( — 2)IBR.
F2 – F1 = (3,14 – 2)100,40,2 = 0,9 Н.
Ответ: F2 – F1 = 0,9
Н.
Задача 2.Прямолинейный проводник длинойL= 0,5 м массойm = 20 г висит горизонтально на двух параллельных нитях равной длины. Магнитное поле с индукцией В = 0,4 Тл создано в вертикальном направлении. На какой угол отклонятся нити с проводником от вертикали, если по проводнику пропустить токI= 1 А?
Решение.
Условие равновесия проводника:
,
где натяжение нити, FA = IBLsin900– сила Ампера.
В проекциях на оси координат:
ох: FA – 2Tsin = 0,
oy: 2Tcos — mg =0.
или
Решая систему данных уравнений, получаем: , следовательно, = 450.
Ответ: = 450.
Задача
3.Квадратная рамка со стороной
а = 0,1 см, по которой протекает
ток силойI=20 А,
помещена в магнитное поле с индукцией
В =0,5 Тл так, что угол между нормалью
к рамке и вектором индукции магнитного
поля равен= 300. Найти вращающий момент М, действующий
на рамку со стороны магнитного поля.
Найти вращающий момент М, действующий
на рамку со стороны магнитного поля.
Решение.
Магнитный момент М, действующий на рамку с током равен
М = рmВsin,
где рm=IS– модуль магнитного момента рамки,S= а2– площадь рамки.
Следовательно, М = Iа2Bsin
М = 200,120,50,87 = 0,087 Нм.
Ответ: М = 0,087 Нм.
Задача 4.Тонкий равномерно заряженный стержень вращается с постоянной угловой скоростью вокруг оси, перпендикулярной стержню и проходящей через один из его концов. Линейная плотность заряда стержня= 2 мкКл/м, линейная плотность стержня= 0,4 кг/м. Найти отношение магнитного момента стержня к его моменту импульса.
Решение.
Пустьl– длина стержня,- его угловая скорость, ось ох проходит
вдоль стержня перпендикулярно оси
вращения ОО. Мысленно разобьем стержень на бесконечно
малые элементыdx. Элементdх имеет элементарный
зарядdQ = dх.
Сила эквивалентного тока при вращении
зарядаdQравна
Мысленно разобьем стержень на бесконечно
малые элементыdx. Элементdх имеет элементарный
зарядdQ = dх.
Сила эквивалентного тока при вращении
зарядаdQравна
,
где — период вращения.
Модуль магнитного момента эквивалентного тока равен
dpm = SdI,
где S = x2– площадь круга.
С учетом вышесказанного .
Проинтегрируем dрmпо х в пределах от 0 доl:
.
Модуль момента импульса стержня:
L = J,
где J– момент инерции стержня относительно оси, проходящей через конец стержня. По теореме Штейнера ,
где m = l– масса стержня. Следовательно,.
Отношение магнитного момента к моменту импульса равно
Кл/кг;
Кл/кг.
Ответ:
Кл/кг.
Задача 5.Контур, имеющий форму окружности радиусаR= 0,1 м, помещен в однородное магнитное поле с индукцией В = 0,8 Тл так, что плоскость контура параллельна вектору магнитной индукции. Найти работу сил магнитного поля А по повороту контура на 900вокруг диаметра окружности, перпендикулярного вектору магнитной индукции. Сила тока в контуреI= 10 А.
Решение.
Работа по повороту контура:
А = I(Ф2– Ф1),
где Ф1=BScos900– начальный магнитный поток вектора магнитной индукции через контур, Ф2=BScos00– конечный магнитный поток,S=R2– площадь контура.
Следовательно, А = IBR2.
А = 3,14100,80,12 = 0,25 Дж.
Ответ: А = 0,25 Дж.
3.7.Сила ампера
Ампер исследовал действие магнитного поля на проводники с током и показал, что сила F, действующая на прямолинейный проводник с током, находящийся в однородном магнитном поле, прямо пропорциональна силе тока I в проводнике, его длине , магнитной индукциии синусу угламежду направлениями тока в проводнике и вектором:
.
В случае неоднородного магнитного поля и проводника произвольной формы перейдем к бесконечно малым приращениям, имеем:
.
-коэффициент пропорциональности, зависящий от выбора единицы измерения. В СИ .
Будем считать, что элемент проводника перпендикулярен вектору, тогда
-магнитная индукция численно равна силе, действующей со стороны поля на единицу длины проводника, по которому течет электрический ток единичной силы и который расположен перпендикулярно к направлению магнитного поля. Т.е. магнитная индукцияявляется силовой характеристикой поля.
Направление
силы
определяется по правилу левой руки:
если ладонь левой руки расположить так,
чтобы в нее входили линии магнитной
индукции, а четыре вытянутых пальца
расположить по направлению электрического
тока в проводнике, то отставленный
большой палец укажет направление силы,
действующей на проводник со стороны
поля.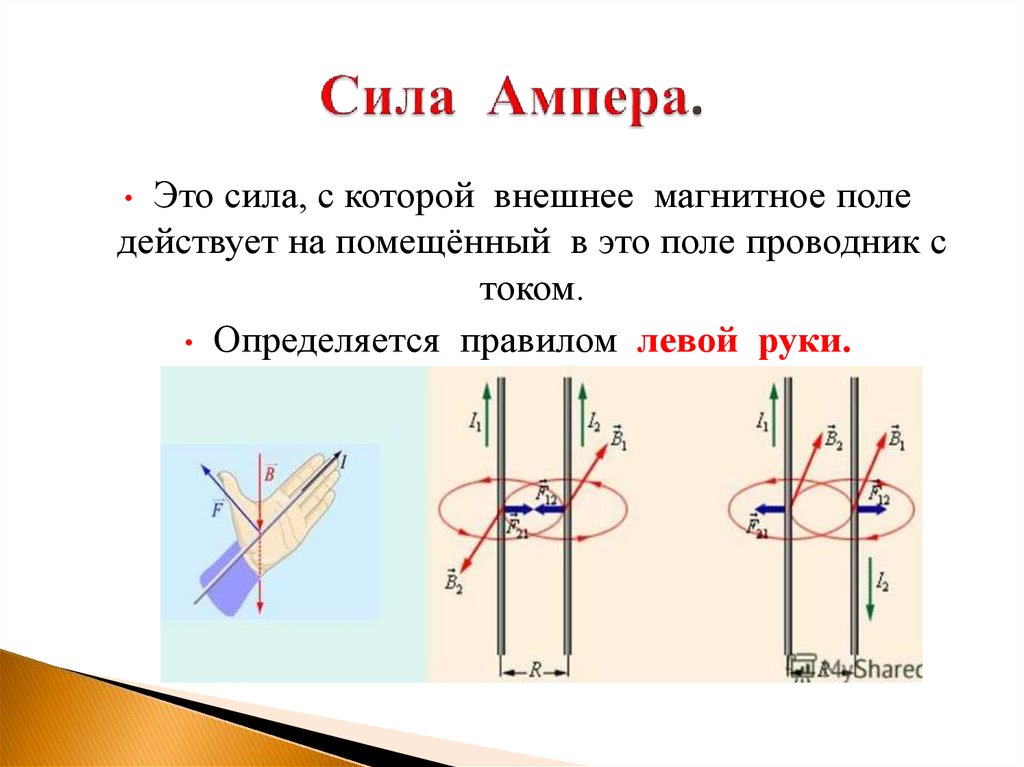
Если не перпендикулярен, то векторсовпадает по направлению с векторным произведением- векторнаправлен перпендикулярно к плоскости, образованной векторамиитаким образом, чтобы из конца векторавращение от векторак векторупо кратчайшему пути происходило против часовой стрелки.
Закон Ампера в векторной форме имеет вид:
.
Силы электромагнитного взаимодействия не являются центральными и всегда перпендикулярны к линиям магнитной индукции.
Рассмотрим два длинных прямолинейных проводника, которые расположены параллельно друг к другу. Расстояние между проводниками а. При пропускании тока по проводникам между ними возникает сила взаимодействия. Рассмотрим некоторые частные случаи.
1.Пусть токи
ив проводниках направлены в одну сторону
(рис.3.9а). В этом случае проводники
притягиваются друг к другу. Каждый из
проводников создает вокруг себя магнитное
поле, которое действует по закону Ампера
на другой проводник. При этом на элементвторого проводника с токомдействует сила:
Каждый из
проводников создает вокруг себя магнитное
поле, которое действует по закону Ампера
на другой проводник. При этом на элементвторого проводника с токомдействует сила:
.
Если а << , то проводник можно считать бесконечно длинным, тогда
, при этом ,, имеем.
Для выражение примет такой же вид. Оно симметрично для обоих проводников, поэтому
, тогда .
2. Если токи противоположны по направлению, то проводники отталкиваются (рис.9б).
Единицы измерения в системе СИ: магнитная индукция — B=[Тл] – тесла; напряженность магнитного поля H=[] — ампер на метр.
Экспериментально
было установлено, что пучок электронов,
испускаемых катодной трубкой, отклоняется
во внешнем магнитном поле. Направление
отклонения перпендикулярно к вектору
индукции
и векторускорости упорядоченного движения
электронов. Таким образом, на заряды,
движущиеся в магнитной поле, действует
сила, направление которой совпадает с
направлением векторного произведения,
если частицы отрицательно заряженные,
или,
если частицы заряжены положительно.
Таким образом, на заряды,
движущиеся в магнитной поле, действует
сила, направление которой совпадает с
направлением векторного произведения,
если частицы отрицательно заряженные,
или,
если частицы заряжены положительно.
Определим силу, действующую на электрический заряд, движущийся в магнитном поле. По закону Ампера на элемент проводника с токомI, действует сила
.
Ток в проводнике определяется движением зарядов, которые движутся со скоростью :, гдеdn — число частиц в элементе проводника ,.
Определим силу, действующую на один заряд:
—
—
это сила Лоренца. Направление
определяется знаком зарядаq.
Сила Лоренца всегда направлена
перпендикулярно к скорости движения
заряда и играет роль центростремительной
силы. Сила Лоренца не совершает работы.
Она изменяет только направление скорости
движения заряда в магнитном поле. Абсолютная величина скорости заряда и
его кинетическая энергия при движении
в магнитном поле не изменяется
Абсолютная величина скорости заряда и
его кинетическая энергия при движении
в магнитном поле не изменяется
.
Но неизменность величины скорости и кинетической энергии заряженной частицы имеет место лишь в случае постоянного магнитного поля, не зависящего от времени, т.е. стационарного. Переменное же магнитное поле ускоряет заряженные частицы (т.е. меняет величину и направление скорости).
Рассмотрим движение частицы в однородном магнитном поле. Будем считать, что на частицу не действуют никакие электрические поля.
Пусть частица движется вдоль линий индукции магнитного поля (рис.3. 10), тогда угол между векторамииравен 0 или,, т.е. магнитное поле не действует на частицу. Она будет двигаться по инерции – прямолинейно и равномерно.
Рассмотрим теперь частицу, которая движется перпендикулярно к линиям магнитной индукции(рис.
 3. 11): и .
В этом случае частица движется в
плоскости, перпендикулярной к вектору
магнитной индукции, и сила Лоренца
является центростремительной силой:
3. 11): и .
В этом случае частица движется в
плоскости, перпендикулярной к вектору
магнитной индукции, и сила Лоренца
является центростремительной силой:
,
где m – масса заряженной частицы, r – радиус кривизны ее траектории. Найдем r:
.
Скорость частицы не меняется, индукция =const, значит, r=const, и заряженная частица будет двигаться по окружности, плоскость которой перпендикулярна к магнитному полю.
Направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле зависит от знака зарядаq. Поэтому по направлению отклонения можно судить о знаке заряда.
Частица движется
в магнитном поле по окружности радиуса r равномерно. Период обращения, т.е. время
одного полного оборота:
Период обращения, т.е. время
одного полного оборота:
— период обращения частицы не зависит от ее скорости. Этот период прямо пропорционален индукции магнитного поля.
Рассмотрим более общий случай, когда скорость частицы направлена под произвольным острым угломк вектору(рис.3.12). Разложим векторна две составляющие:
— параллельную вектору — и перпендикулярную к -:
.
Скорость в магнитном поле не меняется, это скорость поступательного движения частицы. Благодаря же скоростичастица движется по окружности в плоскости, перпендикулярной к, тогда радиус этой окружности:
.
Таким
образом, частица одновременно совершает
два движения – поступательное со
скоростью
в направлении поля, т. е. перпендикулярном
к скорости вращения, и вращательное.
При этом траекторией движения будет
винтовая линия, ось которой совпадает
с линией индукции магнитного поля,
радиус витков
е. перпендикулярном
к скорости вращения, и вращательное.
При этом траекторией движения будет
винтовая линия, ось которой совпадает
с линией индукции магнитного поля,
радиус витков
.
Шаг винта .
СилаАмпер: значение, формула и эксперимент
Мы знаем, что проводник с током создает магнитное поле и силу. Но как рассчитать эту силу и от чего она зависит. А что, если два токонесущих проводника расположить вплотную друг к другу. К счастью для нас, физик Андре-Мари Ампер обнаружил, что провод, по которому течет ток, притягивает или отталкивает другой провод, находящийся поблизости. Это единственное открытие привело к формированию того, что мы знаем сегодня как электромагнетизм. Основная единица тока была названа в честь Ампера в честь его работы. Его эксперименты и работа в области электромагнетизма привели к формулировке закона, называемого законом силы Ампера. Этот закон означает зависимость между индуцированной силой и другими факторами, такими как сила тока и длина провода. В этой статье мы рассмотрим закон силы Ампера и законы, которые легли в его основу. Мы также рассмотрим его уравнение и поработаем над несколькими примерами. Счастливого обучения!
В этой статье мы рассмотрим закон силы Ампера и законы, которые легли в его основу. Мы также рассмотрим его уравнение и поработаем над несколькими примерами. Счастливого обучения!
Закон силы Ампера
Закон силы Ампера гласит, что сила притяжения или отталкивания между двумя проводниками с током пропорциональна их длине и току, протекающему по ним.
Направление магнитной силы зависит от направления тока в обоих проводах, Wikimedia Commons CC-BY-SA-4.0
Если направление тока одинаково в обоих проводах, то сила привлекательна. Если ток течет в противоположных направлениях, то сила отталкивающая. Фундаментальную основу закона силы Ампера составляют следующие существовавшие ранее законы.
Правило большого пальца правой руки
Правило большого пальца правой руки изображено здесь; он показывает взаимосвязь между током, проходящим через провод, и создаваемым им магнитным полем, Wikimedia Commons CC-BY-SA-4. 0
0
Правило гласит, что если вы держите проводник с током, направив большой палец на поток тока , то направление, в котором скручиваются пальцы, будет представлять магнитное поле вокруг него.
Правило левой руки Флеминга
Правило левой руки Флеминга показывает направление тяги на проводник с током в магнитном поле, Wikimedia Commons CC-BY-SA-3.0
Правило гласит, что если мы растягиваем большой, средний палец и указательный палец левой руки так так, чтобы они составляли угол 90 градусов. Тогда большой палец будет указывать в направлении индуцированной силы, средний палец будет указывать в направлении тока, а указательный палец будет представлять направление магнитного поля 9.0007
Эксперимент с силой Ампера Ампер впервые открыл явление силы, действующей между двумя проводами. Он заметил, что стрелка компаса отклоняется перпендикулярно, если ее приблизить к проводнику с током. Его следующие опыты заключались в изучении силы, действующей на два проводника с током путем изменения:
Его следующие опыты заключались в изучении силы, действующей на два проводника с током путем изменения:
тока, проходящего по ним
направления токов
Расстояние между проводами и
Наконец, длина проводов
Он обнаружил, что два параллельных провода, по которым течет ток в одного направления будут притягиваться друг к другу и отталкиваться, если направления тока, проходящего через них, противоположны. А если две проволоки расположить перпендикулярно друг другу, то сила, действующая между ними, будет равна нулю.
Уравнение силы Ампера
Существует сложный математический вывод силы между двумя проводами, который вам не нужно знать для экзамена GCSE!
Мы знаем, что сила Ампера пропорциональна длине провода и протекающему по нему току. Сила Ампера между двумя параллельными проводами может быть получена следующим образом:
Сила Ампера между двумя параллельными проводами, Wikimedia Commons
Если мы поместим два провода, по которым течет ток параллельно друг другу, на расстоянии . Тогда сила между ними будет равна . Это также можно использовать для определения значения . Мы знаем, что ампер является стандартной единицей силы тока. Его также можно определить как ток, протекающий по параллельным проводам на расстоянии друг от друга, который создает силу.
Тогда сила между ними будет равна . Это также можно использовать для определения значения . Мы знаем, что ампер является стандартной единицей силы тока. Его также можно определить как ток, протекающий по параллельным проводам на расстоянии друг от друга, который создает силу.
Есть несколько интересных свойств силы Ампера.
Сила имеет притягательный характер, когда ток в обоих проводах течет в противоположном направлении.
Сила носит отталкивающий характер, когда ток течет в одном направлении.
Сила равна нулю, когда два провода перпендикулярны друг другу.
Сила увеличивается по мере увеличения величины тока в проводах.
Также обратно пропорциональна расстоянию между проводами.
Продольная сила Ампера
Позже Ампер обнаружил дополнительную силу, которая действовала вдоль оси проводника с током. Эта сила называется продольной силой Ампера . Эта растягивающая сила имела тенденцию растягивать провода, по которым текут большие токи. Это также называют напряжением Ампера. Провод при воздействии его магнитного поля испытывает продольную силу, которая его растягивает.
Эта растягивающая сила имела тенденцию растягивать провода, по которым текут большие токи. Это также называют напряжением Ампера. Провод при воздействии его магнитного поля испытывает продольную силу, которая его растягивает.
Сила Ампера — Ключевые выводы
- Закон силы Ампера гласит, что сила притяжения или отталкивания между двумя проводниками с током пропорциональна их длине и току, протекающему по ним.
- Проводник с током, помещенный в магнитное поле , будет испытывать силу , перпендикулярную обоим полям. Направление силы зависит от направления течения тока.
- можно также определить как ток, протекающий по параллельным проводам на расстоянии друг от друга, который создает силу .
- Позже Ампер обнаружил дополнительную силу, которая действовала бы вдоль оси провода с током. Эта сила называется продольной силой Ампера.
22.9 Магнитные поля, создаваемые токами: Закон Ампера – Колледж физики 2e
Цели обучения
К концу этого раздела вы сможете:
- Рассчитайте ток, создающий магнитное поле.

- Используйте правило правой руки 2, чтобы определить направление тока или направление контуров магнитного поля.
Какой ток необходим для создания значительного магнитного поля, возможно такого же сильного, как поле Земли? Геодезисты скажут вам, что воздушные линии электропередач создают магнитные поля, которые мешают показаниям их компаса. Действительно, когда в 1820 году Эрстед обнаружил, что ток в проводе влияет на стрелку компаса, он не имел дело с чрезвычайно большими токами. Как форма проводов, по которым течет ток, влияет на форму создаваемого магнитного поля? Ранее мы отмечали, что токовая петля создает магнитное поле, подобное магнитному стержню, но как насчет прямого провода или тороида (бублика)? Как направление создаваемого током поля связано с направлением тока? Ответы на эти вопросы исследуются в этом разделе вместе с кратким обсуждением закона, управляющего полями, создаваемыми токами.
Магнитное поле, создаваемое длинным прямым проводом с током: Правило правой руки 2
Магнитные поля имеют как направление, так и величину. Как отмечалось ранее, одним из способов определения направления магнитного поля является использование компаса, как показано для длинного прямого провода с током на рис. 22.37. Датчики Холла могут определять величину поля. Обнаружено, что поле вокруг длинного прямого провода представляет собой кольцевые петли. Правило правой руки 2 (RHR-2) вытекает из этого исследования и справедливо для любого текущего сегмента — большой палец указывают в направлении тока, а пальцы скручиваются в направлении создаваемых им петель магнитного поля .
Как отмечалось ранее, одним из способов определения направления магнитного поля является использование компаса, как показано для длинного прямого провода с током на рис. 22.37. Датчики Холла могут определять величину поля. Обнаружено, что поле вокруг длинного прямого провода представляет собой кольцевые петли. Правило правой руки 2 (RHR-2) вытекает из этого исследования и справедливо для любого текущего сегмента — большой палец указывают в направлении тока, а пальцы скручиваются в направлении создаваемых им петель магнитного поля .
Рисунок
22.37
(а) Компасы, расположенные рядом с длинным прямым проводом с током, показывают, что силовые линии образуют круглые петли с центром на проводе. (b) Правило правой руки 2 гласит, что если большой палец правой руки указывает в направлении течения, остальные пальцы сгибаются в направлении поля. Это правило согласуется с полем, отображаемым для длинного прямого провода, и справедливо для любого текущего сегмента.
Напряженность (величина) магнитного поля, создаваемого длинным прямым проводом с током, экспериментально определена как
B=μ0I2πr(длинный прямой провод), B=μ0I2πr(длинный прямой провод),
22,24
где II — сила тока, rr — кратчайшее расстояние до провода, а константа μ0=4π×10−7T⋅ m/Aµ0=4π×10−7T⋅m/A — проницаемость свободного пространства. (μ0(μ0 — одна из основных констант в природе. Позже мы увидим, что μ0μ0 связана со скоростью света.) Поскольку проволока очень длинная, величина поля зависит только от расстояния до проволоки rr, а не на позиции вдоль провода
Пример 22,6
Вычисление тока, создающего магнитное поле
Найдите силу тока в длинном прямом проводе, который создает магнитное поле в два раза сильнее земного на расстоянии 5,0 см от провода.
Стратегия
Поле Земли составляет около 5,0×10−5T5,0×10−5T, поэтому здесь BB из-за провода принимается равным 1,0×10−4T1,0×10−4T. Уравнение B=µ0I2πrB=µ0I2πr можно использовать для нахождения
II, так как все остальные величины известны.
Уравнение B=µ0I2πrB=µ0I2πr можно использовать для нахождения
II, так как все остальные величины известны.
Решение
Решение для II и ввод известных значений дает
I=2πrBμ0=2π5,0×10−2m1,0×10−4T4π×10−7T⋅m/A=25 A.I=2πrBμ0=2π5,0× 10−2m1.0×10−4T4π×10−7T⋅m/A=25 A.
22,25
Обсуждение
Таким образом, умеренно большой ток создает значительное магнитное поле на расстоянии 5,0 см от длинного прямого провода. . Обратите внимание, что ответ указан только с двумя цифрами, поскольку в этом примере поле Земли указано только с двумя цифрами.
Закон Ампера и другие
Магнитное поле длинного прямого провода имеет больше значений, чем вы можете предположить на первый взгляд. Каждый отрезок тока создает магнитное поле, подобное магнитному полю длинного прямого провода, а полное поле тока любой формы представляет собой векторную сумму полей, создаваемых каждым отрезком.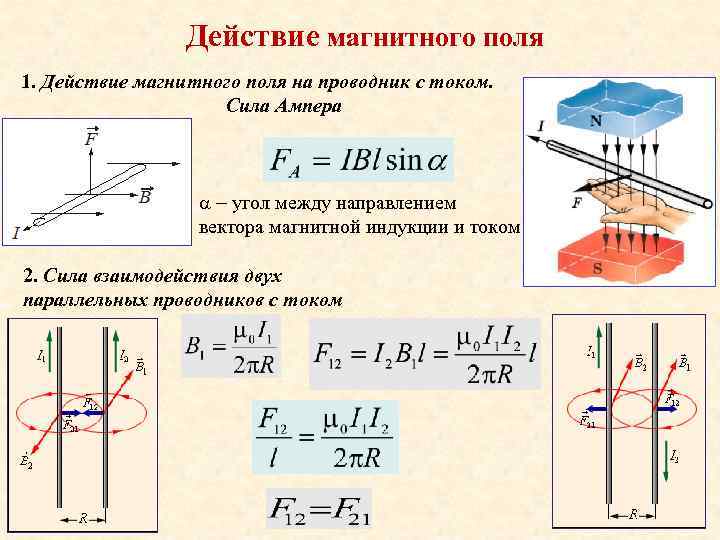 Формальная формулировка направления и величины поля, обусловленного каждым сегментом, называется законом Био-Савара. Интегральное исчисление необходимо для суммирования поля для тока произвольной формы. Это приводит к более полному закону, называемому законом Ампера, который связывает магнитное поле и ток в общем виде. Закон Ампера, в свою очередь, является частью уравнений Максвелла, дающих полную теорию всех электромагнитных явлений. Рассмотрение того, как уравнения Максвелла кажутся разным наблюдателям, привело к современной теории относительности и осознанию того, что электрические и магнитные поля — это разные проявления одного и того же явления. Большая часть этого выходит за рамки этого текста как на математическом уровне, требующем исчисления, так и на том количестве места, которое может быть уделено этому. Но для заинтересованных студентов, и особенно для тех, кто продолжает заниматься физикой, инженерией или подобными занятиями, дальнейшее углубление в эти вопросы откроет описания природы, которые элегантны и глубоки.
Формальная формулировка направления и величины поля, обусловленного каждым сегментом, называется законом Био-Савара. Интегральное исчисление необходимо для суммирования поля для тока произвольной формы. Это приводит к более полному закону, называемому законом Ампера, который связывает магнитное поле и ток в общем виде. Закон Ампера, в свою очередь, является частью уравнений Максвелла, дающих полную теорию всех электромагнитных явлений. Рассмотрение того, как уравнения Максвелла кажутся разным наблюдателям, привело к современной теории относительности и осознанию того, что электрические и магнитные поля — это разные проявления одного и того же явления. Большая часть этого выходит за рамки этого текста как на математическом уровне, требующем исчисления, так и на том количестве места, которое может быть уделено этому. Но для заинтересованных студентов, и особенно для тех, кто продолжает заниматься физикой, инженерией или подобными занятиями, дальнейшее углубление в эти вопросы откроет описания природы, которые элегантны и глубоки.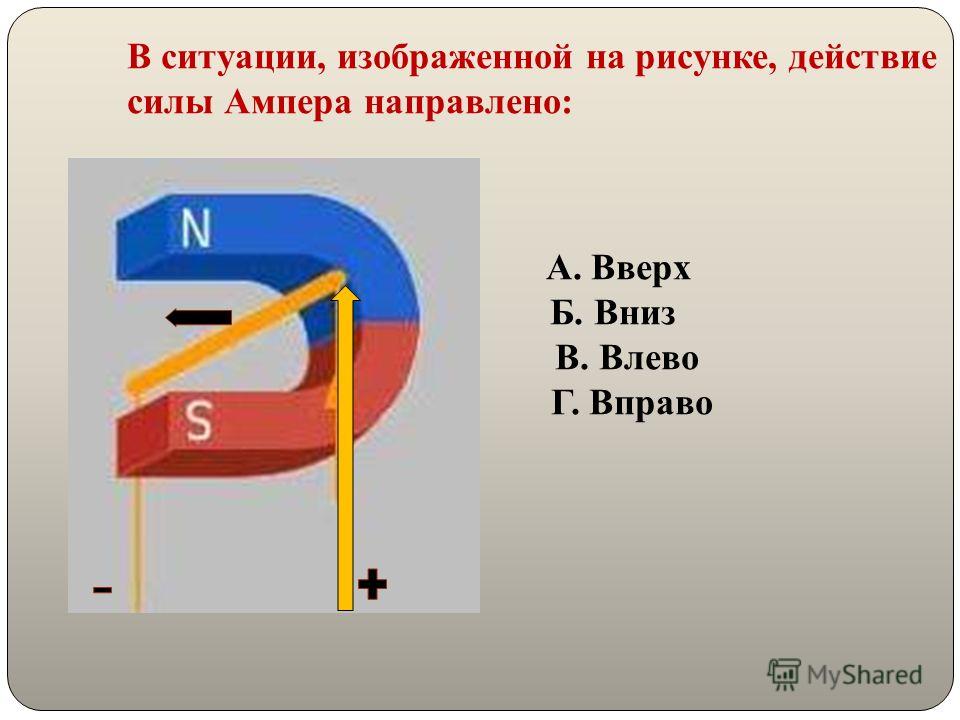 В этом тексте мы будем помнить об общих особенностях, таких как RHR-2 и правила для линий магнитного поля, перечисленные в Магнитных полях и Линии магнитного поля, концентрируясь на полях, создаваемых в определенных важных ситуациях.
В этом тексте мы будем помнить об общих особенностях, таких как RHR-2 и правила для линий магнитного поля, перечисленные в Магнитных полях и Линии магнитного поля, концентрируясь на полях, создаваемых в определенных важных ситуациях.
Установление связей: относительность
Слушая все, что мы делаем об Эйнштейне, у нас иногда создается впечатление, что он изобрел теорию относительности из ничего. Напротив, одним из мотивов Эйнштейна было решить трудности, связанные с пониманием того, как разные наблюдатели видят магнитные и электрические поля.
Магнитное поле, создаваемое круговым контуром с током
Магнитное поле вблизи проволочной петли с током показано на рис. 22.38. Как направление, так и величина магнитного поля, создаваемого петлей с током, сложны. RHR-2 можно использовать для определения направления поля вблизи контура, но для получения более подробной информации необходимо картографирование с помощью компаса и правил относительно силовых линий, приведенных в разделе «Магнитные поля и линии магнитного поля». Существует простая формула для напряженности магнитного поля в центре круглой петли. это
Существует простая формула для напряженности магнитного поля в центре круглой петли. это
B=µ0I2R(в центре петли),B=µ0I2R(в центре петли),
22,26
где RR — радиус петли. Это уравнение очень похоже на уравнение для прямого провода, но оно действительно только в центре круглой петли из проволоки. Сходство уравнений указывает на то, что аналогичная напряженность поля может быть получена в центре контура. Один из способов увеличить поле — использовать NN петель; тогда поле равно B=Nµ0I/(2R)B=Nµ0I/(2R). Обратите внимание, что чем больше петля, тем меньше поле в ее центре, поскольку ток проходит дальше.
Рисунок 22.38 (а) RHR-2 дает направление магнитного поля внутри и снаружи контура с током. (b) Более детальное картографирование с помощью компаса или зонда Холла дополняет картину. Поле похоже на поле стержневого магнита.
Магнитное поле, создаваемое токоведущим соленоидом
Соленоид представляет собой длинную катушку провода (с множеством витков или петель, в отличие от плоской петли). Из-за своей формы поле внутри соленоида может быть очень однородным, а также очень сильным. Поле сразу за катушками почти равно нулю. Рисунок 22.39показывает, как выглядит поле и как его направление задается RHR-2.
Из-за своей формы поле внутри соленоида может быть очень однородным, а также очень сильным. Поле сразу за катушками почти равно нулю. Рисунок 22.39показывает, как выглядит поле и как его направление задается RHR-2.
Рисунок 22.39 (а) Из-за своей формы поле внутри соленоида длиной ll удивительно однородно по величине и направлению, на что указывают прямые и равномерно расположенные силовые линии. Поле вне катушек почти равно нулю. (b) На этом разрезе показано магнитное поле, создаваемое током в соленоиде.
Магнитное поле внутри соленоида с током очень однородно по направлению и величине. Лишь ближе к концам он начинает ослабевать и менять направление. Поле снаружи имеет ту же сложность, что и плоские петли и стержневые магниты, но напряженность магнитного поля внутри соленоида просто
B=μ0nI(внутри соленоида), B=μ0nI(внутри соленоида),
22,27
где nn — количество витков на единицу длины соленоида (n=N/l(n=N/l, где NN — количество витков, а ll — длина).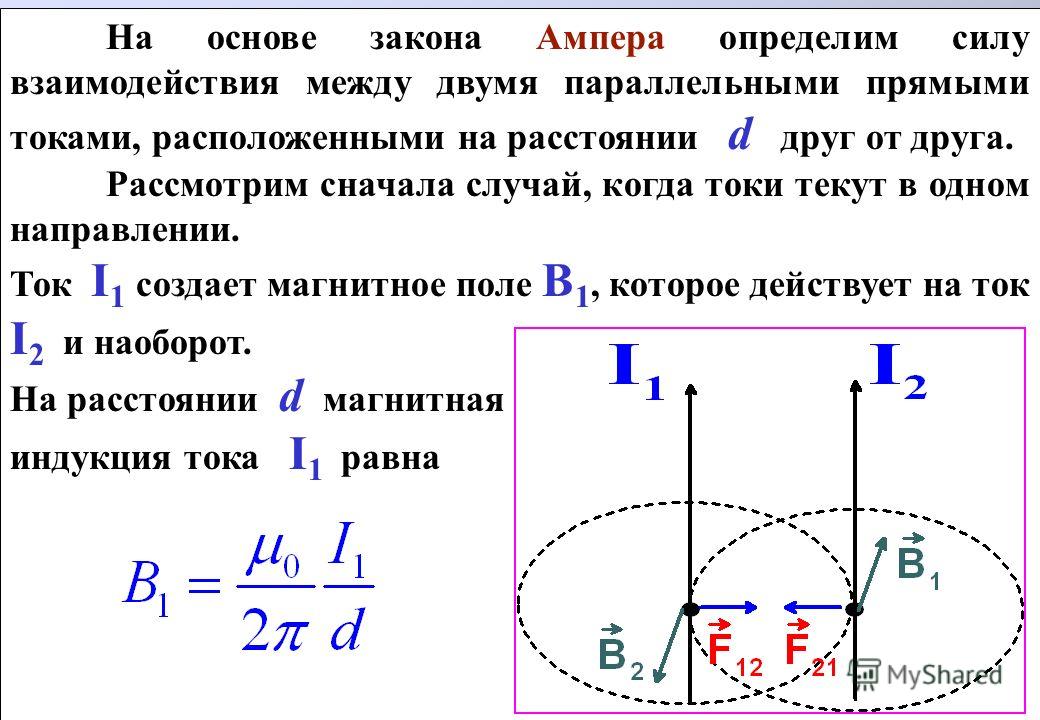 Обратите внимание, что BB — это напряженность поля в любом месте внутри однородной области, а не только в центре. Большие однородные поля, распределенные по большому объему, возможны с соленоидами, например 22.7 подразумевает
Обратите внимание, что BB — это напряженность поля в любом месте внутри однородной области, а не только в центре. Большие однородные поля, распределенные по большому объему, возможны с соленоидами, например 22.7 подразумевает
Пример 22,7
Расчет напряженности поля внутри соленоида
Каково поле внутри соленоида длиной 2,00 м, имеющего 2000 витков и пропускающего ток силой 1600 А?
Стратегия
Чтобы найти напряженность поля внутри соленоида, мы используем B=µ0nIB=µ0nI. Во-первых, отметим, что количество петель на единицу длины составляет
n=Nl=20002,00 м=1000 м-1=10 см-1.n=Nl=20002,00 м=1000 м-1=10 см-1.
22,28
Решение
Подстановка известных значений дает Т.
22,29
Обсуждение
Это большая напряженность поля, которая может быть установлена на соленоиде большого диаметра, например, при медицинском использовании магнитно-резонансной томографии (МРТ).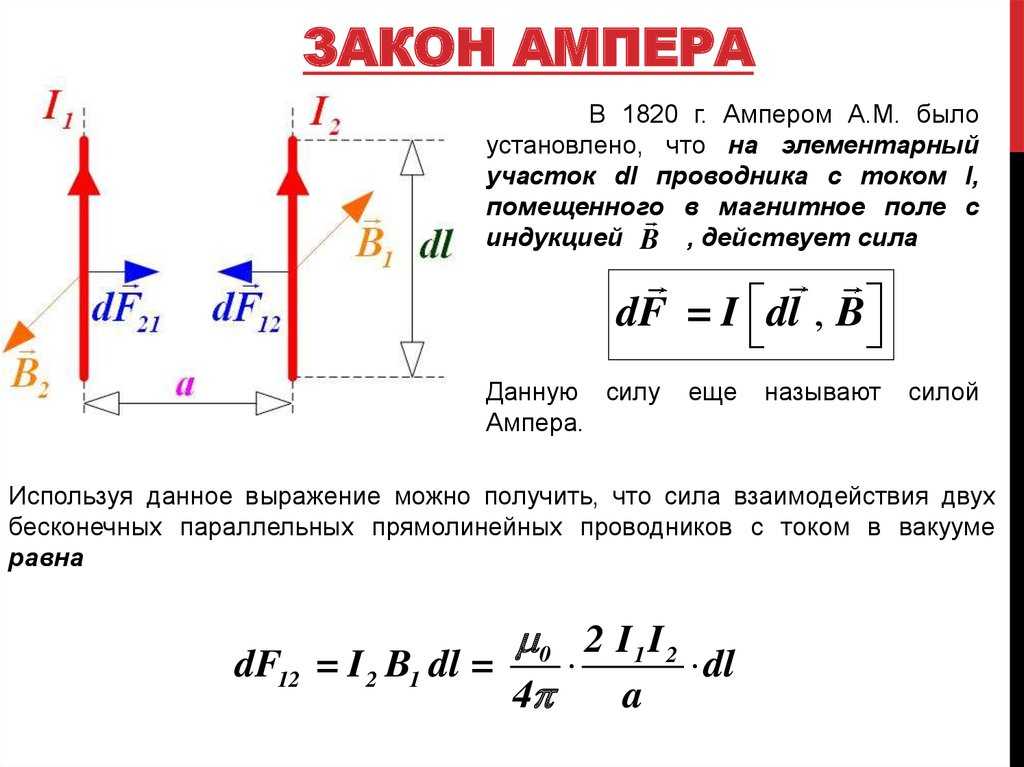 Однако очень большой ток указывает на то, что поля такой силы получить нелегко. Такой большой ток через 1000 витков, втиснутых в длину метра, произвел бы значительный нагрев. Более высокие токи могут быть достигнуты с помощью сверхпроводящих проводов, хотя это дорого. Существует верхний предел тока, поскольку сверхпроводящее состояние нарушается очень большими магнитными полями.
Однако очень большой ток указывает на то, что поля такой силы получить нелегко. Такой большой ток через 1000 витков, втиснутых в длину метра, произвел бы значительный нагрев. Более высокие токи могут быть достигнуты с помощью сверхпроводящих проводов, хотя это дорого. Существует верхний предел тока, поскольку сверхпроводящее состояние нарушается очень большими магнитными полями.
Есть интересные варианты плоской катушки и соленоида. Например, тороидальная катушка, используемая для удержания реактивных частиц в токамаках, очень похожа на соленоид, согнутый в окружность. Поле внутри тороида очень сильное, но круглое. Заряженные частицы движутся по кругу, следуя линиям поля, и сталкиваются друг с другом, возможно, вызывая синтез. Но заряженные частицы не пересекают силовые линии и не покидают тороид. Целый ряд форм катушек используется для создания всевозможных форм магнитного поля. Добавление ферромагнитных материалов увеличивает напряженность поля и может существенно повлиять на форму поля. Ферромагнитные материалы имеют тенденцию улавливать магнитные поля (силовые линии изгибаются в ферромагнитный материал, оставляя более слабые поля вне его) и используются в качестве экранов для устройств, на которые неблагоприятно влияют магнитные поля, в том числе магнитное поле Земли.
Ферромагнитные материалы имеют тенденцию улавливать магнитные поля (силовые линии изгибаются в ферромагнитный материал, оставляя более слабые поля вне его) и используются в качестве экранов для устройств, на которые неблагоприятно влияют магнитные поля, в том числе магнитное поле Земли.
Исследования ФЕТ
Генератор
Генерируйте электричество с помощью стержневого магнита! Откройте для себя физику этого явления, исследуя магниты и то, как вы можете использовать их, чтобы зажечь лампочку.
Нажмите, чтобы просмотреть содержимое.
SCIRP Открытый доступ
Издательство научных исследований
Журналы от A до Z
Журналы по темам
- Биомедицинские и медико-биологические науки.
- Бизнес и экономика
- Химия и материаловедение.
- Информатика.
 и общ.
и общ. - Науки о Земле и окружающей среде.
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные науки. и гуманитарные науки
Журналы по тематике
- Биомедицина и науки о жизни
- Бизнес и экономика
- Химия и материаловедение
- Информатика и связь
- Науки о Земле и окружающей среде
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные и гуманитарные науки
Публикация у нас
- Подача статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Публикуйте у нас
- Представление статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Подпишитесь на SCIRP
Свяжитесь с нами
клиент@scirp.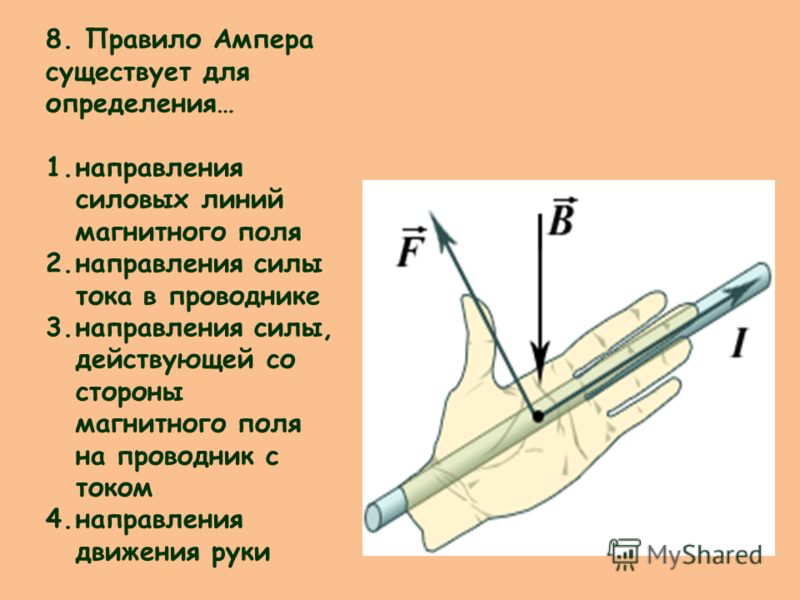 org org | |
| +86 18163351462 (WhatsApp) | |
| 1655362766 | |
| Публикация бумаги WeChat |
| Недавно опубликованные статьи |
| Недавно опубликованные статьи |
Наведение мостов в высшем образовании: мультимодальные программы наставничества для поддержки удержания и подготовки к карьере ()
Джеймс Хатсон, Роджер Нассер, Майкл Марцано, Райан Кертис, Элизабет Макдональд, Сью Эделе, Барбара Хосто-Марти
Креативное образование Том 13 №9, 16 сентября 2022 г.

DOI: 10.4236/ce.2022.139178 12 загрузок 63 просмотров
Морфологический признак и физико-химическая характеристика почв под Festuca вид. Доминирующая степь у Высокой горы и горы Хувсгул, Монголия()
Саруул Нарангерел, Ундармаа Джамсран, Маки Асано, Кенджи Тамура
Открытый журнал почвоведения Том 12 № 9, 16 сентября 2022 г.
DOI: 10.4236/ojss.2022.129018 16 загрузок 90 просмотров
Исследование рассеяния энергии волн в зоне прибоя Гвинейского залива: пример автономного порта Котону в прибрежной зоне Бенина()
Освальд Г.
 Акклассато, Ноукпо Бернар Токпохозин, Кристиан Д. Аковану, Аджимон Матиас Хуекпоэха, Ги Эрве Унге, Бруно Базиль Куноухева
Акклассато, Ноукпо Бернар Токпохозин, Кристиан Д. Аковану, Аджимон Матиас Хуекпоэха, Ги Эрве Унге, Бруно Базиль КуноухеваJournal of Modern Physics Vol.13 No.9, 16 сентября 2022 г.
DOI: 10.4236/jmp.2022.139076 10 загрузок 59 просмотров
Модель скалярного поля обеспечивает возможный мост между общей теорией относительности и квантовой механикой()
Рики В. Остин
Международный журнал астрономии и астрофизики Том 12 № 3, 16 сентября 2022 г.
DOI: 10.4236/ijaa.2022.123014 10 загрузок 57 просмотров
Характеристики состава тела и взаимосвязь между мышечной массой и мышечной силой у пожилых женщин в разных возрастных группах ()
Нао Нишиока Ниси, Норико Танака, Наоми Хирано
Успехи в исследованиях старения Том 11 № 5, 16 сентября 2022 г.

DOI: 10.4236/aar.2022.115010 7 загрузок 40 просмотров
Профиль черепно-мозговой травмы в отделениях неотложной помощи больниц — ретроспективное исследование в Республике Молдова (
)Светлана Кочу, Анжела Казаку-Страту, Лилия Киосеа, Георге Ройновяну, Сергей Чебану, Коринн Пик-Аса
Открытый журнал профилактической медицины Том 12 № 9, 16 сентября 2022 г.
DOI: 10.4236/ojpm.2022.129013 13 загрузок 83 просмотров
Подпишитесь на SCIRP
Свяжитесь с нами
клиент@scirp. org org | |
| +86 18163351462 (WhatsApp) | |
| 1655362766 | |
| Публикация бумаги WeChat |
Бесплатные информационные бюллетени SCIRP
Copyright © 2006-2022 Scientific Research Publishing Inc. Все права защищены.
верхнийЗакон Ампера — Ключ физики
Электрические заряды имеют силовые линии электрического поля, которые начинаются или заканчиваются на зарядах. Линии электрического поля для положительного заряда начинаются у положительного заряда и распространяются радиально наружу, а при наличии отрицательного заряда линии заканчиваются у отрицательного заряда.
Следовательно, электрический поток через замкнутую поверхность, заключающую в себе суммарный заряд, не равен нулю, но магнитный поток через замкнутую поверхность всегда равен нулю. Однако до сих пор не было найдено никаких доказательств существования магнитных монополий, несмотря на то, что исследования продолжаются, силовые линии магнитного поля всегда образуют замкнутые петли; это означает, что они никогда не начинаются и не заканчиваются на полюсах, а образуют замкнутые петли.
Однако до сих пор не было найдено никаких доказательств существования магнитных монополий, несмотря на то, что исследования продолжаются, силовые линии магнитного поля всегда образуют замкнутые петли; это означает, что они никогда не начинаются и не заканчиваются на полюсах, а образуют замкнутые петли.
Вы можете подумать, что силовые линии магнитного поля начинаются на северном полюсе и заканчиваются на южном полюсе, но это не так, они продолжают свой путь даже внутри магнита, образуя замкнутые петли. Таким образом, если вы формируете замкнутую поверхность, чистый магнитный поток через поверхность всегда равен нулю, то есть линии, которые входят в поверхность, должны выходить из поверхности. Теперь у нас есть закон Ампера для магнитных полей.
Это похоже на закон Гаусса, но он основан на линейном интеграле вокруг замкнутого пути, а не на магнитном потоке через замкнутую поверхность. Линейный интеграл равен $\oint \vec B \cdot d\vec l$, где $d\vec l$ — малый элемент длины на пути. Линейный интеграл дает сумму каждого $\vec B \cdot d\vec l$ для всего пути. Линейный интеграл также может быть выражен через параллельную компоненту $\vec B$ с $d\vec l$, то есть $\oint B_\parallel dl$. Обратите внимание, что кружок в знаке интеграла означает, что он находится над замкнутым путем.
Линейный интеграл дает сумму каждого $\vec B \cdot d\vec l$ для всего пути. Линейный интеграл также может быть выражен через параллельную компоненту $\vec B$ с $d\vec l$, то есть $\oint B_\parallel dl$. Обратите внимание, что кружок в знаке интеграла означает, что он находится над замкнутым путем.
Силовые линии магнитного поля прямого проводника с током всегда образуют окружности вокруг проводника, то есть магнитное поле в точке окружности всегда касательно в этой точке или параллельно $d \vec l$. Хорошо доказано, что силовые линии магнитного поля всегда образуют окружности для прямого проводника с током. Это можно продемонстрировать с помощью стрелки компаса. Стрелки компаса размещаются случайным образом в любом направлении без тока. Когда в проводнике есть ток, стрелки компаса тангенциально выравниваются по траектории.
Используйте правило правой руки, чтобы определить направление пути интегрирования; указатель большого пальца в направлении тока и направление согнутых пальцев определяют направление пути интеграции. Мы уже определили магнитное поле бесконечно длинного проводника с током $I$ на перпендикулярном расстоянии $r$, равном
\[B = \frac{\mu_0I}{2\pi \, r}\]
9\circ$. Таким образом, линейный интеграл в этом случае равен просто $\oint B\,dl$. А величина магнитного поля постоянна на всем пути, знаете ли\[\oint B\,dl = B\oint dl = \frac{\mu_0I}{2\pi\,r} (2\pi \, r) = \mu_0 I \tag{1}\label{1 }\]
Приведенное выше уравнение называется законом Ампера. Закон Ампера не зависит от формы пути интегрирования. На рисунке 2 путь интегрирования не является идеальной окружностью, а охватывает ток $I$.
Рис. 3 Закон Ампера не зависит от формы пути интегрирования.Для более общего случая, показанного на рисунке 1, мы имеем
\[\oint \vec B . d\vec l = \oint B\,dl\cos \phi\]
d\vec l = \oint B\,dl\cos \phi\]
Мы знаем $dl\cos\phi = r\,d\theta$ и
\[\точка B\,r\,d\theta = B\,r\oint d\theta = \frac{\mu_0Ir}{2\pi\,r} (2\pi) = \mu_0I\]
Если путь интегрирования охватывает несколько токов, линейный интеграл вокруг замкнутого пути является произведением суммы этих токов $I_\text{enc}$ и $\mu_0$. Магнитное поле $\vec B$ представляет собой векторную сумму всех магнитных полей, обусловленных всеми токами.
\[\oint \vec B \cdot d\vec l = \mu_0I_\text{enc} \tag{2} \label{2}\]
Приведенное выше уравнение называется законом Ампера для всех токов, заключенных в замкнутом пути, и его можно сформулировать как
.ЗАКОН АМПЕРА: Линейный интеграл магнитного поля по замкнутому пути равен произведению $\mu_0$ на полный ток, проходящий через путь.
Обратите внимание, что магнитное поле, вызванное током вне замкнутого пути, также может вносить вклад в векторную сумму магнитных полей, но линейный интеграл, обусловленный любым таким током вне замкнутого пути, всегда равен нулю. Это означает, что магнитное поле тока вне замкнутого пути не дает вклада в линейный интеграл, а линейный интеграл вокруг замкнутого пути по-прежнему равен произведению суммы токов, заключенных в замкнутом пути, на $\mu_0$. Ток вне замкнутого пути не включается в сумму, даже если полное магнитное поле $\vec B$ представляет собой векторную сумму всех магнитных полей, обусловленных токами внутри или вне замкнутого пути. Вы можете легко понять это на Рисунке 2, изображающем ток вне замкнутого пути, тогда линейный интеграл от $d\theta$ равен нулю, а не $2\pi$.
Это означает, что магнитное поле тока вне замкнутого пути не дает вклада в линейный интеграл, а линейный интеграл вокруг замкнутого пути по-прежнему равен произведению суммы токов, заключенных в замкнутом пути, на $\mu_0$. Ток вне замкнутого пути не включается в сумму, даже если полное магнитное поле $\vec B$ представляет собой векторную сумму всех магнитных полей, обусловленных токами внутри или вне замкнутого пути. Вы можете легко понять это на Рисунке 2, изображающем ток вне замкнутого пути, тогда линейный интеграл от $d\theta$ равен нулю, а не $2\pi$.
Линейный интеграл $\oint \vec B \cdot d\vec l = 0$ не означает, что $\vec B$ равен нулю.
Магнитное поле все еще может быть снаружи, но если вы возьмете линейный интеграл по замкнутому пути, который не содержит никакого тока, но ток находится вне замкнутого пути, линейный интеграл равен нулю, и это, очевидно, не означает $\vec B$ равен нулю.
Первоначально считалось, что $\vec B \cdot d\vec l$ — это работа, совершаемая магнитной силой над «магнитным зарядом», аналогичная $\vec E \cdot d\vec l$ (работа, совершаемая электрическая сила на электрический заряд). Но ни одного магнитного монополя никогда не было обнаружено, так называемого «магнитного заряда» не существует. А магнитная сила всегда перпендикулярна скорости движущегося заряда и также пропорциональна скорости, то есть $\vec F = q\vec v \times \vec B$, поэтому работа магнитной силы равна всегда ноль. Это означает, что $\vec B \cdot d\vec l$ не связан с проделанной работой, но связан с током, если мы определяем его интеграл по замкнутому пути, охватывающему этот ток. Это также означает, что магнитная сила является неконсервативной силой.
Но ни одного магнитного монополя никогда не было обнаружено, так называемого «магнитного заряда» не существует. А магнитная сила всегда перпендикулярна скорости движущегося заряда и также пропорциональна скорости, то есть $\vec F = q\vec v \times \vec B$, поэтому работа магнитной силы равна всегда ноль. Это означает, что $\vec B \cdot d\vec l$ не связан с проделанной работой, но связан с током, если мы определяем его интеграл по замкнутому пути, охватывающему этот ток. Это также означает, что магнитная сила является неконсервативной силой.
Кроме того, работа, совершаемая электрической силой на замкнутом пути, всегда равна нулю, это означает, что заряд движется из одной точки и возвращается в ту же точку. Электрическая сила не пропорциональна скорости движущегося заряда. Линии электрического поля представляют собой силовые линии , то есть они действуют в направлении, параллельном или антипараллельном полю, и поэтому работа, совершаемая на замкнутом пути, равна нулю. Но работа, совершаемая электрической силой, при чистом смещении не равна нулю. Обратите внимание, что электрическая сила пропорциональна положению заряда, а не скорости. Следовательно, электрическая сила является консервативной силой (пока мы считаем, что электрическое поле консервативно, позже вы увидите, что электрическое поле также может быть неконсервативным по закону Фарадея).
Но работа, совершаемая электрической силой, при чистом смещении не равна нулю. Обратите внимание, что электрическая сила пропорциональна положению заряда, а не скорости. Следовательно, электрическая сила является консервативной силой (пока мы считаем, что электрическое поле консервативно, позже вы увидите, что электрическое поле также может быть неконсервативным по закону Фарадея).
Закон Ампера полезен для расчета магнитного поля токовых конфигураций высокой степени симметрии, так что мы можем легко вычислить интеграл магнитного поля подобно тому, как мы использовали соображения симметрии в законе Гаусса для определения электрического поля, даже если закон Ампера действительны для любых текущих конфигураций.
Была ли эта статья полезной?
электромагнетизм | Определение, уравнения и факты
электрическое поле
Посмотреть все СМИ
- Ключевые люди:
- Майкл Фарадей
Уильям Томсон, барон Кельвин
Джеймс Клерк Максвелл
Карл Фридрих Гаусс
Дж.
 Дж. Томсон
Дж. Томсон
- Похожие темы:
- электромагнитное излучение электричество Кулоновская сила магнитная сила электромагнитное поле
Просмотреть весь связанный контент →
Резюме
Прочтите краткий обзор этой темы
электромагнетизм , наука о заряде и силах и полях, связанных с зарядом. Электричество и магнетизм — два аспекта электромагнетизма.
Электричество и магнетизм долгое время считались отдельными силами. Лишь в 19 веке к ним, наконец, стали относиться как к взаимосвязанным явлениям. В 1905 году специальная теория относительности Альберта Эйнштейна вне всяких сомнений установила, что оба явления являются аспектами одного общего явления. Однако на практическом уровне электрические и магнитные силы ведут себя совершенно по-разному и описываются разными уравнениями. Электрические силы создаются электрическими зарядами либо в состоянии покоя, либо в движении. Магнитные силы, с другой стороны, создаются только движущимися зарядами и действуют исключительно на движущиеся заряды.
Поймите, как концепция прикосновения меняется при наличии электронов между двумя объектами
Посмотреть все видео к этой статьеЭлектрические явления происходят даже в нейтральной материи, потому что силы действуют на отдельные заряженные составляющие. В частности, электрическая сила отвечает за большинство физических и химических свойств атомов и молекул. Она невероятно сильна по сравнению с гравитацией. Например, отсутствие хотя бы одного электрона из каждого миллиарда молекул у двух 70-килограммовых (154 фунтов) людей, стоящих на расстоянии двух метров (двух ярдов) друг от друга, отталкивало бы их с силой в 30 000 тонн. В более привычном масштабе электрические явления ответственны за молнии и гром, сопровождающие некоторые грозы.
Электрические и магнитные силы можно обнаружить в областях, называемых электрическими и магнитными полями. Эти поля фундаментальны по своей природе и могут существовать в пространстве вдали от заряда или тока, которые их породили. Примечательно, что электрические поля могут создавать магнитные поля и наоборот независимо от внешнего заряда. Изменяющееся магнитное поле создает электрическое поле, как обнаружил английский физик Майкл Фарадей в работе, которая лежит в основе производства электроэнергии. И наоборот, изменяющееся электрическое поле создает магнитное поле, как пришел к выводу шотландский физик Джеймс Клерк Максвелл. Математические уравнения, сформулированные Максвеллом, включили световые и волновые явления в электромагнетизм. Он показал, что электрические и магнитные поля путешествуют вместе в пространстве как волны электромагнитного излучения, при этом изменяющиеся поля взаимно поддерживают друг друга. Примерами электромагнитных волн, распространяющихся в пространстве независимо от материи, являются радио- и телевизионные волны, микроволны, инфракрасные лучи, видимый свет, ультрафиолетовый свет, рентгеновские лучи и гамма-лучи. Все эти волны распространяются с одинаковой скоростью, а именно со скоростью света (примерно 300 000 километров или 186 000 миль в секунду). Они отличаются друг от друга только частотой, с которой колеблются их электрическое и магнитное поля.
Изменяющееся магнитное поле создает электрическое поле, как обнаружил английский физик Майкл Фарадей в работе, которая лежит в основе производства электроэнергии. И наоборот, изменяющееся электрическое поле создает магнитное поле, как пришел к выводу шотландский физик Джеймс Клерк Максвелл. Математические уравнения, сформулированные Максвеллом, включили световые и волновые явления в электромагнетизм. Он показал, что электрические и магнитные поля путешествуют вместе в пространстве как волны электромагнитного излучения, при этом изменяющиеся поля взаимно поддерживают друг друга. Примерами электромагнитных волн, распространяющихся в пространстве независимо от материи, являются радио- и телевизионные волны, микроволны, инфракрасные лучи, видимый свет, ультрафиолетовый свет, рентгеновские лучи и гамма-лучи. Все эти волны распространяются с одинаковой скоростью, а именно со скоростью света (примерно 300 000 километров или 186 000 миль в секунду). Они отличаются друг от друга только частотой, с которой колеблются их электрическое и магнитное поля.
Викторина «Британника»
Викторина «Все о физике»
Кто был первым ученым, проведшим эксперимент по управляемой цепной ядерной реакции? Какова единица измерения циклов в секунду? Проверьте свою физику с помощью этого теста.
Уравнения Максвелла до сих пор дают полное и элегантное описание электромагнетизма вплоть до субатомного масштаба, но не включая его. Однако интерпретация его работ была расширена в 20 веке. Специальная теория относительности Эйнштейна объединила электрические и магнитные поля в одно общее поле и ограничила скорость всего вещества скоростью электромагнитного излучения. В конце 19В 60-х годах физики обнаружили, что другие силы в природе имеют поля с математической структурой, аналогичной электромагнитному полю. Этими другими силами являются сильное взаимодействие, ответственное за выделение энергии при ядерном синтезе, и слабое взаимодействие, наблюдаемое при радиоактивном распаде нестабильных атомных ядер. В частности, слабое и электромагнитное взаимодействия были объединены в общую силу, называемую электрослабой силой. Цель многих физиков объединить все фундаментальные силы, включая гравитацию, в одну великую единую теорию до сих пор не достигнута.
Цель многих физиков объединить все фундаментальные силы, включая гравитацию, в одну великую единую теорию до сих пор не достигнута.
Важным аспектом электромагнетизма является наука об электричестве, которая занимается изучением поведения агрегатов заряда, включая распределение заряда в материи и перемещение заряда с места на место. Различные типы материалов классифицируются как проводники или изоляторы в зависимости от того, могут ли заряды свободно перемещаться через составляющие их вещества. Электрический ток является мерой потока зарядов; законы, управляющие токами в материи, важны в технике, особенно в производстве, распределении и контроле энергии.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Понятие напряжения, так же как заряда и тока, является фундаментальным для науки об электричестве. Напряжение — это мера склонности заряда перетекать из одного места в другое; положительные заряды обычно имеют тенденцию перемещаться из области высокого напряжения в область более низкого напряжения. Распространенной проблемой в электричестве является определение соотношения между напряжением и током или зарядом в данной физической ситуации.
Распространенной проблемой в электричестве является определение соотношения между напряжением и током или зарядом в данной физической ситуации.
В этой статье делается попытка дать качественное понимание электромагнетизма, а также количественную оценку величин, связанных с электромагнитными явлениями.
Повседневная жизнь современного человека пронизана электромагнитными явлениями. Когда лампочка включена, через тонкую нить в колбе течет ток, который нагревает нить до такой высокой температуры, что она светится, освещая все вокруг. Электрические часы и соединения связывают простые устройства такого типа в сложные системы, такие как светофоры, которые отсчитывают время и синхронизируются со скоростью транспортного потока. Радиоприемники и телевизоры получают информацию, переносимую электромагнитными волнами, распространяющимися в пространстве со скоростью света. Чтобы запустить автомобиль, токи в электростартере генерируют магнитные поля, которые вращают вал двигателя и приводят в движение поршни двигателя, сжимая взрывоопасную смесь бензина и воздуха; искра, инициирующая горение, представляет собой электрический разряд, образующий мгновенный ток.
Андре-Мари Ампер: основатель электромагнетизма
|
Датский физик Ганс Кристиан Эрстед случайно обнаружил в 1820 году, что магнитная стрелка отклоняется, когда ток в близлежащем проводе изменяется — явление, устанавливающее связь между электричеством и магнетизмом.
В течение сентября и октября 1820 г. Ампер, под влиянием открытия Эрстеда, провел серию экспериментов, предназначенных для выяснения точной природы взаимосвязи между потоком электрического тока и магнетизмом, а также взаимосвязей, управляющих поведением электрических токов в различных виды проводников. Среди прочего, Ампер показал, что два параллельных провода, по которым текут электрические токи, магнитно притягиваются друг к другу, если токи одного направления, и отталкиваются, если токи противоположны.
Эти эксперименты привели Ампера к формулировке его знаменитого закона электромагнетизма, названного в его честь законом Ампера , который математически описывает магнитную силу между двумя электрическими токами.
Его исследования, о которых сообщалось еженедельно перед Académie des Sciences , положили начало новой науке электродинамики.
Он также был первым, кто разработал методы измерения электричества для проведения своих экспериментов. Ампер построил прибор, использующий свободно движущуюся намагниченную стрелку (компас) для измерения потока электричества. Более позднее усовершенствование этого прибора известно как гальванометр.
По сути, простой современный гальванометр представляет собой прибор, в котором свободно вращающаяся катушка и прикрепленная к ней игла помещаются в магнитное поле постоянного магнита. Когда электрический ток проходит через катушку, он испытывает крутящий момент из-за взаимодействия тока с магнитным полем. В результате катушка поворачивается, а стрелка отклоняется пропорционально току, проходящему через катушку.
Единица электрического тока, ампер , названа в честь Андре-Мари Ампера.
Предупреждение : эксперименты с электричеством должны проводиться под наблюдением учителей или взрослых, знакомых с правилами техники безопасности при работе с электричеством.
Чтобы пойти по стопам Ампера, надо прежде всего повторить опыт Эрстеда.
В 1820 году Эрстед демонстрировал нагревательные эффекты токов, протекающих по проводу и стрелке компаса, случайно оказавшейся под отклоненным проводом.
Чтобы повторить этот эксперимент, положите карманный компас на стол лицевой стороной вверх. Подождите, пока он не укажет на север. Положите середину довольно толстого провода длиной 30 см, изолированного или неизолированного, над стрелкой компаса, также в направлении север-юг. Согните концы проволоки так, чтобы они были близко друг к другу. Если провод не оголен, очистите его концы и присоедините их к клеммам аккумулятора. Стрелка будет сильно отклоняться. Повторите этот короткий эксперимент, поменяв местами соединения батареи. Теперь стрелка качается в противоположном направлении.
Подробнее:
http://www-istp.gsfc.nasa.gov…
http://www.physicsdemos…
Под влиянием открытия Эрстеда прозорливости Ампер пришел к выводу, что если провод с током оказывает магнитное воздействие на стрелку компаса, два таких провода также должны взаимодействовать магнитным образом. Он обнаружил, что параллельные токи, протекающие по проводам в одном направлении, притягиваются друг к другу, а токи, протекающие в противоположных направлениях, отталкиваются.
Он обнаружил, что параллельные токи, протекающие по проводам в одном направлении, притягиваются друг к другу, а токи, протекающие в противоположных направлениях, отталкиваются.
Подробнее: http://dev.physicslab.org…
Эти два первых опыта качественно демонстрируют Закон Ампера (закон Ампера).
Ампер продолжил свои исследования и обнаружил, что сила между двумя длинными прямыми параллельными токами обратно пропорциональна расстоянию между ними и пропорциональна силе тока, протекающего в каждом из них.
Чтобы проверить этот закон, он использовал простой токовый баланс (прибор, используемый для измерения силы между двумя токоведущими проводами), который состоял из двух фиксированных, прямых, вертикальных и параллельных токопроводов (проводов) и чувствительной пружинной шкалы. Он смог отрегулировать расстояние между проводами и измерить различные токи через них с помощью простого компаса-гальванометра, а также измерить силу, действующую между проводами, с помощью своей пружинной шкалы.
Для получения дополнительной информации:
http://books.google.com… (Лернер Дж., Физика для ученых и инженеров, том 2, стр. 795-797.)
Хотя эта установка выглядит просто, для ее реализации требуются некоторые продвинутые навыки механики. Вместо этого для этого эффекта можно использовать современный текущий баланс.
Для получения дополнительной информации:
http://oldkampalass.com…
http://ocw.mit.edu…
http://www.usna.edu…
http://www.millersville .edu…
http://web.me.com…
Этот эксперимент демонстрирует закон силы Ампера (не путать с законом Ампера)
Вы можете измерить токи в вышеописанных экспериментах с помощью современного амперметра или попробовать исторический способ Ампера. Как указывалось выше, Ампер использовал для своих текущих измерений намагниченную движущуюся стрелку или компасный гальванометр. Вы можете построить его сами или использовать коммерческий компас, но помните, что получить точные результаты будет не так просто.


 30)
30) 32)
32) 3. 11): и .
В этом случае частица движется в
плоскости, перпендикулярной к вектору
магнитной индукции, и сила Лоренца
является центростремительной силой:
3. 11): и .
В этом случае частица движется в
плоскости, перпендикулярной к вектору
магнитной индукции, и сила Лоренца
является центростремительной силой: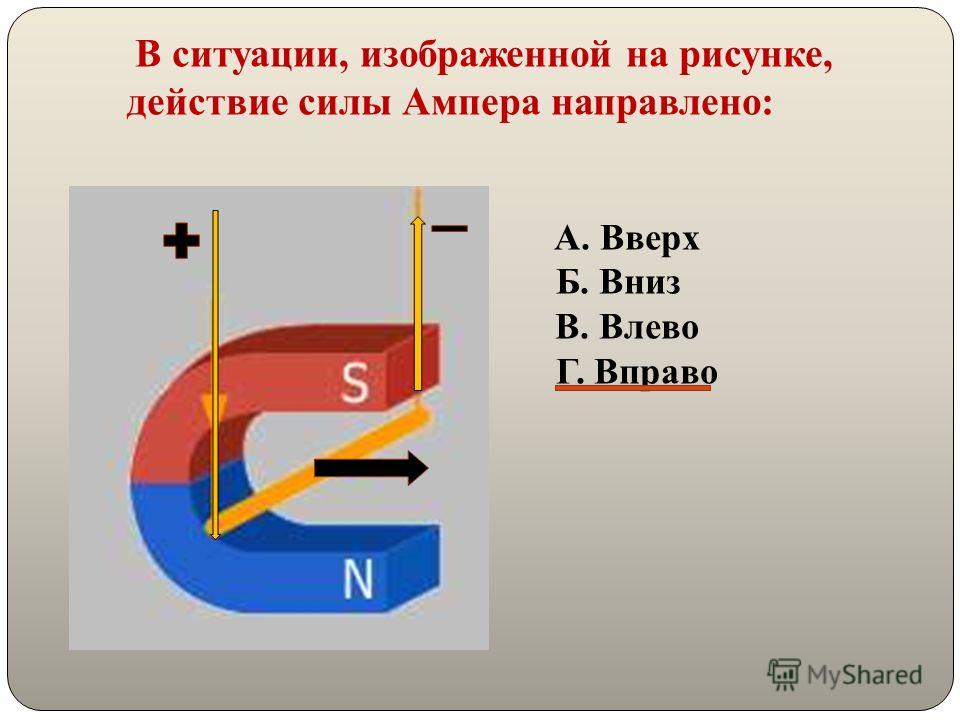
 и общ.
и общ.