Универсальный алькулятор
Универсальный алькулятор| УНИВЕРСАЛЬНЫЙ КАЛЬКУЛЯТОР |
Представлены несколько калькуляторов для электро-радио расчетов.
Индуктивности указаны в наногенри (nH).
Емкости указаны в пикофарадах (pF).
Сопротивления указаны в омах (Om).
Десятичные значения не учитываются в полях ввода, если Вы введете значение 1.9925
то это будет воспринято как 1.
Параллельное соединение двух резисторов
(или последовательное конденсаторов)
Формула: Общее сопротивление = (R1 x R2) / (R1 + R2)
| R1 |
R2 |
| Общее сопротивление |
Реактивное сопротивление конденсатора
= 1 / (2 * Pi * F * C)
| Частота (Hz) [F] |
Емкость (pF) [C] |
| Реактивность |
Реактивное сопротивление катушки индуктивности
Формула: Реактивное сопр. = 2 * Pi * F * L
Частота контура
Формула: F = 1 / (2 * Pi * Sqrt(LC))
Колличество витков однослойной катушки индуктивности
| Формула: |
Колличество витков многослойной катушки
| Формула: |
Аттенюаторы — «T» и «H» типа
| Формулы: |
Входная/выходная мощности могут быть в любых электрических единицах, которые
Вы предпочитаете, например: Мегаватты, милливатты, джоули, и т.
п.
Отрицательные значения получаются при вводе недопустимых значений аттенюаторов. Например, невозможно подключить устройство с 50-омной линией от 600-омной линии и имеющее ослабление более чем 6.78
Аттенюаторы — мостового типа
| Формулы: |
Входная/выходная мощности могут быть в любых электрических единицах, которые Вы предпочитаете, например: Мегаватты, милливатты, джоули и т.п.
Отрицательные значения получаются при недопустимых значениях аттенюаторов.
Дальность радиосвязи при прямой видимости
Дальность радиосвязи при прямой видимости и нормальной атмосферной рефракции зависит от высоты подвеса антенн и определяется нижеприведенной формулой:
Емкостное реактивное сопротивление Калькулятор | Вычислить Емкостное реактивное сопротивление
✖Угловая скорость относится к тому, как быстро объект вращается или вращается относительно другой точки, т. | Степень / деньСтепень / часСтепень / минСтепень / месяцГрадус в секундуСтепень / неделяСтепень в годрадиан / деньрадиан / часРадиан в минутурадиан / месяцРадиан в секундурадиан / неделюрадиан / годРеволюция в деньоборотов в часоборотов в минутуоборотов в секунду | +10% -10% | |
✖Емкость – это отношение количества электрического заряда, хранящегося на проводнике, к разности электрических потенциалов.ⓘ Емкость [C] | AbfaradАттофарадсантифарадаКл / вольтдекафарадДецифарадEMU конденсаторнойESU конденсаторнойэксафарадафарадафемтофарадагигафарадагектофарадкилофарадМегафарадаМикрофарадМиллифараднанофарадапетафарадапикофарадаStatfaradтерафарада | +10% -10% |
е. как быстро изменяется угловое положение или ориентация объекта со временем.ⓘ Угловая скорость [ω]|
✖Емкостное реактивное сопротивление является мерой сопротивления конденсатора переменному току. |
AbohmEMU сопротивленияESU сопротивленияExaohmГигаомкилооммегаоммикроомМиллиомНаномомПетаомПланка сопротивлениеКвантованная Hall СопротивлениеВзаимный СименсStatohmВольт на АмперYottaohmZettaohm |
⎘ копия |
👎
Формула
сбросить
👍
Емкостное реактивное сопротивление Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.
Преобразование входов в базовый блок
Угловая скорость: 2 Радиан в секунду —> 2 Радиан в секунду Конверсия не требуется
Емкость: 3 фарада —> 3 фарада Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.166666666666667 ом —> Конверсия не требуется
< 10+ Электромагнитная индукция Калькуляторы
Емкостное реактивное сопротивление формула
Емкостное реактивное сопротивление = 1/(Угловая скорость*Емкость)
Xc = 1/(ω*C)
Что такое емкостное реактивное сопротивление?
Емкостное реактивное сопротивление (обозначение Xc) — это мера сопротивления конденсатора переменному току (переменному току). Как и сопротивление, оно измеряется в омах, но реактивное сопротивление более сложное, чем сопротивление, поскольку его значение зависит от частоты (f) сигнала, проходящего через конденсатор.
Share
Copied!
23.2: Реактивное, индуктивное и емкостное сопротивление
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2717
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Зарисовывать зависимость напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.
- Рассчитать индуктивное и емкостное сопротивление.
- Расчет тока и/или напряжения в простых индуктивных, емкостных и резистивных цепях.
Многие схемы также содержат конденсаторы и катушки индуктивности в дополнение к резисторам и источнику переменного напряжения.
Катушки индуктивности и индуктивное реактивное сопротивление
Предположим, что катушка индуктивности подключена непосредственно к источнику переменного напряжения, как показано на рисунке. Разумно предположить пренебрежимо малое сопротивление, так как на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что оно окажет незначительное влияние на цепь. Также показан график зависимости напряжения и тока от времени.
Рисунок \(\PageIndex{1}\): (a) Источник переменного напряжения последовательно соединен с катушкой индуктивности, сопротивление которой пренебрежимо мало. (б) График тока и напряжения на катушке индуктивности в зависимости от времени. График на рисунке (b) начинается с максимального напряжения.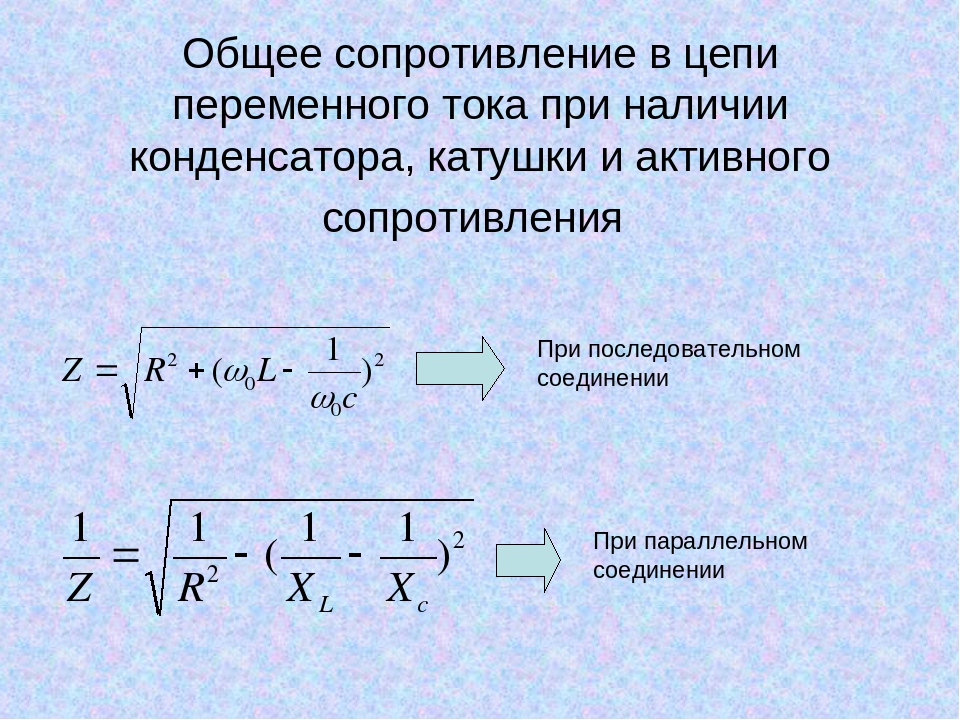
Обратите внимание, что ток начинается с нуля и достигает своего пика 90 050 после 90 051 напряжения, управляющего им, точно так же, как это было в случае, когда напряжение постоянного тока было включено в предыдущем разделе. Когда напряжение в точке а становится отрицательным, ток начинает уменьшаться; он становится равным нулю в точке b, где напряжение является самым отрицательным. Затем ток становится отрицательным, снова следуя за напряжением. Напряжение становится положительным в точке с и начинает делать ток менее отрицательным. В точке d ток проходит через нуль как раз в тот момент, когда напряжение достигает своего положительного пика, чтобы начать новый цикл. Это поведение резюмируется следующим образом: 9о\) фазовый угол.
Ток отстает от напряжения, так как катушки индуктивности препятствуют изменению тока. Изменение тока индуцирует противо-ЭДС \(V = -L(\Delta I/\Delta t)\). Это считается эффективным сопротивлением катушки индуктивности переменному току. Действующее значение тока \(I\) через катушку индуктивности \(L\) определяется версией закона Ома: vo
\[I = \dfrac{V}{X_L},\], где \(V\) равно среднеквадратичное напряжение на катушке индуктивности и \(X_L\) определяется как \[X_L = 2\pi fL,\] с \(f\) частотой источника переменного напряжения в герцах (анализ схемы с использованием метода Кирхгофа).
правило цикла и исчисление фактически производят это выражение). \(X_L\) называется индуктивным реактивным сопротивлением, потому что индуктор реагирует, препятствуя току. \(X_L\) имеет единицы измерения в омах (\(1 \, H = 1 \, \Omega \cdot s\), так что частота, умноженная на индуктивность, имеет единицы (циклы/с)\((\Omega \cdot s) = \Омега\)), в соответствии с его ролью эффективного сопротивления. Имеет смысл, что \(X_L\) пропорциональна \(L\), поскольку чем больше индукция, тем больше ее сопротивление изменению. Также разумно, что \(X_L\) пропорциональна частоте \(f\), поскольку большая частота означает большее изменение тока. То есть \(\Delta I/\Delta t\) велико для больших частот (больших \(f\), малых \(\Delta t\)). Чем больше изменение, тем больше сопротивление индуктора.
Пример \(\PageIndex{1}\): расчет индуктивного сопротивления, а затем тока
(a) Рассчитайте индуктивное сопротивление катушки индуктивности 3,00 мГн при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц.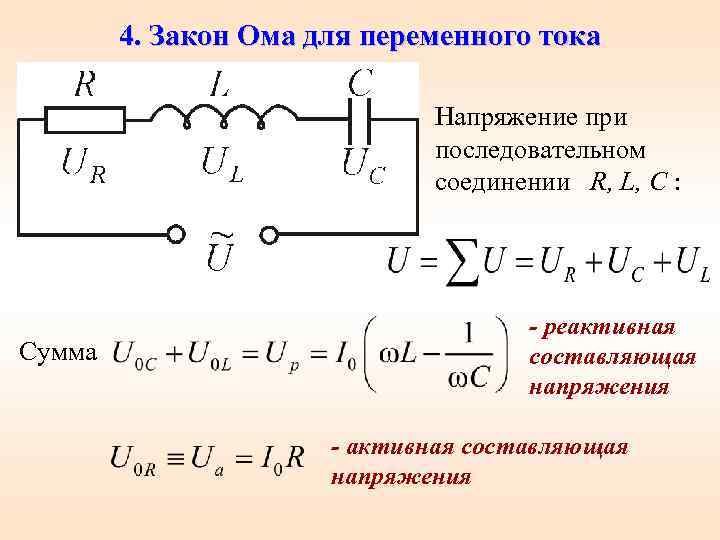
б) Чему равно среднеквадратичное значение тока на каждой частоте, если приложенное среднеквадратичное напряжение равно 120 В?
Стратегия
Индуктивное сопротивление находится непосредственно из выражения \(X_L = 2\pi fL\). Как только \(X_L\) найдено на каждой частоте, можно использовать закон Ома, как указано в уравнении \(I = V/X_L\), чтобы найти ток на каждой частоте. 94/с)(3,00 мкГн) = 188 л, \Омега \, при \, 10 мкГц.\]
Решение задачи (б) закона в уравнении \(I = V/X_L\), при условии, что приложенное среднеквадратичное напряжение равно 120 В. Для первой частоты это дает
\[I = \dfrac{V}{X_L} = \dfrac{120 \, V}{1,13 \, \Omega} = 106 \, A \, при \, 60 \, Гц.\]
Аналогично, при 10 кГц,
\[I = \dfrac{V}{X_L} = \ dfrac{120 \, V}{188 \, \Omega} = 0,637 \, A \, at \, 10 \, кГц.\]
Обсуждение
Катушка индуктивности очень по-разному реагирует на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток мал, что соответствует тому, как индуктор препятствует быстрому изменению.
Таким образом, высокие частоты препятствуют больше всего. Индукторы можно использовать для фильтрации высоких частот; например, большой индуктор можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выходящий из ваших динамиков, или высокочастотные скачки мощности в вашем компьютере.
Обратите внимание, что хотя сопротивление в рассматриваемой цепи незначительно, переменный ток не очень велик, поскольку индуктивное сопротивление препятствует его протеканию. При переменном токе нет времени для того, чтобы ток стал чрезвычайно большим.
Конденсаторы и емкостное реактивное сопротивление
Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рисунке. Сопротивление такой цепи можно сделать настолько малым, что оно оказывает незначительное влияние по сравнению с конденсатором, и поэтому мы можем предположить пренебрежимо малое сопротивление.
Напряжение на конденсаторе и ток представлены на рисунке как функции времени.
График на рисунке начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, а ток становится отрицательным по мере разряда конденсатора. В точке а конденсатор полностью разряжен (на нем \(Q = 0\)) и напряжение на нем равно нулю. Ток между точками a и b остается отрицательным, что приводит к изменению напряжения на конденсаторе. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и сводя напряжение к нулю в точке c, что позволяет току достигать своего максимума.
Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла:
Напряжение переменного тока в конденсаторе
Когда к конденсатору прикладывается синусоидальное напряжение, напряжение следует за током на одну четвертую периода или на фазовый угол.
Конденсатор влияет на ток, имея возможность полностью остановить его при полной зарядке. Поскольку применяется переменное напряжение, существует среднеквадратичное значение тока, но оно ограничено конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока в цепи, содержащей только конденсатор \(I\), согласно другой версии закона Ома, равно
\[I = \dfrac{V}{X_C},\], где \(V\) — среднеквадратичное значение напряжения, а \(X_C\) определяется (как и в случае \(X_L\), это выражение для \(X_C \) получается в результате анализа схемы с использованием правил и исчисления Кирхгофа) как
\[X_C = \dfrac{1}{2\pi fC},\], где \(X_C\) называется емкостным сопротивлением, потому что конденсатор реагирует на сопротивление току.
\(X_C\) измеряется в омах (проверка оставлена читателю в качестве упражнения). \(X_C\) обратно пропорциональна емкости \(C\), чем больше конденсатор, тем больший заряд он может хранить и тем больший ток может протекать. Он также обратно пропорционален частоте \(f\), чем больше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.
Пример \(\PageIndex{2}\): расчет емкостного реактивного сопротивления, а затем тока
(a) Рассчитайте емкостное реактивное сопротивление конденсатора емкостью 5,00 мФ при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока, если приложенное среднеквадратичное напряжение равно 120 В?
Стратегия
Емкостное реактивное сопротивление находится непосредственно из выражения \(X_C = \frac{1}{2\pi fC}\). Как только \(X_C\) найдено на каждой частоте, закон Ома формулируется как \(I = V/X_C\) 94/с)(5,00 мкФ)}.
\]
\[= 3,18 мк, \Омега \, при \, 10 мкГц\]
Решение для (б)
Среднеквадратичное значение ток теперь находится с использованием версии закона Ома в \(I = V/X_C\), учитывая приложенное среднеквадратичное напряжение 120 В. Для первой частоты это дает
\[I = \dfrac{V}{X_C } = \dfrac{120 \, V}{531 \, \Omega} = 0,226 \, A \, при \, 60 \, Гц.\]
Аналогично, при 10 кГц,
\[I = \dfrac {V}{X_C} = \dfrac{120 \, V}{3,18 \, \Omega} = 37,7 \, A \, at \, 10 \, кГц.\]
Обсуждение
Конденсатор очень по-разному реагирует на двух разных частотах, и совершенно противоположным образом реагирует индуктор. На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы способствуют изменениям, тогда как индукторы сопротивляются изменениям. Конденсаторы больше всего препятствуют низким частотам, поскольку низкая частота дает им время зарядиться и остановить ток. Конденсаторы можно использовать для фильтрации низких частот.
Например, конденсатор, включенный последовательно со звуковоспроизводящей системой, избавляет ее от гула частотой 60 Гц.
Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с переменным напряжением, приложенным к конденсатору, существует среднеквадратичное значение тока. Это связано с тем, что напряжение постоянно меняется, заряжая и разряжая конденсатор. Если частота стремится к нулю (DC), \(X_C\) стремится к бесконечности, а ток равен нулю после зарядки конденсатора. На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет пренебрежимо малое реактивное сопротивление и не препятствует протеканию тока (он действует как простой провод). Конденсаторы действуют на цепи переменного тока противоположно действию катушек индуктивности .
Резисторы в цепи переменного тока
В качестве напоминания рассмотрите рисунок, на котором показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени.
Напряжение и ток равны в
Глоссарий
- индуктивное реактивное сопротивление
- противодействие катушки индуктивности изменению тока; рассчитывается как \(X_L = 2\pi fL\)
- емкостное реактивное сопротивление
- сопротивление конденсатора изменению тока; рассчитывается как \(X_C = \frac{1}{2\pi fC}\)
Авторы
Пол Питер Урон (почетный профессор Калифорнийского государственного университета, Сакраменто) и Роджер Хинрихс (Государственный университет Нью-Йорка, Колледж в Освего) с соавторами: Ким Диркс (Оклендский университет) и Манджула Шарма (Сиднейский университет) ). Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.
0).
Эта страница под названием 23.2: Reactance, Inductive and Capacitive распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- емкостный
- емкостное реактивное сопротивление
- Индуктивный
- индуктивное сопротивление
- Реактивное сопротивление
- источник@https://openstax.
org/details/books/college-physics
org/details/books/college-physicsЕмкостное реактивное сопротивление — Как решить последовательные и параллельные конденсаторы — Технические примечания
TestGuy
#1
Шаг 1: Найдите общую емкость цепи
Предположим, у нас есть три конденсатора: 12 мкФ, 20 мкФ и 30 мкФ, подключенные к источнику с частотой 60 Гц. Каково общее емкостное сопротивление (X C ) при последовательном или параллельном соединении?
1А. Для последовательных конденсаторов
Когда конденсаторы соединены последовательно, общая емкость меньше любой из отдельных емкостей последовательных конденсаторов. Если два или более конденсатора соединены последовательно, общий эффект будет таким же, как у одного (эквивалентного) конденсатора, имеющего суммарное расстояние между пластинами отдельных конденсаторов.
Серийные конденсаторы Пример
1/12 = 0,083, 1/20 = 0,050, 1/30 = 0,033
0,083 + 0,050 + 0,033 = 0,166
1 / 0,163 = 6,02 мкФ
Примечание: математика упрощена для иллюстрации. Используйте калькулятор для более точных цифр.
1Б. Для параллельных конденсаторов
Когда конденсаторы соединены параллельно, общая емкость представляет собой сумму емкостей отдельных конденсаторов. Если два или более конденсатора соединены параллельно, общий эффект будет таким же, как у одного эквивалентного конденсатора, имеющего сумму площадей пластин отдельных конденсаторов.
Параллельные конденсаторы Пример
12 + 20 + 30 = 62 мкФ
Шаг 2: Найдите емкостное реактивное сопротивление
Как и сопротивление, реактивное сопротивление измеряется в омах, но ему присваивается символ X, чтобы отличить его от чисто резистивного значения R, а поскольку рассматриваемым компонентом является конденсатор, реактивное сопротивление конденсатора называется емкостным.
Реактивное сопротивление ( X C ), которое измеряется в Омах.
Поскольку конденсаторы заряжаются и разряжаются пропорционально скорости изменения напряжения на них, чем быстрее изменяется напряжение, тем больше ток будет течь. Аналогично, чем медленнее изменяется напряжение, тем меньше ток будет течь. Это означает, что реактивное сопротивление конденсатора переменного тока «обратно пропорционально» частоте источника питания.
X C — емкостное сопротивление в омах, f — частота в герцах, а C — емкость переменного тока в фарадах. Очень важно преобразовать наш пример из микрофарад в фарады, чтобы получить правильный результат!
1 мкФ = 0,000001 Ф
Пример серии 60 Гц
6,02 мкФ = 0,000006 Ф (упрощенно)
2 x 3,14 x 60 x 0,000006 = 0,0022608
1 / 0,0022608 = 442,32 Ом
Параллельный пример 60 Гц
62 мкф = 0,000062 F
2 x 3,14 x 60 x 0,000062 = 0,0233616
1 / 0,0233616 = 42,805 Ом
теперь, когда это происходит, когда часто происходит на частоту .
