Полное сопротивление цепи переменного тока
Содержание:
Электрическая цепь.
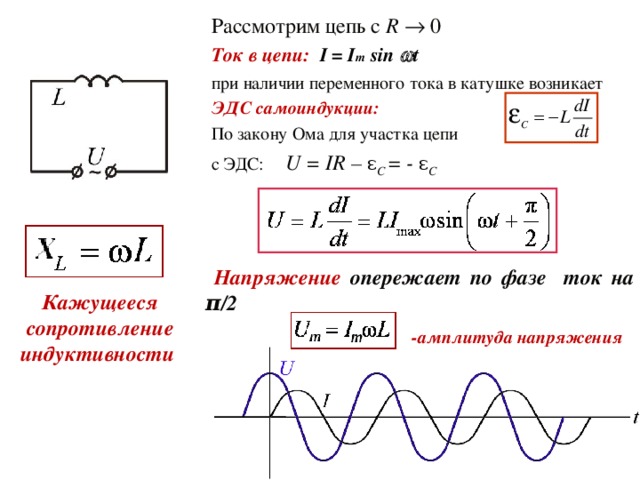
Источник электрического тока, соединенный проводами с различными электроприборами и потребителями электрической энергии, образует электрическую цепь.
Электрическую цепь принято изображать с помощью схем, в которых элементы электрической цепи (сопротивления, источники тока, включатели, лампы, приборы и т. д.) обозначены специальными значками.
Направление тока в цепи — это направление от положительного полюса источника тока к отрицательному. Это правило было установлено в XIX в. и с тех пор соблюдается. Перемещение реальных зарядов может не совпадать с условным направлением тока. Так, в металлах носителями тока являются отрицательно заряженные электроны, и движутся они от отрицательного полюса к положительному, т. е. в обратном направлении. В электролитах реальное перемещение зарядов может совпадать или быть противоположным направлению тока, в зависимости от того, какие ионы являются носителями заряда — положительные или отрицательные.
Включение элементов в электрическую цепь может быть последовательным или параллельным.
Что такое сопротивление
Ток, протекая через провода и различные радиодетали, тратит свою энергию. Это явление количественно выражается величиной сопротивления. В электротехнике его разделяют на активное и реактивное сопротивление. В первом случае при прохождении тока часть его энергии превращается в тепловой вид, а иногда и в другие (например, проявляется в химических реакциях). Величина активного сопротивления зависит от частоты переменного электротока и возрастает с ее увеличением.
Второй тип сопротивления имеет более сложную природу и возникает в момент включения или выключения потребителя электроэнергии в сеть переменного или постоянного тока. В цепи с реактивным сопротивлением энергия электрического тока частично превращается в другую форму, а затем переходит обратно, то есть, наблюдается периодический колебательный процесс. Полное сопротивление цепи включает в себя активный и реактивный типы, которые учитываются по особым правилам.
Виды сопротивления
В электротехнике рассматривается активное электрическое сопротивление, а также две разновидности реактивного: индуктивное и ёмкостное.
Активное сопротивление
Можно представить себе электрическую цепь, в которой к клеммам батарейки через провод последовательно присоединены резистор и электрическая лампочка. Если замкнуть провода, лампочка загорится. Можно использовать вольтметр или мультиметр в соответствующем режиме работы, с помощью которых измеряется разность потенциалов между двумя точками цепи.
Измерив напряжение между клеммами и сравнив его с тем, которое имеется на проводах подсоединённых к лампочке, можно увидеть, что последнее меньше. Это связано с падением напряжения на впаянной в цепь радиодетали. Последняя оказывает противодействие электрическому току, затрудняя его прохождение.
Активным сопротивлением обладает каждая деталь, через которую проходит ток. У металлических проводов оно очень маленькое. Чтобы узнать величину сопротивления радиодетали, нужно изучить обозначение на ее корпусе. Если из рассматриваемой электроцепи убрать резистор, то сила тока, проходящего через лампочку, увеличится.
Если из рассматриваемой электроцепи убрать резистор, то сила тока, проходящего через лампочку, увеличится.
Формула для расчета активного сопротивления соответствует закону Ома:
R = U / I, где
- R — величина активного сопротивления между двумя точками в цепи;
- U — напряжение или разность потенциалов между ними;
- I — сила тока на рассматриваемом участке цепи.
Для расчета активного сопротивления проводника формула будет другая:
где K-коэффициент поверхностного эффекта, который равен 1,
- l — длина проводника,
- s — площадь поперечного сечения,
- p — “ро” удельное сопротивление.
Сопротивление принято измерять в Омах. Оно существенно зависит от формы и размеров объекта, через который протекает ток: сечения, длины, материала, а также от температуры. Действие активного сопротивления уменьшает энергию электрического тока, превращая её в другие формы (преимущественно в тепловую).
Реактивное сопротивление
Этот вид возникает тогда, когда переменный ток проходит сквозь элемент, который обладает индуктивностью или емкостью. Основной особенностью реактивного сопротивления является преобразование электрической энергии в другую форму в прямом и обратном направлениях. Часто это происходит циклически. Реактивное сопротивление проявляется только при изменениях силы тока и напряжения. Существует два его вида: индуктивное и емкостное.
Основной особенностью реактивного сопротивления является преобразование электрической энергии в другую форму в прямом и обратном направлениях. Часто это происходит циклически. Реактивное сопротивление проявляется только при изменениях силы тока и напряжения. Существует два его вида: индуктивное и емкостное.
Индуктивное сопротивление
При увеличении силы тока порождается магнитное поле, обладающее различными характеристиками. Наиболее важной из них является индуктивность. Магнитное поле, в свою очередь, воздействует на проводник, по которому протекает ток. Влияние является противоположным направлению изменения тока. То есть, если сила тока увеличилась, то магнитное поле будет уменьшать его, и наоборот, если снизилась, то поле усилит его. Когда ток не меняется, реактивное сопротивление катушки индуктивности будет равно нулю.
Индуктивное сопротивление зависит от частоты тока. Чем она выше, тем выше скорость изменения данного параметра. Это значит, что будет образовано более сильное магнитное поле. Возникающая при этом ЭДС препятствует изменению электрического тока.
Возникающая при этом ЭДС препятствует изменению электрического тока.
Расчет реактивного индуктивного сопротивления осуществляется по такой формуле:
XL = L×w = L×2π×f, где буквами обозначаются:
- L — индуктивность магнитного поля, которое порождается изменением силы тока;
- W — круговая частота изменения, которая используется в описании синусоидального изменения силы тока;
- Π — число «пи»;
- f — частота тока в обычном смысле.
При синусоидальном изменении напряжения сила тока будет меняться, отставая от него по фазе. Поэтому реактивное сопротивление трансформатора существенно зависит от его индуктивности.
Емкостное сопротивление
Оно имеет иную природу, чем индуктивное. Это понятие удобно проиллюстрировать на примере электрической цепи, состоящей из источника питания, клеммы которого соединены с обкладками конденсатора. Сразу после подключения на них будет постепенно накапливаться заряд, создавая ток в цепи.
После достижения предельной величины, которая определяется ёмкостью детали, ток не будет проходить по цепи. Если после этого отключить провода от клемм, а затем последние соединить, то между ними начнётся перемещение зарядов до тех пор, пока разность потенциалов станет равной нулю.
Если к конденсатору подключить источник переменного тока, то будет происходить следующее. С увеличением разности потенциалов заряд на обкладках конденсатора будет расти. Когда напряжение перейдёт в фазу уменьшения, накопленный заряд начнёт стекать с них, образуя ток противоположного направления. Затем разность потенциалов станет отрицательной, но по абсолютной величине будет расти до максимального значения. При этом конденсатор начнет вновь заряжаться, но при этом знак поступающих зарядов будет не такой, который был раньше.
Когда напряжение начнёт увеличиваться (уменьшаясь по абсолютной величине), заряд с обкладок конденсатора будет стекать. Когда разность потенциалов у источника достигнет нуля и продолжит увеличиваться, начнётся новый цикл изменений.
На каждом этапе описанной ситуации ток с обкладок конденсатора будет иметь направление противоположное тому, которое порождается переменной разностью потенциалов источника питания.
Происходящее таким образом уменьшение силы тока представляет собой физический смысл ёмкостного сопротивления. Оно обозначается буквами ХС и рассчитывается по формуле:
XС = 1/(w×C) = 1/(2π×f×C), где
- C — ёмкость используемого конденсатора;
- w — круговая частота переменного тока;
- π — число «пи»;
- f — частота переменного тока.
В рассматриваемом случае изменения тока отстают от напряжения.
Полное сопротивление
При использовании нескольких разновидностей важно знать, как они сочетаются между собой. Активное сопротивление присутствует в любых схемах. Оно способствует превращению части электрической энергии в нагрев. Реактивное сопротивление возникает лишь в цепи переменного тока. Чтобы определить его величину, необходимо из индуктивного вычесть ёмкостное. 2 ), где
2 ), где
- Z — полное сопротивление;
- R — величина активной составляющей;
- XL и XC — значение индуктивного и емкостного параметра соответственно.
Следовательно, при расчёте полного сопротивления или импеданса нужно учитывать, что такое ёмкость и индуктивность и как они могут проявляться в электрических схемах. Эти величины называются еще паразитными, так как они могут отрицательно влиять на работу электроприбора. Их возникновение относят к непредсказуемым факторам. При этом емкостным или индуктивным сопротивлением, имеющим небольшое значение, при выполнении расчетов можно пренебречь.
Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.
В любом сечении цепи, изображенной на рисунке 2,а, мгновенные значения тока должны быть одинаковыми, так как в противном случае наблюдались бы скопления и разрежения электронов в каких-либо точках цепи. Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения UL (напряжение на индуктивном сопротивлении) и напряжения UR (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°.
Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения UL (напряжение на индуктивном сопротивлении) и напряжения UR (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°.
Рисунок 2. Полное сопротивление цепи с активным сопротивлением и индуктивностью. а) – схема цепи; б) – сдвиг фаз тока и напряжения; в) – треугольник напряжений; д) – треугольник сопротивлений.
Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов UL и UR. Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор UAB является гипотенузой прямоугольного треугольника.
Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов.
По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление.
Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z2) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. е.
(1)
Извлекая квадратный корень из обеих частей этого равенства, получим,
(2)
Таким образом, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений
Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т. е. полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.
Полное сопротивление цепи, изображенной на рис.2,а, не является ни чисто активным, ни чисто реактивным; оно содержит в себе оба эти вида сопротивлений. Поэтому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, то есть он будет больше 0°, но меньше 90°. К которому из этих двух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и наоборот, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°.
В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления. Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи.
Рисунок 3. Полное сопротивление цепи с активным сопротивлением и емкостью. а) – схема цепи; б) – треугольник сопротивлений.
Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его.
Для данного случая:
(3)
В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.
Рисунок 4. Полное сопротивление цепи содержащей R, L и C. а) – схема цепи; б) – треугольник сопротивлений.
Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности, т. е.
(4)
Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений (XL или XC преобладает).
После того как мы по формуле (4) определили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.
(5)
Или
(6)
Способ построения треугольника сопротивлений для этого случая изображен на рис. 4 б.
Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.
Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.
Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.
Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) – параллельное соединение R и L; б) – параллельное соединение R и C.
а) – параллельное соединение R и L; б) – параллельное соединение R и C.
Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z
Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.
(7)
Приводя к общему знаменателю подкоренное выражение, получим:
(8)
откуда:
(9)
Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.
Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.
Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С будет равно:
(10)
Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.
В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).
Рисунок 6. Эквивалентная схема колебательного контура.
Формула полного сопротивления для этого случая будет:
(11)
Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:
(12)
В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие
(13)
При соблюдении этого условия полное сопротивление колебательного контура будет равно:
(14)
где L—индуктивность катушки в Гн;
С—емкость конденсатора в Ф;
R—активное сопротивление катушки в Ом.
Закон Ома для полной цепи.
Рассмотрим электрическую цепь, состоящую из источника тока и резистора R.
Закон Ома для полной цепи устанавливает связь между силой тока в цепи, ЭДС и полным сопротивлением цепи, состоящим из внешнего сопротивления R и внутреннего сопротивления источника тока r.
Работа сторонних сил Aст источника тока, согласно определению ЭДС (ɛ) равна Aст = ɛq, где q — заряд, перемещенный ЭДС. Согласно определению тока q = It, где t — время, в течение которого переносился заряд. Отсюда имеем:
Aст =ɛIt.
Тепло, выделяемое при совершении работы в цепи, согласно закону Джоуля — Ленца, равно:
Q = I2Rt + I2rt.
Согласно закону сохранения энергии А = Q. Приравнивая (Aст =ɛIt) и (Q = I2Rt + I2rt), получим:
ɛ = IR + Ir.
Закон Ома для замкнутой цепи обычно записывается в виде:
.
Сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.
Если цепь содержит несколько последовательно соединенных источников с ЭДС ɛ1, ɛ2, ɛ3 и т. д., то полная ЭДС цепи равна алгебраической сумме ЭДС отдельных источников. Знак ЭДС источника определяется по отношению к направлению обхода контура, который выбирается произвольно, например, на рисунке ниже — против часовой стрелки.
д., то полная ЭДС цепи равна алгебраической сумме ЭДС отдельных источников. Знак ЭДС источника определяется по отношению к направлению обхода контура, который выбирается произвольно, например, на рисунке ниже — против часовой стрелки.
Сторонние силы внутри источника совершают при этом положительную работу. И наоборот, для цепи справедливо следующее уравнение:
ɛ = ɛ1 + ɛ2 + ɛ3 = | ɛ1| – | ɛ2| -| ɛ3| .
В соответствии с
сила тока положительна при положительной ЭДС — направление тока во внешней цепи совпадает с направлением обхода контура. Полное сопротивление цепи с несколькими источниками равно сумме внешнего и внутренних сопротивлений всех источников ЭДС, например, для рисунка выше:
Rn = R + r1 + r2 + r3.
Как измерить полное электрическое сопротивление
Соединим все детали вместе в простую электрическую цепь. Взглянем на рисунок ниже: это цепь с источником питания постоянного тока. Ток течет через резистор. Весьма просто, верно? Чем больше сопротивление резистора в цепи, тем меньше будет ток.
Простая цепь постоянного тока с резистором
на 100 Ом для ограничения силы тока
Что произойдет, если мы добавим в электрическую цепь источник питания переменного тока, катушку индуктивности и конденсатор? Теперь в цепи есть два дополнительных компонента, каждый из которых по своему оказывает сопротивление электрическому току. Как и резистор, они оба препятствуют прохождению электрического тока, при этом также воздействуют на ток. Если суммировать активное сопротивление резистора и активное и реактивное сопротивления конденсатора и катушки индуктивности, то получится полное электрическое сопротивление или импеданс.
В цепи переменного тока последовательно соединены резистор, катушка индуктивности и конденсатора
Постойте! Чтобы рассчитать полное электрическое сопротивления недостаточно просто сложить активные и реактивные сопротивления. Обычно в большинстве учебных пособий с этого момента начинается изобилие математических формул, поэтому дальше читайте не спеша.
Практическое применение полного электрического сопротивления
Становится понятно, в конце концов, что после всех наших объяснений разобраться, что такое полное электрическое сопротивление, несложно, не так ли? Существуют десятки бесплатных калькуляторов , которые помогут вам выполнить расчеты. Что вам на самом деле нужно – это знать, что полное сопротивление работает так же, как активное сопротивление, ограничивая ток в цепи переменного тока.
Способность таких компонентов, как конденсаторы и катушки индуктивности реагировать на постоянные изменения переменного тока, делает их уникальными. Благодаря полному сопротивлению в вашей цепи можно организовать нечто похожее на электрический щит с защитными автоматами, которые реагируют на неожиданные скачки электричества, защищая от выгорания домашнюю электропроводку. Можно также сказать спасибо полному сопротивлению за то, что вы можете носить с собой ноутбук с полностью заряженным аккумулятором, не опасаясь его взрыва.
Когда дело доходит до работы с устройствами с питанием от источника переменного тока, будь то ноутбук или электрощит в вашем доме, стоит быть благодарным полному электрическому сопротивлению. И помните, полное электрическое сопротивление – это просто старший брат привычного активного сопротивления, который объединяет активное и реактивное сопротивления в одной простой формуле.
Расчет полного электрического сопротивления конденсатора
Чтобы найти полное электрическое сопротивление конденсатора, вы можете воспользоваться следующей формулой. В ней Xc – полное электрическое сопротивление, которое необходимо найти. Оно измеряется в Омах. Переменная f – это частота сигнала, проходящего через конденсатор, а C – емкость конденсатора.
Расчёт индуктивного сопротивления катушки
Любая индуктивность, в т.ч. катушка, оказывает переменному току некоторое сопротивление. Как его рассчитать, было описано выше. Из формулы XL=2pfL видно, что сопротивление дросселя в первую очередь зависит от частоты протекающего по нему тока и его индуктивности. При этом с обоими параметрами связь прямо пропорциональная.
При этом с обоими параметрами связь прямо пропорциональная.
Частота – это характеристика внешней среды, индуктивность катушки зависит от ряда её геометрических свойств:
где:
- u0 – магнитная проницаемость вакуума – 4p*10-7 Гн/м;
- ur – относительная проницаемость сердечника;
- N – количество витков дросселя;
- S – его поперечное сечение в м2;
- l – длина катушки в метрах.
Располагая вышеописанными формулами и информацией о материале и размерах катушки, можно достаточно точно прикинуть её индуктивное сопротивление без каких-либо измерительных приборов.
Дополнительная информация. Некоторые цифровые мультиметры имеют режим замера индуктивности. Подобная функция встречается редко, однако иногда оказывается очень полезной. Поэтому при выборе прибора стоит обратить внимание на то, способен ли он измерять индуктивность.
Калькулятор импеданса катушки индуктивности
Калькулятор определяет импеданс катушки индуктивности для заданной частоты синусоидального сигнала. Определяется также угловая частота.
Определяется также угловая частота.
Пример. Рассчитать импеданс катушки индуктивности 10 мкГн на частоте 25 МГц.
Введите значения индуктивности и частоты, выберите единицы измерения и нажмите кнопку Рассчитать. Для ввода значения бесконечность наберите inf.
Отметим, что величина импеданса идеальной катушки индуктивности равна ее реактивному сопротивлению. Однако это не идентичные величины, так как между током и напряжением в индуктивной цепи существует фазовый сдвиг. Для расчетов используются указанная ниже формула:
Здесь
XL — реактивное сопротивление катушки в омах (Ом),
ZL — импеданс катушки в омах (Ом),
ω = 2πf — угловая частота в рад/с,
f — частота в герцах (Гц),
L — индуктивность в генри (Гн),
j — мнимая единица.
Для расчета выберите единицы измерения и введите индуктивность и частоту. Импеданс катушки индуктивности будет показан в омах.
Катушка индуктивности представляет собой пассивный электрический элемент с двумя выводами, изготовленный, как правило, из изолированного провода в форме спирали, намотанного на магнитный сердечник или на оправку (без сердечника). Магнитный сердечник обычно изготовляется из ферромагнитного металла, например, железа или ферромагнитной керамики (феррита) и используется для усиления магнитного поля и, таким образом, для увеличения индуктивности катушки. Как и конденсаторы, катушки индуктивности используются для накопления и сохранения энергии. Однако, в отличие от конденсаторов, энергия в катушке хранится в форме окружающего ее магнитного поля. Катушки индуктивности применяются, в частности, в фильтрах для сглаживания постоянного тока или для предотвращения передачи высокочастотных помех по кабелям. Катушки индуктивности широко используются в колебательных контурах радиопередатчиков и радиоприемников, а также для изготовления трансформаторов.
Магнитный сердечник обычно изготовляется из ферромагнитного металла, например, железа или ферромагнитной керамики (феррита) и используется для усиления магнитного поля и, таким образом, для увеличения индуктивности катушки. Как и конденсаторы, катушки индуктивности используются для накопления и сохранения энергии. Однако, в отличие от конденсаторов, энергия в катушке хранится в форме окружающего ее магнитного поля. Катушки индуктивности применяются, в частности, в фильтрах для сглаживания постоянного тока или для предотвращения передачи высокочастотных помех по кабелям. Катушки индуктивности широко используются в колебательных контурах радиопередатчиков и радиоприемников, а также для изготовления трансформаторов.
Высокодобротная катушка индуктивности без сердечника, установленная в радиопередатчике
В отличие от конденсаторов, которые препятствуют изменению напряжения, приложенного к их обкладкам, катушки индуктивности препятствуют изменению текущего в них тока. В отличие от конденсаторов, которые не пропускают постоянный ток, катушки индуктивности пропускают его легко. Они препятствуют только прохождению переменного тока или иного изменяющегося тока и их способность препятствовать прохождению тока и называется индуктивностью. Индуктивность обозначается символом L в честь российского физика Эмиля Ленца и измеряется в генри — единицах, названных в честь американского ученого Джозефа Генри.
Они препятствуют только прохождению переменного тока или иного изменяющегося тока и их способность препятствовать прохождению тока и называется индуктивностью. Индуктивность обозначается символом L в честь российского физика Эмиля Ленца и измеряется в генри — единицах, названных в честь американского ученого Джозефа Генри.
В отличие от резисторов, которые препятствуют прохождению электрического тока вследствие падения напряжения на них, пропорционального протекающему току, катушки индуктивности препятствуют изменению протекающего через них тока. На них создается падение напряжения, прямо пропорциональное скорости изменения тока. Полярность индуцированного напряжения всегда такова, что это напряжение поддерживает изменяющийся ток в его текущем состоянии. Например, если ток растет, то напряжение препятствует этому росту и старается уменьшить ток. В то же время, если ток через катушку уменьшается, напряжение мешает этому уменьшению и поддерживает более высокий ток. Чем выше скорость изменения тока, тем больше амплитуда этого обратного напряжения. В связи с указанным свойством, это напряжение часто называют индуктивными выбросами или обратным током. Для того, чтобы как-то отличить это свойство от сопротивления, используют понятие реактивного сопротивления. Если к катушке индуктивности приложено синусоидальное напряжение, то при бóльших частотах катушка оказывает току большее сопротивление, следовательно, ее реактивное сопротивление также увеличивается, как показано на графике.
В связи с указанным свойством, это напряжение часто называют индуктивными выбросами или обратным током. Для того, чтобы как-то отличить это свойство от сопротивления, используют понятие реактивного сопротивления. Если к катушке индуктивности приложено синусоидальное напряжение, то при бóльших частотах катушка оказывает току большее сопротивление, следовательно, ее реактивное сопротивление также увеличивается, как показано на графике.
График зависимости реактивного сопротивления катушки XL индуктивности и текущего через нее тока I от частоты f для нескольких величин индуктивности показывает прямую пропорциональную зависимость от частоты реактивного сопротивления и обратную зависимость от частоты протекающего через катушку тока
Полное сопротивление Z, как и реактивное сопротивление, измеряется в омах (Ом) и состоит из двух частей — действительной и мнимой. Первая из них представляет собой активное сопротивление R, которое затрудняет протекание тока в материале с плохой проводимостью и зависит от формы этого материала. Вторая часть — это рассмотренное выше реактивное сопротивление X. Оно также затрудняет протекание тока, но не вследствие свойств и формы проводящего материала, а из-за того, что протеканию тока мешает электрическое и магнитное поля.
Вторая часть — это рассмотренное выше реактивное сопротивление X. Оно также затрудняет протекание тока, но не вследствие свойств и формы проводящего материала, а из-за того, что протеканию тока мешает электрическое и магнитное поля.
Если реальная катушка индуктивности подключена к источнику постоянного напряжения, через нее протекает постоянный ток, ограниченный только сопротивлением провода, из которого намотана катушка. Когда катушка подключается к источнику постоянного напряжения, ток через нее медленно повышается от нуля до максимального значения, которое определяется внутренним сопротивлением источника и внутренним сопротивлением витков катушки. ЭДС самоиндукции, возникающая в катушке, препятствует резкому увеличению тока в ней. Эта ЭДС противодействует приложенному напряжению до тех пор, пока ток не достигнет максимального значения.
Если источник постоянного напряжения отключить от катушки, протекающий через нее ток постепенно падает до нуля. В этом случае опять возникает ЭДС самоиндукции, которая снова препятствует, на этот раз, уменьшению тока и которая старается поддержать ток в неизменном состоянии. В конце концов, ток постепенно уменьшается до нуля.
В конце концов, ток постепенно уменьшается до нуля.
В чисто индуктивной цепи ток отстает от напряжения на π/2 радиан или 90°. 1 — в момент отрицательного максимума тока скорость его изменения нулевая и напряжение равно нулю; 2 — ток нулевой, скорость его изменения максимальная и напряжение равно положительному максимуму; 3 — ток положительный и максимальный, скорость его изменения нулевая и напряжение равно нулю; 4 — ток нулевой, скорость его изменения максимальная и напряжение равно отрицательному максимуму
Если к катушке индуктивности приложено переменное синусоидальное напряжение, ток отстает от напряжения на некоторый фазовый угол, как показано на графике. В идеальной катушке индуктивности этот угол будет равен точно 90° или четверти цикла. В точке (ωt = π/2), временнóй оси, где ток нулевой, напряжение на катушке достигает своего положительного максимума. Затем ток постепенно увеличивается и вокруг катушки создается магнитное поле, которое, в свою очередь, создает ЭДС самоиндукции, направленную противоположно току.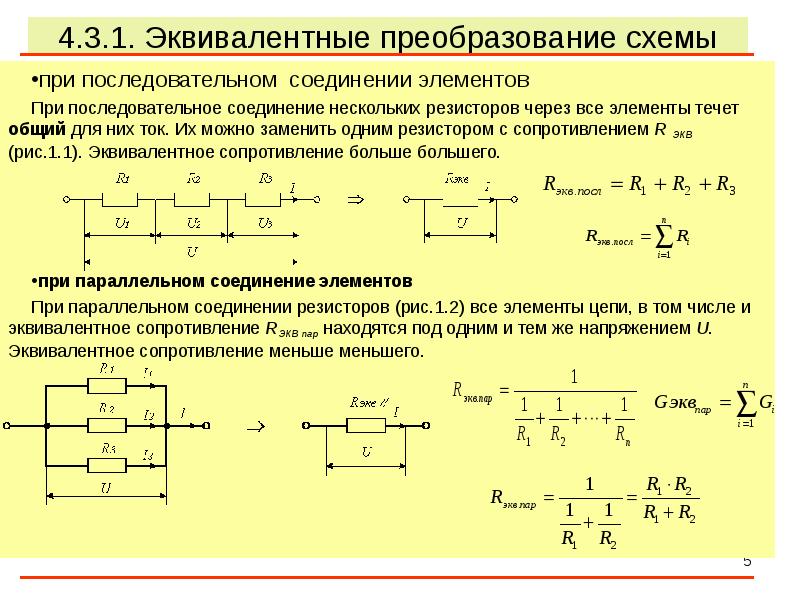 Эта ЭДС является реакцией катушки на изменение протекающего через нее тока, и она максимальна, когда ток нулевой, так как в этой точке скорость изменения тока максимальная. Когда же ток достигает своего максимального значения (положительного или отрицательного), скорость изменения синусоидального тока становится нулевой и в этих точках максимумов ток ЭДС самоиндукции (определяемая этой скоростью) также равна нулю. Это приводит к тому, что синусоида напряжения не совпадает по фазе с током на угол 90° или π/2 радиан. То есть, напряжение опережает ток или ток отстает от напряжения.
Эта ЭДС является реакцией катушки на изменение протекающего через нее тока, и она максимальна, когда ток нулевой, так как в этой точке скорость изменения тока максимальная. Когда же ток достигает своего максимального значения (положительного или отрицательного), скорость изменения синусоидального тока становится нулевой и в этих точках максимумов ток ЭДС самоиндукции (определяемая этой скоростью) также равна нулю. Это приводит к тому, что синусоида напряжения не совпадает по фазе с током на угол 90° или π/2 радиан. То есть, напряжение опережает ток или ток отстает от напряжения.
Аналогичное явление можно наблюдать и в природе. Сравните: Солнце светит сильнее всего в астрономический полдень (солнечный свет — напряжение), однако самая жаркая часть дня обычно бывает через несколько часов после полудня (температура — ток). Или другой пример. День зимнего солнцестояния в северном полушарии (самый короткий день) — в конце декабря, однако самые холодные месяцы еще впереди. В зависимости от того, где вы живете, это будет январь или февраль. Вспомните поговорку «Солнце — на лето, зима — на мороз». Это как раз о поведении индуктивности, только в природной аналогии. Такой сезонный «сдвиг фаз» или отставание вызван поглощением энергии Солнца огромными массами воды в океанах. Они отдадут эту запасенную энергию, но позже — точно так же, как это делают катушки индуктивности.
Вспомните поговорку «Солнце — на лето, зима — на мороз». Это как раз о поведении индуктивности, только в природной аналогии. Такой сезонный «сдвиг фаз» или отставание вызван поглощением энергии Солнца огромными массами воды в океанах. Они отдадут эту запасенную энергию, но позже — точно так же, как это делают катушки индуктивности.
День зимнего солнцестояния в северном полушарии — в конце декабря, однако самые холодные месяцы еще впереди. Именно так ведет себя ток в катушке индуктивности
Рассчитанный этим калькулятором импеданс представляет собой меру сопротивления катушки индуктивности протекающему через нее току на определенной частоте. Индуктивное реактивное сопротивление изменяется при изменении частоты приложенного переменного напряжения. Приведенные выше формула и график показывают, что реактивное сопротивление катушки индуктивности XL велико при высоких частотах и мало при низких частотах (конденсаторы ведут себя с точностью до наоборот). При высоких частотах индуктивное реактивное сопротивление становится очень большим и очень сильно противодействует протекающему току. С другой стороны, при очень низких частотах или при постоянном напряжении катушка индуктивности проводит очень хорошо — отсюда правило, которое мы выучили в школе: катушки индуктивности не пропускают переменный ток и пропускают постоянный. Если частота очень низкая, катушки индуктивности пропускают сигнал очень хорошо. Именно поэтому их устанавливают в фильтрах громкоговорителей (кроссоверах), чтобы высокие частоты не попадали на низкочастотные динамические головки.
С другой стороны, при очень низких частотах или при постоянном напряжении катушка индуктивности проводит очень хорошо — отсюда правило, которое мы выучили в школе: катушки индуктивности не пропускают переменный ток и пропускают постоянный. Если частота очень низкая, катушки индуктивности пропускают сигнал очень хорошо. Именно поэтому их устанавливают в фильтрах громкоговорителей (кроссоверах), чтобы высокие частоты не попадали на низкочастотные динамические головки.
Импеданс измеряется в омах, так же, как и сопротивление. Импеданс мешает прохождению электрического тока так же, как и сопротивление, и показывает как сильно катушка противодействует прохождению тока через нее. Но тогда возникает вопрос: в чем же разница между импедансом и сопротивлением? А разница заключается в зависимости импеданса от частоты приложенного сигнала. Сопротивление от частоты не зависит, а импеданс катушек индуктивности от частоты зависит. С увеличением частоты импеданс катушек уменьшается.
Этот калькулятор предназначен для расчета импеданса идеальных катушек индуктивности. Реальные катушки всегда имеют сопротивление, которое на эквивалентной схеме изображают включенным последовательно с индуктивностью. Для расчета импеданса реальных катушек индуктивности пользуйтесь калькулятором импеданса RL-цепей.
Реальные катушки всегда имеют сопротивление, которое на эквивалентной схеме изображают включенным последовательно с индуктивностью. Для расчета импеданса реальных катушек индуктивности пользуйтесь калькулятором импеданса RL-цепей.
Катушки индуктивности в высокочастотном модуле телевизионного приемника
Предыдущая
РазноеЧто такое фазное и линейное напряжение?
Следующая
РазноеБлуждающие токи и способы борьбы с ними
Закон Ома для цепи переменного тока. Мощность в цепи переменного тока. Резонанс в электрической цепи.
Основные ссылки
CSS adjustments for Marinelli theme
Объединение учителей Санкт-Петербурга
Форма поиска
Поиск
Вы здесь
Главная » Закон Ома для цепи переменного тока. Мощность в…
Закон Ома для полной цепи переменного тока. | |
Если в цепи переменного тока имеются нагрузки разных типов, то закон Ома выполняется только для максимальных (амплитудных) и действующих значений тока и напряжения. В этом случае: — полное сопротивление переменному току. | |
Учитывая, что отношение напряжения к силе тока – это сопротивление, и подставляя конкретные выражения для соответствующих сопротивлений, получим: . | |
Сдвиг фаз в цепи переменного тока определяется характером нагрузки: или . |
|
Мощность в цепи переменного тока. | |
Активной мощностью переменного тока называется средняя за период мощность необратимых преобразований в цепи переменного тока (преобразование энергии электрического тока во внутреннюю энергию): | |
или, переходя к действующим значениям, . | |
Величина наз. коэффициентом мощности. При малом коэффициенте мощности потребляется лишь малая часть мощности, вырабатываемой генератором. Остальная часть мощности периодически перекачивается от генератора к потребителю и обратно и рассеивается в линиях электропередач. | коэффициент мощности |
Резонанс в электрической цепи. | |
Резонанс в электрической цепи — явление резкого возрастания амплитуды вынужденных колебаний тока при приближении частоты внешнего напряжения (эдс) и собственной частоты колебательного контура. |
|
Из выражения для полного сопротивления переменному току видим, что сопротивление будет минимальным (сила тока при заданном напряжении – максимальной) при условии или .
| |
Следовательно, — т.е. частота изменения внешнего напряжения равна собственной частоте колебаний в контуре. | |
Амплитуды колебаний напряжения на индуктивности и емкости будут равны
и — т.е. они равны по величине и противоположны по фазе (напряжение на индуктивности опережает по фазе напряжение на емкости на p). |
|
Следовательно, . |
|
Полное падение напряжения в контуре равно падению напряжения на активном сопротивлении. Амплитуда установившихся колебаний тока будет определяться уравнением |
|
При этом если величина , то напряжения на емкостной и индуктивной нагрузках могут оказаться много больше внешнего напряжения (эдс генератора)! | |
На рисунке представлена зависимость тока в колебательном контуре от частоты при значениях R, где R1<R2<R3. | |
В параллельном контуре при малых активных сопротивлениях R1 и R2 токи в параллельных ветвях противоположны по фазе. Тогда, согласно правилу Кирхгофа . | |
В случае резонанса . Резкое уменьшение амплитуды силы тока во внешней цепи, питающей параллельно соединенные емкостное и индуктивное сопротивления при приближении частоты внешнего напряжения к собственной частоте колебательного контура наз. резонансом токов. |
|
Применение: одно из основных применений резонанса в электрической цепи – настройка радио и телевизионных приемников на частоту передающей станции. Необходимо учитывать резонансные явления, когда в цепи, не рассчитанной на работу в условиях резонанса, возникают чрезмерно большие токи или напряжения (расплавление проводов, пробой изоляции и т. |
|
Теги:
конспект
Как найти полное сопротивление
Полное сопротивление
В любой цепи переменного тока наряду с чисто реактивным сопротивлением присутствует омическое (активное) сопротивление, которое нужно учитывать при определении полного сопротивления.
| Z | полное сопротивление, | Ом |
|---|---|---|
| R | омическое (активное) сопротивление, | Ом |
| X | реактивное сопротивление, | Ом |
| Y = 1/Z | полная проводимость, | сименс |
| G | активная проводимость, | сименс |
| B | реактивная проводимость, | сименс |
| U | полное напряжение (эффективное значение), | Вольт |
| I | полный ток (эффективное значение), | Ампер |
Полное сопротивление при последовательном соединении R и X
При последовательном соединении активное и реактивное сопротивления складываются геометрически
X определяется по формулам реактивного сопротивления и Величина Ux определяется, как произведение IX.
Сопротивление Z не зависит от времени. Вектор, изображающий сопротивление на векторной диаграмме, не вращается.
Полное сопротивление при параллельном соединение R и X
При параллельном соединении активная и реактивная проводимости складываются геометрически
Величина В = 1/Х определяется но формулам реактивного сопротивления. Ix определяется как произведение UB.
Величина Y не зависит от времени. Вектор, изображающий на векторной диаграмме проводимость, не вращается.
Как вычислить полное сопротивление цепи
Импеданс (impedance) – комплексное, полное сопротивление переменному току электрической цепи с активным и реактивным сопротивлением.
Импеданс и общий сдвиг фаз для синусоидального тока можно рассчитать исходя из последовательного или параллельного соединения элементов цепи.
Последовательное соединение
При последовательном соединении, согласно Закону Ома для переменного тока, во всех элементах цепи ток будет общим I = U/Z, а значения напряжений на каждом элементе определятся пропорционально его сопротивлению:
на выводах резистора UR = IR; на выводах конденсатора UC = IXC; на выводах катушки UL = IXL.
Векторы индуктивной и ёмкостной составляющих напряжения направлены в противоположные стороны.
С учётом отрицательного ёмкостного сдвига, общее напряжение на реактивных элементах UX = UL — UC .
Пропорционально напряжению, получим общее реактивное сопротивление X = XL — XC .
Векторы напряжений на активной и реактивной составляющей импеданса имеют угол сдвига фаз 90 градусов.
U , UR и UX представим в виде прямоугольного треугольника напряжений с углом сдвига фаз φ.
Тогда получим соотношение, согласно Теореме Пифагора, U ² = UR² + UX² .
Следовательно, с учётом пропорциональности элементов R, L, C значениям напряжений на их выводах, определим импеданс, который будет равен квадратному корню из суммы квадратов активного и реактивного сопротивлений цепи.
XL = ωL = 2πfL — реактивное сопротивление индуктивности.
XC = 1/(ωC) = 1/(2πfC) — реактивное сопротивление ёмкости.
Угол сдвига фаз φ и его дополнение до 90° δ определятся тригонометрическими функциями из треугольника сопротивлений с катетами R, X и гипотенузой Z, как показано на рисунке:
Обычно, для облегчения расчётов, импеданс представляют в виде комплексного числа, где действительной его частью является активное сопротивление, а мнимой — реактивное.
Для последовательного соединения импеданс можно записать в комплексном виде следующим образом:
Тогда в тригонометрической интерпретации модулем этого числа будет импеданс, а аргументом — угол φ.
В соответствии с формулой Эйлера, запишем показательную форму комплексного импеданса:
Отсюда активная составляющая импеданса R = Zcosφ
Реактивная составляющая X = Zsinφ.
Параллельное соединение
Для вычисления импеданса при параллельном соединении активных и реактивных сопротивлений будем исходить из суммы обратных им величин — проводимостей y = 1/Z, G = 1/R, b = 1/X.
y = 1/Z = √(G 2 + b 2 )
Сдвиг фаз в этом случае будет определён треугольником сопротивлений следующим образом:
Комплексную проводимость, как величину, обратную комплексному импедансу, запишем в алгебраической форме:
Либо в показательной форме:
Здесь:
Y — комплексная проводимость.
G — активная проводимость.
b — реактивная проводимость.
y — общая проводимость цепи, равная модулю комплексной проводимости.
e — константа, основание натурального логарифма.
j — мнимая единица.
φ — угол сдвига фаз.
Онлайн-калькулятор расчёта импеданса и угла сдвига фаз
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Похожие страницы с расчётами:
Замечания и предложения принимаются и приветствуются!
1. Находим полное сопротивление цепи
где R = R1 + R2 = 2 + 2 = 4 – арифметическая сумма всех активных сопротивлений, Ом;
Х L = Х L1 + Х L2 = 4 + 5 = 9, X C = X C1 + X C2 = 4 + 2 = 6 – арифметические суммы однотипных индуктивного и емкостного сопротивлений, Ом.
Подставляем полученные значения в формулу.
2. По закону Ома для цепи переменного тока определим ток в цепи:
I = U / Z = 220 / 5 = 44 А
3. Из треугольника сопротивлений следует: Сos φ = R / Z = 4 / 5 = 0,8 ;
Sin φ= =( 9 – 6) / 5 = 0,6
По таблицам тригонометрических величин найдем значения угла сдвига фаз: φ = 36 0
4. Подсчитываем мощности:
полная мощность S = U· I = 220 · 44 = 9680 ВА = 9,6 кВА
активная Р = S ·Сos φ = 9680 · 0,8 = 7744 Вт =7,744 кВт
реактивная Q = S· Sin φ = 9680· 0,6 = 5808 вар = 5,808 квар
При построении векторных диаграмм тока и напряжений следует исходить из следующих условий:
· ток одинаков для любого участка цепи, т. к. разветвлений в ней нет;
· на каждом сопротивлении при прохождении тока создается падение напряжения, значение которого определяют по закону Ома для цепи и называют напряжением на данном сопротивлении: UА = I ·R – на активном, UL = I ·Х L – на индуктивном; U С = I ·Х С – на емкостном.
Построение векторной диаграммы
1. Выписываем значение тока и напряжений: I= 44 А; U L1 = I ·Х L1 = 44· 4 = 176 В; U А1 = I· R1 = 44 · 2 = 88 В; UL2 = I ·Х L2 = 44 ·5 = 220 В; U А2 = I ·R2 =
44 · 2 = 88 В; Uc1 =I ·Х С1 = 44 · 4 = 176 В; U С2 = I· Х С2 = 44 · 2 = 88 В.
2. Исходя из размеров бумаги (миллиметровки, или тетрадного листа в клетку), задаемся масштабом по току и напряжению. Для рассматриваемого примера принимаем масштаб: по току m I= 10 А /см, по напряжению
m U =44 В/ см. Тогда длины векторов ℓ следующие:
длина вектора тока
ℓI = I / m I = 44 / 10 = 4,4 см;
длины векторов напряжений
ℓ UА 1 = U А1 / m U = 88 В / 44 В / см = 2 см
ℓ UА 2 = U А2 / m U = 88 В / 44 В / см = 2 см
ℓ UС 2 = U С 2 / m U = 88 В / 44 В см = 2 см
3. Выполняем построение диаграммы в такой последовательности:
Выполняем построение диаграммы в такой последовательности:
а) за начальный принимается вектор тока, так как ток имеет одинаковое значение для всех участков цепи.
Строим этот вектор горизонтально в масштабе (рисунок 15)
Далее следует строить векторы напряжений на каждом сопротивлении с учетом сдвига фаз относительно вектора тока.
При этом целесообразно придерживать схемной ( рисунок 14) последовательности расположения сопротивлений и напряжений на них.
б) вектор напряжения на первом индуктивном сопротивлении строим от начало вектора тока под углом 90 0 в сторону опережения этого вектора (вверх) ( рисунок 16)
Опережение или отставание вектора определяется характером нагрузки и принятым направлением вращения векторов против часовой стрелки;
в) вектор напряжения на первом активном сопротивлении UА1 строим от конца вектора UL1, параллельно вектору тока, т. к. между этими векторами I и UА1 сдвига фаз нет (рисунок 17)
m U = 44 В / см m U = 44 В / см
Рисунок 16 Рисунок 17
г) вектор напряжения на втором индуктивном сопротивлении UL2 строим от конца вектора UА1 в сторону опережения на 90 0 (вверх) (рисунок 18)
m U = 44 в / см m U = 44 в / см m U = 44 в / см
Рисунок 18 Рисунок 19 Рисунок 20
д) вектор напряжения на втором активном сопротивлении UА2 строим от конца вектора UL2 параллельно вектору тока аналогично построению вектора UА1 (рисунок 19) .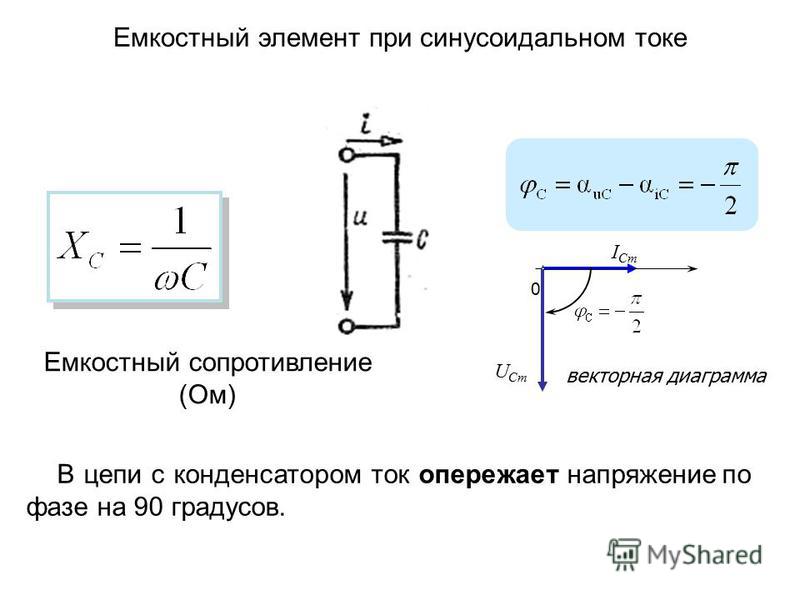
е) векторы напряжений на первом и втором емкостных сопротивлений UС1 и UС2 строим от конца вектора UА2 под углом 90 0 в сторону отставания от вектора тока (вниз) ( риcунок 20).
ж) вектор полного напряжения U находим геометрическим сложением векторов по правилу многоугольника; начало принятого за первый вектор UL1 соединением с концом последнего вектора UС2 (рисунок 21).
Угол между векторами тока I и общего ( приложенного) напряжения U обозначают φ и называют углом сдвига фаз данной цепи.
Следует проверить аналитическое решение и построение векторной диаграммы путем их сопоставления следующим образом.
1. Проверка угла φ производится с помощью транспортира и сравнением полученного угла в градусах с расчетным значением решения в данном случае по расчету φ = 36 0 по диаграмме этот угол также равен φ = 36 0 .
2. Проверка значения приложенного напряжения по диаграмме длина этого вектора ℓ U = 5 см, значение напряжения
U = ℓ U ·m U = 5 см · 44 В / см = 220 В,
что соответствует условием задачи. Значит , диаграмма построена верно. В случае значительных расхождений при такой проверке следует найти ошибку.
Значит , диаграмма построена верно. В случае значительных расхождений при такой проверке следует найти ошибку.
4 Экзаменационные вопросы
1. Определение и изображение электрического поля. Закон Кулона.
2. Напряженность электрического поля. Электрическое напряжение.
3. Электроизоляционные материалы.
4. Электрическая емкость. Плоский конденсатор. Соединение конденсаторов. Энергия электрического поля.
5. Преобразование электрической энергии в тепловую энергию.
6. Электрическая цепь, электрический ток, сила тока.
7. Проводниковые материалы. Зависимость сопротивления от температуры.
8. Закон Ома для участка и полной электрической цепи.
9. Способы соединения сопротивлений.
10. Законы Кирхгофа.
11. Электрическое сопротивление. Проводимость.
12. Энергия и мощность электрической цепи, их единицы измерения.
13. Магнитная индукция и магнитная проницаемость.
14. Магнитные материалы, применяемые в электрических приборах и машинах.
15. Действие магнитного поля на проводник с током.
16. Классификация измерительных приборов, классы точности.
17. Расширение пределов измерения приборов в цепях переменного и постоянного тока.
18. Измерение тока, напряжения, сопротивления.
19. Ваттметр, электрический счетчик, способ включения в цепь переменного тока.
20. Приборы электромагнитной системы ,устройство, принцип действия, достоинства и недостатки.
21. Приборы магнитоэлектрической системы, устройство, принцип действия, достоинства и недостатки.
22. Приборы электродинамической системы, устройство, принцип действия, достоинства и недостатки.
23. Получение однофазного переменного тока.
24. Переменный ток. Амплитудное, действующее и мгновенное значение величины переменного тока, период, частота, фаза, сдвиг фаз.
25. Цепь с последовательным соединением активного и индуктивного сопротивления.
26. Электрическая цепь с последовательным включением активного и емкостного сопротивления.
27. Цепь с последовательным соединением активного, индуктивного и емкостного сопротивлений. Условия резонанса напряжений.
28. Условия и принцип действия трехфазных синхронных электрических двигателей.
29. Треугольник сопротивления и мощности при последовательном соединении R,L,C.
30. Понятие об электроприводе, структурная схема. Режимы работы электродвигателей.
31. Электрическая цепь с параллельным включением активного, индуктивного и емкостного сопротивления. Резонанс токов.
32. Передача и распределение электрической энергии.
33. Активная, реактивная и полная мощность электрической цепи
34. Принципы получения трехфазной ЭДС
35. Транзистор. Устройство, назначение и принцип действия. Условное обозначение.
36. Соединение электроприемников в «звезду». Линейные, фазные токи и напряжения.
37.Двух – полупериодная схема выпрямления с использованием средней точки вторичной обмотки трансформатора.
38. Соединение электроприемноков в «треугольник». Линейные и фазные токи и напряжения.
Линейные и фазные токи и напряжения.
39. Устройство и принцип действия трансформаторов и автотрансформаторов.
40. Электрическая схема реверсивного магнитного пускателя.
41. Источники света и осветительная аппаратура на строительной площадке
42. действие электрического тока на организм человека.
43. Виды электрической сварки.
44. Использование сварочных аппаратов в строительных технологиях..
45. Особенности работы электрооборудования грузоподъемных машин.
46. Простейшие схемы электроснабжения.
47. Защитное заземление и зануление.
48. Требования к крановым электродвигателям.
49. Классификация электрических машин.
50. Классификация электрических сетей.
51. Трансформаторные подстанции и особенности их размещения на строительной площадке.
5 Список рекомендуемой литературы
1. Зайцев В.Е. Нестерова Т.А. Электротехника. Электроснабжение, электротехнология и электрооборудование строительных площадок. М.: Мастерство, 2001.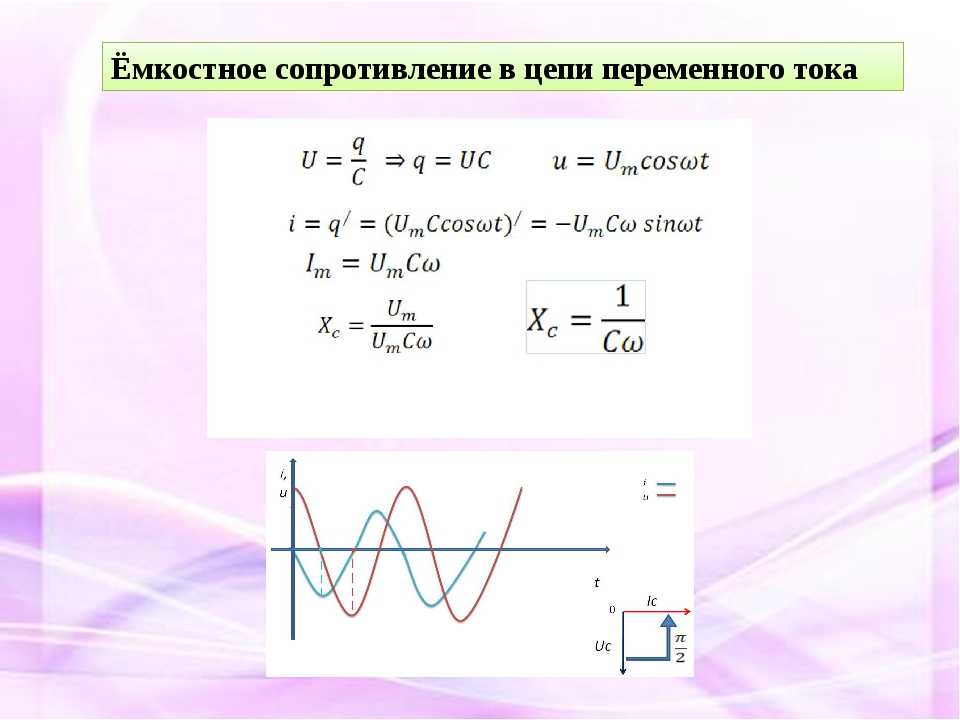
2. Данилов И.А., Иванов П.М. Общая электротехника с основами электроники. М.: Высшая школа, 1989.
3. Зайцев В.Е., Нестерова Т.А. «Задания на лабораторные работы по электронике». Смоленск, 1966.
4. Евдокимов Ф.Е. Общая электротехника. М.: Высшая школа.
5. Чикаев Д.С., Федуркина М.Д. Электрооборудование строительных машин и энергоснабжение строительных площадок.
6. Рабинович Э.А. Сборник задач по общей электротехнике. М.: Стройздат, 1981.
Дата добавления: 2015-05-06 ; Просмотров: 1098 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
В предыдущих статьях мы узнали, что всякое сопротивление, поглощающее энергию, называется активным, а сопротивление, не поглощающее энергии, безваттным или реактивным. Кроме того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные.
Однако существуют цепи, где сопротивление не является чисто активным или чисто реактивным. То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности.
То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности.
Введем понятие полного сопротивления цепи переменному току — Z, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных). Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока
На рисунке 1 представлены варианты электрических цепей и их классификация в зависимости от того какие элементы (активные или реактивные) включены в цепь.
Рисунок 1. Классификация цепей переменного тока.
Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи.
Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление.
Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.
В любом сечении цепи, изображенной на рисунке 2,а, мгновенные значения тока должны быть одинаковыми, так как в противном случае наблюдались бы скопления и разрежения электронов в каких-либо точках цепи. Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения UL (напряжение на индуктивном сопротивлении) и напряжения UR (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°.
Рисунок 2. Полное сопротивление цепи с активным сопротивлением и индуктивностью. а) — схема цепи; б) — сдвиг фаз тока и напряжения; в) — треугольник напряжений; д) — треугольник сопротивлений.
Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов UL и UR. Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор UAB является гипотенузой прямоугольного треугольника.
Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов.
По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление.
Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z 2 ) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. е.
(1)
Извлекая квадратный корень из обеих частей этого равенства, получим,
(2)
Таким образом, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений
Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т. е. полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.
е. полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.
Полное сопротивление цепи, изображенной на рис.2,а, не является ни чисто активным, ни чисто реактивным; оно содержит в себе оба эти вида сопротивлений. Поэтому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, то есть он будет больше 0°, но меньше 90°. К которому из этих двух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и наоборот, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°.
В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления. Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи.
Рисунок 3. Полное сопротивление цепи с активным сопротивлением и емкостью. а) — схема цепи; б) — треугольник сопротивлений .
Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его.
Для данного случая:
(3)
В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.
Рисунок 4. Полное сопротивление цепи содержащей R, L и C. а) — схема цепи; б) — треугольник сопротивлений .
Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности, т. е.
(4)
Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений (XL или XC преобладает).
После того как мы по формуле (4) определили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.
(5)
(6)
Способ построения треугольника сопротивлений для этого случая изображен на рис. 4 б.
Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.
Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.
Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.
Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) — параллельное соединение R и L; б) — параллельное соединение R и C .
Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z
Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.
(7)
Приводя к общему знаменателю подкоренное выражение, получим:
(8)
(9)
Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.
5а.
Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.
Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно:
(10)
Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.
В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).
Рисунок 6. Эквивалентная схема колебательного контура.
Формула полного сопротивления для этого случая будет:
(11)
Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:
(12)
В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие
(13)
При соблюдении этого условия полное сопротивление колебательного контура будет равно:
(14)
где L—индуктивность катушки в Гн;
С—емкость конденсатора в Ф;
R—активное сопротивление катушки в Ом.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Что такое активное сопротивление
При прохождении тока в электрической цепи он подвергается противодействию ее отдельных частей, которое в электротехнике называется сопротивлением. Это приводит к потере части мощности. Чтобы правильно рассчитать параметры электрической цепи, нужно учитывать природу сопротивления и знать, в чем заключается действие различных его видов.
Что такое сопротивление
Ток, протекая через провода и различные радиодетали, тратит свою энергию. Это явление количественно выражается величиной сопротивления. В электротехнике его разделяют на активное и реактивное сопротивление. В первом случае при прохождении тока часть его энергии превращается в тепловой вид, а иногда и в другие (например, проявляется в химических реакциях). Величина активного сопротивления зависит от частоты переменного электротока и возрастает с ее увеличением.
Второй тип сопротивления имеет более сложную природу и возникает в момент включения или выключения потребителя электроэнергии в сеть переменного или постоянного тока. В цепи с реактивным сопротивлением энергия электрического тока частично превращается в другую форму, а затем переходит обратно, то есть, наблюдается периодический колебательный процесс. Полное сопротивление цепи включает в себя активный и реактивный типы, которые учитываются по особым правилам.
Виды сопротивления
В электротехнике рассматривается активное электрическое сопротивление, а также две разновидности реактивного: индуктивное и ёмкостное.
Активное сопротивление
Можно представить себе электрическую цепь, в которой к клеммам батарейки через провод последовательно присоединены резистор и электрическая лампочка. Если замкнуть провода, лампочка загорится. Можно использовать вольтметр или мультиметр в соответствующем режиме работы, с помощью которых измеряется разность потенциалов между двумя точками цепи.
Измерив напряжение между клеммами и сравнив его с тем, которое имеется на проводах подсоединённых к лампочке, можно увидеть, что последнее меньше. Это связано с падением напряжения на впаянной в цепь радиодетали. Последняя оказывает противодействие электрическому току, затрудняя его прохождение.
Активным сопротивлением обладает каждая деталь, через которую проходит ток. У металлических проводов оно очень маленькое. Чтобы узнать величину сопротивления радиодетали, нужно изучить обозначение на ее корпусе. Если из рассматриваемой электроцепи убрать резистор, то сила тока, проходящего через лампочку, увеличится.
Формула для расчета активного сопротивления соответствует закону Ома:
- R — величина активного сопротивления между двумя точками в цепи;
- U — напряжение или разность потенциалов между ними;
- I — сила тока на рассматриваемом участке цепи.
Для расчета активного сопротивления проводника формула будет другая:
где K-коэффициент поверхностного эффекта, который равен 1,
- l — длина проводника,
- s — площадь поперечного сечения,
- p — “ро” удельное сопротивление.
Сопротивление принято измерять в Омах. Оно существенно зависит от формы и размеров объекта, через который протекает ток: сечения, длины, материала, а также от температуры. Действие активного сопротивления уменьшает энергию электрического тока, превращая её в другие формы (преимущественно в тепловую).
Реактивное сопротивление
Этот вид возникает тогда, когда переменный ток проходит сквозь элемент, который обладает индуктивностью или емкостью. Основной особенностью реактивного сопротивления является преобразование электрической энергии в другую форму в прямом и обратном направлениях. Часто это происходит циклически. Реактивное сопротивление проявляется только при изменениях силы тока и напряжения. Существует два его вида: индуктивное и емкостное.
Основной особенностью реактивного сопротивления является преобразование электрической энергии в другую форму в прямом и обратном направлениях. Часто это происходит циклически. Реактивное сопротивление проявляется только при изменениях силы тока и напряжения. Существует два его вида: индуктивное и емкостное.
Индуктивное сопротивление
При увеличении силы тока порождается магнитное поле, обладающее различными характеристиками. Наиболее важной из них является индуктивность. Магнитное поле, в свою очередь, воздействует на проводник, по которому протекает ток. Влияние является противоположным направлению изменения тока. То есть, если сила тока увеличилась, то магнитное поле будет уменьшать его, и наоборот, если снизилась, то поле усилит его. Когда ток не меняется, реактивное сопротивление катушки индуктивности будет равно нулю.
Индуктивное сопротивление зависит от частоты тока. Чем она выше, тем выше скорость изменения данного параметра. Это значит, что будет образовано более сильное магнитное поле. Возникающая при этом ЭДС препятствует изменению электрического тока.
Возникающая при этом ЭДС препятствует изменению электрического тока.
Расчет реактивного индуктивного сопротивления осуществляется по такой формуле:
XL = L×w = L×2π×f, где буквами обозначаются:
- L — индуктивность магнитного поля, которое порождается изменением силы тока;
- W — круговая частота изменения, которая используется в описании синусоидального изменения силы тока;
- Π — число «пи»;
- f — частота тока в обычном смысле.
При синусоидальном изменении напряжения сила тока будет меняться, отставая от него по фазе. Поэтому реактивное сопротивление трансформатора существенно зависит от его индуктивности.
Емкостное сопротивление
Оно имеет иную природу, чем индуктивное. Это понятие удобно проиллюстрировать на примере электрической цепи, состоящей из источника питания, клеммы которого соединены с обкладками конденсатора. Сразу после подключения на них будет постепенно накапливаться заряд, создавая ток в цепи.
После достижения предельной величины, которая определяется ёмкостью детали, ток не будет проходить по цепи. Если после этого отключить провода от клемм, а затем последние соединить, то между ними начнётся перемещение зарядов до тех пор, пока разность потенциалов станет равной нулю.
Если к конденсатору подключить источник переменного тока, то будет происходить следующее. С увеличением разности потенциалов заряд на обкладках конденсатора будет расти. Когда напряжение перейдёт в фазу уменьшения, накопленный заряд начнёт стекать с них, образуя ток противоположного направления. Затем разность потенциалов станет отрицательной, но по абсолютной величине будет расти до максимального значения. При этом конденсатор начнет вновь заряжаться, но при этом знак поступающих зарядов будет не такой, который был раньше.
Когда напряжение начнёт увеличиваться (уменьшаясь по абсолютной величине), заряд с обкладок конденсатора будет стекать. Когда разность потенциалов у источника достигнет нуля и продолжит увеличиваться, начнётся новый цикл изменений.
На каждом этапе описанной ситуации ток с обкладок конденсатора будет иметь направление противоположное тому, которое порождается переменной разностью потенциалов источника питания.
Происходящее таким образом уменьшение силы тока представляет собой физический смысл ёмкостного сопротивления. Оно обозначается буквами ХС и рассчитывается по формуле:
XС = 1/(w×C) = 1/(2π×f×C), где
- C — ёмкость используемого конденсатора;
- w — круговая частота переменного тока;
- π — число «пи»;
- f — частота переменного тока.
В рассматриваемом случае изменения тока отстают от напряжения.
Полное сопротивление
При использовании нескольких разновидностей важно знать, как они сочетаются между собой. Активное сопротивление присутствует в любых схемах. Оно способствует превращению части электрической энергии в нагрев. Реактивное сопротивление возникает лишь в цепи переменного тока. Чтобы определить его величину, необходимо из индуктивного вычесть ёмкостное. Эта характеристика показывает энергию, которая пульсирует в цепи, переходя из одной формы в другую.
Эта характеристика показывает энергию, которая пульсирует в цепи, переходя из одной формы в другую.
Полное сопротивление представляет собой сумму активного и реактивного сопротивления в цепи переменного тока, но такое сложение необходимо выполнять особым образом. Для этого нужно начертить прямоугольный треугольник, катеты в котором должны иметь длину, равную величине активного и реактивного сопротивлений соответственно.
Длина гипотенузы будет численно выражать полное сопротивление электрической цепи. Для его определения используется правило, говорящее о том, что сумма квадратов катетов равна квадрату гипотенузы. Это правило называют теоремой Пифагора. Следовательно, формула, с помощью которой можно найти полное сопротивление, выглядит так:
- Z — полное сопротивление;
- R — величина активной составляющей;
- XL и XC — значение индуктивного и емкостного параметра соответственно.
Следовательно, при расчёте полного сопротивления или импеданса нужно учитывать, что такое ёмкость и индуктивность и как они могут проявляться в электрических схемах. Эти величины называются еще паразитными, так как они могут отрицательно влиять на работу электроприбора. Их возникновение относят к непредсказуемым факторам. При этом емкостным или индуктивным сопротивлением, имеющим небольшое значение, при выполнении расчетов можно пренебречь.
Эти величины называются еще паразитными, так как они могут отрицательно влиять на работу электроприбора. Их возникновение относят к непредсказуемым факторам. При этом емкостным или индуктивным сопротивлением, имеющим небольшое значение, при выполнении расчетов можно пренебречь.
Заключение
Как видим, при расчете электрической цепи необходимо учитывать и активное, и реактивное, и полное сопротивление. Они отличаются друг от друга не только названием. Физика этих сопротивлений также разная. Если под воздействием активного сопротивления электроэнергия превращается в другой вид и поступает в окружающую среду, то реактивное возвращает ее обратно в сеть. Без понятия о сопротивлении и знания формул расчета невозможно конструировать электросхемы.
Как вычислить полное сопротивление цепи
Содержание
- Последовательное соединение
- Параллельное соединение
- Онлайн-калькулятор расчёта импеданса и угла сдвига фаз
- Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.

- Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.
Импеданс (impedance) – комплексное, полное сопротивление переменному току электрической цепи с активным и реактивным сопротивлением.
Импеданс и общий сдвиг фаз для синусоидального тока можно рассчитать исходя из последовательного или параллельного соединения элементов цепи.
Последовательное соединение
При последовательном соединении, согласно Закону Ома для переменного тока, во всех элементах цепи ток будет общим
на выводах резистора UR = IR; на выводах конденсатора UC = IXC; на выводах катушки UL = IXL.
Векторы индуктивной и ёмкостной составляющих напряжения направлены в противоположные стороны.
С учётом отрицательного ёмкостного сдвига, общее напряжение на реактивных элементах UX = UL — UC .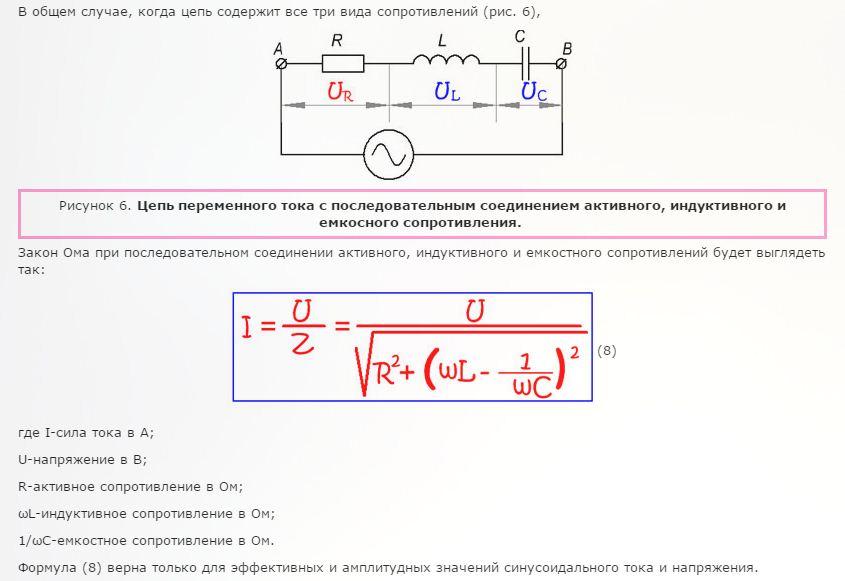
Пропорционально напряжению, получим общее реактивное сопротивление
Векторы напряжений на активной и реактивной составляющей импеданса имеют угол сдвига фаз 90 градусов.
U , UR и UX представим в виде прямоугольного треугольника напряжений с углом сдвига фаз φ.
Тогда получим соотношение, согласно Теореме Пифагора, U ² = UR² + UX² .
Следовательно, с учётом пропорциональности элементов R, L, C значениям напряжений на их выводах, определим импеданс, который будет равен квадратному корню из суммы квадратов активного и реактивного сопротивлений цепи.
XL = ωL = 2πfL
XC = 1/(ωC) = 1/(2πfC) — реактивное сопротивление ёмкости.
Угол сдвига фаз φ и его дополнение до 90° δ определятся тригонометрическими функциями из треугольника сопротивлений с катетами R, X и гипотенузой Z, как показано на рисунке:
Обычно, для облегчения расчётов, импеданс представляют в виде комплексного числа, где действительной его частью является активное сопротивление, а мнимой — реактивное.
Для последовательного соединения импеданс можно записать в комплексном виде следующим образом:
Тогда в тригонометрической интерпретации модулем этого числа будет импеданс, а аргументом — угол φ.
В соответствии с формулой Эйлера, запишем показательную форму комплексного импеданса:
Отсюда активная составляющая импеданса R = Zcosφ
Реактивная составляющая X = Zsinφ.
Параллельное соединение
Для вычисления импеданса при параллельном соединении активных и реактивных сопротивлений будем исходить из суммы обратных им величин — проводимостей y = 1/Z, G = 1/R, b = 1/X.
y = 1/Z = √(G 2 + b 2 )
Сдвиг фаз в этом случае будет определён треугольником сопротивлений следующим образом:
Комплексную проводимость, как величину, обратную комплексному импедансу, запишем в алгебраической форме:
Либо в показательной форме:
Здесь:
Y — комплексная проводимость.
G — активная проводимость.
b — реактивная проводимость.
y — общая проводимость цепи, равная модулю комплексной проводимости.
e — константа, основание натурального логарифма.
j — мнимая единица.
φ — угол сдвига фаз.
Онлайн-калькулятор расчёта импеданса и угла сдвига фаз
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Похожие страницы с расчётами:
Замечания и предложения принимаются и приветствуются!
wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 9 человек(а).
Количество источников, использованных в этой статье: 15. Вы найдете их список внизу страницы.
Полное сопротивление, или импеданс, характеризует сопротивление цепи переменному электрическому току. Данная величина измеряется в омах. Для вычисления полного сопротивления цепи необходимо знать значения всех активных сопротивлений (резисторов) и импеданс всех катушек индуктивности и конденсаторов, входящих в данную цепь, причем их величины меняются в зависимости от того, как меняется проходящий через цепь ток. Импеданс можно рассчитать при помощи простой формулы.
Данная величина измеряется в омах. Для вычисления полного сопротивления цепи необходимо знать значения всех активных сопротивлений (резисторов) и импеданс всех катушек индуктивности и конденсаторов, входящих в данную цепь, причем их величины меняются в зависимости от того, как меняется проходящий через цепь ток. Импеданс можно рассчитать при помощи простой формулы.
В предыдущих статьях мы узнали, что всякое сопротивление, поглощающее энергию, называется активным, а сопротивление, не поглощающее энергии, безваттным или реактивным. Кроме того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные.
Однако существуют цепи, где сопротивление не является чисто активным или чисто реактивным. То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности.
Введем понятие полного сопротивления цепи переменному току — Z, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных).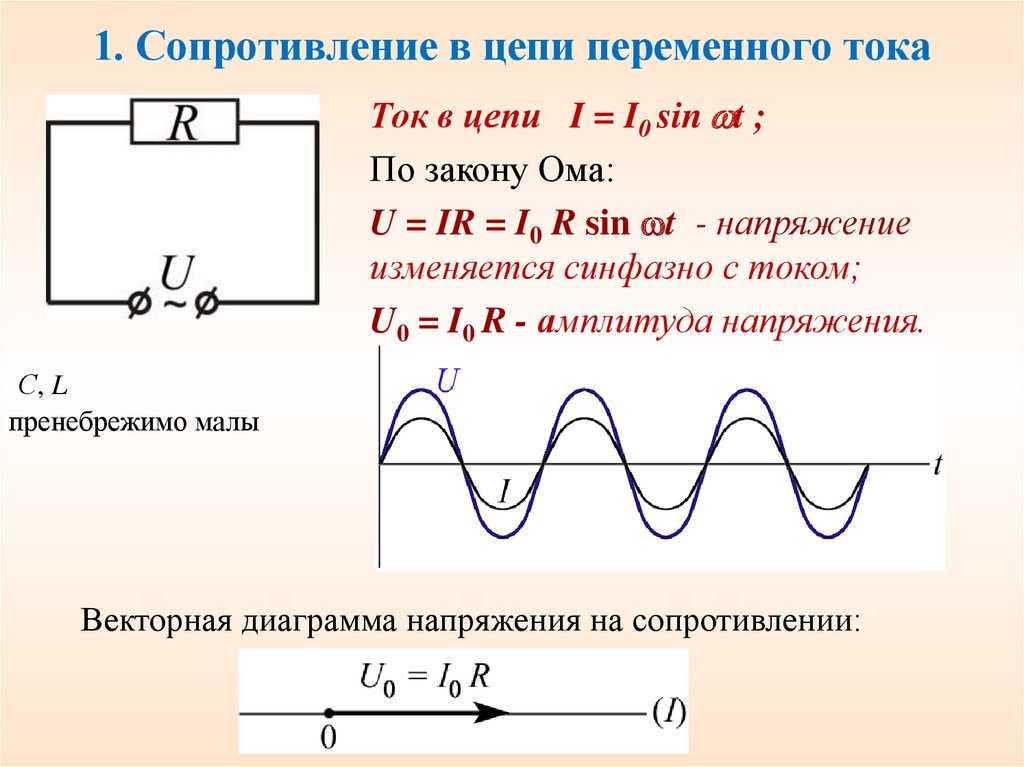 Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока
Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока
На рисунке 1 представлены варианты электрических цепей и их классификация в зависимости от того какие элементы (активные или реактивные) включены в цепь.
Рисунок 1. Классификация цепей переменного тока.
Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи.
Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление.
Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.
В любом сечении цепи, изображенной на рисунке 2,а, мгновенные значения тока должны быть одинаковыми, так как в противном случае наблюдались бы скопления и разрежения электронов в каких-либо точках цепи. Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения UL (напряжение на индуктивном сопротивлении) и напряжения UR (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°.
Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения UL (напряжение на индуктивном сопротивлении) и напряжения UR (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°.
Рисунок 2. Полное сопротивление цепи с активным сопротивлением и индуктивностью. а) — схема цепи; б) — сдвиг фаз тока и напряжения; в) — треугольник напряжений; д) — треугольник сопротивлений.
Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов UL и UR. Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор UAB является гипотенузой прямоугольного треугольника.
Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов.
По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление.
Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z 2 ) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. е.
(1)
Извлекая квадратный корень из обеих частей этого равенства, получим,
(2)
Таким образом, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений
Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т. е. полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.
Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.
Полное сопротивление цепи, изображенной на рис.2,а, не является ни чисто активным, ни чисто реактивным; оно содержит в себе оба эти вида сопротивлений. Поэтому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, то есть он будет больше 0°, но меньше 90°. К которому из этих двух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и наоборот, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°.
В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления. Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи.
Рисунок 3. Полное сопротивление цепи с активным сопротивлением и емкостью. а) — схема цепи; б) — треугольник сопротивлений .
Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его.
Для данного случая:
(3)
В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.
Рисунок 4. Полное сопротивление цепи содержащей R, L и C. а) — схема цепи; б) — треугольник сопротивлений .
Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности, т. е.
е.
(4)
Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений (XL или XC преобладает).
После того как мы по формуле (4) определили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.
(5)
(6)
Способ построения треугольника сопротивлений для этого случая изображен на рис. 4 б.
Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.
Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.
Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.
Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) — параллельное соединение R и L; б) — параллельное соединение R и C .
Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z
Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.
(7)
Приводя к общему знаменателю подкоренное выражение, получим:
(8)
(9)
Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.
Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.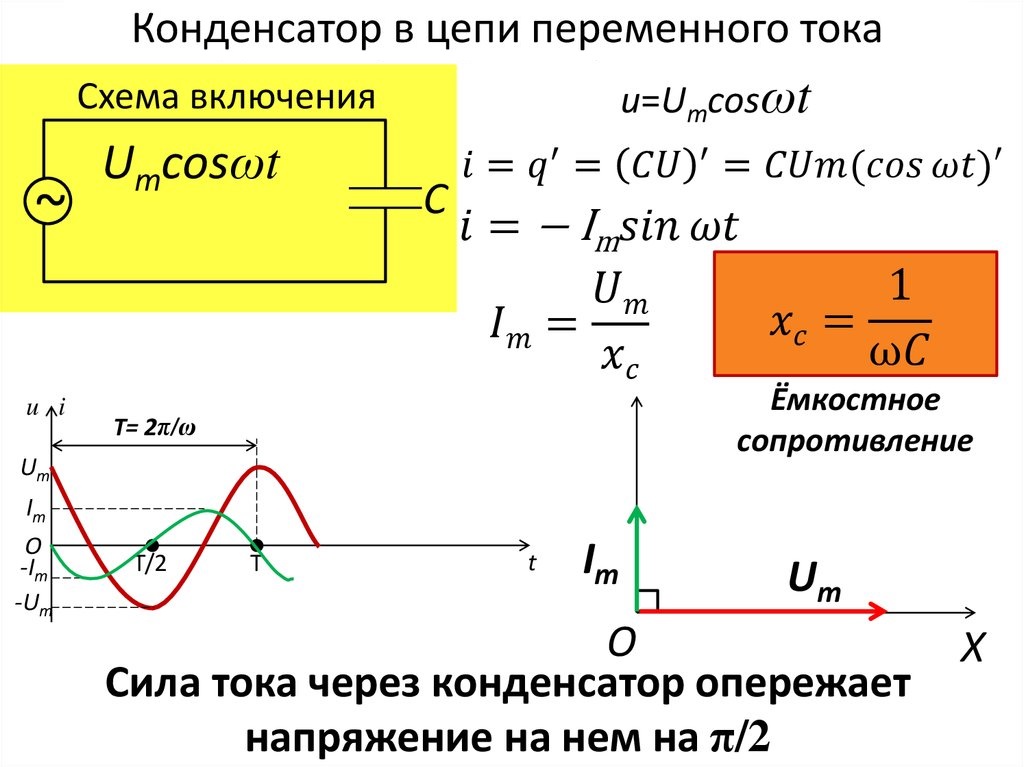
Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно:
(10)
Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.
В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).
Рисунок 6. Эквивалентная схема колебательного контура.
Формула полного сопротивления для этого случая будет:
(11)
Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:
(12)
В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие
е. чтобы соблюдалось условие
(13)
При соблюдении этого условия полное сопротивление колебательного контура будет равно:
(14)
где L—индуктивность катушки в Гн;
С—емкость конденсатора в Ф;
R—активное сопротивление катушки в Ом.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
формула, от чего зависит, в чем измеряется активное сопротивление
При прохождении тока в электрической цепи он подвергается противодействию ее отдельных частей, которое в электротехнике называется сопротивлением. Это приводит к потере части мощности. Чтобы правильно рассчитать параметры электрической цепи, нужно учитывать природу сопротивления и знать, в чем заключается действие различных его видов.
Что такое сопротивление
Ток, протекая через провода и различные радиодетали, тратит свою энергию. Это явление количественно выражается величиной сопротивления. В электротехнике его разделяют на активное и реактивное сопротивление. В первом случае при прохождении тока часть его энергии превращается в тепловой вид, а иногда и в другие (например, проявляется в химических реакциях). Величина активного сопротивления зависит от частоты переменного электротока и возрастает с ее увеличением.
В первом случае при прохождении тока часть его энергии превращается в тепловой вид, а иногда и в другие (например, проявляется в химических реакциях). Величина активного сопротивления зависит от частоты переменного электротока и возрастает с ее увеличением.
Второй тип сопротивления имеет более сложную природу и возникает в момент включения или выключения потребителя электроэнергии в сеть переменного или постоянного тока. В цепи с реактивным сопротивлением энергия электрического тока частично превращается в другую форму, а затем переходит обратно, то есть, наблюдается периодический колебательный процесс. Полное сопротивление цепи включает в себя активный и реактивный типы, которые учитываются по особым правилам.
Индуктивное сопротивление
При увеличении силы тока порождается магнитное поле, обладающее различными характеристиками. Наиболее важной из них является индуктивность. Магнитное поле, в свою очередь, воздействует на проводник, по которому протекает ток. Влияние является противоположным направлению изменения тока. То есть, если сила тока увеличилась, то магнитное поле будет уменьшать его, и наоборот, если снизилась, то поле усилит его. Когда ток не меняется, реактивное сопротивление катушки индуктивности будет равно нулю.
То есть, если сила тока увеличилась, то магнитное поле будет уменьшать его, и наоборот, если снизилась, то поле усилит его. Когда ток не меняется, реактивное сопротивление катушки индуктивности будет равно нулю.
Индуктивное сопротивление зависит от частоты тока. Чем она выше, тем выше скорость изменения данного параметра. Это значит, что будет образовано более сильное магнитное поле. Возникающая при этом ЭДС препятствует изменению электрического тока.
Расчет реактивного индуктивного сопротивления осуществляется по такой формуле:
XL = L×w = L×2π×f, где буквами обозначаются:
- L — индуктивность магнитного поля, которое порождается изменением силы тока;
- W — круговая частота изменения, которая используется в описании синусоидального изменения силы тока;
- Π — число «пи»;
- f — частота тока в обычном смысле.
При синусоидальном изменении напряжения сила тока будет меняться, отставая от него по фазе. Поэтому реактивное сопротивление трансформатора существенно зависит от его индуктивности.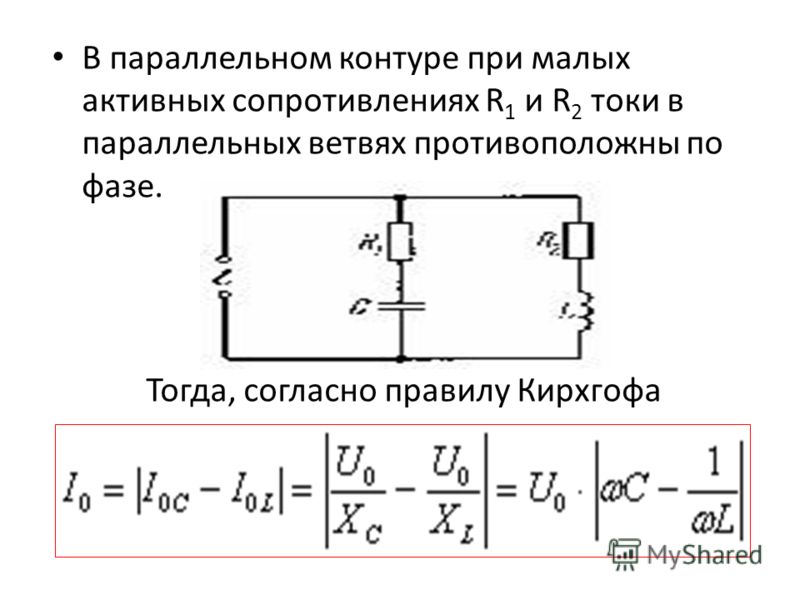
Какое сопротивление называется реактивным, какое активным
Активное электросопротивление — это важный параметр электрической сети, который обуславливает превращение электрической энергии, поступающей в участок электроцепи или в отдельный элетроэлемент в любой другой тип энергии: химическую, механическую, тепловую, электромагнитную. Процесс превращения при этом считаю необратимым.
Типы рассматриваемой величины и формулы ее расчета
Реактивное сопротивление по-другому называется реактансом и представляет собой сопротивляемость элементов электроцепи, которые вызывается измерением силы электротока или напряжения из-за имеющейся емкости или индуктивности этого элемента. При реактансе происходит обменный процесс между отдельным компонентом сети и источником энергии. Часто это понятие относят к простому электрическому сопротивлению, однако оно отличается некоторыми моментами.
Течение переменного электротока не зависит от типа сопротивляемости элементов и всей сети
Различия между активным и реактивным сопротивлением
Разница между активным и реактивным сопротивлением состоит в том, что при прохождении электротока по компонентам цепи, несущим активную нагрузку, имеют место мощностные потери в виде выделения тепла, которое не может быть снова превращено в электрическую энергию. В качестве наглядного примера можно привести конфорку электроплиты, выделяющую тепловую энергию. Такими свойствами обладают и осветительные устройства, электрические двигатели, различные кабели. Фазы проходящих через такие компоненты напряжения и электротока будут совпадать.
В качестве наглядного примера можно привести конфорку электроплиты, выделяющую тепловую энергию. Такими свойствами обладают и осветительные устройства, электрические двигатели, различные кабели. Фазы проходящих через такие компоненты напряжения и электротока будут совпадать.
Будет интересно➡ Режимы работы транзистора
От чего зависит сопротивление проводника
Реактивные нагрузки отличаются наличием емкостных свойств либо способностью к индукции. В первом случае величина рассматриваемого сопротивления зависит от емкости, во втором – от электродвижущей силы самоиндукции.
Важно! Величина, в противоположность активной, может иметь плюсовой и минусовой знаки. Это зависит от того, в какую сторону идет фазовый сдвиг. При опережении электрическим током напряжения будет иметь место отрицательный показатель, в обратном случае – положительный.
Какие отличия
Отличия этих типов электросопротивления в том, что «внутри» активностного типа энергия не накапливается, так как она попадает в активностый элемент и отдается окружающей среде в виде другого ее типа. Это может быть тепло или механическое поднятие груза, свечение, химическая реакция, задание чему-либо скорости.
Это может быть тепло или механическое поднятие груза, свечение, химическая реакция, задание чему-либо скорости.
Индуктивная величина и ее формулы
Важно! Преданная электроэлементу с активностным электросопротивлением энергия преображается и конвертируется, но не возвращается в сеть.
Сопротивляемость же реактивная, наоборот, копит энергию внутри себя за ¼ всего периода синусоидального электротока, а за следующую четверть возвращает ее обратно в сеть. То есть, в окружающую среду полученная энергия не передается.
Комплексная сопротивляемость отдельного элетроэлемента сети R
В активностном типе фазы электрических токов и напряжения совпадают, следовательно, выделяется некоторое количество электроэнергии. В реактивном виде фазы электротока и напряжения расходятся, поэтому энергия передается обратно. Это во многом объясняет то, что активностные электроэлементы нагреваются, а реактивные — нет.
Активная сопротивляемость в цепи переменного синусоидального тока
Как измерить полное электрическое сопротивление
Соединим все детали вместе в простую электрическую цепь.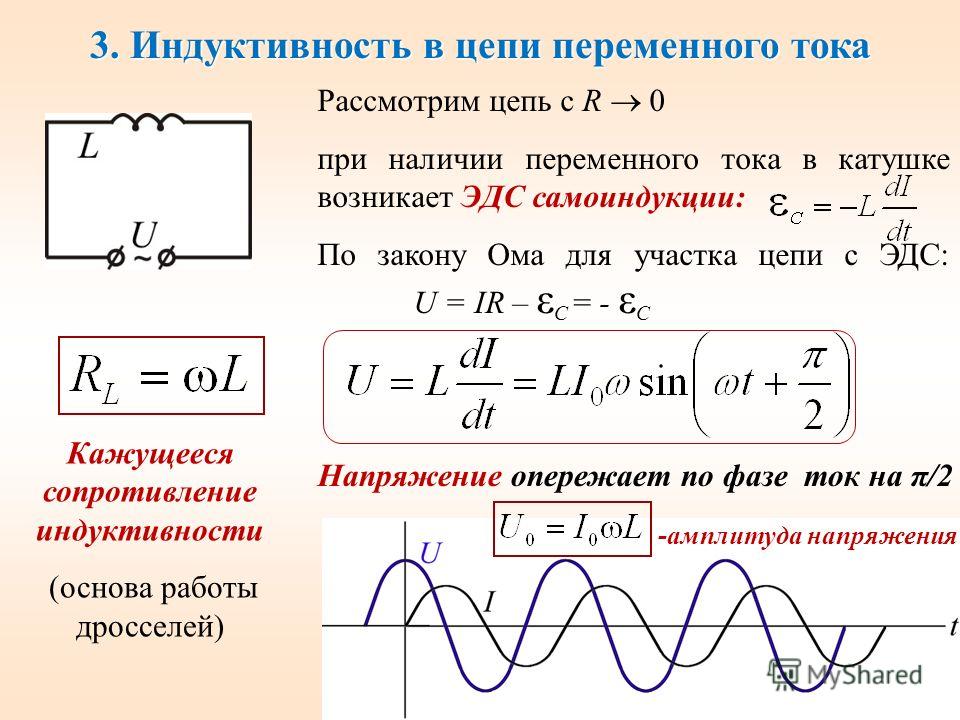 Взглянем на рисунок ниже: это цепь с источником питания постоянного тока. Ток течет через резистор. Весьма просто, верно? Чем больше сопротивление резистора в цепи, тем меньше будет ток.
Взглянем на рисунок ниже: это цепь с источником питания постоянного тока. Ток течет через резистор. Весьма просто, верно? Чем больше сопротивление резистора в цепи, тем меньше будет ток.
Простая цепь постоянного тока с резистором
на 100 Ом для ограничения силы тока Что произойдет, если мы добавим в электрическую цепь источник питания переменного тока, катушку индуктивности и конденсатор? Теперь в цепи есть два дополнительных компонента, каждый из которых по своему оказывает сопротивление электрическому току. Как и резистор, они оба препятствуют прохождению электрического тока, при этом также воздействуют на ток. Если суммировать активное сопротивление резистора и активное и реактивное сопротивления конденсатора и катушки индуктивности, то получится полное электрическое сопротивление или импеданс.
В цепи переменного тока последовательно соединены резистор, катушка индуктивности и конденсатора
Постойте! Чтобы рассчитать полное электрическое сопротивления недостаточно просто сложить активные и реактивные сопротивления. Обычно в большинстве учебных пособий с этого момента начинается изобилие математических формул, поэтому дальше читайте не спеша.
Обычно в большинстве учебных пособий с этого момента начинается изобилие математических формул, поэтому дальше читайте не спеша.
Области проявления
Реактанс электросопротивления проявляется в емкости и индукции. Первое обуславливается наличием емкости проводниках и обмотках или включением в электрическую цепь переменного тока различных конденсаторов. Чем выше емкость потребителя и угловой частоты сигнала электротока, тем меньше емкостная характеристика.
Вам это будет интересно Особенности активно-емкостной нагрузки
Сопротивляемость, которую оказывает проводник переменному току и электродвижущей силе самоиндукции, называется индуктивным. Оно зависит от индуктивности потребителя. Чем выше его индуктивность и выше частота переменного электротока, тем выше индуктивное электросопротивление. Выражается оно формулой: xl = ωL, где xl — это электросопротивление индукции, L — индуктивность, а ω — угловая частота тока.
Емкостный реактанс электросопротивление проявляется, например, в конденсаторе, который накапливает электроэнергию в виде электромагнитного поля между своими обкладками. Индуктивное электросопротивление можно наблюдать в дросселе, который накапливает энергию в виде магнитного поля внутри своей обмотки.
Индуктивное электросопротивление можно наблюдать в дросселе, который накапливает энергию в виде магнитного поля внутри своей обмотки.
Активностным же электросопротивлением может обладать любой резистор, линии электропередач, обмотки трансформатора или электрического двигателя.
Индукция ЭДС может наблюдаться в дросселе
Таким образом, активный резист и реактанс во многом отличаются друг от друга не только разницей по названию, но и по физическим свойствам. Первый вид превращает электроэнергию в другой вид и отдает ее в окружающую среду. Второй же — возвращает ее обратно в электросеть.
Электрическая цепь.
Источник электрического тока, соединенный проводами с различными электроприборами и потребителями электрической энергии, образует электрическую цепь.
Электрическую цепь принято изображать с помощью схем, в которых элементы электрической цепи (сопротивления, источники тока, включатели, лампы, приборы и т. д.) обозначены специальными значками.
Направление тока в цепи — это направление от положительного полюса источника тока к отрицательному. Это правило было установлено в XIX в. и с тех пор соблюдается. Перемещение реальных зарядов может не совпадать с условным направлением тока. Так, в металлах носителями тока являются отрицательно заряженные электроны, и движутся они от отрицательного полюса к положительному, т. е. в обратном направлении. В электролитах реальное перемещение зарядов может совпадать или быть противоположным направлению тока, в зависимости от того, какие ионы являются носителями заряда — положительные или отрицательные.
Это правило было установлено в XIX в. и с тех пор соблюдается. Перемещение реальных зарядов может не совпадать с условным направлением тока. Так, в металлах носителями тока являются отрицательно заряженные электроны, и движутся они от отрицательного полюса к положительному, т. е. в обратном направлении. В электролитах реальное перемещение зарядов может совпадать или быть противоположным направлению тока, в зависимости от того, какие ионы являются носителями заряда — положительные или отрицательные.
Включение элементов в электрическую цепь может быть последовательным или параллельным.
Переменный ток
Для того чтобы понять, что такое активное сопротивление, необходимо разобраться в самом явлении переменного тока. Переменным является такой тип тока, который непрерывно изменяет направление своего протекания. Во время протекания потенциалы переменного тока постоянно изменяются. Это происходит благодаря работе генератора, а точнее за счет взаимодействия магнитного поля с медной обмоткой. Движение хорошо прослеживается при помощи осциллографа. Своей формой оно напоминает синусоиду.
Движение хорошо прослеживается при помощи осциллографа. Своей формой оно напоминает синусоиду.
Будет интересно➡ Устройство люминесцентной лампы
Роль переменного тока сложно переоценить. Главное его достоинство заключается в простоте передачи от источника к потребителю, возможность занижать или увеличивать напряжение при помощи трансформаторов. Также, переменные электрические токи можно доставлять потребителю с гораздо меньшими затратами.
Практическое применение полного электрического сопротивления
Становится понятно, в конце концов, что после всех наших объяснений разобраться, что такое полное электрическое сопротивление, несложно, не так ли? Существуют десятки бесплатных калькуляторов , которые помогут вам выполнить расчеты. Что вам на самом деле нужно – это знать, что полное сопротивление работает так же, как активное сопротивление, ограничивая ток в цепи переменного тока.
Способность таких компонентов, как конденсаторы и катушки индуктивности реагировать на постоянные изменения переменного тока, делает их уникальными. Благодаря полному сопротивлению в вашей цепи можно организовать нечто похожее на электрический щит с защитными автоматами, которые реагируют на неожиданные скачки электричества, защищая от выгорания домашнюю электропроводку. Можно также сказать спасибо полному сопротивлению за то, что вы можете носить с собой ноутбук с полностью заряженным аккумулятором, не опасаясь его взрыва.
Благодаря полному сопротивлению в вашей цепи можно организовать нечто похожее на электрический щит с защитными автоматами, которые реагируют на неожиданные скачки электричества, защищая от выгорания домашнюю электропроводку. Можно также сказать спасибо полному сопротивлению за то, что вы можете носить с собой ноутбук с полностью заряженным аккумулятором, не опасаясь его взрыва.
Когда дело доходит до работы с устройствами с питанием от источника переменного тока, будь то ноутбук или электрощит в вашем доме, стоит быть благодарным полному электрическому сопротивлению. И помните, полное электрическое сопротивление – это просто старший брат привычного активного сопротивления, который объединяет активное и реактивное сопротивления в одной простой формуле.
Активное сопротивление
Переменный ток доставляется потребителю с целью его преобразования в иные виды энергии, например, тепло и свет. В бытовых сетях преобладает использование однофазного переменного тока. При подключении потребителя создается активное сопротивление.
Простые цепи переменного тока с активным сопротивлением включает в себя генератор тока и идеальный резистор. При этом должны соблюдаться необходимые условия для идеальной цепи:
- Активное сопротивление не должно равняться нулю, обязательное условие.
- Емкость и индуктивность цепи должны быть равны нулю.
Также, для идеального активного сопротивления должны соблюдаться следующие условия:
- Соблюдаются закон Ома для мгновенных, среднеквадратичных и амплитудных параметров цепи.
- Значение полностью независимо от амплитудных колебаний.
- Между током и напряжением отсутствует сдвиг фаз.
- Элемент, находящийся под напряжением, выделяет долю тепловой энергии, то есть нагревается.
Все эти условия позволяют электрическим приборам работать в пределах точно установленных параметров с максимальным КПД. Любое изменение может быть причиной отсутствия надежного контактного соединения или неисправностью самого потребителя.
Для того чтобы рассчитать величину активного сопротивления в цепи, необходимо знать величину напряжения и силы тока. Для расчета используется формула: R=U/I. Формула состоит из следующих значений:
Для расчета используется формула: R=U/I. Формула состоит из следующих значений:
- «R» — сопротивление, Ом;
- «U» — величина напряжения, вольт;
- «I» — величина силы тока, ампер.
Далее можно сделать простой расчет. В качестве потребителя выступает электрическая печь, включенная в цепь однофазного переменного тока:
- Напряжение цепи 240 вольт.
- При замере силы тока получено значение 4 ампера.
- R= 240/4=60 Ом.
Расчетная величина активного сопротивления — это не окончательное значение. На нее влияет прежде всего сечение проводов включенных в цепь, схема взаимодействия между цепями емкостных и полупроводниковых элементов.
Активное значение цепи также вызывает безвозвратную потерю первоначальной электрической энергии, а так же приводит к снижению мощности.
Полное сопротивление
При использовании нескольких разновидностей важно знать, как они сочетаются между собой. Активное сопротивление присутствует в любых схемах. 2 ), где
2 ), где
- Z — полное сопротивление;
- R — величина активной составляющей;
- XL и XC — значение индуктивного и емкостного параметра соответственно.
Следовательно, при расчёте полного сопротивления или импеданса нужно учитывать, что такое ёмкость и индуктивность и как они могут проявляться в электрических схемах. Эти величины называются еще паразитными, так как они могут отрицательно влиять на работу электроприбора. Их возникновение относят к непредсказуемым факторам. При этом емкостным или индуктивным сопротивлением, имеющим небольшое значение, при выполнении расчетов можно пренебречь.
Зависимость
Величина активного сопротивления во многом зависит от диаметра проводников. При подаче высокочастотных токов, сопротивление проводника может быть снижено, только если его поверхностный слой намного тоньше основного. Для того чтобы добиться идеального сечения, этот слой должен состоять из материала с очень высокой проводимостью, например, золота или серебра. Данный эффект возникает по причине взаимодействия напряжения и магнитного поля, образованного им. Поле сильно влияет на ток, протекающий по проводнику и выталкивает его на поверхностный слой. Таким образом ближе к поверхности проводника проводимость снижается и становится критично малой в его верхнем слое.
Данный эффект возникает по причине взаимодействия напряжения и магнитного поля, образованного им. Поле сильно влияет на ток, протекающий по проводнику и выталкивает его на поверхностный слой. Таким образом ближе к поверхности проводника проводимость снижается и становится критично малой в его верхнем слое.
Так же присутствуют следующие эффекты: потери утечки и диэлектрические потери. Оба эффекта связаны с наличием конденсатора в цепи. Диэлектрические потери возникают за счет увеличения температуры диэлектрика внутри конденсатора. Потеря утечки возникает в следствии доли пробоя изолятор конденсатора.
Гистерезис. Это тоже тип потери энергии переменного тока. Такая потеря возникает при формировании магнитного поля вокруг предметов из металла. Электромагнитное воздействие приводит к нагреванию металла, а значит преобразованию энергии.
Последним фактором утечки является радиоизлучение. Радиоволны появляются по причине сильного магнитного поля и его взаимодействия с металлами цепи. Для подавления, особенно в радиоаппаратуре, используются экраны, которые впитывают часть поля и отталкивают остальную долю.
Для подавления, особенно в радиоаппаратуре, используются экраны, которые впитывают часть поля и отталкивают остальную долю.
Как найти сопротивление в цепи
Так, R называется отношение напряжения к силе тока: R = U/I.
Эту формулу для закона Ома можно записать еще двумя способами:
Чтобы найти I надо напряжение поделить на сопротивление: I = U/R,
А напряжение, умножив силу тока на сопротивление: U= I*R
Все эти 3 значения Ом объединил в один треугольник, поделив его на 3 части. Вершиной является R, левым боком I, правым — U.
Зная, в чем измеряется сила тока, напряжение, сопротивление, вы всегда сможете сориентироваться в задачах по физике.
Мгновенная мощность в цепи переменного тока с активным сопротивлением.
При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока: p = Umsinωt * Imsinωt = UmImsin2ωt
Из тригонометрии найдём
Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени t. Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = Pm√2 = UmIm√2,то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:
Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = Pm√2 = UmIm√2,то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:
Таким образом, в первоначальной системе координат мгновенная, мощность равна сумме постоянной величины Р= UmIm√2 и перемен- ной р’:
р = Р + р’
Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпадению по фазе напряжения и тока.
Будет интересно➡ Как работает термосопротивление?
Постоянство знака мощности говорит о том, что направление потока электрической энергии остается в течение периода неизменным, в данном случае от сети (от источника энергии) в приемник с сопротивлением R, где электрическая энергия необратимо преобразуется в другой вид энергии. В этом случае электрическая энергия называется активной.
Если R — сопротивление проводника, то в соответствии с законом Ленца — Джоуля электрическая энергия в нем преобразуется в тепло.
Похожие темы:
[ads-pc-1]
Ток и напряжение.
При включении в цепь переменного тока активного сопротивления R (рис. 175, а) напряжение и источника создает в цепи ток i. Если напряжение и изменяется по синусоидальному закону u = Uтsin ?t, то ток i также изменяется синусоидально:
i = Iтsin ?t
При этом
Iт= Uт/ R
Таким образом, ток и напряжение изменяются по одному и тому же закону; они одновременно достигают своих максимальных значений и одновременно проходят через нуль (рис.
175,б). Следовательно,при включении в цепь переменного тока активного сопротивления ток и напряжение совпадают по фазе (рис. 175, в).
Если обе части равенства Iт= Uт/ Rразделить на ?2, то получим выражение закона Ома для рассматриваемой цепи для действующих значений напряжения и тока:
I = U / R
Следовательно, для цепи переменного тока, содержащей только активное сопротивление, этот закон имеет такую же математическую форму, как и для цепи постоянного тока.
Электрическая мощность.Электрическая мощность р в цепи с активным сопротивлением в любой момент времени равна произведению мгновенных значений силы тока i и напряжения и. Следовательно, мгновенная мощность р не является постоянной величиной, как при постоянном токе, а изменяется по кривой (см.
рис. 175,б). Эту кривую можно также получить графически, перемножая ординаты кривых силы тока i и напряжения и при различных углах ?t.
Изменение мощности происходит с двойной частотой ?t по отношению к изменению тока и напряжения, т. е. один период изменения мощности соответствует половине периода изменения тока и напряжения.
Все значения мощности являются положительными. Физически положительное значение мощности означает, что энергия передается от источника электрической энергии к приемнику. Максимальное значение мощности при ?t = 90° и ?t = 270°
Pmax= UтIт= 2UI
Рис. 175. Схема включения в цепь переменного тока активного сопротивления (а), кривые тока i, напряжения и, мощности р (б) и векторная диаграмма (в)
Практически об энергии W, создаваемой электрическим током, судят не по максимальной мощности, а по средней мощности Рср= Р, так как эта энергия может быть выражена как произведение среднего значения мощности Р на время протекания тока:
W = Pt.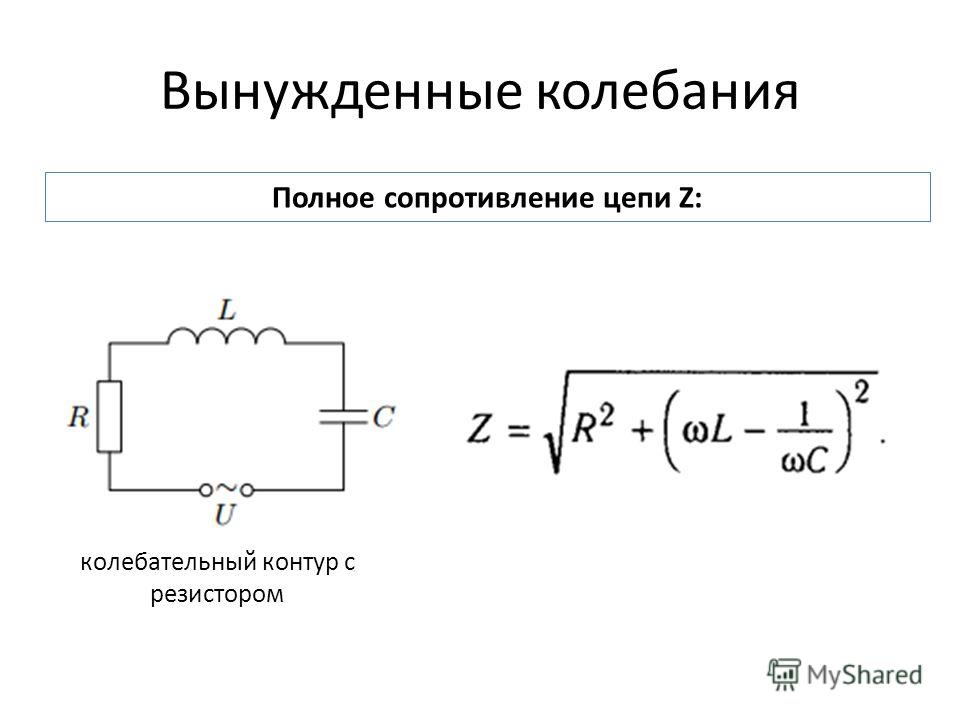
Кривая мгновенной мощности симметрична относительно линии АБ, которая соответствует среднему значению мощности Р. Поэтому
P = Pmax/ 2 = UI
Используя формулу (67) закона Ома, активную мощность можно выразить также в виде P = I2R или P=U2/R.
В электротехнике среднюю мощность, потребляемую активным сопротивлением, обычно называют активной мощностью, или просто мощностью, и обозначают буквой Р.
Поверхностный эффект. Следует отметить, что активное сопротивление проводников в цепи переменного тока всегда больше их сопротивления в цепи постоянного тока.
Переменный ток i не протекает равномерно по всему поперечному сечению проводника, как постоянный ток i, а вытесняется на его поверхность (рис. 176, а). Поэтому полезное сечение проводника как бы уменьшается и сопротивление его при переменном токе возрастает.
Это явление носит название поверхностного эффекта. Неравномерное распределение переменного тока по поперечному сечению проводника объясняется действием э. д.
д.
с. самоиндукции, индуцированной в проводнике магнитным полем, которое создается проходящим по проводнику током I. Это магнитное поле действует не только в пространстве, окружающем проводник (внешний поток Ф2), но и внутри самого проводника (внутренний поток Ф2) (рис.
176,б). Поэтому слои проводника, расположенные ближе к его центру, будут охватываться большим магнитным потоком, чем слои, расположенные ближе к его поверхности, и э. д.
с. самоиндукции, индуцированная во внутренних слоях, будет большей, чем во внешних. Поскольку э.
д. с. самоиндукции препятствует изменению
Рис. 176. Схема протекания постоянного I и переменного i токов по проводнику (а) и возникновение поверхностного эффекта (б)
Рис. 177. Схема термообработки деталей токами высокой частоты: 1 — высокочастотный индуктор; 2 — закаливаемая деталь; 3 — разогретый слой
тока, последний будет стремиться пройти там, где э. д.
с. самоиндукции имеет наименьшее значение, т. е.
е.
пройдет преимущественно по поверхностным слоям проводника. В результате этого плотность тока У в поверхностных слоях будет больше, чем во внутренних. Чем больше частота тока, тем больше э.
д. с. самоиндукции индуцируется во внутренних слоях проводника и тем в большей степени ток вытесняется на поверхность.
При частоте 50 Гц увеличение сопротивления медных и алюминиевых проводников при малом их диаметре практически ничтожно, и сопротивление таких проводников в цепях переменного и постоянного тока можно считать одинаковым. Но для медных и алюминиевых проводников диаметром свыше 10 мм, а для стальных проводников при еще меньших диаметрах необходимо при расчетах учитывать влияние поверхностного эффекта на их активное сопротивление.
При токах высокой частоты, принятых в радиотехнике, телевидении и различных высокочастотных установках, с целью лучшего использования металла проводников их обычно изготовляют полыми.
На свойстве переменного тока высокой частоты протекать, главным образом, по поверхности проводников основаны различные методы высокочастотной закалки и термообработки.
Например, при высокочастотной термообработке деталей вихревыми токами (рис. 177) эти токи индуцируются в основном в поверхностном слое металла. Они быстро разогревают поверхностные слои обрабатываемой детали, раньше, чем ее внутренняя часть успеет заметно нагреться за счет теплопроводности металла.
[ads-pc-2]
В электрической цепи переменного токасуществует два вида сопротивлений:активноеи реактивное. Это является существенным отличием от цепей постоянного тока.
Активная мощность для цепи переменного тока с активным сопротивлением
Скорость преобразования электрической энергии в другой вид энергии за конечный промежуток времени, значительно больший периода изменения тока, характеризуется средней мощностью. Она равна средней мощности за период, которую называют активной.
Активная мощность — среднее арифметическое мгновенной мощности за период.
Для рассматриваемой цепи активную мощность Р нетрудно определить из графика рис. 13.2. Средняя величина мощности равна высоте прямоугольника с основанием Т, равновеликого площади, ограниченной кривой р(t) и осью абсцисс (на рисунке заштриховано).
Равенство площадей РТ = Sp выполняется, если высоту прямоугольника взять равной половине наибольшей мгновенной мощности Pm.
В этом случае часть площади Sp , находящаяся выше прямоугольника, точно укладывается в оставшуюся незаштрихованной его часть:
P = UI
Активная мощность для данной цепи равна произведению действующих величин тока и напряжения:
P = UI = I2R
С математической точки зрения активная мощность является постоянной составляющей в уравнении мгновенной мощности p(t) [см. выражение (13.2)].
Среднюю мощность за период можно найти интегрированием уравнения (13.2) в пределах периода:
Сопротивление R, определяемое из формулы (13.3) отношением активной мощности цепи к квадрату действующего тока, называется активным электрическим сопротивлением.
Закон Ома для полной цепи.
Рассмотрим электрическую цепь, состоящую из источника тока и резистора R.
Закон Ома для полной цепи устанавливает связь между силой тока в цепи, ЭДС и полным сопротивлением цепи, состоящим из внешнего сопротивления R и внутреннего сопротивления источника тока r.
Работа сторонних сил Aст источника тока, согласно определению ЭДС (ɛ) равна Aст = ɛq, где q — заряд, перемещенный ЭДС. Согласно определению тока q = It, где t — время, в течение которого переносился заряд. Отсюда имеем:
Aст =ɛIt.
Тепло, выделяемое при совершении работы в цепи, согласно закону Джоуля — Ленца, равно:
Q = I2Rt + I2rt.
Согласно закону сохранения энергии А = Q. Приравнивая (Aст =ɛIt) и (Q = I2Rt + I2rt), получим:
ɛ = IR + Ir.
Закон Ома для замкнутой цепи обычно записывается в виде:
.
Сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.
Если цепь содержит несколько последовательно соединенных источников с ЭДС ɛ1, ɛ2, ɛ3 и т. д., то полная ЭДС цепи равна алгебраической сумме ЭДС отдельных источников. Знак ЭДС источника определяется по отношению к направлению обхода контура, который выбирается произвольно, например, на рисунке ниже — против часовой стрелки.
Сторонние силы внутри источника совершают при этом положительную работу. И наоборот, для цепи справедливо следующее уравнение:
И наоборот, для цепи справедливо следующее уравнение:
ɛ = ɛ1 + ɛ2 + ɛ3 = | ɛ1| – | ɛ2| -| ɛ3| .
В соответствии с сила тока положительна при положительной ЭДС — направление тока во внешней цепи совпадает с направлением обхода контура. Полное сопротивление цепи с несколькими источниками равно сумме внешнего и внутренних сопротивлений всех источников ЭДС, например, для рисунка выше:
Rn = R + r1 + r2 + r3.
В чем измеряется реактивное сопротивление
Само по себе, явление реактанса характерно только для цепей с электрическим током переменного типа. Обозначается оно латинской буквой «X» и измеряется в Омах. В отличие от активностного варианта, реактанс может иметь как положительное, так и отрицательное значение. Знак «+» или «-» соответствует знаку, по которому сдвигается фаза электротока и напряжения. Знак положительный, когда ток отстает от напряжения и отрицателен, когда кот опережает напряжение.
Важно! Абсолютно чистое реактивное электросопротивление имеет сдвиг фазы на ± 180/2. То есть, фаза «двигается» на π/2.
То есть, фаза «двигается» на π/2.
Емкостное сопротивление
Оно имеет иную природу, чем индуктивное. Это понятие удобно проиллюстрировать на примере электрической цепи, состоящей из источника питания, клеммы которого соединены с обкладками конденсатора. Сразу после подключения на них будет постепенно накапливаться заряд, создавая ток в цепи.
После достижения предельной величины, которая определяется ёмкостью детали, ток не будет проходить по цепи. Если после этого отключить провода от клемм, а затем последние соединить, то между ними начнётся перемещение зарядов до тех пор, пока разность потенциалов станет равной нулю.
Если к конденсатору подключить источник переменного тока, то будет происходить следующее. С увеличением разности потенциалов заряд на обкладках конденсатора будет расти. Когда напряжение перейдёт в фазу уменьшения, накопленный заряд начнёт стекать с них, образуя ток противоположного направления. Затем разность потенциалов станет отрицательной, но по абсолютной величине будет расти до максимального значения. При этом конденсатор начнет вновь заряжаться, но при этом знак поступающих зарядов будет не такой, который был раньше.
При этом конденсатор начнет вновь заряжаться, но при этом знак поступающих зарядов будет не такой, который был раньше.
Когда напряжение начнёт увеличиваться (уменьшаясь по абсолютной величине), заряд с обкладок конденсатора будет стекать. Когда разность потенциалов у источника достигнет нуля и продолжит увеличиваться, начнётся новый цикл изменений.
На каждом этапе описанной ситуации ток с обкладок конденсатора будет иметь направление противоположное тому, которое порождается переменной разностью потенциалов источника питания.
Происходящее таким образом уменьшение силы тока представляет собой физический смысл ёмкостного сопротивления. Оно обозначается буквами ХС и рассчитывается по формуле:
XС = 1/(w×C) = 1/(2π×f×C), где
- C — ёмкость используемого конденсатора;
- w — круговая частота переменного тока;
- π — число «пи»;
- f — частота переменного тока.
В рассматриваемом случае изменения тока отстают от напряжения.
Как правильно измерять сопротивление
При работе с радиоаппаратурой иногда требуется измерять не только активностное, но и реактивное электросопротивление (индуктивность и емкость). Для измерений применяют косвенный метод использования мультиметра, а более точные значения получают при мостовом методе.
Для измерений применяют косвенный метод использования мультиметра, а более точные значения получают при мостовом методе.
Косвенный метод наиболее прост в своей реализации, так как не требует дополнительных схем включения. Одна требуется наличие трех отдельных приборов: амперметра, вольтметра и ваттметра. Если измерить напряжение и силу электротока в цепи, то можно получить полное электросопротивление: Z=U*I После измерения активностной мощности P, можно получить величину активного сопротивления отдельного элемента: R= P/I².
Приложения с емкостным реактивным сопротивлением
Фильтры верхних частот, фильтры нижних частот, мостовые схемы для измерения емкости и индуктивности и схемы фазового сдвига являются одними из основных применений схем, которые содержат емкостные реактивные сопротивления в сочетании с индуктивностями и электрическими сопротивлениями.
В стереосистемах некоторые динамики поставляются с отдельными динамиками. вуфер (больше) для низких частот и твитер или небольшой рог для высоких частот. Это улучшает производительность и качество звука.
Это улучшает производительность и качество звука.
В них используются конденсаторы, которые предотвращают попадание низких частот в высокочастотный динамик, а в низкочастотном динамике добавлен индуктор, чтобы избежать высокочастотных сигналов, поскольку индуктивность имеет реактивное сопротивление, пропорциональное частоте: XL = 2πfL.
Катушка
Катушка индуктивности представляет собой металлический или ферритный сердечник, на который намотано несколько витков медного провода. Элемент обладает следующими свойствами:
- За счет индуктивности ограничивается скорость изменения токов.
- С увеличением частоты тока катушка способна увеличить свое сопротивление (скин-эффект).
- Создает магнитное поле.
- Увеличивает и накапливает напряжение.
- Создает сдвиг фаз переменного тока.
- Пропорционально скорости движения тока создает ЭДС самоиндукции.
Все эти свойства находят применение при разработке радиоприемных устройств, генераторов частоты, тестеров, магнитометров и других видов сложного оборудования.
Конструкция и разновидности
Все типы катушек индуктивности имеют одинаковую конструкцию, независимо от области их использования. Особенности, внесенные для получения индивидуальных параметров, влияют на тип детали.
- Соленоид. Компонент с увеличенной общей длиной обмоточного провода. Обмотка больше диаметра детали.
- Тороидальная. В такой катушке соленоид выполнен в форме «тора».
- Многослойный тип, имеет несколько рядов обмотки.
- Секционированная. Обмотка имеет несколько разделенных секций, иногда из провода разного сечения. Наиболее известной катушкой этого типа является трансформатор или дроссель.
- Универсальная, может совмещать сразу несколько вариантов обмотки.
Независимо от конструкции, все катушки работают по одному и тому же принципу.
Индуктивность
Индуктивностью катушки является способность к накапливанию электричества. Этот параметр зависит от:
- Числа витков.
- Сечения и длины провода.

- Конструктивных особенностей детали.
- От материала, длины, диаметра и формы сердечника.
- От расстояния между витками.
- Наличия экрана.
В радиоэлектронике не принято указывать значение индуктивности. Производители маркируют детали числом витков и указывают тип сердечника.
Замер сопротивления и формула расчета
Замерить активное сопротивление катушки индуктивности можно только в обесточенном виде. Делается это при помощи мультиметра.
- Мультиметр надо перевести в режим омметра.
- Красный измерительный щуп соединить с первым выходом катушки.
- Черный измерительный щуп соединить со вторым выходом.
- Прибор покажет только активное сопротивление обмотки.
Будет интересно➡ Что такое УЗО?
При помощи тестера можно определить только целостность витков. Если элемент включен в цепь под напряжением, то величину сопротивления находят за счет простого вычисления по формуле: Z=U/I.
Для расчета по этой формуле, при помощи тестера определяют сначала величину тока (I) и напряжения (U). Активное сопротивление измеряется в Омах.
Активное сопротивление измеряется в Омах.
Зная формулу расчета активного и индуктивного сопротивления, полное сопротивление элемента может быть найдено с помощью формулы:
Z= 2×(R×R+XL×XL)
В этом выражении R является активным сопротивлением, а XL — индуктивным.
Как рассчитать емкостное реактивное сопротивление
Рассмотрим пример расчета емкостного реактивного сопротивления: предположим, что конденсатор 6 мкФ подключен к розетке переменного тока с напряжением 40 В и частотой F 60 Гц.
Для определения емкостного реактивного сопротивления используется определение, данное в начале. Угловая частота ω определяется как:
Будет интересно➡ Что понимается под напряжением прикосновения?
ω = 2πf = 2π x 60 Гц = 377 с-1
Затем этот результат подставляется в определение:
ИксC = 1 / ωC = 1 / (377 с-1х 6 х10 -6 F) = 442,1 Ом
Теперь посмотрим на амплитуду тока, циркулирующего в цепи. Поскольку источник предлагает напряжение амплитудой VC = 40 В, мы используем соотношение между емкостным реактивным сопротивлением, током и напряжением для вычисления амплитуды тока или максимального тока:
яC = VC / ИКСC = 40 В / 442,1 Ом = 0,09047 А = 90,5 м А.
Если частота становится очень большой, емкостное реактивное сопротивление становится небольшим, но если частота становится равной 0 и у нас есть постоянный ток, реактивное сопротивление стремится к бесконечности.
Активное сопротивление катушки
Активное сопротивление обуславливается омической характеристикой проводов обмотки. При работе на низких частотах, омическое сопротивление не зависит от частоты. В мощных устройствах необходимо учитывать эффект близости, который заключается в том, что токи и образуемое ими магнитное поле вызывают вытеснение тока в проводах соседних витков. В результате, снижается эффективное используемое сечение провода и растет его омическое сопротивление.
Обратите внимание! На высоких частотах проявляется скин-эффект, который заключается в том, что ток вытесняется в поверхностные слои провода. В результате этого снижается используемое сечение кабеля. Для снижения скин-эффекта вместо одного проводника используют жгут из нескольких более тонких – литцендрат, либо поверхность провода покрывают слоем серебра, поскольку оно обладает наименьшим удельным сопротивлением.
Скин-эффект
В мощных электромагнитных системах (ускорители частиц) для снижения активного сопротивления, используется свойство сверхпроводимости – полное исчезновение сопротивления при охлаждении некоторых материалов ниже критической температуры.
Провод литцендрат
Во многих случаях применения катушек индуктивности следует учитывать влияние активного сопротивления обмоток. Данный параметр может отрицательно влиять не только путем снижения добротности, но и вызывать повышенный нагрев проводников обмоток в том случае, когда устройство работает с большими токами.
Емкостная проводимость линий
Электрические линии, кроме активного и индуктивного сопротивлений, характеризуются и емкостной проводимостью, которая обусловлена емкостью между проводами и между проводам и землей.
Величину рабочей емкости в трехфазной воздушной линии приближенно можно определить по формуле:
Из данной формулы видно, что рабочая емкость будет увеличиваться с увеличением сечения проводов и уменьшением расстояния между ними. Поэтому при равных сечениях токоведущих частей линии низкого напряжения имеют большую рабочую емкость, чем линии высокого напряжения. В следствии небольших расстояний между токоведущими жилами кабеля и большей диэлектрической проницаемости изоляции по сравнению с воздухом рабочая емкость кабельной линии значительно больше, чем емкость воздушной линии.
Поэтому при равных сечениях токоведущих частей линии низкого напряжения имеют большую рабочую емкость, чем линии высокого напряжения. В следствии небольших расстояний между токоведущими жилами кабеля и большей диэлектрической проницаемости изоляции по сравнению с воздухом рабочая емкость кабельной линии значительно больше, чем емкость воздушной линии.
Емкостная проводимость одноцепной воздушной линии определяется по формуле:
Определение рабочей емкости кабельной линии по формулам, в которые входят диэлектрическая проницаемость изоляции кабеля, геометрические размеры и другие конструктивные особенности, задача не из легких, поэтому значения рабочей емкости определяют по специальным таблицам, составленным заводом изготовителем для различных марок кабелей, в зависимости от их номинального напряжения.
Емкостной ток вначале линии при холостом ходе (при отключенных электроприемниках) можно определить из формулы:
Где: U – линейное напряжение сети, В; l – длина линии, км;
Емкостные токи имеют серьезное значение в воздушных линиях с рабочим напряжением 110 кВ и выше и в кабельных линиях с напряжением выше 10 кВ.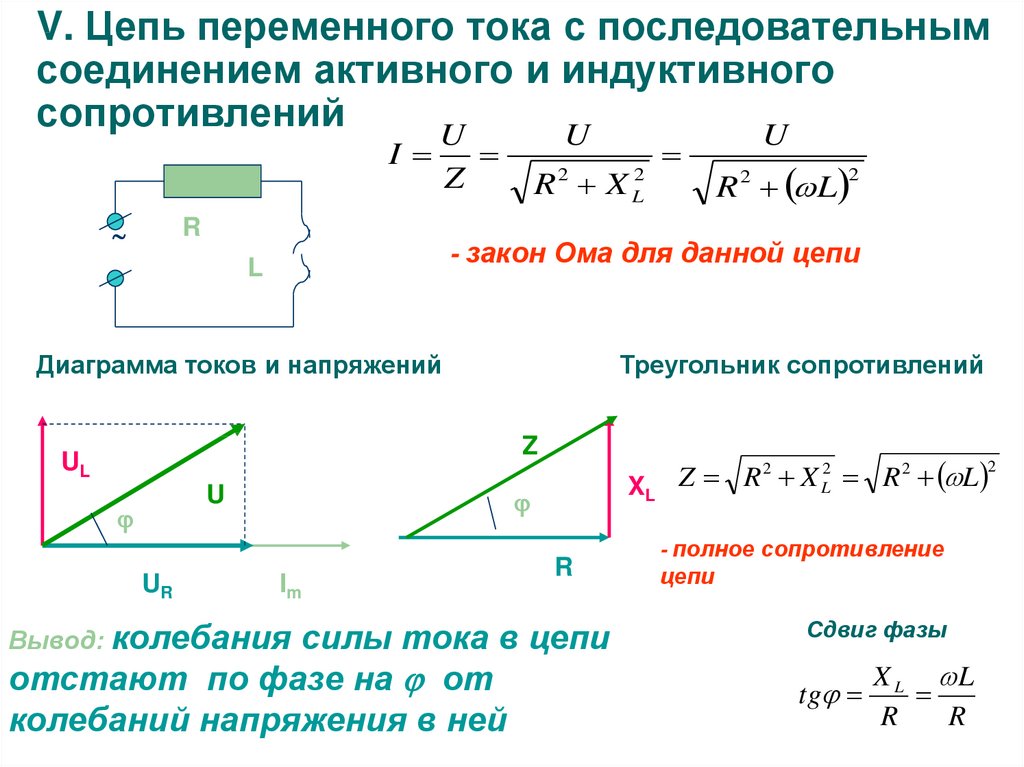 При расчете электрических сетей с напряжениями ниже, чем выше перечисленные, емкость линии могут не учитывать. Емкость токопроводящих частей линии по отношению к земле имеет значение при расчете заземляющих устройств и защиты.
При расчете электрических сетей с напряжениями ниже, чем выше перечисленные, емкость линии могут не учитывать. Емкость токопроводящих частей линии по отношению к земле имеет значение при расчете заземляющих устройств и защиты.
В сети с изолированной нейтралью величину емкостного тока однофазного замыкания на землю приближенно можно определить по формулам:
- Для воздушной линии:
- Для кабельной линии:
Определение активного сопротивления проводов
Активное сопротивлении проводов проще всего определять по справочным данным, составленным на основании ГОСТ 839-80 – «Провода неизолированные для воздушных линий электропередач» таблицы 1 – 4. Данные таблицы вы сможете найти непосредственно в самом ГОСТ, приведу лишь не которые. Пользоваться всеми известными формулами по определению активного сопротивления — не рекомендуется [Л1. с.18],связано это с тем, что действительное сечение отличается от номинального сечения, провода выпускались в разное время, по разным ГОСТ и ТУ и величины удельной проводимости (ρ) и удельного сопротивления (γ) у них разные:
где:
- γ – значение удельной проводимости для медных и алюминиевых проводов при температуре 20 °С принимается: для медных проводов – 53 м/Ом*мм2; для алюминиевых проводов – 31,7 м/Ом*мм2;
- s – номинальное сечение провода(кабеля),мм2;
- l – длина линии, м;
- ρ – значение удельного сопротивления принимается: для медных проводов — 0,017-0,018 Ом*мм2/м; для алюминиевых проводов – 0,026 — 0,028 Ом*мм2/м, см.
 таблицу 1.14 [Л2. с.30].
таблицу 1.14 [Л2. с.30].
Активные сопротивления стальных проводов математическому расчету не поддаются. Поэтому рекомендую для определения активного сопротивления использовать приложения П23 – П25 [Л1. с.80,81].
Удельное сопротивление
Еще раз проговорим, что сопротивление возникает при взаимодействии электронов с ионами кристаллической решетки. Причем, чем больше проводник, тем и сильнее само сопротивление. Поэтому можно и предположить, что толщина проводника так же влияет на R. А разные вещества по-разному проводят ток.
Исходя из всех этих знаний, можно установить следующие физические законы:
- чем длиннее проводник, тем больше его R;
- чем толще проводник, тем меньше его сопротивление;
- R проводников одинаковой длины и ширины могут быть разными, важен сам материал, по которому проходят электроны и ионы.
Удельное сопротивление (p) — это зависимость площади поперечного сечения, длины и сопротивления проводника из данного вещества.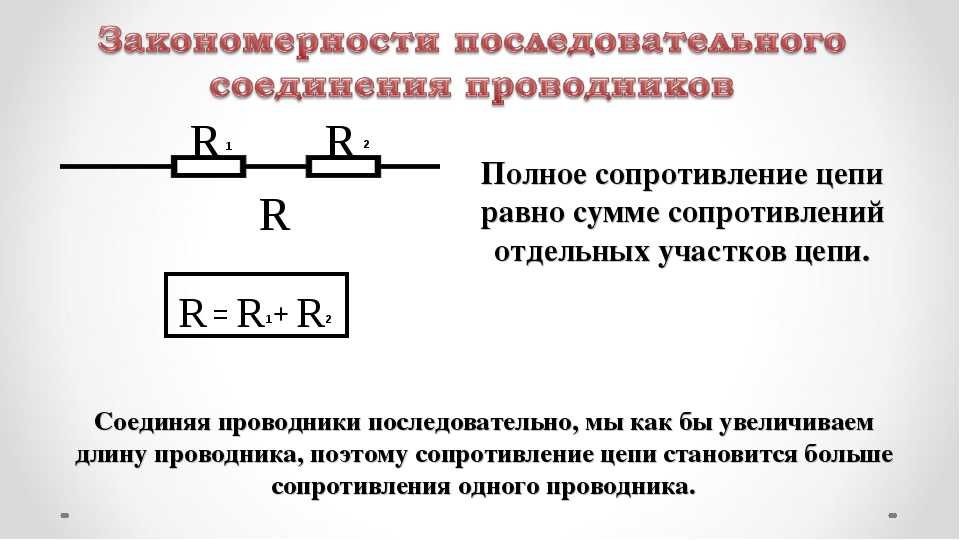 2/м
2/м
Например, удельное сопротивление алюминия 0,28 Ом, ртути 0,96 Ом, удельное сопротивление меди 0,017 Ом.
Формула: p = RS/l
Что такое активное сопротивление. Активное, реактивное и полное сопротивление цепи
Полное сопротивление, или импеданс, характеризует сопротивление цепи переменному электрическому току. Данная величина измеряется в омах. Для вычисления полного сопротивления цепи необходимо знать значения всех активных сопротивлений (резисторов) и импеданс всех катушек индуктивности и конденсаторов, входящих в данную цепь, причем их величины меняются в зависимости от того, как меняется проходящий через цепь ток. Импеданс можно рассчитать при помощи простой формулы.
Формулы
- Полное сопротивление Z = R или X L или X C (если присутствует что-то одно)
- Полное сопротивление (последовательное соединение) Z = √(R 2 + X 2) (если присутствуют R и один тип X)
- Полное сопротивление (последовательное соединение) Z = √(R 2 + (|X L — X C |) 2) (если присутствуют R, X L , X C)
- Полное сопротивление (любое соединение) = R + jX (j – мнимое число √(-1))
- Сопротивление R = I / ΔV
- Индуктивное сопротивление X L = 2πƒL = ωL
- Емкостное сопротивление X C = 1 / 2πƒL = 1 / ωL
Шаги
Часть 1
Вычисление активного и реактивного сопротивлений
Импеданс обозначается символом Z и измеряется в омах (Ом). Вы можете измерить импеданс электрической цепи или отдельного элемента. Импеданс характеризует сопротивление цепи переменному электрическому току. Есть два типа сопротивления, которые вносят вклад в импеданс:
Вы можете измерить импеданс электрической цепи или отдельного элемента. Импеданс характеризует сопротивление цепи переменному электрическому току. Есть два типа сопротивления, которые вносят вклад в импеданс:
- Активное сопротивление (R) зависит от материала и формы элемента. Наибольшим активным сопротивлением обладают резисторы, но и другие элементы цепи обладают небольшим активным сопротивлением.
- Реактивное сопротивление (X) зависит от величины электромагнитного поля. Наибольшим реактивным сопротивлением обладают катушки индуктивности и конденсаторы.
Сопротивление – это фундаментальная физическая величина, описываемая законом Ома: ΔV = I * R. Эта формула позволит вам вычислить любую из трех величин, если вы знаете две другие. Например, чтобы вычислить сопротивление, перепишите формулу так: R = I / ΔV. Вы также можете при помощи мультиметра.
- ΔV – это напряжение (разность потенциалов), измеряемое в вольтах (В).
- I – сила тока, измеряемая в амперах (А).

- R – это сопротивление, измеряемое в омах (Ом).
Реактивное сопротивление имеет место только в цепях переменного тока. Как и активное сопротивление, реактивное сопротивление измеряется в омах (Ом). Есть два типа реактивного сопротивления:
Вычислите индуктивное сопротивление. Это сопротивление прямо пропорционально быстроте изменения направления тока, то есть частоты тока. Эта частота обозначается символом ƒ и измеряется в герцах (Гц). Формула для расчета индуктивного сопротивления: X L = 2πƒL , где L – индуктивность, измеряемая в генри (Гн).
Вычислите емкостное сопротивление. Это сопротивление обратно пропорционально быстроте изменения направления тока, то есть частоты тока. Формула для вычисления емкостного сопротивления: X C = 1 / 2πƒC . С – это емкость конденсатора, измеряемая в фарадах (Ф).
- Вы можете .
- Эту формулу можно переписать так: X C = 1 / ωL (объяснения см.
 выше).
выше).
Часть 2
Вычисление полного сопротивления
Если цепь состоит исключительно из резисторов, то импеданс вычисляется следующим образом. Сначала измерьте сопротивление каждого резистора или посмотрите значения сопротивления на схеме цепи.
- Если резисторы соединены последовательно, то полное сопротивление R = R 1 + R 2 + R 3 …
- Если резисторы соединены параллельно, то полное сопротивление R = 1 / R 1 + 1 / R 2 + 1 / R 3 …
Сложите одинаковые реактивные сопротивления. Если в цепи присутствуют исключительно катушки индуктивности или исключительно конденсаторы, то полное сопротивление равно сумме реактивных сопротивлений. Вычислите его следующим образом:
- Последовательное соединение катушек: X total = X L1 + X L2 + …
- Последовательное соединение конденсаторов: C total = X C1 + X C2 + …
- Параллельное соединение катушек: X total = 1 / (1/X L1 + 1/X L2 .
 ..)
..) - Параллельное соединение конденсаторов: C total = 1 / (1/X C1 + 1/X C2 …)
Активное сопротивление зависит от материала, сечения и температуры. Активное сопротивление обусловливает тепловые потери проводов и кабелей. Определяется материалом токоведущих проводников и площадью их сечения.
Различают сопротивление проводника постоянному току (омическое) и переменному току (активное). Активное сопротивление больше активного (R а > R ом) из-за поверхностного эффекта. Переменное магнитное поле внутри проводника вызывает противоэлектродвижущую силу, благодаря которой происходит перераспределение тока по сечению проводника. Ток из центральной его части вытесняется к поверхности. Таким образом, ток в центральной части провода меньше, чем у поверхности, то есть сопротивление провода возрастает по сравнению с омическим. Поверхностный эффект резко проявляется при токах высокой частоты, а также в стальных проводах (из-за высокой магнитной проницаемости стали).
Для ЛЭП, выполненных из цветного металла, поверхностный эффект на промышленных частотах незначителен. Следовательно, R а ≈ R ом.
Обычно влиянием колебания температуры на R а проводника в расчётах пренебрегают. Исключение составляют тепловые расчеты проводников. Пересчет величины сопротивления выполняют по формуле:
где R 20 – активное сопротивление при температуре 20 о;
текущее значение температуры.
Активное сопротивление зависит от материала проводника и сечения:
где ρ –удельное сопротивление, Ом мм 2 /км;
l – длина проводника, км;
F – сечение проводника, мм 2 .
Сопротивление одного километра проводника называют погонным сопротивлением:
где удельная проводимость материала проводника, км См/мм 2 .
Для меди γ Cu =53×10 -3 км См/мм2 , для алюминия γ Al =31.7×10 -3 км См/мм2 .
На практике значение r 0 определяют по соответствующим таблицам, где они указаны для t 0 =20 0 С.
Величина активного сопротивления участка сети рассчитывается:
R = r 0 ×l .
Активное сопротивление стальных проводов намного больше омического из-за поверхностного эффекта и наличия дополнительных потерь на гистерезис (перемагничивание) и от вихревых токов в стали:
r 0 = r 0пост + r 0доп,
где r 0пост – омическое сопротивление одного километра провода;
r 0доп – активное сопротивление, которое определяется переменным магнитным полем внутри проводника, r 0доп = r 0поверх.эф + r 0гистер. + r 0вихр.
Изменение активного сопротивления стальных проводников показано на рисунке 4.1.
При малых величинах тока индукция прямо пропорциональна току. Следовательно, r 0 увеличивается. Затем наступает магнитное насыщение: индукция и r 0 практически не изменяются. При дальнейшем увеличении тока r 0 уменьшается из-за снижения магнитной проницаемости стали (m ).
Сопротивление, оказываемое проводником проходящему на нему переменному току, называется активным сопротивлением .
Если какой-либо потребитель не содержит в себе индуктивности и емкости (лампочка накаливания, нагревательный прибор), то он будет являться для переменного тока также активным сопротивлением.
Активное сопротивление зависит от частоты переменного тока, возрастая с ее увеличением.
Однако многие потребители обладают индуктивными и емкостными свойствами при прохождении через них переменного тока. К таким потребителям относятся трансформаторы, дроссели, электромагниты, конденсаторы, различного рода провода и многие другие.
При прохождении через них переменного тока необходимо учитывать не только активное, но и реактивное сопротивление , обусловленное наличием, в потребителе индуктивных и емкостных свойств его.
Активное сопротивление определяет действительную часть импеданса:
Где — импеданс, — величина активного сопротивления, — величина реактивного сопротивления, — мнимая единица.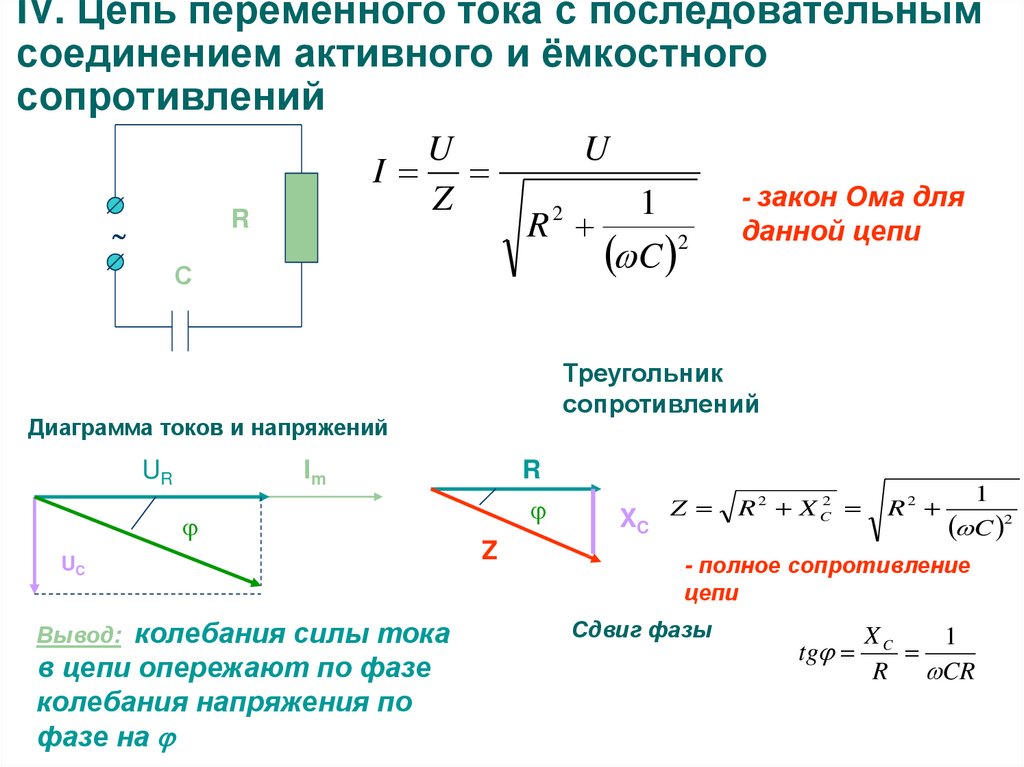
Активное сопротивление — сопротивление электрической цепи или её участка, обусловленное необратимыми превращениями электрической энергии в другие виды энергии(в тепловую энергию)
Реакти́вное сопротивле́ние — электрическое сопротивление, обусловленное передачей энергии переменным током электрическому или магнитному полю (и обратно).
Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений:
Величина полного реактивного сопротивления
Индуктивное сопротивление () обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи.
Ёмкостное сопротивление ().
Здесь — циклическая частота
Полное сопротивление цепи при переменном токе:
| z = | √ | r 2 + x 2 | = | √ | r 2 +(x L −x C) 2 |
Билет №12.
1. 1) Согласование генератора с нагрузкой — обеспечение требуемой величины активного эквивалентного сопротивления нагрузки генераторной лампы, R э, при всех возможных значениях входного сопротивления антенного фидера, которое зависит от его волнового сопротивления и коэффициента бегущей волны (КБВ)
Согласование (в электронике) сводится к правильному выбору сопротивлений генератора (источника), линии передачи и приёмника (нагрузки).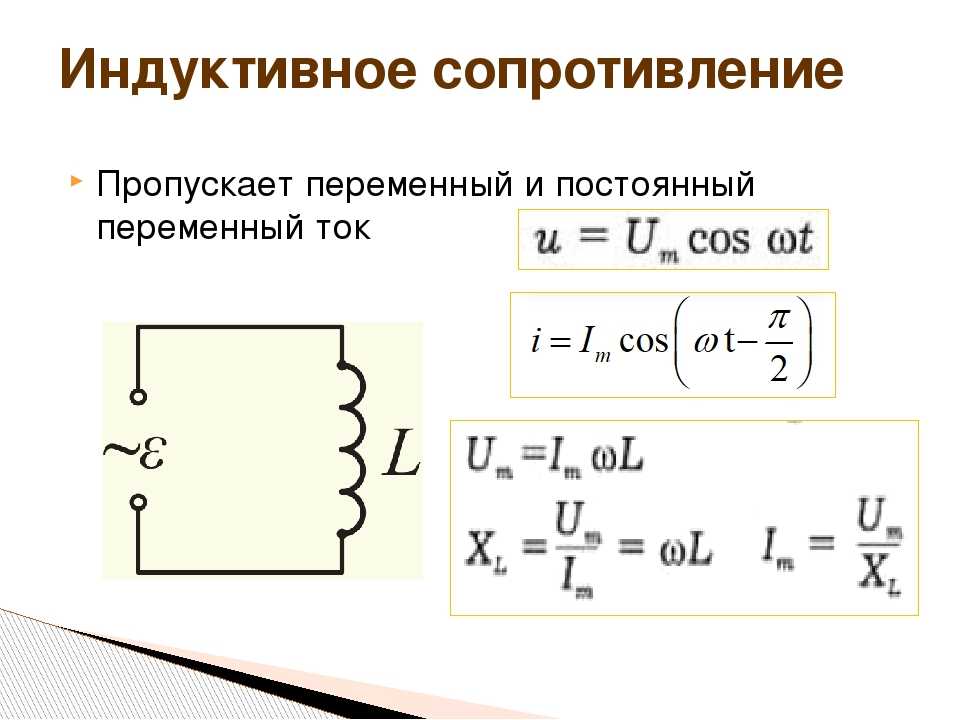 Идеального Согласование (в электронике) между линией и нагрузкой можно достичь при равенстве волнового сопротивления линии r полному сопротивлению нагрузки Zh = RH + j ХН, или при RH= r и XH= 0, где RH -активная часть полного сопротивления, XH — его реактивная часть. В этом случае в передающей линии устанавливается режим бегущих волн и характеризующий их коэффициент стоячей волны (КСВ) равен 1. Для линии с пренебрежимо малыми потерями электрической энергии Согласование и, благодаря ему, максимально эффективная передача энергии из генератора в нагрузку достигаются при условии, что полные сопротивления генератора Zr и нагрузки ZH являются комплексно-сопряжёнными, т. е. Zr = Z*H, или Rr = r = R Н =Xr- XH. В этом случае реактивное сопротивление цепи равно нулю, и соблюдаются условия резонанса, способствующие повышению эффективности работы радиотехнических систем (улучшается использование частотных диапазонов, повышается помехозащищенность, снижаются частотные искажения радиосигналов и т.
Идеального Согласование (в электронике) между линией и нагрузкой можно достичь при равенстве волнового сопротивления линии r полному сопротивлению нагрузки Zh = RH + j ХН, или при RH= r и XH= 0, где RH -активная часть полного сопротивления, XH — его реактивная часть. В этом случае в передающей линии устанавливается режим бегущих волн и характеризующий их коэффициент стоячей волны (КСВ) равен 1. Для линии с пренебрежимо малыми потерями электрической энергии Согласование и, благодаря ему, максимально эффективная передача энергии из генератора в нагрузку достигаются при условии, что полные сопротивления генератора Zr и нагрузки ZH являются комплексно-сопряжёнными, т. е. Zr = Z*H, или Rr = r = R Н =Xr- XH. В этом случае реактивное сопротивление цепи равно нулю, и соблюдаются условия резонанса, способствующие повышению эффективности работы радиотехнических систем (улучшается использование частотных диапазонов, повышается помехозащищенность, снижаются частотные искажения радиосигналов и т. п.). Оценку качества Согласование (в электронике) производят, измеряя коэффициент отражения и КСВ. Практически Согласование (в электронике) считают оптимальным, если в рабочей полосе частот КСВ не превышает 1,2-1,3 (в измерительных приборах 1,05). В отдельных случаях косвенными показателями Согласование (в электронике) могут служить реакции параметров генератора (частоты, мощности, уровня шумов) на изменение нагрузки, наличие электрических пробоев в линии, разогрев отдельных участков линии.
п.). Оценку качества Согласование (в электронике) производят, измеряя коэффициент отражения и КСВ. Практически Согласование (в электронике) считают оптимальным, если в рабочей полосе частот КСВ не превышает 1,2-1,3 (в измерительных приборах 1,05). В отдельных случаях косвенными показателями Согласование (в электронике) могут служить реакции параметров генератора (частоты, мощности, уровня шумов) на изменение нагрузки, наличие электрических пробоев в линии, разогрев отдельных участков линии.
При таком режиме работы в приёмнике выделяется наибольшая мощность, равная половине мощности источника. В этом случае К.П.Д. =0,5. Такой режим используется в измерительных цепях, устройствах средств связи.
При передаче больших мощностей, например по высоковольтным линиям электропередач, работа в согласованном режиме, как правило, недопустима.
Сопротивление одного и того же проводника для переменного тока будет больше, чем для постоянного.
Это объясняется явлением так называемого поверхностного эффекта, заключающегося в том, что переменный ток вытесняется от центральной части проводника к периферийным слоям. В результате плотность тока во внутренних слоях будет меньше, чем в наружных. Таким образом, при переменном токе сечение проводника используется как бы не полностью. Однако при частоте 50 Гц различие в сопротивлениях постоянному и переменному токам незначительно и практически им можно пренебречь.
В результате плотность тока во внутренних слоях будет меньше, чем в наружных. Таким образом, при переменном токе сечение проводника используется как бы не полностью. Однако при частоте 50 Гц различие в сопротивлениях постоянному и переменному токам незначительно и практически им можно пренебречь.
Сопротивление проводника постоянному току называют омическим, а переменному току –активным сопротивлением.
Омическое и активное сопротивление зависят от материала (внутренней структуры), геометрических размеров и температуры проводника. Кроме того, в катушках со стальным сердечником на величину активного сопротивления влияют потери в стали (далее для самоподготовки).
К активным сопротивлениям относят электрические лампы накаливания, электрические печи сопротивления, различные нагревательные приборы, реостаты и провода, где электрическая энергия практически почти целиком превращается в тепловую.
Если цепь переменного тока содержит только резистор R лампа накаливания, электронагревательный прибор и т. д.), к которому приложено переменное синусоидальное напряжение и (рис. 1-5, а):
д.), к которому приложено переменное синусоидальное напряжение и (рис. 1-5, а):
то ток i в цепи будет определяться значением этого сопротивления:
где — амплитуда тока; при этом ток i и напряжение и совпадают по фазе. Обе эти величины, как видно, можно изобразить на временной (рис. 1-5, б) и векторной (1-5, в) диаграммах. Теперь установим, как изменяется мощность в любой момент времени — мгновенная мощность, характеризующая собой скорость преобразования электрической энергии в другие виды энергии в данный момент времени
где IU — произведение действующих значений тока и напряжения.
Из полученного следует, что мощность в течение периода остается положительной и пульсирует с удвоенной частотой. Графически это можно представить так, как показано на рисунке 1-6. В этом случае электрическая энергия превращается необратимо, например, в теплоту независимо от направления тока в цепи.
Кроме мгновенного значения мощности различают еще среднюю мощность за период:
но так как второй интеграл равен нулю, то окончательно имеем:
Средняя за период мощность переменного тока называется активной мощностью, а соответствующее ей сопротивление — активным.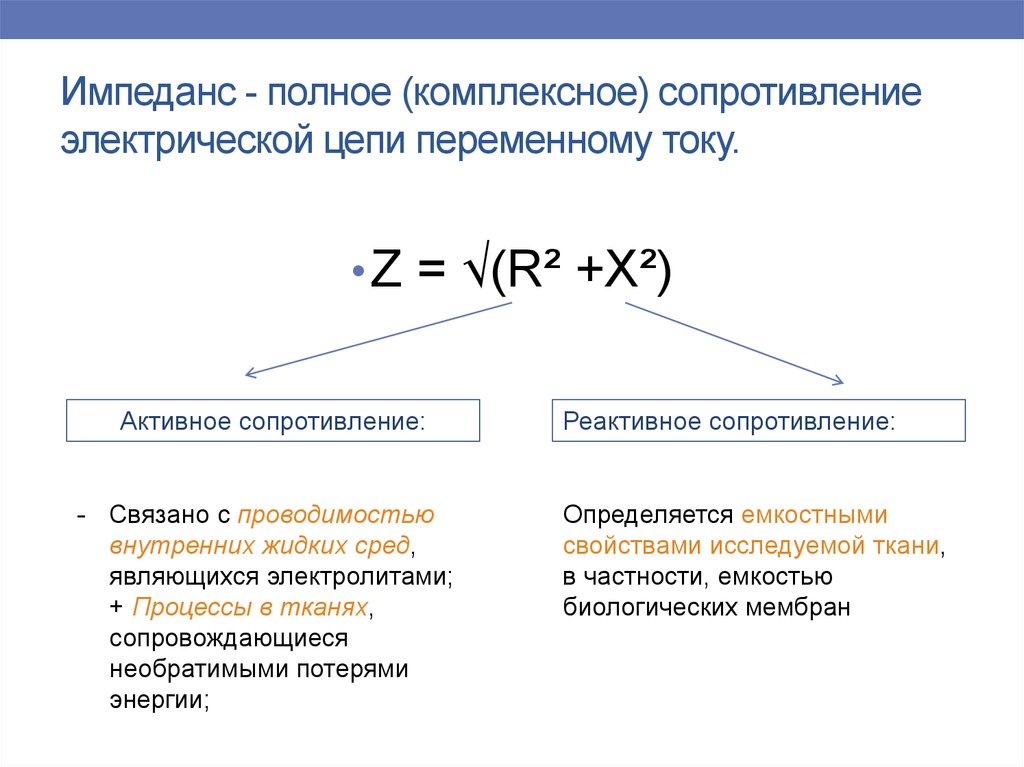
Средняя мощность и активное сопротивление связаны с безвозвратным преобразованием электрической энергии в другие виды энергии. Активное сопротивление электрической цепи не сводится только к
сопротивлению проводников, в которых электрическая энергия превращается в теплоту. Это понятие значительно шире, так как средняя мощность электрической цепи равна сумме мощностей всех видов энергии, полученной из электрической, на всех участках цепи (теплота, механическая и др.).
Из полученных соотношений следует, что
которое является математической записью закона Ома для цепи переменного тока с активным сопротивлением.
Как определить импеданс цепи
Импеданс влияет на то, как сигналы распространяются через плату, как происходит обмен питанием между компонентами и как сигналы просачиваются в нежелательные участки печатной платы. Существует несколько методов определения импеданса цепи, но они не всегда дают реалистичные результаты, если вы не включите в свои модели соответствующие паразитные элементы.
Полное сопротивление цепи
Полное сопротивление — это характеристика цепи переменного тока, которая может изменяться в зависимости от рабочей частоты. Обычно обозначается Z = R – j/ ωC + jωL, где ω= 2πf.
В чем разница между импедансом и сопротивлением?
Основное различие между сопротивлением и импедансом заключается в том, что сопротивление противостоит протеканию как постоянного, так и переменного тока, тогда как импеданс противостоит переменному току. Импеданс не имеет значения в цепи постоянного тока.
Некоторые ключевые отличия приведены в таблице ниже:
| Сопротивление | Импеданс |
|---|---|
| Обозначается буквой «R» | Обозначается буквой «Z» |
| Не зависит от частоты питания. | В основном зависит от частоты питания. |
Два или более сопротивлений, соединенных последовательно, могут быть добавлены арифметически. | Для суммирования импедансов необходимо выполнить сложение векторов. |
| Ток через сопротивление всегда совпадает по фазе с напряжением на нем. | Ток и напряжение не совпадают по фазе. Разность фаз зависит от индуктивности или емкости, присутствующих в импедансе. |
Почему согласование импеданса важно для печатных плат?
На высоких частотах дорожки на плате действуют как линии передачи с определенными значениями импеданса в каждой точке. Согласование импеданса гарантирует, что он остается постоянным в каждой точке на протяжении всей трассы. Колебания импеданса в линии передачи приводят к отражению сигнала, нарушающему целостность сигнала. Контролируемый импеданс гарантирует, что сигналы не ухудшаются по мере их распространения по трассе.
Факторы, влияющие на контролируемый импеданс
Импеданс дорожки определяется физическими размерами дорожки (шириной и толщиной дорожки), диэлектрической проницаемостью и расстоянием до опорной плоскости (толщиной диэлектрика) материала платы.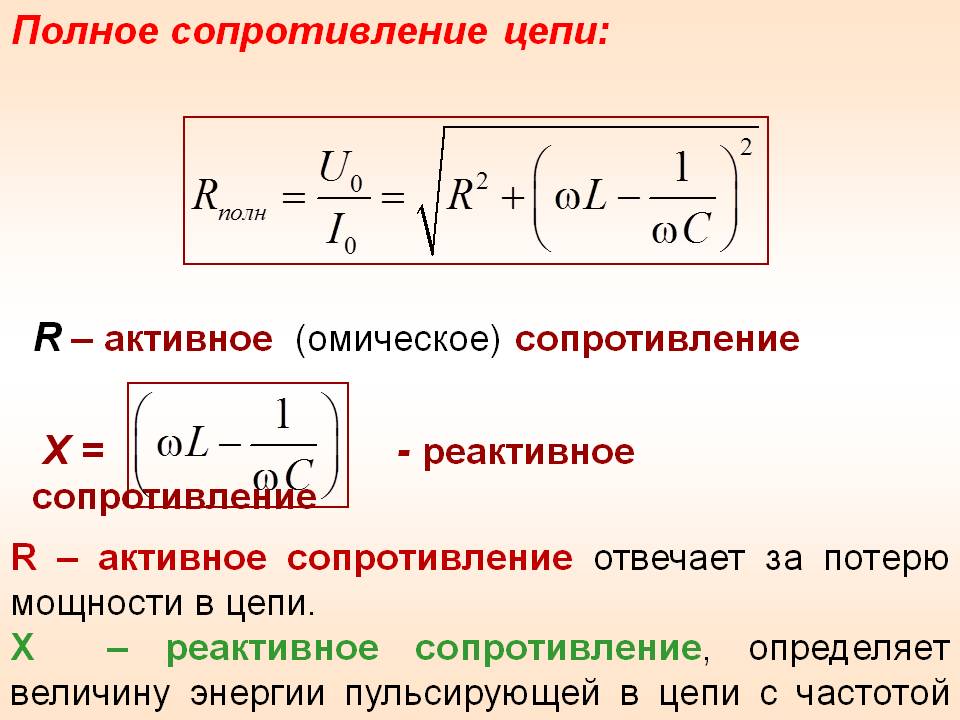 Оно колеблется между 25 и 125 Ом. На импеданс печатной платы влияют следующие факторы:
Оно колеблется между 25 и 125 Ом. На импеданс печатной платы влияют следующие факторы:
Факторы, влияющие на импеданс дорожки печатной платы
- Ширина (w) и толщина (T) медной сигнальной дорожки (вверху и внизу)
- Толщина (H) материала сердечника или препрега с обеих сторон медной дорожки
- Диэлектрическая проницаемость (ER) материала сердечника и препрега
- Расстояние от других медных элементов
Контролируемый импеданс необходим для высокоскоростных приложений, таких как процессоры сигналов, телекоммуникации и радиочастотная передача.
Что определяет полное сопротивление печатной платы?
Полное сопротивление цепи определяется расположением компонентов. Резисторы, конденсаторы и катушки индуктивности являются одними из основных элементов схемы. Резисторы препятствуют протеканию тока, и значение сопротивления не зависит от частоты питания. Принимая во внимание, что конденсаторы и катушки индуктивности имеют реактивное сопротивление, которое зависит от частоты входного сигнала. В идеальном мире реактивное сопротивление конденсатора должно быть обратно пропорционально угловой частоте сигнала. Катушки индуктивности должны иметь реактивное сопротивление, прямо пропорциональное угловой частоте сигнала.
Принимая во внимание, что конденсаторы и катушки индуктивности имеют реактивное сопротивление, которое зависит от частоты входного сигнала. В идеальном мире реактивное сопротивление конденсатора должно быть обратно пропорционально угловой частоте сигнала. Катушки индуктивности должны иметь реактивное сопротивление, прямо пропорциональное угловой частоте сигнала.
Помимо указанных выше параметров, импеданс цепи зависит от подложки печатной платы и внутренних проводящих слоев. Изолятор вместе с внутренними слоями создает паразитную емкость и индуктивность. Эти паразитные элементы вызывают перекрестные помехи и влияют на общий импеданс цепи. Теперь мы увидим несколько факторов, от которых зависит импеданс.
Руководство по проектированию с регулируемым импедансом
6 глав — 56 страниц — 60 минут чтения
Полное сопротивление линии передачи
Характеристическое сопротивление трассы
Полное сопротивление линии передачи в основном зависит от ее характеристического сопротивления, которое, по сути, представляет собой полное сопротивление линии передачи при полной изоляции. Другими показателями, используемыми для количественной оценки импеданса линии передачи, являются импедансы четной и нечетной мод. Четный и нечетный режимы — это два основных режима распространения сигнала по парной линии передачи.
Другими показателями, используемыми для количественной оценки импеданса линии передачи, являются импедансы четной и нечетной мод. Четный и нечетный режимы — это два основных режима распространения сигнала по парной линии передачи.
Нечетная мода – это полное сопротивление линии передачи, когда две дорожки в паре работают по-разному (сигналы с одинаковой амплитудой и противоположной полярностью).
Четный режим – это импеданс линии передачи, когда две дорожки в паре работают равномерно (сигналы с одинаковой амплитудой и направлением).
Полное сопротивление линии передачи также зависит от того, как расположены дорожки относительно друг друга. Две дорожки, расположенные близко друг к другу, испытывают индуктивную и емкостную связь. Эта связь обычно приводит к перекрестным помехам, а также изменяет импеданс на каждой линии.
Чтобы понять, как уменьшить рассогласование импеданса на трассе печатной платы, см. как ограничить скачки импеданса и отражение сигнала в линиях передачи печатной платы.
Полное сопротивление сети подачи электроэнергии
На более низких частотах сеть подачи энергии будет иметь емкостное сопротивление, снижающее сопротивление шины питания, которая питает компоненты и ток обратного тока. Физическое разделение между шинами питания, дорожками и внутренними слоями определяет импеданс PDN. По мере увеличения входной частоты растет и импеданс PDN.
Импеданс PDN в зависимости от частоты. Изображение предоставлено: Cadence
Спектр импеданса полезен для определения полосы пропускания с наименьшим импедансом сети подачи энергии. Он должен оставаться ровным по всему рабочему диапазону доски. Для поддержания целостности питания платы решающее значение имеет расположение заземляющего слоя. При перемещении к заземляющему слою сигналы будут проходить по пути с наименьшим реактивным сопротивлением. Путь с наименьшим реактивным сопротивлением должен проходить непосредственно под проводниками на плате. Это гарантирует, что цепи будут иметь наименьшую индуктивность контура и будут менее восприимчивы к электромагнитным помехам.
Выбор материала платы и укладка
Укладка печатных плат с требованиями к контролируемому импедансуУкладка — это расположение материалов платы в последовательном порядке. На изображении выше показан 4-слойный стек. L1 и L4 — внешние слои, L2 и L3 — внутренние слои. Как упоминалось ранее, соседние проводящие слои в сборке платы создают паразитный эффект, влияющий на общий импеданс схемы. Несоответствие импеданса, вызванное паразитными помехами, приведет к отражениям на трассе, что в конечном итоге приведет к перекрестным помехам и проблемам с электромагнитными помехами.
Стек также выступает в качестве документации, выражающей ваши ожидания производителям. Отсутствие части информации может затруднить или сделать невозможным для производителей точное понимание требований.
Чтобы узнать об эффективной документации по контролируемому импедансу, см. Указание требований к контролируемому импедансу.
Выбор правильного материала, который наилучшим образом соответствует дизайну, является ключом к тому, чтобы избежать этих обстоятельств. Диэлектрическая проницаемость (Dk) влияет на геометрию трассы с определенным значением импеданса. Содержание смолы и толщина материала являются двумя критическими компонентами, определяющими Dk материала. Она уменьшается по мере увеличения толщины. Это означает, что чем выше содержание смолы, тем ниже значение Dk.
Диэлектрическая проницаемость (Dk) влияет на геометрию трассы с определенным значением импеданса. Содержание смолы и толщина материала являются двумя критическими компонентами, определяющими Dk материала. Она уменьшается по мере увеличения толщины. Это означает, что чем выше содержание смолы, тем ниже значение Dk.
Приведенные ниже указатели помогут разработчикам печатных плат выбрать соответствующие материалы и избежать отклонений в общем значении импеданса.
- Определите правильную толщину слоя: Более тонкие слои уменьшают площадь контура и паразитную индуктивность, увеличивая паразитную емкость. Чтобы найти подходящую толщину слоя, вы можете использовать инструменты моделирования с различными стеками слоев.
- Выбирайте материал с более низкой диэлектрической проницаемостью: Подложки с более высоким значением Dk создают большую паразитную емкость. Всегда выбирайте подложку с более низким значением Dk, особенно для высокоскоростных применений.

- Избегайте выбора субстрата с очень низким содержанием смолы: Очень низкое содержание смолы может привести к нехватке смолы, что, в свою очередь, приведет к изменению импеданса.
- Не используйте более трех разных типов препрегов в стопке. : Наличие разных типов препрегов может быть рискованным, так как увеличивает вероятность больших различий в конечной толщине. При использовании нескольких типов препрегов эффективную диэлектрическую проницаемость композиционного материала следует рассчитывать методом средневзвешенного значения.
Руководство по проектированию высокоскоростных печатных плат
8 глав — 115 страниц — 150 минут чтения
Полное сопротивление переходных отверстий
Переходные отверстия и сквозные отверстия в многослойной плате будут иметь паразитные значения между соседними проводящими элементами. Индуктивность переходного отверстия будет порядка наногенри и в основном определяется соотношением сторон. Импеданс переходных отверстий обычно составляет от 25 до 35 Ом. Следовательно, существует значительная разница между импедансами переходных отверстий и дорожек (около 50 Ом). Когда сквозное отверстие помещается на проводящие дорожки, возникает шумовая связь, вызывающая разрывы импеданса. Всегда избегайте размещения переходных отверстий между дифференциальными парами, чтобы уменьшить разрывы.
Импеданс переходных отверстий обычно составляет от 25 до 35 Ом. Следовательно, существует значительная разница между импедансами переходных отверстий и дорожек (около 50 Ом). Когда сквозное отверстие помещается на проводящие дорожки, возникает шумовая связь, вызывающая разрывы импеданса. Всегда избегайте размещения переходных отверстий между дифференциальными парами, чтобы уменьшить разрывы.
Методы определения полного сопротивления цепи
Полное сопротивление цепи можно рассчитать с помощью следующих методов.
Моделирование схемы
Блок-схема моделирования схемы Моделирование схемы — это метод, используемый для проверки функциональности конструкции платы перед ее производством. Расчет импеданса теперь включен во многие программы проектирования печатных плат. Одним из основных преимуществ здесь является то, что расчетные параметры импеданса могут быть изменены для выполнения различных симуляций. После проведения моделирования вы можете выбрать лучший дизайн для производства.
Онлайн-калькуляторы
Контролируемый импеданс или параметры трассы можно определить с помощью онлайн-калькуляторов. Хотя они и не такие подробные, как инструменты моделирования, они могут достаточно приблизить вас к тому, где для технологичности требуются лишь минимальные корректировки со стороны вашего контрактного производителя (CM).
Калькулятор импеданса Sierra Circuits использует двумерное численное решение уравнений Максвелла для линий передачи на печатных платах. Он производит данные, которые являются достаточно точными и пригодными для производства печатных плат. Инструмент оценивает параметры трассы, такие как емкость, индуктивность, задержка распространения на единицу длины и эффективная диэлектрическая проницаемость структуры.
В отличие от нашего инструмента импеданса, большинство бесплатных онлайн-калькуляторов импеданса не очень точны, потому что они основаны на эмпирических формулах и не учитывают трапециевидную форму дорожки или влияние многочисленных диэлектрических материалов.
Практический метод
Выполните следующие шаги, чтобы быстро получить приблизительное значение контролируемого импеданса.
Рассчитайте время нарастания кривой по формуле
t r = 0,35 / f max , где f max – максимальная рабочая частота.
Теперь рассчитайте максимальную длину дорожки,
l = t r x 2 дюйма/нс
Волновое сопротивление дорожки можно рассчитать по следующей формуле:
Формула для расчета волнового сопротивления печатной платы traceГде,
- εr — диэлектрическая проницаемость материала (согласно техпаспорту)
- H — высота трассы над землей
- W — ширина дорожки
- T — толщина следа
Независимо от того, как вы определяете импеданс печатной платы, вам следует сотрудничать с вашим контрактным производителем (CM), поскольку стандарты DFM и доступность материалов будут влиять на производство вашей платы. Дайте нам знать в разделе комментариев, если вам нужна помощь в разработке дизайна с контролируемым импедансом. Мы будем рады помочь вам. Проверьте наши возможности контроля импеданса, чтобы узнать больше о наших услугах. Как легко найти эквивалентное сопротивление для цепей переменного тока — Wira Electrical Это очень важно для анализа электрической цепи.
Дайте нам знать в разделе комментариев, если вам нужна помощь в разработке дизайна с контролируемым импедансом. Мы будем рады помочь вам. Проверьте наши возможности контроля импеданса, чтобы узнать больше о наших услугах. Как легко найти эквивалентное сопротивление для цепей переменного тока — Wira Electrical Это очень важно для анализа электрической цепи.
Эквивалентное полное сопротивление, исходя из его названия, означает одно полное сопротивление нескольких элементов, не влияющее на другие элементы, такие как источник напряжения и тока.
Эквивалентное полное сопротивление необходимо для анализа цепи переменного тока.
Сначала обязательно прочитайте, что такое цепь переменного тока.
Эквивалентное полное сопротивление для цепей переменного тока
Рассмотрим полное сопротивление последовательного соединения N, показанное на рисунке (1). Один и тот же ток I протекает через импедансы. Применение КВЛ вокруг петли дает
| (1) |
Figure 1. N impedances in series N impedances in series |
The equivalent impedance at the input terminals is
| (2) |
showing that the total or equivalent impedance of последовательно соединенные импедансы представляют собой сумму индивидуальных импедансов. Это похоже на последовательное соединение сопротивлений.
Если N = 2, как показано на рис. (2), ток через полное сопротивление равен
| Figure 2. Voltage division |
| (3) |
Since V 1 = Z 1 I and V 2 = Z 2 I , затем
| (4) |
, который составляет 333333.
Таким же образом мы можем получить эквивалентный импеданс и проводимость N параллельно соединенных импедансов, как показано на рисунке (3).
| Рис. 3. N сопротивлений, включенных параллельно |
Напряжение на каждом сопротивлении одинаково. Применение KCL в верхнем узле,
| (5) |
Эквивалентное сопротивление
| (6) |
, а эквивалентный допуск —
| (7) | ||||||||||||||
| (7) | ||||||||||||||
| . сумма индивидуальных допусков. Когда N = 2, как показано на рисунке (4),
the equivalent impedance becomes
Also, since V = Z eq I = I 1 Z 1 = I 2 Z 2 the currents in the impedances are
which is the текущий отдел принцип. Преобразования дельта-звезда и звезда-треугольник, которые мы применяли к резистивным цепям, также действительны для импедансов. Со ссылкой на рис. (5), формулы преобразования следующие.
Wye-delta conversion :
Преобразование треугольник-звезда:
Когда сбалансированная схема дельта-Wye, уравнения. (10) и (11) становятся
, где Z 9 9029 |
, где Z 9 9029 . 1
Как вы можете видеть в этом посте, принципы разделения напряжения, разделения тока, сокращения цепи, эквивалентности импеданса и преобразования звезда-треугольник применимы к цепям переменного тока. В следующем посте мы рассмотрим другой метод для цепей переменного тока, таких как:
- Суперпозиция
- Узловой анализ
- Анализ сетки
- Преобразование источника
- Теорема Тевенина
- Теорема Нортона.
Применение синусоидальной схемы и формулы импеданса приводит к фазовращателю и мосту переменного тока.
Читайте также: теорема суперпозиции
Примеры эквивалентного импеданса для цепей переменного тока
Для лучшего понимания рассмотрим примеры ниже:
1. Найдите входное сопротивление цепи на рисунке (6). Предположим, что схема работает при ω = 50 рад/с.
| Figure 6 |
Solution :
Let
Z 1 = Impedance of the 2 mF capacitor
Z 2 = Полное сопротивление резистора 3 Ом последовательно с конденсатором 10 мФ
Z 3 = полное сопротивление катушки индуктивности 0,2 Гн последовательно с резистором 8 Ом
Затем
Входное сопротивление равно
Hence,
2. Determine v o (t) in the circuit of Figure.(7)
| Figure 7 |
Solution :
Чтобы провести анализ в частотной области, мы должны сначала преобразовать схему домена на рис. (7) в векторную область, эквивалентную на рис. (8). Преобразование дает
(7) в векторную область, эквивалентную на рис. (8). Преобразование дает
Пусть
Z 1 = полное сопротивление резистора 60 Ом
Z 2 = полное сопротивление параллельной комбинации конденсатора 10 мФ и катушки индуктивности 5 Гн.
| Рисунок 8 |
Тогда Z 1 = 60 ω и
по домену
.3. Найти ток I в цепи рис.(9).).
| Figure 9 |
Solution :
The delta network connected to nodes a , b , and c can be converted to the Y network Рис. (10). Мы получаем импеданс Y следующим образом, используя уравнение (11):
Общий импеданс на клеммах источника равен
Требуемый ток равен
Реактивное сопротивление и импеданс – Формула
Значение импеданса. Это мера общего сопротивления цепи переменного тока току, обозначаемому буквой Z. Проще говоря, это количество цепи, препятствующей потоку изменений. Импеданс подобен сопротивлению, которое также учитывает влияние индуктивности и емкости. Единицей измерения импеданса является ом.
Это мера общего сопротивления цепи переменного тока току, обозначаемому буквой Z. Проще говоря, это количество цепи, препятствующей потоку изменений. Импеданс подобен сопротивлению, которое также учитывает влияние индуктивности и емкости. Единицей измерения импеданса является ом.
Поскольку импеданс учитывает влияние индуктивности и емкости и зависит от частоты тока, проходящего через цепь, он является более сложным, чем сопротивление. По сравнению с сопротивлением, которое постоянно независимо от частоты, импеданс зависит от частоты.
Когда дело доходит до определения реактивного сопротивления, это мера сопротивления индуктивности и емкости току. Давайте вкратце узнаем больше об этих двух терминах.
Формула импеданса
Математический символ импеданса — Z, единица измерения — ом. Это надмножество сопротивления и реактивного сопротивления вместе взятых.
В терминах фазора импеданс Z характеризуется как сумма сопротивления R и реактивного сопротивления X как:
X = R + j X
Где реактивное сопротивление X представляет собой сумму индуктивного реактивного сопротивления X\[_{L}\] и емкостного сопротивления X\[_{C}\].
X = X\[_{L}\] — X\[_{C}\]
Полное сопротивление, Z = \[\frac{V}{I}\]
В = напряжение в вольтах (В )
I = ток в амперах (А)
Z= полное сопротивление в омах (Ом)
R= сопротивление в омах (Ом)
Полное сопротивление можно разделить на две части:
Переменный ток отстает или опережает напряжение в зависимости от характера реактивной составляющей импеданса (преимущественно индуктивной или емкостной). 9{2}}\]
Импеданс (Z) цепи определяют четыре электрические величины: сопротивление (R), емкость (C), индуктивность (L) и частота (f).
Что такое реактивное сопротивление?
Мера сопротивления индуктивности и емкости току в цепи переменного тока называется реактивным сопротивлением и обозначается буквой X. Оно зависит от частоты электрических сигналов и измеряется в омах.
Реактивное сопротивление бывает двух типов:
Формула реактивного сопротивления
Полное реактивное сопротивление (X) равно разнице между двумя:
Полное реактивное сопротивление, X = X\[_{L}\]– X\[_{C}\]
a. Емкостное реактивное сопротивление X\[_{C}\]
Емкостное реактивное сопротивление X\[_{C}\]
Реактивное сопротивление, большое на низких частотах и малое на высоких частотах, известно как емкостное реактивное сопротивление ( X\[_{C}\] ). X\[_{C}\] бесконечно для устойчивого постоянного тока при нулевой частоте (f=0Hz). Это означает, что конденсатор пропускает переменный ток, но блокирует постоянный ток.
Емкостное реактивное сопротивление, X\[_{C}\] = 1/2fC
Где,
X\[_{C}\] = реактивное сопротивление в омах (Ом)
f = частота в герцах (Гц)
C = емкость в фарадах (Ф)
Например, конденсатор емкостью 1 мкФ имеет реактивное сопротивление 3,2. k для сигнала 50 Гц, но когда частота выше 10 кГц, реактивное сопротивление составляет всего 16,
b. Индуктивное реактивное сопротивление, X\[_{L}\]
Реактивное сопротивление, малое на низких частотах и большое на высоких частотах, известно как индуктивное реактивное сопротивление. X\[_{L}\] равно нулю для установившегося постоянного тока на нулевой частоте (f=0Hz). Это означает, что катушка индуктивности пропускает постоянный ток, но блокирует переменный ток.
X\[_{L}\] равно нулю для установившегося постоянного тока на нулевой частоте (f=0Hz). Это означает, что катушка индуктивности пропускает постоянный ток, но блокирует переменный ток.
Формула для расчета индуктивного сопротивления катушки:
Индуктивное сопротивление, или X\[_{L}\] является произведением 2-кратного (pi), или 6,28, частоты переменного тока в герцах, индуктивность катушки в генри.
X\[_{L}\] = 2x f x L
L = значение индуктивности катушки в генри.
Индуктивное сопротивление, X\[_{L}\] = 2fL
Где,
X\[_{L}\] = реактивное сопротивление в омах (Ом)
f = частота в герцах (Гц)
L = индуктивность в генри (Гн)
Например, дроссель 1 мГн имеет реактивное сопротивление всего 0,3 для сигнала частотой 50 Гц, но когда частота выше 10 кГц, его реактивное сопротивление равно 63 Ом.
Формула реактивного сопротивления и импеданса
Элемент в цепи постоянного тока можно легко описать, используя только его сопротивление. Сопротивление конденсатора в цепях постоянного тока считается открытым соединением, тогда как сопротивление катушки индуктивности в цепи постоянного тока будет рассматриваться как короткое соединение или нулевое сопротивление. В отличие от цепей постоянного тока видно, что в цепях переменного тока импеданс элемента представляет собой значение того, насколько элемент имеет тенденцию противодействовать протеканию тока, когда на него подается переменное напряжение. Импеданс может быть представлен в виде комплексного числа, состоящего как из действительной, так и из мнимой частей, и может быть представлен следующим образом:
Сопротивление конденсатора в цепях постоянного тока считается открытым соединением, тогда как сопротивление катушки индуктивности в цепи постоянного тока будет рассматриваться как короткое соединение или нулевое сопротивление. В отличие от цепей постоянного тока видно, что в цепях переменного тока импеданс элемента представляет собой значение того, насколько элемент имеет тенденцию противодействовать протеканию тока, когда на него подается переменное напряжение. Импеданс может быть представлен в виде комплексного числа, состоящего как из действительной, так и из мнимой частей, и может быть представлен следующим образом:
Z = R + jX
Где Z представляет импеданс
R представляет значение сопротивления
X, мнимая часть, представляет реактивное сопротивление
Видно, что сопротивление в цепи всегда будет положительным, а наблюдаемое реактивное сопротивление будет либо положительным, либо отрицательным.
Вы знаете?
Когда ток и напряжение не соответствуют друг другу, это означает наличие фазового сдвига. Например, когда вы заряжаете конденсатор, напряжение на нем равно нулю. Но ток максимальный. Когда конденсатор заряжен, напряжение будет максимальным, а ток минимальным. Зарядка и разрядка происходят непрерывно с переменным током, где ток достигает максимума незадолго до того, как напряжение достигает максимума, поэтому это называется опережающим напряжением по току.
Например, когда вы заряжаете конденсатор, напряжение на нем равно нулю. Но ток максимальный. Когда конденсатор заряжен, напряжение будет максимальным, а ток минимальным. Зарядка и разрядка происходят непрерывно с переменным током, где ток достигает максимума незадолго до того, как напряжение достигает максимума, поэтому это называется опережающим напряжением по току.
Соотношения реактивного сопротивления, импеданса и мощности в цепях переменного тока Физика
До этого момента индуктивность и емкость объяснялись отдельно в цепях переменного тока. Остальная часть этой части будет посвящена комбинации индуктивности, емкости и сопротивления в цепях переменного тока.
Для объяснения различных свойств цепей переменного тока будет использоваться последовательная цепь RLC. Рисунок (4) представляет собой принципиальную схему последовательной цепи RLC. Символ E, показанный на рис. 4-4, является общим символом, используемым для обозначения источника переменного напряжения.
Цепь серии RLC
РЕАКТИВНОЕ СОПРОТИВЛЕНИЕЭффект индуктивного реактивного сопротивления заключается в том, что ток отстает от напряжения, в то время как эффект емкостного реактивного сопротивления заставляет ток опережать напряжение. Следовательно, поскольку индуктивное сопротивление и емкостное сопротивление прямо противоположны по своим эффектам, каков будет результат их объединения? Нетрудно заметить, что чистый эффект представляет собой тенденцию компенсировать друг друга, при этом совокупный эффект равен разнице между их значениями. Эта результирующая называется РЕАКТИВНОСТЬ; обозначается символом X; и выражается уравнением X = X L – X C или X = X C – X L . Таким образом, если цепь содержит 50 Ом индуктивного сопротивления и 25 Ом емкостного сопротивления последовательно, чистое реактивное сопротивление, или X, составляет 50 Ом — 25 Ом или 25 Ом индуктивного сопротивления.
Для практического примера предположим, что у вас есть цепь, содержащая катушку индуктивности 100 мкГн последовательно с конденсатором 0,001 мкФ и работающая на частоте 4 МГц. Каково значение чистого реактивного сопротивления, или X?
Каково значение чистого реактивного сопротивления, или X?
Дано f = 4 МГц, L = 100 мкГн, C = 0,001 мкФ
Решение: x L = 2πfl
= 6,28 x 4 МГц x 100 мкН = 2512 ω
x C = 1/2πFC
= 1/6,28 x 4 МГц x 0,001 мкф
= 1/26,28 x 4 МГц x 0,001 м.= 39,8 Ом
X = X L – X C
X = 24722 Ом (индуктивная) цепь переменного тока. Однако есть еще один фактор, сопротивление, которое также препятствует протеканию тока. Поскольку на практике цепи переменного тока, содержащие реактивное сопротивление, также содержат сопротивление, они объединяются, чтобы противостоять протеканию тока. Это комбинированное сопротивление сопротивления и реактивного сопротивления называется ИМПЕДАНСОМ и обозначается символом Z.
Поскольку значения сопротивления и реактивного сопротивления даны в омах, на первый взгляд может показаться возможным определить значение импеданса, просто сложив их вместе. Однако сделать это так просто не получится. Вы знаете, что в цепи переменного тока, содержащей только сопротивление, ток и напряжение будут идти в такт (то есть в фазе) и достигать своих максимальных значений в один и тот же момент. Вы также знаете, что в цепи переменного тока, содержащей только реактивное сопротивление, ток либо опережает, либо отстает от напряжения на четверть периода или на 90 градусов. Следовательно, напряжение в чисто реактивной цепи будет отличаться по фазе на 90 градусов от напряжения в чисто резистивной цепи, и по этой причине реактивное сопротивление и сопротивление объединяются простым их сложением.
Вы знаете, что в цепи переменного тока, содержащей только сопротивление, ток и напряжение будут идти в такт (то есть в фазе) и достигать своих максимальных значений в один и тот же момент. Вы также знаете, что в цепи переменного тока, содержащей только реактивное сопротивление, ток либо опережает, либо отстает от напряжения на четверть периода или на 90 градусов. Следовательно, напряжение в чисто реактивной цепи будет отличаться по фазе на 90 градусов от напряжения в чисто резистивной цепи, и по этой причине реактивное сопротивление и сопротивление объединяются простым их сложением.
При объединении реактивного сопротивления и сопротивления значение импеданса будет больше любого из них. Верно также и то, что ток не будет идти в ногу с напряжением и не будет отличаться по фазе точно на 90 градусов от напряжения, а будет где-то между совпадающим и 90 градусов.0-градусные условия отклонения от шага. Чем больше реактивное сопротивление по сравнению с сопротивлением, тем ближе разность фаз будет приближаться к 90°. Чем больше сопротивление по сравнению с реактивным сопротивлением, тем ближе разность фаз будет приближаться к нулю градусов.
Чем больше сопротивление по сравнению с реактивным сопротивлением, тем ближе разность фаз будет приближаться к нулю градусов.
Если значение сопротивления и реактивного сопротивления нельзя просто сложить вместе, чтобы найти импеданс или Z, как его определить? Поскольку ток через резистор находится в шаге от напряжения на нем, а ток в реактивном сопротивлении отличается на 90 градусов от напряжения на нем, они находятся под прямым углом друг к другу. Следовательно, их можно комбинировать тем же методом, что и при построении прямоугольного треугольника.
Предположим, вы хотите найти полное сопротивление последовательной комбинации сопротивления 8 Ом и индуктивного сопротивления 5 Ом. Начните с рисования горизонтальной линии R, представляющей сопротивление 8 Ом, в качестве основания треугольника.
Тогда, поскольку действие реактивного сопротивления всегда происходит под прямым углом, или 9От 0 градусов к сопротивлению нарисуйте линию X L , представляющую индуктивное сопротивление 5 Ом, как высоту треугольника. Это показано на рисунке (5). Теперь достройте гипотенузу (самую длинную сторону) треугольника. Тогда гипотенуза представляет импеданс цепи.
Это показано на рисунке (5). Теперь достройте гипотенузу (самую длинную сторону) треугольника. Тогда гипотенуза представляет импеданс цепи.
Векторная диаграмма, показывающая соотношение сопротивления, индуктивного сопротивления и полного сопротивления в последовательной цепи.
Одно из свойств прямоугольного треугольника:
(гипотенуза) 2 = (База) 2 + (высота) 2
Гипотеновая = √ (базу) 2 (высота) 2
, применяемый к импу = (resistence) 2 + (reactance) 2
Impedance = √(resistance) 2 + (reactance) 2
Impedance = √(resistance) 2 + (reactrance) 2
Z = √R 2 + X 2
Теперь предположим, что вы применяете это уравнение для проверки результатов в приведенном выше примере.
Дано: r = 8 Ом, x L = 5 Ом
Решение: z = √r 2 + x L 2
= √ (8 Ом) 2 + (5ω) 2
6969696969696969696969 2 2 2 2 2 2 2 2 2 2 2 2 9063 2 2= √ (8 Ом) 2 + (5ω)
= √64 + 25
= √89 Ом = 9,4 Ом
Когда вам нужно иметь дело с емкостным реактивным сопротивлением вместо индуктивного реактивного сопротивления, как в предыдущем примере, обычно чертят линию, представляющую емкостное реактивное сопротивление в нисходящем направлении. направление. Это показано на рисунке (6). Линия проведена вниз для емкостного реактивного сопротивления, чтобы указать, что оно действует в направлении, противоположном индуктивному реактивному сопротивлению, которое направлено вверх. В последовательной цепи, содержащей емкостное реактивное сопротивление, уравнение для нахождения импеданса принимает вид:
направление. Это показано на рисунке (6). Линия проведена вниз для емкостного реактивного сопротивления, чтобы указать, что оно действует в направлении, противоположном индуктивному реактивному сопротивлению, которое направлено вверх. В последовательной цепи, содержащей емкостное реактивное сопротивление, уравнение для нахождения импеданса принимает вид:
Z = √R 2 + X C 2
Во многих последовательных цепях сопротивление сочетается как с индуктивным, так и с емкостным сопротивлением. Поскольку вы знаете, что значение реактивного сопротивления X равно разнице между значениями индуктивного сопротивления X L и емкостного сопротивления X C , уравнение для импеданса в последовательной цепи, содержащее R, X L и X C тогда становятся:
z = √r 2 + (x L — x C ) 2 или z = √r 2 + x 2
ПРИМЕЧАНИЕ: ФОРМАЛАС Z = √ √ √ √ Qu + X C 2 , Z = √R 2 + X 2 и Z = √R 2 + X L 2 соединены последовательно.
В приведенных выше выражениях вы увидите метод, который можно использовать для определения импеданса в последовательной цепи, состоящей из сопротивления, индуктивности и емкости.
Предположим, что индуктивное сопротивление 10 Ом и емкостное сопротивление 20 Ом соединены последовательно с сопротивлением 40 Ом. Пусть горизонтальная линия представляет собой сопротивление R. Линия, проведенная вверх от конца R, представляет собой индуктивное реактивное сопротивление, X L . Представьте емкостное сопротивление линией, проведенной вниз под прямым углом от одного и того же конца R. Результирующая X L и X C находится путем вычитания X L из X C . Этот результат представляет собой значение X.
Таким образом: X = X C – X L = 20 Ом – 10 Ом
= 10 Ом
Примечание. Если индуктивное сопротивление меньше емкостного, то оно вычитается из емкостного.
Эти два примера иллюстрируют важный момент: при последовательном соединении емкостного и индуктивного сопротивлений меньшее всегда вычитается из большего, и результирующее реактивное сопротивление всегда принимает характеристики большего.
Вопрос
- Дано X L = 10 Ом, X C = 20 Ом, R = 40 Ом, рассчитайте импеданс.
- 40 Ом B. 41,2 Ом C. 56 Ом D. 45,3 Ом
Дано F = 1 МГц, L = 100 мкН, C = 0,0002 мкф
- Рассчитайте для индуктивного реагирования
- 352 Ом B. 702 Ом.
- Расчет емкостного реактивного сопротивления
- 801 Ом B. 235 Ом C. 769 Ом D. 745 Ом
- Теперь предположим, что имеется цепь, содержащая катушку индуктивности 100 мкГн, последовательно соединенную с конденсатором 0,0002 мкФ, и работающая на частоте 1 МГц. Какова величина результирующего реактивного сопротивления в этом случае?
- 168 Ом B. 200 Ом C. 265 Ом D. 158 Ом
- Как и в случае с емкостным сопротивлением, напряжение на катушке индуктивности определяется выражением
Присоединяйтесь к дискуссионному форуму и выполняйте задание :
Найдите вопросы в конце каждого урока. Щелкните здесь, чтобы обсудить свои ответы на форуме
Щелкните здесь, чтобы обсудить свои ответы на форуме
Объявление: Получите БЕСПЛАТНУЮ Библию : Обрести истинный покой. Нажмите здесь, чтобы узнать, как получить БЕСПЛАТНУЮ Библию.
По вопросам размещения рекламы/партнерства пишите [email protected]
Загрузите наше бесплатное мобильное приложение для Android : Сохраняйте свои данные при использовании нашего бесплатного приложения. Нажмите на картинку, чтобы скачать. Нет подписки.
Мы заинтересованы в продвижении БЕСПЛАТНОГО обучения. Расскажите своим друзьям о Stoplearn.com. Нажмите кнопку «Поделиться» ниже!
Зависимость цепи переменного тока между импедансом, током и подаваемым напряжением
Для этого ответа, всякий раз, когда я говорю ток , я конкретно имею в виду условный ток ; и всякий раз, когда я говорю резистор , конденсатор или индуктор , я конкретно имею в виду резистор постоянного сопротивления , конденсатор постоянной емкости и индуктор постоянной индуктивности соответственно. Поскольку вы изучаете цепи переменного тока, я предполагаю, что вы уже по отдельности изучали резисторы, конденсаторы и катушки индуктивности. Я также предполагаю, что вы знакомы с производными и некоторыми тригонометрическими тождествами.
Поскольку вы изучаете цепи переменного тока, я предполагаю, что вы уже по отдельности изучали резисторы, конденсаторы и катушки индуктивности. Я также предполагаю, что вы знакомы с производными и некоторыми тригонометрическими тождествами.
Во-первых, давайте вспомним некоторые уравнения.
В резисторе мгновенный ток через резистор прямо пропорционален мгновенному напряжению на резисторе:
\$v(t) = R \, i(t) \tag 1\$
В конденсаторе, мгновенный ток через конденсатор прямо пропорционален скорости изменения мгновенного напряжения на конденсаторе во времени:
\$i(t) = C \, \dfrac{\mathrm dv(t)}{\mathrm dt} \тег 2\$
В индукторе мгновенное напряжение на индукторе прямо пропорционально скорости изменения мгновенного тока через индуктор:
\$v(t) = L \, \dfrac{\mathrm di(t)} {\mathrm dt} \tag 3\$
Рассмотрим резистор. Предположим, что мгновенный ток через него представляет собой синусоиду вида \$i(t) = I_\text{m} \cos{(\omega t + \phi_i)}\$. Тогда из уравнения (1) мгновенное напряжение на нем равно:
Тогда из уравнения (1) мгновенное напряжение на нем равно:
\$\begin{align} v(t) &= R \, [I_\text{m} \cos{(\omega t + \phi_i )}] \\ &= R \, I_\text{m} \cos{(\omega t + \phi_i)} \tag 4 \end{align}\$
, то есть это тоже синусоида той же частоты, что и мгновенный ток. Ток находится в фазе во времени с напряжением.
Далее, в конденсаторе предположим, что мгновенное напряжение на нем представляет собой синусоиду вида \$v(t) = V_\text{m} \cos{(\omega t + \phi_v)}\$. Тогда из уравнения (2) мгновенный ток через него равен:
\$\begin{align} i(t) &= C \, \dfrac{\mathrm d}{\mathrm dt} [V_\text{ m} \cos{(\omega t + \phi_v)}] \\ &= C \, [- \omega \, V_\text{m} \sin{(\omega t + \phi_v)}] \\ & = — C \, \omega \, V_\text{m} \cos{(\omega t + \phi_v — 9\circ)} \tag 5 \end{align}\$
то есть это также синусоида той же частоты, что и мгновенное напряжение. Ток опережает напряжение на 90° во времени.
Далее, в катушке индуктивности предположим, что мгновенный ток через нее представляет собой синусоиду вида \$i(t) = I_\text{m} \cos{(\omega t + \phi_i)}\$. Тогда из уравнения (3) мгновенное напряжение на нем равно:
Тогда из уравнения (3) мгновенное напряжение на нем равно:
\$\begin{align} v(t) &= L \, \dfrac{\mathrm d}{\mathrm dt} [I_\text{ m} \cos{(\omega t + \phi_i)}] \\ &= L \, [- \omega \, I_\text{m} \sin{(\omega t + \phi_i)}] \\ & = — L \, \omega \, I_\text{m} \cos{(\omega t + \phi_i — 9\circ)} \tag 6 \end{align}\$
то есть это также синусоида той же частоты, что и мгновенный ток. Напряжение опережает ток на 90° во времени или, что то же самое, ток отстает от напряжения на 90° во времени.
Из уравнений (4)-(6) мы видим, что всякий раз, когда мы подаем синусоидальный ток или напряжение на резистор, конденсатор или катушку индуктивности, результирующее напряжение или ток также является синусоидальным с той же частотой . Имейте в виду этот факт. Назовем это наблюдение №1 . (На самом деле, это так, по прошествии некоторого времени так называемые переходные процессы затухли до нуля и было достигнуто установившееся состояние, но давайте проигнорируем это. )
)
Также, как вы знаете, мы можем комбинировать синусоиды разной амплитуды и разного фазового угла, но одинаковой частоты в одну синусоиду разной амплитуды, разного фазового угла, но одинаковой частоты. Прочтите эту страницу, если не знаете. Назовем это наблюдение #2 .
9{N} i_n(t) = 0 \tag 8\$В цепи, состоящей только из резисторов, катушек индуктивности, конденсаторов и независимых синусоидальных источников напряжения и тока одинаковой частоты, законы Кирхгофа вместе с наблюдением № 1 показывают, что в цепях переменного тока мы будем суммировать мгновенные напряжения и токи одной частоты . Назовем это наблюдение №3 . Эти суммы синусоидальных сигналов приведут к синусоидальным сигналам той же частоты, как мы видели в наблюдении № 2. 9{j \omega t}]}\$.
Обратите внимание, что вектор не включает циклическую или угловую частоту сигнала и, таким образом, не полностью представляет сигнал. Но это не имеет значения, потому что, как мы видели, все сигналы в цепи переменного тока, состоящей из независимых источников одинаковой частоты, резисторов, конденсаторов и катушек индуктивности, будут иметь одинаковую частоту.
(Комплексный) импеданс равен , определяемый как отношение векторного напряжения к векторному току:
\${\hat Z} = \dfrac{\tilde V}{\tilde I} \tag 9\circ \tag {12} \end{align}\$
Если вы проверите уравнения (10) — (12), вы увидите в уравнении (9), фазовый угол между мгновенным током и мгновенным напряжением резистор, конденсатор и катушка индуктивности учитываются в фазовом угле (комплексного) импеданса . Я думаю, что это отвечает на ваш вопрос:
Как можно рассчитать ток, используя I = V/Z, даже если I и источник V не совпадают по фазе?
В случае, если вы имеете в виду амплитуды/пиковые значения/максимальные значения, возьмите величину (комплексного) импеданса уравнения (9{j \phi_i}|} \\ &= \dfrac{V_\text{m}}{I_\text{m}} \tag {13} \end{align},\$
и вот оно, предыдущее уравнение показывает, что мы можем рассчитать величину (комплексного) импеданса просто как отношение пикового напряжения к пиковому току .
Если вы имеете в виду среднеквадратичное/действующее значение, вспомните, что среднеквадратичное значение синусоидального сигнала равно \$X_\text{RMS} = X_\text{m}/\sqrt{2}\$, из что мы получаем пиковое значение как \$X_\text{m} = \sqrt{2} \, X_\text{RMS}\$. Подставляя это в уравнение (13):
\$\begin{align}|{\hat Z}| &= \dfrac{\sqrt{2} \, V_\text{RMS}}{\sqrt{2} \, I_\text{RMS}} \\ &= \dfrac{V_\text{RMS}}{I_ \text{RMS}} \tag {14} \end{align},\$
и вот оно, предыдущее уравнение показывает, что мы можем рассчитать величину (комплексного) импеданса просто как отношение Среднеквадратичное значение напряжения к среднеквадратичному току .
Обратите внимание, что в уравнениях (13) и (14) фазовые углы не нужны; мы работаем только с величинами в этих уравнениях. 9{N} {\tilde V}_n = 0, \tag*{}\$
что имеет тот же вид, что и КВЛ для мгновенных напряжений! Таким образом, KVL верен для фазоров. То же самое можно сказать и о KCL.
Итак, мы можем использовать обобщенный закон Ома и законы Кирхгофа для анализа и проектирования цепей переменного тока, используя комплексные числа.
23.12 Цепи переменного тока серии RLC – College Physics
Глава 23 Электромагнитная индукция, цепи переменного тока и электрические технологии
Сводка
- Рассчитайте импеданс, фазовый угол, резонансную частоту, мощность, коэффициент мощности, напряжение и/или ток в последовательной цепи RLC.
- Нарисуйте принципиальную схему последовательной цепи RLC.
- Объясните значение резонансной частоты.
Катушки индуктивности, конденсаторы и резисторы в цепи переменного тока сами по себе препятствуют току. Как они ведут себя, когда все три встречаются вместе? Интересно, что их индивидуальные сопротивления в омах не просто складываются. Поскольку катушки индуктивности и конденсаторы ведут себя противоположным образом, они частично или полностью компенсируют эффект друг друга. На рис. 1 показана цифра 9.1169 Цепь серии RLC с источником переменного напряжения, поведение которой рассматривается в этом разделе. Суть анализа схемы RLC заключается в частотной зависимости [latex]{X_L}[/latex] и [latex]{X_C}[/latex] и влиянии, которое они оказывают на фазу зависимости напряжения от тока. (установлено в предыдущем разделе). Это приводит к частотной зависимости схемы с важными «резонансными» свойствами, которые лежат в основе многих приложений, таких как радиотюнеры.
Суть анализа схемы RLC заключается в частотной зависимости [latex]{X_L}[/latex] и [latex]{X_C}[/latex] и влиянии, которое они оказывают на фазу зависимости напряжения от тока. (установлено в предыдущем разделе). Это приводит к частотной зависимости схемы с важными «резонансными» свойствами, которые лежат в основе многих приложений, таких как радиотюнеры.
Суммарный эффект сопротивления [латекс]{R}[/латекс], индуктивного сопротивления [латекс]{X_L}[/латекс] и емкостного сопротивления [латекс]{X_C}[/латекс] определяется как импеданс , аналог переменного тока для сопротивления в цепи постоянного тока. Ток, напряжение и импеданс в цепи RLC связаны версией закона Ома для переменного тока:
[латекс] {I_0 =} [/латекс] [латекс] {\ гидроразрыва {V_0} {Z}} [/латекс] [латекс] {\ текст {или} \; I _{\text{rms}} =}[/latex] [латекс]{\frac{V _{\text{rms}}}{Z}}. [/latex]
[/latex]
Здесь [latex]{I_0}[/latex] — пиковый ток, [latex]{V_0}[/latex] — пиковое напряжение источника, а [latex]{Z}[/latex] — импеданс цепи. Единицами импеданса являются омы, и его влияние на цепь, как и следовало ожидать: чем больше импеданс, тем меньше ток. Чтобы получить выражение для [латекса]{Z}[/латекс] через [латекс]{R}[/латекс], [латекс]{X_L}[/латекс] и [латекс]{X_C}[/латекс ], теперь мы рассмотрим, как напряжения на различных компонентах связаны с напряжением источника. Эти напряжения обозначены [латекс]{V_R}[/латекс], [латекс]{V_L}[/латекс] и [латекс]{V_C}[/латекс] на рисунке 1.
Сохранение заряда требует, чтобы ток был одинаковым в каждой части цепи все время, так что мы можем сказать, что токи в [латекс]{R}[/латекс], [латекс]{L}[/латекс], и [latex]{C}[/latex] равны и находятся в фазе. Но из предыдущего раздела мы знаем, что напряжение на индукторе [латекс]{V_L}[/латекс] опережает ток на одну четвертую периода, напряжение на конденсаторе [латекс]{V_C}[/латекс] следует за ним. ток на одну четвертую периода, а напряжение на резисторе [латекс]{V_R}[/латекс] точно совпадает по фазе с током. На рис. 2 эти отношения показаны на одном графике, а также показано общее напряжение в цепи [latex]{V = V_R + V_L + V_C}[/latex], где все четыре напряжения являются мгновенными значениями. Согласно петлевому правилу Кирхгофа, полное напряжение вокруг цепи VV также является напряжением источника. 92}},[/латекс]
ток на одну четвертую периода, а напряжение на резисторе [латекс]{V_R}[/латекс] точно совпадает по фазе с током. На рис. 2 эти отношения показаны на одном графике, а также показано общее напряжение в цепи [latex]{V = V_R + V_L + V_C}[/latex], где все четыре напряжения являются мгновенными значениями. Согласно петлевому правилу Кирхгофа, полное напряжение вокруг цепи VV также является напряжением источника. 92}},[/латекс]
, где [латекс]{V_{0R}}[/латекс], [латекс]{V_{0L}}[/латекс] и [латекс]{V_{0C}}[/латекс] — пиковые напряжения на [ латекс]{R}[/латекс], [латекс]{L}[/латекс] и [латекс]{C}[/латекс] соответственно. Теперь, используя закон Ома и определения из главы 23.11 Реактивное, индуктивное и емкостное сопротивление, подставим [латекс]{V_0 = I_0Z}[/латекс] в приведенное выше, а также [латекс]{V_{0R} = I_0R}[/ латекс], [латекс]{V_{0L} = I_0X_L}[/латекс] и [латекс]{V_{0C} = I_0X_C}[/латекс], что дает
92}},[/латекс], который представляет собой импеданс цепи переменного тока серии RLC . Для цепей без резистора возьмите [латекс]{R = 0}[/латекс]; для тех, у кого нет индуктора, возьмите [латекс]{X_L = 0}[/латекс]; а для тех, у кого нет конденсатора, возьмите [латекс]{Х_С = 0}[/латекс].
Для цепей без резистора возьмите [латекс]{R = 0}[/латекс]; для тех, у кого нет индуктора, возьмите [латекс]{X_L = 0}[/латекс]; а для тех, у кого нет конденсатора, возьмите [латекс]{Х_С = 0}[/латекс].
Пример 1: Расчет импеданса и тока
Цепь серии RLC имеет [латексный] {40,0 \;\Омега}[/латексный] резистор, катушку индуктивности 3,00 мГн и [латексный] {5,00 \;\мю F}[/латекс] конденсатор. (a) Найдите полное сопротивление цепи при 60,0 Гц и 10,0 кГц, отметив, что эти частоты и значения для [латекс]{L}[/латекс] и [латекс]{С}[/латекс] такие же, как в главе 23.11. Пример 1 и Глава 23.11 Пример 2. (b) Если источник напряжения имеет [латекс]{V_{\text{среднеквадратичное значение}} = 120 \;\текст{V}}[/латекс], что такое [латекс]{I_ {\text{rms}}}[/latex] на каждой частоте? 92}}[/latex], чтобы найти импеданс, а затем закон Ома, чтобы найти силу тока. 2}}[/латекс] дает 92}} \\[1em]\;= & {190 \;\Omega \;\text{at} \; 10,0 \;\text{кГц}}. \end{array}[/latex]
2}}[/латекс] дает 92}} \\[1em]\;= & {190 \;\Omega \;\text{at} \; 10,0 \;\text{кГц}}. \end{array}[/latex]
Обсуждение для (a)
В обоих случаях результат почти одинаков для наибольшего значения, а импеданс определенно не является суммой отдельных значений. Понятно, что [латекс]{X_L}[/латекс] доминирует при высокой частоте, а [латекс]{Х_С}[/латекс] доминирует при низкой частоте.
Решение для (b)
Текущий [латекс]{I_{\text{среднеквадратичное значение}}}[/латекс] можно найти, используя версию закона Ома для переменного тока в уравнении [латекс]{I_{среднеквадратичное значение} = V_{rms} / Z}[/латекс]:
[латекс] {I _ {\ text {rms}} =} [/ латекс] [латекс] {\ frac {V _ {\ text {rms}}} {Z}} [/ латекс] [латекс] {=} [/латекс] [латекс]{\ гидроразрыва {120 \;\текст{V}}{531 \;\Омега}}[/латекс] [латекс]{= 0,226 \;\текст{А}}[/латекс] при 60,0 Гц
Наконец, при 10,0 кГц мы находим
[латекс] {I _ {\ текст {среднеквадратичное значение}} =}[/латекс] [латекс] {\ гидроразрыва {V _ {\ текст {среднеквадратичное значение}}} { Z}}[/латекс] [латекс]{=}[/латекс] [латекс]{\гидроразрыва{120 \;\текст{V}}{190 \;\Омега}}[/латекс] [латекс]{= 0,633 \;\text{A}}[/latex] на частоте 10,0 кГц
Обсуждение для (a)
Ток на частоте 60,0 Гц такой же (с точностью до трех цифр), что и для одного конденсатора в примере 1. 2}}[/латекс] дает 92}}}.[/латекс]
2}}[/латекс] дает 92}}}.[/латекс]
Реактансы зависят от частоты: [латекс]{X_L}[/латекс] велик на высоких частотах и [латекс]{Х_С}[/латекс] велик на низких частотах, как мы видели в трех предыдущих примерах. На некоторой промежуточной частоте [латекс]{f_0}[/латекс] реактивные сопротивления будут равны и сокращаются, что дает [латекс]{Z = R}[/латекс] — это минимальное значение импеданса и максимальное значение для [латекс] {I _ {\ текст {rms}}}[/латекс] результаты. Мы можем получить выражение для [латекс]{f_0}[/латекс], взяв
[латекс]{X_L = X_C}.[/латекс]
Замена определений [латекс]{X_L}[/латекс] и [латекс]{X_C}[/латекс],
[латекс] {2 \pi f_0 L =}[/латекс] [латекс] {\ гидроразрыва {1} {2 \пи f_0 C}}.[/латекс]
Решение этого выражения для [латекс]{f_0}[/латекс] дает
[латекс] {f_0 =} [/латекс] [латекс] {\ гидроразрыва {1} {2 \ pi \ sqrt {LC}}}, [/латекс]
, где [latex]{f_0}[/latex] – резонансная частота цепи серии RLC . это тоже собственная частота , при которой схема колебалась бы, если бы не приводилась в действие источником напряжения. При [латексе]{f_0}[/латексе] эффекты катушки индуктивности и конденсатора компенсируются, так что [латекс]{Z = R}[/латекс] и [латекс]{I_{\текст{среднеквадратичное значение}}} [/latex] это максимум.
это тоже собственная частота , при которой схема колебалась бы, если бы не приводилась в действие источником напряжения. При [латексе]{f_0}[/латексе] эффекты катушки индуктивности и конденсатора компенсируются, так что [латекс]{Z = R}[/латекс] и [латекс]{I_{\текст{среднеквадратичное значение}}} [/latex] это максимум.
Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденные колебания — в данном случае вызванные источником напряжения — на собственной частоте системы. Приемник в радио — это RLC , которая лучше всего колеблется в своем [латексе]{f_0}[/латексе]. Переменный конденсатор часто используется для настройки [латекс]{f_0}[/латекс] для получения желаемой частоты и отклонения других. Рисунок 3 представляет собой график зависимости тока от частоты, иллюстрирующий резонансный пик в [латексе]{I_{\текст{среднеквадратичное значение}}}[/латекс] в точке [латекс]{f_0}[/латекс]. Две кривые относятся к двум разным цепям, которые отличаются только величиной сопротивления в них. Пик ниже и шире для схемы с более высоким сопротивлением. Таким образом, цепь с более высоким сопротивлением не резонирует так сильно и не будет такой избирательной, например, в радиоприемнике.
Пик ниже и шире для схемы с более высоким сопротивлением. Таким образом, цепь с более высоким сопротивлением не резонирует так сильно и не будет такой избирательной, например, в радиоприемнике.
Пример 2: Расчет резонансной частоты и тока
Для той же цепи серии RLC , имеющей [латексный] {40,0 \;\Omega}[/латексный] резистор, катушку индуктивности 3,00 мГн и [латексный] {5,00 \ ;\mu F}[/latex] конденсатор: (a) Найдите резонансную частоту. (b) Рассчитайте [латекс]{I_{\text{среднеквадратичное значение}}}[/латекс] в резонансе, если [латекс]{V_{\текст{среднеквадратичное значение}}}[/латекс] равно 120 В.
Стратегия
Резонансная частота находится с помощью выражения в [latex]{f_0 = \frac{1}{2 \pi \sqrt{LC}}}[/latex]. {-6} \;\text{F})}} = 1,30 \;\text{кГц}.} \ конец{массив}[/латекс]
{-6} \;\text{F})}} = 1,30 \;\text{кГц}.} \ конец{массив}[/латекс]
Обсуждение для (a)
Мы видим, что резонансная частота находится между 60,0 Гц и 10,0 кГц, двумя частотами, выбранными в предыдущих примерах. Этого и следовало ожидать, поскольку на низкой частоте преобладал конденсатор, а на высокой частоте — катушка индуктивности. Их эффекты одинаковы на этой промежуточной частоте.
Решение для (b)
Ток определяется законом Ома. В резонансе два реактивных сопротивления равны и компенсируются, так что импеданс равен одному сопротивлению. Таким образом,
[латекс] {I _ {\ text {rms}} =} [/ латекс] [латекс] {\ frac {V _ {\ text {rms}}} {Z}} [/ латекс] [латекс] {=} [/латекс] [латекс]{\ гидроразрыва {120 \;\текст{V}}{40,0 \;\Омега}}[/латекс] [латекс]{= 3,00 \;\текст{А}}.[/латекс ]
Обсуждение для (b)
При резонансе ток больше, чем на более высоких и более низких частотах, рассмотренных для той же цепи в предыдущем примере.
Если ток в цепи RLC зависит от частоты, то подводимая к ней мощность также зависит от частоты. Но средняя мощность — это не просто ток, умноженный на напряжение, как в чисто резистивных цепях. Как видно на рисунке 2, напряжение и ток не совпадают по фазе в 9{\circ}}[/latex] и что напряжение и ток совпадают по фазе, как и ожидается для резисторов. На других частотах средняя мощность меньше, чем на резонансе. Это связано как с тем, что напряжение и ток не совпадают по фазе, так и с тем, что [латекс] {I _ {\ текст {среднеквадратичное значение}}}[/латекс] ниже. Тот факт, что напряжение и ток источника не совпадают по фазе, влияет на мощность, подаваемую в цепь. Можно показать, что средняя мощность равна
[латекс] {P _ {\ text {ave}} = I _ {\ text {rms}} V _ {\ text {rms}} \ text {cos} \;\phi}, [/latex]
Таким образом, [латекс] {\ текст {cos} \; \ фи} [/ латекс] называется коэффициентом мощности , который может варьироваться от 0 до 1. Коэффициенты мощности, близкие к 1, желательны при разработке эффективного двигателя, например . На резонансной частоте [латекс] {\ текст {кос} \; \ фи = 1} [/ латекс].
Коэффициенты мощности, близкие к 1, желательны при разработке эффективного двигателя, например . На резонансной частоте [латекс] {\ текст {кос} \; \ фи = 1} [/ латекс].
Пример 3: Расчет коэффициента мощности и мощности
Для той же цепи серии RLC , имеющей [латексный] {40,0 \;\Omega}[/латексный] резистор, катушку индуктивности 3,00 мГн, [латексный] {5,00 \ ;\mu F}[/latex] конденсатор и источник напряжения с [latex]{V_{\text{rms}}}[/latex] 120 В: (a) Рассчитайте коэффициент мощности и фазовый угол для [ латекс]{f = 60,0 \текст{Гц}}[/латекс]. (b) Какова средняя мощность при 50,0 Гц? в) Найдите среднюю мощность на резонансной частоте контура.
Стратегия и решение для (a)
Коэффициент мощности при 60,0 Гц определяется из R}{Z}}.[/latex]
Мы знаем [latex]{Z = 531 \;\Omega}[/latex] из примера 1, поэтому
[latex]{cos \;\phi =} [/латекс] [латекс]{\ гидроразрыва {40,0 \;\Омега}{531 \;\Омега}}[/латекс] [латекс]{= 0,0753 \;\текст{ат} \; 60,0 \;\text{Гц}}. [/latex]
[/latex]
Это небольшое значение указывает на то, что напряжение и ток значительно не совпадают по фазе. На самом деле фазовый угол равен 9{\circ}}[/latex] не в фазе).
Стратегия и решение для (b)
Средняя мощность при 60,0 Гц составляет
[латекс]{P_{ave} = I_{\text{rms}}V_{\text{rms}} \text{ кос} \; \phi}[/latex]
[латекс]{I_{\text{среднеквадратичное значение}}}[/латекс] равно 0,226 А в примере 1. Ввод известных значений дает
[латекс]{P_{\ text{ave}} = (0,226 \;\text{A})(120 \;\text{V})(0,0753) = 2,04 \;\text{W at} \; 60,0 \;\text{Гц}}.[/latex]
Стратегия и решение для (c)
На резонансной частоте мы знаем, что [латекс]{\текст{коиз} \;\фи = 1}[/латекс], и [латекс]{I_{\текст{среднеквадратичное значение}}}[/латекс] было в примере 2 значение равно 6,00 А. Таким образом,
[латекс]{P_{\text{ave}} = (3,00 \;\text{A})(120 \;\text{V})(1) = 360 \;\text{W}}[/latex] при резонансе (1,30 кГц)
Обсуждение
И ток, и коэффициент мощности выше при резонансе, производя значительно большую мощность, чем на более высоких и более низких частотах.
Мощность поставлена на RLC серии Цепь переменного тока рассеивается только за счет сопротивления. Катушка индуктивности и конденсатор имеют входную и выходную энергию, но не рассеивают ее из цепи. Скорее они передают энергию туда и обратно друг другу, при этом резистор рассеивает именно то, что источник напряжения помещает в цепь. Это предполагает отсутствие значительного электромагнитного излучения от катушки индуктивности и конденсатора, такого как радиоволны. Такое излучение может происходить и может быть даже желательным, как мы увидим в следующей главе об электромагнитном излучении, но его также можно подавить, как в случае с этой главой. Схема аналогична колесу автомобиля, движущегося по неровной дороге, как показано на рис. 4. Равномерно расположенные неровности на дороге аналогичны источнику напряжения, приводящему в движение колесо вверх и вниз. Амортизатор аналогичен сопротивлению, демпфирующему и ограничивающему амплитуду колебаний. Энергия внутри системы переходит туда и обратно между кинетической (аналогично максимальному току и энергии, хранящейся в индукторе) и потенциальной энергией, запасенной в автомобильной пружине (аналогично отсутствию тока и энергии, запасенной в электрическом поле конденсатора). Амплитуда движения колес максимальна, если удары о неровности дороги происходят на резонансной частоте.
Амплитуда движения колес максимальна, если удары о неровности дороги происходят на резонансной частоте.
Чистая цепь LC с незначительным сопротивлением колеблется на частоте [latex]{f_0}[/latex], той же резонансной частоте, что и цепь RLC . Он может служить эталоном частоты или тактовой схемой, например, в цифровых наручных часах. При очень малом сопротивлении для поддержания колебаний требуется лишь очень небольшая затрата энергии. Схема аналогична автомобилю без амортизаторов. Как только он начинает колебаться, он некоторое время продолжает работать на своей собственной частоте. На рис. 5 показана аналогия между LC схема и масса на пружине.
Рисунок 5. Цепь LC аналогична массе, колеблющейся на пружине без трения и движущей силы. Энергия движется вперед и назад между катушкой индуктивности и конденсатором точно так же, как она движется от кинетической к потенциальной в системе масса-пружина.
Цепь LC аналогична массе, колеблющейся на пружине без трения и движущей силы. Энергия движется вперед и назад между катушкой индуктивности и конденсатором точно так же, как она движется от кинетической к потенциальной в системе масса-пружина.PhET Explorations: комплект для построения цепей (AC+DC), виртуальная лаборатория
Создавайте схемы с конденсаторами, катушками индуктивности, резисторами и источниками переменного или постоянного напряжения и проверяйте их с помощью лабораторных приборов, таких как вольтметры и амперметры.
Рис. 6. Набор для построения схемы (AC+DC), виртуальная лаборатория- Аналогом сопротивления переменного тока является импеданс [латекс]{Z}[/латекс], комбинированный эффект резисторов, катушек индуктивности и конденсаторов, определяемый версией закона Ома для переменного тока:
[латекс] {I_0 =} [/латекс] [латекс] {\ гидроразрыва {V_0} {Z}} [/латекс] [латекс] {\ текст {или} \; I _{\text{rms}} =}[/latex] [латекс]{\frac{V _{\text{rms}}}{Z}},[/latex]
, где [latex]{I_0}[/latex] — пиковое значение тока, а [latex]{V_0}[/latex] — пиковое напряжение источника.
 9{\ circ}} [/latex] для чисто резистивной цепи или цепи RLC в резонансе.
9{\ circ}} [/latex] для чисто резистивной цепи или цепи RLC в резонансе. - Средняя мощность, подаваемая в цепь RLC , зависит от фазового угла и определяется выражением
[латекс] {P _ {\ text {ave}} = I _ {\ text {rms}} V _ {\ text {rms}} \; \ text {cos} \; \ phi}, [/latex]
[latex]{\text{cos} \;\phi}[/latex] называется коэффициентом мощности, который принимает значения от 0 до 1.
Задачи и упражнения
1: An Схема RL состоит из резистора [латекс]{40,0 \;\Омега}[/латекс] и катушки индуктивности 3,00 мГн. (a) Найдите его импеданс [латекс]{Z}[/латекс] при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения [латекс]{Z}[/латекс] со значениями, найденными в примере 1, в котором также был конденсатор.
2: Схема RC состоит из [латексного] {40,0 \;\Омега}[/латексного] резистора и [латексного] {5,00 \;\мкФ}[/латексного] конденсатора. (а) Найдите его импеданс на частотах 60,0 Гц и 10,0 кГц. (b) Сравните эти значения [латекс]{Z}[/латекс] с найденными в примере 1, в котором также присутствовал индуктор.
(b) Сравните эти значения [латекс]{Z}[/латекс] с найденными в примере 1, в котором также присутствовал индуктор.
3: Схема LC состоит из катушки индуктивности [латекс]{3,00 \;\text{мГн}}[/латекс] и конденсатора [латекс]{5,00 \;мкФ}[/латекс]. . (а) Найдите его импеданс на частотах 60,0 Гц и 10,0 кГц. (b) Сравните эти значения [латекс]{Z}[/латекс] со значениями, найденными в примере 1, в котором также был резистор.
4: Какова резонансная частота катушки индуктивности 0,500 мГн, подключенной к [латексу] {40,0 \; \mu F}[/latex] конденсатор?
5: Чтобы принимать AM-радио, вам нужен RLC , которую можно заставить резонировать на любой частоте от 500 до 1650 кГц. Это достигается с помощью фиксированного [латексного] {1,00 \;\mu \text{H}}[/латексного] индуктора, соединенного с переменным конденсатором. Какой диапазон емкости нужен?
6: Предположим, у вас есть запас катушек индуктивности от 1,00 нГн до 10,0 Гн и конденсаторов емкостью от 1,00 пФ до 0,100 Ф. один конденсатор?
один конденсатор?
7: Какая емкость необходима для получения резонансной частоты 1,00 ГГц при использовании катушки индуктивности 8,00 нГн?
8: Какая индуктивность нужна для получения резонансной частоты 60,0 Гц при использовании конденсатора 2,00 мкФ2,00 мкФ?
9: Самая низкая частота в диапазоне FM-радио — 88,0 МГц. а) Какая индуктивность необходима для получения этой резонансной частоты, если он подключен к конденсатору емкостью 2,50 пФ? (b) Конденсатор переменный, что позволяет регулировать резонансную частоту до 108 МГц. Какая должна быть емкость на этой частоте?
10: Цепь серии RLC имеет резистор [латекс]{2,50 \;\Омега}[/латекс], резистор [латекс]{100 \;\mu \text{H}}[/латекс] индуктор и [латексный] {80,0 \;\mu \text{F}}[/латексный] конденсатор. (а) Найдите полное сопротивление цепи на частоте 120 Гц. (b) Найдите полное сопротивление цепи на частоте 5,00 кГц. (c) Если источник напряжения имеет [латекс]{V_{\text{среднеквадратичное значение}}} = 5,60 \;\текст{В}}[/латекс], что такое [латекс]{I_{\текст{среднеквадратичное значение}}} [/latex] на каждой частоте? г) Какова резонансная частота цепи? (e) Что такое [латекс] {I _ {\ text {среднеквадратичное значение}}} [/латекс] в резонансе?
11: Цепь серии RLC имеет [латекс]{1,00 \;\text{k} \Omega}[/latex] резистор, [латекс]{150 \;\mu \text{H} }[/latex] индуктор и конденсатор 25,0 нФ. а) Найдите полное сопротивление цепи на частоте 500 Гц. (b) Найдите полное сопротивление цепи на частоте 7,50 кГц. (c) Если источник напряжения имеет [латекс]{V_{\text{среднеквадратичное значение}} = 408 \;\текст{В}}[/латекс], что такое [латекс]{I_{\текст{среднеквадратичное значение}}} [/latex] на каждой частоте? г) Какова резонансная частота цепи? (e) Что такое [латекс] {I _ {\ text {среднеквадратичное значение}}} [/латекс] в резонансе?
а) Найдите полное сопротивление цепи на частоте 500 Гц. (b) Найдите полное сопротивление цепи на частоте 7,50 кГц. (c) Если источник напряжения имеет [латекс]{V_{\text{среднеквадратичное значение}} = 408 \;\текст{В}}[/латекс], что такое [латекс]{I_{\текст{среднеквадратичное значение}}} [/latex] на каждой частоте? г) Какова резонансная частота цепи? (e) Что такое [латекс] {I _ {\ text {среднеквадратичное значение}}} [/латекс] в резонансе?
12: Цепь серии RLC имеет [латексный] {2,50 \;\Омега}[/латекс] резистор, [латексный] {100 \;\мкГн}[/латексный] индуктор и [латекс]{80,0 \;\мю \текст{F}}[/латекс] конденсатор. (a) Найдите коэффициент мощности при [латексе]{f = 120 \;\текст{Гц}}[/латекс]. (b) Каков фазовый угол на частоте 120 Гц? в) Какова средняя мощность на частоте 120 Гц? г) Найдите среднюю мощность на резонансной частоте контура.
13: Цепь серии RLC имеет [латекс]{1,00 \;\text{k} \Omega}[/latex] резистор, [латекс]{150 \;\mu \text{H} }[/latex] индуктор и конденсатор 25,0 нФ.




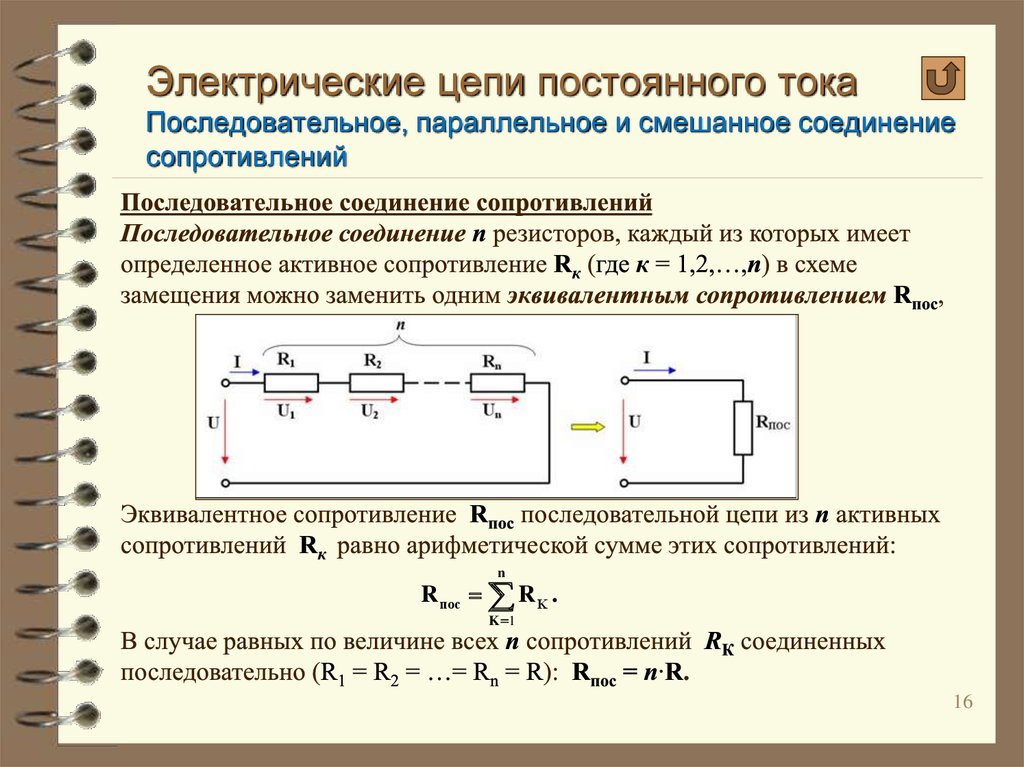




 таблицу 1.14 [Л2. с.30].
таблицу 1.14 [Л2. с.30].
 выше).
выше). ..)
..)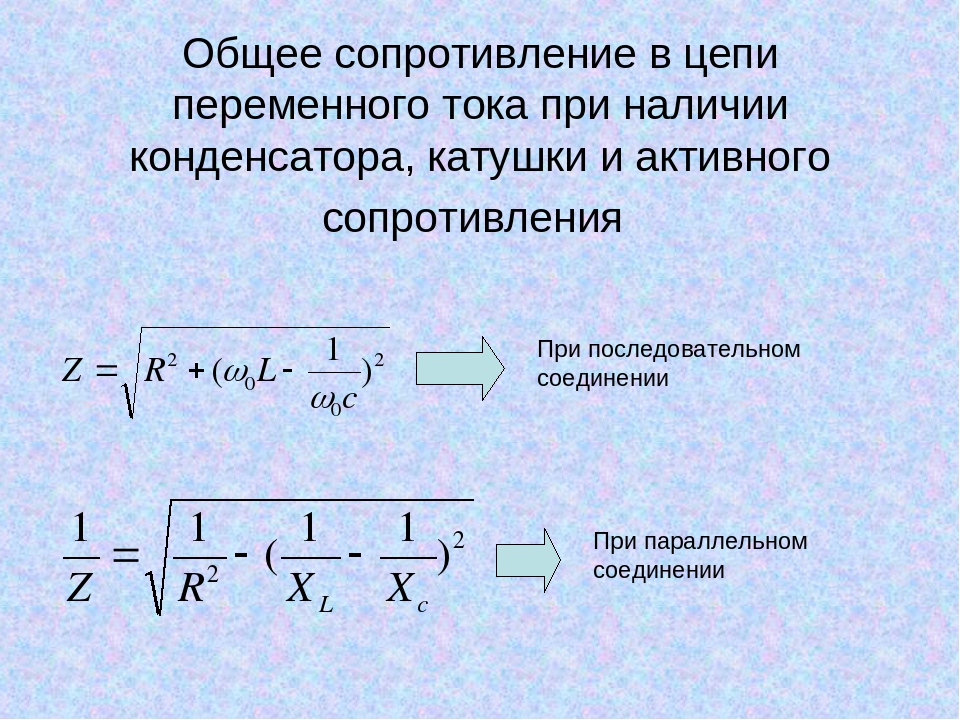
 Текущее деление
Текущее деление