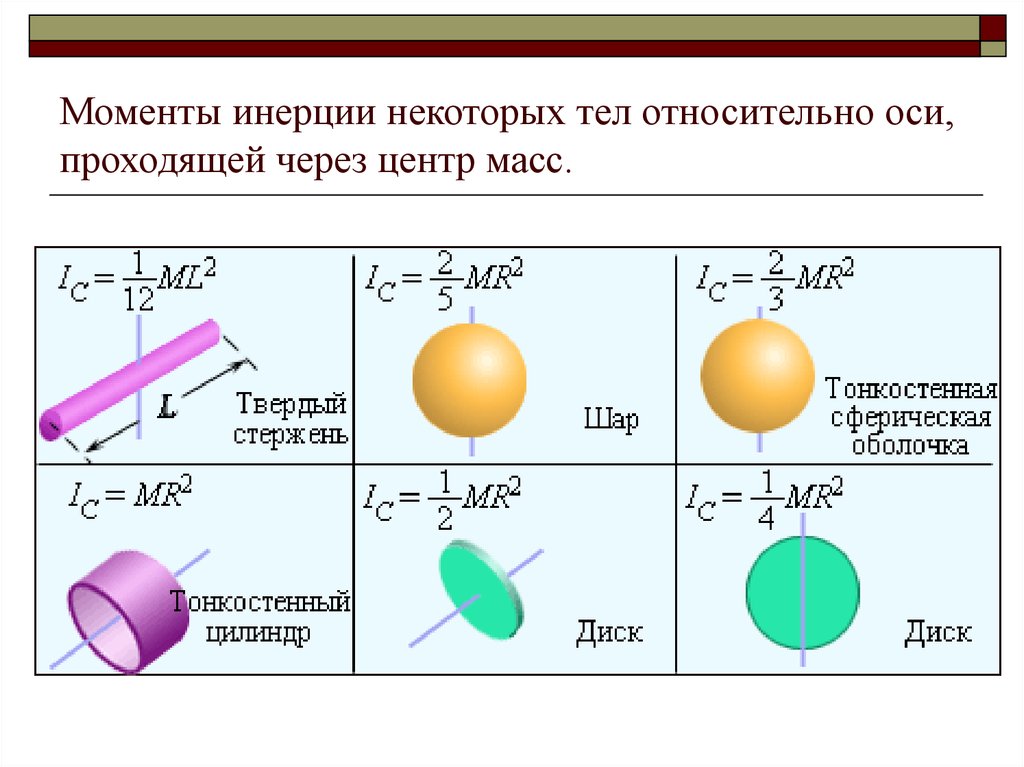
Момент инерции тела.

При описании поступательного движения тел мы вводили понятие массы тела – меры инертности тела при действии на него кокой — либо силой. Именно масса тела определяет ускорение, с которым будет двигаться тело под воздействием силы.

А достаточно ли знания массы тела, чтобы описать вращательное движение тела вокруг какой либо оси? Оказывается, что для описания вращательного движения кроме массы тела необходимо знать и его момент инерции относительно выбранной оси вращения.

Пусть тело вращается относительно оси, проходящей через точку О (см. рис. 6.3). При вращательном движении точки, обладающие одинаковой массой, но находящиеся на разном расстояние от оси вращения, будут иметь разную инертность.

Во вращательном движении материального тела мерой его инертности является момент инерции. Моментом инерции материальной точки относительно оси вращения

О называется величина равная произведению массы этой точки на квадрат расстояние от точки до оси вращения:

. .( 6.2 )

Рис. 6.3. К понятию инертности тела.

Чтобы найти момент инерции всего материального тела, необходимо сложить моменты инерции всех материальных точек, составляющих это материальное тело:

. ( 6.3 )

Выражения ( 6.2 ) и ( 6.3 ) показывают, что момент инерции любого материального тела есть величина

скалярная и аддитивная, аналогично массе при поступательном движении. Аддитивность момента инерции означает, что если мы имеем 2 или более материальных тел с моментами инерции Ii относительно выбранной оси вращения, то если мы соединим эти тела в одно целое и заставим эту совокупность материальных тел вращаться как единое целое относительно той же самой выбранной оси вращения, то в соответствии с формулой ( 6.3 ).

Если в формуле ( 6. 3 ) сделать предельный переход, учитывая, что суммирование производится по непрерывно меняющейся величине, то суммирование заменится интегрированием, т.е. для точки с

m_i = dm, находящейся на расстоянии r от оси вращения:

, ( 6.4 )

где интегрирование производится по всему объему однородного материального тела. Величина r в этом случае есть функция положения точки с координатами (x, y, z ).

Выражение ( 6.4 ) однако несколько некорректно, поскольку не вполне понятно, как вычислять элементы dm . В случае,если плотность материального тела однородна, т.е. , где

dV— элементарный объем, то момент инерции можно выразить иначе; учитывая, что dm=dV :

. ( 6.5 )

В качестве примера применения формул ( 6.4 ) и ( 6.5 ) рассмотрим случаи вычисления момента инерции конкретных материальных тел.

1.Момент инерции однородного стержня относительно оси, проходящей через центр масс.

Пусть однородный стержень имеет длину l массу m и площадь поперечного сечения S ( см. рис. 6.4 ). Для вычисления момента инерции будем использовать формулу ( 6.5 ):

Рис. 6.4. К вычислению момента инерции однородного стержня.

Выберем на расстояние r от оси вращения участок стержня толщиной dr, имеющий объем dV=Sdr. Поскольку стержень предполагается однородным то:

, (6.6)

т.к. Sl = m.

2.

Момент инерции однородного цилиндра относительно оси, параллельной образующей и проходящей через центр масс.

На расстоянии r от оси ОО вращение цилиндра выберем слой толщиной dr (см. рис 6.5 ). Объем этого бесконечно тонкого слоя будет равен:

. ( 6.7 )

Подставим это выражение в формулу (6.5) и получим::

( 6.8 )

Рис. 6.5. К вычислению момента инерции однородного цилиндра.

формулы для стержня и колеса :: SYL.ru

Любые перемещения тел в пространстве, траектория которых является окружностью, предполагают знание не только угловой скорости, но и момента инерции для описания этого движения. Что такое момент инерции, а также чему он равен для стержня и колеса, ответит данная статья.

Вращение и момент инерции

Физическая величина, которая называется моментом инерции, обозначается, как правило, буквой I и появляется в физике при рассмотрении момента импульса материальной точки, которая вращается вокруг оси. Момент импульса L в скалярной форме записывается следующим выражением:

L = r*m*v

Здесь r — дистанция до оси материальной точки, m — ее масса, v — линейная скорость. Используя связь последней со скоростью угловой ω, получаем выражение:

L = r²*m*ω, где ω = v/r

Отвечая на вопрос о том, что такое момент инерции, следует сказать, что это величина I = r²*m. То есть она зависит от массы вращающегося объекта, быстро растет с увеличением расстояния до оси и измеряется в кг*м².

Общее выражение для момента инерции

Введенная в предыдущем пункте формула для величины I справедлива, если размеры объекта пренебрежимо малы по сравнению с дистанцией до оси r (вращение Земли вокруг нашей звезды). Если же линейные размеры объекта становятся сравнимыми с расстоянием r, тогда необходимо для вычисления I пользоваться более общей формулой, которая дана ниже:

I = ∫_m(r²*dm)

Из нее видно, что подынтегральное выражение представляет собой момент инерции материальной точки. Сумма же всех моментов от точек с массой dm составляет полный момент инерции I для всего тела.

Эта формула является мощным инструментом для определения I тела абсолютно любой формы. Согласно формуле величина I является аддитивной, то есть позволяет разбить тело на отдельные части, вычислить их моменты инерции, а затем сложить полученные результаты для получения величины I тела.

Физический смысл величины I

Зная, что такое момент инерции, необходимо сказать несколько слов о том, как его значение отражается на поведении и характеристиках вращения реальных объектов.

Большая величина I приводит к тому, что тело очень тяжело раскрутить вокруг оси. Для этого приходится выполнить значительную работу и приложить существенные усилия. Примером тела с большим I является автомобильный маховик — тяжелый металлический диск, жестко закрепленный на коленвале двигателя. Наоборот, если величина I системы невелика, то ее можно быстро раскрутить и так же быстро и легко остановить.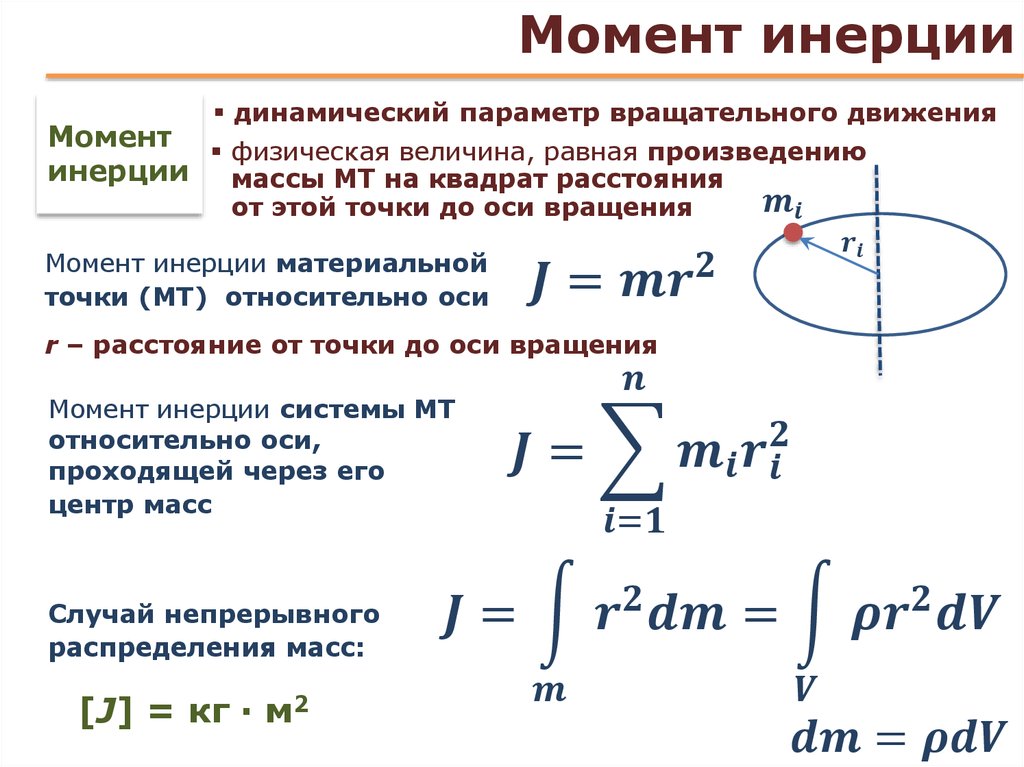 Примером для этого случая является алюминиевый обод велосипедного колеса.

Приведенное выше обсуждение говорит о том, что момент инерции характеризуется инерционностью процесса вращения, то есть выполняет ту же самую роль, что и масса тела при приложении к ней силы с целью придания ускорения.

Отличие массы и момента инерции заключается не только в единицах измерения, но и в том, что последний является функцией вращательной системы, а не только геометрии тела и его массы.

Момент инерции относительно оси вращения, пересекающей центр масс стержня

Рассмотрим пример использования интегральной формулы для решения реальных задач. Первым делом решим простую проблему: имеется стержень тонкий длиной l и массой m. Вращения оси проходит перпендикулярно этому стержню через центр массы объекта. Необходимо определить величину I для этой системы.

Выпишем общую формулу для инерции момента стержня относительно оси, имеем:

I = ∫_m(r²*dm)

Поскольку ось перпендикулярна рассматриваемому телу, и сам стержень имеет бесконечно малую толщину, то можно мысленно разрезать его на тонкие слои плоскостями, параллельными оси.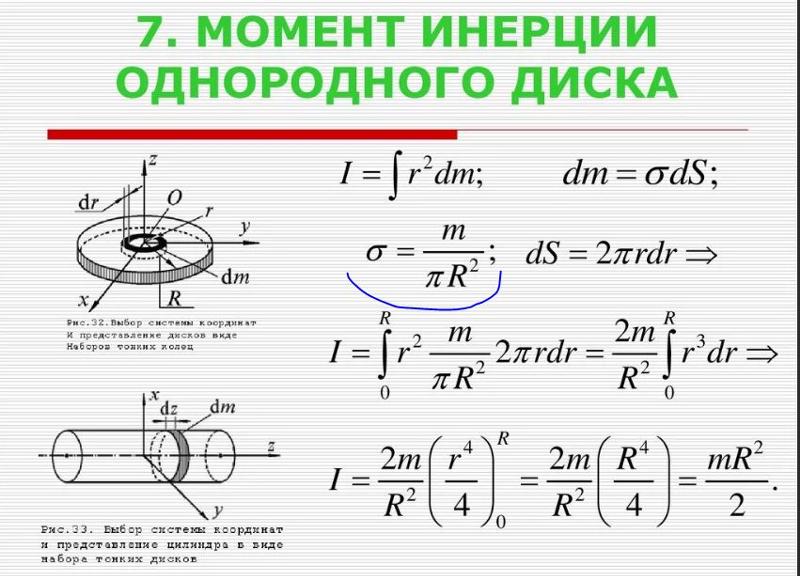 В таком случае получаем, что элемент массой dm может быть представлен следующим равенством:

dm = ρ*S*dr

Здесь ρ — плотность материала, S — поперечное сечение, которое является постоянной величиной и стремится к нулю (стержень бесконечно тонкий). Подставим это выражение в общую формулу:

I = ρ*S*∫^+l/2_-l/2(r²*dr)

Заметим, что подставленные пределы интегрирования по r соответствуют условию задачи (ось делит стержень на две равные части). Выполняя интегрирование, получаем:

I = ρ*S*(r³/3)|^+l/2_-l/2 = m*l²/12, где m = ρ*S*l

Таким образом, момент инерции стержня тонкого, когда ось проходит через центр масс, в 12 раз меньше такового для материальной точки той же массы, находящейся на расстоянии l от оси.

Величина I для стержня с осью вращения на конце объекта

Рассмотрим, что такое момент инерции, в несколько иной ситуации. Имеем тот же самый объект (тонкий стержень), но теперь ось проходит через конец. Как изменится момент инерции в этом случае? Применяем тот же метод разбиения стержня и последующего интегрирования, как в предыдущем пункте, получаем:

I = ρ*S*∫^l₀(r²*dr)

Заметим, что изменились лишь пределы интегрирования. Решением будет следующее равенство:

I = m*l²/3

Выражение показывает, что тот же самый стержень будет обладать в 4 раза большим моментом инерции (труднее раскрутить), если ось вращения переместить с его центра на край.

Рассматривая решение этих двух задач, следует сделать важный вывод: при расчете величины I нельзя сводить всю массу объекта в его центр и выполнять расчет, как для материальной точки. Вычисление следует проводить только с использованием интегрального выражения.

Значение I для колеса со спицами

Момент инерции колеса можно определить, используя свойство аддитивности рассматриваемой величины. Для этого мысленно разберем колесо на отдельные части, которые представляют собой спицы и обод.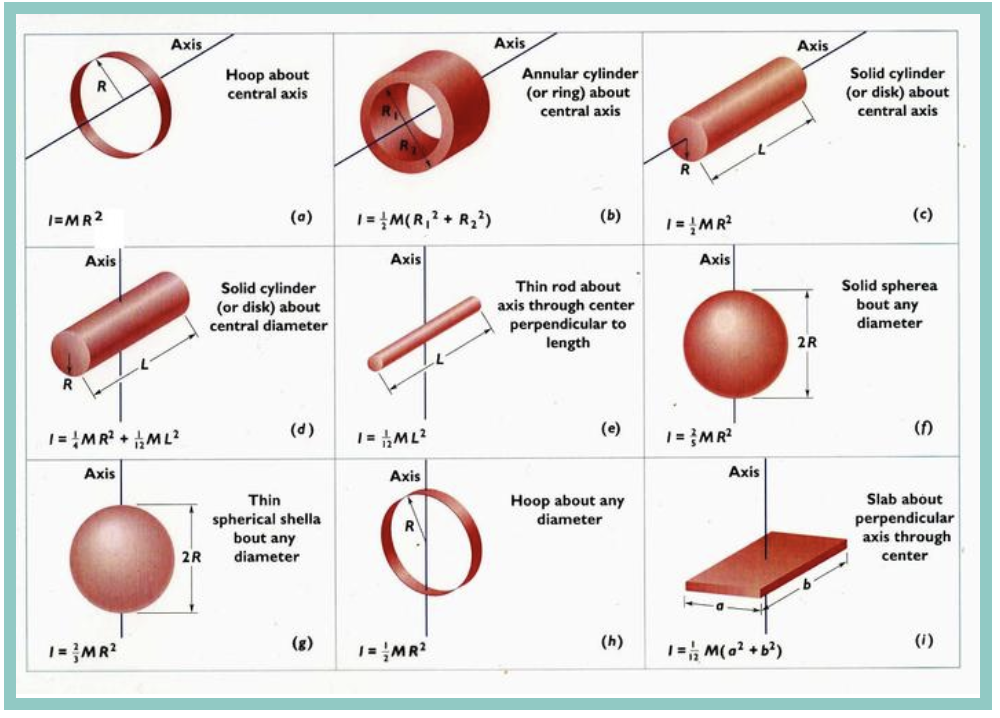 Поскольку спица — это тонкий стержень, и ось ее вращения проходит через конец, то для нее справедлива формула, полученная в предыдущем пункте.

Что касается обода колеса, то его момент инерции аналогичен таковому для материальной точки, находящейся на расстоянии радиуса колеса и имеющей массу обода.

Складывая моменты инерции всех элементов, получаем:

I = n*m_c*r²/3 + m_o*r²

Здесь m_c и m_o — массы спицы и обода, соответственно, n — число спиц. Если все спицы весят намного меньше обода, тогда момент инерции колеса будет равен:

I =m_o*r², если n*m_c<<m_o

Знание величины I для колеса является важным при расчете скорости угловой и момента импульса вращения колес любого транспортного средства (автомобиля, велосипеда).

Момент инерции | Определение, формула и расчет

Пожалуйста, заполните следующую форму, чтобы ваше ответственное контактное лицо могло связаться с вами.

Тема (*)

Продажи

Сервис

Недостаточный вход

Компания (*)

Пожалуйста, заполните название компании

г -н

Ms.

Invalid.

Имя

Пожалуйста, введите имя

Фамилия (*)

Пожалуйста, введите фамилию

Фамилия

Неверный ввод

Улица, номер

Укажите улицу и номер

Почтовый индекс (*)

Пожалуйста, заполните почтовый индекс

Город (*)

Неверный ввод

Country (*)

Please Select—United KingdomUnited StatesIrelandIndia—AfghanistanAland IslandsAlbaniaAlgeriaAmerican SamoaAndorraAngolaAnguillaAntarcticaAntigua and BarbudaArgentinaArmeniaArubaAustraliaAustriaAzerbaijanBahamasBahrainBangladeshBarbadosBelarusBelgiumBelizeBeninBermudaBhutanBoliviaBonaire, Sint Eustatius and SabaBosnia and HerzegovinaBotswanaBouvet IslandBrazilBritish Indian Ocean TerritoryBruneiBulgariaBurkina FasoBurundiCambodiaCameroonCanadaCape VerdeCayman IslandsCentral African RepublicChadChileChinaChristmas IslandCocos (Keeling) IslandsColombiaComorosCongoCook IslandsCosta RicaCote d’ Ивуар (Берег Слоновой Кости)ХорватияКубаКюрасаоКипрЧехияДемократическая Республика КонгоДанияДжибутиДоминикаДоминиканская РеспубликаЭквадорЕгипетСальвадорЭкваториальная ГвинеяЭритреяЭстонияЭфиопияФолклендские (Мальвинские) островаФарерские островаФиджиФинляндияФранцияФранцузская ГвианаФранцузская ПолинезияФранцузские Южные ТерриторииГабонГрибияГамбияГрецияГрузияГермания landGrenadaGuadaloupeGuamGuatemalaGuernseyGuineaGuinea-BissauGuyanaHaitiHeard Island and McDonald IslandsHondurasHong KongHungaryIcelandIndiaIndonesiaIranIraqIrelandIsle of ManIsraelItalyJamaicaJapanJerseyJordanKazakhstanKenyaKiribatiKosovoKuwaitKyrgyzstanLaosLatviaLebanonLesothoLiberiaLibyaLiechtensteinLithuaniaLuxembourgMacaoMacedoniaMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall IslandsMartiniqueMauritaniaMauritiusMayotteMexicoMicronesiaMoldavaMonacoMongoliaMontenegroMontserratMoroccoMozambiqueMyanmar (Burma)NamibiaNauruNepalNetherlandsNew CaledoniaNew ZealandNicaraguaNigerNigeriaNiueNorfolk IslandNorth KoreaNorthern Mariana IslandsNorwayOmanPakistanPalauPalestinePanamaPapua New GuineaParaguayPeruPhillipinesPitcairnPolandPortugalPuerto RicoQatarReunionRomaniaRussiaRwandaSaint BarthelemySaint HelenaSaint Kitts and NevisSaint LuciaSaint MartinSaint Pierre and MiquelonSaint Vincent and the GrenadinesSamoaSan MarinoSao Tome and PrincipeSaudi ArabiaSenegalSerbiaSeychellesSierra LeoneS ingaporeSint MaartenSlovakiaSloveniaSolomon IslandsSomaliaSouth AfricaSouth Georgia and the South Sandwich IslandsSouth KoreaSouth SudanSpainSri LankaSudanSurinameSvalbard and Jan MayenSwazilandSwedenSwitzerlandSyriaTaiwanTajikistanTanzaniaThailandTimor-Leste (East Timor)TogoTokelauTongaTrinidad and TobagoTunisiaTurkeyTurkmenistanTurks and Caicos IslandsTuvaluUgandaUkraineUnited Arab EmiratesUnited KingdomUnited StatesUruguayUzbekistanVanuatuVatican CityVenezuelaViet NamVirgin Islands, BritishVirgin Islands, USWallis and FutunaWestern SaharaYemenZambiaZimbabwe

Выберите страну

Код страны

Неверный ввод

Телефон

Неверный ввод

CompletePhone

Неверный ввод

Сообщение

Неверный ввод

Spamschutz (*)

Защита от спама не удалась.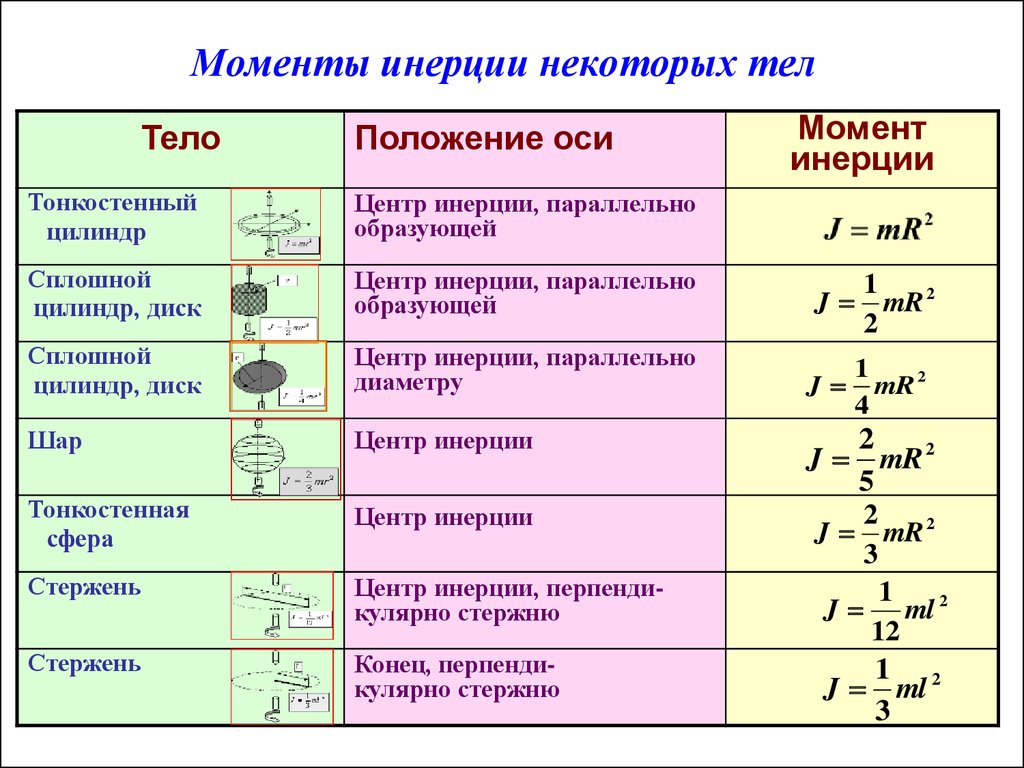

Поля, отмеченные звездочкой (*), обязательны для заполнения.

Как рассчитать импульс инерции для различных форм и твердых тел

В физике при расчете момента инерции объекта необходимо учитывать не только массу объекта, но и распределение массы. Например, если два диска имеют одинаковую массу, но у одного вся масса приходится на ободок, а другой твердый, то диски будут иметь разные моменты инерции.

Вычисление моментов инерции довольно просто, если вам нужно исследовать орбитальное движение небольших точечных объектов, где вся масса сосредоточена в одной конкретной точке на заданном радиусе р . Например, для мяча для гольфа, который вы вращаете на веревке, момент инерции зависит от радиуса круга, по которому вращается мяч:

I = мр ²

Здесь r — радиус окружности от центра вращения до точки, в которой сосредоточена вся масса мяча для гольфа.

Однако, когда вы входите в мир без мячей для гольфа, хруст чисел может стать немного затруднительным, потому что вы можете не знать, какой радиус использовать.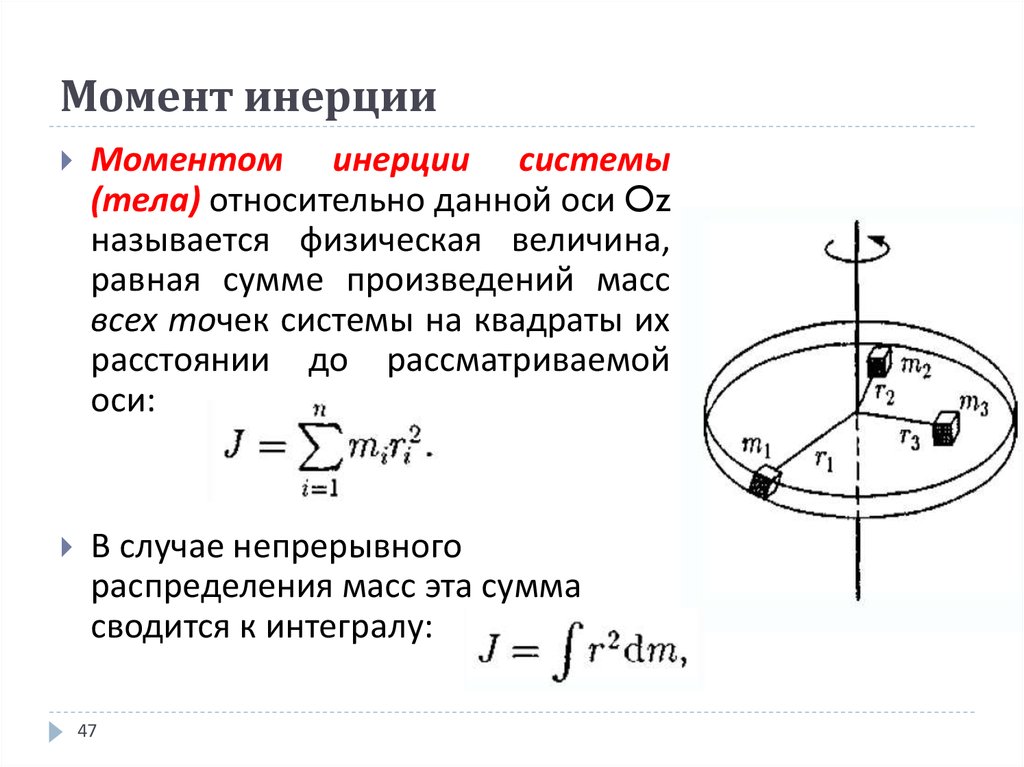 Что делать, если вы крутите удочку? Вся масса стержня не сосредоточена на одном радиусе. Когда у вас есть протяженный объект, такой как стержень, каждая частица массы находится на другом радиусе. У вас нет простого способа справиться с этим, поэтому вы должны суммировать вклад каждой частицы массы на каждом другом радиусе следующим образом:

Вы можете использовать эту концепцию суммирования моментов инерции всех элементов, чтобы получить сумму, чтобы вычислить момент инерции любого распределения массы. Вот пример использования двух точечных масс, который немного сложнее, чем одна точечная масса. Скажем, у вас есть два мяча для гольфа, и вы хотите узнать, каков их суммарный момент инерции. Если у вас есть мяч для гольфа с радиусом r ₁ и другой с радиусом r ₂ , общий момент инерции равен

Так как же найти момент инерции, скажем, диска, вращающегося вокруг оси, проходящей через его центр? Вы должны разбить диск на крошечные шарики и сложить их все вместе. Вы завершаете это, используя исчисление процесса интегрирования.

Формы, соответствующие моментам инерции в таблице.

Надежные физики уже выполнили эту задачу для многих стандартных форм; В следующей таблице приведен список объектов, с которыми вы, вероятно, столкнетесь, и их моменты инерции. На рисунке изображены формы, которым соответствуют эти моменты инерции.

Эта статья из книги:

• Физика I для чайников,

Об авторе книги:

Доктор Стивен Хольцнер написал более 40 книг по физике и программированию. Он был редактором журнала PC Magazine и преподавал в Массачусетском технологическом институте и Корнелле. Он является автором книг для чайников, в том числе «Физика для чайников», и «Основы физики для чайников». Доктор Хольцнер получил докторскую степень в Корнелле.