Переменный ток — Википедия

     Синусоидальный

Переме́нный ток — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным^[1].

Хотя переменный ток часто переводят на английский как alternating current, эти термины не эквивалентны. Термин alternating current (AC) в узком смысле означает синусоидальный ток, в широком смысле — периодический знакопеременный ток (то есть периодический двунаправленный ток). Условное обозначение на электроприборах: ∼{\displaystyle \thicksim } или ≈{\displaystyle \thickapprox } (знак синусоиды), или латинскими буквами AC{\displaystyle AC}.

Так как переменный ток в общем случае меняется в электрической цепи не только по величине, но и по направлению, то одно из направлений переменного тока в цепи считают условно положительным, а другое, противоположное первому, условно отрицательным. В соответствии с этим и величину мгновенного значения переменного тока в первом случае считают положительной, а во втором случае — отрицательной.

Переменный ток — величина алгебраическая, знак его определяется тем, в каком направлении в рассматриваемый момент времени протекает ток в цепи — в положительном или отрицательном.

Величина переменного тока, соответствующая данному моменту времени, называется мгновенным значением переменного тока.

Максимальное мгновенное значение переменного тока, которое он достигает в процессе своего изменения, называется

амплитудой тока Im{\displaystyle I_{m}}.

График зависимости переменного тока от времени называется развёрнутой диаграммой переменного тока.

Развёрнутая диаграмма переменного синусоидального тока

На рисунке приведена развёрнутая диаграмма переменного тока, изменяющегося с течением времени по величине и направлению. На горизонтальной оси 0t{\displaystyle 0t} отложены в определённом масштабе отрезки времени, а по вертикальной оси — величины тока, вверх — от начальной точки 0{\displaystyle 0} — положительные, вниз — отрицательные. Часть развёрнутой диаграммы тока, расположенная выше оси времени 0t{\displaystyle 0t}, характеризует изменение положительных величин во времени, а часть, расположенная ниже оси времени 0t{\displaystyle 0t}, — изменение отрицательных величин.

В начальный момент времени t=0{\displaystyle t=0} ток равен нулю (i=0){\displaystyle (i=0)}. Затем он с течением времени растёт в положительном направлении, в момент времени t=T4{\displaystyle t={\frac {T}{4}}} достигает максимального значения, после чего убывает по величине и в момент времени t=T2{\displaystyle t={\frac {T}{2}}} становится равным нулю. Затем, пройдя через нулевое значение, ток меняет свой знак на противоположный, то есть становится отрицательным, затем растёт по абсолютной величине, затем достигает максимума при t=34T{\displaystyle t={\frac {3}{4}}T}, после чего убывает и при t=T{\displaystyle t=T} становится равным нулю.

Развёрнутая диаграмма периодического переменного тока

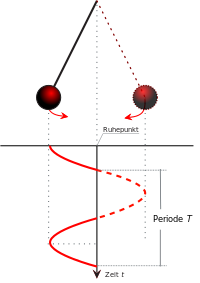
Периодическим переменным током называется такой электрический ток, который через равные промежутки времени повторяет полный цикл своих изменений, возвращаясь к своей исходной величине.

На представленной диаграмме мы видим, что через равные промежутки времени T{\displaystyle T} график тока воспроизводится полностью без каких-либо изменений.

Время T{\displaystyle T}, в течение которого переменный периодический ток совершает полный цикл своих изменений, возвращаясь к своей исходной величине, называется

периодом переменного тока.

Величина, обратная периоду, называется частотой переменного тока:

f=1T{\displaystyle f={\frac {1}{T}}}, где

f{\displaystyle f} — частота переменного тока;

T{\displaystyle T} — период переменного тока.

Если выразить время T{\displaystyle T} в секундах (sec), то будем иметь:

f=1T[1sec]{\displaystyle f={\frac {1}{T}}\left[{\frac {1}{sec}}\right]}, то есть размерность частоты переменного тока выражается в 1/с.

Частота переменного тока численно равна числу периодов в секунду.

За единицу измерения частоты переменного тока принят 1 герц (

1 гц, 1 Гц, 1 Hz).

Герц — единица Международной системы единиц (СИ), названа в честь Генриха Герца. Через основные единицы СИ герц выражается следующим образом: 1 Гц = 1 с⁻¹. Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.

Частота переменного тока равна одному герцу, если период тока равен одной секунде (один полный цикл за одну секунду).

Стандарты частоты[править | править код]

В большинстве стран в электротехнике применяются частоты 50 или 60 Гц (60 Гц — этот вариант принят в США и Канаде). В некоторых странах, например, в Японии, используются оба стандарта (см. Промышленная частота переменного тока).

Частота 16 ⅔ Гц до сих пор используется в некоторых европейских железнодорожных сетях (Австрия, Германия, Норвегия, Швеция и Швейцария), частота 25 Гц — на старых железнодорожных линиях США.

(См. Электрификация железных дорог переменным током пониженной частоты).

В авиации и военной технике для снижения массы устройств или с целью повышения частоты вращения электродвигателей переменного тока применяется частота 400 Гц.

Число оборотов ротора n[1min]{\displaystyle n\left[{\frac {1}{min}}\right]} синхронного электродвигателя определяется по формуле:

n=60fp{\displaystyle n={\frac {60f}{p}}}, где

f{\displaystyle f} — частота переменного тока;

p{\displaystyle p} — число пар полюсов.

Так как минимальное число пар полюсов равно единице, тогда синхронный электродвигатель, работающий на переменном токе частотой 50 герц разовьёт 3 000 оборотов в минуту, а электродвигатель, работающий на переменном токе частотой 400 герц, разовьёт 24 000 оборотов в минуту. Частота вращения ротора асинхронного электродвигателя меньше, чем частота питающего его тока и зависит от нагрузки. Скольжение — разность между частотой вращения вращающегося магнитного поля и частотой вращения ротора.

В технике связи применяются частоты более высокие, и в частности в радиотехнике — порядка миллионов и миллиардов герц.

Синусоидальным током называется периодический переменный ток, который с течением времени изменяется по гармоническому закону синуса.

Синусоидальный ток — элементарный, то есть его невозможно разложить на другие более простые переменные токи^[2].

Переменный синусоидальный ток выражается формулой:

i=Imsin⁡ωt{\displaystyle i=I_{m}\sin \omega t}, где

Im{\displaystyle I_{m}} — амплитуда синусоидального тока;

ωt{\displaystyle \omega t} — некоторый угол, называемый фазой синусоидального тока.

Фаза синусоидального тока ωt{\displaystyle \omega t} изменяется пропорционально времени t{\displaystyle t}.

Множитель ω{\displaystyle \omega }, входящий в выражение фазы ωt{\displaystyle \omega t} — величина постоянная, называемая угловой частотой переменного тока (круговой частотой переменного тока).

Угловая частота ω{\displaystyle \omega } синусоидального тока зависит от частоты f{\displaystyle f} этого тока и определяется формулой:

ω=2πf=2πT{\displaystyle \omega =2\pi f={\frac {2\pi }{T}}}, где

ω{\displaystyle \omega } — угловая (круговая) частота синусоидального тока;

f{\displaystyle f} — частота синусоидального тока;

T{\displaystyle T} — период синусоидального тока;

2π{\displaystyle 2\pi } — центральный угол окружности, выраженный в радианах.

Исходя из формулы ω=2πf=2πT{\displaystyle \omega =2\pi f={\frac {2\pi }{T}}}, можно определить размерность угловой (круговой) частоты:

[ω]=[2πT]=[1sec]{\displaystyle \left[\omega \right]=\left[{2\pi \over T}\right]=\left[{1 \over sec}\right]}, где

sec{\displaystyle sec} — время в секундах,

2π{\displaystyle 2\pi } — угол в радианах, является безразмерной величиной.

Фаза ωt{\displaystyle \omega t} синусоидального тока измеряется радианами.

1 радиан = 57,29° = 57°17′, угол 90° = π2{\displaystyle \pi \over 2} радиан, угол 180° = π{\displaystyle \pi } радиан, угол 270° = 3π2{\displaystyle 3\pi \over 2} радиан, угол 360° = 2π{\displaystyle 2\pi } радиан,
где π=3,14{\displaystyle \pi =3,14} радиан; π{\displaystyle \pi } — число «Пи»,

° — угловой градус и ′ — угловая минута.

---

Формула i=Imsin⁡ωt{\displaystyle i=I_{m}\sin \omega t} описывает случай, когда наблюдение за изменением переменного синусоидального тока начинается с момента времени t=0{\displaystyle t=0}. Если начальный момент времени не равен нулю, тогда формула для определения мгновенного значения переменного синусоидального тока принимает следующий вид:

i=Imsin⁡(ωt+ψ){\displaystyle i=I_{m}\sin(\omega t+\psi )}, где

(ωt+ψ){\displaystyle (\omega t+\psi )} — фаза переменного синусоидального тока;

ψ{\displaystyle \psi } — угол, называемый начальной фазой переменного синусоидального тока

.

Если в формуле i=Imsin⁡(ωt+ψ){\displaystyle i=I_{m}\sin(\omega t+\psi )} принять t=0{\displaystyle t=0}, то будем иметь

ωt=0{\displaystyle \omega t=0}, ωt+ψ=ψ{\displaystyle \omega t+\psi =\psi } и it=0=Imsin⁡ψ{\displaystyle i_{t=0}=I_{m}\sin \psi }.

Начальная фаза — это фаза синусоидального тока в момент времени t=0{\displaystyle t=0}.

Начальная фаза переменного синусоидального тока может быть положительной (ψ>0){\displaystyle (\psi >0)} или отрицательной (ψ<0){\displaystyle (\psi <0)} величиной. При ψ>0{\displaystyle \psi >0} мгновенное значение синусоидального тока в момент времени t=0{\displaystyle t=0} положительно, при ψ<0{\displaystyle \psi <0} — отрицательно.

Если начальная фаза ψ=π2{\displaystyle \psi ={\frac {\pi }{2}}}, то ток определяется по формуле i=Imsin⁡(ωt+π2){\displaystyle i=I_{m}\sin(\omega t+{\frac {\pi }{2}})}. Мгновенное значение его в момент времени t=0{\displaystyle t=0} равно

it=0=Imsin⁡π2=Im{\displaystyle i_{t=0}=I_{m}\sin {\frac {\pi }{2}}=I_{m}}, то есть равно положительной амплитуде тока.

Если начальная фаза ψ=−π2{\displaystyle \psi =-{\frac {\pi }{2}}}, то ток определяется по формуле i=Imsin⁡(ωt−π2){\displaystyle i=I_{m}\sin(\omega t-{\frac {\pi }{2}})}. Мгновенное значение его в момент времени t=0{\displaystyle t=0} равно

it=0=Imsin⁡(−π2)=−Im{\displaystyle i_{t=0}=I_{m}\sin(-{\frac {\pi }{2}})=-I_{m}}, то есть равно отрицательной амплитуде тока.

Два синусоидальных тока совпадают по фазе друг с другом

Синусоидальные токи сдвинуты по фазе на угол π2{\displaystyle {\frac {\pi }{2}}}

Два переменных синусоидальных тока совпадают по фазе, если они имеют одинаковые фазы и, следовательно, одновременно достигают своих нулевых и максимальных значений одинакового знака.

На левой иллюстрации представлены развёрнутые диаграммы токов i1{\displaystyle i_{1}} и i2{\displaystyle i_{2}}. Токи i1=I1msin⁡ωt{\displaystyle i_{1}=I_{1m}\sin \omega t} и i2=I2msin⁡ωt{\displaystyle i_{2}=I_{2m}\sin \omega t} совпадают по фазе.

Два переменных синусоидальных тока сдвинуты по фазе относительно друг друга, если они имеют различные фазы.

На правой иллюстрации токи i1=I1msin⁡(ωt+π2){\displaystyle i_{1}=I_{1m}\sin(\omega t+{\frac {\pi }{2}})} и i2=I2msin⁡ωt{\displaystyle i_{2}=I_{2m}\sin {\omega t}} сдвинуты по фазе на угол π2{\displaystyle {\frac {\pi }{2}}}, так как

(ωt+π2)−ωt=π2{\displaystyle (\omega t+{\frac {\pi }{2}})-{\omega t}={\frac {\pi }{2}}}.

Ток i1{\displaystyle i_{1}} опережает по фазе ток i2{\displaystyle i_{2}} на угол π2{\displaystyle {\frac {\pi }{2}}}, или, иначе, ток i2

типы проводников электрического тока, характеристики

Открытия, которые связаны с электричеством, существенно поменяли жизнь современного человека. Применяя электроток в качестве источника энергии, удалось сделать технологический прорыв, облегчивший существование человечества. На сегодняшний день электричество приводит в действие токарные станки, авто, роботизированную технику, предоставляет связь. В связи с этим важно понять, какие бывают виды тока и принцип их действия.

Что это такое

Электроток — направленное передвижение электрическим полем заряженных элементов. Носители зарядов металлопроводников — электроны, а кислотных и солевых растворов — ионы. Полупроводниковые носители зарядов именуются электронами и «дырками».

Электрический ток

Чтобы ток существовал, требуется постоянно поддерживать электрополе. Должна быть разница потенциалов, которая поддерживает само поле. Пока такие условия не будут выполнены, заряды упорядоченно перемещаются по замкнутой электроцепи.

Подобные условия возможно создать, к примеру, посредством электрофорной машины. Когда 2 диска вращаются в обратных направлениях, они заряжаются разноименными зарядами. На щётках, которые прилегают к дискам, возникает разница потенциалов. Соединяя контакты, частицы начинают перемещаться упорядоченно. В такой ситуации машина становится электрическим источником.

Что представляет собой ток 

Характеристики

Исследовав электрический ток и его ключевые характеристики, возможно понять принцип его функционирования. Главными величинами электрической энергии являются напряжение, сила и сопротивление.

Сила и плотность тока

Чтобы описать характеристики электричества, зачастую применяют термин «сила тока». Он определяет интенсивность перемещения зарядов, которые проходят сквозь поперечное сечение проводника.

Плотность тока является векторной величиной. Вектор направляется в сторону движения положительно заряженных зарядов. Его модуль равняется соотношению силы электротока на определенном перпендикулярном по направлению перемещения зарядов сечении проводника к его площади. Измерение происходит в амперах на метр.

Плотность тока

Мощность

Электрические силы осуществляют работу против активного и реактивного сопротивления. На пассивных работах будет преобразовываться в теплоэнергию. Производительностью называется работа, которая выполнена за 1 врем. ед. Относительно электричества применяется понятие «мощность теплопотерь». Мощность теплопотерь проводника равняется силе тока, которая умножена на напряжение. Измеряется мощность в ваттах.

Мощность

Частота

Ток характеризует частота. Такой параметр покажет, как за врем. ед. меняется число колебаний. Частота измеряется в герцах. Обычная промышленная частота составит 50 Гц.

Частота

Ток смещения

Такой термин был введен для комфорта, хотя в привычном понимании его не назовешь током, поскольку нет переноса заряда. Интенсивность электромагнитного поля находится в зависимости от токопроводимости и смещения.

Токи смещения возможно увидеть в конденсаторе. Невзирая на то, что во время зарядки и разрядки меж обкладок конденсатора не перемещается заряд, ток смещения будет протекать сквозь конденсатор и замыкать электроцепь.

Ток смещения

Как работает

Условия существования электротока предполагают действие заряженных частиц, проводника и напряжения. Большинство специалистов исследовали электричество и установили, что есть 2 его разновидности: статическая и текущая.

Непосредственно текущая имеет важное значение в ежедневной жизни каждого человека, поскольку является электротоком, проходящим через электроцепь. Человек каждый день использует его, чтобы питать дома и др.

Типы проводников

Процессы образования электротока в разных средах отличаются определенными особенностями:

• В металлах заряд перемещается свободными отрицательными частицами — электронами. Само вещество не переносится — ионы металла останутся в узлах кристаллической решетки. В процессе нагрева хаотичные колебания ионов усилятся, что препятствует упорядоченному передвижению электронов.
• В жидкостях заряд перемещают ионы, формирование которых вызывает электролитическая диссоциация. Упорядоченное передвижение в такой ситуации является их перемещением к противоположно заряженным электродам, где они будут нейтрализованы и осядут.
• В газах под воздействием разницы потенциалов формируется плазма. Заряженные частицы — ионы, положительные и отрицательные, и свободные электроны, которые формируются под действием ионизатора.
• В вакууме электроток присутствует как электроны, движущиеся от катода к аноду.
• В полупроводниках будут участвовать электроны, которые перемещаются от 1 атома к 2, и формируются вакантные участки — дырки, считающиеся плюсовыми.

При невысокой температуре полупроводники приблизятся по качествам к изоляторам. В процессе повышения температурных показателей валентные электроны получат необходимую, чтобы разорвать связи, энергию и станут свободными. С увеличением температуры улучшается проводимость полупроводника.

Важно! Положительно заряженные ионы направляются к отрицательному электроду, отрицательные ионы — к плюсовому. Во время увеличения температурных показателей проводимость электролита возрастет, поскольку увеличивается количество разложившихся на ионы молекул.

Проводники тока

Виды

По типу генерации и характеристикам электроток бывает постоянным и переменным. Постоянный является таковым, который не обладает своим направлением. Он будет течь в любом случае в одну сторону. Переменный время от времени изменяет направленность. Таковым считается любой ток, помимо постоянного. Когда мгновенные показатели повторятся в той же последовательности спустя одинаковые временные интервалы, то подобный электрический ток называется периодическим.

Постоянный

Рассматриваемый ток тот, который на протяжении определенного временного промежутка не изменит собственной величине и направлению. Довольно часто постоянным считают пульсирующий электроток. Он отливается тем, что одинаковое число зарядов регулярно сменяются между собой в одну сторону.

Важно! В процессе определения направления бывают разбежности. Когда электроток формируется передвижением положительных частиц, то направление будет соответствовать перемещению частиц. Когда он сформирован передвижением отрицательных частиц, то направление считается противоположным движению частиц.

Основным достоинством станет то, что его возможно накопить. Делается это собственноручно, с помощью аккумуляторов либо конденсаторов.

Постоянный ток

Переменный

Для понимания сущности переменного электротока требуется представить синусоиду. Непосредственно она наилучшим образом сможет охарактеризовать изменения в постоянном токе. Переменный электроток постоянно изменяет собственную полярность. Во время одного интервала он положительный, других отрицательный. Для него немаловажным фактором станет скорость смены полярности (частота).

Большинство техники функционирует на переменном токе отличных частот. Благодаря изменениям в частоте возможно менять скорость вращения мотора.

Важно! Увидеть наглядный пример возможно, осмотрев обыкновенную лампу. В частности это заметно на некачественной диодной лампочке. В процессе функционирования на постоянном электротоке они будут гореть равномерным светом, а на переменном еле уловимо мерцать.

Переменный ток

Источники тока

Первоисточниками электроэнергии, которые нашли применение на практике, стали гальванические элементы. После усовершенствования они используются и сегодня. Их применяют для энергопитания дистанционных пультов, электронных часов, устройств для детей и различных приборов. С появлением генераторов переменного тока электроэнергия стала использоваться еще интенсивнее. В связи с этим, следует ознакомиться с основными типами источников тока.

Механические источники

В них преобразуется механическая энергия в электричество. Процесс происходит в спецустройствах — генераторах. Главными из них считаются турбогенераторы, где электромашина будет приведена в действие с помощью газового либо парового потока, и гидрогенераторы, которые преобразуют энергию воды в электричество. Основная часть электрической энергии на планете производят непосредственно механические преобразователи.

Механические источники

Тепловые источники

Тут происходит преобразование теплоэнергии в электрическую. Появление электротока обусловливается разницей температурных показателей 2 пар контактирующих металлов. В такой ситуации заряженные частицы перемещаются в сторону холодного участка. Величина электротока будет зависеть непосредственно от температурной разницы: чем она выше, тем сильнее ток. Термопары из полупроводников дают термоэдс выше, чем биметаллические, потому они используются для изготовления источников электротока. Термопары из металла применяют только, чтобы измерять температурные показатели.

Тепловые источники

Световые источники

Когда начала развиваться физика полупроводников, стали появляться новые токоисточники — солнечные аккумуляторы, где световая энергия будет преобразовываться в электрическую. Они используют качество полупроводников выдачи напряжения во время действии на них светопотока. В частности такой эффект заметен в полупроводниках из кремния. Однако коэффициент полезного действия подобных элементов не превысит 15%. Солнечные аккумуляторы нашли свое применение в космической сфере, в бытовой. Стоимость на данные источники энергопитания регулярно уменьшается, однако по-прежнему высока.

Световые источники

Химические источники

Их возможно разделить на несколько групп:

• Гальванические;
• Аккумуляторы;
• Тепловые.

Гальванические функционируют благодаря взаимодействию 2 различных металлов, которые помещены в электролит. В виде пар металлов и электролита выступают различные химэлементы и соединения. Это определяет разновидность и параметры элемента.

Важно! Гальванические элементы применяются лишь 1 раз, когда разрядятся их не удастся восстановить.

Дешевизна материалов и простота производства аккумуляторов делает их наиболее дешевыми из доступных. Однако по параметрам они существенно уступят щелочным и литиевым.

Химические источники

 

Тепловые выступают в качестве источников резервного энергопитания. Они обладают отличными характеристиками по удельной плотности электротока, однако отличаются непродолжительным сроком эксплуатации (до 60 минут). Используются преимущественно в космической отрасли, где требуются точность и кратковременное функционирование.

Как правильно применяются

Вне зависимости от принципа функционирования какого-либо источника электротока, в каждом из разделяются электрозаряды физ.тел. Происходит преобразование какой-либо разновидности энергии в электричество.

Такая энергия в технике применяется повсюду. В любом жилище возможно отыскать быттехнику, существенно облегчающую ведение хозяйства. Помимо этого, предотвращается появление пыли, копоти и других неприятных эффектов использования плит и прочих приборов, актуальных до возникновения электричества.

В промышленной сфере электрическая энергия имеет важную роль. Использование тока дает возможность существенно уменьшить траты, так как такой тип энергии дешевле горючего.

Меры безопасности

Главным правилом безопасности во время работы с токами станет то, что перед любыми действиями требуется обесточить электросеть. В процессе работ также необходимо следовать таким рекомендациям:

• Запрещено ремонтировать включенное в электросеть приспособление.
• При осуществлении работ на электрощитке должно присутствовать предупреждение.
• Работа с высоким напряжением допустимо лишь с помощником.
• Требуется наблюдать за изоляцией каждого провода и контролировать заземление.

Напряжение свыше 24 вольт будет опасно для жизни. Во время работы с напряжением больше данного параметра требуется спецдопуск. При работах необходимо пользоваться специнструментами с повышенным уровнем защиты.

Правила безопасности

Использование электротока разнообразно, так как без него нельзя представить сегодня жизнь. Необходимо понять принципы его функционирования для направления электроэнергии в правильное русло. Электроток течет по законам физики, используемым для создания разнообразных приспособлений. Чтобы грамотно использовать его, требуется ознакомиться с основными электровеличинами.

2. Формы волн переменного тока | 1. Основы теории переменного тока | Часть2

2. Формы волн переменного тока

Формы волн переменного тока

Когда генератор вырабатывает напряжение переменного тока, это напряжение определенным образом меняет свою полярность с течением времени. Если посмотреть на график изменения полярности переменного напряжения, то можно увидеть «волну», известную как синусоида:

 

 

На графике напряжения, генерируемого электромеханическим генератором, изменение полярности происходит плавно, уровень напряжения меняется наиболее быстро на нулевой линии («точка пересечения») и наиболее медленно на пике. Если графически изобразить синусоидальную функцию в диапазоне от 0 до 360 градусов, то мы получим то же чередование, что представлено в таблице ниже:

 

Угол (o)	Синус угла	волна	Угол (o)	Синус угла	волна
0	0.0000	ноль	180	0.0000	ноль
15	0.2588	+	195	-0.2588	—
30	0.5000	+	210	-0.5000	—
45	0.7071	+	225	-0.7071	—
60	0.8660	+	240	-0.8660	—
75	0.9659	+	255	-0.9659	—
90	1.0000	+максимум	270	-1.0000	-минимум
105	0.9659	+	285	-0.9659	—
120	0.8660	+	300	-0.8660	—
135	0.7071	+	315	-0.7071	—
150	0.5000	+	330	-0.5000	—
165	0.2588	+	345	-0.2588	—
180	0.0000	ноль	360	0.0000	ноль

 

Причина, по которой электромеханический генератор  выдает переменный ток в виде синусоиды, тесно связана с физическими процессами его работы. Напряжение, возникающее на неподвижных обмотках при вращении магнита, пропорционально скорости изменения магнитных силовых линий, расположенных перпендикулярно обмоткам (Закон электромагнитной индукции Фарадея). Эта скорость будет наибольшей в моменты прохождения полюсов магнита в непосредственной близости от обмоток, и наименьшей, когда полюсы магнита находятся дальше всего от обмоток. Математически, скорость изменения магнитного потока при вращении магнита соответствует функции синусоиды, из чего можно сделать вывод, что напряжение, возникающее на обмотках, подчиняется той же функции.

Если проследить за изменением напряжения (возникающего на генераторе переменного тока) от любой точки синусоиды до точки, в которой форма волны начинает повторяться, мы увидим один цикл волны. Его легче всего заметить, если посмотреть на часть синусоиды между двумя максимумами или минимумами, а также между любыми соответствующими точками на графике. Отметки на горизонтальной оси графика представляют собой область синусоиды, а также угловое положение вала генератора при вращении (см. рисунок ниже).

 

 

Поскольку горизонтальная ось данного графика может обозначать как положение вала в градусах, так и время, циклы чаще всего измеряются в единицах времени: в секундах или долях секунды. В ходе измерений один цикл часто называют периодом волны. Период волны всегда составляет 360°, и время его прохождения зависит от скорости колебаний напряжения.

Более популярной мерой описания изменений напряжения переменного тока является скорость его колебаний или частота. Единицей измерения частоты является герц (Гц). Один Герц означает одно колебание волны (один полный цикл) за одну секунду.  В Соединенных Штатах Америки стандартом сетевого напряжения принята частота 60 Гц. Это означает, что напряжение переменного тока совершает 60 полных циклов колебаний в секунду. В Европе и России, где стандарт частоты для линий электропередач составляет 50 Гц,  напряжение переменного тока совершает 50 полных циклов колебаний в секунду. Радиопередатчик, вещающий на частоте 100 МГц, совершает 100 миллионов циклов колебаний в секунду.

До введения Герца частота просто выражалась как количество циклов в секунду. На старых измерительных приборах вместо Гц можно встретить старое обозначение ЦВС (Циклов В Секунду). Многие думают, что замена такой понятной единицы как «цикл в секунду» на герц влечет за собой потерю ясности. Подобное изменение произошло, когда стоградусная шкала для измерения температуры была заменена шкалой Цельсия. В наименовании «стоградусная шкала»  отражены температуры таяния и кипения воды.  Использование же имени собственного (Цельсий),  никак не объясняет происхождение и значение единицы измерения.

Период и частота математически обратны друг другу. То есть, если период волны составляет 10 секунд, ее частота будет равна 0,1 Гц, или 1/10 цикла в секунду:

 

 

На рисунке ниже вы можете увидеть осциллограф. Этот прибор используется для  отображения изменений напряжения во времени на графическом экране. Вам  наверняка знакомы электрокардиографы, используемые в медицине для определения частоты сердечных ударов пациента в определенный промежуток времени. Электрокардиограф – это особый вид осциллографа, специально сконструированный для медицинских целей. Осциллографы общего назначения способны отображать на своем экране напряжения любых источников, представляя их в виде графика (с учётом времени в качестве независимой переменной). Знание взаимосвязи между периодом и частотой очень поможет вам при анализе напряжения переменного тока на экране осциллографа. Измеряя период волны на горизонтальной оси экрана осциллографа, и соотнося его со значением времени (в секундах), можно определить частоту в герцах.

 

 

Напряжение и ток никоим образом не являются единственными физическими переменными, подверженными изменению во времени. В повседневной жизни мы гораздо чаще сталкиваемся с таким явлением, как звук. Звук представляет собой попеременное сжатие и декомпрессию  молекул воздуха (продольные волны), субъективно интерпретируемые слухом как физическое ощущение. Поскольку переменный ток – это волновое явление, его поведение сходно с другими волновыми явлениями, в том числе и со звуком. По этой причине, звук (в особенности структурированная музыка) представляет собой отличную аналогию для понимания концепции переменного тока.

В музыкальных терминах частота эквивалентна высоте звука. Низкие ноты (туба или фагот) состоят из относительно медленных вибраций воздушных молекул (низкая частота). Высокие ноты (флейта или свисток) состоят из тех же вибраций воздуха, но колеблющихся с много большей скоростью (высокая частота). На рисунке ниже представлена таблица, представляющая фактические частоты для ряда обычных музыкальных нот.

 

 

Самые наблюдательные из вас заметят, что все ноты данной таблицы, обозначенные одним буквенным символом, имеют соотношение по частоте равное 2:1. Например, частота первой ноты, обозначенной буквой А (нота ля), составляет 220 Гц. Частота следующей по высоте ноты ля составляет уже 440 Гц (ровно в два раза больше циклов звуковой волны в секунду). Тот же коэффициент 2:1 имеет место для первой ноты ля-диез (233,08 Гц) и для следующей ноты ля-диез (466,16 Гц), а также для всех подобных пар нот в таблице.

На слух две ноты, частота которых различается в два раза, звучат как один и тот же звук. Такое сходство в звучании общепризнано в музыке, а самый короткий промежуток звукоряда, разделяющий одинаковые пары нот, называется октавой. Согласно этому правилу, следующая по высоте нота ля (на одну октаву выше от 440 Гц) будет иметь частоту 880 Гц, а частота ноты ля одной октавой ниже 220 Гц. будет равна 110 Гц. Вид клавиатуры пианино поможет нам расставить все по своим местам (cм. рисунок ниже).

 

 

Как видно, одна октава равна семи белым клавишам на клавиатуре пианино. Известная музыкальная символика (до-ре-ми-фа-соль-ля-си) –, а именно этот шаблон обессмертил причудливую песенку Роджерса и Хаммерстайна в «Звуках музыки» — составляет одну октаву от одной ноты «до» до другой.

Несмотря на то, что электромеханические генераторы  и многие другие физические явления как правило выдают синусоиды, это не единственный существующий вид переменной волны. Электронные схемы могут генерировать и другие формы волн переменного тока. На рисунке ниже вы можете увидеть некоторые из них.

 

 

Эти формы волн ни в коем случае не охватывают все существующие волны в природе. Они представляют собой лишь зафиксированные под определенными названиями наиболее распространенные типы волн. Даже в цепях, в которых теоретически должны возникать «чистая» синусоида, квадрат, треугольник или зуб пилы, в реальности формируются искаженные версии перечисленных типов волн. Некоторые формы волн имеют настолько сложную структуру, что она не поддается какой либо классификации. Для упрощения ситуации можно сказать, что любая форма кривой, имеющая близкое сходство с правильной синусоидой именуется синусоидальной, а любая другая классифицируется как несинусоидальная.  При разработке электронных схем всегда нужно учитывать формы волн переменного тока, так как от этого зависит функционирование схемы в целом.

Переменный электрический ток

В данной статье расскажем что такое переменный электрический ток и трехфазный переменный переменный ток.

Понятие переменного электрического тока даётся в учебнике физики общеобразовательного учебного заведения — школы. Переменный электрический ток — ток имеющий форму гармонического синусоидального сигнала, основными характеристиками которого являются действующее напряжение и частота, с течением времени изменяется по направлению и величине.

Частота – это количество полных изменений полярности переменного электрического тока за одну секунду. Это означает, что ток, в обычной бытовой розетке частотой 50 Герц за одну секунду меняет своё направление с положительного значения на отрицательное и обратно ровно пятьдесят раз. Одно полное изменение направления (полярности) электрического тока с положительного значения на отрицательное и снова на положительное называют — периодом колебания электрического тока. В течение периода Т переменный электрический ток меняет своё направление дважды.

Для визуального наблюдения синусоидальной формы переменного тока обычно используют осциллограф. Для исключения поражения электрическим током и защиты осциллографа от сетевого напряжения по входу, используют разделительные трансформаторы. Для измерения периода нет разницы, по каким равнозначным (равноамплитудным) точкам его измерять. Можно по максимальным положительным, или отрицательным вершинам, а можно и по нулевому значению. Это поясняется на рисунке.

Синусоидальная форма переменного тока

Из учебника физики мы знаем, что переменный электрический ток вырабатывается с помощью электрической машины – генератора. Простейшая модель генератора это магнитная рамка, вращающаяся в магнитном поле постоянного магнита.

Представим себе прямоугольную проволочную рамку с несколькими витками, равномерно вращающуюся в однородном магнитном поле. Возникающая в этой рамке э.д.с. индукции меняется по синусоидальному закону. Период колебания Т переменного электрического тока – это один полный оборот магнитной рамки вокруг своей оси.

магнитная рамка

Одними из важных характеристик электрического тока являются две величины переменного электрического тока – максимальное значение и среднее значение.

Максимальное значение напряжения электрического тока Umax — это величина напряжения, соответствующая максимальному значению синусоиды.

Среднее значение напряжения электрического тока Uср — это величина напряжения, равная значению 0,636 от максимального. Математически это выглядит так:

U_ср = 2 * U_max / π = 0,636 U_max

Синусоиду максимального напряжения можно проконтролировать на экране осциллографа. Понять, что такое среднее значение переменного электрического напряжения можно проведя эксперимент по рисунку и описанию ниже.

Осциллограмма полуволны

Используя осциллограф, подключите к его входу синусоидальное напряжение. Ручкой вертикального смещения развёртки переместите «ноль» развёртки на самую нижнюю линию шкалы экрана осциллографа. Растяните и сместите горизонтальную развёртку так, чтобы одна полуволна синусоидального напряжения поместилась в десять (пять) клеток экрана осциллографа. Ручкой вертикальной развёртки (усилением) растяните развёртку так, чтобы максимальная амплитуда полуволны поместилась ровно в десять (пять) клеток экрана осциллографа. Определите амплитуду синусоиды на десяти участках. Суммируйте все десять значений и поделите на десять – найдите его «средний балл». В результате Вы получите значение напряжения, приблизительно равное 6,36 от его максимального значения — 10.

Измерительные приборы – вольтметры, цешки, мультиметры для измерения переменного напряжения имеют в своей схеме выпрямитель и сглаживающий конденсатор. Эта цепочка «округляет» множитель разницы максимального и измеряемого напряжения до числа 0,7. Поэтому, если Вы будете наблюдать на экране осциллографа синусоиду напряжения амплитудой 10 вольт, то вольтметр (цешка, мультиметр) покажет не 10, а около 7 вольт. Вы думаете что в Вашей домашней розетке – 220 вольт? Так и есть, но не совсем так! 220 вольт – это среднее значение напряжения бытовой розетки, усреднённое измерительным прибором — вольтметром. Максимальное же напряжение следует из формулы:

U_max = U_изм / 0,7 = 220 / 0,7 = 314,3 вольт

Именно поэтому, когда Вас «бъёт» током от электрической розетки 220 вольт, знайте, что это Ваша иллюзия. На самом деле, Вас трясёт напряжение около 315 вольт.

Трехфазный ток

Наряду с простым синусоидальным переменным током в технике широко используется так называемый трехфазный переменный ток. Мало того, трёхфазный электрический ток — это основной вид энергии используемый во всём мире. Трёхфазный ток приобрёл популярность по причине менее затратной передачи энергии на большие расстояния. Если для обычного (однофазного) электрического тока требуется два провода, то для трёхфазного тока, у которого энергия в три раза больше, требуется всего три провода. Физический смысл Вы узнаете в этой статье позже.

Представьте, если вокруг общей оси вращается не одна, а три одинаковые рамки, плоскости которых повернуты друг относительно друга на 120 градусов. Тогда возникающие в них синусоидальные э.д.с. также будут сдвинуты по фазе на 120 градусов (см. на рис).

Трехфазный электрический ток

Такие три согласованных переменных тока называют трехфазным током. Упрощённое расположение проволочных обмоток в генераторе трёхфазного тока иллюстрируется на рисунке.

Генератор трехфазного электрического тока

Подключение обмоток генератора по трём независимым линиям показано на рисунке ниже.

схема питания по независимым линиям

Такое подключение шестью проводами довольно громоздко. Так как для явлений в электрических цепях важны только разности потенциалов, то один проводник может использоваться сразу для двух фаз, без снижения нагрузочной способности по каждой из фаз. Другими словами, в случае подключения обмоток генератора по схеме «звезда» с использованием «нуля», передача энергии от трёх источников производится по четырём проводам (см. рис.), в которых один является общим – нулевым проводом.

схема питания по общим линиям

По трём проводам может передаваться энергия сразу от трёх (фактически независимых) источников электрического тока соединённых «треугольником».

схема питания по треугольнику

В промышленных генераторах и преобразующих трансформаторах «треугольником» обычно подключается межфазное напряжение 220 вольт. При этом «нулевой» провод отсутствует.

«Звезда» применяется для передачи напряжения сети с использованием «нуля». При этом на фазе относительно «нуля» действует напряжение 220 вольт. Межфазное напряжение при этом равно 380 вольт.

Частым явлением во времена «нагло ворующей демократии» было сгорание бытовой аппаратуры в квартирах добропорядочных граждан, когда из-за слабой проводки сгорал общий «ноль», тогда в зависимости от того, какое количество бытовых приборов включено в квартирах, горели телевизоры и холодильники у того, кто их меньше всего включал. Вызвано это явлением «перекоса фаз», которое возникало при обрыве нуля. В розетку добропорядочных граждан вместо 220 вольт устремлялось межфазное напряжение 380 вольт. До настоящего времени во многих коммуналках и сооружениях напоминающих жильё наших российских городов и весей это явление до конца не искоренилось.

Форма — ток — Большая Энциклопедия Нефти и Газа, статья, страница 1

Форма — ток

Cтраница 1

Форма тока зависит от числа фаз и имеет иные соотношения между средними, амплитудными и действующими значениями по сравнению с токами синусоид.  [2]

Форма тока через диод определяется по вольтамперной характеристике диода при заданной форме напряжения. Например, если диод Ганна работает в режиме с задержкой образования домена при пороговом напряжении, времена рекомбинации и формирования домена малы по сравнению с периодом колебаний и форма напряжения на диоде синусоидальная, то форма тока определяется по вольтамперной характеристике ( см. рис. 8.16) в виде цикла ABCDEFA.  [3]

Форма тока 1 К1 отличается от прямоугольной, так как в цепи транзистора 7 / включено индуктивное сопротивление обмотки wy ( рис. XJ.  [4]

Форма тока та же, что и у напряжения питания, — синусоидальная.  [6]

Форма тока во вторичной обмотке выпрямительного трансформатора отличается от синусоидальной главным образом потому, что включенные последовательно с обмоткой вентили пропускают через нее ток не в течение всего периода, как это имеет место в обычных трансформаторах, а лишь в течение некоторой его части. В зависимости от схемы выпрямления и способа соединения обмоток трансформатора ток в его вторичных обмотках может содержать как переменную, так и постоянную составляющую. Постоянная составляющая тока не может передаваться электромагнитным путем; поэтому кривая тока первичной обмотки не может содержать постоянной составляющей. В результате различия формы токов в первичной и вторичной обмотках их приведенные эффективные значения, а следовательно, и расчетные мощности обмоток могут отличаться по величине друг от друга. Если в обычном трансформаторе расчетные мощности обмоток примерно равны друг другу, то в выпрямительном трансформаторе расчетная мощность первичной обмотки может быть и меньше расчетной мощности вторичной обмотки. Указанное обстоятельство является основной особенностью выпрямительного трансформатора и должно быть учтено в процессе его расчета. Это обстоятельство, характерное для выпрямительных трансформаторов, работающих в однополупериодной, трехфазной и некоторых других схемах выпрямления, также должно быть учтено в процессе их расчета.  [7]

Форма тока в нагрузке id изображена на рис. 5.8 г. Как видно, ток в нагрузке пульсирует 6 раз за период частоты сети. Кривая напряжения Ud на нагрузке повторяет форму кривой тока.  [9]

Форма тока в анодной цепи зависит от режима работы.  [11]

Форма тока i, содержащего высшие гармоники, существенно отличается от формы напряжения ик на колебательном контуре, которая весьма близка к синусоидальной. Высшие гармоники проходя-т в основном через конденсатор С, почти не вызывая на нем падения напряжения.  [13]

Форма токов, проходящих через эти диоды, юказана на рис. 7 6 и в.  [15]

Страницы:      1    2    3    4    5

1. Электрический ток. Его виды.

Электрическим током называется направленное движение заряженных частиц. За направление тока принимается движение положительных зарядов.

Характеристики тока:

1. Сила тока — это скалярная физическая величина, равная отношению заряда, протекающего через поперечное сечение проводника, ко времени его протекания.

I = q/t

[ I ] = 1A

2. Плотность тока – величина, равная отношению силы тока к площади поперечного сечения проводника.

j = I/S

[ j ] = 1 A/м²

Постоянным называется ток, сила и направление которого с течением времени не изменяется.

I

t

Переменным называется ток, величина и направление которого изменяется с течением времени (например, это может быть периодический ток — здесь заряд , сила тока и напряжение изменяются по периодическим законам .

Различают ток проводимости– он обусловлен перемещением электронов металла относительно ионов решетки. При перемене полюсов заряды создают колебательное движение.

Различают также ток смещения– он обусловлен смещением электрических зарядов на границе проводник- диэлектрик.

По форме кривой зависимости Iотtразличают:

• синусоидальный ток;

• прямоугольный ток;

• треугольный ток;

• трапециевидный ток;

• игольчатоэкспаненциальный ток.

I

t

t

t

t

t

Для практических целей чаще применяется синусоидальный ток.

Переменный ток характеризуется действующими (эффективными) значениями силы тока и напряжения.

Iдейств. = Imax / 2

Uдейств. =Umax / 2

Действующее значение силы переменного тока равно значению силы постоянного тока, эквивалентного данному переменному по своему тепловому действию.

Первичное действие переменного тока заключается в смещении ионов в растворах электролитов и их перераспределении, а также в изменении поляризации диэлектрика. Т.к. подвижность ионов различна, то происходит изменение их концентрации по обе стороны клеточной мембраны. Это вызывает изменение функционального состояния клетки.

Наиболее сильное раздражающее действие оказывает импульсный ток.

Виды импульсных токов:

1.прямоугольный

2.треугольный

3.пилообразный.

I

t

t

t

Где t– длительность импульса,

to– длительность паузы,

х- амплитуда (максимальное значение тока).

Раздражающее действие зависит от длительности импульса, его формы, частоты, амплитуды. Оно проявляется для возбудимых тканей – нервной, мышечной, железистой.

В зависимости от условийток оказывает лечебное или поражающее действие. К лечебным действиям относятся:

Вопрос № 2.

Особенности импеданса живых тканей.

Импеданс – суммарное сопротивление цепи переменному току.

R C L

R – активное сопротивление

Xc реактивное

X сопротивление

Xc- емкостное сопротивление

Xc=1/wc=1/2πνс

X — индуктивное сопротивление

X =wL=2πνL

Z=R²+(Xc-X) ² — импеданс (суммарное сопротивление).

При пропускании переменного тока живую ткань можно рассматривать, как электрическую цепь, состоящую из определенных элементов. Экспериментально установлено, что эта цепь обладает активным и емкостным сопротивлениями. Аналогов индуктивности в живых тканях не обнаружено.

Т.о. живая ткань, как цепь переменного тока , является неполной цепью.

R C

Z=R²+Xc²

С увеличением частоты тока емкостное сопротивление, а, следовательно, и импеданс, снижаются.

2.1 Основные параметры тока и напряжения

Электрические сигналы в виде напряжения характеризуются прежде всего мгновенным значением, т.е. значением напряжения в заданный момент времени. Мгновенные значения напряжений представляют интерес при исследовании формы сигналов, например, с помощью осциллографа. К измеряемым параметрам относятся, в частности, наибольшее и наименьшее мгновенные значения сигнала в заданном интервале времени, называемые максимальным U_max и минимальным U_min значениями напряжения.

Пиковое значение U_m (для гармонического колебания — амплитудное) — это наибольшее мгновенное значение напряжения u(t) за время измерения Т. Если напряжение за время измерения или период изменяет знак, а кривая напряжения несимметрична, то различают положительные U_m+ и отрицательные U_m-пиковые значения.

Если сигнал содержит постоянную составляющую, она называется средним значением сигнала и определяется, как правило, за период (интервал усреднения) T.

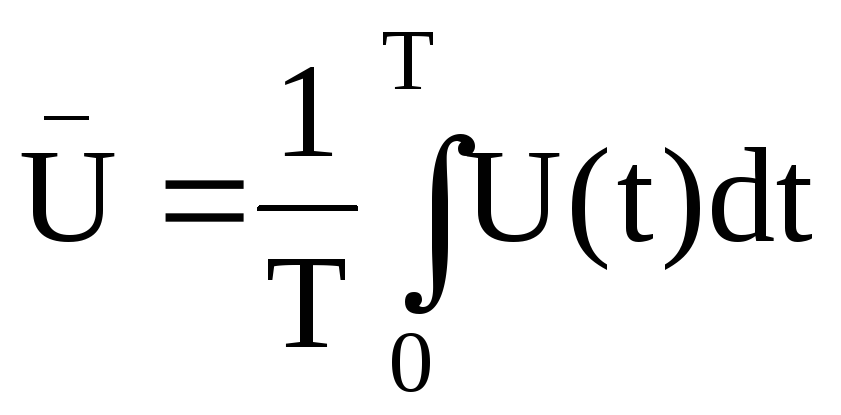. (2.1)

В том случае важными параметрами сигнала являются наибольшее и наименьшее значения переменной составляющей сигнала, называемые соответственно пиковым отклонением «вверх» (U_в) и пиковым отклонением «вниз» (U_н).

Если сигнал не содержит постоянной составляющей (например, гармонический сигнал или меандр), он будет характеризоваться средневыпрямленным значением

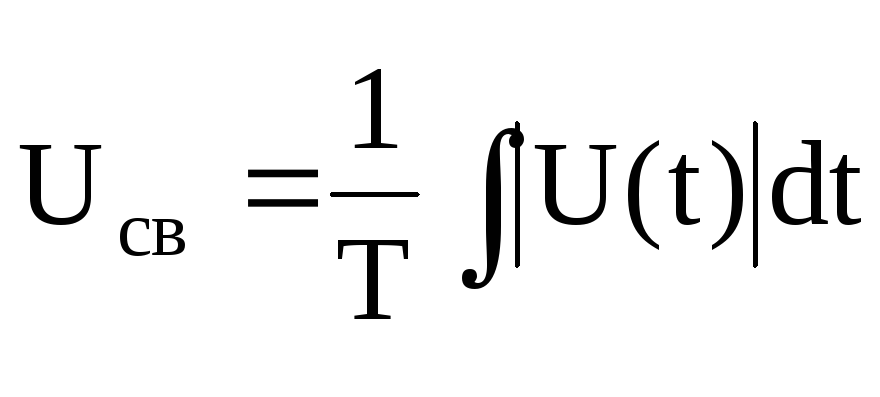(2.2)

и амплитудой U_m. Величина

А = U_max — U_min = U_в — U_н = 2U_m (2.3)

называется размахом сигнала. Для однополярных сигналов

U_св =

Наконец, важным параметром является среднеквадратическое значение сигнала, определяемое по формуле

(2.4)

и характеризующее энергетический уровень его (в литературе U_ск называют еще действующим или эффективным значением сигнала).

Существует определенная связь между всеми перечисленными параметрами, зависящая от формы сигнала. Эту связь принято характеризовать коэффициентами амплитуды (пиковости) k_а, формы k_ф, и усреднения k_у, причем

(2.5)

В таблице 2.1 в качестве примеров приведены значения k_а, k_ф и k_у для гармонического и пилообразного напряжений, а также для меандра.

Таблица 2.1

Значения k_а, k_ф и k_у для напряжений различной формы

Форма напряжения	kа	kф	kу
Гармоническая (синусоидальная)	1,41	1,11	1,56
Однополярная пилообразная	1,73	1,16	2,00
Прямоугольной формы с симметричными полупериодами — меандр	1,00	1,00	1,00

Коэффициенты k_а, k_ф и k_у позволяют получать значения переменного напряжения, если известно одно из них и форма напряжения.

2.2 Зависимость показаний вольтметров от формы напряжения

Многочисленные электронные вольтметры, выпускаемые промышленностью, Содержат преобразователи различных типов: пиковые, квадратичные, средневыпрямленного значения. Шкалы электронных вольтметров градуируют в значениях различных параметров напряжения, причем далеко не всегда в значениях того параметра, который соответствует типу преобразователя. Например, преобразователь может быть пиковым, а шкала проградуирована в среднеквадратических значениях синусоидального напряжения. Поэтому при подключении нескольких вольтметров к одному источнику напряжения результаты измерений могут быть неодинаковыми.

Оператор, измеряющий напряжение, должен уметь правильно определить результат измерения по показаниям прибора. Решая эту задачу, опираются на градуировочную характеристику вольтметра (зависимость между значениями величины на входе и выходе средства измерения), устанавливающую соотношение между показанием прибора U_n и значением определенного параметра U напряжения, подаваемого на вход прибора:

U_n = k U,

где k — градуировочный коэффициент, зависящий от типа преобразователя и измеряемого параметра. Коэффициент k обеспечивает получение прямого отсчета при измерении данного параметра.

k =	параметр напряжения, в значениях которого проградуирована шкала
	параметр того же напряжения, соответствующий типу преобразователя

Из этой формулы видно, что если шкала вольтметра проградуирована в значениях параметра, соответствующего типу преобразователя, то градуировочный коэффициент k = 1.

Определим градуировочные коэффиценты для случаев, когда нет соответствия между типом преобразователя и значениями параметра, нанесенными на шкалу вольтметра.

1. Преобразователь пиковый, шкала проградуирована в среднеквадратических значениях синусоидального напряжения. (В таких ситуациях обязательно следует указать форму напряжения, по которому градуировалась шкала прибора).

Тогда

k =	среднеквадратическое значение синусоидального напряжения	=	1
	пиковое значение синусоидального напряжения

Шкалы подавляющего большинства стрелочных электронных вольтметров переменного тока градуируются в среднеквадратических значениях синусоидального напряжения. Если преобразователь вольтметра квадратичный, то k = 1. Тогда показания прибора непосредственно соответствуют среденеквадратическому значению напряжения, т.е. U_n = U. Для преобразователей других типов коэффициент k отличен от 1.

Иногда при измерении синусоидального напряжения вольтметром, шкала которого проградуирована в среднеквадратических значениях этого напряжения, интересуются другими параметрами — амплитудным (пиковым) или средневыпрямленным значениями. Данную задачу несложно решить, но измерения в этом случае будут косвенными. Для нахождения интересующего параметра используют известную зависимость между необходимым параметром и непосредственно измеряемым среднеквадратическим значением

U_m = 1,41 U; U_св = 0,9 U.

Данные соотношения справедливы только для синусоидальной формы напряжения.

При измерении напряжений несинусоидальной формы следует ответить на четыре следующих вопроса:

1. Какой параметр несинусоидального напряжения может быть измерен данным вольтметром?

2. Дает ли показание вольтметра непосредственно значение этого параметра?

3. Если не дает, то как по показанию вольтметра найти значение параметра, измеряемого данным вольтметром?

4. Как определить значения других параметров?

Последовательно ответим на эти вопросы.

1. Фактически измеряемый вольтметром параметр напряжения определяется типом преобразователя: каков преобразователь — пиковый, среднеквадратического или средневыпрямленного значений, таков и фактически измеряемый параметр. Данный вольтметр измеряет только тот параметр напряжения, который соответствует типу преобразователя.

2. Необходимо знать, в значениях какого параметра проградуирована шкала вольтметра. Если в формуле

U_n = U,

коэффициент k = 1, то прибор показывает непосредственно значение измеряемого параметра.

3. Вычисляем градуировочный коэффициент k согласно приведенной формуле и, пользуясь градуировочной характеристикой, записываем уравнение, связывающее конкретный параметр напряжения с показанием вольтметра

.

Так, если преобразователь данного вольтметра пиковый, а шкала проградуирована в среднеквадратических значениях синусоидального напряжения, то k = 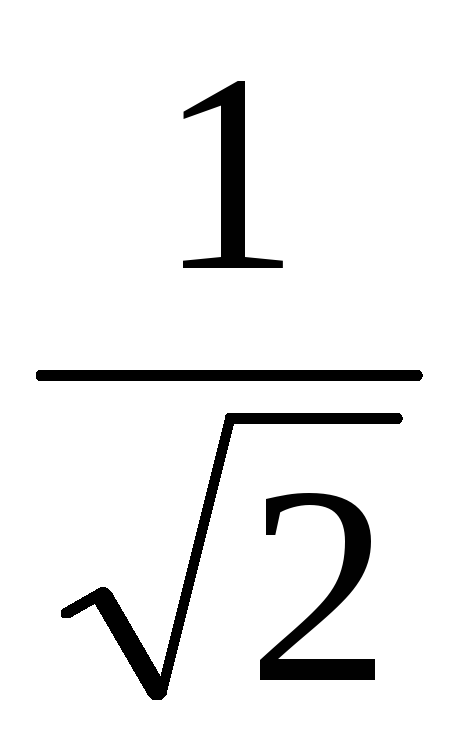, U = U_m и, следовательно U_m = .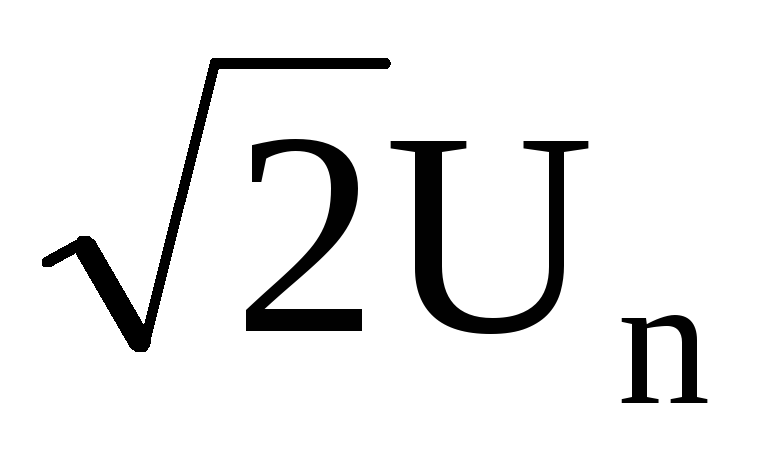

4. Чтобы найти значения параметров напряжения, не соответствующих типу преобразователя, необходимо располагать знаниями коэффициентов амплитуды и формы или моделью исследуемого сигнала (описанием формы напряжения), подаваемого на вход вольтметра.

U_ск = ; U_св = ,

где К_а и К_ф — коэффициенты амплитуды и формы исследуемого сигнала.

Измеряя параметры несинусоидального напряжения вольтметром с закрытым входом, следует учитывать, что на преобразователь поступает напряжение исследуемого сигнала без постоянной составляющей. Форма этого напряжения будет отличаться от формы напряжения исходного сигнала и будет характеризоваться «своими» значениями коэффициентов амлитуды и формы:

и

Причем в общем случае 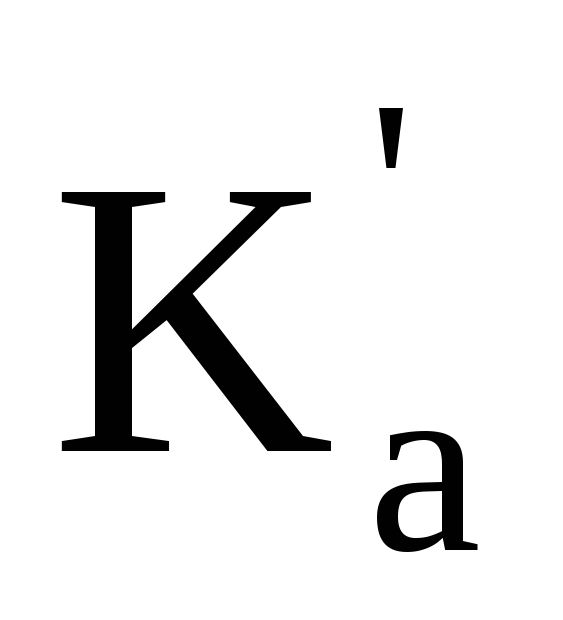 К_а и  K_ф.