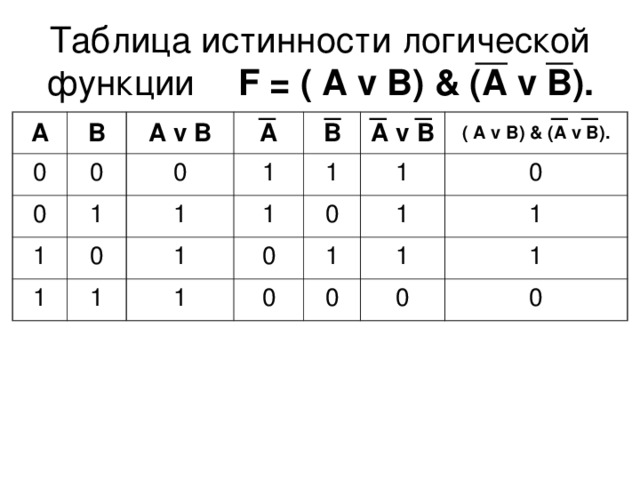
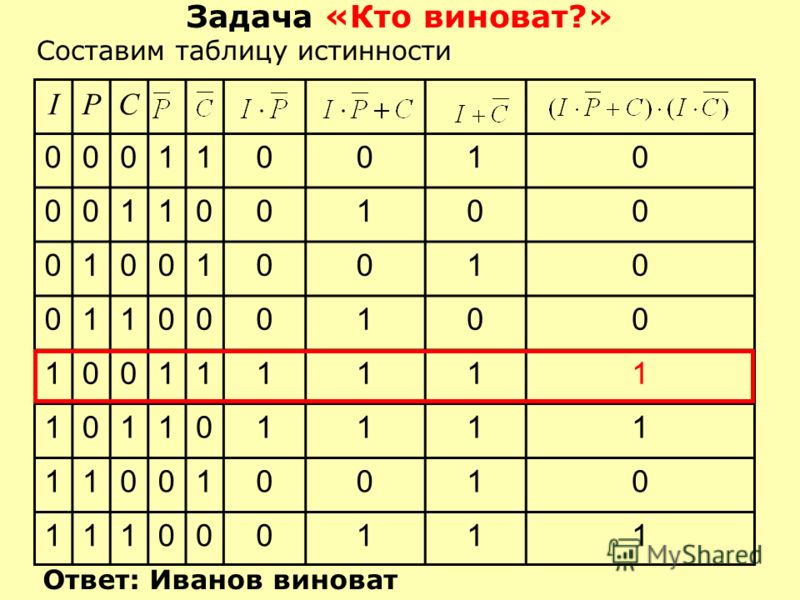
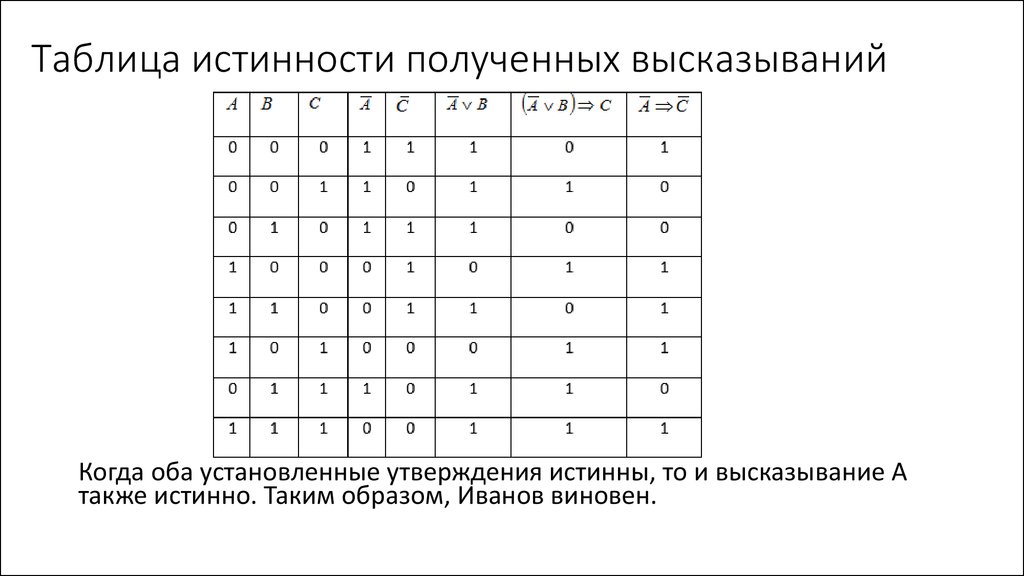
Математическая логика — презентация онлайн

1. Математическая логика

1
Математическая
логика
§ 8. Логика и компьютеры
§ 9. Логические элементы
§ 10. Другие логические операции
§ 11. Логические выражения
§ 12. Множества и логика

2. Математическая логика

2
Математическая
логика
§ 5. Логика и компьютер

3. Логика, высказывания

3
Логика, высказывания
Логика (др.греч. λογικος) – это наука о том, как
правильно рассуждать, делать выводы,
доказывать утверждения.
Формальная логика отвлекается от
конкретного содержания, изучает только
истинность и ложность высказываний.
Аристотель
(384-322 до н.э.)
Логическое высказывание – это
повествовательное предложение, относительно
которого можно однозначно сказать, истинно оно
или ложно.

4. Высказывание или нет?

4
Высказывание или нет?
Сейчас идет дождь.
Жирафы летят на север.
История – интересный предмет.
У квадрата – 10 сторон и все разные.
Красиво!
В городе N живут 2 миллиона человек.
Который час?

5. Логика и компьютер

5
Логика и компьютер
!
двоичная логика
Любое высказывание может быть ложно (0)
или истинно (1).
Логика изучает операции между 0 и 1!
!
Связь с двоичным кодированием!
Алгебра логики — это математический
аппарат, с помощью которого
записывают, упрощают и преобразуют
логические высказывания, вычисляют
их значения.
Алгебра высказываний,
булева алгебра
Джордж Буль

6. Простые и составные высказывания

6
Простые и составные высказывания
A – Сейчас идет дождь.
B – Форточка открыта.
}
простые
высказывания
(элементарные)
Составные высказывания строятся из простых с
помощью логических связок (операций) «и», «или»,
«не», «если … то», «тогда и только тогда» и др.
AиB
A или не B
Сейчас идет дождь и открыта форточка.
Сейчас идет дождь или форточка закрыта.
если A, то B
Если сейчас идет дождь, то форточка открыта.
A тогда и только
тогда, когда B
Дождь идет тогда и только тогда, когда открыта
форточка.

7. Операция НЕ (инверсия)

7
Операция НЕ (инверсия)
Если высказывание A истинно, то «не А» ложно, и
наоборот.
А
не А
0
1
1
0
также A, not A
таблица
истинности
операции НЕ
Таблица истинности логического выражения Х – это
таблица, где в левой части записываются все
возможные комбинации значений исходных данных,
а в правой – значение выражения Х для каждой
комбинации.

8. Разные операции с одной переменной

8
Разные операции с одной переменной
?
Сколько всего?
22 = 4
А
не А
А
0
1
0
1
0
0
1
1
0
1
0
1

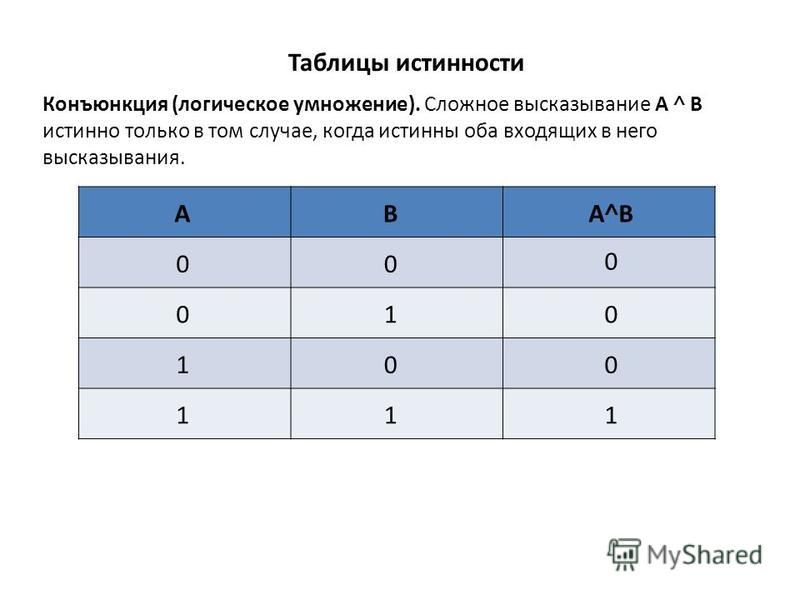
9. Операция И

9
Операция И
Высказывание «A и B» истинно тогда и только тогда,
когда А и B истинны одновременно.
AиB
A
B
220 В

10.

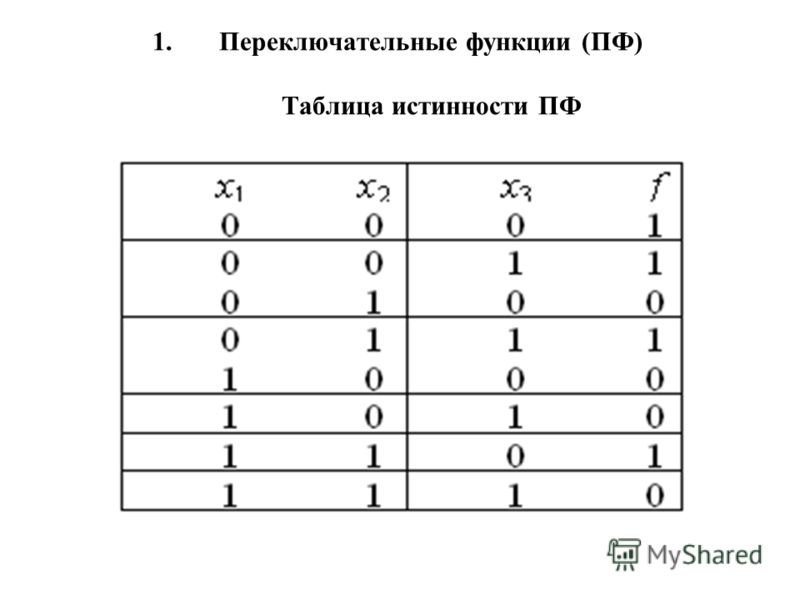Операция И (логическое умножение, конъюнкция)10
Операция И (логическое умножение, конъюнкция)
0
1
2
3
A
B
АиB
0
0
1
1
0
1
0
1
0
0
0
1
также A·B, A and B
?
Почему
умножение?
конъюнкция – от лат. conjunctio — соединение
A и B = min(A, B)

11. Операция ИЛИ (логическое сложение, дизъюнкция)

11
Операция ИЛИ (логическое сложение, дизъюнкция)
Высказывание «A или B» истинно тогда, когда
истинно А или B, или оба вместе.
A или B
A
B
220 В

12. Операция ИЛИ (логическое сложение, дизъюнкция)

12
Операция ИЛИ (логическое сложение, дизъюнкция)
A
B
А или B
0
0
1
1
0
1
0
1
0
1
1
1
также: A+B, A or B
?
!
Почему
сложение?
1+1=1
дизъюнкция – от лат. disjunctio — разъединение
A или B = max(A, B)

13. Упрощение логических выражений

13
Упрощение логических выражений
Aи0=A∙0=0
Aи1=A∙1=A
A или 0 = A + 0 = A
A или 1 = A + 1 = 1
A и не A = A ∙ A = 0
A или (не A) = A + A = 1

14.

Математическая логика14
Математическая
логика
§ 6. Логические элементы

15. Элемент «НЕ»

15
Элемент «НЕ»
значок
инверсии
A
не A
A
?A
A
A
не A
?

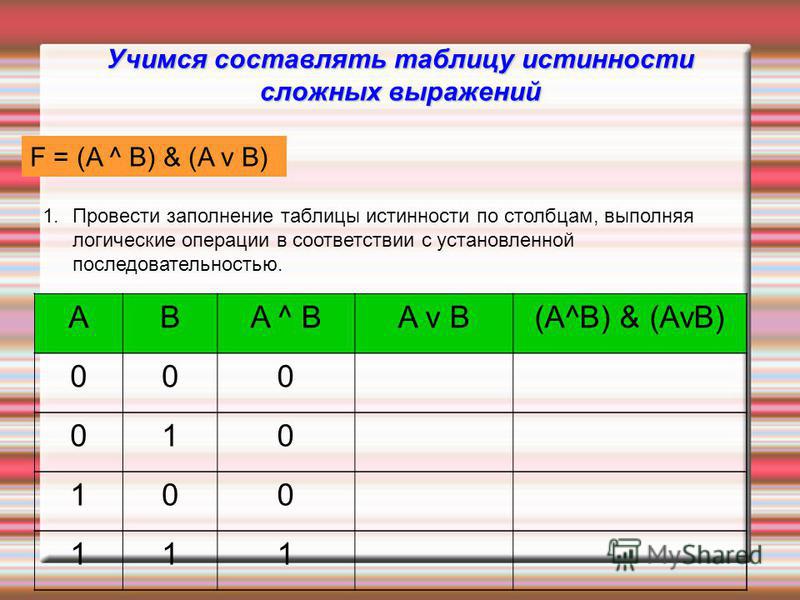
16. Элементы «И» и «ИЛИ»

16
Элементы «И» и «ИЛИ»
«И»
A
&
B
«ИЛИ»
AиB
A B
A
«И-НЕ»
B
&
A или B
B
Двойные элементы:
A
не (A и B)
&
B
A B
A
1
A B
A
1
B
не (A или B)
A B
«ИЛИ-НЕ»
не (A и B)
A
B
1
не (A или B)

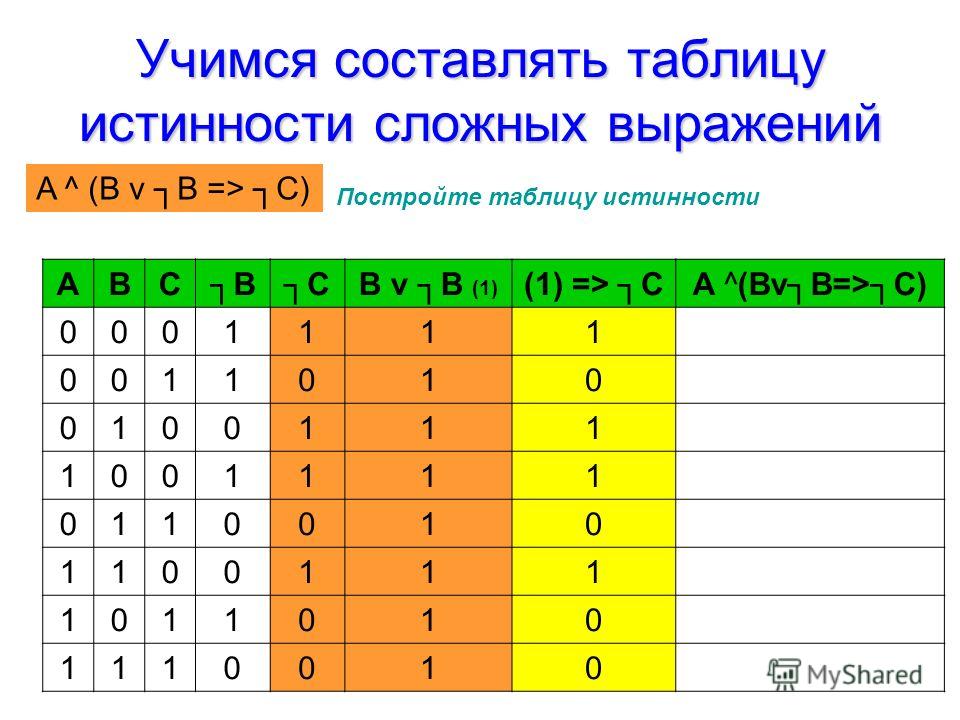
17. Составьте таблицы истинности

17
Составьте таблицы истинности
A
A
&
B
1
C
A
&
F
B
F
A
B
A
A
B
F
&
C
B
1
1
B
1
F
&
F
F

18. Математическая логика

18
Математическая
логика
§ 7. Другие логические
операции

19. Операции с двумя переменными

19
Операции с двумя переменными
?
Сколько всего?
A
0
0
1
1
B
0
1
0
1
F
?
?
?
?
0 или 1
24 = 16

20.

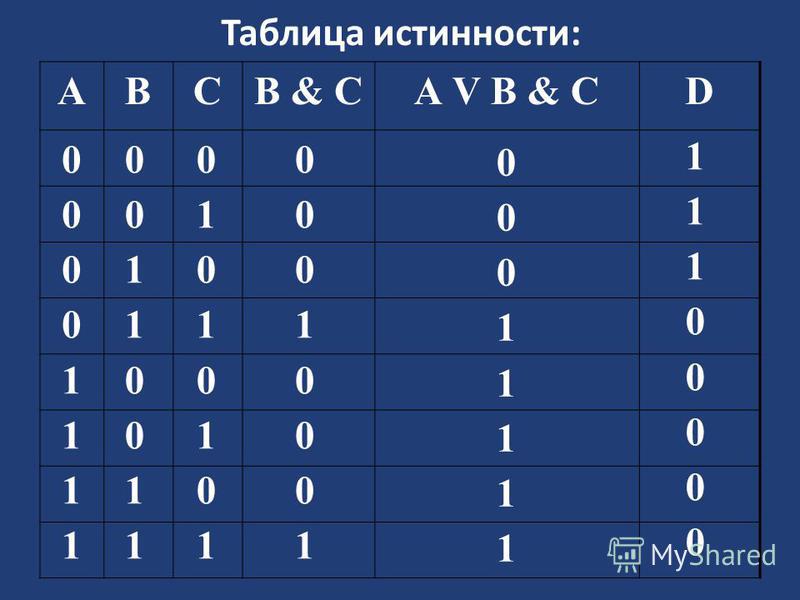Импликация20
Импликация
A
X=A B
X = Если идёт дождь, то
Лена раскрывает зонтик.
B
Импликация A → B истинна, если не исключено,
что из A следует B.
A
0
0
1
1
B
0
1
0
1
F
1
1
0
1
Идёт дождь, но Лена
не раскрыла зонтик.

21. Постройте таблицы истинности

21
Постройте таблицы истинности
X=B A
B A A B
X A B
A B A B
X B A
A B B A

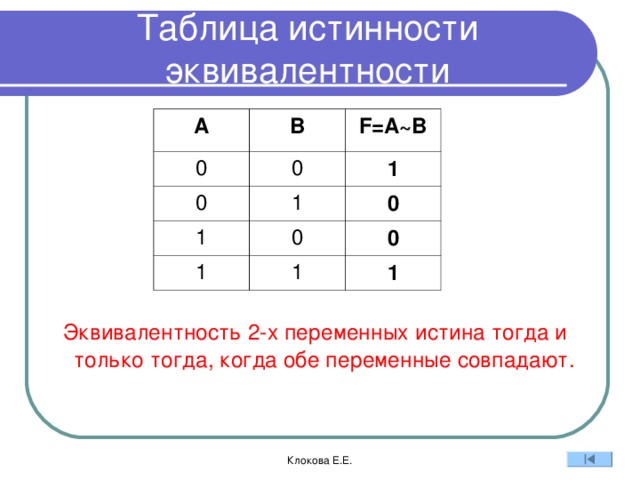
22. Эквиваленция

22
Эквиваленция
Высказывание «A B» истинно тогда и только
тогда, когда А и B равны.
A
0
0
1
1
B
0
1
0
1
А B
1
0
0
1

23. Постройте таблицы истинности

23
Постройте таблицы истинности
X A B A B
A B A B A B
X ( A B ) ( A B)
A B (A B ) (A B)
X A B A B
A B (A B A B)

24. Исключающее «ИЛИ»

24
Исключающее «ИЛИ»
Высказывание «A B» истинно тогда, когда
истинно А или B, но не оба одновременно (A B).
«Либо пан, либо пропал».
A
B
А B
0
0
1
1
0
1
0
1
0
1
1
0
арифметическое
сложение, 1+1=2
остаток
сложение по модулю 2: А B = (A + B) mod 2

25. Постройте таблицы истинности

25
Постройте таблицы истинности
X A B A B
A B A B A B
X ( A B) ( A B )
A B (A B) (A B )

26. Упрощение логических выражений

26
Упрощение логических выражений
A 0= A
A 1= A
A A= 0
(A B) B = A
!
операция обратима
Повторное применение операции с тем
же B восстанавливает исходное A!

27. Шифрование

27
Шифрование
данные
ключ
(A B) B = A
шифровка
дешифровка
A=1001
B=0101
(A B) = 1 1 0 0
B=0101
1001=A

28. Математическая логика

28
Математическая
логика
§ 8. Логические выражения

29. Логические выражения

29
Логические выражения
Логическое выражение — это выражение,
результат вычисления которого — логическое
значение (истина или ложь).
Авария = вышли из строя 2 из 3-х двигателей.
A – «Двигатель № 1 неисправен».
логическое
B – «Двигатель № 2 неисправен».
выражение
C – «Двигатель № 3 неисправен».
Аварийный сигнал: X ( A B) ( A C) (B C)
X = «Неисправны два двигателя»
= (A и B) или (A и C) или (B и C)
!
Формализация – это переход к записи на
формальном языке!

30. Порядок вычисления

30
Порядок вычисления
• скобки
• НЕ
•И
• ИЛИ , исключающее ИЛИ
• импликация
• эквиваленция
5
6
1 3
4 2
X A B (A B B )

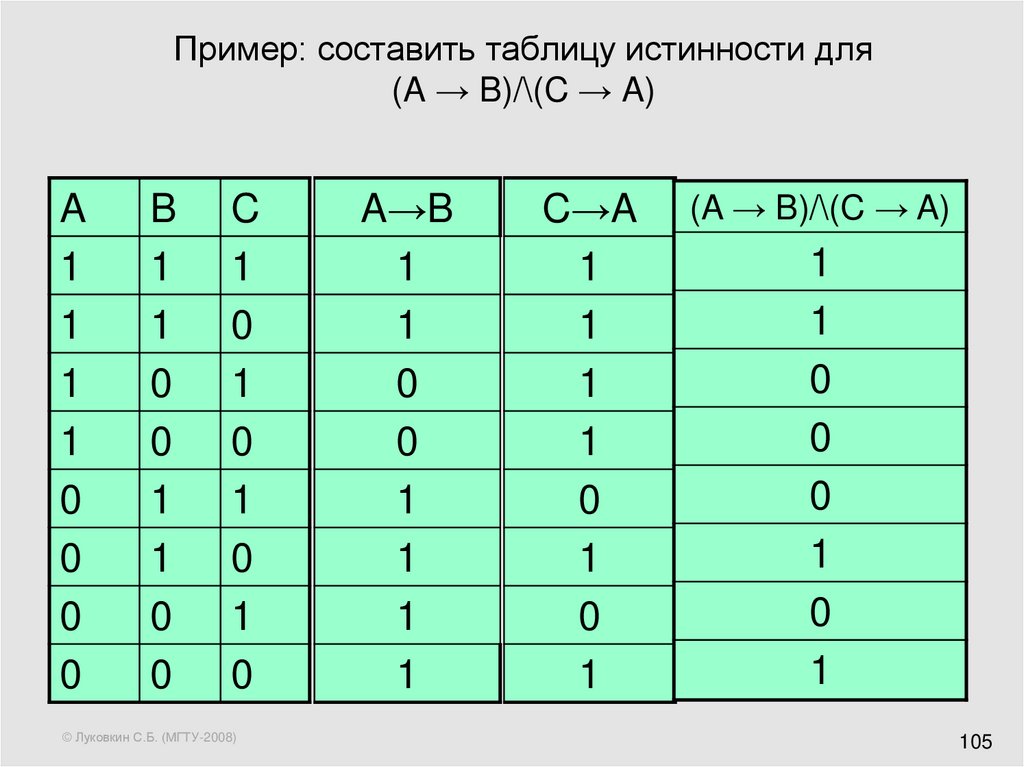
31. Таблицы истинности

31
Таблицы истинности
X A B A B
0
1
2
3
A
B
A B
A B
X
0
0
1
1
0
1
0
1
0
0
1
0
0
1
0
0
0
1
1
0
Логические выражения могут быть:
• вычислимыми (зависят от исходных данных)
• тождественно истинными (всегда 1, тавтология)
• тождественно ложными (всегда 0, противоречие)

32.

Таблицы истинности32
Таблицы истинности
X ( A B) ( A B )
0
1
2
3
A
B
0
0
1
1
0
1
0
1
A B A B
0
1
1
1
1
1
1
0
равносильны
X
A B A B
0
1
1
0
0
1
1
0
Если два выражения принимают одинаковые
значения при всех значениях переменных, они
называются равносильными (определяют
одну и ту же логическую функцию).

33. Неполные таблицы истинности

33
Неполные таблицы истинности
A
B
C
F
0
0
1
0
1
1
1
1
1
1
0
0
?
?
Сколько строк в полной
таблице?
3
2 =8
Сколько подходящих
функций?
25 = 32
а) F A B C
один ноль в таблице
F A C B
в) F A B C
по 1-й строке
б)
г)
F A B C
по 2-й строке

34. Сколько нулей и единиц?

34
Сколько нулей и единиц?
в таблице истинности функции от 3-х переменных:
A B C
A B C
A B C
A B C
A ( B C)
нулей
единиц
1
7
7
1
5
7
1
1
7
3

35.

Неполные таблицы истинности35
Неполные таблицы истинности
A
0
1
B
C
F
1
0
1
1
0
1
один ноль,
две единицы
а)
F A B C
по 1-й строке
1 B 0 0
б)
F A B C
по 2-й строке
0 0 C 1
в)
F A B C
г)
F A B C
только 1 единица,
все строки разные!

36. Составление условий

36
Составление условий
0
1
2
3
4
5
(x 3) и (x 6)
0
1
2
3
6
7
8
x
(3 x) и (x 6)
4
5
6
7
8
x
(1 x) и (x 3) или (5 x) и (x 8)
0
1
2
3
4
5
6
7
8
x

37. Составление условий

37
Составление условий
x 1 y
x –1
нижняя граница: y – 1
верхняя граница: y – x
левая граница:
-1
y 1 — 1
1 x
y x
!
Всё одновременно!
(x – 1) и (y – 1) и (y – x)

38. Составление условий

38
Составление условий
y
x2 y 2 1
1 x
-1
y
-1
x y 1
2
2
1 x
y x
левая
правая
(x2+y2 1) и (x 0)
левая
нижняя
(x 0) и (x2+y2 1)
и (y – x)
верхняя

39.

Составление условий39
Составление условий
y
x2 y 2 1
y
-1
1 x
=
-1
y
x2 y 2 1
1 x
+
x2 y 2 1
1 x
-1
y x
(…) или (…)
y x
((x2+y2 1) и (x 0)) или
? Как упростить?
((x2+y2 1) и (x 0) и (y – x))
А ещё?
?
(x2+y2 1) и ((x 0) или ((x 0) и (y – x)))
(x2+y2 1) и ((x 0) или (y – x))

40. Определение истинности выражений

40
Определение истинности выражений
Для каких из указанных значений числа X
истинно высказывание:
(X < 5) И НЕ (X < 1) ?
X = 2:
( 1 ) И НЕ ( 0 )
(1И1)
X = 4:
X = 8:
=1
( 1 ) И НЕ ( 0 )
(1И1)
=1
( 0 ) И НЕ ( 0 )
( 0 И 1)
=0
можно не
вычислять!

41. Табличный метод

41
Табличный метод
Для каких из указанных значений числа X
истинно высказывание:
R = (X < 5) И НЕ (X < 1) ?
X
2
4
8
X < 5 X < 1 НЕ(X < 1)
1
0
1
1
0
1
0
0
1
И
R
1
1
0

42.

Задачи42
Задачи
Для каких из указанных значений числа X
ЛОЖНО высказывание:
(НЕ (X ≥ 3) И НЕ (X = 8)) ИЛИ (X ≤ 5) ?
X = 4:
X = 1:
X = 8:
?+1
(НЕ (1) И НЕ (0)) ИЛИ (1) = 1
(НЕ (0) И НЕ (0)) ИЛИ (1) = 1
(НЕ (1) И НЕ (1)) ИЛИ (0)
( 0 И 0 ) ИЛИ (0) = 0

43. Задачи

43
Задачи
Для каких значений числа X истинно
высказывание:
(X < 5) И НЕ (X < 1) ?
(X < 5) И (X >= 1)
1
1, 2, 3, 4
2
3
4
5

44. Задачи

44
Задачи
Для каких из приведённых имён ЛОЖНО
высказывание:
(Первая буква согласная)
НЕ(Первая буква гласная) ИЛИ
(Последняя буква гласная) ?
ПервСогл
ПослГлас
R
Никита
1
1
1
Антон
0
0
0
Даниил
1
0
1
Инна
0
1
1
Кирилл
1
0
1

45. Задачи

45
Задачи
Для каких из приведённых имён ЛОЖНО
высказывание:
НЕ(Первая буква гласная) ИЛИ
(Последняя буква гласная) ?
(Первая буква согласная) ИЛИ
(Последняя буква гласная)
Никита
Антон
Даниил
Инна
Кирилл
Егор
Мефодий
Игнат
ЛОЖНО
A+B=0
A·B=1
ИЛИ И,
обратные условия

46.

Задачи46
Задачи
Для каких из приведённых имён ЛОЖНО
высказывание:
НЕ(Первая буква гласная) И
(Последняя буква гласная) ?
(Первая буква согласная) И
(Последняя буква гласная) ЛОЖНО
A·B=0
Никита
Кирилл
Антон
Егор
A+B=1
Даниил
Мефодий
И ИЛИ,
Инна
Игнат
обратные условия

47. Задачи

47
Задачи
Для каких значений числа X ЛОЖНО
высказывание:
(НЕ (X ≥ 3) И НЕ (X = 8)) ИЛИ (X ≤ 5) ?
ЛОЖНО ( (X < 3) И (X <> 8)) ИЛИ (X ≤ 5)
И ИЛИ,
обратные условия
ИСТИННО ( (X ≥ 3) ИЛИ (X = 8)) И (X > 5)
3
5
6
7 8
9
6, 7, 8, …

48. Логические схемы

48
Логические схемы
?
X A B A C B C
A
B
A
&
B
C
A
&
C
A B
A C 1
A B A C
B C
B
&
C
Какая последняя
операция?
1
X

49. Математическая логика

49
Математическая
логика
§ 12. Множества и логика

50.

Что такое множество?50
Что такое множество?
Множество – некоторый набор элементов, каждый из
которых отличается от остальных.
пустое множество:
конечное число элементов: буквы русского алфавита
бесконечное число элементов: натуральные числа
Как задать множество?
• перечислением элементов
{Вася, Петя, Коля}
• логическим выражением:
{x: x > 0}

51. Изображение множеств

51
Изображение множеств
Диаграммы Эйлера-Венна
A
пересечение
A
B
B
AиB
не A
A
A или B
A
A
B
A и (не B)
A
B
(не A) или B
объединение
B
(не A) и (не B)

52. Количество элементов множеств

52
Количество элементов множеств
Поисковые запросы в Интернете:
& = и (and)
| = или (or)
NA – количество элементов множества A
?
Что больше?
? NA & B
NA
NA
?
A
A
A &B
!
B
NA | B
B
A|B
& всегда сужает область, | — расширяет!

53.

Задачи53
Задачи
В таблице приведены запросы к поисковому серверу.
Расположите номера запросов в порядке возрастания
количества страниц, которые найдет поисковый сервер
по каждому запросу.
А: принтеры & сканеры & продажа
Б: принтеры | продажа
В: принтеры & продажа
Г: принтеры | сканеры | продажа
АВБГ

54. Использование диаграмм

54
Использование диаграмм
принтеры & сканеры & продажа
сканеры
принтеры
продажа
принтеры & продажа
сканеры
принтеры
продажа
принтеры | продажа
сканеры
принтеры
продажа
принтеры | сканеры | продажа
сканеры
принтеры
продажа

55. Задачи

55
Задачи
В таблице приведены запросы к поисковому серверу.
Расположите номера запросов в порядке убывания
количества страниц, которые найдет поисковый сервер
по каждому запросу.
А: принтеры & сканеры & продажа
Б: (принтеры & сканеры) | продажа
В: (принтеры | сканеры) & продажа
Г: принтеры | сканеры | продажа
ГБВА

56.

Количество элементов множеств56
Количество элементов множеств
Известно количество сайтов, которых находит
поисковый сервер по следующим запросам :
Запрос
огурцы
помидоры
огурцы & помидоры
Количество сайтов
N
A
100
200
50
Сколько сайтов будет найдено по запросу
огурцы | помидоры
NA|B
NB
NA&B

57. Количество элементов множеств

57
Количество элементов множеств
В общем виде:
A
B
A|B
A
NA&B = 0?
NA | B = NA + NB
NA&B =
B
NA | B =
NA + NB =
+
NA | B = NA + NB – NA & B
+
+
= NA | B +
Формула включений
и исключений

58. Задачи с тремя областями

58
Задачи с тремя областями
Известно количество сайтов, которых находит
поисковый сервер по следующим запросам:
Запрос
собаки & лемуры
кошки & лемуры
(кошки | собаки) & лемуры
Количество
сайтов
320
280
430
Сколько сайтов будет найдено по запросу
собаки & кошки & лемуры

59.

Задача с тремя областями59
Задача с тремя областями
собаки
кошки
лемуры
A = собаки & лемуры
B = кошки & лемуры
A
B
NA&B = NA+ NB – NA|B

60. Задачи с тремя областями

60
Задачи с тремя областями
Известно количество сайтов, которых находит
поисковый сервер по следующим запросам:
Запрос
A
собаки & лемуры
B
кошки & лемуры
A | B
(кошки | собаки) & лемуры
Количество
сайтов
320
280
430
A & B
Сколько сайтов будет найдено по запросу
собаки & кошки & лемуры
!
Общее условие с & можно отбросить !
NA&B = NA+ NB – NA|B = 320 + 280 – 430 = 170

61. Задачи с тремя областями

61
Задачи с тремя областями
Известно количество сайтов, которых находит
поисковый сервер по следующим запросам:
Запрос
Количество сайтов
сканер
принтер
монитор
принтер | сканер
принтер & монитор
сканер & монитор
200
250
450
450
40
50
Сколько сайтов будет найдено по запросу
(принтер | сканер) & монитор
!
Обычно две области не пересекаются!

62.

Задачи с тремя областями62
Задачи с тремя областями
А (сканер) B (принтер) 450
принтер | сканер
0
NA|B = NA+ NB – NA&B
сканер
сканер
200
принтер
250
принтер
50
40
принтер & монитор = 40
сканер & монитор = 50
монитор
(принтер | сканер) & монитор
40 + 50 = 90

Кафедра технологии бетона и строительных материалов — Технологии определяют всё

Является одним из старейших подразделений современного Брестского технического университета.

История кафедры начинается с 1967 года, когда ещё в Брестском инженерно-строительном институте (сегодня Брестский государственный  технический университет)  была основана кафедра «Строительные материалы».

Кафедру возглавляли:
Жоров Владимир Леонтьевич, к.т.н., доцент (с 1967  по 1977 год)
Зайцев Анатолий Алексеевич, к.т.н., доцент (с 1977 по 1987 год)
Волкова Флора Николаевна, к.т.н., доцент (с 1987-1988 год).

В 1988 году кафедра «Строительные материалы» была объединена с кафедрой «Технология строительного производства». Объединённая кафедра стала называться «Технология строительного производства и строительные материалы», которую возглавляли:
Бобко Фадей Александрович к.т.н., доцент (с 1988 по 1989 год)
Голубицкая Галина Андреевна, к.т.н., доцент  (с 1989 по1991 год)

Плосконосов Владимир Николаевич, к.т.н., доцент  ( с 1991 по 1992 год).

В 1991 году в институте открывается подготовка инженеров-технологов-строителей по специальности  «Производство строительных изделий и конструкций». Организация учебного процесса по данной специальности возложена на кафедру «Технологии строительного производства и строительных материалов». Разнообразие направлений работы кафедры не позволяет эффективно управлять её деятельностью и требует совершенствования структуры управления учебным процессом. В связи с чем приказом ректора по Брестскому политехническому  институту №67 от 12 июня 1992 года в отдельное подразделение выделяется уже кафедра  «Технологии бетона и строительных материалов» которую с 1992 по1993 год возглавляет Довнар Надежда Ивановна, к.

т.н., доцент.

С 1993 года кафедрой  руководит Тур Виктор Владимирович, профессор, доктор технических наук.

Кафедра технологии бетона и строительных материалов является выпускающей кафедрой по специальности 70 01 01 «Производство строительных изделий и конструкций» и готовит специалистов, имеющих квалификацию инженер-строитель-технолог, что позволяет им работать практически в любом направлении строительного, и не только, производства.

Так же на кафедре изучают специальные дисциплины строительного профиля студенты следующих специальностей очного и заочного обучения: «Промышленное и гражданское строительство» (1-70 02 01), «Автомобильные дороги» (1-70 03 01), «Экспертиза и управление недвижимостью» (1-70 02 02), «Архитектура» (1-69 01 01), «Сельское строительство и обустройство территорий» (1-74 04 0), «Автоматизация технологических процессов и производств» (1-53 01 01), «Водоснабжение, водоотведение и охрана водных ресурсов» (1-70 04 03),  «Мелиорация и водное хозяйство» (1-74 05 01), «Коммерческая деятельность» (1-25 01 10).

На кафедре проводится подготовка  аспирантов по специальности «Строительные конструкции, здания и сооружения», «Строительные материалы и изделия».

 

Генератор таблиц истинности онлайн для студентов колледжа — Полная помощь по заданию

Вас беспокоит решение таблицы истинности для логических вентилей, исчисления высказываний или булевой алгебры? Если да, используйте наш генератор таблиц истинности . Студенты со всего мира и из каждого университета по всему миру используют наш генератор таблиц истинности для получения точных результатов и экономии времени. Если эта концепция таблицы истинности для вас является чем-то новым, прочитайте эту статью, чтобы понять, о чем эта таблица и как работает генератор таблиц истинности ABC.

Переменные (разделенные запятыми)

Выражения (разделенные запятыми)

Таблица истинности показывает, как истинность и ложность сложносочиненного предложения зависят от истинности и ложности ясного предложения, из которого оно получено. В таблице есть столбец для всех входных переменных, обычно представленных как P и Q, a и b или x и y. В другом столбце представлены все результаты логических операций, как А и Б. Все строки таблицы содержат возможную конфигурацию вставленных в них переменных и результат операции для вставленных значений.

Если вы новичок и ничего не знаете о таблицах истинности, то генератор таблиц истинности с сайта totalassignment.com может показаться вам просто еще одним приложением, в котором вы вставляете символы и показываете какие-то случайные предложения. Но не беспокойся; статья расскажет вам о таблице и о том, как использовать генератор логических вентилей из таблицы истинности.

Прочитав приведенные выше указатели, вы поймете, что использовать наш генератор таблиц истинности ABC легко. Когда вы поймете каждый из операторов, вы сможете ввести любую переменную и работать с ней без помощи друзей или членов семьи.

Плата за использование генератора таблиц истинности для решения операций AND, XOR или NOR не взимается.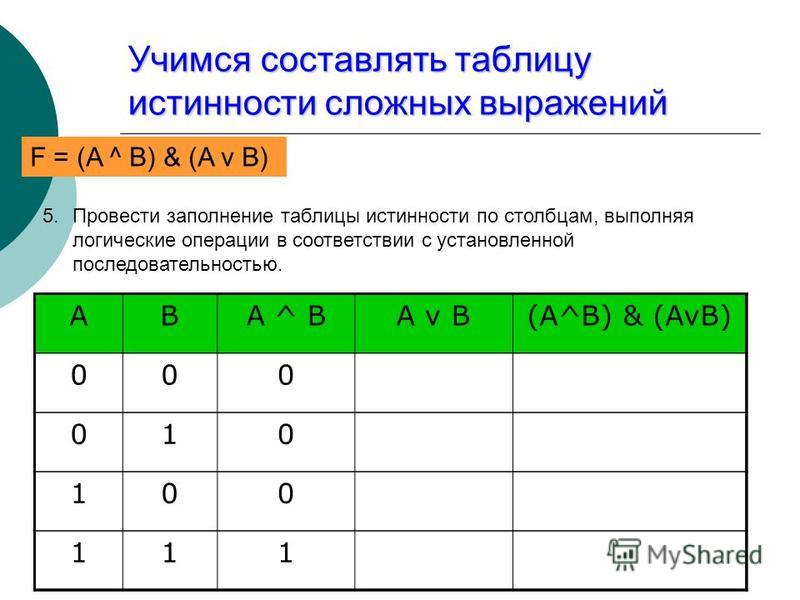

Вы можете самостоятельно управлять инструментом, не нанимая услуги эксперта, связанного с totalassignment.com, или вкладывать деньги в найм услуг любого другого онлайн-инструмента. Генератор таблицы истинности логических вентилей обладает следующими качествами:

Использование без каких-либо ограничений : Нет никаких условий, связанных с использованием генератора таблицы истинности для логических вентилей. Генератор можно использовать любое количество раз, не ограничивая частоту его использования. Задачи, связанные с булевой алгеброй или исчислением высказываний, можно быстро решить с помощью 9Генератор таблиц истинности 0004 от totalassignment.com.

Современный алгоритм : Мы использовали современный алгоритм глубокого обучения при разработке генератора логической схемы на основе таблицы истинности. Обновленные функции стола помогают работать лучше при каждом использовании. Это, в свою очередь, позволяет получать 100-процентно точные результаты при каждом использовании. Итак, зачем ждать, чтобы использовать наш генератор таблиц истинности для решения всех задач на основе таблиц.

Круглосуточная поддержка службы поддержки клиентов : Если вы столкнулись с какой-либо ошибкой при использовании нашего генератора таблиц истинности, вы можете связаться с нашим отделом обслуживания клиентов, который остается онлайн весь день. Если вы не можете связаться с нами по телефону или в сообщениях, вы можете зайти в онлайн-режим на нашем веб-сайте и пообщаться с нами, или вы даже можете отправить электронное письмо на наш идентификатор с указанием ошибок, с которыми вы столкнулись при работе с инструментом.

Генератор логической таблицы истинности может решить все проблемы, связанные с И-НЕ, бинарными логическими операторами, вентилями ИЛИ-НЕ и т. д. Более того, за использование таблицы с вашего кармана не будет взиматься никаких денег.

Способен ли генератор таблицы истинности пропозициональной логики давать быстрые результаты?

У вас есть задание, связанное с булевой алгеброй или цифровой электроникой, которое нужно срочно сдать? Если да, вы можете использовать наш генератор таблиц истинности логики высказываний для получения ответов на все задачи независимо от крайнего срока.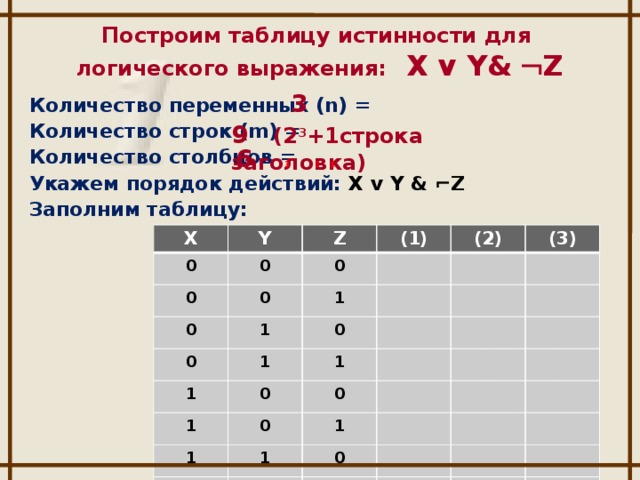 Вы получите точный результат, не тратя время на каждое использование. Генератор дискретных математических таблиц истинности имеет следующие особенности:

Может работать с любого устройства : Страница, связанная с генератором таблиц истинности, может быть открыта на любой платформе, будь то телефон, планшет, настольный компьютер или ноутбук. Инструмент был создан для совместимости с платформами IOS, Windows и Android. Таким образом, вам не требуется приобретать какое-либо конкретное устройство для открытия или запуска результатов при использовании нашего генератора таблиц истинности.

Его можно использовать в любое время : Как уже говорилось ранее, нет никаких скрытых затрат, связанных с использованием услуг генератора таблицы истинности логики высказываний. Плата за подписку не взимается, и инструмент можно использовать в любое время дня. Его можно использовать из любого места, и единственным требованием является устройство и стабильное подключение к Интернету.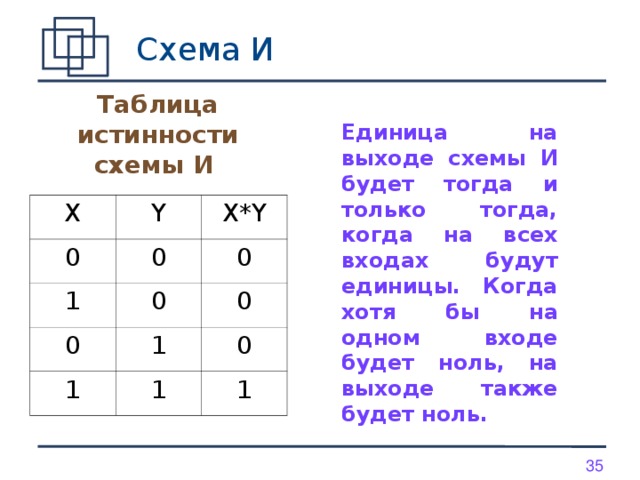

Быстрый результат : Как только вы поместите формулу или задачу в таблицу, вы сможете быстро получить результат. Генератор таблицы истинности пропозициональной логики быстро генерирует результаты. Если у вас есть готовый оператор или выражение для ввода в инструмент, вы увидите, что генератор отразит результаты в течение нескольких секунд.

Итак, не тратя время на поиски других онлайн-генераторов таблиц истинности , воспользуйтесь услугами totalassignment.com.

Ограничены ли услуги totalassignment.com генераторами таблиц истинности?

Нет, наши услуги не ограничиваются набором инструментов. Эти услуги являются дополнительными услугами, которые мы предоставляем вместе с услугами по написанию. Наша основная цель — удовлетворить потребности студентов в академическом письме, включая написание заданий, отчеты, эссе, диссертации, домашние задания и т. д. У нас есть группа экспертов из разных академических областей, которые предоставляют безупречные услуги по написанию работ для студентов. Например, если у вас есть набор вопросов, связанных с логикой высказываний или булевой алгеброй, которые требуют некоторого объяснения, вы можете воспользоваться нашими услугами академического письма.

Эксперты, которых мы наняли для решения ваших академических проблем, обладают высокой квалификацией и хорошо разбираются в своих дисциплинах, включая таблицу истинности, выражения, операторы и т. д. Таким образом, использование наших услуг принесет вам следующие преимущества:

Выполнение заданий в срок : Когда эксперта просят ответить на логический вопрос или вопрос, связанный с условными воротами, он использует правильную логику для ответа на все вопросы, независимо от их сложности. Они гарантируют подачу задания вовремя, чтобы представить его без каких-либо предпоследних при опоздании. Но если у вас мало времени и вы не можете разместить запрос на задание, используйте наш генератор таблиц истинности для проверки ответов.

Помощь в рамках вашего бюджета : Наши услуги недороги, и каждый студент может выбрать сумму из своего кармана. Бюджетные задания не ограничиваются набором конкретных студентов; вместо этого они доступны для всех студентов со всего мира. Наряду с низкими ценами на выполнение заданий, мы предоставляем значительные скидки студентам, оформившим у нас оптовые заказы, первокурсникам, реферальные бонусы и т. д. Мы также проверяем все задания на плагиат и их качество после сдачи экспертом. , и эти услуги бесплатны.

Неограниченное количество исправлений : После получения задания, если учащийся считает, что оно не на должном уровне, он всегда может попросить внести исправления на основе своих входных данных. Если вы считаете, что решить ваши задачи с помощью генератора таблиц истинности невозможно, вы всегда можете обратиться к нам за услугами по написанию заданий. После того, как задание выполнено, вносимые нами исправления не подлежат оплате. Мы рассматриваем запросы на доработку как возможность выполнить качественную работу, исправив ранее допущенные ошибки. Для авторов это полезный опыт, позволяющий избежать таких ошибок в будущих задачах.

Бесплатный доступ к образцам : Мы подготовили набор образцов, относящихся к разным темам и дисциплинам. Если студент застрял при решении каких-либо проблемных вопросов, он может проверить наши бесплатные образцы, доступные на нашем веб-сайте. Образцов много, и вы можете отсортировать их по своему усмотрению. Например, у нас есть образцы, связанные с темами управления, техническими описаниями, обзорами литературы, задачами по программированию, таблицами истинности, операциями P и Q и т. д.

Работа без плагиата : Задания, которые мы делаем, или проблемы, которые мы решаем, не содержат плагиата. Мы с гордостью можем сказать, что наши специалисты могут выполнять работу без плагиата, даже если они работают над несколькими задачами одновременно. Нелегко выполнить задачу без плагиата, но наши специалисты всегда старались предоставить оригинальный контент. Подлинность содержания в заданиях оценивается с помощью различных программ для проверки на плагиат, таких как Turn-it-in и Grammarly. com.

Поддержание качества : Если вы обращаетесь за помощью к письменному онлайн-сайту для написания своего задания и не получаете качественной услуги, то такая помощь бесполезна. Мы думаем, что было бы лучше написать свои задания, а не помощь от низкопробных поставщиков услуг. О нашем качестве можно судить по отзывам, опубликованным разными студентами, и по чтению содержания наших образцов работ на нашем веб-сайте. Поддержание качества является приоритетом, который наша внутренняя команда по контролю качества тщательно проверяет перед тем, как передать какое-либо задание учащемуся.

Поэтому, если вы хотите получить полные оценки за незавершенные задания, воспользуйтесь нашей помощью прямо сейчас.

Заказать сейчас

Заказать сейчас

Популярные вопросы, которые ищут в Интернете

Что такое генератор таблиц истинности?

Генератор таблиц истинности используется для построения таблицы истинности для формулы пропозициональной логики.

Логические операторы могут быть вставлены в таблицу в различных форматах. Единственное, что необходимо сделать, это выбрать оператора и ввести свое требование. Наконец, введите выражение и получите нужную таблицу из инструмента.

Как решить логическое выражение?

Чтобы решить логическое выражение, вам необходимо выполнить следующие шаги:

Какое значение имеют P и Q в таблице истинности?

P и Q — это связки, используемые в таблице истинности для отображения составных предложений. Отрицание представлено как «¬p», что означает «не p», а союз представлен как «p ∧ q», что означает «p и q». Дизъюнкция представлена ​​как «p ∨ q», что означает «p или q или оба». Исключающее ИЛИ представляется как «p ⊕ q», что означает «либо p, либо q, но не оба». Импликация представлена ​​как «p → q», что означает «если p, то q». Бикондиционал представлен как «p ↔ q», что означает «p тогда и только тогда, когда q».

Что означает ∨ таблица истинности?

(∨) на самом деле таблица представляет собой клин, представляющий слово, которое соединяет два дизъюнкта с выражением «или» в качестве наиболее знакомого примера. Другими словами, включающее «или» означает истинную природу одного из дизъюнктов, тогда как исключающее «или» означает, что одно дизъюнктное является истинным, но не оба.

Применимы ли таблицы истинности в реальных сценариях?

Таблица истинности в математике используется для определения истинности сложного утверждения. Возможно, вам не потребуется ежедневно составлять таблицу истинности, но важно применять логику таблицы, чтобы установить, является ли утверждение истинным или ложным. Возьмите, например. это можно обосновать с помощью таблицы истинности, что «если я выиграю, я перейду на следующий уровень».

Что в логике означают P и Q?

Если значение истинности утверждения одинаково, то можно сказать, что предложение идентично или логически похоже. Следовательно, p считается истинным, если q истинно, и наоборот. P считается ложным, если q ложно, и наоборот. Следовательно, можно сказать, что p и q логически эквивалентны. Подводя итог, можно сказать, что p = q, если p и q логически равны.

Какие пять символов логического оператора?

Пять символов логических операторов: точка, клин, тильда, тройная черта и подкова. Используйте наш генератор таблиц истинности для решения математических задач.

Другие бесплатные академические инструменты

Мы предлагаем ряд инструментов и множество академических ресурсов, чтобы вывести ваши задания на новый уровень! Максимально используйте наш генератор эссе, генератор ссылок и инструменты перефразирования, чтобы вывести свои задания на новый уровень!

Ищу свое задание

На этом ваши поиски отличного задания заканчиваются. Нажмите на ссылку ниже, чтобы найти свое задание в нашей огромной базе данных работ.

Булевы функции (формы SOP, POS)

Схема

Представление булевых функций

Использование переключающих устройств, таких как транзисторы, порождает особый случай булевой алгебры, называемый алгеброй переключения. В алгебре переключений все переменные принимают одно из двух значений: 0 и 1.

[адсенс1]

В булевой алгебре 0 используется для представления «открытого» или «ложного» состояния логического элемента. Точно так же 1 используется для представления «закрытого» состояния или «истинного» состояния логического элемента.

Логическое выражение — это выражение, состоящее из переменных, констант (0 — ложь и 1 — истина) и логических операторов, результатом которых является истина или ложь.

Булева функция — это алгебраическая форма логического выражения. Булева функция n-переменных представлена ​​как f(x1, x2, x3….xn). Используя булевы законы и теоремы, мы можем упростить булевы функции цифровых схем. Краткое примечание о различных способах представления булевой функции показано ниже.

• Форма суммы произведений (СОП)
• Суммарное произведение (POS) форма
• Канонические формы

Существует два типа канонических форм:

• Сумма минимальных членов или каноническая СОП
• Product-of-max terms или Canonical POS

Булевы функции могут быть представлены с помощью логических элементов И-НЕ, а также с использованием метода K-карты (карты Карно). Мы можем стандартизировать логические выражения, используя две стандартные формы.

Форма СОП – Сумма произведений, форма

Форма POS – произведение сумм форма

Стандартизация логических уравнений сделает внедрение, развитие и упрощение более простым и систематическим.

Форма суммы произведений (SOP)

Форма суммы произведений (SOP) представляет собой метод (или форму) упрощения логических выражений логических вентилей. В этой SOP-форме представления булевой функции переменные обрабатываются по И (продукт) для формирования термина продукта, и все эти термины продукта объединяются по ИЛИ (суммируются или складываются) вместе, чтобы получить окончательную функцию.

[адсенс2]

Форма суммы произведений может быть сформирована путем сложения (или суммирования) двух или более членов произведения с использованием логической операции сложения. Здесь термины произведения определяются с помощью операции И, а термин суммы определяется с помощью операции ИЛИ.

Форма суммы произведений также называется дизъюнктивной нормальной формой, поскольку термины произведения объединяются вместе, а операция дизъюнкции является логическим ИЛИ. Форма суммы продуктов также называется стандартной СОП. Представление формы

SOP наиболее подходит для их использования в FPGA (программируемых вентильных матрицах).

Примеры

AB + ABC + CDE

(AB) ̅ + ABC + CD E ̅

Форма SOP может быть получена с помощью

• Запись условия И для каждой входной комбинации, которая производит ВЫСОКИЙ выход.
• Запись входных переменных, если значение равно 1, и запись дополнения переменной, если ее значение равно 0.
• ИЛИ условия И для получения выходной функции.

Пример: логическое выражение для функции большинства F = A’BC + AB’C + ABC ‘ + ABC

Таблица истинности:

Теперь запишите комбинацию входных переменных с высоким выходом. F = АВ + ВС + АС.

Проверка

По закону идемпотентности мы знаем, что

([ABC + ABC)] + ABC) = (ABC + ABC) = ABC

Теперь функция F = A’BC + AB’C + ABC ‘ + ABC

= A’BC + AB’C + ABC’ + ([ABC + ABC)] + ABC)

= (ABC + ABC’) + (ABC + AB’C) + (ABC + A’ ВС)

= АВ (С + С’) + А (В + В’) С + (А + А’) ВС

= АВ + ВС + АС.

Форма произведения сумм (POS)

Форма произведения сумм — это метод (или форма) упрощения логических выражений логических вентилей. В этой форме POS все переменные объединяются по ИЛИ, т. е. записываются как суммы для формирования суммирующих условий.

Все эти составляющие суммы объединяются по И (умножаются) вместе, чтобы получить форму произведения суммы. Эта форма прямо противоположна форме СОП. Так что это также можно назвать «двойной формой SOP».

Здесь условия суммы определяются с помощью операции ИЛИ, а условия произведения определяются с помощью операции И. Когда два или более членов суммы умножаются с помощью логической операции ИЛИ, результирующее выходное выражение будет иметь форму произведения сумм или форму POS.

Форма произведения сумм также называется конъюнктивной нормальной формой, поскольку члены суммы объединяются вместе, а операция конъюнкции является логическим И. Форма произведения сумм также называется стандартной POS.

Примеры

(A+B) * (A + B + C) * (C +D)

(A+B) ̅ * (C + D + E ̅)

Форма POS может быть получена по телефону

• Запись условия ИЛИ для каждой комбинации входов, которая дает НИЗКИЙ выходной сигнал.
• Запись входных переменных, если значение равно 0, и запись дополнения переменной, если ее значение равно 1.
• И условия ИЛИ для получения выходной функции.

Пример: логическое выражение для функции большинства F = (A + B + C) (A + B + C ‘) (A + B’ + C) (A’ + B + C)

Теперь запишите ввод комбинация переменных с высокой производительностью. F = АВ + ВС + АС.

Проверка

По закону идемпотентности мы знаем, что

[(A + B + C) (A + B + C)] (A + B + C) = [(A + B + C)] ( A + B + C) = (A + B + C)

Теперь функция

F = (А + В) (В + С) (А + С)

= (А + В + С) (А + В + С’) (А + В’ + С) (А’ + В + В)

= [(А + В + С) (А + В + С)] (А + В + С) (А + В + С’) (А + В’ + С) (А’ + В + В)

= [(А + В + С) (А + В + С’)] [(А + В + С) (А’ + В + С)] [(А + В + С) (А + Б’ + В)]

= [(А + В) + (С * С’)] [(В + С) + (А * А’)] [(А + С) + (В * В’)]

= [(A + B) + 0] [(B + C) + 0] [(A + C) + 0] = (A + B) (B + C) (A + C)

Каноническая форма (Стандартная форма SOP и POS)

Любая логическая функция, которая выражается как сумма minterms или как произведение maxterms, называется «канонической формой».

Он в основном включает два логических термина: «minterms» и «maxterms».

Когда форма SOP логического выражения находится в канонической форме, каждый из его терминов продукта называется «minterm». Таким образом, каноническая форма функции суммы произведений также известна как «каноническая форма minterm», или «Sum-of-minterms», или стандартная каноническая форма SOP.

Аналогичным образом, когда POS-форма логического выражения находится в канонической форме, каждый из его суммирующих терминов называется «maxterm». Таким образом, каноническая форма функции произведения сумм также известна как «каноническая форма maxterm или произведение суммы или стандартная каноническая форма POS».

Минимальные термины

Минтерм определяется как произведение n переменных, в котором каждая из n переменных появляется один раз либо в дополненной, либо в недополненной форме. Минимальный член обозначается как mi, где i находится в диапазоне 0 ≤ i <2ⁿ.

Переменная находится в дополненной форме, если ее значение присвоено 0, и переменная находится в недополненной форме, если ее значение присвоено 1.

Для логической функции с 2 переменными (x и y) возможные минтермы:

x’y’, x’y, xy’ и xy.

Для булевой функции с 3 переменными (x, y и z) возможные minterms:

x’y’z’, x’y’z, x’yz’, x’yz, xy’z’ , xy’z, xyz’ и xyz.

• 1 – Minterms = minterms, для которых функция F = 1,
• 0 – Minterms = minterms, для которых функция F = 0.

Любая логическая функция может быть выражена как сумма (ИЛИ) ее 1-минутных членов. Представление уравнения будет

• F (список переменных) = Σ (список 1-минутных индексов)

Пример: F (x, y, z) = Σ (3, 5, 6, 7)

Обратная функция может быть выражена как сумма (ИЛИ) ее нулевых членов. Представление уравнения будет

• F (список переменных) = Σ (список индексов 0-минутного члена)

Пример: F’ (x, y, z) = Σ (0,1, 2, 4)

Примеры канонической формы выражения суммы произведений (каноническая форма минимального члена):

i) Z = XY + XZ’

ii) F = XYZ’ + X’YZ + X’YZ’ + XY’Z + XYZ

В стандартной форме СОП максимально возможные условия произведения для n переменных задаются как 2ⁿ.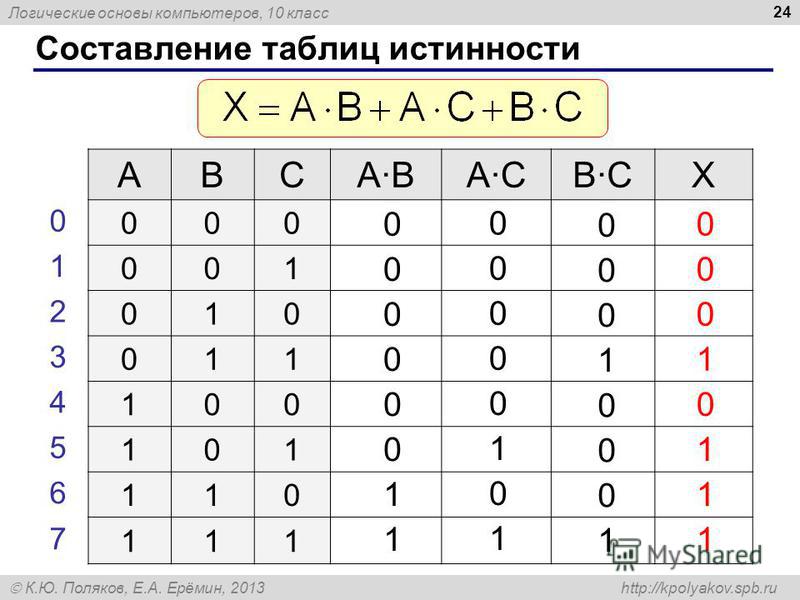 Таким образом, для уравнений с 2 ​​переменными произведение составляет 22 = 4. Аналогично, для уравнений с 3 переменными произведение составляет 23 = 8.

Максимальное число членов

Максимальный термин определяется как произведение n переменных в диапазоне 0 ≤ i < 2ⁿ. Максимальный член обозначается как Mi. В термине max каждая переменная дополняется, если ее значение равно 1, и каждая переменная не дополняется, если ее значение присваивается 0.

термины:

x + y, x + y’, x’ + y и x’ + y’.

Для булевой функции с тремя переменными (x, y и z) возможные maxterms:

x + y + z, x + y + z’, x + y’ + z, x + y’ + z ‘, x’ + y + z, x’ + y + z’, x’ + y’ + z и x’ + y’ + z’.

• 1 – Максимальное число членов = максимальное число членов, для которых функция F = 1.
• 0 – максимальное число членов = максимальное число членов, для которых функция F = 0.

Любая логическая функция может быть выражена произведением (И) ее 0-макс.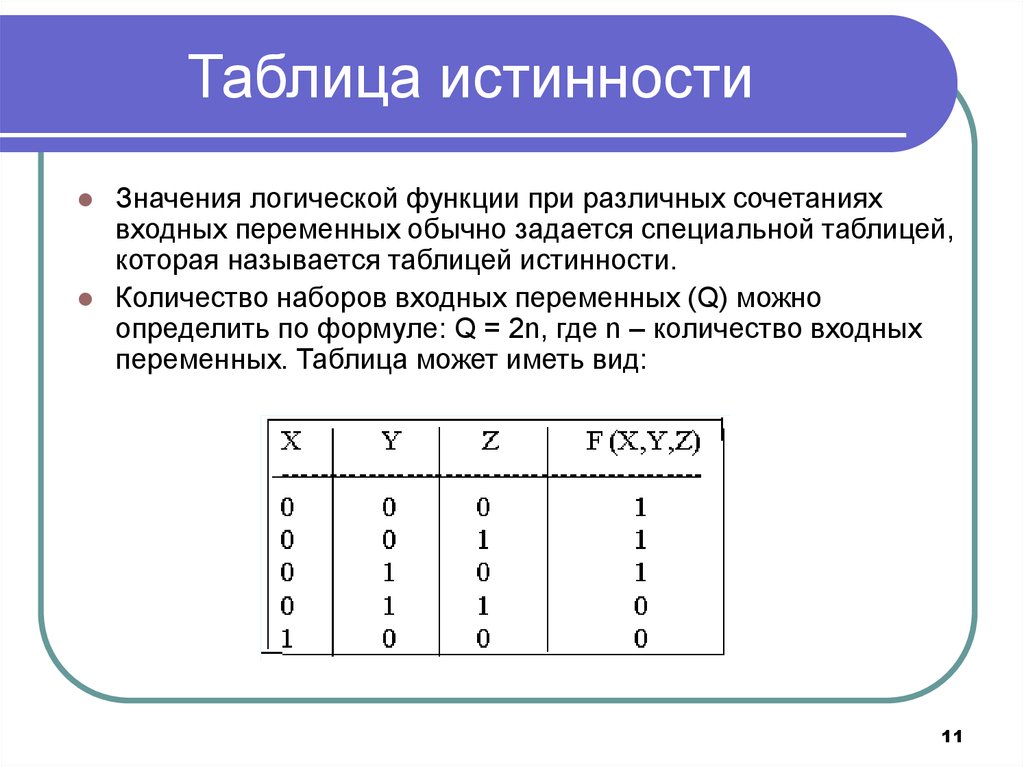 членов. Представление уравнения будет

• F (список переменных) = Π (список индексов 0-max)

Пример: F (x, y, z) = Π (0, 1, 2, 4)

Обратная функция может быть выражена как произведение (И) ее 1-макс. членов. Представление уравнения будет

• F(список переменных) = Π(список индексов 1-max)

Пример: F’ (x, y, z) = Π (3, 5, 6, 7)

Примеры канонической формы произведения выражений сумм (каноническая форма максимального члена):

i. Z = (X + Y) (X + Y′)

ii. F = (X′ + Y + Z′) (X′ + Y + Z) (X′ + Y′ + Z′)

В стандартной форме POS максимально возможные члены суммы для n переменных задаются как 2ⁿ . Итак, для уравнений с 2 ​​переменными сумма членов равна 22 = 4. Аналогично, для уравнений с 3 переменными сумма членов равна 23 = 8,9.0006

Таблица для 2n минимальных членов и 2n максимальных членов

Следующая таблица поможет вам понять представление средних и максимальных членов 3 переменных.

Преобразование канонических форм

Мы можем представить одно каноническое сформированное уравнение в другой канонической форме, т.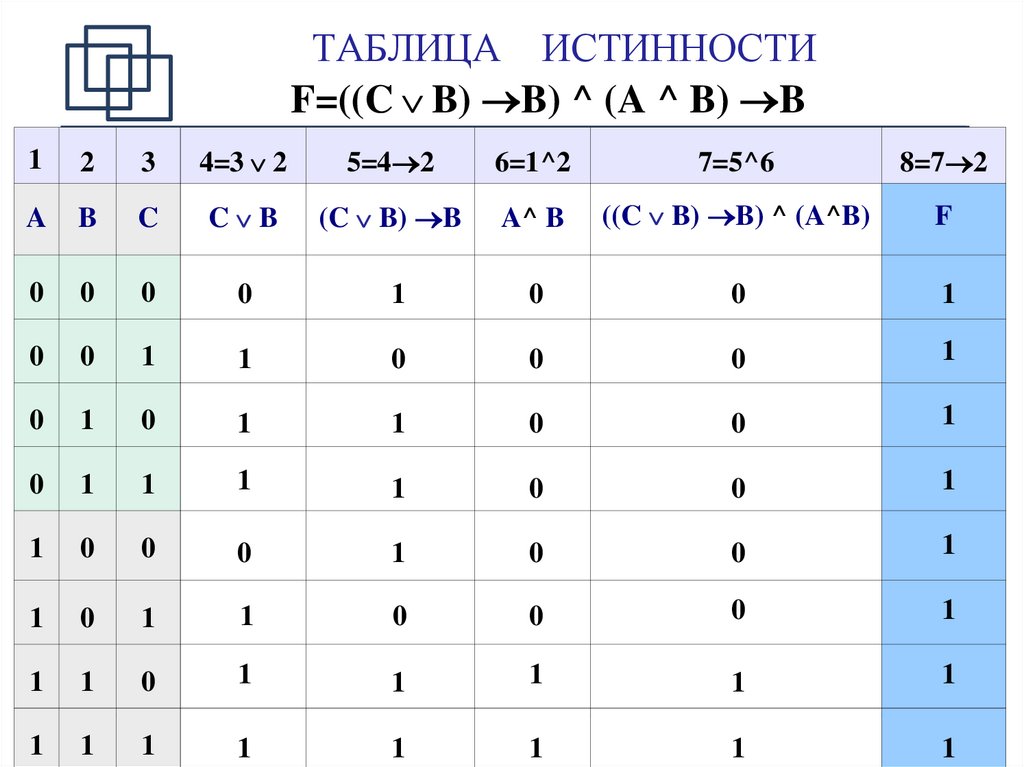 е. мы можем представить форму уравнения SOP в форме POS и уравнение формы POS в форме SOP. Чтобы преобразовать канонические уравнения, мы поменяем местами символы Σ и Π после перечисления порядковых номеров уравнений, которые исключены из исходной формы уравнения.

Важно помнить о логических функциях, что формы SOP и POS дублируют друг друга. Чтобы преобразовать каноническую форму уравнений, необходимо выполнить 2 шага. Это

. Шаг 1: Поменяйте местами рабочие символы Σ и Π в уравнении.

Шаг 2: Примените принцип двойственности Де Моргана к порядковым номерам булевой функции или запишите индексы членов, которые не представлены в данной форме уравнения.

Преобразование формы SOP в форму POS

Чтобы преобразовать форму SOP в форму POS, сначала мы должны изменить Σ на Π, а затем записать числовые индексы отсутствующих переменных данной булевой функции.

Пример:

Функция SOP

F = ∑ A, B, C (0, 2, 3, 5, 7) = A’ B’ C’ + A B’ C’ + A B’ C + ABC ‘ + ABC  записывается в форме POS как

Шаг 1: изменение операционного знака на Π

Шаг 2: запись недостающих индексов терминов, 001, 100 и 110.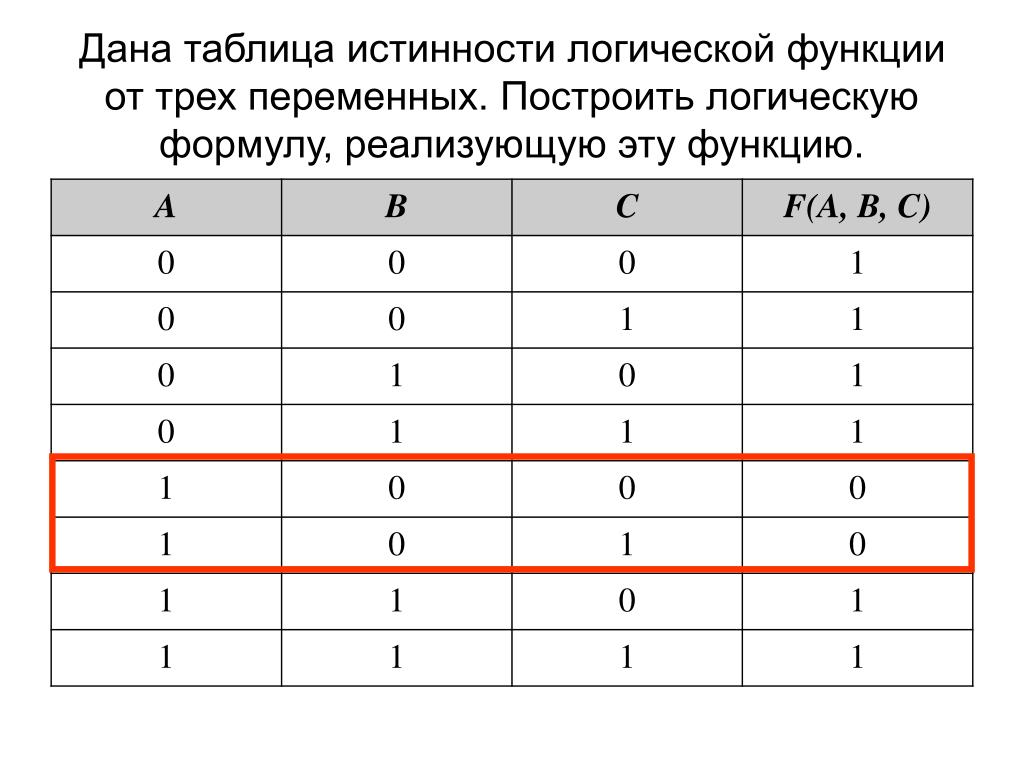 Теперь напишите форму суммы для этих отмеченных терминов.

001 = (A + B + C) 100 = (A + B’ + C’) 110 = (A + B’ + C’)

Запись нового уравнения в виде формы POS,

F = Π A, B, C (1, 4, 6) = (A + B + C) * (A + B’ + C’) * (A + B’ + C’)

Преобразование формы POS в SOP form

Чтобы преобразовать форму POS в форму SOP, сначала мы должны изменить Π на Σ, а затем написать числовые индексы отсутствующих переменных данной булевой функции.

Пример: Функция POS F = Π A, B, C (2, 3, 5) = A B’ C’ + A B’ C + ABC’ записывается в форме SOP как

Шаг 1: изменение знака операции на Σ

Шаг 2: запись отсутствующих индексов терминов 000, 001, 100, 110 и 111. Теперь напишите форму произведения для этих отмеченных термов.

000 = A’ * B’ * C’ 001 = A’ * B’ * C 100 = A * B’ * C’

110 = A * B* C’ 111 = A * B * C

Запись вниз новое уравнение в виде формы СОП,

F = Σ A, B, C (0, 1, 4, 6, 7) = (A’ * B’ * C’) + (A’ * B’ * C) + (A * B’ * C’) + (A * B * C’) + (A * B * C)

Преобразование формы СОП в стандартную форму СОП или форму канонической СОП

Мы можем включить все переменные в каждый член произведения уравнения формы СОП, в котором нет всех переменных, путем преобразования в стандартную форму СОП. Функцию нормальной формы SOP можно преобразовать в стандартную форму SOP, используя закон булевой алгебры (A + A’ = 1) и выполнив следующие шаги.

Шаг 1:

Путем умножения каждого нестандартного термина продукта на сумму его отсутствующей переменной и ее дополнения, что дает 2 термина продукта

Шаг 2:

Повторяя шаг 1 до тех пор, пока все полученные условия продукта не будут содержать все переменные

С помощью этих двух шагов мы можем преобразовать функцию SOP в стандартную функцию SOP. В этом процессе для каждой отсутствующей переменной в функции количество терминов продукта будет удваиваться.

Пример:

Преобразование нестандартной SOP-функции F = x y + x z + y z

Sol:

F = x y + x z + y z

= x y (z + z’) + x (y + y’) г + (х + х’) у г

= x y z + x y z’ + x y z + x y’ z + x y z + x’ y z

= x y z + x y z’ + x y’ z + x’ y z

Стандартная форма SOP: F = x y z + x y z’ + x y’ z + x’ y z

Преобразование формы POS в стандартную форму POS или каноническую форму POS

Мы можем включить все переменные в каждый термин продукта уравнения формы POS, который не имеет всех переменные путем преобразования в стандартную форму POS. Обычную функцию формы POS можно преобразовать в стандартную форму POS, используя закон алгебры логики (A * A’ = 0) и выполнив следующие шаги.

Шаг 1:

Добавляя каждый нестандартный член суммы к произведению его отсутствующей переменной и ее дополнения, что дает 2 члена суммы

Шаг 2:

Применяя булев алгебраический закон, A + BC = (A + B) * (A + C)

Шаг 3:

Повторяя шаг 1, пока все результирующие члены суммы не будут содержать все переменные

Этими тремя шагами мы можем преобразовать функцию POS в стандартную функцию POS.

Пример:

F = (A’ + B + C) * (B’ + C + D’) * ​​(A + B’ + C’ + D)

В первом члене переменная D или D’ отсутствует, поэтому мы добавляем к ней D*D’ = 1. Тогда

(A’ + B + C + D*D’) = (A’ + B + C + D) * (A’ + B + C + D’)

Аналогично, во втором члене переменная A или A’ отсутствует, поэтому мы добавляем к нему A*A’ = 1. Тогда

(B’ + C + D’ + A*A’) = (A + B’ + C + D’) * (A’ + B’ + C + D’)

Третий член уже в стандартная форма, так как она имеет все переменные.